第四章 管道内的黏性流动与管路计算基础
黏性是流体的重要属性之一,自然界中存在的流体都具有黏性。由于流体黏性的影响,必然伴随着流体机械能的损失,即所谓的流动损失。因此在管内流动中,确定流动损失是管道设计与计算的关键。
在工程中,涉及许多的管道计算问题,除了工程中常见的各种管道外,航空上诸如发动机的起动管路系统、滑油系统、空调系统和空气系统等管路设计问题都与流动损失有关。此外,减少和利用流动损失也是研究流动损失的目的之一
本章首先介绍黏性流体的两种流态,然后讨论管内层流流动和湍流流动,并讨论沿程损失和局部损失。在讨论流动损失(沿程损失和局部损失)的计算时,一般是指不可压缩流体的流动损失的计算。对于液体,因为可以认为是不可压缩的,所以用本章介绍的方法计算压力损失产生的误差较小;但对于气体,因为不能认为是不可压缩的,所以计算会产生一定的误差,其大小取决于气体流动的速度和所研究的管道或附件的损失大小。最后讨论管道设计与计算基础。
4.1 管道中黏性流动的状态
由于实际流体具有黏性,因此流体在管道中流动时,紧贴管壁的流体其速度必然为零,即与管壁没有相对运动。而离开管壁越远,由于一层层流体之间的相互影响,流速逐渐增大,到管道中心处的流速最大。经过大量的科学实验发现,黏性流体流动中存在着两种不同的流动状态。一种状态是流体质点作有序的、有规则的运动。在这种运动中,流体质点的迹线互不交错,相邻两层之间没有无规则的脉动,流体是在作层状运动,这种流动称之为层流流动。与层流流动完全不同的流动状态是另一种流态,这种流态是流体质点作毫无规则的混乱运动,各层流体作复杂的、无规则的和随机的非定常运动。在这种流动中,每个流动质点的迹线十分复杂,流体各部分互相掺混,流体的这种运动称为湍流流动(或紊流流动)。
一、雷诺实验
黏性流动的两种流态首先是由雷诺实验得到证明,并确定了流态的判别方法。
雷诺实验是在尺寸足够大的水箱中充满水,并不断补充水使水箱的水位保持一定的高度。在水箱中插入一根透明的玻璃管,此管进口做成圆滑的喇叭形,玻璃管出口前某位置装一阀门 K,以控制玻璃管内流速的大小。另用一细管引出一条有色液体(有色液体的比重与水相同,但与水不相溶),如图4. 1(a)所示。阀门C用于调节有色液体。
实验时,当阀门K开得不大时,玻璃管内的流速不大。然后打开阀门C,则有色液体流入玻璃管。这时可以观察到破璃管内有色水从头到尾保持各清晰的流线。移动细管,可以观察到破璃管中若干条有色的流线,这些流线互不相混。这说明管中的流体在流动过程中是分层的一层一层的流动,各层之间互不干扰、互不掺混,如图4.I ( b)所示,这种流动称为层流。当阀门K开大时,流速逐渐增大,开始仍保留层流流动。当阀门开到一定程度,管内流速增加到某个临界值时,有色水流开始弯曲,层流流动状态被破坏,如图4. 1(c)所示。如果继续增加流速,有色水流便会突然散开,而发生断裂,如图1. 1(d)所示。这说明流体质点除了沿管道轴线方向的纵向流动外,还有流体质点的无规则横向运动。结果把各层流体搅混而形成了一系列小旋涡,流体处于亳无规则的混乱运动状态,这种流态称为湍流流动。如果出现湍流流动后,逐渐关小阀门K,就会观察到从上述的湍流过渡为层流的流动现象,但是由湍流转变为层流的流速却不相同。由以上实验可知,流体在管道内的实际流动中,存在着两种性质截然不同的流动,即层流和湍流。而层流和湍流之间存在着一个过渡的流动状态。这些状态是流体运动普遍存在的物理现象。
雷诺实验不但揭示了这两种流动状态,同时也揭示了不同流动状态下的流动损失机理。层流和湍流的流动损失机理有所不同。在层流中,由于分于间的吸引力和分子无规则运动的动量交换产生的黏性阻力而引起流动损失。在湍流中,除了上述黏性阻力外更重要的是由于大量流体质点脉动运动,大量旋涡的无规则迁移引起的动量交换产生的阻力而引起流动损失。因此其损失规律的不同是由于它们的流动结构不同而造成的,前者称为黏性阻力(或黏性应力),通常以\({{\tau }_{\text{t}}}\)表示;后者称为湍流应力,以\({{\tau }_{\text{t}}}\)表示。
二、雷诺数及流态判别
在雷诺实验中,若以不同的管径、不同的流体进行实验,其各种流态的转变也是不同的。实验研究发现这种流态的转变不仅取决于阀门开启的大小(即流速大小),而且还决定于流速V,特征长度d(管径)和流体的运动黏度三者的组合量,该组合量叫雷诺数,记为Re。其定义为
Re=Vd/v=ρVd/μ (4.1)
从层流转变为湍流的现象称为转捩,转捩是一种自然的不稳定现象。当雷诺数较小时,层流流动是稳定的;当雷诺数大到一定数量时,这种不稳定现象便出现了。之外,影响稳定的因素还有管壁的粗糙度,管道入囗的形状等。管道壁面越粗糙,越容易转变为湍流。进口形状不光滑,也越容易转变为湍流。实验发现,当管壁十分光滑,入口处的形状也非常光滑时,实验曾做到雷诺数超过40000才转变为湍流。但是,实验时,从湍流转变为层流的雷诺数可以低到 2320此时,层流变得非常稳定,不论管壁多么粗糙,流动也不会转变为湍流。因此,流态转变的雷诺数与实验条件、管壁粗糙度、管道进口形状等因素有关。从层流转变为湍流的雷诺数称为上临界雷诺数,用Re′(13800~40000)表示;而从湍流转变为层流的雷诺数称为下临界雷诺数,用Re cr(2320)表示。当雷诺数大于Re′时为湍流,当雷诺数小于Re cr时为层流,介于这两个雷诺数之间的流动可能是层流,也可能是湍流,还可能是从层流向湍流转变的过渡状态,但多数为湍流。这是由于在雷诺数较高时,层流极易转变为湍流的原因。在工程应用中,取下临界雷诺数作为判别的准则,该雷诺数叫临界雷诺数。从雷诺实验得知,对于管内流动:
Re≤2320 层流
Re>2320 湍流
对于特殊形状的管道,判别流态的临界雷诺数也有所不同。例如,圆形橡胶管的临界雷诺数为1600,同心环缝的临界雷诺数为1100,边长为a的正方形管道的临界雷诺数为2070,偏心环缝的临界雷诺数为1 000。
雷诺数是一个无量纲的参数。根据雷诺数的定义,有
Re=ρVd/μ~ρV²/(μV/l)
可以看出,上式分子表示单位时间内通过单位面积的流体动量,即表示流体惯性力的大小;而分母中V/l表示速度梯度,因此雷诺数反映了流体质点的惯性力与黏性力之比。根据雷诺数的定义和物理意义可知,雷诺数越小,则惯性力相对于黏性力也越小,黏性力的作用也越大,因而流体能保持平稳的层流状态,能够消除流体发生紊乱的运动。雷诺数越大,则惯性力的作用大,惯性力容易使流体质点发生湍流运动。
需要说明的是,空气和水的黏度都很小,因而在管内流动问题中,速度取平均速度,特征长度取管道直径来定义雷诺数,因此管内流动的雷诺数一般在几千以上。对于高速运动的飞行器,速度取飞行速度,特征长度取飞机机翼的平均弦长,机翼的雷诺数可能在千万以上。气体在管内流动的气体雷诺数也较大。
对于非圆形的管道,雷诺数定义中的特征长度用当量直径de表示,即
\[{{d}_{e}}=\frac{4A}{\chi }\] (4.2)
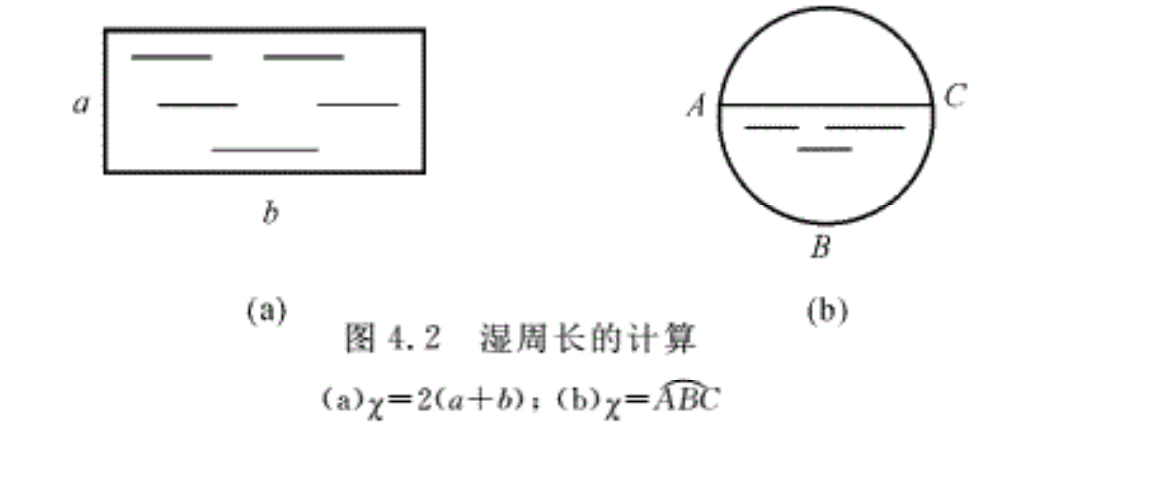
式中,A表示充满流体部分的截面面积;\(\chi \)表示流体的湿周长,即指流动截面上流体与固体壁面接触的周界长度,或被流体湿润的固体壁面周界长度。图4. 2给出了两种湿周长的例子。
以当量直径作为特征尺寸时,雷诺数表示为
Re=ρVde/μ (4.3)
三、流动损失的分类
根据流动中能量损失产生的机理和表现形式,可将流动损失分为两种类型。
1.沿程损失
沿程损失是指沿流动路程上由于各流体层之间黏性摩擦而产生的流动损失(又叫摩擦损失)。流体在流动中沿流程克服内摩擦力所消耗的机械能称为沿程能量损失,以hf表示。
沿程能量损失hf可根据量纲分析法(见第九章)得出,并写成如下形式:
\[{{h}_{f}}=\lambda \frac{l}{d}\frac{V_{{}}^{2}}{2g}\] (4.4)
式中,λ称为沿程损失(阻力)因数,它与流动状态(层流或湍流)、雷诺数和管壁粗糙度等因素有关,通常需要由实验确定。
2.局部损失
局部损失是流体在流动中因遇到局部障碍物,例如,管道截面突然扩大或减小、流道突然弯曲、流道中设置有各种管件(如阀门、三通)等而产生的流动损失。由于流体的黏性摩擦和流体与局部障碍物之间发生剧烈碰撞而产生旋涡等消耗机械能,这种能量损失发生在局部故称其为局部损失,以hζ表示。由大量实验可知,单位质量流体的局部损失与流体的动能成正比,可写成
\[{{h}_{\zeta }}=\zeta \frac{V_{{}}^{2}}{2g}\] (4.5)
式中,ζ称为局部损失因数,由实验确定。它与雷诺数和管件几何形状等有关。
在各种设备和管道计算中,上述两种损失一般都存在,即在管路系统中既存在直管也存在弯管和阀门等各种各样的管件。因此整个流动的机械能损失既有沿程损失又有局部损失,即总的能量损失为
\[{{h}_{w}}=\sum\limits_{i=1}^{n}{{{\lambda }_{i}}\frac{{{L}_{i}}}{{{d}_{i}}}\frac{V_{i}^{2}}{2g}}+\sum\limits_{j=1}^{m}{{{\zeta }_{j}}\frac{V_{j}^{2}}{2g}}=\sum {{h}_{f}}+\sum {{h}_{\zeta }}\] (4.6)
在实际工程中,如果产生局部损失的管件相距较近,还应该考虑其相互干扰损失。
4.2 圆管中充分发展的层流流动及沿程损失
当雷诺数较低时,即流速、管径较小而黏度较大时常会出现层流流动。工程中遇到的液体的层流流动较多,如轴承润滑、液压传动、燃油供给、石油传送和化工管道等都会遇到层流流动。气体在发动机各部件中的流动多数为湍流流动。
本节仅讨论圆管入囗段之后的流动,即黏性流体充满整个管道的,或称为充分发展的管内层流流动。这种流动可以直接用数值求解黏性流动的动量方程(纳维尔一斯托克斯方程,见第十章),也可以用本节介绍的方法即建立常微分方程的方法求解。
一、管内速度分布
取水平放置的直管,沿轴线方向为x方向。显然流动是轴对称的,对于不可压缩流动,根据连续方程可知流体流动的速度与x无关,因此沿x方向不同截面相同半径处的流速相等,即V=V(r)。
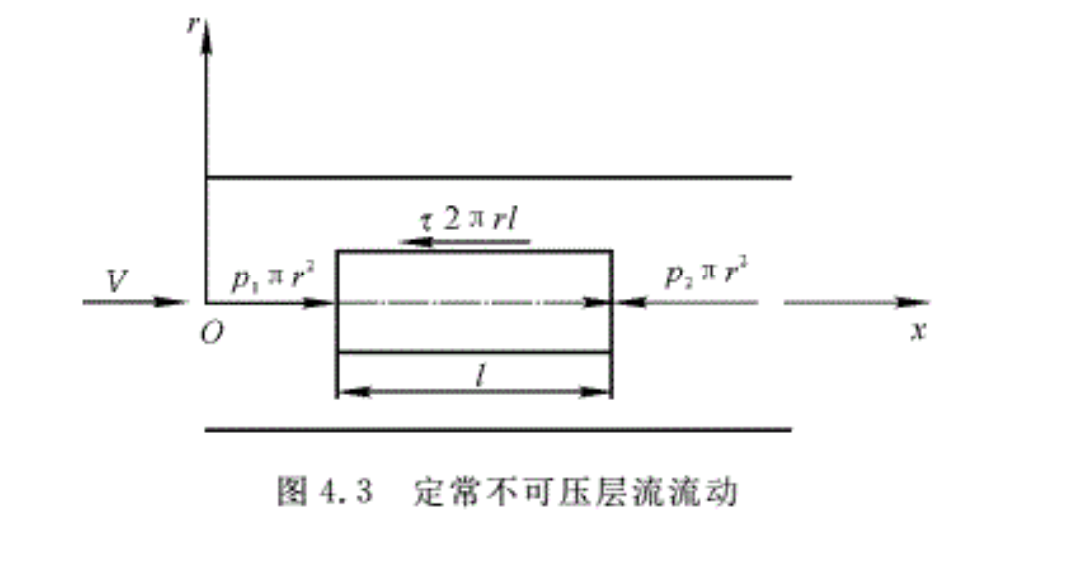
取如图4.3所示的小圆柱体,长度为l,半径为r,分析作用在其上的作用力。由于没有径向和周向的速度分量,因而同一截面上的压强相同。又由于各截面的速度分布相同,因此,相同半径处速度梯度也相同,故切应力也相同。圆柱体受力分析示于图4.3中,根据牛顿第二定律,得
\[{{p}_{1}}\pi r_{{}}^{2}-{{p}_{2}}\pi r_{{}}^{2}-\tau 2\pi rl=0\]
若记p1-p2=∆p,则上式为
\[\tau =\frac{\Delta pr}{2l}\] (4.7)
由上式可知,圆管中的层流切应力与半径r成正比。壁面上,r=ro(圆管半径),τ=τw ,切应力达到最大值。而在轴线上,r=0,τ=0。
将牛顿内摩擦定律,τ=-μdV/dy(负号表示随着r的增加,速度是减小的,仅取τ的大小)代入式(4.7),得
\[-\mu \frac{dV}{dr}=\frac{\Delta pr}{2l}\]
则
\[\int_{0}^{V}{dV=-\frac{\Delta p}{2\mu l}\int_{{{r}_{0}}}^{r}{rdr}}\]
于是得到圆管中的速度分布为
\[V=\frac{\Delta p}{4\mu l}\left( {{r}_{0}}^{2}-{{r}^{2}} \right)\] (4.8)
由式(4. 8)可以看出,在层流流动中,速度分布为抛物线分布规律。
在圆管中心处速度最大,将r=0代入式(4.8),得
\[{{V}_{\max }}=\frac{\Delta p}{4\mu l}{{r}_{0}}^{2}\] (4.9)
通过圆管的流量为
\[{{q}_{v}}=\int\limits_{0}^{{{r}_{0}}}{V2\pi rdr=\int\limits_{0}^{{{r}_{0}}}{\frac{\Delta p}{4\mu l}\left( {{r}_{0}}^{2}-{{r}^{2}} \right)2\pi rdr=}}\frac{\pi \Delta p{{r}_{0}}^{4}}{8\mu l}=\frac{\pi \Delta p{{d}^{4}}}{128\mu l}\] (4.10)
式(4.10)与实验结果完全一致。用该式可作为测定液体黏度的依据。只要在一根己知的管道中,保证流动为稳定的充分发展的层流流动,测出通过管内的流量和压差,代入式(4. 10),就可以确定流体的黏度。
截面上的平均流速为
\[\overline{V}=\frac{{{q}_{v}}}{\pi {{r}_{0}}^{2}}=\frac{\int\limits_{0}^{{{r}_{0}}}{V2\pi rdr}}{\pi {{r}_{0}}^{2}}\]
将式(4.10)代入上式,考虑到式(4.9),得到平均速度
\[\overline{V}=\frac{\Delta p{{r}_{0}}^{2}}{8\mu l}=\frac{\Delta p}{32\mu l}{{d}^{2}}=\frac{1}{2}{{V}_{\max }}\] (4.11)
二、壁面切应力分布及摩擦力
式(4. 7)已经导出了切应力分布规律,τ=∆pr/2l;在壁面上,r=ro,τ=τw,切应力达到最大值,即
\[{{\tau }_{w}}=\frac{\Delta p{{r}_{0}}^{{}}}{2l}\]
因此,切应力分布为
\[\tau ={{\tau }_{w}}\frac{r}{{{r}_{0}}}\] (4.12a)
作用在管壁上的摩擦力为
\[F={{\tau }_{w}}2\pi {{r}_{0}}l=\frac{\Delta p{{r}_{0}}^{{}}}{2l}2\pi {{r}_{0}}l=\Delta p\pi {{r}_{0}}^{2}\] (4.12b)
式(4.12)不仅适合于层流流动,也适合于湍流流动。由式(4.12)可以看出,当管内流动处于平衡状态时,作用在管壁上的摩擦力与两端截面上的压强差相平衡。
三、沿程损失计算
由于黏性摩擦的影响,流体在等截面直管中的流动也会产生沿程能量损失。沿程能量损失可以表示成压强损失、功率损失和水头损失。
对图4. 3所示的管道的任意两个截面应用伯努利方程,并考虑到沿程的能量损失,可得管内黏性流体的伯努利方程,即
\[\frac{{{p}_{1}}}{\gamma }+\frac{V_{1}^{2}}{2g}+{{z}_{1}}=\frac{{{p}_{2}}}{\gamma }+\frac{V_{2}^{2}}{2g}+{{z}_{2}}+{{h}_{f}}\]
由于各截面的平均流速相等,即V1=V2,且管道水平放置z1=z2。,并考虑到式(4.4),沿程能量损失可以表示为沿程压力损失的关系,即
hf=∆p/γ=(p1-p2)/γ=4μlVmax/γro²=64lV²/Red2g=λlV²/d2g (4.13a)
式中,V是管道截面上的平均流速;对于层流流动,λ=64/Re,即沿程损失因数仅仅与雷诺数有关,与管壁粗糙度无关。
工程上常用压差形式表示沿程损失,由式(4.13 a),可得
\[\Delta p=\lambda \frac{l}{d}\frac{\rho V_{{}}^{2}}{2}={{\lambda }_{p}}\frac{\rho V_{{}}^{2}}{2}\] (4.13b)
式中,λp=64l/Red,称为压力损失因数。
由式(4.13a)可以看出,对于层流流动,沿程能量损失与速度和管长成正比,与管径的平方成反比。层流流动的沿程损失因数仅与雷诺数有关,而与管壁粗糙度无关。对于介质为油的情况,工程中常用下式计算沿程损失因数:
λ=75/Re
功率损失指输送流体时克服沿程阻力所消耗的功率。设管道流量为qv,则由于沿程摩擦所损失的功率为
\[N=\gamma {{q}_{v}}{{h}_{f}}={{q}_{v}}\Delta p=\frac{32\mu l\overline{{{V}_{{}}}}{{q}_{v}}}{d_{{}}^{2}}=\frac{128\mu lq_{v}^{2}}{\pi d_{{}}^{4}}\] (4.14)
由式(4.14)可见,沿程摩擦所损失的功率与黏度成正比,与管径成反比。适当降低黏度或适当加大管径可降低功率损失。当流量与管径不变时,黏度越小,损失的功率也越小。因此在输送油液时,为了降低功率损失,常将油液加热。
需要说明一点,计算气体在管内流动的压强损失时,通常指的是流动气体的总压损失,关于总压的概念将在第五章中介绍。
例4.1 一个等截面的圆管垂直放置,流体从入囗截面1到出口截面2,假设流体在其中作定常不可压缩层流流动,若不考虑圆管进出囗的影响,流动可以看为充分发展的管流。试确定圆管内的速度分布。
解:本例题与流体在水平放置的圆管内流动分析类似,不同的是需要考虑重力的影响。选取z方向沿流动方向,r方向沿径向。同样取一个小圆柱体,对该圆柱体受力分析,写出牛顿第二定理,得
\[{{p}_{1}}A-{{p}_{2}}A-\tau 2\pi rl+\gamma A\left( {{z}_{1}}-{{z}_{2}} \right)=0\]
进一步可得
\[\left( {{p}_{1}}+\gamma {{z}_{1}} \right)-\left( {{p}_{2}}+\gamma {{z}_{2}} \right)=\frac{2\tau l}{r}\] (1)
将 τ=-μdV/dr代入式(1 ),得
\[\frac{\left( {{p}_{1}}+\gamma {{z}_{1}} \right)-\left( {{p}_{2}}+\gamma {{z}_{2}} \right)}{l}=-\frac{2}{r}\mu \frac{dV}{dr}\] (2)
式(2)等号左端的压强p仅是z的函数,故该式左端各项与r无关;而等号右端项的V只是r 的函数,故该式右端也只是r的函数。因此只有当式(2)等号左、右两端都等于常数时,式(2)才能成立。因此,单位长度上的压强差∆p/l不变。令B=\(\frac{\left( {{p}_{1}}+\gamma {{z}_{1}} \right)-\left( {{p}_{2}}+\gamma {{z}_{2}} \right)}{l}\),B称为单位长度上的有效压差,则由式(2)可得
dV=-0.5Brdr/μ
对上式积分后,得
V=-0.25Br²/μ+C
当r=ro(圆管的半径)时,v=0,代入上式得C=Bro²/4μ,因此速度为
\[V=\frac{B}{4\mu }\left( {{r}_{0}}^{2}-{{r}^{2}} \right)\]
可见,速度分布仍然为抛物线的分布规律。
显然,最大速度为
\[{{V}_{\max }}=0.25Br_{0}^{2}/\mu \]
4.3 圆管中充分发展的湍流流动及沿程损失
4.3.1 湍流流动的时均化及湍流度
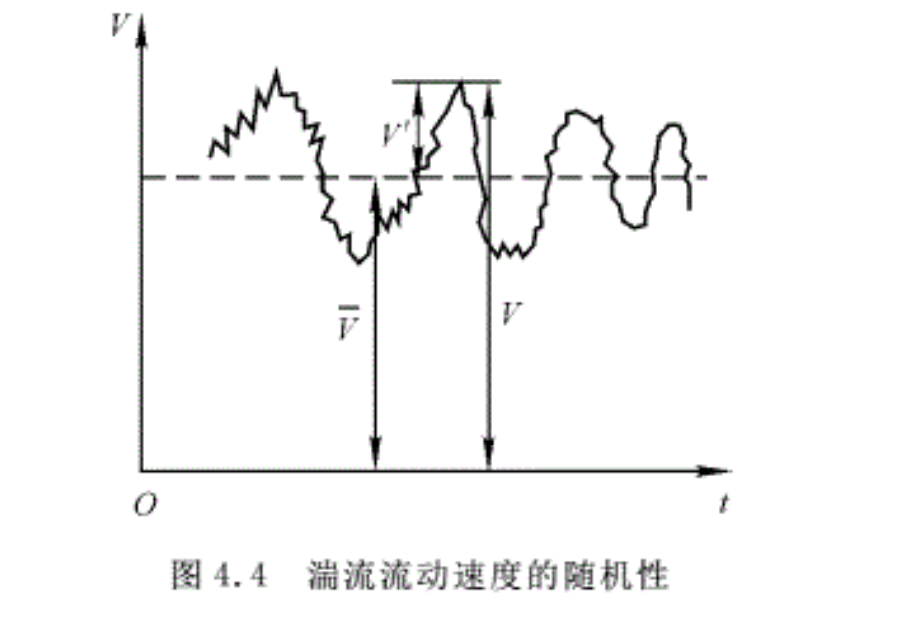
在湍流中,流体质点作混杂的、无规则和随机的非定常运动,它们在向下游流动的同时,不断与邻近的流体质点相互掺混,流体质点作无规则的横向脉动。所以湍流流动中的各流动物理量对于时间和空间坐标来说,呈现着随机性的脉动。图4.4给出了流体以湍流运动时,流场中某点处的速度变化。在任一瞬时,湍流流场中各点处的速度也是不相同的。由图4.4可以看出,湍流流动的速度(含其他物理参数)虽然是脉动的,但却在某一平均值上下变动,即服从统计规律。因此引进流动参数时均值的概念来分析湍流运动是方便的。下面以速度为例进行分析。
在图4.4中,取一时间间隔T,T相对于整个运动来说是很短的,但相对于脉动运动来说又足够得长,把流体的瞬时速度V在时间T内取平均值,得到时均速度\(\overline{V}\)为
\[\overline{V}=\frac{1}{T}\int_{0}^{T}{Vdt}\] (4.15)
通常把各个物理量,例如瞬时速度V表示成时均速度\(\overline{V}\)与脉动速度V′之和,即
\[V=\overline{V}+V_{{}}^{\prime }\]
显然,脉动速度的时均值等于零,即
\[V_{{}}^{\prime }=\frac{1}{T}\int_{0}^{T}{\left( V-\overline{V} \right)dt=\overline{V}-\overline{V}=0}\] (4.16)
对于流场中的压强、密度、温度等都可以将其瞬时值表示为时均值与脉动值之代数和。
一般来说,取时均值后的物理量\(\overline{V}\)仍是时间t和空间坐标的函数,这种湍流称为非定常湍流。
引入湍流时均值的概念之后,对于湍流的一切概念都是从时均值的意义上定义的。对于工程中的大多数问题都是稳定的湍流流动(即时均化后的物理量与时间t无关)。如果流动是一维的,则前面讨论的一维定常流基本方程(如连续方程、动量方程、伯努利方程)都是适用的。引入时均值的概念后,给处理湍流流动带来了很大的方便。但是它掩盖了湍流脉动运动的物理本质。因此在分析诸如湍流流动阻力时,就必须考虑流体质点及微团相互掺混进行动量交换的影响,即计算流体质点及微团混杂运动引起的阻力,否则会引起较大的误差。
为了描述湍流流动的随机性质,在工程中常采用湍流度的概念。湍流度用ε表示,则
\[\varepsilon =\frac{\sqrt{\overline{V\prime _{{}}^{2}}}}{\overline{V}}\] (4.17)
式中,把脉动速度先平方,使之为正值,再作时间平均,然后取方根值。可以反映出脉动量绝对值的平均大小。
在普通风洞中,ε小于1%。
需要说明的是,在讨论湍流的时均特性时,其流动参数均指时均参数,因此以下的研究均略去了时均参数的符号“—”。
4.3.2 圆管中湍流流动的切应力及速度分布
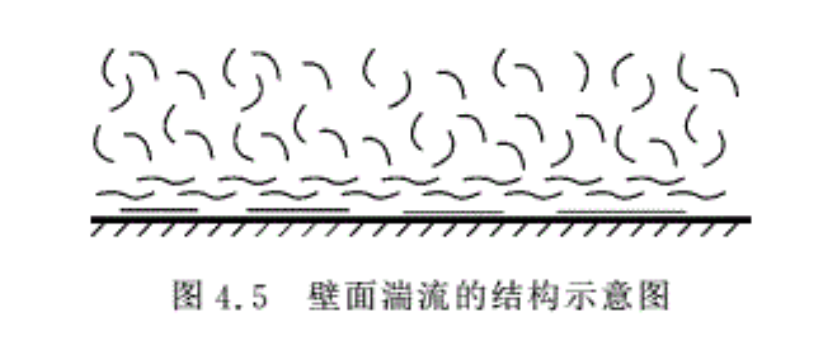
实验观察发现,在管内和绕物面的流动中,流动可以分为三层,即黏性底层、过渡区和湍流核心区。由于流动受壁面的限制,在靠近壁面的簿层内,流体质点没有横向的脉动,因此在壁面附近,流体质点的运动仍然保持有序的层流流动,该层流体称为黏性底层。离开壁面一段距离后,壁面的影响逐渐减弱,流动呈现出波动状态,流线弯曲,该区域称为过渡区。过渡区之外的是湍流核心区,即完全发展的湍流核心区,该区域内的流动完全不受壁面粗糙度的影响。图4 . 5给出了壁面湍流的结构示意图。
黏性底层的厚度很薄,其厚度大概仅有几分之一亳米。根据理论分析和实验结果知,黏性底层的厚度为
δt=32.8d/Re√λ (4.18)
可见随着雷诺数的增加,黏性底层的厚度减小。
一、湍流流动的切应力分布及摩擦力
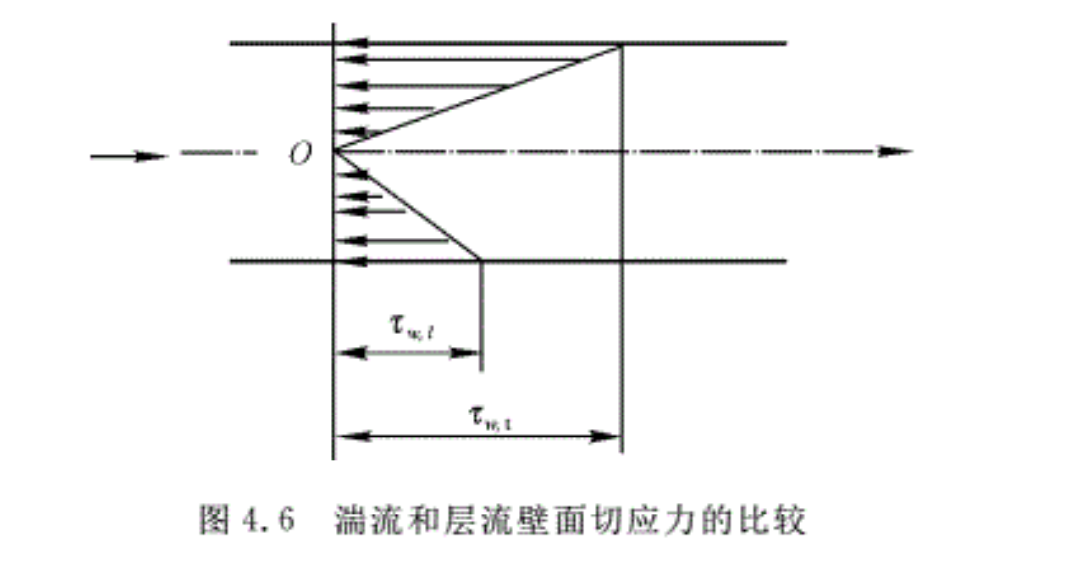
湍流流动的切应力分布与层流流动的表达形式完全相同,即
\[\tau ={{\tau }_{w}}\frac{r}{{{r}_{0}}}\]
不过,对于湍流流动,流过截面上的壁面切应力τw与层流不同,因此其切应力分布的斜率也不同。图4. 6给出了壁面切应力τw的比较,图中τ w,t,τ w,t分别表示湍流壁面切应力和层流壁面切应力。
在湍流流动中,由于流体质点的大量混杂运动,其阻力损失大大超过了层流的阻力损失。
在层流区或黏性底层,由于流体流动的有序性或壁面的限制,流体质点横向脉动引起的切应力很小,因此切应力主要是分子黏性切应力,可以用牛顿内摩擦定律表示。
在湍流核心区,既有层流流动的分子黏性切应力τt,也有湍流流动的流体质点横向脉动引起的湍流切应力τt。根据普朗特混合长度理论,平面定常均匀湍流的切应力可以表示为
\[\tau ={{\tau }_{t}}+{{\tau }_{t}}=\mu \frac{d\overline{V}}{dy}+\rho {{l}^{2}}\left( \frac{d\overline{V}}{dy} \right)_{{}}^{2}\]
式中:l——普朗特混合长度,由实验确定;
\(\frac{d\overline{V}}{dy}\)——y方向上的时均速度梯度。
在计算湍流流动时,由于τt《τt。因此为了研究方便,通常略去式中等号右端的第一项。下面在导出速度分布时同样忽略了分子黏性应力τt。
二、湍流流动的速度分布
由于湍流流动的复杂性,到目前为止,还无法像层流流动那样,严格地按理论分析导出湍流流动的速度分布规律。这里在一定的假设前提下,根据理论分析和实验相结合的方法来研究湍流流动的速度分布。
1.黏性底层速度分布
在黏性底层中,由于厚度很薄,因此可以认为是层流流动,切应力可以用壁面切应力表示,即τ=τw,而且速度分布也可认为是线性的。由牛顿内摩擦定律得到
τw=μdV/dy,即dV=τwdy/μ
积分得
V=τwy/μ (4.19a)
并引进摩擦速度的定义,即
\[{{V}_{*}}=\sqrt{\frac{{{\tau }_{w}}}{\rho }}\]
代入式(4.19a),得到
\[\frac{V}{{{V}_{*}}}=\frac{\rho {{V}_{*}}}{\mu }y=\frac{{{V}_{*}}y}{v}\] (4.19b)
式(4.19)即为黏性底层的速度分布规律。
可见黏性底层的速度分布为线性分布。这实际上是层流速度抛物线分布规律在黏性底层中的近似处理。
2.过渡区的速度分布
在过渡区内,由于黏性应力与湍流切应力具有相同的数量级,因此难以进行理论分析。其速度分布要用实验来确定。工程中常将过渡区按湍流流动的速度分布规律来确定。
3.湍流核心区的速度分布
在湍流流动中,由于黏性底层的存在,壁面的粗糙度∆对流动损失的影响与黏性底层厚度δt有关。当δt≥∆时,黏性底层完全掩盖了管壁的粗糙部分,核心区中的流动完全感受不到粗糙度的影响,这种状态下的流动管道称为水力光滑管。当δt<∆时,管壁的粗糙度暴露在黏性底层之外,粗糙表面造成的旋涡增了流动损失,这种情况下的管道称为水力粗糙管。因此两种管道中的速度分布也不相同。
假设湍流切应力τt与壁面切应力具有同样的数量级,因此则有τt≈τw。
湍流核心区的速度分布可以从普朗特混合长度理论得出。其基本思想是把湍流脉动与气体分子运动相比拟,认为流体微团脉动引起的切应力和分子运动引起的黏性应力非常相似。当湍流流动的时均流线为直线时,认为脉动引起的湍流可以表示为与黏性切应力具有类似的形式,即
\[{{\tau }_{t}}={{\mu }_{t}}\frac{dV}{dy}=\rho l_{{}}^{2}\left( \frac{dV}{dy} \right)_{{}}^{2}\] (4.20)
式中,μt为湍流黏度;混合长度l一般假设为l=ky,k由实验确定。
根据以上假设和式(4.20),可得
\[{{\tau }_{{}}}={{\tau }_{t}}=\rho l_{{}}^{2}\left( \frac{dV}{dy} \right)_{{}}^{2}={{\tau }_{w}}\]
引进摩擦速度的定义,得
\[{{V}_{*}}=l\frac{dV}{dy}=ky\frac{dV}{dy}\]
积分可得
\[\frac{V}{{{V}_{*}}}=\frac{1}{k}\ln y+{{C}_{1}}\]
令\({{C}_{1}}=C-\frac{1}{k}\ln \frac{v}{{{V}_{*}}}\),则上式可写为
\[\frac{V}{{{V}_{*}}}=\frac{1}{k}\ln \frac{y{{V}_{*}}}{v}+C\] (4.21)
式(4. 21)表明,湍流流动的速度分布是按对数规律分布的。式中的常数要由实验确定。
对于光滑的直圆管,根据实验可取k=0.4,C=5.5,代入式(4. 21 ),得
\[\frac{V}{{{V}_{*}}}=5.75\lg \frac{y{{V}_{*}}}{v}+5.5\] (4.22)
工程上,式(4.22)适合于除黏性底层以外的任何区域。
湍流流动的速度分布除了对数分布规律外,人们还根据实验结果归纳出了幂次方的速度分布规律,即
\[\frac{V}{{{V}_{\max }}}=\left( \frac{y}{{{r}_{0}}} \right)_{{}}^{\frac{1}{n}}\] (4.23)
式中,n随雷诺数而变化,具体数值见表4.1。
由表4.1可知,指数n随雷诺数的增大而增大,一般取n=6~10。当Re=1.1×105时,n=7,于是可得
\[\frac{V}{{{V}_{\max }}}=\left( \frac{y}{{{r}_{0}}} \right)_{{}}^{\frac{1}{7}}\] (4.24)
式(4. 24)称为布拉休斯的1 / 7速度分布规律。
由式(4.22),可得,y=ro的圆管轴线上的最大速度为
\[{{V}_{\max }}={{V}_{*}}\left( 5.75\lg \frac{{{r}_{0}}{{V}_{*}}}{v}+5.5 \right)\] (4.25)
通过圆管的平均速度为
\[\overline{V}=\frac{{{q}_{v}}}{\pi r_{0}^{2}}=\frac{1}{\pi r_{0}^{2}}2\pi \int_{0}^{{{r}_{0}}}{V\left( {{r}_{0}}-y \right)}dy\] (a)
当y=ro时,V=Vmax,代入式(4. 21),可得
\[{{V}_{\max }}/{{V}_{*}}=\frac{1}{k}\ln \frac{{{r}_{0}}{{V}_{*}}}{v}+C\] (b)
因此,由式(4.21)和式(b)得
\[V-{{V}_{\max }}=\frac{{{V}_{*}}}{k}\ln \left( \frac{y}{{{r}_{0}}} \right)\]
代入式(a)积分,得平均速度为
\[\overline{V}={{V}_{\max }}-1.5{{V}_{*}}/k={{V}_{\max }}-3.75{{V}_{*}}\] (4.26a)
经实验修正后的平均速度为
\[\overline{V}={{V}_{\max }}-4.07{{V}_{*}}\] (4.26b)
湍流流动的速度分布规律按照对数规律或幂次方的速度分布规律,其特点是在靠近壁面处的速度变化很大,在湍流区速度变化较小,这是由于湍流区流体质点的剧烈掺混,使得速度分布更加均匀。根据平均速度与最大速度之比可以得出,对于湍流流动,若用1 / 7幂次方的速度分布,则V/Vmax=0.817,而层流流动V/Vmax=0.5。可见湍流的速度分布比较均匀。
对于水力粗糙管,流速分布公式为
\[\frac{V}{{{V}_{*}}}=5.75\lg \frac{y}{\Delta }+8.5\] (4.27)
其平均速度仍为式(4.26a)。
4.3.3 圆管内沿程损失的实验研究
尽管对于湍流流动的研究可以借助于计算机技术的发展从理论上进行研究,但是,从4.3.2小节的讨论可以看出湍流流动是非常复杂的,因此对于湍流流动的研究,目前大多数问题还需要借助于实验才能够得到解决。从沿程损失的计算公式式(4.4)可以看出,沿程能量损失计算的关键仍然是沿程损失因数的确定。大量研究表明,在不可压缩流动中,沿程损失因数λ=f(Re,∆/d),为确定这一数关系的具体表达形式,必须经过大量实验的研究。本节主要介绍著名的尼古拉兹实验曲线。
尼古拉兹对不同直径的管道进行了一系列的实验。为了模拟管壁的粗糙度,采用了人工粗糙的管壁,即以颗粒均匀的砂粒黏附在经过油漆后的管壁上,用砂粒直径∆表示绝对粗糙度,∆与管径之比∆/d称为相对粗糙度。用6种不同粗糙度的圆管进行实验,测出了hf,V,并计算出λ,得到了λ与Re的关联曲线,并以对数规律示于图4.7中。
由图可以看出,尼古拉兹的实验曲线可以分为5个阻力区域,每个阻力区域的λ计算经验和半经验公式归纳如下。
1.层流区
当Re≤2 320时,λ与Re的关联曲线在对数坐标图上为一直线(见图4.7中的Ⅰ)。所有的不同相对粗糙度的实验点都落在这一直线上,这条直线的方程正是λ=64/Re。表明实验规律只与Re有关,而与∆/d无关。
2.过渡区
当2 320≤Re≤4000时,出现了从层流向湍流过渡的不稳定现象。在该区域中,虽然实验点上下波动,但总的趋势是λ随Re的增大而增大(见图4.7中Ⅱ)。此区可用扎依钦柯的经验公式计算,即
λ=0.0025Re^(1/3) (4.28)
3.光滑管区
此区中的管壁粗糙度对几乎没有什么影响,不同粗糙度的实验点都落在同一直线上(见图 4.7中的Ⅲ)。这种情况只能是黏性底层厚度δt大于壁面粗糙度∆时才可能出现的。流体就好像流过光滑的壁面一样。这个区域的范围为4000≤Re≤80(d/∆),λ可用下列经验公式计算。
当4000≤Re≤105时,可以用布拉休斯公式计算,即
λ=0.3164/Re^(0.25) (4.29)
当105<Re≤3×106时,采用尼古拉兹光滑管的经验公式,即
λ=0.0032+0.221Re^(-0.237) (4.30)
根据湍流的速度分布规律,尼古拉兹提出了一个适用于整个光滑管区的半经验公式,即
λ=[2lg(Re√λ)-0.8]^(-2) (4.31)
4. 粗糙管区
当80(d/∆)≤Re≤ 4160(d/2∆)^(0.85)时,为粗糙管区(见图4. 7中的Ⅳ)。随着Re的增大,黏性底层厚度逐渐减小,以至于不能掩盖粗糙不平的管壁表面,管壁粗糙度对流动产生影响。由图4. 7可以看出,粗糙度越大,光滑管转变为粗糙管的雷诺数也越小。该区的λ可用考尔布鲁克公式计算,即
1/√λ=-2lg(2.51/Re√λ+∆/3.7d) (4.32)
考尔布鲁克公式不仅适合于粗糙管区,而且也适合于4000≤Re<106的整个区域。这是一个湍流沿程损失的综合计算公式。
5.阻力平方区
当Re>4160(d/2∆)^(0.85)时,为阻力平方区(见图4.7中的V)。该区的流动特点是黏性底层厚度趋近于零,粗糙表面全部暴露出来,沿程损失因数与雷诺数无关。沿程损失因数的计算公式为
\(\lambda \text{=}{{\left( 2\lg \frac{d}{2\Delta }+1.74 \right)}^{-2}}\) (4.33)
为了便于计算,工程上还提出了一个适合于整个湍流的经验公式为
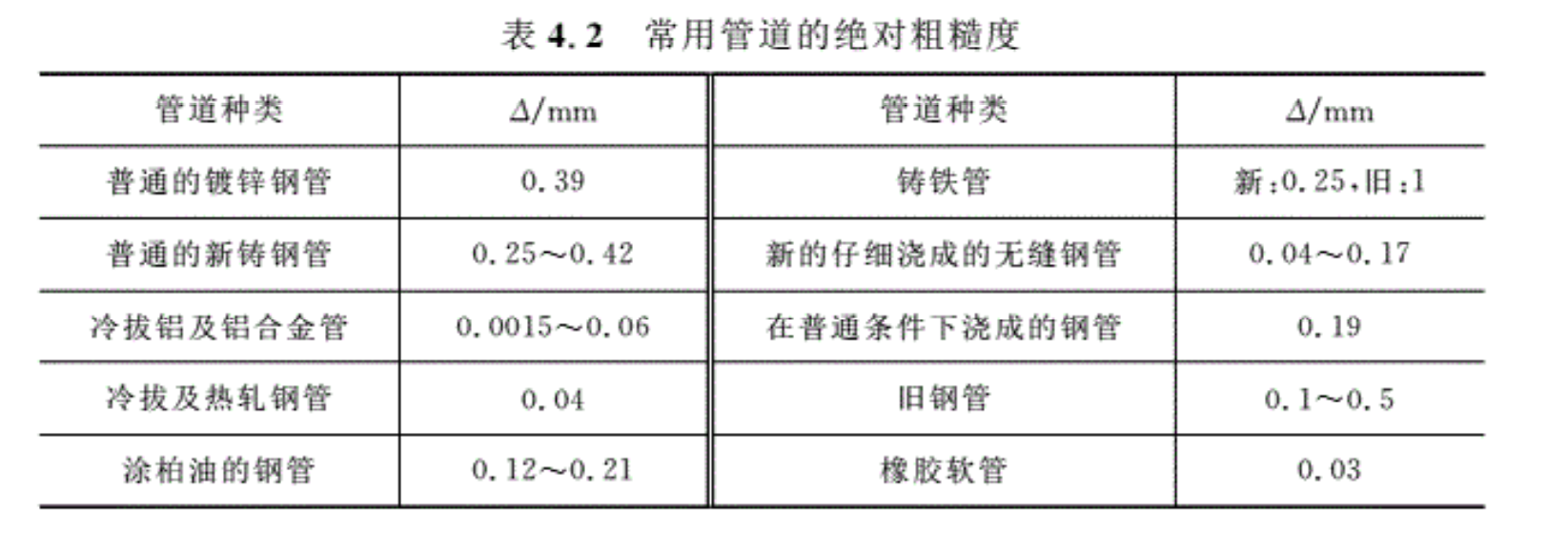
在粗糙管区和阻力平方区,即从式(4.32)~式(4.33)可以看出,沿程损失因数与管壁粗糙度∆有关。由前所述,尼古拉兹实验曲线揭示了管道中的沿程损失的规律,但这些规律的得出是有前提的一一该实验是在人工粗糙的管道(管壁粗糙度比较均匀)内进行的。实际的商品管道的壁面粗糙度不会像人工粗糙管那么均匀,而且实际管道粗糙部分的高度、形状和分布规律也不相同。因此实际中要把各种管壁的真实粗糙度通过实验换算成砂粒粗糙度。表4. 2给出了几种常用管道的绝对粗糙度,即与真实粗糙度相当的砂粒直径。
在实际计算中,适合于工业管道使用的实验曲线类似于尼古拉兹的实验曲线,使用时可以查阅流体力学手册。
例4.2 设有一个截面尺寸为(1. 2 ×0.6)mm²的矩形通风管道,通过截面的流量为qv = 11.67m³/s,空气的温度t=45 ℃,在L=12 m长的管道中,用倾斜30°的装有酒精的斜管微压计测量沿程损失,斜管中的读数l=7.5 mm,酒精密度ρ=860 kg/m³。求风道的沿程损失因数λ。
解:在标准状态下,t=45 ℃时的空气密度为
\[\rho =\frac{p}{RT}=\frac{1.0133\times {{10}^{5}}}{287.06\times \left( 273.15+45 \right)}=1.1095kg/{{m}^{3}}\]
风道中的流速
\[V=\frac{{{q}_{v}}}{A}=\frac{11.67}{0.72}=16.21m/s\]
管道的当量直径
\[{{d}_{e}}=\frac{4A}{\chi }=\frac{4\times 0.72}{2\left( 1.2+0.6 \right)}=0.8m\]
由
\[\Delta p=\lambda \frac{L}{{{d}_{e}}}\frac{\rho V_{{}}^{2}}{2}\]
得
\[\lambda =\frac{2\Delta p{{d}_{e}}}{L\rho {{V}^{2}}}=\frac{2\times 7.5\times {{10}^{-3}}\times 0.5\times 860\times 9.81\times 0.8}{12\times 1.11\times {{16.2}^{2}}}=0.01448\]
例4.3 一输油管道的管长L=300m,直径d=0.2 m,绝对粗糙度∆=0.5mm,输送流量qv=0.33 m³/s,油的运动黏度v=3.0×10-6㎡ / s。求单位质量流体通过管道的能量损失。
解:首先求出雷诺数,然后判别流动状态,即
\[V=\frac{4{{q}_{v}}}{\pi {{d}^{2}}}=\frac{4\times 0.33}{3.14\times {{0.2}^{2}}}=10.5m/s\]
Re=Vd/v=10.5×0.2/3.0×10-6=7.00637×105
因为
\[4160{{\left( \frac{d}{2\Delta } \right)}^{0.85}}=4160{{\left( \frac{200}{2\times 0.5} \right)}^{0.85}}=3.758\times {{10}^{5}}\]
所以流动属于阻力平方区,由式(4.33)得
\[\lambda ={{\left( 2\lg \frac{d}{2\Delta }+1.74 \right)}^{-2}}={{\left( 2\lg \frac{200}{2\times 0.5}+1.74 \right)}^{-2}}=0.0248\]
故
\[{{h}_{f}}=\lambda \frac{l}{d}\frac{{{V}^{2}}}{2g}=0.0248\times \frac{300}{0.2}\times \frac{{{10.5}^{2}}}{2\times 9.8}=209.6m\]
4.3.4 压缩性对沿程损失因数的影响
由前面讨论可知,在不可压缩(液体或低速流动的气体)情况下,对于光滑管,沿程损失因数仅仅取决于雷诺数,对于粗糙管,除了与雷诺数有关外,还与管壁的相对粗糙度有关。
一般情况下,在可压流动中,沿程损失因数除了与雷诺数和相对粗糙度有关外,还与马赫数有关。因此考虑压缩性影响时的沿程损失因数要用实验来确定。在黏性可压流动中,压缩性对沿程损失因数的影响如图4.8所示。图中以λ c/λ inc表示在相同雷诺数下可压流动的沿程损失因数与不可压流动的沿程损失因数之比。
由图4. 8可以看出:
(1)当Ma <0.7时,压缩性对沿程损失因数影响较小,按不可压流动的沿程损失因数计算不会引起太大的误差。
(2)在0.7 < Ma <0.9范围内,λc随Ma的增加而逐渐减小。在Ma>0. 9以后,沿程损失因数迅速下降。
(3)在超声速气流中,可压流动的沿程损失因数比不可压流动的要小一些,由实验知,对于管道长度L在10~50倍的管径时,当1.2 < Ma ≤ 3.0,0.25 × 105< Re≤ 7 × 105时,沿程损失因数在0.008~0.012之间,大约为不可压流动沿程损失因数的50%。
4.4 管道内的局部阻力及损失计算
在实际的管路系统中,不但存在第4.3节所讲的在等截面直管中的沿程损失,而且也存在着因有各种各样的其他管件,如弯管、流道突然扩大或缩小、阀门、三通等,所以当流体流过这些管道的局部区域时,流速大小和方向被迫急剧地发生改变,从而出现流体质点的撞击,产生旋涡、二次流以及流动的分离及再附壁现象。此时由于黏性的作用,流体质点间发生剧烈的摩擦和动量交换,因而阻碍着流体的运动。这种在局部障碍物处产生的损失称为局部损失,其阻力称为局部阻力。因此,在一般的管路系统中,既有沿程损失,又有局部损失。
4.4.1 局部损失产生的原因及计算
一、产生局部损失的原因
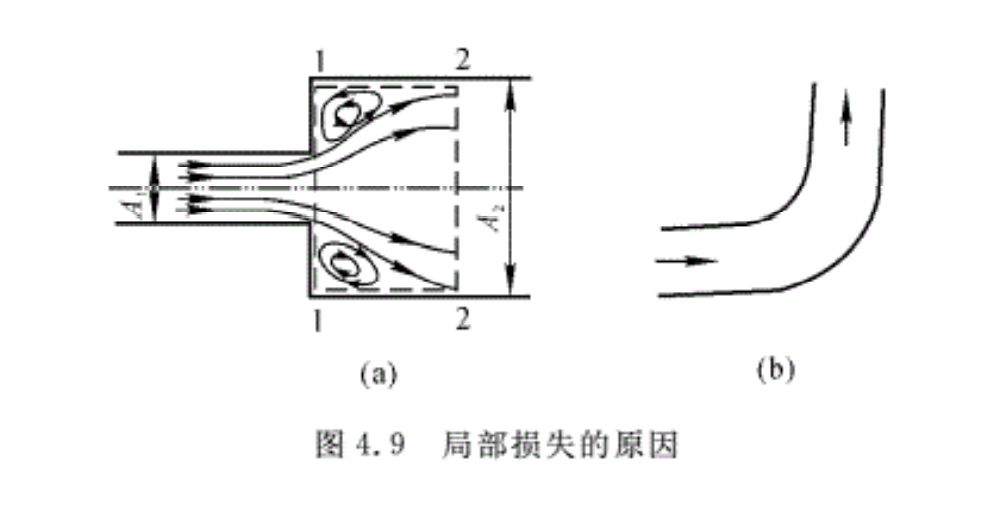
产生局部损失的原因多种多样,而且十分复杂,因此很难概括全面。这里结合几种常见的管道来说明。
对于突然扩张的管道,由于流体从小管道突然进入大管道,如图4.9(a)所示,而且由于流体惯性的作用,流体质点在突然扩张处不可能马上贴附于壁面,而是在拐角的尖点处离开了壁面,出现了一系列的旋涡。进一步随着流体流动截面面积的不断扩张,直到2截面处流体充满了整个管截面。在拐角处由于流体微团相互之间的摩擦作用,一部分机械能不可逆地转换成热能,在流动过程中,不断地有微团被主流带走,同时也有微团补充到拐角区,这种流体微团的不断补充和带走,必然产生撞击、摩擦和质量交换,从而消耗一部分机械能。同时,进入大管流体的流速必然重新分配,增了流体的相对运动,并导致流体的进一步摩擦和撞击。局部损失就发生在从旋涡开始到消失的一段距离上。
图4. 9(b)示出了流体在弯曲管道的流动。由于管道弯曲,流线会发生弯曲,流体在受到向心力的作用下,管壁外侧的压力高于内侧的压力。在管壁的外侧,压强先增加而后减小,同时内侧的压强先减小后增加,这样流体在管内形成螺旋状的交替流动。
综上所述,碰撞和旋涡是产生局部损失的主要原因。当然在1一2之间也存在沿程损失,一般来说,局部损失比沿程损失要大得多。在测量局部损失的实验中,实际上也包括了沿程损失。
二、局部损失的计算
如前所述,单位重量流体的局部能量损失以\({{h}_{\zeta }}\)表示
\[{{h}_{\zeta }}=\zeta \frac{{{V}^{2}}}{2g}\]
式中:\({{h}_{\zeta }}\)一一局部损失(阻力)因数,是一个无量纲数,它的大小与局部障碍物的结构形式有关,由实验确定;
V—— 管中流体的平均速度(通常指局部损失之后的速度)。
局部压强损失为 \(\Delta p=\zeta \frac{\rho {{V}^{2}}}{2}\)
式中,∆p为流经局部障碍物前后的压强差(或总压差)。
1.突然扩张管道的局部损失计算
由于产生局部损失的情况多种多样及其流动情况的复杂性,所以对于大多数情况局部损失只能通过实验来确定。只有极少数情况下的局部损失可以进行理论计算。
对于突然扩大的情况,可以通过理论推导得到局部损失的计算公式。流体在如图4. 9(a) 所示的突然扩张的管道内流动,由于流体的碰撞、惯性和附面层的影响,在拐角区形成了旋涡,引起能量损失。由图可见,流体到2一2截面充满整个管道。取1一1和2一2截面以及侧表面为控制体,并设截面1一1处的管道面积为A1,参数为p1,V1;截面2一2处的管道面积为A2,参数为p2,V2,则根据伯努利方程,有
\[\frac{{{p}_{1}}}{\gamma }+\frac{V_{1}^{2}}{2g}+{{z}_{1}}=\frac{{{p}_{2}}}{\gamma }+\frac{V_{2}^{2}}{2g}+{{z}_{2}}+{{h}_{\zeta }}\]
于是局部损失为
\[{{h}_{\zeta }}=\frac{{{p}_{1}}-{{p}_{2}}}{\gamma }+\frac{V_{1}^{2}-V_{2}^{2}}{2g}\] (a)
对1一1和2一2截面运用连续方程,即
V1A1=V2A2
对所取的控制面应用动量方程,考虑到1一1和2一2截面之间的距离比较短,通常可以不计侧表面上的表面力,于是动量方程可写为
p1A1-p2A2=ρV2A2(V2-V1)
将动量方程和连续方程代入式(a),得
\[{{h}_{\zeta }}=\frac{V_{2}^{2}-{{V}_{1}}{{V}_{2}}}{2g}+\frac{V_{1}^{2}-V_{2}^{2}}{2g}=\frac{{{\left( {{V}_{1}}-{{V}_{2}} \right)}^{2}}}{2g}=\frac{V_{1}^{2}}{2g}{{\left( 1-\frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}}=\frac{V_{2}^{2}}{2g}{{\left( \frac{{{A}_{2}}}{{{A}_{1}}}-1 \right)}^{2}}\]
令\({{\zeta }_{1}}={{\left( 1-\frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}},{{\zeta }_{2}}={{\left( \frac{{{A}_{2}}}{{{A}_{1}}}-1 \right)}^{2}}\),则局部损失可写为
\[{{h}_{\zeta }}={{\zeta }_{1}}\frac{V_{1}^{2}}{2g}={{\zeta }_{2}}\frac{V_{2}^{2}}{2g}\] (4.35)
式中ζ1,ζ2分别表示局部损失(阻力)因数。式(4.35)表明,用公式计算局部损失时,采用的速度可以是损失前的也可以是损失后的,但局部损失因数也不同。由式(4. 35)及局部损失因数的表达式可以看出,突然扩大的局部损失因数仅与管道的面积比有关而与雷诺数无关。实际上,根据实验结果可知,当在雷诺数不很大时,局部损失因数随着雷诺数的增大而减小,只有当雷诺数足够大(流动进入阻力平方区)时,局部损失因数才与雷诺数无关。如果流体从管道流入一大容器,此时A1/A2≈0,则ζ1=1。
下面介绍几种比较常见的局部损失因数的计算,而且在一般情况下,局部损失因数均是由对应发生损失后的速度给出的。
2.渐扩管
流体流过逐渐扩张的管道时,由于管道截面积的逐渐扩大,使得流速沿流向减小,压强增高,而且由于黏性的影响,在靠近壁面处,流速小,以至于动量不足以克服逆压的倒推作用,因而在靠近壁面处可能出现倒流现象从而引起旋涡,产生能量损失。渐扩管的扩散角θ越大,旋涡产生的能量损失也越大;θ越小,要达到一定的面积比所需要的管道也越长,因而产生的摩擦损失也越大。所以存在着一个最佳的扩散角θ。在工程中,一般取θ=6°~12°,其能量损失最小。θ在60°左右损失最大。渐扩管的局部损失因数为
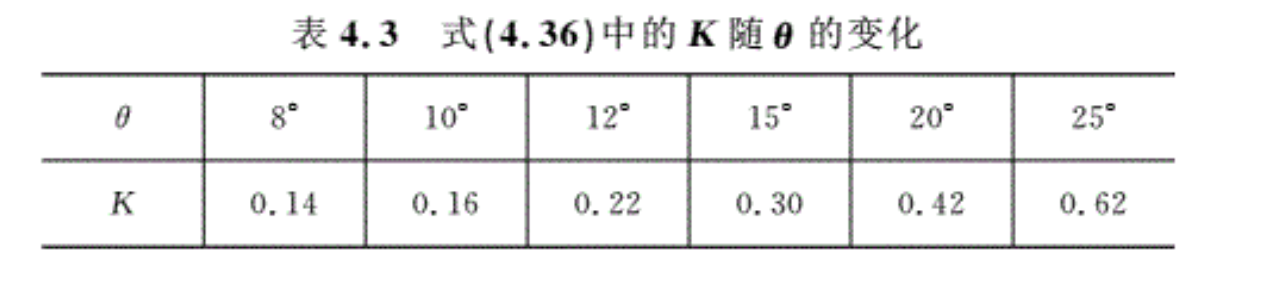
\[\zeta =\frac{\lambda }{8\sin \left( \frac{\theta }{2} \right)}\left[ 1-{{\left( \frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}} \right]+K{{\left( 1-\frac{{{A}_{1}}}{{{A}_{2}}} \right)}^{2}}\] (4.36)
式中,K随θ的变化见表4.3。
3.突然缩小
流体在管道截面积突然缩小的管道中流动,如图4.10所示。当管道的截面积突然收缩时,流体首先在大管的拐角处发生分离,形成分离区,然后在小管内也形成一个分离区。最后才占据管道的整个截面。局部损失因数的确定可以根据实验确定。对于不可压流动,根据实验结果,有
\[\zeta =0.5\left( 1-\frac{{{A}_{2}}}{{{A}_{1}}} \right)\] (4.37)
在特殊情况下,A2/A1→0,即流体从一个大容器进入管道且进口处具有尖锐的边缘时,局部损失因数为ζ=0.5。若将进口处的尖锐边缘改成圆角后,则局部损失因数ζ随着进口的圆滑程度而大大降低,对于圆形匀滑的边缘,ζ=0.2;入口极圆滑时ζ=0.05。
4. 渐缩管
为了减小管道截面积突然缩小的流动损失,通常采用渐缩管。在渐缩管中,流线不会脱离壁面,因此流动阻力主要是由沿流程的摩擦引起的。对应于截面积缩小后的流速的局部损失因数为ζ=0.05~0.06,由此可见,在渐缩管中的流动损失很小。
5.弯管
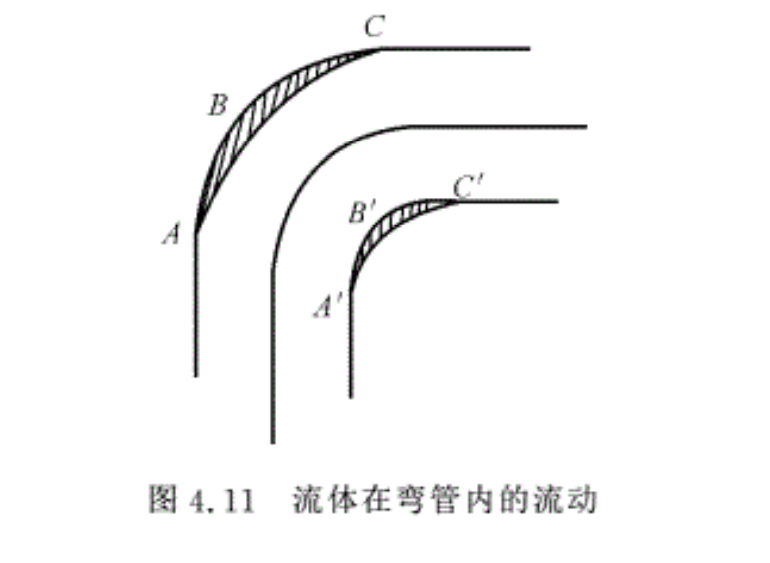
在弯管内的流动由于流体的惯性,流体在流过弯管时内、外壁面的压力分布不同而流线发生弯曲,流体受到向心力的作用。这样,弯管外侧的压强就高于内侧的压强,如图4.11所示。图中AB区域内,流体压强升高,B点以后,流体的压强渐渐降低。与此同时,在弯管内侧的A′B′区域内,流体作增速降压的流动,在B′C′区域内是增压减速流动。在AB和B′C′这两个区域内,由于流动是减速增压的,会引起流体脱离壁面,形成旋涡区,造成损失。此外,由于黏性的作用,管壁附近的流体速度小,在内、外压力差的作用下,会沿管壁从外侧向内侧流动。
同时,由于连续性,管中心流体会向外侧壁面流去,从而形成一个双旋涡形状的横向流动,整个流动呈螺旋状。横向流动的出现,也会引起流体能量的损失。弯管的局部损失因数计算的经验公式为
ζ=kθ/90° (4.38a)
式中,θ表示弯管弯曲的角度,以(°)为单位;系数k的计算式为
K=0.131+0.159(d/r)^3.5 (4.38b)
式中 ,r——弯管中线的曲率半径;
d——管径。
4.4.2 减小和利用局部损失
在各种管道的设计中,应尽量减小局部损失。为了减小局部损失,应尽量避免流通截面积发生突然的变化。在截面积有较大变化的地方常采用锥形过渡,在要求比较高的管道中应采用光滑的流线形壁面。
以下举几个例子来说明减小局部损失的方法。
1.弯曲管道
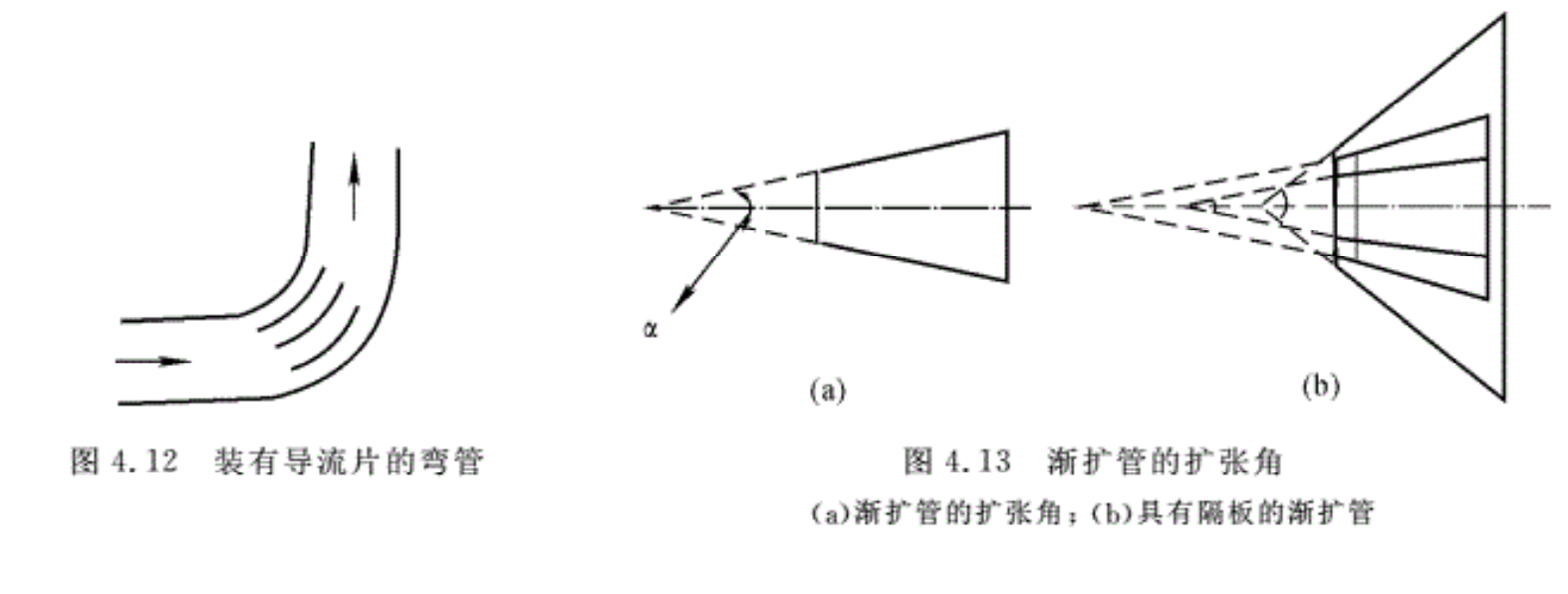
由弯管的局部损失计算公式可知,弯管的局部损失取决于管道的直径(d)、曲率半径(r)和管道的转弯角。因此在设计管道时,为了减小局部损失,应尽量避免采用转弯角过小的死弯。对于直径较小的热力设备管道,通常采用r/d> 3.5。对于直径较大的排烟风道来说,横向的二次流动比较突出。为了减小二次流动损失,一方面可以适当地加大管道的曲率半径,以减小流体转弯时的离心力;另一方面通常在弯管内安装导流叶片,如图4.12所示。这样既可以减小弯道两侧的压强差,又可以减小二次流影响的范围。根据实验,在没有安装导流叶片的情况下,直角弯管的ζ=1.1;安装薄板弯成的导流叶片后,ζ=0.4;当导流叶片呈流线月牙形时,ζ=0.25。可见,安装导流叶片后,并适当选择导流叶片的形状,对减小局部损失有明显的效果。
2.流通截面的变化
将突然扩张的管道改为渐扩管,由于涡流区的大小和涡流强度的减小,其局部损失有很大的改善。但是当扩张(或收缩)的面积比一定时,渐变管的长度相应地加长,使得沿程损失有所增加,所以设计时应取最佳值。管长的增加会增加管道设计的成本或带来制造上的困难。有些情况下,还要受到几何空间的限制,因此在管道设计中,应根据具体问题、具体情况全面折中考虑。
在设计渐扩管时,如果面积比较大,则可用隔板或用几个同心扩张管来达到正常的扩张角(见图4. 13)。扩张角一般控制在α=6°~12°的范围内。
3.三通
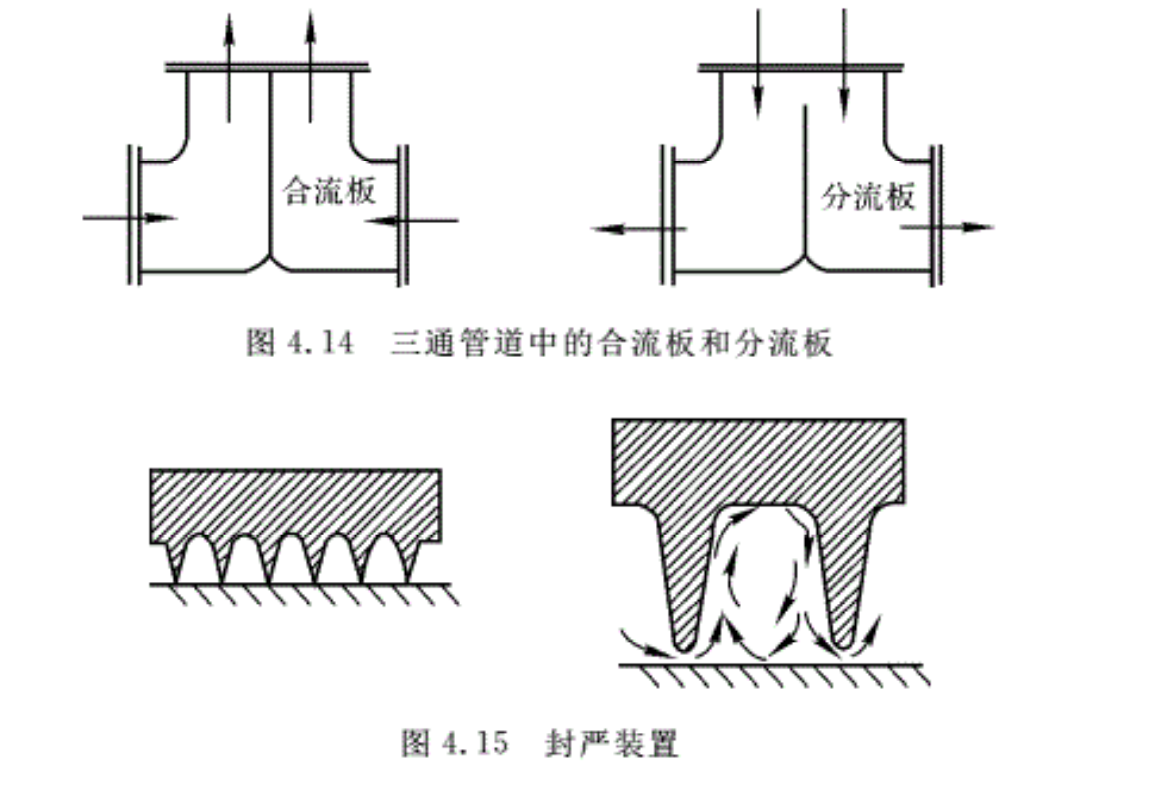
工程中有各种各样的三通接头,其局部阻力因数也各不相同,使用时可查阅流体力学手册。这里说的是为了减少流体流过三通的能量损失,可以在总管中根据支管的流量安装分流板和合流板,如图4.14所示。从减小局部损失的角度来讲,应尽量避免采用直角三通。
4.局部损失的利用
在日常生活中,局部损失还可以被利用。阀门就是利用局部损失来控制流量的一个例子。在航空发动机上,为了防止燃烧室出口的高温高压燃气进入滑油腔内,可以利用如图4.15所示的封严装置将燃气和滑油腔隔开。封严装置的原理是根据气每经过一个密封齿,压强就有所降低,经过几个密封齿后,压强就降低到与滑油腔内的压强基本相等。这样最后一个齿的前、后的压强差很小,达到阻隔燃气流入滑油腔的目的,起到密封的作用。
4.4.3 流动损失叠加及当量长度法
1.流动损失的计算
一般情况下,流体在管路系统中的流动必将存在若干沿程损失和局部损失,总的能量损失符合叠加原理。在不考虑其相互干扰的情况下,单位质量流体沿流程的总损失的计算式为式(4.6)。
2.当量长度法
由上面的沿程损失和局部损失计算公式可知,这两种损失均与流速的平方成正比。假定能够找出在流速相同的条件下,某段长度的管件能产生同样长度的沿程损失,这段长度就叫做该管件的当量长度。它能在流动损失等效的条件下,以某段等径直管的沿程损失代替局部损失。这种当量长度法对于管路系统的计算是非常方便的。这种当量关系为
\[\lambda {{\frac{L}{d}}^{\prime }}\frac{{{V}^{2}}}{2g}=\zeta \frac{{{V}^{2}}}{2g}\]
即 \({{L}^{\prime }}=\frac{\zeta }{\lambda }d\) (4.39)
式中,L′称为该管件的当量长度,或者称为此局部损失的等价管长。
如果管路系统的管径和沿程阻力损失因数处处相等,则有
∑L′=(d/λ)∑ζ
于是
\[{{h}_{w}}=\sum \frac{\lambda }{d}\left( L+{{L}^{\prime }} \right)\frac{{{V}^{2}}}{2g}=\frac{\lambda }{d}\frac{{{V}^{2}}}{2g}\sum \left( L+{{L}^{\prime }} \right)\] (4.40)
引用了当量长度的概念,可在总损失中方便地估计出局部损失所占的比例,这为复杂管路系统的能量损失计算提供了简便的分析方法。
4.4.4 进口起始段内的流动
在各种管路计算中,会遇到管路起始段的流动问题,本节讨论进囗起始段的沿程能量损失。在这段管流中,流体质点的运动与完全发展的管内流动完全不同,流体质点的速度在不断地变化。图4.16表示了进囗比较圆滑的圆管进口段内的流动。一方面流体从进口几乎均匀地流入管内,由于黏性的影响,在壁面上速度为零,然后沿法线方向流速逐步增加到中心线上的速度;另一方面,随着流体的不断流入,管壁对流动的影响加大,但因在流动中要满足连续方程,即流量保持不变,因此,管轴附近的流体将相应加速。在这个过程中,流体质点存在着从管壁到管轴的横向运动,且横截面上的速度分布也发生了变化,直到轴线上的速度达到该流量下的完全发展的最大速度为止,此时即可认为进口初始段的流动过程结束。下面分别讨论进口起始段长度的计算方法和能量损失。
1.进囗起始段长度
从进口开始到管中形成完全发展的流动时对应的这段流程定义为进口起始段。进口起始段的长度用Le表示。
一般情况下,对于比较光滑的进囗,管中完全发展的流动是层流流动,则起始段长度为
Le=0.065Red (4.41)
将Re=2320代入式(4.41),可得
Le=150d
由实验得到的层流起始段长度为
Le=0.02875Red (4.42)
将Re=2320代入式(4.42),可得
Le=66.5d (4.43)
如果管中完全发展的流动为湍流流动,则根据大量实验结果可知,起始段长度为Le=(25~40)d。
从以上分析可知,通常湍流起始段比层流起始段要短。这是由于湍流质点相互掺混,流体进入管口后很快就达到了湍流速度分布规律。
对于进口比较尖锐的管道,流体进入管道时将出现先收缩后扩张的离壁现象,其间管壁对流体的影响减弱,相应起始段的长度将有所增加。
2.进囗起始段的能量损失
在进口起始段内,不仅存在着由于摩擦影响引起的沿程损失,而且也存在流体质点横向脉动而引起的局部损失,因此进囗起始段的能量损失应为这两者之和。设局部损失因数为ζ,则起始段单位质量流体的能量损失为
\[{{h}_{w}}=\left( \lambda \frac{{{L}_{e}}}{d}+\zeta \right)\frac{{{V}^{2}}}{2g}\] (4.44)
对于层流流动,当管道进囗尖锐时,ζ=2.7;当管道进囗圆滑时,ζ=2.2~2.4。
对于湍流流动,当管道进囗尖锐时,ζ=0.5;当管道进囗圆滑时,ζ=0.005~0.06。
从以上数据可以看出,在同样流速下,湍流流动的局部损失比层流时小得多,这主要是由于湍流流动时,流体质点的无规则横向脉动,使得进囗段湍流脉动所占的比例相对较小。
工程计算中,常常将局部损失折合到沿程损失中一起计算。
当起始段内的流动为层流时,取沿程损失因数λ=A/Re。当L >Le时,能量损失为
hW=[A x Le/Re x d+λ(L-Le)/d]V²/2g (4.45)
式中,A为实验常数。层流流动状态下,水的实验常数列入表4.4中。
如果当L<Le时,则单位质量流体的能量损失为
hW=A x Le x V²/Re x d x 2g (4.46)
对于管内的湍流流动,或管长L > 10Le,通常不计进囗段的流动损失。
4.5 管路设计与计算基础
在工程中,会涉及许多管路设计与计算问题。除了工程中的石油、化工、建筑、供暖和水利中的管路系统外,在航空、航天中诸如飞机滑油系统和发动机起动管路系统、飞机空调系统等都会遇到管路计算问题。
工程中所遇到的管路设计与计算问题是多种多样的,遇到的管件类型以及所涉及的物理量也很多,但管路设计与计算中所遇到的典型情况一般有三类。
(1)已知管路布局、几何尺寸和管路系统允许的压力降,求通过的流量(确定管路的输送能力)。
(2)已知管路布局、几何尺寸和通过的流量,求流动损失,即确定管路系统的压力降。
(3)已知管路布局、通过的流量和允许的压力降,确定管路几何尺寸。
对于上述(1),(3)两类问题,通常需要多次的迭代计算。具体计算可假设一个沿程损失因数λ,按总的损失计算确定流速V,并计算雷诺数Re,判别流动状态,然后对假设的λ进行校核,直到求出较为准确的λ后,最后用总的能量损失公式计算速度V,从而求出通过管路的流量或管径d。对于上述的第(2)种情况,若能事先计算出Re,则根据Re可以确定流动状态及该流动所属的流动范围,亦即确定λ,从而可直接确定管路的压力降。
根据前面的讨论,一条管路中的能量损失等于各段上的沿程损失和局部损失之和,即
\[{{h}_{W}}=\sum {{\lambda }_{i}}\frac{{{l}_{i}}}{{{d}_{i}}}\frac{V_{i}^{2}}{2g}+\sum {{\zeta }_{j}}\frac{V_{j}^{2}}{2g}\]
在管路设计之前,通常要进行经济核算。若管径大,则初期投资大,但流动损失小,所需动力设备小,经常运转的费用就小。
工程中需要先定出经济流速,可根据输送的流量定出合适的管径。可见管路中能量损失的计算是管路计算的关键。
在水力机械中经常用到管路特性曲线。所谓的管路特性曲线是指一条管路上的能量损失与流量之间的函数关系。
4.5.1 串联管路的计算
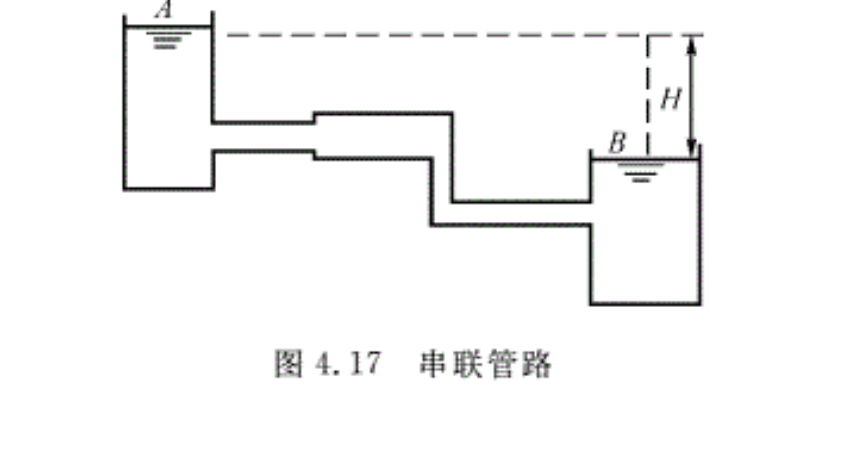
串联管路是指各种不同(或相同)直径的管路依次连接组成的管路系统,如图4.17所示。
在不可压缩流动中,对于直径相同的串联管路,由于管路截面积相同,通过管路各截面上的流量相等,因此通过各截面上的平均流速也相等。对于直径不同的串联管路,根据连续方程,通过管路各截面上的流量仍相等,但平均流速不再相等。无论是同径管路还是异径串联管路,计算的基本原则如下:
(1)在串联管路中,各管段的流量相等;
(2)串联管路系统的总损失等于各管段的沿程损失和局部损失之和,即
\[{{h}_{W}}=\sum {{\lambda }_{i}}\frac{{{l}_{i}}}{{{d}_{i}}}\frac{V_{i}^{2}}{2g}+\sum \zeta \frac{V_{j}^{2}}{2g}\] (4.47)
\[{{q}_{v1}}={{q}_{v2}}={{q}_{vn}}\] (4.48)
对于如图4.17所示的管路系统,流体自容器A经串联管路系统流入容器B,对两容器的自由液面应用伯努利方程得
\[\frac{{{p}_{A}}}{\gamma }+\frac{V_{A}^{2}}{2g}+{{z}_{A}}=\frac{{{p}_{B}}}{\gamma }+\frac{V_{B}^{2}}{2g}+{{z}_{B}}+{{h}_{W}}\]
当自由液面的压强为大气压强时,Pa=pB,当容器足够大时,VA=VB,代入上式得
hW=H (4.49)
即水位的降低用来克服各种流动损失。
当已知通过管路的流量和管路的几何尺寸时,即可利用连续方程求出流量和雷诺数,由 Re可以确定λ,并由管件具体形式确定局部损失因数ζ,从而确定总的流动损失。
当已知总的流动损失和通过管路的流量时,采用迭代法确定管路的直径。可以先假设一个流速V,由此求出d,Re,λ和h′W,比较计算出的h′W与已知的总损失hW的差别,调整流速 V,重新计算,直到两者误差在允许的范围内即可确定。
当已知总的流动损失和管路的几何尺寸时,也同样采用迭代法确定管路的流量。可以先假设一个λ,求出流速V,之后计算Re,再求新的λ值,由λ计算新的速度,直到收敛为止。
例4.4 供水系统(见图4.18)由三种不同的管段组成,水从管1和2两截面分流,流量为qv1=qv2=0.05m³/s,从3截面流出的流量为qv3=0. 05 m³/s,己知管径d1=0.3 m,d2=0.2m,d3=0.15m,管长l1=l2=l3=100m,管壁粗糙度∆= 0.125 mm,水的运动黏度系数v=1.003×10-6㎡/s。若不计局部损失,要达到正常的供水量,试求水塔中的水位高度ho。
解: 由图可见,这是一个有泄流的串联管路系统。对于第一管段,其平均流速为
\[{{V}_{1}}=\frac{{{q}_{v1}}+{{q}_{v2}}+{{q}_{v3}}}{\pi {{\left( {{d}_{1}}/2 \right)}^{2}}}=\frac{4\times 0.05\times 3}{\pi \times {{0.3}^{2}}}=2.123m/s\]
Re1=V1 x d1/v=0.635×10^6
4160 (d1/2∆)^0.85=1.723×106>Re1>80(d1/∆)=1.92×105
可见,流动属于粗糙管区。于是沿程损失因数可按下式计算:
1/√λ=-2lg(2.51/Re1√λ1+∆/3.7d1) (a)
解得 λ1=0.0169
于是可得
\[{{h}_{W1}}={{\lambda }_{1}}\frac{{{l}_{1}}}{{{d}_{1}}}\frac{V_{1}^{2}}{2g}=0.0169\times \frac{100}{0.3}\times \frac{{{2.123}^{2}}}{2\times 9.8}=1.2954m\]
第二段的沿程损失
\[{{V}_{2}}=\frac{{{q}_{v2}}+{{q}_{v3}}}{\pi {{\left( {{d}_{2}}/2 \right)}^{2}}}=\frac{4\times 0.05\times 2}{\pi \times {{0.2}^{2}}}=3.184m/s\]
Re2=V2 x d2/v=0.6349×10^6
4160 (d2/2∆)^0.85=1.221×10^6>Re2>80(d2/∆)=1.28×10^5
流动属于粗糙管区。于是将λ2代入式(a ),解得
λ2=0.0182
从而可得
\[{{h}_{W2}}={{\lambda }_{2}}\frac{{{l}_{2}}}{{{d}_{2}}}\frac{V_{2}^{2}}{2g}=0.0182\times \frac{100}{0.2}\times \frac{{{3.184}^{2}}}{2\times 9.8}=4.707m\]
第三段的沿程损失
\[{{V}_{3}}=\frac{4{{q}_{v3}}}{\pi d_{3}^{2}}=\frac{4\times 0.05}{\pi \times {{0.15}^{2}}}=2.831m/s\]
Re3=V3 x d3/v=0.423×10^6
4160 (d3/2∆)^0.85=0.956×10^6>Re3>80(d3/∆)=0.96×10^5
流动属于粗糙管区。于是将λ3代入式(a),解得
λ3=0.0196
从而可得
\[{{h}_{W3}}={{\lambda }_{3}}\frac{{{l}_{3}}}{{{d}_{3}}}\frac{V_{3}^{2}}{2g}=0.0196\times \frac{100}{0.15}\times \frac{{{2.831}^{2}}}{2\times 9.8}=5.343m\]
求水位高度,沿水箱自由液面至流道出口截面应用伯努利方程,得
\[\frac{{{p}_{a}}}{\gamma }+\frac{V_{{}}^{2}}{2g}+z=\frac{{{p}_{a}}}{\gamma }+\frac{V_{3}^{2}}{2g}+{{z}_{3}}+{{h}_{W\sum }}\]
式中: z=h,V=0,z3=0
h (W∑)=h (W1)+h (W2)+h (W3)
所以
h=h (W1)+h (W2)+h (W3)+V²(3)/2g=11.85m
4.5.2 并联管路的计算
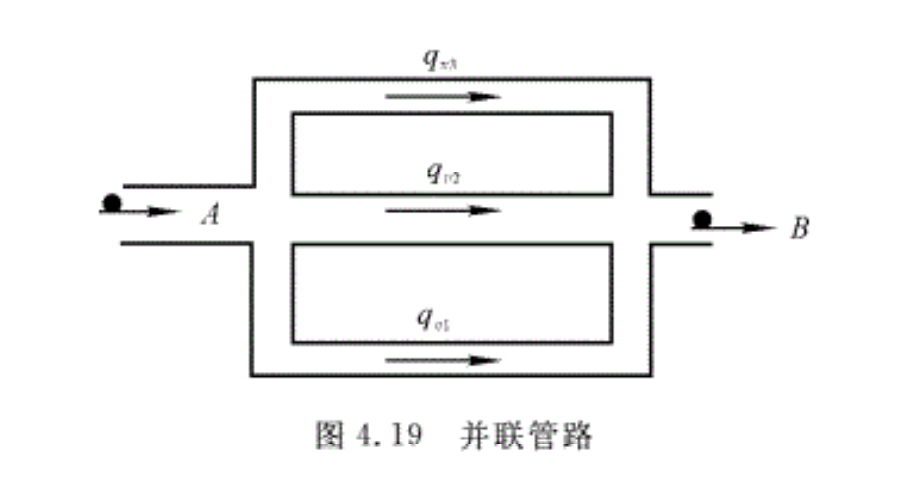
并联管路是指如图4.19所示的各管道进囗汇合在一起,出囗也汇合在一起,即从一点分叉又在另一点汇合的管路称为并联管路。并联管路系统各支管可以是同径并联管路,也可以是异径并联管路。
并联管路的特点是各支管的流量不同,但总流量等于各支管流量之和。在并联管路中,各支管的流动损失h wi相同(这里假设汇合后的流体参数己经掺混均匀),根据并联管路的特点即可得出并联管路两个重要的计算公式为
\[\begin{align}
& {{q}_{v}}\text{=}\sum {{q}_{vi}} \\ (4.50)
& {{h}_{Wi}}={{h}_{WAB}} \\
\end{align}\] (4.51)
在并联管路的计算中,虽然各管段的流动损失标h wi相同,但由于各管段的流量和管径不同,因此各支管的沿程损失因数λ并不相同。为了简化计算,对工程中的湍流问题常按阻力平方区计算。己知总流量和管道尺寸,求流量分配,用试凑法的计算步骤如下:
(1)设过管1的流量q′v1,求管1的流动损失h′W。
(2)用h’W求其他管的流量q′v2,q′v3,…………….,q′vn及∑q′v。
(3)设总流量qv在各管中按q′vi相同的比例分配,即
\({{\text{q}}_{vi}}=\frac{q_{vi}^{\prime }}{\sum q_{v}^{\prime }}{{q}_{v}}\)
(4)根据q vi计算各管中的流动损失并校正流量的正确性。
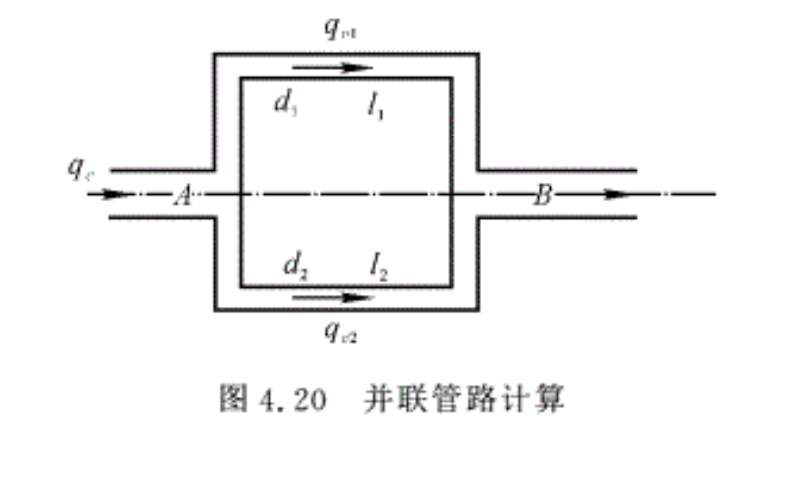
例4.5 并联管路如图4.20所示,设d1=0.1m,l1=150m,λ1= 0.025,总管流量qv =0.1m³/ s,d2=0.15 m ,l2=180 m,λ2=0.02,不计局部损失。求各支管中的流量qv1和qv2。
解:依题意可知
\({{\text{q}}_{v1}}+{{\text{q}}_{v2}}=0.1{{m}^{3}}/s\) (a)
又因 h W1=h W2
即 \({{\lambda }_{1}}\frac{{{l}_{1}}}{{{d}_{1}}}\frac{1}{2g}{{\left( \frac{4{{q}_{v1}}}{\pi d_{1}^{2}} \right)}^{2}}={{\lambda }_{2}}\frac{{{l}_{2}}}{{{d}_{2}}}\frac{1}{2g}{{\left( \frac{4{{q}_{v2}}}{\pi d_{2}^{2}} \right)}^{2}}\) (b)
将有关数据代入式(b)并整理,得
2.81q v1=q v2 (c)
联立式(a)和式(c),解得
q v1=26.25 × 103m³/s, q v2=73.75 × 103m³/s
4.5.3 管网计算基础
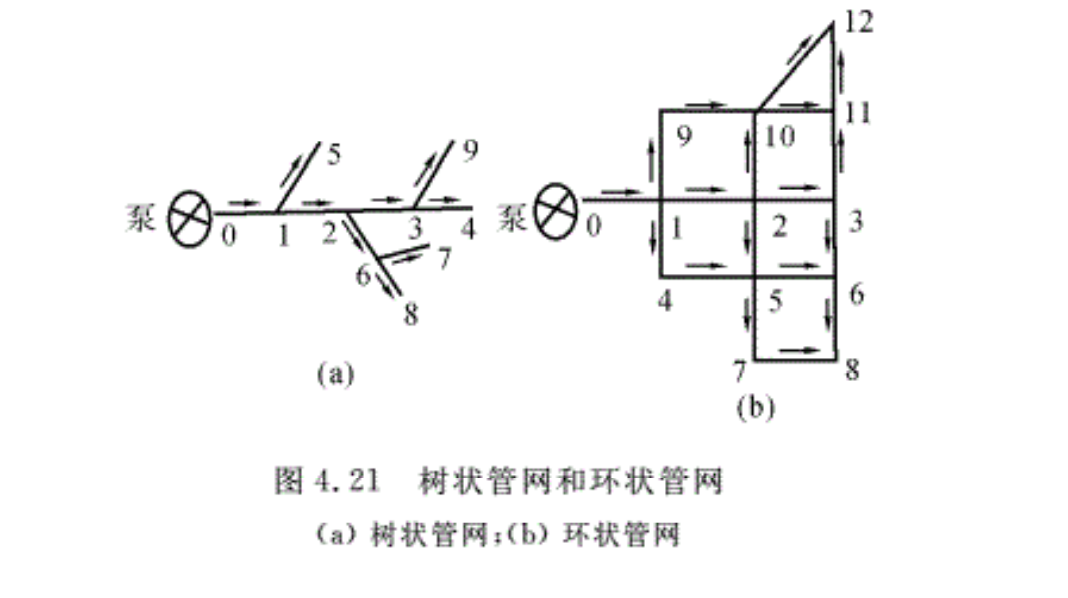
管网是指有一系列管道相互连接组成的管路系统,分为树状管网和环状管网。树状管网管线短,投资少,但可靠性较差。环状管网管线长,投资高,但当局部管线损坏时,可以用其他管线代替,便于维护。
树状管网:几条管道自一点分叉而不再汇合的管路系统叫分叉管路系统。分叉管路系统中的分支上可又有分叉管路,可一直分下去形似树状,故称树状管网。
树状管网是工程中常见的管路形式,在供水、供气管路中广泛采用。树状管路是将主干道中的流体引向不同的地点,以满足用户的需求。图4.21(a)给出了树状管网的示意图,假设管路中各段的长度、直径和流量己知,可以计算出管路系统中的能量损失。每一分支可以按串联管路计算,即
\[\begin{align} & {{h}_{Wi}}=\left( \frac{{{\lambda }_{i}}{{l}_{i}}}{{{d}_{i}}}+\sum \zeta \right)\frac{V_{i}^{2}}{2g} \\& {{H}_{i}}=\sum {{h}_{Wi}} \\\end{align}\]
计算出每一分支管路上的Hi,其中的最大者即是所要求的树状管网系统的能量损失。
环状管网:图4.21 (b)为环状管网示意图。环状管网计算的基本出发点为,根据能量方程,环状管网的任意闭合环路上各管段的流动损失总和等于零。每一节点上流入的流量等于流出的流量。
在设计新管网时,其计算步骤如下:
(1)确定管网布局方式(树状、环状或混合状),管线位置和各管段的长度。
(2)根据用户的流量需求,确定各管段的流量,选择各管段的经济流速,并根据流量确定各管段的管径。
(3)计算各管段的流动损失,根据水头控制点确定供流设备的供流水头(如水塔高度等)。一般选取供流设备的最远供流端(见图4.2 1(a)中的点4、点9和(b)中的点8、点12)为水头的控制点,应满足这些最不利点的水头要求。
(4)对于环状管网,需要调整流量分配来满足各闭合环路的流动损失为零的要求。
小结
本章讨论了管内黏性不可压缩流体流动基础及有关概念。
(1)讨论了黏性流动的两种流态,即层流和湍流流动。讨论了层流和湍流的特点、差别。在黏性流动中用雷诺数判别流动状态。
(2)讨论管内层流流动和管内湍流流动的分析方法、速度分布、切应力分布等。
(3)流动损失(沿程损失和局部损失)及其计算,流动损失的计算归结为求沿程损失因数和局部损失因数。计算时必须首先确定流动状态,然后根据流动状态的特点确定相应的损失因数,进一步确定总的能量损失和压力损失。
(4)以单管的计算为基础,为串、并联管路和管网的计算奠定基础。
思考与练习题
4.1 思考雷诺数的物理意义,并写出直径为d1和d2(d2>d1)的同心圆环的雷诺数的表达式。
4.2 思考产生沿程损失和局部损失的物理原因。
4.3 一等截面的圆管其轴线与水平面的夹角为α,假设流体在其中作定常不可压层流流动,若不考虑圆管进出口的影响,流动可以看做充分发展的管流。试导出管内的速度分布,以及最大速度和单位长度上的压差。
4.4 分别确定水(v=1.13 ×10-6 ㎡/s)和重质柴油(v=205 × 10-6 ㎡/s)以1. 067 m/s 的速度在直径为305 mm的管道中流动时的流动状态。
4.5 直径为多大的管道可以在层流状态下输送qv=5.67 × 10-3m³/s的中质柴油(v=6.08 x 10-6㎡/s)?
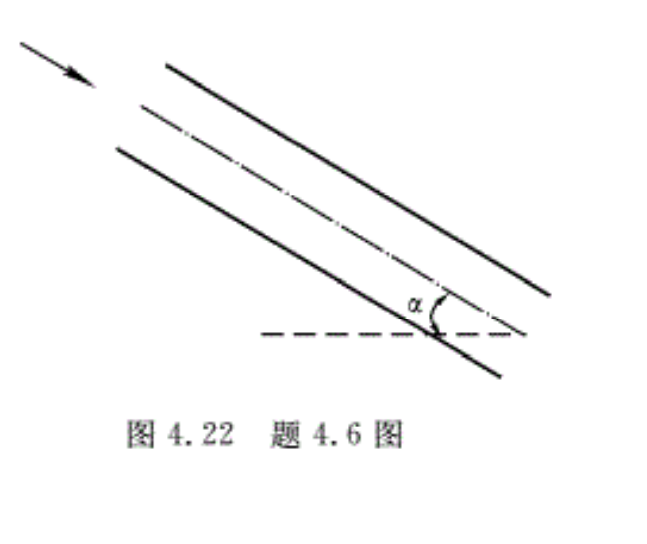
4.6 如图4. 22所示,黏性流体在重力作用下流过斜管,管的半径为ro,α=30°。求:
(1)当管内压力为常数时,定常流动的运动微分方程;
(2)管内的流速分布;
(3)黏性系数与流量qv的关系。
4.7 试证明两无限大固定平行平板间层流流动的平均流速与最大流速之比为2/3。
4.8 水在直径为305 mm的管道中流动时,在300 m 长度上的沿程损失为15m水柱。试求:
(1)管壁上的切应力;(2)离管道中心线51 mm处的切应力,摩擦速度;
(3)当λ=0.05时的平均流速。
4.9 大气压力下20 ℃的水和空气流过同一光滑管道。若沿程损失因数和沿程损失相同,且己知空气的密度为ρ=1.225 kg/m³,求两者的体积流量之比。
4.10 当Re=3500时,光滑管内的流动可能是层流或湍流。设有20 ℃的水流过内径为50.8 mm,长为1. 3 m的光滑管,求:
(1)湍流和层流时的平均流速比;
(2)湍流时的沿程损失;(3)层流时管中心的流速。
4.11 方形光滑管道的边长为a和b,截面积一定,求流过一定流量时,沿程损失最小的a /b值(设流动为层流)。
4.12 设在两个水位不同的水箱之间,在同一高度上用管道连通。若管道的直径为
(1)d;(2)d/2
求层流和湍流时两种管道的流量比(不计局部损失)。
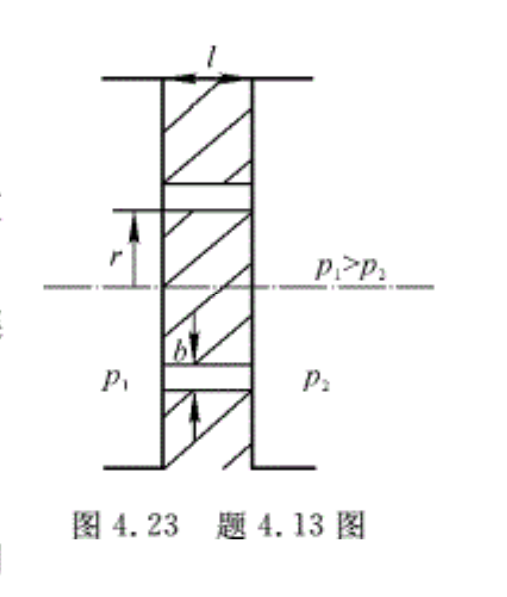
4.13 流体经过如图4. 23所示的环状间隙,自左向右流过,间隙两边的压强为p1和p2。已知p1>p2,设间隙通道的沿程损失因数为λ,进出间隙的局部损失因数为∑ζ,求流过间隙的体积流量。
4.14 流体从容器A经过串联管路1和2到达容器B。已知由容器A到管1的局部损失为ζ1=0.5,管1的长度和直径分别为l1=300 m,d1=0.6 m;∆1=2 mm;管2的长度和直径分别为l2=240 m,d2=1 m,∆2=0.3 mm;流体的运动黏度v=3 x 10-6㎡/ s,两容器的液面差H=6 m。求流过管路的流量。
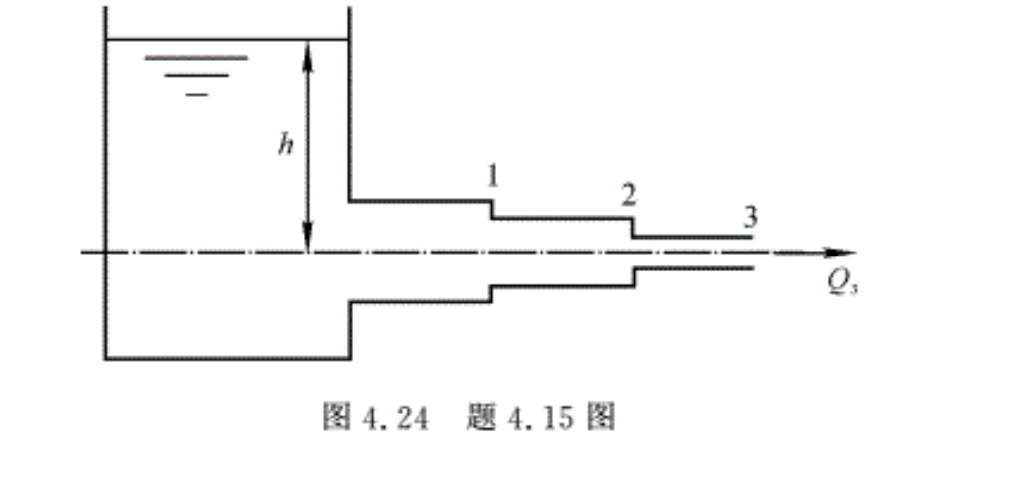
4.15 有一种供水系统由三种不同管道组成,如图4.24所示。已知管径d1=0.3 m,d2=0.2 m ,d3=0.15 m,管长l1=l2=l3=100 m,粗糙度为∆=0.125 mm,水的运动黏度v=1.003 × 10-6㎡ /s。若不计局部损失,求当供水量为q v3=0.05 m³/s时,管道中的沿程损失。
4.16 水电站管路直径D=0.5 m,长L=1000m,水头H=400 m,出口端喷嘴直径d=0.3 m(见图4.25),管路的沿程损失因数λ=0.02,喷嘴的局部损失因数ζ=0.04,不计入口处的局部损失。求:
(1)喷嘴出口流速及流量;
(2)射流功率γqvV²/2g,输水管效率η)指出囗可用动能与流体原有能量之比V²/(2gγH))。
4.17 对沿程均布泄流的管段如图4.26所示。设均布泄流的总量为qv,下游流量为q vT;该段的沿程损失因数λ为常数。试证明该段的沿程损失为
\[{{h}_{Wi}}=S\left( q_{vT}^{2}+{{q}_{vT}}{{q}_{v}}+\frac{q_{v}^{2}}{3} \right)\]
其中, \(S=\frac{\lambda }{d}\frac{l}{2g{{A}^{2}}}\),d为管径,l为管长,A为管截面积。
4.18 由水塔供水的输水管路由三段串联而成,各管段尺寸为:l1=300 m,l2=200 m, l3=100 m,d1=200mm,d2=150 mm,d3=100 mm。沿程损失因数λ=0.03,在l2段内均匀泄流流量qv=20 L/s ,在l3段内流量q vT=10 L/s。求所需水头H。
4.19 油泵以qv=0.070 8 m³/ s的流量通过长L=5000 m和管径d=0.3 m的管路抽送密度ρ=950 kg/m³的重油。试求运动黏度v=1.8cm²/s时的沿程压强损失∆p。



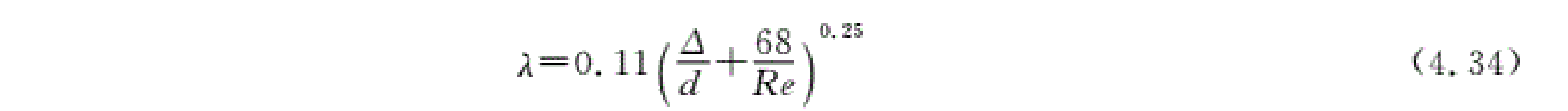






请问非牛顿流体管内流动的压力损失也可以用上述方法进行计算吗?