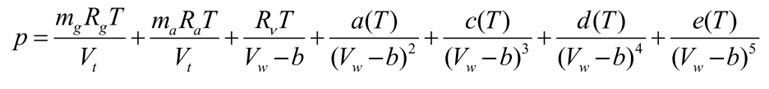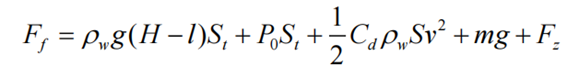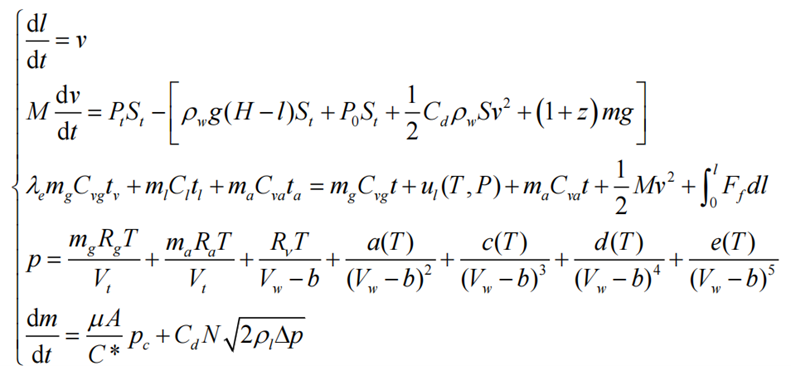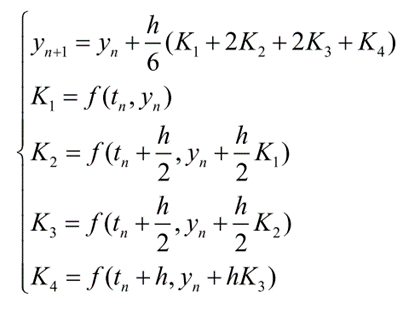燃气蒸汽式水下弹射内弹道仿真数学模型

1 引言

水下弹射内弹道学旨在研究水下弹射过程中运动速度、加速度的变化规律和弹射筒内 混合工质气体状态参数的变化规律，为弹射内弹道的设计和仿真计算提供理论和方法。水 下弹射过程包含多种运动形式，各种运动形式并不孤立存在，而是相互依存、相互制约， 因此需要建立描述水下弹射过程主要现象的基本方程，构成水下弹射内弹道仿真数学模型。

本文介绍了水下弹射动力系统的组成，阐述了水下弹射内弹道调能控制机理，对实际 水下弹射过程进行了分析，并结合内弹道设计基本要求及基本简化假设，介绍了水下弹射 过程的质量守恒方程、能量守恒方程、气体状态方程及弹射运动方程，构成了描述水下弹 射过程的内弹道仿真数学模型，并介绍了水下弹射内弹道仿真计算的基本方法和一般步骤。

2 水下弹射内弹道基础

2.1 动力系统组成

水下弹射动力系统经过一系列的发展，从最初的压缩空气式、液压式，发展到燃气式、燃气-蒸汽式，再到新兴的电磁式和二氧化碳相变式。目前工程上应用最成熟的主要是燃气-蒸汽式动力系统，通过推进剂燃烧产生工质气体膨胀做功，将弹体弹射出筒，为弹体提供稳定的入水初始条件，筒内弹道性能满足相应弹道指标的要求。

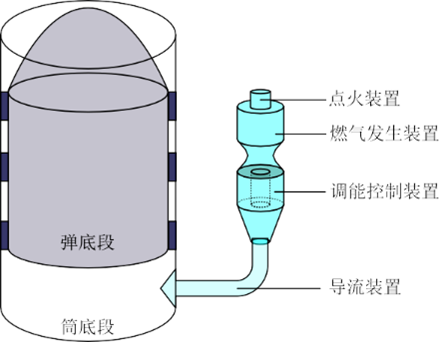
燃气-蒸汽式动力系统由点火装置、燃气发生装置、调能控制装置和导流装置等部分组成，点火装置位于燃气发生装置的顶端，是确保安全可靠点火的重要部件；燃气发生装置通过推进剂燃烧产生大量高温燃气，是产生燃气的动力源；调能控制装置通过控制进入高温燃气流的冷却水量，实现到达筒底段的有用能量的调节。其结构如图 1 所示：

图 1 水下弹射系统示意图

2.2 调能控制机理

为了适应变深度弹射的要求，必须对弹射能量加以控制，使出筒速度满足不同深度弹射时的要求。在燃气发生装置状态确定的情况下，通过改变冷却水量的方法对有用能量加以调节，是实现变深度弹射的有效途径，具有简单可靠、连续可调、容易实现等优点。

燃气—蒸汽弹射动力系统工质气体为燃气、蒸汽以及筒内初始容积中一定量空气组成的混合气体，在弹射过程中混合工质气体的膨胀功就是动力系统的有用能。为探究变能量设计的核心问题，以筒内空间为热力学系统，忽略掉一些量值小的项，能量方程可简化为

如(1)所示：

\({i}_{0}=\alpha{u}_{l}+\int\limits_{{V}_{0}}^{{V}_{e}}{{P}_{c}dV/{m}_{r}+{C}_{vg}{T}_{c}}\)      (1)

式中： \({i}_{0}\)为每 kg 燃气对应的总能量，为定值；\(\alpha{u}_{i}\) 为水蒸汽的比内能； \(\int\limits_{{V}_{0}}^{{V}_{e}}{P}_{c}dV/{m}_{r}\)为参与做功的有用能， C_vgT_c 为燃气的内能。在设计推进剂质量一定的情况下：

增大有用能。减少冷却水量，降低被冷却水吸收汽化的部分能量，水蒸汽的内能减小，即减小αu_l ，筒内的混合工质气体的温度上升，有用能增大。

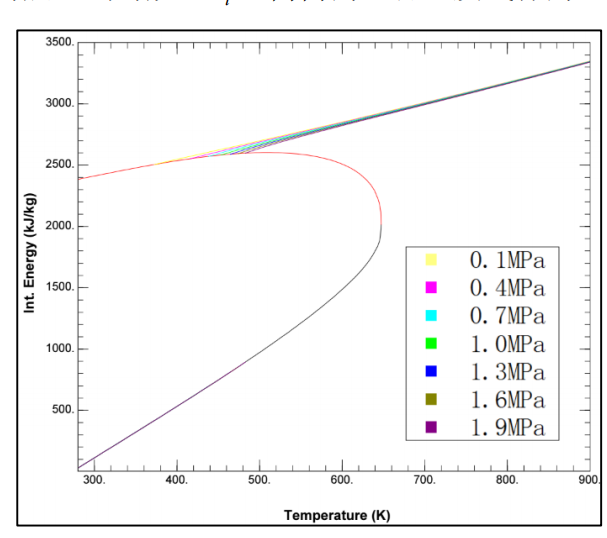
图 2 水蒸汽比内能变化曲线

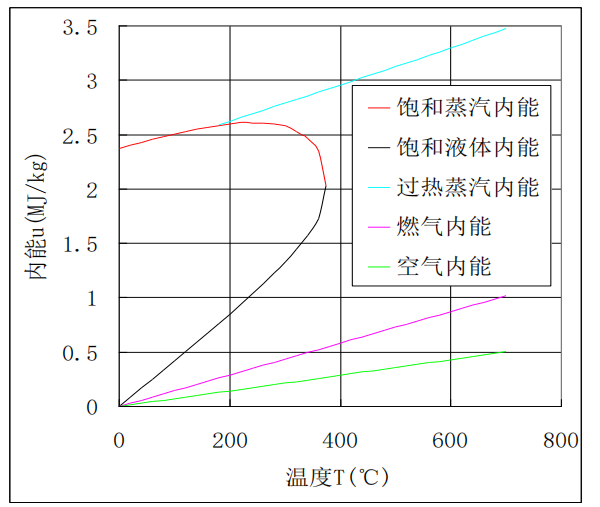
图 3 工质气体比内能变化曲线

减小有用能。增加冷却水量，提高被冷却水吸收汽化的部分能量，水蒸汽的内能增加，即增大aul，筒内的混合工质气体的温度下降，有用能减小。为了研究冷却水量改变对有用能产生的影响，需了解混合工质气体的比内能随温度变化的情况。冷却水又分为液体、饱和蒸汽和过热蒸汽三种状态，其中过热蒸汽的比内能是温度和压强的函数，图2是水蒸汽比内能随着温度和压强变化的情况，由图中可以看出， 压强对过热蒸汽比内能的影响要比温度对其的影响小得多，当压强小于1MPa时，压强对水蒸汽的内能几乎没有影响。图3是冷却水、燃气和空气的比内能随温度变化的情况，图中只画出压强为1MPa的过热蒸汽比内能曲线，从图中可以看出，在相同温度下，无论水处于何种状态，其比内能均远大于燃气和空气的比内能，一般情况下水蒸汽的比内能又远大于液态水的比内能。因此，水蒸汽质量的变化对有用能量的调节起主导作用。

在燃气质量一定的条件下，当冷却水量增加时，一方面会使水蒸汽的质量上升，另一 方面会使混合工质气体的温度降低。混合工质气体的温度降低会导致水蒸汽的比内能减小， 但仍处在很高的水平上，因此水蒸汽的内能主要受本身质量的控制，当冷却水量增加时， 水蒸汽的内能随之增加。虽然筒内燃气的内能由于温度降低也有一定程度的降低，但由于 水蒸汽的内能占比较大（一般为70%以上），弹射动力系统的有用能依然是减小的，因此通 过改变冷却水量是实现对有用能量的调节有效途径。

3 水下弹射过程分析

水下弹射过程伊始，点火装置首先开始工作点燃燃气发生装置内的推进剂，燃气发生 装置内推进剂开始剧烈燃烧产生大量高温燃气，高温燃气在压力作用下流入调能控制装置。调能控制装置内的冷却水与高温燃气相遇，发生掺混、传热和相变等过程，并且在很短时 间内达到接近平衡的状态。在开始阶段，弹射筒内液态水的含量比较高，随着筒内工质燃 气含量的不断增加，液态水含量不断减小，到某一时刻时液态水全部汽化，进入过热状态 阶段。随着燃气和水蒸汽的混合气体通过导流装置进入弹射筒底部的初容空间，燃气和水 蒸汽的混合气体与初容空间内存在的部分空气掺混，筒内压强不断上升，对弹体底部的作 用力也不断增大，当作用力足以克服各种阻力时，推动弹底开始运动并不断加速直至弹射 出发射筒。

通过对水下弹射过程进行分析可以发现水下弹射过程包括若干阶段。按不同方法可以划分为以下几个阶段：

• 按弹体是否运动可以划分为两个阶段

静力学阶段：这一阶段的特点是筒内压力小于起动压力，近似于定容增压过程，混合工质气体的容积保持不变，当筒内压力等于起动压力时该阶段结束。

动力学阶段；这一阶段的特点是筒内压力大于起动压力，混合工质气体的容积逐渐加大，弹射速度从零开始不断加速，直至弹射出弹射筒时该阶段结束。

• 按弹射筒内是否有新的工质气体加入划分为两个阶段

变量气体阶段：这一阶段的特点是不断有新的工质气体加入，弹射筒内混合工质气体的质量不断增加，当弹射动力系统停止工作时，该阶段结束。

定量气体阶段：这一阶段的特点是弹射筒内不再有新的气体加入，弹射筒内的混合工质气体质量基本不变。

3.1 内弹道设计基本要求

水下弹射系统内弹道主要研究水下弹射过程中的运动变化规律和伴随的物理化学现象规律^[52]。运动规律主要有水下弹射过程中加速度、速度随时间的变化规律，以及混合工质气体状态参数随时间的变化规律。伴随的现象包含由于推进剂燃烧而引起的剧烈的化学反应，释放出燃气和能量，并且伴随着水蒸汽的掺混、传热和相变等，以及混合工质气体膨胀做功和能量传递现象。从一般力学范围来看，水下弹射具有瞬态特征。从热力学范围来看，水下弹射过程是一个不可逆过程。

针对整个水下弹射过程，对内弹道设计的基本要求有：

• 水下弹射出筒速度Ve需在允许的速度范围内；
• 水下弹射过程中在弹射筒内运动加速度A 不超过允许值 Atmax ；
• 水下弹射出筒压差DPe不超过允许值DPe_max 。

3.2 基本简化假设

水下弹射系统的实际弹射过程是非常复杂的能量交换和能量转换过程，从抓主要矛盾入手，在建立水下弹射内弹道数学模型时做如下假设：

• 弹射筒内气流无流动，并且把气流沿管路的流动看作是工质能量从动力源向弹射筒的输送过程，弹射内弹道为零维内弹道，假设把弹射筒内工质气体的状态参数按整个弹射筒内的自由容积进行平均，不考虑温度、压强、密度沿长度的变化。
• 燃气和空气按理想气体处理，水蒸汽为实际气体，燃气、空气和水蒸汽之间符合温度函数混合法则，它们无摩擦、无粘性，各自的化学组分与热力性质完全一致。
• 连续进入弹射筒的燃气、水蒸汽和弹射筒内的空气每瞬时都能均匀混合，进行能量交换，形成各点状态参数均匀一致的混合物。
• 混合工质气体的动能和势能为零，在工质气体的总储存能量中，其动能和势能所占的比例非常小，可以忽略不计。
• 不具体考虑燃气气体各组成成分的作用，将燃气视作一个整体发挥作用，也不具体考虑燃气的组分变化及其与水蒸汽、空气之间的化学作用。
• 弹射筒内的热力学过程为绝热、等熵过程，对于工质气体与各个壁面间的对流换热、热传递等热损失，设置相应的能量系数加以修正。
• 将调能控制过程中的参与掺混、传热和相变的最小冷却水量视为定值，并以最小冷却水量单元数N 来描述参与调能控制过程的冷却水量。

3.3 质量守恒方程

弹射筒内的混合工质气体是由燃气、水蒸汽和弹底初始容积内存在的空气三种气体组成的混合气体，准确计算进入弹射筒的各种工质质量是保证弹射内弹道计算准确的基础。弹射筒内混合工质气体的质量守恒关系为弹射筒内混合工质气体的质量变化量等于流入

的气体质量，如式(2)所示：

\(\frac{dm}{dt}={\dot m}_{i}\)    (2) 

式中： m 为弹射筒内混合工质气体的总质量； m& i  为流入弹射筒的质量流量。

设某时刻弹射筒内的燃气、水蒸汽以及空气的质量分别为mg 、m_w 和m_a ，则质量方程可化为式(3)所示：

\(\frac{{m}_{g}}{dt}={\dot m}_{gi}\)

\(\frac{{m}_{a}}{dt}=0\)

\(\frac{{m}_{w}}{dt}={\dot m}_{wi}\)    (3)

其中流入弹射筒的燃气质量流量与推进剂的特征速度、喷管截面面积、燃气弹射装置

内部压强等因素有关，则燃气质量如式(4)所示：

\(\frac{{m}_{g}}{dt}=\frac{{\mu}{A}}{{C}^{*}}{p}_{c}\)         (4) 

式中： m 为压力修正系数； A 为喷管截面面积； C * 为推进剂特征速度； p_c 为燃气发生装置内部压强。

在实际调能控制过程中，将参与调能冷却的最低冷却水量作为最小调能冷却单元，通过控制调能冷却单元数 N 实现对水下弹射过程的调能控制，则水蒸气质量如式(5)所示：

\(\frac{{m}_{w}}{dt}={C}_{d}{N}\sqrt{2{\rho}_{l}{\Delta}{p}}\)     (5)

式中： Cd 为修正系数。

3.4 能量守恒方程

假设某时刻有 mg kg 燃气流经调能冷却装置与 m_l kg 冷却水掺混再进入弹射筒内和m_akg 空气混合，并对外做功W 。根据上文基本假设，混合工质气体瞬时均匀混合，对外作膨胀功，则根据热力学第一定律建立能量守恒方程如式(6)所示：

\({U}_{1}+Q={U}_{2}+W\)       (6）

方程左边，U₁ 为mg kg 燃气、 m_l kg 和m_akg 空气具有的初态能量，如式(7)所示：

U₁ = U_g1 +U_l1 +U_a1 = m_gC_vgt_v + m_lC_lt_l + m_aC_vat_a      (7)

Q 表示对外热耗散损失的能量，根据基本假设引入能量损失系数修正，则能量守恒方程左边如式(8)所示：

U₁ + Q = U_g1 +U_l1 +U_a1 + Q = l_em_gC_vgt_v + m_lC_lt_l + m_aC_vat_a      (8)

方程右边，U₂ 为mg kg 燃气、 m_l kg 和m_akg 空气具有的末态能量，如式(9)所示：

U₂ = U_g 2 +U_l 2 +U_a2 = m_gC_vgt + u_l (T , P) + m_aC_vat    (9)

式中，u_l(T , P) 为某温度和压强下水蒸汽的能量，可通过查饱和水蒸汽热力性质表得到。W 表示热力系统膨胀做功，表现为克服阻力所做功与动能之和，如式(10)所示：

\(W=\int_{1}^{2}{{p}dV}=\frac{1}{2}M{v}^{2}+\int_{0}^{1}{{{F}_{f}}dl}\)    （10）

可得能量守恒方程如式(2-11)所示：

   （11）

3.5 气体状态方程

混合工质气体中燃气和空气为理想气体，可直接应用理想气体状态方程描述工质气体的状态，水蒸气为实际气体，应用马丁-侯实际气体状态方程来描述其气体状态，因此混合工质气体的状态方程如式(12)所示：

（12）

3.6 弹射运动方程

根据水下弹射过程的基本简化假设，由牛顿第二定律有弹射运动方程如式(13)所示：

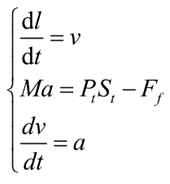     （13）

式中： S_t 为弹底截面积； Ff 为运动阻力。

水下弹射过程中受到的运动阻力有重力、摩擦力^[54]、静水压力和流体阻力，则弹射运动方程如式(14)所示：

  （14） 

4 内弹道方程组及其解法

4.1 内弹道方程组

根据上文各节推导出的各个方程，则得到水下弹射内弹道方程组如式(15)所示：

(15)

方程组中含有l, v, m, p,T 共五个独立变量，变量数等于方程数，因此内弹道方程组是封闭的，可以求解。

4.2 内弹道计算基本方法及步骤

涉及到的常微分方程常用龙格-库塔方法进行近似求解，给定时间步长和时间终点就可求出所需各变量在每一时刻的数值解，并且画出相应的曲线图形。设初值 y ‘ =dy/dt= f (t, y ) ，y (t₀ ) = y₀ ，四阶经典 Runge-Kutta 计算公式如式(16)所示：

(16)

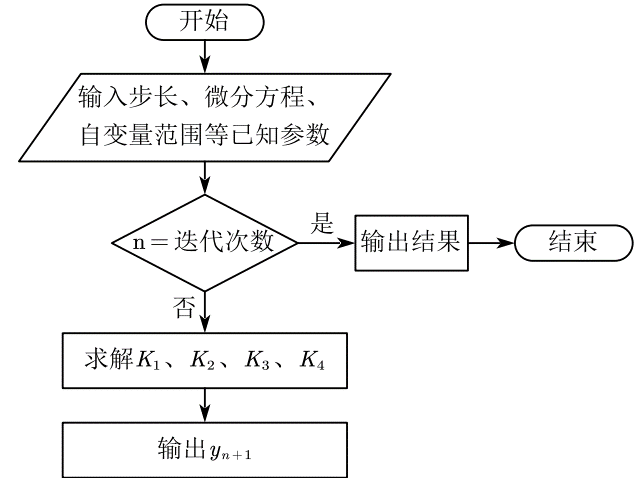
四阶经典 Runge-Kutta 算法流程图如图 4 所示：

图 4 四阶 Runge-Kutta 公式求解流程图

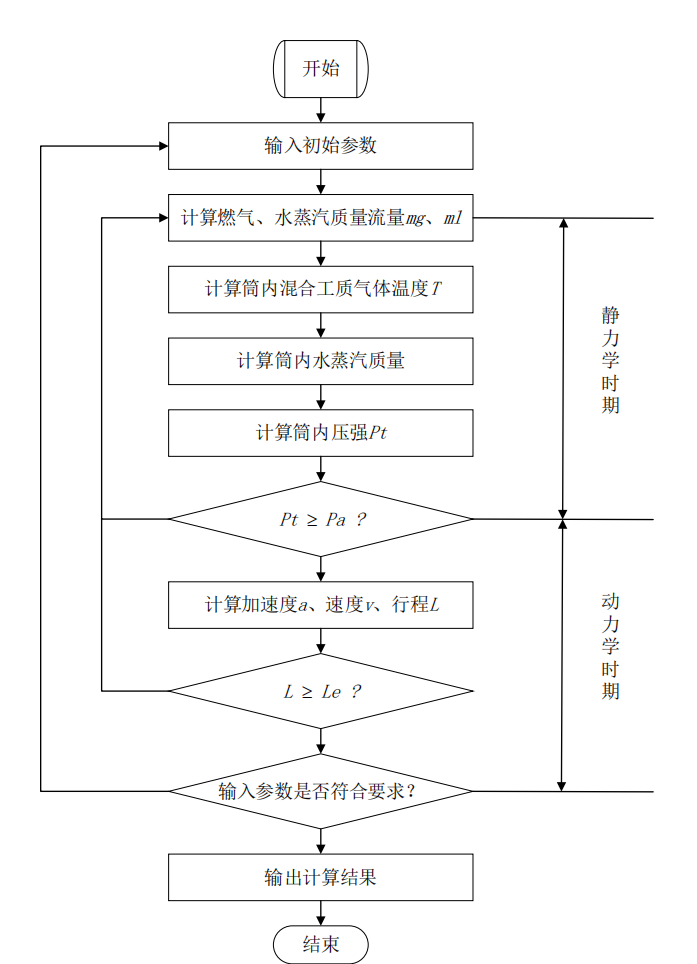
利用质量守恒方程、能量守恒方程、气体状态方程、弹射运动方程构建内弹道方程组， 采用适当的求解方法，即可计算出筒内混合工质气体的温度、水蒸汽质量、压强，以及水下弹射过程中的速度、加速度以及位移随时间变化的规律。水下弹射内弹道计算流程如图

图 5 水下弹射内弹道计算流程图

5 小结

本文介绍了水下弹射动力系统的组成，分析了水下弹射内弹道调能控制机理，基于燃气-蒸汽式弹射做功机理及实际水汽掺混过程，对水下弹射实际物理过程进行了基本简化假设，通过水下弹射过程中的质量守恒方程、能量守恒方程、气体状态方程及弹射运动方程， 构成了描述水下弹射过程的内弹道仿真数学模型，并介绍了水下弹射内弹道仿真计算的基本方法和一般步骤，为数值仿真计算、内弹道参数敏感度分析的开展、内弹道调能控制品质的综合评价以及调能控制的多目标优化提供了计算基础和理论支撑。