第三章流体动力学基本方程和基本概念
本章讲述流体动力学的基本知识、基本原理和基本方程,是整个课程的重点。首先讨论流体运动的数学描述、几何表示方法和基本概念;其次讨论流体微团的运动和变形;最后讨论流体动力学的基本方程。由于流体动力学涉及的内容广泛,因此以后各章内容均与本章内容有一定的联系。
3.1 描述流体运动的两种方法及基本概念
3.1.1 系统和控制体
在分析流体运动时,主要有两种方式。一种是描述流场中每一个点的流动细节,另一种是针对一个有限区域,通过研究某物理量流入和流出的平衡关系来确定总的作用效果,如作用在这个区域上的力、力矩、能量交换等等。其中,前一种方法也称为微分方法,而后者则被称为积分方法或“控制体”方法。
力学的基本物理定律都是针对一定的物质对象来陈述的。在流体力学中,这个对象就是系统(System)。所谓系统,是指某些确定的物质集合。系统以外的物质称为环境。系统的边界定义为把系统和环境分开的假想表面,在边界上可以有力的作用和能量的交换,但没有质量的通过。系统的边界随着流体一起运动。
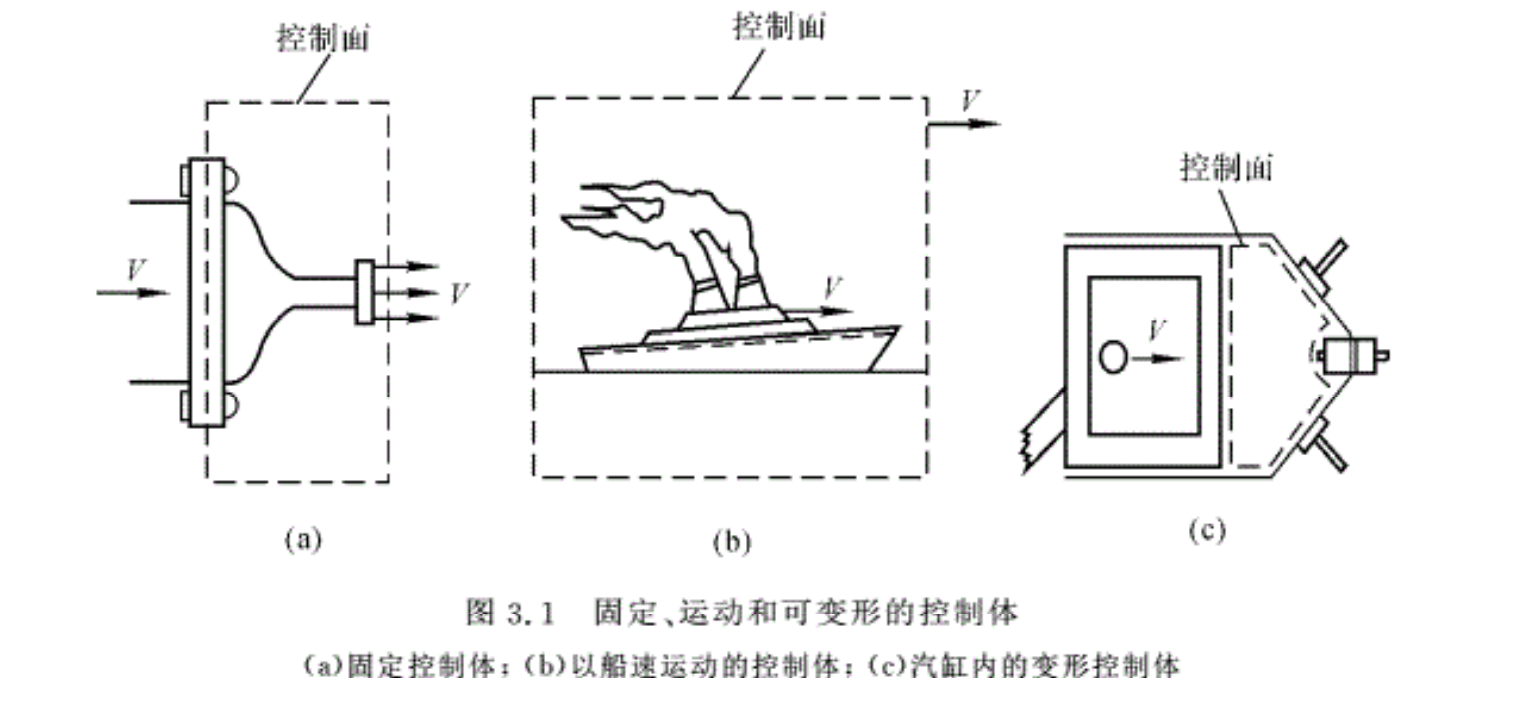
在流体动力学中,因为流体运动的复杂性,对于任何有限长的时间,很难确定流体系统的边界,因此,采用系统的分析方法一般情况下是比较困难的。在实际研究中,人们往往需要研究的是某一个特定的流动区域,在这个区域中流体和所研究的对象发生作用,例如,建筑物受到的风载、活塞受到的流体压力、飞行物的升力和阻力等等。因此提出了控制体的分析方法。所谓控制体(control volume),是指流体流过的、固定在空间的一个任意体积,占据控制体的流体是随时间改变的,控制体的边界称为控制面(control surface),它总是封闭的表面。通过控制面,可以有流体流入或流出。在控制面上可以有力的作用和能量的交换。引入了控制体的概念后,在分析问题时,就可以把注意力放在所确定的控制体上,研究流体流过控制体时诸参数的变化情况,以及控制体内流体与控制体外物质的相互作用。根据所研究对象的运动情况,控制体主要有三种类型,分别为静止、运动和可变形,其中,前两种控制体为固定形状,如图3.1 所示。本书主要考虑刚性的、没有运动的控制体。
3.1.2 描述流体运动的两种方法
目前,研究流体运动有两种不同的观点,因而形成两种不同的方法。一种方法是从分析流体各个质点的运动着手,即跟踪流体质点的方法来研究整个流体的运动,称之为拉格朗日法;另一种方法则是从分析流体所占据的空间中各固定点处流体的运动着手,即设立观察站的方法来研究流体在整个空间里的运动,称其为欧拉法。在理论力学中,以质点、质点系和刚体为研究对象,在流体力学中,以流体为研究对象。由于流体无固定的形状,因而研究流体要复杂得多。对于表征运动流体的各物理量,诸如流体质点的速度、速度、压强、密度、温度等统称为流体的流动参数。描述流体的运动即是要研究流体流动参数随时间和空间的变化规律。要研究流体运动,就要解决用什么方法描述流体的运动问题。这就是下面要解决的问题。
1.拉格朗日(Lagrange)法
用拉格朗日法研究流体运动时,着眼点是流体质点。其实质就是研究个别流体质点的速度、加速度、压强和密度等参数随时间t的变化,以及由某一流体质点转向另一流体质点时这些参数的变化,然后再把全部流体质点的运动情况综合起来,就得到整个流体的运动情况。此法实质上就是质点动力学研究方法的延续。
通常利用初始时刻流体质点的坐标来标注不同流体质点的坐标。设初始时刻流体质点的坐标是(a,b,c),不同的(a,b,c)代表不同的流体质点。显然质点的空间位置不但与时间有关,而且还与该质点起始时刻的空间位置有关。于是t时刻任意流体质点的位置在空间的坐标可表示为
x=f1(a,b,c,t) (3.1)
y=f2(a,b,c,t) (3.1)
z=f3(a,b,c,t) (3.1)
式中,(a,b,c)称为拉格朗日坐标,(a,b,c,t)称为拉格朗日变数。拉格朗日变数是各自独立的,质点的初始坐标(a,b,c)与t无关,t仅影响运动坐标、速度和加速度。显然,流体质点不管什么时候运动到哪里,拉格朗日坐标并不改变。
当(a,b,c)一定时,式(3.1 )代表某个流体质点的运动轨迹,代表t时刻流体质点所处的位置。因此,任一流体质点的速度和加速度均可表示为
\(\left. \begin{align}
& {{V}_{x}}=\frac{\partial x}{\partial t}=\frac{\partial {{f}_{1}}\left( a,b,c,t \right)}{\partial t} \\
& {{V}_{y}}=\frac{\partial y}{\partial t}=\frac{\partial {{f}_{2}}\left( a,b,c,t \right)}{\partial t} \\
& {{V}_{z}}=\frac{\partial z}{\partial t}=\frac{\partial {{f}_{3}}\left( a,b,c,t \right)}{\partial t} \\
\end{align} \right\rangle
\) (3.2)
\(\left. \begin{align}
& {{a}_{x}}=\frac{\partial {{V}_{x}}}{\partial t}=\frac{\partial _{{}}^{2}{{f}_{1}}\left( a,b,c,t \right)}{\partial \text{t}_{{}}^{2}} \\
& {{a}_{y}}=\frac{\partial {{V}_{y}}}{\partial t}=\frac{\partial _{{}}^{2}{{f}_{2}}\left( a,b,c,t \right)}{\partial t_{{}}^{2}} \\
& {{a}_{z}}=\frac{\partial {{V}_{z}}}{\partial t}=\frac{\partial _{{}}^{2}{{f}_{3}}\left( a,b,c,t \right)}{\partial t_{{}}^{2}} \\
\end{align} \right\rangle
\) (3.3)
式中采用求偏导数是因为fi同时是时间t和质点标号(即质点初始位置坐标(a,b,c))的函数,而在求导数时要求a,b,c不变,即求导是针对同一流体质点所作的。
用拉格朗日方法来研究流体运动时,由于该方法研究的是各个流体质点的运动,对于由无穷多个流体质点所构成的流体来说,往往会遇到数学上的困难,所以一般很少采用,只有在研究像流体的波动、振动等某些问题时才使用。
2.欧拉(Euler)法
采用欧拉法研究流体运动,其着眼点是流场中的空间点即着眼于控制体。其实质是研究运动流体所占空间中某固定空间点流体的速度、压强和密度等物理量随时间的变化,以及找出任意相邻空间点之间这些物理量的变化关系,即分析由空间某一点转到另一点时流动参数的变化,从而得出整个流体的运动情况。可见,用欧拉法不需要注意各个流体质点的运动过程,而是研究运动流体所占空间各点的流体参数的变化;研究一切描述流体运动的物理参数在空间的分布,即研究各流动参数的场,如速度场、压强场、密度场等向量场和标量场。所以,数学中的连续数和场论知识是欧拉法的强有力的工具。
在欧拉法中,用流体质点的空间坐标(x,y,z)与时间变量t来表达流体的运动规律,(x,y,z)叫欧拉变数。欧拉变数不是各自独立的,因为流体质点在场中的空间位置x,y,z与时间t有关,不同的时间t,流体质点有不同的空间坐标。因此,对于任一个流体质点的位置变量x,y,z都是时间t的函数,即
x=x(t) (3.4)
y=y(t) (3.4)
z=z(t) (3.4)
设Vx,Vy,Vz分别代表流体质点的速度V在x,y,z轴上的分量,则
\(\left. \begin{align}
& {{V}_{x}}=\frac{dx}{dt}={{V}_{x}}\left( x,y,z,t \right) \\
& {{V}_{y}}=\frac{dy}{dt}={{V}_{y}}\left( x,y,z,t \right) \\
& {{V}_{z}}=\frac{dz}{dt}={{V}_{z}}\left( x,y,z,t \right) \\
\end{align} \right\rangle
\) (3.5)
式(3.5)表示在空间点(x,y,z)处t时刻的流体速度。这个速度是某一流体质点的速度,即在t时刻运动到空间点(x,y,z)处的那个流体质点的速度。
同样,压强、温度和密度等物理量都可以表示x,y,z,t的函数。
应该强调的是,由于某个时刻在空间点(x,y,z)上必有一个流体质点占据,因此用欧拉法描述的物理量实际上是占据该空间点的流体质点的物理量。
用欧拉法描述实际上最终提供了一切物理量的场,如速度场、压强场、温度场等等,因此可以使用数学中有关场论的数学工具。所以在流体力学中,欧拉法得到了广泛的应用。
例3.1 分别用拉格朗日法和欧拉法求流体质点的速度。
\(\begin{align}
& x=-t-1+{{c}_{1}}e_{{}}^{t} \\
& y=t-1+{{c}_{2}}e_{{}}^{-t} \\
\end{align}
\)
解:用拉格朗日法求解。当t=0时,对应流体质点的坐标为(a,b),代入上式得
c1=a+1 c2=b+1
因此,用拉格朗日法描述的流体质点的坐标为
\(\left\{ \begin{align}
& x=-t-1+\left( a+1 \right)e_{{}}^{t} \\
& y=t-1+\left( b+1 \right)e_{{}}^{-t} \\
\end{align} \right.
\)
流体质点的速度和加速度分别为
\(\left\{ \begin{align}
& {{V}_{x}}=\frac{\partial x}{\partial t}=-1+\left( a+1 \right)e_{{}}^{t} \\
& {{V}_{y}}=\frac{\partial y}{\partial t}=1-\left( b+1 \right)e_{{}}^{-t} \\
\end{align} \right.
\)
\(\left. \begin{align}
& {{a}_{x}}=\frac{\partial {{V}_{x}}}{\partial t}=\left( a+1 \right)e_{{}}^{t} \\
& {{a}_{y}}=\frac{\partial {{V}_{y}}}{\partial t}=\left( b+1 \right)e_{{}}^{-t} \\
\end{align} \right\}
\) (a)
用欧拉法求解。流体质点的速度为
\(\begin{align}
& {{V}_{x}}=\frac{dx}{dt}=-1+{{c}_{1}}e_{{}}^{t}=t+x \\
& {{V}_{y}}=\frac{dy}{dt}=1-{{c}_{2}}e_{{}}^{-t}=t-y \\
\end{align}
\)
流体质点的加速度可根据多元函数微分法则对速度求导得到,即
\(\left. \begin{align}
& {{a}_{x}}=\frac{d{{V}_{x}}}{dt}=\frac{\partial {{V}_{x}}}{\partial t}+{{V}_{x}}\frac{\partial {{V}_{x}}}{\partial x}+{{V}_{y}}\frac{\partial {{V}_{x}}}{\partial y}+{{V}_{z}}\frac{\partial {{V}_{x}}}{\partial z}=1+x+t={{c}_{1}}e_{{}}^{t} \\
& {{a}_{y}}=\frac{d{{V}_{y}}}{dt}=\frac{\partial {{V}_{y}}}{\partial t}+{{V}_{x}}\frac{\partial {{V}_{y}}}{\partial x}+{{V}_{y}}\frac{\partial {{V}_{y}}}{\partial y}+{{V}_{z}}\frac{\partial {{V}_{y}}}{\partial z}=1+y-t={{c}_{2}}e_{{}}^{-t} \\
\end{align} \right\}
\) (b)
可见,式(a)和式(b)是一致的。
式(a)表示初始时刻坐标为(a,b)的那个流体质点在给t(给定)时刻的加速度,而式(b)给出的加速度则表示t(给定)时刻的加速度在空间的分布。当空间点给定时,表示位于该空间点的流体质点不同时刻的加速度,不同的空间点有不同的速度。因此,我们并不关心是哪个流体质点的加速度,而是关心加速度在空间的分布,这就是欧拉法的描述方法。
3.1.3 随流导数
1.随流导数
在流动过程中,流体质点的各物理量随时间的变化率称为相应物理量的随流导数,也称为随体导数或质点导数。例如,流体质点的加速度是流体质点速度随时间的变化率。随流导数意味着跟随流体质点运动时观测到的质点物理量随时间的变化率。
在拉格朗日法中,物理量的随流导数是跟随质点(a,b,c)的物理量随时间的导数,这时(a,b,c)是不变的。例如,速度是矢径r(a,b,c,t)对时间的偏导数,加速度是速度对时间的偏导数,即
\(V\left( a,b,c,t \right)=\frac{\partial r\left( a,b,c,t \right)}{\partial t}\) (3.6)
\(a\left( a,b,c,t \right)=\frac{\partial V\left( a,b,c,t \right)}{\partial t}\) (3.7)
可见,在拉格朗日法中随流导数是偏导数。
在欧拉法中,随流导数必须是跟随t时刻位于空间点(x,y,z)上的那个流体质点的物理量随时间的变化率(该物理量是同一流体质点而非同一空间点)。由于流体质点是运动的,因此,流体质点的空间位置x,y,z是变化的,可见该物理量的随流导数是d/dt。若该物理量用N(x,y,z,t)表示,则N的随流导数为
\(\frac{d}{dt}N\left( x,y,z,t \right)=\frac{\partial N}{\partial x}\frac{dx}{dt}+\frac{\partial N}{\partial y}\frac{dy}{dt}+\frac{\partial N}{\partial z}\frac{dz}{dt}+\frac{\partial N}{\partial t}=\frac{\partial N}{\partial x}{{V}_{x}}+\frac{\partial N}{\partial y}{{V}_{y}}+\frac{\partial N}{\partial z}{{V}_{z}}+\frac{\partial N}{\partial t}=\frac{\partial N}{\partial t}+\left( V\bullet \nabla \right)N\) (3.8)
式中 \(\frac{d}{dt}=\frac{\partial }{\partial t}+{{V}_{x}}\frac{\partial }{\partial x}+{{V}_{y}}\frac{\partial }{\partial y}+{{V}_{z}}\frac{\partial }{\partial z}\)
\(\nabla =i\frac{\partial }{\partial x}+j\frac{\partial }{\partial y}+k\frac{\partial }{\partial z}\)
式(3.8)表明,用欧拉法求质点物理量的随流导数由两项构成。第一项是∂N/∂t,表示在给定点上物理量N随时间的变化率,称为局部导数或当地导数。它是由于流动的非定常性引起的,对定常流,该项等于零。第二项(V∙▽)N,表示物理量N在空间分布不均匀的情况下,流体质点运动时引起N的变化率,称为对流导数或迁移导数。它是在非均匀的流场中(有梯度▽N)由空间位置变化引起的。该项反映了流场的非均匀性,对于均匀流场,该项为零。
在圆柱坐标系中,随流导数的表达式为
\(\begin{align}
& \frac{dN}{dt}=\frac{\partial N}{\partial t}+\left[ {{V}_{r}}\frac{\partial N}{\partial r}+\frac{{{V}_{\theta }}}{r}\frac{\partial N}{\partial \theta }+{{V}_{z}}\frac{\partial N}{\partial z} \right] \\
& \nabla ={{i}_{r}}\frac{\partial }{\partial r}+{{i}_{\theta }}\frac{\partial }{r\partial \theta }+{{i}_{z}}\frac{\partial }{\partial z} \\
\end{align}
\)
对于不可压缩流体,流体质点在运动过程中密度保持不变,因此它的随流导数等于零,即dρ/dt=0。它表示每个流体质点的密度在流动过程中保持不变,但不同的流体质点密度可以互不相同,所以dρ/dt=0并不意味着整个流场的密度为常数。只有均质不可压缩流体,其密度才处处相等,即ρ=C。
对于可压缩流体,一般情况下dρ/dt≠0,但∂ρ/∂t可以等于零,即表示空间各点流体质点的密度不随时间变化。
由随流导数的定义式可以看出,流动参数的随流导数把该参数的瞬时变化率与流场中该参数的导数联系起来了。在欧拉法描述中,特性场是直接可以利用的,所以随流导数在拉格朗日法与欧拉法之间建立了一种联系。由以上讨论可知,随流导数是对流体质点的,它反映了流体质点物理量随时间的变化率,因此随流导数本质上是拉格朗日观点下的概念。
2.速度的随流导数(加速度)
将式(3.8)中的N用流体质点的速度代入得到流体质点运动的加速度。它表示流体质点沿迹线运动时的速度变化率。加速度矢量形式的表达式为
a=dV/dt=∂V/∂t=(V·▽)V (3.9)
由式(3.9)可见,速度的随流导数由两部分组成。
(1) ∂V/∂t一一局部加速度或当地加速度。它表示在固定空间点上(流体质点没有空间位置变化)流体质点的运动速度对时间的变化率。它是由流场的非定常性引起的。显然,对于定常流动,该项等于零。
(2)(V∙▽)V一一一对流加速度或迁移加速度。它表示流体质点经过dt时间运动到不同的位置时,质点速度对时间的变化率,即流体质点位置改变引起的速度变化率。它是由流场的不均匀性引起的。对于均匀流动该项等于零。
同样质点的其他物理量如压强、温度和密度等,都有其相应的随流导数。
对于直角坐标系,流体质点运动速度可表示为
V=Vxi+Vyj+Vzk
根据速度的随流导数(或从多元函数微分法)可知,通过流场中某点的流体质点的加速度在直角坐标系中表示为
\(\left. \begin{align}
& {{a}_{x}}=\frac{d{{V}_{x}}}{dt}=\frac{\partial {{V}_{x}}}{\partial t}+{{V}_{x}}\frac{\partial {{V}_{x}}}{\partial x}+{{V}_{y}}\frac{\partial {{V}_{x}}}{\partial y}+{{V}_{z}}\frac{\partial {{V}_{x}}}{\partial z} \\
& {{a}_{y}}=\frac{d{{V}_{y}}}{dt}=\frac{\partial {{V}_{y}}}{\partial t}+{{V}_{x}}\frac{\partial {{V}_{y}}}{\partial x}+{{V}_{y}}\frac{\partial {{V}_{y}}}{\partial y}+{{V}_{z}}\frac{\partial {{V}_{y}}}{\partial z} \\
& {{a}_{z}}=\frac{d{{V}_{z}}}{dt}=\frac{\partial {{V}_{z}}}{\partial t}+{{V}_{x}}\frac{\partial {{V}_{z}}}{\partial x}+{{V}_{y}}\frac{\partial {{V}_{z}}}{\partial y}+{{V}_{z}}\frac{\partial {{V}_{z}}}{\partial z} \\
\end{align} \right\}
\) (3.10)
对于圆柱坐标系,\(V={{V}_{r}}{{i}_{r}}+{{V}_{\theta }}{{i}_{\theta }}+{{V}_{z}}{{i}_{z}}\),代入式(3.9),并考虑到ir,iθ的方向在不断变化可得流体质点的加速度为
\(\left. \begin{align}
& {{a}_{r}}={{\left( \frac{dV}{dt} \right)}_{r}}=\frac{\partial {{V}_{r}}}{\partial t}+{{V}_{r}}\frac{\partial {{V}_{r}}}{\partial r}+{{V}_{\theta }}\frac{\partial {{V}_{r}}}{r\partial \theta }+{{V}_{z}}\frac{\partial {{V}_{r}}}{\partial z}-\frac{V_{\theta }^{2}}{r}=\frac{d{{V}_{r}}}{dt}-\frac{V_{\theta }^{2}}{r} \\
& {{a}_{\theta }}={{\left( \frac{dV}{dt} \right)}_{\theta }}=\frac{\partial {{V}_{\theta }}}{\partial t}+{{V}_{r}}\frac{\partial {{V}_{\theta }}}{\partial r}+{{V}_{\theta }}\frac{\partial {{V}_{\theta }}}{r\partial \theta }+{{V}_{z}}\frac{\partial {{V}_{\theta }}}{\partial z}+\frac{{{V}_{r}}V_{\theta }^{{}}}{r}=\frac{d{{V}_{\theta }}}{dt}+\frac{{{V}_{r}}V_{\theta }^{{}}}{r} \\
& {{a}_{z}}={{\left( \frac{dV}{dt} \right)}_{z}}=\frac{\partial {{V}_{z}}}{\partial t}+{{V}_{r}}\frac{\partial {{V}_{z}}}{\partial r}+{{V}_{\theta }}\frac{\partial {{V}_{z}}}{r\partial \theta }+{{V}_{z}}\frac{\partial {{V}_{z}}}{\partial z}=\frac{d{{V}_{z}}}{dt} \\
\end{align} \right\}
\) (3.11)
在圆柱坐标系中,加速度有如下特点.
(1)径向加速度由两项组成:\(\frac{d{{V}_{r}}}{dt}\)表示径向速度分量的随流导数;\(-\frac{V_{\theta }^{2}}{r}\)表示流体质点作圆周运动时产生的向心加速度,向心加速度指向转动中心,与r方向相反。
(2)周向加速度也由两项组成:\(\frac{d{{V}_{\theta }}}{dt}\)表示周向速度分量的随流导数;\(\frac{{{V}_{r}}V_{\theta }^{{}}}{r}\)表示流体质点以Vθ作圆周运动时,径向速度分量Vr,因圆周运动改变方向使得流体质点沿周向产生的附加加速度。
(3)轴向加速度:由于圆柱坐标系的z轴与直角坐标系中的z轴重合,因此z轴方向的加速度分量表达式相同。
从以上分析可知,在拉格朗日法中,(x,y,z)是指一个流体质点在空间的位置坐标,而欧拉法中的(x,y,z)则是空间点的坐标,不同时刻有许多不同的流体质点通过。
由于欧拉法比拉格朗日法要优越得多,所以在流体力学的研究中多用欧拉法。在本课程中,都采用欧拉法。
例3.2 已知用拉格朗日法表示的质点坐标
\(x=ae_{{}}^{t}y=be_{{}}^{-t}\)
试求流体质点的速度和加速度。
解:拉格朗日法描述的速度和加速度分别为
\({{V}_{x}}=\frac{\partial x}{\partial t}=ae_{{}}^{t},{{V}_{y}}=\frac{\partial y}{\partial t}=-be_{{}}^{-t}\) (a)
\({{a}_{x}}=\frac{\partial {{V}_{x}}}{\partial t}=ae_{{}}^{t},{{a}_{y}}=\frac{\partial {{V}_{y}}}{\partial t}=be_{{}}^{-t}\) (b)
用欧拉法描述的速度和加速度分别如下:
根据己知条件得
\(a=xe_{{}}^{-t}b=ye_{{}}^{t}\)
则将a,b代入式(a),式(b),得
\(\begin{align}
& {{V}_{x}}=\frac{dx}{dt}=ae_{{}}^{t}=x{{V}_{y}}=\frac{dy}{dt}=-be_{{}}^{-t}=-y \\
& {{a}_{x}}=\frac{d{{V}_{x}}}{dt}=ae_{{}}^{t}=x{{a}_{y}}=\frac{d{{V}_{y}}}{dt}=be_{{}}^{-t}=y \\
\end{align}
\)
也可由式(3.10),得
\(\begin{align}
& {{a}_{x}}=\frac{\partial {{V}_{x}}}{\partial t}+{{V}_{x}}\frac{\partial {{V}_{x}}}{\partial x}+{{V}_{y}}\frac{\partial {{V}_{x}}}{\partial y}=x \\
& {{a}_{y}}=\frac{\partial {{V}_{y}}}{\partial t}+{{V}_{x}}\frac{\partial {{V}_{y}}}{\partial x}+{{V}_{y}}\frac{\partial {{V}_{y}}}{\partial y}=y \\
\end{align}
\)
例3. 3 已知用欧拉法表示的速度为
\({{V}_{x}}=e_{{}}^{\left( x+1 \right)t}{{V}_{y}}=e_{{}}^{\left( y+1 \right)t}\)
试确定流体质点在位置(1,1) ,当t =0时的加速度。
解:由
\(\begin{align}
& {{a}_{x}}=\frac{\partial V_{x}^{{}}}{\partial t}+{{V}_{x}}\frac{\partial V_{x}^{{}}}{\partial x}+{{V}_{y}}\frac{\partial V_{x}^{{}}}{\partial y} \\
& {{a}_{y}}=\frac{\partial V_{y}^{{}}}{\partial t}+{{V}_{x}}\frac{\partial V_{y}^{{}}}{\partial x}+{{V}_{y}}\frac{\partial V_{y}^{{}}}{\partial y} \\
\end{align}
\)
得
\(\begin{align}
& {{a}_{x}}=e_{{}}^{\left( x+1 \right)t}\left[ x+1+te_{{}}^{\left( x+1 \right)t} \right] \\
& {{a}_{y}}=e_{{}}^{\left( y+1 \right)t}\left[ y+1+te_{{}}^{\left( y+1 \right)t} \right] \\
\end{align}
\)
将x=1 , y=1和t=0代入上式,得
\({{a}_{x}}=2{{a}_{y}}=2\)
例3.4 通过一收敛喷管的流场可以用一维速度分布V=Vo(1+2x/L)来近似,式中, L 为喷管长度,Vo为入口速度,出囗速度为V=3Vo。试求:
( 1 )加速度分布;
( 2 )若入口速度Vo=10m/ s , L=1 m ,试求进、岀口的加速度。
解:该流动为一维流动,且V与时间无关。
( 1 )求加速度即求速度的随流导数,因此有
\(\frac{dV}{dt}=V\frac{\partial V}{\partial x}={{V}_{0}}\left( 1+2x/L \right)2{{V}_{0}}/L\)
由此可以看出,即使流动是定常流动,流体加速度并不为零。
( 2 )入囗处x=0 ,将Vo , L代入上式得进口的加速度为
\({{\left( \frac{dV}{dt} \right)}_{x=0}}=V\frac{\partial V}{\partial x}=2V_{0}^{2}/L=200m/s_{{}}^{2}\)
出口处x=L ,加速度为
\({{\left( \frac{dV}{dt} \right)}_{x=L}}={{V}_{0}}\left( 1+2 \right)2{{V}_{0}}/L=\frac{6V_{0}^{2}}{L}=3{{\left( \frac{dV}{dt} \right)}_{x=0}}=600m/s_{{}}^{2}\)
3.1.4 迹线、流线、流管和脉线
为了清楚地了解流场的详细情况,常用流场的几何表示方法,它能帮助我们直观形象地分析流体运动。常用到的有迹线、流线和流管等概念。
1.迹线
任何一个流体质点在空间中的运动轨迹,称为迹线。或者说,迹线是同一个流体质点,在不同时刻的空间坐标的连线,显然,如果流体的运动是以拉格朗日变数给岀的,那么流场的描述则由迹线给岀。
2.流线和流管
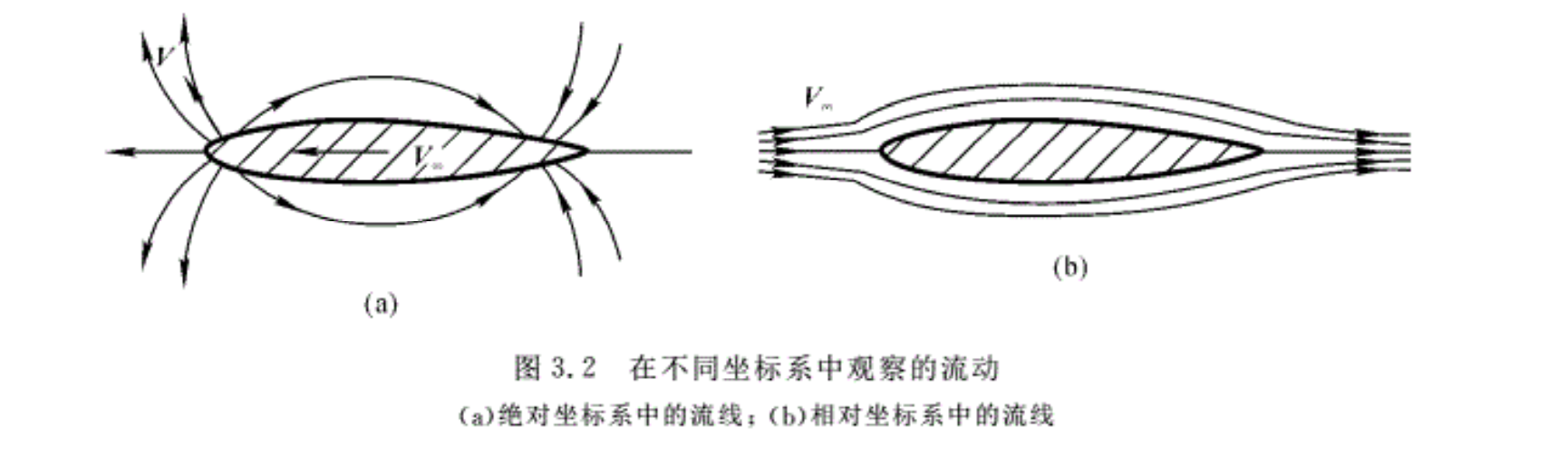
用欧拉法研究流体运动时,流线的概念相当重要。所谓的流线是指在给定的瞬时t,流场中位于流线上的各流体质点的速度向量均与曲线在相应点的切线相重合。换句话说,在给定的瞬时t ,流线上任一点的切线方向与位于该点流体质点的速度方向一致。图3.2表示的是对于同一种流动在不同坐标系中的流线。图3.2(a)表示在绝对坐标系中的非定常流动的流线,图3.2(b)则表示在相对坐标系中定常流动的流线。
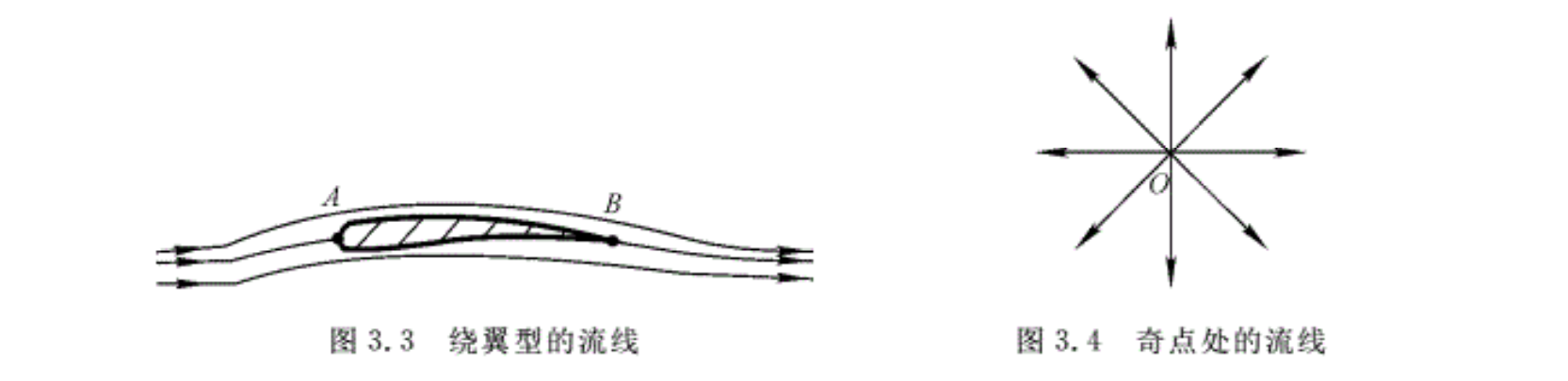
流线有两个重要的特性。一是在定常流动中,流体质点的流线与迹线一定重合;而在非定常流动中,一般它们不重合,是两条不稳定的曲线。另一个特性是在一般的情况下,流线不能彼此相交。这可用反证法证明,即如果相交,则在交点处的流体质点必有两个切线方向,这是不可能的,所以流线不能彼此相交。
在特殊的情况下,流线可能相交。例如,理想的直匀流绕一个静止的物体运动,如图3.3所示,在驻点A处,流线与上、下翼面(上、下两条流线)彼此相交。此时前驻点处的流体质点的速度必为零,而零向量的方向可以是任意的。同样,在机翼后缘B处,上、下两条流线也相交而成一流线。此时,上下两条流线必须在后缘处相切。流线相交的第三种情况就是在流场中速度接近无限大的点处(通常称为奇点),如图3.4所示。
在某一时刻,流场中,任取一条非流线的曲线C,通过C上的每一个点做该瞬时t的流线,这些无限多条流线就构成了一个曲面,称其为流面。如果曲线C是条封闭的非流线,则该流面形成为流管。如果流管的横截面积足够小,则这条流管就叫基元流管。基元流管的任一截面上流体参数都是均匀的。根据流线的特点,可以推出,流体质点不能穿越流管。对无黏性流体,其固体壁面即可视为流面。
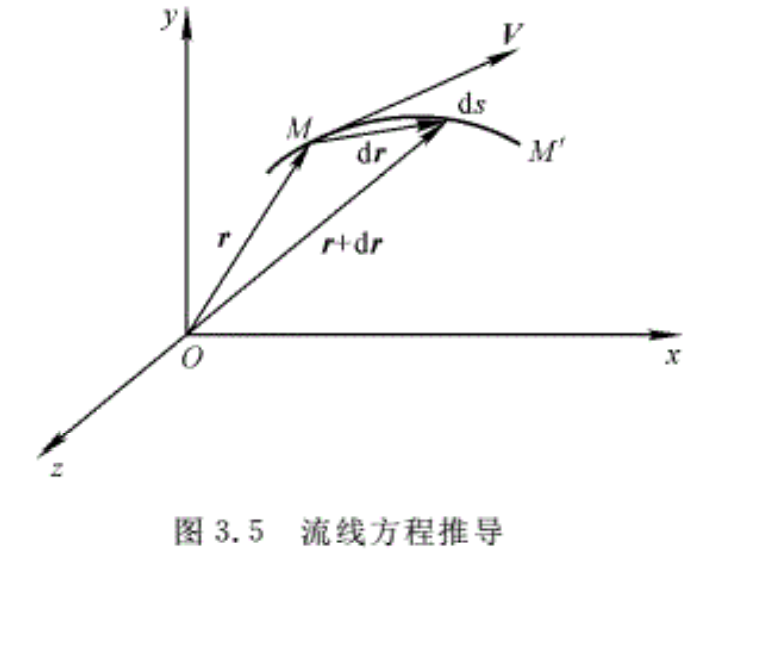
现在来确定流线方程。在流线上任取一点M(x,y,z)(见图3.5)。其速度V在三个坐标轴上的投影分别为Vx,Vy和Vz,于是向量V与三个坐标轴的夹角的余弦是
\(\frac{{{V}_{x}}}{V}\frac{{{V}_{y}}}{V}\frac{{{V}_{z}}}{V}\)
在点M(x,y,z)附近沿流线取无限小线段ds,则过点M的流线与坐标轴之间的夹角的余弦是
dx/ds,dy/ds,dz/ds
式中,dx,dy和dz是ds在坐标轴x,y,z上的投影。根据流线的定义,流线上任一点处流体质点的速度向量与该点的切线相重合,即
\(\frac{{{V}_{x}}}{V}=\frac{dx}{ds}\frac{{{V}_{y}}}{V}=\frac{dy}{ds}\frac{{{V}_{z}}}{V}=\frac{dz}{ds}\) (3.12)
从而得 \(\frac{dx}{{{V}_{x}}}=\frac{dy}{{{V}_{y}}}=\frac{dz}{{{V}_{z}}}=\frac{ds}{V}\) (3.13)
这就是直角坐标系流线的微分方程式,积分后得到流线方程。
同理,可得圆柱坐标系中的流线方程为
\(\frac{dr}{{{V}_{r}}}=\frac{rd\theta }{{{V}_{\theta }}}=\frac{dz}{{{V}_{z}}}\) (3.14)
流线方程写成向量形式则为
dr x V=0 (3.15)
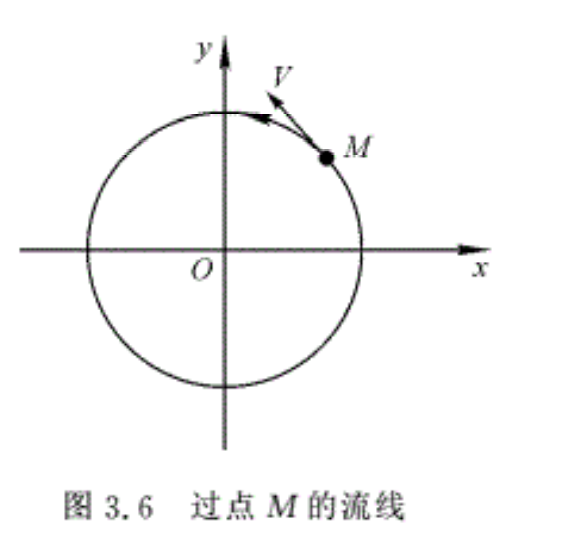
例3.5 设己知流体运动的速度分量为\({{V}_{x}}=-\frac{y}{x_{{}}^{2}+y_{{}}^{2}}{{V}_{y}}=\frac{x}{x_{{}}^{2}+y_{{}}^{2}}\),试求流线方程,并求过点(1,1)的流线。
解:显然这是平面定常流动。按流线方程定义,将Vx,Vy代入式(3.13),即
\(\frac{dx}{{{V}_{x}}}=\frac{dy}{{{V}_{y}}}\)
得 ydy=-xdx
积分得 x²+y²=C
式中,C为常数。流线为一族圆心在坐标原点的同心圆。
将点(1,1 )代入流线方程,得C=2,即过点M(1,1)流线方程x²+y²=2,如图3.6所示。速度是个矢量,所以流线应有方向。为了确定流体运动的方向,需要计算速度V与x,y方向夹角的余弦,即
\(\begin{align}
& \cos \theta =\frac{{{V}_{x}}}{V}=-\frac{y}{\sqrt{{{x}^{2}}+{{y}^{2}}}} \\
& \cos \alpha =\frac{{{V}_{y}}}{V}=\frac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}}} \\
\end{align}
\)
对于点M(1,1),则有\(\cos \theta =-\frac{1}{\sqrt{2}}\),而\(\cos \alpha =\frac{1}{\sqrt{2}}\),则V与x方向成钝角,与y方向成锐角,即流线的方向为逆时针方向,如图3.6所示。
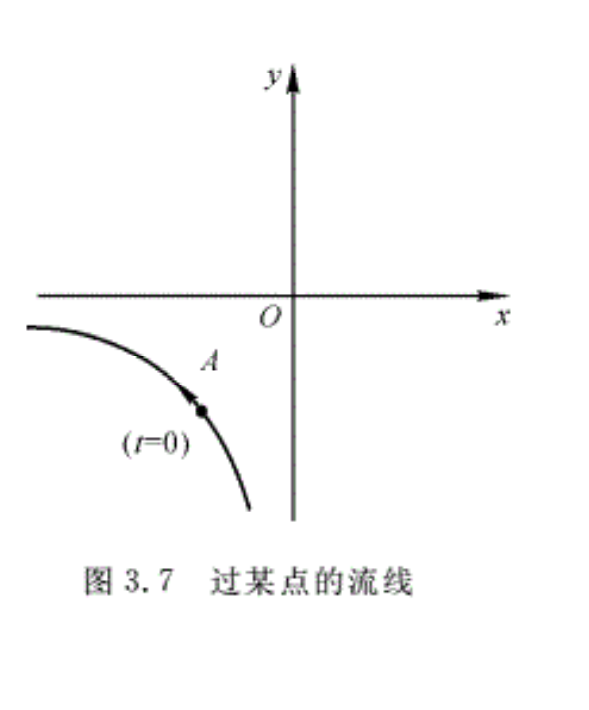
例3.6 设已知流体运动的各速度分量为Vx=x+t,Vy=-y+t,Vz=0。试求流线族及 t=0瞬时通过点A(-1,-1)的流线。
解:这是一个平面非定常流动。根据式(3.13),可得
\(\frac{dx}{x+t}=\frac{dy}{-y+t}\)
当求在瞬时t的流线时,可将t视为常数,积分后得
\(\ln \left( x+t \right)=-\ln \left( -y+t \right)+\ln C\)
式中,C为常数,或
(x+t)(-y+t)=C (a)
即在某一瞬时t的流线族是一族双曲线。为了确定t=0时通过点A(-1,-1)的流线,可以将 t=0时的坐标x=-1,y=-1代入式(a),得积分常数C=-1。将C=-1代入方程式(a),可得当t=0时通过点A的流线为
xy=1
如图3.7所示。流线与x方向夹角的余弦为
\(\cos \theta =\frac{{{V}_{x}}}{V}=\frac{x+t}{\sqrt{{{\left( x+t \right)}^{2}}+{{\left( -y+t \right)}^{2}}}}\)
当t=0时,\(\cos \theta =\frac{{{V}_{x}}}{V}=\frac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}}}\)
显然,在A点,COSθ<0,故V与x方向成钝角。同理可知,与y方向夹角α为锐角。流线方向如图3.7所示。
除了流线、迹线和流管外,对有旋流动的描述还有涡线和涡管等概念。
3.脉线
所谓脉线是指在一段时间内,将相继通过某一空间固定点的不同流体质点,在某一瞬时(即观察的瞬时)连成的曲线。如果该空间固定点是释放染色的源,则在某一瞬时观察到一条染色线,故脉线也称为染色线。染色线也是同一时刻不同流体质点的连线。经过烟头和烟囱冒出的烟都是形成脉线的例子。
在流动显示技术中,对气体,在流场中的固定点可加入烟或氢气以形成烟线或氢气泡等显示流场结构和流动图像。对液体经常加入有色液体,从而在流场中形成染色线。在实验室里,经常采用染色线、烟线和氢气泡等流场显示技术来显现流场的结构。
3.1.5 流体运动分类
一、定常与非定常流动
1.定常流动
在一般情况下,流体的速度、压强、温度、密度等流体运动参数都是坐标和时间的数。但是在某些情况下,在任意空间点上,流体质点的全部流动参数都不随时间而变化,这种流动称为定常流动。例如,飞机作匀速直线运动时,相对于飞机来看(即将坐标系固定在飞机上)空气绕飞机的运动可认为是定常的,即所有的流动参数都不随时间而变化,满足∂/∂t=0的条件。对于定常流动,由于与时间无关,因此定常流动的研究要简单得多。所以往往将某些流动参数随时间变化不大的非定常流动作适当的假设,将其简化为定常流动。
2.非定常流动
在任意空间点上,流体质点的流动参数(全部或一部分)随时间发生变化的流动称为非定常流动,用数学表示为 ∂/∂t≠0。发动机在起动或减速工作过程中,发动机内的气流则为非定常流动。非定常流动常常可以通过选取适当的坐标系而转变为定常流动,如飞行器的匀速直线运动,在地面上观察为非定常运动,而在飞行器上看则是定常运动。这种转化方法在气体动力学中经常被采用。
虽然为处理问题的方便,常常把非定常的流动转化为定常流动或看做是定常流动来处理,但在数值计算中,都常常把定常流动看做非定常流动来处理,即求非定常流动的渐近解,这样使数值求解更为方便。
二、一维流动与多维流动
如果流体在流动中,其流动参数仅是一个空间坐标的函数,则这样的流动称为一维流动,如果流动参数是两个空间坐标的函数,则称为二维流动,二维流动又称为平面流动。如果流动参数是三个空间坐标的函数,则称为三维流动。二维和三维流动均称为多维流动。如果把时间也考虑进去,则有一维定常流动、一维非定常流动,二维定常流动和二维非定常流动,三维定常流动和三维非定常流动,等等。
在圆柱坐标系中,轴对称流动属于二维流动,它的特点是流动参数仅是坐标r,z的数,而与θ无关,即∂/∂θ=0.例如,空气沿着一个圆锥物体的对称轴线方向流动,流动参数仅仅沿轴线方向(z方向)和垂直于轴线方向(r方向)发生变化。
3.2 流体微团运动分析
在理论力学中,刚体的复杂运动可以分解为平动和绕某一瞬时轴的转动问题来简化求解过程。那么在流体力学中,是否可以像分解刚体的运动那样,将流体微团的复杂运动也分解为类似的几个简单的运动呢?这就要对流体质点的运动进行分析。本节分析流体质点运动的组成部分,以便对复杂的流体运动进行分类研究,着重分析直角坐标系中的流体微团的运动。
3.2.1 直角坐标系中流体微团的速度分解
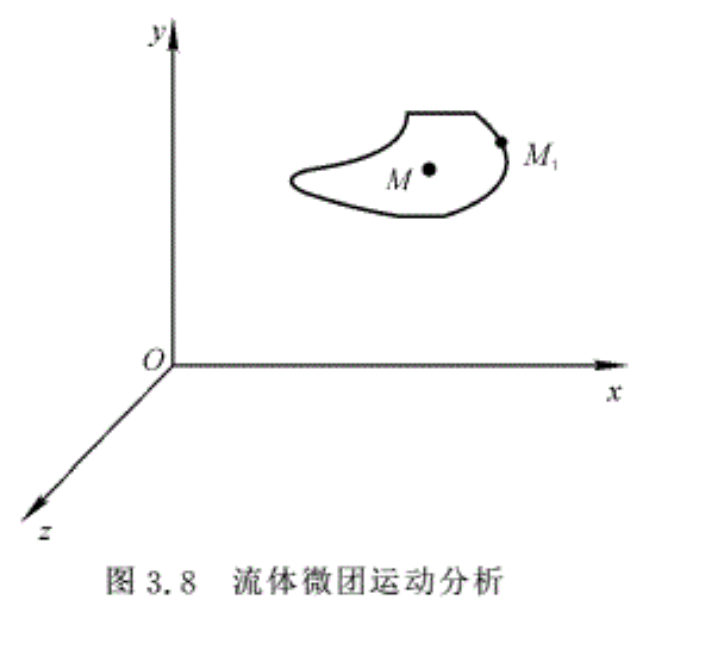
在运动流体中取一流体微元体(见图3.8),设其中心点M(x,y,z),在某一瞬时的速度为
\(V={{V}_{x}}i+{{V}_{y}}j+{{V}_{z}}k\)
流体微元体上邻近的另一点M1(x+δx,y+δy,z+δz)在同一瞬时的速度用泰勒级数展开,略去二阶以上的小量,得
\(\left. \begin{align}
& {{V}_{x1}}={{V}_{x}}+\frac{\partial {{V}_{x}}}{\partial x}\delta x+\frac{\partial {{V}_{x}}}{\partial y}\delta y+\frac{\partial {{V}_{x}}}{\partial z}\delta z \\
& {{V}_{y1}}={{V}_{y}}+\frac{\partial {{V}_{y}}}{\partial x}\delta x+\frac{\partial {{V}_{y}}}{\partial y}\delta y+\frac{\partial {{V}_{y}}}{\partial z}\delta z \\
& {{V}_{z1}}={{V}_{z}}+\frac{\partial {{V}_{z}}}{\partial x}\delta x+\frac{\partial {{V}_{z}}}{\partial y}\delta y+\frac{\partial {{V}_{z}}}{\partial z}\delta z \\
\end{align} \right\}
\) (3.16)
在第一式中人为地增加四项,即\(\text{ }\!\!\pm\!\!\text{ }\frac{1}{2}\frac{\partial {{V}_{y}}}{\partial x}\delta y\text{ }\!\!\pm\!\!\text{ }\frac{1}{2}\frac{\partial {{V}_{z}}}{\partial x}\delta z\) ,然后将第一式改写为
\({{V}_{x1}}={{V}_{x}}+\frac{\partial {{V}_{x}}}{\partial x}\delta x+\frac{1}{2}\left( \frac{\partial {{V}_{x}}}{\partial y}+\frac{\partial {{V}_{y}}}{\partial x} \right)\delta y+\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial x}+\frac{\partial {{V}_{x}}}{\partial z} \right)\delta z-\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}-\frac{\partial {{V}_{x}}}{\partial y} \right)\delta y+\frac{1}{2}\left( \frac{\partial {{V}_{x}}}{\partial z}-\frac{\partial {{V}_{z}}}{\partial x} \right)\delta z\)
同理,将第二式和第三式分别增加\(\text{ }\!\!\pm\!\!\text{ }\frac{1}{2}\frac{\partial {{V}_{x}}}{\partial y}\delta x\text{ }\!\!\pm\!\!\text{ }\frac{1}{2}\frac{\partial {{V}_{z}}}{\partial y}\delta z\)和\(\text{ }\!\!\pm\!\!\text{ }\frac{1}{2}\frac{\partial {{V}_{x}}}{\partial z}\delta x\text{ }\!\!\pm\!\!\text{ }\frac{1}{2}\frac{\partial {{V}_{y}}}{\partial z}\delta y\),则可将第二式和第三式改写为
\(\begin{align}
& {{V}_{y1}}={{V}_{y}}+\frac{\partial {{V}_{y}}}{\partial y}\delta y+\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}+\frac{\partial {{V}_{x}}}{\partial y} \right)\delta x+\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial y}+\frac{\partial {{V}_{y}}}{\partial z} \right)\delta z-\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial y}-\frac{\partial {{V}_{y}}}{\partial z} \right)\delta z+\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}-\frac{\partial {{V}_{x}}}{\partial y} \right)\delta x \\
& {{V}_{z1}}={{V}_{z}}+\frac{\partial {{V}_{z}}}{\partial z}\delta z+\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial y}+\frac{\partial {{V}_{y}}}{\partial z} \right)\delta y+\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial x}+\frac{\partial {{V}_{x}}}{\partial z} \right)\delta x-\frac{1}{2}\left( \frac{\partial {{V}_{x}}}{\partial z}-\frac{\partial {{V}_{z}}}{\partial x} \right)\delta x+\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial y}-\frac{\partial {{V}_{y}}}{\partial z} \right)\delta y \\
\end{align}
\)
引用以下符号:
\(\left. \begin{align}
& {{\varepsilon }_{x}}=\frac{\partial {{V}_{x}}}{\partial x} \\
& {{\varepsilon }_{y}}=\frac{\partial {{V}_{y}}}{\partial y} \\
& {{\varepsilon }_{z}}=\frac{\partial {{V}_{z}}}{\partial z} \\
\end{align} \right\}
\) (3.17)
\(\left. \begin{align}
& {{\gamma }_{x}}=\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial y}+\frac{\partial {{V}_{y}}}{\partial z} \right) \\
& {{\gamma }_{y}}=\frac{1}{2}\left( \frac{\partial {{V}_{x}}}{\partial z}+\frac{\partial {{V}_{z}}}{\partial x} \right) \\
& {{\gamma }_{z}}=\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}+\frac{\partial {{V}_{x}}}{\partial y} \right) \\
\end{align} \right\}
\) (3.18)
\(\left. \begin{align}
& {{\omega }_{x}}=\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial y}-\frac{\partial {{V}_{y}}}{\partial z} \right) \\
& {{\omega }_{y}}=\frac{1}{2}\left( \frac{\partial {{V}_{x}}}{\partial z}-\frac{\partial {{V}_{z}}}{\partial x} \right) \\
& {{\omega }_{z}}=\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}-\frac{\partial {{V}_{x}}}{\partial y} \right) \\
\end{align} \right\}
\) (3.19)
则可得亥姆霍兹(Helmholts)速度分解定理为
\(\left. \begin{align}
& {{V}_{x1}}={{V}_{x}}+\left[ {{\varepsilon }_{x}}\delta x+\left( {{\gamma }_{z}}\delta y+{{\gamma }_{y}}\delta z \right)+\left( {{\omega }_{y}}\delta z-{{\omega }_{z}}\delta y \right) \right] \\
& {{V}_{y1}}={{V}_{y}}+\left[ {{\varepsilon }_{y}}\delta y+\left( {{\gamma }_{x}}\delta z+{{\gamma }_{z}}\delta x \right)+\left( {{\omega }_{z}}\delta x-{{\omega }_{x}}\delta z \right) \right] \\
& {{V}_{z1}}={{V}_{z}}+\left[ {{\varepsilon }_{z}}\delta z+\left( {{\gamma }_{y}}\delta x+{{\gamma }_{x}}\delta y \right)+\left( {{\omega }_{x}}\delta y-{{\omega }_{y}}\delta x \right) \right] \\
\end{align} \right\}
\) (3.20a)
用矢量表示为
V1=V+ε x δr+ω x δr (3.20b)
式中,第一项为平移速度;第二项为变形(包括线变形和角变形)引起的速度增量;第三项为旋转引起的速度增量。ε为变形速度矩阵,即
\(\varepsilon =\left[ \begin{align}
& {{\varepsilon }_{x}}{{\gamma }_{z}}{{\gamma }_{y}} \\
& {{\gamma }_{z}}{{\varepsilon }_{y}}{{\gamma }_{x}} \\
& {{\gamma }_{y}}{{\gamma }_{x}}{{\varepsilon }_{z}} \\
\end{align} \right]
\)
3.2.2 流体微团的运动和变形
进一步分析式(3.20)可以看出,点M1处的速度(Vx1,Vy1,Vz1)由点M处的速度(Vx,Vy,Vz)和后边的几项构成。如果后边的几项等于零,则点M1处的速度与点M处的速度相等。说明该流体微团上各点的速度相等,该流体微团只可能作平动。如果速度不相等,则流体微团不但有平动,而且还可能会存在转动和变形运动。为了说明流体微团运动的形式,下面以流体微团的平面运动来讨论式(3.17)~式(3.19)的物理意义。
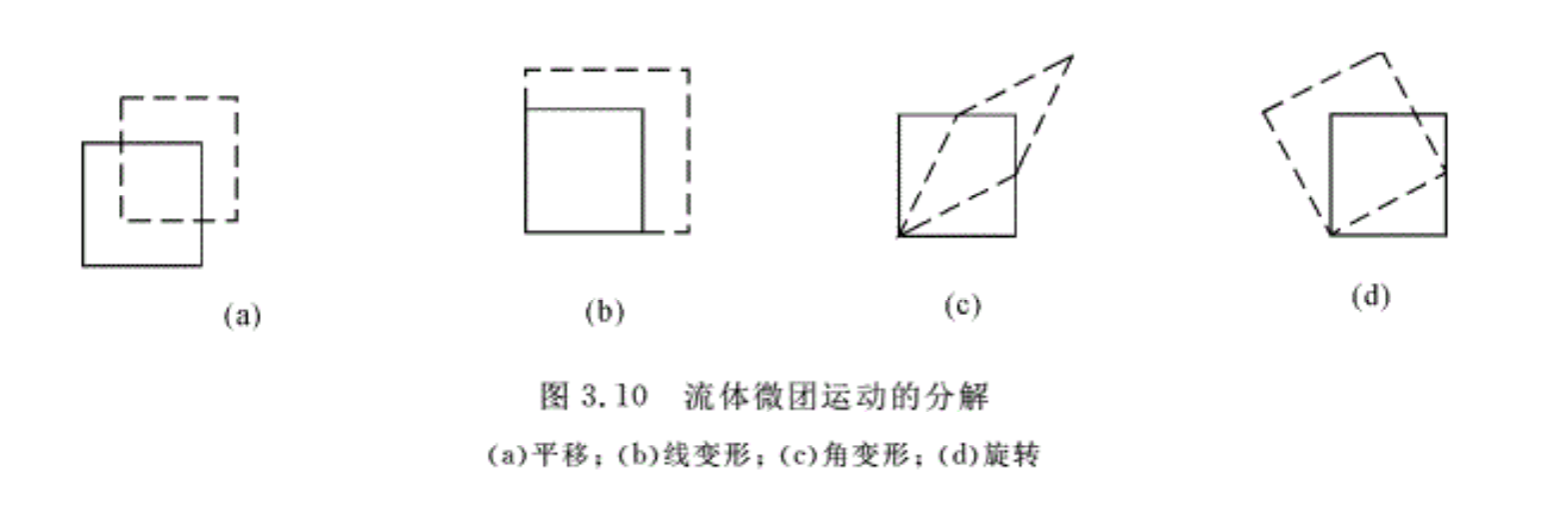
为了简单起见,在二维流动中,考察一个正方形的流体微团,其边长为δx=δy,如图3.9所示。一般情况下流场是不均匀的,即流场中的各点速度的大小和方向都可能变化。因此该微团从t时刻的位置ABCD 运动到t+dt时刻的位置A’B’C’D’上,流体微团的体积、形状都发生了变化,而且也发生了旋转。整个运动是同时发生的,可以将这样的一个复杂的一般运动分解为几个简单运动的合成,如图3.10所示。
1.平移
在式(3.20b)中,若ε=0,ω= 0,则V1=V,表示流体微团上各点的速度都相等,经过dt时间后,流体微团运动到新的位置,其大小、形状、方位等均没有发生变化。流体微团作平移运动如图(3.10a)所示。
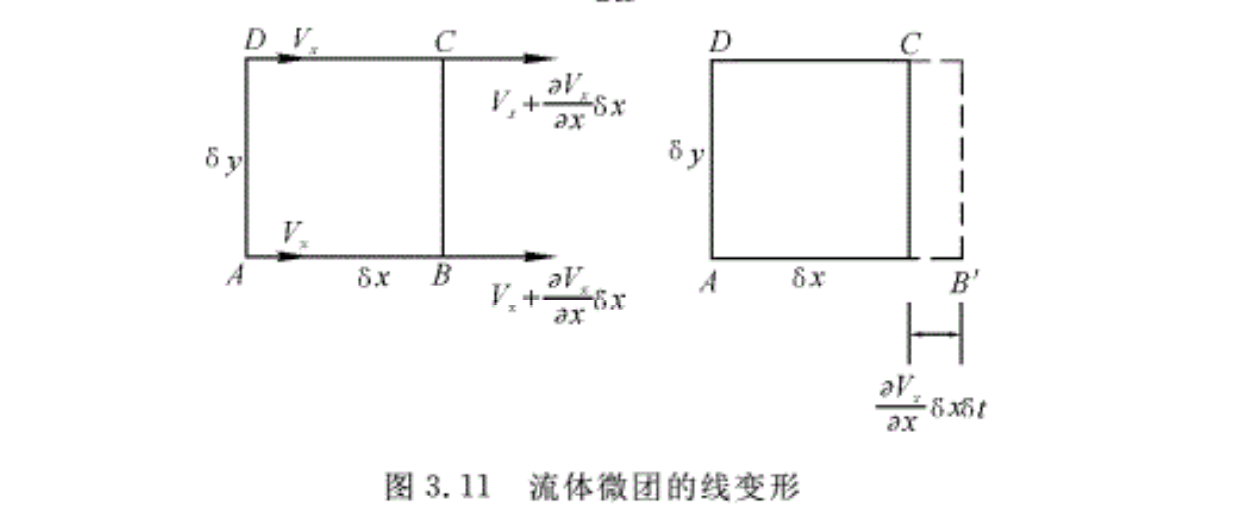
2.线变形(体变形)
当式(3.20b)中的V=ω= 0,且变形速度矩阵ε中除了εx= ∂Vx/∂x≠0外,其余各项均为零。即如果速度变化仅有∂Vx/∂x,则此时如图3.11所示的点A与点D的x方向的速度分量都是Vx,而点c与点B的x方向的速度分量都是Vx+∂Vx·δx/∂x。
由于速度的不同将会引起流体边线的拉伸,在δt时间内x方向的拉伸量为∂Vx·δx·δt/∂x,则在 x方向单位时间内流体边线的相对伸长量为
\( \frac{1}{\delta x}\frac{d\left( \delta x \right)}{dt}\text{=}\frac{1}{\delta x}\frac{\frac{\partial {{V}_{x}}}{\partial x}\delta x\delta t}{dt}\text{=}\frac{\partial {{V}_{x}}}{\partial x}\text{=}{{\varepsilon }_{x}}\)
如果同时考虑三个方向的速度变化,则x,y,z方向的流体边线的相对伸长量为∂Vx/∂x,∂Vy/∂y,∂Vz/∂z。因此,式εx= ∂Vx/∂x,εy= ∂Vy/∂y,εz= ∂Vz/∂z表示流体微团边线的相对伸长量。它们又称为线应变速度。从以上的讨论可以看出,只要存在流体微团的线应变速度,就会产生线变形,其结果就会使流体微团的体积产生膨胀和收缩,即所谓的体变形。
设瞬时t流体微团的体积为δv=δxδyδz,则经过δt时间后,由于流体微团产生线变形,其体积变为
δv′=\(\left( \delta x+\frac{\partial {{V}_{x}}}{\partial x}\delta x\delta t \right)\left( \delta y+\frac{\partial {{V}_{y}}}{\partial y}\delta y\delta t \right)\left( \delta z+\frac{\partial {{V}_{z}}}{\partial z}\delta z\delta t \right)\)
将上式展开,略去高阶小量,则得
δv′=\(\delta v+\left( \frac{\partial {{V}_{x}}}{\partial x}+\frac{\partial {{V}_{y}}}{\partial y}+\frac{\partial {{V}_{z}}}{\partial z} \right)\delta t\delta v\)
于是,单位时间内流体体积的相对变化率(即流体微团的体积膨胀率)为
\[\frac{1}{\delta v}\frac{d\left( \delta v \right)}{dt}=\frac{1}{\delta v}\underset{\delta t\to 0}{\mathop{\lim }}\,\frac{\delta v_{{}}^{\prime }-\delta v}{\delta t}=\frac{\partial {{V}_{x}}}{\partial x}+\frac{\partial {{V}_{y}}}{\partial y}+\frac{\partial {{V}_{z}}}{\partial z}\]
上式第二个等号的右端可表示为速度的散度,即
divV=▽ x V= ∂Vx/∂x+∂Vy/∂y+∂Vz/∂z=εx+εy+εz (3.21)
由以上推导可以看出,流体微团三个线变形速度之和等于流体微团的体积膨胀率,也等于流体运动速度的散度。
3.剪切变形(角变形)
当流体微团速度的变化率∂Vx/∂y≠∂Vy/∂x时,则伴随有流体微团的旋转和剪切变形,导致流体微团的形状发生变化。剪切变形用剪切变形角速度来表示,其定义为流体微团上任意两条相互垂直的流体边线夹角的时间变化率的一半。流体边线是由流体质点所组成的线段。同样考虑xOy平面上的运动,在时刻t流体微团各点的速度分布如图3.12所示。
经过dt时间之后,流体微团的边线AB和AD分别转过的角度为δα和δβ,即
\[\begin{align}
& \delta \alpha =\left( \frac{\partial {{V}_{y}}}{\partial x}\delta x \right)\delta t/\delta x \\
& \delta \beta =\left( \frac{\partial {{V}_{x}}}{\partial y}\delta y \right)\delta t/\delta y \\
\end{align}\]
这两条流体边线间的夹角变化了δα+δβ,则根据剪切变形角速度的定义,在xOy平面上,剪切变形角速度为
\[{{\gamma }_{z}}=\underset{\delta t\to 0}{\mathop{\lim }}\,\frac{1}{2}\left( \frac{\delta \alpha +\delta \beta }{\delta t} \right)=\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}+\frac{\partial {{V}_{x}}}{\partial y} \right)\]
同理,可以得出在另外两个平面内的剪切变形角速度γx和γy分别为
\[\begin{align}
& {{\gamma }_{x}}=\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial y}+\frac{\partial {{V}_{y}}}{\partial z} \right) \\
& {{\gamma }_{y}}=\frac{1}{2}\left( \frac{\partial {{V}_{x}}}{\partial z}+\frac{\partial {{V}_{z}}}{\partial x} \right) \\
\end{align}\]
流体微团的剪切变形速度为
\[\gamma ={{\gamma }_{x}}i+{{\gamma }_{y}}j+{{\gamma }_{z}}k\]
当γ为正时,微元体角变形减小,即流体微元体产生了收缩切变形;当γ为负时,微元体角变形增大,即流体微元体产生了扩展切变形。
4.转动
由于从流体微团中某一点引出的各流体线的旋转角速度互不相同,因此需要用平均旋转的概念来描述流体微团的转动,即定义流体微团的旋转角速度为微团上两条相互垂直的流体线的平均旋转角速度。或者说两条相互垂直的流体线角平分线的旋转角速度。考察微团上相互垂直的流体边线AB线和AD线,并规定逆时针旋转角速度为止,顺时针为负,则图3.12所示的AB线和AD线的旋转角速度分别为
\[\begin{align}
& \underset{\delta t\to 0}{\mathop{\lim }}\,\frac{\delta \alpha }{\delta t}=\frac{\partial {{V}_{y}}}{\partial x} \\
& \underset{\delta t\to 0}{\mathop{\lim }}\,\frac{\delta \beta }{\delta t}=-\frac{\partial {{V}_{x}}}{\partial y} \\
\end{align}\]
定义流体微团绕Oz轴的旋转角速度为AB线和AD线的旋转角速度的平均值,即
\[{{\omega }_{z}}=\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}-\frac{\partial {{V}_{x}}}{\partial y} \right)\]
同理,可以导出绕Ox,Oy轴的旋转角速度分别为
\[\begin{align}
& {{\omega }_{x}}=\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial y}-\frac{\partial {{V}_{y}}}{\partial z} \right) \\
& {{\omega }_{y}}=\frac{1}{2}\left( \frac{\partial {{V}_{x}}}{\partial z}-\frac{\partial {{V}_{z}}}{\partial x} \right) \\
\end{align}\]
通常可以用矢量形式表示流体微团的旋转角速度,即
\[\omega ={{\omega }_{x}}i+{{\omega }_{y}}j+{{\omega }_{z}}k=\frac{1}{2}\left( \frac{\partial {{V}_{z}}}{\partial y}-\frac{\partial {{V}_{y}}}{\partial z} \right)i+\frac{1}{2}\left( \frac{\partial {{V}_{x}}}{\partial z}-\frac{\partial {{V}_{z}}}{\partial x} \right)j+\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}-\frac{\partial {{V}_{x}}}{\partial y} \right)k=\frac{1}{2}\left| \begin{align}
& ijk \\
& \frac{\partial }{\partial x}\frac{\partial }{\partial y}\frac{\partial }{\partial z} \\
& {{V}_{x}}{{V}_{y}}{{V}_{z}} \\
\end{align} \right|\]
根据场论的表示法,上式可表示为
\[\omega =\frac{1}{2}\nabla \times V=\frac{1}{2}\Omega \] (3.22)
式中
\[\Omega =\nabla \times V=\left| \begin{align}
& \text{i}\text{j}\text{k} \\
& \frac{\partial }{\partial x}\frac{\partial }{\partial y}\frac{\partial }{\partial z} \\
& {{V}_{x}}{{V}_{y}}{{V}_{z}} \\
\end{align} \right|\]
式(3.22)中Ω=▽xV,称为速度的旋度,它构成了一个矢量场称为涡旋场,Ω又称为涡量。
由上面讨论亥姆霍茨速度分解定理(式(3.20))中各项的物理意义可知,流体微团的运动可以分解为平移(见图3.10(a))、线变形(体变形,见图3.10(b)、剪切变形(见图3.10(c))和旋转(见图3.10(d)。如果流场中的流体微团不绕其自身轴旋转,即旋转角速度矢量为零(ω=0),则这样的运动称为无旋运动,否则称为有旋运动或旋涡运动。此部分内容将在第八章讨论。
例3.7(1 )已知速度分布为V=3ti+xzj+ty²k,试计算流体微团的体积膨胀率,并判别该速度场是否为无旋场。
(2)若速度场为Vx=x(1+y²),Vy=x-y²求在此流场中的点(2,1)处的旋转角速度、剪切变形角速度和体积膨胀率。
解:(1)流体微团的体积膨胀率(即速度的散度)为
\[\nabla \times V=\frac{\partial }{\partial x}\left( 3t \right)+\frac{\partial }{\partial y}\left( xz \right)+\frac{\partial }{\partial z}\left( ty_{{}}^{2} \right)=0\]
此速度场并没有产生膨胀或压缩,这样的流场为不可压缩的。速度的旋度为
\[\nabla \times V=\left| \begin{align}
& \text{i}\text{j}\text{k} \\
& \frac{\partial }{\partial x}\frac{\partial }{\partial y}\frac{\partial }{\partial z} \\
& 3\text{t}\text{xz}\text{t}y_{{}}^{2} \\
\end{align} \right|=\left( 2ty-x \right)i+zk\ne 0\]
所以流动为有旋的。由速度分布还可以看出,该流场为三维非定常流动。
(2)流体微团在点(2,1)处的旋转角速度、剪切变形角速度和体积膨胀率分别为
\[\begin{align}
& \omega =\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}-\frac{\partial {{V}_{x}}}{\partial y} \right)=\frac{1}{2}\left( 1-2xy \right)=-1.5 \\
& \gamma =\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}+\frac{\partial {{V}_{x}}}{\partial y} \right)=\frac{1}{2}\left( 1+2xy \right)=2.5 \\
& \nabla \times V=\frac{\partial {{V}_{y}}}{\partial y}+\frac{\partial {{V}_{x}}}{\partial x}=\left( 1+y_{{}}^{2} \right)-2y=0 \\
\end{align}\]
可以看出,此流场为二维定常流场;在点(2,1)处流体微团顺时针旋转,虽然没有产生体积膨胀变形,但是产生了剪切变形。
3.3 适合于系统的基本方程及雷诺输运定理
3.3.1 适合于系统的基本方程
在分析流体运动时,主要有两种方式:一种是描述流场中每一个点的流动细节;另一种是针对一个有限区域,通过研究某物理量流入和流出的平衡关系来确定总的作用效果,如作用在这个区域上的力、力矩、总能量交换等等。其中,前一种方法也称为微分方法,而后者则称为积分方法。
如果系统的质量用m来表示,则根据质量守恒定律,有
M=const或dm/dt=0 (3.23a)
如果环境对系统施加的合力为F,则根据牛顿第二定律,有
F=mdV/dt=d(mV)/dt (3.23b)
如果环境对系统施加关于某一轴的合力矩为M,则有
M=dH/dt (3.23c)
式中H=∑(r×V)δm为系统关于同一轴的动量矩(也叫角动量)。如果传给系统的热量为 dQ或系统对外做功dW,则系统的能量会发生变化dE,根据热力学第一定律,有
dQ-dW=dE
或 dQ/dt-dW/dt=dEdt (3.23d)
式(3.23a)~式(3.23d)分别称为适合于系统的连续方程、动量方程、角动量(或动量矩)方程和能量方程。这些方程都包含热力学参量,所以在研究某些具体流动时还要补充完全气体状态方程。
3.3.2 雷诺输运定理
在流体力学中为了便于研究,常常采用控制体的方法,因此就需要将描述系统的力学基本方程转化成对控制体的方程,这个过程就是通过雷诺输运定理来完成的。方程式(3.23a)~式(3.23d)都是基本量(m,V,H,E)对时间导数的关系式,因此,需要将系统中物理量对时间的导数转化为控制体中相应量的时间导数。为了方便,首先推导一维流动的雷诺输运方程,然后再推广到一般形式。
图3.13表示速度场V=V(s)的一维流动,选取控制体11一22 ( Ⅰ,Ⅱ区),如图所示。选t时刻占据该控制体的流体为系统,经过dt时间后系统运动到1’1’一2’2′ (Ⅲ,Ⅱ区)位置,流入、流出控制体的流体体积分别为∆v1=A1V1dt,∆v2=A2V2dt。令Ф为与流体质量有关的随流物理量(能量、动量等),β表示单位质量流体所具有的Ф,整个控制体内流体所具有的Ф应为
\[{{\phi }_{cv}}=\int_{cv}{\beta dm}=\int_{cv}{\beta \rho dv}\] (3.24a)
式中,pdv为微元体中流体的质量;下标cv表示控制体(体积)。
显然,在同一瞬间t,与控制体相重合的流体系统所具有的物理量Фs(t)=Фcv(t),在t+∆t瞬时,系统移动到新的位置,不再与控制体重合,计算Фs随时间的变化率,即
\[\frac{d{{\phi }_{s}}}{dt}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\phi }_{s}}\left( t+\Delta t \right)-{{\phi }_{s}}\left( t \right)}{\Delta t}\] (3.24b)
式中
\[{{\phi }_{s}}\left( t+\Delta t \right)={{\phi }_{cv}}\left( t+\Delta t \right)-{{\left( \beta \rho \Delta v \right)}_{I}}+{{\left( \beta \rho \Delta v \right)}_{II}}\] (3.24c)
而(βρ∆v)Ⅰ是∆t时间内通过截面A1流入控制体cv的Ф值,即
\[{{\left( \beta \rho \Delta v \right)}_{I}}=\beta {{\rho }_{1}}{{A}_{1}}{{V}_{1}}\Delta t\]
(βρ∆v)Ⅱ是同一时间通过截面A2流出控制体的Ф值,即
\[{{\left( \beta \rho \Delta v \right)}_{II}}=\beta {{\rho }_{2}}{{A}_{2}}{{V}_{2}}\Delta t\]
由于Фs(t)=Фcv(t),故式(3.24b)可改写为
\[\frac{d{{\phi }_{s}}}{dt}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\phi }_{s}}\left( t+\Delta t \right)-{{\phi }_{cv}}\left( t \right)}{\Delta t}\] (3.24d)
下面推导t时刻Фcv对时间的导数和系统所具有的Фs对时间导数之间的关系。将式(3.24c)代入式(3.24d),可以得出
\[\begin{align}
& \frac{d{{\phi }_{s}}}{dt}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\phi }_{s}}\left( t+\Delta t \right)-{{\phi }_{cv}}\left( t \right)}{\Delta t}= \\
& \underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\phi }_{cv}}\left( t+\Delta t \right)-{{\left( \beta \rho \Delta v \right)}_{I}}+{{\left( \beta \rho \Delta v \right)}_{II}}}{\Delta t}= \\
& \underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\phi }_{cv}}\left( t+\Delta t \right)-\left( \beta {{\rho }_{1}}{{A}_{1}}{{V}_{1}} \right)\Delta t+\left( \beta {{\rho }_{2}}{{A}_{2}}{{V}_{2}} \right)\Delta t-{{\phi }_{cv}}\left( t \right)}{\Delta t}= \\
& \frac{d{{\phi }_{cv}}}{dt}+{{\left( \beta {{\rho }_{2}}{{A}_{2}}{{V}_{2}} \right)}_{out}}-{{\left( \beta {{\rho }_{1}}{{A}_{1}}{{V}_{1}} \right)}_{in}} \\
\end{align}\] (3.25a)
如果控制体是静止的,则
\[\frac{d{{\phi }_{s}}}{dt}=\frac{\partial {{\phi }_{cv}}}{\partial t}+{{\left( \beta {{\rho }_{2}}{{A}_{2}}{{V}_{2}} \right)}_{out}}-{{\left( \beta {{\rho }_{1}}{{A}_{1}}{{V}_{1}} \right)}_{in}}\] (3.25b)
式(3.25)即为一维运动的雷诺输运定理数学表达式。式中,等号右边三项分别为:第一项表示控制体内Ф随时间的变化率;第二项表示流出控制面的Ф流率;第三项表示流入控制面的Ф流率;后两项称为流率项(Flux一Term),代表流体通过控制面时物理量Ф值的净通量率。
对于定常流动,在静止的固定形状的控制体中Фcv不随时间变化,因此
∂Фcv/∂t=0
式(3.25)可以很容易地推广到一般的形式。
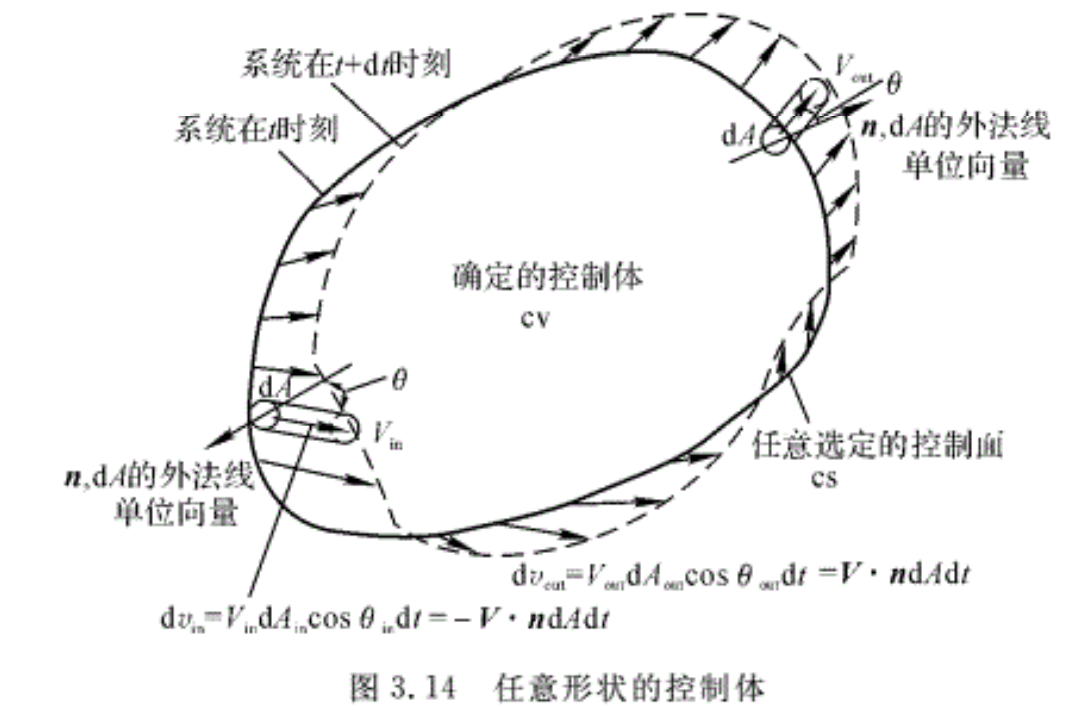
图3.14表示了一个任意形状的控制体,在控制面上的每个微元面积dA上,都有相应的流速V,与dA的外法线夹角为θ。在控制面处,有的部分为流体流入控制体,有的部分为流体流出控制体,有的部分为流线或固壁(V=0),没有流体流入或流出控制体。因此对于任意固定形状的控制体,方程式(3.25)可推广为
\[\begin{align}
& \frac{d{{\phi }_{s}}}{dt}=\frac{d{{\phi }_{cv}}}{dt}+\int_{cs}{\beta \rho V\cos \theta }d{{A}_{out}}-\int_{cs}{\beta \rho V\cos \theta }d{{A}_{in}}= \\
& \frac{d{{\phi }_{cv}}}{dt}+\int_{cs}{\beta }d{{q}_{m,out}}-\int_{cs}{\beta }d{{q}_{m,in}} \\
\end{align}\] (3.26)
对静止控制体,则
\[\frac{d{{\phi }_{s}}}{dt}=\frac{\partial {{\phi }_{cv}}}{\partial t}+\int_{cs}{\beta \rho {{V}_{n}}}d{{A}_{out}}-\int_{cs}{\beta \rho {{V}_{n}}}d{{A}_{in}}\] (3.27)
式中,cs表示控制体的表面,式(3.27)即为适用于静止控制体的雷诺输运定理数学表达式。
将式(3.24a)的代入式(3.27),并将时间导数放在积分号内,式(3.27)可写为
dΦs/dt=∫(cv) ∂(βρ)dv/∂t+∮(cs) βρ(V x n)dA (3.28)
方程式(3.28)说明,在某一时刻,,控制体内流体所构成的系统具有的随流物理量随时间的变化率,等于该瞬时与系统重合的控制体中所含同一物理量的增加率与相应物理量通过控制面的净流出率之和。
在许多实际应用中,流体通过多个进、出囗流入和流出控制体,在这些进、出口截面流动近似一维,因此式(3.28)中积分形式的流率项可以简化为所有出口截面流率减去进囗截面流率,即
∮(cs) βρ(V x n)dA=∑(βiρiViAi)out-∑(βiρiViAi)in (3.29)
图3.15所示为多进、出口控制体,其中, ①,④截面为进口,②,③,⑤截面为出口。对于该流动情况,流率项应为
∮(cs) βρ(V x n)dA=β2ρ2V2A2+β3ρ3V3A3+β5ρ5V5A5-β1ρ1V1A1-β4ρ4V4A4 (3.30)
除了这五个截面外,控制面上其他部分没有流体进出,因此对流率项没有贡献。
将式(3.27)或式(3.28)中的Ф分别换为质量、动量、动量矩或能量,代入到式(3.23a)~式(3.23d)中,即可以得到控制体形式的力学基本方程。
3.4 连续方程
根据质量守恒定律,系统的质量保持不变,数学方程为式(3.23a)。在雷诺输运表达式中,令Ф=m,则β=dm/dm=1,将它们代入式(3.28)并根据(3.23a),得出
∫(cv) ∂ρdv/∂t+∮(cs) ρ(V x n)dA=0 (3.31)
如果控制体只有若干个进、出口,且流动为一维,则式(3.31)可以与成
∫(cv) ∂ρdv/∂t+∑(ρiViAi)out-∑(ρiViAi)in=0 (3.32)
下面讨论几种特殊情况下连续方程的形式。
(1)定常流动,则∂ρ/∂t=0,由式(3.31)可得出
∮(cs) ρ(V x n)dA=0 (3.33)
式(3.33)说明,对于定常流动,流入和流出控制体的质量流量恒等。进一步,如果控制体只有若干个一维进、出口,则连续方程为
∑(ρiViAi)out=∑(ρiViAi)in (3.34)
可以证明,在定常流动的条件下,对于任意形状的控制体,只要在控制体的进、出口截面上流体参数是均匀的,而不论流体在控制体内部的流动情况如何,所导出的连续方程与式(3.34)的是相同的。该式在解决实际工程问题中应用非常广泛。
例如在图3.15中,如果控制体内的流动定常,则三个出囗的质量流率应等于两个进口的质量流率,即
ρ2V2A2+ρ3V3A3+ρ5V5A5=ρ1V1A1+ρ4V4A4 (3.35)
质量流率或称为质量流量,常用qm表示,其SI单位为千克/秒(kg/ s)。因此式(3.35)还可以写成一维定常流动的连续方程,即
qm=ρVA=C (3.36)
对于一般形式,有
qm = ∫(cs) ρ(V x n)dA (3.37)
(2)不可压流动, ∂ρ/∂t=0,又因为ρ≠ 0,方程式(3.33)可简化为
∮(cs) (V x n)dA=0 (3.38)
如果进、出口均为一维流动,则有
qv=VA=C (3.39)
式中,qv称为通过某截面的体积流量,其SI单位为立方米/秒(m³/ s)。对于一般形式,体积流量可表示为
qv = ∫(cs) (V x n)dA (3.40)
例3.8 图3.16所示为一维定常流管,①,②分别为进、出口截面。试写出其质量守恒关系式。
解:根据定常流动的连续方程式(3.36),可以得出
qm=ρ1V1A1=ρ2V2A2=const
上式说明,通过定常流管任意截面的质量流量处处相等,为同一个常数。如果是不可压的,则有
qv=V1A1=V2A2=const
或 V2=A1V1/A2
因此,在一维定常不可压流管中体积流量也是一个常数,流速和截面积成反比。
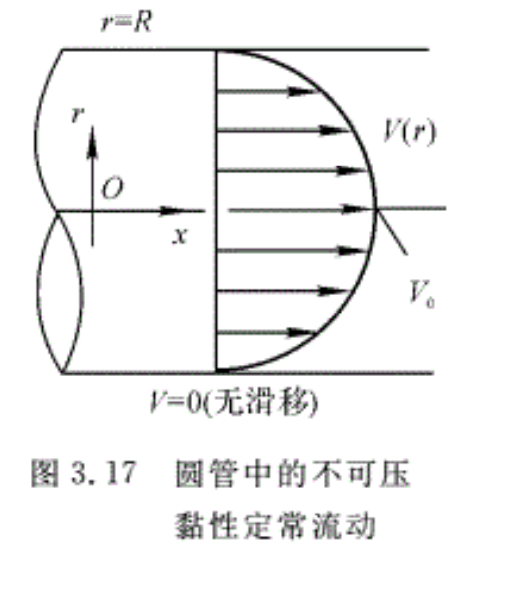
例3.9 图3.17所示为一圆管中的不可压黏性定常流动,其轴向速度分布近似为
\[{{V}_{x}}={{V}_{0}}\left( 1-\frac{r}{R} \right)_{{}}^{m}\]
对于层流m≈1/2,对于湍流m≈1 / 7,计算平均流速。
解:该流动的体积流量为
\[{{q}_{v}}=\int{{{V}_{x}}dA=\int_{0}^{R}{{{V}_{0}}\left( 1-\frac{r}{R} \right)_{{}}^{m}}2\pi rdr}\]
平均流速为
\[\begin{align}
& {{V}_{av}}=\frac{{{q}_{v}}}{A}=\frac{1}{\pi R{{_{{}}^{2}}_{{}}}}\int_{0}^{R}{{{V}_{0}}\left( 1-\frac{r}{R} \right)_{{}}^{m}2\pi rdr} \\
& {{V}_{av}}={{V}_{0}}\frac{2}{\left( 1+m \right)\left( 2+m \right)} \\
\end{align}\]
对于层流m≈1/2,Vav≈0.53Vo。对于湍流m≈1 / 7,Vav≈0.82Vo。对比两种流动可见,湍流的平均速度略小于最大速度,速度分布相对均匀。
例3.10 某涡轮喷气发动机在设计状态下工作时,已知在尾喷管进口截面气流参数为:p1=2.05×105pa,T1=865 K,V1= 288 m/s,A1=0. 19㎡;出口截面的气流参数为:p2=1.143×105pa,T2=766 K,A2=0.1538㎡。试求通过尾喷管的燃气质量流量和出囗速度。给定燃气(k=1.33)的气体常数R=287.4 J/(kg·K)。
解:根据连续方程,质量流量为
\[{{q}_{m}}=\rho AV=\frac{p}{RT}AV=\frac{{{p}_{1}}{{A}_{1}}{{V}_{1}}}{R{{T}_{1}}}=45.1kg/s\]
由于\[{{q}_{m}}=\frac{{{p}_{1}}{{A}_{1}}{{V}_{1}}}{R{{T}_{1}}}=\frac{{{p}_{2}}{{A}_{2}}{{V}_{2}}}{R{{T}_{2}}}\]
所以\[{{V}_{2}}={{V}_{1}}\frac{{{A}_{1}}}{{{A}_{2}}}\frac{{{P}_{1}}}{{{P}_{2}}}\frac{{{T}_{2}}}{{{T}_{1}}}=565.1m/s\]
3.5 动量方程
将雷诺输运定律表达式(式(3.28))中的Ф换为动量mV,则β=dФ/dm=V,根据牛顿第二定律(式(3.23b)),有
\(\frac{d}{dt}{{\left( mV \right)}_{s}}=\sum F\)=∫(cv) ∂(ρV)dv/∂t+∮(cs) ρV(V x n)dA (3.41)
式(3.41)即为动量方程。关于此式需要强调以下三点:
(1)V是流体相对于某一惯性坐标系的速度,如果坐标系运动则应考虑相对速度,而且,在非惯性系中作用力必须要考虑惯性力。
(2)∑F是作用在控制体上所有力的矢量和,包括表面力以及质量力(体积力)。等号右边第一项表示控制体内流体所具有的动量随时间的变化率,对定常流该项为零。第二项表示通过控制体表面的流体动量通量,它等于单位时间内净流出控制体的流体动量。
(3)整个方程为矢量关系式,在直角坐标系中有三个分量式,其x方向的分量式为
\[\sum {{F}_{x}}=\int_{cv}{\frac{\partial \left( \rho {{V}_{x}} \right)}{\partial t}}dv+\oint_{cs}{\rho {{V}_{x}}{{V}_{n}}}dA\] (3.42)
同理,将∑Fy,∑Fz,Vy和Vz代入,可分别得到y,z方向的分量式。
对于定常流动,式(3.41)为
∑F=∮(cs) ρV(V x n)dA (3.43)
式中,(V·n)为速度矢量与控制面外法向单位矢量的点积,对于流入控制体应为负,流出为正。对于一维流动,其动量为
M=qmV=ρVnAV (3.44)
如果控制体的所有进、出囗参数均匀,则式(3.42)为
∑F=∫(cv) ∂(ρV)dv/∂t+\(\sum {{\left( {{q}_{mi}}{{V}_{i}} \right)}_{out}}-\sum {{\left( {{q}_{mi}}{{V}_{i}} \right)}_{in}}\) (3.45)
式(3.45)说明,作用在控制体上的合力等于该控制体内动量随时间的变化率加上单位时间进、出口动量的矢量和。式(3.45)在具体应用时常采用直角坐标系分量形式。此外,对于固定形状控制体在定常流动的情况下,式(3.45)等号右边第一项为零。因此,其x方向的分量式(其他方向类同)为
\[\sum {{F}_{x}}=\sum {{\left( {{q}_{mi}}{{V}_{xi}} \right)}_{out}}-\sum {{\left( {{q}_{mi}}{{V}_{xi}} \right)}_{in}}\] (3.46)
同样可以证明,在定常流动的条件下,对于任意形状的控制体,只要在控制体的进、出口截面上流体参数是均匀的,而不论流体在控制体内部的流动情况如何,所导出的动量方程与式(3.46)是相同的。
控制体形式的动量方程是流体动力学中最常用的基本方程之一。其优点在于,只要知道控制体进、出口的流动情况,就可以得出作用在控制体上的力,而无须知道控制体内部的流动细节。
动量方程式中的作用力为质量力和表面力。质量力的合力可表示为
\[{{F}_{B}}=\int_{cv}{R\rho dv}\] (3.47)
一般情况下,控制体受到的表面力包括两部分一一压力和黏性力,即法向力和切向力。对于理想流体,切向力为零,因此,表面力仅为法向压力。
下面首先来分析压力的作用。由第二章已经知道,作用在流体表面的压力与表面垂直并指向内部。因为表面单位矢量向外为正,所以压力可以表示为
\[{{F}_{p}}=\oint_{cs}{p\left( -n \right)}dA\] (3.48)
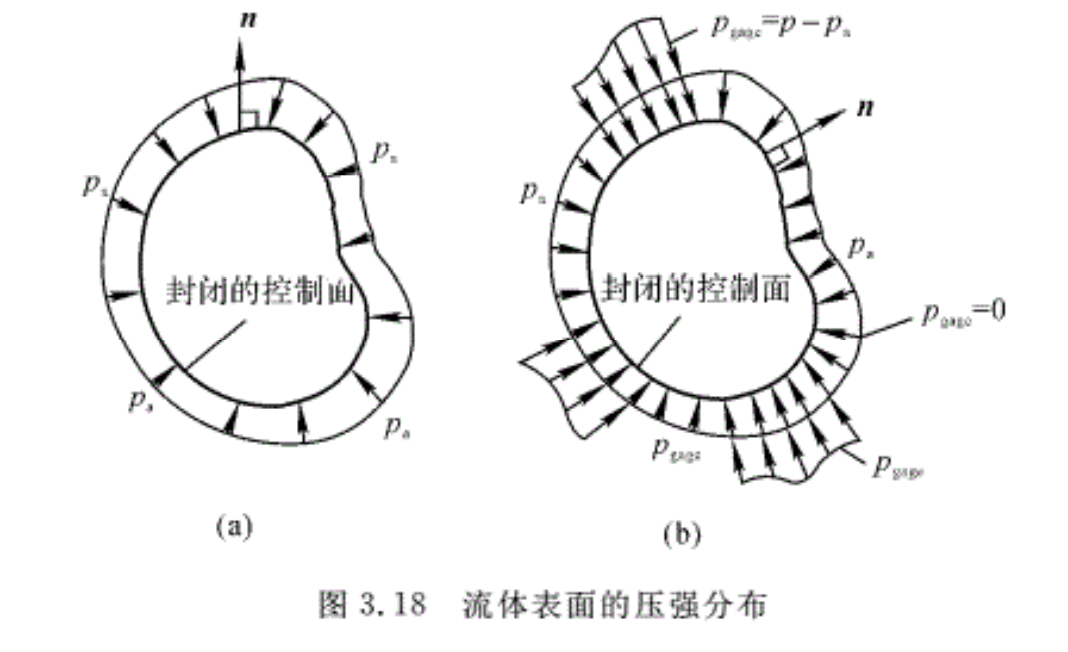
如果整个表面上压强相等都为pa,如图3.18(a)所示,则对于封闭的表面,压力的合力为零,即
\[{{F}_{p}}=-{{p}_{a}}\oint_{cs}{n}dA=0\]
这一结果表明,只要表面封闭且压强处处相等,无论表面形状如何,合力恒为零。当控制面上压强并非处处相等时,如图3.18(b)所示,则pa相互抵消,剩下的只有表压p(gage)=p-pa的作用,即
\[{{F}_{p}}=\oint_{cs}{\left( p-{{p}_{a}} \right)}\left( -n \right)dA=\oint_{cs}{{{p}_{gage}}\left( -n \right)}dA\]
将式(3.47)和式(3.48)代入式(3.41),得到适合于控制体的动量方程为
∫(cv) ∂(ρV)dv/∂t+∮(cs) ρV(V x n)dA = ∫(cv) Rρdv-∮(cs) pndA (3.49)
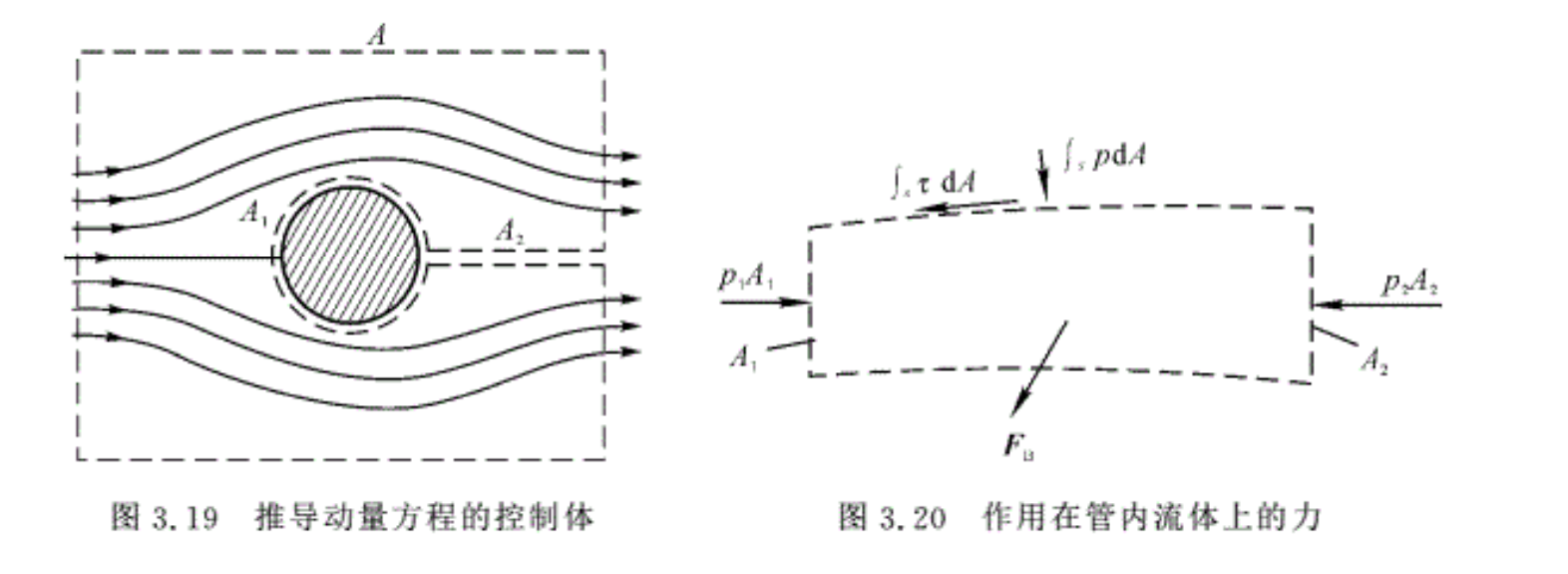
考虑到动量方程的实际应用大多数是在于求对物体的作用力Fe,为此取如图3.19所示的控制体,控制面由A,A1,A2组成。为了方便,把表面力分解成两部分,即物体(通过控制面A1)对控制体内流体的作用力-Fe和控制体外流体作用于控制面A上的压力\(-\int\limits_{A}{pndA}\),A2控制面是双层的,因此压力合力为零。在求流体对物体的作用力时,所取控制体只要把物体包围在内即可,并且动量方程式(3.41)可写成
∫(cv) ∂(ρV)dv/∂t+∮(cs) ρV(V x n)dA = –Fe+ ∫(cv) Rρdv-∮(cs) pndA (3.50a)
式(3.50a)还可以写成在三个坐标轴上的投影式,例如x方向的分量式为
∫(cv) ∂(ρVx)dv/∂t+∮(cs) ρVnVxdA = -F(ex)+∫(cv) Xρdv-∫(cs) pcosθdA (3.50b)
对于一维流动,图3.20表示了作用于控制体内流体的质量力,记为FB;控制体外的流体或固体作用在控制面上的表面力,一部分为控制面的进、出囗截面上表面力的法向力p1A1,p2A2(均指向作用面),由于A1,A2分别与气流速度方向垂直,故无剪切力;另一部分为作用在控制面的侧表面上的法向力∫(cs) pdA 和剪切力 ∫(cs) τdA 。在大多数情况下,后两种力是未知的,因此,侧表面上的法向力和剪切力的合力用Fi表示。这样,动量方程式中的合力为
\[\sum F=\overrightarrow{{{p}_{1}}{{A}_{1}}}+\overrightarrow{{{p}_{2}}{{A}_{2}}}+{{F}_{i}}+{{F}_{B}}\] (3.51)
则一维定常流动的动量方程可表示为
\[\overrightarrow{{{p}_{1}}{{A}_{1}}}+\overrightarrow{{{p}_{2}}{{A}_{2}}}+{{F}_{i}}+{{F}_{B}}={{q}_{m}}\left( {{V}_{2}}-{{V}_{1}} \right)\] (3.52)
对于流体在管道中的流动,Fi即为管壁施加于管内流体上的作用力。根据牛顿第三运动定律,管内流体作用于管壁上的力Fd和Fi大小相等,方向相反。
在具体解决问题时,动量方程运用成功与否,与所选的控制体是否恰当很有关系,但是很难给出普遍适用的控制面选取的原则,一般尽量包括所要研究的边界面、己知物理量尽量多的面和流面等。
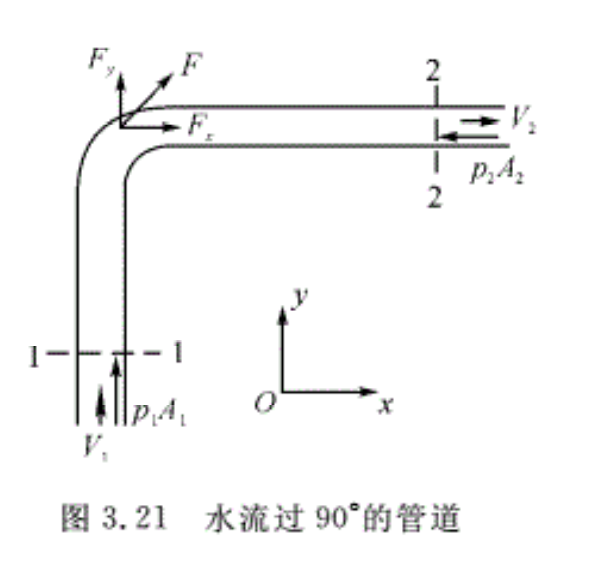
例3.11 如图3.21所示,水流过一弯曲90°的管道,在进口1一1截面处水流的压强为4.91 × 105 Pa,在出口截面2一2 处压强为4.19 × 105 Pa,水的流量为78.5kg/s。截面1一1的直径为10cm,2一2的直径为8 cm,如果忽略水流的自重,求水对管壁的作用力。
解:选弯管内侧面和进、出口截面为控制面,如图3.21中虚线所示。因为忽略水自重,所以控制体受力只有表面力包括进出口的压力和侧面管壁的作用力,其中后者的反作用力即为所求的力。
在如图3.21所示直角坐标系下,设管壁对控制体内水流的作用力为F=Fxi+Fyj,对所选控制体在x和y方向分别使用动量方程,有
\({{F}_{x}}-{{p}_{2}}{{A}_{2}}={{q}_{m}}{{V}_{2}}\) (a)
\({{F}_{y}}+{{p}_{1}}{{A}_{1}}={{q}_{m}}{{\left( 0-{{V}_{1}} \right)}_{{}}}\) (b)
式中
\[\begin{align}
& {{V}_{1}}=\frac{{{q}_{m}}}{{{\rho }_{1}}{{A}_{1}}}=\frac{78.5}{1000\times \frac{\pi }{4}\times 0.01}=10m/s \\
& {{V}_{2}}=\frac{{{q}_{m}}}{{{\rho }_{2}}{{A}_{2}}}=\frac{78.5}{1000\times \frac{\pi }{4}\times 0.08_{{}}^{2}}=15.6m/s \\
\end{align}\]
将V1,V2等代入式(a),式(b),得
Fx=+(4.19 x 105 x π/4 x 0.08²+78.5 x 15.6)=+3329.6N
Fy=-(4.91 x 105 x π/4 x 0.1²+78.5 x 10)=-4639.4N
负号说明Fy的方向与图中假设方向相反。根据作用力与反作用力定律,水流对弯管的作用力与管壁对水流的作用力大小相等、方向相反,即Fdx=-Fx,Fdy=-Fy。作用力的合力为
\[{{F}_{d}}=\sqrt{{{F}_{dx}}^{2}+{{F}_{dy}}^{2}}=\sqrt{{{4640}^{2}}+{{3329.6}^{2}}}=5712N\]
Fd与x的负方向(第2象限)的夹角为
\[\alpha =\arctan \frac{{{F}_{dy}}}{{{F}_{dx}}}=\arctan \left( -\frac{4639.4}{3329.6} \right)=-54.3{}^\circ \]
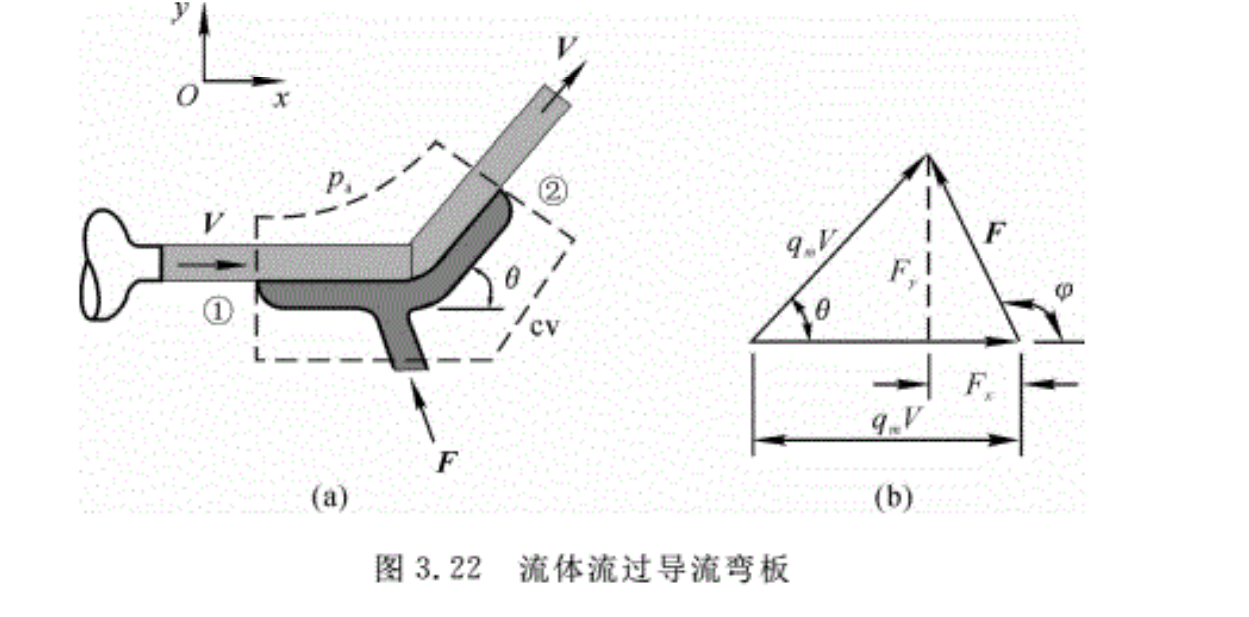
例3.12 流体流过导流弯板,如图3.22所示,己知射流截面积为A,射流速度为V,其大小不变,弯板转角为θ,流动定常,压强处处为pa,忽略摩擦,求弯板的支撑力F。
解:选控制体如图3.22中虚线所示,如忽略流体和弯板的自重,而且控制面上压强处处为pa,所以对整个封闭的控制面其合力为零,则控制体所受的外力只有弯板支撑处的F。根据动量方程,有
\[F={{q}_{m2}}{{V}_{2}}-{{q}_{m1}}{{V}_{1}}\]
由连续方程,qm2=qm1=qm=ρAV,在如图3.22所示的直角坐标系中,x,y方向的动量方程有
\[\begin{align}
& {{F}_{x}}={{q}_{m}}\left( {{V}_{2x}}-{{V}_{1x}} \right)={{q}_{m}}V\left( \cos \theta -1 \right) \\
& {{F}_{y}}={{q}_{m}}\left( {{V}_{2y}}-{{V}_{1y}} \right)={{q}_{m}}V\sin \theta \\
\end{align}\]
合力大小为
\[F=\sqrt{{{F}_{x}}^{2}+{{F}_{y}}^{2}}={{q}_{m}}V\sqrt{\sin {{\theta }^{2}}+{{\left( \cos \theta -1 \right)}^{2}}}=2{{q}_{m}}V\sin \frac{\theta }{2}\]
方向为
\[\tan \alpha =\frac{{{F}_{y}}}{{{F}_{x}}}=\frac{\sin \theta }{\cos \theta -1}\]
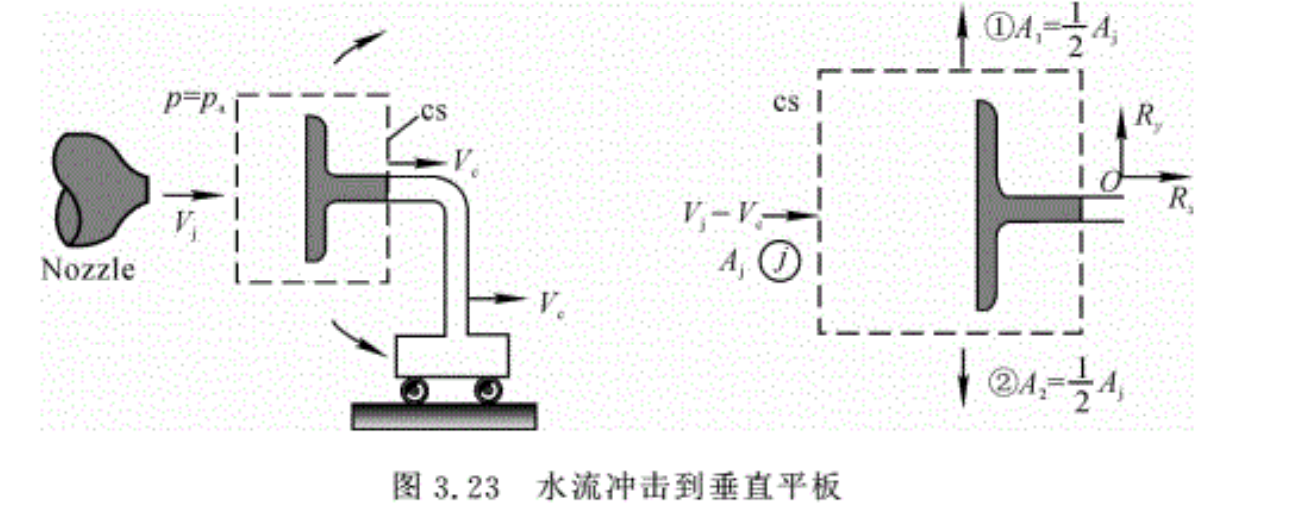
例3.13 一股水流以水平速度Vj冲击到一垂直平板,该平板同时以水平速度Vc向右运动,如图3.23所示。如果水的密度为1 000 kg/m³,射流的截面积为3cm²,Vj,Vc分别为 20 m/ s和15 m/ s,如果忽略水和板的自重,水流相对于平板为定常,且上、下平均分开。试求保持平板匀速运动所需的力。
解:选控制体如图中虚线所示,该控制体随平板以Vc运动,因此相对平板来说,控制体是静止的,根据相对运动原理,此时流入控制体的来流速度应为Vj—Vc:,控制体所受的外力,只有平板后的水平支撑在与控制面切割处作用到控制体上的力,此力即为所求之力。
根据连续方程,有
\( {{q}_{m,out}}\text{=}{{q}_{m,in}}\)
\[{{\rho }_{1}}{{A}_{1}}{{V}_{1}}+{{\rho }_{2}}{{A}_{2}}{{V}_{2}}={{\rho }_{j}}{{A}_{j}}\left( {{V}_{j}}-{{V}_{c}} \right)\]
流动不可压,有ρ1=ρ2=ρj,所以,
\[{{A}_{1}}{{V}_{1}}+{{A}_{2}}{{V}_{2}}\text{=}{{A}_{\text{j}}}\left( {{V}_{j}}-{{V}_{c}} \right)\]
己知上、下对称,有V1=V2,A1=A2=Aj/2,所以,
\({{V}_{1}}\text{=}{{V}_{2}}\text{=}{{V}_{j}}-{{V}_{c}}=20-15=5m/s\)
由动量方程,得
x方向:
\(\sum {{F}_{x}}={{R}_{x}}={{q}_{m1}}{{V}_{1x}}+{{q}_{m2}}{{V}_{2x}}-{{q}_{mj}}{{V}_{jx}}=-\left[ {{\rho }_{j}}{{A}_{j}}\left( {{V}_{j}}-{{V}_{c}} \right) \right]\left( {{V}_{j}}-{{V}_{c}} \right)\)
Rx=-1000 x 0.0003 x 5=-1.5N
y方向:
\(\begin{align}
& {{R}_{y}}={{q}_{m1}}{{V}_{1y}}+{{q}_{m2}}{{V}_{2y}}-{{q}_{mj}}{{V}_{jy}} \\
& {{R}_{y}}={{q}_{m1}}{{V}_{1}}+{{q}_{m2}}\left( -{{V}_{2}} \right)=\frac{1}{2}{{q}_{mj}}\left( {{V}_{1}}-{{V}_{2}} \right)=0 \\
\end{align}
\)
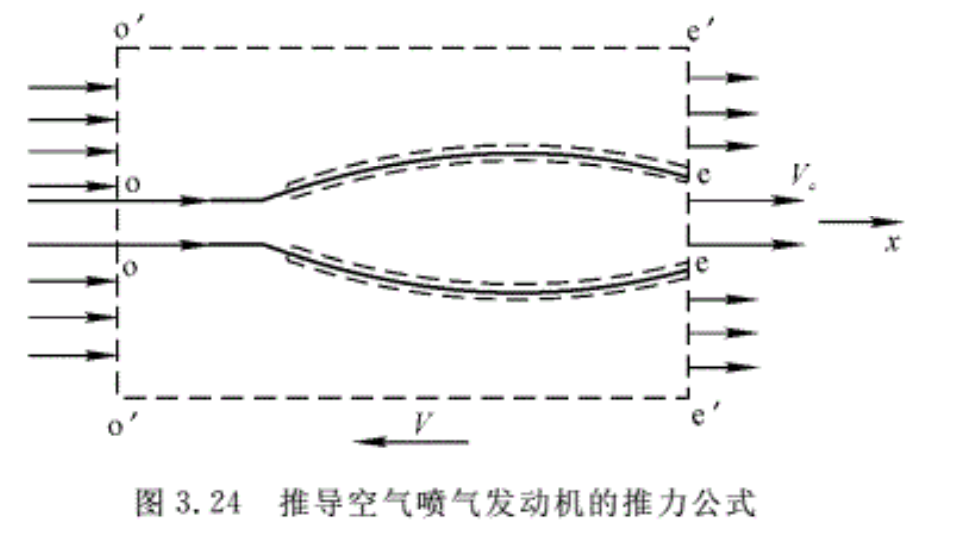
例3.14 推导空气喷气发动机的推力公式。
解:发动机的推力是发动机所产生的推动发动机前进的力。推力的物理实质是内、外气流作用在发动机所有湿表面上的轴向力的合力。如果直接按定义求推力是非常困难的。但是,如果将发动机看成一个整体,根据动量定理,直接从气流经过发动机时的动量变化率来计算推力,可以不涉及发动机内部的流动细节,这样就会简单很多。
设发动机以飞机飞行速度V相对地面运动。为了便于研究,将坐标系固定在发动机上,且x方向与来流方向一致。因此在此坐标系观察到的情况是发动机静止,而空气则以与V大小相等、方向相反的速度流入发动机,以Ve表示从发动机尾喷囗射出的速度(见图3.24)。取控制体如图中虚线所示。控制面o’—e’为圆柱面,母线与发动机的轴向即x方向平行,且离发动机足够远,因此可以认为它是一个流面,其上的压强为大气压强pa。控制面o’—o’为圆截面,垂直于发动机的轴线,取在未受进口扰动的足够远前方,这是因为发动机进口截面处的气流参数一般不易确定。o’—o’面上的气体压强为大气压强pa,气流速度为V。控制面e一e为发动机尾喷管的出口平面,在该截面上,燃气的喷射速度与x方向近似平行,速度的平均值为Ve,压强的平均值为pe。e’一e’和e一e位于同一平面内,它是环形截面,假定不计气流从外部流过时的摩擦,并且与发动机内部的燃气无热量交换,因此可以近似地认为,从发动机外部流过的空气在截面e’一e’上,各参数与远前方来流o’一o’处相同。
下面对控制体在轴线方向写出动量方程。
首先分析受力情况:
截面e一e所受外界气体的压力:peAe(Ae是e一e面的面积);
截面o’—o’所受外界气体的压力:paA’o(Ao是o’—o’面的面积);
环形截面e一e’所受外界气体的压力:pa(A’e-Ae)(A’e是e’一e’截面的面积且A’e=A’o)。
假定发动机湿表面对内、外气流在轴向的作用力的合力为Rx,其方向与气流方向一致,则 Rx与发动机的推力互为作用力和反作用力。
作用在控制体上的合力为
\({{R}_{x}}+{{p}_{a}}{{A}^{\prime }}_{0}-{{p}_{a}}\left( {{A}^{\prime }}_{e}-{{A}_{e}} \right)-{{p}_{e}}{{A}_{e}}={{R}_{x}}-{{A}_{e}}\left( {{p}_{e}}-{{p}_{a}} \right)\)
流流过控制体在x方向的动量变化率(外流的动量变化率为零)为
\({{q}_{m,bg}}{{V}_{e}}-{{q}_{m}}{{V}_{{}}}\)
其中,qm表示空气由o一o截面流入发动机的流量;qm,bg表示燃气从e一e截面流出发动机的流量,它等于空气流量qm和燃油流量qm,f之和,即
\({{q}_{m,bg}}={{q}_{m}}+{{q}_{m,f}}={{q}_{m}}\left( 1+\frac{{{q}_{m,f}}}{{{q}_{m}}} \right)\)
然后根据控制体受力情况,写出其轴向的动量方程。在x方向,气流流经控制体时的动量变化率,应等于作用在控制体上的合力,故有
\(\begin{align}
& {{R}_{x}}-{{A}_{e}}\left( {{p}_{e}}-{{p}_{a}} \right)={{q}_{m,bg}}{{V}_{e}}-{{q}_{m}}V \\
& {{R}_{x}}={{q}_{m,bg}}{{V}_{e}}-{{q}_{m}}V+{{A}_{e}}\left( {{p}_{e}}-{{p}_{a}} \right) \\
\end{align}
\) (3.53)
因此,发动机的推力为-Rx,其方向与x方向相反。在近似计算时,可假设qm,bg≈qm,则推力的大小可写成
\({{R}_{{}}}={{q}_{m}}\left( {{V}_{e}}-V \right)+{{A}_{e}}\left( {{p}_{e}}-{{p}_{a}} \right)\) (3.54)
需要说明的是,推力公式(式(3.53))是在假设气流从发动机外部流过无摩擦等理想条件下导出的,因而它未计入外部阻力。通常把该式称为发动机的内推力或额定推力公式。
例3.15 某涡轮喷气发动机在地面试车时,当地的大气压强为1.0133 × 105 Pa,发动机的尾喷管出口面积为0.1543m²,出口气流参数为pe=1.141×105Pa,Ve—542 m/s,流量 qm=43.4kg/s.试求发动机的推力。
解:因为在地面试车,V=0,所以
\({{R}_{{}}}={{q}_{m}}{{V}_{e}}+{{A}_{e}}\left( {{p}_{e}}-{{p}_{a}} \right)=43.4\times 542+\left( 1.141-1.0133 \right)\times {{10}^{5}}\times 0.1543=25493N\)
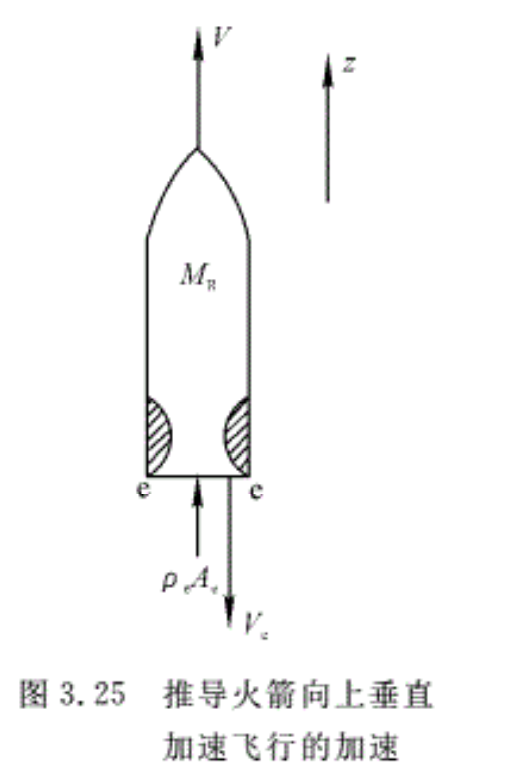
例3.16 运用动量定理导出火箭向上垂直加速飞行(见图 3.25)的速度公式(设火箭内气体的运动相对火箭是定常的)。
解:取火箭本身的外壳表面和喷管的出口平面为控制面。对此控制面沿火箭飞行方向(z方向)写动量方程。为方便起见,取与火箭以同样速度运动的相对坐标系。因为火箭作加速运动,故该坐标系为非惯性系。在本节开始的时候曾强调,对于非惯性坐标系,在运用动量方程时,要将惯性力考虑到合力中,并把速度改为相对速度。由此,对所取的控制面沿z方向的动量方程,可以写为
\(-{{M}_{R}}g+{{A}_{e}}\left( {{p}_{e}}-{{p}_{a}} \right)-{{F}_{d}}-{{M}_{R}}\frac{dV}{dt}=-{{q}_{m,bg}}{{V}_{e}}\)
式中:第一项——用在控制体的重力(MR为火箭整体的瞬时质量);
第二项——作用在控制面上压强的合力在z方向上的投影(pe为喷管出囗处的压强,pa为大气压强,Ae为喷管出口处的截面积);
第三项——作用在控制面上的全部阻力的合力在z方向上的投影;
第四项——火箭的惯性力,方向与火箭的加速度相反(V为火箭飞行的瞬时速度);
第五项——从控制面e一e气体动量的流出率(qm,bg为燃气的流量,ve为气体相对于所取坐标的速度)。
将上式整理后得
\({{M}_{R}}\frac{dV}{dt}=\left[ {{q}_{m,bg}}{{V}_{e}}+{{A}_{e}}\left( {{p}_{e}}-{{p}_{a}} \right) \right]-\left( {{F}_{d}}+{{M}_{R}}g \right)\)
3.6 动量矩方程
与第3.5节建立动量方程的方法相同,控制体的方法同样可以运用到对动量矩的分析中。取雷诺输运定律表达式(式(3.27))中的Ф为动量矩H。对于流体系统,关于某一坐标轴的动量矩为
\(H=\int_{cv}{\left( r\times V \right)}dm\) (3.55)
式中:r——流体微元质量dm距坐标原点的矢径;
V——微元流体的速度。
那么,单位质量的角动量为
β=dH/dm=r x V (3.56)
代入雷诺输运定理表达式(式(3.28)),得
(dH/dt)s=∂/∂t[∫(cv) (r x V)ρdv+∫(cs) (r x V)(V x n)ρdA] (3.57)
根据动量矩方程,系统关于某一轴的动量矩的变化率应等于该时刻系统所受所有外力对同一轴的力矩之和,故式(3.57)可写成
∑M=∑(r x F)= ∂/∂t[∫(cv) (r x V)ρdv+∫(cs) (r x V)(V x n)ρdA] (3.58)
如果控制体的进、出囗为一维流动,则动量矩流率为
∫(cs) (r x V)(V x n)ρdA= ∑(r x V)out qm,out—∑(r x V)in qm,in (3.59)
对于定常流动,\(\frac{\partial }{\partial t}\left[ \int\limits_{cv}{\left( r\times V \right)\rho dv} \right]=0\)。因此,一维定常流动的动量矩方程为
\(\sum M=\sum {{\left( r\times V \right)}_{out}}{{q}_{m,out}}-\sum {{\left( r\times V \right)}_{in}}{{q}_{m,in}}\) (3.60)
方程式(3.60)表明:对于流动定常且进、出口为一维的固定控制体,作用在控制体上诸外力对于某轴的力矩总和,等于单位时间内从控制面流出与流入的流体对该轴的动量矩之和。
在对叶轮机械的研究中,经常采用圆柱坐标系,如图3.26所示,而且主要应用于建立对旋转轴的动量矩方程。对于Oz轴的动量矩方程可写为
\(\sum {{M}_{z}}={{q}_{m}}\left( {{V}_{2}}{{r}_{2}}-{{V}_{1}}{{r}_{1}} \right)\) (3.61)
例3.17 流体在如图3.27所示的径流式叶轮机中作定常流动,流过整个叶轮的质量流量为qm,进入叶轮时的流体速度为V1,流出叶轮时的速度为V2。试写出对于旋转轴(Oz轴)的动量矩方程。
解:取控制体如图3.27(b)中虚线所示,它包围整个转子,并切割转轴。设在控制面的进、出口截面1一1和2一2上,流体参数沿周向是均匀的,则单位时间内进、出控制体的动量矩之差为
\({{q}_{m}}\left( {{V}_{2u}}{{r}_{2}}-{{V}_{1u}}{{r}_{1}} \right)\)
现在分析作用在控制面上诸外力对Oz轴的力矩:作用在截面1一1和2一2上的压强对于Oz轴的矩为零。如果忽略由于转子与充满在叶轮机壳体内的流体之间的摩擦所产生的力矩,则单位时间作用在控制体中流体上的外力矩就等于外界通过转轴加于叶轮的转矩Mz,根据式(3.61)可得
\({{M}_{z}}={{q}_{m}}\left( {{V}_{2u}}{{r}_{2}}-{{V}_{1u}}{{r}_{1}} \right)\) (3.62)
方程式(3.62)是动量矩定理应用于流体在叶轮机中的定常流动的解析式,称为动量矩的欧拉方程。如果将式(3.62)两端同乘以叶轮机的旋转角速度ω,则可得外界给予叶轮机的功率,即
\(N={{M}_{z}}\omega ={{q}_{m}}\left( {{V}_{2u}}{{r}_{2}}-{{V}_{1u}}{{r}_{1}} \right)\omega\)
或 \(N={{q}_{m}}\left( {{V}_{2u}}{{U}_{2}}-{{V}_{1u}}{{U}_{1}} \right)\) (3.63)
式中,U1,U2表示叶轮在半径r1及r2处的圆周速度。
功率是外力对每秒流过叶轮机的流体所做的功,所以外力对流过叶轮机的单位质量流体做功的功率为
\(\omega =\frac{N}{{{q}_{m}}}={{V}_{2u}}{{U}_{2}}-{{V}_{1u}}{{U}_{1}}\) (3.64)
这就是在分析和计算压气机或涡轮的功时经常用到的公式。
如果作用在流体上的外力矩为零,根据动量矩方程式(3.62),得出
\({{V}_{2u}}{{r}_{2}}={{V}_{1u}}{{r}_{1}}={{V}_{u}}{{r}_{{}}}=const\) (3.65)
式(3.65)就是著名的面积定律。它说明,在没有外力矩作用而流体只依靠本身的惯性运动的情况下,气流的切向速度与半径成反比。半径越大,气流的切向速度越小;反之则相反。例如,气体在离心式压气机的扩压器内的流动,燃料在离心式喷嘴内的旋转运动等,均属于这种情形。
3.7 能量方程
将雷诺输运定理运用到热力学第一定律,可以得出控制体形式的能量方程。令雷诺输运定律表达式(式(3.27))中的Ф为能量E,则单位质量流体所具有的能量为β=dE/dm=e。对固定的控制体,其能量方程形式为
dQ/dt-dW/dt=dE/dt=∫(cv) ∂(eρ)dv/∂t+∮(cs) eρ(V x n)dA (3.66)
在第3.3节中己经说明,正的Q表示传给系统热量,正的W表示系统对外做功。
系统中单位质量流体所具有的能量e由以下几部分组成:
式中,等号右边4项分别为内能、动能、势能及其他形式的能量。其中,其他形式能量主要包括化学反应、核反应、电磁场作用等形式的能量。如果忽略其他形式的能量,且势能中仅考虑重力势能,并令z坐标向上为正,则单位质量流体的能量可表示为
e=u+V²/2+gz (3.67)
将系统做功(功率)分为三部分:
Ẁ=Ẁs+Ẁp+Ẁv
下标s,p,v分别表示轴功、压力做功和黏性切应力做功。
其中,轴功表示系统中的流体通过某种机械对外所做的功。
压力做功只产生在控制面上,对于控制面上的某一微元面积,压力做功应为微元面上的压力乘以微元面上速度的法向分量,即
dẀp=(pdA)Vn=p(V x n)dA
通过对dẀp在整个控制面上积分便得到流体对外做的压力功功率,即
Ẁp=∫(cs) p(V x n)dA (3.68)
黏性切应力做功的功率也是发生在控制面上,其值应为黏性力与速度的点积,即
dẀv=-τ x VdA
或者 Ẁv=-∫(cs) τ x VdA (3.69)
式中,负号表示是外界对控制体做功。
根据控制体的选择不同,黏性力做功项也会有不同的形式。如果控制面为固壁,则根据无滑移条件,速度为零,所以黏性力做功也为零;对于机械的表面黏性力做功项将与轴功合并;对于进、出囗面速度近似与截面垂直,只有黏性正应力做功,一般情况下,因为黏性正应力很小,因此这一项也常常可以忽略掉。但是对于某些特殊情况,如激波等,此项必须考虑。
对于控制面为流面的情况,如果流动无黏性,则无黏性力之功,否则应计入该项作用。
经过上述讨论,得出系统对外做功的功率为
Ẁ=Ẁs+∫(cs) p(V x n)dA-∫(cs) (τ x V)ssdA (3.70)
将式(3.70)、式(3.67)代入式(3.66)发现压力做功项可以和能量流率项合并,因为都含有 V·n的面积分,得出控制体的能量方程为
Q′-Ẁs-(Ẁv)ss=∂/∂t[∫(cv) (eρ)dv]+∫(cs) (e+p/ρ)ρ(V x n)dA (3.71)
式中,下标ss表示流面。己知焓h=u+p/ρ,代入式(3.71),得出对于固定控制体一般形式的能量方程为
Q′-Ẁs-Ẁv=∂/∂t[∫(cv) (u+V²/2+gz)ρdv]+∫(cs) (h+V²/2+gz)ρ(V x n)dA (3.72)
如果控制体具有若干个一维进、出囗截面,则式(3.72)中的面积分将简化为流出控制体能量流率和流入控制体能量流率的差。对于流动定常、进出口一维的固定控制体,能量方程式(3.72)为
Q′-Ẁs-Ẁv=∑ (h+V²/2+gz)out qm,out-∑ (h+V²/2+gz)in qm,in (3.73)
对于只有一个进口(1截面)和一个出口(2截面)的控制体,有
Q′-Ẁs-Ẁv= (h2+V2²/2+gz2) qm,2- (h1+V1²/2+gz1) qm,1 (3.74)
考虑到连续方程qm1=qm2=qm,式(3.73)可以写成
\({{h}_{1}}+\frac{1}{2}V_{1}^{2}+g{{z}_{1}}={{h}_{2}}+\frac{1}{2}V_{2}^{2}+g{{z}_{2}}-q+{{\omega }_{s}}+{{\omega }_{v}}\) (3.75)
式中:q——传给单位质量流体的热量,q=Q′/qm=dQ/dm;
ωs——单位质量流体对外做的轴功,ωs=Ẁs/qm=dWs/dm;
ωv——单位质量流体由于黏性力对外做的功,ωv=Ẁv/qm=dWv/dm.
式(3.75)说明,上游1截面处单位质量流体所具有的总能量h1+V²1/2+gz1,等于下游2截面的总能量加上单位质量流体对外做的轴功和黏性力功再减去单位质量流体吸收的热量。
当研究对象为气体时,在高度变化不是很大的情况下,可以略去位能的变化,如果所选控制面使得黏性力做功为零,这样式(3.75)可以写成
\[q-{{\omega }_{s}}=\left( {{h}_{2}}-{{h}_{1}} \right)+\frac{1}{2}\left( V_{2}^{2}-V_{1}^{2} \right)\] (3.76)
式(3.76)是大多数工程热力学教科书中常见的一维定常流动的能量方程式,又叫热焓形式能量方程式。它表明,外界加给气流的热量用来对外界做功和增加气体的焓和动能。在推导式(3.76)时并未涉及气体在控制体内流动的具体情况,因此该式对流动是否是可逆过程都适用。
对于微元控制体,式(3.76)为
\[\delta q-\delta {{\omega }_{s}}=d\left( \frac{V_{{}}^{2}}{2} \right)+dh\] (3.77)
式(3.77)是一维定常流动的微分形式的能量方程。
对于绝能流动过程,因为q=0(δq=0),ωs=0(δωs=0),能量方程式(3.76)和式(3.77)简化为
\[{{h}_{1}}+\frac{1}{2}V_{1}^{2}={{h}_{2}}+\frac{1}{2}V_{2}^{2}=const\] (3.78)
\[d\left( \frac{V_{{}}^{2}}{2} \right)+dh=0\] (3.79)
对于完全气体,气体的焓h=cpT,代入方程式(3.78)和式(3.79)中,得
\[{{c}_{p}}{{T}_{1}}+\frac{1}{2}V_{1}^{2}={{c}_{p}}{{T}_{2}}+\frac{1}{2}V_{2}^{2}=const\] (3.80)
\[d\left( \frac{V_{{}}^{2}}{2} \right)+{{c}_{p}}dT=0\] (3.81)
式(3.78)表明,在绝能流动中,管道各个截面上气流的焓和动能之和保持不变,但两者之间却可以相互转换。如果气体的焓减小(表现为温度降低),则气体的动能增大(表现为气体的速度增大);反之,如果气体的动能减小,则气体的焓增大。
在涡轮喷气发动机中,对于气体在进气道、尾喷管、压气机(或涡轮)静子通道内的流动,可以近似地认为是绝能流动。
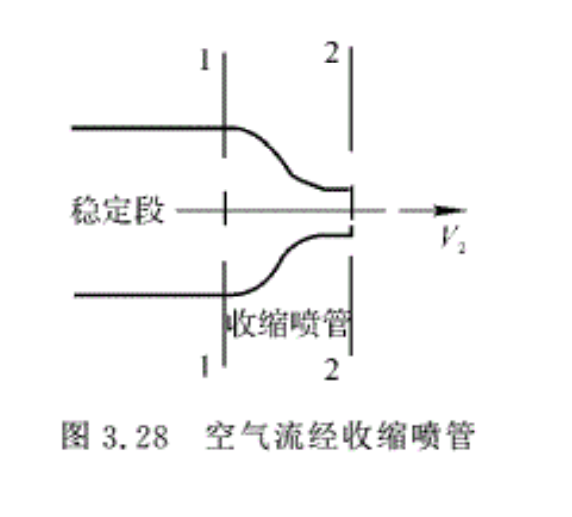
例3.18 空气从图3.28所示的收缩喷管射出,在稳定段中空气压强p1=1.47×105Pa,温度T1=293 K,在喷管出囗处,气流的压强等于外界大气压强pa=1.0133×105Pa。忽略空气在喷管中的摩擦影响,并假设在流动中与外界无热量交换,空气的比定压热(cp=kR/(k+1))为常数。求喷管出口截面上空气的速度及温度。
解:由于稳定段直径比喷囗出囗直径大得多,所以稳定段中气流的速度相当小,可以忽略不计,近似认为V1≈0。
根据式(3.80),喷管出囗截面上的空气速度为
\[{{V}_{2}}=\sqrt{2{{c}_{p}}\left( {{T}_{1}}-{{T}_{2}} \right)}=\sqrt{\frac{2k}{k-1}R{{T}_{1}}\left( 1-\frac{{{T}_{2}}}{{{T}_{1}}} \right)}\]
由于忽略空气在喷管内流动时的摩擦影响,并假设在流动中与外界无热量交换,故可以认为空气在喷管内流动为等熵过程。因此
\[\frac{{{T}_{2}}}{{{T}_{1}}}=\left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)_{{}}^{\frac{k-1}{k}}\]
将此式代入前式,得
\[{{V}_{2}}=\sqrt{\frac{2k}{k-1}R{{T}_{1}}\left[ 1-\left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)_{{}}^{\frac{k-1}{k}} \right]}\]
将己知数据代入,得
\[\begin{align}
& {{T}_{2}}={{T}_{1}}\left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)_{{}}^{\frac{k-1}{k}}=263.7K \\
& {{V}_{2}}=244m/s \\
\end{align}\]
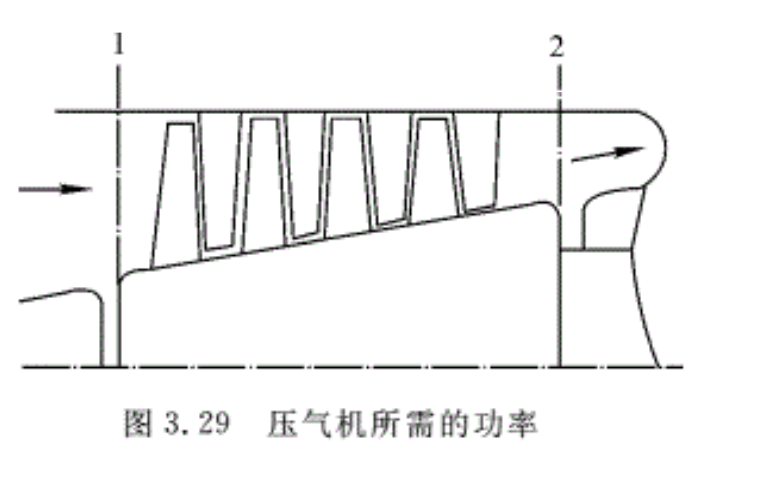
例3.19 某涡轮喷气发动机,空气进入压气机时的温度T1=290 K,经压气机压缩后,出口温度上升至T2=450 K,如图3.29所示。假设压气机进出口的空气流速近似相等,如果通过压气机的空气流量为13.2kg/s,求带动压气机所需的功率(设空气的比定压热容为常数)。
解:在压气机中,外界并未向气体加入热量,气体向外界散出的热量也可以忽略不计,故空气通过压气机可以近似地认为是绝热过程,即q=0,又因V1≈V2,故由式(3.76),有
\[-{{\omega }_{s}}={{h}_{2}}-{{h}_{1}}={{c}_{p}}\left( {{T}_{2}}-{{T}_{1}} \right)=\frac{k}{k-1}R\left( {{T}_{2}}-{{T}_{1}} \right)\]
将己知数据代入得 ωs=-160.8kJ/kg
即压气机压缩1kg的空气所消耗的功为160.8kJ,负号表示外界对气体做功。
带动压气机所需的功率为
\[{{N}_{s}}={{q}_{m}}{{\omega }_{s}}=2122kW\]
3.8 伯努利方程
伯努利方程是一个和定常流动能量方程形式非常接近的方程,它给出了无黏性流动中压力、速度和高度位置之间的关系。该关系是伯努利在1738年口述给出的,1755年欧拉推导出完整的公式。伯努利方程非常著名而且应用很广,但必须要注意,该方程只适用于黏性作用可以忽略的流动。下面推导伯努利方程。
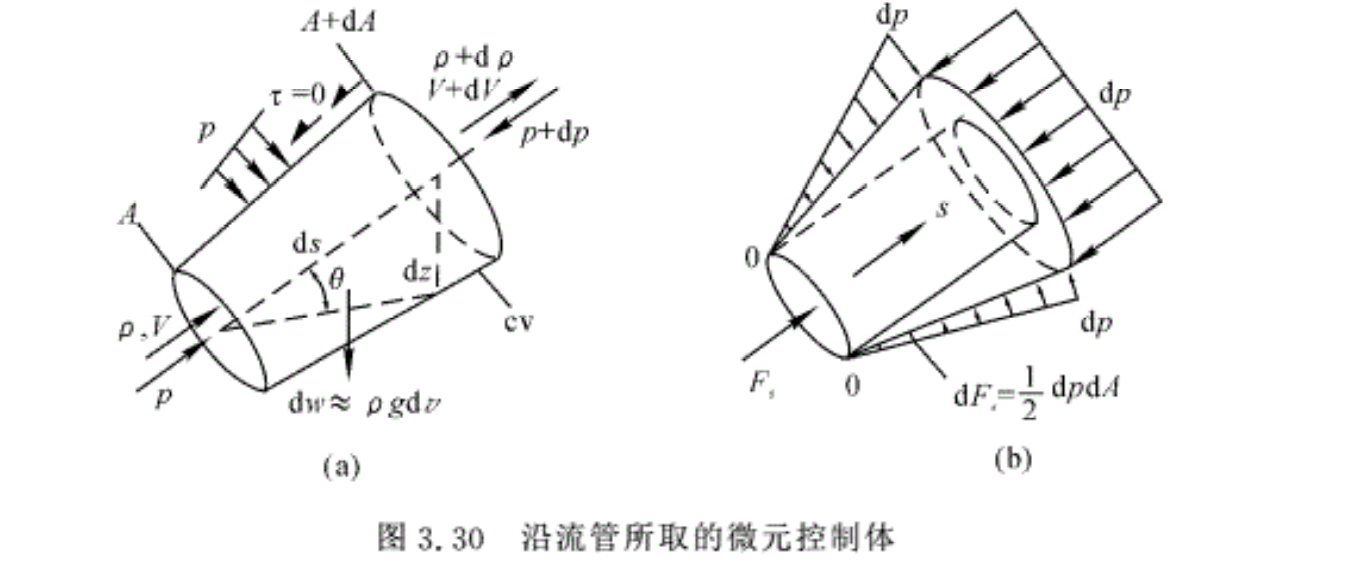
图3.30所示为沿流管所取的微元控制体,长度为ds,s为流线方向,流动参量(ρ,V,p)随s及时间变化,并且在各个垂直于s的截面上是均匀的。根据质量守恒式(3.32),有
∫(cv)∂ρdv/∂t+q m,out-q m,in=0
对于微元控制体,可表示为
∂ρdv/∂t+dqm=0
式中,qm=ρAV,dv≈Ads,因此有
\[d{{q}_{m}}=d\left( \rho AV \right)=-\frac{\partial \rho }{\partial t}Ads\] (3.82a)
流线方向的动量方程为
∑dFs=∂[∫(cv)Vρdv]/∂t+(qmV)out-(qmV)in=∂(ρV)Ads/∂t+d(qmV) (3.82b)
式( 3. 82b )由于是在流线方向的动量方程,因此V就是Vs。如果忽略黏性力作用,即对于理想流体,流体受到的力为压力和重力,重力在流线方向的分量为
\[d{{F}_{s,g}}=-dW\sin \theta =-\gamma Ads\sin \theta =-\gamma Adz\]
求整个控制面的压强在沿流向的合力时,可以将所有部分的压强都减去p ,然后再求和,如图 3.30 ( b )所示,即
\[d{{F}_{s,p}}=\frac{1}{2}dpdA-dp\left( A+dA \right)\approx -Adp\]
将上述两个力项代入动量方程式( 3. 82b ) ,得
\[\begin{align}
& \sum d{{F}_{s}}=-\gamma Adz-Adp=\frac{\partial \left( \rho V \right)}{\partial t}Ads+d\left( {{q}_{m}}V \right)= \\
& \frac{\partial \rho }{\partial t}VAds+\frac{\partial V}{\partial t}\rho Ads+{{q}_{m}}dV+Vd{{q}_{m}} \\
\end{align}\]
将上式两边除以ρA并考虑到式(3.82a) ,得
\[\frac{\partial V}{\partial t}ds+\frac{dp}{\rho }+VdV+gdz=0\] (3.83a)
式( 3. 83a )即为非定常、无黏性流动,沿流线方向的微分形式动量方程,又称为一维流动的欧拉运动微分方程。
如果流动为定常,则式( 3.83a )可改写为
\[\frac{dp}{\rho }+VdV+gdz=0\] (3.83b)
对于气体,由于重度很小,通常忽衉重力能,则式( 3.83b )为
\[\frac{dp}{\rho }+VdV=0\] (3.83c)
此式说明,当dp为正值时,dV必为负值,也就是说,当压强增加时,流体的速度必定要减小,而当压强减小时,速度一定要增加。这是气体流动时的重要规律之一。
对式(3.83a)从点1到点2进行积分,得
\[\int_{1}^{2}{\frac{\partial V}{\partial t}}ds+\int_{1}^{2}{\frac{dp}{\rho }}+\frac{1}{2}\left( V_{2}^{2}-V_{1}^{2} \right)+g\left( {{z}_{2}}-{{z}_{1}} \right)=0\] (3.84)
对于定常不可压流动,式(3.84)变为
\[\frac{{{p}_{2}}-{{p}_{1}}}{\rho }+\frac{1}{2}\left( V_{2}^{2}-V_{1}^{2} \right)+g\left( {{z}_{2}}-{{z}_{1}} \right)=0\]
或
\[\frac{{{p}_{1}}}{\rho }+\frac{V_{1}^{2}}{2}+g{{z}_{1}}=\frac{{{p}_{2}}}{\rho }+\frac{V_{2}^{2}}{2}+g{{z}_{2}}=const\] (3.85)
式(3.85)两端同时除以g得
\[\frac{{{p}_{1}}}{\gamma }+\frac{V_{1}^{2}}{2g}+{{z}_{1}}=\frac{{{p}_{2}}}{\gamma }+\frac{V_{2}^{2}}{2g}+{{z}_{2}}=const\] (3.86)
式(3.86)即为定常不可压无黏性流动沿流线的伯努利方程。
从力学观点来看,伯努利方程表示无黏性流体定常流动中的能量守恒定律。式中,p/γ代表单位重力流体的压力能;V²/(2g)表示单位重力流体所具有的动能;z表示单位重力流体所具有的位能。
式(3.86)表明,对于无黏性定常流动,单位重力流体的压力能、位能和动能的总和沿流线是一个常数。可以证明,对于多维定常无黏性流动,此式沿流线仍然成立。
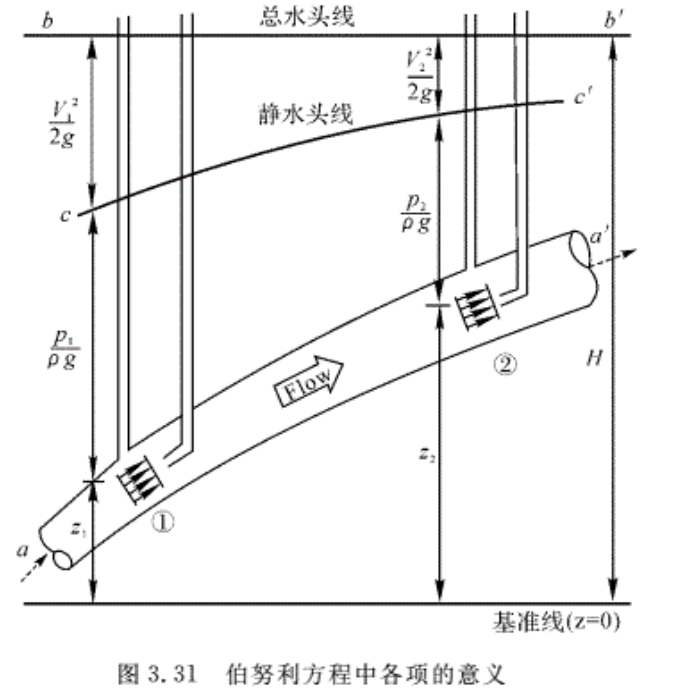
式(3.86)中各项都具有长度量纲,因此又称为“头”, p/γ称为压力头又叫静水头,V²/(2g)称为速度头,又称为动水头,z称为位置水头。在流体力学中常常采用水头线来直观地表示伯努利方程中各项之间的关系,如图3.31所示。流管各截面中心线联成的曲线aa’称为位置水头线,位置水头线上再加上压力水头线的高度,则可得到反映p/γ和z之和的曲线cc’,这条曲线称为静水头线,在静水头线上加上速度水头的高度,则得到反映单位重力流体总机械能量的曲线bb’,它被称为总水头线。
如果流动是在同一水平面内进行,或者流场中坐标z的变化与其他流动参量相比可以忽略不计时,则从式(3.86)可得
p+ρV²/2=C=p* (3.87)
式中p,ρV²/2,p*分别称为静压、动压和总压(驻点压强)。式(3.87)表示,流管每个横截面上的总压相等。
对于气体可压缩定常流动,气体本身的重力忽略不计。由式(3.84)得出
\[\int_{1}^{2}{\frac{dp}{\rho }}+\frac{1}{2}\left( V_{2}^{2}-V_{1}^{2} \right)=0\] (3.88)
对于等熵过程,根据工程热力学可知,\(\frac{p}{\rho _{{}}^{k}}=C\)故
\[\frac{1}{\rho }=\frac{p_{1}^{1/k}}{{{\rho }_{1}}}\frac{1}{p_{{}}^{1/k}}=C_{{}}^{1/k}/p_{{}}^{1/k}\]
所以有
\[\int_{1}^{2}{\frac{dp}{\rho }}=\frac{k}{k-1}R{{T}_{1}}\left[ \left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)_{{}}^{\frac{k-1}{k}}-1 \right]\]
代入式(3.88),得出
\[\frac{k}{k-1}R{{T}_{1}}\left[ \left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)_{{}}^{\frac{k-1}{k}}-1 \right]+\frac{V_{2}^{2}-V_{1}^{2}}{2}=0\] (3.89)
式(3.89)的适用条件为一维定常绝能等熵流动。该式说明了在一维定常绝能等熵流动过程中速度和压强之间的变化关系。在喷管中气体等熵膨胀,压强降低,而气流速度增加;在扩压器内,气流速度减小,压强升高。
当实际的黏性气体流过叶轮机时,如果忽略重力位能的变化,伯努利方程将有如下的形式:
\[-{{\omega }_{s}}=\int_{1}^{2}{\frac{dp}{\rho }}+\frac{1}{2}\left( V_{2}^{2}-V_{1}^{2} \right)+{{\omega }_{f}}\] (3.90)
式中,ωf为单位质量气体克服摩擦阻力所消耗的功(流动损失);ωs为单位质量气体通过叶轮机对外所做的机械功(涡轮内的情况),规定为正,或外界通过叶轮机对单位质量气体所做的机械功(压气机内的情况),规定为负。
式(3.90)是伯努利方程在具有摩擦及机械功条件下的推广,称为推广的伯努利方程或通用的伯努利方程。
伯努利方程是能量守恒与转换定律的另一种表现形式。它与热焓形式的能量方程式的不同点是,热焓形式能量方程式表示气流的各种能量(包括热能和机械能)的守恒与转换关系,突出了气流的速度与温度之间的关系;伯努利方程式却表示流体的各种机械能的守恒与转换关系,突出了流体的速度与压强之间的关系,所以伯努利方程又叫做机械能形式的能量方程。
下面通过一些例题来说明如何用伯努利方程解决问题。
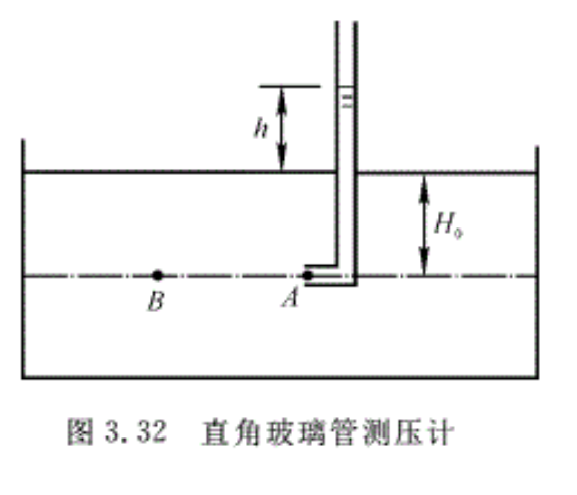
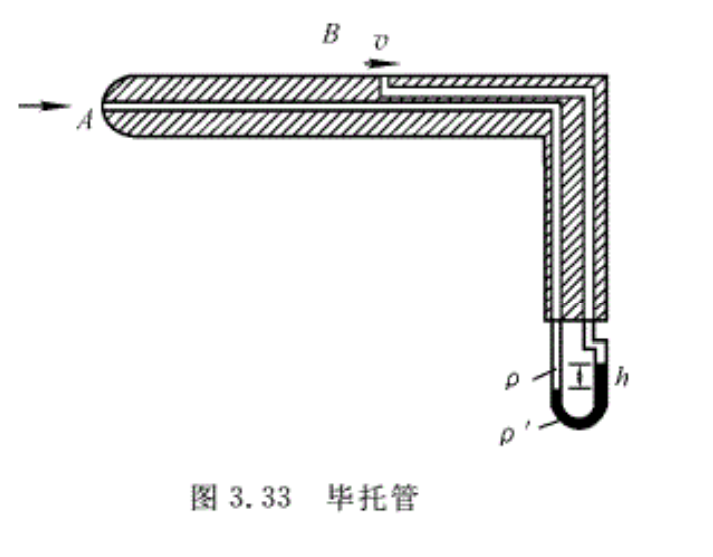
例3.20 如图3.32所示,用开口直角玻璃管量水渠中水的流速。玻璃管的一端点在水面下的深度为Ho,玻璃管中水面高度为h,A点是水流中的驻点,驻点处的压强称为滞止压强或总压,在上游和A点处于同一水平上的B 点,流动未受测压管的影响。试求B点的流速。
解:应用伯努利方程于A,B两点,即
\[\frac{{{p}_{A}}}{\gamma }+\frac{V_{A}^{2}}{2g}+{{z}_{A}}=\frac{{{p}_{B}}}{\gamma }+\frac{V_{B}^{2}}{2g}+{{z}_{B}}\]
由于A点是驻点,故VA=0,A,B处于同一水平线,因而zA=zB,另外,PB=γHo,pA=γ(Ho+h),将这些数值代入上述方程后,可得
\[{{V}_{B}}=\sqrt{\frac{2g}{\gamma }\left( {{p}_{A}}-{{p}_{B}} \right)}=\sqrt{2gh}\]
上述弯管也称为毕托管或总压管。本题中A点的总压与未受干扰的B点的总压是相同的,实际上PA—pB是B点总压和静压之差,因此只要测得某点的总压和静压,就可得出该点的流速。如图3.33所示为一测速管示意结构。在毕托管的基础上,在驻点之后适当距离的外壁上沿圆周钻几个小孔,称为静压孔。将静压孔和毕托管中心孔分别连接于压差计的两端,由此得出总压和静压的差值。这种仪器被称为毕托一静压管或动压管。假定测点B附近的气流是直匀流,总压孔对准来流,来流撞在孔上,速度降为零,相应的压强达到了总压(即pA=p*),沿AB流线应用伯努利方程,得
\[{{V}_{B}}=\sqrt{\frac{2g}{\gamma }\left( {{p}_{A}}-{{p}_{B}} \right)}\]
而\[{{p}_{A}}-{{p}_{B}}=h\left( \gamma \prime -\gamma \right)=hg\left( \rho \prime -\rho \right)\] ,故
\[{{V}_{B}}=\sqrt{\frac{2gh\left( \rho \prime -\rho \right)}{\rho }}\]
式中:ρ——被测流体的密度;
ρ’——U形管中的液体密度;
h——U形管中液体的高度差。
例3.21 试求出小孔出流速度和水箱液面高度之间的关系式(见图3.34)。假定流动定常无黏性。
解:我们选①处表示上游,②处表示下游。确定具体位置时,应考虑的原则就是能够得到最多的己知信息、要包含所求的未知量,所以②应该定在小孔的出口处。在这里已知压强为大气压,出口速度为所求量;而①应选在水箱的上表面,这里压强为大气压,距小孔的高度为h。
根据连续方程,有 A1V1=A2V2 (1)
列①—②之间的伯努利方程,为
\[\frac{{{p}_{1}}}{\gamma }+\frac{V_{1}^{2}}{2g}+{{z}_{1}}=\frac{{{p}_{2}}}{\gamma }+\frac{V_{2}^{2}}{2g}+{{z}_{2}}\] (2)
由于p1=p2=pa,所以有
\[V_{2}^{2}-V_{1}^{2}=2g\left( {{z}_{1}}-{{z}_{2}} \right)=2gh\] (3)
将式(1)代入式(3),有
\[V_{2}^{2}=\frac{2gh}{1-A_{2}^{2}/A_{1}^{2}}\] (4)
一般情况下,小孔出囗的截面A2要远远小于水箱的截面A1,所以A²2/A²1≈0,最后有
\[{{V}_{2}}\approx \left( 2gh \right)_{{}}^{1/2}\] (5)
式(5)说明,小孔出口的速度近似为无黏性流体微团由①自由下落到时的速度,势能完全变成了机械能。该式是托里赛里(Evangelista Torricelli)在1644年导出的。
在实际流动中,由于黏性的作用,小孔出口的速度不是均匀一维的,所以在工程计算中求解出囗平均流速,还需要乘以一个系数cd,即
\[{{\left( {{V}_{2}} \right)}_{av}}={{c}_{d}}\left( 2gh \right)_{{}}^{1/2}\]
出口系数cd=0.6~1.0,随流动条件和小孔形状不同而变化。
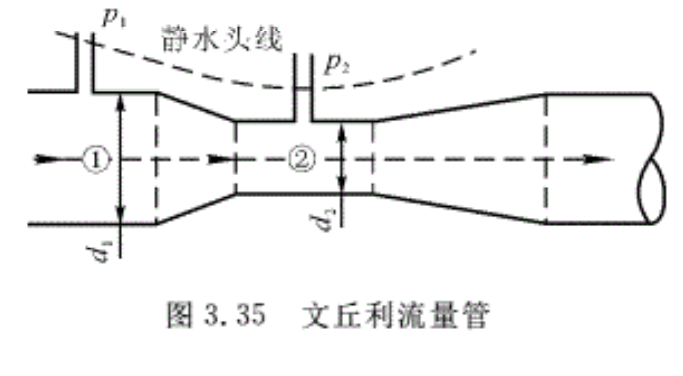
例3.22 图3.35所示为文丘利流量管。收缩管可以使得②面处流速增加、压强减小。试通过压力下降求出管中流体的流量。
解:沿中心线列①—②的伯努利方程为
\[\frac{{{p}_{1}}}{\gamma }+\frac{V_{1}^{2}}{2g}+{{z}_{1}}=\frac{{{p}_{2}}}{\gamma }+\frac{V_{2}^{2}}{2g}+{{z}_{2}}\]
如果管中心线水平,则z1=z2因此
\[\begin{align}
& V_{2}^{2}-V_{1}^{2}=\frac{2\Delta p}{\rho } \\
& \Delta p={{p}_{1}}-{{p}_{2}} \\
\end{align}\] (1)
对于不可压流,由连续方程得
A1V1=A2V2
或 V1=β²V2,β=d2/d1 (2)
将式(2)代入式(1 ),得出收缩管处的速度为
\[{{V}_{2}}=\left[ \frac{2\Delta p}{\rho \left( 1-\beta _{{}}^{4} \right)} \right]_{{}}^{1/2}\] (3)
质量流量为
\[{{q}_{m}}=\rho {{A}_{2}}{{V}_{2}}=\rho {{A}_{2}}\left[ \frac{2\Delta p}{\rho \left( 1-\beta _{{}}^{4} \right)} \right]_{{}}^{1/2}\] (4)
式(4)即为通过管道的质量流量,在实际流动中考虑黏性的作用时还要乘以一个修正系数。
例3.23 消火栓喷头如图3.36所示,水以1. 5 m³/min的流量喷出。假设流动无黏性,试求连接喷头和消火栓之螺栓所受的力。
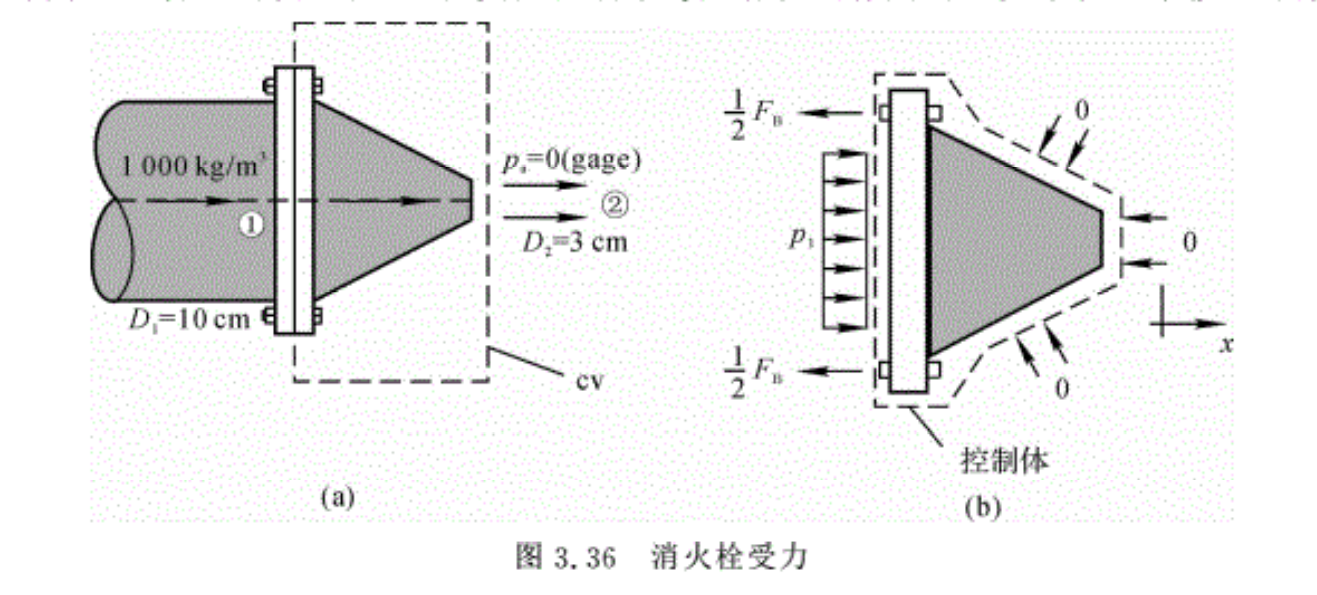
解:首先采用伯努利方程和连续方程求出喷头上游的压强,然后再用控制体的动量分析计算出螺栓受力。
根据喷嘴进、出囗①和②截面之间的伯努利方程,可得出
\[{{p}_{1}}={{p}_{2}}+\frac{1}{2}\rho \left( V_{2}^{2}-V_{1}^{2} \right)\] (1)
己知流量为qv=1.5m³/ min=0.025m/s,因此进、出囗速度分别为
\[\begin{align}
& {{V}_{1}}=\frac{{{q}_{m}}}{{{A}_{1}}}=\frac{0.025}{\left( \pi /4 \right)\times 0.01}=3.2m/s \\
& {{V}_{2}}=\frac{{{q}_{m}}}{{{A}_{2}}}=\frac{0.025}{\left( \pi /4 \right)\times 0.03_{{}}^{2}}=35.4m/s \\
\end{align}\]
己知p2=pa=0(表压),则由方程式(1 ),可得
\[{{p}_{1}}=\frac{1}{2}\times 1000\times \left( {{35.4}^{2}}+{{3.2}^{2}} \right)=620kPa\]
控制体所受合力,如图3.36(b)所示,为
\[\sum {{F}_{x}}=-{{F}_{B}}+{{p}_{1}}{{A}_{1}}\]
其他各面上的大气压相互抵消,x方向的动量流量为
\[{{q}_{m}}{{V}_{2}}-{{q}_{m}}{{V}_{1}}={{q}_{m}}\left( {{V}_{2}}-{{V}_{1}} \right)\]
对图中虚线所示控制体,根据动量方程有
\[-{{F}_{B}}+{{p}_{1}}{{A}_{1}}={{q}_{m}}\left( {{V}_{2}}-{{V}_{1}} \right)\]
或
\[{{F}_{B}}={{p}_{1}}{{A}_{1}}-{{q}_{m}}\left( {{V}_{2}}-{{V}_{1}} \right)\]
将所有的数据代入,得出 FB=4067N
由此可以得出,为什么在灭火时需要几个消防队员来把握消防栓喷头的原因。
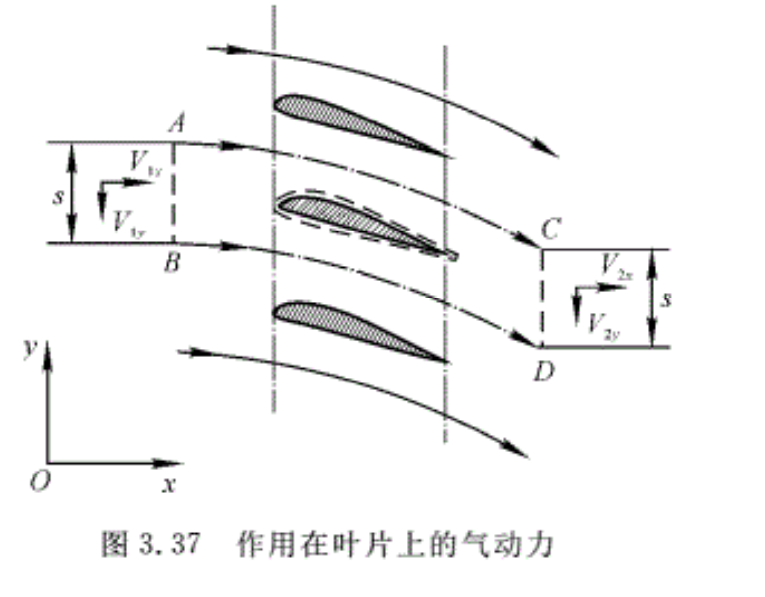
例3.24 如图3.37中所示的平面叶栅,由无限多个形状相同的叶片所组成。试求出气流作用在叶片上的气动力。
解:取控制体如图中虚线所示。在垂直于纸面的方向为单位长度。AB和CD分别取在上、下游足够远的地方,此处气流的参数是均匀的、AC和BD是两个状态完全相同的流面。假定气流是无黏性不可压流。
由于AC和BD两个面上的压强完全相同但方向相反,因此力的作用相互抵消。
x方向的动量方程为
\[{{F}_{x}}+{{p}_{1}}s-{{p}_{2}}s={{q}_{m}}\left( {{V}_{2x}}-{{V}_{1x}} \right)\]
或
\[{{F}_{x}}={{q}_{m}}\left( {{V}_{2x}}-{{V}_{1x}} \right)+\left( {{p}_{2}}-{{p}_{1}} \right)s\] (1)
式中,Fx为叶片给予气流的作用力在x方向的分量。
y方向的动量方程为
\[{{F}_{y}}={{q}_{m}}\left[ -{{V}_{2y}}-\left( -{{V}_{1y}} \right) \right]={{q}_{m}}\left( {{V}_{1y}}-{{V}_{2y}} \right)\] (2)
式中,Fy为叶片给予气流的作用力在y方向的分量。
气流作用在叶片上的作用力P应该为F的反作用力,所以有
\[\begin{align}
& -{{P}_{y}}={{q}_{m}}\left( {{V}_{1y}}-{{V}_{2y}} \right) \\
& -{{P}_{x}}={{q}_{m}}\left( {{V}_{2x}}-{{V}_{1x}} \right)+\left( {{p}_{2}}-{{p}_{1}} \right)s \\
\end{align}\]
根据连续方程\({{q}_{m}}=\rho {{V}_{1x}}s=\rho {{V}_{2x}}s\),得出
\[{{V}_{1x}}={{V}_{2x}}\]
根据伯努利方程,可得
\[{{p}_{2}}-{{p}_{1}}=\frac{\rho }{2}\left[ \left( V_{1x}^{2}+V_{1y}^{2} \right)-\left( V_{2x}^{2}+V_{2y}^{2} \right) \right]=\frac{\rho }{2}\left( V_{1y}^{2}-V_{2y}^{2} \right)\]
将上两式代入式(1 ),式(2),得
\[\begin{align}
& {{P}_{x}}=\frac{\rho }{2}\left( V_{2y}^{2}-V_{1y}^{2} \right)s \\
& {{P}_{y}}=\rho {{V}_{x}}s\left( V_{2y}^{{}}-V_{1y}^{{}} \right) \\
\end{align}\]
小结
本章主要讨论了流体动力学的基本方程。这些方程是以后各章要用到的,是分析动力学的基本数学工具。除此之外,本章介绍了描述流体运动的两种方法、流体微团运动的分解以及有关动力学的基本概念。介绍雷诺输运定理的目的主要是为了更方便地导出基本方程,把适合于系统的方程转化成适合于控制体的方程。
思考与练习题
3.1 分析描述流体运动的两种方法有何不同。
3.2 思考速度的随流导数的意义。
3.3 已知速度场分别为
(1)\[\begin{align}
& {{V}_{x}}=-Cy \\
& {{V}_{y}}=Cx \\
\end{align}\] (C为正的常数);
(2)\[\begin{align}
& {{V}_{x}}=\frac{y}{{{x}^{2}}+{{y}^{2}}} \\
& {{V}_{y}}=\frac{x}{{{x}^{2}}+{{y}^{2}}} \\
\end{align}\]
(3)\[\begin{align}
& {{V}_{x}}=Ky \\
& {{V}_{y}}=0 \\
\end{align}\] (K为正的常数)
求各流线方程,并画出过点A(1,1)的流线。
3.4 己知二维流场的速度分布为
\[\begin{align}
& {{V}_{x}}=\frac{x}{1+t} \\
& {{V}_{y}}=y \\
\end{align}\]
试求当t=0时过点(1,1 )的流线及迹线。
3.5 己知流体的速度分布为Vx=1-y,Vy=t(t为时间)。试求当t=1时过点(0,0)的流线。
3.6 已知速度场V=x²yi-4yj+3z²k。试求过点(3,2,1)的加速度。
3.7 已知速度场V=(x+t)i+(t-y)j。试求过点(2,1)的加速度。
3.8 通过一收敛喷管的流场可以用一维速度分布为Vx=Vo(1+2x/L)来近似,式中,L 为喷管长度,Vo为入口速度,出囗速度为Vx=2Vo,试求:
(1)加速度分布;
(2)若入口速度Vo=100m/ s,L=1 m,试求进、出囗的加速度。
3.9 已知速度分量为Vx=2xt,Vy=yt,Vz=zt²,且密度场为ρ=(x²+y³+zt)。求流体质点的密度变化率。
3.10 有一二维流场,其速度分布为Vx=x²y+y²,Vy=x²-y²x。求流场在点(1,2)处的旋转角速度、剪切变形角速度和体积膨胀率。
3.11 己知流场的速度分布为Vr=2rsinθ,Vθ=2rcosθ。试求旋转角速度、剪切变形角速度和体积膨胀率。
3.12 一速度大小为\(\left| V \right|=kr_{{}}^{n}\)的流动,其流线为绕坐标原点的同心圆。求流体微团的旋转角速度ωz;若ωz=0,求剪切变形角速度的表达式。
3.13 己知速度分布为\(V/{{V}_{\infty }}=\left( y/\delta \right)_{{}}^{1/7}\)。试问这种流动是无旋流动还是有旋流动?
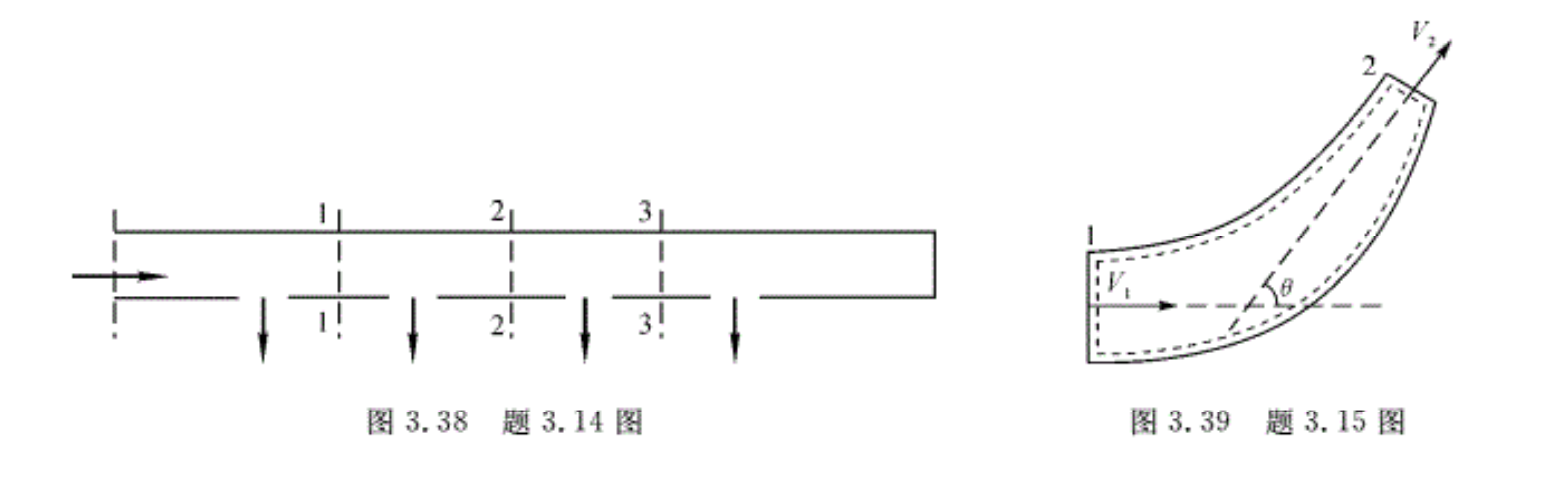
3.14 横截面积为(0.5 × 0.5)㎡的空气导管如图3.38所示,通过四个面积为(0.4× 0.4)㎡的侧向管囗流出,出口气流平均流速均为5 m/s。求通过1一1,2一2,3一3各截面的流速和体积流量。
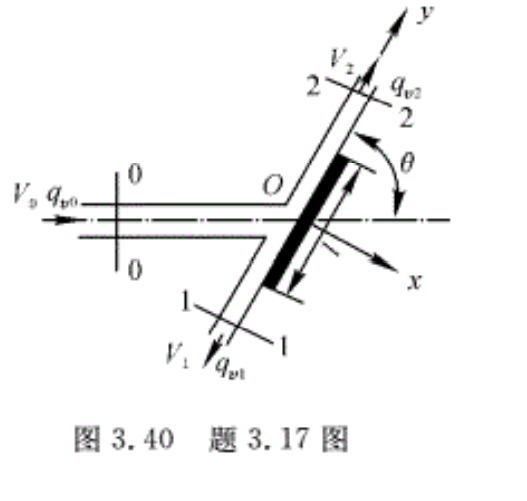
3.15 一个水平放置的渐缩弯管如图3.39所示,进、出口流体的压强、速度、面积、流体的密度和通过的体积流量均己知。求流体对管壁的作用力(设流动为不可压、气流方向角θ给定)。
3.16 已知尾喷管进口燃气参数p1=1. 76 × 104Pa,流速V1=300m/ s,进口截面积A1=0.85㎡,出口速度V2=500 m/s, 出口截面积A2=0.67㎡,若燃气流量为qm=160 kg/ s,设流动为绝能等熵的,求燃气作用于喷管上的轴向力R。
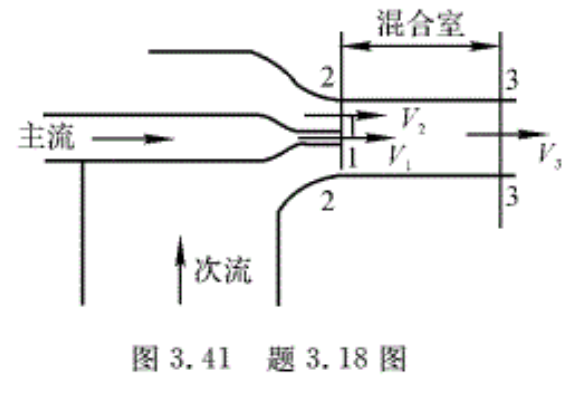
3.17 一股射流冲击板面,如图3.40所示,己知流动为定常,入射流股速度为Vo,流量为qto,斜板倾角为θ。设各流股在垂直纸面方向的厚度均为1,不计重力及阻力作用(假设Vo=V1=V2),求流体对斜板的冲击总作用力F及分流流量qv1,qv2。
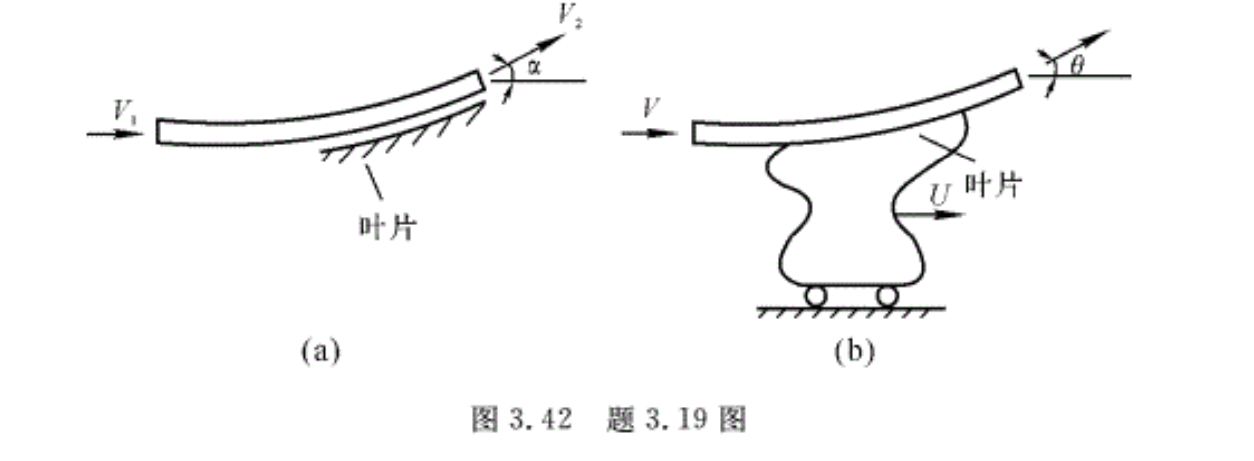
3.18 在图3.41所示中给出一台射流泵,截面1处的高速液体主流引动截面2处的一股低速次流(流体与主流相同),在等直径混合室的末端,即截面3处,由于液流之间摩擦的结果,两股液流己经完全掺混,而且速度均匀。己知V1=30. 48 m/s,V2=3.048 m/s,ρ=103 kg/m³ A1=0.0093㎡,A2=0.0837㎡,为了便于分析起见,假设在截面1和2处两股的静压相同,且假设混合室壁上的切应力可略去不计。试计算出口截面3与截面1的压强差为多少。
3.19 (1 )参看图3.42(a),水(射流)流过一固定叶片后,流速方向改变了α角。如果射流截面不变,且不计摩擦力的影响,则V2=V1,p2=p1。试确定液体射流对叶片的作用力。
提示:计算液体射流与叶片间的作用力时,因pa(大气压)的作用远较动量变化为小,故一般可略去pa的影响。
(2)参看图3.42(b),当导流叶片的小车以恒速U向右移动时,忽略射流的质量力和黏性力。试问当U/V为多大时,射流对小车的作用功率最大?
3.20 (1 )海平面上,大气从管道被吸入真空箱,在翼型上某点B处气流的速度为122 m/s,试求点B(见图3.43(a))处的气流静压。
(2)如在同样的条件下,若机翼在静止大气中以等速度61 m/ s向左运动(见图3.43(b) ),在翼型上B点处,翼型与空气的相对速度为122 m/ s,试求点B处的气流静压pB。
3.21 (1 )火箭发动机作地面试验,从尾喷口排出的质量流量为qmj,喷口处的压强为pj,喷气速度为Vj,喷管出囗面积为A,大气压强为pa。设为定常流动,求实验台所受的推力。
(2)如果发动机相对于地面做匀速直线运动,试推导发动机的推力公式。