第二章流体静力学基础与基本概念
本章主要讨论流体处于静止或相对静止时的平衡规律,描述这种规律的数学关系是流体静平衡微分方程。在此基础上,讨论流体静平衡微分方程的应用,即讨论只有重力作用时以及流体在相对静止(平衡)时的平衡规律;讨论流体运动学基础及基本概念。本章讲述的这些概念是研究流体动力学所必须具各的基本知识。
2.1 作用在流体上的力及静压强特性
任何流体的运动都是在力的作用下进行的。因此,在研究流体的运动规律时,应该首先研究作用在流体上的力。
2.1.1 作用在流体上的力
作用在流体上的力可以分成两大类:质量力和表面力。分述如下。
1.质量力(也称为体积力)
质量力是指作用在体积v内每一个流体质点上的力,其大小与流体体积或质量成正比,而与体积v以外的流体存在无关。这类力中最常见的有重力。此外,对于非惯性坐标系,质量力还包括惯性力。例如,气体在压气机或涡轮内运动时,取与转子以相同角速度旋转的动坐标系来研究气体的运动时,就要考虑惯性力和哥氏力。
若规定用R表示作用在单位质量流体上的质量力,X,Y,Z分别表示其在坐标轴x,y,z方向上的分量,则
\(R\text{=}X\text{i}+Y\text{j}+Z\text{k}\) (2.1)
式中,i,j,k分别表示沿坐标轴x,y,z方向上的单位向量。
作用在微元体积dv上的质量力为
\(\text{d}F=\rho R\text{dv}\)
作用在流体体积v上的质量力为
\(F\text{=}\int_{\text{v}}{\rho R\text{dv}}\) (2.2)
2.表面力和应力
所谓表而力是指作用在所取流体表面上的力,是由与这块流体相接触的流体或物体的作用而产生的。根据连续介质的概念,这个力连续分布在所取流体表面上(见图2.1)。在所取流体表面S上点C附近划出一微元面积∆A,作用在其上的表面力为∆F,当微元面积∆A无限减小时,比值∆F/∆A的极限值为
\({{\text{p}}_{\text{n}}}\text{=}\underset{\Delta A\to \Delta {{A}_{0}}}{\mathop{\lim }}\,\frac{\Delta F}{\Delta A}\) (2.3)
pn表示以n为法向的单位面积上的表面力,常称其为表面应力。应力pn的方向一般与作用面的外法向n并不重合,它是空间点和坐标的函数,且与作用而在空间的方位有关。通常pn可以分解为垂直于表面的法向应力(称为正应力)和平行于表面的切向应力(称为切应力)。
式(2.3)中的∆Ao是和流体质点的体积∆vo可以相比拟的微小面积。
作用于整个流体表面上的表面力可表示为
\(F\text{=}\int\limits_{\text{s}}{{{\text{p}}_{\text{n}}}\text{d}A}\) (2.4)
2.1.2 流体静压强及其特性
在静止流体中,由于流体间没有相对运动(dV/dy=0),或者在运动的无黏性流体(忽略黏度系数μ)中,切向力等于零,流体内部仅存在法向力。这时,作用在某点附近单位面积上的法向力就定义为该点流体的压强(法向应力),以符号p表示,其单位是Pa或N/㎡。
流体压强具有下列两个重要的特性。
(1)因为流体分子之间的距离比固体的大得多,一般流体抵抗拉伸的能力很小,故压强的方向永远沿着作用面的内法线方向,即压强的方向永远指向作用面。
(2)在静止流体或运动的无黏性流体中,某一点压强的数值与过该点所取作用面在空间的方位无关。下面就来证明这个问题。
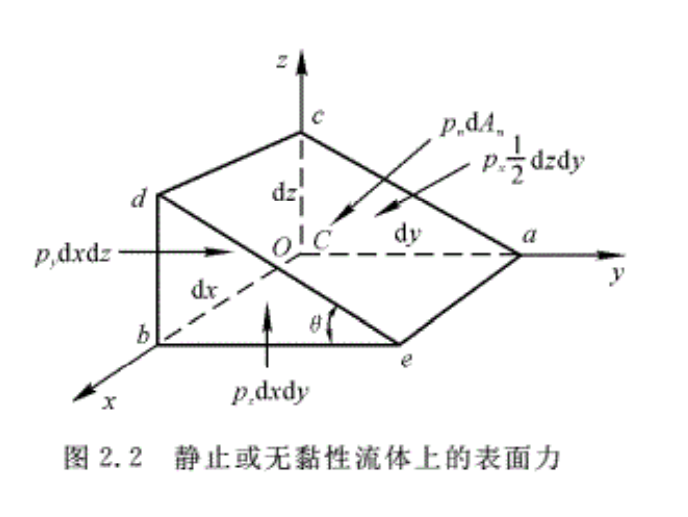
首先考虑静止流体的情况(见图2.2)。设在静止流体中,围绕点C取一流体体积元,并将它放大为微元体,使该微元体的顶点C与坐标系Oxyz的原点重合,微元体的三个边长分别是dx,dy和dz。因为流体没有相对运动,于是流体内的切应力等于零。作用在微元体上的力仅有质量力和表面力中的法向力(静压强)。设质量力仅有重力,且沿z方向的负向(图中没有标出)。由于所取的微元体无限小,可以认为作用在表面Cbdc上各点的流体压强均匀分布。因此,可以得出作用在表面Cbdc上的法向力为pydxdz。写出y方向的平衡方程。
\({{\text{p}}_{\text{y}}}\text{dxdz-}{{\text{p}}_{\text{n}}}\text{d}{{A}_{\text{n}}}\sin \theta \text{=}0\)
由图2.2可以看出,\(\text{d}{{A}_{\text{n}}}\sin \theta \text{=dxdz}\),因此\[{{\text{p}}_{\text{y}}}\text{=}{{\text{p}}_{\text{n}}}\].
类似地,可以写出z方向的平衡方程为
\[{{\text{p}}_{\text{z}}}\text{dxdy-}{{\text{p}}_{\text{n}}}\text{d}{{A}_{\text{n}}}\cos \theta \text{-}\frac{1}{2}\rho \text{gdxdydz=}0\]
式中,ρ为流体的密度,且有\[\text{d}{{A}_{\text{n}}}\cos \theta \text{=dxdy}\],上式可化简为
\[{{\text{p}}_{\text{z}}}\text{-}{{\text{p}}_{\text{n}}}\text{-}\frac{1}{2}\rho \text{gdz=}0\]
略去高阶小量,则有
\[{{\text{p}}_{\text{z}}}\text{=}{{\text{p}}_{\text{n}}}\]
同理,在x方向也可以作同样推导,最后得
\[{{\text{p}}_{\text{x}}}\text{=}{{\text{p}}_{\text{y}}}\text{=} {{\text{p}}_{\text{z}}}\] (2.5)
由于微元体的位置和方向是可以任选的,因此,我们己经证明了在静止流体中,一点处的压强与过该点所取作用面在空间的方位无关,即压强是各向同性的。
其次,讨论运动的无黏性流体的情况。对于运动的无黏性流体,同样可以得到式(2.5),所不同的是在质量力中多出了一项惯性力。惯性力是质量力,也是三阶无限小量,在建立动平衡关系式时,将和重力同时略去,因而可以得出和式(2.5)相同的结果。
综上所述,可得如下结论:在静止流体或运动的无黏性流体中,任一点处的压强沿各个方向都是相同的。也就是说,流体内部一点的压强大小与该点所在的作用面在空间的方位无关。因此,可以把流体压强看做是标量,即它只是空间点和时间的函数。
2.2 流体静平衡微分方程及其应用
平衡流体的最大特点是没有切应力。本节讨论静止或相对静止流体的平衡规律,并由此得到其压强分布规律。
2.2.1 流体静平衡微分方程
在惯性坐标系中,任何物体处于静止状态的必要条件是作用在物体上的外力之和以及外力矩之和均为零。现在利用力的平衡条件导出流体压强的变化规律。
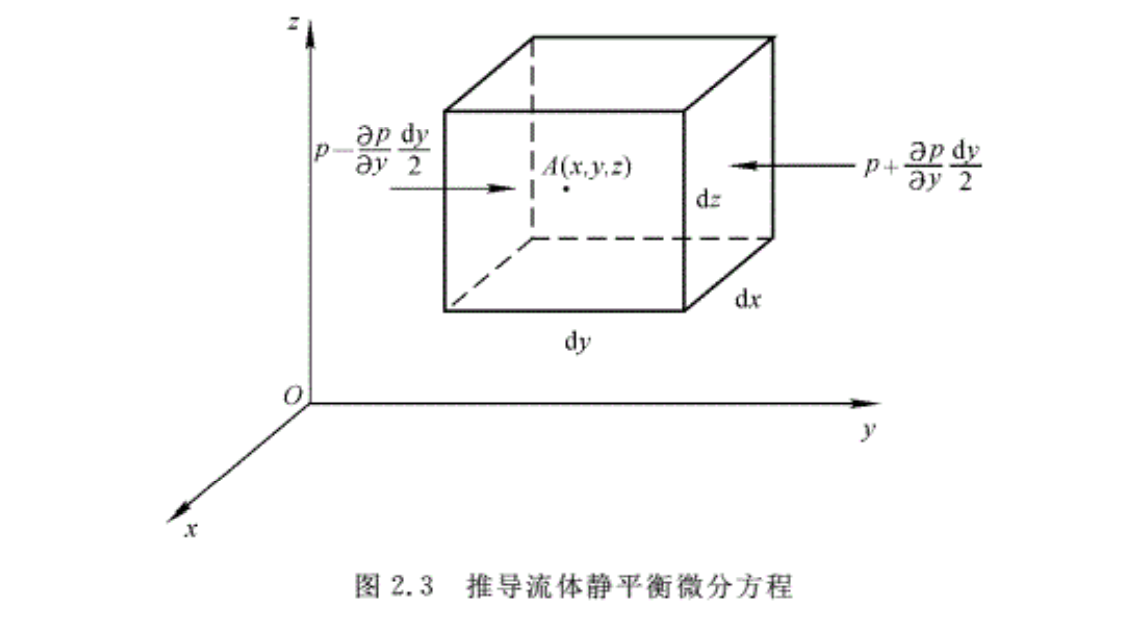
在静止流体中任取一点A(x,y,z),如图2.3所示,围绕点A取一微元六面体,其表面分别与坐标面平行,点A在其中心,六面体边长分别为dx,dy,dz,体积为δv,其压强为p。
作用在此微元六面体上的力有质量力和表面力。其质量力在x,y,z方向上的分力分别是Xρδv,Yρδv,Zρδv。对于静止或相对静止的流体,切向力等于零,表面力中仅有压力。所以,作用于此微元六面体的表面力分别和6个面垂直。沿y方向的表面力,只有垂直于xOz面的两个表面的法向力。将这两个面上的压强p按泰勒级数展开且保留一次项,分别为
\[\text{p-}\frac{\partial \text{p}}{\partial \text{y}}\bullet \frac{\text{dy}}{2}\]
和
\[\text{p+}\frac{\partial \text{p}}{\partial \text{y}}\bullet \frac{\text{dy}}{2}\]
作用在六面体上沿y方向的表面力则为
\[\text{p-}\frac{\partial \text{p}}{\partial \text{y}}\frac{\text{dy}}{2}\text{dxdz-}\text{p+}\frac{\partial \text{p}}{\partial \text{y}}\frac{\text{dy}}{2}\text{dxdz=-}\frac{\partial \text{p}}{\partial \text{y}}\text{dxdydz}\]
同理,可得作用于该六面体上沿x和z方向的表面力分别为
\[\text{-}\frac{\partial \text{p}}{\partial \text{x}}\delta \text{v}\]和
\[\text{-}\frac{\partial \text{p}}{\partial \text{z}}\delta \text{v}\]
作用于此六面体上的质量力在x,y,z方向上的分力分别是Xρδv,Yρδv,Zρδv,因为流体处于平衡状态,则沿x,y,z方向的各力的总和应等于零。沿x方向则有
\[\text{-}\frac{\partial \text{p}}{\partial \text{x}}\delta \text{v}+X\rho \delta \text{v=0}\]
或\(\frac{\partial \text{p}}{\partial \text{x}}\text{=}\rho X\) (2.6a)
同理可得\(\frac{\partial \text{p}}{\partial \text{y}}\text{=}\rho Y\) (2.6a)
\(\frac{\partial \text{p}}{\partial \text{z}}\text{=}\rho Z\) (2.6a)
写成向量形式则为
\(\nabla \text{p=}\rho R\) (2.6b)
式(2.6)称为流体静平衡微分方程式,是由欧拉在1755年首先推导出来的,因此也称它为欧拉静平衡微分方程式。它表明了在静止流体中,压强的变化和质量力是密切相关的,描述了静平衡时压强、密度和单位质量的质量力之间的关系。
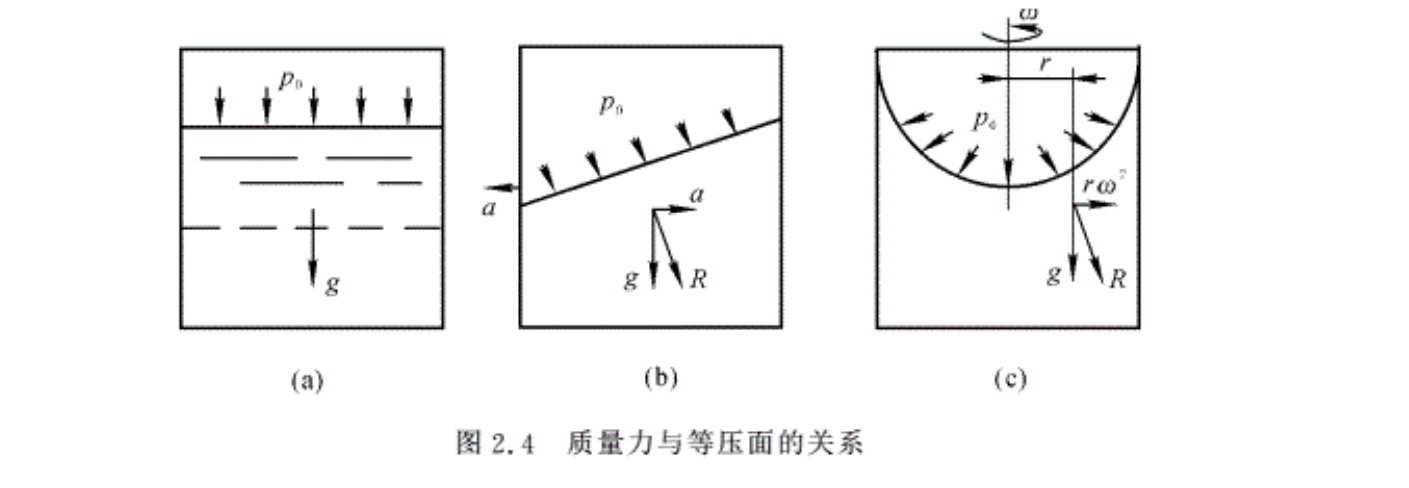
由式(2.6)可见,在静止流体中压强的变化是由质量力决定的,只有在质量力不等于零的方向,才有压强的变化。故在垂直于质量力的方向,压强保持不变。由此可以推论,在静止流体中的等压面和质量力垂直。
图2.4表示当容器中的液体的质量力方向不同时,等压面变化的情况。图2.4(a)表示只有重力的情况;图2.4(b)表示容器以加速度a往左运动的情况;如果是飞机的油箱,则从图可以看出,飞机水平加速飞行时油箱中液面的形状,从而可确定出油囗的位置。图2.4(c)表示容器以角速度ω转动时的情形,此时惯性力则为液体的重力和离心力rω²之合力。半径r愈大,惯性离心力也愈大,这时等压面是个抛物面。
2.2.2 重力作用下流体内部的压强
在一般情况下,静止流体只受到重力作用。现在来讨论在这种情况下压强变化的规律。此时,图2.3所示的微元六面体所受的质量力只有重力,显然,单位质量流体的质量力为g,其方向垂直向下,与图2.3中所选择的z方向相反。因此,单位质量流体的质量力在各个坐标轴方向的分量为
X=0,Y=0,Z=-g
代入式(2.6a),得\(\frac{\partial \text{p}}{\partial \text{x}}\text{=}0\),\( \frac{\partial \text{p}}{\partial \text{y}}\text{=}0\),\(\frac{\partial \text{p}}{\partial \text{z}}\text{=}-\rho \text{g}\)
由此可见,压强p只是密度ρ和坐标z的函数,而与x,y无关。则可得
\(\frac{d\text{p}}{d\text{z}}\text{=}-\rho \text{g}\)
或
\(\text{dp=}-\rho \text{gdz}\) (2.7)
这就是流体静力学的基本关系式。
在重力作用下平衡的液体,可以认为是不可压缩的,即ρ=常数。对式(2.7)两边积分可得
\(\text{p=}-\rho \text{gz}+C\text{=}-\gamma \text{z}+C\)
或
\(\text{p}+\gamma \text{z=}C\) (2.8)
式中,γ=ρg为液体的重度;C是积分常数,由给定的边界条件决定。
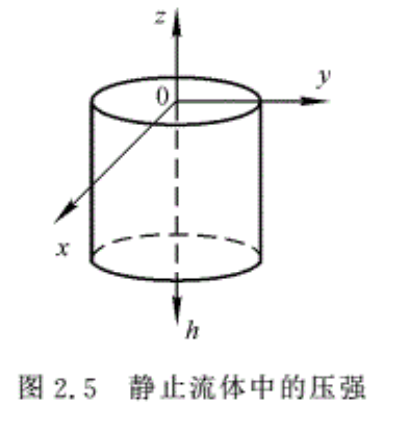
通常说明液体内部某一点的位置时,总是以这一点在液体自由表面以下的深度来说明的。因此,引用深度h的零点在液体的自由表面上,方向向下,如图2.5所示。这时式(2.8)就变为
\(\text{p=}\gamma \text{h}+C\)
如果在液面(h=0)上的压强po为已知,则可求得积分常数C=po,则
\(\text{p=}{{\text{p}}_{0}}+\gamma \text{h}\) (2.9)
可见,在重力作用下,液体内部的压强随深度的增加按线性规律变化。液体中任一点处的压强均由两部分组成。一部分是液体自由表面上的压强po;另一部分是该点附近单位面积上液体柱的重量γh。它清楚地表明了压强和重力之间的平衡关系。运用式(2.9),可以计算出在重力作用下静止的流体内部任一点的压强、压强沿着深度变化的规律以及作用在固体壁面上的力等等。
对于在重力作用下平衡的气体,也就是一般所谓的静止气体,在所处的空间不是十分大的情况下,可以不考虑气体的压缩性,而认为密度ρ是个常数,此时式(2.9)仍然是适用的;此外,对于存在于大多数工程设备中的气体,由于高度差h并不很大,而气体本身的重度γ又很小,故可以不考虑重力对气体压强分布的影响,认为空间各点的压强具有同一的数值。但对于大气来说,其密度、压强等状态参数随高度变化是很大的,因此大气的密度就不再作为常数看待了。
2.2.3 大气结构与国际标准大气
1.大气结构
围绕在地球表面的一层空气,叫做大气层。由于重力场的作用,空气在大气层中的分布是不均匀的,靠近地面的空气较稠密,离开地面越远就越稀薄,最后逐渐过渡到宇宙空间。
大气层内部情况随高度不同而异,通常把它分成几层来研究。
在靠近地面的一层是对流层。这一层占据了大气的大部分质量(约占3/4)。这一层空气受地面的加热和起伏不平的影响,处于不断运动的状况,有水平方向和垂直方向的风,同时还会发生像云、雨、雪、雷、电等现象;空气的密度、压强、温度等参数不断改变,且可随高度的增大而减小。对流层的平均高度可取为11 km。
高度从11~24km为同温层(或平流层),这层的特点是空气的温度几乎不变,平均等于-56.5 ℃(216.5K)。这一层中的空气没有垂直方向的流动,而只有水平方向的流动,所以同温层又叫平流层。
在高度24~85 km之间为中间大气层。这一层气温变化比较强烈,先随高度增大而增大,然后随高度增大而减小。
电离层由85 km一直延伸到800 km的高空。此层空气己电离,导电性较大,可以反射无线电波,而且空气较稀薄,太阳光线辐射作用较强,气温随高度的增加迅速增高。
越过800 km以上是外层大气,是过渡到宇宙空间的区域,此层空气极其稀薄。
一切以空气中的氧气作为氧化剂进行燃料烧的发动机都只能在大气层中工作,以此类发动机为动力的飞机只能在大气层中飞行,因而更高的高度,由于空气过于稀薄的缘故,目前空气喷气发动机还不能在那样稀薄的大气中工作。
2.国际标准大气
大家知道,在某一高度上,大气的温度、压强、密度等参数会随纬度、地区、季节和昼夜等因素而剧烈改变,这会影响到飞机的飞行性能或发动机的工作性能,从而对在试飞或试车时所得的结果不好进行分析比较。为了便于整理飞行试验或试车数据,便于对同类型飞机或发动机的性能进行比较,以及便于作设计计算,国际航空界共同规定了一种国际标准大气。国际标准大气主要是按照中纬度地区各季节中大气的平均值定出的。其具体规定如下所述。
(1)空气被看做是完全气体。
(2)大气的相对湿度为零。
(3)以海平面作为高度计算的起点H=0,To=288.15K,po=1.01325×105Pa,ρo=1.225 kg/m³。
(4)在高度H=11000m以下,气温随高度呈直线变化,高度每升高1 m,气温下降0065K,即
T=288.15-0.0065H (2.10)
式中:T——对流层中任一高度上的大气温度(K);
H——高度(m)
(5)在高度H=11000~24000m的范围内,气温保持不变,此时,T=216.5K。
根据上述规定,由流体静力学知识和完全气体的状态方程式就可以计算出大气压强和大气密度随高度的变化规律。由式(2.7)可得在流体内部某点压强随高度H的变化关系式为
dp=-ρgdH
用完全气体的状态方程式p=ρRT等号两边分别除上式两边,得
\(\frac{d\text{p}}{\text{p}}\text{=}-\frac{\text{g}}{RT}\text{d}H\)
将T=288.15-0.0065H代入上式,积分后得
\(\ln \text{p=}\frac{\text{g}}{0.0065R}\ln 288.15-0.0065H+C\) (a)
当H=0时,有 p=po=1.01325×105 Pa
解得 \(C\text{=}\ln {{\text{p}}_{0}}-\frac{\text{g}}{0.0065R}\ln 288.15\)
代入式(a),得
\(\frac{\text{p}}{{{\text{p}}_{0}}}\text{=}(1-\frac{0.0065H}{288.15})_{{}}^{\frac{g}{0.0065R}}\) (2.11)
同理,对同温层T=216.7K,也可得到
\(\frac{\text{p}}{{{\text{p}}_{1}}}\text{=e}_{{}}^{\left[ \frac{\text{g}{{H}_{1}}-H}{216.7R} \right]}\) (2.12)
式中,p1,H1分别为对流层上界的压强和海拔高度。
有了温度和压强随高度的变化觌律后,就可算得大气的密度随高度的变化规律。列成表格,就是国际标准大气表(见附录表1)。只要给出海拔高度,就可查到相应该高度大气的状态参数。
国际标准大气表给出了各国设计、实验有关航空产品的统一标准。各国、各厂生产的航空发动机的性能都是以国际标准大气为基准给出的。
2.3 流体的相对平衡
我们己经研究了静止流体中的压强分布。对于等加速运动的流体,如果每个流体质点与其直接相邻的质点之间没有相对运动,流体的运动像刚体运动一样,则可以将坐标系与加速运动的流体相固连,此时流体处于相对平衡状态,且流体内各处的切应力为零,仍可以用静平衡微分方程式(2.6)来研究其压强分布规律。下面以两个具体的例子来说明。
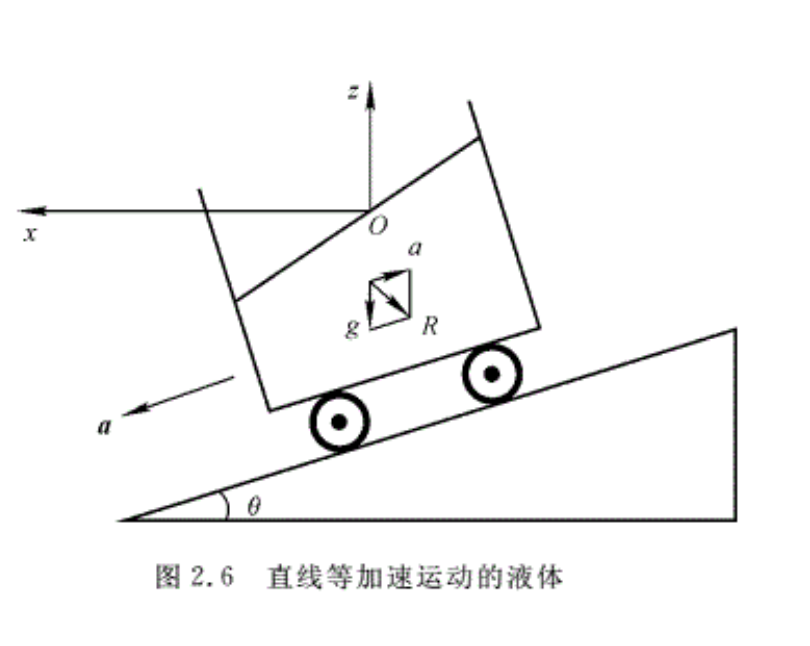
2.3.1 直线等加速运动
考虑一个沿直线作等加速运动的载有液体容器的小车,如图2.6所示。加速度a为
a=a cosθi-a sinθk
将坐标系与小车固连,则在此非惯性坐标系中,质量力由两部分组成:重力及惯性力,即单位质量的质量力为
R=-a cosθi+(a sinθ-g)k
根据式(2.6),得
\(\frac{\partial \text{p}}{\partial {{\text{x}}^{{}}}}\text{=}-\rho \text{a}\cos \theta\)
\(\frac{\partial \text{p}}{\partial \text{y}}\text{=}0\)
\(\frac{\partial \text{p}}{\partial \text{z}}\text{=}\rho \text{a}\sin \theta -\rho \text{g}\)
即 dp=-ρa cosθdx+(ρa sinθ-ρg)dz (2.13a)
积分式(2.13a),得
p=-ρax cosθ-ρz(g-a sinθ)+C (2.13b)
式中,C为积分常数
由式(2.13b)可以看出存在下述几种情况。
1.等压面为倾斜平面
在等压面上压强为常数,故由式(2.13b)可得等压面方程为
\( \text{z}+\frac{\text{a}\cos \theta }{\text{g}-\text{a}\sin \theta }\text{x=常数}\) (2.14)
即等压面是斜率为-a cosθ/(g-asinθ)的平面。
2.自由液面为倾斜平面
由于自由液面上的压强pa为常数,故自由液面为等压面,而且也是倾斜平面。
对于过零点的自由液面,其边界条件可写成x=0,z=0时(p)x,z=pa ,代入式(2.13b)得C=pa,故压强分布可写成
\(\text{p=}{{\text{p}}_{\text{a}}}-\rho \text{g}-\text{a}\sin \theta \frac{\text{a}\cos \theta }{\text{g}-\text{a}\sin \theta }\text{x}+\text{z}\) (2.15)
由此可求出自由液面方程,即p=pa的平面为
\({{\text{z}}_{0}}\text{=}-\frac{\text{a}\cos \theta }{\text{g}-\text{a}\sin \theta }\text{x}\) (2.16)
将式(2.16)代入式(2.15),得
\(\text{p=}{{\text{p}}_{\text{a}}}-\rho \text{g}-\text{a}\sin \theta \text{z}-{{\text{z}}_{0}}\) (2.17)
若令h=zo-z则式(2.17)可写成
\(\text{p=}{{\text{p}}_{\text{a}}}+\rho \text{g}-\text{a}\sin \theta \text{h}\) (2.18)
式中,h为自由液面下方液体的深度,如图2.7所示。
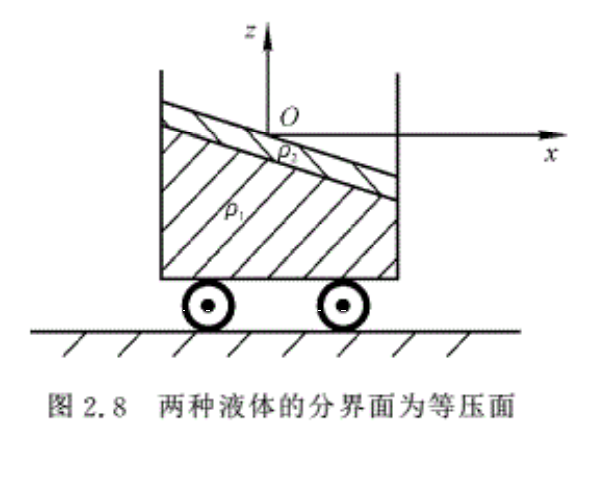
3.两种不同液体的分界面为等压面
图2.8中所示的两种密度不同而又不相混的流体处于平衡时,可以证明,它们的分界面必为等压面。
在分界面上任取相邻两点,设这两点的压强差为dp,则由式(2.13a),得
\(\begin{align}
& \text{d}{{\text{p}}_{1}}\text{=}{{\rho }_{1}}\left[ -\text{a}\cos \theta \text{dx}+-\text{g}+\text{a}\sin \theta \text{dz} \right] \\
& \text{d}{{\text{p}}_{2}}\text{=}{{\rho }_{2}}\left[ -\text{a}\cos \theta \text{dx}+-\text{g}+\text{a}\sin \theta \text{dz} \right] \\
\end{align}
\)
式中θ=0。由以上两式可得
\(\frac{d{{\text{p}}_{1}}}{{{\rho }_{1}}}\text{=}\frac{d{{\text{p}}_{2}}}{{{\rho }_{2}}}\)
要使该式成立,则必有dp1=dp2=0,可见分界面为等压面。
综上所述,在直线等加速坐标系中,相对静止液体的等压面、自由液面、分界面均为倾斜的平面。
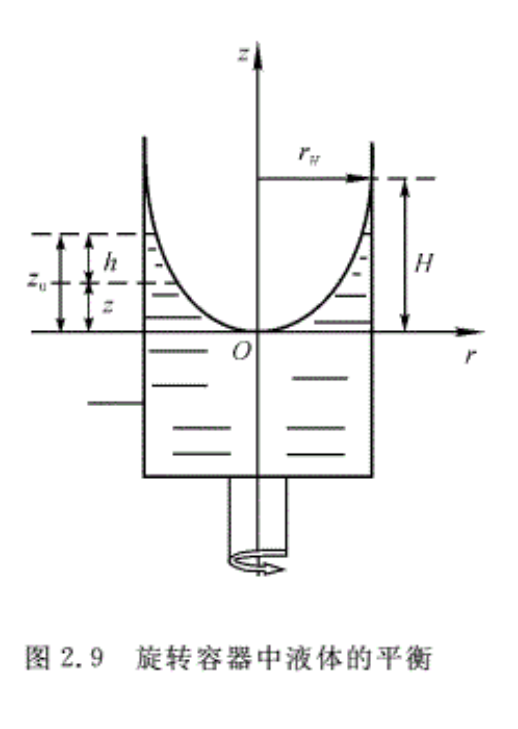
2.3.2 等角速度旋转容器中液体的平衡
图2.9所示为盛有液体的开口容器,绕某一固定轴作等角速度转动。此时,相对于容器而言,液体处于相对平衡。
在相对坐标系中,各点的加速度为
\(\text{a=-r}\omega _{{}}^{2}{{\text{i}}_{\text{r}}}\)
式中,ir为柱坐标沿r方向的单位向量。
由于液体旋转时有向心加速度,因此质量力有重力和离心力,即
\(R\text{=r}\omega _{{}}^{2}{{\text{i}}_{\text{r}}}-\text{g}{{\text{i}}_{\text{z}}}\)
由方程式(2.6),得
\(\frac{\partial \text{p}}{\partial \text{r}}\text{=}\rho \text{r}\omega _{{}}^{2} ,\frac{\partial \text{p}}{\partial \text{z}}\text{=}-\rho \text{g}, \frac{\partial \text{p}}{\text{r}\partial \theta }\text{=}0\)
所以 \(\text{dp=}\rho \text{r}\omega _{{}}^{2}\text{dr}-\text{gdz}\)
积分上式,可得
\( \text{p=}\frac{1}{2}\rho \text{r}_{{}}^{2}\omega _{{}}^{2}-\rho \text{gz}+C\) (2.19)
式中,C为积分常数。
由式(2.19)可得下述结论。
1.等压面为抛物面
在等压面上,压强为常数,由式(2.19)可以看出,等压面方程为
\(\text{z=}\frac{\omega _{{}}^{2}}{2\text{g}}\text{r}_{{}}^{2}+常数\) (2.20)
即等压面为一组旋转的抛物面。
2.自由液面为抛物面
在自由液面上,压强为大气压强pa,则边界条件可写成z=0,r=0时(p)z,r=pa,代入式(2.19),得C=pa,可得压强分布公式为
\(\text{p=}{{\text{p}}_{\text{a}}}-\rho \text{g}\left( \text{z}-\frac{\text{r}_{{}}^{2}\omega _{{}}^{2}}{2\text{g}} \right)\) (2.21)
在自由液面上p=pa,故得自由液面方程为
\({{\text{z}}_{0}}\text{=}\frac{\text{r}_{{}}^{2}\omega _{{}}^{2}}{2\text{g}}\) (2.22)
可见,液面上升的高度与角速度的平方成正比,ω越大,液面升得也越高。当\(\text{r=}{{\text{r}}_{H}}\) 时,液面升到最高点,此时\(H\text{=}\frac{\text{r}_{H}^{2}\omega _{{}}^{2}}{2\text{g}}\) ,由此可得到角速度\(\omega \text{=}\frac{\sqrt{2\text{g}H}}{{{\text{r}}_{H}}}\)。可通过测定H,直接求出旋转角速度ω,且ω与流体种类无关。
将式(2.22)代入式(2.21),得
\(\text{p=}{{\text{p}}_{\text{a}}}-\rho \text{g}\left( \text{z}-{{\text{z}}_{0}} \right)\text{=}{{\text{p}}_{\text{a}}}+\rho \text{gh}\) (2.23)
式中,h为自由液面以下的深度,h=zo-z,如图2.9所示。
2.4 静止流体对平面和曲面的作用力
2.4.1 静止流体对物体的作用力
静止流体对物体的表面力的合力,可以通过对整个表面上各面积元表面力的积分而获得,即
\(F\text{=}\int\limits_{A}{\text{pd}A\text{=}\int\limits_{A}{\left( {{\text{p}}_{\text{a}}}+\gamma \text{h} \right)}}\text{d}A\) (2.24)
式中:pa——自由液面上的压强;
h——物体离开自由液面的深度。
2.4.2静止流体对平面的作用力
如果一水平平板位于液体下深度为h处,则作用在物体表面一侧的力,由式(2.24),可得
\(F\text{=}\int\limits_{A}{\left( {{\text{p}}_{\text{a}}}+\gamma \text{h} \right)}\text{d}A\text{=}\left( {{\text{p}}_{\text{a}}}+\gamma \text{h} \right)A\) (2.25)
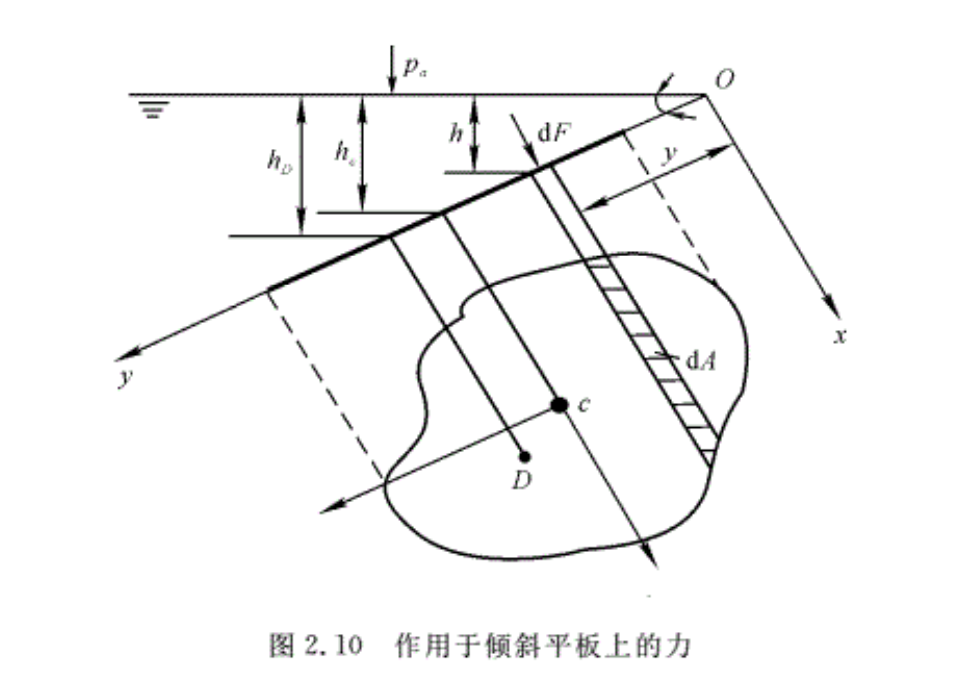
如果任意形状的平板倾斜放置在液体中,如图2.10所示,该平板垂直于纸面,与水平面之夹角为θ,液体自由表面的压强等于大气压强,试求作用于平板上的合力及其合力的作用点。
为研究方便起见,假设将平板绕Oy轴旋转90°,使它与图面重合,就能显平板的形状。
在平面上取一微面积dA,液体作用于此微元面积上的压力为pdA,作用在整个平板上的压力为
\(F=\int\limits_{A}{\text{pd}A\text{=}\int\limits_{A}{\left( {{\text{p}}_{\text{a}}}+\gamma \text{h} \right)}}\text{d}A\)
积分上式,便可得到作用在整个平面上的合力,即
\(F=\int\limits_{A}{\left( {{\text{p}}_{\text{a}}}+\gamma \text{y}\sin \theta \right)\text{d}A\text{=}{{\text{p}}_{\text{a}}}A+\gamma \sin \theta \int\limits_{A}{\text{y}}}\text{d}A\)
式中,\(\int\limits_{A}{\text{y}}\text{d}A\)为平板面积A对Ox轴的面积静矩,它等于\({{\text{y}}_{\text{c}}}A\),\({{\text{y}}_{\text{c}}}\)是平板的形心c与Ox轴间的距离,所以
\(\text{F=}{{\text{p}}_{\text{a}}}A+\gamma {{\text{h}}_{\text{c}}}A\text{=}{{\text{p}}_{\text{c}}}A\) (2.26)
式中,\({{\text{h}}_{\text{c}}}\)是几何中心c在自由液面下的深度,\({{\text{p}}_{\text{c}}}\text{=}{{\text{p}}_{\text{a}}}+\gamma {{\text{h}}_{\text{c}}}\)
由式(2.26)的可见,作用力F的大小等于平板面积A和平板形心c处的绝对压强pc之积,而与平板倾斜角θ无关;作用力的方向与平板垂直。
下面再研究合力作用点(压力中心)的计算方法。设作用点为D。根据平行力系对某轴的力矩之和应等于合力对同一轴力矩的原理,先对Ox轴取矩,得到
\({{F}_{{}}}{{\text{y}}_{D}}\text{=}\int\limits_{A}{\text{yd}F\text{=}\int\limits_{A}{\left( {{\text{p}}_{\text{a}}}+\gamma \text{h} \right)\text{yd}A\text{=}{{\text{p}}_{\text{a}}}\int\limits_{A}{\text{yd}A+\gamma \sin \theta }}}\int\limits_{A}{\text{y}_{{}}^{2}}\text{d}A\)
式中,\(\int\limits_{A}{\text{y}_{{}}^{2}}\text{d}A\)是平面对Ox轴的惯性矩,以Jx表示。又根据平行移轴定理,\({{J}_{\text{x}}}\text{=}{{J}_{\text{c}}}\text{+y}_{\text{c}}^{2}A\),Jc是平面面积对通过其几何中心c并与Ox轴平行的轴x*的惯性矩(附录表7列出了几种常见平面的惯性矩),将这些关系代入上式,得出
\(\text{y}_{D}^{{}}\text{=}\frac{{{\text{p}}_{\text{a}}}{{\text{y}}_{\text{c}}}A+\gamma \sin \theta \left( {{J}_{\text{c}}}+\text{y}_{\text{c}}^{2}A \right)}{\left( {{\text{p}}_{\text{a}}}+\gamma {{\text{y}}_{\text{c}}}\sin \theta \right)A}\text{=}{{\text{y}}_{\text{c}}}+\frac{{{J}_{\text{c}}}\gamma \sin \theta }{\left( {{\text{p}}_{\text{a}}}+\gamma {{\text{y}}_{\text{c}}}\sin \theta \right)A}\)
如果仅需求出相对压强γh作用在面积A上的合力作用点(即相对压力中心)时,可由上式令pa=0(不考虑自由液面的压强)得到,即
\(\text{y}_{D}^{{}}\text{=}{{\text{y}}_{\text{c}}}+\frac{{{J}_{\text{c}}}}{{{\text{y}}_{\text{c}}}A}\) (2.27)
\(\text{h}_{D}^{{}}\text{=}{{\text{h}}_{\text{c}}}+\frac{{{J}_{\text{c}}}\sin \theta }{{{\text{y}}_{\text{c}}}A}\) (2.28)
式(2.28)表明,压力中心总是在平面几何中心之下。
再对Oy轴取矩,可以得到压力中心到Oy轴的距离为
\(\text{x}_{D}^{{}}\text{=}\frac{{{\text{p}}_{\text{a}}}{{\text{x}}_{\text{c}}}A+\gamma \left( {{J}_{\text{xyc}}}+{{\text{x}}_{\text{c}}}{{\text{y}}_{\text{c}}}A \right)\sin \theta }{F}\)
对于相对压力中心,则为
\(\text{x}_{D}^{{}}\text{=}{{\text{x}}_{\text{c}}}\frac{{{J}_{\text{xyc}}}}{{{y}_{c}}A}\) (2.29)
式中,\({{J}_{\text{xyc}}}={{J}_{\text{xy}}}+{{x}_{c}}{{y}_{c}}A\),\({{J}_{\text{xy}}}=\int\limits_{A}{xydA}\)是平面惯性积,Jxyc是平面对通过c点且平行于Ox和Oy轴的惯性积。
2.4.3 静止流体对曲面的作用力
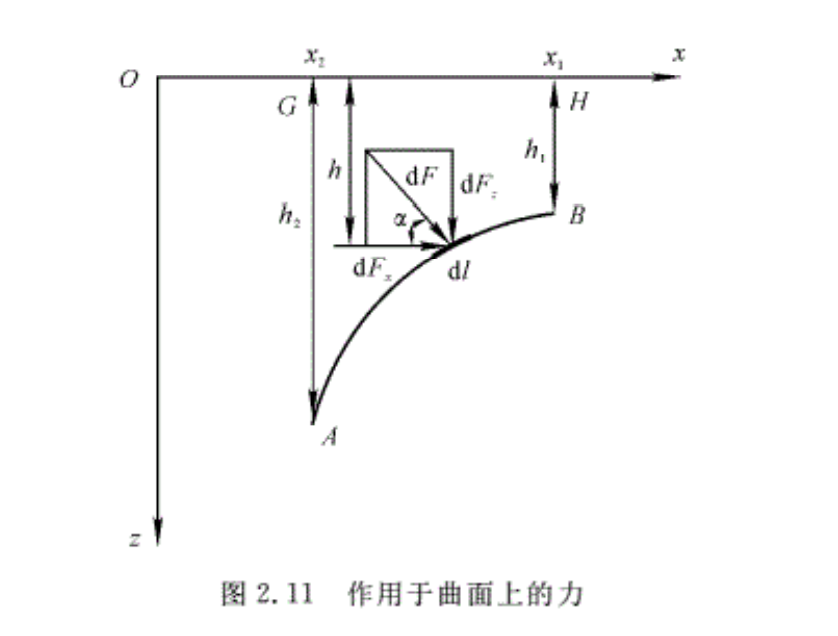
设流体作用在柱形曲面AB上,如图2.11所示,那么,静止的流体对曲面AB的作用力如何计算呢?
在曲面AB上取一微元面积dA,它距流体的自由表面深度为h。显然曲面AB各点只受流体沿内法线方向的压强作用,其大小为
\(p={{p}_{a}}+\gamma h\) (a)
在AB上取一微元长度dl,曲面的高度为b,则微元面积dA=bdl。若作用在dA上的合力为dF,则
dF= pdA=pbdl (b)
dF在x方向的分量为
\(d{{F}_{x}}=dF\cos \alpha =pb\cos \alpha dl=pbdh\)
所以
\({{F}_{x}}=\int_{{{h}_{1}}}^{{{h}_{2}}}{pbdh=\int_{{{h}_{1}}}^{{{h}_{2}}}{\left( {{p}_{a}}+\gamma h \right)}}bdh={{p}_{a}}b\left( {{h}_{2}}-{{h}_{1}} \right)+b\gamma \frac{h_{2}^{2}-h_{1}^{2}}{2}=b\left( {{h}_{2}}-{{h}_{1}} \right)\left( {{p}_{a}}+\gamma \frac{h_{2}^{{}}+h_{1}^{{}}}{2} \right)\)
式中,\(b\left( {{h}_{2}}-{{h}_{1}} \right)={{A}_{x}}\)为曲面AB在zOy面上的投影,而\(\frac{h_{2}^{{}}+h_{1}^{{}}}{2}\)则为Ax面的几何中心在自由液面下的深度hc,则
\({{F}_{x}}=\left( {{p}_{a}}+\gamma {{h}_{c}} \right){{A}_{x}}\) (2.30)
即静止液体作用在柱形曲而AB上的合力在水平方向的分量等于柱面在该方向的投影面积与该面积几何中心压强的乘积。也就是对柱面AB作用力的水平分量等于某一个垂直平板上所受的作用力。这个平板就是柱面AB在yOz坐标面上的投影。而水平分力的大小和压力中心的位置根据2.4.2节即可确定。如果柱形曲面是封闭的,则Ax=0,因此Fx=0。
将式(a)代入式(b),可得柱面AB所受的表面力在铅垂方向上的分力,即
\(d{{F}_{z}}=dF\sin \alpha =\left( {{p}_{a}}+\gamma h \right)d{{A}_{z}}={{p}_{a}}d{{A}_{z}}+\gamma hd{{A}_{z}}\)
\({{F}_{z}}=\int_{{{x}_{2}}}^{{{x}_{1}}}{\left( {{p}_{a}}+\gamma h \right)bdx}\)
积分后,得
\({{F}_{z}}={{p}_{a}}{{A}_{z}}+\gamma v\) (2.31)
式中,v为压力体的体积。
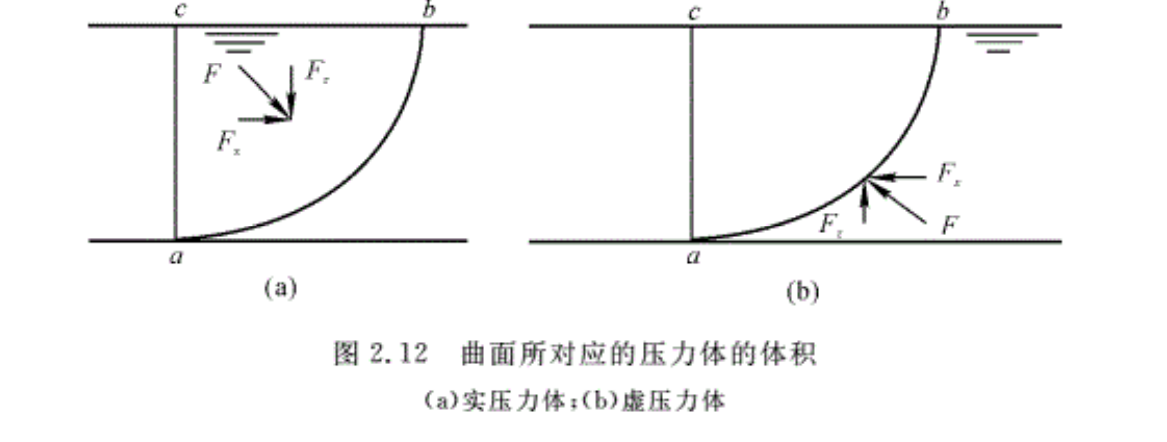
静止流体对柱面AB的作用力沿铅垂方向上的分力可分为两个部分。一部分是由于自由液面上的压强pa所引起的压力paAz;另一部分则是曲面上方压力体内流体的重力γv。前者作用力合力的中心在Az的面积中心,而后者则通过体积v中流体的重心。值得注意的是,压力体的体积v是指具有压强pa的自由表面和曲面ab间所包围的体积。它可以是充满了流体的体积,也可以是假想的体积。当曲面所受的垂直作用力Fz向下时,压力体的体积等于曲面上方液体的体积,此时压力体称为实压力体,如图2.12(a)所示。当Fz是向上时,这时曲面上方并没有液体,此时压力体的体积仍等于曲面上方的体积abc。这种情况下的压力体称为虚压力体,如图2.12(b)所示。
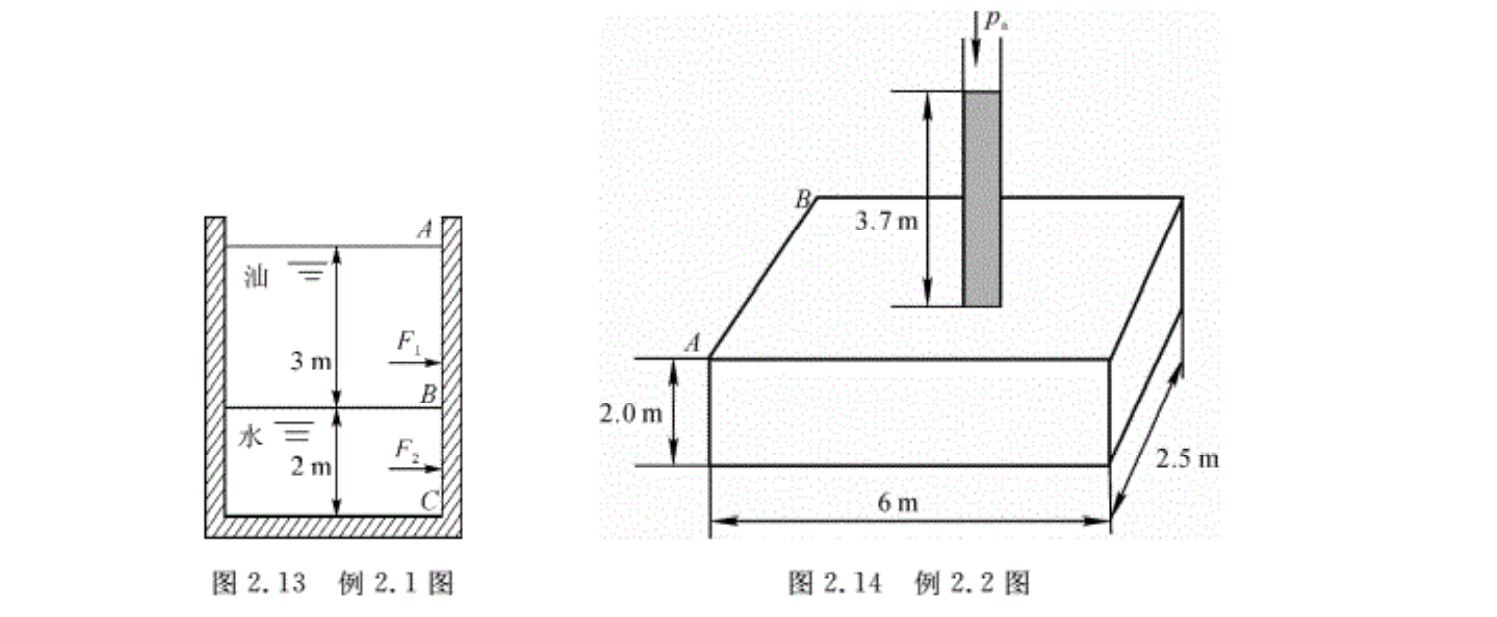
例2.1 如图2.13所示,水箱内装有水和油,油的重度为7.8×103N/m³,求作用在 1. 2 m宽的侧面ABC上的合力。
解:作用在ABC上的合力可由AB和BC两部分所受的力合成。因水箱周围和自由液面上均受大气压强的作用,所以只需要考虑相对压强的作用。
AB面上的作用力F1为
\({{F}_{1}}={{\gamma }_{1}}{{h}_{{{c}_{1}}}}{{A}_{1}}\)=7.8×1.5x3x1200=42.12kN
BC面上的作用力F2为BC面形心处的压强与面积Az的乘积,即
\({{F}_{2}}=\left( {{\gamma }_{1}}\text{x}3+{{\gamma }_{2}}\text{x}1 \right){{A}_{2}}\)=(3×7800+9810×1)(2×1.2)=79.7kN
总得合力
F=F1+F2=121.8kN
设F1的作用点离开自由液面深度为\({{\text{h}}_{{{D}_{1}}}}\),则有
\(\begin{array}{c}F_{1} h_{D_{1}}=\int_{A B} p h \mathrm{~d} A=\int_{0}^{3} 1.2 \gamma_{1} h^{2} \mathrm{~d} h=1.2 \gamma_{1} \times \frac{1}{3} \times 3^{3}= \\10.8 \times 7.8 \times 10^{3}=84.24 \mathrm{kN} \cdot \mathrm{m}\end{array}\)
\({{\text{h}}_{{{D}_{1}}}}=\frac{1}{{{F}_{1}}}\int_{AB}{phdA=\frac{84.24\times 10_{{}}^{3}}{42.12\times 10_{{}}^{3}}}=2m\)
F2的作用点离两种液体交界面的距离为h ‘,则F2的作用点离开自由液面的深度为
\({{\text{h}}_{{{D}_{2}}}}=3+h_{{}}^{/}\)
根据
\(\begin{aligned}F_{2} h^{\prime}=& \int_{B C} p L \mathrm{~d} A=\int_{0}^{2}\left(3 \gamma_{1}+\gamma_{2} L\right) L(1.2 \mathrm{~d} L)=\\& \int_{0}^{2} 3.6 \gamma_{1} L \mathrm{~d} L+\int_{0}^{2} 1.2 \gamma_{2} L^{2} \mathrm{~d} L=87.552 \mathrm{kN} \cdot \mathrm{m}\end{aligned}\)
得\(h^{\prime}=\frac{1}{F_{2}} \int_{B C} p L \mathrm{~d} A=87552 / 79700=1.0985 \mathrm{~m}\)
所以\({{\text{h}}_{Dz}}=4.0985m\)
合力作用点\({{\text{h}}_{D}}=\frac{{{F}_{1}}{{h}_{{{D}_{1}}}}+{{F}_{2}}{{h}_{{{D}_{2}}}}}{F}=3.3735m\)
例2.2 一水箱与管道相连,如图2.14所示,水的自由液面高度为3.7 m,水箱底面宽度为2.5 m,水箱高度为2.0 m,管道截面积A=0.1㎡,忽略水箱与管道的重量。试计算:
(1)作用在水箱底面上的合力;
(2)作用在水箱侧面AB上的合力及作用点;
(3)水的总重力,分析为什么与水箱底面上的合力不相等。
解:(1)由于水箱底面上的压强是均匀的,因此合力为
\(F=\gamma hA=9810\times 5.7\times 6\times 2.5=839kN\)
(2)水箱侧面的几何中心在自由液面下的深度为hc=4. 7 m,因此所受作用力为
\(F=\gamma {{h}_{c}}A=9810\times 4.7\times 2\times 2.5=230kN\)
作用点到自由液面的距离为
\({{h}_{D}}={{h}_{c}}+\frac{{{J}_{c}}}{{{y}_{c}}A}=4.7+\frac{2.5\times 8/12}{4.7\times 2\times 2.5}=4.77m\)
(3)水的总重力
\(G=\gamma v=9810\times \left( 6\times 2\times 2.5+3.7\times 0.1 \right)=298kN\)
与(1)相比可以看出,水箱底面上所受的合力F与水的总重力G不相等,原因是水箱上壁所受流体向上的作用力F ′为
F ′=\(\gamma hA=9810\times 3.7\times \left( 2.5\times 6-0.1 \right)=541kN\)
因此
F-F ′=839-541=298=G
2.5 流体静压强的测量原理
2.5.1 绝对压强、相对压强和真空度
压强常用压强表和真空表测量。压强表用于测量高于大气压的压强,称为表压强\({{p}_{gage}}\);真空表用于测量低于大气压的压强,称为真空度\({{p}_{va}}\)。一般用这类测压计所得的压强(如\({{p}_{gage}}\),\({{p}_{va}}\))是实际压强与当地大气压强的差值,称为相对压强,即
\({{p}_{gage}}=p-{{p}_{a}}\)
\({{p}_{va}}={{p}_{a}}-p\)
2.5.2 流体静压强的测量
压强测量是流体力学实验技术中最基本的测量技术。不仅压强本身是表征流体运动过程的重要参数,而且流速、流量等参数的测量,也往往转换为压强测量问题。因此,压强测量几乎成为每一项流体力学实验所不可缺少的项目。从被测压强的性质来看,压强的测量可分为静态压强(稳定压强)和动态压强(非稳定压强)的测量。静态压强的测量是指流体压强不随时间而变,或者变化很慢,称其为常规量。动态压强是指流体压强随时间快速变化,或周期性变化,它是研究非定常流动所必须进行的特殊测量项目。
在流体力学实验中,测量压强的范围非常广泛,可以由负压到中、高压。在这样宽的压强范围内,需要采用各种类型的测压计。
压力指示仪有各种各样的结构形式。按被测压强高低,可以分为压强表、真空表和压力传感器。它们多数是利用金属的弹性变形来度量压强大小的。
各种压力表、真空表和压力传感器都必须进行校准和标定,这些测压计在出厂前和使用了一段时间后都须进行校准,以保证测量精度。测压计按其转换原理的不同,大致可分为液柱式压力计、弹性式压强表、活塞式压强表和电压式压强表等。
1.液柱式压力计
液柱式压力计基本原理是将被测压强转换成液柱高度差进行压力测量的,用于测量低压、负压或压力差。常用的液柱式压力计有单管式测压计、U形管测压计和斜管测压计等。
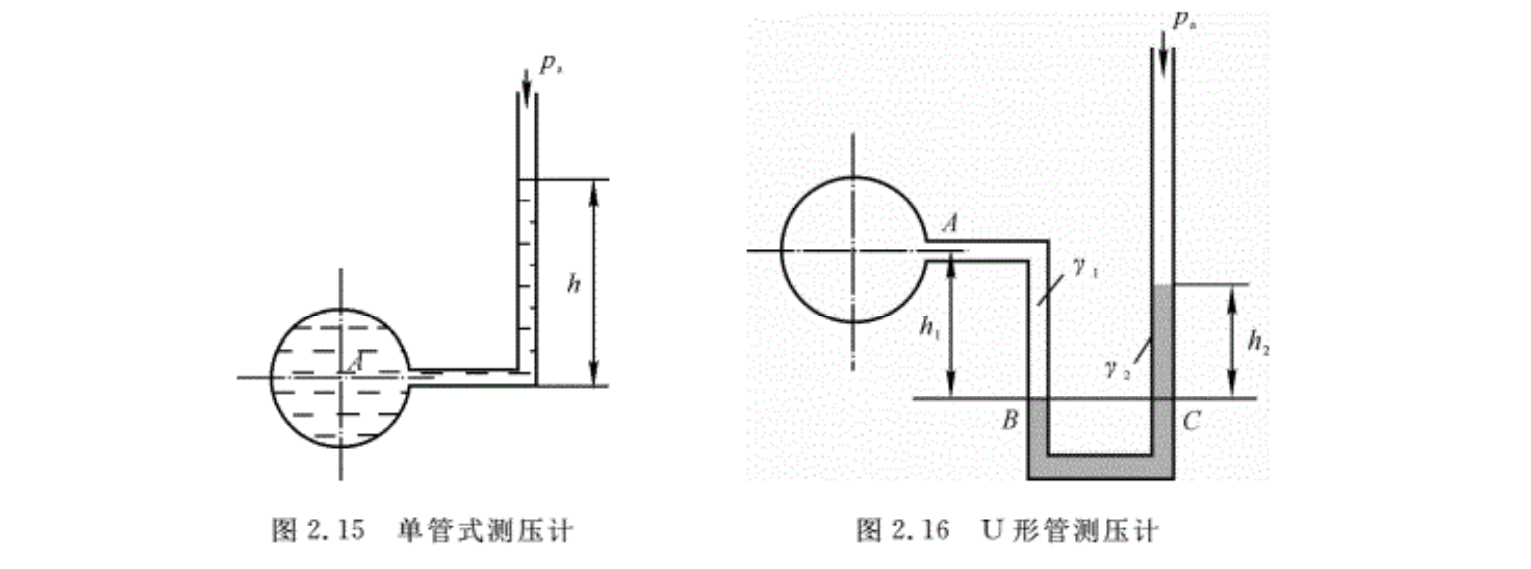
(1)单管式测压计:单管式测压计是最简单的液柱式测压计。通常由一根内径大于5 mm 的直玻璃管组成。玻璃管一端直接连在盛有液体的压力容器上,另一端与大气相通,如图2.15所示。若液体在玻璃管内上升的高度为h,液体的重度为γ,则容器中A点的压强为
\({{p}_{A}}={{p}_{a}}+\gamma h\)
用单管式测压计测量压强简单、准确。但其缺点是只能用来测量液体的压强,而不能用来测量气体的压强,而且容器内压强必须大于大气压强,否则空气被抽吸进容器;同时也不能用来测量很高的压强,否则测压管很长,用起来很不方便。
(2)U形管测压计:U形管测压计的一端与大气相通,另一端连接到所要测量压强的容器上,如图2.16所示。U形管测压计克服了单管式测压计的缺点。它的优点是既可以测量液体的压强,也可以测量气体的压强(因为U形管中的液体可将被测流体与大气隔开)。如果被测流体的压强较小时,U形管中装较轻的液体,如水或酒精。当被测流体的压强较大时,U形管中装较重的液体,如水银。
当多个U形管并联使用时,其压强计算较为复杂,但只要注意在连通的同一种静止液体中,如果两点高度相同,则它们的压强也相等。由此可以建立A(见图2.16)点压强与大气压强之间的关系,即
\({{p}_{A}}+{{\gamma }_{1}}{{h}_{1}}={{p}_{a}}+{{\gamma }_{2}}{{h}_{2}}\)
如果被测流体是气体,则由于气体重度γ1比液体重度小得多,可以略去γ1h1项,得
\({{p}_{A}}={{p}_{a}}+{{\gamma }_{2}}{{h}_{2}}\)
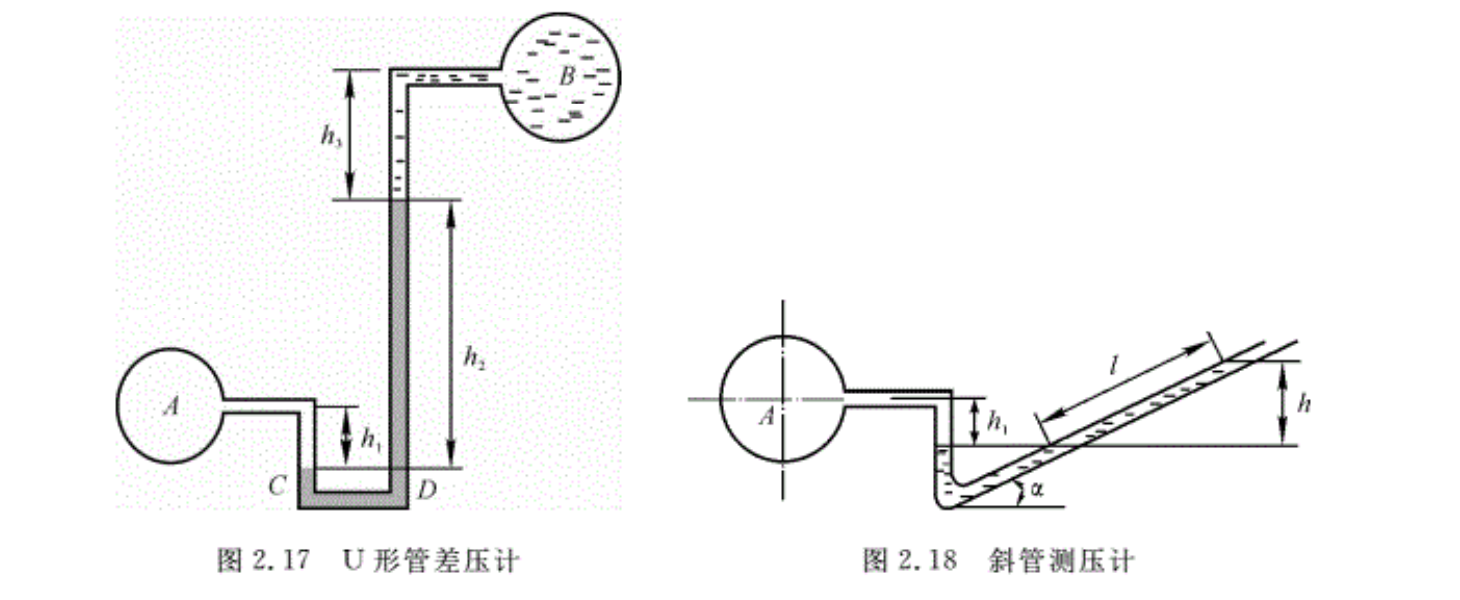
U形管测压计还可以用来测量两点间的压强差,即构成所谓的U形管差压计如图2.17 所示。U形管两端分别连接在容器A和B上。用U形管差压计可测量任意两点之间的压强差,由图2.17可知,C,D面是等压面,因此可得
\({{p}_{A}}+{{\gamma }_{1}}{{h}_{1}}={{p}_{B}}+{{\gamma }_{2}}{{h}_{2}}+{{\gamma }_{3}}{{h}_{3}}\)
于是A,B两点的压强差为\({{p}_{A}}-{{p}_{B}}={{\gamma }_{2}}{{h}_{2}}+{{\gamma }_{3}}{{h}_{3}}-{{\gamma }_{1}}{{h}_{1}}\) 。需要注意的是,在高精度测量过程中,要考虑温度对液体密度的影响。
(3)斜管测压计:为了提高测量精度,对于微小压强的测量,可以将测压管倾斜放置,即利用斜管测压计将读数放大。图2.18所示为斜管测压计,倾斜管一端和容器A相接,另一端与大气相通,测压管倾斜角为α,容器内的压强为
\({{p}_{A}}+{{\gamma }_{1}}{{h}_{1}}={{p}_{a}}+{{\gamma }_{2}}l\sin \alpha \)
即 \({{p}_{A}}={{p}_{a}}-{{\gamma }_{1}}{{h}_{1}}+{{\gamma }_{2}}l\sin \alpha \)
斜管测压计常用来测量气体的压强,根据图中几何关系,得
\(\frac{l}{h}=\frac{1}{\sin \alpha }\)
可见,l比h放大了1/sinα倍,α愈小,l愈长,从而提高了读数和测量精度。
2.弹性式压强表
弹性式压强表是利用弹性元件在受到压强作用下产生压缩和伸长变形的原理来测量压强大小的。它用于测量稳态压强,可以用来测量中等或较高的压强。这类压强表的形式有管环式、弹簧式和隔膜式等。这类压强表的测量精度和灵敏度不太高,且不能测量脉动压强的变化。
3.活塞式压强表
此种压强表是一种标准的压强测量仪表。它是将被测压强转换成活塞上所加的平衡砝码的重量进行压强测量的。
4.电压式压强表
电压式压强表是将被测压强转换成各种电量进行压强测量的。这是一种采用电测技术对流体压强进行测量的方法。
在发动机实验中,压强测量点数越来越多,要迅速准确地记录这些数据,液柱式压强计及弹性式压强表是难以实现的。这就需要采用压力传感器。
压力传感器是利用电子元件制成的传感器,它将压强的变化转变成电量(如电压、电容、电流或电感等)的变化,然后经过相应的换算而求得压强的变化值。这类传感器可以测量脉动压强。常见的传感器有电阻应变式压力传感器、电容式压力传感器、电感式脉动压力传感器、电压式压力传感器和压阻式压力传感器等。下面仅简单介绍两种传感器。
电阻应变式压力传感器:这种传感器的工作原理是当电阻应变片上的金属丝受力变形时,其电阻值发生变化的大小与被测压强之间建立一定的联系,量出电阻值变化后,就可求出被压强的大小。
电阻应变式压力传感器的优点是结构简单,使用方便。
电容式压力传感器:这种传感器是利用量电容量的大小来测量压强大小的。只要使所测压强能引起电容压力传感器的两极板间的距离发生变化,就可以使用这种传感器。
电容式压力传感器的优点是结构简单,灵敏度高,动态响应快。缺点是测量低频脉动压强时,输出功率很小;测量高频脉动压强时,寄生电容较大,使抗干扰能力下降。
小结
连续介质与流体质点的概念、流体的黏性、压缩性和导热性等是研究流体运动的基础。
作用在流体上的力可分为两类,即质量力和表面力。当流体处于静平衡(静止流体)和相对平衡(流体质点作等加速运动或等角速度旋转)时,导致剪切应力处处为零。因此作用在流体上的力只有质量力和压强(垂直于表面的力)。
静止流体或运动的无黏性流体中,任意一点的压强具有两个重要特点:
(1)任意一点处的压强都是各向同性的,因此压强是时间和空间坐标的标量数,而与作用而在空间的方位无关;
(2)压强的方向永远沿着作用而的内法线方向。
流体静平衡微分方程为
\(\nabla p=\rho R\)
对于静平衡流体,如果质量力只有重力,则压强随高度变化为
\(\frac{dp}{dz}=-\rho g\)
对于作等加速度直线运动或等角速度转动的流体,如果没有流体之间的相对运动,仍可以运用流体静平衡微分方程。
对于等加速直线运动,在相对坐标系中,其等压面、自由液面和分界面均为倾斜平面。
对于等角速度旋转的液体,在转动坐标系中,其等压面、自由液面和分界面均为抛物面。
静止流体对任意平板的作用力F的大小等于平板面积A和平板形心c处的绝对压强pc的乘积,即\(F={{p}_{c}}A=\left( {{p}_{a}}+\gamma {{h}_{c}} \right)A\) ,而与平板的倾角θ无关,其方向与平板垂直。
静止流体对柱面的作用力在水平方向上的投影Fx,等于作用在投影平面Ax上的作用力。
在铅垂方向上的分力为
\({{F}_{z}}={{p}_{a}}{{A}_{z}}+\gamma v\)
式中,v为压力体的体积。
思考练习题
2.1思考流体静平衡微分方程的意义。
2.2有一油槽车在水平轨道上作等减速运动,其减加速度a=0.02m/s²。试求此车油罐内油的自由液面倾斜角。
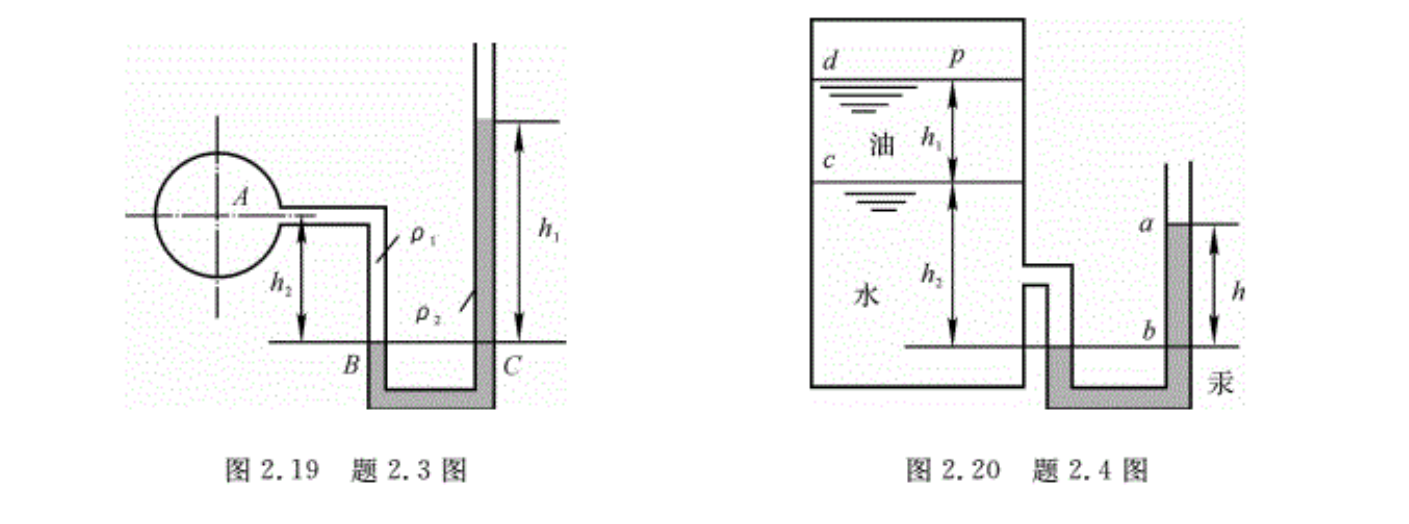
2.3如图2.19所示,其中ρ1=850 kg/m³,ρ2=1000kg/m³,h1=15 cm,h2=7.0cm。 试求A点的相对压强。
2.4图2.20所示的封闭容器中盛有ρ=800 kg/m³的油,h1=300 mm,下面为水,h2=500mm,测压管中汞柱液面的读数h=400mm。试求封闭容器中油面相对压强的大小。
2.5直径为d=0.2m,高度为h=0.1m的圆柱形容器,装水2/3容量后,绕垂直轴旋转。求:
(1)自由液面达到顶部边缘时的转速;
(2)自由液面达到底部中心时的转速。
2.6半径r=15cm,高H=50cm的圆柱形离心分离器,充水深度h=30cm,容器绕圆柱中心线以等角速度ω旋转。求圆柱以多大的极限角速度旋转时,才能不使水从容器中溢出
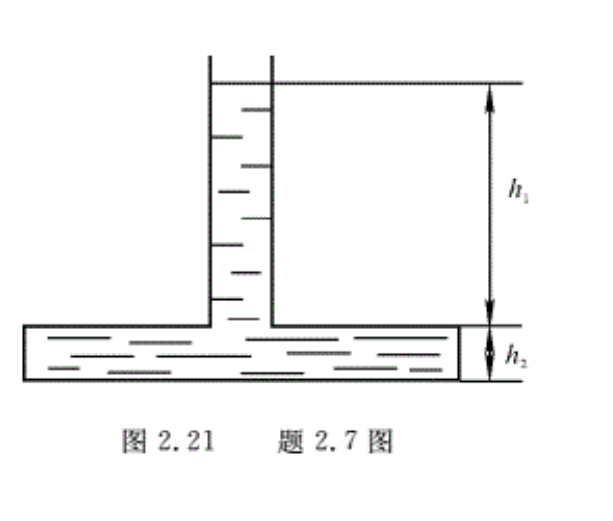
2.7一根横截面面积为1cm²的管子连在一个容器的上面(见图2.21)。容器的高度为h1=1 cm,横截面积为100cm²,今把水注入,使水到容器上部的深度为h2=99cm。问:
(1)水对容器底面的作用力是多大?
(2)系统内水的重力是多少?
(3)解释(1 )和(2)中求得的数值为何不同。
2.8在海半面上海水密度ρo=1024kg/m³,求海洋8000m深处的压强(表压)。假设:
(1)海水是不可压缩的;
(2)海水是可压缩的,其中弹性模量E=2.34×109Pa。
2.9一矩形水箱长3m,自由液面离箱底1. 5m(见图2.22 )。如果水箱以加速度a=3m/s²作水平运动,试确定自由液面与水平面之间的夹角以及作用在箱底的最小压强与最大压强。已知流体密度ρ=1000kg/m³。
2.10如图2.23所示,巨型闸门AB,宽1m,左侧油深h1=1 m,水深h2=2 m,油的重度γ=7.84 kN/m³,闸门的倾角α=60°。求闸门上的流体总压力及作用点的位置(平板右侧受大气压强的作用)。
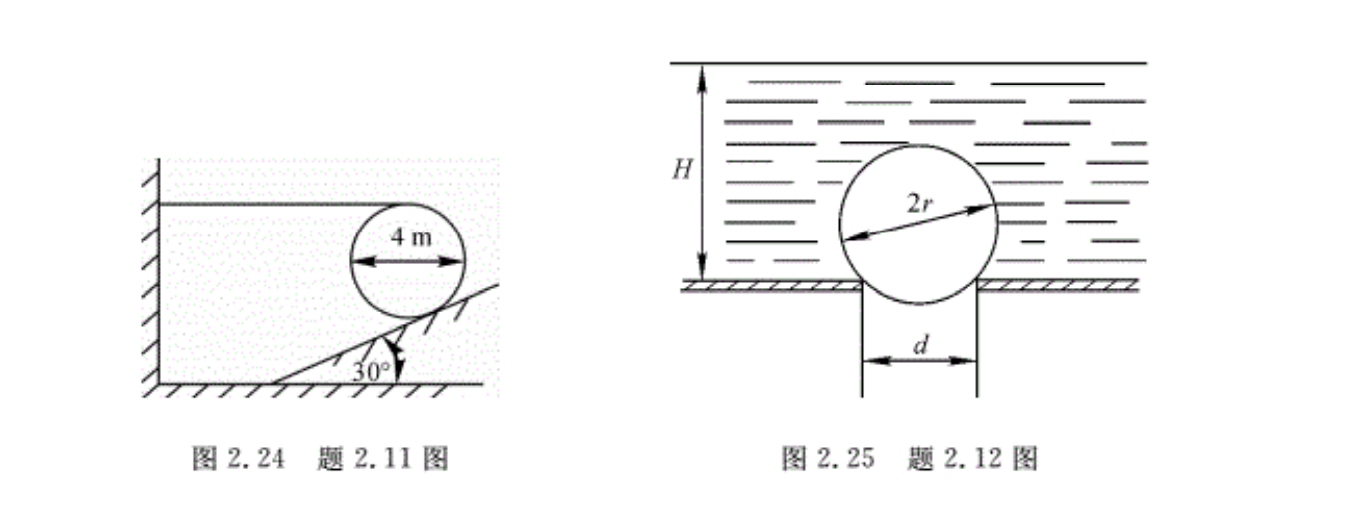
2.11计算图2.24所示水平圆柱体每1m长度上的流体作用力。
(1)若圆柱体左侧是限制在密闭容器中的气体,容器内气体表压强为35 kPa;
(2)若圆柱体左侧是具有自由表面的水。计算时计及圆柱体右侧大气压强的作用。
2.12如图2.25所示,盛水容器底部开有d=5cm的孔,用空心金属球封住,球重力G=2.45N,r=4cm,水深H=20cm。求升起该球所需的力。
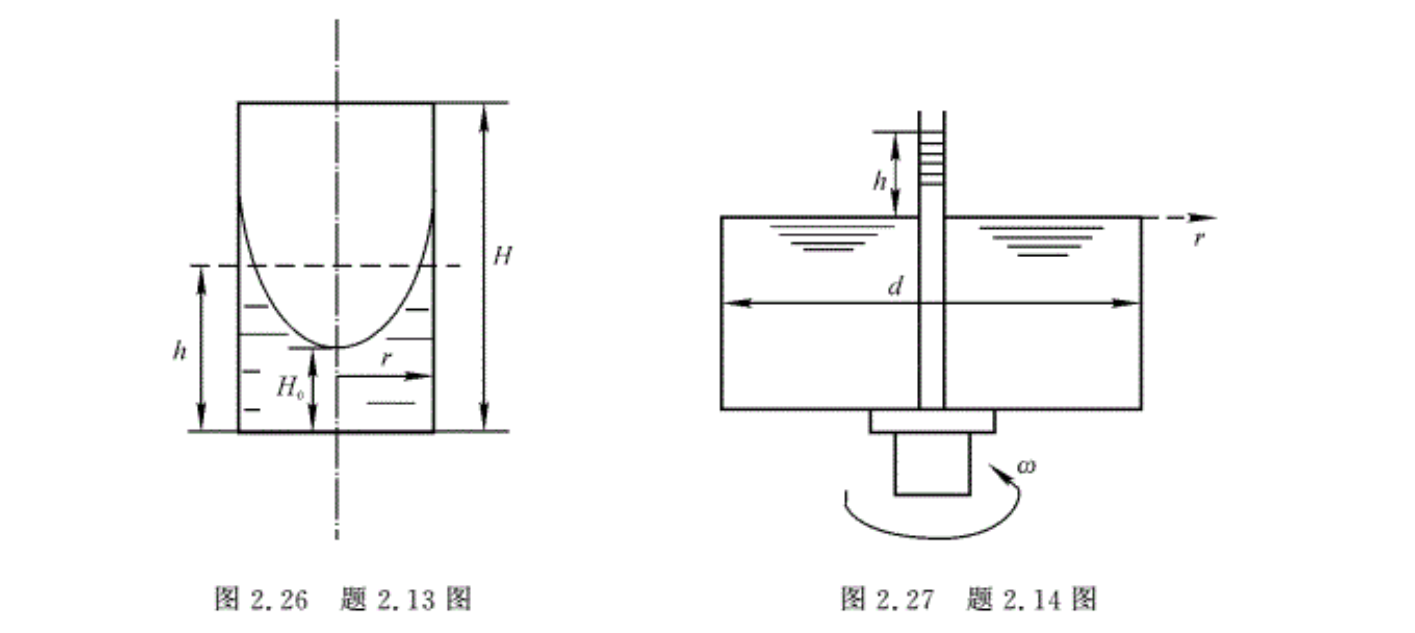
2.13盛有水的圆桶(见图2.26),以角速度ω绕自身轴旋转,试问:ω超过多大值时可露出桶底?设水的初始高度为h。
2.14一圆柱形容器,其顶盖中心装有一敞口的测压管,如图2.27所示,容器装满水,测压管中的水面比顶盖高h,容器直径为d。当它绕自身中心轴以角速度ω旋转时,试问:顶盖收到液体向上的作用力有多大?
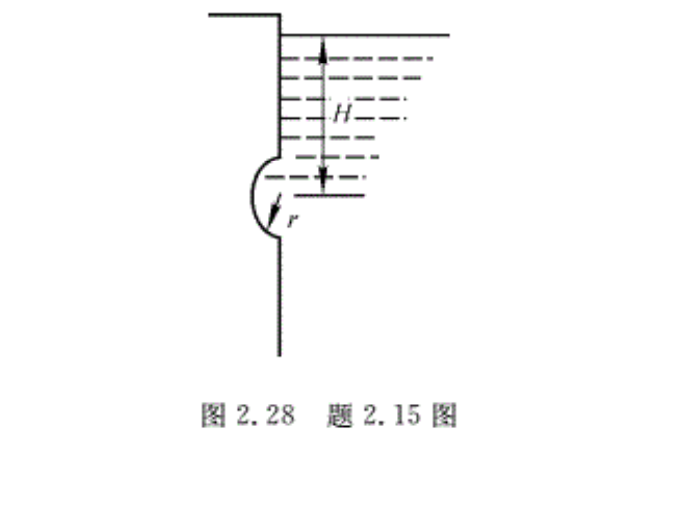
2.15在水下竖壁上有一半圆柱形的穴腔,半径r,长L,轴线在水面下H处,H>r,如图2.28所示,水的密度为ρ。求水对腔壁的铅垂方向的力及水平方向的力。