第五章滞止参数与气动函数
在气体动力学中,尤其在发动机的气动计算中,经常用到滞止参数、临界参数和气体动力学函数的概念。因此,本章将讨论微扰动的传播规律;引出声速与马赫数的概念,并讨论滞止参数、临界参数、极限速度和气体动力学函数。在此基础上,将前文讨论过的一维定常流动的基本方程用本章所介绍的滞止参数和气动函数来表示,以利于在发动机中的应用。
5.1 微扰动的传播及马赫数
5. 1. 1 微扰动的传播
在气体所占据的空间中,若某点的压强、密度和温度等参数发生了变化,则这种现象被称为气体受到了扰动。造成扰动的根源(如击鼓时鼓膜的振动,说话时声带的振动)叫做扰动源。根据扰动所造成的气体参数变化的大小,把扰动分为微扰动和强扰动。如果气体的压强、密度和温度等参数的变化量与参数原来的数值相比极其微小时,则称其为微扰动(鼓膜和声带的振动所引起的扰动均为微扰动),否则为强扰动。扰动在介质中是以波的形式向四周传播的。
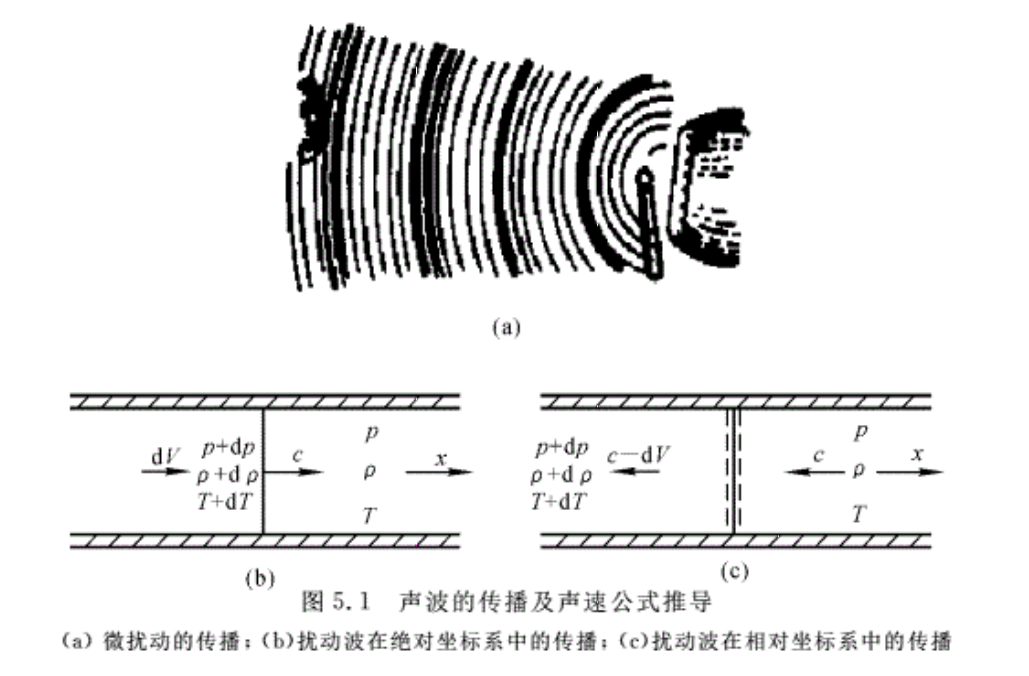
如图5.1(a)所示,用锤击鼓时,会引起鼓膜的振动。当鼓膜向外凸起时,会压缩其邻近的一层空气,使周围静止空气的压强、密度和温度略有增加。这层被压缩的空气因其压强稍大于外层空气的压强,就挤靠近它的较远的一层空气。这层较远的空气受到压缩后,又会压缩更远的一层空气,击鼓这样的一个扰动就会从鼓膜处向四周传播出去。而扰动气体与未受扰动气体的分界面即是扰动波。由于扰动很弱,且空气受到压缩,故称为微弱压缩波。同理,当鼓膜向内凹时,其邻近的空气又会膨胀,压强、密度和温度略微减小。这种微弱膨胀扰动也会从鼓膜处向些周传播出去。只要鼓膜连续振动,就产生一系列的压力升高和降低的微扰动波,不管是压缩或膨胀,只要是微扰动,所产生的微扰动波都是以声速向外传播的。
5.1.2 声速
由5.1.1小节的分析可知,微扰动波在介质中的传播速度,就是声速。声速的大小与介质的可压缩性有非常紧密的联系,因而它是介质的重要属性之一
将上述微扰动波的传播过程用量化的形式表示。鼓膜压缩邻近空气的这一扰动,即所产生的微扰动波相当于活塞在一个半无限长直管中,由于活塞速度从零增加到dV,这一扰动将压缩邻近气体而产生微扰动波。该微扰动波以声速c向右传播,如图5.1(b)所示。
波扫过的气体,压强为p+dp加密度为ρ+dρ,温度为T+ dT,并以微小速度dV向右运动。波前方的气体压强为p,密度为ρ,温度为T,并且气体是静止不动的。而微扰动波是以声速向右传播的。显然,对一个静止的观察者来说,这是一个非定常的一维流动。为了使分析简单起见,选用与扰动波一起运动的相对坐标系。对于位于该坐标系的观察者来说,上述的流动过程就转化为定常的了。这就表明了观察者以声速c向右运动时所看到的这一过程的现象,即扰动波不动,而压强为p,密度为ρ,温度为T的未被扰动的气体以声速c向着扰动波(即由右向左)运动。气体经过扰动波之后,速度降为c-dV,同时压强增大为p+dp,密度增加到ρ+dρ,温度也升高到T+ dT,如图5.1(c)所示。包围扰动波取控制体(即图中虚线),并忽略作用在这个控制体上的黏性力,然后对此控制体沿x方向应用动量方程,则有
-pA+(p+dp)A=ρAc[-(c-dV)-(-c)]
式中,A为直管的横截面面积。经整理后得
dp=ρcdV (a)
对此控制体应用连续方程,则有
ρAc= (ρ+dρ)A(c-dV)
经整理并略去高阶无穷小量后,可得
dV/c=dρ/ρ (b)
将式(b)代入式(a),得 c=dp/dρ (5.1)
由气体属性的讨论可知,气体中的声速c大小直接代表了气体的可压缩性的大小。
不难理解,如果活塞以速度dV在管内向左运动,即在管内(活塞右边)产生膨胀波向右运动,同样它的运动速度仍然是声速c。并由式(5.1)决定。也就是说,在相同介质的条件下,微压缩扰动波与微膨胀扰动波的传播速度是一样的。显然,由微压缩扰动波和微膨胀扰动波交替组成的微弱扰动波(例如在空气中的声波)的传播速度也是由式(5.1)决定的。
要想具体计算声速,还必须知道在微扰动传播过程中的压强p和密度ρ之间的关系。因
为在微扰动传播过程中,气体参数变化量都是无限小量。即dp→0,dρ→0和dT→0。若忽略黏性作用,则整个过程接近于可逆的过程。此外,由于扰动传播过程进行得非常迅速,介质来不及和外界交换热量,这就使得此过程接近于绝热过程。所以,可以认为微扰动的传播过程是个等熵过程。对于完全气体来讲,在等熵过程中压强p和密度ρ之间的关系是
p/ρk=常数
对此式取对数并微分,得
\(c=\sqrt{{{\left( \frac{\partial p}{\partial \rho } \right)}_{s}}}=\sqrt{k\frac{p}{\rho }}=\sqrt{kRT}\) (5.2)
对于空气,气体常数R=287.06 J /(kg··K),k=1.4,则c=20.05√T(m/s)。对于涡轮喷气发动机使用的燃气,一般取R=287.41 J /(kg·K),k=1.33,则c=19.55√T(m/s)。
从式(5.2)可知,气体中声速的大小与气体的性质和绝对温度有关。气体温度愈高,气体中的声速愈大,则气体的可压缩性就愈小(即dρ/ dp愈小)。对于不可压缩流体来说,密度为常数,即dρ/dp趋近于0,则c=√(dp/dρ)→∞。对任何一个微小的扰动,都会立即传遍到整个流场。可见声速的大小与气体的可压缩性有关。
5.1.3 马赫数
流体的压缩性与声速有关,但由伯努利方程和微分形式的动量方程可知,气流的速度变化,也影响到气流的密度和压强的变化。因此对流动的气体来讲,气流的压缩性除了与气体中的声速有关外,还与气流的速度大小有关。为了同时考虑这两个因素,需要用气流的马赫数来表示流动气体的压缩性。马赫数用Ma表示,它的定义是
Ma=V/c (5.3)
即流体质点的运动速度与流体质点当地的声速之比。流场中各点的气体参数不同,马赫数的值也就不同。马赫数是可压缩流动理论中的重要相似参数。因为它除了表征气流的压缩性以外,对于研究气体的高速运动规律以及气体流动问题的计算和分析等方面,均有极其重要的用途。由马赫数的定义式可以看出,\(M{{a}^{2}}=\frac{{{V}^{2}}}{{{c}^{2}}}=\frac{2}{k\left( k-1 \right)}\frac{{{V}^{2}}/2}{{{c}_{v}}T}\) ,即马赫数的平方是与气流的动能与内能之比成正比的,因此,马赫数的平方可以作为衡量气体宏观运动的动能与分子无规则运动的内能比值大小的一种度量。
气流的可压缩性与马赫数的关系可由欧拉运动微分方程式揭示出来。因为气体在流动过程中,满足下列关系式:
\[-VdV=\frac{dp}{\rho }=\frac{d\rho }{\rho }\frac{dp}{d\rho }\]
将式(5.1 )代入上式,并应用式(5.3),得
\[-M{{a}^{2}}\frac{dV}{V}=\frac{d\rho }{\rho }\] (5.4)
式中,dV/V和dρ/ρ分别表示气流速度和密度的相对变化量。式(5.4)表明,在绝能等熵流动中,气流速度相对变化量所引起的密度相对变化量与Ma²是成正比,且V与ρ变化方向相反。在绝能等熵流动中,当Ma≤0.3时,比值丨(dρ/ρ)/(dV/V)丨在0.09以下,一般可以不考虑密度的变化。即认为气体是不可压缩的,从而可以使问题简化,当Ma >0.3时,就必须考虑气体的压缩性。
对于不可压流动,由于密度不变(即认为密度是己知的),只需要求出流场中的压强和速度,在无特殊加热和冷却的情况下,可以不考虑能量方程。如果需要知道温度的变化,例如有加热的情况,此时温度、压强和速度存在着相互的耦合关系,就一定要用到能量方程来求解温度场。
对于气体绕物体的流动,当气流速度小于当地声速(即Ma<1)时,称这种气流为亚声速气流;当气流速度大于当地声速(即Ma> 1)时,称其为超声速气流。当物体上一部分区域的流动为Ma< 1,而其余部分的流动为Ma> 1时,则在该物体上的某点(或线)必定有Ma=1,这种既有亚声速,又有超声速的混合流动叫跨声速流动。跨声速流动兼有亚声速和超声速流动的某些特征,因而使流动更为复杂。
例5.1 飞机在12000m的高空飞行,其速度为1 800 km/h,求该飞机的飞行马赫数。若在发动机尾喷管出口处,燃气流的温度为873K,燃气速度为560 m/s,燃气的比热比k=1.33,气体常数R=287.4 J/(kg·K)。求尾喷管出口处燃气流的声速和马赫数。
解:由国际大气表查得,H=12000m时的声速为295.1 m/ s,因此飞机的飞行马赫数为
Ma=V/c=1800 x 103/3600 x 295.1=1.694
据定义即可算出尾喷管出口的声速和马赫数分别为
c=√(kRT)= 19.55√873=577 m/s
Ma=V/c=560/577.6=0.97
5.2 几个气流的参考参数
5.2.1 气流的滞止参数
1.滞止状态与滞止参数(或称总参数)
在气体动力学中,为了计算方便,引入了滞止参数的概念。滞止参数又叫总参数,而一般流动中一点处的流体压强、温度与密度又叫静参数。这里的静参数是指相对于测量仪器静止时所测得的参数。气流从某一状态绝能等熵地滞止到速度为零的状态称为滞止状态,滞止状态下的气流参数称为滞止参数,用上标“*”表示。在实际中,由于滞止参数便于测量,因而在气动计算中得到了广泛的应用。
滞止状态是一种假想的参考状态(也可以是真实状态),在实际流动中,气流每一个状态都有相应的滞止状态,因而每一点都有相应的滞止参数。因此,滞止参数是点函数。在实际流动中,从一点到另一点的滞止参数可能不同。一般滞止参数的变化与实际流动中气体与外界的热交换和功交换以及耗散(摩擦即是一种耗散)等因素有关。
由于滞止参数是人为引入的参考参数,其定义与所研究的实际流动过程无关。但滞止参数可以是流场中实际存在的参数,如飞行器飞行时驻点处的参数和高压容器中气体的参数,高速风洞前的储气罐中的气体参数等。
2.滞止焓和滞止温度
根据一维定常绝能流动的能量方程
\[h+\frac{{{V}^{2}}}{2}={{h}_{1}}+\frac{V_{1}^{2}}{2}\]
可知,在绝能流动中,当速度减小时,气流的(静)焓h将会增加。如果把气流由速度V1绝能地滞止到零(V1=0),此时所对应的焓值(h1)就称为滞止焓,用h*表示,则
\({{h}^{*}}=h+\frac{{{V}^{2}}}{2}\) (5.5)
此式只要求绝能,不要求等熵,因此式(5.5)既可适用于可逆过程也适用于不可逆过程。滞止焓也称为气流的总焓。式(5.5)中的h称为静焓。静焓与气流动能之和,代表气流所具有的总能量的大小(即总焓)。
对于完全气体,h=cpT,则有
\[{{T}^{*}}=T+\frac{{{V}^{2}}}{2{{c}_{p}}}\] (5.6)
式中,T*称为气流的滞止温度或称总温。它是把气流速度绝能滞止到零时的温度,它也反映气流总能量的大小,而T称为静温。
因为\({{c}_{p}}=\frac{k}{k-1}R\),而\(M{{a}^{2}}=\frac{{{V}^{2}}}{{{c}^{2}}}=\frac{{{V}^{2}}}{kRT}\), 代入式(5.6),得
\[{{T}^{*}}=T\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)\]
或 \(\frac{{{T}^{*}}}{T}=1+\frac{k-1}{2}M{{a}^{2}}\) (5.7)
由式(5.7)可见,总温与静温之比取决于气流的Ma。当Ma很小时,T*/ T接近于1,气流Ma 越大,则T*与T差别就越大。例如,当Ma=0.3时,k=1.4,则由式(5.7)可得
T*/T=1.018
可见,当Ma≤0. 3时,T *与T差别不超过2%。式(5.7)中三个参数T*,T和Ma中己知任何两个,就可用式(5.7)求出第三个。
从式(5.6)可以看出,要想测出以速度V运动的气体静温T,必须使温度计与气流没有相对速度,此时温度计所指示的温度即为气流的静温。显然,这是不容易办到的。实际中所测得的温度都接近于气流的总温。例如在实验室中,测温计是固定在气流通道壳体上的,所以这时测温计所显示的温度是气流的总温(不计测温探头的热传导及黏性的影响)。
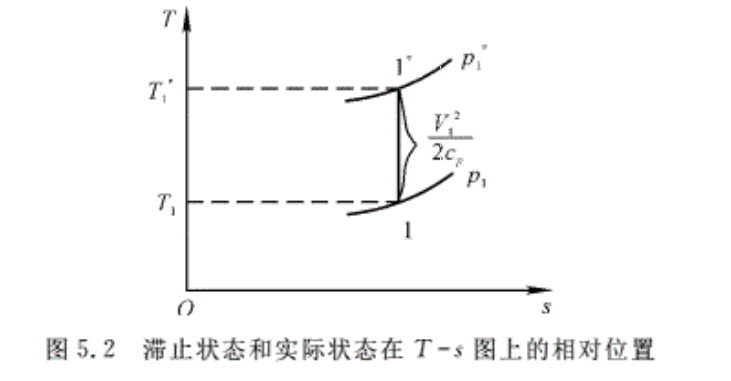
利用T—s图可以清楚地把滞止状态和实际状态表示出来。图5.2中点1代表气流被滞止之前的状态,即实际状态,其静温为T1,速度为V1,静压强为p1。根据滞止参数的定义,气流滞止前后的状态位于一条等熵线上。因此图中点1*代表气流的滞止状态,其温度为T*1,压强为p*1。其线段1一1*的长度应为诟V²1/(2cp)。
3.用滞止焓和滞止温度表示能量方程
引用总温的概念后,气流的能量方程式(3.76)可以表示为
\[q-{{\omega }_{s}}=\left( {{h}_{2}}+\frac{V_{2}^{2}}{2} \right)-\left( {{h}_{1}}+\frac{V_{1}^{2}}{2} \right)=h_{2}^{*}-h_{1}^{*}={{c}_{p}}\left( T_{2}^{*}-T_{1}^{*} \right)\] (5.8a)
即加给气流的热量和机械功用以增大气流的总焓。当气体作绝能流动时,能量方程式则为
\[h_{2}^{*}=h_{1}^{*}\] (5.8b)
对于完全气体有
\[T_{2}^{*}=T_{1}^{*}\] (5.8c)
对于作绝能流动的气体,气流的总焓(或总温)保持不变。这是绝能流动的一个基本性质。
对于燃烧室内的流动,能量方程式可写成
\[q=h_{2}^{*}-h_{1}^{*}={{c}_{p}}\left( T_{2}^{*}-T_{1}^{*} \right)\] (5.8d)
即加给气流的热量用以增大气流的总焓。
对于压气机(ωs<0)、涡轮(ωs> 0)内的流动,能量方程式可写成
\[-{{\omega }_{s}}=h_{2}^{*}-h_{1}^{*}={{c}_{p}}\left( T_{2}^{*}-T_{1}^{*} \right)\] (5.8e)
即加给气流的机械功用以增大气流的总焓,或气流的总焓降低转变成对外做的机械功。
例5.2 某压气机在地面试验时,测得出口气流总温为T2*=310 K,空气流量为qm=50 kg/s,求带动压气机所需要的功率。设空气的比定压热容cp=1 004 J/(kg • K)。
解:对压气机,q=0,则
\[-{{\omega }_{s}}={{c}_{p}}\left( T_{2}^{*}-T_{1}^{*} \right)\]
压气机在地面试验时,空气由静止状态逐渐加速吸入压气机,在这个过程中,气流是绝能的,所以总温不变,即在压气机进口截面上空气的总温T1*应等于静止空气的温度。由国际标准大气表查得,地面大气的温度为288 K,故压气机进囗气流总温为
T1*=288 K
所以 \({{\omega }_{s}}={{c}_{p}}\left( T_{1}^{*}-T_{2}^{*} \right)=1004\left( 288-310 \right)=-22.09kJ/kg\)
所求得的机械功ωs为负值,表明是外界对气体做功,带动压气机所需要的功率为
\[N={{q}_{m}}{{\omega }_{s}}=50\times 22.09=1104.5kW\]
对应于气流滞止状态的声速,称为滞止声速,以符号c*表示,显然
\[{{c}^{*}}=\sqrt{kR{{T}^{*}}}\] (5.9)
在绝能流动中,c*是一个常数,它也常被用来作为一个参考速度。
4.滞止压强和滞止密度
将气流速度绝能等熵地滞止到零时的压强和密度就称为滞止压强和滞止密度,分别用p*和ρ*表示。对于完全气体,由等熵关系式得
\[\frac{{{p}^{*}}}{p}={{\left( \frac{{{T}^{*}}}{T} \right)}^{\frac{k}{k-1}}}\]
将式(5.7)代入上式,得
\[\frac{{{p}^{*}}}{p}={{\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)}^{\frac{k}{k-1}}}\] (5.10)
由式(5.7)、式(5.10)和完全气体的状态方程式可以得到滞止密度ρ*、静密度ρ和Ma之间的关系。将完全气体状态方程式分别用于气流滞止前后的状态可得
\[\begin{align}& {{\rho }^{*}}=\frac{{{p}^{*}}}{R{{T}^{*}}} \\& \rho =\frac{p}{RT} \\\end{align}\]
两式相除,则得
\[\frac{{{\rho }^{*}}}{\rho }=\frac{{{p}^{*}}}{p}\frac{T}{{{T}^{*}}}={{\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)}^{\frac{1}{k-1}}}\] (5.11)
式(5.7)、式(5.10)的和式(5.1 1)给出了滞止参数与静参数之间的关系。可以看出,如果给定了流场中任一点的气流滞止温度T*、滞止压强p*、滞止密度ρ*和马赫数Ma,那么就可由式(5.7)、式(5.10)和式(5.11)三式,分别算出该点的气流温度T、压强p和密度ρ并进一步计算出速度V。反之,也可以通过某点气流的静参数确定其总参数。
应该指出,在气体动力学中引进滞止状态是个参考状态,它是假想地把一点处的气流绝能等熵地流入一个无限大的储气箱内,使其速度滞止到零时的箱内气体状态。在流场内每一点都有一个当地的滞止状态,因此,在任意流动过程中的每一点都有确定的滞止参数的数值,即滞止参数是点函数。在实际流动中,气体与外界有能量交换和黏性耗散时,流场中各点的滞止参数也是可以变化的。
5.2.2 关于总压的讨论
1.总压的物理意义
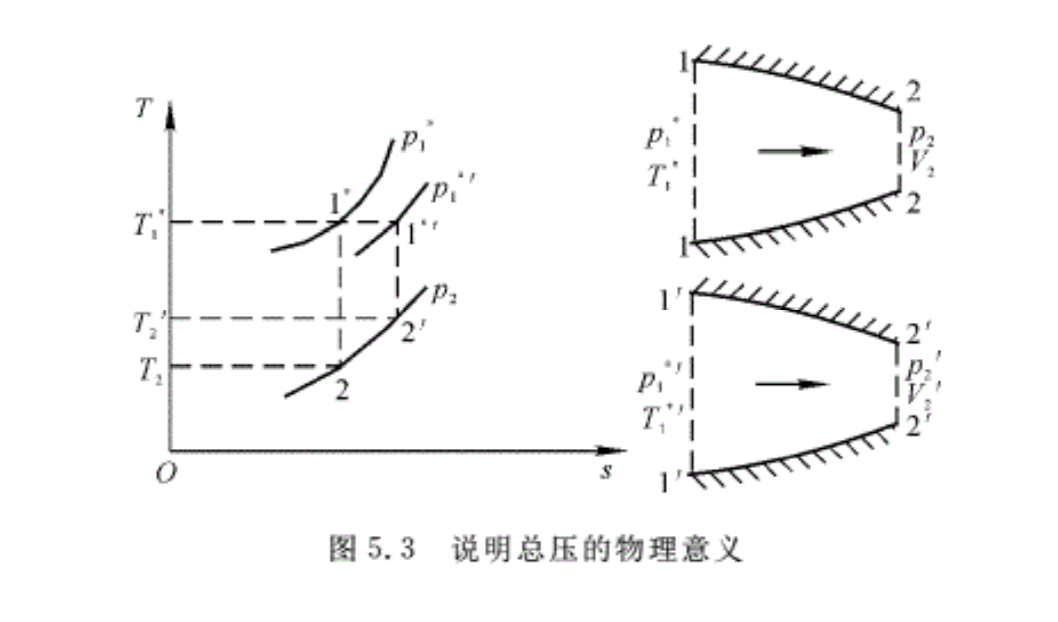
在流体动力学中,总压是一个非常重要的物理量,它代表了气流做功能力的大小。下面通过具休例子来说明这个问题。图5.3表示两股气流分别在收缩形管道内绝能等熵加速流动。在管道入口,气流的总温相等,即T1*=T1*′,也就是说,两股气流的总能量是一样的,但两股气流的总压不等,p1*>p1*′。根据伯努利方程式,气体在管道内作加速流动,必定膨胀降压。如果两股气流在各自管道的出口处的压强相等,p2=p2′,问在上述条件下,管道出口流速V2和 V2′哪个大?
可以用T一s图来分析这个问題。图5.3中点1*和1*′分别代表两个管道进口气流的滞止状态,T1*=T1*′,p1*>p1*′,故点1*与1*’在同一水平线上,而点1*’位于点1*的右方。点2 和2′分别表示两个管道出囗的气流状态,因为两管出口压强相等,故点2和2′位于同一条压强线上。由图可以看出,T2′必高于T2。由能量方程式
\[\begin{align}& {{c}_{p}}T_{1}^{*}={{c}_{p}}{{T}_{2}}+\frac{V_{2}^{2}}{2} \\& {{c}_{p}}T{{_{1}^{*}}^{\prime }}={{c}_{p}}{{T}_{2}}^{\prime }+\frac{{{V}^{\prime}}_{2}^{2}}{2} \\\end{align}\]
比较两式,显然V2>V2′这就是说,在其他条件相同时,总压高的气流可以在管道出囗得到更大的流速。从而有更大的动能。管道出口气流的动能可以用来做功(如可用来推动涡轮做功),故出口速度大则意味着气流有较大的做功能力。
通过此例,可以看出,尽管两股气流有同样的总能量,但两者的做功能力却不相同,总压越高,做功能力也越大。如果保持流动过程中气流的总温不变,而进口总压降低到和出口压强p2一样时,那么气流就不可能膨胀降压而加速了。这样的气流虽有同样的总温,但由于总压过低,己失去了做功能力。所以,我们可以用气流的总压的高低来代表气流做功能力的大小。从热能转变成功的方面看,当然希望气流有更大的做功能力。气流做功能力强,就是说气流可以把更多的热能转变成为机械功。为此在发动机里需要有压气机来提高气流的总压,以提高气流的做功能力,改善热能转变为功的有效程度。因此气流的总压也可看做气流能量可利用程度的度量。
2.影响总压的因素
影响总压变化的因素有黏性耗散、轴功与加热量。
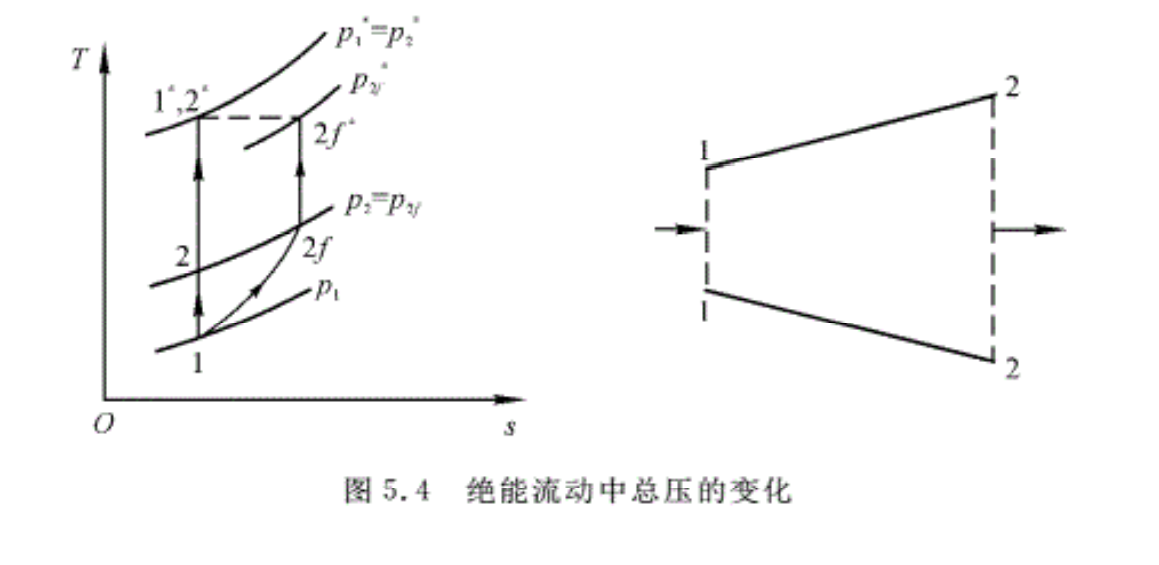
分析气流在图5.4所示的管道内作无摩擦的理想绝能流动。两个截面上气流参数可用 T一s图上点1,2表示(即1一2过程为等熵流动),把1和2两个截面上的气流参数分别绝能等熵滞止,则得到1*和2*两点。因为T1*=T2*,则1*和2*两点必重合,即气流作理想绝能流动,气体的滞止参数不变,因而p1*=p2*。这是绝能等熵流动的重要性质。
若气流在管道内作绝能不等熵(有摩擦等不可逆因素)流动,则管道出口截面2的气流参数可用图5.4中的点2f来表示,把点2f的的参数绝能等熵滞止,便得到2f*点。因为T2f*=T1*,点2f*必落在点1*之右方,所以p1*>p2f*。可见气体作绝能不等熵流动时,总压必下降。总之,绝能流动中总压的变化规律可表示为
P1*≥p2* (5.12)
当流动为绝能等熵时取等号,绝能不等熵时取大于号。
由以上分析可知耗散及不可逆因素是影响总压的重要因素之一。
对于只存在耗散的绝能流动有p2*<p1*,因而p2*/p1*< 1。为了表征绝能流动中总压的下降程度或不可逆因素的影响大小,我们定义总压恢复因数σ为
σ=p2*/p1* (5.13)
即出囗总压与进口总压之比。
根据熵增与状态参数之间的关系,可以得到熵增与总压恢复因数之间的关系如下:
\[\begin{align}& {{s}_{2}}-{{s}_{1}}={{c}_{p}}\ln \frac{{{T}_{2}}}{{{T}_{1}}}-R\ln \frac{{{p}_{2}}}{{{p}_{1}}}={{c}_{p}}\ln \frac{{{T}_{2}}/{{T}_{1}}}{{{\left( {{p}_{2}}/{{p}_{1}} \right)}^{\frac{k-1}{k}}}}= \\& {{c}_{p}}\ln \frac{\frac{{{T}_{2}}/T_{2}^{*}}{{{T}_{1}}/T_{1}^{*}}}{{{\left( {{p}_{2}}/{{p}_{1}} \right)}^{\frac{k-1}{k}}}}={{c}_{p}}\ln {{\left( \frac{p_{1}^{*}}{p_{2}^{*}} \right)}^{\frac{k-1}{k}}}=-R\ln \frac{p_{2}^{*}}{p_{1}^{*}}=-R\ln \sigma \\\end{align}\] (5.14)
可见,在绝能流动中,耗散愈大,σ就愈小,气流的熵增将加大。对理想气体的绝能流动,σ=1,则s2=s1。对绝能不等熵流动,通常用总压恢复因数σ来衡量流动过程的不可逆性的程度(即熵增的大小)是非常方便的。
对于绝热流动,由能量方程可得
\[-{{\omega }_{s}}={{h}_{2}}-{{h}_{1}}+\frac{V_{2}^{2}-V_{1}^{2}}{2}=h_{2}^{*}-h_{1}^{*}\]
对完全气体 \(-{{\omega }_{s}}={{c}_{p}}\left( T_{2}^{*}-T_{1}^{*} \right)\) (5.15)
若对于定熵流动,式(5.15)可表示为
\[{{\omega }_{s}}=\frac{kR}{k-1}T_{1}^{*}\left[ 1-{{\left( \frac{p_{2}^{*}}{p_{1}^{*}} \right)}^{\frac{k-1}{k}}} \right]\] (5.16 )
式(5.15)和式(5.16)是计算轴功的重要关系式。由式(5.16)可以看出,对气体做功将使总压增加,而气流对外做功将使气流总压下降。因此,轴功是影响总压变化的另一个因素。
式(5.16)还可写成如下形式:
\[{{\omega }_{s}}={{c}_{p}}T_{1}^{*}\left[ 1-{{\left( \frac{p_{2}^{*}}{p_{1}^{*}} \right)}^{\frac{k-1}{k}}} \right]=h_{1}^{*}\left[ 1-{{\left( \frac{p_{2}^{*}}{p_{1}^{*}} \right)}^{\frac{k-1}{k}}} \right]\] (5.17)
由式(5.17)可以看出,由于h1*代表气流的总能量,则式(5.17)代表了气流总能量可以转化为机械功的比例大小。由此也可看出,p*代表了气流的做功能力大小,即气流总能量所能转化为机械能的部分。
关于热交换对总压的影响,将在换热管流中讨论。
3.能量方程的应用
在绝能流动中(ωs=0,q=0,如喷气发动机的扩压器或尾喷管中的流动等),能量方程可表示为
h1*=h2* 或 T1*=T2*
即 h1+V1²/2=h+V²/2
对于理想流体等熵过程,上式可改与为
\[\frac{1}{2}\left( V_{1}^{2}-{{V}^{2}} \right)=h-{{h}_{1}}={{c}_{p}}\left( T-{{T}_{1}} \right)=\frac{kRT}{k-1}\left[ 1-{{\left( \frac{p_{1}^{{}}}{p} \right)}^{\frac{k-1}{k}}} \right]\]
上式即为一维定常绝能等熵流动的伯努利方程。
如果令V1→0,可得滞止压强的表达式(式(5.10)),即
\[\frac{{{p}^{*}}}{p}={{\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)}^{\frac{k}{k-1}}}\]
根据数学上的二项式定理,有
\[{{\left( 1+x \right)}^{n}}=1+nx+\frac{n\left( n-1 \right)}{2!}{{x}^{2}}+…\]
当马赫数不大时,可将(k-1)Ma²/2看做x,k/(k-1)看做n,则讲上式展开,得
\[{{p}^{*}}=p+\frac{1}{2}\rho {{V}^{2}}\left( 1+\frac{1}{4}M{{a}^{2}}+… \right)\] (5.18)
当气流为不可压缩,即Ma <0.3时,式(5.18)等号右端括号中后边的项可以忽略,则得到不可压流动的伯努利方程,即
\[{{p}^{*}}=p+\frac{1}{2}\rho {{V}^{2}}\] (5.19)
比较式(5.18)和式(5.19)可以看出,当Ma ≤0.3时,忽略气体压缩性所引起的动压变化不大。因此,对于等熵流动,只要马赫数很小,就可以看做是不可压流动,这将会使问题得到较大的简化。
有功交换的绝热流动(如在叶轮机械内的流动)此时能量方程为式(5.15),若流动为绝热定熵流动则能量方程为式(5.17)。
有热交换的绝功流动(如在燃烧室内的流动),此时能量方程为式(5.8d)。
需要强调一点,滞止参数与坐标系的选取有关,不同坐标系,滞止参数的数值不同。
例5.3 涡轮导向器进囗燃气参数为p1*=1. 2 × 106Pa,总温T1*=1110K,出口静压p2=7.0× 105Pa。求燃气在导向器内做绝能等熵流动时的出口流速。
解:在绝能等熵流动中气流的总温、总压不变,所以
p2*=p1*=1. 2 × 106Pa
T2*=T1*=1110K
由式(5.10),得
\(M{{a}_{2}}=\sqrt{\frac{2}{k-1}\left[ {{\left( \frac{{{p}^{*}}}{p} \right)}^{\frac{k-1}{k}}}-1 \right]}=\sqrt{\frac{2}{k-1}\left[ {{\left( \frac{12}{7} \right)}^{0.248}}-1 \right]}=0.93\) (k=1.33)
由式(5.7),得
\[\begin{align}& {{T}_{2}}={T_{2}^{*}}/{\left( 1+\frac{k-1}{2}Ma_{2}^{2} \right)=\frac{1110}{1+0.143}=971K}\; \\ & {{c}_{2}}=\sqrt{kR{{T}_{2}}}=\sqrt{1.33\times 287.4\times 971}=609m/s \\\end{align}\]
所以
\[{{V}_{2}}={{c}_{2}}M{{a}_{2}}=609\times 0.93=567m/s\]
例5.4 涡轮导向器进口总温、总压以及出口静压均与上例相同,由于摩擦,导向器出口流速降为V2=555 m/ s。求导向器的总压恢复因数σ。设cp=1.17kJ/(kg • K)。
解:因为流动为绝能的,进、出口总温仍保持不变,故
\[{{T}_{2}}=T_{2}^{*}-\frac{V_{2}^{2}}{2{{c}_{p}}}=1110-\frac{{{555}^{2}}}{2\times 1170}=978.4K\]
由出囗截面上总、静参数间的关系为
\[\frac{p_{2}^{*}}{{{p}_{2}}}={{\left( \frac{T_{2}^{*}}{{{T}_{2}}} \right)}^{\frac{k}{k-1}}}={{\left( \frac{1110}{978.4} \right)}^{4.03}}=1.663\]
得 \(p_{2}^{*}=1.663{{p}_{2}}=1.663\times 7.0\times {{10}^{5}}=11.6\times {{10}^{5}}Pa\)
所以
\[\sigma =\frac{p_{2}^{*}}{p_{1}^{*}}=\frac{11.6}{12}=0.97\]
由此可见,由于摩擦的影响,使得总压减小,总压恢复因数下降。由题可知,相应的动能(流速)也减小。
例5.5 若飞机在11000 m高空以Ma=2.5的速度等速飞行,问机翼表面可能达到的最高温度是多少?假定流动是绝热的。
解:把坐标系固定在飞机上,气流则以Ma=2.5的速度流向飞机。飞机机翼前缘驻点处的温度最高。由大气参数表查得11000m高空的温度为T=216.7 K。所以驻点温度为
\[{{T}^{*}}=T\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)=216.7\left( 1+0.2\times {{2.5}^{2}} \right)=487.6K\]
如果在大气中飞行的马赫数很高(如返回地球的高超声速飞行器),由这种气动加热所造成的高温将会产生严重的烧蚀问题。
5.2.3 极限速度和临界参数
除了滞止参数外,在分析和计算气体的流动过程中还经常应用极限速度、临界参数等。
1.极限速度
气流的极限速度是气流经过绝能过程所能达到的最大速度,记作Vmax。可根据完全气体绝能过程的能量方程式来决定Vmax,即
\[\frac{k}{k-1}RT+\frac{{{V}^{2}}}{2}=\frac{k}{k-1}R{{T}^{*}}\]
可见,在绝能流动中,随着气流的温度降低,气流速度则必然增加,如果气流的绝对温度降到零,即气流的热焓全部转化为动能,这时气流的速度将达到最大值,即极限速度,或称最大速度。上式中,令T=0K,V=Vmax ,可得
\[{{V}_{\max }}=\sqrt{\frac{2}{k-1}kR{{T}^{*}}}\]
显然,Vmax仅仅是一个理论上的极限值,因为任何气体在未达到Vmax时,早已液化了。对于绝能流动,由上式可知Vmax是个常数,因此,常用极限速度作为一个参考速度。
2.临界参数
在绝能流动中,流体速度和声速的关系是
\(\frac{{{c}^{2}}}{k-1}+\frac{{{V}^{2}}}{2}=\frac{{{c}^{*}}^{2}}{k-1}+\frac{V_{\max }^{2}}{2}\) (a)
气流的速度V与声速c之间的关系用曲线表示,如图5.5所示。由图可见,当速度从零连续增加到Vmax时,相应的声速从c*连续减小到零,即气体的温度由T*下降为零。
在气流速度由零绝能等熵地增加到Vmax的过程中,必然会有气流速度恰好等于当地声速(即Ma=1 )的状态,该状态称为临界状态。该状态的声速称为临界声速,以c cr表示,相应的速度称为临界速度,以V cr表示。显然V cr=c cr。临界状态的压强、密度和温度称之为临界压强、临界密度和临界温度,并分别以p cr,ρ cr和T cr表示。
以V cr=c cr代入式(a),得
\[\frac{V_{\max }^{2}}{2}=\frac{{{c}^{*}}^{2}}{k-1}=\frac{c_{cr}^{2}\left( k+1 \right)}{2\left( k-1 \right)}\]
则临界声速、极限速度及滞止声速的关系式为
\[{{c}_{cr}}=\sqrt{\frac{k-1}{k+1}}{{V}_{\max }}=\sqrt{\frac{2}{k+1}}{{c}^{*}}=\sqrt{\frac{2k}{k+1}R{{T}^{*}}}\] (5.21)
可见对于一定的气体,临界声速c cr只决定于其总温T*,在绝能流动中是一个不变的常数。因此,在气体动力学中,临界声速c cr也是一个方便的参考速度。对空气,k=1. 4,则c cr=18.3√T*,对燃气,k=1.33,c cr=18.1√T*。
利用总、静参数与马赫数之间的关系即式(5.7)、式(5.10)和式(5.11 ),将Ma=1代入,可求出其临界参数与滞止参数之间的关系,即
\[\frac{{{T}_{cr}}}{{{T}^{*}}}=\frac{2}{k+1}\] (5.22)
\[\frac{{{p}_{cr}}}{{{p}^{*}}}={{\left( \frac{2}{k+1} \right)}^{\frac{k}{k-1}}}\] (5.23)
\[\frac{{{\rho }_{cr}}}{{{\rho }^{*}}}={{\left( \frac{2}{k+1} \right)}^{\frac{1}{k-1}}}\] (5.24)
显然,气体的临界参数与其滞止参数之比,仅是气体比热比k的函数。在定常绝能等熵气流中,沿同一流线上,临界参数均是常数。
对于空气,k=1.4,有T cr/T*=0.8333,p cr/p*=0.5283,ρ cr/ρ=0.6339。
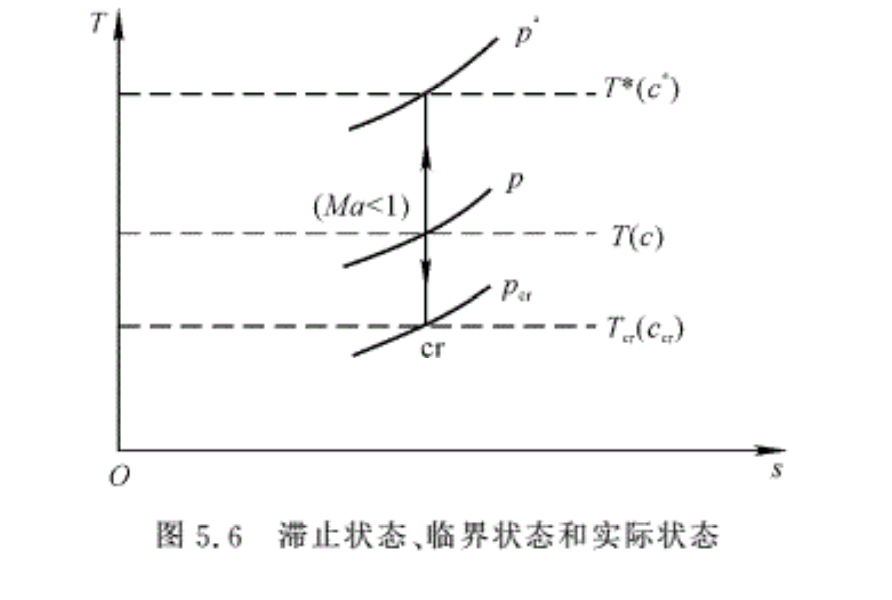
应该指出,在一维流动的每一个截面上,都有相应于该截面的临界参数,就好像在气流中每个截面上都有相应的滞止参数一样。若气流在某一个截面上Ma=1,则该截面上气流的状态就是临界状态,该截面上的气流参数就是临界参数,该截面叫做临界截面。气流Ma≠1的截面仍有临界参数,只是该截面气流的静参数不等于临界参数;但如果假想把该截面的气流绝能等熵地转变到Ma=1,则可得到该截面的临界参数。应该特别注意的是,在某个截面上的声速和临界声速的区别,前者由该截面的气流静温决定,而后者则由该截面的临界温度确定,只有在临界截面上(Ma=1的截面)的声速c才等于临界声速c cr。图5.6表示了某个气流 Ma<1的截面上的气流状态参数、滞止参数和临界参数在T -s图上的相对位置。例如,对于气流在管内做绝能等熵速流动,如果出口截面Ma=1,即出口截面为临界截面,则该截面的参数为整个流管的临界参数。
5.2.4 速度因数
在气体动力学的计算中,有时用气流速度与临界声速之比代替马赫数更为方便。这个比值λ称为速度因数,即
λ=V/c cr (5.25)
速度因数和马赫数一样,也是一个无量纲的参数。采用λ的好处是,在绝能流动中,临界声速c cr是个常数,所以流场中某截面上气流速度V只与该截面上速度因数λ有关(即与λ成正比)。使用λ比使用Ma要方便得多。因为在绝能流动中,各截面的声速是不同的,要想确定某截面上的流速,除了要知道该截面上气流马赫数之外,还必须要知道该截面上的声速,即还必须确定该截面上气流的静温T。另外,当V=Vmax时,Ma→∞,而λ趋近于有限值,即\({{\lambda }_{\max }}=\frac{{{V}_{\max }}}{{{c}_{cr}}}=\sqrt{\frac{k+1}{k-1}}\)。由上可知,λ与Ma之间必然有确定的对应关系。实际上
\[M{{a}^{2}}=\frac{{{V}^{2}}}{{{c}^{2}}}={{\lambda }^{2}}\frac{c_{cr}^{2}}{{{c}^{2}}}={{\lambda }^{2}}\frac{2}{k+1}\frac{{{T}^{*}}}{T}\]
即 \(\lambda =Ma\sqrt{\frac{k+1}{2+\left( k-1 \right)M{{a}^{2}}}}\) (5.26a)
或 \(Ma=\lambda \sqrt{\frac{2}{\left( k+1 \right)-\left( k-1 \right){{\lambda }^{2}}}}\) (5.26b)
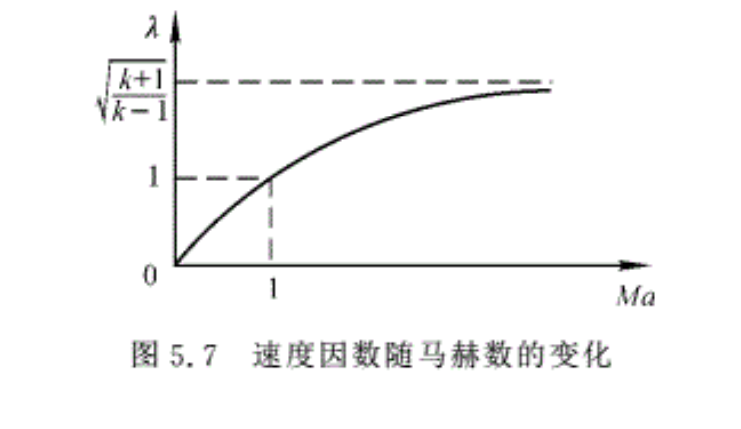
上述的Ma与λ一一对应关系可以用图5.7上的曲线表示。
从图可知:
当Ma=0时,λ=0;当Ma<1时,λ<1;
当Ma=1时,λ=1;当Ma>1时,λ>1。
当Ma→∞时,V→Vmax,而λ→λmax=√[(k+1)/(k-1)]。这样用曲线和数值表形式研究气流参数时,当V→Vmax时,用马赫数表示不太方便,所以很多气动函数表都是用λ表示的,λ与Ma的关系可制成数值表,见附录表2。
将式(5.26)代入式(5.27)、式(5.10)和式(5.11),可以分别得到用λ表示的气流滞止参数与静参数的关系式,即
\[\frac{T}{{{T}^{*}}}=1-\frac{k-1}{k+1}{{\lambda }^{2}}\] (5.27)
\[\frac{p}{{{p}^{*}}}={{\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)}^{\frac{k}{k-1}}}\] (5.28)
\[\frac{\rho }{{{\rho }^{*}}}={{\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)}^{\frac{1}{k-1}}}\] (5.29)
同理,也可以分别得到用λ表示的气流临界参数与静参数的关系式,即
\[\begin{align}& \frac{T}{{{T}_{cr}}}=\frac{\left( k+1 \right)-\left( k-1 \right){{\lambda }^{2}}}{2} \\& \frac{p}{{{p}_{cr}}}={{\left[ \frac{\left( k+1 \right)-\left( k-1 \right){{\lambda }^{2}}}{2} \right]}^{\frac{k}{k-1}}} \\& \frac{\rho }{{{\rho }_{cr}}}={{\left[ \frac{\left( k+1 \right)-\left( k-1 \right){{\lambda }^{2}}}{2} \right]}^{\frac{1}{k-1}}} \\\end{align}\]
例5.6 已知某发动机尾喷管进口燃气参数为p1*=2.4× 105Pa,T1*=790 K,出囗截面处于临界状态,尾喷管总压恢复因数σ=0.98。求出囗流速、静温和静压。其中,k=1.33,R=287.4 J /(kg·K)。
解:尾喷管内气流是绝能流动,则T1*=T2*,而λ2=1. 0,故
\[{{V}_{2}}={{c}_{cr}}{{\lambda }_{2}}=\sqrt{\frac{2k}{k+1}R{{T}^{*}}}=18.1\sqrt{{{T}^{*}}}=509.1m/s\]
由式(5.27),得
\[\begin{align}& {{T}_{2cr}}=T_{2}^{*}\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)=790\left( 1-\frac{0.33}{2.33} \right)=677.8K \\& p_{2}^{*}=\sigma p_{1}^{*}=0.98\times 2.4\times {{10}^{5}}=2.35\times {{10}^{5}}Pa \\& {{p}_{2cr}}=p_{2}^{*}{{\left( \frac{2}{k+1} \right)}^{\frac{k}{k-1}}}=2.35\times {{\left( 0.858 \right)}^{4.03}}\times {{10}^{5}}=1.27\times {{10}^{5}}Pa \\\end{align}\]
5.3 气体动力学函数及其应用
在引入了无量纲速度Ma,λ之后,不仅气流的总参数与静参数之比可以用气流的Ma或λ的函数表示,下面还会看到,连续方程和动量方程也可以用Ma或λ的函数表示出来。这些以 Ma或λ为自变量的函数叫气体动力学函数(简称气动数)。给定λ或Ma,编制计算机程序,很容易求得这些数值表。气体动力学函数在气动计算中有着广泛的应用。为了方便计算,往往列出以Ma或λ为自变量的各种气动函数的数值表,供计算时查用,这样的数值表称为气动函数表(见附录表2)。
5.3.1 气动函数τ(λ),π(λ),ε(λ)
将式(5.27)、式(5.28)和式(5.29)分别用τ(λ),π(λ),ε(λ)表示,即
\[\tau \left( \lambda \right)=\frac{T}{{{T}^{*}}}=1-\frac{k-1}{k+1}{{\lambda }^{2}}\] (5.30a)
\[\pi \left( \lambda \right)=\frac{p}{{{p}^{*}}}={{\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)}^{\frac{k}{k-1}}}\] (5.30b)
\[\varepsilon \left( \lambda \right)=\frac{\rho }{{{\rho }^{*}}}={{\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)}^{\frac{1}{k-1}}}\] (5.30c)
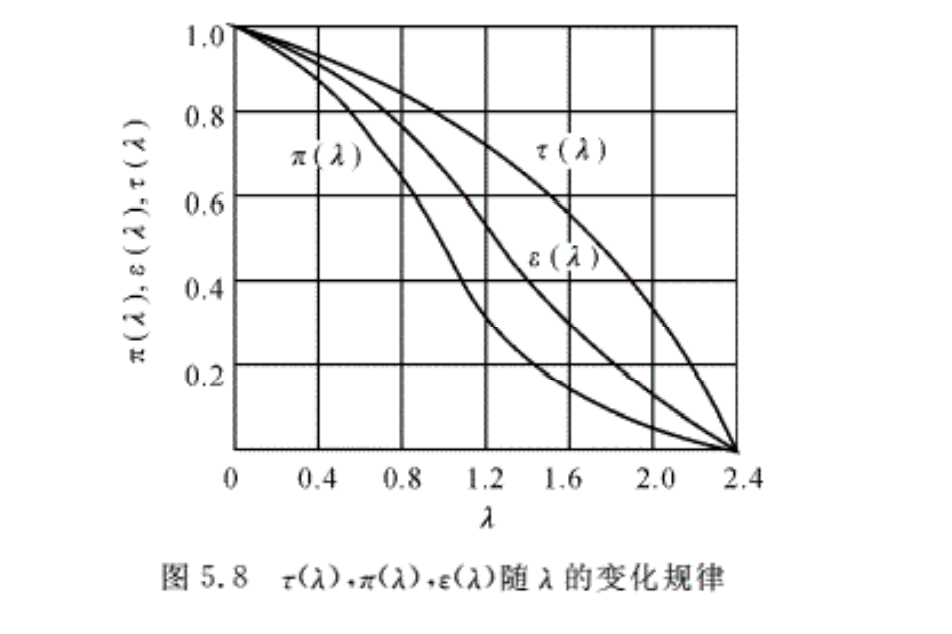
在发动机和各种气动计算中它们是用得最多的。以上三式中对于一定的气体(即k己知),每式只有三个未知数,即静参数、总参数和λ。如果已知两个,则第三个就可用相应的公式求出。对于空气来说k=1.4,函数τ(λ),π(λ)和ε(λ)随λ的变化关系如图5.8所示。如果用Ma表示以上三个函数式,则为
\[\tau \left( Ma \right)=\frac{T}{{{T}^{*}}}={{\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)}^{-1}}\] (5.31a)
\[\pi \left( Ma \right)=\frac{p}{{{p}^{*}}}={{\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)}^{-\frac{k}{k-1}}}\] (5.31b)
\[\varepsilon \left( Ma \right)=\frac{\rho }{{{\rho }^{*}}}={{\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)}^{-\frac{1}{k-1}}}\] (5.31c)
在气动函数表中给出了上述气动函数的数值。下面通过几个例题说明气动函数的运用。
例5.7 用气动函数表解例5.4。
解:对燃气k=1.33,R=287.4J /(kg·K) ,有
\[\begin{align}& {{c}_{cr}}=18.1\sqrt{T_{2}^{*}}=18.1\sqrt{1110}=603m/s \\& {{\lambda }_{2}}=\frac{{{V}_{2}}}{{{c}_{cr}}}=\frac{555}{603}=0.92 \\\end{align}\]
由k=1.33查气动函数表,当λ2= 0.92时,查得
\[\pi \left( {{\lambda }_{2}} \right)=\frac{{{p}_{2}}}{p_{2}^{*}}=0.5977\]
所以
\[\begin{align}& p_{2}^{*}=\frac{{{p}_{2}}}{\pi \left( {{\lambda }_{2}}\right)}=\frac{7.0\times {{10}^{5}}}{0.5977}=11.7\times {{10}^{5}}Pa \\& \sigma =\frac{p_{2}^{*}}{p_{1}^{*}}=\frac{11.7}{12}=0.97 \\\end{align}\]
5.3.2 流量函数q(λ),y(λ)
在一维定常流动中,流量公式为qm=ρAV。如果己知流场中某截面的气流密度ρ,截面积 A和该截面上的流速V,可按上式确定通过此截面的流量qm。而在一般气动计算中,往往是先给出气流的总参数(如用仪器测量出总参数等)和某截面的λ(或Ma),如果能把流量公式表示成气流总参数和λ的关系式,将使计算大大简化。
\[{{q}_{m}}=\rho AV=\frac{\rho V}{{{\rho }_{cr}}{{V}_{cr}}}{{\rho }_{cr}}{{V}_{cr}}A\] (a)
式中
\[{{\rho }_{cr}}={{\rho }^{*}}{{\left( \frac{2}{k+1} \right)}^{\frac{1}{k-1}}}=\frac{{{p}^{*}}}{R{{T}^{*}}}{{\left( \frac{2}{k+1} \right)}^{\frac{1}{k-1}}}\] (b)
\[{{V}_{cr}}=\sqrt{\frac{2kR{{T}^{*}}}{k+1}}\] (c)
\[\frac{\rho V}{{{\rho }_{cr}}{{V}_{cr}}}=\lambda \frac{\rho /{{\rho }^{*}}}{{{\rho }_{cr}}/\rho }=\lambda \frac{\varepsilon \left( \lambda \right)}{\varepsilon \left( \lambda =1 \right)}={{\left( \frac{k+1}{2} \right)}^{\frac{1}{k-1}}}\lambda {{\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)}^{\frac{1}{k-1}}}\] (d)
对于给定的气体,式(d)右端是λ的函数,用q(λ)表示,则有
\[q\left( \lambda \right)=\frac{\rho V}{{{\rho }_{cr}}{{V}_{cr}}}={{\left( \frac{k+1}{2} \right)}^{\frac{1}{k-1}}}\lambda {{\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)}^{\frac{1}{k-1}}}\] (5.32)
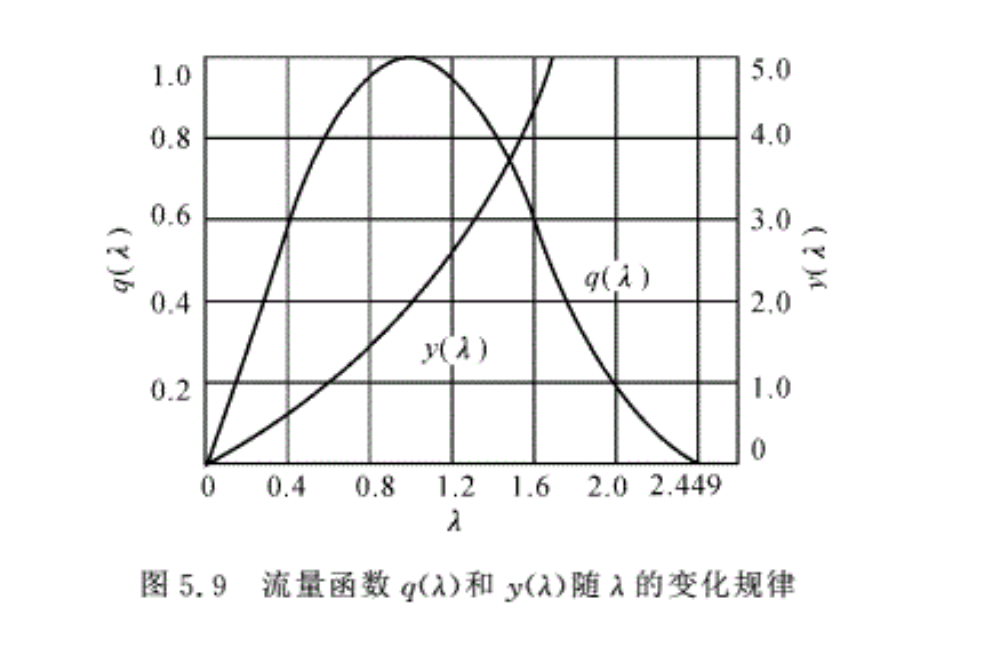
q(λ)构成一个新的气动函数,从式(5.32)可以看出,式中ρV表示通过单位面积上的质量流量,称为密流,因此q(λ)的的意义表示无量纲密流。分析式(5.32)可知q(λ)的变化规律,即对于空气,q(λ)与λ变化的规律如图5.9所示,从图中可看出:
当λ=0时,q(λ)=0;当λ=1时,q(λ)=1;当λ=λmax时,q(λ)=0。
需要注意的是,在一个q(λ)值下对应有两个值。
将式(b)、式(c)、式(d)和式(5.32)代入式(a),得
\[\begin{align}& {{q}_{m}}=\sqrt{\frac{2}{k+1}\frac{k}{R}}{{\left( \frac{2}{k+1} \right)}^{\frac{1}{k-1}}}q\left( \lambda \right)\frac{{{p}^{*}}A}{\sqrt{{{T}^{*}}}}= \\& \sqrt{\frac{k}{R}{{\left( \frac{2}{k+1} \right)}^{\frac{k+1}{k-1}}}}\frac{{{p}^{*}}A}{\sqrt{{{T}^{*}}}}q\left( \lambda \right)=K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}Aq\left( \lambda \right) \\\end{align}\] (5.33)
式中,\(K=\sqrt{\frac{k}{R}{{\left( \frac{2}{k+1} \right)}^{\frac{k+1}{k-1}}}}\),对于一定的气体k和R均是一定的,则K也是一个常数。例如,对于空气,k=1.4,R=287.06J/(kg • K),则K=0.0404√(kg·K/N·m)。对于燃气,k=1.33,R=287.4J/(kg • K),则K=0.0397√(kg·K/N·m)。在式(5.33)中,p*,A和T*的单位分别是Pa,㎡和K。
由图5.9可知,在临界状态下(λ=1),q(λ)达到最大值,由此可知,在λ=1的截面上,即临界截面上,单位面积上通过的流量最大。
由流量公式(式(5.33))可见,流量可以表示为总压、总温和λ的函数。当λ己知时,对于一定的气体,密流(qm/A)与总压成正比,而与总温的平方根成反比。在发动机的计算中,往往qm√T*/p*作为流量组合参数整理实验数据并绘制发动机的特性曲线,使得某一特定的实验结果可以应用于总压、总温改变的情况。
对于一维绝能等熵(总压、总温保持不变)流动,根据连续方程,同一管道各个截面的流量保持不变,因此
q(λ1)A1=q(λ2)A2=const (5.34)
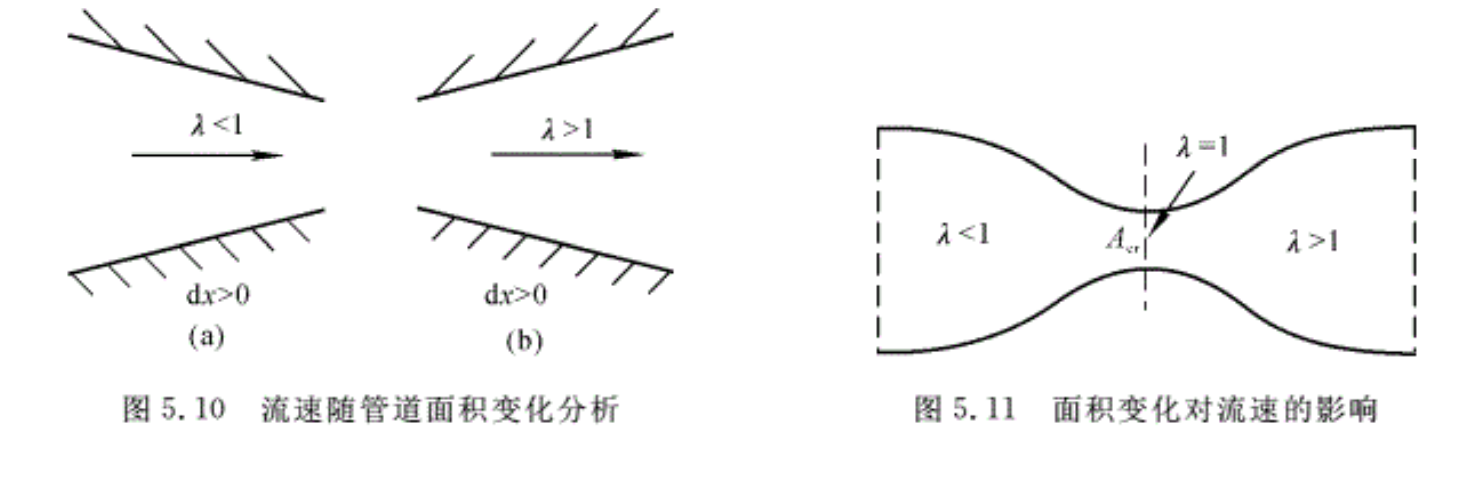
由式(5.34)可以看出,q(λ)值大,则面积A小;反之,q(λ)的值小,则A变大。由图5.9可以看出,在亚声速(即λ< 1)范围内,随着λ增大,q(λ)值增加。因此,管道面积应当减小,即管道形状应当是收缩的(见图5.10(a));在超声速(即λ> l)范围内,随着气流加速,λ数增大,q(λ)值减小,则管道截面积应当增大,即管道形状应当是扩张形的(见图5.10(b))。显然,若要求气体在管道内由亚声速加速到超声速,随着λ增大,q(λ)值是先增加,直到q(λ)=1的最大值,然后q(λ)值又逐渐减小。而管道截面应做成如图5.11所示的先收缩后扩张的形状。其中最小截面是临界截面。
将式(5.34)用于管道中的临界截面A cr和任意另一个截面Ai之间(见图5.11),则由于在临界截面上q(λ)=1.0,因此得
\[{{A}_{i}}q\left( {{\lambda }_{i}} \right)={{A}_{cr}}\]
或 \(q\left( {{\lambda }_{i}} \right)=\frac{{{A}_{cr}}}{{{A}_{i}}}\) (5.35)
此式说明,在绝能等熵流动中,如果最小截面上的气流处于临界状态,则任一截面上的q(λ)值等于临界截面积与该截面积之比。
当p*,T*和面积A一定时,在绝能等熵条件下,通过截面A的气体流量qm与q(λ)成正比。当该截面为临界截面时,q(λ)达到最大值,此时通过该截面的流量为最大,即
\[{{q}_{m,\max }}=K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}{{A}_{cr}}\] (5.36)
因此,如果实际流量超过q m,max ,则多余的流量不可能通过临界截面,这就出现了所谓“堵塞” (或称“壅塞”)现象。在本书第七章将研究气流的“堵塞”现象。
有时己知条件不是气流的总压,而是气流在A截面上的静压,此时用另一个气动函数 y(λ)来代替q(λ)。由式(5.33)和式(5.30b),可得
\[{{q}_{m}}=K\frac{pA}{\sqrt{{{T}^{*}}}}\frac{q\left( \lambda \right)}{\pi \left( \lambda \right)}=K\frac{p}{\sqrt{{{T}^{*}}}}Ay\left( \lambda \right)\] (5.37)
式中,y(λ)=q(λ)/π(λ)。图5.9给出了y(λ)随λ变化的规律,y(λ)随λ的增加而单调地上升。y(λ)和q(λ)的数值同样可在气动函数表(见附录表2)中查到。
例5.8 一扩压器的出口截面积A2与进囗截面积A1之比A2/A1=2.5,己知进口截面空气流的速度因数λ1=0.8,求出囗截面上空气的λ2。
解:假设流动过程为绝能等熵的,则T1*=T2*,p1*=p2*,根据连续方程,得
\[K\frac{p_{1}^{*}q\left( {{\lambda }_{1}} \right)}{\sqrt{T_{1}^{*}}}{{A}_{1}}=K\frac{p_{2}^{*}q\left( {{\lambda }_{2}} \right)}{\sqrt{T_{2}^{*}}}{{A}_{2}}\]
故 \(q\left( {{\lambda }_{2}} \right)=\frac{{{A}_{1}}}{{{A}_{2}}}q\left( {{\lambda }_{1}} \right)\)
由气动函数表查得,当λ1=0.8时,q(λ1)=0.9519,代入上式,得q(λ2)=0.38,然后查得λ2的两个值,即λ2=0.247或1.825。这一点由图5.9可以看出,对应一个q (λ)值,有两个λ与之相对应,一个小于1,另一个大于1,宄竟取哪个值,要由其他条件决定。本题的λ1=0.8,说明扩压器进囗为亚声速气流,而亚声速气流在扩张通道中流速减小,因此应取λ2=0.247。
例5.9 液体火箭发动机在地面试车时,高速喷气所产生的推力为F=4.905 × 105 N,在喷管进口处燃气总温T*=2700 K,总压p*=30.99 × 105 Pa,喷管出口处气压强等于大气压强pa=1.0133 ×105 Pa。设燃气的气体常数R=287.4J/(kg·K),k=1.33,求喷管出囗处燃气速度Ve,燃气流量qm,喷管最小截面及出口截面面积。假设流动为绝能等熵的。
解:发动机在地面试车时,V=0,又流动是绝能等熵的,故T1*=T*,p1*=p*,所以,pe/p*=pa/p*=π(λ)=0.0327,查气动函数表,得λe=2.01,故有
\[{{V}_{e}}={{\lambda }_{e}}{{c}_{cr}}={{\lambda }_{e}}\times \sqrt{\frac{2kR{{T}^{*}}}{k+1}}=2.01\times \sqrt{\frac{2\times 1.33\times 287.4\times 2700}{2.33}}=1891.8m/s\]
通过喷管的流量可根据发动机的内推力公式计算,即
\[F={{q}_{m}}\left( {{V}_{e}}-V \right)+\left( {{p}_{e}}-{{p}_{a}} \right){{A}_{e}}\]
将pe=pa,V=0代入上式,得
\[{{q}_{m}}=\frac{F}{{{V}_{e}}}=\frac{4.905\times {{10}^{5}}}{1891.8}=259.27kg/s\]
由流量公式,得
\[{{A}_{cr}}=\frac{{{q}_{m}}}{K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}}=\frac{259.27}{0.0397\times 30.99\times {{10}^{5}}/\sqrt{2700}}=0.1096{{m}^{2}}\]
据连续方程,有
\[K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}{{A}_{cr}}=K\frac{{{p}^{*}}q\left( {{\lambda }_{e}} \right)}{\sqrt{{{T}^{*}}}}{{A}_{e}}\]
得
\[{{A}_{e}}=\frac{{{A}_{cr}}}{q\left( {{\lambda }_{e}} \right)}=\frac{0.1096}{0.2436}=0.4498{{m}^{2}}\]
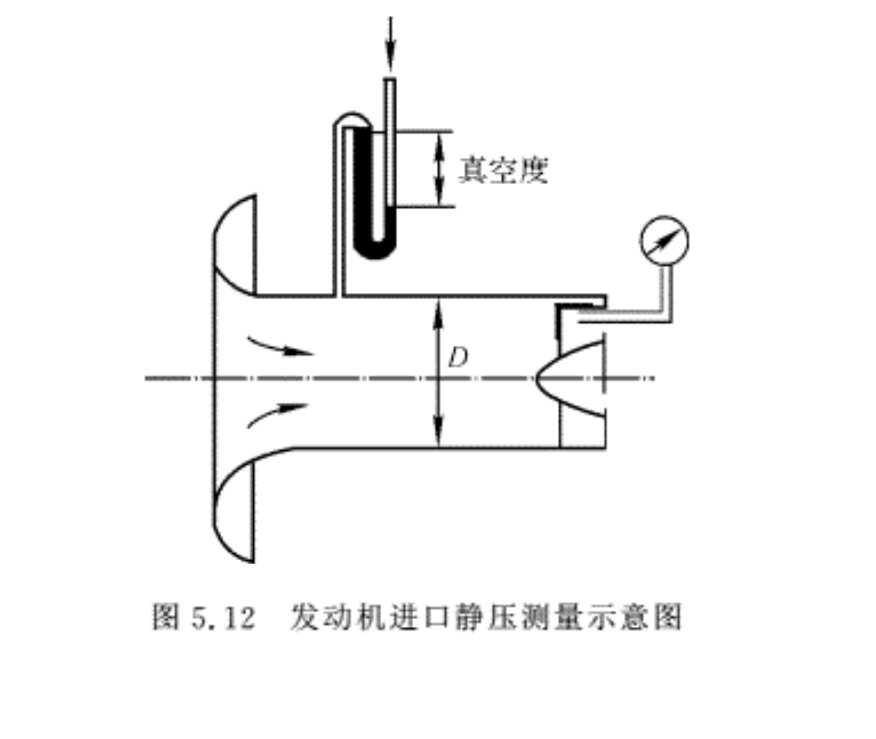
例5.10 有一压气机实验装置如图5.12所示,在进口截面(A1=0.29㎡)处,开有静压孔,与装水银的U形管接通。在压气机出口截面处装有总压管与压力表接通。在实验时,U 形管上的读数h=76 mm,压力表测得的表压强为6.0 × 105 Pa。由气压计测得当时的大气压强pa=1. 0133 × 105Pa,由温度计测得当时大气温度Ta=289 K。求压气机压缩空气所需要的功率为多少(设流动过程是等熵的)。
解:由题意知 p1*=pa,T1*=Ta
P2*=p2+pa=6.0×105+1.0133×105=7.0133x105Pa
进口截面上的压强为
P1=pa-γh=1.0133×105-76 × 133.3一91199.2 Pa
由式(5.30b),得
\[\pi \left( {{\lambda }_{1}} \right)=\frac{{{p}_{1}}}{p_{1}^{*}}=\frac{{{p}_{1}}}{{{p}_{a}}}=\frac{9.1199\times {{10}^{4}}}{1.0133\times {{10}^{5}}}=0.9\]
由气动函数表(k=1.4)的查得,当π(λ)=0.9时,q(λ)=0.6149。 由式(5.33),得
\[\begin{align}& {{q}_{m}}=K\frac{p_{1}^{*}}{\sqrt{{{T}^{*}}}}Aq\left( {{\lambda }_{1}} \right)=0.0404\times \frac{1.0133\times {{10}^{5}}}{\sqrt{289}}\times 0.29\times 0.6149=42.94kg/s \\& N={{q}_{m}}{{\omega }_{s}}={{q}_{m}}\frac{kR}{k-1}T_{1}^{*}\left[ 1-{{\left( \frac{p_{2}^{*}}{p_{1}^{*}} \right)}^{\frac{k-1}{k}}} \right]=42.94\times \frac{1.4\times 287.06\times 289}{0.4}\left[ 1-{{\left( \frac{7.0133}{1.0133} \right)}^{0.286}} \right]=-8335.3kW \\\end{align}\]
负号表示压气机对气流做功。
例5.11 求某压气机出口截面上气流的总压。设其出口截面积A=0.1㎡,由测量得知出口静压p=4.12 × 105Pa,空气流量qm=50 kg/s,总温T*=480 K。
解:由式(5.37),可得
\(y\left( \lambda \right)=\frac{{{q}_{m}}\sqrt{{{T}^{*}}}}{KAp}=\frac{50\sqrt{480}}{0.0404\times 0.1\times 4.12\times {{10}^{5}}}=0.658\)
查表,当k=1.4时,得π(λ)=0.907,则
\({{p}^{*}}=\frac{p}{\pi \left( \lambda \right)}=\frac{4.12\times {{10}^{5}}}{0.907}=4.52\times {{10}^{5}}Pa\)
5.3.3 冲量函数z(λ),f(λ),r(λ)
动量方程式也可以用气流的总参数和气动函数来表示。将动量方程应用于图5.13所示的控制体内的气流,如果不计气体质量力时,则得
\({{F}_{i}}=\left( {{q}_{m}}{{V}_{2}}+{{p}_{2}}{{A}_{2}} \right)-\left( {{q}_{m}}{{V}_{1}}+{{p}_{1}}{{A}_{1}} \right)\)
式中,Fi是管壁作用于控制面内气体上的轴向力。通常定义组合量qmV+pA为某个截面上气流的冲量。它也可以用λ的气动函数z(λ),f(λ),r(λ)来表示,推导如下。
将连续方程式代入冲量关系式,有
\({{q}_{m}}V+pA={{q}_{m}}\left( V+\frac{p}{\rho V} \right)\)
而 \(V=\lambda {{c}_{cr}}\)
\(\frac{p}{\rho }=RT=R{{T}^{*}}\tau \left( \lambda \right)=\frac{k+1}{2k}\tau \left( \lambda \right)c_{cr}^{2}\)
代入冲量公式,得
\(\begin{align}& {{q}_{m}}V+pA={{q}_{m}}\left[ \lambda {{c}_{cr}}+\frac{k+1}{2k}\frac{\tau \left( \lambda \right)}{\lambda }{{c}_{cr}} \right]= \\& {{q}_{m}}\left[ \lambda {{c}_{cr}}+\frac{k+1}{2k}\frac{{{c}_{cr}}}{\lambda }\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right) \right]= \\& {{q}_{m}}\frac{k+1}{2k}{{c}_{cr}}\left( \frac{1}{\lambda }+\lambda \right)= \\& \frac{k+1}{2k}{{q}_{m}}{{c}_{cr}}z\left( \lambda \right) \\\end{align}\)
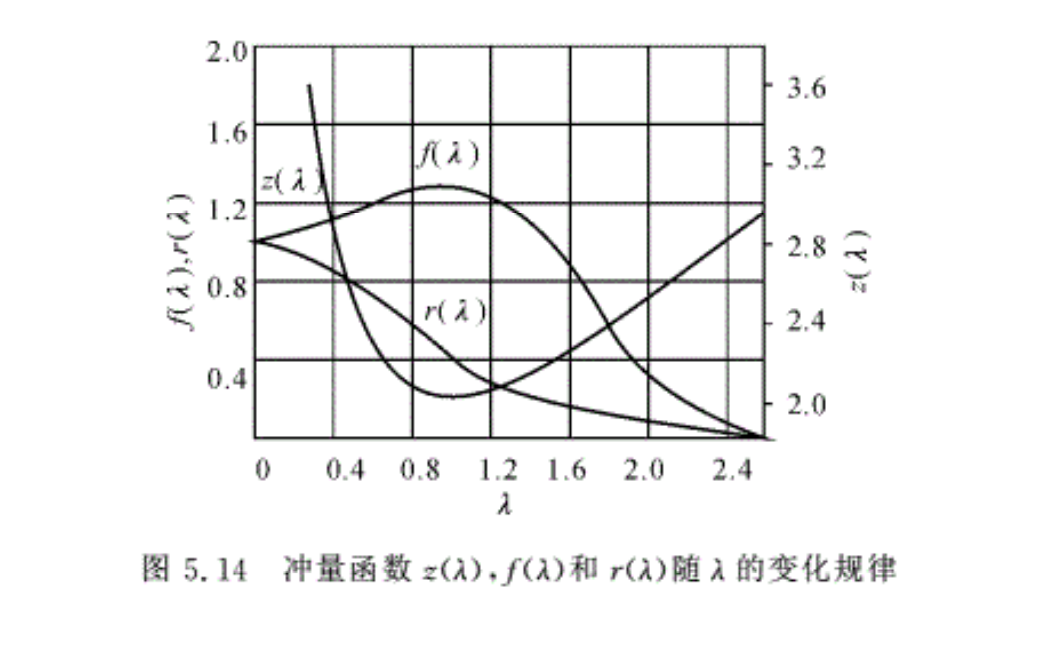
式中,z(λ)=1/λ+λ,又是一个气动函数,称其为冲量函数。它随λ的变化规律表示在图5.14上。当λ< 1时,z(λ)随λ的增加而迅速下降;当λ=1时,z(λ)降低到最小值为2,;当λ> 1时,z(λ)随λ的增加而增大。需要指出的是z(λ)函数与气体的比热比k无关,且在同一个z(λ)值下有两个λ值与其对应。
管壁作用于控制体内气体上的轴向力Fi等于管道内气体冲量的增量。引用气动函数z(λ)后,动量方程为
\({{F}_{i}}=\frac{k+1}{2k}{{q}_{m}}\left[ {{c}_{cr2}}z\left( {{\lambda }_{2}} \right)-{{c}_{cr1}}z\left( {{\lambda }_{1}} \right) \right]\) (5.38)
气体冲量还可以用气流的滞止压强p*表示,因此还可以引出另一个气动函数f(λ)。
将式(5.21)、式(5.33)代入冲量关系式,得
\(\begin{align}& {{q}_{m}}V+pA=\frac{k+1}{2k}{{q}_{m}}{{c}_{cr}}z\left( \lambda \right)= \\& \frac{k+1}{2k}K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}q\left( \lambda \right)A\sqrt{\frac{2kR{{T}^{*}}}{k+1}}z\left( \lambda \right)= \\& \frac{k+1}{2k}\sqrt{\frac{k}{R}{{\left( \frac{2}{k+1} \right)}^{\frac{k+1}{k-1}}}}\sqrt{\frac{2k}{k+1}R}{{p}^{*}}Aq\left( \lambda \right)z\left( \lambda \right)= \\ & {{\left( \frac{2}{k+1} \right)}^{\frac{1}{k-1}}}{{p}^{*}}Aq\left( \lambda\right)z\left( \lambda \right)={{p}^{*}}Af\left( \lambda \right) \\\end{align}\) (5.39)
式中 \(f\left( \lambda \right)={{\left( \frac{2}{k+1} \right)}^{\frac{1}{k-1}}}q\left( \lambda \right)z\left( \lambda \right)\)
如果冲量用静压p表示,又可得到另一个气动函数r(λ),即将式(5.39)中的总压p*用静压p代替,可得
\({{q}_{m}}V+pA=\frac{p}{\pi \left( \lambda \right)}Af\left( \lambda \right)=\frac{pA}{r\left( \lambda \right)}\) (5.40)
式中,r(λ)=π(λ)/f(λ)。它和f(λ)随λ的变化关系均表示在图5.14上。从式(5.39)、式(5.40)式可以看出,如果用气流的总压或静压表示气流冲量时,冲量大小则与气流的温度高低无关。这是因为qmV项中温度的影响刚好抵消。这样,动量方程中的作用力又可表示为
\({{F}_{i}}=p_{2}^{*}{{A}_{2}}f\left( {{\lambda }_{2}} \right)-p_{1}^{*}{{A}_{1}}f\left( {{\lambda }_{1}} \right)\) (5.41)
\({{F}_{i}}=\frac{{{p}_{2}}{{A}_{2}}}{r\left( {{\lambda }_{2}} \right)}-\frac{{{p}_{1}}{{A}_{1}}}{r\left( {{\lambda }_{1}} \right)}\) (5.42)
到此为止,一般的8个气动函数己全部讨论完毕,这些气动函数可以在附录表2中查到。需要指出的是,在实际应用中,将会遇到很多不同版本的气动函数表,其中有的气动含糊定义稍有不同。例如,在苏联的有些科技资料中定义,q(λ)=λε(λ),因此当λ=1. 0时,它的q(λ)=0.62……。另外有的厂、所用的气动函数表中定义,z(λ)=1/2(λ+1/λ)。应用中要注意气动函数的定义。
例5.12 燃气(k=1. 33)在等截面直管中流动,进口参数为T1*=750 K,p1*=2.55 × 105 Pa,λ1=0.35,己知给燃气加入的热量为q=1.17 × 103kJ / kg,不计燃气与管壁间的摩擦力,求出囗气流参数T2*,p2*,λ2(cp=1.16 kJ/(kg • K))。
解:取直管进、出口及侧面为控制体,由能量方程可得
\(T_{2}^{*}=\frac{q}{{{c}_{p}}}+T_{1}^{*}=\frac{1.17\times {{10}^{3}}}{1.16}+750=1760K\)
对于直管且无壁面摩擦力,故F=0,沿流动方向列动量方程为
\({{c}_{cr1}}z\left( {{\lambda }_{1}} \right)={{c}_{cr2}}z\left( {{\lambda }_{2}} \right)\)
故 \(z\left( {{\lambda }_{2}} \right)=\sqrt{\frac{T_{1}^{*}}{T_{2}^{*}}}z\left( {{\lambda }_{1}} \right)=\sqrt{\frac{750}{1760}}\left( 0.35+\frac{1}{0.35} \right)=2.1\)
解得λ2=0.73或λ2=1.37 。本题为亚声速流动,应取λ2=0.73。
动量方程还可写为
\(p_{2}^{*}Af\left( {{\lambda }_{2}} \right)=p_{1}^{*}Af\left( {{\lambda }_{1}} \right)\)
故 \(p_{2}^{*}=p_{1}^{*}\frac{f\left( {{\lambda }_{1}} \right)}{f\left( {{\lambda }_{2}} \right)}=2.55\times {{10}^{5}}\times \frac{1.0645}{1.2085}=2.25\times {{10}^{5}}Pa\)
例5.13 某收缩喷管在截面积为0.25m²的位置处空气的静压为2.0 × 105 Pa,温度为 300K,速度为100 m/s,不计摩擦影响。问该喷管内气流最大可能的流速是多大?其出口气流参数(p*,T*,p,T,Ma)和流量是多少?出口面积为多大?
解:在截面A1=0.25m2位置处,各参数分别为
\(\begin{align}& {{c}_{1}}=\sqrt{kR{{T}_{1}}}=\sqrt{1.4\times 287.06\times 300}=347.2m/s \\& M{{a}_{1}}=\frac{{{V}_{1}}}{{{c}_{1}}}=\frac{100}{347.2}=0.288 \\& p_{1}^{*}=\frac{{{p}_{1}}}{\pi \left( M{{a}_{1}} \right)}=\frac{2.0\times {{10}^{5}}}{0.943}=2.119\times {{10}^{5}}Pa \\ & T_{1}^{*}=\frac{{{T}_{1}}}{\tau \left( M{{a}_{1}} \right)}=\frac{300}{0.9837}=305.0K \\\end{align}\)
通过喷管的流量为
\({{q}_{m}}=K\frac{p_{1}^{*}}{\sqrt{T_{1}^{*}}}q\left( M{{a}_{1}} \right){{A}_{1}}=58.56kg/s\)
由于流动是绝能等熵的,因此喷管出口总压、总温不变。在收缩喷管中,最大可能的马赫数为1,即最大可能的流速为
\({{V}_{2}}={{c}_{cr}}=\sqrt{\frac{2kR{{T}^{*}}}{k+1}}=319.5m/s\)
出口压强、温度和截面积分别为
\(\begin{align}& {{p}_{2}}={{p}_{cr}}=0.5283{{p}^{*}}=1.119\times {{10}^{5}}Pa \\& {{T}_{2}}={{T}_{cr}}=0.8333\times 305.0=254.2K \\& {{A}_{2}}={{A}_{cr}}={{A}_{1}}q\left( M{{a}_{1}} \right)=0.25\times 0.4739=0.1185{{m}^{2}} \\\end{align}\)
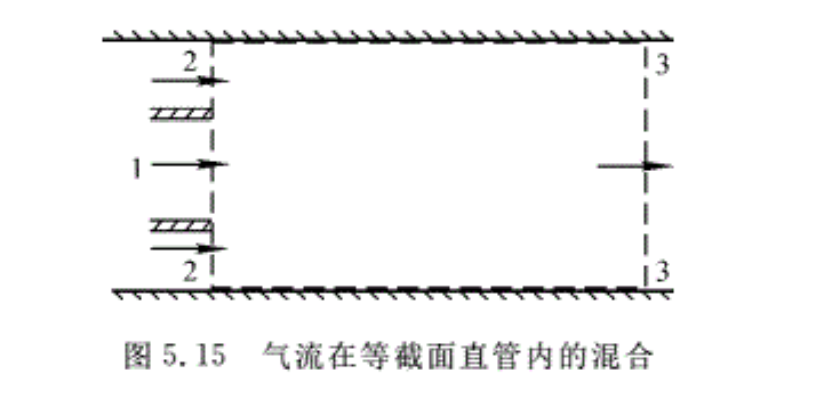
例5.14 亚声速气流在如图5.15所示的等截面管内流动(引射器),两股空气混合前的参数分别为T1*=900 K,p1*=3 × 105 Pa,T2*=300 K,p2*=2 × 105Pa,空气流量qm1=80 kg/s,qm2= 20 kg/s,截面面积A1=A2=0.22㎡,A3=A1+A2。略去管壁与气流间的摩擦,气流与外界也无热量交换。求混合后气流的参数T3*,p3*和Ma3。设气流的比定压热容cp为常数。
解:这是一个亚声速引射器问题,主动气流1与被动气流2在混合室进口混合,在出囗截面3混合均匀。对于亚声速引射器,两股气流在混合室进口处必须满足静压相等的条件,即有p1=p2。由于两股气流的总压不同,所以流速并不相等。
取控制体如图5.15所示,对其用能量方程,可得
\({{q}_{m1}}{{c}_{p}}T_{1}^{*}+{{q}_{m2}}{{c}_{p}}T_{2}^{*}={{q}_{m3}}{{c}_{p}}T_{3}^{*}\)
故 \(T_{3}^{*}=\frac{{{q}_{m1}}}{{{q}_{m3}}}T_{1}^{*}+\frac{{{q}_{m2}}}{{{q}_{m3}}}T_{2}^{*}=\frac{80}{80+20}\times 900+\frac{20}{80+20}\times 300=780K\)
由流量公式,有
\(\begin{align}& q\left( {{\lambda }_{1}} \right)=\frac{{{q}_{m1}}\sqrt{T_{1}^{*}}}{Kp_{1}^{*}{{A}_{1}}}=\frac{80\times \sqrt{900}}{0.0404\times 3.0\times {{10}^{5}}\times 0.22}=0.9 \\& q\left( {{\lambda }_{2}} \right)=\frac{{{q}_{m2}}\sqrt{T_{2}^{*}}}{Kp_{2}^{*}{{A}_{2}}}=\frac{20\times \sqrt{300}}{0.0404\times 2.0\times {{10}^{5}}\times 0.22}=0.195 \\\end{align}\)
查表,得λ1=0.714,Ma1=0.68,λ2=0.125,Ma2=0.112,所以,
\[\begin{align}& z\left( {{\lambda }_{1}} \right)={{\lambda }_{1}}+\frac{1}{{{\lambda }_{1}}}=2.1146 \\& z\left( {{\lambda }_{2}} \right)={{\lambda }_{2}}+\frac{1}{{{\lambda }_{2}}}=8.125 \\\end{align}\]
由于略去管壁与气流间的摩擦,且气流与外界无热量交换,所以管壁对气流沿流向的作用力Fi=0 ,因此由动量方程式(5.38 ) ,可得
\[\begin{align} & {{q}_{m1}}{{c}_{cr1}}z\left( {{\lambda }_{1}} \right)+{{q}_{m2}}{{c}_{cr2}}z\left( {{\lambda }_{2}} \right)={{q}_{m3}}{{c}_{cr3}}z\left( {{\lambda }_{3}} \right) \\& z\left( {{\lambda }_{3}} \right)=\frac{{{q}_{m1}}}{{{q}_{m3}}}\frac{{{c}_{cr1}}}{{{c}_{cr3}}}z\left( {{\lambda }_{1}} \right)+\frac{{{q}_{m2}}}{{{q}_{m3}}}\frac{{{c}_{cr2}}}{{{c}_{cr3}}}z\left( {{\lambda }_{2}} \right)= \\& 0.8\sqrt{\frac{900}{780}}\times 2.1146+0.2\sqrt{\frac{300}{780}}\times 8.125=2.825 \\\end{align}\]
由气动函数表,查得 λ3=0.415,Ma3=0.382
由式( 5 .41 ) ,得
\[p_{1}^{*}{{A}_{1}}f\left( {{\lambda }_{1}} \right)+p_{2}^{*}{{A}_{2}}f\left( {{\lambda }_{2}} \right)=p_{3}^{*}{{A}_{3}}f\left( {{\lambda }_{3}} \right)\]
由气动函数表,查得
f(λ1)=1.208,f(λ2)=1.009,f(λ3)=1.09
故
\[\begin{align}& p_{3}^{*}=p_{1}^{*}\frac{{{A}_{1}}}{{{A}_{3}}}\frac{f\left( {{\lambda }_{1}} \right)}{f\left( {{\lambda }_{3}} \right)}+p_{2}^{*}\frac{{{A}_{2}}}{{{A}_{3}}}\frac{f\left( {{\lambda }_{2}} \right)}{f\left( {{\lambda }_{3}} \right)}= \\& 3\times {{10}^{5}}\times \frac{1}{2}\times \frac{1.208}{1.09}+2.0\times {{10}^{5}}\times \frac{1}{2}\times \frac{1.009}{1.09}=2.585\times {{10}^{5}}Pa \\\end{align}\]
由本例可知,一方面,混合后主流的总压有所损失,虽然未计气流与管壁间的摩擦力,但是由于两股气流混合前的速度不同会引起混合后气流总压的下降。气体混合是一个不可逆过程,一定会产生混合损失。另一方面,引射器出口的气流总压大于被动气流的总压。这说明引射器起到一个抽气泵的作用,可以使较低总压的气流总压提高,而引射器的主要作用就在于此。
小结
本章主要讨论了声速、马赫数与速度因数的定义,以及与压缩性的关系;讨论了几个重要的气流参数,即滞止参数、临界参数和最大速度;为了计算方便,引进了气体动力学函数。进一步将一维定常流动的基本方程用滯止参数、临界参数和气动函數来表示。
主要掌握这些基本概念的定义,熟练掌握滞止参数与临界参数的变化规律以及影因素。
( 1 )流场中每一点都有相应该点的滞止参数、临界参数和最大速度,只有在速度等于零的截面上,实际参数与滞止参数相等;只有在速度等于当地声速的截面上,实际参数与临界参数相等。
( 2 )影响总压的因素有摩擦、热交换和机械功的交换。
( 3 )基本方程的表示:
流量公式
\[{{q}_{m}}=\rho VA=K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}Aq\left( \lambda \right)=K\frac{p}{\sqrt{{{T}^{*}}}}Ay\left( \lambda \right)\]
因此,连续方程可相应地有三种表达式。
动量方程求作用力
\[\begin{align}& {{F}_{i}}=\left( {{p}_{2}}{{A}_{2}}+{{q}_{m2}}{{V}_{2}} \right)-\left( {{p}_{1}}{{A}_{1}}+{{q}_{m1}}{{V}_{1}} \right)= \\& \frac{k+1}{2k}{{q}_{m}}\left[ {{c}_{cr2}}z\left( {{\lambda }_{2}} \right)-{{c}_{cr1}}z\left( {{\lambda }_{1}} \right) \right]= \\& p_{2}^{*}{{A}_{2}}f\left( {{\lambda }_{2}} \right)-p_{1}^{*}{{A}_{1}}f\left( {{\lambda }_{1}} \right)=\frac{{{p}_{2}}{{A}_{2}}}{r\left( {{\lambda }_{2}} \right)}-\frac{{{p}_{1}}{{A}_{1}}}{r\left( {{\lambda }_{1}} \right)} \\\end{align}\]
能量方程
\[q-{{\omega }_{s}}={{h}_{2}}-{{h}_{1}}+\left( V_{2}^{2}-V_{1}^{2} \right)/2=h_{2}^{*}-h_{1}^{*}={{c}_{p}}\left( T_{2}^{*}-T_{1}^{*} \right)\]
思考与练习题
5.1 什么叫气流的滞止参数和临界参数?在绝能流动中,它们是如何变化的?
5.2 用T -s图分析在绝能流动中,总压的变化规律。
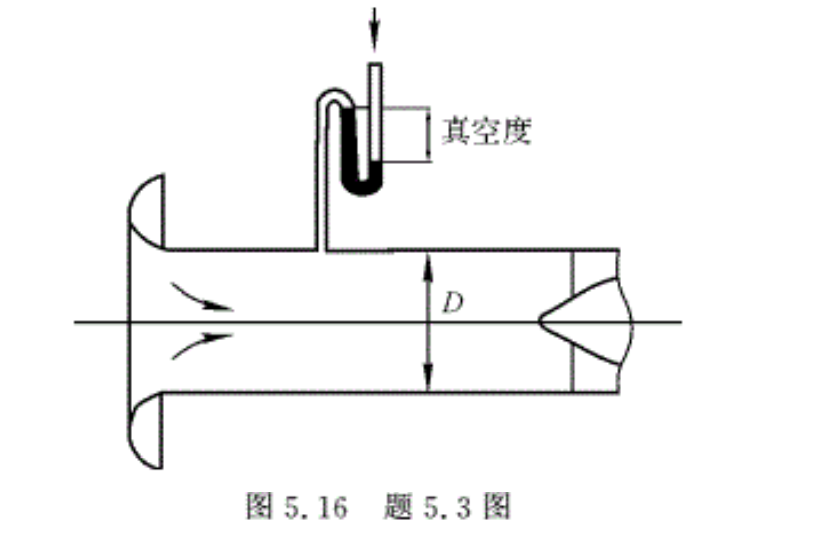
5.3 某发动机在台架试车,当地的大气压强pa=1.0059 ×105 Pa,大气温度Ta=296 K,发动机的进口直径为D=0. 6 m,如图5.16所示。试车时,得进口处的静压(真空度)为0.032 × 105 Pa,求在该工作状态下,通过发动机的空气流量qm。
5.4 空气沿着扩散管道流动,在进囗截面1一1处,空气压强p1=1. 0133 × 103 Pa,温度 T1=288 K,速度V1=272 m/s,截面1一1的面A1=1 × 10-3m2,在出囗截面2一2处空气速度降低到V2=72.2 m/s。设空气在扩散形管道中为绝能等熵流动。试求:
(1)气流作用于管道内壁的力;
(2)进、出囗气流的马赫数Ma1及Ma2;
(3)进、出口气流的总温及总压。
5.5 己知在超声速喷管的收缩段某截面1处的空气流压强p1=5.88 × 105 Pa,总温 T1*=310 K,速度因数λ1=0.6,在扩张段某截面2处气流温度T2=243 K。假设气流在喷管中的流动为绝能等熵的,求空气流在截面2上的压强和速度因数。
5.6 设储气箱中空气的压强p1=2.943 ×105 Pa,温度T1=288 K,通过喷管向外喷入大气中,大气压强pa=9.81 × 104Pa。如果在喷管出囗截面上的气流压强和外界大气压强相等,试求出囗截面上的气流速度。假定空气在喷管中的流动是绝能等熵的。
5.7 编写以马赫数为自变量的气体动力学函数表的计算机程序。
5.8 承上题,设气流从储气箱流到喷管出口的过程中,由于气体在流动中有摩擦损失,故为不可逆的绝能流动过程,此时,出口处的气流总压p²(2f)必小于储气箱中的压强p1。设p*(2f)=0.95p1,其他条件同上题,试求出口处气流的速度。
5.9 用测压管和温度计测得空气流参数:p*=2.0 × 105 Pa,p=1.5 × 105 Pa,T*=290 K。求空气流的Ma、速度和静温。
5.10 设发动机进气道的空气流量qm=50 kg/s,在进气道入囗截面上的速度因数λ1=0.4,出口截面上的λ2=0.2,气流的总温T*=322 K。求气流作用在进气道内壁上的推力。
5.11 海平面标准大气经管道被吸入真空箱。假设在所有温度下,空气均保持完全气体的性质,而且空气经管道为绝能流动。试求空气所能达到的最大速度Vmax
5.12 空气自气瓶经超声速喷管流出时的速度等于最大速度之半,求空气流出时的声速、速度因数λ。已知气瓶中空气的温度400 K。
5.13 空气沿着收敛扩散形管道流动,在进口截面1一1处,空气压强p1=6 × 105Pa,总温T1*= 310 K,速度因数λ1=0.4;在出囗截面2一2处空气流压强p2=1.457 × 105 Pa,求在截面2一2处气流的马赫数和温度(假设流动为绝能等熵过程)。
5.14 己知某扩散管的进出囗的面积比A1/A2=0.8,进囗速度因数λ1=0.8,气流在出口的总压为进囗总压的90%,求出口气流的速度因数λ2。
5.15 已知管流中某截面(A=13 × 10-4m2)上的Ma=0.6,p=1.3 × 105 Pa,流量qm=0.5 kg/s。求该空气总温T*及最小截面处之速度、温度和压强(设管中流动为等熵,且在最小截面处Ma= 1)。
5.16 空气流在等直径圆管进口处的参数是T1*=600K,λ1=0. 4。进入管道后,因受到管道外面加热的作用,在圆管出口处气流的总温升高到T2*=1200 K,求速度因数λ2(忽略气流与管壁间的摩擦力)。
5.17 燃烧室出囗气流参数为p*=8 × 105 Pa,T*=1150 K,V=150 m/ s。通过烧室的燃气流量qm= 50 kg/s。求燃烧室出囗所需要的面积A。
5.18 亚声速气流在如图5.15所示的等截面直管内流动(引射器),测得两股气流混合均匀后的总压、总温和流量,即p3*,T3*,qm3,并己知掺混前的主流参数为p1*,T1*,qm1,截面面积 A1=A2,出口截面面积A3=A1+A2。略去管壁与气流间的摩擦,并设气流与外界无热量交换,气流的比定压热容cp为常数。求进囗次流在环形截面2处的总温T2*、速度因数λ2和总压p2*。