第六章膨胀波与激波

在绝能等熵流动中，当Ma < 0.3时，流体可近似看做是不可压缩的。随着流速的不断提高，压缩性的影响将变得愈来愈严重。当Ma > 1时，绕物体的流动是超声速的，在物体上会形成激波和膨胀波（这将在下面详细讨论)。当流动既有亚声速流动，又有超声速流动时，物体上会出现激波等现象，这种流动称为跨声速流动。在跨声速流动中，物体上可以出现Ma< 1， Ma=1，Ma＞1的流动区域，流动现象要复杂得多。当Ma>5时，流动为高超声速的，其流动特点与低超声速差别很大。关于高超声速流动的特点将在最后一章讨论。本章仅讨论超声速气流中的激波与膨胀波的产生、特点及计算公式。

膨胀波与激波是超声速气流中的重要现象，超声速气流减速时一般会产生激波，超声速气流加速时，会产生膨胀波。随着飞机和发动机性能的提高，超声速进气道、超声速压气机和超声速喷管己经广泛地被采用。超声速燃烧室和超声速涡轮也在研究之中。在分析和研宄这些部件中气流的运动规律时，首先就要遇到膨胀波与激波问题。

本章首先讨论微扰动在气流中的传播规律，其次讨论膨胀波和激波的产生、特点、参数变化规律以及激波的相交与反射等问题，最后讨论圆锥激波以及激波在实际中的应用。

6.1  微扰动在气流中的传播及马赫锥

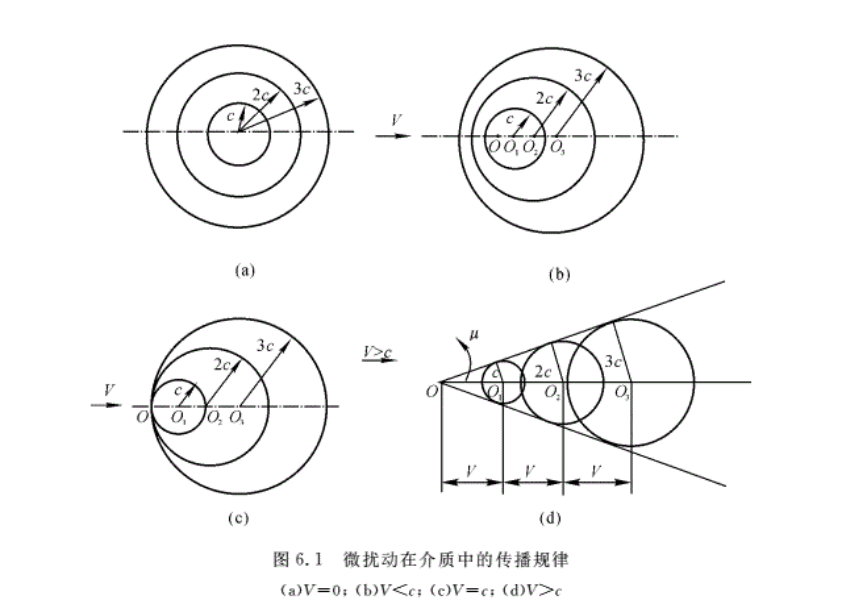
本节将讨论微扰动在气流中的传播规律，特别是在超声速流动中的传播规律。如图6.1 （a）所示，在静止的气体中，有一个微扰动源位于点O，它所发出的扰动波以声速向外传播，且扰动波为球面波。假设不计气体黏性的影响，且参数分布均匀，则随着时间的推移，扰动可以传遍整个流场。图6.1(a）给出了t=1 s，2 s，3 s末微扰动波所达到的位置。如果静止的扰动源在点O连续不断地发出扰动，则在不同时刻所发出的扰动波将构成一系列的同心球面。

当气流以小于声速的速度运动时，扰动波相对气流仍以声速c向外传播，同时球面中心又以气流速度V向下游运动。因此，扰动波在下游顺气流方向的绝对速度为c+V，在上游逆气流方向的绝对速度为c-V，其他方向的绝对速度则介于这两者之间。由于扰动传播的速度大于气流的速度，因此扰动仍可以逆流传播。图6.1(b）给出了t=3 s末扰动波所在的位置。可以看出在亚声速气流中，微扰动波仍可以传遍整个流场。这是微扰动在亚声速气流中传播的特点。

随着气流速度的不断提高，当气流速度恰好等于当地声速（V=c）时，在逆气流方向的绝对速度等于零，因此微扰动波不能逆流传播，即扰动源O点的上游不会受到任何影响，扰动被限制在以扰动源O为公切点的各球面波的公切平面的下游。其扰动传播的图形如图6.1（c）所示。

若气流速度超过声速，则由于气体的运动速度比扰动波相对于气体本身的传播速度还要大，因此，扰动不能逆流传播。扰动影响局限于以O点为顶点，以μ角为半顶角的圆锥内。如图6.1（d）所示。此圆锥称为马赫锥，μ角称为马赫角。此马赫锥以内的区域称为扰动的影响区，马赫锥以外的流动不受任何影响。显然，其半锥角满足：

sin μ= c/V = 1/Ma           （6.1 )

由式（6.1）可知，当Ma=1时，μ=90°，即此时扰动被限制在过扰动源O的公切平面内，该公切平面与流动方向垂直。当Ma > 1时，μ< 90°，而在亚声速气流中，μ角无意义。

由以上分析可见，微扰动在亚声速气流中，随着时间的推移，扰动可以传遍整个流场。而在超声速气流中，微扰动波不仅不能逆流传播，而且扰动影响范围仅限制在一个以扰动源为顶点的马赫锥之内。这是亚声速气流与超声速气流的根本差别，如图6.1（b）和6.1（d）所示。

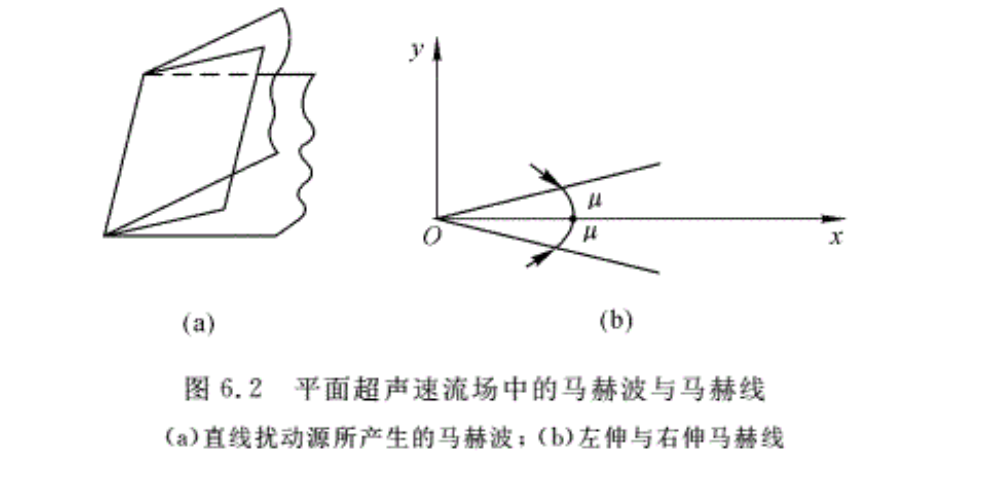
图6.1（d）中所示的马赫锥的锥面即为马赫波，马赫波不仅可以是微弱压缩波，也可以是膨胀波。

对于直线的扰动源（如无限薄的平板）所产生的微弱扰动波，扰动波的波面为一楔面，如图 6.2（a）所示。气流通过扰动波受到了微弱的压缩，气流的压强、密度、温度有微小的增加，而速度则有所减小。

在平面超声速流场中，马赫波在xOy平面上的投影称为马赫线。通常对于面向下游（顺气流方向）的观察者，把从扰动源伸向左方的称为左伸马赫线（图6.2（b）中Ox轴上方的线），把伸向右方的称为右伸马赫线（图6.2（b）中Ox轴下方的线）。

最后还要指出，如果超声速来流速度沿其垂直方向（y向）气流参数不均匀，则由于当地马赫数随马赫角变化，因此马赫线将变成曲线。

6.2  膨胀波的形成及普朗特一迈耶流动

6.2.1  膨胀波的形成及特点

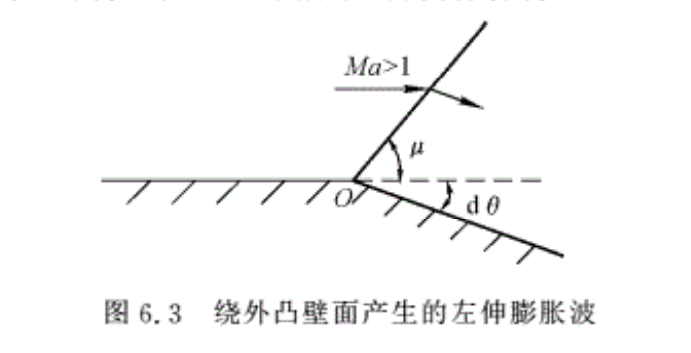
二维平面超声速气流沿如图6.3所示的外凸壁面（相对于气流向外折转）流动，壁面在O 点向外折转一个无限小的角度dθ。由于壁面的微小折转，对原来的均匀来流产生了扰动，使原来的直匀来流的参数发生了微小的变化。因此，在壁面的折转处，产生一道马赫波，其马赫角μ=arcsin（1/Ma）。气流通过马赫波之后，流动方向将沿波后壁面流动，即气流通过马赫线一定要折转一个角度dθ，dθ称为气流折转角。通常规定相对于来流方向逆时针方向折转角dθ为正，而顺时针方向折转角dθ为负（图6.3中所示的折转角为负)。

从图6.3可以看出，马赫波后的流通面积比波前流通面积有所增加。如前所述，超声速气流流过截面积增加的管道，其流速必然增大，相应的压强、温度、密度减小，如果不考虑气流的黏性和与壁面间的热交换，则流动可看做是绝能等熵的。因此，超声速气流流过微小折转的外凸壁面所产生的马赫波，使气流加速，压强和密度下降。这种马赫波使气流得到了膨胀，因此称为膨胀波。可见壁面外凸即是一种产生膨胀波的扰动源。

如果超声速气流绕过一个有限折转角的外凸壁流动，如图6.4所示，此时气流可以看做是流过由一系列折转无限小的外凸壁（每次的折转角为dθ）的流动，气流每折转一个角度dθ，就产生一道膨胀波（见图6.5），而气流每经过一道膨胀波，马赫数增大，μ角减小，同时壁面又向外折转了dθ，因此，后面的膨胀波的倾斜角都比前面的倾斜角小，即这些膨胀波既不会平行也不会彼此相交，而是发散的，即形成了一个扇形区。显然，如果壁面的几个折转点都无限接近O点时，就形成了如图6.4所示的普朗特一迈耶流动。也就是说，超声速气流绕图6.5所示的外凸壁面的流动与如图6.4所示的流动在本质上并没有什么差别。除了壁面的曲壁和直壁不同之外，其他并没有什么差别。由此可以看出，超声速气流绕外凸壁面的流动时，流动参数的变化取决于来流条件和总的折转角，而与壁面的折转方式无关，一次折转与多次折转的效果是相同的。

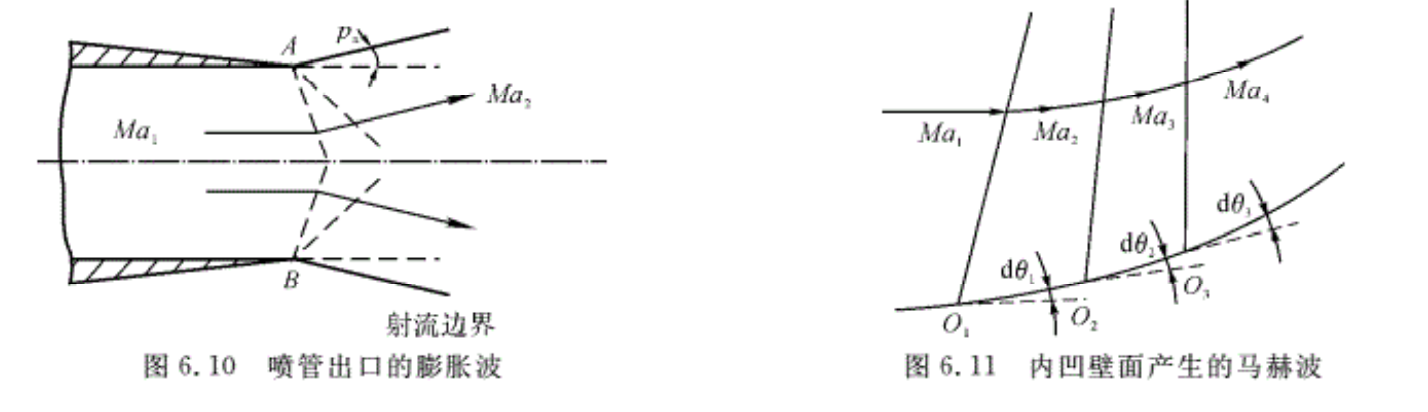
除了超声速气流沿外凸壁流动外，在另外一种情况下，如扰动源为压强差，也会产生膨胀波。例如，当气体由超声速喷管以超声速射出时，如果气体在出口截面上的压强pe大于外界环境压强pa，气流自喷管流出后将继续膨胀加速，这个膨胀加速过程直到气体在射流边界上的压强等于外界环境压强为止。这时在喷管出口就必然会产生膨胀波。

同样，对于超声速气流沿内凹的壁面流动，dθ为正值。只要dθ足够得小，这时产生的微弱压缩波仍然可看做是等熵流动，只不过此时流速减小，相应的压强、温度和密度增加一个微量。这种马赫波使气流得到了微弱压缩，因此称为微弱压缩波。微弱压缩波是等熵压缩波。

6.2.2  膨胀波的计算

气流通过膨胀波是绝能等熵的，亦即在整个膨胀加速过程中，气流的总参数都保持不变。因此只要求出流场中的马赫数，就可以求出流场中的其他静参数。但由图6.4可以看出，气流每经过一道膨胀波，马赫数与气流方向角都在变化，因此必须建立两者之间的关系。由于图 6.5所示各区的流动是均匀的，且各区中马赫数不变，因而图6.4所示的扇形区中的马赫线为直线。对于给定的起始条件，扇形区中气流速度和马赫数及其他参数仅仅是气流方向角θ的函数。

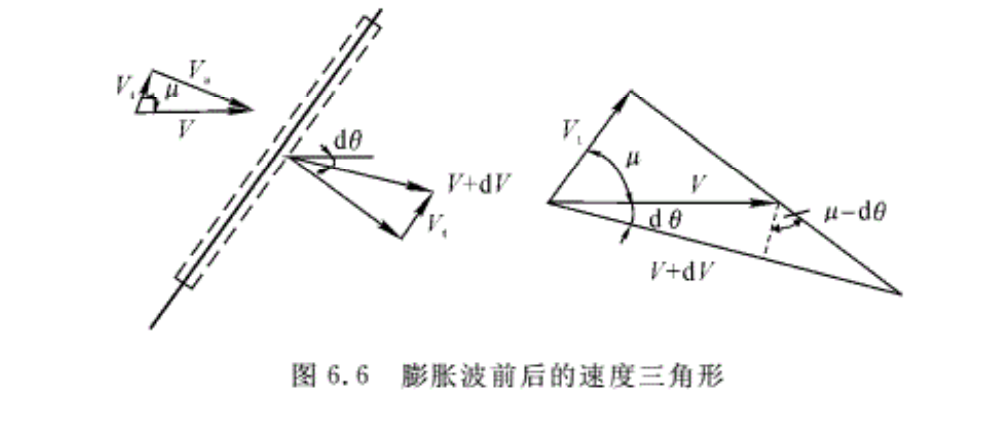
对图6.3的左伸膨胀波，将波前、后的流速V1，V2分解为与波面平行和与波面垂直的分量，如图6.6所示。沿波面取控制体，对该控制体应用连续方程

                                ρVn=常数             （6.2）

又沿波面方向的动量方程，由于∑Ft=0，因此动量方程为

\(\sum {{F}_{t}}=\rho {{V}_{n}}A\left( V_{t}^{\prime }-{{V}_{t}} \right)=0\)             （6.3）

因此可得                        \(V_{t}^{\prime }={{V}_{t}}\)                   (6.4)

即超声速气流经过膨胀波后，气流沿膨胀波波面方向的分速不变。而气流速度的变化仅仅取决于垂直于波面的速度分量。显然，经过膨胀波，气流方向必定要向离开波面的方向折转。

在起始条件一定的情况下，通过膨胀波气流速度的增量dV与dθ的关系，可根据图6.6所示的速度三角形得出，即

\(\tan \left( \mu -d\theta  \right)=-\frac{dV}{Vd\theta }\)                 (a)

式中，dθ为负值。

当dθ比马赫角小得很多时，则可以认为tan（μ-dθ）≈tanμ，则式（a）可写成

dV/V=-tanμdθ                     （b）

又由式（6.1 )，得                    \(\tan \mu =\frac{1}{\sqrt{M{{a}^{2}}-1}}\)

代入式（b)，得                      \(\frac{dV}{V}=-\frac{d\theta }{\sqrt{M{{a}^{2}}-1}}\)                     (6.5)

这就是超声速气流沿外凸壁流动的基本微分方程。

由V=Mac，对其两边取对数后微分，可得

dV/V = dMa/Ma + dc/c                  (6.6）

由\({{c}^{2}}=kRT=kR{{T}^{*}}/\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)\)，对该式取对数后微分，得

\(\frac{dc}{c}=-\frac{\frac{k-1}{2}MadMa}{1+\frac{k-1}{2}M{{a}^{2}}}\)

将上式代入式（6.6），得

\(\frac{dV}{V}=\frac{dMa}{Ma}\left[ 1-\frac{\frac{k-1}{2}M{{a}^{2}}}{1+\frac{k-1}{2}M{{a}^{2}}} \right]\)             (6.7)

将式（6.7）代入微分方程式（6.5），得

\(d\theta =-\frac{\sqrt{M{{a}^{2}}-1}dM{{a}^{2}}}{2M{{a}^{2}}\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)}\)

积分后

\(\theta =-\sqrt{\frac{k+1}{k-1}}\arctan \sqrt{\frac{k-1}{k+1}\left( M{{a}^{2}}-1 \right)}+\arctan \sqrt{M{{a}^{2}}-1}+{{C}_{1}}\)

式中，C1为积分常数。

令                 \(\upsilon \left( Ma \right)=-\sqrt{\frac{k+1}{k-1}}\arctan \sqrt{\frac{k-1}{k+1}\left( M{{a}^{2}}-1 \right)}-\arctan \sqrt{M{{a}^{2}}-1}\)                (6.8)

则                           \(\theta =-\upsilon \left( Ma \right)+{{C}_{1}}\)

式中，υ（Ma）称为普朗特一迈耶函数，对于空气，k=1. 4，υ（Ma）的变化规律如图6.7所示。

因此气流马赫数与气流方向角之间的关系为

θ+υ（Ma）=C1                    (6.9a)

对于右伸波，有                             θ-υ（Ma）=C2                   (6.9b)

式中的积分常数取决于起始马赫数与气流方向角，即

\({{\theta }_{1}}\pm \upsilon \left( M{{a}_{1}} \right)={{\theta }_{2}}\pm \upsilon \left( M{{a}_{2}} \right)\)                      (6.10)

“ + ”号对应于左伸波，“-”对应于右伸波。

若Ma1=1，显然υ（Ma1）=0，且以Ma1（即来流）的方向为基准，即当θ1=0°时，由式（6.10)对于左伸波，得

\(\upsilon \left( M{{a}_{2}} \right)={{\theta }_{1}}-{{\theta }_{2}}=-\delta \)

可见普朗特一迈耶角就是气流由声速气流膨胀到Ma（Ma> 1)时气流所折转的角度，如图6.8所示。

当气流由声速膨胀速到马赫数为无穷大时，气流须折转的角度为

\(\upsilon \left( Ma \right)=\upsilon \left( M{{a}_{\max }} \right)=\frac{\pi }{2}\left( \sqrt{\frac{k+1}{k-1}}-1 \right)\)

对空气，k=1. 4，则

υ（Ma max）=130°27′

如图6.9所示，超过θmax时就会在局部区域出现真空。可见普朗特一迈耶函数的确代表一个角度。最大的普朗特一迈耶角是将气流绕外凸壁由声速膨胀加速到马赫数为无穷大时，气流的最大折转角。显然υ（Ma max）只是一个理论上的极限值。

由式（6.10）可以看出，在给定波前气流参数的情况下，只要知道壁面的总折转角δ，就可以确定υ（Ma2），从而可确定波后气流的Ma2（或λ2）以及其他气流参数。因此可以推论：超声速气流绕外凸壁流动时，气流参数的总变化只决定于波前气流参数和气流总的折转角度，而与气流的折转方式无关。即不论一次折转，还是分两次或多次折转，只要总折转角度相同，其最后的气流参数值必定相等。

附录表3给出了普朗特一迈耶函数随λ或Ma的变化数值表。实际上，对于空气 k=1. 4，取一系列Ma代入式（6.8），即可得υ（Ma）。编写计算机程序，很容易列出该数表，但若已知 υ（Ma），则需要迭代计算才能求出Ma。

图6.8中还给出了马赫角的极角的大小。马赫角的极角定义为气流从声速膨胀到某个马赫数时，膨胀波扇形区所张的角度，用φ表示。如果己知波前、后的马赫数，则可计算出马赫角μ，再根据几何关系可以求出马赫角的极角φ。如果超声速来流马赫数为Ma1，则根据Ma1和Ma2分别求出相应的极角φ1和φ2，则可得超声速气流绕外凸壁面流动所产生的扇形区的大小为

∆φ=φ2-φ1

另一方面，根据通过膨胀波前后的连续方程可以得出流线方程，留给读者自行推导。

例6.1  设平面超声速喷管出口处气流马赫数Ma1=1. 4，压强p1=1.25 × 10⁵Pa,外界大气压强pa=1. 0 × 10⁵ Pa。求气流经膨胀波后的Ma2及气流的折转角δ。

解：由膨胀波表查得，当Ma=1. 4时，υ（Ma1）=9渡，π（Ma1）=p1/p*=0.314。因为超声速气流排到大气中，所以气流的压强也膨胀到大气压强，即p2=pa，则

\(\frac{{{p}_{2}}}{{{p}^{*}}}=\frac{{{p}_{a}}}{{{p}_{1}}}\frac{{{p}_{1}}}{{{p}^{*}}}=\frac{1}{1.25}\times 0.314=0.2512\)

查气动函数表，得

Ma2=1.557

查膨胀波表，得

υ（Ma2）=13.6°

以喷管上半部为例，出口处的膨胀波系为右伸波，则

δ=θ2-θ1=υ（Ma2）-υ（Ma1）=13.6°-9°=4.6°

即超声速气流向外折转δ=4.6°。因为喷管是上、下对称的，则出囗气流也是上、下对称的，下边界也向外折转4. 6°，如图6.10所示。

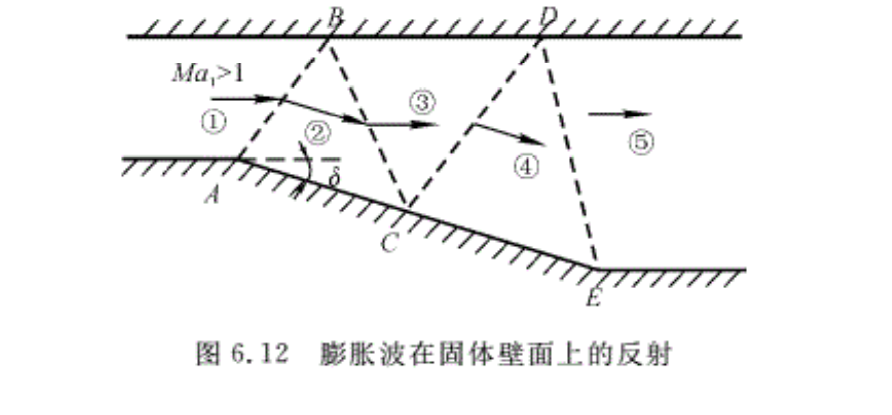
需要指出的是，图6.11给出的超声速气流沿内凹壁面流动时，只要壁面折转角dθ无限小，在壁面转折点处就产生微压缩波（也是马赫波）。气流通过弱的压缩波时，气流参数也将有微小的变化（即气流速度降低、压强和密度、温度均增加），而总参数不变。不难想象，如果超声速气流连续流过具有多个无限小转折角的壁面（见图6.11），则由每个折点必然产生相应的微压缩波，流动仍为等熵流动。不难推断出Ma1 > Ma2 > Ma3…而马赫角μ1<μ2 <μ3…则各个微压缩波在延伸一定距离后，它们会相交。而很多微压缩波相交成一道波时，它就再也不是弱的压缩波而成激波了。不过在各微压缩波未相交时，气流流经各波的过程仍为等熵的。

例6.2  要将Ma1=2.0的超声速气流（空气）膨胀加速到Ma2=3.0，问壁面要折转到多大角度？

解：由Ma1=2.0和Ma2=3.0分别查普朗特一迈耶函数表得到对应的角度υ（Ma1）=26.38°，υ（Ma2）=49.76°，因此壁面需要向外折转

∆θ=θ2-θ1=23.38°

6.3  膨胀波的相交与反射

6.3.1  膨胀波在固体壁面上的反射与消波

图6.12所示为一均匀超声速气流沿壁面流动，这时由于壁面外折，在点A必产生一束膨胀波，我们用一道波AB来表示。均匀的超声速气流经膨胀波AB后沿下壁而流动，由于上壁面是直固体壁面，则波后气流方向与上壁面不平行，因而膨胀波AB必然在点B 反射出一道膨胀波。②区气流经反射膨胀波BC后进入③区，又沿上壁面方向流动。由于气流在C点与下壁面不平行，相当于③区气流在C点遇到了一个向外折转的壁面，因此在点C又产生一道膨胀波CD。同理，由于④区气流方向在D点与壁面不平行，而再次产生膨胀波DE。由此可见，膨胀波在固体壁面上反射仍为膨胀波。同理可知，压缩波在固体壁面上反射为压缩波。

气流经（见图6.12）膨胀波DE后，以平行于D点和E点以后的壁面方向流动。由于⑤区气流方向一致且沿壁面方向，压强也相等，所以在E点膨胀波将消失，不再反射。可以利用膨胀波的消失（无反射）来设计超声速喷管。

图6.12中所示各区中的参数可根据式（6.10）逐区计算。如果给定来流的马赫数、静压、静温和壁面折转角δ，求各区参数。其计算思路如下：

第一步，可以根据Ma，p1，T1计算出总压、总温。

第二步，根据Ma1，查气动函数表得υ（Ma1），然后根据式（6.10），求出左伸波AB后的Ma2。

由于通过膨胀波总压、总温保持不变，所以可以根据总、静参数与马赫数的关系或气动函数计算出第一道膨胀波后的压强、温度等参数。

第三步，以同样的方法求其他各区的气流参数，并注意到AB和CD为左伸波，而BC和 DE为右伸波。

6.3.2  膨胀波的相交

如果管道的上、下壁面在A，B处都向外转折一个有限角度δ，则超声速气流流过时，在A， B两点处均会产生一束膨胀波，它们的平均马赫波相交于点C，如图6.13所示。超声速气流流过AC,BC后，分别向外折转一个角度δ，沿波后壁面流动。②，③区气流参数分别可按膨胀波计算公式求得。②，③区气流方向不平行而在点C又一次膨胀，从而产生膨胀波CD和CE，气流经过这两道波后进入④区和⑤区，气流方向向内折转一个δ角，直到④，⑤两区气流方向一致，压强平衡为止。可见膨胀波相交时，在交点处必定又产生两道膨胀波。

同理可知，压缩波相交后仍然是压缩波。

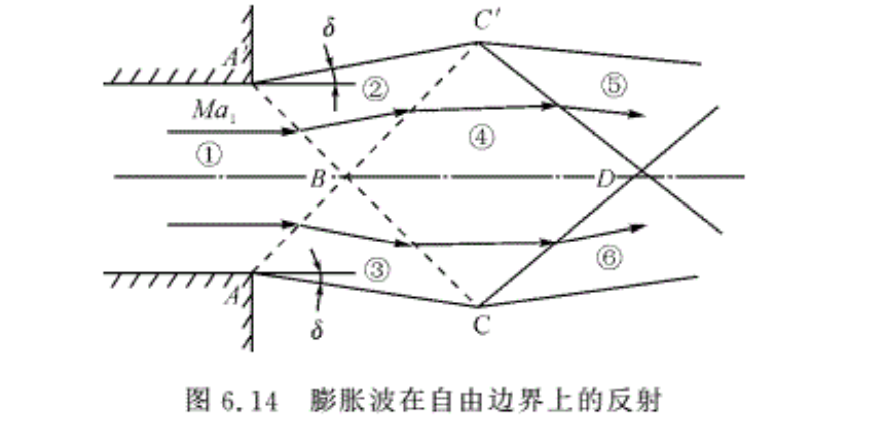
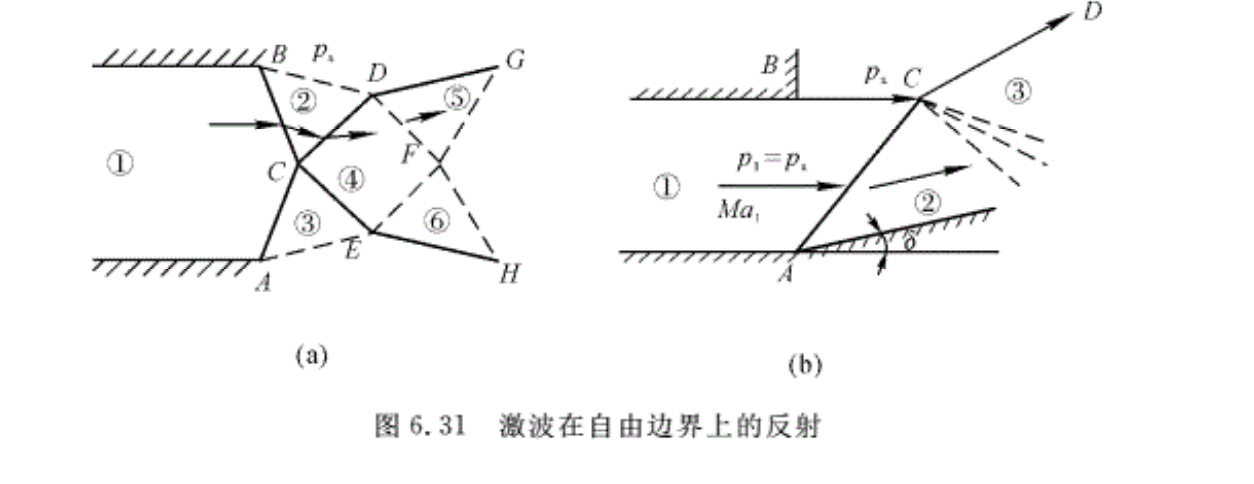
6.3.3  膨胀波在自由边界上的反射

运动介质与其他介质之间的切向（与速度平行的方向）交界面称为自由边界。自由边界上的特点是接触面两边的压强相等。

如果喷管出口截面的超声速气流其压强pe大于外界压强pa，则在喷管出囗产生膨胀波 AB和A’B（用平均马赫波代替），并交于点B(见图6.14)。气流经过膨胀波AB和A′B后，压强降到外界大气压强pa，并向外折转一个角度δ，AC和A′C′即是自由边界。气流流过点B之后必产生膨胀波BC和BC′。②、③区气流经膨胀波BC，BC’进入④区；并向内折转角度δ，且 p4<p2（或p3），即p4<pa。因为气流到自由边界上必须满足压强相等，所以气流过点C和C′后，必然受到压缩而产生压缩波，即气流经过压缩波CD和C’D后，速度降低，压强升高，气流方向向内折转δ角。由此可见，膨胀波遇到自由边界时，反射出压缩波。

由以上分析可知，喷管出囗之后的无黏性超声速流场是膨胀波和压缩波交替出现的流场，仍可以按逐区计算的方法计算各区的流动参数。

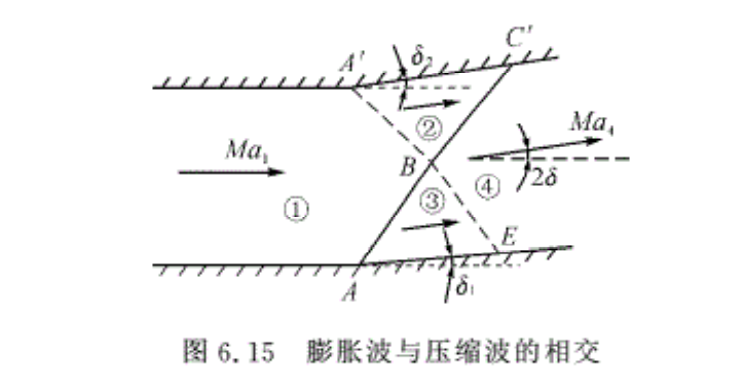
6.3.4  膨胀波与压缩波的相交

如果平面通道的上、下壁面都向上折转无限小角度δ1=δ2=δ,如图6.15所示，则在 AA’两处必分别产生膨胀波A’B和压缩波AB，两波相交于点B。在②区和③区内气流均向上偏转δ角。虽然这两区气流方向一致，但气流压强不等，即p2<p3。这两股气流平行地流下去是不可能的。在点B两股气流相遇后，②区的低压气流将受到③区高压气流压缩，而产生一道压缩波BC’；同时，③区高压气流必向低压气流膨胀，从而产生一道膨胀波BE。这样，高、低压区分别经过膨胀波BE和压缩波BC’后进入④区，它们的压强和气流方向都一致了。可以形象地看，膨胀波和压缩波相交时，两波可以相互穿过（波的方向要改变)。

研究了上述几种典型的膨胀波的相交与反射问题后，可以总结出处理这类问题的一个重要原则就是：在流场中的同一个区内，气流的方向一致，静压必须相等；不同方向，不同静压的超声速气流相接触必定会产生波。这个原则，在解决其他波的相交与反射问题时，同样也适用。

例6.3  已知膨胀波前气流参数为Ma1=2.0，T1=250 K，p1=1.8 × 10⁵ Pa，壁面向外转折δ=18°。求膨胀波后的气流参数。

解：以来流为准，θ1=0°，θ2=18°，膨胀波束系左伸波，由式（6.2），得

υ（Ma1）=θ2+υ（Ma2）

由Ma1=2.0查表，得

υ（Ma1）=26.5°

即

υ（Ma2）=18°+ 26.5°=44.5°

由膨胀波表查得，当υ（Ma2）=44.5°时，

Ma2=2.74，λ2=1.898

气流通过膨胀波是等熵过程，即T1*=T2*，p1*=p2*，由气动函数表，查得

π（λ1）=0.1278，τ（λ1）=0.5554

π（λ2）=0.0404，τ（λ2）=0.3995

所以

\(\begin{align}& {{T}_{2}}=T_{2}^{*}\tau \left( {{\lambda }_{2}} \right)=\frac{{{T}_{1}}}{\tau \left( {{\lambda }_{1}} \right)}\tau \left( {{\lambda }_{2}} \right)=\frac{0.3995}{0.5544}\times 250=179.8K \\& {{p}_{2}}=p_{2}^{*}\pi \left( {{\lambda }_{2}} \right)=\frac{{{p}_{1}}}{\pi \left( {{\lambda }_{1}} \right)}\pi \left( {{\lambda }_{2}} \right)=\frac{0.0404}{0.1278}\times 1.8\times {{10}^{5}}=0.569\times {{10}^{5}}Pa \\\end{align}\)

需要注意的是，当壁面折转角δ比较大时，或喷管出口截面压强pe比周围大气压强pa大得很多时，就不能用一道平均膨胀波来代替膨胀波束了，而应当用若干膨胀波来求解。在扇形区内取波数愈多，则解的精度愈高，但是计算工作量也将随之加大。

6.4  激波的形成及传播速度

激波是气体在超声速运动过程中最重要的现象之一。它是气体受到强烈压缩后产生的强压缩波，也叫强间断面*(即两侧气体参数发生间断的面），这种间断称之为激波。气流经过激波后，流速减小，相应的压强、温度和密度均升高。

由于气体经过激波时，气体参数在极短的瞬间和极短的距离内发生极大的变化，因此不但激波厚度很薄，而且参数变化的每一状态不可能是热力学平衡状态。这种过程必然是一个不可逆的耗散过程，因而必然会引起熵的增加，即气体经过激波是一个不可逆的绝热过程。在这个过程中，气体的黏性、热传导占有重要的地位，使得激波内部的结构非常复杂。本教材中研究激波时，都忽略激波的厚度（一般情况下，激波厚度大约是2.5 ×10^-5 cm），只研究激波前后气流参数的变化关系，不讨论其内部的复杂过程。

按照激波的形状，将激波分为以下几种．

（1）正激波：气流方向与波面垂直，如图6.16（a）所示；

（2）斜激波：气流方向与波面不垂直，如图6.16（b）所示；

（3）曲线激波：波形为曲线形，例如当超声速气流流过钝头物体时，在物体前面往往产生脱体激波，这种激波就是曲线激波，如图6.16（c）所示。

6.4.1  激波的形成

在第6.1节中讨论的是微弱压缩波，本节讨论的是强压缩波（或有限强度的扰动波），即激波。但是强压缩扰动波可以看成是由许多微弱压缩波在一定条件下累积形成的。现以活塞在半无限长直管内的加速运动为例来说明激波形成的物理过程。设想将活塞从静止状态加速到某一速度V的过程分解为若干阶段，每一阶段活塞只有一个微小的速度增量，因而产生微弱的压缩波。当活塞速度从零增加到∆V时，活塞左边的气体先受到压缩，其压强、密度、温度略有提高。所产生的压缩波的传播速度是尚未被压缩的气体中的声速c1。由于活塞以速度∆V移动，所以弱压缩波左边的气体被活塞推着也以同样的速度∆V向右移动。经历1 s后，压强有微小变化处就是弱压缩波所在位置，如图6.17(b)所示。

之后，活塞速度由∆V增加到2∆V，在管内便产生第二道弱压缩波。第二道弱压缩波的传播速度是c2+∆V（绝对速度），由于该波是在第一道压缩波后的气流中传播，因此c2>c1，可见第二道波的传播速度必大于第一道波的传播速度，到第二秒末，管内气体压强分布如图6.17（c）所示。

依此类推，活塞每加速一次，在管内就多一道微弱压缩波（见图6.17（d）），每道波总是在经过前几次压缩后的气体中以当地声速相对于气体向右传播。气体每受到一次压缩，声速便增大一次，而且随活塞速度的增大，活塞附近的气体跟随活塞一起向右移动的速度也增加，所以后面产生的微弱压缩波的传播速度必定比前面的快。

经过若干次加速，活塞速度达到了V，在管内形成了若干道微弱压缩波，因为后面的波比前面的波传播得快，波与波之间距离逐渐缩小。最终，后面的波赶上了前面的波，使所有这些微压缩波汇集成一道强的压缩波（即激波）。只要活塞仍以不变的速度V继续运动，在管内就能维持一个强度不变的激波。

从以上讨论可以看出，气体被压缩而产生的一系列压缩波聚集在一起，就转化为一道激波。这种量的变化引起了质的飞跃，使激波的性质与微弱压缩波有着本质的区别。其主要表现如下．

（1）激波是强压缩波，经过激波的气流参数变化是突跃的；

（2）气体经过激波受到突然、强烈地压缩，必然在气体内部造成强烈的摩擦和热传导，因此气流经过激波是绝能不等熵流动；

（3）激波的强弱与气流受压缩的程度（或扰动的强弱）有直接关系。

6.4.2  激波的传播速度

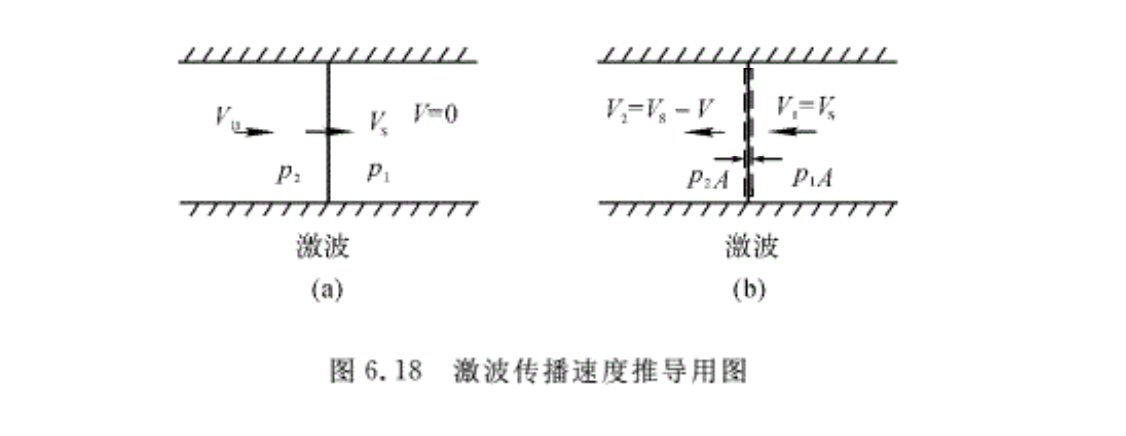
现以在管内产生的激波为例，导出激波的传播速度。

图6.18（a）表示由于活塞的加速运动，在管内气体中形成的激波在某一瞬时的位置。用Vs和VB分别代表激波传播速度和激波后气体向右的运动速度，即活塞向右移动的速度。为了把非定常流动转化为定常流动，和讨论声速的情况一样，在以激波速度Vs运动的相对坐标系中，激波相对于观察者是静止的，而整个流动则为定常的流动，图6.18（b）表示在相对坐标系中，定常流动的气体参数分布情况。取激波运动方向为x的方向，则激波前气流运动速度为-Vs，而波后的气流速度则为-（Vs-VB)，沿激波前后波面取控制体（即图6.18（b）中的虚线)。波前为1区，波后为2区，管道横截面积为A。对控制体沿x方向应用动量方程，得

\(A\left( {{p}_{2}}-{{p}_{1}} \right)={{q}_{m}}\left[ -\left( {{V}_{s}}-{{V}_{B}} \right)-\left( -{{V}_{s}} \right) \right]\)                (a)

由连续方程，可得

\({{q}_{m}}={{\rho }_{1}}{{V}_{s}}A={{\rho }_{1}}\left( {{V}_{s}}-{{V}_{B}} \right)A\)                (b)

即                                                \({{V}_{B}}=\frac{{{\rho }_{2}}-{{\rho }_{1}}}{{{\rho }_{2}}}{{V}_{s}}\)               (c)

由式（a）、式（b），可得

\(A\left( {{p}_{1}}-{{p}_{2}} \right)={{\rho }_{1}}{{V}_{s}}A\left[ \left( {{V}_{s}}-{{V}_{B}} \right)-{{V}_{s}} \right]\)

或                                          \({{V}_{s}}{{V}_{B}}=\frac{{{p}_{2}}-{{p}_{1}}}{{{\rho }_{1}}}\)                  (d)

将式（c）代入式（d），可得

\({{V}_{s}}=\sqrt{\frac{{{p}_{2}}-{{p}_{1}}}{{{\rho }_{2}}-{{\rho }_{1}}}\frac{{{\rho }_{2}}}{{{\rho }_{1}}}}=\sqrt{\frac{{{p}_{1}}}{{{\rho }_{1}}}\frac{\frac{{{p}_{2}}}{{{p}_{1}}}-1}{1-\frac{{{\rho }_{1}}}{{{\rho }_{2}}}}}={{c}_{1}}\sqrt{\frac{\frac{{{p}_{2}}}{{{p}_{1}}}-1}{k\left( 1-\frac{{{\rho }_{1}}}{{{\rho }_{2}}} \right)}}\)                (6.11)

代入式（d），可得

\({{V}_{B}}=\sqrt{\frac{\left( {{p}_{2}}-{{p}_{1}} \right)\left( {{\rho }_{2}}-{{\rho }_{1}} \right)}{{{\rho }_{2}}{{\rho }_{1}}}}=\sqrt{\frac{{{p}_{1}}}{{{\rho }_{1}}}\left( \frac{{{p}_{2}}}{{{p}_{1}}}-1 \right)\left( 1-\frac{{{\rho }_{1}}}{{{\rho }_{2}}} \right)}\)               (6.12)

从式（6.11)可以看出激波的传播速度与激波前、后的气流参数间的关系。显然随着激波强度的增加（即p2/p1或ρ2/ρ1的值加大），激波的传播速度也增加。若激波强度很弱很弱（即p2/p1→1，或ρ2/ρ1→1)，此时激波己成为微弱压缩波，波前、波后的气体参数变化关系为等熵关系。例如，式（6.11)中，

\[\begin{align}
& \frac{{{p}_{2}}-{{p}_{1}}}{{{\rho }_{2}}-{{\rho }_{1}}}=\frac{\Delta p}{\Delta \rho }\to {{\left( \frac{dp}{d\rho } \right)}_{s}}={{c}^{2}} \\
& \frac{{{\rho }_{2}}}{{{\rho }_{1}}}\to 1 \\
\end{align}\]

所以                                              \({{V}_{s}}\to \sqrt{{{\left( \frac{dp}{d\rho } \right)}_{s}}}=c\)

可见，当激波很弱时，其传播速度为声速，这时激波已转化为微压缩波了。若激波无限增强时，即p2/p1→∞，ρ2/ρ1→(k+1)/(k-1)（参看后文介绍的朗金一雨贡纽关系式），由式（6.11）可以推出Vs→∞。可见，随激波强度的增加，激波的传播速度加大，当激波无限增加时，其传播速度趋向无限大；实际中所产生的激波强度增加是有限的，因此，激波是以一定的超声速的速度在气体中传播的。

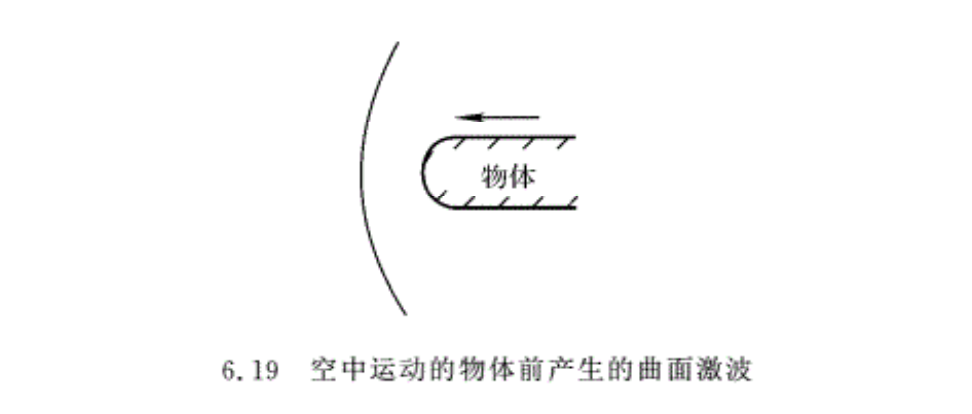
在图6.17所示的气缸中，只要物体作加速度运动，就能在管内气体中产生激波。当物体在大气中运动时，只有当物体以超声速运动时，才有可能形成稳定的激波。因为波后气流没有像图6.17（a）所示气缸侧壁的限制，所以气体能够自由地向四周运动，从而使得波后气体压强降低，激波强度减弱，如图6.19所示。若物体运动速度V小于Vs，则物体与激波间的距离逐渐加大，波后向四周运动的气体也加多，所以波后气体压强逐渐降低，激波逐渐减弱，直到最后消失。只有物体的运动速度与激波传播速度相同时，才能维持物体与激波之间相对位置不变，而形成稳定的激波。在图6.19所示中，在物体上、下两侧较远处，因为波后气流压强的沟通，故激波强度随气体横向流动而越来越弱，从而形成曲面激波，通常为弓形波。

例6.4  设长管中静止空气的参数为p1=9.81 × 10⁴Pa，ρ1=1.225 kg/m³，T1=288 K。经活塞压缩后，在气体中产生一道激波，波后空气的参数为p2=1.765 × 10⁵Pa,ρ2=1.85 kg/m³。求激波的传播速度和激波后空气的运动速度，并与气体中的声速比较。

解：由式（6.11)和式（6.12），可得

\[\begin{align}& {{V}_{s}}=\sqrt{\frac{\left( {{p}_{2}}-{{p}_{1}} \right)}{\left( {{\rho }_{2}}-{{\rho }_{1}} \right)}\frac{{{\rho }_{2}}}{{{\rho }_{1}}}}=\sqrt{\frac{\left( 1.765-0.981 \right)\times {{10}^{5}}\times 1.85}{\left( 1.85-1.225 \right)\times 1.225}}=435m/s \\& {{V}_{B}}=\sqrt{\frac{\left( {{p}_{2}}-{{p}_{1}} \right)\left( {{\rho }_{2}}-{{\rho }_{1}} \right)}{{{\rho }_{1}}{{\rho }_{2}}}}=\sqrt{\frac{\left( 1.765-0.981 \right)\times {{10}^{5}}\times \left( 1.85-1.225 \right)}{1.225\times 1.85}}=147m/s \\\end{align}\]

而激波前气体中的声速为

\[{{c}_{1}}=\sqrt{kR{{T}_{1}}}=\sqrt{1.4\times 287.06\times 288}=340m/s\]

由此例题可以看出，激波传播速度大于激波前气体中的声速，即激波传播速度大于微压缩波在气体中的传播速度。

6.4.3  斜激波的形成

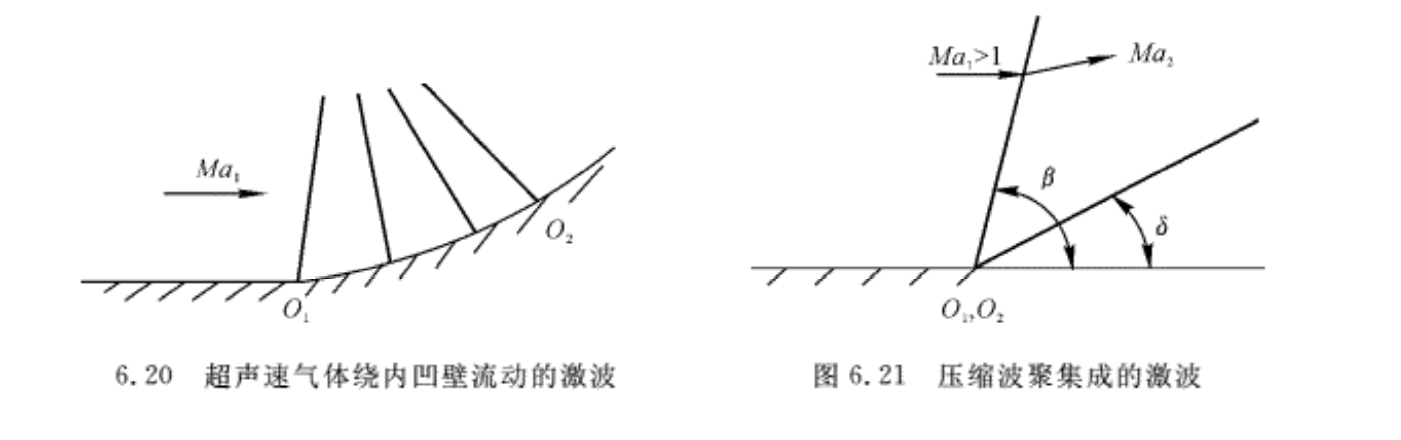
当超声速气流被压缩时，即当超声速气流沿内凹壁流动，或自低压区流向高压区时，就会在折转点产生强压缩波即激波。实际上，当超声速气流流过内凹的曲壁时（见图6.20），曲壁上的每一个点都相当于一个折点，而每一个折点都发出一道微弱压缩波。如果把曲壁O1O2 逐渐靠近，极限情况下O2与O1重合，即形成了如图6.21所示的情况，这些微弱的压缩波聚集在一起，就形成一道斜激波。

斜激波波面与波前来流方向的夹角定义为激波角，用β表示，如图6.21所示。

当β=90°时，斜激波变为正激波，激波强度最大。

当β=arcsin（1/Ma1）时，激波退化为马赫波，且激波强度最小。一般斜激波的激波角β变化范围为

arcsin（1/Ma1）＜β＜π/2

6.5  激波计算公式

6.5.1  激波前、后参数之间的关系

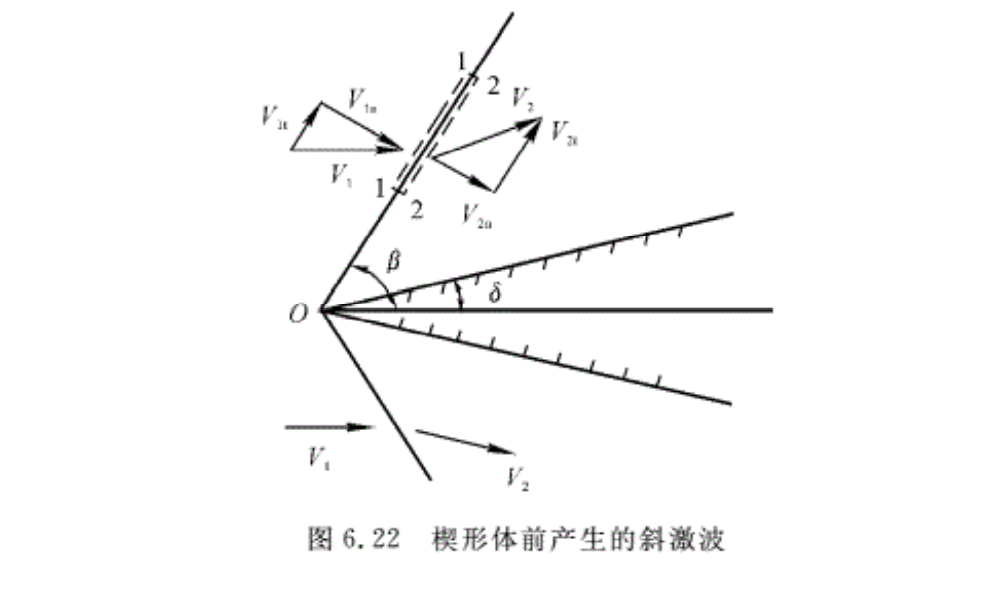
对于超声速气流流过如图6.22所示的半顶角为δ的楔形体，在O点产生一道斜激波，经过斜激波后，气流折转δ角而沿楔面流动。沿斜激波取控制体11一22，将激波前、后气流速度分解为平行于波面的分量V1t，V2t和垂直于波面的分量V1n，V2n。对所取的控制体可与出下列基本方程：

连续方程           \({{\rho }_{1}}{{V}_{1n}}={{\rho }_{2}}{{V}_{2n}}\)           （6.13）

动量方程：法向                     \({{p}_{1}}-{{p}_{2}}={{\rho }_{1}}V_{2n}^{2}-{{\rho }_{1}}V_{1n}^{2}\)                (6.14)

                 切向                     \({{\rho }_{1}}{{V}_{1n}}{{V}_{1t}}={{\rho }_{2}}{{V}_{2n}}{{V}_{2t}}\)

即                                         \({{V}_{1t}}={{V}_{2t}}\)               (6.15)

能量方程                               \({{c}_{p}}{{T}_{1}}+\frac{V_{1}^{2}}{2}={{c}_{p}}{{T}_{2}}+\frac{V_{2}^{2}}{2}\)                (6.16)

或                                         \({{c}_{p}}{{T}_{1}}+\frac{V_{1n}^{2}}{2}={{c}_{p}}{{T}_{2}}+\frac{V_{2n}^{2}}{2}\)                  (6.17)

状态方程                               \(p=\rho RT\)                 (6.18)

由式（6.13）~式（6.17）可以看出，超声速气流经过斜激波时，气流平行于波面的切向分速度不变，而法向分速度则要减小，且气流向着波面折转。

显然，对于正激波，V1t=V2t=0。因此，将以上各式中的法向分速度换成速度V，则得到正激波前后的基本关系式为

ρ1V1=ρ2V2               (6.19)

\({{p}_{1}}-{{p}_{2}}={{\rho }_{2}}V_{2}^{2}-{{\rho }_{1}}V_{1}^{2}\)             (6.20)

\({{V}_{1t}}={{V}_{2t}}=0\)             (6.21)

\({{c}_{p}}{{T}_{1}}+\frac{V_{1}^{2}}{2}={{c}_{p}}{{T}_{2}}+\frac{V_{2}^{2}}{2}\)             (6.22)

6.5.2  基本方程

1.朗金一雨贡纽关系式

朗金一雨贡纽（Rankine一Hugoniot）关系式揭示了激波前后压强比、密度比、温度比之间的关系。从斜激波前后的连续方程、动量方程和能量方程式（6.13）~式（6.18）可导出朗金一雨贡纽关系式。

将状态方程式（6.18）代入能量方程式（6.17），得

\(\frac{k}{k-1}\left( \frac{{{p}_{2}}}{{{\rho }_{2}}}-\frac{{{p}_{1}}}{{{\rho }_{1}}} \right)=\frac{1}{2}\left( V_{1n}^{2}-V_{2n}^{2} \right)\)                     (a)

又根据动量方程式（6.14）和连续方程式（6.13），得

\[{{p}_{1}}-{{p}_{2}}={{\rho }_{1}}V_{1n}^{2}-{{\rho }_{2}}V_{2n}^{2}={{\rho }_{1}}V_{1n}^{2}\left( 1-\frac{{{\rho }_{1}}}{{{\rho }_{2}}} \right)\]

解得                                    \(V_{1n}^{2}=\frac{{{p}_{2}}-{{p}_{1}}}{{{\rho }_{2}}-{{\rho }_{1}}}\frac{{{\rho }_{2}}}{{{\rho }_{1}}}\)                 (b)

同理可得                             \(V_{2n}^{2}=\frac{{{p}_{2}}-{{p}_{1}}}{{{\rho }_{1}}-{{\rho }_{2}}}\frac{{{\rho }_{1}}}{{{\rho }_{2}}}\)                 (c)

将式（b）、式（c）两式代入式（a），得

\[\frac{2k}{k-1}\left( \frac{{{p}_{2}}}{{{\rho }_{2}}}-\frac{{{p}_{1}}}{{{\rho }_{1}}} \right)=\frac{{{p}_{2}}-{{p}_{1}}}{{{\rho }_{2}}-{{\rho }_{1}}}\left( \frac{{{\rho }_{2}}}{{{\rho }_{1}}}-\frac{{{\rho }_{1}}}{{{\rho }_{2}}} \right)\]

最后化简，解得

\[\frac{{{p}_{2}}}{{{p}_{1}}}=\frac{\left( k+1 \right)\frac{{{\rho }_{2}}}{{{\rho }_{1}}}-\left( k-1 \right)}{\left( k+1 \right)-\left( k-1 \right)\frac{{{\rho }_{2}}}{{{\rho }_{1}}}}\]             (6.23a)

类似地，有

\[\frac{{{\rho }_{2}}}{{{\rho }_{1}}}=\frac{\left( k+1 \right)\frac{{{p}_{2}}}{{{p}_{1}}}+\left( k-1 \right)}{\left( k+1 \right)+\left( k-1 \right)\frac{{{p}_{2}}}{{{p}_{1}}}}\]              (6.23b)

\[\frac{{{T}_{2}}}{{{T}_{1}}}=\frac{\frac{{{p}_{2}}}{{{p}_{1}}}\left[ \left( k+1 \right)+\left( k-1 \right)\frac{{{p}_{2}}}{{{p}_{1}}} \right]}{\left( k+1 \right)\frac{{{p}_{2}}}{{{p}_{1}}}+\left( k-1 \right)}\]               (6.23c)

以上三式称为朗金一雨贡纽关系式。三式中均不包含激波角β。即对任一激波，其一定的压强比对应着一定的密度比和温度比。以上三式既适合于斜激波，也适合于正激波。

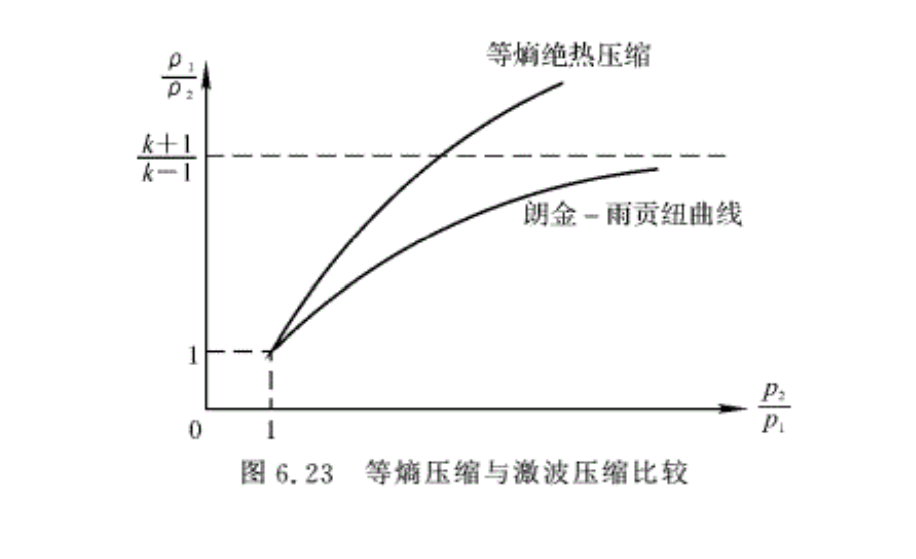
图6.23给出了等熵绝热压缩过程曲线和激波压缩曲线，比较两条曲线可得如下结论：

（1）对于微弱压缩波（即当p2/p1=1时），这两条曲线都可得到ρ2/ρ1=0，即只有对微弱压缩波，不等熵压缩过程才无限接近等熵压缩过程。两条曲线在点（1，1 )处的斜率相等。

（2）当激波强度p2/p1无限增大时，激波前后的密度比ρ2/ρ1最多增加到(k+1)/(k-1)，而对于等熵绝热压缩过程，理论上ρ2/ρ1可以足够大。

（3）由图6.23可以看出，若压缩前气体状态相同，压缩到相同的p2/p1，经过激波压缩的ρ2/ρ1小于等熵压缩的ρ2/ρ1，即等熵压缩比激波压缩更有效。

2.普朗特关系式

普朗特Prandtl关系式反映了激波前、后速度的关系。由基本方程式（6.13）和式（6.14），可得

\[{{V}_{1n}}-{{V}_{2n}}=\frac{{{p}_{2}}}{{{\rho }_{2}}{{V}_{2n}}}-\frac{{{p}_{1}}}{{{\rho }_{1}}{{V}_{1n}}}\]            （a）

将式（6.18）代入能量方程式（6.16），得

\[\frac{k}{k-1}\frac{{{p}_{1}}}{{{\rho }_{1}}}+\frac{V_{1}^{2}}{2}=\frac{k}{k-1}\frac{{{p}_{2}}}{{{\rho }_{2}}}+\frac{V_{2}^{2}}{2}=\frac{kR{{T}^{*}}}{k-1}=\frac{k+1}{2\left( k-1 \right)}c_{cr}^{2}\]               (b)

由式（b）可解得

\[\frac{{{p}_{1}}}{{{\rho }_{1}}}=\frac{k+1}{2k}c_{cr}^{2}-\frac{k-1}{2k}V_{1}^{2}\]             (c)

\[\frac{{{p}_{2}}}{{{\rho }_{2}}}=\frac{k+1}{2k}c_{cr}^{2}-\frac{k-1}{2k}V_{2}^{2}\]                 (d)

将式（c）、式（d）代入式（a），整理后得

\[{{V}_{1n}}{{V}_{2n}}=c_{cr}^{2}-\frac{k-1}{k+1}V_{t}^{2}\]            (6.24)

式（6.24）称为普朗特关系式。

对于正激波，Vt=0，普朗特关系式为

\[{{V}_{1}}{{V}_{2}}=c_{cr}^{2}\]

或                                        λ1λ2=1             （6.25）

因为正激波前气流的速度因数λ1> 1，由式（6.25）可见，波后的速度因数λ2 < 1，即相对于正激波，波后的气流永远是亚声速的。同理，对斜激波波前气流的法向分速度必定是超声速的，波后的法向分速度则是亚声速的。但斜激波后的合成速度可能是超声速的，也可能是亚声速的。

例6.5  利用动量方程证明式（6.25）。

证明：对围绕正激波所取的控制体写出动量方程，忽略控制体侧面上的黏性力，根据

\[{{F}_{i}}=\frac{k+1}{2k}{{c}_{cr}}{{q}_{m}}\left[ z\left( {{\lambda }_{2}} \right)-z\left( {{\lambda }_{1}} \right) \right]\]

因为Fi=0，故可得z（λ2）= z（λ1），此方程有两个解，即λ2=λ1和λ1λ2=1。其中第一个解对正激波无意义，而第二个解即为式（6.25）。

6.5.3  激波计算公式

除了上面给出的一些激波计算公式之外，为了计算方便，这里给出另外一些常用的激波计算公式。

1.正激波参数计算

对于正激波，由连续方程式ρ2/ρ1=V1/V2和普朗特关系式V1V2=c²(cr)联立，可导出如下关系式：

\[\frac{{{V}_{2}}}{{{V}_{1}}}=\frac{2}{k+1}\frac{1}{Ma_{1}^{2}}+\frac{k-1}{k+1}=\frac{2+\left( k-1 \right)Ma_{1}^{2}}{\left( k+1 \right)Ma_{1}^{2}}\]       （a）

再将式（a）代入连续方程得正激波前、后的密度比和速度比与Ma1的关系，即

\[\frac{{{\rho }_{2}}}{{{\rho }_{1}}}=\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{\left( k+1 \right)Ma_{1}^{2}}{2+\left( k-1 \right)Ma_{1}^{2}}\]              （6.26）

由动量方程式（6.20)、连续方程式（6. 19）、状态方程和式（a）联立，可得

\[\frac{{{p}_{2}}}{{{p}_{1}}}=\frac{2k}{k+1}Ma_{1}^{2}-\frac{k-1}{k+1}\]       （6.27）

由式（6.18）、式（6.26）、式（6.27），可得

\[\frac{{{T}_{2}}}{{{T}_{1}}}=\frac{1}{Ma_{1}^{2}}{{\left( \frac{2}{k+1} \right)}^{2}}\left( kMa_{1}^{2}-\frac{k-1}{2} \right)\left( 1+\frac{k-1}{2}Ma_{1}^{2} \right)\]              （6.28）

由式（6.26）~式（6.28）可以看出，当Ma1≥1时，p2/p1≥1，ρ2/ρ1≥1，T2/T1≥1，即激波过程一定是压缩过程，气流经过激波后，压强、温度和密度增大。进一步还可以看出，对于正激波，当比热比k一定时，激波前后的密度比、压强比和温度比只决定于来流的马赫数，来流马赫数越大，激波越强。当来流马赫数趋近于1时，p2/p1，ρ2/ρ1，T2/T1趋近于1，此时激波退化为马赫波。

气流通过激波为绝能流动，即总温保持不变，因此

\[\frac{{{T}_{2}}}{{{T}_{1}}}=\frac{{{T}_{2}}/{{T}^{*}}}{{{T}_{1}}/{{T}^{*}}}=\frac{1+\frac{k-1}{2}Ma_{1}^{2}}{1+\frac{k-1}{2}Ma_{2}^{2}}\]            （6.29）

对于正激波，将式（6.28）代入式（6.29），得激波前、后马赫数之间的关系为

\[Ma_{2}^{2}=\frac{Ma_{1}^{2}+\frac{2}{k-1}}{\frac{2k}{k-1}Ma_{1}^{2}-1}\]         （6.30）

由式（6.30）可见，Ma1 > 1，必有Ma2 < 1；再次证明了正激波后一定是亚声速的。Ma1愈大，Ma2则愈小，激波压缩也愈强。

根据总、静参数与Ma的关系，即

\[\frac{p_{2}^{*}}{{{p}_{2}}}={{\left( 1+\frac{k-1}{2}Ma_{2}^{2} \right)}^{\frac{k}{k-1}}}\]           （b）

\[\frac{p_{1}^{*}}{{{p}_{1}}}={{\left( 1+\frac{k-1}{2}Ma_{1}^{2} \right)}^{\frac{k}{k-1}}}\]              （c）

得                                               \(\frac{p_{2}^{*}}{p_{1}^{*}}=\frac{p_{2}^{*}}{{{p}_{2}}}\frac{{{p}_{2}}}{{{p}_{1}}}\frac{{{p}_{1}}}{p_{1}^{*}}\)                     (d)

将式（b）、式（c）和式（6.27）代入式（d），得正激波前、后的总压比为

\[\sigma =\frac{p_{2}^{*}}{p_{1}^{*}}=\frac{{{\left[ \frac{\left( k+1 \right)Ma_{1}^{2}}{2+\left( k-1 \right)Ma_{1}^{2}} \right]}^{\frac{k}{k-1}}}}{{{\left[ \frac{2k}{k+1}Ma_{1}^{2}-\frac{k-1}{k+1} \right]}^{\frac{1}{k-1}}}}\]   （6.31）

气体通过激波，熵的变化为

\[{{s}_{2}}-{{s}_{1}}=-R\ln \frac{p_{2}^{*}}{p_{1}^{*}}\]          （6.32）

显然有                               s2-s1＞0

即通过激波，气体的熵必增大。超声速气流经过激波时，气流受到剧烈的压缩，在激波内部存在着剧烈的热传导和黏性作用，该过程是个不可逆的绝热压缩过程，气流做功能力下降，熵增加。

2.斜激波前、后参数的计算

由图6. 22所示的几何关系可以看出,斜激波前的法向马赫数Ma 1n=Ma1sinβ，将Ma 1n代替式( 6.26 ) ~式( 6.28 )中的Ma1 ,可得到斜激波前、后的关系式,即

\[\frac{{{\rho }_{2}}}{{{\rho }_{1}}}=\frac{\left( k+1 \right)Ma_{1}^{2}{{\sin }^{2}}\beta }{2+\left( k-1 \right)Ma_{1}^{2}{{\sin }^{2}}\beta }\]           （6.33）

\[\frac{{{p}_{2}}}{{{p}_{1}}}=\frac{2k}{k+1}Ma_{1}^{2}{{\sin }^{2}}\beta -\frac{k-1}{k+1}\]                （6.34）

\[\frac{{{T}_{2}}}{{{T}_{1}}}=\frac{1}{Ma_{1}^{2}{{\sin }^{2}}\beta }{{\left( \frac{2}{k+1} \right)}^{2}}\left( kMa_{1}^{2}{{\sin }^{2}}\beta -\frac{k-1}{2} \right)\left( 1+\frac{k-1}{2}Ma_{1}^{2}{{\sin }^{2}}\beta  \right)\]          （6.35）

显然,对于斜激波,波前、后的密度比、压强比和溫度比只决定于波前的法向马赫数,波前的法向马赫数越大,激波也愈强。

将式( 6. 35 )代入式( 6.29 )等号的左边,经整理可得

\[Ma_{2}^{2}=\frac{Ma_{1}^{2}+\frac{2}{k-1}}{\frac{2k}{k-1}Ma_{1}^{2}{{\sin }^{2}}\beta -1}+\frac{Ma_{1}^{2}{{\cos }^{2}}\beta }{\frac{k-1}{2}Ma_{1}^{2}{{\sin }^{2}}\beta +1}\]             （6.36）

显然,当来流马赫数一定时,随着激波角β的增加,波后的马赫数减小。

将Ma 1n= Ma1sinβ代替式( 6. 31 )中的马赫数,可得斜激波前、后的总压比为

\[\frac{p_{2}^{*}}{p_{1}^{*}}=\frac{{{\left[ \frac{\left( k+1 \right)Ma_{1}^{2}{{\sin }^{2}}\beta }{2+\left( k-1 \right)Ma_{1}^{2}{{\sin }^{2}}\beta } \right]}^{\frac{k}{k-1}}}}{{{\left[ \frac{2k}{k+1}Ma_{1}^{2}{{\sin }^{2}}\beta -\frac{k-1}{k+1} \right]}^{\frac{1}{k-1}}}}\]              （6.37）

由式( 6. 36 )和式( 6.37 )可以看出,随着斜激波前的法向马赫数的增大,通过激波的总压恢复因数σ=p2*/p*下降,即激波越强,通过激波损失越大;当Ma1sinβ=1时,p2*=p1*,此时激波退化为弱压缩波。通过斜激波的熵仍可按式( 6. 32 )计算。

通过斜激波,气流的方向必有折转。事实上,斜激波的强度除了取决于Ma1和波前状态外,还取决于通过激波气流的偏转角。很显然,当Ma1及波前状态不变时,波后气流偏转角越大,激波强度也越大(即对来流的压缩也越强)。所以,对于斜激波来说,除M及波前状态之外,尚须给定气流偏转角δ与激波角β之间的关系,即建立Ma1, δ和β的关系式。据图6. 22 所示的几何关系,考虑到V1t=V2t ,可得

\[\frac{{{V}_{2n}}}{{{V}_{1n}}}=\frac{\tan \left( \beta -\delta  \right)}{\tan \left( \beta  \right)}\]             （6.38）

将式( 6.13 )及式( 6. 33 )代入式( 6. 38 ) ,得

\[\frac{\tan \left( \beta -\delta  \right)}{\tan \left( \beta  \right)}=\frac{{{\rho }_{1}}}{{{\rho }_{2}}}=\frac{2}{k+1}\frac{1}{Ma_{1}^{2}{{\sin }^{2}}\beta }+\frac{k-1}{k+1}\]               （a）

由三角函数公式

\[\tan \left( \beta -\delta  \right)=\frac{\tan \left( \beta  \right)-\tan \left( \delta  \right)}{1+\tan \left( \beta  \right)\tan \left( \delta  \right)}\]     （b）

将式( b )代入式( a ) ,化简可得

\[\tan \delta =\frac{Ma_{1}^{2}{{\sin }^{2}}\beta -1}{\left[ Ma_{1}^{2}\left( \frac{k+1}{2}-{{\sin }^{2}}\beta  \right)+1 \right]\tan \beta }\]         （6.39）

式（6.39）表示，附体斜激波的波后气流折转角δ与来流Ma1和激波角β有关，对于一定的气体，三个变量Ma1，δ和β，己知其中任意两个，则可求出第三个。通常Ma1和δ是己知的，于是可确定β。

从式（6.39）可以推出如下参数变化规律：

（1）当δ=0时，Ma 1n= Ma1sinβ=1。说明此斜激波已退化成弱的压缩波了，β→μ（马赫角）。

（2）当Ma1和δ(即楔形角）一定时，可以解出两个大小不同的激波角β1和β2。它们代表两个强度不等的斜激波。

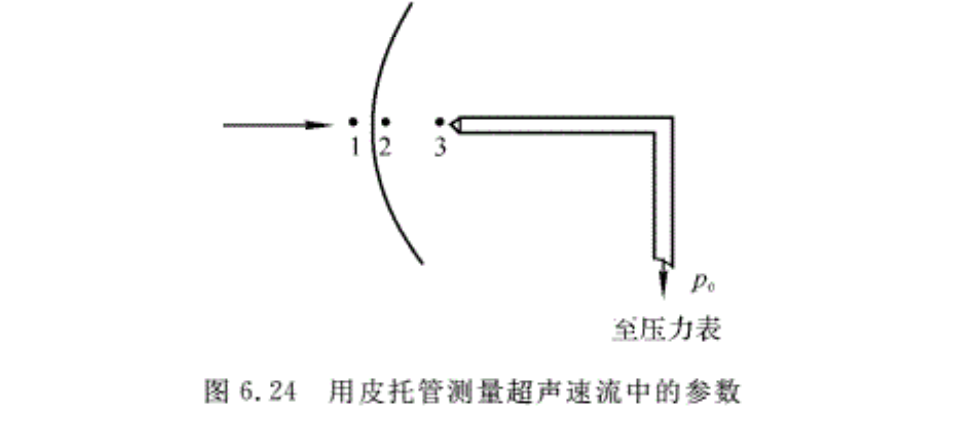
例6.6  超声速皮托管（总压管）测量高速气流中的马赫数和流速。

解：在高速气流中，皮托管前驻点上的密度与来流密度相比有较大的增量。若来流为定常亚声速气流，则可由皮托管总静压孔，测出p*及p，并根据p*，p与Ma的关系式求出Ma。要计算流速，尚须测量出驻点温度。对定常的超声速流动，皮托管只能测出波后总压p2*，欲由此计算气流Ma，尚须出波前压强p1。

首先对流动过程进行分析，然后根据相互关系进行求解。气流由图6.24中的点1到点2 通过激波的流动过程是一绝热过程，由点2到点3为一等熵过程，由于探头点3是驻点，故该点压强相当于激波后气流的滞止压强p2*。

气流经过正激波后，压强与马赫数的变化关系为

\[\frac{{{p}_{2}}}{{{p}_{1}}}=\frac{2k}{k+1}Ma_{1}^{2}-\frac{k-1}{k+1}\]

波后总压p2*与波前压强p1的关系，可写成

\[\frac{p_{2}^{*}}{p_{1}^{{}}}=\frac{p_{2}^{*}}{{{p}_{2}}}\frac{p_{2}^{{}}}{p_{1}^{{}}}={{\left( 1+\frac{k-1}{2}Ma_{2}^{2} \right)}^{\frac{k}{k-1}}}\left( \frac{2k}{k+1}Ma_{1}^{2}-\frac{k-1}{k+1} \right)\]

利用激波前、后马赫数之间的关系式（6.30），上式可写成

\[\frac{p_{2}^{*}}{p_{1}^{{}}}={{\left( \frac{k+1}{2}Ma_{1}^{2} \right)}^{\frac{k}{k-1}}}{{\left( \frac{2k}{k+1}Ma_{1}^{2}-\frac{k-1}{k+1} \right)}^{\frac{-1}{k-1}}}\]          （6.40）

测出p2*和p1后，由式（6.40）可计算出波前马赫数，要计算流速，还须测量出驻点温度。

例6.7  已知ρ1=1.6 kg／m³，p1=68.95 × 10³Pa的完全气体经正激波后，速度从V1=456 m／s降低到V2=152 m/s。试求气体的比热比k。

解：根据正激波关系式，可得

ρ2=ρ1V1/V2=1.6 x 456 / 152=4.8kg/m³

由动量方程

\[{{p}_{1}}-{{p}_{2}}={{\rho }_{2}}V_{2}^{2}-{{\rho }_{1}}V_{1}^{2}\]

得

\[{{p}_{2}}={{p}_{1}}-{{\rho }_{2}}V_{2}^{2}+{{\rho }_{1}}V_{1}^{2}=68.95\times {{10}^{3}}-4.8\times {{152}^{2}}+1.6\times {{456}^{2}}=2.9075\times {{10}^{5}}Pa\]

由能量方程

\[{{c}_{p}}{{T}_{1}}+\frac{V_{1}^{2}}{2}={{c}_{p}}{{T}_{2}}+\frac{V_{2}^{2}}{2}\]

得

\[\frac{k}{k-1}\frac{{{p}_{1}}}{{{\rho }_{1}}}+\frac{V_{1}^{2}}{2}=\frac{k}{k-1}\frac{{{p}_{2}}}{{{\rho }_{2}}}+\frac{V_{2}^{2}}{2}\]

即

\[\frac{k}{k-1}\left( \frac{{{p}_{2}}}{{{\rho }_{2}}}-\frac{{{p}_{1}}}{{{\rho }_{1}}} \right)=\frac{V_{1}^{2}-V_{2}^{2}}{2}=\frac{{{456}^{2}}-{{152}^{2}}}{2}=92416\]

进一步解得                                       k=1.213

6.5.4  激波曲线和激波表

1.激波曲线

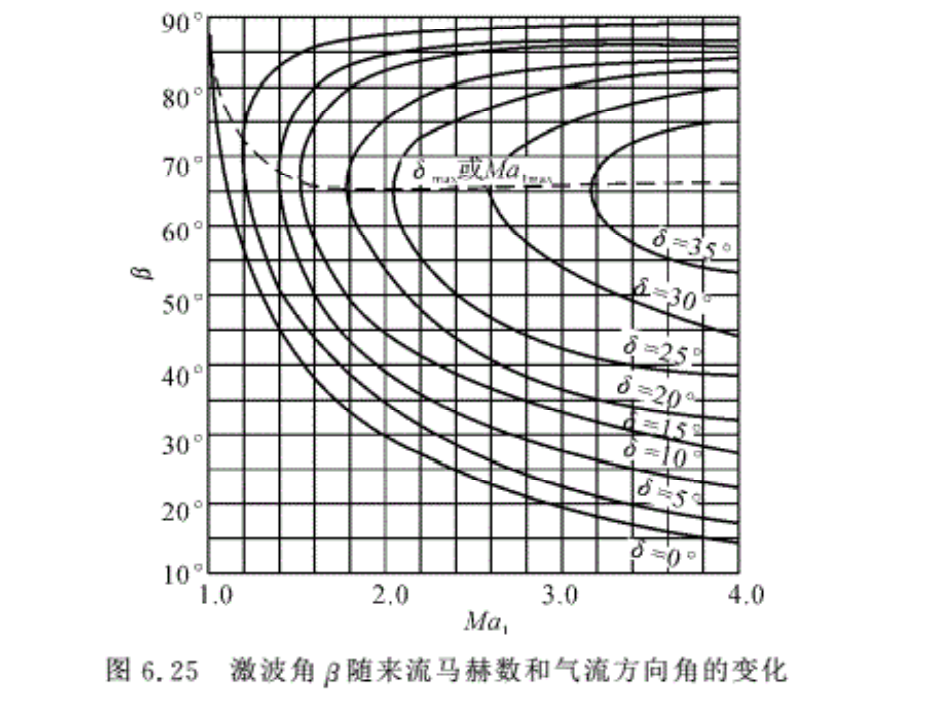
在6.5.3小节介绍的激波计算公式，都是比较复杂的。工程上为了方便计算，通常是将激波各个参数间的依赖关系用曲线和表格清楚地表示出来，通常把来流Ma1和气流折转角δ作为自变量来绘制各激波曲线和图表。

图6.25表示了式（6.39）中的β，Ma1和δ的变化关系（k=1.4）。下面仅讨论曲线下半支。从图中曲线可以看出如下的一些规律：

（1）当δ=0时，激波退化为马赫波，即相当于微弱压缩波的情况，β随来流Ma1的增加而减小（即最下边的曲线）。对于正激波，β不随来流Ma1改变，当β=90°时，β与Ma1的关系曲线为过β=90°的水平直线。

（2）在相同的Ma1下，当波后气流折转角δ一定时，可有两个大小不等的激波角β。β越大，p2/p1值越高，表示激波越强。因此β大代表强的斜激波，β小则代表弱的斜激波。实际流动中究竟是弱激波还是强激波视具体情况而定。一般情况下，工程中由于壁面折转产生的附体激波可视为弱激波；当超声速气流从低压区流向高压区时，所产生的激波可能为弱激波也可能为强激波，可根据激波前、后压强比的大小确定。图6.25中所示的虚线上方部分为强激波区，虚线下方部分为弱激波区。

（3）对于弱激波区，当δ一定时，激波角随着波前来流Ma1的增大而减小。对于强激波区则相反。

（4）当β一定时，δ随Ma1的增加而加大，即要产生相同的激波角，尖楔的角度必须随来流马赫数的增加而增大。

（5）当Ma1一定时，必有一个相应的δmax存在。如果δ<δmax，则产生附体斜激波，如图6.26所示。如果δ>δmax，则曲线与过Ma1的垂线无交点，即说明式（6.39）此时无解。其物理意义，就是不可能产生附体斜激波而只能产生一个脱体的曲线激波，如图6.27所示。

（6）当δ一定时，存在一个最小的来流Ma1 min，如果Ma1 <Ma1 min，式（6.39）也无解。此时也产生一个脱体激波。脱体激波的β沿波面是逐渐变化的，在楔形体正前方近似正激波，激波角最大，激波最强，沿波面向两侧逐渐减弱，最后退化成微弱压缩波。图6.25中的虚线表示在各Ma1数值下，对应的δmax或是在各δ数值下Ma1 min点的连线。连线之下的曲线即为弱斜激波区，之上则为强斜激波。

同样，根据式（6.34）、式（6.36）、式（6.37）和式（6.39），可以计算得出激波前后的压力比、总压比和波后马赫数随来流马赫数和气流方向角的变化规律。这些变化规律可以绘制成类似的图线，这些关系曲线己经通过编程计算得出正激波表和斜激波表，计算时可查阅附录中的表4、表5。

2.利用正激波表计算斜激波

在本节所介绍的基本方程组和普朗特关系式中，可以清楚地看出斜激波与正激波的关系，即如果在以速度Vt运动的相对坐标系中，显然原来的斜激波就转化为正激波了。波前的来流马赫数为

\(M{{a}_{1n}}=M{{a}_{1}}\sin \beta \)               (6.41)

波后的马赫数为                          \(M{{a}_{2n}}=M{{a}_{2}}\sin \left( \beta -\delta  \right)\)                 (6.42)

式中，Ma1，Ma2，β和δ分别为原斜激波的波前、波后马赫数，激波角和气流的转折角。

这样就可以用Ma1n在正激波表中查得在相对坐标系中的波前、波后其他气流参数之比，因为在两个不同的惯性坐标系中，它们的气流静参数是相同的，而气流的滞止参数，将发生变化。例如，在相对坐标系中将波前的速度滞止下来，得到滞止温度和滞止压强分别记为Tn*和pn*，则有

\(T_{n}^{*}=T+\frac{V_{1n}^{2}}{2{{c}_{p}}}=T\left( 1+\frac{k-1}{2}Ma_{1n}^{2} \right)\)                    (6.43)

\(p_{n}^{*}=p{{\left( 1+\frac{k-1}{2}Ma_{1n}^{2} \right)}^{\frac{k}{k-1}}}=p{{\left( \frac{T_{n}^{*}}{T} \right)}^{\frac{k}{k-1}}}\)                    (6.44)

在正激波表中查得的\({{\sigma }^{\prime }}=\frac{p_{2n}^{*}}{p_{1n}^{*}}\)之值，就是斜激波的总压恢复因数σ。

例6.8  超声速喷管出囗气流马赫数为Ma1=1. 5，出囗截面压强为p1=0.645 × 10⁵ Pa, 出口外的大气压强为p2=1. 0 × 10⁵Pa。求出囗外所产生的斜激波的激波角β，气流经过斜激波后的折转角δ和波后的气流Ma2。

解：设所给的喷管如图6.28所示，由斜激波表可查得：当Ma1=1. 5，p2/p1=1. 55时，β=54°，δ=8°46′(向波main转折），Ma2=1.174。

例6.9  马赫数为Ma1=3.0的空气流过顶角为30°的楔形体，气体静压为p1=1. 0 × 10⁴ Pa，静温为T1=216.5 K。求激波后的静压p2、静温T2、密度ρ2、速度V2、总压p2*和马赫数Ma2。

解：设气流沿楔形体对称面流过，则气流折转角δ(即楔形体半顶角）为15°，由斜激波表查得激波角为β=32.3°。将Ma1，β代入式（6.30），得到

\(\begin{align}& \frac{{{p}_{2}}}{{{p}_{1}}}=\frac{2.8}{2.4}\times {{3}^{2}}{{\sin }^{2}}{{32.3}^{\text{ }\!\!{}^\circ\!\!\text{ }}}-\frac{0.4}{2.4}=2.831 \\& {{p}_{2}}=2.831\times 1.0\times {{10}^{4}}=2.831\times {{10}^{4}}Pa \\\end{align}\)

由连续方程，有                                \(\frac{{{\rho }_{2}}}{{{\rho }_{1}}}=\frac{{{V}_{1n}}}{{{V}_{2n}}}=\frac{\tan \beta }{\tan \left( \beta -\delta  \right)}=\frac{\tan {{32.3}^{\text{ }\!\!{}^\circ\!\!\text{ }}}}{\tan \left( {{32.3}^{\text{ }\!\!{}^\circ\!\!\text{ }}}-{{15}^{\text{ }\!\!{}^\circ\!\!\text{ }}} \right)}=2.03\) 

由状态方程，得

\(\begin{align} & {{\rho }_{2}}=\frac{{{\rho }_{2}}}{{{\rho }_{1}}}{{\rho }_{1}}=2.03\times \frac{{{p}_{1}}}{R{{T}_{1}}}=2.03\times \frac{1.0\times {{10}^{4}}}{287.06\times 216.5}=0.327kg/{{m}^{3}} \\& {{T}_{2}}=\frac{{{p}_{2}}}{R{{\rho }_{2}}}=\frac{2.831\times {{10}^{4}}}{287.06\times 0.327}=301K \\\end{align}\)

由图6.22所示几何关系及连续方程，可得

\(\begin{align}& \frac{{{V}_{2}}}{{{V}_{1}}}=\frac{{{V}_{2n}}}{{{V}_{1n}}}\frac{\sin \beta }{\sin \left( \beta -\delta  \right)}=\frac{{{\rho }_{1}}}{{{\rho }_{2}}}\frac{\sin \beta }{\sin \left( \beta -\delta  \right)}=\frac{\sin {{32.3}^{\text{ }\!\!{}^\circ\!\!\text{ }}}}{2.03\times \sin {{17.3}^{\text{ }\!\!{}^\circ\!\!\text{ }}}}=0.885 \\& {{V}_{1}}=M{{a}_{1}}{{c}_{1}}=3\times 20.05\sqrt{216.5}=885m/s \\\end{align}\)

而                                                \({{V}_{2}}=\frac{{{V}_{2}}}{{{V}_{1}}}{{V}_{1}}=0.888\times 885=783m/s\)

方向是向内折转15°，故有

\(M{{a}_{2}}=\frac{{{V}_{2}}}{{{c}_{2}}}=\frac{783}{20.05\sqrt{301}}=2.25\)

则                                                    \(p_{2}^{*}=\frac{{{p}_{2}}}{\pi \left( M{{a}_{2}} \right)}=\frac{2.831\times {{10}^{4}}}{0.0862}=3.28\times {{10}^{5}}Pa\)

例6.10  用正激波表计算上例。

解：在上例中己查得β=32.3°，所以来流沿斜激波法向马赫数为

Ma1n=Ma1sinβ=3 x sin32.3°=1.6

由Ma1n查正激波表，得

Ma 2n=0.6684，p2/p1=2.82，T2/T1=1.388，ρ2/ρ1=2.032，p2*/p1*=0.8952

因为T1，p1，ρ1和V1己在上例给出，故有

\(\begin{align}& {{p}_{2}}=\frac{{{p}_{2}}}{{{p}_{1}}}{{p}_{1}}=2.82\times 1.0\times {{10}^{4}}=2.82\times {{10}^{4}}Pa \\& {{T}_{2}}=\frac{{{T}_{2}}}{{{T}_{1}}}{{T}_{1}}=1.388\times 216.5=300K \\& {{\rho }_{2}}=\frac{{{\rho }_{2}}}{{{\rho }_{1}}}{{\rho }_{1}}=2.032\times 0.161=0.327kg/{{m}^{3}} \\\end{align}\)

由式（6.42），得

\(\begin{align}& M{{a}_{2}}=\frac{M{{a}_{2n}}}{\sin \left( \beta -\delta  \right)}=\frac{0.6684}{\sin {{17.3}^{\text{ }\!\!{}^\circ\!\!\text{ }}}}=2.25 \\& {{V}_{2}}=2.25\times 20.05\times \sqrt{300}=781m/s \\& p_{2}^{*}=\frac{{{p}_{2}}}{\pi \left( M{{a}_{2}} \right)}=\frac{2.82\times {{10}^{4}}}{0.0852}=3.30\times {{10}^{5}}Pa \\\end{align}\)

6.6  激波的相交与反射

前文讨论的是气流经过一道激波时参数的变化，在实际的超声速流场中，经常遇到的激波系要复杂得多。一般地，只要流场中出现激波，往往都要出现激波反射和相交。例如，超声速气流绕流叶片或叶栅时的流场，超声速风洞模型实验时的流场等，都是复杂的波系，即多波系共存的流场。本节将研究如何运用前面的知识来分析较复杂的激波系。

6.6.1  激波在固体直壁上的反射

马赫数为Ma1的超声速气流在图6.29所示的平直管道內流动,由于管壁的折转,在A点产生入射激波AB，使波后气体偏转δ角。在B点由于平壁面的限制,迫使偏转后的气流重新平行于平壁方向·因此②区超声速气流再次受到偏转压缩,偏转角仍为δ。这一偏转压缩必然在B点产生反射激波BC。激波BC后③区气流与上壁面平行。若希望在B点不产生反射波,则只需要将上壁面在B点转折到和②区气流方向平行即可。

如果Ma数值很大而δ较小,原则上说,这种反射在上、下壁面处可重复多次。但每经过一次反射,Ma都下降,而偏转角δ的大小不变。所以经过几次反射后,由于Ma较低,因此就会出现δ> δmax,的情况·这时上述止常的反射便不能进行下去,即出现不规则的反射激波,如图6. 29所示。在点E附近形成包括滑移流线在內的复杂反射(叫马赫反射或λ反射)的激波。

在正常反射的情况下,即②，③区流动参数的计算可以按单波区逐区计算。

例6.11   在图6.29中,已知马赫数等于2 .0 ,p1=1.0 x 10⁵Pa ,壁面折转角δ= 7°。求 AB和BC的激波角和②，③区的马赫数和压强。

解：由Ma=2.0 , δ= 7° ,查激波表得

β=36. 21°, Ma2=1.75, p2/p1=1.462,p2=1.462 × 10⁵ Pa

由激波表可以看出, Ma2=1.75 , δ= 7°<δmax,所以能在点B处产生斜激波,反射激波BC的激波角、③区气流的马赫数和压强分别为

β23= 41.87° , Ma3=1.509 , p3/p2=1.425 , p3=1. 425 × 10⁵ pa

关于求②，③区气流的总压,留给读者自己求解。

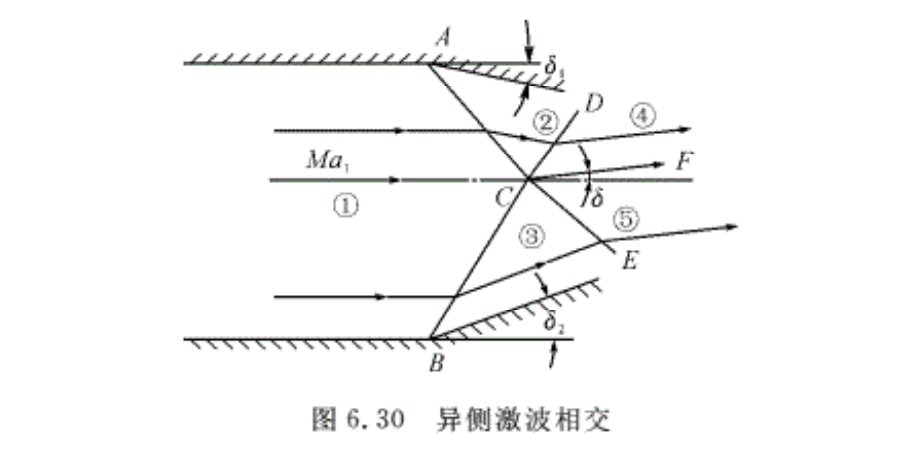
马赫数为Ma1的超声速气流在图6.30所示的不对称的二维进气道内流动,设上、下唇囗的折转角均小于气流的最大折转角,则超声速气流在A , B两处分别产生两道斜激波 AC和BC,并交于点C。①区气流经过激波AC顺时针折转角δ1,经过激波BC则逆时针折转角δ2。 ②，③区气流方向不同,在点C相互压缩又产生了激波CD和CE ,因此异侧激波相交后在交点C处又产生两道激波CD和CE。由于δ1≠δ2,因此,②，③区气流的马赫数、熵值和其他参數均不相同。气流经过激波CD和CE后,虽然④, ⑤区的气流方向一致,压强也相等,但由于两区气流的速度和熵值都不相同,因此④ ,⑤区的气流之间存在一条滑流线CF。滑流线两侧的气流参数不同,就会在两侧产生旋涡·如果δ2＞δ1,则气流经过激波BC和CE的损失大。因此，⑤区的气流总压低于④区气流的总压，⑤区的气流速度也比④区低，两区总温和静压相同。异侧激波相交各区气流参数的计算可通过迭代的方法得到。

如果δ1=δ2，气流沿通道对称地流动，④，⑤区的气流方向一致且参数均相同。这种情况下不产生滑流层。

例6.12  计算④，⑤区的气流参数（见图6.30）。设δ1=5°，δ2=15°，Ma1=3.0，p1=1 × 10⁵ Pa。

解：按δ1=5°，δ2=15°，Ma1=3.0，查激波表，得

Ma2=2.75，p2/p1=1. 46

Ma3=2.25，p3/p1=2.8

计算④，⑤区的气流参数需要采用试凑法迭代计算。

假设δ=9°，按Ma2=2.75和δ1+δ=14°，查激波表得p4/p2=2.48，即

P4=（p4/p2）x（p2/p1）x p1=3.62 x 10⁵Pa

按Ma2=2.25和δ2-δ=6°，查激波表得p5/p3=1.44，即

P5=（p5/p3）x（p3/p1）x p1=4.04 x 10⁵Pa

由于p5＞p4，所以重新假设δ=9.5°，重复以上计算，得

P4=3.8 × 10⁵ Pa, p5=3.82 × 10⁵ Pa

求出的偏差在允许的范围内，因此所假设的δ=9.5°正确，图6.30中所示的气流相对于①区气流向上的折转角δ=9.5°。

6.6.3  激波在自由边界上的反射

设有超声速气流自平面喷管流入大气，如果在管道出口的压强p1小于外界压强pa（pa不能太高，否则会使激波进入管内），则在管道出囗处必然会产生两道平面斜激波AC和BC ,如图6.31（a）所示。这两道激波在C点相交后，会产生两道激波CD和CE。①区气流经过激波 BC和AC后，气流方向内折转一个角度δ，气流进入②，③区后，压强与外界压强相等，即p2=p3=pa，但由于②，③区气流方向不平行，则在C点会产生两道激波CD和CE。②，③区气流穿过激波CD和CE后进入④区，气流方向与①区气流方向一致，但④区压强高于②，③区气流压强，即p4>p2，p4>p3，因而p4>pa，所以激波CD和CE打到自由边界BD和AE上后必然要反射出膨胀波束（用一道波代替）DF和EF，因此激波打到自由边界上反射为膨胀波。

④区气流经膨胀波DF和EF后，进入⑤，⑥区，分别向外折转一个角度，因而在F点又形成两道膨胀波FG和FH。可以看出，在不计黏性的情况下，管道出囗以后的流动中，是激波与膨胀波交替重复发展的过程。

例6.13  超声速气流从如图6.31（b）所示的平面超声速喷管射出，已知壁面折转角δ=10°，来流马赫数Ma1=1.5，外界大气压强为pa=1.013 3 ×10⁵ Pa。求②，③区气流的马赫数和③区气流的折转角。

解：由Ma1=1.5和δ=10°，查斜激波表，得

β=56.68°，Ma2=1. 114， p2/p1=1.666

由于p1=pa，所以

P2=1.688 × 10⁵ Pa

\[p_{2}^{*}={{p}_{2}}{{\left( 1+\frac{k-1}{2}Ma_{2}^{2} \right)}^{\frac{k}{k-1}}}=3.667\times {{10}^{5}}Pa\]

又③区气流的压强p3=pa，p3*=p2*，所以由

\[\pi \left( M{{a}_{3}} \right)=\frac{{{p}_{3}}}{p_{3}^{*}}=\frac{1.0133}{3.667}=0.2763\]

查气动函数表，得Ma3=1.49。

可以根据右伸膨胀波的计算公式求得③区气流的折转角。设用一条平均的膨胀波代替，因此有

\({{\theta }_{2}}-\upsilon \left( M{{a}_{2}} \right)={{\theta }_{3}}-\upsilon \left( M{{a}_{3}} \right)\)           (a)

由Ma2=1.114和Ma3=1.49，查气动函数表，得

v(Ma2)=1. 554°，v(Ma3)=11.69°

带入式（a），得

δ=θ3-θ2= v(Ma3)- v(Ma2)=10.14°

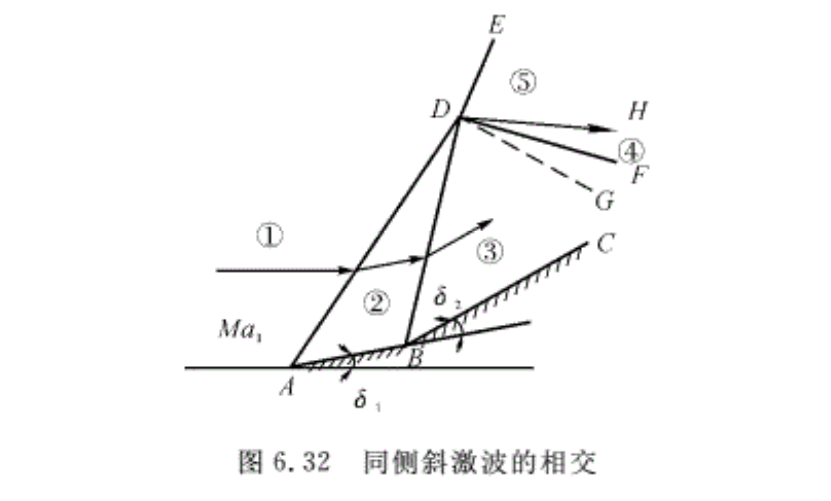
6.6.4  同侧斜激波的相交

在吸气式发动机超声速二维进气道的设计中，就会出现同侧激波相交的情况。如图6.32 所示的超声速二维进气道，在A，B两点分别产生两道斜激波AD和BD，这两道激波相交后形成一道更强的激波DE。来流马赫数为Ma1的超声速气流，一方面经过第一道激波AD后，气流方向折转δ1的角度，进入②区。②区仍为超声速流，经激波BD进入③区，气流方向又折转δ2角，压强进一步得到提高。另一方面，①区气流经过外激波DE后进入⑤区，一般来讲，⑤区气流与③区气流的压强不相等，且方向也不一定一致，因而在D点处根据具体情况还会产生弱激波DF或膨胀波DG。

①区气流马赫数为Ma1，压强为p1，便可求出总压p1*。根据Ma1和气流折转角δ1可求出激波AD的激波角β1和②区气流马赫数Ma2，压强p2，由Ma2和p2可求出p2*。然后根据 Ma2和气流方向角δ2求出激波BD的激波角β2，③区气流的马赫数Ma3，压强p3，进一步计算出③区气流的总压p3*。进而可求出这两道激波的交点D。

在计算外激波DE的激波角时，可先假设气流穿过激波DE时，要向上折转δ1+δ2的角度，即假设气流穿过激波DE以后，沿平行于壁面BC方向流动，然后根据Ma1和气流折转角δ1+δ2算出激波DE的激波角βDE，以及⑤区气流马赫数Ma5和压强p5。一般地，p5不等于p3，如果p5小于p3，就会在D点反射膨胀波束DG(用一道波代替），使③区气流穿过此膨胀波束DG后，把压强降低到与⑤区压强相等，同时气流向上折转一个角度δ。如果p5>p3，则要在D点反射出一道弱激波DF，使③区气流穿过反射波DF时，把压强提高到与⑤区压强相等，并向下折转一个角度δ。因此要计算气流经过膨胀波DG（或激波DF）后的④区气流参数，必须先假设一个δ值，然后根据Ma1和折转角δ1+δ2±δ(对于激波用-δ)重新计算⑤区气流参数Ma5′和p′5。如果新计算的值p′5=p4，则假设的δ是正确的，如果p′5≠p4，就必须重新假设δ值，重复以上步骤，直到

P5-p4≤ε

为止，ε是允许的偏差。此外，由于④，⑤区流速不等，因此两区之间存在滑流线DH。

例6.14   图6.33表示超声速气流沿两个内凹壁流动，两个内凹壁总的折转角都是25°，但一个是一次折转，另一个则是分两次折转，即先折转15°，再折转10°，已知斜激波前气流马赫数为Ma1=2.5。求激波后气流的马赫数Ma2和总压恢复因数σ。

解：（1）一次折转：由激波表查得，当Ma1=2.5，δ=25°时，

β=50°，p2/p1=4.09，Ma2=1.395

由气动函数表，查得

π（λ1）=0.0585，π（λ2）=0.3165

所以                                               \(\sigma =\frac{p_{2}^{*}}{p_{1}^{*}}=\frac{{{p}_{2}}}{{{p}_{1}}}\frac{\pi \left( {{\lambda }_{1}} \right)}{\pi \left( {{\lambda }_{2}} \right)}=4.09\times \frac{0.0585}{0.3165}=0.756\)

（2）两次折转：由图6.33(b)可知，此时必产生两道斜激波。由激波表查得，当Ma1=2.5，δ1=15°时，

β=37°，p′1/p1=2.473， Ma′1=1.87

再查激波表（或计算）得，当Ma′1=1.87，δ2=10°时，

β2=42°，p2/p′1 =1.68， Ma2=1.55

则                                                 \(\frac{{{p}_{2}}}{{{p}_{1}}}=\frac{p_{1}^{\prime }}{{{p}_{1}}}\frac{{{p}_{2}}}{p_{1}^{\prime }}=2.473\times 1.68=4.15\)

由气动函数表查得，当Ma2=1.55时，π（λ2）=0.2533，π（λ1）=0.0585，则

\[\sigma =\frac{p_{2}^{*}}{p_{1}^{*}}=\frac{{{p}_{2}}}{{{p}_{1}}}\frac{\pi \left( {{\lambda }_{1}} \right)}{\pi \left( {{\lambda }_{2}} \right)}=4.15\times \frac{0.0585}{0.2533}=0.958\]

由此可见，在同样的来流Ma1和总的折转角度也相同的情况下，两次转折和一次转折后的气流参数变化不相同。一般来讲，在上述条件下，气流折转的次数愈多，即经过的激波压缩的次数愈多，气流总压损失越小。

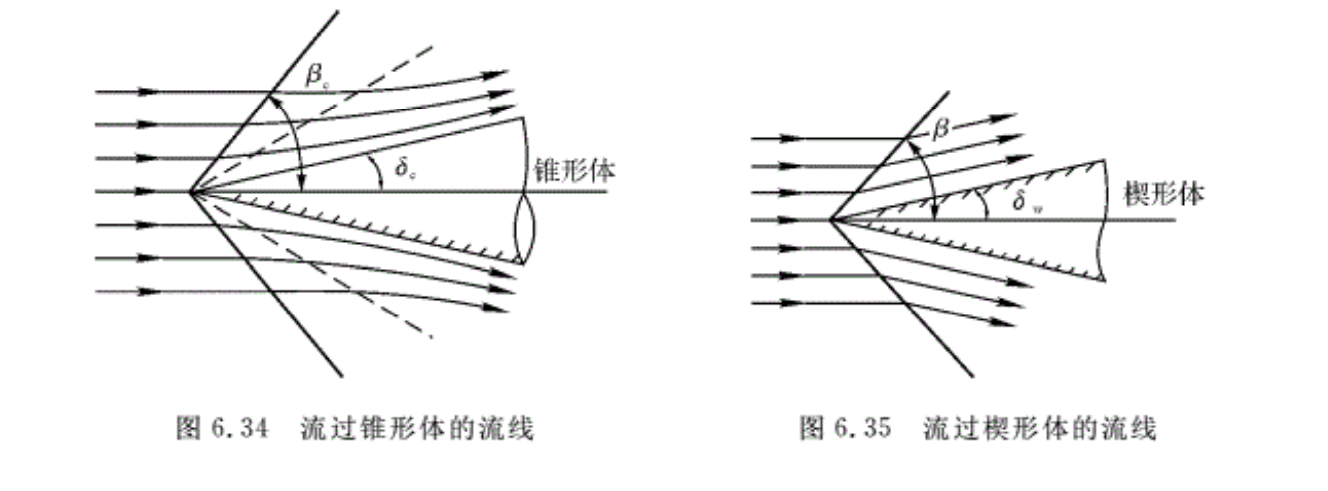
6.7  锥面激波及其数值解

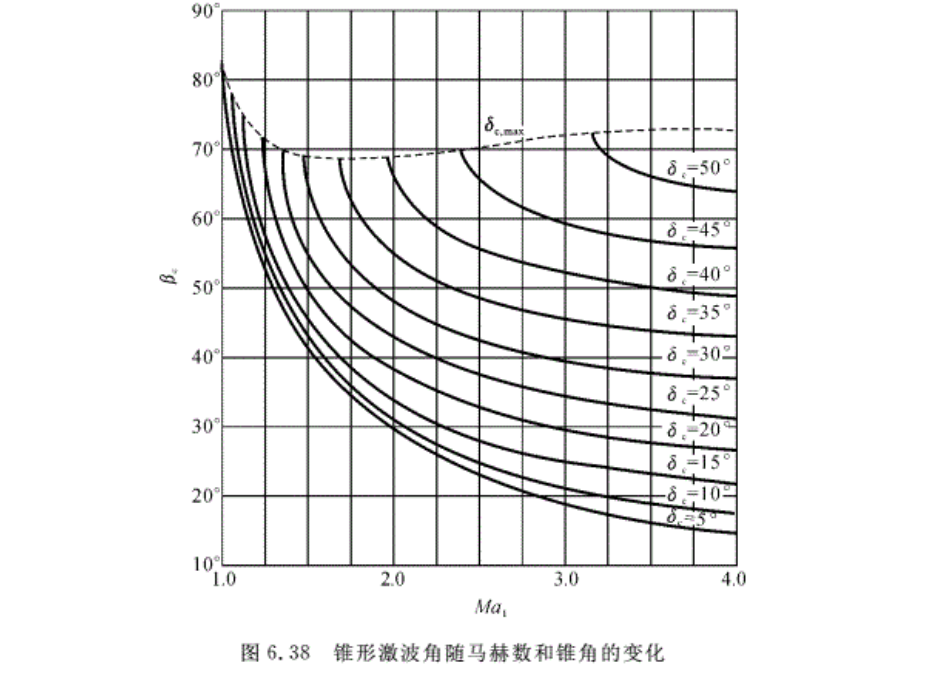
超声速气流沿对称轴方向流过锥形体时，如果来流马赫数不是过小或是半锥角δc不是太大，则在锥体顶端产生一个锥形激波。其激波角为βc，如图6.34所示。锥形激波与锥体共轴。

超声速进气道的中心锥以及大多数超声速飞行器的头部都是圆锥或接近于圆锥。因此在其圆锥头部尖端处会产生圆锥激波。圆锥激波与二维尖楔产生的平面斜激波的前、后气流参数变化规律一样，但波后流场的性质却完全不同。

6.7.1  锥面激波的特点及与平面斜激波的比较

图6.34和图6.35分别表示了超声速气流流过锥形体和楔形体时所产生的激波和流场，从两个流场比较，可以看出下述几个特点。

（1）平面斜激波后的流场是均匀的，波后各条流线都平行于楔形体的壁面，且波后的气流参数处处相等，即来流通过斜激波时，一次完成压缩。而圆锥激波波后流场不均匀。圆锥激波后各条流线都是以锥体壁面的母线为渐近线而逐渐向它靠近。流线方向逐渐折转，且沿流线各点参数不相等。由于圆锥激波后沿流线方向是等熵压缩过程，所以流动速度逐渐减小，压强、温度逐渐提高。在不计黏性的情况下，从激波后到锥面之间的总压相等。即来流经过圆锥激波波面不等熵压缩后，波后连续地等熵压缩直至锥面。

（2）如果来流马赫数Ma1和半顶角（半楔角和半锥角）均相等，则由尖锥产生的圆锥激波角βc小于由尖楔产生的平面激波角β。因此，在同样的条件下，锥形激波比平面斜激波要弱一些。

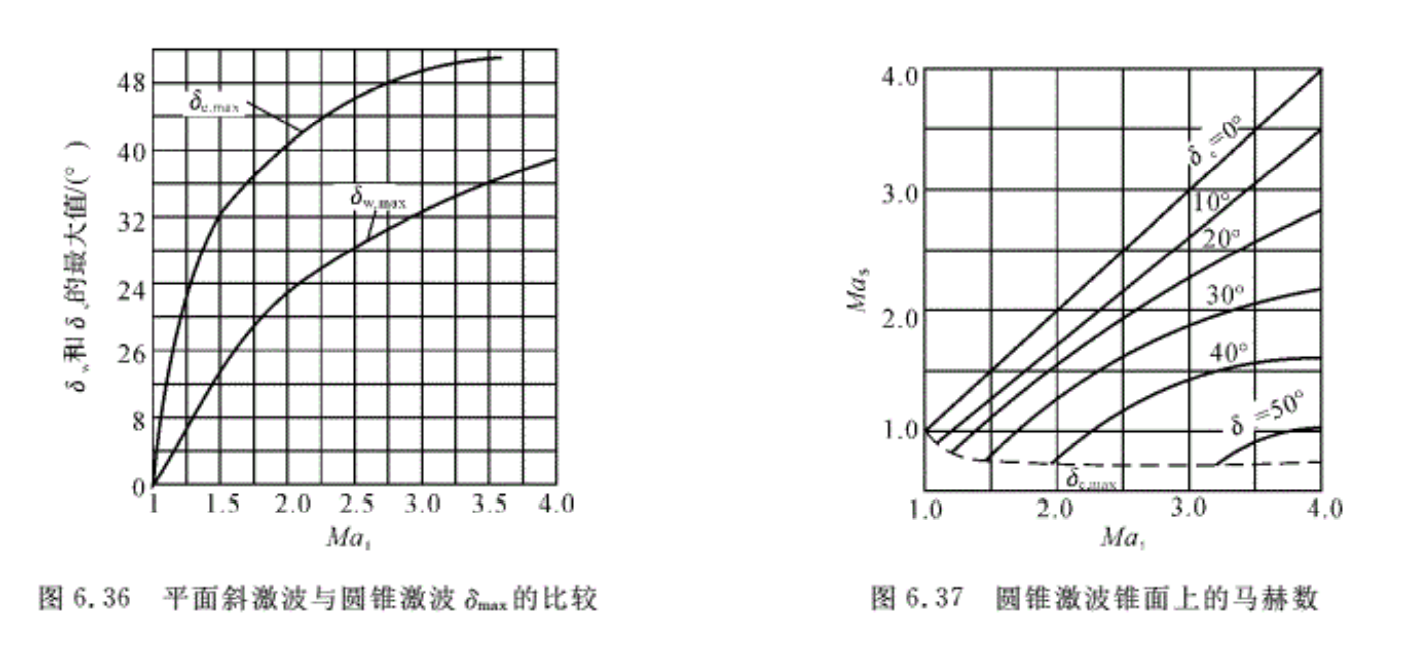
（3）对于相同的来流马赫数，圆锥激波脱体时的半顶角δc,max大于由楔形体产生的平面斜激波脱体时的半顶角δw,max，即δc,max>δw,max，如图6.36所示。同样，对于一定的半顶角δ，两者都各自存在Ma1 min。当δ相同时，圆锥的Ma1 min小于气流流过楔形体的Ma1 min。因此，尖楔激波比圆锥激波更容易脱体。

（4）通过锥形流理论可以证明，在锥形激波后，通过锥顶的任一条射线（见图6.34中的虚线）上，各点气流参数都是相同的。

图6.37表示了锥体表面上的马赫数Mas与来流马赫数Ma1及锥体半顶角δc的关系曲线。

图6.38所示是用锥形流理论计算的锥面激波角βc与Ma1和δc之间的关系曲线。从曲线还可看出，曲线族只有下半部（和平面激波相比），即表明超声速气流流过锥形体时，只产生弱的激波。

例6.15  如图6.34所示，己知Ma1=2.0，p1=1.0 × 10⁴Pa，δc=30°。求βc，波后气流的折转角δ和压强、马赫数以及锥面上气流的马赫数Mas，和压强ps。

解：由Ma1=2.0及δc=30°，由图6.38查得βc=48.2°；由图6.37查得Mas=1.25。

因为在圆锥激波前后气流参数间的关系和平面激波是一样的，所以为了求出波后气流的折转角δ，可以利用平面激波的图线或数值表，即利用Ma1及βc由平面激波曲线或查表，得 δ=17°。再按Ma1，δ查得，圆锥激波波后的Ma2=1.36，激波前、后的压强比p2/p1=2.427。

所以

\[\begin{align}& {{p}_{2}}=\frac{{{p}_{2}}}{{{p}_{1}}}{{p}_{1}}=2.42\times 1.0\times {{10}^{4}}Pa \\& {{p}_{s}}=\frac{{{p}_{s}}}{p_{2}^{*}}\frac{p_{2}^{*}}{{{p}_{2}}}{{p}_{2}}=\frac{\pi \left( M{{a}_{s}} \right)}{\pi \left( M{{a}_{2}} \right)}{{p}_{2}} \\\end{align}\]

查气动函数表，则得π(Mas）=0.3861，π(Ma2）=0.3370，所以

\[{{p}_{s}}=\frac{0.3861}{0.3370}\times 2.42\times {{10}^{4}}=2.77\times {{10}^{4}}Pa\]

可见，超声速气流在锥形激波后是继续减速增压的。从波后到锥面Ma减小，而压强升高。

6.7.2  锥形流场数值计算方法

1.锥形流

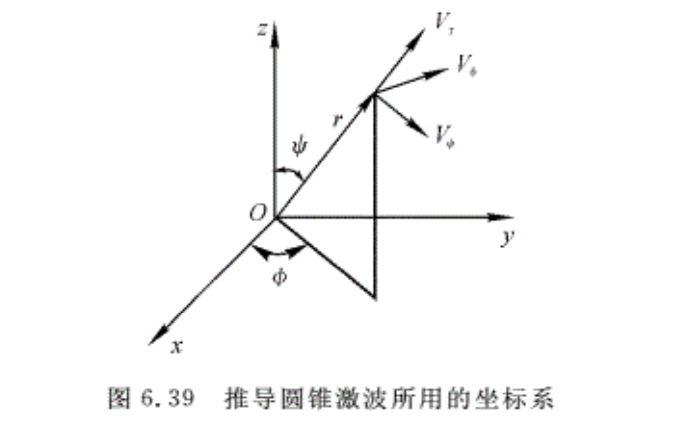
上面讨论了圆锥激波的特点。如果半锥角δc与自由流马赫数Ma∞在合适的范围内，就会在圆锥前产生一附体的圆锥激波，且激波本身是锥形的，这样的流动称为锥形流。对于一个超声速定常直匀流沿对称轴流过圆锥的流动，其流动满足锥形流动的特点，即沿着任意一条从圆锥顶端发出的射线上，流动参数处处均匀。这种锥形流动的特点己被实验所证明。取如图 6.39所示的球坐标系，对于圆锥无攻角超声速定常绕流，由于流场的圆锥特性，所有的待求物理量都有∂/∂r=0的性质。又由于流场的轴对称性，∂/∂ф=0，因此，圆锥无攻角绕流中的所有待求函数只是ψ (球面角）的函数。

由以上分析可知，圆锥无攻角超声速定常绕流必定可简化为只有一个自变量ψ的常微分方程。

可以证明，对一般有攻角的锥体（不一定是圆锥）超声速定常绕流，只要产生附体激波，则同样满足锥形流的条件，即∂/∂r=0。但是这时不存在对称性，即∂/∂ф≠0，所以流动参数是ψ和ф的函数。

2.Taylor-Maccoll数值解

如图6.40所示的一直匀来流沿对称轴流过圆锥，在顶端产生一圆锥激波。

由于顶端的斜激波是圆锥形的，所以它处处与来流成相同的角度，即圆锥激波角βc和激波强度保持不变，紧靠激波后的流动参数是均匀的。

根据可压流动的气体动力学基本方程，按照锥形流场的基本特征，取球坐标系如图6.39所示，便可推导出描述超声速直匀流绕圆锥流动的控制方程（这里仅给出公式而不作详细推导）如下：

\[{{\overline{V}}_{\psi }}=\frac{d{{\overline{V}}_{r}}}{d\psi }\]           (6.45)

\[\frac{d{{\overline{V}}_{\psi }}}{d\psi }=-{{\overline{V}}_{r}}+{{\overline{c}}^{2}}\frac{{{\overline{V}}_{r}}+{{\overline{V}}_{\psi }}\cot \psi }{\overline{V}_{\psi }^{2}-{{\overline{c}}^{2}}}\]           （6.46）

式中，\({{\overline{V}}_{\psi }}\left( =\frac{{{V}_{\psi }}}{{{c}_{cr}}} \right)\)，\({{\overline{V}}_{r}}\left( =\frac{{{V}_{r}}}{{{c}_{cr}}} \right)\)分别是ψ，r方向上的速度分量与临界声速之比；\(\overline{c}\left( =\frac{c}{\overline{c}} \right)\)是声速与临界声速之比。声速表达式为

\[{{\overline{c}}^{2}}=\frac{k+1}{2}-\frac{k-1}{2}{{\left( \frac{V}{{{c}_{cr}}} \right)}^{2}}=\frac{k+1}{2}-\frac{k-1}{2}{{\lambda }^{2}}\]                 （6.47）

\[{{\lambda }^{2}}={{\left( \frac{V}{{{c}_{cr}}} \right)}^{2}}=\overline{V}_{r}^{2}+\overline{V}_{\psi }^{2}\]         （6.48）

式（6.46）为一二阶常微分方程，可以用任何一种积分方法对其进行积分，例如，可以用四阶龙格一库塔法。

3.控制方程的数值积分方法

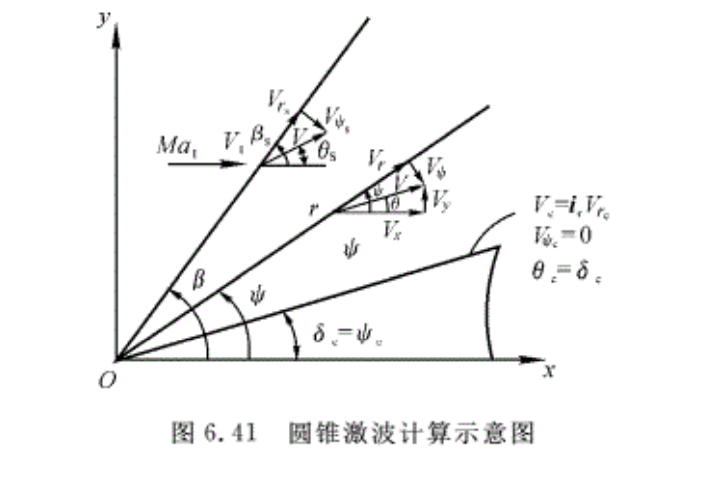
当给定自由流流动参数后V1，p1，T1和半锥角δc时，要确定激波角βc和速度分布Vr(ψ)及Vψ(ψ)。因为激波角βc未知，所以在激波后或锥面上的参数都是未知的，因此需要迭代求解。下面给出一种简单的迭代方法。

首先假定激波角\({{\beta }^{\left( i \right)}}\)的一个试算值，上标(i)表示试算的次数，其次确定数值积分的步长。根据锥形流的特点，在激波与锥面之间，从锥尖发出的每条射线上，其流动参数均匀一致，因此步长可以按等角度∆ψ来划分。最后求解控制方程确定相应的半锥角\(\delta _{c}^{\left( i \right)}\)的数值。如果计算的\(\delta _{c}^{\left( i \right)}={{\delta }_{c}}\)，则假定的激波角\({{\beta }^{\left( i \right)}}\)是正确的；若不满足该条件，则重新设定\({{\beta }^{\left( i \right)}}\)，直到当假设的\({{\beta }^{\left( i \right)}}\)的试算值使得\(\delta _{c}^{\left( i \right)}={{\delta }_{c}}\)时，求解过程就完成了，即求出了每条射线上的流动参数，也就求解出激波后的锥形流场。其求解步骤如下：

（1）假定激波角\({{\beta }^{\left( 1 \right)}}\)为初始试算值，可按下式设定：

\({{\beta }^{\left( 1 \right)}}\text{=}{{\delta }_{c}}+\frac{1}{2}\arcsin \frac{1}{M{{a}_{1}}}\)            (6.49)

（2）确定数值积分算法的角度步长，即

\(\Delta \psi =-\frac{{{\beta }^{\left( i \right)}}-{{\delta }_{c}}}{N}\)      （6.50）

式中，N是激波与锥面间所取的步数。

（3）根据给定的自由来流参数V1，p1，T1，以及假设的激波角\({{\beta }^{\left( i \right)}}\)去计算紧靠激波波而后的流动参数\({{\overline{V}}_{{{r}_{s}}}}\)和\({{\overline{V}}_{{{\psi }_{s}}}}\)，如图41所示。用\({{\overline{V}}_{{{r}_{s}}}}\)和\({{\overline{V}}_{{{\psi }_{s}}}}\)这个值作为对方程式（6.46）进行数值积分的初始条件。斜激波前后的各种参数比，重写如下:

\(\frac{{{p}_{2}}}{{{p}_{1}}}=\frac{2k}{k+1}Ma_{1}^{2}{{\sin }^{2}}\beta -\frac{k-1}{k+1}=\frac{2k}{k+1}\left( Ma_{1}^{2}{{\sin }^{2}}\beta -\frac{k-1}{2k} \right)\)                (6.51)

\(\frac{{{\rho }_{2}}}{{{\rho }_{1}}}=\frac{\left( k+1 \right)Ma_{1}^{2}{{\sin }^{2}}\beta }{2+\left( k-1 \right)Ma_{1}^{2}{{\sin }^{2}}\beta }=\frac{\tan \beta }{\tan \left( \beta -{{\theta }_{s}} \right)}\)              (6.52)

或                                                       \(\frac{{{\rho }_{1}}}{{{\rho }_{2}}}=\frac{\tan \left( \beta -{{\theta }_{s}} \right)}{\tan \beta }=\frac{2}{k+1}\left( \frac{1}{Ma_{1}^{2}{{\sin }^{2}}\beta }+\frac{k-1}{2} \right)\)     

\(\frac{{{V}_{2}}}{{{V}_{1}}}=\frac{{{\lambda }_{2}}}{{{\lambda }_{1}}}=\frac{\sin \beta }{\sin \left( \beta -{{\theta }_{s}} \right)}\left[ \frac{2}{\left( k+1 \right)Ma_{1}^{2}{{\sin }^{2}}\beta }+\frac{k-1}{k+1} \right]\)              (6.53)

式中，下标2表示紧靠激波后面的参数;θs为紧靠波后的气流方向角。\({{\overline{V}}_{{{r}_{s}}}}\)和\({{\overline{V}}_{{{\psi }_{s}}}}\)由下式确定：

\[{{\overline{V}}_{{{r}_{s}}}}=\frac{{{V}_{{{r}_{s}}}}}{{{c}_{cr}}}={{\lambda }_{2}}\cos \left( \beta -{{\theta }_{s}} \right)\]              (6.54)      

\[{{\overline{V}}_{{{\psi }_{s}}}}=\frac{{{V}_{{{\psi }_{s}}}}}{{{c}_{cr}}}=-{{\lambda }_{2}}\sin \left( \beta -{{\theta }_{s}} \right)\]             （6.55）

速度因数

\[{{\lambda }_{1}}={{\left[ \frac{\left( k+1 \right)Ma_{1}^{2}}{2+\left( k-1 \right)Ma_{1}^{2}} \right]}^{\frac{1}{2}}}\]              （6.56）

（4）由第（3）步所确定的初始条件开始，从激波到锥面积分控制方程式（6.46）。锥面上的边界条件为速度平行于锥表面（无黏性流体)。因此，在锥面上，\({{\overline{V}}_{\psi }}=0\)。激波后面\({{\overline{V}}_{\psi }}\)的初始值是负的，当球面角ψ减小时，\({{\overline{V}}_{\psi }}\)增加到零。对于假定的一个激波角\({{\beta }^{\left( i \right)}}\)，当计算到锥面上时，\({{\overline{V}}_{{{\psi }_{c}}}}=0\)，此时，球面角ψc必须用迭代法来确定（见图6.41）。这样的ψc值找到后，即是对应于激波角\({{\beta }^{\left( i \right)}}\)的圆锥半顶角\(\delta _{c}^{\left( i \right)}\)。

（5）当第（4）步所计算的\(\delta _{c}^{\left( i \right)}\)不等于实际的圆锥半顶角δc时，必须对假定的激波角\({{\beta }^{\left( i \right)}}\)重新修改，然后再重复进行上面的第（2）步到第（4）步，直到找出的\(\delta _{c}^{\left( i \right)}={{\delta }_{c}}\)时为止。对假定的激波角\({{\beta }^{\left( 1 \right)}}\)值的第一次修正值，可以用\(\delta _{c}^{\left( 1 \right)} \)偏离实际δc的差值来修正，即

\({{\beta }^{\left( 2 \right)}}={{\beta }^{\left( 1 \right)}}+\left( {{\delta }_{c}}-\delta _{c}^{\left( 1 \right)} \right)\)               (6.57)

\({{\beta }^{\left( i \right)}}\)的以后各次试算值可以对于相邻的两组\({{\beta }^{\left( i \right)}}\)和\(\left( {{\delta }_{c}}-\delta _{c}^{\left( 1 \right)} \right)\)用割线法来确定。重复进行第（2）步到第（4）步，直到\(\left( {{\delta }_{c}}-\delta _{c}^{\left( 1 \right)} \right)\)达到允许的误差范围内，即迭代收敛为止。

（6）在解收敛后，速度分量\({{\overline{V}}_{r}}\left( \psi  \right)\)和\({{\overline{V}}_{\psi }}\left( \psi  \right)\)（\({{\overline{V}}_{\psi }}\)为负）可以被变换成二维速度分量\({{\overline{V}}_{x}}\left( \psi  \right)\)和\({{\overline{V}}_{y}}\left( \psi  \right)\)，然后再计算出流动参数V（ψ），θ（ψ），p（ψ）和ρ（ψ），由图6.41，可得

\[\lambda =\sqrt{\overline{V}_{x}^{2}+\overline{V}_{y}^{2}}\]           (6.58)

\[{{\overline{V}}_{x}}={{\overline{V}}_{r}}\cos \psi -{{\overline{V}}_{\psi }}\sin \psi \]               （6.59）

\[{{\overline{V}}_{y}}={{\overline{V}}_{r}}\sin \psi +{{\overline{V}}_{\psi }}\cos \psi \]                （6.60）

\[\theta =\tan \frac{{{\overline{V}}_{y}}}{{{\overline{V}}_{x}}}\]              （6.61）

式中，符号上的“一”表示物理量与c cr之比。

激波后任一点的滞止参数都相等，即p*=p2*，ρ*=ρ2*。波后任一点静参数、总参数与λ的关系为

\[\frac{p}{{{p}^{*}}}={{\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)}^{\frac{k}{k-1}}}\]                （6.62）

\[\frac{\rho }{{{\rho }^{*}}}={{\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)}^{\frac{1}{k-1}}}\]                 （6.63）

上述的数值积分求解方法很简单，一般地，取3~4次β的试算值后就能收敛到10^-6的相对误差范围内。

6.8  激波在超声速进气道及飞行器设计中的应用

6.8.1  激波与膨胀波的组合

在许多实际问题中，超声速气流流过某一物体时，会在物体上同时出现激波和膨胀波，从而形成了更为复杂的流动图形，图6.42表示出了几种常见的激波与膨胀波同时出现在同一物体上的情况。

图6.42（a）所示是超声速气流流过一个菱形翼型时所产生的激波和膨胀波系。气流在翼型前缘产生两道斜激波（δ＜δmax），经激波后，②区仍然是超声速气流，经过翼型顶部的膨胀波束进入③区，最后在翼型后缘处经过一道斜激波进入④区，与下翼面气流汇合。

图6.42（b）所示是超声速气流流过一个有攻角α的平板形翼型。在平板前缘处，下翼面产生斜激波，压强增大，上翼面产生膨胀波，压强减小，由于翼型上、下翼而存在压力差，从而使平板产生升力。而超声速翼型在流动方向上由于压力分量而产生的阻力，称为波附，这是与亚声速翼型完全不同的概念。

图6.42（c）所示是同侧的激波与膨胀波相交的情况。每一道激波与膨胀波相交后，在交点以上形成一道更弱的激波，所以膨胀波束与激波相交后，形成了曲线形的激波。

图6.42中所示的各个区域的流动参数的计算，根据激波和膨胀波理论，借助数值表或编制计算机程序均可计算出来。

6.8.2  超声速进气道的激波系

进气道的功用是把一定的高速气流均匀地引入发动机，并满足发动机在不同条件下所需求的空气流量，同时气流在其中减速增压。

对进气道的主要要求是：总压恢复因数尽可能得高，阻力小，结构简单且重量轻。

当气流以超声速流入进气道时，超声速气流受到压缩时必然要产生激波，而激波会引起较大的总压损失，使气流的做功能力下降。因此，在设计进气道时，如何组织进气道进口前的激波系，降低进气道的总压损失是非常重要的。

超声速气流流经锥体时便产生锥形激波，流经楔形体时便产生平面斜激波。按照压缩形式来化分，进气道可分为外压式、内压式和混合式进气道。如果超声速气流的压缩过程是在进气道进口截面以外进行的，则称该进气道为外压式进气道；若压缩过程是在进气道进口截面以内进行的，则称为内压式进气道；如果既有外压又有内压缩，则称为混压式进气道。按照波系数目的多少来划分，又可分为正激波式、双波系和多波系进气道。

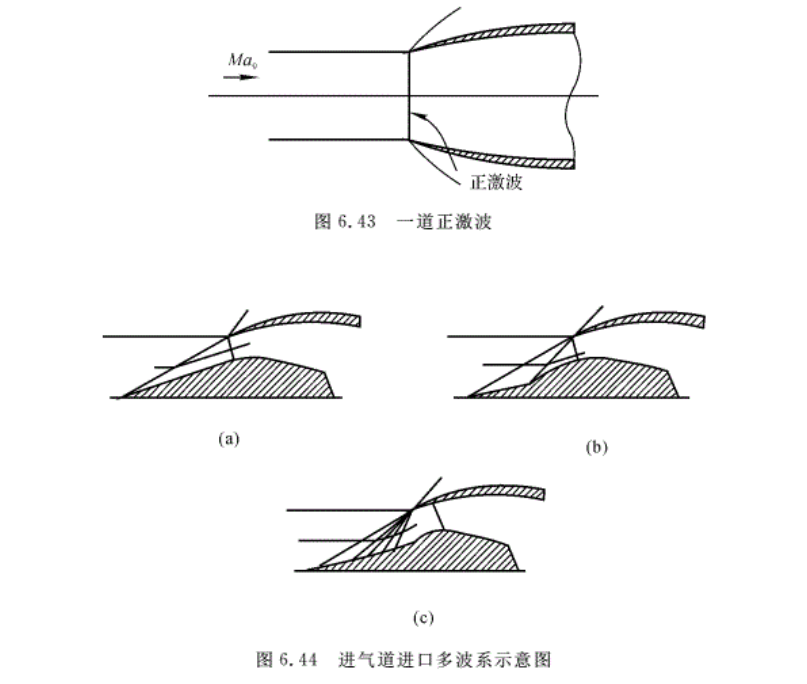
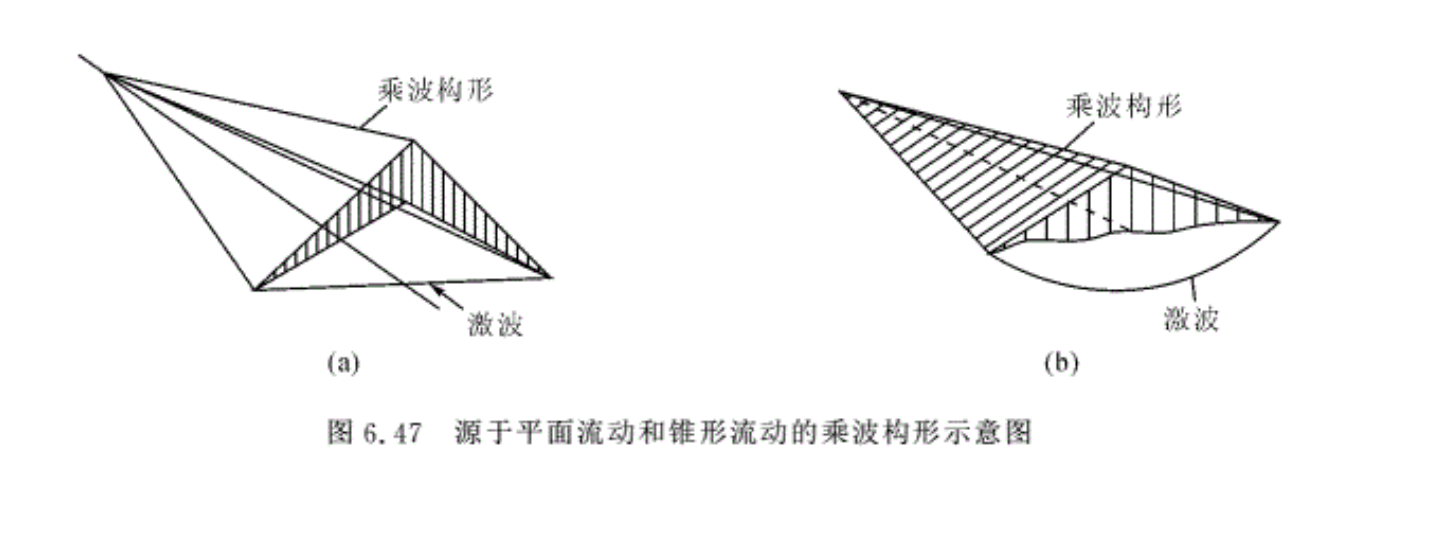
图6.43表示的是一道正激波的超声速进气道（又叫皮托式进气道）。当超声速气流流过进气道时，在一定的出口反压作用下，进气道进口截面上会产生一道正激波（外罩上产生斜激波）。正激波后的亚声速气流在进气道内的扩张通道内继续减速增压。这种进气道结构简单、工艺性好且重量轻。但当来流速度高时，单一正激波的总压损失太大，所以，当来流马赫数 Ma1≤1. 5~1. 7时，才被采用。当Ma1> 1. 7时，就要采用结构比较复杂的带有中心锥的进气道（对腹部或两侧进气的飞机，采用楔形体进气道），目的是要产生斜激波，以降低正激波前的气流马赫数，减弱正激波的强度，提高总压恢复因数。图6.44表示了不同波系的外压式进气道。图6.44（a）表示的是一道斜激波和一道正激波，即双波系外压式进气道。它比图6.43表示的单波系进气道有较高的总压恢复因数。例如，当飞机飞行马赫数Ma0=2.5时，皮托式进气道的总压恢复因数为0.5；而用一道斜激波角为43°的双波系进气道，则其总压恢复因数为 0.76。通常在1.5< Ma0 ≤2.0时，多采用双波系进气道。如果在中心锥上再多设计一个折转面，则中心锥要产生两道锥激波（楔形体产生斜激波），与最后的正激波共同组成三波系进气道，如图6.44(b)所示。显然，波系越多，则总压恢复因数越高。图6.44（c）给出了曲母线中心锥的进气道。在光滑连续的曲面上，超声速气流连续地向内折转。即经过无数的微弱压缩波，气流接近等熵压缩，故称其为等熵外压式超声速进气道。它的总压损失最小。但是随着波数的增多中心锥体就愈复杂，而且，气流经过同侧的波数愈多，气流折转角度将愈大，这样在进气道的外壳前端内壁（要与正激波后气流方向相同）的倾角也就愈大，使得外罩波阻也急速增加。所以多波系外压式进气道使用受到很大限制。图6.45给出了总压恢复因数随飞行马赫数与进气道的激波数目变化的关系。其中，N=1表示一道正激波的压缩；2表示二道激波（一斜一正）的压缩；3表示三道激波（二斜一正）的压缩；4表示四道激波（三斜一正）的压缩减速过程。

为了减小进气道的外罩唇囗的波阻，可以采用通道截面积先收缩后扩张的内压式超声速进气道。这种进气道像一个倒置的拉伐尔喷管。超声速来流进入进气道，经过通道收缩段的激波系减速增压。内压式超声速进气道的优点是外部阻力小，但主要缺点是存在着所谓的“起动”问题，因此单纯的内压式超声速进气道在实际中很少使用。

为了克服外压式超声速进气道的总压恢复因数提高与外罩波阻增加的矛盾，出现了混压式进气道。超声速气流流经如图6.46所示的混压式进气道，先经过进口前的激波系减速到低超声速气流，再经过通道内的激波系减速到亚声速流。这种进气道兼顾了外压式和内压式进气道的优点，因此在实际中得一到了广泛的应用。

6.8.3  激波在乘波构形中的应用

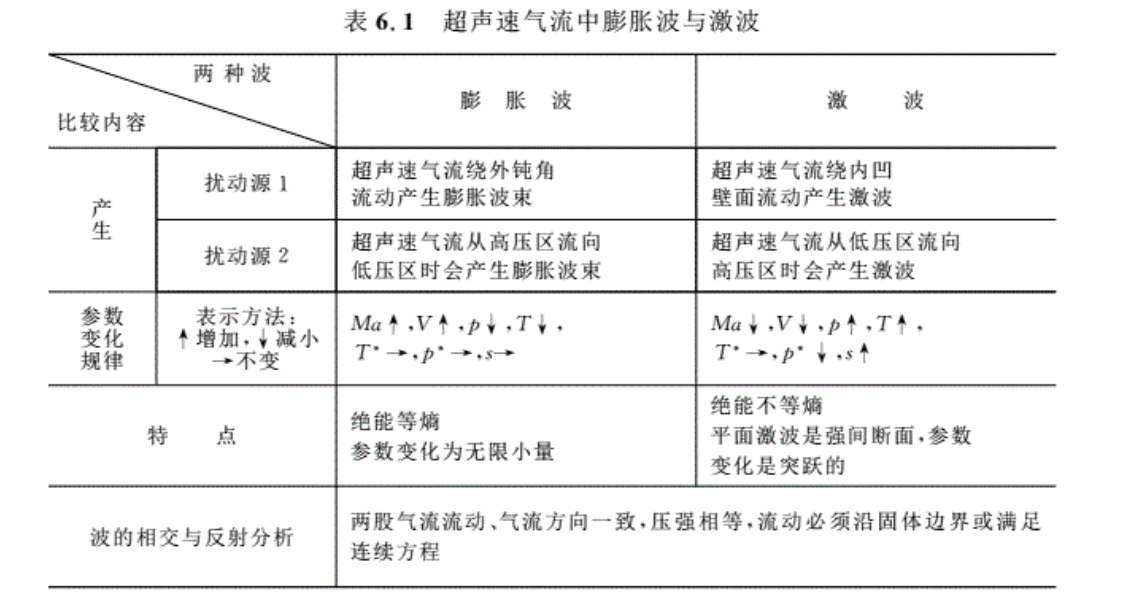
作用在飞行器上的气动力在飞行方向上投影定义为阻力，在垂直于飞行方向上的投影即为升力，升力主要是由飞行器上、下表面的压强差构成的，升力与阻力之比定义为升阻比。对于普通外形的飞机，在超音速飞行时，飞行器上、下表面之间存在压力沟通，从而大大减小了飞行器的升力和升阻比。为了克服普通外形的诸多缺陷，1959年Nonweiler最早提出了乘波构形的概念。认为在高超声速飞行（当Ma > 5.0时，一般称之为高超声速）时，利用激波后压强较高的特点设计一种飞行器，并使得上、下表面的压力不产生沟通，保证下表面的高压气流，提高飞行器的升阻比。这种构形形状独特，在设计飞行条件下，这种外形恰似踏波而行，故冠之以“乘波构形”（waverider)。

乘波构形的显著气动特性是高升阻比，特别适合于高超声速飞行器。常规外形在超声速气流中前缘大都产生脱体激波，激波前后存在的压差使得外形上的波阻非常大，而乘波构形的上表面与自由流平行，所以上表面的压差阻力较小，而下表面在设计马赫数下受到一个与常规外形一样的高压，这个流动的高压抑不会绕过前缘影响到上表面，这样上、下表面的压差不会像常规外形一样相互沟通而降低下表面的压力，因此乘波机具有较高的升阻比。

乘波构形具有以下优点：

（1）在设计马赫数下，下表面在激波后的高压不会绕过前缘泄漏到上表面，波后高压与上表面低压之间没有压力沟通，这使乘波构形和普通外形相比具有很高的升阻比。

（2）来流经激波压缩后，沿着压缩面的流动被限制在前缘激波内，形成较均匀的下表面流场，可以消除发动机进口处的横向流动，利于提高吸气式发动机的进气效率，使得这一构形便于进行飞机机体/发动机／进气道一体化设计。

（3）由于上、下表面没有压力沟通，飞行器上表面和下表面的流场不存在干涉问题，上、下表面可以分开处理，有效地简化了飞行器的初步设计和计算过程。

图6.47给出了源于平面流动和锥形流动的乘波构形。

小结

本章介绍了二维可压流动。在讨论了微扰动在介质中传播的基础上，主要讨论了超声速气流中的激波与膨胀波的产生、特点、参数变化规律以及有关的计算公式，同时讨论了多波系共存的流场，即波的相互作用。本章得到的结论如下：

（1）亚声速气流和超声速气流的流动规律截然不同。在亚声速气流中，扰动可以传遍整个流场，在超声速气流中，扰动被限制在以扰动源为顶点的马赫锥之间，马赫锥的半顶角为

μ=arcsin（1/Ma）

马赫角Ma的大小即表示了扰动的影响范围。

（2）膨胀波和微弱压缩波统称为马赫波。

（3）通过膨胀波，若不计黏性和壁面与外界气体间的热交换，则流动是绝能等熵的。

（4）激波为强扰动波，是强间断面，通过激波时具有强烈的黏性作用和剧烈的热交换。因此是绝能不等熵流动。

（5）膨胀波、激波的产生、特点及参数变化规律的比较见表6.1。

思考与练习题

6.1  用示意图画出超声速气流和亚声速气流绕物体流动时，其流动图形有何差别。

6.2  超声速气流绕外凸壁流动时，气流参数值的总变化取决于什么？而与什么因素无关？

6.3试分别定性地指出超声速气流流过膨胀波和激波时参数（V，λ，h，s，h*，p，T，ρ，p*，T*，ρ*）的变化趋势。

6.4  激波的传播速度与什么有关？

6.5  试述v（Ma）的物理意义。

6.6   Ma=2.0的超声速气流，其扰动的影响区域是多大？

6.7  从平面超声速喷管射出的超声速直匀空气流，设在出囗截面上Ma1=2.0，p1=2 × 10⁵Pa，而喷管外部介质的压强pa=1. 0133 × 10⁵ Pa。求射流边界相对于喷管轴线的偏斜角δ及膨胀后的马赫数Ma2。

6.8   Ma1=1. 0的空气绕外钝角壁面向下折转后，Ma2=2.245。求气流转折角δ及膨胀区扇形角φ。

6.9  具有速度V1=498.34 m／s、温度T1=300K和压强p1=1.0133 × 10⁵ Pa的空气，绕外凸壁面流动，气流折转角δ=-15°。试求膨胀波后气流的速度V2、温度T2和压强p2及膨胀波所占区域的扇形角φ。

6.10  用超声速气流在如图6.48所示的管道中流动，已知Ma1=2.028 ，a=20 × 10^-2 m, δ=5°，假设在B点产生膨胀波束用一道平均马赫波代替。要求在管道出口得到平行于壁面GE的均匀气流，求管道长度l。

6.11  计算图6.14中所示各个区域的流动参数。已知来流空气的马赫数和压强分别为 Ma1=2.0，p1=1.1 × 10⁵ pa，外界大气压强为pa=1.0133 × 10⁵ Pa。

6.12   ρ1=1. 6 kg/m³，p1=0.69 × 10⁵Pa的完全气体经正激波后，速度从V1=450 m/ s 降低到V2=150 m/s。试求ρ2/ρ1，p2/p1，T2/T1以及该气体的比热比k；波前气流马赫数Ma1及波后气流马赫数Ma2。

6.13  速度V1=530 m/ s，Ma1=2.0的空气流，流过内折壁向内转折20°（见图6.49）。求激波后的气流速度V2。

6.14  速度V1=800m/ s的气流经过半顶角为20°的尖劈时，测得激波角β=53°(见图6.50)。试求波后气流速度V2。

6.15  （1）如图6.51所示，设Ma1=2.5，δ=10°，求激波角β，p2/p1 ,T2/T1，ρ2/ρ1，p2*/p1*和Ma2。

（2）对应Ma1=2.5，为了使激波不脱体，求尖劈角δ允许的最大值。

6.16  一正激波以速度V1=722.4 m/s在静止空气中运动，静止空气的静压为1 × 10⁵ Pa，温度为294.4K试计算波后（相对于静止观察者）空气的马赫数、静压、温度和速度。

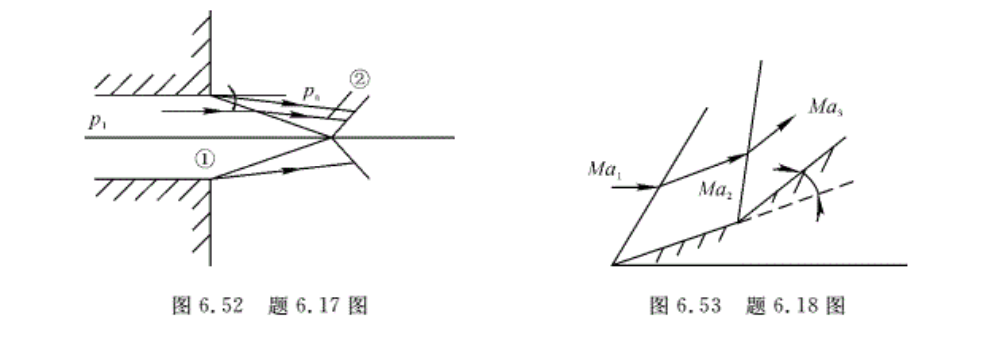
6.17  超声速空气流由平面喷管中射出，如图6.52所示。已知喷管出口的流动参数 Ma1=1. 5，p1=0.7825 × 10⁵ Pa，管外大气压强pa=1 × 10⁵ Pa。试求喷管出囗②区内的 Ma2，并求激波角β和气流折转角δ的大小。

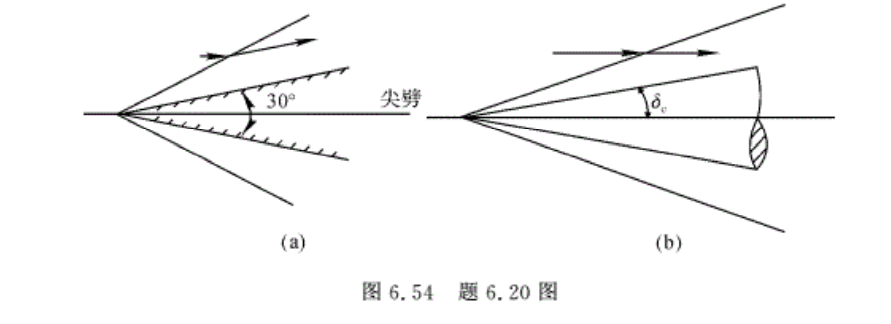
6.18  如图6.53所示，Ma1=2.0，p1=1 × 10⁵ Pa的超声速气流遇尖劈折转20°。求激波角β，p2，M2和p2*/p1*。若分两次折转，每次折转10°时，再求p2*/p1*。

6.19  己知斜激波前、后静压比p2/p1=2.6003（介质为空气），求此斜激波前、后总压比p2*/p1*。

6.20  （1）如图6.54（a）所示，Ma1=2.0，p1=1.0133 ×10⁵ Pa，T1=288.15K的空气流对称地流过一尖劈角为30°的尖劈。试计算激波角β、波后气流的马赫数Ma2和静压p2、静温T2。

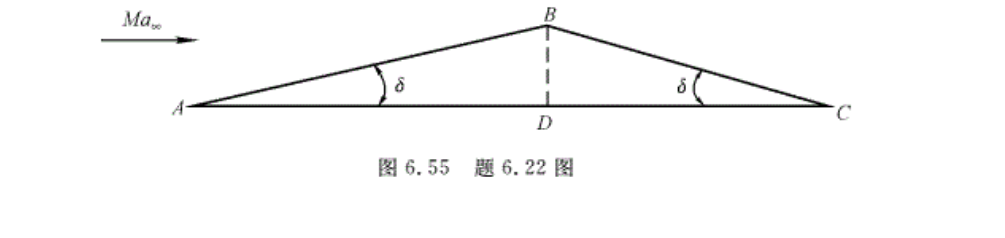
（2）Ma1=2.0，p1=1.0133 ×10⁵ Pa，T1=288.15K的空气流对称地流过一半顶角为δc=15°的圆锥体（见图6.54（b）)。试计算激波角βc、波后气流的折转角δ、压强p、温度T和马赫数，以及锥面上气流的Mas，ps和Ts。

6.21  在p1=1.0133 × 10⁵ Pa的超声速空气流中，放一个皮托总压管，测得的压强为 2.6 × 10⁵ Pa。试求该超声速气流的马赫数。

6.22  空气流过如图6.55所示的物体，来流方向与下壁面平行。己知Ma1=3.0，p1=1 × 10⁴Pa，δ=18°。试计算物面上气流的马赫数和静压。若设BD=0.1m，垂直于纸面的厚度为1. 0 m，计算沿来流方向气流作用于物体上的力。