第七章 一维定常可压缩管內流动
所谓的一维定常可压缩管流是指垂直于管道轴线的每个截面上的流动参数保持均匀一致,且不随时间变化的流动。在这种流动中,气体压缩性影响显著,对于超声速流动,还可能会出现激波和膨胀波等一些特有的现象。对于工程中所遇到的管内高速流动,其管道的截面积可以是圆形的,也可以是方形或任意的形状。管道的中心线可以是直线,也可以是曲线,但曲率半径应足够大。一维定常可压缩管流所涉及的内容很广,例如,截面积无急剧变化的变截面管流(如超声速风洞的尾喷管,亚声速和超声速扩压器,喷气发动机的尾喷管和叶栅通道内的流动等),气流在等截面摩擦管内的流动(各种各样的气体输送管道、煤气管道、天然气管道、蒸汽管道等),以及等截面的有热交换的管流(如发动机燃烧室),等等,我们把这些流动看做一维流动来分析计算,虽然有一定的近似,但大大地简化了问题的难度,是工程问题常采用的方法。
气体在管道内的实际流动,通常涉及的因素很多。例如,管道截面积的变化、传热、摩擦、加入或引出气流和化学反应等;在实际管流中,往往又是多种因素同时在起作用;除此之外,当马赫数较高、温度较高或温度变化较大时,还必须考虑变比热容的影响;等等。但是,在各类实际管流中,各种因素的作用时强时弱。例如,在变截面管流中,如果没有加热或冷却,而且管道较短,流速很高,黏性摩擦对气流参数的影响较小,同时高速气流与管壁接触的时间很短,则对外界的散热量也较小。这种情况下可以先忽略摩擦和散热等因素,而仅仅考虑截面积变化对气流参数的影响,把这种流动看做是无黏性的、无热交换的一维定常变截面管流来分析是方便的。如果气体温度不高且变化不太大,则可以作为定比热的完全气体来处理。如果管道较长,截面面积变化不大,可以作为等截面的摩擦管流来处理。如果有热量的交换而截面面积变化不大,则可以看做等截面的换热管流(如发动机的燃烧室)来处理。这样可抓住主要因素分析其流动规律,然后根据具体问题做必要的修正。
本章主要讨论一维定常可压缩的变截面管流、等截面摩擦管流、换热管流等和变流量加质管流。
7.1 理想气体在变截面管道中的流动
本节主要讨论管道截面积变化对气流参数的影响,以及在变截面管道中的流动分析及计算问题。在讨论中假设:
(1)管内气流与外界没有热量和功的交换;
(2)不计管壁与气体间的摩擦作用;
(3)没有质量的加入或引出;
(4)流动是一维定常的;
(5)所讨论的气体为定比热的完全气体。
气体在航空涡轮喷气发动机压气机的静于叶片、涡轮导向器以及各种吸气式发动机的进气道、尾喷管等部件内的流动,如果气流中没有激波且不计气流与管壁的摩擦,则可将它们看做是一维定常变截面等熵流动。
一、基本方程
为了更清楚地了解截面积变化对流动参数影响的物理过程,本节从微分形式的基本方程出发,来讨论截面积变化对气流参数的影响。
一维定常流动连续方程的微分形式为
\(\frac{d\rho }{\rho }+\frac{dA}{A}+\frac{dV}{V}=0\) (7.1)
一维定常理想流动的动量方程的微分形式为dp=-ρVdV,考虑到
\(M{{a}^{2}}=\frac{{{V}^{2}}}{{{c}^{2}}}=\frac{\rho {{V}^{2}}}{kp}\)
则
\(\frac{dp}{p}+kM{{a}^{2}}\frac{dV}{V}=0\) (7.2)
绝能流动能量方程的微分形式为
\({{c}_{p}}dT+VdV=0\)
进一步可化成
\(\frac{dT}{T}+\left( k-1 \right)M{{a}^{2}}\frac{dV}{V}=0\) (7.3)
由状态方程p=ρRT,取对数后并进行微分得
\(\frac{dp}{p}-\frac{d\rho }{\rho }-\frac{dT}{T}=0\) (7.4)
根据Ma的定义,Ma=V/√(kRT),取对数后微分得
\(\frac{dMa}{Ma}-\frac{dV}{V}+\frac{dT}{2T}=0\) (7.5)
在式(7.1)~式(7.5)的5个等熵流动的基本方程中,包含6个变量,即dp/p,dρ/ρ,dT/ T,dV/V,dMa/Ma和dA/A。若将dA/A看做独立变量,则可从上述方程组中解出其余5个变量与dA/A的关系式,即
\(\frac{dp}{p}=\frac{kM{{a}^{2}}}{1-M{{a}^{2}}}\frac{dA}{A}\) (7.6)
\(\frac{d\rho }{\rho }=\frac{M{{a}^{2}}}{1-M{{a}^{2}}}\frac{dA}{A}\) (7.7)
\(\frac{dT}{T}=\frac{\left( k-1 \right)M{{a}^{2}}}{1-M{{a}^{2}}}\frac{dA}{A}\) (7.8)
\(\frac{dV}{V}=-\frac{1}{1-M{{a}^{2}}}\frac{dA}{A}\) (7.9)
\(\frac{dMa}{Ma}=-\frac{2+\left( k-1 \right)M{{a}^{2}}}{2\left( 1-M{{a}^{2}} \right)}\frac{dA}{A}\) (7.10)
二、管道截面积变化对气流参数的影响
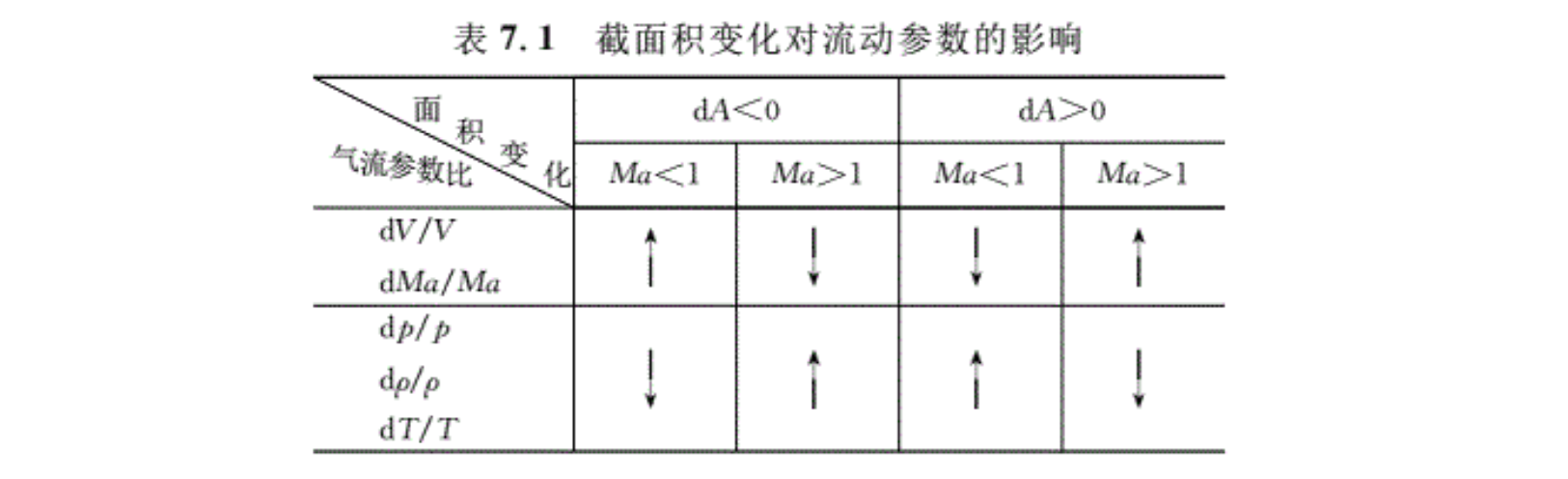
根据方程式(7.6)~式(7.10)的,可以分析面积变化对气流参数的影响,其结果综合成表7.1。表中,“↑”表示增,“↓”表示减小。由表7.1可以看出下述问题。
(1)对亚声速流(Ma < 1):
在收缩形管道中,速度和马赫数增大,压强、密度和温度减小;
在扩张形管道中,速度和马赫数减小,压强、密度和温度增加。
在亚声速气流中,dV与dA异号,表明速度变化与面积变化的方向相反。可见,在收缩形管道内(dA< 0),亚声速气流加速(dV> 0),这种使亚声速气流加速的管道叫亚声速喷管,如图 7.1(a)所示;而在扩张形管道内(dA>0),亚声速气流减速(dV<0),压强增加,这种使亚声速气流减速增压的管道叫亚声速扩压器,如图7.1(b)所示。
因此,亚声速气流在收缩形管道内(dA < 0),气流加速(dV >0);在扩张形管道内 (dA>0),气流减速(dV<0)。
(2)对超声速流(Ma > 1 ):
在收缩形管道中,速度和马赫数减小,压强、密度和温度增加;
在扩张形管道中,速度和马赫数增加,压强、密度和温度则减小。
在超声速气流中,dV与dA同号,表明速度变化与面积变化的方向相同。可见超声速流动与亚声速流动规律完全相反。在收缩形管道内(dA < 0),沿流动方向,超声速气流减速,压力、密度和温度增,这种使超声速气流减速增压的管道叫超声速扩压器,如图7.1(c)所示。反之,在扩张形管道内(dA>0),沿流动方向,超声速气流加速,压强、密度和温度下降。这种使超声速气流速的管道叫超声速喷管,如图7.1(d)所示。
因此,超声速气流在收缩形管道内(dA < 0),气流减速(dV < 0);在扩张形管道内(dA > 0),气流是加速的(dV> 0) 。
(3)在声速气流(Ma=1)中:由式(7.6)~式(7.10)可知,实际上,由于dV,dT,dp,dρ, dMa都不会趋于无穷大,因此,当Ma=1时,必有dA=0,该截面即为临界截面。在第六章中己经证明过临界截面一定是管道的最小截面。这就是说,气流速度只能在管道的最小截面处达到当地声速。因为当Ma < 1时,要使气体加速,必有dA < 0,所以根据dA=0的这一条件,流动达到声速时管道的截面积必定最小,即声速截面必定是管道的最小截面,叫管道的喉部。但需要强调的是,最小截面不一定是管道的临界截面,因为最小截面是否达到声速还必须要由一定的前后压强差来决定。例如,当进出口压强差不大时,如果进口是亚声速气流,则整个管内的流动可能都是亚声速的,最小截面处速度最大。同样当进出口压强差不大时,若进口马赫数大于1,则整个管内的流动可能都是超声速的,最小截面处速度最小。
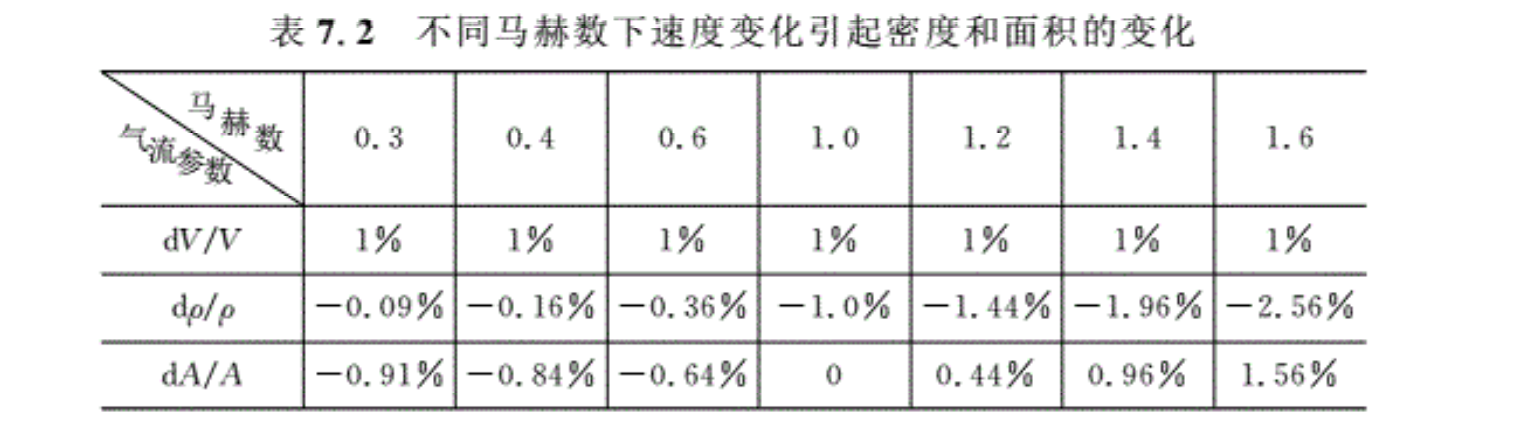
通过上面的讨论,可以看出,管道截面积的变化,对亚声速流动和超声速流动有本质上的区别,这种本质上差别的物理原因是由于在不同马赫数时气流的压缩性不同。由表7.2可知,无论是超声速气流,还是亚声速气流,密度ρ的变化和速度V的变化方向总是相反的。气流加速时,密度减小;气流减速时,密度增大。但是,对于不同Ma的气流,两者密度随气流速度变化的大小是不同的。表7.2列出了按照式(7.7)和式(7.9)计算的一些数值,这是按速度增加1%时,相应的不同Ma时的气流密度变化和面积变化的百分数。例如,对于Ma=0.6的亚声速气流,当速度增大1%时,气流密度减小0.36%,由微分形式的连续方程可知,面积应减小0.64%;而对于Ma=1. 6的超声速气流,当速度增大1%时,气流密度减小2.56%,要满足连续方程,截面积应增加1. 56%,对于Ma < 0.3的气流,速度变化1%,密度变化不到0.09%。
在绝能等熵流动中,一般认为当Ma <0.3时,可以忽略压缩性的影响,而把气流当做不可压流动来处理。Ma较大时,密度变化也较大,这表明气流压缩性随Ma增大而增大。但是在亚声速气流中,密度变化总是小于速度变化;对于超声速气流(Ma > 1 ),密度变化则比速度变化大。因此,对于影响流量的乘积,在亚声速流动的情况下,速度变化起着主要的作用,而在超声速流动的情况下,则是密度变化起着主要的作用。
通过上面的讨论,可以看出,在连续的流动中,由于气流压缩性的影响,要使亚声速气流加速,管道截面积必须逐渐收缩;而要使超声速气流加速,管道截面积必须是逐渐扩张的。因此,要使气流从亚声速加速到超声速,管道形状就应该是先收缩后扩张的。
7.2 收缩喷管
使气流不断加速的管道称为喷管。亚声速气流在截面积逐渐缩小的管道内将不断速,这种管道称为收缩喷管或收敛喷管。收缩喷管在许多试验设备(如校准风洞、叶栅风洞和各种管路系统的喷嘴等)和涡轮喷气发动机中均得到了广泛的应用。在涡轮喷气发动机中,喷管进口的燃气具有较高的总压和总温,在喷管进出口压差的作用下,高温燃气在喷管内膨胀,将气体的热焓转变成动能,到喷管出口,燃气以很高的速度流出,高速喷气使发动机产生很大的反作用推力。
一、喷管出口气流参数的计算
已知收缩喷管进口的总压p*和总温T*,如图7.2所示,喷管出口的外界反压(或称背压)为pb。如果不考虑气体黏性和与外界的热交换,则喷管中的流动为理想的绝能等熵流动,即喷管各截面上的总温和总压都相同。
在这种情况下,面积变化是引起流动参数变化的主要原因。以注脚e和o分别表示喷管出口和进口截面上的气流参数,则由绝能流动的能量方程,有
\[{{c}_{p}}T_{o}^{*}={{c}_{p}}T_{e}^{*}={{c}_{p}}{{T}_{e}}+\frac{V_{e}^{2}}{2}\]
得
\[{{V}_{e}}=\sqrt{2{{c}_{p}}\left( T_{e}^{*}-{{T}_{e}} \right)}=\sqrt{2{{c}_{p}}T_{e}^{*}\left( 1-\frac{{{T}_{e}}}{T_{e}^{*}} \right)}=\sqrt{\frac{2k}{k-1}RT_{e}^{*}\left[ 1-{{\left( \frac{{{p}_{e}}}{p_{e}^{*}} \right)}^{\frac{k-1}{k}}} \right]}\] (7.11a)
根据p*,p与Ma的关系,得
\[M{{a}_{e}}=\sqrt{\frac{2}{k-1}\left[ {{\left( \frac{p_{e}^{*}}{{{p}_{e}}} \right)}^{\frac{k-1}{k}}}-1 \right]}\] (7.11b)
因此,如果知道气流的马赫数或速度因数,也可以用下式计算速度:
\[{{V}_{e}}=M{{a}_{e}}{{c}_{e}}={{\lambda }_{e}}{{c}_{cr}}\] (7.11c)
从式(7.11a)可以看出,喷管出口截面上的气流速度主要取决于气流总温Te*和压强比pe/pe*。对于给定的气体,气体总温越高,喷管出口截面上气流速度越大,压强比pe/pe*越小,气流速度也越大,发动机所获得的反作用推力也越大。
在喷管流动计算中,一般喷管的几何形状和气体性质是己知的,即喷管出口面积、气体性质R和k是己知的。若进囗总压和总温己知,则只需求出出口压强或出口马赫数,即可由以上各式求出出口截面上的其他所有气流参数和通过喷管的流量。
二、临界压强比
亚声速气流在收缩形管道中的最小截面(出囗截面),速度最大只能等于当地声速,即出口截面上的气流Mae。最大只能达到1。若记当Mae=1时的压强比p e,cr/pe*为临界压强比,用βcr表示,则有
\[{{\beta }_{cr}}=\frac{{{p}_{e,cr}}}{p_{e}^{*}}={{\left( \frac{2}{k+1} \right)}^{\frac{k}{k-1}}}\] (7.12)
对于空气,k=1.4,βcr=0.5283;对于燃气k=1.33,βcr=0.5404。
通过喷管的流量为
\[{{q}_{m}}=K\frac{p_{e}^{*}}{\sqrt{T_{e}^{*}}}q\left( {{\lambda }_{e}} \right){{A}_{e}}\] (7.13a)
或
\[{{q}_{m}}={{\rho }_{e}}{{V}_{e}}{{A}_{e}}\] (7.13b)
当压强比pe/pe*下降时,λe将随之增大,因而q(λe)也随之增大,由上式可见,通过喷管的流量也相应地增大。当出囗截面上的气流压强比达到βcr时,由于λe=1,q(λe)=1,则流量达最大值,即
\[{{q}_{m,\max }}=K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}{{A}_{e}}\] (7.14)
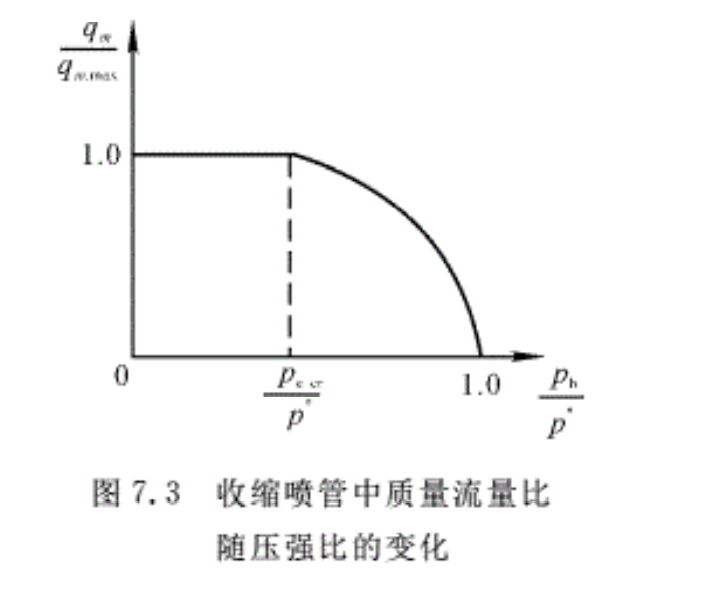
其流量比随pb/p*的变化如图7.3所示。
由图可见,当pb/p*较大时(大于p e,cr/p*)由于反压较大(p*给定),因而喷管出口流速小于当地声速,此时喷管出口压强与外界反压相等,反压增加,出口压强也增加;反压减小,出口压强pe也减小。因此,在来流总压不变的情况下,随着pb减小,λe增大,q(λ)也随之增大,相应地pe/p*减小。由式(7.11a)可知,排气速度Ve提高,因而通过喷管的流量增大。一旦pb/p*=βcr,,由于喷管出囗马赫数等于1,因此流量达到最大值qm,max,之后随pb减小,流量保持最大值。
三、收缩喷管的工作状态
气流在收缩喷管内膨胀加速的程度既取决于管后压强pb,也取决于喷管进囗的总压p*,因此,用压强比pb/p*来代表气流的膨胀加速的程度是方便的。在分析喷管内的流态时,假设来流p*,T*不变,而反压pb变化。
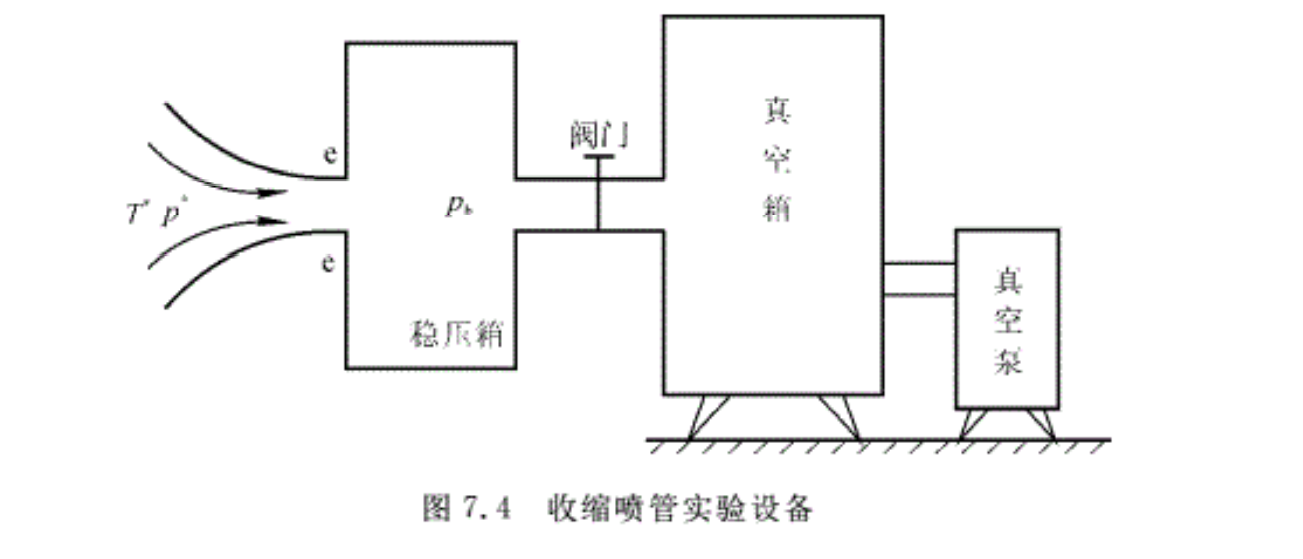
下面来分析如图7.4所示收缩喷管内的流动。收缩喷管后接一个稳压箱,稳压箱内的压强(即管后压强pb,叫反压或背压)随着阀门的逐渐开大而减小,当反压略低于来流总压时,气流在管内不断加速流动。若反压逐渐减小(或来流总压p*增大),则pb/p*不断减小,管内流速开始加大,即气流在收缩喷管内加速流动,通过喷管的流量也相应地加大。此种情况下,整个喷管是亚声速流动,如果此时改变反压pb,则这种扰动可以向管内传播。由于Mae< 1,所以pb/p* >βcr,这种流动状态称为亚临界流动状态,喷管出口压强等于反压,即然pe=pb,气体在喷管内得到完全膨胀,出囗后的流动是平行流动,如图7.5(a)所示。
随着pb/p*的不断降低,喷管出口流速进一步加大,当喷管出口速度等于当地声速时,出口马赫数等于1,此时pe=pb,且气流在喷管内仍能得到完全膨胀,流量达到最大值qm,max。这种Mae=1,pe/p*=pb/p*=βcr的流动状态称为临界流动状态。喷管出囗后的气流仍是平行流动,如图7.5(a)所示。
Pb/p*进一步减小,由于喷管出口已是临界截面,反压变化引起的扰动不会逆流传播,所以扰动不能影响管内的流动。出口截面仍维持pe=βcrp*,Mae=1的临界状态,这种流动状态称为超临界流动状态。此时在喷管出囗处的气流压强没有完全膨胀到外界反压,pe>pb,即pb/p*< βcr。这种流态又称为未完全膨胀状态,气流在出口截面之后继续膨胀,如图7.5(b)所示。气流在出口之后经历一个由膨胀波和压缩波组成的复杂波系。
上面所述是在进口气流总压不变的情况下,改变反压pb所得到的结果。如果来流总压不断增大,出口反压不变,则此时pb/p*将不断减小,也可以得到同样的结论。
总之,收缩喷管的流动状态及特点如下:
(1) pb/p*>βcr时,为亚临界流动状态,此时Mae< 1,pe=pb,气流在喷管内得到完全膨胀;
(2)当pb/p*=βcr时,为临界流动状态,此流态的特点是Mae=1,pe=pb=p*βcr,气流在喷管内得到完全膨胀;
(3)当pb/p*<βcr时,为超临界流动状态,此时喷管出口马赫数 Mae=1,pe>pb,且pe=p*βcr,气流在喷管出口未达到完全膨胀状态。
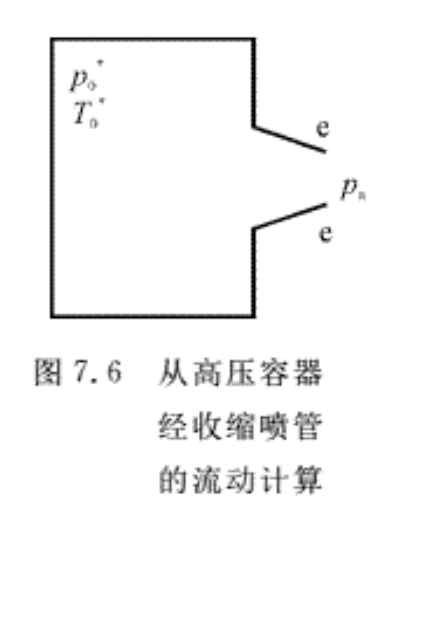
例7.1 高压容器内的空气通过一收缩形喷管等熵地膨胀到外界大气压强,如图7.6所示。己知容器内的压强为7.0 × 105 Pa,温度为 288 K,大气压强为1. 0133 ×105 Pa,喷管出囗面积为0.0015㎡。求:
(1)初始空气的出口速度Ve和通过喷管的流量qm。
(2)设容器体积为1m³,求保持此状态的时间。
解:高压容器内的初始压强为初始总压po*,温度为总温To*。
(1) \(\frac{{{p}_{a}}}{p_{0}^{*}}=\frac{1.0133}{7.0}=0.1448{{\beta }_{cr}}\)
流动为超临界状态,因此,Mae=1. 0,有
\[\begin{align}& {{p}_{e}}=p_{0}^{*}{{\beta }_{cr}}=7.0\times {{10}^{5}}\times 0.5283=3.6981\times {{10}^{5}}Pa \\& {{V}_{e}}={{c}_{cr}}=\sqrt{\frac{2kRT_{0}^{*}}{k+1}}=\sqrt{\frac{2.8\times 287.06\times 288}{2.4}}=310.57m/s \\\end{align}\]
通过喷管的流量为
\[{{q}_{m}}={{q}_{m,\max }}=K\frac{p_{0}^{*}}{\sqrt{T_{0}^{*}}}{{A}_{e}}=0.0404\times \frac{7.0\times {{10}^{5}}}{\sqrt{288}}\times 0.0015=2.5kg/s\]
(2)求维持超临界状态的时间。随着空气的不断流出,容器内的压强不断下降,当容器内的压强值降低到临界状态的压强值时,即p*=pcr*=pa/βcr时,该流态将不能再维持下去,故终了状态的总压
\[p_{cr}^{*}=\frac{1.0133\times {{10}^{5}}}{0.5283}=1.918\times {{10}^{5}}Pa\]
根据连续方程,有
\[-\frac{dm}{dt}=K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}{{A}_{e}}={{q}_{m,\max }}\]
即 \(d\left( -\frac{{{p}^{*}}}{R{{T}^{*}}}\upsilon \right)=K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}{{A}_{e}}dt\)
故
\[\begin{align}& t=-\int{\frac{\sqrt{{{T}^{*}}}}{K{{p}^{*}}{{A}_{e}}}}d\left( \frac{{{p}^{*}}}{R{{T}^{*}}}\upsilon \right)=-\int\limits_{p_{0}^{*}}^{p_{cr}^{*}}{\frac{\upsilon }{RK\sqrt{{{T}^{*}}}{{A}_{e}}}}\frac{d{{p}^{*}}}{{{p}^{*}}}=\frac{\upsilon }{RK\sqrt{{{T}^{*}}}{{A}_{e}}}\ln \frac{p_{0}^{*}}{p_{cr}^{*}}= \\& \frac{1}{0.0104\times 287.06\times 0.0015\sqrt{288}}\ln \frac{7.0\times {{10}^{5}}}{1.918\times {{10}^{5}}}=4.39s \\\end{align}\]
四、收缩喷管的壅塞状态
当气流处于临界和超临界状态时,喷管出囗截面上的气流Mae=1,出囗截面是临界截面,通过喷管的流量达到最大值,即qm=qm,max=Kp*Ae/√T*。由于喷管出囗截面气流速度等于声速,因而反压进一步降低,不能使出口截面上的气流马赫数继续增大,也不能使喷管流量继续增大,因此称流量达到最大值,Mae=1的流动状态为壅塞状态。一旦喷管处于壅塞状态,喷管出口外界反压便不再能影响喷管内的流动。而且由q(Ma)=Ae/A可知,无论是改变出口外界的反压,还是改变进口气流的总压、总温,都不能使喷管中任一截面上的无量纲参数发生变化。这些无量纲参数有Mac(或λc)、压强比p/p*和温度比T/T*等等。
当pe/p*=pcr/p*时,喷管内的流动处于壅塞(附塞)流动状态,此时,如果单纯增加总温,则马赫数Mae,压力比pe/p*保持不变,而Ve=λeccr将增大。因此,在涡轮喷气发动机中,常通过采用提高燃气总温的办法来增加排气速度,以提高发动机的推力。如果单纯增加进口气流总压,则马赫数Mae和压力比pe/p*仍保持不变,由式(7.11a)可知,出口气流速度保持不变。而出口气流的压强pe随总压的提高而增大,流量也随总压成比例地增大。在壅塞状态下,由于扰动不会越过声速面而逆流传播,因此,降低反压也无法使喷管出口截面参数和通过喷管的流量发生变化。在壅塞状态下,如果只增加喷管出口面积,则Mae,pe/p*,Ve和pe均保持不变,仅流量qm随出囗面积Ae成比例地增加。
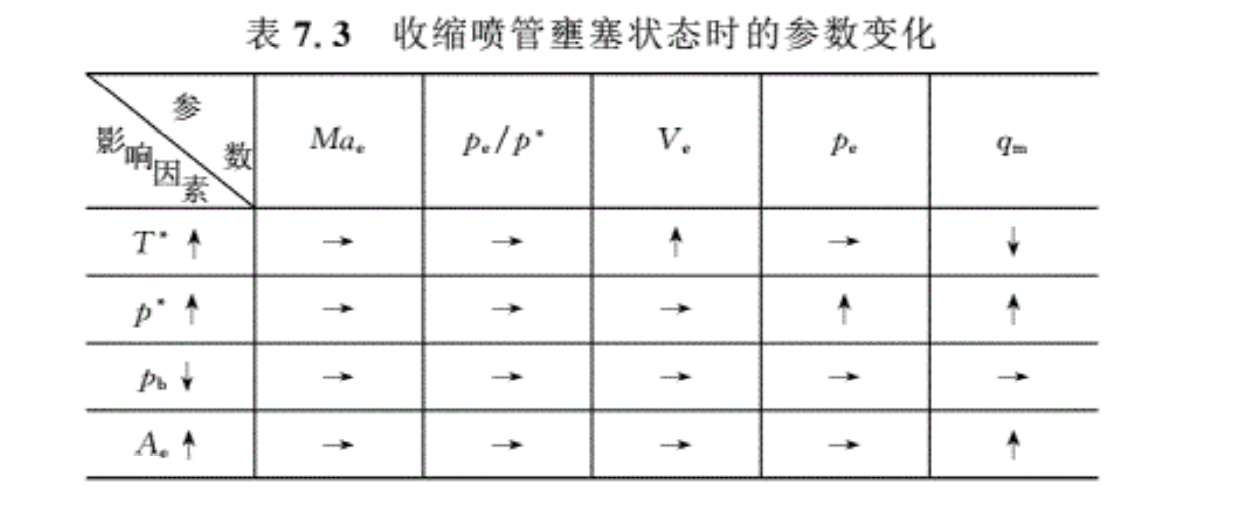
按照壅塞状态的特点,可以归纳出在壅塞状态下各种因素对气流参数的影响,见表7.3。表中,“→”表示不变,“ ↑”表示增,“↓”表示减小。
从表7.3可以看出,在壅塞状态下,对流量的影响因素有喷管进口的总压、总温和喷管出口的面积。因此,在涡轮喷气发动机中,常在喷管前对燃气进行二次喷油燃烧(称为加力燃烧),以提高气流的总温,同时增大出囗面积以保持流量不变,采取这样的方式可以增加推力。
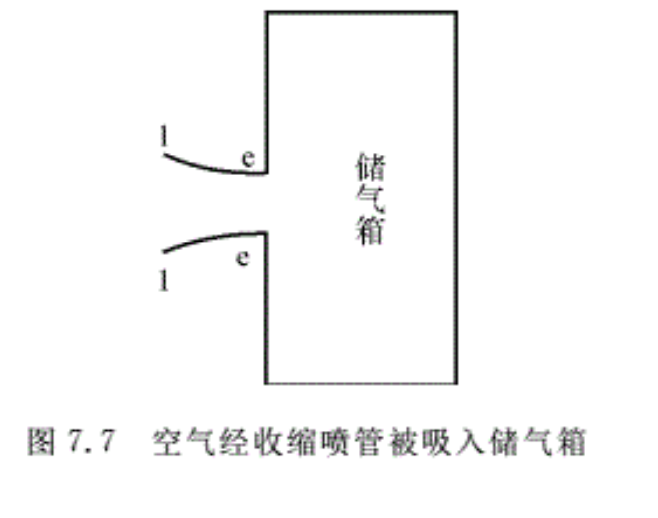
例7.2 空气在如图7.7所示的收缩喷管中流动,己知进囗参数为V1=250 m/s,p1=2.22 × 105 Pa,T1=899 K,反压pb=0.98 × 105Pa,试计算喷管出口处的压强、温度、速度和马赫数。
解:设流动是绝能等熵的,则滞止参数保持不变。由进口参数可计算出总温和总压分别为
\[\begin{align}& T_{1}^{*}={{T}_{1}}+\frac{V_{1}^{2}}{2{{c}_{p}}}=899+\frac{{{250}^{2}}}{2\times 1004.5}=930K \\& p_{1}^{*}={{p}_{1}}{{\left( \frac{T_{1}^{*}}{{{T}_{1}}} \right)}^{\frac{k}{k-1}}}=2.22\times {{10}^{5}}\times {{\left( \frac{930}{899} \right)}^{3.5}}=2.5\times {{10}^{5}}Pa \\\end{align}\]
因为pb/p*=0.392,pb/p*小于临界压强比βcr,所以喷管处于超临界状态,即该喷管在壅塞状态下运行,出口Mae=1. 0,故可求得出囗参数为
\[\begin{align}& {{p}_{e}}={{p}^{*}}{{\beta }_{cr}}=2.5\times {{10}^{5}}\times 0.5283=1.32\times {{10}^{5}}Pa \\& {{T}_{e}}={{T}^{*}}\tau \left( {{\lambda }_{2}} \right)=930\times 0.8333=774.9K\left( {{\lambda }_{2}} \right)=1 \\& {{V}_{e}}={{c}_{e}}=\sqrt{kR{{T}_{e}}}=\sqrt{1.4\times 287.06\times 774.9}=558m/s \\\end{align}\]
五、收缩喷管壁面设计
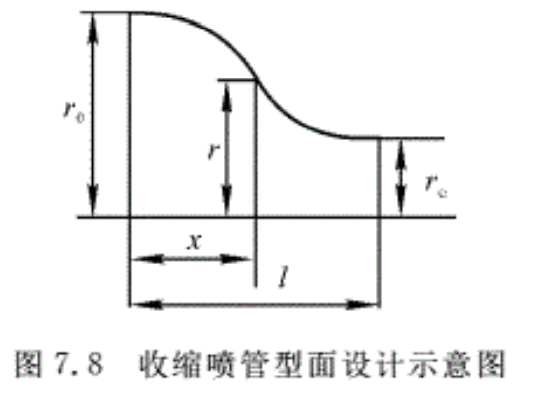
设计收缩喷管时,一般要求在喷管出口产生均匀的流动。只有设计得很平滑的壁面,才能使气流在喷管中逐渐得到膨胀。保证进口截面产生的横向压强梯度和径向分速逐渐减小,并在出口截面上趋于零,从而获得均匀的出口流场。一般认为比较满意的是用维托辛斯基公式来计算壁面的型线,其公式为
\[{{\left( \frac{{{r}_{e}}}{r} \right)}^{2}}=1-\left( 1-\frac{1}{C} \right)\frac{{{\left[ 1-{{\left( \frac{x}{l} \right)}^{2}} \right]}^{2}}}{{{\left[ 1+\frac{1}{3}{{\left( \frac{x}{l} \right)}^{2}} \right]}^{3}}}\] (7.15)
式中,C表示收缩比,C=(ro/re)²,其他各参数的意义示与图7.8中。其中l是选定的(l>ro),它可以在宽广的范围内变动,这种型面的喷管适合于连接两个不同尺寸的管道,它用在亚声速风洞上;而ro是给定的尺寸;re是喷管的喉部半径。在具体设计时,根据经验,若取ro=2re,且当l=2ro/3,收缩曲线可以获得较好的气流品质。此种方法既适用于轴对称喷管,又适用于矩形或二维收缩喷管。此时C为单边的收缩比。当收缩比较大(C> 4)时,则曲线前部分收缩很陡,而后段却很近似平直,这样对得到均匀的气流是不利的。在这样的情况下,可以采用移轴(即“加R “)的办法来修正。采用这种方法设计收缩型线,可得到较好的气流品质。具体做法如下:
\[\begin{align}& r_{0}^{\prime }={{r}_{0}}+R \\& r_{e}^{\prime }={{r}_{e}}+R \\\end{align}\]
令 ro=2re′
得 R=ro-2re
式中,R为半径的移轴量。用ro′,re′代入式(7.15)计算出来的曲线坐标,再减去R后即得到收缩比C=(ro/re)²情况下的收缩喷管型线的坐标。
经验表明,用维氏公式来计算壁面的型线,一直到λ=0.9~0.95的宽广速度范围内,喷管后的速度场是足够均匀的。
由于附面层的影响,在设计喷管时,还要对型面修正一个附面层位移厚度(见第十章)。当喷管直接连接在储气罐后面时,其壁面型线可以是圆弧线、双曲线或抛物线等。
7.3 拉伐尔喷管
一、基本概念与等熵面积比公式
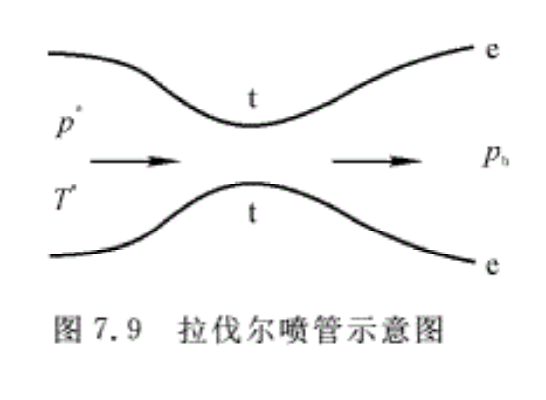
使气流由亚声速加速到超声速的收缩一扩张喷管称为拉伐尔喷管,如图7.9所示。它主要用来产生超声速气流。拉伐尔喷管在超声速及高超声速风洞喷管、超声速飞机、火箭的尾喷管上得到广泛应用。
在实际发动机中,当涡轮出囗的气流压强较高时,若采用收缩喷管,则由于气流在喷管内不能得到完全膨胀而造成较大的推力损失。为了提高发动机的推力,需要采用拉伐尔喷管。
由于采用拉伐尔喷管是为了在其扩张段产生超声速气流,因此在这种情况下就有可能会出现激波。超声速气流通过激波是非等熵流动,因此拉伐尔喷管内的流动在一般情况下,是绝能非等熵流动。但是在不出现激波时,或出现激波时的激波前、激波后的流动区域,可作为绝能等熵(不计摩擦影响)流动来处理。
对于己设计好的拉伐尔喷管,要分析拉伐尔喷管内的流动状态及特点。通常已知的条件有:进口气流总压p*、总温T*,喷管出口外界反压pb和面积比Ae/At(下标e,t分别表示喷管出囗和喉部处的参数,如图7.9所示)。
亚声速气流在如图7.9所示的拉伐尔喷管的收缩段加速,到最小截面(喉部)速度等于当地声速(即Mat=1),在扩张段内进一步加速到出口的超声速气流。在这种流动中没有激波存在,如果不计摩擦,流动是绝能等熵的。对喉部与任一截面写出连续方程,即可得到所谓的等熵而积比公式,即
\[\frac{{{A}_{cr}}}{A}=q\left( \lambda \right)\] (7.16a)
或 \(\frac{A}{{{A}_{cr}}}=\frac{1}{Ma}{{\left[ \left( 1+\frac{k-1}{2}M{{a}^{2}} \right)\frac{2}{k+1} \right]}^{\frac{k+1}{2\left( k-1 \right)}}}\) (7.16b)
式中A——喷管任一截面的面积;
Acr——喷管喉部面积。
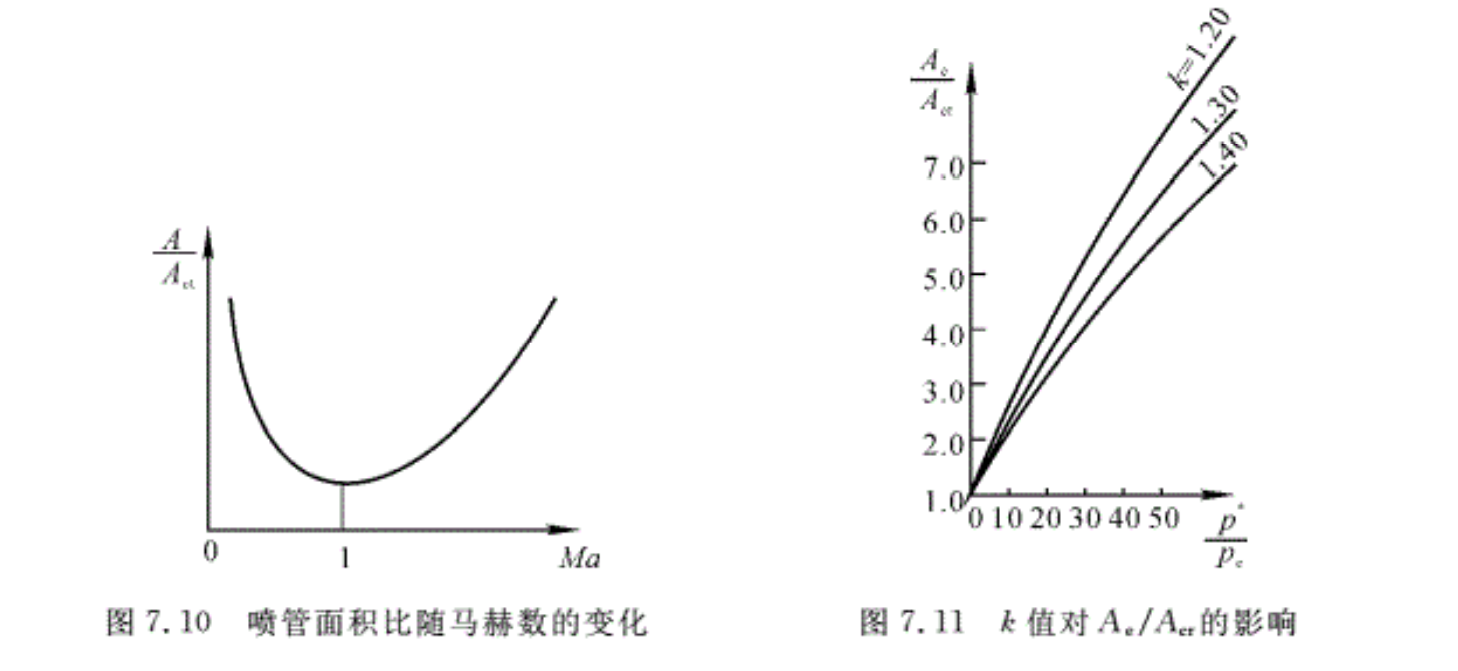
应当注意,式(7.16a)在喉部与截面A之间不存在激波时才能使用。当然截面A可以位于喷管的超声速段,也可以位于亚声速段。由式(7.16)可以看出,对于给定的气体,面积比仅与Ma有关,其变化规律如图7.10所示。由图可以看出,要在喷管出口截面上产生一定Mae 的超声速气流,所对应的喷管面积比Ae/Acr是唯一的。另外,每一个面积比,对应着两个马赫数,一个是亚声速气流的Ma,一个是超声速气流的Ma。
拉伐尔喷管出口截面上的气流速度仍可按式(7.11)计算。对于拉伐尔喷管,由于Mae与面积比Ae/Acr对应,而Mae又与压强比有关,因此,压强比也对应一定的面积比。从面积比公式(式(7.16))可以看出,造成一定出口马赫数Mae的喷管面积比Ae/Acr还与k值有关,不同比热比k,对喷管面积比有一定影响,这一点在喷管型面设计时应当注意。图7.11表示出了不同压强比下k值对面积比Ae/Acr的影响。
二、拉伐尔喷管的流动状态
由等熵面积比公式可知,要在喷管出口建立一定马赫数的超声速气流,就必须有一定的管道面积比,但是具备了管道面积比的条件后,能否实现超声速流动,还要由喷管进口的总压p*和外界反压pb来决定。下面分析给定面积比的拉伐尔喷管内可能出现的几种流动状态。
1.临界状态
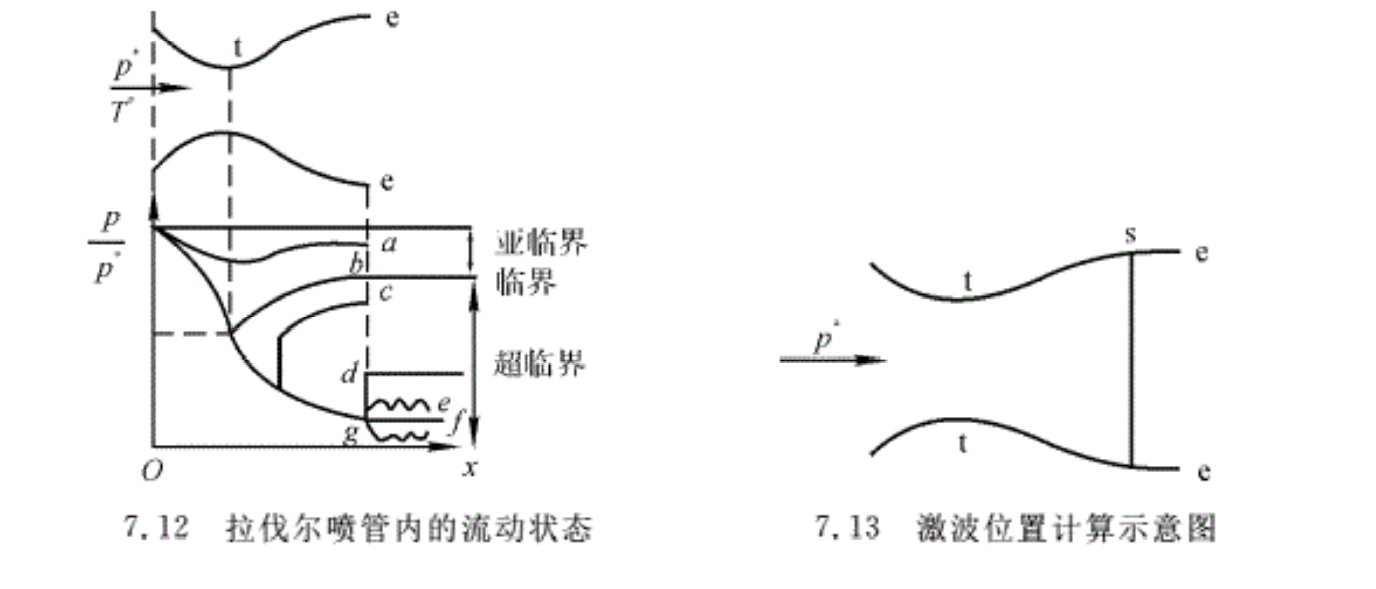
在一个恰当的压强比pb/p*下,气流在收缩段内加速,至喉部马赫数Mat=1,然后在扩张段内减速,至出口Mae< 1,且pe=pb,这种流动状态称为拉伐尔喷管的临界状态。气流的静压沿喷管轴线的变化如图7.12中的曲线b所示。临界状态的特点是Mat=1,Mae< 1,pe=pb(完全膨胀),喷管内无激波,如果不计摩擦,管内的整个流动可视为等熵流动。记临界状态下的出囗压强为p3,即压强比为p3/p*。可见,当pb/p*=p3/p*时,喷管的流动为临界状态。临界状态下的有关参数计算如下:
喷管出口马赫数Mae:由面积比公式(式(7.16a))可计算得到Mae,即
\(q\left( M{{a}_{e}} \right)=\frac{{{A}_{cr}}}{{{A}_{e}}}\) (Mae<1)
出口静压pe与进囗总压p*之比
\(\frac{{{p}_{e}}}{{{p}^{*}}}=\frac{{{p}_{b}}}{{{p}^{*}}}={{\left( 1+\frac{k-1}{2}Ma_{e}^{2} \right)}^{-\frac{k}{k-1}}}=\pi \left( M{{a}_{e}} \right)\)
由于 p3/p*=pe/p*=pb/p* (7.17)
所以p3/p*是面积比Acr/Ae的函数。
通过尾喷管的质量流量
\({{q}_{m,\max }}=K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}{{A}_{t}}\) (7.18)
2.亚临界状态
尾喷管内的流动全部为亚声速时,称为亚临界状态。例如,当pb/p*1时,整个喷管内无流动,静压等于总压且沿尾喷管不变,如图7.12中平行于s方向的直线所示,这是亚临界状态的一种极限情况。
当1.0> pb/p*> p3/p*时,气流在喷管收缩段内加速,至喉部仍然是Mat< 1,之后在扩张段内减速,至出囗Mae< 1,pe=pb,如图7.12中所示的曲线a属于亚临界的流动状态。因此亚临界状态的特点是Mat< 1,Mae< 1,pe=pb,气流在喷管内得到完全膨胀,整个喷管为亚声速流动。亚临界状态的有关参数计算如下:
出口马赫数可按下式计算:
\({{\left( 1+\frac{k-1}{2}Ma_{e}^{2} \right)}^{\frac{k}{k-1}}}=\frac{{{p}^{*}}}{{{p}_{e}}}\)
出口静压 pe=pb
通过喷管的流量 \({{q}_{m}}=K\frac{{{p}^{*}}q\left( {{\lambda }_{e}} \right)}{\sqrt{{{T}^{*}}}}{{A}_{e}}\) (7.19)
3.超临界状态
当pb/p*< p3/p*时,尾喷管内的流动称为超临界状态。
气流在喷管收缩段加速,至喉部Mat=1,之后在扩张段内的流动根据pb/p*的大小不同,可能有下述几种情况。
(1)气流在扩张段内继续加速,至出口Mae> 1,同时气流在喷管出口达到完全膨胀,pe=pb,整个扩张段内无激波,出口外也无激波和膨胀波,静压沿喷管的变化如图7.12中的曲线f所示。这种情况即是所谓的设计状态,记该状态下的压强比pe/p*=p1/p*=pb/p*。可见,当pb/p*=p1/p*时,尾喷管内的流动为超临界状态,且气流在喷管出口达到完全膨胀。
其特点是Mat=1,Mae>1,pe=pb,因此喷管出口的马赫数可用等熵面积比公式计算,即
\(q\left( M{{a}_{e}} \right)=\frac{{{A}_{cr}}}{{{A}_{e}}}\) (Mae>1)
出口静压 pe/p*=pb/p*=p1/p*=π(Mae) (7.20)
pe=pb=p1
通过喷管的流量,由于Mat=1,所以流量达到最大值,仍可用式(7.18)计算。
(2)当pb/p* <p1/p*时,气流在扩张段加速到出口的Mae> 1,气流在喷管内没有得到完全膨胀,即pe/p*>pb/p*,因此超声速气流在喷管出口产生膨胀波束。在这个压强比范围内,反压的变化不会影响喷管内的流动,因为外界的扰动是以声速传播的,而喷管出囗为超声速流动。其流动特点为Mat=1,qm=qm,max,Mae> 1。通常称为欠膨胀流动状态。如图7.12 中的曲线g所示。出口马赫数和通过喷管的流量的计算方法与(1)相同,出口压强pe>pb,pe=p1。对应于超临界状态中管口有膨胀波的流动状态。
(3)当p1/p*<pb/p*≤p2/p*时,在这个压强比范围内,气流在扩张段加速到出口的 Mae> 1,气流在出口将产生斜激波,如图7.12中的曲线e所示。通过斜激波后的压强与外界反压相等,激波强度由压强比pb/p1决定。随着压强比的不断增大,激波不断增强,激波角逐渐加大,当激波角增加到90°,即斜激波变成正激波时,激波后的压强与总压之比记为p2/p*,如图7.12中的曲线d所示。这种流动通常称为过渡膨胀状态。该状态对应于管口有激波的超临界流动状态。
可见,在超临界状态的((1 ),(2)和(3))三种情况下,喷管内部的流动特点完全相同,计算方法也完全一致,不同的仅是喷管出囗后的流动。
压强比p2/p*可以根据激波关系式确定,即
\(\frac{{{p}_{2}}}{{{p}_{1}}}=\frac{2k}{k+1}Ma_{e}^{2}-\frac{k-1}{k+1}\)
因此,可得 \(\frac{{{p}_{2}}}{{{p}^{*}}}=\left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)\times \left( \frac{{{p}_{1}}}{{{p}^{*}}} \right)\) (7.21)
由于Mae,p1/p*与面积比Ae/At有关,所以,p2/p*也与面积比Ae/At有关。
(4)当p2/p*<pb/p*<p3/p*时,在这个压强比范围内,在喷管扩张段内会产生激波,该激波可看做是由于随压强比pb/p*的不断提高,使正激波不断向管内移动的结果。在扩张段内的激波前加速到超声速,压强减小,通过正激波后,压强升高,波后亚声速气流在扩张段减速增压,直到出口处Mae< 1,pe=pb。此时的压强比沿轴线的变化如图7.12中的曲线c所示。此种情况对应于超临界状态管内有激波的流动状态。其流动特点为喉部Mat=1,qm=qm,max。
在一维流动的情况下,当己知喷管面积比、来流总压和反压时,可按下述方法计算管内流动参数和激波位置。设As表示激波所在截面面积,如图7.13所示,则根据出口截面气流压强等于反压的条件,对临界截面和出口截面应用连续方程,即
\(K\frac{p_{t}^{*}}{\sqrt{T_{t}^{*}}}{{A}_{t}}=K\frac{{{p}_{e}}}{\sqrt{T_{e}^{*}}}{{A}_{e}}y\left( {{\lambda }_{e}} \right)\)
式中 \(\begin{align}& {{p}_{e}}={{p}_{b}} \\& T_{t}^{*}=T_{e}^{*} \\& p_{t}^{*}={{p}^{*}} \\\end{align}\)
所以 \(y\left( {{\lambda }_{e}} \right)=\frac{{{p}^{*}}}{{{p}_{b}}}\frac{{{A}_{t}}}{{{A}_{e}}}\) (7.22)
由y(λe)查气动函数表得喷管出口的λe和Mae,然后再次使用连续方程,即
\(K\frac{p_{t}^{*}}{\sqrt{T_{t}^{*}}}{{A}_{t}}=K\frac{p_{e}^{*}}{\sqrt{T_{e}^{*}}}{{A}_{e}}q\left( {{\lambda }_{e}} \right)\)
由此可以计算出通过激波的总压恢复因数,即
\(\sigma \left( M{{a}_{s}} \right)=\frac{p_{e}^{*}}{p_{t}^{*}}=\frac{{{A}_{t}}}{{{A}_{e}}}\frac{1}{q\left( {{\lambda }_{e}} \right)}\) (7.23)
由正激波表可查得激波前的马赫数Mas。由于喉部与激波前之间的流动为绝能等熵的,故由连续方程可得
\(\frac{{{A}_{s}}}{{{A}_{t}}}=\frac{1}{q\left( {{\lambda }_{s}} \right)}\) (7.24)
式中,As为激波所在的截面积。
由以上的分析可知,拉伐尔喷管的流动状态及其特点如下:
Pb/p*>p3/p* 管内全为亚声速流动,为亚临界状态
Pb/p*>p3/p* Mat=1,收缩段和扩张段流动全为亚声速流动,为临界状态
p2/p* <pb/p*<p3/p* 扩张段内有激波,Mat=1,Mae< 1,pe=pb
pb/p*=p2/p* 正激波位于喷管出口,Mat=1,Mae> 1,pe<pb
p1/p* <pb/p*<p2/p* 过膨胀状态,出口有斜激波,Mat=1,Mae> 1,pe<pb
pb/p*=p1/p* 完全膨胀状态,Mat=1,Mae> 1,pe=pb
pb/p*<p2/p* 欠膨胀状态,出口有膨胀波,Mat=1,Mae> 1,pe>pb
总之,三个特征压强比是由面积比At/Ae确定的,即q(λe=At /Ae,查气动函数表,可得两个速度因数,即λe> 1,λe< 1,从而可求出p1/p*=π(λe>1)和p3/p*=π(λe>1),而p2/p*是由λe> 1(Mae> 1 )查正激波表,得到p2/p1,从而计算出p2/p*=(p2/p1)x(p1/p*)。
以上按照一维无黏性流动讨论了拉伐尔喷管的流动特点及其计算方法,实际上的多维黏性流动要复杂得多。
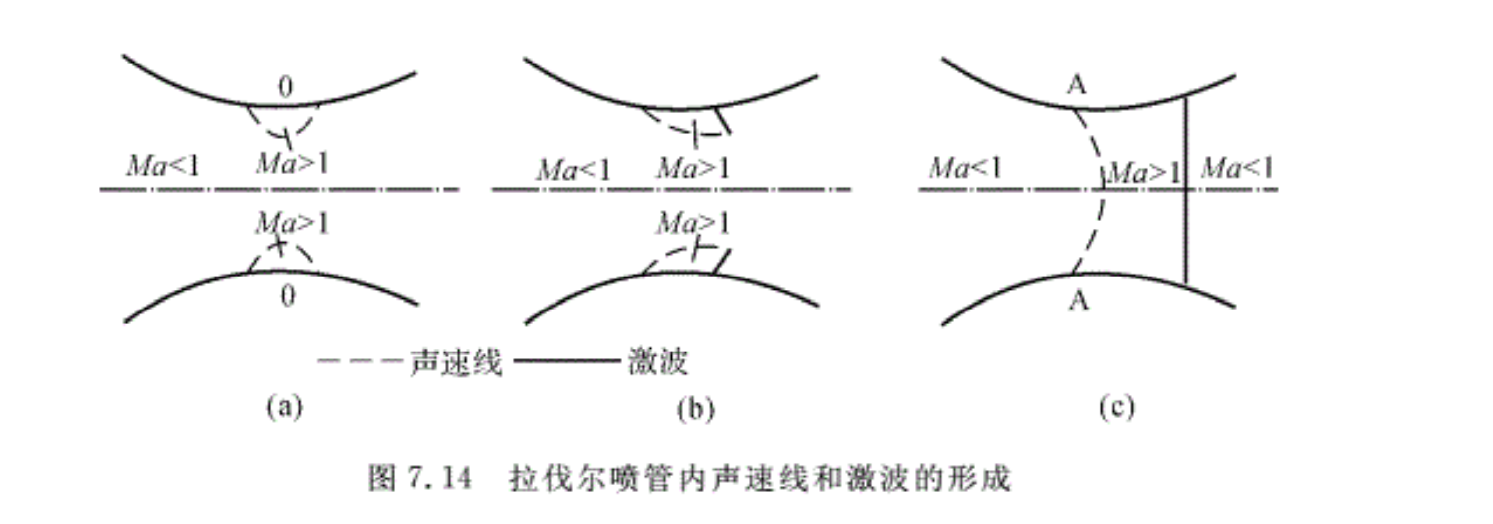
在实际流动中,当气流在喷管内加速时,最大速度点最先出现在喉部壁面的凸点处。如果反压不变,来流总压不断提高,则随着pb/p*的逐渐下降,在凸点附近逐渐形成局部超声速区,如图7.14(a)所示。若pb/p*继续下降,则超声速区继续扩大,会在凸点附近下游局部产生尾激波,如图7.14(b)所示。这是由于随着局部超声速区受到下游亚声速流动的压缩而产生的。由于上、下壁面的对称性,上、下壁面的超声速区逐步相连,形成一个连接亚声速区与超声速区的分界面,即声速线A一A,同时上、下壁面产生的尾激波也连接在一起,最终形成一道正激波,如图7.14(c)所示。
三、拉伐尔喷管计算
拉伐尔喷管内的流动计算一般有两类。一类是正问题,即给定喷管面积比At /Ae、反压与总压之比pb/p*和总温T*,需要计算喷管内的流动状态及参数。这类问题求解步骤是,首先按面积比公式确定三个特征压强比;其次根据给定的pb/p*与三个特征压强比相比较,从而判别实际的流动状态;最后根据流动状态的特点进行计算。
第二类是逆问题,即给定喷管出口Mae,须确定面积比Ae/At和反压比pb/p*。
若Mae< 1,通常不需要采用拉伐尔喷管,利用收缩喷管即可达到要求。
若Mae> 1,此时喉部必然是临界截面,即Mat=1,而且扩张段没有激波。可以使用等熵面积比公式(式(7.16))确定喷管的面积比Ae/At,由Mae可以计算出pe/p*。
根据要求的马赫数分布Ma(x),可以由式(7.16)确定整个喷管的截面积分布A (x)/At。
例7.3 已知某拉伐尔喷管最小截面面积At=4. 0 × 10-4㎡,出口截面面积Ae=6.76 ×10-4㎡。喷管周围的大气压强pa=1 × 105 Pa,气源的温度T*=288 K。当气源的压强p*=1 × 105 Pa时,求:
(1)喷管出口处空气的Ma和空气的流量;
(2)若管中有激波,求激波的位置。
解:这是一个正问题,需要先确定三个特征压强比。首先由面积比公式q(λe)=At/Ae=0.5917,查气动函数表,得λe=1.634 ,Mae=2.0 ,pe/p*=π(λe)=0.128;其次求激波在出囗截面时的压强比p2/p*,即
p2/p*=(p2/p1) x (p1/p*)
由Mae=2.0查正激波表,得p2/p1=4.5,因此有
p2/p*=(p2/p1) x (p1/p*)=4.5 x 0.128=0.576
再求p3/p*,它对应于出口截面和扩张段是亚声速流动,但喉部是处于临界状态的流动,所以仍可用面积比公式。查气动函数表,得λe=0.406,p3/p*=0.909。根据pb/p*=1/1.5=0.6667,又由于p2/p*<pb/p*<p3/p*,所以喷管扩张段内有激波。
(1)计算出口Mae和通过喷管的流量qm。对喉部及出口运用连续方程,即
\(K\frac{p_{{}}^{*}}{\sqrt{T_{{}}^{*}}}{{A}_{t}}=K\frac{p_{e}^{{}}}{\sqrt{T_{{}}^{*}}}{{A}_{e}}y\left( {{\lambda }_{e}} \right)\)
由于出口为亚声速流动,所以 pe=pa
故得 \(y\left( {{\lambda }_{e}} \right)=\frac{{{p}^{*}}{{A}_{t}}}{{{p}_{b}}{{A}_{e}}}=1.5\times 0.5917=0.8876\)
查表得Mae=0.5,λe=0.534,因为λt=1,所以通过喷管的流量为
\({{q}_{m}}=K\frac{p_{{}}^{*}}{\sqrt{T_{{}}^{*}}}{{A}_{t}}=0.0404\times \frac{1.5\times {{10}^{5}}}{\sqrt{288}}\times 4.0\times {{10}^{-4}}=0.1428kg/s\)
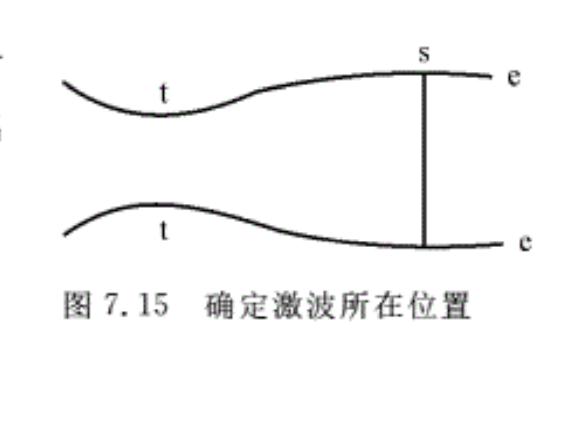
(2)确定激波位置及出口截面速度与总压。设激波位于扩张段某处,其所在处的面积为As,如图7.15所示。由(1 )已求出y(λe),所以由y(λe)=0.8876,查气动函数表,得q(λe)=0.75。
对喉部及出口运用连续方程,即
\[K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}{{A}_{t}}=K\frac{p_{e}^{*}q\left( {{\lambda }_{e}} \right)}{\sqrt{{{T}^{*}}}}{{A}_{e}}\]
得总压恢复因数
\[\sigma =\frac{p_{e}^{*}}{{{p}^{*}}}=\frac{{{A}_{t}}}{{{A}_{e}}}\frac{1}{q\left( {{\lambda }_{e}} \right)}=\frac{4.0}{6.76}\times \frac{1}{0.75}=0.7889\]
由σ=0.7889查正激波表得激波前的马赫数Mas=1.85,由气动函数表查得q(λs)=0.67。
对喉部及激波前运用连续方程,即
\[K\frac{{{p}^{*}}}{\sqrt{{{T}^{*}}}}{{A}_{t}}=K\frac{p_{{}}^{*}q\left( {{\lambda }_{s}} \right)}{\sqrt{{{T}^{*}}}}{{A}_{s}}\]
得
\[\frac{{{A}_{s}}}{{{A}_{t}}}=\frac{1}{q\left( {{\lambda }_{s}} \right)}=\frac{1}{0.67}=1.4925\]
所以激波所处的面积
\[{{A}_{s}}=1.4925\times {{A}_{t}}=1.4925\times 4.0\times {{10}^{-4}}=5.79\times {{10}^{-4}}{{m}^{2}}\]
还可以求出出囗截面的其他参数,例如Ve,pe*等,留给读者自己完成。
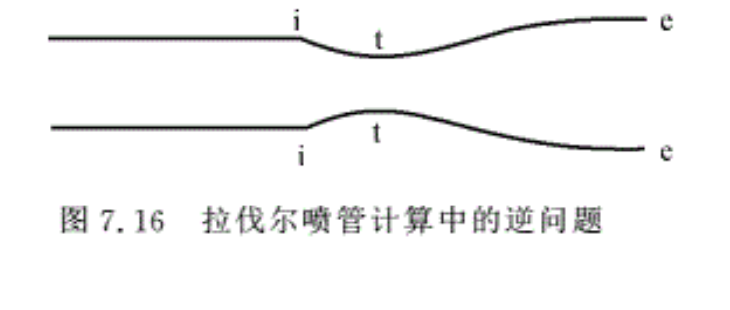
例7.4 一等截面直管后接一拉伐尔喷管,如图 7.16所示,已知直管的截面积为0.15㎡,拉伐尔喷管入口处的压强pi=3.5 × 105 Pa,温度Ti=340 K,马赫数Mai=0.15,喷管出口处的马赫数Mae=1.5。不计摩擦损失,求喷管喉部面积At及出口面积Ae,并计算喉部及出口截面的压强、温度和速度。
解:这是一个逆问题。因为Mae> 1,故喉部是临界截面,即At=Acr,Mat=1,故
\[\begin{align}& T_{i}^{*}={{T}_{i}}\left( 1+\frac{k-1}{2}Ma_{i}^{2} \right)=340\times \left( 1+\frac{0.4}{2}\times {{0.15}^{2}} \right)=341.53K \\& p_{i}^{*}={{p}_{i}}{{\left( 1+\frac{k-1}{2}Ma_{i}^{2} \right)}^{\frac{k}{k-1}}}=3.5\times {{10}^{5}}\times {{\left( 1+\frac{0.4}{2}\times {{0.15}^{2}} \right)}^{3.5}}=3.555\times {{10}^{5}}Pa \\\end{align}\]
喷管进口与喉部运用连续方程,即
\[K\frac{p_{t}^{*}}{\sqrt{{{T}^{*}}}}{{A}_{t}}=K\frac{p_{i}^{*}q\left( {{\lambda }_{i}} \right)}{\sqrt{{{T}^{*}}}}{{A}_{i}}\]
由于不计摩擦损失,绝能等熵流动,故有
\[\begin{align}& T_{i}^{*}=T_{t}^{*}=T_{e}^{*} \\& p_{t}^{*}=p_{i}^{*}=p_{e}^{*} \\\end{align}\]
由Mai=0.15,查气动函数表,得q(λi)=0.260,所以,有
\[{{A}_{t}}={{A}_{i}}q\left( {{\lambda }_{i}} \right)=0.15\times 0.260=0.039{{m}^{2}}\]
喉部与喷管出口运用连续方程,且由于流动为绝能等熵的,由Mae=1.5,查表得q(λe)=0.849,故
\[{{A}_{e}}=\frac{{{A}_{t}}}{q\left( {{\lambda }_{e}} \right)}=\frac{0.039}{0.849}=0.046{{m}^{2}}\]
喉部气流参数
\[\begin{align}& {{p}_{cr}}=p_{i}^{*}{{\left( \frac{2}{k+1} \right)}^{\frac{k}{k-1}}}=3.555\times {{10}^{5}}\times 0.5283=1.8781\times {{10}^{5}}Pa \\& {{T}_{cr}}=T_{i}^{*}\left( \frac{2}{k+1} \right)=341.53\times 0.8333=284.61K \\& {{V}_{cr}}={{c}_{cr}}=\sqrt{kR{{T}_{cr}}}=\sqrt{1.4\times 287.06\times 284.61}=338.2m/s \\\end{align}\]
喷管出口气流参数,由Mae=1. 5查气动函数表,得
pe/p*=π(λe)=0.273,Te/T*=τ(λe)=0.69,λe=1.366
故
\[\begin{align}& {{p}_{e}}=p_{i}^{*}\pi \left( {{\lambda }_{e}} \right)=3.555\times {{10}^{5}}\times 0.273=0.9705\times {{10}^{5}}Pa \\& {{T}_{e}}=T_{i}^{*}\tau \left( {{\lambda }_{e}} \right)=341.53\times 0.69=235.66K \\& {{V}_{e}}={{\lambda }_{e}}{{C}_{cr}}=1.366\times 338.2=461.98m/s \\\end{align}\]
例7.5 已知空气在拉伐尔喷管中流动时,进囗气流总压为1. 523 × 105 Pa,总温为900K,出囗反压为1.0133 ×105 Pa,喷管面积比At/Ae0.2857。
(1)确定喷管内的流动状态;
(2)若管内有激波,求激波位置以及喷管出口速度。
解:这是一个正问题。
(1)首先根据面积比公式,计算三个特征压强比,然后确定拉伐尔喷管内的流动状态。由面积比公式确定p1/p*,p2/p*和p3/p*。根据q(λe)=At/Ae=0.2857查气动函数表,得
λe=1.914,Mae=2.80,p1/p*=π(λe)=0.0369
再由Mae=2.8查正激波表,得p2/p1=8.98,故
\[\frac{{{p}_{2}}}{{{p}^{*}}}=\frac{{{p}_{2}}}{{{p}_{1}}}\frac{{{p}_{1}}}{{{p}^{*}}}=8.98\times 0.0369=0.3314\]
求p3/p*,它对应出口截面是亚声速气流,喷管喉道Mat=1,所以仍可由面积比公式,q(λe)= At /Ae=0.2857,查气动函数表,得
λe=0.1857, p3/p*=π(λe)=0.98
根据题意,有
Pb/p*=1.0133/1.523=0.665
可见p2/p*< pb/p* < p3/p*,超临界流动,管内有激波的流态。
(2)求激波位置As/At及喷管出口的速度Ve。
对出口及喉部运用连续方程,即
\[K\frac{p_{t}^{*}}{\sqrt{T_{t}^{*}}}{{A}_{t}}=K\frac{{{p}_{e}}y\left( {{\lambda }_{e}} \right)}{\sqrt{T_{e}^{*}}}{{A}_{e}}\]
因为管内有激波,所以出口是亚声速(λe<1),且pe=pb,故
\[y\left( {{\lambda }_{e}} \right)=\frac{{{p}^{*}}}{{{p}_{b}}}\frac{{{A}_{t}}}{{{A}_{e}}}=1.5\times 0.2857=0.4286\]
由此查表得λe=0.269 ,q(λe)=0.411。然后,再用一次连续方程,即
\[K\frac{p_{t}^{*}}{\sqrt{T_{t}^{*}}}{{A}_{t}}=K\frac{p_{e}^{*}q\left( {{\lambda }_{e}} \right)}{\sqrt{T_{e}^{*}}}{{A}_{e}}\]
求出气流通过正激波的总压恢复因数
\[\sigma =\frac{p_{e}^{*}}{p_{t}^{*}}=\frac{{{A}_{t}}}{{{A}_{e}}}\frac{1}{q\left( {{\lambda }_{e}} \right)}=\frac{0.2857}{0.411}=0.6955\]
查正激波表,得到波前马赫数Mas1=2.054,q(λs1)=0.5681。最后,对波前截面As及喉部再次运用连续方程,即
\[K\frac{p_{t}^{*}}{\sqrt{T_{t}^{*}}}{{A}_{t}}=K\frac{p_{s1}^{*}q\left( {{\lambda }_{s1}} \right)}{\sqrt{T_{s1}^{*}}}{{A}_{s}}\]
式中,下标s1表示激波前参数。因为激波之前的流动是绝能等熵的,所以pt*=ps1*,Tt*=Ts1*,面积比为
\[\frac{{{A}_{s}}}{{{A}_{t}}}=\frac{1}{q\left( {{\lambda }_{s1}} \right)}=\frac{1}{0.5681}=1.76\]
喷管出口的速度Ve为
\[{{V}_{e}}={{\lambda }_{e}}{{c}_{cr}}={{\lambda }_{e}}\sqrt{\frac{2kR{{T}^{*}}}{k+1}}=0.269\times \sqrt{\frac{2\times 1.4\times 287.06\times 900}{1.4+0}}=147.7m/s\]
7.4 内压式超声速进气道及其他变截面管流
内压式超声速进气道的一个经典问题就是起动问题,这对于超声速和高超声速进气道同样重要。本节利用变截面管内流动的知识讨论内压式超声速进气道内的流动及其起动问题。理解起动过程的关键是清楚地了解气体在管道中流动的一系列流动状态。本节最后讨论其他变截面管内的流动。
7.4.1 内压式超声速进气道
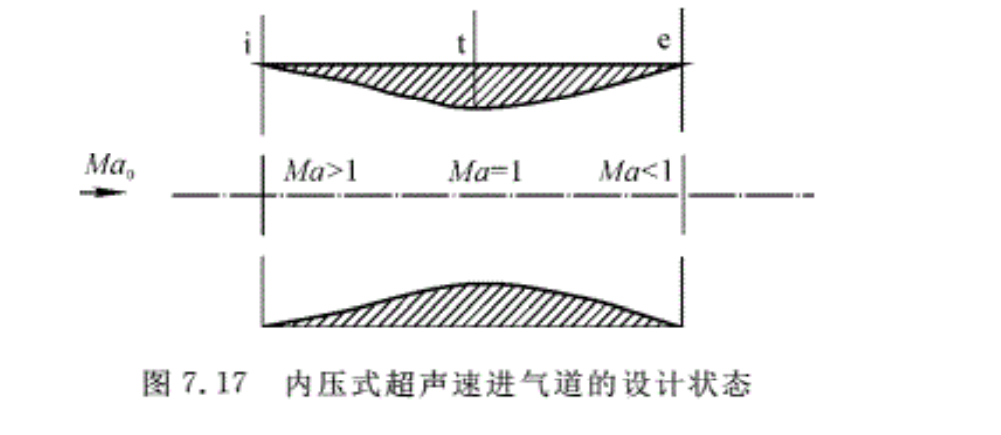
第7.3节讨论了气流在拉伐尔喷管中的流动规律。本节讨论的则是一个倒置的拉伐尔喷管,即迎面的超声速气流在如图7.17所示的管道内流动。如果流动中没有激波,则可假设流动为一维定常、无摩擦、无热交换、无化学反应,且喉道下游流通能力足够大。
内压式超声速进气道也属于变截面管流。它是靠内部压缩超声速气流使其达到减速增压的目的。内压式超声速进气道包括收缩段、喉部和扩张段。收缩段可以是直壁或曲壁,气体在其中经过一系列波系减速增压,到达喉部时马赫数一般大于1。然后在扩张段内加速再经过一道正激波,变为亚声速气流。
一、设计状态
内压式超声速进气道的理想流动状态如图7.17所示,迎面超声速气流在进囗之前气流参数不发生变化。进入进气道后,在收缩段(设为曲壁)中进行连续地微弱压缩,气流速度不断减小,到喉部气流速度刚好减小到当地声速,Mat=1,然后气流在扩张段内进一步减速,变为亚声速气流,到出口截面得到所需要的气流马赫数。在这样的流动中,不存在激波,因此流动损失很小。这种流动称为最佳流动状态,又叫设计状态。
对于超声速进气道,对进口截面和喉部运用连续方程,则有
\[K\frac{p_{t}^{*}}{\sqrt{T_{t}^{*}}}{{A}_{t}}q\left( {{\lambda }_{t}} \right)=K\frac{p_{i}^{*}q\left( {{\lambda }_{i}} \right)}{\sqrt{T_{i}^{*}}}{{A}_{i}}\] (7.25)
因为流动绝能,所以Ti*=Tt*=To*,如果不计摩擦,则pi*=pt*=po*。在最佳流动状态时,λt= 1,因而q(λt)=1,此外λi=λod。这样,式(7.25)就可简化成
\[{{\left( \frac{{{A}_{t}}}{{{A}_{i}}} \right)}_{d}}=q\left( {{\lambda }_{0d}} \right)\] (7.26)
这就是设计状态时的面积比公式。
图7.18表示了按式(7.26)所确定的面积比随来流Ma的变化关系。由图可见,对于不同的来流马赫数Mao,为了实现最佳流动,所需的面积比(At/Ai)是不同的,Mao越大,进口段需要收缩的程度也越大。因此,最佳面积比(At /Ai)是与Mao一一对应的,这就是说,一定面积比的进气道,只有在确定的Mao下,进气道内的流动才是最佳的,Mao不合适,流动就不会是最佳的。
二、非设计状态
马赫数小于或大于设计马赫数的流动状态称为非设计状态。下而讨论内压式超声速进气道非设计状态下的流动特点。
1.Ma03>Ma0d(Ma01)
对于面积比为(At/Ai)d=(At/Ai)1的进气道,设计状态(最佳流动)所对应的来流马赫数为Ma0d=Ma01,由等熵面积比公式可得(At/Ai)d=q(λ0d),对于这样面积比的进气道,若迎面气流马赫数不是Ma0d,而是Ma03(Ma03 > Ma0d),那么,超声速气流在进气道的收缩段内减速后,喉部截面上的气流马赫数并不等于1,根据通过进气道任一截面的质量流量不变的条件,可以导出
\[q\left( {{\lambda }_{t}} \right)=\frac{{{A}_{0}}q\left( {{\lambda }_{03}} \right)}{{{A}_{t}}}=\frac{q\left( {{\lambda }_{03}} \right)}{q\left( {{\lambda }_{0d}} \right)}\]
式中,A0表示自由流管面积。
由于λ03> λ0d> 1,所以q(λt)< 1,喉部气流马赫数Mat> 1,即在喉部仍是超声速气流。气流在喉部后而的扩张段又重新加速,然后经过由于反压作用而引起的正激波,才变为亚声速气流(见图7.19(a)),由于正激波的存在,总压损失较大。
2.Ma02 <Mad
若此进气道的迎面气流马赫数Ma02小于设计马赫数Ma0d,这时进口截面通过的流量将为
\[\begin{align}& {{q}_{m,i}}=K\frac{p_{0}^{*}}{\sqrt{T_{0}^{*}}}{{A}_{i}}q\left( {{\lambda }_{02}} \right)=K\frac{p_{0}^{*}}{\sqrt{T_{0}^{*}}}\frac{{{A}_{i}}}{{{A}_{t}}}q\left( {{\lambda }_{02}} \right)= \\& K\frac{p_{0}^{*}}{\sqrt{T_{0}^{*}}}{{A}_{t}}\frac{q\left( {{\lambda }_{02}} \right)}{q\left( {{\lambda }_{0d}} \right)}\rangle K\frac{p_{0}^{*}}{\sqrt{T_{0}^{*}}}{{A}_{t}} \\\end{align}\]
而喉部能通过的最大流量为\({{q}_{m,i}}=K\frac{p_{0}^{*}}{\sqrt{T_{0}^{*}}}{{A}_{t}}\),结果,qm,i>qm,t 。这说明,面积比为(At/Ai)d的进气道对马赫数为Ma02的超声速气流来说,喉部的截面积就显得小了,进口截面放进来的流量不能从喉部全部排出。这样,气体将在收缩段内积聚,压强升高,因而产生一道正激波。气流经激波后,总压降低,喉部的流通能力更小,因而激波强度增大,激波传播速度增大,直到被推出进气道。于是,在进口之前产生一道脱体弓形波,气流经过脱体弓形波后,变为亚声速气流,流线在进口前发生偏转,使喉部不能通过的那部分流量溢出进气道,其流动图形如图 7.19(b)所示。进入进气道的亚声速气流在进气道中的流动情况和拉伐尔喷管一样,将由进气道出口的反压来决定。
如果在进气道进口前的超声速气流中出现激波,即使将迎面气流马赫数增大到Ma0d,也不可能建立最佳流动状态,这是因为有激波存在时,喉部所能通过的最大流量为
\[{{q}_{m,i}}=K\frac{\sigma p_{0}^{*}}{\sqrt{T_{0}^{*}}}{{A}_{t}}\]
激波使气流总压有损失,从而减小了喉部的通流能力。所以在进气道前仍需要溢流,即激波仍然存在。
综上所述,在迎面气流马赫数为Ma0d时,可能有两种流动状态。一种是进囗前有脱体激波,气流总压有很大的损失;另一种是最佳流动状态,但这种最佳流动状态是不稳定的,因为只要有一点微小的扰动,就会在进口前产生脱体弓形波,一旦出现弓形波后,即使扰动消失后,流动也不可能恢复到最佳状态。空气喷气发动机的飞行马赫数总是由小到大变化的,而且在飞行中,飞行马赫数也总会受到扰动,因此,按面积比确定的内压式超声速进气道,实际上是不可能建立起最佳流动状态的,进口总会有脱体弓形波。流动损失也将是很大的。那么如何消除进气道进口前的弓形波,在进气道中建立起最佳流动状态或接近于最佳流动状态呢?这个问题就是内压式超声速进气道的起动问题。在讨论进气道起动之前,先介绍一个气动函数,以便为下文的讨论做准备。
3.气动函数θ(λ)
若用Ao表示进入进气道的气流流管截面面积,当进气道进口前有激波时,则有Ao<Ai(见图7.19(b)),若这时进气道出囗反压足够低,则Mat=1.0。对进气道进口前与喉部运用连续方程,即
\[K\frac{p_{0}^{*}}{\sqrt{T_{0}^{*}}}{{A}_{0}}q\left( {{\lambda }_{0}} \right)=K\frac{p_{t}^{*}q\left( {{\lambda }_{t}} \right)}{\sqrt{T_{t}^{*}}}{{A}_{t}}\]
当进囗前有脱体激波时,pt*=σ(λo)po*,式中,σ(λo)是气流通过正激波时的总压恢复因数,它仅是波前气流速度因数λo的函数。在进气道的流动中,To*=Tt*,并注意到q(λt)=1,则有
\[\frac{{{A}_{t}}}{{{A}_{0}}}=\frac{q\left( {{\lambda }_{0}} \right)}{\sigma \left( {{\lambda }_{0}} \right)}\]
此式等号右边仅是λo的函数,记作θ(λo),即
\[\theta \left( {{\lambda }_{0}} \right)=\frac{q\left( {{\lambda }_{0}} \right)}{\sigma \left( {{\lambda }_{0}} \right)}\]
这就是所要介绍的气动函数。它与λ及Ma的关系如下:
由 \(q\left( \lambda \right)={{\left( \frac{k+1}{2} \right)}^{\frac{1}{k-1}}}\lambda {{\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)}^{\frac{1}{k-1}}}\)
得 \(\theta \left( \lambda \right)={{\left( \frac{k+1}{2} \right)}^{\frac{1}{k-1}}}\frac{1}{\lambda }{{\left( 1-\frac{k-1}{k+1}\frac{1}{{{\lambda }^{2}}} \right)}^{\frac{1}{k-1}}}\) (λ≥1) (7.28)
图7.20表示出了θ(λ)与λ的关系曲线,图上同时也画出了q(λ)曲线。当λ=1时,不形成激波,σ=1所以θ(λ)=q(λ)=1。当1 ≤λ ≤λmax=√(k+1)/(k-1)时,比较q(λ)与θ(λ)的的表达式,可以看出θ(λ)=q(1/λ)。当λ=λmax时,θ=θ(λmax)。对于空气,θ(λmax)=0.60019。
4.超声速进气道的起动
超声速进气道的起动是设计进气道时所需要考虑的问题。下面将利用气动函数θ(λ),来讨论超声速进气道的起动问題。
进气道的起动过程也就是如何消除进气道进囗前的脱体弓形波,建立起最佳流动的过程。有两种途径可以建立起进气道的最佳流动状态,一种是增大迎面气流的马赫数;另一种是增大喉部截面面积。
首先讨论用增大来流Ma起动进气道的过程。设进气道几何不可调,即截面尺寸是固定的,At/Ai是根据设计状态的迎面气流马赫数确定的,用Mad表示设计马赫数,相应的速度因数为λd,进气道的面积比和速度因数符合等熵面积比公式,即
At/Ai=q(λd)
假设气流在进气道内的流通能力足够大,即通过喉部的流量都能从出囗流出;并不计进气道内的摩擦损失。在来流马赫数逐渐加大的过程中,当1<Mao<Mad时,根据前面的讨论可知,在进口前会出现脱体弓形波,喉部气流Mat=1,发生堵塞。这时,进气道的流管截面积 Ao ,可由连续方程求得,即
\[\begin{align}& {{A}_{0}}q\left( {{\lambda }_{0}} \right)=\sigma \left( {{\lambda }_{0}} \right){{A}_{i}}q\left( {{\lambda }_{i}} \right) \\& \frac{{{A}_{0}}}{{{A}_{i}}}=\frac{q\left( {{\lambda }_{i}} \right)\sigma \left( {{\lambda }_{0}} \right)}{q\left( {{\lambda }_{0}} \right)}=\frac{q\left( {{\lambda }_{i}} \right)}{\theta \left( {{\lambda }_{0}} \right)} \\\end{align}\]
再对Ai,At截面运用连续方程Aiq(λi)=At,代入上式,并注意At /Ai=q(λd),则得
\[\frac{{{A}_{0}}}{{{A}_{i}}}=\frac{q\left( {{\lambda }_{i}} \right)}{\theta \left( {{\lambda }_{0}} \right)}=\frac{\frac{{{A}_{t}}}{{{A}_{i}}}}{\theta \left( {{\lambda }_{0}} \right)}=\frac{q\left( {{\lambda }_{d}} \right)}{\theta \left( {{\lambda }_{0}} \right)}\langle 1\]
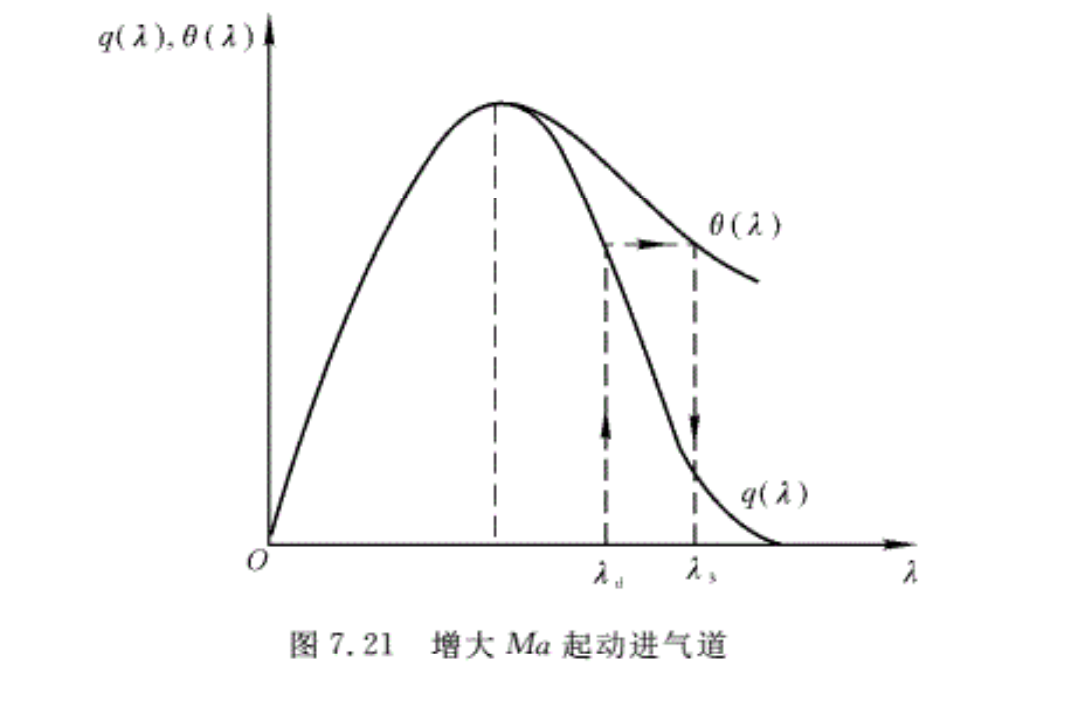
由上式可知,Ao<Ai,即在进囗处气流通过激波溢流,随着λo的增大,θ(λo)的数值减小,所以出Ao/Ai增大,这意味着溢流减小,激波向进口靠近,但只要λo<λd,则总是存在出Ao/Ai< 1,脱体激波始终存在,一直要到λo=λ3(>λd)时,θ(λ3)=q(λd) (见图7.21 ),才有Ao /Ai=1。这表示此时流线在进口前没有偏折,溢流消失,激波贴到进口。当激波位于进囗时,由于激波不可能稳定在收缩通道内,流动是不稳定的。这是因为激波从进口向喉部移动时波前的Ma减小,强度减弱,总压恢复因数增大,通过喉部的流量加大。当Mao增大到Ma3时,就能将进口激波吸入进气道内。但在Ma3时,如前所说,由于Ma3>Mad,所以喉部的Mat > 1,为了使 Mat=1,还要将起动后的来流Mao再降下来,直到Mao=Mad时,才能使Mat=1,这时进气道总压损失较小。
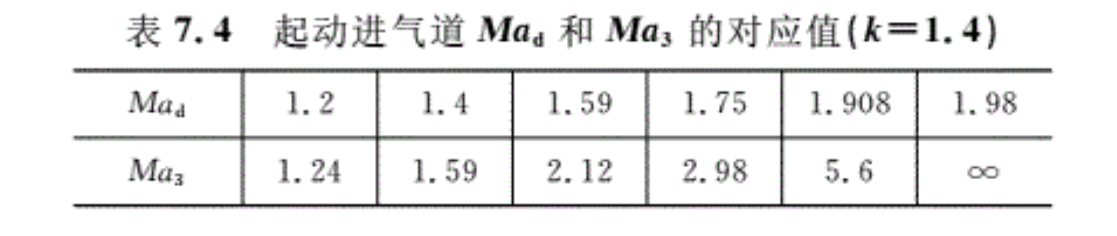
需要指出,用这种方式起动进气道,迎面气流的马赫数Ma比设计的Mad需要大很多,具体数值可按θ(λ3)=q(λd)确定。表7.4列出了一系列Mad和Ma3的对应值。
由表7.4可以看出,当设计Mad=1.98时,理论上,要求Ma3→∞。因此,当设计马赫数 Mad > 1.98时,即使在理论上也不可能用提高迎面气流Ma的办法来起动进气道。
第二种起动进气道的方法是增大喉部面积。由前分析可知,进气道起动问题之所以存在,是由于进口前出现激波,气流总压有损失,减小了喉部的流通能力。所以,为了使进气道起动,需要将喉部面积(用At3表示)放大。放大的喉部面积应恰好能弥补由于激波所造成的流通能力的减小,使Ao=Ai的迎面气流完全从喉部流出,即
\[K\frac{p_{0}^{*}}{\sqrt{T_{0}^{*}}}{{A}_{i}}q\left( {{\lambda }_{d}} \right)=K\frac{p_{t}^{*}q\left( {{\lambda }_{t}} \right)}{\sqrt{T_{t}^{*}}}{{A}_{t3}}\]
式中,pt*=σ(λd)po*,To*=Tt*,λt=1。所以上式可以与成
\[\frac{{{A}_{t3}}}{{{A}_{i}}}=\frac{q\left( {{\lambda }_{d}} \right)}{\sigma \left( {{\lambda }_{d}} \right)}=\theta \left( {{\lambda }_{d}} \right)\]
图7.22表示起动面积比At3/Ai与设计马赫数Mad的关系,同时也给出了最佳流动状态的面积比(At/Ai)与Mad的关系。
最后来观察一下喉部面积按起动要求放大了的进气道在起动时各阶段的流动图形。此进气道是在设计马赫数下工作的,其面积比为(At3/Ai)d。当Mao<Mad时,以超声速进入进口截面的气体流量,喉部吞不掉,从而在进口前出现脱体激波(见图7.22(a))。当Mao略低于Mad时,激波贴于进口(见图7.22(b))。当速度达到设计值时,激波被吞入进气道,由于激波不能稳定在收缩段中,所以一直顺流移动,通过喉部,然后在扩张段内稳定下来,具体位置由进气道出口的反压决定。由于放大了喉部,所以在喉部截面上,Mat > 1(见图7.22(c))。若激波不靠近喉部,则波前Ma也很大,因而损失也很大。为了减小损失,最好使激波处在喉部截面上(见图7.22(d))。但这种流动稍有扰动,激波就会被吐出来。所以,实际上是将激波配置在喉部之后不远的截面上,这样工作的进气道,损失较小,工作稳定。
这种进气道工作时有一种滞后现象,气流马赫数Ma从低速开始增大时,直到Mad以前,激波吞不进去,但是起动后,即激波被吞入后,Ma 再减小下来时,直到Mab(见图7.23上的b点),激波吐不出来。这样,两个面积比的两条曲线就将图7.23所示的区域分成三部分,在起动面积比(At3/Ai)线以上,进气道进囗无激波;在最佳面积比(At/Ai)线下方,进气道进囗前有激波;在两条曲线之间的区域则可能有激波,也可能无激波。
采用放大喉部面积的办法来起动进气道时,起动后喉部处的气流并不是声速气流,而是 Ma > 1的气流,所以还不是最佳流动状态,仍有一定的损失。为了获得最佳流动状态,需要采用几何面积可调的办法。起动前先将喉部面积放大,将进口前的激波吸入后,再减小喉部面积,使喉部处的气流变成声速气流。在适当的反压配合下,喉部之后是亚声速气流,这样,进气道内将是无激波的流动过程,损失最小。
7.4.2 其他变截面管流
一、气体在引射喷管内的流动
前面讨论的收缩喷管,因其结构简单、重量轻而被广泛地应用于亚声速飞机的发动机上。但是收缩喷管在出口处只能膨胀到马赫数等于1。随着喷管进囗总压不断提高,要求喷管具有更大的膨胀能力,因此可采用收缩一扩张喷管,从而提高了发动机的推力。对于固定面积比Ae/At的拉伐尔喷管,气流的膨胀程度也是一定的。而为了适应于涡轮喷气发动机在飞行过程中发动机的转速、飞行高度和飞行速度在宽广的飞行范围内变化,就要求拉伐尔喷管扩张段的几何尺寸随压力比的变化而变化,即采用可变面积比的拉伐尔喷管。这样会增结构上的困难,并导致喷管重量的增加。为了克服这个困难,同时也为了解决对发动机部件的冷却以及提高部件性能等这些问题,在涡轮喷气发动机上常采用引射喷管。
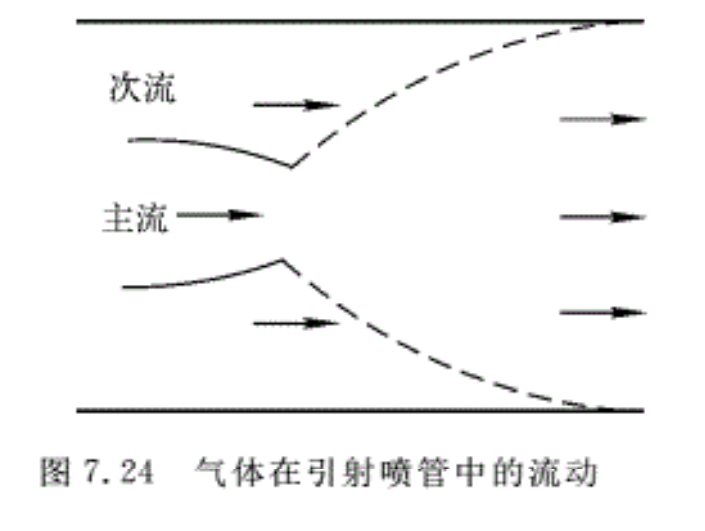
引射喷管是由发动机原来的尾喷管(叫主喷管)和尾喷管外面套的一个外罩所形成的第二个喷管(叫次喷管)构成的,如图7.24所示。主喷管可以是收缩喷管,也可以是面积比Ae/At不大的收缩一扩张喷管。
从发动机排出的燃气通过主喷管流出,在主喷管出囗与外部亚声速次流(从次喷管排出的空气流)混合,而由于主流在主喷管内没有得到完全膨胀,喷管中次流的压强、温度比主流的要低得多,因此在喷管出囗之后的外罩内,主流继续膨胀速,压强降低。周围的次流形成主流的”流体”壁面,起着拉伐尔喷管扩张段的作用。调节次流的压强可以控制主流在外罩内的膨胀程度,这样在外罩内形成一个相当于截面积可以随工作状态变化的拉伐尔喷管。
在设计状态,可使得引射喷管外罩出囗截面上气流压强与周围压强相等,即主流在引射喷管中得到完全膨胀。
二、气体在斜切口管内的流动
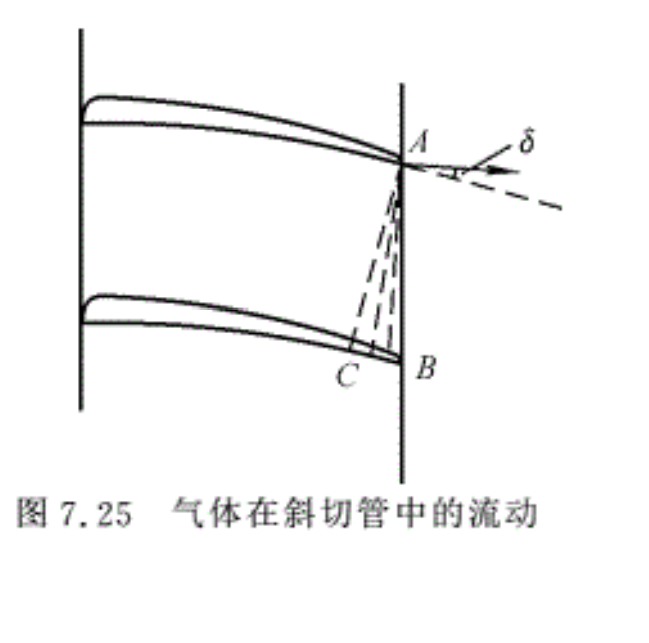
除了收缩喷管和拉伐尔喷管之外,还有采用斜切囗管使气流加速。所谓的斜切口管是一种出口截面不垂直于管道轴线的管道,例如涡轮导向器叶片间的通道。由于管道出口截面不与管道轴线垂直,在管道出口处就会形成一个斜切囗,如图7.25所示。该斜切口具有拉伐尔喷管扩张段的作用,因此,斜切口管可以使气流从亚声速加速到超声速。
气流在收缩段从亚声速不断加速,到最小截面处气流速度达到声速而进入斜切口ACB。由于外界反压比较低,因而气流过点A产生膨胀波束。经膨胀波,气流加速到超声速,同时气流向外折转一定角度δ。
如果反压与来流总压之比(即压强比)等于临界压强比,则管道最小截面处的马赫数等于 1,而出口压强刚好等于外界反压,此种情况下,气体流过斜切囗时,不能继续膨胀。
如果压强比大于临界压强比,气流在管道内速度增大得不多,管道最小截面处气流的速度小于声速,出口压强等于外界反压,这里斜切口只起到引导气流的作用,即气流在斜切口处既不转折,也不膨胀。
三、气体在扩散形管内的流动
超声速气流在扩散形管内的流动与在拉伐尔喷管扩张段内的流动一样。这里主要讨论亚声速气流在扩散形管内的流动。
亚声速气流绝能无摩擦地流过扩散形管时,气流速度减小,压力、温度和密度相应地增大。空气喷气发动机的进气道内管道常采用扩散形管道,以便达到提高压强的目的。
若在扩散形管进口处气体温度保持不变,气体在流动过程中,动能减小量越大,说明压缩气体提高压强也越多,即出口与进口压强的比值越大。反之动能减小量越小,压强比也越小。所以在空气喷气发动机的进气道中应尽可能减小损失。
四、塞式喷管
对于用于大气层和航天飞行器上的推进系统,要求飞行器在宽广范围的飞行马赫数及高度的飞行条件下具有良好的性能,从而采用了塞式喷管,如图7.26所示。如果采用精心设计的可变几何的塞式喷管,其飞行器可以在很高的高度和很宽的飞行马赫数的范围内持续飞行。图中示出了一种外膨胀的塞式喷管,气流绕外罩唇口流出时,突然膨胀到外界大气压强,即气流经一系列膨胀波扇形区完成膨胀。通过适当的设计,马赫线(特征线)可以聚集于一点。设计塞体表面时,应使气流从进强膨胀到外界大气压强,而出口气流转折到平行于喷管轴线方向,并使最后一道波落在塞体顶点A上。
对于一架必须在很宽的速度范围内飞行的飞机而言,采用可变喷管面积比是现代高性能战斗机所要求的。在实际中,采用矩形喷管更容易实现面积的调节,即可以用两块或三块可控制的铰接板来近似喷管的弯曲部分,以实现有效的调节。此外,采用矩形喷管还可以加速燃气与外界空气的掺混,降低红外辐射,提高飞行器的隐身能力。
7.5 等截面摩擦管流
在第7.4节讨论变截面管流时,没有考虑摩擦的影响,但摩擦在实际的管道流动中总是存在的。特别是可压缩流体在等截面管道内的流动是许多工程中的重要问题,诸如天然气在管道中的流动,气体在动力装置内通道中的流动以及化工设备中各类气体的输送和流动等。
为了着重分析摩擦对气流参数的影响,在讨论中假设:
流动是一维定常的;管道是等截面的;气体与外界没有机械功和热量的交换;气体为定比热的完全气体。
如果管道比较短,流动速度又比较大,气体与固体壁面之间的热交换影响与摩擦作用相比可忽略不计,则这种流动称为一维定常等截面的绝热摩擦管流。可以把这种流动看做是纯摩擦过程。如果管道比较长,有足够的时间进行热交换,流动接近于等温过程,则这种流动称为等截面的等温摩擦管流。
本节只讨论一维定常等截面绝热的摩擦管流。
一、摩擦对气流参数的影响
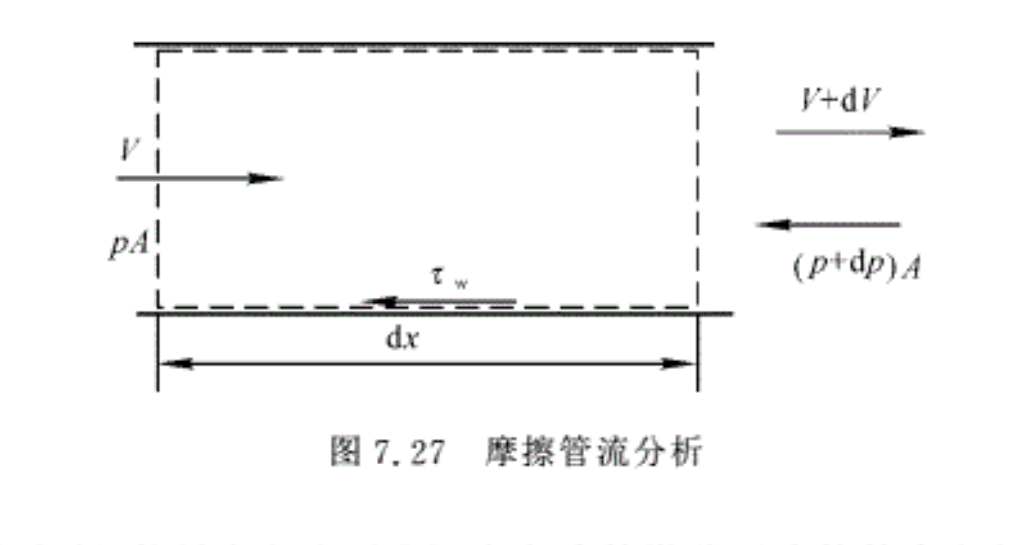
为了讨论摩擦对绝热流动中气流参数的影响,需要对如图7.27所示的微元控制体写出微分形式的基本方程。
连续方程、状态方程、能量方程和对Ma定义式的微分形式的基本方程与变截面管流的方程相同。对于本节的等截面流动,dA=0。于是,这几个方程为
\[\frac{d\rho }{\rho }+\frac{dV}{V}=0\] (7.30)
\[\frac{dp}{p}-\frac{d\rho }{\rho }-\frac{dT}{T}=0\] (7.31)
\[\frac{dT}{T}+\left( k-1 \right)M{{a}^{2}}\frac{dV}{V}=0\] (7.32)
\[\frac{dM{{a}^{2}}}{M{{a}^{2}}}=\frac{d{{V}^{2}}}{{{V}^{2}}}-\frac{dT}{T}\] (7.33)
动量方程的微分形式 \(-Adp-{{\tau }_{w}}d{{A}_{w}}=\rho VAdV\) (a)
式中,dAw=πddx是控制体内气流与管壁接触的面积。在摩擦管流中一般都利用摩擦因数Cf来进行分析。摩擦因数Cf定义为壁面切应力与气流动压头之比,即
\[{{C}_{f}}=\frac{{{\tau }_{w}}}{\frac{1}{2}\rho {{V}^{2}}}\]
将摩擦因数及dAw=πddx代入式(a)后,通除以ρV²,并引入声速和马赫数的定义式,得
\[\frac{dV}{V}+\frac{1}{kM{{a}^{2}}}\frac{dp}{p}+4{{C}_{f}}\frac{dx}{2d}=0\] (7.34)
在摩擦管流中,根据总压与静压和马赫数间的关系式,取对数微分后得
\[\frac{d{{p}^{*}}}{{{p}^{*}}}=\frac{dp}{p}+\frac{kM{{a}^{2}}}{1+\frac{k-1}{2}M{{a}^{2}}}\frac{dMa}{Ma}\] (7.35)
由冲量函数
\[F=pA+\rho {{V}^{2}}A=pA\left( 1+kM{{a}^{2}} \right)\]
取对数再微分得
\[\frac{dF}{F}=\frac{dp}{p}+\frac{2kM{{a}^{2}}}{1+kM{{a}^{2}}}\frac{dMa}{Ma}\] (7.36)
根据熵和总压的关系,微分得
\[ds=-R\frac{d{{p}^{*}}}{{{p}^{*}}}\] (7.37)
这样,得到上述从式(7.30)~式(7.37)8个联立线性方程组。这8个方程中联系着9个变量 :dp/p,dρ/ρ,dT/T,dV/V,dMa/Ma,dp*/p*,ds/cp,dF/F和4Cfdx/d 。在等截面摩擦管流中,引起气流参数变化的物理原因是黏性摩擦。因此,取4Cfdx/d作为独立变量,其余8个变量可以由上述8个方程用4Cfdx/d表示。这样可以方便地分析摩擦对气流参数的影响。解上述8个方程可得如下绝热摩擦管流的关系式:
\[\begin{align}& \frac{dp}{p}=-\frac{kM{{a}^{2}}\left[ 1+\left( k-1 \right)M{{a}^{2}} \right]}{2\left( 1-M{{a}^{2}} \right)}4{{C}_{f}}\frac{dx}{d} \\& \left( 7.38 \right) \\& \frac{d\rho }{\rho }=-\frac{kM{{a}^{2}}}{2\left( 1-M{{a}^{2}} \right)}4{{C}_{f}}\frac{dx}{d} \\& \left( 7.39 \right) \\& \frac{dT}{T}=-\frac{k\left( k-1 \right)M{{a}^{4}}}{2\left( 1-M{{a}^{2}} \right)}4{{C}_{f}}\frac{dx}{d} \\& \left( 7.40 \right) \\& \frac{dV}{V}=\frac{kM{{a}^{2}}}{2\left( 1-M{{a}^{2}} \right)}4{{C}_{f}}\frac{dx}{d} \\& \left( 7.41 \right) \\& \frac{dM{{a}^{2}}}{M{{a}^{2}}}=\frac{kM{{a}^{2}}\left[ 1+\frac{k-1}{2}M{{a}^{2}} \right]}{\left( 1-M{{a}^{2}} \right)}4{{C}_{f}}\frac{dx}{d} \\& \left( 7.42 \right) \\& \frac{d{{p}^{*}}}{{{p}^{*}}}=-\frac{kM{{a}^{2}}}{2}4{{C}_{f}}\frac{dx}{d} \\& \left( 7.43 \right) \\& \frac{dF}{F}=-\frac{kM{{a}^{2}}}{2\left( 1+kM{{a}^{2}} \right)}4{{C}_{f}}\frac{dx}{d} \\& \left( 7.44 \right) \\& \frac{ds}{{{c}_{p}}}=\frac{\left( k-1 \right)M{{a}^{2}}}{2}4{{C}_{f}}\frac{dx}{d} \\& \left( 7.45 \right) \\\end{align}\]
从式(7.38)~式(7.45)可以看出在摩擦管流中气流各参数沿管长方向的变化规律,即不论是亚声速气流还是超声速气流,摩擦的作用都是使气流的总压下降,冲量减小而熵值增大。所以壁面摩擦降低了气流的机械能,减小喷气推进装置的推力;摩擦作用对气流参数(V,Ma,p,ρ,T)的影响,在亚声速气流中与在超声速气流中刚好相反,各种参数的变化列入表7.5中。
由以上分析可见,单纯的摩擦不能使亚声速气流转变为超声速气流,也不可能使超声速气流连续地转变为亚声速气流。
二、摩擦管流的计算
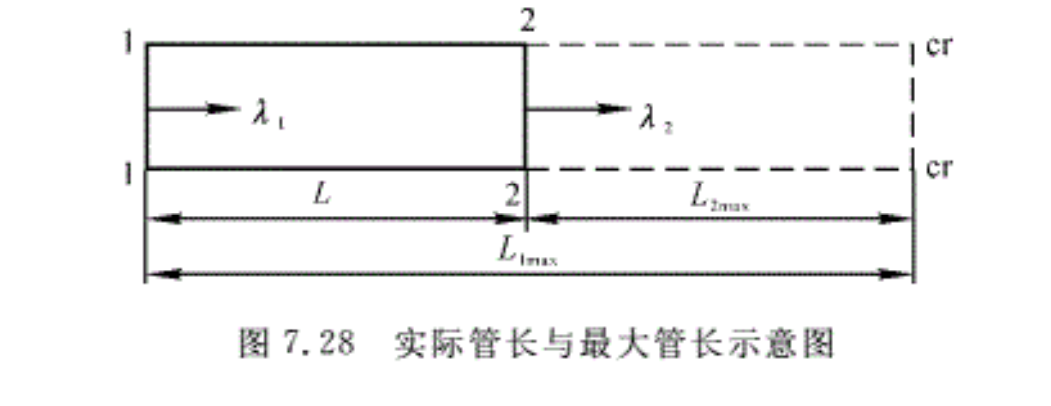
在摩擦管中,任意取如图7.28所示的两个截面1和2。它们之间的距离为L,管径为d,对以上各式在两个截面之间积分,便可得到各流动参数间的关系。将式(7.42)改写为速度因数λ的形式,则有
\(\left( \frac{1}{{{\lambda }^{2}}}-1 \right)\frac{d\lambda }{\lambda }=\frac{k}{k+1}4{{C}_{f}}\frac{dx}{d}\)
积分上式,有
\(\int_{0}^{L}{\frac{k}{k+1}4{{C}_{f}}\frac{dx}{d}=\int_{{{\lambda }_{1}}}^{{{\lambda }_{2}}}{\left( \frac{1}{{{\lambda }^{2}}}-1 \right)\frac{d\lambda }{\lambda }}}\)
得 \(\left( \frac{1}{\lambda _{1}^{2}}-\frac{1}{\lambda _{2}^{2}} \right)-\ln \frac{\lambda _{2}^{2}}{\lambda _{1}^{2}}=\frac{2k}{k+1}4\overline{{{C}_{f}}}\frac{L}{d}\) (7.46)
式中,\(\overline{{{C}_{f}}}\)为按长度L平均的摩擦因数,即
\(\overline{{{C}_{f}}}=\frac{1}{L}\int_{0}^{L}{{{C}_{f}}}dx\)
对于绝热的亚声速完全发展的湍流,根据实验测量,马赫数在0~1的范围内,气体的压缩性对摩擦因数的影响可以忽略。对于绝热的超声速流的摩擦因数,不仅包括壁面切向应力的影响,而且还包括速度分布不断变化引起的动量交换的影响。对于相对管长L/d=10~50的管道,在Ma=1. 2~3.0、管流Re=2.5 × 104~ 7 × 105的范围内,\(\overline{{{C}_{f}}}\)=0.002~0.003。对于中等长度的管道可取\(\overline{{{C}_{f}}}\)=0.0025。
有了λ的关系后,截面1,2上其他气流参数的关系,可以用气动函数求得。
密度比与速度比为
\(\frac{{{\rho }_{2}}}{{{\rho }_{1}}}=\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{{{\lambda }_{1}}}{{{\lambda }_{2}}}=\frac{M{{a}_{1}}}{M{{a}_{2}}}{{\left( \frac{1+\frac{k-1}{2}Ma_{2}^{2}}{1+\frac{k-1}{2}Ma_{t}^{2}} \right)}^{\frac{1}{2}}}\) (7.47)
温度比
\(\frac{{{T}_{2}}}{{{T}_{1}}}=\frac{\tau \left( {{\lambda }_{2}} \right)}{\tau \left( {{\lambda }_{1}} \right)}=\frac{1+\frac{k-1}{2}Ma_{t}^{2}}{1+\frac{k-1}{2}Ma_{2}^{2}}\) (7.48)
压强比
\(\frac{{{p}_{2}}}{{{p}_{1}}}=\frac{y\left( {{\lambda }_{1}} \right)}{y\left( {{\lambda }_{2}} \right)}=\frac{M{{a}_{1}}}{M{{a}_{2}}}{{\left( \frac{1+\frac{k-1}{2}Ma_{t}^{2}}{1+\frac{k-1}{2}Ma_{2}^{2}} \right)}^{\frac{1}{2}}}\) (7.49)
总压比
\(\frac{p_{2}^{*}}{p_{1}^{*}}=\frac{q\left( {{\lambda }_{1}} \right)}{q\left( {{\lambda }_{2}} \right)}=\frac{M{{a}_{1}}}{M{{a}_{2}}}{{\left( \frac{1+\frac{k-1}{2}Ma_{2}^{2}}{1+\frac{k-1}{2}Ma_{t}^{2}} \right)}^{\frac{k+1}{2\left( k-1 \right)}}}\) (7.50)
冲量比
\(\frac{{{F}_{2}}}{{{F}_{1}}}=\frac{z\left( {{\lambda }_{2}} \right)}{z\left( {{\lambda }_{1}} \right)}=\frac{M{{a}_{1}}\left( 1+kMa_{2}^{2} \right)}{M{{a}_{2}}\left( 1+kMa_{1}^{2} \right)}{{\left( \frac{1+\frac{k-1}{2}Ma_{1}^{2}}{1+\frac{k-1}{2}Ma_{2}^{2}} \right)}^{\frac{1}{2}}}\) (7.51)
熵增
\(\frac{{{s}_{2}}-{{s}_{1}}}{R}=\ln \frac{p_{1}^{*}}{p_{2}^{*}}=\ln \frac{q\left( {{\lambda }_{2}} \right)}{q\left( {{\lambda }_{1}} \right)}=\ln \left\{ \frac{M{{a}_{2}}}{M{{a}_{1}}}{{\left( \frac{1+\frac{k-1}{2}Ma_{1}^{2}}{1+\frac{k-1}{2}Ma_{2}^{2}} \right)}^{\frac{k+1}{2\left( k-1 \right)}}} \right\}\) (7.52)
由式(7.47)~式(7.52)可知,只要求出出囗截面的速度因数或马赫数,就可以计算出各参数比。为了简化计算,一般都设想管子有一个临界截面,然后把进口截面的气流参数和需要计算的那个截面上的参数都和临界截面建立联系。若以x=Lmax表示气流速度达到声速时的管长,如图7.28所示,对应于x=Lmax的气流速度因数λ2=1,代入式(7.46),得
\(\left( \frac{1}{{{\lambda }^{2}}}-1 \right)+\ln {{\lambda }^{2}}=\frac{2k}{k+1}4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d}\) (7.53)
式中 \(4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d}\)——摩擦管流的临界折合长度;
Lmax——对应于临界截面的管长,即最大管长。
利用临界截面的概念,式(7.47)~式(7.51)可以化为
\(\frac{\rho }{{{\rho }_{cr}}}=\frac{{{V}_{cr}}}{V}=\frac{1}{\lambda }=\frac{1}{Ma}\sqrt{\frac{2+\left( k-1 \right)M{{a}^{2}}}{k+1}}\) (7.54)
\(\frac{T}{{{T}_{cr}}}=\frac{k+1}{2+\left( k-1 \right)M{{a}^{2}}}\) (7.55)
\(\frac{p}{{{p}_{cr}}}=\frac{1}{Ma}{{\left( \frac{k+1}{2+\left( k-1 \right)M{{a}^{2}}} \right)}^{\frac{1}{2}}}\) (7.56)
\(\frac{{{p}^{*}}}{p_{cr}^{*}}=\frac{1}{Ma}{{\left[ \left( \frac{1}{k+1} \right)\left( 2+\left( k-1 \right)M{{a}^{2}} \right) \right]}^{\frac{k+1}{2\left( k-1 \right)}}}\) (7.57)
\(\frac{F}{{{F}_{cr}}}=\frac{1+kM{{a}^{2}}}{Ma{{\left[ \left( k+1 \right)\left( 2+\left( k-1 \right)M{{a}^{2}} \right) \right]}^{\frac{1}{2}}}}\) (7.58)
对于不同的k值,可将这些函数制成表格(见附录表6),利用这些表格,就可以进行摩擦管流的计算。上述这些计算公式很容易编制计算机程序,计算更为快速、准确。
实际上,管道出口气流马赫数不一定等于1,即L不一定等于Lmax,在此情况下,可按进口马赫数Ma1计算出\({{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{M{{a}_{1}}}}\),再计算出实际折合管长\(4\overline{{{C}_{f}}}\frac{L}{d}\),而对应出囗截面Ma2的临界折合管长为
\({{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{M{{a}_{2}}}}={{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{M{{a}_{1}}}}-4\overline{{{C}_{f}}}\frac{L}{d}\) (7.59)
然后,再利用式(7.53)计算出口截面的λ2(或Ma2)值,从而可计算出其他参数。附录表6 给出了k=1. 4的绝热摩擦管流函数表。
例7.6 空气沿着直径d=0.1 m的等截面直管流动,要使Ma1=0.45的气流加速到Ma2=0.6,求管道的长度L(设气流的平均摩擦因数\(\overline{{{C}_{f}}}\)=0.003)。
解:从附录表6可查出Ma1=0.45和Ma2=0.6时的临界折合管长分别为\({{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{M{{a}_{1}}}}=1.5664\),\({{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{M{{a}_{2}}}}=0.4908\),因此根据式(7.59),可得
\[4\overline{{{C}_{f}}}\frac{L}{d}={{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{M{{a}_{1}}}}-{{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{M{{a}_{2}}}}=1.5664-0.4908=1.0756\]
所以 \(L=\frac{D\times 1.0756}{4\overline{{{C}_{f}}}}=\frac{0.1\times 1.0756}{4\times 0.003}=8.9633m\)
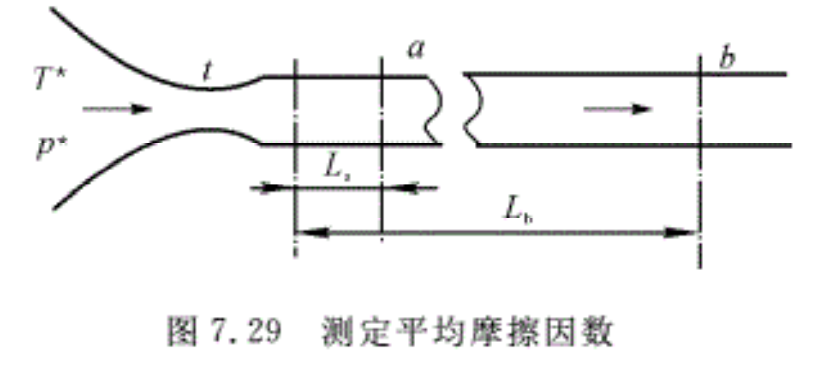
例7.7 空气沿拉伐尔喷管加速成超声速气流后进入一光滑的等截面直管,如图7.29所示。己知喷管进口气流总压po*=6.89 × 105Pa,总温T*=315K,距圆管进口1.75d的a处气流压强pa=2.432 × 104pa,距圆管进口29.6d的b处气流压强pb=4.95 × 104Pa,拉伐尔喷管喉部直径为6.14 ×10-3 m,圆管直径d=12.7 ×10-3 m,设喷管喉部之前的流动是等熵的,整个流动是绝能流动,求a,b之间这段直管的平均摩擦因数(\overline{{{C}_{f}}}\)。
解:根据连续方程\(p_{0}^{*}{{A}_{t}}={{p}_{a}}y\left( {{\lambda }_{a}} \right){{A}_{a}}\),得
\[y\left( {{\lambda }_{a}} \right)=\frac{p_{0}^{*}{{A}_{t}}}{{{p}_{a}}{{A}_{a}}}=\frac{6.89}{0.2432}\times \frac{{{6.14}^{2}}}{{{12.7}^{2}}}=6.6219\]
查气动函数表,得Maa=2.538,由Maa查表,得
\[\begin{align}& {{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{a}}=0.44 \\& {{\left( \frac{p}{{{p}_{cr}}} \right)}_{a}}=0.288 \\& {{\left( \frac{T}{{{T}_{cr}}} \right)}_{a}}=0.528 \\\end{align}\]
又
\[\frac{{{p}_{b}}}{{{p}_{a}}}={{\left( \frac{p}{{{p}_{cr}}} \right)}_{b}}/{{\left( \frac{p}{{{p}_{cr}}} \right)}_{a}}\]
得
\[{{\left( \frac{p}{{{p}_{cr}}} \right)}_{b}}=\frac{{{p}_{b}}}{{{p}_{a}}}{{\left( \frac{p}{{{p}_{cr}}} \right)}_{a}}=\frac{4.95}{2.432}\times 0.288=0.5862\]
由(p/pcr)b=0.5862,查表得
Mab=1.542,
\[{{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{b}}=0.1514\]
于是
\[{{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{a}}-{{\left( 4\overline{{{C}_{f}}}\frac{{{L}_{\max }}}{d} \right)}_{b}}=4\overline{{{C}_{f}}}\frac{{{L}_{b}}-{{L}_{a}}}{d}=0.44-0.1514=0.2886\]
故有
\[\overline{{{C}_{f}}}=\frac{0.2886d}{4\left( {{L}_{b}}-{{L}_{a}} \right)}\]
即得平均摩擦因数
\[\overline{{{C}_{f}}}=\frac{0.2886}{4\left( 29.6-1.75 \right)}=0.00259\]
该例题提供了测定绝热摩擦管流中平均摩擦因数的方法。
三、摩擦壅塞
由式(7.53)可以看出,对于给定的进口速度因数λ1(或Ma1),就有一个相应的管道最大长度(最大管长Lmax),若实际管长超过此λ对应的最大管长,即使出口反压足够低,以λ1流入管道的流量也无法从出口排出,流动将出现壅塞现象。壅塞将使气流的压强升高,对流动造成扰动。
对于亚声速气流,压强升高的这一扰动将会逆流传播,扰动一直影响到管道进口,使进口流速降低。对应的最大管长加长,临界截面后移,一直移到出口,气流能够从出口通过为止。此时出口截面上的速度因数λ2=1,其进囗气流Ma1由实际管长确定。
对于超声速气流,压强升高的扰动将会在气流中产生激波。当管长超过最大管长不多时,激波位于管内,这时进口的没有变化。而激波之后的亚声速气流在同样管长上造成的总压损失要比超声速气流小得多,从而使进囗流量能够从口通过,在出口截面上气流达到临界状态,激波位置可按出口气流达到临界状态的条件来确定。
由于实际气体的黏性作用,管内激波结构是十分复杂的。近似计算可按一道正激波来处理。运用式(7.46),从管道进囗到激波前以及从激波后到管道出囗列出两个关系式,并注意到管道出口的λ2=1,则有
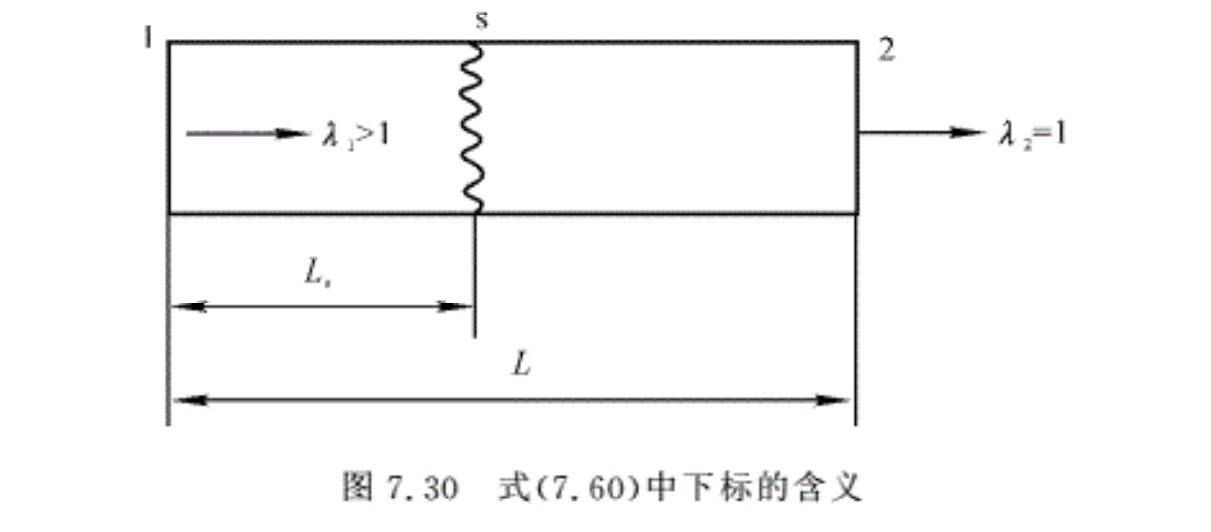
\[\begin{align}& \left( \frac{1}{\lambda _{1}^{2}}-\frac{1}{\lambda _{s}^{2}} \right)-\ln \frac{\lambda _{s}^{2}}{\lambda _{1}^{2}}=\frac{2k}{k+1}4\overline{{{C}_{f}}}\frac{{{L}_{s}}}{d} \\& \left( 7.60a \right) \\& \left( \frac{1}{\lambda {{_{s}^{\prime }}^{2}}}-1 \right)-\ln \frac{1}{\lambda {{_{s}^{\prime }}^{2}}}=\frac{2k}{k+1}4\overline{{{C}_{f}}}\frac{L-{{L}_{s}}}{d} \\& \left( 7.60b \right) \\\end{align}\]
式中,下标的含义示于图7.30中。
对于正激波,λs′=1/λs,所以式(7.60b)变为
\[\left( \lambda _{s}^{2}-1 \right)-\ln \lambda _{s}^{2}=\frac{8k}{k+1}\overline{{{C}_{f}}}\frac{L-{{L}_{s}}}{d}\] (7.61)
联立求解式(7.60a)和式(7.61 ),可得两个未知数λs和Ls。
综上所述,对于每一个起始的λ,都存在一个最大的\(4\overline{{{C}_{f}}}\frac{L}{d}\)值,超过这个值,流动就会壅塞。对于给定的\(4\overline{{{C}_{f}}}\frac{L}{d}\)值,在亚声速气流中,存在着一个最大的进口λ,大于它,流动就会发生壅塞;而在超声速气流中存在着一个最小的进口λ,小于它,流动也要发生壅塞。
关于反压对绝热摩擦管流的影响此处就不再讨论了。
7.6 气体在有热交换的管道内的流动
本节着重讨论热量交换对气体流动的影响。有热交换的实际流动是很多的。例如,气体在燃烧室中因燃料的燃烧而获得大量的热能;向高温气流中喷水,借水的蒸发使气流冷却;高超声速风洞前室常用电热器对气体加热等。之外,实际的流动过程都伴随有摩擦的作用。气流在燃烧室中的流动,不仅喷油燃烧使流量改变,而且气体的化学成分也发生变化。但是,对于管道长度不大而且流速又低的燃烧室来说,摩擦作用可以略去。此外,油和水汽的量与气体的流量相比要小得多,在初步计算中也可以忽略。以上这些假设虽然有一定的近似,但是,突出了现象的物理本质,也使问题得到了简化,而且可以得到具有实际意义的认识和结论。特别是当所假设的情况与实际情况相接近时,所得结论就有较高的准确度。因此,本节将讨论一维定常、定比热容、无摩擦完全气体在等截面直管内的流动过程,并且不考虑功的交换和气体化学成分的变化。这种流动就成了滞止焓或滞止温度变化的流动过程,或看做是纯滞止温度的变化过程。
一、瑞利线
利用瑞利线可以分析加热管流的一些特点。无黏等截面管流的连续方程与动量方程分别为
\[\begin{align}& \rho V=\frac{{{q}_{m}}}{A}=const \\& \left( 7.62 \right) \\& p+\rho {{V}^{2}}=\frac{F}{A}=const \\& \left( 7.63 \right) \\\end{align}\]
式中,qm是质量流量;F是冲量函数。合并上述两个方程,得到
\[p+\frac{{{\left( \frac{{{q}_{m}}}{A} \right)}^{2}}}{\rho }=\frac{F}{A}=const\] (7.64)
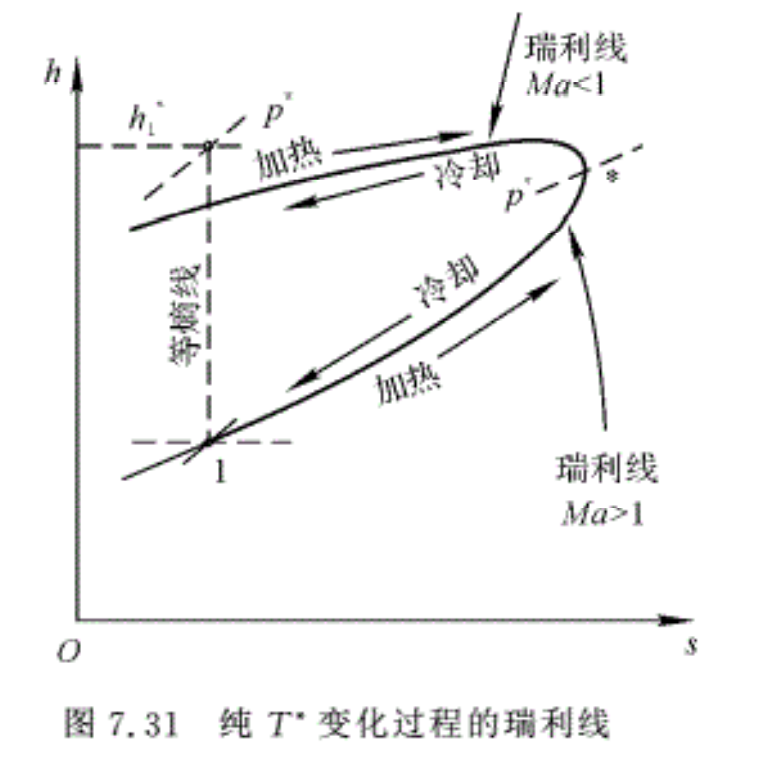
当单位面积的冲量函数F/A和单位面积的质量流量qm/A 为定值时,式(7.64)就确定了压强与密度间的唯一关系,称此关系所画的曲线为瑞利线。由于焓和熵都是压强和密度的函数,因此,由式(7.64)在焓一熵图上可画出瑞利线(见图7.31)。从图中可以看到以下几个特点:
(1)借助于方程式(7.62)和式(7.64)可求得管内速度与压强和密度的关系式V=√(dp/dρ),当此变化过程是在等熵条件下进行时,此速度就是当地声速c。图7.31中标以*的点代表ds=0,Ma=1和s=smax的状态。
(2)在最大熵值点上方的瑞利线分支对应于亚声速流动,而下方分支则对应于超声速流动。因为单纯换热过程在热力学上是可逆的,故加入热量必定对应于熵的增加,而放出热量则对应于熵的减小。因此,加热使亚声速流的马赫数增大,冷却使马赫数减小;而对于超声速流,加热反而使马赫数减小,冷却使马赫数增大。总之,加热使马赫数趋近于1,而冷却则使马赫数向离开1的方向变化。
(3)无论是亚声速或超声速气流,在加热时,所加入的热量都不能大于出口马赫数等于1 时的热量。如果超过了它,气流就将壅塞,这将在后面细述。
二、热交换对气流参数的影响
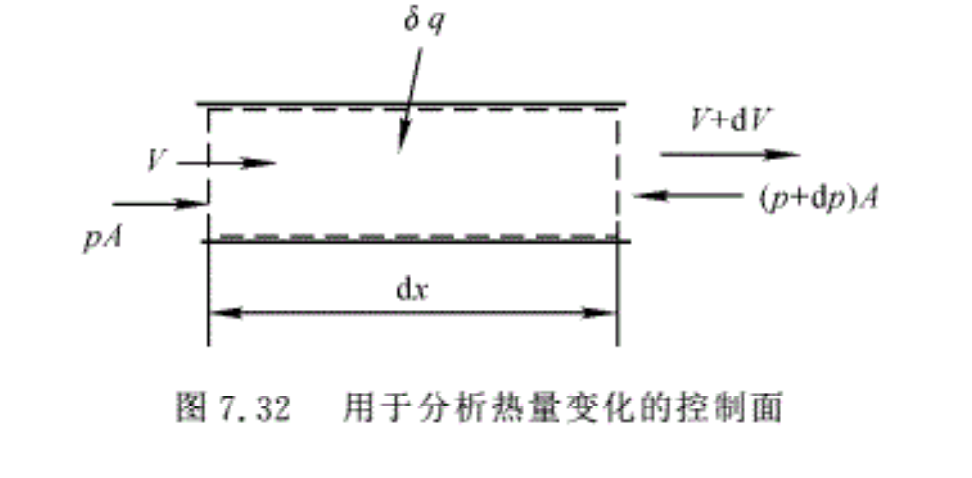
在换热管流中,取无限小的控制体如图7.32虚线所示,在dx长度上,单位质量气体与外界交换的热量为δq,对该控制体写出微分形式的基本关系式为
能量方程 δq=cpdT* (7.65)
动量方程 \(\frac{dp}{p}+kM{{a}^{2}}\frac{dV}{V}=0\) (7.66)
连续方程、状态方程、Ma的定义式和总、静压与Ma的关系的微分形式的基本方程与等截面摩擦管流方程相同,即
dρ/ρ+dV/V=0 (7.67)
dp/p-dρ/ρ-dT/T=0 (7.68)
dMa/Ma=dV/V-dT/2T (7.69)
\(\frac{d{{p}^{*}}}{{{p}^{*}}}=\frac{dp}{p}+\frac{kM{{a}^{2}}}{2+\left( k-1 \right)M{{a}^{2}}}\frac{dM{{a}^{2}}}{M{{a}^{2}}}\) (7.70)
由总、静温与Ma的关系,取对数微分,得
\[\frac{d{{T}^{*}}}{{{T}^{*}}}=\frac{dT}{T}+\frac{\left( k-1 \right)M{{a}^{2}}}{2+\left( k-1 \right)M{{a}^{2}}}\frac{dM{{a}^{2}}}{M{{a}^{2}}}\] (7.71)
因为
\[\frac{ds}{{{c}_{p}}}=\frac{dT}{T}-\frac{k-1}{k}\frac{dp}{p}\]
将式(7.70)和式(7.71)代入上式,得
\[\frac{ds}{{{c}_{p}}}=\frac{d{{T}^{*}}}{{{T}^{*}}}-\frac{k-1}{k}\frac{d{{p}^{*}}}{{{p}^{*}}}\]
从能量方程式(7.65)可以看出,总温的变化直接反映了热量交换的大小和方向,所以可以用总温的变化来反映热量交换的影响。这样,以dT*/T*来体现换热的影响,联立求解式(7.66)~式(7.72)7个方程,就可找出其他7个气流参数与总温变化的关系,由此可以分析热量交换对这些气流参数的影响。联立解得的方程为
\[\begin{align}& \frac{dMa}{Ma}=\frac{\left( 1+kM{{a}^{2}} \right)\left[ 2+\left( k-1 \right)M{{a}^{2}} \right]}{4\left( 1-M{{a}^{2}} \right)}\frac{d{{T}^{*}}}{{{T}^{*}}} \\& \left( 7.73 \right) \\& \frac{dV}{V}=\frac{2+\left( k-1 \right)M{{a}^{2}}}{2\left( 1-M{{a}^{2}} \right)}\frac{d{{T}^{*}}}{{{T}^{*}}} \\& \left( 7.74 \right) \\& \frac{dp}{p}=-\frac{\left[ 2+\left( k-1 \right)M{{a}^{2}} \right]kM{{a}^{2}}}{2\left( 1-M{{a}^{2}} \right)}\frac{d{{T}^{*}}}{{{T}^{*}}} \\& \left( 7.75 \right) \\& \frac{d\rho }{\rho }=-\frac{2+\left( k-1 \right)M{{a}^{2}}}{2\left( 1-M{{a}^{2}} \right)}\frac{d{{T}^{*}}}{{{T}^{*}}} \\& \left( 7.76 \right) \\& \frac{dT}{T}=\frac{\left( 1-kM{{a}^{2}} \right)\left[ 2+\left( k-1 \right)M{{a}^{2}} \right]}{2\left( 1-M{{a}^{2}} \right)}\frac{d{{T}^{*}}}{{{T}^{*}}} \\& \left( 7.77 \right) \\& \frac{d{{p}^{*}}}{{{p}^{*}}}=-\frac{kM{{a}^{2}}}{2}\frac{d{{T}^{*}}}{{{T}^{*}}} \\& \left( 7.78 \right) \\& \frac{ds}{{{c}_{p}}}=\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)\frac{d{{T}^{*}}}{{{T}^{*}}} \\& \left( 7.79 \right) \\\end{align}\]
由式(7.73)~式(7.79)可以分析热量对气流参数的影响,见表7.6。
可以看出,热量交换对气流速度的影响在亚声速和超声速气流中恰恰相反,加热使亚声速气流加速,使超声速气流减速,放热时情况刚好相反。因此,单独的加热不可能使亚声速气流加速到超声速,也不可能使超声速气流连续地降为亚声速。
无论是超声速气流还是亚声速气流,加热时气流总压都是下降的,这一物理现象称为热阻。而且加热量愈大,总压下降也愈大;气流马赫数愈大,总压下降也愈大。为了减小加热时的总压降低,应尽量减小气流的马赫数。例如,在空气喷气发动机的烧室进口,气流的速度就比较低。但在超声速燃烧的冲压发动机燃烧室内,应综合考虑激波损失和加热使得总压下降这两个因素。
在理论上使气流总温减小的冷却过程可以使气流总压增大,但是,由于摩擦等影响因素的存在,实际上这是难以实现的。
三、换热管流的计算
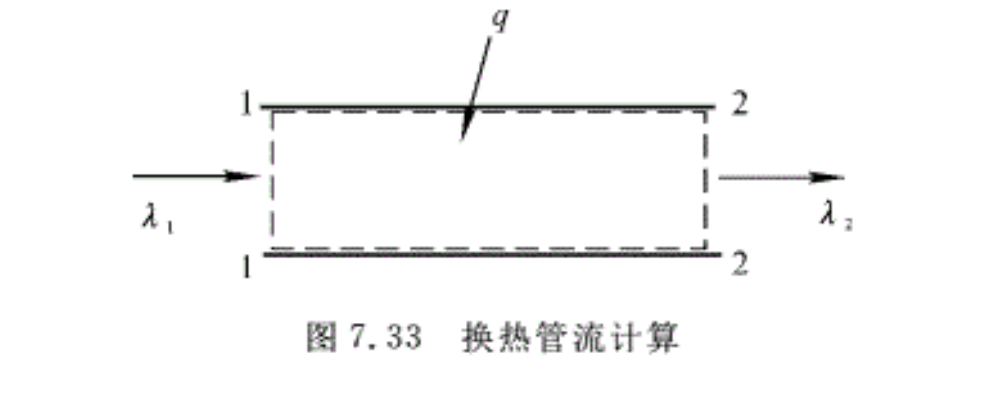
如图7.33所示的换热管流,设气流从1一1截面流入,从2一2截面流出,单位质量气体与外界交换的热量为q,则此两截面间的气流参数可以由下面导出的基本关系式求出。
能量方程 \(q={{c}_{p}}\left( T_{2}^{*}-T_{1}^{*} \right)\) (7.80)
动量方程
\[{{c}_{cr}}z\left( {{\lambda }_{1}} \right)={{c}_{cr2}}z\left( {{\lambda }_{2}} \right)\]
即
\[\frac{z\left( {{\lambda }_{1}} \right)}{z\left( {{\lambda }_{2}} \right)}=\sqrt{\frac{T_{2}^{*}}{T_{1}^{*}}}\]
或
\[\frac{T_{2}^{*}}{T_{1}^{*}}={{\left( \frac{z\left( {{\lambda }_{1}} \right)}{z\left( {{\lambda }_{2}} \right)} \right)}^{2}}\] (7.81)
由连续方程,得
\[\frac{{{\rho }_{2}}}{{{\rho }_{1}}}=\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{{{\lambda }_{1}}{{c}_{cr1}}}{{{\lambda }_{2}}{{c}_{cr2}}}=\frac{{{\lambda }_{1}}}{{{\lambda }_{2}}}\sqrt{\frac{T_{1}^{*}}{T_{2}^{*}}}=\frac{{{\lambda }_{1}}z\left( {{\lambda }_{2}} \right)}{{{\lambda }_{2}}z\left( {{\lambda }_{1}} \right)}\] (7.82)
温度比
\[\frac{{{T}_{2}}}{{{T}_{1}}}=\frac{T_{2}^{*}\tau \left( {{\lambda }_{2}} \right)}{T_{1}^{*}\tau \left( {{\lambda }_{1}} \right)}={{\left( \frac{z\left( {{\lambda }_{1}} \right)}{z\left( {{\lambda }_{2}} \right)} \right)}^{2}}\frac{\tau \left( {{\lambda }_{2}} \right)}{\tau \left( {{\lambda }_{1}} \right)}\] (7.83)
由动量方程可得压力比和总压比,即
\[\begin{align}& \frac{{{p}_{2}}}{{{p}_{1}}}=\frac{r\left( {{\lambda }_{2}} \right)}{r\left( {{\lambda }_{1}} \right)} \\& \left( 7.84 \right) \\& \frac{p_{2}^{*}}{p_{1}^{*}}=\frac{f\left( {{\lambda }_{1}} \right)}{f\left( {{\lambda }_{2}} \right)} \\& \left( 7.85 \right) \\\end{align}\]
以上是以λ为自变量的基本关系式,也可以得到以马赫数为自变量的基本关系式。
例7.8 把某涡轮喷气发动机的燃烧室可近似地看做等截面加热管来计算。设气体在进口截面处的速度V1=62.1 m/s,温度T1=323K,压强p1=0.4 × 105 Pa,在燃烧室中气体吸热量q=1088kJ/ kg。求出口截面上的气体参数。燃气k=1.33,cp=1.088 kJ/(kg • K)。
解:进口处
\[M{{a}_{1}}=\frac{{{V}_{1}}}{\sqrt{kR{{T}_{1}}}}=\frac{62.1}{352}=0.1765\]
查表,得 λ1=0.19
\[\begin{align}& {{T}^{*}}=\frac{{{T}_{1}}}{\tau \left( {{\lambda }_{1}} \right)}=\frac{323}{0.9949}=325K \\& p_{1}^{*}=\frac{{{p}_{1}}}{\pi \left( {{\lambda }_{1}} \right)}=\frac{0.4\times {{10}^{5}}}{0.9796}=0.409\times {{10}^{5}}Pa \\\end{align}\]
出口处
\[\begin{align}& T_{2}^{*}=T_{1}^{*}+\frac{q}{{{c}_{p}}}=325+\frac{1008}{1.008}=1325K \\& z\left( {{\lambda }_{2}} \right)=z\left( {{\lambda }_{1}} \right)\sqrt{\frac{T_{1}^{*}}{T_{2}^{*}}}=5.453\sqrt{\frac{325}{1325}}=2.7 \\\end{align}\]
查表,得 λ2=0.445
\[\begin{align}& p_{2}^{*}=p_{1}^{*}\frac{f\left( {{\lambda }_{1}} \right)}{f\left( {{\lambda }_{2}} \right)}=0.409\times {{10}^{5}}\times \frac{1.0202}{1.0991}=0.38\times {{10}^{5}}Pa \\& \sigma =\frac{p_{2}^{*}}{p_{1}^{*}}=\frac{0.38}{0.409}=0.929 \\& {{T}_{2}}=T_{2}^{*}\tau \left( {{\lambda }_{2}} \right)=1325\times 0.972=1288K \\& {{p}_{2}}=p_{2}^{*}\pi \left( {{\lambda }_{2}} \right)=0.38\times {{10}^{5}}\times 0.892=0.339\times {{10}^{5}}Pa \\\end{align}\]
四、加热壅塞
无论Ma < 1或Ma > 1,加热总使得气体速度向声速趋近。但在等截面直管内加热不可能使亚声速气流加速到超声速,也不能使超声速气流连续地减速为亚声速。可见,对于给定的初始马赫数和温度,必定存在着一个最大的加热量,超过此加热量时,加热后的气流速度将达到声速而发生壅塞。将气流在加热管出口的马赫数Ma2=1时的加热量叫做临界加热量,记为 qcr,对应的加热后气流的总温叫临界总温Tcr*。根据Ma2=1的条件,由式(7.81)和式(7.80)可得
\[\begin{align}& \frac{T_{cr}^{*}}{T_{1}^{*}}=\frac{{{\left[ z\left( {{\lambda }_{1}} \right) \right]}^{2}}}{4} \\& \left( 7.86 \right) \\& {{q}_{cr}}={{c}_{p}}\left( T_{cr}^{*}-T_{1}^{*} \right)={{c}_{p}}T_{1}^{*}\left\{ \frac{{{\left[ z\left( {{\lambda }_{1}} \right) \right]}^{2}}}{4}-1 \right\} \\& \left( 7.87 \right) \\\end{align}\]
可以看出,qcr随λ1的变化趋势与的是一致的。亚声速气流的起始λ1越大,或者超声速气流的起始λ1越小,临界加热量就越小。
当q>qcr时,流动就会发生壅塞。发生壅塞后,由于管道出口q(λ)值已经达到1,而加入过多热量使总压下降,总温上升,根据流量公式不能够调整满足流量相等的要求。因此,气体在管内堆积,使管内气流压强上升。对于亚声速气流,这种壅塞作用一直影响到管道上游,使起始马赫数下降,因而进入管道的质量流量减小,直到所加入的热量能够使管道出口气流顺畅通过为止,此时,气流出口马赫数等于1。对于超声速气流,壅塞的影响将以激波的形式向上游传播,由于激波后气流总压损失更大,若进囗流量不减小,管内壅塞更严重。所以超声速气流因热发生壅塞时,激波将一直向上游推进,直到管口外,使进囗气流马赫数改变,以适应流量的要求。这时整个直管的流动完全变成亚声速流动。
由上述分析可见,对于给定的起始马赫数,存在着一个临界加热量。换句话说,对于给定的起始总温和加热量,亚声速气流的起始马赫数存在一个最大值,超声速气流的起始马赫数存在一个最小值。
例7.9 k=1.33,R=287.04 J /(kg • K)的气体流过等截面直管道。现给气体加热,使其达到滞止温度的3倍,希望马赫数不超过0.8。试求初始的马赫数和加给单位质量气体的热量q。己知初始滞止温度为310 K,且不计摩擦影响。
解:取如图7.33所示的控制体,根据题意,T1*=310 K,T2*=3T1*=930 K,Ma2=0.8,求Ma1和q。
根据能量方程,可得加给气体的热量为
\[q={{c}_{p}}\left( T_{2}^{*}-T_{1}^{*} \right)=\frac{kR}{k-1}\left( T_{2}^{*}-T_{1}^{*} \right)=\frac{1.33\times 287.4}{1.33-1}\left( 930-310 \right)=718.2kJ/kg\]
由动量方程 \({{c}_{cr}}z\left( {{\lambda }_{1}} \right)={{c}_{cr2}}z\left( {{\lambda }_{2}} \right)\)
得 \(z\left( {{\lambda }_{1}} \right)=\sqrt{\frac{T_{2}^{*}}{T_{1}^{*}}}z\left( {{\lambda }_{2}} \right)\) (a)
根据Ma与λ之间的关系,得
\[{{\lambda }_{2}}=\sqrt{\frac{\left( k+1 \right)Ma_{2}^{2}}{2+\left( k-1 \right)Ma_{2}^{2}}}=\sqrt{\frac{\left( 1.33+1 \right)\times {{0.8}^{2}}}{2+\left( 1.33-1 \right)\times {{0.8}^{2}}}}=0.821\]
所以
\[z\left( {{\lambda }_{2}} \right)={{\lambda }_{2}}+\frac{1}{{{\lambda }_{2}}}=0.821+\frac{1}{0.821}=2.04\]
将上式代入式(a),得
\[z\left( {{\lambda }_{1}} \right)=\sqrt{\frac{930}{310}}\times 2.04=3.533\]
查气动函数表,得 λ1=0.31,Ma1=0.285
即进囗马赫数不超过0.285,若超过0. 285,则出囗马赫数不能保证0.8的数值。
如果要求热管不发生壅塞,则此时的进口马赫数计算如下:
由
\[z\left( {{\lambda }_{1}} \right)=\sqrt{\frac{T_{2}^{*}}{T_{1}^{*}}}z\left( {{\lambda }_{2}} \right)\]
因为
\[z\left( {{\lambda }_{2}} \right)={{\lambda }_{2}}+\frac{1}{{{\lambda }_{2}}}=2\] (λ2=1)
所以
\[z\left( {{\lambda }_{1}} \right)=\sqrt{\frac{930}{310}}\times 2=3.464\]
查气体函数表,得 λ1=0.318,Ma1=0.29
即进囗马赫数大于0.29,就会发生壅塞。
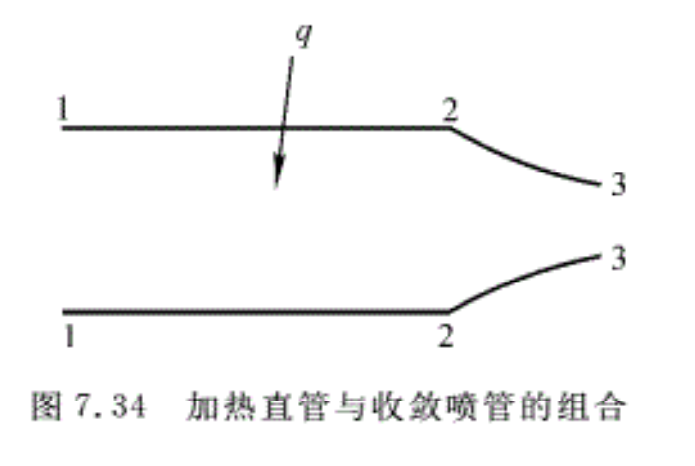
例7.10 理想气体流经等截面加热直管,在位置2 完成加热,之后气体在收缩喷管内等熵膨胀,如图7.34 所示,忽略表main摩擦,已知比热比k=1. 33,Ma1=0.3, T1*=300 K,T2*/T1*=2,A3/A2=0.9。求速度因数λ3,以及恰好引起流动壅塞时的T2*/T1*及加热量。
解:设加热管进口为1截面,则可与出气流在加热管内的动量方程为
\[\begin{align}& {{c}_{cr1}}z\left( {{\lambda }_{1}} \right)={{c}_{cr2}}z\left( {{\lambda }_{2}} \right) \\& z\left( {{\lambda }_{2}} \right)=\sqrt{\frac{T_{1}^{*}}{T_{2}^{*}}}z\left( {{\lambda }_{1}} \right) \\\end{align}\] (a)
由Ma1=0.3查表,得
λ1=0.322, z(λ1)=λ1+1/λ1=3.4276
代入式(a),得
z(λ2)=2.4236
查气动函数表,得
λ2=0.528,Ma2=0.498,q(λ2)=0.74
由连续方程
\[K\frac{p_{2}^{*}}{\sqrt{T_{2}^{*}}}q\left( {{\lambda }_{2}} \right){{A}_{2}}=K\frac{p_{3}^{*}}{\sqrt{T_{3}^{*}}}q\left( {{\lambda }_{3}} \right){{A}_{3}}\]
又
T3*=T2* ,p3*=p2*
解得
\[q\left( {{\lambda }_{3}} \right)=\frac{{{A}_{2}}}{{{A}_{3}}}q\left( {{\lambda }_{2}} \right)=0.8222\]
查气动函数表,得
λ3=0.612
壅塞时,λ3=1,所以
\[q\left( {{\lambda }_{2}} \right)=\frac{{{A}_{3}}}{{{A}_{2}}}=0.9\]
查气动函数表,得
λ2=0.708,z(λ2)=2.12
故
\[\frac{T_{2}^{*}}{T_{1}^{*}}={{\left[ \frac{z\left( {{\lambda }_{1}} \right)}{z\left( {{\lambda }_{2}} \right)} \right]}^{2}}={{\left( \frac{3.4276}{2.12} \right)}^{2}}=2.61\]
加热量
\[q={{c}_{p}}\left( T_{2}^{*}-T_{1}^{*} \right)=\frac{kRT_{1}^{*}}{k-1}\left( \frac{T_{2}^{*}}{T_{1}^{*}}-1 \right)=\frac{1.33\times 287.4}{0.33}\left( 2.61-1 \right)\times 300=559kJ/kg\]
五、凝结突跃
凝结突跃是换热管流中出现的一种现象。气体沿着超声速或高超声速风洞的拉伐尔喷管流动时,由于气流的迅速降压膨胀,使其温度迅速下降,其温度可能低于水蒸气的凝结温度。根据实验,刚低于凝结温度不多时,无明显的凝结现象,即可以允许有一定的过冷度。过冷度达到一定的值时,空气中所含的水汽就会凝结。例如,过冷度在50 ℃左右就会出现显著的凝结现象。一旦出现凝结,凝结过程便进行得十分迅速,该过程所占的距离很小,几乎是集中在一个截面上完成的。水蒸气凝结时放出潜热,这部分热量突然加入超声速气流中,使超声速气流速度突然下降,密度、压强、总温突然上升,总压突然下降,这种现象称为凝结突跃。显然,凝结突跃不同于正激波突跃,因为凝结突跃使总温突然上升,而激波突跃使总温保持不变。从实验可知,虽然凝结突跃的波面与气流方向接近垂直,但其后的气流仍是超声速的。而正激波突跃后气流一定是亚声速的。
一旦出现凝结突跃,不仅会引起流场中参数的大小发生变化,而且也会改变流场的均匀度,因此超声速和高超声速风洞喷管中应避免凝结突跃。为了避免凝结突跃,通常采用特殊的干燥设备,把空气中的水分减少到万分之五以下,以避免凝结突跃放出过多的热量使气流参数变化过大。
7.7 变流量加质管流
本章的前几节讨论了变截面管流、摩擦管流和换热管流,其共同点是在管道各截面上流量是不变的。在工程实际中还有许多是变流量的管内流动。例如,在火箭发动机上,固体空心药柱燃烧时,燃气不断增加就是变流量的问题。本节将讨论质量添加对主流的影响,仅考虑由于流量变化所引起的参数变化,而不考虑其他因素的影响,即假设没有摩擦、机械功和热量的交换,没有化学反应,等等;同时假设,附加气流是和主流的分子量、比热容都相同的完全气体,且具有相同的总焓h*,在控制体内完全混合,离开控制面时具有均匀参数。
一、基本方程
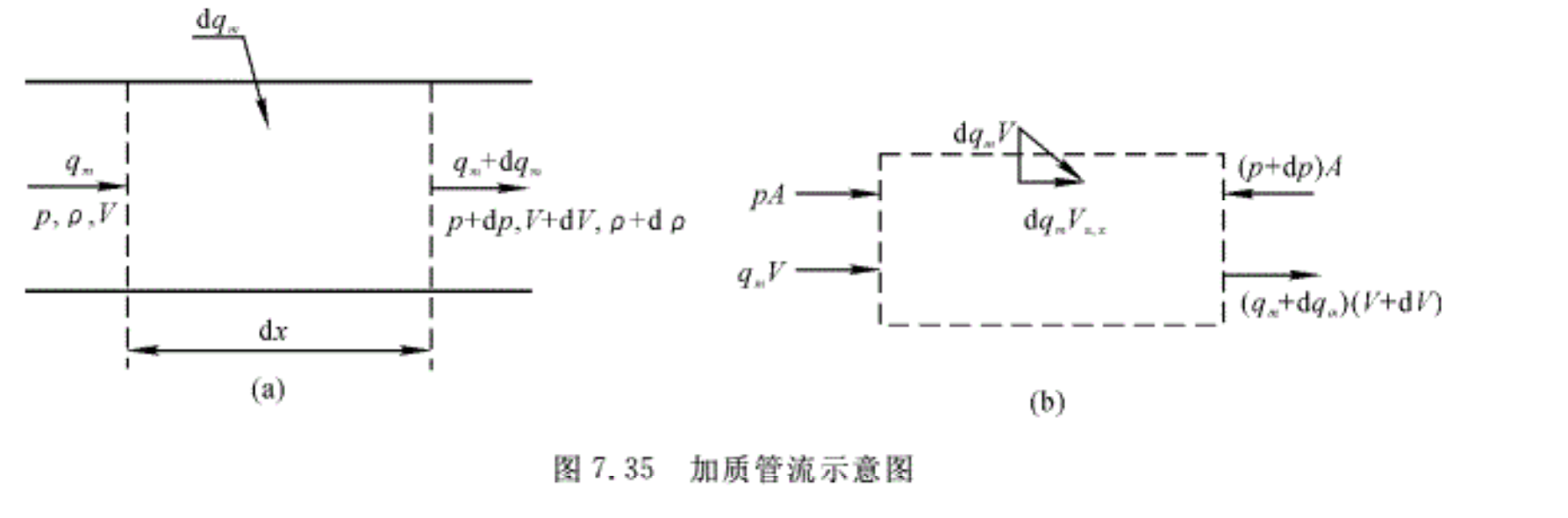
取图7.35(a)所示的微元控制体,对此控制体写出基本方程。
1.连续方程
由流量公式qm=ρAV,取对数微分,则有
\(\frac{d{{q}_{m}}}{{{q}_{m}}}=\frac{d\rho }{\rho }+\frac{dV}{V}\) (7.88)
式中 qm——主流的流量;
dqm——附加的气流流量。
2.动量方程
图7.35(b)表示了在x方向上作用在控制面上的作用力和单位时间通过控制面的动量。其中,Va,x表示附加气流速度在x方向的分量,则在x方向上列出动量方程得
\(pA-\left( p+dp \right)A=\left( {{q}_{m}}+d{{q}_{m}} \right)\left( V+dV \right)-{{q}_{m}}V-d{{q}_{m}}{{V}_{ax}}\)
令y=Va,x/V,并利用qm=ρAV,则动量方程可化成
\(dp+\rho VdV+\rho {{V}^{2}}\left( 1-y \right)\frac{d{{q}_{m}}}{{{q}_{m}}}=0\)
将上式通除以p,引进p/ρ=c²/k,简化后得
\(\frac{dp}{p}+kM{{a}^{2}}\frac{dV}{V}+kM{{a}^{2}}\left( 1-y \right)\frac{d{{q}_{m}}}{{{q}_{m}}}=0\) (7.89)
3.能量方程
因为己假设主流和附加气流单位质量气体具有相同的总焓,所以两股气流混合后单位质量气体总焓也保持原有的数值,因此能量方程为
\(${{h}^{*}}={{c}_{p}}{{T}^{*}}={{c}_{p}}T+\frac{{{V}^{2}}}{2}=$\)
将上式微分并考虑到c=kR/(k-1),c²=kRT,则有
\(\frac{dT}{T}+\left( k-1 \right)M{{a}^{2}}\frac{dV}{V}=0\) (7.90)
4.其他关系式
状态方程、马赫数的定义式及总静压与马赫数的关系的微分形式基本方程为
\(\frac{dp}{p}=\frac{d\rho }{\rho }+\frac{dT}{T}\) (7.91)
\(\frac{dMa}{Ma}=\frac{dV}{V}-\frac{1}{2}\frac{dT}{T}\) (7.92)
\(\frac{d{{p}^{*}}}{{{p}^{*}}}=\frac{dp}{p}+\frac{kM{{a}^{2}}}{1+\frac{k-1}{2}M{{a}^{2}}}\frac{dMa}{Ma}\) (7.93)
气流冲量的变化由\(F=\frac{k+1}{2k}{{q}_{m}}{{c}_{cr}}z\left( \lambda \right)=pA\left( 1+kM{{a}^{2}} \right)\),同样两边取对数微分,得
\(\frac{dF}{F}-\frac{dp}{p}-\frac{2kM{{a}^{2}}}{1+kM{{a}^{2}}}\frac{dMa}{Ma}=0\) (7.94)
在T*=C的情况下,由熵和总压恢复因数的关系,可得
\(\frac{ds}{{{c}_{p}}}=-\frac{k-1}{k}\frac{d{{p}^{*}}}{{{p}^{*}}}\) (7.95)
式( 7 .94 )中的F表示气流的冲量。
二、流量变化对气流参数的影响
从式( 7.88 ) ~式( 7.95 )的8个方程中有9个未知量,只要将影响气流参数变化的流量参数dqm/qm作为独立的变量,即可解得其他8个参数与dqm/qm的关系,即
\(\frac{dMa}{Ma}=\frac{1+\frac{k-1}{2}M{{a}^{2}}}{1-M{{a}^{2}}}\left[ 1+\left( 1-y \right)kM{{a}^{2}} \right]\frac{d{{q}_{m}}}{{{q}_{m}}}\) (7.96)
\(\frac{dV}{V}=\frac{1}{1-M{{a}^{2}}}\left[ 1+\left( 1-y \right)kM{{a}^{2}} \right]\frac{d{{q}_{m}}}{{{q}_{m}}}\) (7.97)
\(\frac{dp}{p}=-\frac{kM{{a}^{2}}}{1-M{{a}^{2}}}\left[ 2\left( 1+\frac{k-1}{2}M{{a}^{2}} \right)\left( 1-y \right)+y \right]\frac{d{{q}_{m}}}{{{q}_{m}}}\) (7.98)
\(\frac{d\rho }{\rho }=-\frac{1}{1-M{{a}^{2}}}\left[ M{{a}^{2}}+\left( 1-y \right)kM{{a}^{2}} \right]\frac{d{{q}_{m}}}{{{q}_{m}}}\) (7.99)
\(\frac{dT}{T}=-\frac{\left( k-1 \right)M{{a}^{2}}}{1-M{{a}^{2}}}\left[ 1+\left( 1-y \right)kM{{a}^{2}} \right]\frac{d{{q}_{m}}}{{{q}_{m}}}\) (7.100)
\(\frac{d{{p}^{*}}}{{{p}^{*}}}=-kM{{a}^{2}}\left( 1-y \right)\frac{d{{q}_{m}}}{{{q}_{m}}}\) (7.101)
\(\frac{ds}{{{c}_{p}}}=\frac{k-1}{k}\frac{d{{p}^{*}}}{{{p}^{*}}}=\left( k-1 \right)M{{a}^{2}}\left( 1-y \right)\frac{d{{q}_{m}}}{{{q}_{m}}}\) (7.102)
\(\frac{dF}{F}=\frac{ykM{{a}^{2}}}{1+kM{{a}^{2}}}\frac{d{{q}_{m}}}{{{q}_{m}}}\) (7.103)
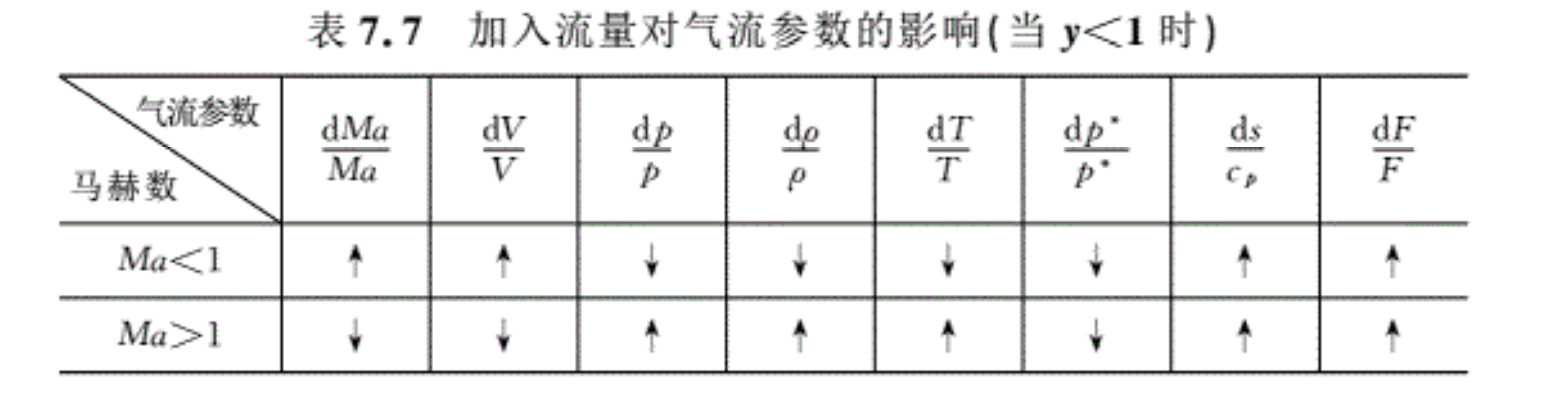
从式( 7.96 ) ~式( 7.103 )可以看岀,在dqm /qm的系数中包含Ma和y ,因此,流量对气流参数的影响不仅与气流的马赫数有关,还与参数y有关。表7.7列出了当y< 1时,加入流量对气流参数的影响。
由表7. 7可见,当y< 1时,加入流量使总压下降,单位质量流体的机械能降低。加入流量将使亚声速气流加速,使超声速气流减速。因此,与前几节讨论的情况相类似,加入流量使气流向临界状态逼近,因而流量加到一定程度时,气流速度达到当地声速, Ma等于1 ,主流开始出现壅塞现象,流量加入过多,则会改变主流的起始状态。
三、附加流量垂直于主流的情况
当附加气流流动方向垂直与主流方向时, Vax=0 , y= 0 ,方程变得比较容易积分。与摩擦管流中所用的方法相类似,应用临界状态的概念,即流量增加到使Ma=1 ,此时对应的流量为界流量qm,cr,这样式( 7.96 )的积分形式为
\(\int_{{{q}_{m}}}^{{{q}_{mcr}}}{\frac{d{{q}_{m}}}{{{q}_{m}}}=\int_{Ma}^{1}{\frac{1-M{{a}^{2}}}{Ma\left( 1+kM{{a}^{2}} \right)\psi }}}dMa\)
式中 \(\psi =1+\frac{k-1}{2}M{{a}^{2}}\)
积分后得
\(\frac{{{q}_{m}}}{{{q}_{mcr}}}=\frac{Ma{{\left[ 2\left( k+1 \right)\psi \right]}^{\frac{1}{2}}}}{1+kM{{a}^{2}}}\) (7.104)
同样,积分式( 7 . 97 ) ~式( 7.103 ) ,可得岀其他参数。这里从原始方程岀发可以更容易地得出。根据T *=Tcr* =常数的假设,得
\(\frac{T}{{{T}_{cr}}}=\frac{k+1}{2\psi }\) (7.105)
又
\(\frac{V}{{{V}_{cr}}}=\lambda =Ma{{\left( \frac{k+1}{2\psi } \right)}^{\frac{1}{2}}}\) (7.106)
从 qm=ρVA=pVA/RT
得 \(\frac{p}{{{p}_{cr}}}=\frac{{{q}_{m}}}{{{q}_{mcr}}}\frac{T}{{{T}_{cr}}}\frac{{{V}_{cr}}}{V}=\frac{Ma{{\left[ 2\left( k+1 \right)\psi \right]}^{\frac{1}{2}}}}{1+kM{{a}^{2}}}\frac{k+1}{2\psi }\frac{1}{Ma}{{\left( \frac{2\psi }{k+1} \right)}^{\frac{1}{2}}}\)
化简得
\(\frac{p}{{{p}_{cr}}}=\frac{k+1}{1+kM{{a}^{2}}}\) (7.107)
从状态方程得
\(\frac{\rho }{{{\rho }_{cr}}}=\frac{p}{{{p}_{cr}}}\frac{{{T}_{cr}}}{T}=\frac{2\psi }{1+kM{{a}^{2}}}\) (7.108)
从总压、静压和马赫数的关系,得
\(\frac{{{p}^{*}}}{p_{cr}^{*}}=\frac{k+1}{1+kM{{a}^{2}}}{{\left( \frac{2\psi }{k+1} \right)}^{\frac{k}{k-1}}}\) (7.109)
以上方程中的各参数比值与马赫数的关系可制成表格,也可直接编程借助于计算机计算。
例7.11 图7.36所示的固体火箭发动机的火药柱内孔直径d=0.025 m,烧在靠近火药柱的内表面非常薄的燃烧区内进行。设燃烧速度Vb=0.025 m/s保持不变,推进剂的密度ρp=2500 kg/m³,燃气的比热比k=1. 2,气体常数R=320 J/( kg.K),火焰温度Tf=3000K,火药柱长L=0.3 m,喷管喉部面积At=0.0003 m2,出囗直径与火药柱内孔直径相等。火药柱始端以下标0表示,末端以e表示。试计算:
(1)推进剂的燃气流量;
(2)喷管进口气流的马赫数和总压;
(3)始端总压po*、密度ρo;
(4)始端和末端的静压差。
解 :(1)在微元段dx上,\(d{{q}_{m}}={{V}_{b}}{{\rho }_{b}}\pi ddx\),则
\[{{q}_{m,e}}=\int_{0}^{L}{d{{q}_{m}}=}{{V}_{b}}{{\rho }_{b}}\pi dL=0.025\times 2500\times \pi \times 0.025\times 0.30=1.473kg/s\]
(2) \(q\left( {{\lambda }_{e}} \right)=\frac{{{A}_{t}}}{{{A}_{e}}}=\frac{4\times 0.0003}{\pi \times {{0.025}^{2}}}=0.6111\)
查气动函数表(k=1. 2),得
\[\begin{align}& M{{a}_{e}}=0.3938 \\& {{\lambda }_{e}}=0.4099 \\& p_{e}^{*}=\frac{{{q}_{m,e}}\sqrt{{{T}^{*}}}}{K{{A}_{t}}}=\frac{1.473\times \sqrt{3000}}{0.0362\times 0.0003}=74.29\times {{10}^{5}}Pa \\\end{align}\]
(3)由式(7.109),当Mae=0.3938时,
\[\begin{align}& \frac{p_{e}^{*}}{p_{cr}^{*}}=\frac{k+1}{1+kMa_{e}^{2}}{{\left[ \left( \frac{2}{1+k} \right)\left( 1+\frac{k-1}{2}Ma_{e}^{2} \right) \right]}^{\frac{k}{k-1}}}= \\& \frac{1.2+1}{1+1.2\times {{0.3938}^{2}}}\times {{\left[ \frac{2}{2.2}\times \left( 1+\frac{0.2}{2}\times {{0.3938}^{2}} \right) \right]}^{\frac{1.2}{0.2}}}=1.1483 \\\end{align}\]
于是 \(p_{cr}^{*}=\frac{74.29\times {{10}^{5}}}{1.1483}=64.7\times {{10}^{5}}Pa\)
由式(7.109),对Mao=0,有
\[\begin{align}& \frac{p_{0}^{*}}{{{p}_{cr}}}=\left( 1.2+1 \right)\times {{\left( \frac{2}{2.2} \right)}^{\frac{1.2}{0.2}}}=1.2418 \\& p_{0}^{*}=1.2418\times 64.7\times {{10}^{5}}=80.30\times {{10}^{5}}Pa \\& {{\rho }_{0}}=\frac{p_{0}^{*}}{RT}=\frac{80.30\times {{10}^{5}}}{320\times 3000}=8.36kg/{{m}^{3}} \\\end{align}\]
(4) \(\Delta p=p_{0}^{*}-{{p}_{e}}=p_{0}^{*}-p_{e}^{*}\pi \left( {{\lambda }_{e}} \right)=\left( 80.3-74.29\times 0.9118 \right)\times {{10}^{5}}=12.56\times {{10}^{5}}Pa\)
小结
(1)在一维可压缩管内流动中,分析问题的方法是:首先写出一维可压缩流动的微分形式的基本方程;其次突出主要的影响因素,如变截面管内的流动,主要突出截面积变化的因素,把面积变化作为参变量,来分析对其他流动参数的影响;最后得到对各个流动参数的影响规律。其他管内流动,其分析方法类同。
(2)收缩喷管与拉伐尔喷管的流动特点,见表7.8。
(3)内压式超声速进气道的优点是外部阻力小,缺点是存在起动问题。使进气道起动的方法是提高来流马赫数或增加喉部面积。
(4)摩擦对亚声速气流和超声速气流有不同的影响。单纯的摩擦作用不能使亚声速气流变为超声速气流,也不可能使超声速气流连续地变为亚声速气流。
(5)摩擦管流的计算一般都设想管子有一个临界截面,然后把进口截面和需要计算的那个截面上的参数都和临界截面建立联系,最后利用临界截面的概念,即可进行摩擦管流的计算。
(6)换热管流的计算主要用基本方程,即能量方程、动量方程、连续方程以及气动函数来计算。
(7)加热壅塞是指加热管出口马赫数等于1时的状态,此时的加热量叫临界加热量,对应于加热后的总温叫临界总温。
(8)变流量加质管流也是工程中常见的流动,分析的方法与前几节类似,不同点在于将流量参数作为参变量,来分析流量变化对气流参数的影响。
思考与练习题
7.1 当收缩喷管出现壅塞时,此时的流动特点是什么?
7.2 如果要建立Ma=2.5的超声速气流,喷管的出口面积Ae与喉部面积At之比应为多大?
7.3 什么叫加热壅塞?试分析加入过多的热量对亚声速气流和超声速气流是如何影响的。
7.4 临界加热量与什么条件有关?
7.5 某风洞的收缩喷管,进囗空气流的总压为1.724 × 105 Pa,总温为324K,喷管出口通大气,出囗面积为0.03 m2,实验时大气压强pa=1.0133 × 105 Pa。若不考虑喷管内的流动损失,试计算喷管出囗气流速度、压强及通过喷管的空气流量。
7.6 设空气自容器经收缩喷管等熵流出,如图7.37所示,已知p*/pa=3.3,A1/A2=2。求λ1。
7.7 发动机在地面试车时,测得收缩形喷管前燃气总压和总温分别为p*=2.5 × 105 pa,T*=1016 K。己知喷管出口面积Ae=0.168 m2, 喷管出口外界大气压强pa=1.0133 × 105Pa。试求喷管出口处燃气的速度及通过喷管的流量(设燃气的比热比k=1. 33,气体常数R= 287.4 J /(kg.K) ) 。
7.8 己知某拉伐尔喷管最小截面的面积At=4. 0 × 10-4㎡,出口截面的面积Ae=6.76 × 10-4 m2。 喷管出囗外界的大气压强pe=1 × 105 Pa,气源的温度T*=288 K。求当气源的压强p*分别等于1.09 ×105 pa,1. 5 × 105 Pa,2.0 × 105 pa和10 × 105pa时,在喷管出口处空气流的马赫数、速度和空气的流量以及管中有激波时激波的位置。
7.9 给定拉伐尔喷管的出口面积和最小截面面积之比Ae/At=2,试问在计算通过喷管的流量时,pa/p*在什么范围内可采用流量公式qm=0.0404p*At/√T*(流体为空气)?
7.10 空气由气瓶经拉伐尔喷管流出,已知气流总温T*=289 K,Ae/At=4.235。试求当激波位于出囗截面时,出口截面处激波后气流的速度。
7.11 海平面高度的静止大气通过拉伐尔喷管被吸入真空箱,在扩张段的As处产生一正激波。己知喷管的喉道面积为At,出口面积为Ae,假设除激波外的流动为一维等熵流动,求真空箱内的压强。
7.12 空气通过一无摩擦的收缩一扩张喷管流动,已知Ae/At=3,p1*/pe=2.5(pe=pa)。试计算出口马赫数Mae及气流通过喷管时熵的增加。
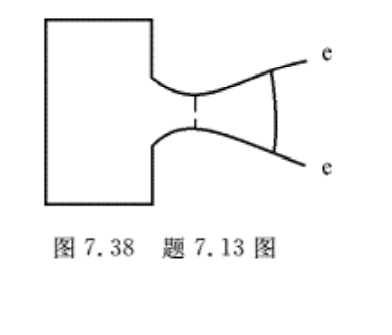
7.13 (1)如图7.38所示的拉伐尔喷管,己知Ae/Acr=2.429,试求当p1*/pa等于多少时,正激波将位于As/Acr=1.7处。
(2)为保持p1*/pa不变,而Ae/Acr=2.005,问激波将移至何处?
7.14 总压为13.6 × 105 Pa的空气流过平面拉伐尔喷管,Acr/Ae=0.4965,问气体流出喷管后,气流方向将连续向外折转的角度是多少度?设喷管出口外界反压pa=1 × 105 Pa。
7.15 内压式超声速进气道的进口面积为Ai,设计马赫数Mad=1. 6,喉道面积按在设计飞行状态下喉道为声速流动确定。为了使进气道起动,采用飞行加速法。若在起动过程中,除激波有总压损失外的流动是等熵的,问飞行马赫数至少加速到多大,激波才被吞入?
7.16 内压式超声速进气道的设计马赫数Mad=2.31,飞行高度H=18000 m,已知进气道的面积比At/Ai=q(λd) ,且Ai=0.15㎡。问:
(1)在该高度以Mad=1.95飞行时,进气道进囗前的流动图形如何?若飞行马赫数加大到Mad=2.31,流动图形有无变化?
(2)为了使进气道起动,喉道面积应放大到多大?
(3)计算喉道面积放大后的喉道马赫数及通过进气道的流量。
7.17 空气在等直径的圆管中无摩擦地流动,由于对气流热,速度由V1=100m/s 增大到V2=300m/s。设加热前气体的密度为ρ1=2.4 kg/m³,试求压强降低的数值,即求p1-p2的值。
7.18 空气在等直径的圆管中无摩擦地流动,进口总温T1*=300K,由于对气流加热,空气流的速度因数由0.5提高到0.9。求对单位质量空气的热量。
7.19 空气在等直径的圆管中无摩擦地流动,进口处,T1*=400K,λ1=0.3,由于对气流加热,所以总温提高,试求达到壅塞状态时的总温T2*。
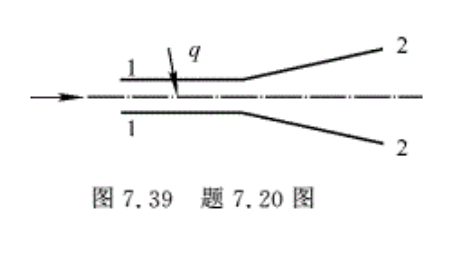
7.20 一个半热力喷管(见图7.39),等截面段为加热段,扩散段为绝热段,不考虑摩擦作用,已知在加热段进口空气流T1*=289 K,V1=62.2 m/s,p1*=20 × 105Pa,扩散段为超声速段,出口截面A2上的气流压强p2=pa=1. 033 × 105 Pa,通过管道的流量qm=9 kg/s。试求气流作用于管壁的轴向力。