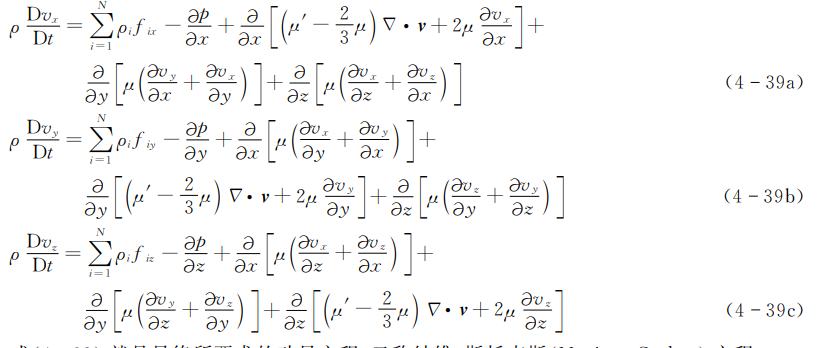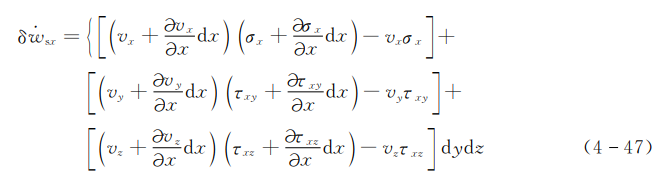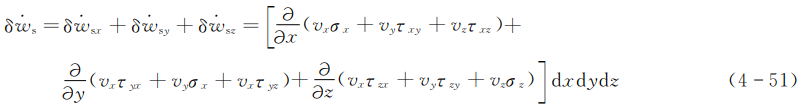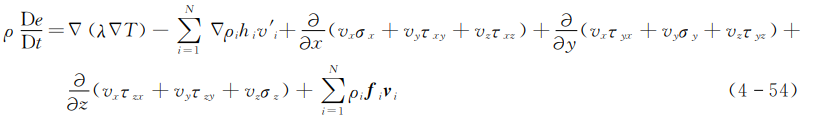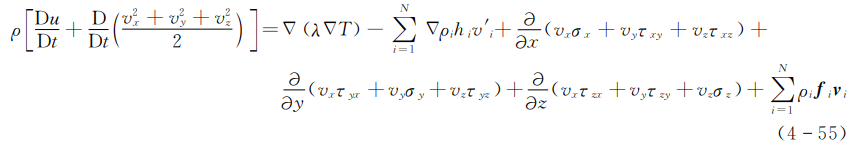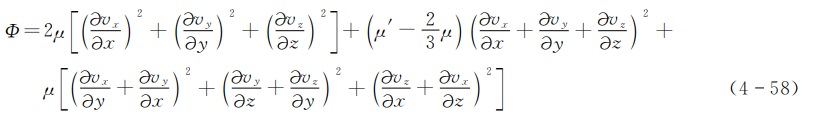第4章多组分反应系统的基本方程

本章针对多组分连续介质,利用有关定律导出描述多组分反应流体混合物的守恒方程。方程推导过程采用控制体法(欧拉法)。所谓反应流体力学,是指利用连续介质力学观点,研究各种有化学反应的流动过程,这些过程都有化学反应和传热、传质的多组分流体的流动。所谓控制体法,是指研究的不是流体的微团本身而是流体微团所流过的空间(流场)

4.1多组分连续介质的主要参数

假定多组分反应气体混合物是由多种连续介质所形成的连续介质,同时也假定各组分气体都是完全气体。

4.1.1密度(浓度)

4.1.1密度(浓度)
组分i在某点的分密度为
\({{\rho }_{i}}(\xi )=\underset{\Delta V\to 0}{\mathop{\lim }}\,=\frac{\Delta {{m}_{i}}}{\Delta V}=\frac{d{{m}_{i}}}{dV}i=1,2,3\cdots ,N\)  (4-1)
总密度为
\(\rho =\sum\limits_{i=1}^{N}{{{\rho }_{i}}}\)   (4-2)
用质量分数Yi来表示组分i的质量在混合气体质量中所占的比例，如
\({{Y}_{i}}=\frac{{{\rho }_{i}}}{\rho }\) (4-3)
\(\sum\limits_{i=1}^{N}{{{Y}_{i}}}=\sum\limits_{i=1}^{N}{\frac{{{\rho }_{i}}}{\rho }}=1\) (4-4)
4.1.2温度
温度用T表示。
4.1.3压力
假如混合气体中存在多种组分，那么每种组分都存在一个分压力。假设各组分为完全气体，分压力和总压力分别定义如下：
(1)分压力混合气体中组分气体分子运动所产生的压力等于它单独存在时的压力，此压力称为气体组分的分压力。
(2)总压力：所有气体组分的分子运动同时作用产生的压力是整个混合气体的总压力。根据道尔顿定律，它等于全部气体组分的分压力之和。
总压力和分压力关系如下:
\(p=\sum\limits_{i=1}^{N}{{{p}_{i}}}\)    (4-5)
由分压力定义可得组分i的状态方程为
\({{p}_{i}}={{\rho }_{i}}\frac{{{R}_{0}}}{{{M}_{i}}}T=\frac{{{Y}_{i}}}{{{M}_{i}}}\rho {{R}_{0}}T\)  (4-6)
混合气体状态方程为
\(p=\sum\limits_{i=1}^{N}{\frac{{{Y}_{i}}}{{{M}_{i}}}\rho {{R}_{0}}T}\)   (4-7)
混合气体平均分子量为
\(M=(\sum\limits_{i=1}^{N}{\frac{{{Y}_{i}}}{{{M}_{i}}}{{)}^{-1}}}\)    (4-8)
摩尔分数与压力分数关系为
\({{X}_{i}}=\frac{{{C}_{i}}}{\sum\limits_{i=1}^{N}{{{C}_{i}}}}=\frac{\frac{{{Y}_{i}}}{{{M}_{i}}}}{\sum\limits_{i=1}^{N}{\frac{{{Y}_{i}}}{{{M}_{i}}}}}=\frac{{{p}_{i}}}{p}\)   (4-9)
4.1.4内能和焓
组分i的比内能为
\({{u}_{i}}={{u}_{i}}^{0}+{{C}_{V,i}}dT\)   (4-10)
组分i的比焓为
\(~{{h}_{i}}={{u}_{i}}+\frac{{{p}_{i}}}{{{\rho }_{i}}}\text{=h}_{i}^{0}{{C}_{p,i}}dT\)    (4-11)
混合气体的比内能为
\(u=\sum\limits_{i=1}^{N}{{{Y}_{i}}}{{u}_{i}}={{u}_{0}}+\int_{{{T}_{0}}}^{T}{{{C}_{V}}dT}\)    (4-12)
混合气体的比焓为
\(h=\sum\limits_{i=1}^{N}{{{Y}_{i}}}{{h}_{i}}={{h}_{0}}+\int_{{{T}_{0}}}^{T}{{{C}_{p}}dT}\)    (4-13)
u和h不仅是温度的函数，还与混合气体的组成有关。
4.1.5速度
混合气体平均运动速度v是各组分的运动速度按其质量分数加权的平均速度，数学表达式如下
\(v=\sum\limits_{i=1}^{N}{{{Y}_{i}}{{v}_{i}}}\)    (4-14)
每一组分的扩散速度 ，也就是每一组分相对混合物的相对运动速度，即
\({{{v}’}_{i}}={{v}_{i}}-v\)    (4-15)
\(\sum\limits_{i=1}^{N}{{{Y}_{i}}{{v}_{i}}}=\sum\limits_{i=1}^{N}{{{Y}_{i}}{{{{v}’}}_{i}}}-\sum\limits_{i=1}^{N}{{{Y}_{i}}v=v-v=0}\)    (4-16)
任一组分i的扩散速度通常由浓度梯度和扩散系数确定。
某一组分的浓度梯度不仅与扩散速度有关而且与压力梯度扩散、彻体力扩散、热扩散有关。
4.1.6 Fick扩散定律
早在1855年，Fick就提出:如果不计热扩散、体力扩散及压力梯度扩散，只考虑浓度梯度扩散，在单位时间内通过垂直于扩散方向的单位截面积的扩散物质流量(扩散通量)与该截面处的浓度梯度成正比，也就是说，浓度梯度越大，扩散通量越大。故扩散通量YiVi，可采用如下方程表示(Fick定律):
\({{Y}_{i}}{{{v}’}_{i}}=-{{D}_{i,0}}\nabla {{Y}_{i}}\)    (4-17)
式中，Di,0为i组分对混合气的双元扩散系数。
4.1.7实导数
用欧拉法描述流场时，流体的各个物理量不仅是时间的函数，也是空间位置的函数。因此，确定流体微团的任一物理量A相对于时间的变化率应包括两部分
(1)t时刻位于空间点P上的流体微团A是时间的函数，在这个点上A随时间变化;
(2)原在P点的微团经dt时间后由于流动到了Q点，一般来说，Q点的A和在P点时有些不同，也就是说，由于迁移引起A的变化。
由一物理量A(x，y，z，t)，具有速度 ，A在空间一点的总变化率为
\(\frac{dA}{dt}=\frac{\partial A}{\partial t}={{V}_{x}}\frac{\partial A}{\partial x}+{{V}_{y}}\frac{\partial A}{\partial y}+{{V}_{z}}\frac{\partial A}{\partial z}\)   (4-18)
由这个算式得到的导数称为随流体运动的导数或实导数。
4.2连续方程
用 代表单位时间、单位体积内由于化学反应生成组分i的净质量，在整个反应中，一种组分可以转变为另一组组分，但是参加化学反应各物质的质量总和保持不变，从而
\(\sum\limits_{i=1}^{N}{{{\omega }_{i}}}=0\)   (4-19)
在这个前提下，分别讨论在有化学反应的情况下组分i的连续方程和混合气体的整体连续方程。
4.2.1组分i的连续方程
设在流场中任取一控制体V(它在空间是固定的)该控制体的表面为控制面S。在有化学反应的情况下，因为占据控制体V的流体内存在着各组分的质量源和汇，所以根据质量守恒定律，单位时间内，组分i从控制面S流出的净质量与其在控制体内质量的变化率之和等于组分i在控制体V内的生成率，即
\(~\iint_{S}{{{\rho }_{i}}}{{v}_{i}}ndS+\frac{\partial }{\partial t}\iint_{S}{{{\rho }_{i}}}dV=\iiint_{V}{{{\omega }_{i}}dV}~~\) (4-20)
根据高斯(Gauss)定理
\(~\iint_{S}{{{\rho }_{i}}}{{v}_{i}}ndS=\iiint_{V}{\nabla {{\rho }_{i}}{{v}_{i}}dV}~~\)
控制体V是固定的，不随时间而变化，因此在积分号之前的对时间偏导数运算符\(\frac{\partial }{\partial t}\)可以移到积分号之内。于是式(4-20)可以写为
\(~\iiint_{V}{\nabla {{\rho }_{i}}{{v}_{i}}dV}~~+\iiint_{V}{\frac{\partial {{\rho }_{i}}}{\partial t}dV}=\iiint_{V}{{{\omega }_{i}}dV}\)    (4-21)
因为V是任意取的，所以式(4-21)中等号两侧积分中的被积分函数应相等，即
\(\nabla {{\rho }_{i}}{{v}_{i}}+\frac{\partial {{\rho }_{i}}}{\partial t}={{\omega }_{i}},i=1,2,\cdots ,N\)          (4-22)
其中\({{\rho }_{i}}=\rho {{Y}_{i}},{{v}_{i}}=v+{{{v}’}_{i}}\) 因此上式又可写成
\(~\frac{\partial ({{Y}_{i}})}{\partial t}+\nabla \left( \rho {{Y}_{i}}{{{{v}’}}_{i}} \right)+\nabla \cdot \left( \rho {{Y}_{i}}{{{{v}’}}_{i}} \right)={{\omega }_{i}}i=12\cdots ,N~\) (4-23)
该式就是最后求得的组分i的连续方程。
4.2.2整体连续方程
将式(4-23)对全部N种组分求和，即
\(~\frac{\partial }{\partial t}\sum\limits_{i=1}^{N}{\rho {{Y}_{i}}}+\nabla \left( \sum\limits_{i=1}^{N}{\rho {{Y}_{i}}}V \right)+\nabla \left( \sum\limits_{i=1}^{N}{\rho {{Y}_{i}}}{{{{v}’}}_{i}} \right)=\sum\limits_{i=1}^{N}{{{\omega }_{i}}}~\)
由于 \(~\sum\limits_{i=1}^{N}{\rho {{Y}_{i}}}=\rho ~,~\sum\limits_{i=1}^{N}{\rho {{Y}_{i}}V}=\rho V~\)
\(~\sum\limits_{i=1}^{N}{\rho {{Y}_{i}}}{{{v}’}_{i}}=0,\sum\limits_{i=1}^{N}{{{\omega }_{i}}}=0~\)
从而有
\(\frac{\partial \rho }{\partial t}+\nabla \cdot \rho V=0\)    (4-24)
该式就是最后求得的反应混合气体的整体连续方程。它同无化学反应的气体动力学中的连续方程是一样的。
4.3动量方程

这里所说的动量方程是指反应气体混合物整体的动量方程。一般认为，混合物整体的动量不因化学反应而增减，这就是说，由于各组分的生成或消耗而引起的总的动量变化应为零，即
\(~\sum\limits_{i=1}^{N}{{{\omega }_{i}}{{M}_{i}}}=0\) (4-25)
式中，Mi为单位质量组分i的动量。因此，在动量方程中，不必考虑化学反应对动量变化率的影响。以下推导反应气体混合物的动量方程。
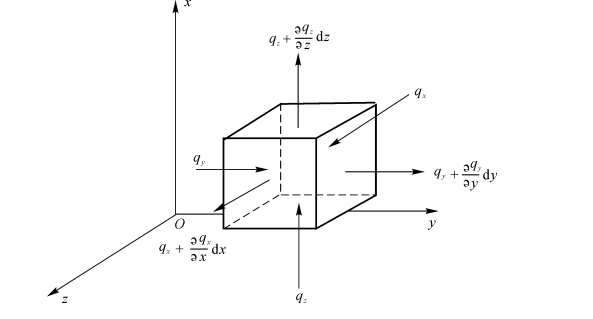
在笛卡儿坐标系中，在流体里划出一块矩形微元六面体，边长分别为dx，dy，dz规定作用在微元体各微元面上的应力如图4-1所示。\({{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}}\)是作用在各微元面上的法向应力，并分别平行于x,y,z轴。\({{\tau }_{xy}},{{\tau }_{xz}},{{\tau }_{yx}},{{\tau }_{yz}},{{\tau }_{zx}},{{\tau }_{zy}},\)  是作用在各微元面上的剪应力，其第一个下角标表示与该应力所在的微元面相垂直的坐标轴，应力的第二个下角标表示该应力的方向。
根据微元体的力矩平衡条件，略去高阶微量，可得
\({{\tau }_{xy}}={{\tau }_{yx}},{{\tau }_{yz}}={{\tau }_{zy}},{{\tau }_{zx}}={{\tau }_{xz}}\)    (4-26)
设各表面应力作用在该微元体dxdydz上的合力为Fs，则其沿x方向的分量为
\({{F}_{xr}}=\frac{\partial {{\sigma }_{x}}}{\partial x}dxdydz+\frac{\partial {{\tau }_{yx}}}{\partial y}dydxdz+\frac{\partial {{\tau }_{zx}}}{\partial x}dzdydz\)  (4-27)
设，\({{f}_{i}}={{f}_{ix}}\overrightarrow{i}+{{f}_{iy}}\overrightarrow{j}+{{f}_{iz}}\overrightarrow{k}\)为单位质量组分i所受的彻体力(\(\overrightarrow{i,}\overrightarrow{j},\overrightarrow{k}\)分别为沿x，y轴的单位向量)，则微元体dxdydz内混合气整体所受的彻体力为
\(~{{F}_{b}}=\sum\limits_{i=1}^{N}{{{\rho }_{i}}{{f}_{i}}}dxdydz\) (4-28)

图4-1微元体上表面力示意图
它在x方向的分量为
\({{F}_{bx}}\text{ }=\sum\limits_{i=1}^{N}{{{\rho }_{i}}{{f}_{ix}}}dxdydz\) (4-29)
现计算单位时间内微元体dxdydz(见图4-1)在x方向动量的增量。首先，从六个表面发散出的x向的净动量为
\((\frac{\partial \rho {{u}_{x}}{{u}_{x}}}{\partial x}+\frac{\partial \rho {{u}_{y}}{{u}_{x}}}{\partial y}+\frac{\partial \rho {{u}_{z}}{{u}_{x}}}{\partial z})dxdydz) (4-30)
其次，在微元体xdyd内部，x向动量变化率为
\(\frac{\partial \rho {{u}_{x}}}{\partial t}dxdydz\) (4-31)
因此，单位时间内微元体的x方向动量的增量为
\((\frac{\partial \rho {{u}_{x}}}{\partial t}\text{+}\frac{\partial \rho {{u}_{x}}{{u}_{x}}}{\partial x}+\frac{\partial \rho {{u}_{y}}{{u}_{x}}}{\partial y}+\frac{\partial \rho {{u}_{z}}{{u}_{x}}}{\partial z})dxdydz\) (4-32)
根据牛顿第二定律，单位时间内微元体在x向动量的增量必等于作用在微元体的x向分力，而该分力正是表面应力和彻体力在x方向的分量之和。写成数学式就是
\((\frac{\partial \rho {{u}_{x}}}{\partial t}\text{+}\frac{\partial \rho {{u}_{x}}{{u}_{x}}}{\partial x}+\frac{\partial \rho {{u}_{y}}{{u}_{x}}}{\partial y}+\frac{\partial \rho {{u}_{z}}{{u}_{x}}}{\partial z})dxdydz={{F}_{bx}}+{{F}_{sx}}\) (4-33)
利用连续方程将式(4-33)左边化简，可得
\(\rho \frac{\partial {{u}_{x}}}{\partial t}\text{+}\rho {{u}_{x}}\frac{\partial {{u}_{x}}}{\partial x}+\rho {{u}_{y}}\frac{\partial {{u}_{x}}}{\partial y}+\rho {{u}_{z}}\frac{\partial {{u}_{x}}}{\partial z}\text{=}\sum\limits_{i=1}^{N}{{{\rho }_{i}}{{f}_{ix}}}+\frac{\partial {{\sigma }_{x}}}{\partial x}+\frac{\partial {{\tau }_{yx}}}{\partial y}+\frac{\partial {{\tau }_{zx}}}{\partial z}\) (4-34)
将式(4-34)左边用实导数的符号表示，则有
\(\rho \frac{D{{u}_{x}}}{Dt}\text{=}\sum\limits_{i=1}^{N}{{{\rho }_{i}}{{f}_{ix}}}+\frac{\partial {{\sigma }_{x}}}{\partial x}+\frac{\partial {{\tau }_{yx}}}{\partial y}+\frac{\partial {{\tau }_{zx}}}{\partial z}\) (4-35)
同理可得沿y,z方向的关系式
\(\rho \frac{D{{u}_{y}}}{Dt}\text{=}\sum\limits_{i=1}^{N}{{{\rho }_{i}}{{f}_{iy}}}+\frac{\partial {{\tau }_{xy}}}{\partial x}+\frac{\partial {{\sigma }_{y}}}{\partial y}+\frac{\partial {{\tau }_{zy}}}{\partial z}\) (4-36)
\(\rho \frac{D{{u}_{z}}}{Dt}\text{=}\sum\limits_{i=1}^{N}{{{\rho }_{i}}{{f}_{iz}}}+\frac{\partial {{\tau }_{xz}}}{\partial x}+\frac{\partial {{\tau }_{yz}}}{\partial y}+\frac{\partial {{\sigma }_{z}}}{\partial z}\) (4-37)
对黏性流体，在三维流动中应力与变形率的关系为

式中 \({{\theta }_{x}}=\frac{\partial {{u}_{x}}}{\partial x},{{\theta }_{y}}=\frac{\partial {{u}_{y}}}{\partial y},{{\theta }_{z}}=\frac{\partial {{u}_{z}}}{\partial z}\)
\({{\gamma }_{x}}=\frac{1}{2}(\frac{\partial {{u}_{y}}}{\partial z}+\frac{\partial {{u}_{z}}}{\partial y}),{{\gamma }_{y}}=\frac{1}{2}(\frac{\partial {{u}_{x}}}{\partial z}+\frac{\partial {{u}_{z}}}{\partial x}),{{\gamma }_{z}}=\frac{1}{2}(\frac{\partial {{u}_{x}}}{\partial y}+\frac{\partial {{u}_{y}}}{\partial x}),\)
\({{\theta }_{x}},{{\theta }_{y}},{{\theta }_{z}}\)分别表示沿x，y，z轴方向的线变形率；\(2{{\gamma }_{x}}2{{\gamma }_{y}}2{{\gamma }_{z}}\)分别表示流体微团在垂直于x，y，z轴平面内的角变形率，p为流体静压力和分别是普通黏性系数和体积膨胀黏性系数。对一定的流体，\(\mu \)和\({\mu }’\)主要是温度的函数，压力对它们只有很微弱的影响。气体的 随温度增高而增大，这个性质与液体的完全不同。从式(4-38)可知 与剪应力及法向应力都有关系，但一般只有剪应力是重要的。其原因是散度\(\nabla \cdot v\)和剪应变相比往往很小。\({\mu }’\)只与法向应力有关，当散度为零时，\({\mu }’\)的作用也是零。所以\({\mu }’\)是与体积膨胀或收缩有关的黏性系数。当分子没有内在自由度时，或内在运动没有激发起来时，\({\mu }’\)的值为零。
至此，只要将式(4-38)代入式(4-37)，即可得下述动量方程。

式(4-39)就是最终所要求的动量方程，又称纳维-斯托克斯( Navier-Stokes)方程

4.4能量方程
这里推导的是反应气体混合物整体的能量方程。当流体流动时，流体微团不仅有内能(包括化学能和物理内能)的变化，而且有动能与位能的变化。为了方便，引入一符号e并令
\(e=u+\frac{{{v}^{2}}}{2}+{{e}_{p}}\) (4-40)
式中 u——单位质量混合物的内能，即此内能;
\(\frac{{{v}^{2}}}{2}\)——单位质量混合物的动能，
ep——单位质量混合物的位能
显然e代表了单位质量流体的总能量，在有些书上，把e称为储存能( stored energy) 根据能量守恒的原理，化学反应只改变能量的形式，而不会改变总的能量。既然内能中已经包括了化学能，在能量方程中就不必考虑化学反应对总能量变化的影响。
考虑如图4-2所示的微元体，其体积为dxdydz，质量为ρdxdydz。根据热力学第一定律，微元体dxdy内的总能量变化率应等于单位时间内外界传入该微元体的势量加上外力对该微元体单位时间内所做的功，亦即

图4-2穿过微元体表面热流量示意图
\(\rho \frac{De}{Dt}dxdydz=\delta \dot{Q}+\delta \dot{\omega }\) (4-41)
该式的左边表示流体微元dxdydz的总能量变化率，而右边的 和 则分别表示单位时间内外界传入该微元体的热量和外力对微元体单位时间内所做的功。下面，讨论上述方程右边各项的组成和数学表达式。
1.第一项\(\delta \dot{Q}\)
设单位时间内通过单位面积的热流v(即热流密度)为\(q={{q}_{x}}\overrightarrow{i}+{{q}_{y}}\overrightarrow{j}+{{q}_{z}}\overrightarrow{k}\) ，于是，从图4-2可见，单位时间通过六个微元表面传给流体微元 dxdydz的净热量为
\(\delta \dot{Q}=-(\frac{\partial {{q}_{x}}}{\partial x}+\frac{\partial {{q}_{y}}}{\partial y}+\frac{\partial {{q}_{z}}}{\partial z})dxdydz=-\nabla \cdot qdxdydz\) (4-42)
q将包括以下几项:
(1)由于控制面上存在着的温度梯度而引起的热传导项:
\({{q}_{c}}=-\lambda \nabla T\)   (4-43)
这里负号表示热流方向与温度梯度方向是相反的。
(2)由于组分i相对于混合气体以扩散速度\({{{v}’}_{i}}\) 运动因此伴随着这种运动热量必然会通过微元体表面进入微元体内。设i组分的比焓为hi，那么单位时间为，单位面积上由于i组分的扩散而传入微元体内的热量为\({{\rho }_{i}}{{h}_{i}}{{{v}’}_{i}}\)。对N种组分求和，则由于扩散速度而引起的热流密度为
\({{q}_{d}}=\rho \sum\limits_{i=1}^{N}{{{Y}_{i}}{{h}_{i}}{{{{v}’}}_{i}}}\) (4-44)
(3)其他还有热辐射和由于杜夫(Dufour)效应引起的热流。然而在燃烧问题中，它们的影响与前两项相比往往可略而不计，因此
\(~q={{q}_{c}}+{{q}_{d}}=-\lambda \nabla T+\rho \sum\limits_{i=1}^{N}{{{Y}_{i}}}{{h}_{i}}{{{v}’}_{i}}~\) (4-45)
由式(4-42)可知
\(\delta \dot{Q}=-\nabla \cdot (-\gamma \nabla T+\rho \sum\limits_{i=1}^{N}{{{Y}_{i}}{{h}_{i}}{{{{v}’}}_{i}}})dxdydz\) (4-46)
2.第二项\(\delta \dot{W}\)
\(\delta \dot{\omega }\)包括两子项，一子项是单位时间内表面力所做的功\(\delta {{\dot{\omega }}_{s}}\);另一子项是单位时间内彻体力所做的功\(\delta {{\dot{\omega }}_{b}}\)。
因为 是沿x，y，z方向表面力对流体微元所做的净功之和，所以对 可以依次求各个微元面上表面力所做的功。
单位时间内，在流体微元的\(A{A}'{B}’B\)面上表面力作用于流体微元的功为
\(~-({{v}_{x}}{{\sigma }_{x}}+{{v}_{y}}{{\tau }_{xy}}+{{v}_{z}}{{\tau }_{xz}})dydz\)
式中负号表示应力与速度方向相反。在与AABB相对的微元面DDCC上作用于流体微元的功为

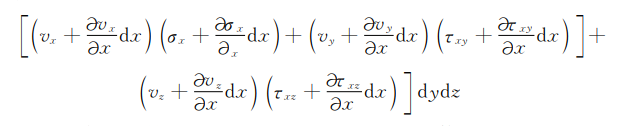
可得垂直于x轴的两个微元表面上表面力对流体微元所做的净功为

将式(4-47)整理并略去高阶微量可得
\(\delta {{\dot{\omega }}_{sx}}=\frac{\partial }{\partial x}({{v}_{x}}{{\sigma }_{x}}+{{v}_{y}}{{\tau }_{xy}}+{{v}_{z}}{{\tau }_{xz}})dxdydz\)   (4-48)
同理，可以计算垂直于y，z轴的微元面上表面力对流体微元所做的净功8w分别为
\(\delta {{\dot{\omega }}_{sy}}=\frac{\partial }{\partial x}({{v}_{x}}{{\tau }_{yx}}+{{v}_{y}}{{\sigma }_{y}}+{{v}_{z}}{{\tau }_{yz}})dxdydz\)   (4-49)
\(\delta {{\dot{\omega }}_{sz}}=\frac{\partial }{\partial x}({{v}_{x}}{{\tau }_{zx}}+{{v}_{y}}{{\tau }_{zy}}+{{v}_{z}}{{\sigma }_{z}})dxdydz\) (4-50)
将式(4-48)、式(4-49)、式(4-50)相加，可得

下面计算 ，前已得出微元体内i组分所受彻体力为 ，因此单位时间内该彻体力所做的功为\({{\rho }_{i}}{{f}_{i}}{{v}_{i}}dxdydz\)。对N种组分求和即可得彻体力对流体微元内混合气整体所做的功 ，即
\(\delta {{\dot{\omega }}_{b}}=\sum\limits_{i=1}^{N}{{{\rho }_{i}}{{f}_{i}}{{v}_{i}}dxdydz}\) (4-52)
最后可得

将式(4-46)、式(4-53)代入式(4-41)，并消去xdydz，可得

该式说明了单位体积反应气体混合物的总能量变化率与传入该体积的热流密度和对其做功速率之间的关系。由于反应气体混合物位能的变化比内能和动能的变化小得多，因此可略去位能的变化率，从而上式变为

可以利用动量方程把式(4-55)简化。以vx，Vy，v2分别与式(4-39a)、式(4-39b)、式(4-39c)相乘，然后把所得的三式相加可得

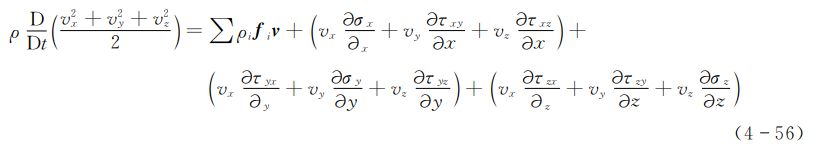
将式(4-55)两边分别减去式(4-56)的两边，并且利用式(4-38)中的关系可得用内能表示的能量方程
\(\rho \frac{Du}{dt}=\nabla (\lambda \nabla T)-\sum\limits_{i=1}^{N}{\nabla {{\rho }_{i}}{{h}_{i}}{{{{v}’}}_{i}}-p\nabla v+}\sum\limits_{i=1}^{N}{\nabla {{\rho }_{i}}{{f}_{i}}{{v}_{i}}}\text{+}\Phi \)  (4-57)
在式(4-57)中，已经使用了关系式
\(\sum\limits_{i=1}^{N}{{{\rho }_{i}}{{f}_{i}}{{v}_{i}}-}\sum\limits_{i=1}^{N}{{{\rho }_{i}}{{f}_{i}}v}=\sum{{{\rho }_{i}}{{f}_{i}}{{{{v}’}}_{i}}}\)
式中的称为耗散函数，是黏性耗散所产生的热量，其表达式为

当然，能量方程式(4-57)也可用焓来表示，因为
\(\frac{Dh}{Dt}=\frac{D}{Dt}(u+\frac{p}{\rho })=\frac{Du}{Dt}+\frac{1}{\rho }\frac{Dp}{Dt}+\frac{p}{\rho }\nabla v\)
从而有
\(\frac{Du}{Dt}=\frac{Dh}{Dt}-\frac{1}{\rho }\frac{Dp}{Dt}-\frac{p}{\rho }\nabla v\)
将此式代入能量方程式(4-57)可导出用焓表示的能量方程如下:
\(\rho \frac{Dh}{dt}=\nabla (\lambda \nabla T)-\sum\limits_{i=1}^{N}{\nabla {{\rho }_{i}}{{h}_{i}}{{{{v}’}}_{i}}+\frac{Dp}{Dt}+}\sum\limits_{i=1}^{N}{\nabla {{\rho }_{i}}{{f}_{i}}{{v}_{i}}}\text{+}\Phi \) (4-59)
可见，对于多组分反应系统，独立的基本方程的个数有N+6个(组分连续方程N个整体连续1个、动量方程3个、能量方程1个、气体状态方程1个)。未知数的个数也是N+6个(\({{Y}_{1}},\cdots ,{{Y}_{N}},\rho ,{{V}_{x}},{{V}_{y}},{{V}_{z}},T,P\))，从原则说，方程的数量和未知数的数量相等，在相应物性参数给定条件下，可求解，实际上困难多多解析解只适用于少量简化的情况。一般情况下，可用数值法求解。大多数情况下，针对不同问题，作一定简化，再求解。
习题
4.1简述Fick扩散定律。
4.2推导微元体整体连续方程。
4.3推导微元六面体(边长分别为dx，dy，dz)的动量方程。
4.4用焓h表示的能量方程如下:
\(\rho \frac{Dh}{dt}=\nabla (\lambda \nabla T)-\sum\limits_{i=1}^{N}{\nabla {{\rho }_{i}}{{h}_{i}}{{{{v}’}}_{i}}+\frac{DP}{Dt}+}\sum\limits_{i=1}^{N}{\nabla {{\rho }_{i}}{{f}_{i}}{{v}_{i}}}\text{+}\Phi \)
推导:低马赫数下用温度T表示的能量方程为
\(\rho {{C}_{p}}\frac{DT}{Dt}=\nabla (\lambda \nabla T)+\frac{\partial p}{\partial t}\) (b)