第3章化学动力学基础
化学动力学是研究化学反应速度和反应机理的学科。它是物理化学的一个重要分支。任何化学反应大致有两方面的问题需要研究:
(1)反应的可能性问题:反应能否发生,反应方向和趋势。
(2)化学反应的速度问题,还有与速度有关的具体途径,也就是反应机理或反应历程的问题。
反应趋势和反应速度是两个不同的概念。研究反应趋势只须研究系统的初态和终态,与过程无关。研究化学反应速度首先是研究反应的具体过程,要了解反应如何一步一步地进行,然后才能从反应的每一个具体步骤的速度来确定反应过程的总的速度。
化学动力学要研究反应的过程,研究此过程中每一个反应步骤的反应速度,研究影响反应速度的各种条件,如浓度、温度、催化剂、化学结构等。
3.1质量作用定律
质量作用定律是关于反应速度与反应浓度关系的定律。
3.1.1浓度
浓度:指单位容积中所含物质的量。常用的浓度表示方式有三种:
(1)摩尔浓度Ci:表示单位容积中i组分物质的摩尔数。
(2)分子浓度ni:表示单位容积中i组分的分子数。
\({{n}_{i}}={{N}_{A}}{{C}_{i}}\) (3-1)
式中,NA=6.023×1023,为阿伏伽德罗常数。
(3)质量浓度p:表示单位容积中i组分的质量。
\({{\rho }_{i}}={{C}_{i}}{{M}_{i}}=\frac{{{n}_{i}}{{M}_{i}}}{{{N}_{A}}}\) (3-2)
单位容积中的全部质量为
\(\rho =\sum{{{\rho }_{i}}}\) (3-3)
此外,还经常用相对浓度,它表示单位容积中某一组分的质量与全部物质质量之比。
一般组分i的质量分数表示为
\({{Y}_{i}}=\frac{{{\rho }_{i}}}{\sum{{{\rho }_{i}}}}\) (3-4)
摩尔分数表示为
\({{X}_{i}}=\frac{{{C}_{i}}}{\sum{{{C}_{i}}}}\) (3-5)
3.1.2反应速度
反应速度指反应系统中单位时间内某一组分物质数量的变化。反应速度取决于系统条件:化合物浓度、温度、压力、是否有催化剂或抑制剂、辐射效应等。
对于容积不变的反应,用单位时间内物质浓度的变化来表示(注意正负号的取向):
\(\omega =\pm \frac{dC}{dt}\) (3-6)
例如反应:
\(~aA+bB\begin{matrix}
\underline{\underline{}} \\
{} \\
\end{matrix}gG+hH~\) (3-7)
反应速度为
\(\omega =\frac{d(A)}{-adt}=\frac{d(B)}{-bdt}=\frac{d(G)}{gdt}=\frac{d(H)}{hdt}\) (3-8)
有时把化学反应式写成和式的形式:
\(\sum\limits_{i=1}^{N}{{{{{v}’}}_{i}}{{A}_{i}}}\to \sum\limits_{i=1}^{N}{{{{{v}”}}_{i}}{{A}_{i}}}\) (3-9)
其中,Ai表示i组分的分子式;\({{{v}’}_{i}}\)和\({{{v}”}_{i}}\)分别表示反应物和生成物中i组分的分子数。
用任一组分Ai的浓度变化率来表示反应速度为,\({{\omega }_{i}}=\frac{d({{A}_{i}})}{dt}\)各组分 的不同,但对各组分, 除以 是相同的,故反应速度可表示为
\(\omega \text{=}\frac{{{\omega }_{i}}}{{{{{v}”}}_{i}}-{{{{v}’}}_{i}}}\) (3-10)
3.1.3质量作用定律
质量作用定律表明反应速度与反应物浓度的关系。当温度不变时,反应速度与当时的反应物浓度的一定方次的乘积成正比。
例如反应:
\(aA+bB\begin{matrix}
\underline{\underline{}} \\
{} \\
\end{matrix}gG+hH~~\) (3-11)
反应速度为
\(~\omega =k{{\left( A \right)}^{a}}{{\left( B \right)}^{b}}~\) (3-12)
对于反应:
\(\sum\limits_{i=1}^{N}{{{{{v}’}}_{i}}{{A}_{i}}}\to \sum\limits_{i=1}^{N}{{{{{v}”}}_{i}}{{A}_{i}}}\) (3-13)
反应速度为
\(\omega =k{{({{A}_{1}})}^{{{{{v}’}}_{1}}}}{{({{A}_{2}})}^{{{{{v}’}}_{2}}}}\cdots {{({{A}_{N}})}^{{{{{v}’}}_{N}}}}=k\prod\limits_{\text{i=1}}^{N}{{{({{A}_{i}})}^{{{{{v}’}}_{i}}}}}\) (3-14)
式中,k是比例常数,称为反应速度常数或比速度。
式(3-14)中各反应物浓度的方次之和叫作反应级数,即
\(v=\sum\limits_{i=1}^{N}{{{v}_{i}}}\) (3-15)
反应级数不同,表示反应物浓度对反应速度的影响不同。
质量作用定律是一个由大量试验总结得到的经验关系式。
注意:应用质量作用定律所根据的化学反应式必须是真正表示实际反应过程的动力学反应式。有的反应式只表示总的反应前后的质量平衡,表示各组分的化学计量关系,不一定表示实际的反应过程。
3.2反应机理
反应机理是指整个反应过程如何一步一步完成,它包括组成整个反应的具体反应步骤,也包括反应过程中的一系列具体的细节。化学反应一般由一个或多个基元反应组成。组成化学反应的每一个最基本的化学变化叫作基元反应。可以认为基元反应是反应物的粒子通过一步实现的一种化学反应,因此,基元反应的反应式就是动力学反应式,可应用质量作用定律写出反应速度的关系式。
学反应按反应复杂程度可分为简单反应和复杂反应。由一个基元反应组成的化学反应称为简单反应。由两个或两个以上的基元反应组成的化学反应叫作复杂反应。简单反应按参加反应的分子数而分成单分子反应、双分子反应和三分子反应。常见的复杂反应有可逆反应、平行反应、连串反应等。
3.2.1单分子反应
例如: \({{I}_{2}}\to 2I\)
上述反应属于一级反应:v=1。
单分子反应速度如下:
\(\omega =-\frac{d({{I}_{2}})}{dt}=k({{I}_{2}})\) (3-16)
3.2.2双分子反应
例如: \(2\text{ }N{{O}_{2}}\to 2NO+{{O}_{2}}\)
上述反应属于二级反应:v=2
双分子反应速度如下:
\(\omega =-\frac{d(N{{O}_{2}})}{dt}=k{{(N{{O}_{2}})}^{2}}\) (3-17)
3.2.3三分子反应
例如: A+B+C→D
上述反应属于三级反应:v=3
三分子反应速度如下: \(\omega =\frac{d(D)}{dt}=k(A)(B)(C)\) (3-18)
3.2.4可逆反应
能在正、反两个方向同时进行的基元反应叫作可逆反应,也称作对峙反应。
例如:\(A+B\underset{{{k}_{2}}}{\overset{{{k}_{1}}}{\longleftrightarrow}}G+H\),k1和k2分别表示正向和逆向的反应速度常数。
正向反应的反应速度: \({{\omega }_{1}}={{k}_{1}}\left( A \right)\left( B \right)\)
逆向反应的反应速度: \({{\omega }_{2}}={{k}_{2}}\left( G \right)\left( H \right)\)
如果以A的净消耗速度或者G的净生成速度表示总反应速度,则
\(\omega =\frac{d(A)}{dt}~=\frac{d(G)}{dt}={{\omega }_{1}}-{{\omega }_{2}}={{k}_{1}}\left( \text{A} \right)\left( B \right)-{{k}_{2}}\left( G \right)\left( H \right)\) (3-19)
3.2.5平行反应
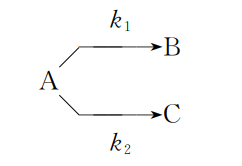
相同的反应物(单分子或多分子)同时进行两个不同的反应,如
上述反应是A分子的两个平行的单分子反应形成的平行反应,对每一个基元反应都可应用质量作用定律。
总的反应速度由A的消耗速度表示
\(\omega =-\frac{d(A)}{dt}~=\frac{d(B)}{dt}+{{\frac{d(C)}{dt}}_{2}}=({{k}_{1}}-{{k}_{2}})\left( A \right)\) (3-20)
k1和k2决定了每个基元反应的反应速度,速度快的为主反应,速度慢的为次反应。总反应速度更多地取决于主反应的速度。
3.2.6连串反应
前一步基元反应的生成物作为下一步反应的反应物,接连进行下一步反应,这样一步反应接着另一步反应,经过几个步骤方能达到最后的结果,叫作连串反应。
如: \(A\xrightarrow{{{k}_{1}}}B\xrightarrow{{{k}_{2}}}C\)
各组分浓度变化如下:
\(~-\frac{d\left( A \right)}{dt}={{k}_{1}}\left( A \right)~~~~~\) (3-21)
\(~\frac{d(B)}{dt}={{k}_{1}}\left( A \right)-{{k}_{2}}\left( B \right)~~\) (3-22)
\(\frac{d(C)}{dt}={{k}_{2}}(B)\) (3-23)
此外,还有其他的复杂反应,如共轭反应、自动催化反应、链反应等。
注意:反应分子数和反应级数,是两个不完全相同的概念。反应分子数指参与反应的分子的数量,直接说明反应机理。反应级数指反应速度同反应物浓度的若干次方的乘积成正比,是在实际过程中表现出来的反应速度同反应物浓度的关系。简单反应中,反应分子数与反应级数相等;复杂反应,两者不一定相等。
3.3简单反应中浓度的变化
3.3.1一级反应
一级反应的反应速度与浓度的关系为
\(\frac{-dC}{dt}=kC\) (3-24)
式中,C为反应物浓度;t为时间;k为反应速度常数。在等温条件下,k为常值。
式(3-24)积分,得
\(~\ln \text{ }C=-kt\text{ }+\ln {{C}_{0}}\) (3-25)
\(\ln \frac{C}{{{C}_{0}}}=-kt\) (3-26)
\(C={{C}_{0}}{{e}^{-kt}}\) (3-27)
可见,对于一级反应,nC与t为线性关系。这是判断反应是否为一级反应的重要判定标准。半衰期是指反应物浓度减少到一半所需的时间。半衰期的长短表征反应的快慢,作为反应的特征时间:
\({{t}_{{}^{1}/{}_{2}}}=-\frac{1}{k}\ln 2=\frac{0.6932}{k}\) (3-28)
3.3.2二级反应
双分子反应: A+B→D
为二级反应,反应速度为
\(-\frac{d{{C}_{A}}}{dt}=k{{C}_{A}}{{C}_{B}}\) (3-29)
式中,C表示浓度;t为时间;k为反应速度常数。
假设A,B的初始浓度相同,则任一时刻A和B的浓度相同:
\(-\frac{dC}{dt}=k{{C}^{2}}\) (3-30)
式(3-30)积分,得
\(\frac{1}{C}=kt+\frac{1}{{{C}_{0}}}\) (3-31)
\(\frac{1}{C}-\frac{1}{{{C}_{0}}}=kt\) (3-32)
可见,对于二级反应,当两种反应物初始浓度相等时,\(\frac{1}{C}\)与t为线性关系这是判断反应是否为二级反应的重要判定标准。
二级反应是最常见的反应。溶液中的反应、相中的反应大部分都是二级反应;燃烧过程中气相反应一般为二级反应。
将\(C=\frac{1}{2}{{C}_{0}}\)代入方程式(3-32),可得二级反应的半衰期为
\({{t}_{{1}/{2}\;}}=\frac{1}{k{{C}_{0}}}\) (3-33)
对于二级反应,半衰期和初始浓度也有关系。
3.3.3三级反应
如果三种分子的初始浓度都相同,反应速度为
\(-\frac{dC}{dt}=k{{C}^{2}}\) (3-34)
式(3-34)积分,得
\(\frac{1}{{{C}^{2}}}=2kt+\frac{1}{{{C}_{0}}}\) (3-35)
当三种反应物初始浓度相等时,与t为线性关系。
半衰期为
\({{t}_{{1}/{2}\;}}=\frac{31}{2k{{C}_{0}}}\) (3-36)
3.3.4v级反应
一般,v级反应的反应速度为
\(-\frac{dC}{dt}=k{{C}^{v}}\) (3-37)
式(3-37)积分,得
\(~\frac{1}{{{C}^{v-1}}}=\left( v-1 \right)kt+\frac{1}{{{C}_{0}}}~\) (3-38)
当初始浓度相等时,与t为线性关系。
半衰期为
\({{t}_{{}^{1}/{}_{2}}}=\frac{{{2}^{v-1}}-1}{v-1}\frac{1}{k{{C}_{0}}}\) (3-39)
对于任何化学反应:
\(\sum\limits_{i=1}^{N}{{{{{v}’}}_{i}}}{{A}_{i}}\to \sum\limits_{i=1}^{N}{{{{{v}”}}_{i}}}A\)
组分反应速度为
\({{\omega }_{i}}=-\frac{d{{C}_{i}}}{dt}=k({{{v}”}_{i}}-{{{v}’}_{i}})\prod\limits_{i=1}^{N}{{{C}_{i}}}\) (3-40)
总反应速度为
\(\omega =\frac{{{\omega }_{i}}}{{{{{v}”}}_{i}}-{{{{v}’}}_{i}}}=k\prod\limits_{i=1}^{N}{{{C}_{i}}}\) (3-41)
3.4连串反应中浓度的变化
连串反应在燃烧中出现较多,这类反应各组分浓度随时间变化的关系比简单反应复杂。对于一级连串反应
\(~A\xrightarrow{{{k}_{1}}}B\xrightarrow{{{k}_{2}}}C\)
各组分浓度变化如下:
\(\frac{d(A)}{dt}=-{{k}_{1}}(A)\) (3-42)
\(\frac{d(B)}{dt}={{k}_{1}}(A)-{{k}_{2}}(B)\) (3-43)
\(\frac{d(C)}{dt}={{k}_{2}}(B)\) (3-44)
将上面三个式子相加:
\(\frac{d(A)}{dt}+\frac{d(B)}{dt}+\frac{d(C)}{dt}=0\) (3-45)
因此 (A)+(B)+(C)=常数
假设,t=0时,[A]=[A]0,[B]=[C]=0,则[A]+[B]+[C]=[A]0
以此为初始条件求解得到
\(~\left( A \right)={{\left( A \right)}_{0}}{{e}^{-{{k}_{1}}t}}~~\) (3-46)
\(~\left( B \right)=\frac{{{k}_{1}}}{{{k}_{2}}-{{k}_{1}}}{{\left( A \right)}_{0}}\left( {{e}^{-{{k}_{1}}t}}-{{e}^{-{{k}_{2}}t}} \right)~~~\) (3-47)
\(~\left( C \right)={{\left( A \right)}_{0}}(1+\frac{1}{{{k}_{1}}-{{k}_{2}}}\left( {{k}_{2}}{{e}^{-{{k}_{1}}t}}-{{k}_{1}}{{e}^{-{{k}_{2}}t}} \right)~)\) (3-48)
三种组分浓度变化随时间关系为式(3-46)至式(3-48),用曲线表示如图3-1所示。
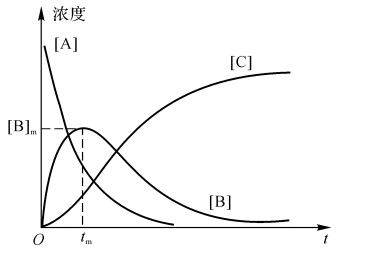
图3-1三种组分浓度变化随时间关系
当B生成速率与消耗速率相同时,(B)达到最大值(B),由此可确定达到的时间tm,如下:
\({{t}_{m}}=\frac{\ln \frac{{{k}_{2}}}{{{k}_{1}}}}{{{k}_{2}}-{{k}_{1}}}\( (3-49)
\({{(B)}_{m}}={{(A)}_{0}}{{(\frac{{{k}_{2}}}{{{k}_{1}}})}^{\frac{{}^{{{k}_{2}}}/{}_{{{k}_{1}}}}{1-{}^{{{k}_{2}}}/{}_{{{k}_{1}}}}}}\) (3-50)
通常把(C)显著增长以前的这段时间称为诱导期或感应期。在此期间,(B)快速增加,为(C)快速增长作准备。
在连串反应中,最慢一步的反应速度决定总反应速度。
常用一种近似方法准稳态法来求解。
3.5压力对反应速度的影响
在气相反应中,压力的大小反映了物质的浓度,根据气体状态方程:
\(C=\frac{N}{V}=\frac{P}{{{R}_{0}}T}\) (3-51)
i组分的摩尔浓度CI,可用其分压pI表示:
\({{C}_{i}}=\frac{{{N}_{i}}}{V}=\frac{{{p}_{i}}}{{{R}_{0}}T}\) (3-52)
摩尔分数为
\({{X}_{i}}=\frac{{{C}_{i}}}{C}=\frac{{{p}_{i}}}{p}\) (3-53)
显然
\({{C}_{i}}=C{{X}_{i}}={{X}_{i}}\frac{p}{{{R}_{0}}T}\) (3-54)
i组分作为反应物的v级反应,反应速度为
\(-\frac{d{{C}_{i}}}{dt}=kC_{i}^{v}=k{{\left( \frac{{{p}_{i}}}{{{R}_{0}}T} \right)}^{v}}=kX_{i}^{v}{{\left( \frac{p}{{{R}_{0}}T} \right)}^{v}}\) (3-55)
对于反应
\(\sum\limits_{i=1}^{N}{{{{{v}’}}_{i}}}{{A}_{i}}\to \sum\limits_{i=1}^{N}{{{{{v}”}}_{i}}}A\) (3-56)
反应速度为
\({{\omega }_{i}}=-\frac{d{{C}_{i}}}{dt}=k({{{v}”}_{i}}-{{{v}’}_{i}}){{\prod\limits_{i=1}^{N}{({{X}_{i}}\frac{p}{{{R}_{0}}T})}}^{{{{{v}’}}_{i}}}}=k({{{v}”}_{i}}-{{{v}’}_{i}}){{(\frac{p}{{{R}_{0}}T})}^{v}}{{\prod\limits_{i=1}^{N}{({{X}_{i}})}}^{{{{{v}’}}_{i}}}}\)
反应级数为
\(v=\sum\limits_{i=1}^{N}{{{v}_{i}}}\) (3-58)
用质量浓度的变化表示,反应速度为
\({{\omega }_{g,i}}={{M}_{i}}k({{{v}”}_{i}}-{{{v}’}_{i}})\prod\limits_{i=1}^{N}{{{({{X}_{i}}\frac{p}{{{R}_{0}}T})}^{{{{{v}’}}_{i}}}}}\) (3-59)
3.6温度对反应速度的影响
质量作用定律反映了一定温度下浓度对化学反应速度的影响。在温度变化的情况下,温度对反应速度的影响也特别显著。
大多数反应的反应速度随温度的升高而迅速增加温度对反应速度的影响规律是什么。目前有两个规律得到研究人员的认同:范特荷规律和阿累尼乌斯定律
范特荷甫(Van’t Hoff)根据试验得到一个近似规律:一般反应,当温度升高10℃时,反应速度大约增加到2~4倍。用反应速度常数k表示此规则为
\(~~~{{k}_{T+10}}/{{k}_{T}}=2\tilde{\ }4\) (3-60)
阿累尼乌斯(S. Arrhenius)根据试验,发现反应速度常数k与T之间有如下关系
\(\text{ln }k=\frac{-A}{T}+B~\) (3-61)
式中,A,B为常数。
\(\frac{\text{dln }k}{dT}=\frac{E}{{{T}^{2}}}\) (3-62)
用通用气体常数R分别乘以右边的分子、母,且让EAR,则得到
\(\frac{\text{dln }k}{dT}=\frac{E}{{{R}_{0}}{{T}^{2}}}\) (3-63)
\(\text{ln }k=-\frac{E}{{{R}_{0}}T}+B~=-\frac{E}{{{R}_{0}}T}+\ln Z\) (3-64)
整理可得
\(k=Z{{e}^{-\frac{E}{{{R}_{0}}T}}}\) (3-65)
式(3-65)就是阿累尼乌斯定律常用的关系式,包括两个常数:活化能E和指前因子Z。
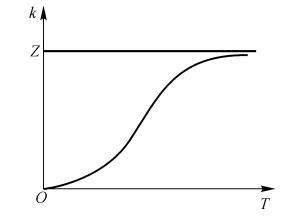
随着温度升高,反应速度常数按指数规律迅速增大。具体关系曲线如图3-2所示。
图3-2阿累尼乌斯定律关系曲线
1889年阿累尼乌斯提出其定律时也提出了理论解释:分子之间要发生反应需要两个分子相遇或碰撞。但不是任何分子相遇都发生反应只有少数特别活泼的分子碰撞才有作用所谓这些分子的活泼就是指它们的碰撞能量比普通的分子要超过一定的数值E,这个超过的能量E使分子变成活化分子,也就是阿累尼乌斯定律中的活化能。
3.6.1活化能
只有碰撞分子所具有的能量超过所需要的活化能才能发生反应。一般化学反应的活化能为10~100kcal/mol。许多燃烧反应的活化能大约为40kcal/mol活化能越小,其反应速度越快。活化能与反应热有一定的关系。
一般说来,活化能与温度无关。但精确试验表明,E随温度稍有变化。
各类化学反应的活化能各不相同,它随反应的种类反应物的结构和反应条件而改变。
3.6.2指前因子
Z表示反应物浓度为单位浓度时在单位时间、单位体积中分子碰撞的总数。它代表碰撞频率,又称频率因子。
温度对反应速度的影响,不仅通过\({{e}^{-\frac{E}{{{R}_{0}}T}}}\) ,而且通过指前因子Z但是由于前者的温度处在指数项上,影响比Z大,因此Z的影响相对可以忽略不计。
阿累尼乌斯定律应用范围广,不仅适用于一般的均相反应,而且也适用于非均相反应。
在燃烧理论中,阿累尼乌斯定律表示化学反应速度随温度的变化。但是,分子碰撞理论的分析只适用于基元反应。对于复杂反应,总的反应速度受温度的影响,只能从各个基元反应的速度来进行计算,不能直接应用阿累尼乌斯公式。
但是,在某些情况下,一定的温度范围内,某些复杂反应的反应速度可以近似用阿累尼乌斯公式来表示,其中包括相应的指前因子和活化能。
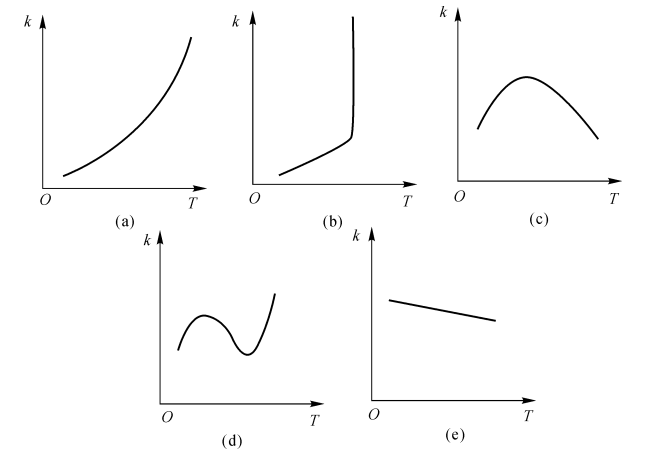
图3-3表示五种类型的反应速度随温度的变化关系。
图3-3反应速度常数随温度变化的五种类型
只有图3-3(a)所示可用阿累尼乌斯定律。
3.7链反应
链反应是一种特殊的化学反应,它由一系列基元反应组成。这种反应一经激发就可以经过一系列连锁步骤自动发展下去。反应的发展依靠激发反应中产生的活化分子(或原子原子团),又称活性中心。
链反应分为直链反应和支链反应两类。
3.7.1直链反应
直链反应中,消耗活性中心的数量与新产生的活性中心数量相等。
直链反应分两步:
(1)首先要产生链载体,这是链反应的第阶段,称为链的开始,又称为链的引发。
(2)第二阶段为链的传递。活性分子参与相应的基元反应,促使生成生成物的反应迅速进行,同时又生成新的活性中心。
从链传递的各个基元反应来看,每一反应消耗活性中心的数量等于新生成的数量,经过这个反应以后,活性中心的数量不增不减,这是直链反应的特征。
但是,有时发生链的终止,又称链的破坏。
例如:
\({{H}_{2}}+B{{r}_{2}}\to 2HBr\)
Bodenstain和Lind提出如下链反应机理:
(1)\(B{{r}_{2}}\to 2Br\)
(2)\({{H}_{2}}+Br\to HBr+H\)
(3)\(H+B{{r}_{2}}\to HBr+Br\)
(4)\(H+HBr\to {{H}_{2}}+Br\)
(5)\(Br+Br\to B{{r}_{2}}\)
其中:(1)为链反应的第一阶段;(2)(3)为第二阶段;(4)也属于链的传递,它消耗HBr影响生成HBr的速度;(5)为链的终止,不利于链反应的完成。
可推导得到该直链反应速度为
\(~\frac{d\left( HBr \right)}{dt}=\frac{2{{k}_{3}}{{k}_{2}}{{\{({k1}/{k5}\;\text{)}\left( B{{r}_{2}} \right)\}}^{\frac{1}{2}}}\left( H \right)\left( Br \right)~~}{~{{k}_{3}}\text{ }\left( Br{}_{2} \right)+\text{ }{{\text{k}}_{\text{4}}}(HBr)}\) (3-66)
3.7.2支链反应
对于支链反应(分支链反应),在链的传递中一个活性中心参与某一基元反应后生成多于一个新的活性中心。
在支链反应中,活性中心的数量有可能愈来愈多总的反应速度也会愈来愈快。其一般机理如下:
(1)\(M\xrightarrow{{{k}_{1}}}R+\cdots \).
(2)\(R+M\xrightarrow{{{k}_{2}}}aR+{M}’\) \(\alpha >1\)
(3)\(R+M\xrightarrow{{{k}_{3}}}\)生成物
(4)\(R\xrightarrow{{{k}_{4}}}\)在容器壁上销毁
(5)\(R\xrightarrow{{{k}_{5}}}\)在气相中销毁
各反应:
(1)为链的开始,同直链反应一样,要通过获得较多的能量才能形成活性中心开始链反应。
(2)为链的分支,通过这个反应,活性中心数量增加,促成后面的反应速度增加。
(3)是生成生成物,同(4)(5)一样,都是链的终止。
可推导得到该支链反应的反应速度为
\(~\omega ={{k}_{3}}\left( R \right)\left( M \right)=\frac{{{k}_{3}}{{k}_{1}}{{\left( M \right)}^{2}}}{{{k}_{3}}\left( M \right)+~{{k}_{4}}+{{k}_{5}}-{{k}_{2}}(\alpha -1)\left( M \right)}~\) (3-67)
将式(3-67)推广,得到支链反应的一般公式为
\(\omega =\frac{F(C)}{{{f}_{s}}+{{f}_{c}}+A(1-\alpha )}\) (3-68)
式中,F(C)为反应物浓度的函数;fs是活性中心在容器壁面销毁速度的因素,同k4有关;fc是活性中心在气相中销毁的因素,与k3(M)和k5有关;A相当于k2(M),是反应物浓度的函数; 是支链反应中活性中心增殖的倍数。
在直链反应中,\(\alpha =1\omega =F\left( C \right)/\left( {{f}_{s}}+{{f}_{c}} \right)\)反应速度是一个有限值。
在支链反应中,\(\alpha >1A\left( 1-\alpha \right)\)为一负值,此负值抵消f+f,使反应速度增大,极端情况,为
\({{f}_{s}}+{{f}_{c}}+A\left( 1-\alpha \right)=0\) (3-69)
则反应速度趋于无限大,在一定条件下就要发生爆炸。这种由于支链反应引起的爆炸称为链爆炸。
链爆炸不靠热的作用,而是靠分支链反应中活性中心的迅速增殖,使反应速度迅速增长,形成爆炸。
3.8爆炸极限
3.8.1 H2-O2系统
在试验中可以观察到,一个装有氢和氧的压力容器,在如图3-4所示的条件下,当压力提高时就会发生爆炸。根据直觉可以假定,当压力提高时,自由基的浓度将增大,以至引起爆炸。但是,在试验中也会发现,当压力降低时也会发生爆炸。
封闭容器中存在爆炸极限可以很简单地理解为,容器表面上及气相内链终止反应与链分支反应相比谁占优势。第一个,亦即较低的爆炸极限,出现在一个较大的温度范围内,并几乎在同样的压力下。链载体在壁面上消失(壁面效应)和链载体在气相反应中产生之间达到平衡,就确定了这个较低的爆炸极限。在这个较低的压力范围内,碰撞次数和链载体产生的速率都很低。
压力愈低, 临界的值愈大,因而爆炸的机会就愈小。但是,这些分析却不能预测爆炸极限的准确位置,只能解释每个区域中的反应机理。
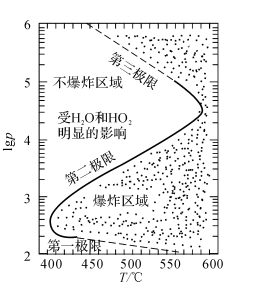
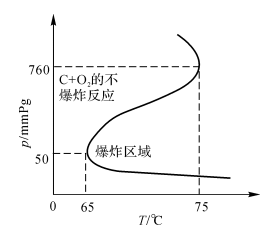
压力升高,气相反应产生链载体的速率增加,到某种程度时,壁面上链载体的消失就不再足以阻止支链爆炸。较低的爆炸极限的条件,就是气相中链的分支与壁面上链的消失达到平衡。球形容器中化学计量比的氢-氧混合物的爆炸极限如图3-5所示。
随着压力上升到爆炸极限,气相中链的分支就变得很重要。关于其反应动力学有两种假设:
20世纪20年代许多研究工作者认为
\(~~{{H}_{2}}\text{ }\to 2H\)-106kcal/mol(离解) (3-71)
Lewis和Von Elbe提出
OH基产生以后
\(OH+H2\text{ }\to {{H}_{2}}O+H+15\text{ }kcal/mol\)
\(H+{{O}_{2}}\to OH+O-16\text{ }kcal/mol\)
\(O+{{H}_{2}}\to OH+H-2\text{ }kcal/mol\)
式(3-71)反应比式(3-72)反应的吸热量更大,但是式(3-72)反应需要一个与离解反应不同的载体反应。所以,在低温下可能是式(3-72)反应,而在高温下则可能是式(3-72)反应。
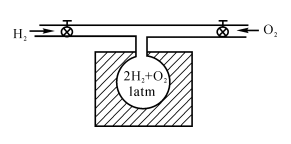
图3-4压力容器中H2和O2的混合物
图3-5球形容器中化学计量比的氢一氧混合物的爆炸极限
在较高的压力下,将达到第二爆炸极限。如果加入一个载体反应
\(~H+{{O}_{2}}+M\to H{{O}_{2}}+M\) (3-73)
就不难解释第二爆炸极限的存在。在这个反应中,M代表能够使H和O2稳定结合的任何第三分子。由于亚稳态的中间产物过氧化氢基(HO2)是相当不活泼的,所以它会向壁面扩散。HO2成为自由价消失的媒介物,从而上面的反应可以看作是一个链终止反应。当压力升高时三元碰撞H+O2+M的频率相对于二元碰撞H+O2的频率而言将会增大,因此就会有这样一个压力,超过了它,自由价消失的速率将会超过链分支反应产生自由价的速率,由此建立了第二爆炸极限。HO2在壁面上消失,可以用下面的反应表示:
至此,可以假设HO2在链传递或链分支中不再起作用,而是在壁面上消失了。
然而,在第二爆炸极限之上的某个压力下,HO2却按下面的反应参与了链传递过程:
\(H{{O}_{2}}+{{H}_{2}}\to \underset{\begin{smallmatrix}
\downarrow \\
2OH
\end{smallmatrix}}{\mathop{{{H}_{2}}{{O}_{2}}}}\,+H\downarrow \) (3-76)
因此,在某一临界压力之上,自由基的数目将激增,这个临界压力就确定了第三爆炸极限。现在,H2O的键频率与HO2的很接近,其结构是
H—O—H
O—O—H
所以H2O是方程式(3-73)的反应中最好的载体。在爆炸极限图上指出了H2O和HO2有显著影响的区域。值得说明的是,当T>60℃时,HO2不稳定,因而在任何压力下都会爆炸。
3.8.2 CO-O2系统
一氧化碳和氧的混合物也存在爆炸极限。
链生成反应是
\(CO+{{O}_{2}}\to C{{O}_{2}}+O\Delta {{H}_{r}}=9kcal/mol\) (放热) (3-77)
一般来说,该混合气在没有H2的情况下较难发生这种链生成反应。 Lewis和 VonElbe认为爆炸极限主要受下列反应的控制:
\(M+CO+O\to C{{O}_{2}}+M\)
\(~M+O+{{O}_{2}}\to {{O}_{3}}+M*\) (放热)
\(~{{O}_{3}}+CO\to C{{O}_{2}}+2O\) (非常迅速)
\(~{{O}_{2}}+CO+M\to C{{O}_{2}}\text{ }+{{O}_{2}}\text{ }+M*\)
必须注意,CO-O2系统的特性之所以会改变,主要是由于混进了少量的H2或H2O的缘故,控制速率的反应机理包括H,OH,H2,HO2,H2O以及O,O2,CO,CO2,O3。
图3-6化学计量比的CO-O2混合物的爆炸极限
水煤气反应最有可能是表面催化反应:
\(~CO+{{H}_{2}}OC{{O}_{2}}+{{H}_{2}}\) (表面)
接着就是氢和氧的表面反应:
\({{H}_{2}}+{{O}_{2}}{{H}_{2}}{{O}_{2}}\) 表面)
链载体的提供,要依靠气相中H2O2的离解:
\({{H}_{2}}{{O}_{2}}\to 2OH\)
\(OH+CO\to C{{O}_{2}}+H\)
\(H+{{O}_{2}}\to OH+O\)
习题
3.1简述质量作用定律。
3.2写出v级反应的判定准则和半衰期。
3.3分析定温条件下压强对化学反应速度的影响。
3.4分析温度对化学反应速度的影响。
3.5分析阿累尼乌斯各参数的意义。
3.6推导\({{H}_{2}}+B{{r}_{2}}\to 2HBr\) 直链反应速度。
3.7一级连串反应\(A\xrightarrow{{{k}_{1}}}B\xrightarrow{{{k}_{2}}}C\) 中,A初始浓度为(A)0,作图分析各组分浓度变化
求出C的反应诱导期,并写出反应诱导期时各组分浓度表达式。