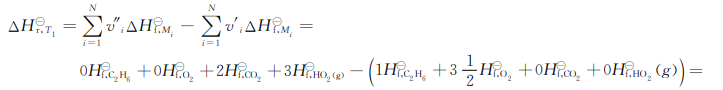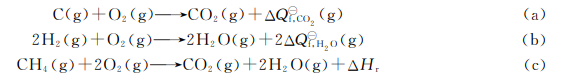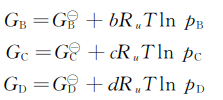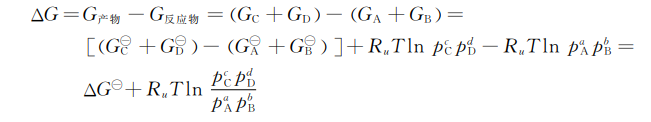第2章化学热力学基础
2.1热力学定律的论述
在讨论热力学定律时,按跨越系统边界所发生的能量(热和功)和质量交换对系统进行分类:
(1)孤立系统:与外界既没有能量交换也没有质量交换。
(2)封闭系统:与外界只有能量交换而无质量交换。
(3)开放系统:与外界既有能量交换也有质量交换。
在热力学的发展过程中,曾提出了三大热力学定律,有些书籍也把气体状态方程称为热力学第零定律。
1热力学第零定律
热力学第零定律表述如下:体系温度和压强、容积、气体摩尔数存在如下关系式:
\(T=T(p,V,{{n}_{i}})\) (2-1)
对于彼此处于平衡状态的所有系统,其值都相同。换言之,当两个物体与第三个物体具有相同温度时,它们彼此的温度也是相同的因此当它们相互接触时,将处于平衡状态。这个定律虽然是在其他几个定律之后提出的,但在逻辑上却居于其他定律之前,故称作第零定律。这个定律指出,温度测量必须有标准刻度。方程式(2-1)也称作气体状态方程。
2.热力学第一定律
存在着一个广义的函数,称作贮能E,它由内能U、动能Ek、势能E三部分组成。因此有
\(E=U+{{E}_{K}}+{{E}_{p}}\) (2-2)
式中
\(E=E(p,V,{{n}_{i}})\) (2-3)
热力学第一定律一般有如下描述:
(1)热可以转化成功,功也可以转化成热。
(2)消耗一定的功必然产生一定的热,一定的热消失时,也必然产生一定的功。
在一个无限小的过程中加入系统的热量可表示为
\(\delta \hat{Q}=dE+\delta \hat{W}\) (2-4)
这里变量上面的符号表示这个量不是热力学参量,表示不严格的微分,因为Q和W是与路径有关的函数。
3.热力学第二定律
对于温度,存在着一个绝对刻度,还有一个叫作熵的广义函数:
\(S=S(p,V,{{n}_{i}})\) (2-5)
热力学第二定律一般有如下描述:
(1)热不可能自发地不付任何代价地从低温转到高温。
(2)熵增加原理:对孤立系统内可逆过程,系统的熵不变,对不可逆过程,系统的熵增加。
因此,对于封闭系统中的一个无限小的过程:
\(TdS\ge \delta \hat{Q}\) (2-6)
式(2-6)等号适用于可逆过程,不等号适用于自然的(不可逆)过程。
4.热力学第三定律
热力学第三定律一般有如下描述:
(1)绝对零度不可能实现。
(2)完全晶体的嫡在温度绝对零度时等于零。
D.w.h. Nernet和M. Planck对热力学第三定律是这样描述的:完全晶体的熵在温度绝对零度时等于零。这一定律为计算各种物质的熵提供了基准值。Van Wylen和 Sonntag曾清楚地阐述过,从统计的观点看,这意味着晶格结构具有最高的等级。因此,当物质在绝对零度时并不具备完全的晶格结构,而是具有一定程度的随机性时(像固体熔液或玻璃状固体)那么即使在绝对零度时它的熵仍具有一定的数值。
2.2状态方程
通常,对于一个体积为V和温度为T的已知物质的封闭系统,当其处于化学平衡时有一组n的值,则
\({{n}_{i}}^{\text{*}}\text{=}{{i}^{*}}(V,T)\) (2-7)
式中,\({{n}_{i}}^{*}\) 是平衡状态下的数值。对于平衡系统,状态方程变成
\(p=p(V,T,{{n}_{1}}^{\text{*}},{{n}_{2}}^{*},\cdots ,{{n}_{N}}^{*})\) (2-8)
根据 Dalton的分压定律,对处于热力学平衡的热理想气体的混合物,得
\(p=\frac{1}{V}\sum\limits_{i=1}^{N}{{{n}_{i}}^{*}{{R}_{u}}T}\) (2-9)
对处于化学不平衡的系统,表示它的压强可简单地将式(2-9)中的星号去掉:
\(p=\frac{1}{V}\sum\limits_{i=1}^{N}{{{n}_{i}}{{R}_{u}}T}\) (2-10)
2.3质量守恒
对一个封闭系统,所含物质的总质量是不变的,但当系统处于化学不平衡状态时,每一组分的量是会改变的。一个简单的任意的化学反应可以写成如下的形式:
\(\sum\limits_{i=1}^{N}{{{{{v}’}}_{i}}}{{M}_{i}}\to \sum\limits_{i=1}^{N}{{{{{v}”}}_{i}}}{{M}_{i}}\) (2-11)
式中,\({{{v}’}_{i}}\) 是组分i作为反应物时的化学计量系数;\({{{v}”}_{i}}\)是组分i作为产物时的化学计量系数,Mi是组分i的化学符号。不参加反应的组分,\({{{v}’}_{i}}=0\),不在产物中出现的组分,\({{{v}”}_{i}}=0\)。哪些组分是反应物,哪些组分是产物,这只是一个选择的问题,一经作出选择,就应保持不变。
从方程式(2-11)可以看出,当有\({{{v}”}_{i}}-{{{v}’}_{i}}\)摩尔的Mi生成时,就有\({{{v}’}_{j}}-{{{v}”}_{j}}\)摩尔的Mj,消失(应注意j≠i)。这个方程给出了各个组分的摩尔数变化之间的关系。
例2.1 \({{H}_{2}}+\frac{1}{2}{{O}_{2}}\to {{H}_{2}}O\)
令 \({{M}_{1}}={{H}_{2}};{{M}_{2}}={{O}_{2}};{{M}_{3}}={{H}_{2}}O\)
那么 \({{{v}’}_{1}}=1{{{v}”}_{1}}=0\)
\({{{v}’}_{2}}=\frac{1}{2}{{{v}”}_{2}}=0\)
\({{{v}’}_{3}}=0{{{v}”}_{3}}=1\)
\({{{v}”}_{3}}-{{{v}’}_{3}}=1\),有1mol的H2O形成,△n3=1;
|({{{v}’}_{1}}-{{{v}”}_{1}}=1\),有1mol的H2消失,△n3=-1
\({{{v}’}_{2}}-{{{v}”}_{2}}=\frac{1}{2}\),有1/2mol的O2消失,△n2=-1/2
因此有 \(\frac{\Delta {{n}_{1}}}{{{{{v}”}}_{1}}-{{{{v}’}}_{1}}}=\frac{\Delta {{n}_{2}}}{{{{{v}”}}_{2}}-{{{{v}’}}_{2}}}=\frac{\Delta {{n}_{3}}}{{{{{v}”}}_{3}}-{{{{v}’}}_{3}}}\)
对于一个无限小的变化,常引用一个简单反应过程的无因次反应度参量,于是
\(d{{n}_{i}}=({{{v}”}_{i}}-{{{v}’}_{i}})d\varepsilon i=1,2,\cdots N\) (2-12)
如果ni表示各种组分在为零的同一初始工况或参考工况下的摩尔数,对式(2-12)积分可得
\({{n}_{i}}-{{n}_{i,r}}=({{{v}”}_{i}}-{{{v}’}_{i}})\varepsilon i=1,2,\cdots ,N\) (2-13)
从方程式(2-13)可以看到,对于发生简单反应的封闭系统,热力学状态关系式中的ni可以用量ni,r和反应度\(\varepsilon \)代替。当某一系统在某一参考工况下的成分已知时,该系统的热力学状态可由下式确定:
\(p=p(V,T,\eta )\) (2-14)
式中,\(\varepsilon \)可以看作一个状态变量。对于V和T为已知量的化学平衡,ni将有其相应的平衡值ni*,因而也有相应的特定值\({{\varepsilon }^{*}}\) 。
令mi,为第i个组分的质量,Wi为其分子量,则由方程式(2-12)可得
\(d{{m}_{i}}=({{{v}”}_{i}}-{{{v}’}_{i}}){{W}_{i}}d\varepsilon i=1,2,\cdots ,N\) (2-15)
由于封闭系统的总质量是不变的,即
\(M=\sum\limits_{i=1}^{N}{{{m}_{i}}=}\)常数 (2-16)
因此有
\(\sum\limits_{i=1}^{N}{d{{m}_{i}}=}0\) (2-17)
将方程式(2-15)代入式(2-17)中得
\(\sum\limits_{i=1}^{N}{(({{{{v}”}}_{i}}-{{{{v}’}}_{i}}){{W}_{i}})d\varepsilon =}0\) (2-18)
如果反应度不等于零(即\)d\varepsilon \)≠0),则
\(\sum\limits_{i=1}^{N}{({{{{v}”}}_{i}}-{{{{v}’}}_{i}}){{W}_{i}}=}0\) (2-19)
这个方程叫作化学量计量方程。将式(2-12)对时间微分,得
\(d{{n}_{i}}/dt=({{{v}”}_{i}}-{{{v}’}_{i}})d\varepsilon /dt\) (2-20)
这个方程叫作速率方程。
2.4热力学第一定律和能量守恒
热力学第一定律指出,在系统所经历的循环中,热的环路积分将与功的环路积分成正比,即
\(\oint{\delta \hat{Q}=}\oint{\delta \hat{W}}\) (2-21)
式中,\(\oint{\delta \hat{Q}}\)是传热量的环路积分或循环中的净传热量;\(\oint{\delta \hat{W}}\)是功的环路积分或循环所做的净功。热力学第一定律还给出了一个状态函数叫作系统的贮能E,并把该函数的变化与来自外界的能量流联系起来。
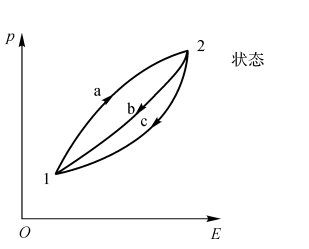
图2-1 热力学参数E的存在性的证明
热力学参量E的存在可作这样的验证:根据方程式(2-21),可以写出热和功沿路径a和b的环路积分(见图2-1):
\(\int_{1a}^{2a}{\delta \hat{Q}}+\int_{2b}^{1b}{\delta \hat{Q}}=\int_{1a}^{2a}{\delta \hat{W}+\int_{2b}^{1b}{\delta \hat{W}}}\) (2-22a)
现设想另有一个循环,系统仍由路径a由状态1变化到状态2,然后由路径c回到状态1,那么
\(\int_{1a}^{2a}{\delta \hat{Q}}+\int_{2c}^{1c}{\delta \hat{Q}}=\int_{1a}^{2a}{\delta \hat{W}+\int_{2c}^{1c}{\delta \hat{W}}}\) (2-22b)
式(2-22a)减去式(2-22b),整理后得到
\(\int_{2b}^{1b}{(\delta \hat{Q}}-\delta \hat{W})=\int_{2c}^{\text{1}c}{(\delta \hat{Q}-\delta \hat{W})}\) (2-23)
由于b和c代表状态1和状态2之间的任意过程,则 \(\delta \hat{Q}-\delta \hat{W}\)对状态1和2之间的所有过程都是相同的。所以,\(\delta \hat{Q}-\delta \hat{W}\)仅仅取决于初始和终了状态,而与这两个状态之间所经历的路径无关。由此可认为,\(\delta \hat{Q}-\delta \hat{W}\)是一个点函数,是系统的真实微分。这个参量就是系统的能量用符号E表示,即
\(dE=\delta \hat{Q}-\delta \hat{W}\) (2-24)
因为 是系统所做的功,所以式(2-24)中\(\delta \hat{W}\)前面是负号。
从物理意义来看,参量E代表系统在某一特定状态下的总能量,这个能量可以多种形式出现,其中包括热能、动能、势能(相对于选定的坐标系)、与分子的运动和位置有关的能量、与原子结构有关的能量、化学能(例如在蓄电池内)静电能(如在充电的电容器内)等等在热力学的研究中,为方便起见,将数值较大的动能和势能分别考虑,然后将系统内所有其他形式的能量合并成一个参量,叫作内能,用符号U表示,则
E=内能+动能+势能=U+EK+EP
式中 \({{E}_{K}}=\frac{1}{2}m{{\left| v \right|}^{2}}\)
\({{E}_{p}}=mgZ\) (2-25)
由方程式(2-24),微分式dE=dU+d(Ek)+d(Ep)可写成
\(\delta \hat{Q}=dU+(\frac{1}{2}m{{\left| v \right|}^{2}})+d(mgZ)+\delta \hat{W}\) (2-26)
假设g是常数,将上述方程在状态1和2之间积分可得
\({{\hat{Q}}_{2}}=({{U}_{2}}-{{U}_{1}})+\frac{m({{\left| {{v}_{2}} \right|}^{2}}-{{\left| {{v}_{1}} \right|}^{2}})}{2}+mg({{Z}_{2}}-{{Z}_{1}}){{+}_{1}}{{\hat{W}}_{2}}\) (2-27)
式中的内能U同动能和势能一样也是一个容积量因为这三种能都取决于系统的质量。
功包括以下三种形式:
(1)传动功 ,是对系统的外观产生影响所做的功,也就是转动一根轴或提起一个重物所做的功。
(2)流动功是在发生质量流的边界上任一点处克服压强效应所做的功。流动功功率可以写成
\(p\frac{dV}{dt}=\frac{p}{\rho }\left( \frac{\rho dV}{dt} \right)=\frac{p}{\rho }\dot{m}\) (2-28)
(3)黏性功\({{\hat{W}}_{\mu }}\) 是发生质量流动的边界上克服流体摩擦效应所做的功。循环所做的净功的功率可写成
\({}^{\delta \hat{W}}/{}_{\delta t}={}^{\delta {{{\hat{W}}}_{s}}}/{}_{\delta t}+{}^{\delta {{{\hat{W}}}_{\mu }}}/{}_{\delta t}+\int{\frac{p}{\rho }}d{{\dot{m}}_{out}}-\int{\frac{p}{\rho }}d{{\dot{m}}_{in}}\) (2-29)
当封闭系统内发生了无限小的可逆过程时,第一定律一般用古典(即平衡的)热力学形式表示,即
\(dU=\delta \hat{Q}-pdV\) (2-30)
式(2-30)中假设没有黏性功或传动功,没有动能或势能的变化,\(\delta \hat{Q}\)表示系统从外界吸收的热量,pdV是系统所做的流动功。此处p和U是与其他参量V和T有关的状态函数,可用下述形式的状态方程表示
p=p(V,T),U=U(V,T) (2-31)
能量守恒定律可以用来研究化学不平衡状态,需要修正的仅仅是状态函数p和U要重新
定义:
\(p=p(V,T,{{n}_{1}},{{n}_{2}},{{n}_{3}},\cdots ,{{n}_{N}})\) (2-32)
\(U=U(V,T,{{n}_{1}},{{n}_{2}},{{n}_{3}},\cdots ,{{n}_{N}})\)
当系统处于平衡状态时,ni变为ni*(V,T,状态方程式(2-32)回到平衡时的关系式(2-31)。因此可以把完全的热力学平衡状态看成是化学不平衡的一种特殊情况。
在热力学不平衡状态中,也可以像热力学平衡状态那样用下式定义焓:
H=U+pV (2-33)
对于化学不平衡状态,H也可以用状态方程的形式表示:
\(H=H(V,T,{{n}_{1}},{{n}_{2}},\cdots ,{{n}_{N}})\) (2-34)
或
\(H=H(V,T,\varepsilon )\) (2-35)
例2.2考虑下面在容积V不变的情况下进行的反应
H2(g)+1/2O2(g)→H2O(g)+57.5kcal①/(温度298.16K)
对于定容过程,第一定律变成
\(dU=\delta \hat{Q}\) (2-36)
因为内能是点函数,与路径无关,所以在化学反应过程中能量的变化就等于热量的变化,即
\(\Delta U={{(\Delta \hat{Q})}_{v}}=57.5kcal/mol\)
如果在定压状态下发生同样的反应,第一定律将为
\(dU=\delta \hat{Q}-pdV\) (2-37)
积分得到
\(\Delta U={{(\Delta \hat{Q})}_{p}}-p\Delta V\) (2-38)
如果反应是在等温T和定压p下进行,那么对于每1mol的H2O,有
\(\Delta U={{(\Delta \hat{Q})}_{p}}-RT\Delta n\)
式中△n=(n产物-n反应物)理理想气体=-1/2,因而
\({{(\Delta \hat{Q})}_{p}}=\Delta V+\frac{1}{2}RT=57.798kcal\)
则
\({{(\Delta \hat{Q})}_{p}}-{{(\Delta \hat{Q})}_{v}}=0.298kcal\)
这表明这个反应在定压状况下进行要比在定容状况下多放出0.298kcal的热量。这部分热量RT△n是外界环境为了维持气体在反应过程中压力p不变所做的功,此时气体的体积是减小的。这也说明化学反应所释放的热量是与反应进行时的物理条件有关的(即与路径有关)。
2.5热力学第二定律
2.5.1平衡热力学
对于封闭系统,当其由一个热力学平衡状态态1变化到另一个平衡状态2时,熵的变化为
\({{S}_{2}}-{{S}_{1}}=\int_{1}^{2}{{{(\delta \hat{Q}/T)}_{rev}}}\) (2-39)
式中,rev表示状态1与2之间的任一可逆路径;\(\delta \hat{Q}\)是系统释放或吸收的热量;T是相应的绝对温度。这里值得注意的是,由于物质的熵的变化与路径无关,因此对所有的过程,可逆的或不可逆的,熵的变化都是相同的。上面的方程仅能计算沿可逆路径的熵的变化,但一经算出,嫡变的值就是这两个状态之间所有过程熵变的值。还有一点值得注意的是,T在这里充当积分因子,它将不确切的微分\(\delta \hat{Q}\)转化为确切的微分\({{(\delta \hat{Q}/T)}_{rev}}\)
如果同样一个系统在同样两个平衡状态1和2之间经历一个不可逆过程或真实过程,则有
①1kcal=4.1868kJ。
\({{S}_{2}}-{{S}_{1}}>\int_{1}^{2}{(\delta \hat{Q}/T)}\) (2-40)
式中\(\delta \hat{Q}\)是在特定过程中加入系统的热量。
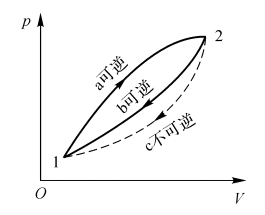
设有某系统在状态1和2之间经历了两个循环,其一由两个可逆过程a和b组成,另一个则由过程a和不可逆过程c组成(见图2-2)。
图2-2 证明熵是物质的一个特征
对于可逆循环a和b,有
\(\oint_{a,b}{\delta \hat{Q}/T=}\int_{1a}^{2a}{\delta \hat{Q}/T\text{+}\int_{\text{2b}}^{1b}{\delta \hat{Q}/T}\text{=0}}\) (2-41)
对于由可逆过程a和不可逆过程c组成的循环,根据Clausius不等式有
\(\oint_{a,c}{\delta \hat{Q}/T}\le 0\) (2-42)
因此:
\(\oint_{a,c}{\delta \hat{Q}/T=}\int_{1a}^{2a}{\delta \hat{Q}/\delta T\text{+}\int_{\text{2c}}^{1c}{\delta \hat{Q}/\delta T}\text{0}}\) (2-43)
将式(2-41)和式(2-43)两个方程相减得
\(\int_{\text{2b}}^{1b}{\delta \hat{Q}/T}>\int_{2c}^{1c}{\delta \hat{Q}/T}\) (2-44)
因为熵是热力学参量,b是可逆过程,且
\(\int_{\text{2b}}^{1b}{\delta \hat{Q}/T}=\int_{2b}^{1b}{dS=}\int_{2c}^{1c}{dS}\) (2-45)
所以
\(=\int_{2b}^{1b}{dS>}\int_{2c}^{1c}{\delta \hat{Q}/T}\) (2-46)
或者在一般情况下
\(dS\ge \delta \hat{Q}/T\) (2-47)
在状态1和2之间对上式积分即可得到:
\({{S}_{2}}-{{S}_{1}}>\int_{\text{1}}^{\text{2}}{(\delta \hat{Q}/T)}\) (2-48)
2.5.2非平衡热力学
确定了状态参量熵S之后,任一封闭系统在经历任一过程时熵的变化dS可以分解为两部分:
dS=deS+diS (2-49)
式中,deS是系统与外界相互作用(例如系统的吸热和放热)产生的熵变;diS是系统内部发生的过程(如化学反应、多种气体的定压混合)产生的熵变。这两个微分量也可分别看作是外界流入系统的熵和系统内部不可逆过程产生的熵。
熵变diS永远不会是负值:
diS=0(可逆过程) (2-50)
diS>0(不可逆过程 (2-51)
对于封闭系统,当其经历任一可逆的或不可逆的过程时,deS由下式给定:
\({{d}_{e}}S=\delta \hat{Q}/T\) (2-52)
当封闭系统经历一个不可逆过程时,方程式(2-48)积分后变成
\(S-S=\int_{1}^{2}{(\delta \hat{Q}/T)+\int_{1}^{2}{{{d}_{i}}S}}\) (2-53)
对于不可逆过程,diS>0,因此方程式(2-53)包含了古典论述的不等式。后一个关系方程式(2-53)比前一个关系方程式(2-48)更实用因为这里用等式代替了前面的不等式,意味着diS实际上是能够计算的。
对于孤立系统,\(\delta \hat{Q}=0\),所以dES=0,方程式(2-49)变成
\(dS={{d}_{i}}S\ge 0\) (2-54)
这个表达式与前面已经熟悉的古典论述是相同的,即孤立系统的熵不会减小。
如果有质量加入到一个不起化学反应的开式可逆系统中,那么与这部分附加质量相关联的熵可以看作是外界流入系统的熵的一部分。因而有
\(dS={{d}_{e}}S=\delta Q/T+\sum\limits_{j=1}^{N}{{{S}_{j}}{{d}_{e}}{{n}_{j}}}\) (2-55)
式中,Sj是每摩尔加入系统的第j种组分的熵;denj是流入系统的第j种组分的摩尔数的变化。考虑到质量的加入,第一定律变为
\(dU=\delta \hat{Q}-pdV+\sum\limits_{j=1}^{N}{{{u}_{j}}{{d}_{e}}{{n}_{j}}}\) (2-56)
式中,uj是每摩尔流入系统的第j种组分的内能。
定义μj为化学势
\({{\mu }_{j}}={{u}_{j}}-T{{S}_{j}}\) (2-57)
方程式(2-56)除以T得
\(\delta \hat{Q}/T=dU/T+pdV/T-\frac{1}{T}\sum\limits_{j=1}^{N}{{{u}_{j}}{{d}_{e}}{{n}_{_{j}}}}\) (2-58)
将方程式(2-57)和式(2-58)代入方程式(2-55)中得
\(dS=dS=\frac{1}{T}dU+\frac{p}{T}dV-\frac{1}{T}\sum\limits_{j=1}^{N}{({{u}_{j}}-T{{S}_{j}}){{d}_{e}}{{n}_{_{j}}}}\) (2-59)
式(2-59)适用于无化学反应的开式可逆系统。
方程式(2-59)是根据这样一个假设建立的,即系统内所有组分在化学上都是惰性的,因而系统内部不存在由化学反应产生的不可逆过程。在有化学反应出现的情况下,来自系统外部的附加质量以及系统内部的化学反应都会使摩尔数改变。在这些情况下,即使P,T和nj,只有无限小变化的过程一般也是不可逆的,为此时可能不存在化学平衡。若dinj(这里d的下标i表示内部微小的变化,n的下标j表示第j种组分)表示第j种组分由于化学反应而造成的摩尔数的变化,那么
\(d{{n}_{j}}={{d}_{i}}{{n}_{j}}+{{d}_{e}}{{n}_{j}}\) (2-60)
如果认为每一个组分j都在总系统中占有一个单独的子系统,那么每一个子系统都可以看成是一个无化学反应的开式系统,这意味着对于每一个组分:
\(d{{S}_{j}}=\frac{1}{T}d{{U}_{j}}+\frac{{{p}_{j}}}{T}dV-\frac{1}{T}{{\mu }_{j}}d{{n}_{j}}\) (2-61)
式中,Pj是组分j的分压;Uj是组分j的内能。将上面的方程对所有的组分也即所有的子系统)求和,并注意到
\(p=\sum\limits_{j=1}^{N}{{{p}_{j}}}\) (2-62)
\(U=\sum\limits_{j=1}^{N}{{{U}_{j}}}\) (2-63)
\(S=\sum\limits_{j=1}^{N}{{{S}_{j}}}\) (2-64)
对总系统可得
\(dS=\frac{1}{T}dU+\frac{p}{T}dV-\frac{1}{T}\sum\limits_{j=1}^{N}{{{\mu }_{j}}d{{n}_{j}}}\) (2-65)
这是开式不可逆化学过程一个基本的化学热力学方程。这个方程与方程式(2-59)去掉d的下标e是相同的。
由状态方程,得
\(S=S(U,T,{{n}_{1}},{{n}_{2}},\cdots ,{{n}_{N}})\) (2-66)
或者表示成微分的形式:
\(dS={{(\frac{\partial S}{\partial U})}_{V,{{n}_{j}}}}dU+{{(\frac{\partial S}{\partial V})}_{U,{{n}_{j}}}}dV+\sum\limits_{j=1}^{N}{{}}{{(\frac{\partial S}{\partial {{n}_{j}}})}_{U,V,{{n}_{j}}}}d{{n}_{j}}\) (2-67)
上式末项中的n表示在求导时除n以外的所有摩尔数都保持不变。将此式与方程式 (2-65)比较得
\({{(\frac{\partial S}{\partial U})}_{V,{{n}_{j}}}}=\frac{1}{T}\) (2-68)
\({{(\frac{\partial S}{\partial V})}_{U,{{n}_{j}}}}=\frac{p}{T}\) (2-69)
\(-T{{(\frac{\partial S}{\partial {{n}_{j}}})}_{U,V,{{n}_{j}}}}={{\mu }_{J}}\) (2-70)
H为系统焓
H=U+pV (2-71)
\(dU=dH-pdV-Vdp\) (2-72)
将方程式(2-72)代入式(2-65)中得
![]()
由式(2-73)可得\(dS=\frac{1}{T}dH-\frac{V}{T}dp-\frac{1}{T}\sum\limits_{j=1}^{N}{{{\mu }_{j}}d{{n}_{j}}}\)
\({{\mu }_{j}}=-T{{(\frac{\partial S}{\partial {{n}_{j}}})}_{H,p,{{n}_{j}}}}\) (2-74)
将式(2-68)~式(2-70)与方程式(2-74)合并得
\({{(\frac{\partial S}{\partial {{n}_{j}}})}_{H,p,{{n}_{j}}}}={{(\frac{\partial S}{\partial {{n}_{j}}})}_{U,V,{{n}_{j}}}}\) (2-75)
下面推导μj与吉布斯自由能G之间的变化关系。
吉布斯自由能G是一个容积量,可由下式定义
G=H-TS=U+pV-TS (2-76)
这里G与H一样,可以看成是一个二次状态参量。需要说明的是在热力学的全部内容里,已经包含了参量p,V,T,U和S,化学热力学的发展也只需要三个一次状态参量就够了,引入附加的函数G仅仅是为了研究的方便。
dG=dH-Tds-SdT (2-77)
方程式(2-73)代入式(2-77)得
\(dG=Vdp-SdT+\sum\limits_{j=1}^{N}{{{\mu }_{j}}d{{n}_{j}}}\) (2-78)
从而可以写出
\(V={{(\frac{\partial G}{\partial p})}_{T,{{n}_{j}}}}\) (2-79)
\(S=-{{(\frac{\partial G}{\partial T})}_{p,{{n}_{j}}}}\) (2-80)
\({{\mu }_{j}}={{u}_{j}}-TS={{(\frac{\partial G}{\partial {{n}_{j}}})}_{p,T,{{n}_{j}}}}=-T{{(\frac{\partial S}{\partial {{n}_{j}}})}_{H,p,{{n}_{j}}}}\) (2-81)
这里,式(2-81)可以作为化学势μ1的定义式在化学热力学中起着很重要的作用。化学势是一个强度量,一般是由p,T和n,给定的系统状态的函数。即使某一组分并不出现在系统内,但它的化学势也无须为零,这是因为常常可能将它引入系统中,这时G的值就会改变,相应的的值也就不为零。
由热力学第一定律得
\(dU=\delta \hat{Q}-pdV+{{d}_{e}}U\) (2-82)
式中,dU是附加质量携带的内能。将此式代式(2-65)可得
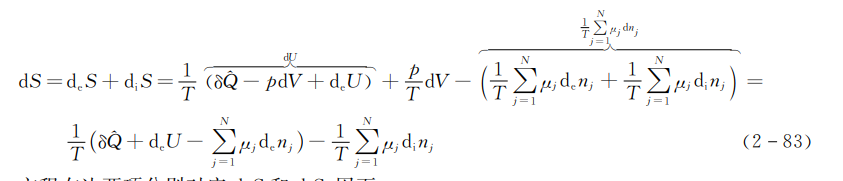
方程右边两项分别对应deS和diS,因而
\({{d}_{e}}S=\frac{1}{T}(\delta \hat{Q}+{{d}_{e}}U-\sum\limits_{j=1}^{N}{{{\mu }_{j}}{{d}_{e}}{{n}_{j}}})\) (2-84)
\({{d}_{i}}S=-\frac{1}{T}\sum\limits_{j=1}^{N}{{{\mu }_{j}}{{d}_{i}}{{n}_{j}}}\) (2-85)
将方程(2-74)代入式(2-84)、式(2-85)得
\({{d}_{i}}S={{(\frac{\partial S}{\partial {{n}_{j}}})}_{H,p,{{n}_{j}}}}{{d}_{i}}{{n}_{j}}\) (2-86)
如果只考虑单个反应,那么对于封闭系统,dn=dn,并可用反应度的变化d表示为
\({{d}_{i}}{{n}_{j}}=({{{v}”}_{j}}-{{{v}’}_{j}})d\varepsilon \) (2-87)
代入方程式(2-85)得
\({{d}_{i}}S=-\frac{1}{T}(\sum\limits_{j=1}^{N}{({{{{v}”}}_{j}}-{{{{v}’}}_{j}}){{\mu }_{j}})}d\varepsilon \) (2-88)
根据第二定律,这个表达式对于不可逆过程是正的,而对于可逆过程则为零。如果说某一过程是可逆的,就等于说这个系统在任何时候都处于化学平衡状态,或者说这个过程是一系列无限缓慢的化学平衡状态中的一个状态。因此,化学平衡的条件就是任何时候dS都为零,这就要求
\(\sum\limits_{j=1}^{N}{({{{{v}”}}_{j}}-{{{{v}’}}_{j}}){{\mu }_{j}}^{*}}=0\) (2-89)
式中,\({{\mu }_{j}}^{*}\)是平衡状态的化学势。这个方程不仅仅只限于气体,在化学文献中,\(-\sum\limits_{j=1}^{N}{({{v}^{\prime \prime }}_{j}-{{{{v}’}}_{j}})}{{\mu }_{j}}\)叫作化学反应的亲和力,通常用符号a表示:
\(a=-\sum\limits_{j=1}^{N}{({{{{v}”}}_{j}}-{{{{v}’}}_{j}}){{\mu }_{j}}}\) (2-90)
化学亲和力在化学热力学中起着很重要的作用。
下面来总结一下关于化学势μ的一些重要特点及物理解释:
(1) 通常看作是吉布斯函数对摩尔数的偏微分,即\({{\mu }_{j}}^{*}={{(\frac{\partial G}{\partial {{n}_{j}}^{*}})}_{p,T,{{n}_{j}}}}\);它表示当有无限小量的组分j加入到系统内而保持压力、温度以及其他组分量不变时,吉布斯自由能的变化。
(2)\({{\mu }_{j}}\)是一个强度量,单位是(能量/摩尔)。
(3)方程式(2-78)可以对这样一个过程积分,在这个过程中系统的尺寸由于加入了相同的强度量而增加,所有的强度量都保持不变,而所有的容积量都成比例地增加,由于此过程中dT=0,dp=0,以及d\({{\mu }_{j}}\)=0,因而方程(2-78)很容易从(G=0,ni=0)的状态积分到(G,ni)的状态,得
\(G=\sum\limits_{i=1}^{N}{{{\mu }_{i}}{{n}_{i}}}\) (2-91)
由于
\(dG=\sum\limits_{i=1}^{N}{{{\mu }_{i}}d{{n}_{i}}+}\sum\limits_{i=1}^{N}{{{n}_{i}}d{{\mu }_{i}}}=\sum\limits_{i=1}^{N}{d({{\mu }_{i}}}{{n}_{i}})=d(\sum\limits_{i=1}^{N}{{{\mu }_{i}}}{{n}_{i}})\) (2-92)
因此, 可以看成是1mol某种成分对系统总G值的影响。根据上面的解释,可以设想\({{\mu }_{j}}\)就等于1mol的组分j在纯净状态下的Gj值,但这只在有限的特定情况下才成立。一般情况下,溶液的\({{\mu }_{j}}\)是不等于纯物质的Gj的,并随系统成分而变。
(4)对于定温和定压的封闭系统,由方程式(2-78)和式(2-92)可以得
\(\sum\limits_{i=1}^{N}{{{n}_{j}}d{{\mu }_{j}}=-SdT+Vdp=0}\) (2-93)
这个关系式叫作Gibbs-Duhem方程,其用途很多,特别是与液汽平衡的研究有密切关系。
(5)如果在给定的温度和压力下系统处于化学平衡,则
\(\sum{{{\mu }_{j}}d{{n}_{j}}=0}\) (2-94)
这里求和包括构成系统的各种物相的所有\(\mu dn\)项。这个关系式为“相准则”奠定了基础。
(6)当一个系统由一些组分组成时,在给定温度和压力的完全平衡状态下这些组分具有多种相,那么每个组分的化学势对所有的相都是相同的,即
\({{\mu }_{j}}={{\mu }_{j}}={{\mu }_{j}}\) 对所有的j (2-95)
(7)如果系统的各相不处于平衡状态,那么组分的化学势对各个相就不是一样的。组分j将会从具有较高化学势 的相自发地向具有较低化学势的相转移。换言之,物质总是由化学势高的区域向化学势低的区域移动,这就是为什么取名为化学势,它可以度量导致发生化学反应的驱动力。
例2.3下面研究封闭系统中均匀混合物发生的化学平衡反应
\({{{v}’}_{B}}\Leftrightarrow {{{v}”}_{R}}R+{{{v}”}_{L}}L\)
证明 \({{{v}’}_{B}}{{\mu }_{B}}^{*}\Leftrightarrow {{{v}”}_{R}}{{\mu }_{R}}^{*}+{{{v}”}_{L}}{{\mu }_{L}}^{*}\)
证明 根据方程式(2-94),平衡条件为
\({{\mu }_{B}}^{*}d{{n}_{B}}+{{\mu }_{R}}^{*}d{{n}_{R}}+{{\mu }_{L}}^{*}d{{n}_{L}}=0\)
式中分子数的变化不是任意的,而由下面的方程决定:
\(d{{n}_{R}}=\frac{{{{{v}”}}_{R}}}{{{v}_{B}}}(-d{{n}_{B}}),d{{n}_{L}}=\frac{{{{{v}”}}_{L}}}{{{{{v}’}}_{B}}}(-d{{n}_{B}})\)
将这两式代入第一个方程得
\({{{v}’}_{B}}{{\mu }_{B}}^{*}={{{v}”}_{R}}{{\mu }_{R}}^{*}+{{{v}”}_{L}}{{\mu }_{L}}^{*}\)
一般情况下,均匀平衡的条件是,产物的化学势之和等于反应物化学势之和,即
\(\sum{{{{{v}’}}_{i}}{{\mu }_{i}}^{*}=}\sum{{{{{v}”}}_{j}}{{\mu }_{j}}^{*}}\)
2.6平衡准则
化学平衡的准则,取决于某些热力学参量保持不变时的条件。为方便起见,对于定容过程,引入另一个二次热力学函数,叫作 Helmholtz自由能A,其定义为
A=U-TS (2-96)
dA=dU-TdS-SdT (2-97)
A代表温度和容积不变时的有用功而不是压力一体积功。
根据热力学第一定律\(dU=\delta \hat{Q}-pdV\),得
\(dU=\delta \hat{Q}-pdV+d\xi \) (2-98)
式中,d表示除压力体积功以外的功。加于系统的功,\(d\xi \)为正,系统做功时\(d\xi \(为负。将方程式(2-98)与热力学第二定律结合起来\(\delta Q=TdS\),得
\(d\xi =dU-\delta \hat{Q}+pdV=dU-TdS+pdV\) (2-99)
将方程式(2-97)代入方程式(2-99),得
\(d\xi =dA+SdT+pdV\) (2-100)
从式(2-100)(当T和V不变时)可以很明显地得到
\(d\xi =dA\) (2-101)
在温度T和容积V不变时,dA代表除压力体积功以外的有用功。一方面,如果dA是负的,那么\(d\xi \)也是负的,该系统做了有用功另一方面,如果\(d\xi \)在某一特定过程中为正值,则必须对系统做功。如果\(d\xi \)=0,则说明系统没有做功,也没有对系统做功,系统是平衡的。
用同样的方法,可以得到用吉布斯自由能G表示的方程。
G=H-TS=U+Pv-TS (2-102a)
dg=dU+pdV+Vdp-SdT-TdS (2-102b)
将方程式(2-102b)代入方程式(2-99),得
\(d\xi =dG+SdT-Vdp\) (2-103)
当T和P不变时,得
\(d\xi =dG\) (2-104)
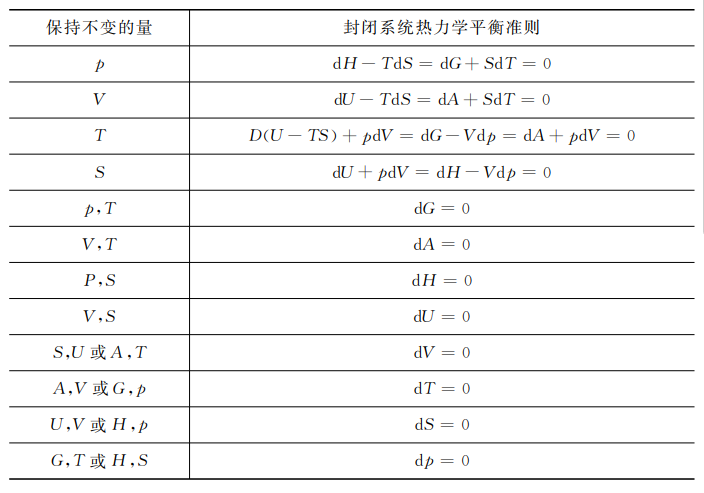
总的平衡准则(\(d\xi \)=0)在不同情况下的结果概括在表2-1中。
表2-1封闭热力学系统的平衡准则
对于开式系统,为了表示开式不可逆化学反应过程A值的变化,方程式(2-65)可改写为
\(dA=-SdT-pdV+\sum\limits_{j=1}^{N}{{{\mu }_{j}}d{{n}_{j}}}\) (2-105)
方程式(2-65)和式(2-73)可以重新组织为
\(dU=TdS-pdV+\sum\limits_{j=1}^{N}{{{\mu }_{j}}d{{n}_{j}}}\) (2-106)
\(dH=TdS+Vdp+\sum\limits_{j=1}^{N}{{{\mu }_{j}}d{{n}_{j}}}\) (2-107)
以上各式以及方程式(2-78)在化学平衡的研究以及热化学计算中是很有用的。
2.7标准生成热
物质的标准生成热△Qf○一(kcal/mol)是这样定义的:由标准状态(298.15K和1atm,即标准温度和压力)下的元素构成1mol物质时所释放出的热量。标准生成热还可以看成是物质在标准状态下的焓△Hf○一(kcal),它与同样温度的标准状态下的元素有关。下标f表示化合物由元素形成,上标○一指所有的产物和反应物均处于标准状态。
标准状态当其涉及元素时是指集态的参考状态。对于气体,参考状态就是在1atm及某一给定温度下的理想气体状态在此状态下,各个孤立的分子之间没有相互作用,并且遵循完全气体的状态方程。对于纯净的液体和固体,其参考状态就是该物质在1atm及某一给定温度下的真实状态。按常规都把标准状态下的各种元素的焓定为零,或其标准生成热为零。些元素的标准状态为:H2(气),O2(气),N2(),Hg(液),C(固,石墨)
例2.4 作为标准生成热的一个例子,可以将下面的反应作为参考:
\({{C}_{(s)}}+{{O}_{2}}\left( g \right)\to C{{O}_{2}}\text{ }\left( g \right)+94.\text{ }054\text{ }kcal/mol\)
-94.054kcal/mol就是298k时的(△Hf○一)co2
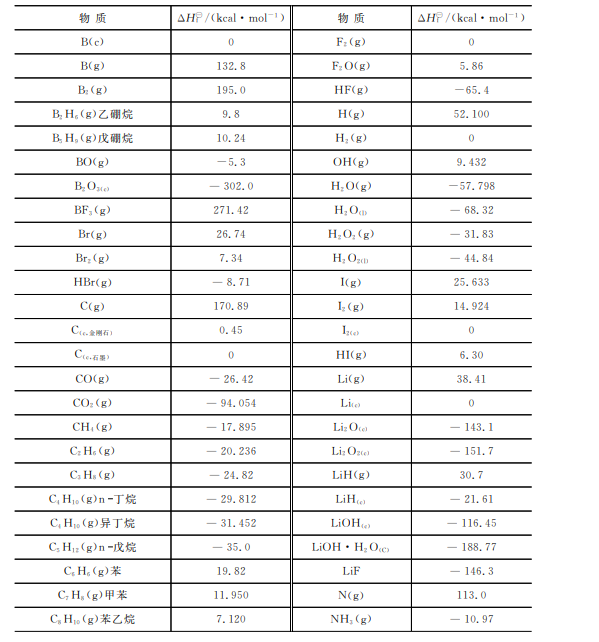
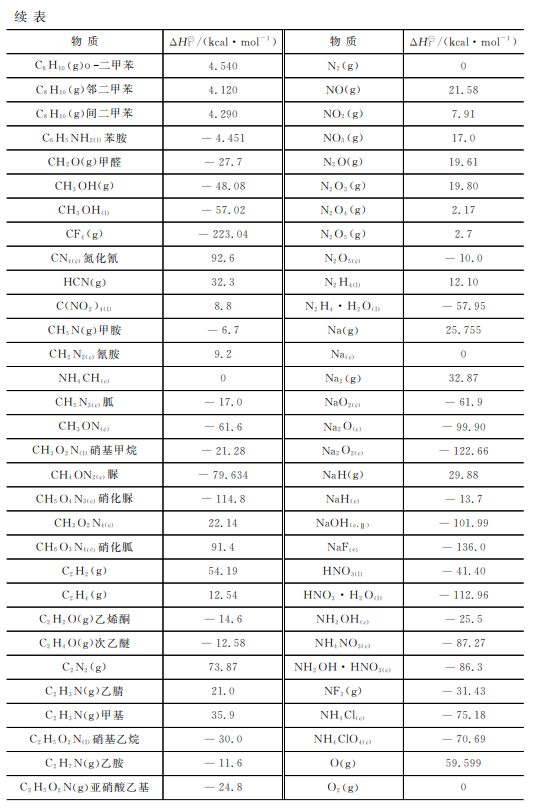
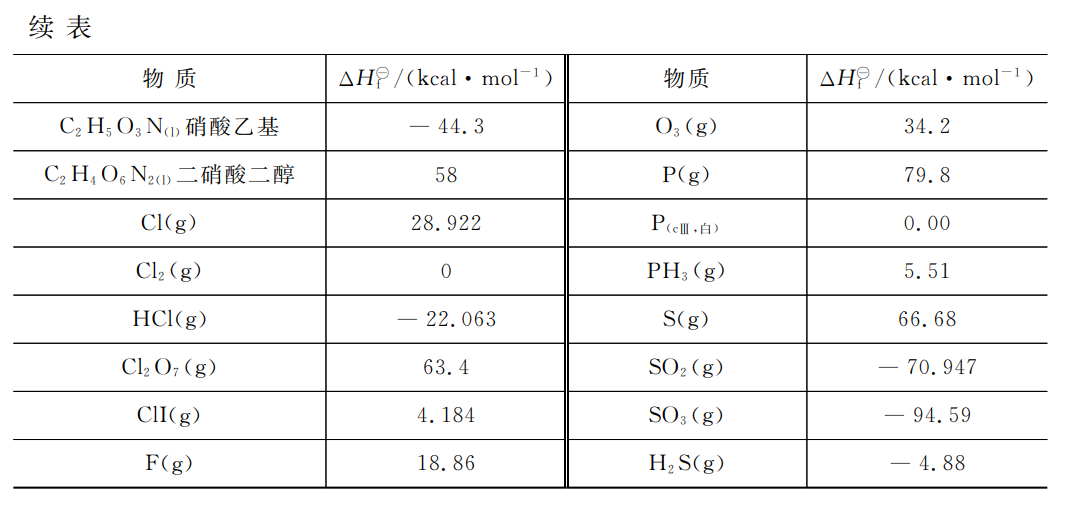
表2-2给出了一些化合物在298.15K或298.6K下的标准生成焓,更详细的数据可查阅 JANAF热化学表或化学物理手册。
表2-2一些物质在298.15K下的标准生成焓
2.8热化学定律
A.l.La Voisier和p.s. Laplacc(1780年)出了这样的定律将化合物分解为元素所须提供的热量,等于由这些元素构成该化合物所释放的热量。这个定律更普遍的叙述是:沿一定方向进行的化学反应,其所引起的热量变化,与同一反应沿反方向进行时的热量变化,在数量上完全相等,但符号却相反。
例2.5 有如下两个反应:
\(\sim C{{H}_{4}}\left( g \right)+2{{O}_{2}}\left( g \right)\to C{{O}_{2}}\left( g \right)+2{{H}_{2}}O\left( 1 \right)+212.8kcal\)
以及
\(C{{O}_{2}}\left( g \right)+2{{H}_{2}}O\left( 1 \right)\to C{{H}_{4}}\left( g \right)+2{{O}_{2}}-212.8kcal\)
这两个反应都是在29816K下进行的。
1840年,G.H.Hess根据经验提出了热量之和不变的定律。这个定律指出:在一定的压力和一定的容积下,对于某一化学反应,论是一步还是分多步进行,其最终的热量变化总是一样的。这意味着反应的净热量只取决于初态和终态。
Hess定律的一个结论是:由于定压过程的△H和定容过程的△U都与路径无关,因此热化学方程就会像代数方程那样可以加减。
例2.6 研究二氧化碳的标准生成热(94.5kcal(gmol))值的确定方法。
\(CO\left( g \right)+\frac{1}{2}{{O}_{2}}\left( g \right)\text{ }\to {298.\text{1}6K}C{{O}_{2}}\text{ }(g)+67.63\text{ }kcal/\left( g.\text{ }mol \right)\)
式中,△H不是标准生成热,因为反应物CO不是标准状态下的元素。在下面的反应中:
\(C\left( s \right)+\frac{1}{2}{{O}_{2}}\left( g \right)\to {\sim 298.16K} \sim CO\left( g \right)+26.42kcal/\left( g\cdot mol \right)\)
26.42kcal/(g·mol)是CO的标准生成热(△Hf○一)因为C和O2在其标准状态下都是元素。将上面两个热化学方程相加可得
\(CO\left( g \right)+\frac{1}{2}{{O}_{2}}\left( g \right)+C\left( s \right)+\frac{1}{2}{{O}_{2}}\left( g \right)\to {298.16K} \sim C{{O}_{2}}\text{ }\left( g \right)+CO\left( g \right)+94.05\text{ }keal/\left( \text{g}\cdot mol \right)\)
将方程两边都出现的分子级分消去得
\(C\left( s \right)+{{O}_{2}}\text{ }\left( g \right)\to {298.16K}C{{O}_{2}}\left( g \right)+94.\text{ }05\text{ }kcal/g\cdot mol\)
这就是正确的二氧化碳形成过程的热化学方程。其所释放的热量94.05kcal/(g·mol)就是CO2的标准生成热( Qf○一)co2,298.16K
由于Hess定律适用于定压(△H)和定容(△U)过程,因此在绝对零度时
△Hf,o○一=△Uf,o○一+(△n)\({{R}_{u}}\underset{\to 0}{\mathop{T}}\,\)= △Uf,o○一 (2-108)
2.9键能和生成热
对于某些还无法合成或不适于在量热计中燃烧的化合物,常用键图和谐振能量来估算它们的标准生成热。键能就是将分子中的某一个键断开使其成为原子所需的能量。为此,常采用破坏分子中的这种键能所需能量的平均值(每摩尔的)这是因为将两个原子间的某个特定键断开所需的能量差不多是相同的,与这种键所在的分子无关。
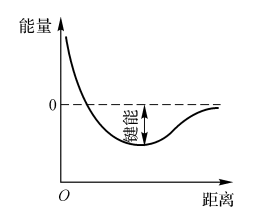
通常,将两个原子分开所需的能量与两个原子间的距离有关。如图2-3所示,键能是势能最低值与无限远时能量值之差。
图2-3两原子间的势能与原子间距离的关系
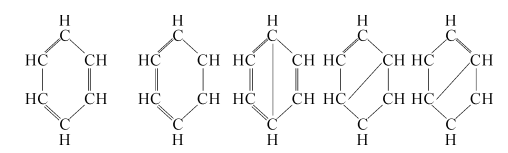
在估算生成热时,除了键能以外还要考虑分子中谐振的可能性。例如苯分子C6H6可以在下列5种结构之间谐振:
由于谐振的结果,△Hf,C,H○一,要比3个 ,3个C-C以及6个C-H的键能之和大得多。这部分附加的能量就是谐振能量,在计算某一给定化合物的实际生成热时,除了要考虑键能外,还要考虑谐振能量。
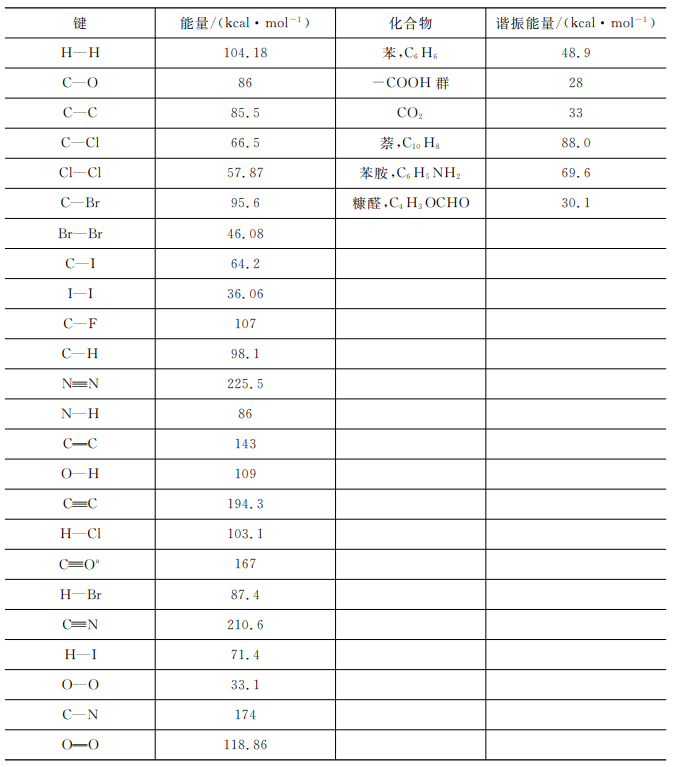
表2-3列出了一些化合物的谐振能量。在这个表中,键能是基于这个物质在气体状态下的数据,所以只能用于气体反应。另外,键能是构成这种键所需能量的负值。
表2-3一些键能和谐振能量的数据
例2.7 确定乙醇C2HO的生成热。
解 C2H6O的结构是
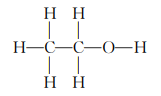
构成1molC2H6O所需的能量为
5(C-H)+(C-C)+(C-O)+(O-H)=5×98.1+85.5+86+109=771kcal/mol
因此可以写出热化学方程为
\(~6H\left( g \right)+O\left( g \right)+2C\left( g \right)\to {{C}_{2}}{{H}_{6}}O\left( g \right)+771\text{ }kcal/\left( g\cdot mol \right)\)
为了求得生成热,需要应用Hess定律以及热化学方程组
\(3{{H}_{2}}(g)\to 6H(g)-312.54kcal/mol\)
\(\frac{1}{2}{{O}_{2}}(g)\to O(g)-59.\text{ }16\text{ }kcal/mol\)
\(2C\left( s \right)\to 2C\left( g \right)-343.4\text{ }kcal/mol\)
得到
\(3{{H}_{2}}\left( g \right)+\frac{1}{2}{{O}_{2}}\left( g \right)+2C\left( s \right)\to {{C}_{2}}{{H}_{6}}O\left( g \right)+\left( 771-715.10 \right)kcal/\left( g\cdot mol \right)\)
因此,△H○一\(_{f,T,{{C}_{2}}{{H}_{6}}O}\)的估算值是-55.90kca/(g·mol),生成热的实际值是53.3kcal/(g·mol),其差值是因为估算值是以平均的键能为依据的。
例2.8求苯甲酸的燃烧热。
解 反应式是
\(~{{C}_{6}}{{H}_{5}}COOH+7\frac{1}{2}{{O}_{2}}\to 7C{{O}_{2}}+3{{H}_{2}}O\)
为了解决这个问题,必须知道苯甲酸的结构式。
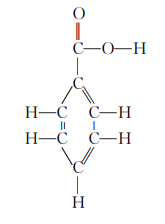
反应物的键能为
4(C-C)+3(C=C)+5(C-H)+1(C=O)+1(C-O)+1(O-H)+7(O=O)+1(C6H6,苯环谐振)+1(-COOH,羧基)
填入数值得
342+429+490.5+167+86+109+891.45+48.9+28=2591.9kcal/mol
产物的键能
14(C=0)+6(O-H)+7(CO2)=2338+654+231=3223kcal/mol
因而苯甲酸的燃烧热为
3223-2591.9=631.1kcal/mol
例2.9 已知下列反应在298.16K下的反应热:
\(~{{C}_{2}}{{H}_{4}}\left( g \right)+\text{3}{{O}_{2}}\left( g \right)\to 2C{{O}_{2}}\left( g \right)+2{{H}_{2}}O\left( l \right)+337.3\text{ }kcal/mol\) (a)
\({{H}_{2}}\left( g \right)+\frac{1}{2}{{O}_{2}}\left( g \right)\to {{H}_{2}}\text{ }O\left( l \right)+68.\text{ }3\text{ }kcal/mol~\) (b)
\({{C}_{2}}{{H}_{6}}\left( g \right)+3{{O}_{2}}\left( g \right)\to 2C{{O}_{2}}\left( g \right)+3{{H}_{2}}O\left( l \right)+372.8kcal/mol\) (c)
求下面反应的反应热:
\(~{{C}_{2}}{{H}_{4}}\left( g \right)+{{H}_{2}}\left( g \right)\to {{C}_{2}}{{H}_{6}}\left( g \right)+\Delta H\)
解 将(a)(b)两式相加再减去式(c),或者将式(a)(b)相加,对式(c)应用Laplace定律,所得结果再与(a)(b)两式的和相加,这样就可以求得结果。
\({{C}_{2}}{{H}_{4}}\left( g \right)+3{{O}_{2}}\left( g \right)\to 2C{{O}_{2}}\left( g \right)+2{{H}_{2}}O\left( l \right)+337.3kcal/mol\)
\({{H}_{2}}\left( g \right)+\frac{1}{2}{{O}_{2}}\text{ }\left( g \right)\to {{H}_{2}}\text{ }O(l)+68.3\text{ }kcal/mol\)
\(~2C{{O}_{2}}\left( g \right)+3{{H}_{2}}O\left( l \right){{C}_{2}}{{H}_{6}}\left( g \right)+3\frac{1}{2}{{O}_{2}}\left( g \right)-372.8kcal/mol\)
\({{C}_{2}}{{H}_{4}}\left( g \right)+{{H}_{2}}(g)\to {{C}_{2}}{{H}_{6}}\left( g \right)+32.\text{ }8\text{ }kcal/mol\)
2.10 反应热
热化学主要研究化学反应中热量的变化,也就是研究化学能向热能的转化和热能向化学能转化。化学反应也和其他过程一样,其中的热量变化一般是一个不确定的量,并与路径有关。只有当反应过程中保持压力或容积不变时,热量的变化才具有确定的值,并且只取决于系统的始态和终态。因此,化学反应的热量变化总是在定压或定容状况下测量的。
反应热的定义方法很多,下面的定义是最普遍的。
设某一封闭系统在温度T和压力p状况下含有给定摩尔数ni的N种不同的组分,这个系统经历一个等压过程,在此过程中ni的值发生变化,而T的初始值与终了值却相同,那么系统释放的热量就是该过程的反应热。
假设系统由状态A变化到状态B,系统的能量增加△E,系统所做的功为6W,系统吸收的热量为Q,那么由热力学第一定律得
\(\Delta E=\delta \hat{Q}-\delta \hat{W}~\) (2-109)
对于流动速度为零并且势能不变的化学反应,则
\(~\Delta E=\Delta U+\Delta \underset{\to 0}{\mathop{P}}\,E+\Delta \underset{\to 0}{\mathop{K}}\,E\)
第一定律将变成
\(~\Delta U=\delta \hat{Q}-\delta \hat{W}\) (2-110a)
\(\Delta \hat{Q}=\Delta U+\delta \hat{W}\) (2-110b)
此外,如果反应在定压下进行,则第一定律可以写成
\(~{{\hat{Q}}_{p}}=\int{{{(\delta \hat{Q})}_{p}}}=\Delta U+P\Delta V~\) (2-111)
当系统由状态A变化到状态B时,得
\({{\hat{Q}}_{p}}=({{U}_{B}}-{{U}_{A}})+p({{V}_{B}}-{{V}_{A}})=({{U}_{B}}+p{{V}_{B}})-({{U}_{A}}-p{{V}_{A}})={{H}_{B}}-{{H}_{A}}=\Delta H\) (2-112)
所以,对于没有流动的定压反应
\({{\hat{Q}}_{p}}=\Delta H\) (2-113)
同理,对于没有流动的定容反应,在没有外部功(W=0)时,第一定律为
\({{\hat{Q}}_{V}}=\Delta U\) (2-114)
对于反应流,如果Ep和EK没有变化,而且除了流动所需的功以外没有其他的功,那么,焓的净变化就等于反应热,即
\(\hat{Q}=\Delta H\) (2-115)
在通常的应用中,要考虑流动系统的摩尔数以及封闭系统的质量。
一个物质在其标准状态下的热含量或焓的符号是H。如前所述,上标表示标准状态,下标T为绝对温度。因此,H表示物质在温度为0K的标准状态下的。
理想气体或完全气体的状态方程为
\(~~pV=mRT=n{{R}_{u}}T\) (2-116)
代入公式H=U+pV,可得
HT○一=UT○一+(pV)○一=UT○一+mRT=UT○一+nRuT (2-117)
当T=0时
H0○一=U0○一+mR(0)=U0○一 (2-118)
将方程式(2-117)减去式(2-118),可以很方便地由UT○一计算HT○一反之亦然。
HT○一-H0○一=UT○一-U0○一+p△V (2-119)
由方程式(2-112)可知,对于无流动的定压反应
△H=△U+p△V (2-120)
如果V是1mol任一理想气体在不变的温度和压力下的体积,那么pV的变化就等于p△V,对理想气体应用方程式(2-116)可得
p△V=(△n)RuT (2-121)
将式(2-121)代入式(2-120)得
△H=△U+(△n)RuT (2-122)
式中
![]() (2-123)
(2-123)
由方程式(2-119)可知,定压过程的反应热可以由定容过程的反应热算出。
设有最普通的反应
\(\sum\limits_{i=1}^{N}{{{{{v}’}}_{i}}{{M}_{i}}\to }\sum\limits_{i=1}^{N}{{{{{v}”}}_{i}}{{M}_{i}}}\)
在T0时标准状态的反应热为
例2.10 求乙烷C2H6(g)的反应热。
解 如果化学反应能按下面的反应式进行,最后的产物不再分解,那么可用方程式(2-124)计算标准状态下的△Hr,
![]()
确定未知反应热的另一个有效方法是应用Hess定律,把已知反应热的一些合适的反应相加。键能和谐振能量也可以用来估算反应热或反应的燃烧热。
例2.11 由CO2和H2O的生成热以及甲烷一氧反应的△H值求CH的生成热。
\(~C{{O}_{2}}(g)+2{{H}_{2}}O\left( g \right)\to C{{H}_{4}}\left( g \right)+2{{O}_{2}}-\Delta {{H}_{r}}\) (d)
把式(a)、式(b)和(d)相加得
![]()
因此
2.11绝热火焰温度的计算
假设有一个绝热的燃烧过程,没有做功也没有动能和势能的变化。对于这样的过程,产物的温度就是绝热火焰温度,这是该反应物所能达到的最高温度,因为反应物的任何传热以及任何不完全的燃烧都会使产物的温度降低。在绝热燃烧过程中,系统释放的热量都用于提高体系温度。
\(\Delta Q=\int_{{{T}_{0}}}^{{{T}_{f}}}{m\bar{C}dT}\( (2-125)
下面给出几个例题说明计算绝热火焰温度的一些步骤。
例2.12 计算气态的H2和O2反应后水蒸气的绝热火焰温度。
解 这个反应可以分解为
![]()
(△Hv=汽化热),将两式相加得
\(~2{{H}_{2}}\left( g \right)+{{O}_{2}}\left( g \right)\to 2{{H}_{2}}O\left( g \right)+115.6kcal\)
因此反应产生的热量为115.6kcal,如果所有的热量都用来加热产物(绝热,没有分解)那么
\(115.6=2\int_{298}^{{{T}_{f}}}{{{C}_{p,{{H}_{2}}O}}dT}\)
![]()
当绝热火焰温度T1=5000K时可以使上面的方程平衡。在这样高的温度下,一般会发生离解现象,实际产物尚未可知,这使得问题变得更为复杂。产物不离解时的绝热火焰温度,通常叫作绝热的凝结火焰温度。
2.12平衡常数
在可逆反应中,当体系达到平衡时,反应物和生成物浓度达到一定平衡,存在一个平衡关系,这里可以用平衡常数来表征。
1.定义
平衡常数:在一定温度下,可逆反应无论从正反应开始还是从逆反应开始,也不管反应物起始浓度大小,最后都达到平衡,这时各生成物浓度的化学计量数次幂的乘积除以各反应物浓度的化学计量数次幂的乘积所得的比值是个常数,用K表示,这个常数叫化学平衡常数。从平衡常数的大小,可确定在该温度下可逆反应中的正反应可能达到的程度
对于aA+bB cC+dD,显然,平衡常数Kp可以用如下函数表示:
![]()
2.平衡常数获取方法
(1)实验测定:通过化学分析法测定反应达到平衡时各物质的浓度。
(2)化学热力学公式推导。
3.平衡常数表达式推导
平衡常数用热力学表达式推导。前提:此过程为等温过程。
(1)自由能方程(用压强表示)。根据定义
G=H-TS=U+pV-TS (2-127a)
有
dG=dU+pdV+Vdp-Tds-SdT (2-127b)
根据热力学定律
\(dU=\delta Q-pdV\delta Q=TdS\)
可得
dU=TdS-pdV (2-128)
将方程式(2-128)代入方程式(2-127b)得
dG=Vdp-SdT (2-129)
假设满足完全气体关系式,对于等温过程
\(~dG=Vdp=\frac{n{{R}_{u}}T~}{p}dp=n{{R}_{u}}Td\left( \ln p \right)~\) (2-130)
因为
\(\frac{dp}{p}=d\left( \text{ln }p \right)\)
将方程式(2-130)在\({{p}^{}}\)至 之间积分得
\(G-{{G}^{}}=n{{R}_{u}}T(\ln p-\ln {{p}^{}})\) (2-131)
若\({{p}^{}}\)=latm,贝
\(G={{G}^{}}+n{{R}_{u}}T\ln p\) (2-132)
对于系统中的组分i
![]()
(2)平衡常数方程推导。反应:\(aA+bB\Leftrightarrow c~C+dD\)
假设:等温条件下,p。=1atm,由方程式(2-133)得到
图2-4 Van’t Hoff平衡箱
假设有a mol的A和b mol的B注入平衡箱在等温状况下进行反应并达到平衡,然后有c mol的C和d mol的D从平衡箱抽出。由此可以得到
由于假设系统处于平衡状态,故
△G=0
以及
![]()
定义
\({{K}_{p}}=\frac{p_{C}^{c}p_{D}^{d}}{p_{A}^{a}p_{B}^{b}}\) (2-135)
从而
![]()
或
![]()
方程式(2-136)给出了标准自由能的变化与任意压力和温度下平衡常数之间的关系。平衡常数K的实际重要性在于它与总的压力无关,仅是温度的函数。如果已知△G○一值,Kp就可以由方程式(2-136)得出。
为了对标准自由能的变化ΔG○一的概念有更清楚的物理认识,就应当注意到,ΔG○一的负值越大, K的值越大,反应也越容易自发进行。
对于一般的化学反应,可以把平衡常数写成更一般的形式。如果反应为
\(\sum\limits_{i=1}^{N}{{{{{v}’}}_{i}}{{M}_{i}}}\Leftrightarrow \sum\limits_{i=1}^{N}{{{{{v}”}}_{i}}{{M}_{i}}}\)
式中, 和 分别代表化学组分;Mi作为反应物和产物时的化学计量系数;N是反应中化学组分的总数。那么
式中,下标p指平衡常数是用分压表示的;下标s表示这些系数与各个化学平衡反应的化学计量系数是相同的。
4.平衡常数的物理意义
平衡常数具有如下物理意义:
(1)平衡常数是化学反应的特性常数。它不随物质的初始浓度(或分压)而改变,仅取决于反应的本性。一定的反应,只要温度一定,平衡常数就是定值。
(2)平衡常数数值的大小是反应进行程度的标志。它能很好地表示出反应进行的完全程度。一个反应的K值越大,说明平衡时生成物的浓度越大,反应物剩余浓度越小反应物的转化率也越大,也就是正反应的趋势越强。反之亦然。
(3)平衡常数表达式表明在一定温度下,体系达成平衡的条件。
例2.13 研究下面的水煤气反应(\(CO+{{H}_{2}}O\to C{{O}_{2}}+{{H}_{2}}\))的平衡常数表达式。
\(C{{H}_{4}}+1.\text{ }5{{O}_{2}}\to CO+2{{H}_{2}}O\)
\(CO+{{H}_{2}}O\to C{{O}_{2}}+{{H}_{2}}\)
混合物为
\((1-\eta )CO+(2-\eta ){{H}_{2}}O+\eta C{{O}_{2}}+\eta {{H}_{2}}\(
解 对于水煤气反应,平衡常数可以写成
\({{K}_{p}}=\frac{{{p}_{C{{O}_{2}}}}{{p}_{{{H}_{2}}}}}{{{P}_{CO}}{{p}_{{{H}_{2}}O}}}\(
\(~{{n}_{T}}=\sum\limits_{i=1}^{N}{{{n}_{i}}}=\left( 1-\eta \right)+\left( 2-\eta \right)+\eta +\eta =3\)
\({{X}_{CO}}=\frac{1-\eta }{3},{{X}_{{{H}_{2}}O}}=\frac{2-\eta }{3},{{X}_{C{{O}_{2}}}}={{X}_{{{H}_{2}}}}=\frac{\eta }{3}\(
\({{p}_{CO}}=\frac{1-\eta }{3}p,{{p}_{{{H}_{2}}O}}=\frac{2-\eta }{3}p,{{p}_{C{{O}_{2}}}}={{p}_{{{H}_{2}}}}=\frac{\eta }{3}p\(
所以
\({{K}_{P}}=\frac{{{(\frac{\eta }{3})}^{2}}{{p}^{2}}}{(\frac{1-\eta }{3})p(\frac{2-\eta }{3})p}=\frac{{{\eta }^{2}}}{(1-\eta )(2-\eta )}\(
Kp(Tf)可从有关表格中查出,则 可以求得,平衡成分也就知道了。
对于化学反应
\(C{{H}_{4}}+1.5{{O}_{2}}\to \left( 1-\eta \right)CO+\left( 2-\eta \right){{H}_{2}}O+\eta C{{O}_{2}}+\eta {{H}_{2}}\)
总焓方程为
此式可写成
例2.14 1 mol的N2和0.5mol的O2的混合物在1atm下被加热到4000K,得到只含有N2,O2和NO的平衡混合物。如果O2和N2的初始温度是298.16K,然后被稳定地加热,以最初的1molN2为准,试求将最终的混合物加热到400K所需的热量。
解 反应可写成
\(~{{N}_{2}}\text{ }+0.\text{ }5{{O}_{2}}\to a{{N}_{2}}\text{ }+b{{N}_{2}}+cNO\)
由原子组分守恒定律得
N2: 2a+c
O1: 2b+c
所以
a=0.5(2-c)=1-c/2
b=0.5(1-c)=-c/2
令c=x,可得
\(~~~{{N}_{2}}+0.5{{O}_{2}}\to \left( 1-\frac{x}{2} \right){{N}_{2}}+\left( \frac{1}{2}-\frac{x}{2} \right){{O}_{2}}+xNO\)
已知TI=298.16K,Tf=4000K,对于\(0.5{{N}_{2}}+0.5{{O}_{2}}NO\)的反应,Kp=0.29793≈0.3
有\(0.09=\frac{4{{x}^{2}}}{(2-x)(1-x)}\(或x2-3x+2=44.5×2,则43.5×2+3x-2=0。故
因此最终的混合物是
0.90875N2+0.40875O2+0.1825NO
可知
2.13有效压力和活性
G.n.Lewis于1901年提出了有效压力的概念它在区别真实气体的实际特性与理想气体的假想特性方面具有很大的价值,特别是在高压下。按照理想气体状态方程,在恒定温度下,一定质量的气体,其压强与体积的乘积p为恒值而与压强p的量值无关。这时在p-V图上画出的等温线是等轴双曲线,但这与实验事实并不一致,而且可能会有很大的差别。例如对于氮气,在273K,100MPa下,偏差可能达100,其他气体也有类似现象。
对于恒定温度下的理想气体
\(dG=n{{R}_{u}}Td\left( \text{ln }p \right)\) (2-138)
对于不具有理想特性的气体,上面的方程不能成立,但可以定义一个叫作有效压力的函数f,无论是否理想气体,都能满足下述关系式:
\(~dG=\text{n}{{\text{R}}_{u}}Td\text{ }\left( \ln f \right)\) (2-139)
对式(2-139)积分得
\({{G}_{2}}-{{G}_{1}}=n{{R}_{u}}T\ln \frac{{{f}_{2}}}{{{f}_{1}}}\) (2-140)
在这方面,有效压力可以看成是修正后的分压
\({{f}_{i}}/{{p}_{i}}=\Gamma \)(比例常数) (2-141)
式中 是许多参数(例如温度和压力)的函数。对于理想气体
f/p=1 (2-142)
随着实际气体的压力降低,其特性就接近于理想气体,所以处于很低压力下的气体常被选取为基准状态,并假定比值f/p接近1,即
\(~\underset{p\to 0}{\mathop{lim}}\,f/p=1\) (2-143)
这里f具有压力的单位。
在温度为T的等温方程中,有效压力可按下式由压缩因子Z和压力p确定:
\(Z\cdot d{{\left( \ln p \right)}_{T}}=d{{(\ln f)}_{T}}~~\) (2-144)
在恒定温度下,从p=0到某一有限的压力对式(2-144)积分,得
\(~\ln \text{ }f/p=\int_{0}^{pT}{\left( Z-1 \right)d\text{ }{{\left( \ln {{p}_{T}} \right)}_{T}}}\) (2-145)
在任何温度下,式(2-145)右边可以进行图解积分,利用通用压缩性图表查得对应每个较小压力pT的Z,从而求出f的值。
习 题
2.1简述热力学第一定律。
2.2简述热力学第二定律。
2.3简述热力学第三定律。
2.4分析定容过程与定压过程的差异。
2.5简述 Clausius不等式。
2.6对于气体化学反应,平衡准则有哪些?
2.7推导等温过程化学反应平衡常数表达式。
2.8化学反应的绝热火焰温度如何计算?