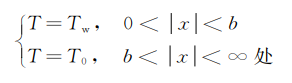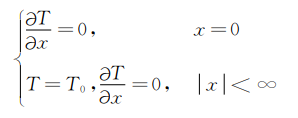第5章预混可燃气着火

着火是燃料由未反应状态到达反应状态的过渡过程,在此过程中,由于外部的激发引起热化学的急剧变化,然后迅速地过渡到自持燃烧过程。

 研究着火是为了对这个过渡过程中详细的物理化学过程有所认识研究着火的基本目的包括:

(1)防止火灾。

(2)为燃料的着火和燃烧设计点火器和能再生的能源。

(3)研究在一定的初始条件下输入一定能量时物质的着火性能。

(4)确定最小点火能。

(5)研究各种物理和化学参数对着火的影响。

一般来说,影响着火的因素很多,如混合物成分及浓度、压力、增压速率、加热的持续时间、系统积存的能量、环境温度、对流速度、湍流尺度和强度、被加热物质的热力特性和输运特性、化剂、抑制剂等。

5.1着火的激发及装置

实现着火的方法很多,外部的激发大致分为如下三类:

(1)热激发:通过导热、对流、辐射或这些传热方式的任意组合对反应物传输热能。

(2)化学激发:引入自燃的易反应的媒介物。

 (3)机械激发:机械碰撞、摩擦或冲击波。

在工业应用和基础研究中常采用许多不同形式的点火装置,包括火花塞、热丝、电爆管、烟火点火器、高温点火器、喷射气流式自发点火装置、击发式点火剂等。此外,还有一些用于着火研究的各种装置,最常用的有振荡管、电弧聚焦炉、大功率CO2激光器、太阳能聚焦器、冲击试验机等。

 5.2着火概念

5.2.1燃烧现象分类

燃烧是一种复杂的物理化学过程,要使燃烧能够进行,首先要有燃料和氧化剂作为反应所 必需的物质。这两种物质还必须有一定的浓度,且通过混合互相接触才能反应。要使反应达到一定的速度,还必须有一定的环境温度而反应过程的放热和反应物的消耗又反过来影响燃烧速度,整个燃烧过程自始至终都受到传热传质的影响。

燃烧包括两个过程:

 (1)燃料和氧化剂混合:预混、流动和扩散。

(2)剧烈化学反应。

燃烧按控制因素分类:

 (1)主要受化学动力学控制;

(2)主要受扩散、流动等物理过程控制;

(3)化学动力学和流动混合过程都起相当的作用。

对于化学动力学控制的化学反应,反应物的混合速度大大超过化学反应的速度,燃烧过程所需时间主要是化学反应的时间。燃烧速度取决于化学反应速度,并由化学动力学因素控制。化学动力学控制的燃烧过程,简称动力燃烧。预混可燃气系统的着火爆炸、熄火等属于动力燃烧。对于扩散过程控制的化学反应,当反应物的混合速度大大小于化学反应速度时,燃烧过程所需时间主要是扩散混合时间,燃烧速度取决于燃料和氧化剂相互的扩散速度。扩散过程控制的燃烧过程简称扩散燃烧,如例如高温高压下,气体化学反应速度很快,但燃料和氧化剂的混合需要较长时间。实际上大多数燃烧都属于扩散燃烧:木柴燃烧、碳粒燃烧、蜡烛燃烧、油滴燃烧、煤气炉燃烧等。

对于化学动力学和扩散共同控制的化学反应,燃料和氧化剂混合流动等物理过程需要时间,化学反应也需要相当时间的过程。预混可燃气的燃烧属于此类。对任一种化学反应,到底由化学动力学控制还是由扩散过程控制达姆科勒(Damkohlor)提出了控制因素判定准则(Damkohlor第一准则):物理过程所需特征时间tph与化学过程所需时间tch之比。

\({{D}_{am1}}=\frac{{{t}_{ph}}}{{{t}_{ch}}}\) (5-1)
对扩散过程来说，tph为扩散时间，有
\({{t}_{ph}}=\frac{l}{D}\) (5-2a)
式中，为燃烧过程的特征长度;D为扩散系数。
对流动过程来说，可取流动时间为
\({{t}_{ph}}=\frac{l}{v}\)  (5-2b)
对化学反应来说，可取反应的半衰期为特征时间，即
\({{t}_{ch}}={{t}_{\frac{1}{2}}}\)  (5-3)
当Dam1≈0时，化学反应由动力学过程控制;当Dam1≈1化学反应由动力学过程和扩散过程共同控制;当\({{D}_{am1}}\gg 1\)化学反应由扩散过程控制。
5.2.2着火方式
依靠反应的热效应而实现着火的过程叫作热着火或热点燃。着火方式有多种，如热自燃和强制着火等。
热自燃是指预混气系统的初始条件达到一定水平依靠系统本身的反应生热而自行达到着火的。强制点燃是指从系统外引入一个点火能源，使预混气的局部反应速度迅速达到着火燃烧，并依靠局部燃烧的效应，使燃烧反应向预混气系统的其他部分传播出去。热自燃和强制点燃都需要一定的外加能源。对于热自燃，必使系统达到一定的初温，这就是外加能源的作用。
此外，还存在化学链着火。对于一个化学反应，化学反应速度急剧增加，除了温度的影响以外，还可以借助于链反应中链载体的增加来实现，这就是化学链着火。
5.3热自燃
5.3.1热自燃临界条件
研究对象如下:密闭容器内充满预混的可燃气体，压力为p，温度为T，混合物因有化学反应而放热，热量通过容器壁传至环境。因此，在一般情况下，整个容器内的温度既随空间位置变化，又随时间变化。
作如下假定:
(1)容器内温度、浓度都均匀分布，只有容器壁有温差;
(2)整个容器内气体反应放热率为Qg；
(3)整个器壁表面的散热率为Q1。
该体系能量方程如下：
\(\rho V{{C}_{V}}\frac{dT}{dt}={{Q}_{g}}-{{Q}_{1}}\)  (5-4)
式中V为容器体积;Cv为气体的定容比热。
假设气体混合物在容器内进行n级反应，其反应速度为
\(\omega =ZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{T}}}}}\)  (5-5)
式中，Z为指前因子;CA为预混可燃气浓度。
容器内气体反应放热率Qg。和器壁表面的散热率Q1分别为
\({{Q}_{g}}=V\omega \Delta H=V\Delta HZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{T}}}}}\)      (5-6)
\({{Q}_{1}}=hS(T-{{T}_{0}})\)     (5-7)
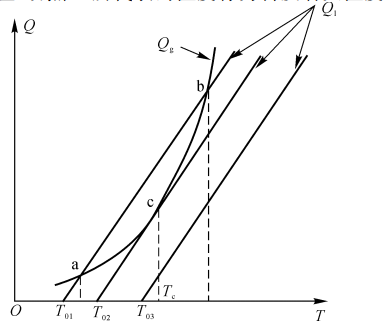
式中，△H为单位质量燃料燃烧热;S为容器表面积;h为换热系数， 为质量反应速率。如图5-1所示，显然，Q随T增加而指数关系增加Q随T增加而线性增加。当两条线相切时，可达到热自燃的临界值，切点C所代表的温度称为自发着火温度。

图5-1着火过程中热平衡示意图
热自燃的临界条件是
\({{\left( {{Q}_{g}} \right)}_{C}}={{\left( {{Q}_{1}} \right)}_{C}}\) (5-8)
\({{\left( \frac{d{{Q}_{g}}}{dT} \right)}_{C}}={{\left( \frac{d{{Q}_{1}}}{dT} \right)}_{C}}\)  (5-9)
可另写成
\(V\Delta HZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{TC}}}}}=hS({{T}_{C}}-{{T}_{0C}})\)   (5-10)
\(V\Delta HZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{TC}}}}}(\frac{E}{{{R}_{0}}T_{C}^{2}})=hS\)   (5-11)
可见，达到热自燃的措施有
(1)提高初始温度;
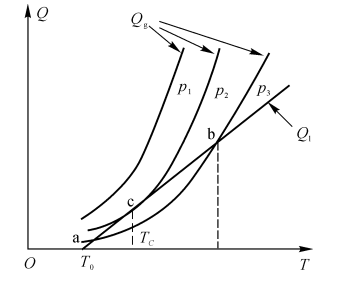
(2)增加气压，以提高浓度CA，提高Qg(见图5-2);
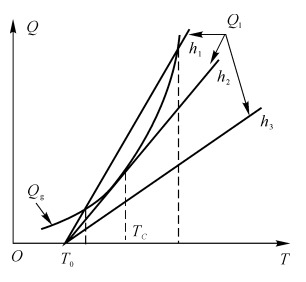
(3)改善系统绝热条件，降低换热系数h，降低Q1(见图5-3)。

图5-2着火时热平衡分析示意图

 

图5-3着火时热平衡分析示意图
5.3.2谢苗诺夫方程
1.自发着火温度和着火临界壁温的关系
用式(5-11)除以式(5-10)可得
\(\frac{{{R}_{0}}T_{C}^{2}}{E}={{T}_{C}}-{{T}_{0C}}\) 
从而有
\({{T}_{C}}=\frac{1-\sqrt{1-\frac{4{{R}_{0}}{{T}_{0C}}}{E}}}{\frac{2{{R}_{0}}}{E}}\)       (5-12)
由于\(\frac{4{{R}_{0}}{{T}_{0C}}}{E}\) 很小，可得
\(\sqrt{1-\frac{4{{R}_{0}}{{T}_{0C}}}{E}}=1-\frac{\frac{4{{R}_{0}}{{T}_{0C}}}{E}}{2}-\frac{{{(\frac{4{{R}_{0}}{{T}_{0C}}}{E})}^{2}}}{8}-\cdots \) (5-13)
将式(5-13)代入式(5-12)，得
\({{T}_{C}}=\frac{\frac{2{{R}_{0}}{{T}_{0C}}}{E}+2{{(\frac{{{R}_{0}}{{T}_{0C}}}{E})}^{2}}+\cdots }{\frac{2{{R}_{0}}}{E}}\) 
略去\(\frac{{{R}_{0}}{{T}_{0C}}}{E}\(的高次项，得
\({{T}_{C}}\approx {{T}_{0C}}+\frac{{{R}_{0}}T_{0C}^{2}}{E}\)     (5-14)
式中，Tc为自发着火温度;Tc为着火临界壁温。
显然，自发着火前的温升为
\(\Delta {{T}_{C}}={{T}_{C}}-{{T}_{0C}}=\frac{{{R}_{0}}T_{0C}^{2}}{E}\) (5-15)
当活化能为30~60kcal/mol，Toc为700K时Tc和Toc只相差约33K，这说明:用自发着火的临界壁温代替自发着火温度所引起的误差很小。
2.谢苗诺夫方程热自燃条件
作如下假定:
(1)用Toc代替Tc或Toc≈Tc;
(2)假定气体为完全气体。
代入点火条件式(5-11)，得
\(\Delta HVZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{0}}{{T}_{0C}}}}}(\frac{E}{{{R}_{0}}T_{0C}^{2}})=hS\)  (5-16)
假定气体为完全气体，且T0C≈TC，从而有
\({{C}_{A}}=\frac{{{P}_{AC}}}{{{R}_{0}}{{T}_{0C}}}={{X}_{AC}}\frac{{{P}_{C}}}{{{R}_{0}}{{T}_{0C}}}\)  (5-17)
将式(5-17)代入式(5-16)，得
\(\frac{\Delta HVZE}{{{R}_{0}}hST_{0C}^{2}}{{\left( \frac{{{X}_{AC}}{{P}_{C}}}{{{R}_{0}}{{T}_{0C}}} \right)}^{n}}{{e}^{-\frac{E}{{{R}_{0}}{{T}_{0C}}}}}=1\) 
或
\(\frac{P_{C}^{n}}{T_{0C}^{n+2}}=\frac{hSR_{0}^{n+1}}{\Delta HVZ{{X}^{n}}E}{{e}^{\frac{E}{{{R}_{0}}{{T}_{0C}}}}}\)    (5-18)
将式(5-18)取对数得
\(\ln \frac{P_{C}^{n}}{T_{0C}^{1+\frac{2}{n}}}=\frac{E}{{{R}_{0}}{{T}_{0C}}}+\ln {{(\frac{hSR_{0}^{n+1}}{\Delta HVZ{{X}^{n}}E})}^{\frac{1}{n}}}\)  (5-19)
当n=1时
\(\ln \frac{{{P}_{C}}}{T_{0C}^{3}}=\frac{E}{{{R}_{0}}{{T}_{0C}}}+\ln (\frac{hSR_{0}^{2}}{\Delta HVZ{{X}_{AC}}E})\)  (5-20)
当n=2时
\(\ln \frac{{{P}_{C}}}{T_{0C}^{2}}=\frac{E}{2{{R}_{0}}{{T}_{0C}}}+\ln {{(\frac{hSR_{0}^{3}}{\Delta HVZX_{AC}^{2}E})}^{\frac{1}{2}}}\)  (5-21)
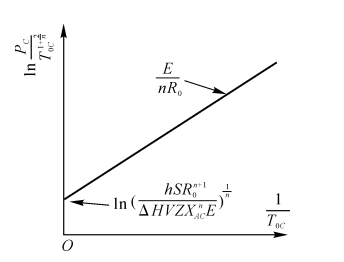
如图5-4所示，\(\ln \frac{{{P}_{C}}}{T_{0C}^{1+\frac{2}{n}}}\)为纵坐标，\(\frac{1}{{{T}_{0C}}}\)为横坐标，式(5-19)为一直线，斜率为\(\frac{E}{n{{R}_{0}}}\)。自发着火条件下PC与TOC的关系如图5-5所示。

图5-4系统达到热自燃地临界条件

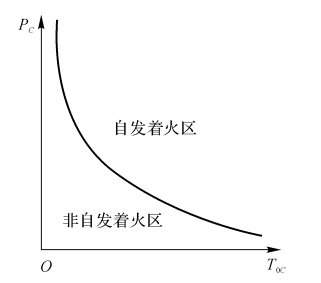
图5-5自发着火条件下Pc与Tx的关系

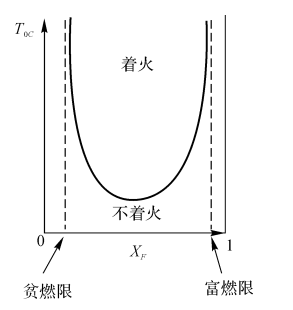
图5-6自发着火条件下T与XF的关系

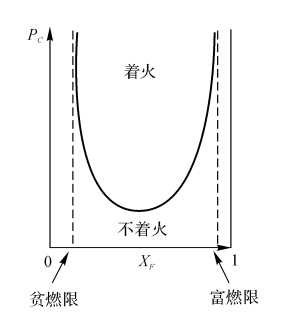
图 5-7自发着火条件下P与X的关系
在TOC-XF和PC-XF曲线中(见图5-6、图57)，能实现着火的都在U形区域内显然，为了实现着火，燃料的浓度XF有其低限和高限。
温度越低或者压力越低，XF可着火区间范围就越窄。
5.4着火延迟期
谢苗诺夫明确地提出了热自燃的临界条件，对热自燃前后系统经历的过程没有做过分析。为了了解系统在着火前后的变化，特别是为了研究着火延迟(着火所经历的时间)，必须进一步分析系统状态随时间的变化，这就是点火过程的非定常分析。
非定常分析所做的基本假设与谢苗诺夫热自燃理论是相同的，其出发点仍是分析热平衡的能量方程:
\(\frac{dT}{dt}=\frac{\Delta H}{\rho {{C}_{V}}}ZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{0}}T}}}-\frac{hS}{\rho V{{C}_{V}}}(T-{{T}_{0}})\)  (5-22)
令△T=T-T0，它是着火前的温升，一般可以认为比T0小得多，即\(\Delta T\ll {{T}_{0}}\)，有
\(\frac{E}{{{R}_{0}}T}=\frac{E}{{{R}_{0}}}(\frac{1}{{{T}_{0}}+\Delta T})\approx \frac{E}{{{R}_{0}}{{T}_{0}}}-\frac{E}{{{R}_{0}}T_{0}^{2}}\Delta T\)  (5-23)
引入无因次温升
\(\theta =\frac{E}{{{R}_{0}}T_{0}^{2}}(T-{{T}_{0}})\)   (5-24)
则式(5-22)变为
\(\frac{d\theta }{dt}=\frac{\Delta H}{\rho {{C}_{V}}}ZC_{A}^{n}\frac{E}{{{R}_{0}}T_{0}^{2}}{{e}^{-\frac{E}{{{R}_{0}}{{T}_{0}}}}}{{e}^{\theta }}-\frac{hS}{\rho V{{C}_{V}}}\theta \)    (5-25)
初始条件当t=0，有T=T0，即\(\theta ={{\theta }_{0}}\)
\({{\tau }_{1}}={{\left( \frac{\Delta H}{\rho {{C}_{V}}}ZC_{A}^{n}\frac{E}{{{R}_{0}}T_{0}^{2}}{{e}^{-\frac{E}{{{R}_{0}}{{T}_{0}}}}} \right)}^{-1}}\)  (5-26)
\({{\tau }_{2}}={{\left( \frac{hS}{\rho V{{C}_{V}}} \right)}^{\text{-1}}}\)  (5-27)
方程式(5-25)写成
\(\frac{d\theta }{dt}=\frac{{{e}^{\theta }}}{{{\tau }_{1}}}-\frac{\theta }{{{\tau }_{2}}}\)   (5-28)
经量纲分析可知\({{\tau }_{1}},{{\tau }_{2}}\)的量纲都是时间，\({{\tau }_{1}}\)代表反应生成热的特征时间，\({{\tau }_{2}}\)代表表面散热的特征时间。引入无因次时间\(\varphi =\frac{t}{{{\tau }_{1}}}\)，则方程式(5-28)又可化为
\(\frac{d\theta }{d\varphi }={{e}^{\theta }}-\frac{{{\tau }_{1}}}{{{\tau }_{2}}}\theta \) (5-29)
可见，方程式(5-29)的解必为
\(\theta =f(\varphi ,\frac{{{\tau }_{1}}}{{{\tau }_{2}}})\) (5-30)
从式(5-30)可以看出，在无因次温度无因次时间的关系中，只有一个无因次参数\({{{\tau }_{1}}}/{{{\tau }_{2}}}\;\)，因而\({{{\tau }_{1}}}/{{{\tau }_{2}}}\;\)的数值便决定了系统是否发生着火。从直观上看，\({{{\tau }_{1}}}/{{{\tau }_{2}}}\;\)代表反应生成热的特征时间与表面散热的特征时间之比，当这个比值越来越小时，则说明反应的放热量越来越大于散热量，从而导致着火点燃。当这个比值越来越大时，则意味着散热量相对于反应加热量逐渐增大，使预混可燃气处于一个稳定的温度，不发生着火。因此，有关着火的临界条件必定相应于\({{{\tau }_{1}}}/{{{\tau }_{2}}}\;\)处在某一特定值上，即\({{{\tau }_{1}}}/{{{\tau }_{2}}}\;\)等于定值。这个关系是由托杰士首先得到的。
如果此定值为\({{{\tau }_{1}}}/{{{\tau }_{2}}}\;\)，即可得到谢苗诺夫有关热自燃的临界条件
下面讨论系统达到着火所需要的时间，即着火感应期。
在自发着火的条件下，方程式(5-29)右边第一项比第二项大得多这时方程(5-29)可化为
\(\frac{d\theta }{d\varphi }={{e}^{\theta }}\) (5-31)
初始条件为t=0或\(\varphi =0\)时，\(\theta =0\)。
这种条件下的热自燃称为绝热热自燃(散热特征时间无限长)，又称为绝热热爆炸。既然达到着火条件发生即意味着θ达到一定值，或\({d\theta }/{d\varphi }\;\) 达到一定值，此定值必然对应一个无量纲时间值。由此条件可求得\({{\varphi }_{i}}\)值对应的时间，即着火延迟或着火感应期用ti表示。由于这是在绝热条件下求得的，因此又把ti称为绝热着火感应期。
为求出t，可对方程式(5-31)积分，得
\(\varphi =1-{{e}^{-\theta }}\)   (5-32)
注意到自发着火的临界温度为TC，临界壁温为T0C，相应的温升为\({{T}_{C}}-{{T}_{0C}}\approx \frac{{{R}_{0}}T_{0C}^{2}}{E}\)，由 的定义可得到着火时，\({{\theta }_{i}}=1\)。因此由式(5-32)可得
\({{\varphi }_{i}}=1-{{e}^{-1}}\) (5-33)
\({{t}_{i}}={{\tau }_{1}}{{\varphi }_{i}}={{\tau }_{1}}(1-{{e}^{-1}})\) (5-34)
此结果是由弗兰克-卡明涅茨基求出的。托杰士利用不同的数学方法求解绝热条件下的点火延迟，他没有利用式(5-23)的近似关系，而是从式(5-21)中略去散热项之后，直接进行积分计算，得到着火感应期为
\({{t}_{i}}={{\tau }_{1}}=\frac{\rho {{C}_{V}}}{\Delta H}\frac{{{R}_{0}}T_{0}^{2}}{E}\frac{1}{ZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{0}}{{T}_{0}}}}}}\) (5-35)
式(5-34)和式(5-35)相差一个因子(1e)，但是t正比于t是共同的，因此常用式(5-35)表示着火感应期。从式(5-35)可以知道:
(1)混合物的比热小，燃烧热值高，初始反应速度大都会使着火感应期变短。
(2)压力的影响也是很清楚的，因为CACP因此tP由于燃烧反应通常是二级的，压力越高，则点火延迟越短。
(3)初温的影响，除了To，还通过CA和p对t产生影响。
由式(5-35)可知:
\({{t}_{i}}\propto T_{0}^{n+1}{{e}^{\frac{E}{{{R}_{0}}{{T}_{0}}}}}\) (5-36)
通常反应级数n=2，\(T_{0}^{n+1}\) 的影响不如\({{e}^{\frac{E}{{{R}_{0}}{{T}_{0}}}}}\)大，主要影响在指数项上，随着T0的增加，点火延迟缩短。
5.5强制着火
强制着火是指利用外部热源对冷的预混可燃气进行局部快速加热，邻近热源的可燃气因温度升高而反应加快、开始着火，火焰在预混气中向其他部分传播。
强制着火一般包括两阶段:
(1)局部加热，局部着火;
(2)火焰传播。
5.5.1热体点燃
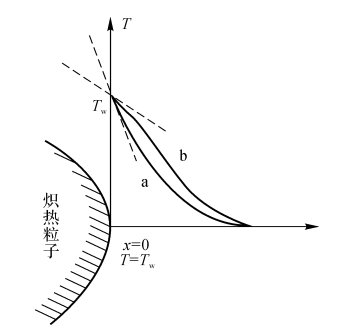
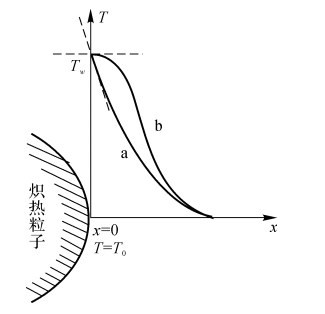
将加热了的高温物体放入预混气中进行强制点燃(见图5-8)。
(1)在X=0处，可燃气的温度梯度比惰性气体的温度梯度小因为可燃气受热发生化学反应，温度的提升有两方面原因;惰性气体温升仅靠热体加热。
(2)在X=0处，当可燃气的温度梯度为零时热体附近的预混可燃气反应速度达到一个临界状态。此时，只要热体的温度比TC稍高一点，热体附近预混气的反应速度就会有突跃性的急剧增加，即着火发生。
(3)泽尔多维奇把预混可燃气中热体(点火源)表面法线方向上的温度梯度达到零作为强制着火的判据:

(4)什么情况下能促成点火呢?

图5-8炽热粒子附近的温度分布
a-惰性气体;b-预混可燃气
实验表明:用一定的热体来点燃一定的预混可燃气，有一个最低的临界温度TC。当热体的温度Tw高于其临界温度TC时，则预混可燃气的着火是可能的。用石英或铂制的热球的实验结果表明:球的临界温度取决于球的尺寸、催化性质、射入速度、预混可燃气的热化学和动力学等参数。若紧靠热球的可燃气体层中，化学反应产生的热量超过该层中散失的热量，则认为着火是能保证的。其着火的临界准则可推断如下:
在球体周围的一个厚度为 的薄层内，假定温度从球的表面温度TW线性地下降至预混气的初温T0，厚度 与球的运动速度直径、流体的黏度以及热力学性质有关。在厚度 层内发生反应的气体体积近似为 球的散热面积是4r2。假设散热是以热传导的方式进行的且化学反应速度符合阿累尼乌斯定律，则只要
\(\Delta H4\pi {{r}^{2}}\delta ZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{0}}{{T}_{w}}}}}\ge 4\pi {{r}^{2}}\lambda \frac{{{T}_{w}}-{{T}_{0}}}{\delta }\)     (5-38)
即可方式着火。
此处，假定反应物的消耗量忽略不计，对式5-38)进行简化，得到
\(\frac{{{T}_{w}}-{{T}_{0}}}{\delta }\le \frac{\Delta H\delta ZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{0}}{{T}_{w}}}}}}{\lambda }\)  (5-39)
当Tw等于临界值TC时，式(5-39)取等号。该式说明在反应层内的温度梯度是控制着火发生的重要因素。厚度δ越大，越有利于着火点燃。
实验证明：球的尺寸越大，射入速度越低，则临界温度TC越低，即越容易着火
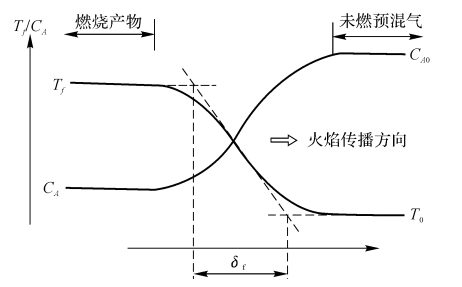
(5)预混气在热体附近组分的浓度分布，如图5-10所示。
(6)火焰速度:火焰前锋的法向传播速度。
(7)火焰厚度:定义为最大温差与最大温度梯度之比，即
\({{\delta }_{f}}=\frac{{{T}_{f}}-{{T}_{0}}}{{{(\frac{dT}{dx})}_{\max }}}\)   (5-40)
若 是整个火焰厚度 内的平均反应速度，产生的热量为
\({{Q}_{g}}\approx \Delta H\bar{\omega }{{\delta }_{f}}A\)  (5-41)
式中，\({{\delta }_{f}}A\(为火焰区体积；A是火焰的横截面积。导热量近似为
\({{Q}_{k}}=\lambda A({{T}_{f}}-{{T}_{0}})\frac{1}{{{\delta }_{f}}}\)  (5-42)

图5-9临界状态时粒子附近温度分布
a一惰性气体;b一预混可燃气

图5-10火焰前沿传播现象
将单位质量的未燃气体从温度T0升高到Tf需要的热量是C(Tf-T0)若\({{\rho }_{0}}\)是未燃气体密度，则单位时间中受到加热的质量是\({{\rho }_{0}}{{V}_{0}}A\)，其得到的热量是
\({{Q}_{h}}={{\rho }_{0}}{{V}_{0}}AC({{T}_{f}}-{{T}_{0}})\) (5-43)
令Qg=Qk，得
\({{\delta }_{f}}={{\left( \frac{\lambda ({{T}_{f}}-{{T}_{0}})}{\Delta H\bar{\omega }} \right)}^{\frac{1}{2}}}\)    (5-44)
式(5-44)说明，当导热系数入与温差(TT)比较大，反应产生得热量比较少时，火焰厚度就比较大。
另外，令Qk=Qh，注意到热扩散率\({{a}_{0}}=\frac{\lambda }{{{\rho }_{0}}C}\)就得到了的另一种表达形式用以说明热扩散和火焰传播速度的关系:
\({{\delta }_{f}}=\frac{{{a}_{0}}}{{{V}_{0}}}\)       (5-45)
令Qg=Qh，得
\({{\delta }_{f}}\approx \frac{{{\rho }_{0}}{{V}_{0}}C({{T}_{f}}-{{T}_{0}})}{\Delta H\omega }\) (5-46)
可得
\({{V}_{0}}\approx \frac{1}{{{\rho }_{0}}C}{{\left( \frac{\lambda \Delta H\bar{\omega }}{{{T}_{f}}-{{T}_{0}}} \right)}^{\frac{1}{2}}}\approx {{\left( \frac{\lambda \bar{\omega }}{{{\rho }_{0}}C{{C}_{A0}}} \right)}^{\frac{1}{2}}}\) (5-47)
其中，使用了\({{\rho }_{0}}C({{T}_{f}}-{{T}_{0}})={{C}_{A0}}\Delta H\)，即单位体积内燃料的全部燃烧热用来把单位体积内的反应物和生成物从T0升高到Tf，CA0为燃料初始浓度。
由于热传导、比热、燃烧热与总的压力无关，因此
\({{V}_{0}}\propto {{\bar{\omega }}^{\frac{1}{2}}}{{\rho }_{0}}^{-1}\) (5-48)
一个n级反应的平均反应速度\(\bar{\omega }\(与总的压力的n次方成正比，因此
\({{V}_{0}}\propto {{P}^{\frac{n}{2}-1}}={{P}^{\frac{n-2}{2}}}\) (5-49)
5.5.2火焰点火
点燃预混可燃气所需的能量，可以通过一个小火焰来提供。着火的可能性取决于混合物的成分、小火焰和混合物之间的接触时间、小火焰的温度和尺寸。
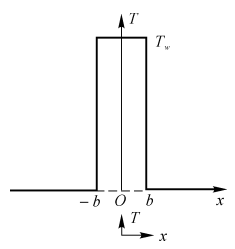
设有一个无限长的片形火焰，其温度为Tw，厚度为2b(实际上，小火焰的尺寸是三维的，有限长的，此处选取一无限长、厚度为2b的薄片，目的是使数学分析简化为一维问题，取得的结果可以推广到二维或三维的小尺寸火焰中)(见图5-11)。
如果时间t=0时，把片形火焰放入温度为T0的可燃混合气中，并假设没有流动的影响，则瞬态能量守恒方程为
\(\rho C\frac{\partial T}{\partial t}=\lambda \frac{{{\partial }^{2}}T}{{{\partial }^{2}}x}+\Delta HZC_{A}^{n}{{e}^{-\frac{E}{{{R}_{0}}T}}}\) (5-50)
受此方程控制，混合气中的温度是随时间和位置而变化的，方程的初始条件和边界条件为
t≤0时

t>0时

图5-11片形火焰温度分布    

               

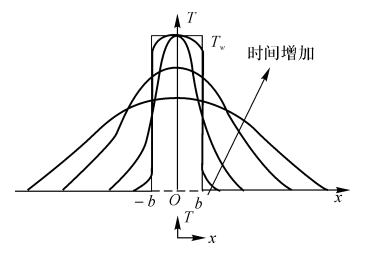
图5-12片形火焰温度随时间变化
当没有化学反应热源项 时，方程式(5-76)的解析解是
\(\frac{T-{{T}_{0}}}{{{T}_{w}}-{{T}_{0}}}=\frac{1}{2}\left( erf(\frac{b-x}{2\sqrt{at}})+erf(\frac{b+x}{2\sqrt{at}}) \right)\) (5-51)
式中，\(a=\frac{\lambda }{\rho C},erf(\varphi )\) 为误差函数，其定义为
\(erf(\varphi )=\frac{2}{\sqrt{\pi }}\int_{0}^{\varphi }{{{e}^{-{{\eta }^{2}}}}}d\eta \) (5-52)
此解析解描述了温度随时间和空间的变化图5-12定性地表示了这种变化。
如果有化学反应热源项，求解解析解是不可能的，只能求数值解。图5-12可以说明，在一开始，化学反应项确实是可以忽略的，到最后，温度分布随时间趋于平缓。现在有两种情况:
(1)原始片形火焰的厚度小于某一临界尺寸，温度分布就连续f衰减，直至火焰熄灭。
(2)火焰的厚度大于临界尺寸，放热反应使火焰能向冷的预混可燃气中传播。火焰的临界厚度大约是稳定传播的火焰区厚度δ的两倍。
\({{b}_{C}}={{\delta }_{f}}\)   (5-53)
可得
\({{b}_{C}}\approx {{\delta }_{f}}\approx \frac{{{a}_{0}}}{{{v}_{0}}}\approx {{\left( \frac{\lambda ({{T}_{f}}-{{T}_{0}})}{\Delta H\bar{\omega }} \right)}^{\frac{1}{2}}}\)    (5-54)
式(5-54)表明，要使导热系数大、火焰温度高的预混气着火，必须要求一较厚的火焰。要是平均放热速度(\(\Delta H\bar{\omega }\))大，则火焰的临界厚度可以比较小。更进一步看到，因为热扩散率a与密度成反比，而\({{v}_{0}}\propto {{P}^{\frac{n-2}{2}}}\)，所以
\({{b}_{C}}\propto \frac{1}{{{\rho }_{\text{0}}}{{v}_{0}}}\propto {{P}^{-\frac{n}{2}}}\)   (5-55)
所以，在压力较高时，火焰的临界厚度比较小如果是二级反应，则\({{b}_{C}}\propto {{P}^{-1}}\) 
5.6自动催化着火
除了普通热着火，还存在自动催化着火。两者差异如下:
(1)普通热着火:系统反应产生的热量大于系统向环境散失的热量。正是这种热量的积累使反应物温度不断增加，反应速度加快，样又放出更多的热量，使反应速度更加增加。这种热量、温度和反应速度之间的依次放大，最终导致着火发生。
(2)自动催化着火:反应温度不变，反应速度一开始就随着生成物浓度增大而加快。这样的反应被称为自动催化反应。其反应速度为
\(-\frac{d{{c}_{A}}}{dt}=Zc_{A}^{n-m}c_{p}^{j}{{e}^{-\frac{E}{{{R}_{T}}}}}\) (5-56)
式中，\({{c}_{p}}\)为生成物浓度；\({{c}_{A}}\)为反应物浓度。在反应开始时，\({{c}_{p}}=0\)，因此反应速度等于零。为了引起自动催化反应，需要通过某些外部手段产生一些初始的、起催化作用的生成物。当反应产生出足够数量的起催化作用的生成物时，热的化学反应速度就会在催化项和温度加速项\({{e}^{-\frac{E}{{{R}_{T}}}}}\)的综合影响下得到加速。
自动催化反应速度受如下两者的影响:①催化项;②温度加速项。
自动催化着火与热自燃具有同样的着火判据。在着火时，反应产生热量的速度超过散热损失的速度。因此谢苗诺夫着火判据或弗兰克卡门涅茨基着火判据同样适用于自动催化着火，只不过要用\(Zc_{A}^{n-m}c_{p}^{j}{{e}^{-\frac{E}{{{R}_{T}}}}}\)代替原来判据中\(Zc_{A}^{n}{{e}^{-\frac{E}{{{R}_{T}}}}}\)但是自动催化着火的感应期比热自燃着火的感应期要长得多。其原因在于:自燃着火中，反应一开始就以很大的速度进行，其感应期是把可燃混合物加热到着火临界温度所需要的时间。而自动催化着火中，其感应期包括两个阶段:第一阶段，反应混合物通过缓慢的反应加热来产生足够的起催化作用的生成物，温度基本是一常数第二阶段与热自燃着火是相同的，即加速反应放热使反应混合物的温度达到着火温度。第二阶段所用的时间与第一阶段相比，是很小的数值，因此可以认为感应期是第一阶段所用的时间。
习   题
5.1简述着火种类或方式。
5.2作图分析谢苗诺夫热自燃的临界条件。
5.3写出泽尔多维奇热体强制着火判据。
5.4推导非定常条件下着火延迟期表达式。
5.5写出火焰厚度表达式。
5.6分析催化着火与普通着火的差异。