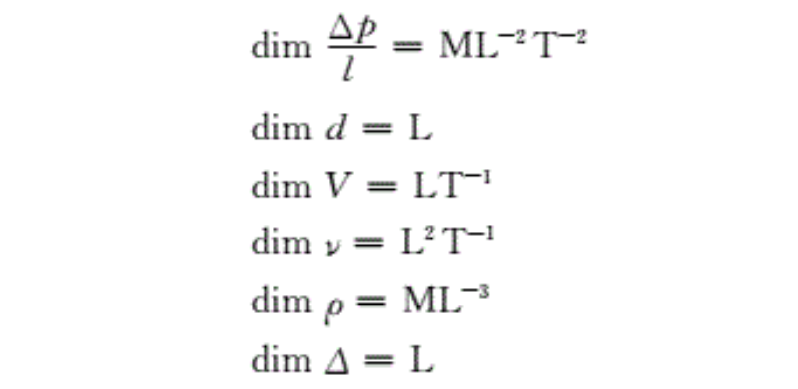第十一章 相似原理及量纲分析

任何流体力学问题的解决不外乎用理论或实验两种方法。在理论方法中，仅极少数简单流动问题可以通过数学分析方法求得解析解，而大部分流动问题只能进行数值求解。然而不管是解析解还是数值解，都需要预先知道主导待求问题的控制方程，这一点对于许多复杂的现象，特别是对于原本就不清楚的未知现象往往是不可能的。这就必须依靠实验方法，即通过实验获取的大量数据研究这类流动问题的内在规律。

任何一个物理现象往往有许多影响因素，要研究每一个因素对这一现象的影响，需要进行大量的实验，有时简直是不可能的。是否存在一种简单的方法使得只进行少量的实验就可达到对流动现象的本质认识呢？本章介绍的相似原理及量纲分析就是指导实验的理论基础。

由于许多流体力学问题很难用数学方法去解决，必须通过实验来研究。然而直接实验方法有很大的局限性，其实验结果只适用于某些特定条件，并不具有普遍意义，因而即使花费巨大，也很难能揭示现象的物理本质，并描述其中各量之间的规律性关系。还有许多流动现象不宜进行直接实验，例如飞机太大，不能在风洞中直接研究飞机原型的飞行问題；而昆虫的原型又太小，也不宜在风洞中直接进行吹风实验；况且，直接实验方法往往只能得出个别量之间的规律性关系，难以抓住现象的本质。我们更希望用缩小的飞机模型或放大的昆虫模型进行研究。那么，最关心的问题就是，从模型的实验结果所描述的物理现象能否真实再现原型的流动现象呢？如果要使从模型实验中得到的精确的定量数据能够准确代表对应原型的流动现象，就必须在模型和原型之间满足下述的相似性。

11.1.1  相似概念

相似是指组成模型的每个要素必须与原型的对应要素相似，包括几何要素和物理要素，其具体体现为由一系列物理量组成的场对应相似。对于同一个物理过程，若两个物理现象的各个物理量在各对应点上以及各对应瞬间大小成比例，且各矢量的对应方向一致，则称这两个物理现象相似。在流动现象中若两种流动相似，一般应满足下述条件。

1.几何相似

几何相似是指模型与其原型形状相同，但尺寸可以不同，而一切对应的线性尺寸成比例，这里的线性尺寸可以是直径、长度及粗糙度等。如果用下标p和m分别代表原型和模型，则

线性比例常数                              \({{C}_{l}}=\frac{{{l}_{p}}}{{{l}_{m}}}\)                (11.1)

面积比例常数                              \({{C}_{A}}=\frac{{{A}_{p}}}{{{A}_{m}}}=\frac{l_{p}^{2}}{l_{m}^{2}}=C_{l}^{2}\)                (11.2)

体积比例常数                              \({{C}_{v}}=\frac{{{v}_{p}}}{{{v}_{m}}}=\frac{l_{p}^{3}}{l_{m}^{3}}=C_{l}^{3}\)                (11.3)

2.运动相似

运动相似是指对不同的流动现象，在流场中的所有对应点处对应的速度和加速度的方向一致，且比值相等，也就是说，两个运动相似的流动，其流线和流谱是几何相似的。

速度比例常数                                 \({{C}_{V}}=\frac{{{V}_{p}}}{{{V}_{m}}}\)              (11.4)

由于时间的量纲是l（长度）/V（速度），因此时间比例常数为

\({{C}_{t}}=\frac{{{t}_{p}}}{{{t}_{m}}}=\frac{{{l}_{p}}/{{V}_{p}}}{{{l}_{m}}/{{V}_{m}}}=\frac{{{C}_{l}}}{{{C}_{V}}}\)                (11.5)

由此加速度比例常数                                     \({{C}_{a}}=\frac{{{a}_{p}}}{{{a}_{m}}}=\frac{{{V}_{p}}/{{t}_{p}}}{{{V}_{m}}/{{t}_{m}}}=\frac{{{C}_{V}}}{{{C}_{t}}}=\frac{C_{V}^{2}}{{{C}_{l}}}\)             (11.6)

3.动力相似

动力相似即对不同的流动现象，作用在流体上相应位置处的各种力，如重力、压力、黏性力和弹性力等，它们的方向对应相同，且对应量大小的比值相等，也就是说，两个动力相似的流动，作用在流体上相应位置处各力组成的力多边形是几何相似的。

一般地说，作用在流体微元上的力有重力（FG）、压力（Fp）、黏性力（FV）、弹性力（FE）和表面张力（FT）。如果流体是作加（减）速运动，则加上惯性力（F1）后，上述各力就会组成一个力多边形，因此，

\({{F}_{G}}+{{F}_{P}}+{{F}_{v}}+{{F}_{E}}+{{F}_{T}}+{{F}_{1}}=0\)

或者                                                   \({{F}_{1}}=-\left( {{F}_{G}}+{{F}_{P}}+{{F}_{v}}+{{F}_{E}}+{{F}_{T}} \right)=-\sum F\)

这些力可以简单表示为

重力                                                   \({{F}_{G}}=mg=\rho {{l}^{3}}g\)

压力                                                   \({{F}_{P}}=pA=p{{l}^{2}}\)

黏性力                                                   \({{F}_{v}}=\mu \left( \frac{dV}{dy} \right)A=\mu \left( \frac{V}{l} \right){{l}^{2}}=\mu Vl\)

弹性力                                                   \({{F}_{E}}=EA=E{{l}^{2}}\)

式中，E为弹性模量，且E=ρdp/dρ，而dp/dρ=c²，这里c是声速，代入上式，因此有

\({{F}_{E}}=E{{l}^{2}}=\rho {{l}^{2}}{{c}^{2}}\)

表面张力                                                   \({{F}_{T}}=\sigma l\)

惯性力                                                   \({{F}_{1}}=ma=\rho {{l}^{3}}\frac{l}{{{T}^{2}}}=\rho {{l}^{4}}{{T}^{-2}}=\rho {{V}^{2}}{{l}^{2}}\)

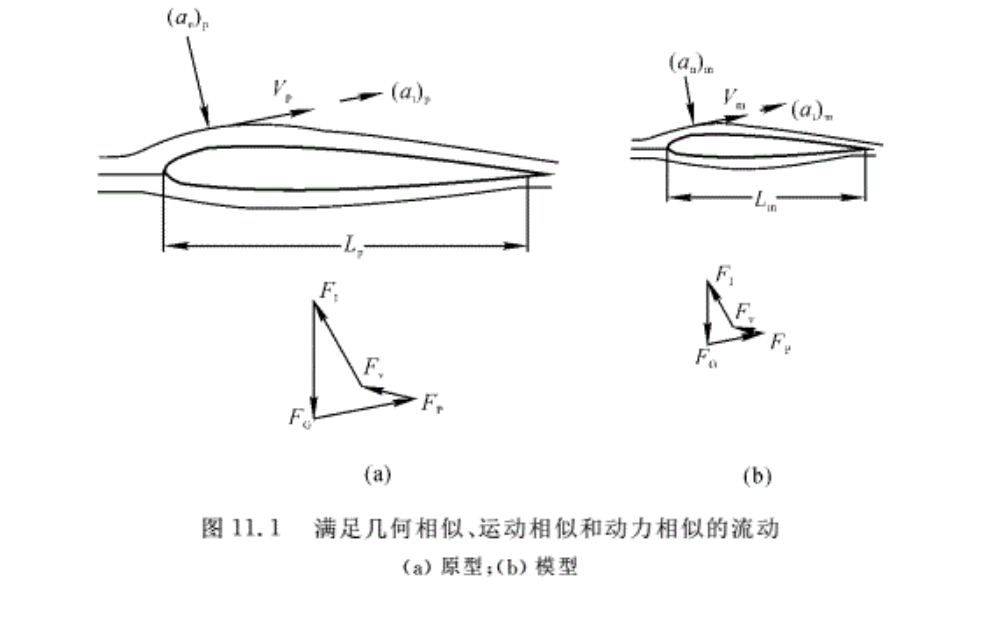
当然，在许多实际问题中，上述各力并非同等重要，有时有些力可能不存在或者小得可以忽略不计。例如，图11.1给出了忽略FE和FT的两种流动，图中，at和an分别表示切向和法向加速度，而下标p和m依然表示原型和模型。如果在满足几何相似及运动相似的两个流动现象中，作用在任何流体微元上的力有FG，Fp，Fv和F1等，那么，如果这些力满足以下条件，则说两个现象是动力相似的：

\({{C}_{F}}=\frac{{{F}_{{{G}_{p}}}}}{{{F}_{{{G}_{m}}}}}=\frac{{{F}_{{{P}_{p}}}}}{{{F}_{{{P}_{m}}}}}=\frac{{{F}_{{{v}_{p}}}}}{{{F}_{{{v}_{m}}}}}=\frac{{{F}_{{{1}_{p}}}}}{{{F}_{{{1}_{m}}}}}=……\)                     （11.7）

同样，用FG，Fp，Fv分别去除惯性力F1，也可以将其表示成下列关系：

\({{\left( \frac{{{F}_{1}}}{{{F}_{G}}} \right)}_{p}}={{\left( \frac{{{F}_{1}}}{{{F}_{G}}} \right)}_{m}},{{\left( \frac{{{F}_{1}}}{{{F}_{P}}} \right)}_{p}}={{\left( \frac{{{F}_{1}}}{{{F}_{P}}} \right)}_{m}},{{\left( \frac{{{F}_{1}}}{{{F}_{v}}} \right)}_{p}}={{\left( \frac{{{F}_{1}}}{{{F}_{v}}} \right)}_{m}}\)

从这4个力得到了3个无量纲量，它们必须满足3个独立的关系式；同理，从3个力可以得到2个无量纲量，同时必须满足2个独立的关系式。

满足以上三种相似条件时，两个流动现象（或流场）在力学上就是相似的。这三种相似条件中，几何相似是运动相似和动力相似的前提和依据，动力相似则是流动相似的主导因素，而运动相似只是几何相似和动力相似的表征；三者密切相关，缺一不可。

11.1.2  相似原理

理论上，任意一个流动由控制该流动的基本微分方程和相应的定解条件唯一确定。两个相似的流动现象，为了保证它们遵循相同的客观规律，其微分方程就应该相同，这是同类流动的通解；此外，要求得某一具体流动的特解，还要求其单值性条件也必须相似。这些单值性条件包括：

（1）初始条件，指非定常流动问题中开始时刻的流速、压力等物理量的分布；对于定常流动不需要这一条件。

（2）边界条件，指所研究系统的边界上（如进囗、出口及壁面处等）的流速、压力等物理量的分布。

（3）几何条件，指系统表面的几何形状、位置及表面粗糙度等。

（4）物理条件，指系统内流体的种类及物性，如密度、黏度等。

因此，如果两个流动相似，则作为单值性条件相似，作用在这两个系统上的惯性力与其他各力的比例应对应相等。在流体力学问题中，若存在上述所有这6种力，而且满足动力相似，则必须使下列各力间的比例对应相等。

惯性力与压力（或压差）之比

\(\frac{{{F}_{1}}}{{{F}_{P}}}=\frac{\rho {{V}^{2}}{{l}^{2}}}{\left( \Delta p \right){{l}^{2}}}=\frac{\rho {{V}^{2}}}{\Delta p}\)               (11.8)

惯性力与重力之比

\(\frac{{{F}_{1}}}{{{F}_{G}}}=\frac{\rho {{V}^{2}}{{l}^{2}}}{\rho {{l}^{3}}g}=\frac{{{V}^{2}}}{gl}\)               (11.9)

惯性力与摩擦力之比

\(\frac{{{F}_{1}}}{{{F}_{v}}}=\frac{\rho {{V}^{2}}{{l}^{2}}}{\mu Vl}=\frac{\rho Vl}{\mu }=\frac{lV}{\upsilon }\)               (11.10)

惯性力与弹性力之比

\(\frac{{{F}_{1}}}{{{F}_{E}}}=\frac{\rho {{V}^{2}}{{l}^{2}}}{E{{l}^{2}}}=\frac{\rho {{V}^{2}}{{l}^{2}}}{\rho {{c}^{2}}{{l}^{2}}}=\frac{{{V}^{2}}}{{{c}^{2}}}\)               (11.11)

惯性力与表面张力之比

\(\frac{{{F}_{1}}}{{{F}_{T}}}=\frac{\rho {{V}^{2}}{{l}^{2}}}{\sigma l}=\frac{\rho {{V}^{2}}l}{\sigma }\)               (11.12)

式（11.8）~式（11.12）分别引入了5个无量纲数。它们依次是：

（1）欧拉数                    Eu=△p/ρV²

欧拉数还可写成2△p/ρV²的形式，例如，在表示物体表面压力分布的压强系数，以及升力系数和阻力系数等中经常用到。物理上，欧拉数表征了压力与惯性力之比。

（2）弗劳德数                    Fr=V²/gl

物理上，弗劳德数表征了惯性力与重力间的量级之比。通常写作Fr=V/√(gl)。 一个表征流速高低的无量纲量。

（3）雷诺数                  Re=ρVl/μ或者Re=Vl/υ

物理上，雷诺数表征了相似流动中惯性力与黏性力间的量级之比。流动的Re小，表示与惯性力的量级相比，黏性摩擦力的量级要大得多，因此可以忽略惯性力的作用；反之，Re大则表示惯性力起主要作用，因此可以当做无黏性流体处理。

（4）马赫数                Ma=²=V²/c²或者Ma=V/c

物理上，马赫数表征了惯性力与弹性力间的量组之比，是气体可压缩性的度量，通常用来表示飞行器的飞行速度或者气流的流动速度。

（5）韦伯数                   We=ρV²l/σ

物理上，韦伯数表征了惯性力与表面张力间的量级之比。

可以看出，Eu，Fr，Re，Ma和We都是无量纲数，在相似理论中称为相似准则或者相似判据。它们是判断两个现象是否相似的依据，因而，彼此相似的现象，其同名相似准则的数值一定相等。反之，如果两个流动的单值性条件相似，而且由单值性条件组成的同名相似准则的数值相等，则这两个现象一定相似。

11.2  量纲分析法及П定理的应用

量纲和谐原理指出，要正确反映一个物理现象所代表之客观规律，其所遵循的物理方程式各项的量纲必须一致。这是量纲分析法的基础，因此也可以用这一原理来校核物理方程和经验公式的正确性和完整性。当某个流动现象未知或复杂得难以用理论分析写出其物理方程时，量纲分析就是一种强有力的科学方法。这时只须仔细分析这些现象所包含的主要物理量，并通过量纲分析和换算，将含有较多物理量的方程转化为数目较少的无量纲数组方程，就能为解决问题理出头绪，找出解决问题的方向。这就是量纲分析的价值。

11.2.1  量纲基本知识

量纲，是用以度量物理量单位种类的。在国际单位制（即SI单位制）中，规定有7个基本单位（或量纲），对于流体力学问题一般涉及其中的4个，即长度单位为米(m)，质量单位为公斤（kg），时间单位为秒（s），温度单位为开尔文（K），对应的量纲即基本量纲，依次是L,M,T和Θ。任何一个物理量的单位都可以用上述基本量纲的某种组合（即导出量纲）来表示；它们都可以写为基本量纲指数幂乘积的形式。常用的量及量纲有：

11.2.2  量纲分析法一一一瑞利（Rayleigh）法

下面举例说明量纲分析方法的具体应用。

例11.1  不可压缩流体在匀直圆管内作定常流动，试分析圆管单位长度上的流动损失△P/l的表达式。

解：根据题意，基本可按以下步骤解题。

（1）分析所求问题的影响因素。这是求解问题正确与否的关键。在本例中，由于是管内流动，显然管壁粗糙高度△将会显著影响流动附力；管长l、管径d、流体流动速度V都将是重要的影响因素；同样，流体的性质，如密度ρ和运动黏度υ也将影响流动辑力的大小。因此，该流动现象共有△p，l，d，V，ρ，υ和△等7个变量，如果研究单位长度上的流动阻力△p/l，则减少一个变量l，它们组成关系式：

\(f\left( \frac{\Delta p}{l},d,V,\rho ,\upsilon ,\Delta  \right)=0\)

（2）写出各变量之间的指数关系式：

\(\frac{\Delta p}{l}=K{{d}^{\alpha }}{{V}^{\beta }}{{\upsilon }^{\gamma }}{{\rho }^{\delta }}{{\Delta }^{\kappa }}\)

其中,α，β，γ，δ和κ都是待定指数，K为常数。

（3）写出各变量的量纲：

（4）与出对应的量纲关系式：

\(\begin{align}& M{{L}^{-2}}{{T}^{-2}}={{L}^{\alpha }}{{\left( L{{T}^{-1}} \right)}^{\beta }}{{\left( {{L}^{2}}{{T}^{-1}} \right)}^{\gamma }}{{\left( M{{L}^{-3}} \right)}^{\delta }}{{L}^{\kappa }}= \\& {{M}^{\delta }}{{L}^{\alpha +\beta +2\gamma -3\delta +\kappa }}{{T}^{-\beta -\gamma }} \\\end{align}\)

（5）比较等号两边对应量纲的指数，并根据量纲一致的原理，解得各待定指数：

δ=1

α+β+2γ-3δ+κ=-2

-β-γ=-2

上述3个方程中包含5个未知数，于是将其中2个，如γ，κ作为待定系数，从而解得：

α=-1-γ-κ

β=2-γ

δ=1

（6）将求得的指数代入上面的指数关系式，并将具有相同待定指数的量组合在一起成为相似准则：

\(\frac{\Delta p}{l}=K{{d}^{-1-\gamma -\kappa }}{{V}^{2-\gamma }}{{\upsilon }^{\gamma }}\rho {{\Delta }^{\kappa }}=K\frac{\rho {{V}^{2}}}{d}{{\left( \frac{\upsilon }{Vd} \right)}^{\gamma }}{{\left( \frac{\Delta }{d} \right)}^{\kappa }}\)

也可写作                                            \(\frac{\Delta p}{\rho }=\lambda \frac{l}{d}\frac{{{V}^{2}}}{2}\)

式中                                                    \(\lambda =f\left( \operatorname{Re},\frac{\Delta }{d} \right)=2K{{\left( \frac{\upsilon }{Vd} \right)}^{\gamma }}{{\left( \frac{\Delta }{d} \right)}^{\kappa }}\)

称为阻力因数，其中，Re=Vd/υ。

可见，圆管流动中的阻力因数λ取决于雷诺数Re和粗糙度△的变化，这与前面所讲的尼古拉兹曲线揭示的规律是一致的。但是必须知道，量纲分析不能得出λ的具体数值，它的数值只能通过实验获得。假定对于粗糙度△一定的圆管，如要得到d，V，ρ，υ对阻力因数的影响，如每次改变其中一个量，每个量取10个不同的值分别进行实验，要建立上述关系式就需要进行10⁴次实验。这不仅需要花费大量的人力、物力、财力和宝贵的时间，而且有时也是难以做得到的。但是如果用上述的无量纲数Re，仅用10次实验就可以确定阻力因数λ和Re之间对应关系的普遍规律，而且不用改变上述每一个量，只须改变容易控制的速度V就可以了。这就是量纲分析的科学价值。

上述量纲分析法仅适用于变量少的简单问题，因为变量的增加（例如4个以上）就会增加待定指数的数目，从而增加求解难度。这时更普遍、更实用的方法是布金汉（E．Buckingham）法。它将诸变量编列成更少的无量纲量，使问题处理起来更方便，此即布金汉(П定理）方法。

11.2.3  П定理

对于某个物理现象，若影响该现象的有量纲变量有n个，其中基本量纲有m个，于是可以将这些有量纲变量以乘积形式分组，编排成（n-m）个独立的无量纲量，并将各无量纲量组成函数关系式。这些无量纲量用П表示，故称П定理。

设变量X1，X2，…，Xi，…，Xn代表n个有量纲变量，如速度、密度及压力等，可以将这些变量写成如下的量纲齐次关系式：

F（X1，X2，…，Xi，…，Xn）=0

重新编排这个方程为以下形式：

\[f\left( {{\Pi }_{1}},{{\Pi }_{2}},…,{{\Pi }_{j}},…,{{\Pi }_{n-m}} \right)=0\]

其中，每个П代表一个独立的由若干个有量纲量Xi以乘积形式组合而成的无量纲量。

下面介绍利用П定理进行求解的步骤。

例11.2   用П定理方法分析例11.1中的流动。

解：（1）列出对所求问题有重要影响的物理量：如上例所述，共有△p，l，d，V，ρ，υ和△等7 个变量，因此有数关系式

△p=F（d，V，ρ，υ，l，△）

或者                           f（△p ，d，V，ρ，υ，l，△）=0

这里，n=7。

（2）用国际单位制（MLT）列出各个变量的量纲，它们依次为

ML^-1T^-2，L,LT^-1，ML^-3，L²T^-1，L,L

涉及M，L，T这3个基本量纲，因此m=3。

（3）选择m个独立的有量纲变量，它们应包括M，L，T三个基本量纲，但不应形成无量纲数组。

在一般流体力学问题中，常选一个与长度有关的量，例如l或d以保证几何相似；一个与速度有关的量，例如V，以保证运动相似；再选一个与质量有关的量，例如ρ，以保证动力相似。这3个变量分别具有量纲L，L/ T和M／L³，它们不会形成无量纲数组，因为M，L不能抵消。因此该例中n-m=4，即只有4个П值。如果在所研究的问题中包含有温度的变化，则还应再增加一个温度作为基本量纲。注意，在这里选择有量纲量时就不能选d，V，l，因为它们未能全部包含M，L，T三个基本量纲，而且d，l互不独立，它们能够组成无量纲量；同时因为同样的原因也不能选d，ρ，△。

（4）将其余每一个变量依次与上述诸独立变量的相应指数的乘积组成无量纲量П，并将各变量的量纲代入：

\[\begin{align}& {{\Pi }_{1}}={{V}^{{{\alpha }_{1}}}}{{d}^{{{\beta }_{1}}}}{{\rho }^{{{\gamma }_{1}}}}\Delta p={{\left( L{{T}^{-1}} \right)}^{{{\alpha }_{1}}}}{{\left( L \right)}^{{{\beta }_{1}}}}{{\left( M{{L}^{-3}} \right)}^{{{\gamma }_{1}}}}\left( M{{L}^{-1}}{{T}^{-2}} \right)={{M}^{0}}{{L}^{0}}{{T}^{0}} \\& {{\Pi }_{2}}={{V}^{{{\alpha }_{2}}}}{{d}^{{{\beta }_{2}}}}{{\rho }^{{{\gamma }_{2}}}}\upsilon ={{\left( L{{T}^{-1}} \right)}^{{{\alpha }_{2}}}}{{\left( L \right)}^{{{\beta }_{2}}}}{{\left( M{{L}^{-3}} \right)}^{{{\gamma }_{2}}}}\left( {{L}^{2}}{{T}^{-1}} \right)={{M}^{0}}{{L}^{0}}{{T}^{0}} \\& {{\Pi }_{3}}={{V}^{{{\alpha }_{3}}}}{{d}^{{{\beta }_{3}}}}{{\rho }^{{{\gamma }_{3}}}}l={{\left( L{{T}^{-1}} \right)}^{{{\alpha }_{3}}}}{{\left( L \right)}^{{{\beta }_{3}}}}{{\left( M{{L}^{-3}} \right)}^{{{\gamma }_{3}}}}L={{M}^{0}}{{L}^{0}}{{T}^{0}} \\& {{\Pi }_{4}}={{V}^{{{\alpha }_{4}}}}{{d}^{{{\beta }_{4}}}}{{\rho }^{{{\gamma }_{4}}}}\Delta ={{\left( L{{T}^{-1}} \right)}^{{{\alpha }_{4}}}}{{\left( L \right)}^{{{\beta }_{4}}}}{{\left( M{{L}^{-3}} \right)}^{{{\gamma }_{4}}}}L={{M}^{0}}{{L}^{0}}{{T}^{0}} \\\end{align}\]

（5）对每一个等式写出指数方程,并使每个量纲的指数之和等于0 ,则对于П1 ,有

L：α1+β1-3γ1-1=0

T：-α1-2=0

M：γ1+1=0

于是,解得指数α1=-2，β1=0，γ1=-1。同理，对于П2，有

L：α2+β2-3γ2+2=0

T：-α2-1=0

M：γ2=0

解得指数α2=-1，β2=-1，γ2=0。对于П3,有

L：α3+β3-3γ3+1=0

T：-α3=0

M：γ3=0

解得指数α3=0，β3=-1，γ3=0。同样,对于П4,有

L：α4+β4-3γ4+1=0

T：-α4=0

M：γ4=0

由此解得                                α4=0，β4=-1，γ4=0

（6）将上面求得的各指数代入对应的П式中,可得

\[\begin{align}& {{\Pi }_{1}}=\frac{\Delta p}{\rho {{V}^{2}}} \\& {{\Pi }_{2}}=\frac{\upsilon }{Vd}=\frac{1}{\operatorname{Re}} \\& {{\Pi }_{3}}=\frac{l}{d} \\& {{\Pi }_{4}}=\frac{\Delta }{d} \\\end{align}\]

（7）建立\(f\left( {{\Pi }_{1}},{{\Pi }_{2}},…,{{\Pi }_{j}},…,{{\Pi }_{n-m}} \right)=0\)型的函数关系，即

\[f\left( \frac{\Delta p}{\rho {{V}^{2}}},\frac{\upsilon }{Vd},\frac{l}{d},\frac{\Delta }{d} \right)=0\]

同时,也可以写成任意一个无量纲数的显式关系式,例如对差求解后,得

\[\frac{\Delta p}{\rho {{V}^{2}}}={{f}_{1}}\left( \frac{1}{\operatorname{Re}},\frac{l}{d},\frac{\Delta }{d} \right)\]

为了方便起见,可对式中的某些项(注意,它们都是无量纲项)或各项间进行一系列算术运算,例如加、减、乗、除,以及指数和开方等运算,而不影响其无量纲的本质。例如这里对第二项,即Re项取倒数后,该式可写成

\[\frac{\Delta p}{\rho {{V}^{2}}}={{f}_{2}}\left( \operatorname{Re},\frac{l}{d},\frac{\Delta }{d} \right)\]

由于管路中的压力降随管长呈线性变化，即管长增一倍，压力降也增加一倍，因此

\[\frac{\Delta p}{\rho {{V}^{2}}}=\frac{l}{d}{{f}_{3}}\left( \operatorname{Re},\frac{\Delta }{d} \right)\]

或者                        \(\Delta p={{f}_{4}}\left( \operatorname{Re},\frac{\Delta }{d} \right)\frac{l}{d}\frac{\rho {{V}^{2}}}{2}=\lambda \frac{l}{d}\frac{\rho {{V}^{2}}}{2}\)

式中,\( \lambda ={{f}_{4}}\left( \operatorname{Re},\frac{\Delta }{d} \right)\)，可见所得结果与量纲分析法的结果是完全一致的。由相似原理知道，原型的阻力因数（无量纲数)λ与模型中是相等的，因此，要用模型实验数据推算原型中的结果，只须将原型的相关数据，如λ，ρ，l，d，V代入即可求得原型管路中的压力降Δp。

这里必须强调，量纲分析不能给流体力学问题提供一个完整解，它只能提供部分解，其中的无量纲量还得通过实验来得到。利用量纲分析求解是否成功完全取决于研究者分析问题的能力，如果研究中遗漏了某个重要的变量，则结论将是不正确的。例如，对于高速流动，可压缩性的影响是显著的，这时，就必须考虑马赫数的影响。反之，如果研究中过多考虑了一些无关紧要的因素，则会使问题复杂化。因此，要成功地应用量纲分析，首先必须熟悉所研究的现象，并且对各变量的影响程度进行深入分析，除去相对次要的影响因素，只保留一些主要因素，既能使问题的求解简捷，又能揭示问題的本质。

11.3  方程分析法

相似理论的关键是导出与物理现象有关的相似准则。前而所述的量纲分析方法，即是通过分析与物理现象有关的变量，再使用П定理确定相似准则的方法。这种方法对于任何流动问题都是适用的，但是对研究人员要求较高，因为如果对所研究问题理解不深，以致遗漏了一个甚至多个重要的变量，将导致错误的结论。另外一种确定相似准则的方法是方程分析法。该方法是从主导流动的基本方程出发，不存在多余或遗漏变量的问题，因此所得到的相似准则是可靠的。但是这种方法仅仅适用于那些己知描述该流动的基本方程及其全部定解条件的流动现象，而对那些大量的未知流动现象却无能为力。下面通过例题对方程分析法加以说明。

例11.3  某流动现象可用不可压缩流体定常流动的N一S方程来描述，试用方程分析法确定其相似准则。

解：以N一S方程的x方向投影式为例，即

\(\frac{d{{V}_{x}}}{dt}=X-\frac{1}{\rho }\frac{\partial p}{\partial x}+\upsilon \left( \frac{{{\partial }^{2}}{{V}_{x}}}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}{{V}_{x}}}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}{{V}_{x}}}{\partial {{z}^{2}}} \right)\)                (a)

与其相似的模型流动中的主导方程为

\(\frac{dV_{x}^{\prime }}{d{{t}^{\prime }}}={{X}^{\prime }}-\frac{1}{{{\rho }^{\prime }}}\frac{\partial {{p}^{\prime }}}{\partial {{x}^{\prime }}}+{{\upsilon }^{\prime }}\left( \frac{{{\partial }^{2}}V_{x}^{\prime }}{\partial {{x}^{\prime }}^{2}}+\frac{{{\partial }^{2}}V_{x}^{\prime }}{\partial {{y}^{\prime }}^{2}}+\frac{{{\partial }^{2}}V_{x}^{\prime }}{\partial {{z}^{\prime }}^{2}} \right)\)                (b)

既然二现象相似，必有

\(\left. \begin{align}& {{x}^{\prime }}\text{=}{{C}_{l}}x,{{y}^{\prime }}\text{=}{{C}_{l}}y,{{z}^{\prime }}\text{=}{{C}_{l}}z \\& {{t}^{\prime }}\text{=}{{C}_{t}}t=\frac{{{C}_{l}}}{{{C}_{V}}}t \\& {{\rho }^{\prime }}={{C}_{\rho }}\rho ,{{p}^{\prime }}={{C}_{p}}p,{{\upsilon }^{\prime }}={{C}_{\upsilon }}\upsilon ,{{X}^{\prime }}={{C}_{g}}X \\\end{align} \right\}\)                (c)

式中，各比例常数Cl,Ct,CV,Cp,Cρ,Cυ,Cg等称为相似倍数。

将式（c）代入式（b），整理后得

\(\frac{C_{V}^{2}}{{{C}_{l}}}\frac{d{{V}_{x}}}{dt}={{C}_{g}}X-\frac{{{C}_{p}}}{{{C}_{\rho }}{{C}_{t}}}\frac{1}{\rho }\frac{\partial p}{\partial x}+\frac{{{C}_{\upsilon }}{{C}_{V}}}{C_{l}^{2}}\upsilon \left( \frac{{{\partial }^{2}}{{V}_{x}}}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}{{V}_{x}}}{\partial {{y}^{2}}}+\frac{{{\partial }^{2}}{{V}_{x}}}{\partial {{z}^{2}}} \right)\)                     (d)

既然两个流动现象完全相同，它们的主导方程就应该一致，于是比较式（a）和式（d），则有

\(\frac{C_{V}^{2}}{{{C}_{l}}}={{C}_{g}}=\frac{{{C}_{p}}}{{{C}_{\rho }}{{C}_{t}}}=\frac{{{C}_{\upsilon }}{{C}_{V}}}{C_{l}^{2}}=1\)                     (e)

由此，各相似倍数不能任意选取，它们依式（e）而相互制约。将式（e）第一项分别除以后三项，则有

\(\left. \begin{align}& \left( 1 \right)\frac{C_{V}^{2}}{{{C}_{g}}{{C}_{l}}}=1,\frac{{{V}^{2}}}{gl}=\frac{{{V}^{\prime }}^{2}}{{{g}^{\prime }}{{l}^{\prime }}},Fr=F{{r}^{\prime }} \\& \left( 2 \right)\frac{C_{V}^{2}{{C}_{\rho }}}{{{C}_{p}}}=1,\frac{p}{\rho {{V}^{2}}}=\frac{{{p}^{\prime }}}{{{\rho }^{\prime }}{{V}^{\prime }}^{2}},Eu=E{{u}^{\prime }} \\& \left( 3 \right)\frac{{{C}_{V}}{{C}_{l}}}{{{C}_{\upsilon }}}=1,\frac{Vl}{\upsilon }=\frac{{{V}^{\prime }}{{l}^{\prime }}}{{{\upsilon }^{\prime }}},\operatorname{Re}={{\operatorname{Re}}^{\prime }} \\\end{align} \right\}\)                     (f)

至此，从基本方程导出了两个相似的不可压缩定常流动现象的相似准则，它们是弗劳德数 Fr、欧拉数Eu和雷诺数Re。综上所述，相似原理可表述为：两种流动现象相似的充分必要条件是：凡是同一种现象，必能用同一个微分方程所描述；单值性条件相似；由单值性条件中的物理量所组成的相似准则在数值上相等。

11.4  模型实验

11.4.1  全面力学相似

按照上述分析，如果要两个流动达到全面相似，就必须使模型和原型两种流动完全满足几何相似、运动相似和动力相似，且具有相似的初始条件和边界条件，也应使所有相似准则（Re，Eu ,Fr ,Ma ,•••)分别相等，且初始条件和边界条件相似，这实际上是困难的，有时甚至是办不到的。例如，对于黏性不可压缩流体定常流动，尽管只有2个相似准则Re和Fr，但也很难满足。

其原因分析如下：

（1）要满足\({{\left( \operatorname{Re} \right)}_{p}}={{\left( \operatorname{Re} \right)}_{m}}\)，即\(\frac{{{V}_{p}}{{l}_{p}}}{{{\upsilon }_{p}}}=\frac{{{V}_{m}}{{l}_{m}}}{{{\upsilon }_{m}}}\),假设两种流动的介质一样，即υp=υm，且模型尺寸为原型尺寸的1/10，即\({{C}_{V}}=\frac{{{V}_{p}}}{{{V}_{m}}}=\frac{{{l}_{m}}}{{{l}_{p}}}=\frac{1}{{{C}_{l}}}=\frac{1}{10}\)，则应有，即要求模型中的流速应为原型中的10倍。

（2）要满足\({{\left( Fr \right)}_{p}}={{\left( Fr \right)}_{m}\) ，即\(\frac{{{g}_{p}}{{l}_{p}}}{V_{p}^{2}}=\frac{{{g}_{m}}{{l}_{m}}}{V_{m}^{2}}\),假设gp=gm,在\({{C}_{l}}=\frac{{{l}_{p}}}{{{l}_{m}}}=10\)的情况下，则应有\(\frac{{{V}_{p}}}{{{V}_{m}}}={{C}_{V}}=\sqrt{{{C}_{l}}}=3.16\)，即要求模型中的流速应为原型中流速的1／3.16。显然这与第一项的要求是矛盾的。

解决这一矛盾的办法只有在模型中使用与原型中不同黏度的流体：假定取CV=3.16，以满足Fr相等的要求，而同时要满足Re相等的要求，就应使\({{C}_{\upsilon }}=\frac{{{V}_{p}}}{{{V}_{m}}}\frac{{{l}_{p}}}{{{l}_{m}}}={{C}_{V}}{{C}_{l}}=31.6\)，这就是说，模型实验中只有使用运动黏度υ为原型1 / 31.6的流体，这是很难做到的。

由此看出，即使仅有2个相似准则也是难以满足的，若有3个以上相似准则时，其模型实验就难以进行，除介质的选择受限制外，其他物理量也会受到限制。为此，工程上通常采用近似模化方法。

11.4.2  近似模化法

全面力学相似几乎不可能，为了使模型研究得以进行，就必须对各相似条件逐一分析，对那些主要的、起决定作用的条件，应当尽量加以保证；而对那些次要的条件只须近似满足，甚至忽略，这样不会引起大的误差。这种近似模化法也是完全可能的。

（1）气体是可压缩流体，但是当Ma≤0.3时，压缩性影响很小，可以近似认为是不可压缩流体，因此可以用气体模化液体的流动。

（2）在工程和无压明渠流动中，重力起主导作用，而黏性力则处于次要地位，因此，重力相似准则Fr就是主要相似准则。这在水利工程上得到广泛的应用。

（3）实际流体在管内流动时，黏性力决定流动阻力的大小，而重力则处于次要地位，因此雷诺数Re成了主要相似准则。这种方法在管内流动、液压技术、流体机械的模化实验中得到广泛应用。

（4）在上述管内流动中，Re是主要相似准则，那么，是否一定需要Rem=Rep呢？如此，假设在小得多的模型实验中使用与原型同样的流体，从Re=Vd/υ，则需要实验流速大大增加；如果流动介质是气体，则高速度可能使得必须要考虑压缩性的影响。幸亏流动的一种特性——“自模性”——给我们带来极大的方便。当Re小于某一数值（第一临界值，下临界雷诺数）时，流动处于层流状态。在层流状态范围内，流体的速度分布彼此相似，与Re不再有关，这种现象便称为自模性。例如，流体在圆管中作层流流动时，只要Re≤2320，沿横截面的流速分布都是一个轴对称的旋转抛物面，而与Re无关；当Re=2320即Recr1（第一临界值）时，常将Re＜Recr1的范围叫做“第一自模化区”。当Re＞Recr1时，流动处于由层流向湍流的过渡状态，这时流动速度分布随Re变化较大；但是当Re>Recr2（第二临界值）时，流体的速度分布又一次彼此相似，阻力的相似并不要求Re相等，即与Re无关，流动再次进入自模化状态，称Re> Recr2的范围叫做“第二自模化区”。只要原型设备的Re处于自模化区以内，模型与原型的Re就不必相等，只须与原型处于同一自模化区就可以了。也就是说，在同一自模化区内，即使Re不相等，其黏性力也是自动相似的。如果流场中的流体是气体，可忽略重力的影响，因此Fr不必考虑；这时只须考虑压强的影响，即保证Eu相等就可以了。

在这种模化区中进行的模型实验应用很广，如管内流动、低速风洞实验、气体绕流实验等。

11.4.3  实验研究的基本要点

实验研究的理论基础是相似原理，因此在进行实验研究时应注意下述几个问题。

（1）所研究的问题有几个相似准则？相似准则是控制流动的参数。对于一个具体的实验，首先要分析所研究现象的相似准则，并分清主次，找出决定性准则，忽略次要准则。例如，物体在空气中做低速运动时，决定性准则是Re，而在高速（Ma＞0.3）运动时，反映压缩性影响的相似准则Ma则成了决定性准则。

（2）有哪些决定性相似准则？根据决定性相似准则相等的条件设计实验，包括模型设计、实验设备及实验条件的选择，实验中流体介质的选择及运动状态的确定等。

（3）实验中应测量哪些物理量？由于彼此相似的现象必定具有数值相同的相似准则，因此实验中就要测定各个相似准则中所包含的一切物理量。

（4）怎样整理实验数据？所有实验结果必须整理成无量纲量的形式。因为在彼此相似的现象中只有无量纲量的数值才相等，只有这种结果在几何相似的流动中才具有普遍意义。

（5）怎样将实验结果换算到原型系统中去？根据相似原理，在相似准则相等的条件下，将实验得到的无量纲量推广到原型系统中，进而得到所需的有量纲量。

小结

（1）本章讨论了两种流动相似应满足的条件为几何相似、运动相似和动力相似；根据相似原理，导出了相似准则。

（2）量纲分析法对于分析任何流动都是适用的。对于变量数目较少的简单问题，可以用瑞利法求解；对于变量数目较多的问题，可采用史普遍、更实用的布金汉(П定理）方法求解。

（3）用瑞利和布金汉方法要求不能遗漏某个重要的物理变量，否则会导致错误结论。

（4）方程分析法是从主导流动的基本方程出发，不存在遗漏变量的问题，可靠性高，但仅适用于已知描述流动的基本方程及其全部定解条件的流动现象。

（5）工程中要求所有的相似准则对应相等是难以满足的，故常采用近似模化法。对起决定作用的条件应尽量保证，对次要的条件可近似满足或忽略。