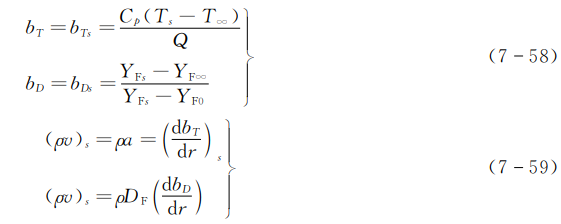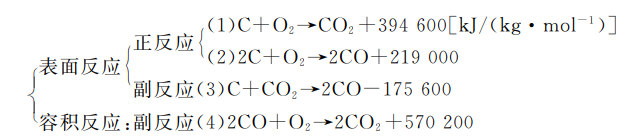第7章扩散燃烧

预混燃烧是指燃料气体与氧化剂预先混合均匀再燃烧的现象。预混燃烧速度一般受化学反应速度控制。但实际上,绝大部分情况是两者没有事先混合好,而是边混合边燃烧。对固态或液态燃料来说,必须先通过热解、升华等,在气相中燃料气体与氧化剂气体先混合再燃烧,这种燃烧现象称为扩散燃烧。扩散燃烧一般受扩散速度控制。 扩散燃烧可分为如下两类:

(1)均匀相扩散燃烧:燃料和氧化剂都是气态的,如煤气炉、乙炔。

(2)非均匀相扩散燃烧:液体或固体的凝相燃料的燃烧,如木柴、蜡烛、油滴。

对于气体的扩散燃烧燃烧反应在薄层空间中进行,薄层外只是分子输运;燃料气体和氧 化剂气体浓度不均,依靠分子浓度的梯度形成扩散。由于存在扩散现象,扩散火焰中的氧化剂、燃料及产物的浓度、温度在比较宽的区域内变化着,而真正的燃烧反应只是发生在一个其厚度可以忽略不计的区域中。但是对于预混火焰,其组分浓度、温度等参数在一个非常窄的火焰区内才有显著变化,在火焰区外是均匀的。

一般来说,扩散燃烧速度比预混燃烧速度慢,因为混合过程比较慢(扩散燃烧中分子扩散速度较慢)。例如对于乙烯和氧的燃烧,在预混火焰燃烧中其燃烧速度为4mol/(cm3·s),而在扩散燃烧中,燃烧速度为6×10-5mol/(cm3·s)本章介绍三种扩散燃烧:气体燃料射流燃烧、料液滴的蒸发与燃烧、碳粒的燃烧。

7.1气体燃料射流燃烧

7.1.1气体燃料射流燃烧定义

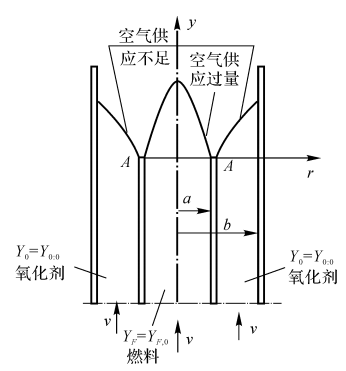
气体燃料射流燃烧是指气体燃料射流进入氧化剂气体环境中的燃烧现象。如果气体边界受限制,则称为受限制的射流燃烧。现有两根同心管，内管为燃料，内外管之间的环形管内为空气(见图7-1)。在同心管出口截面点燃混合气，研究混合气燃烧特性。
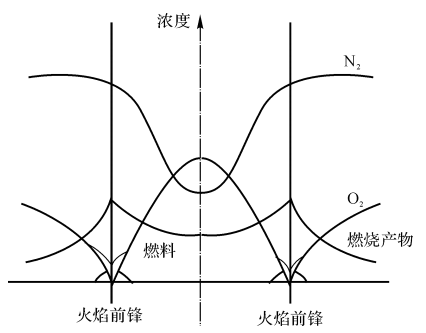
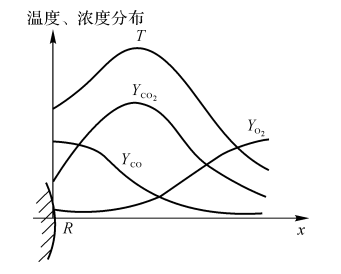
Hottel和 Hanthone在1949年对层流的H2-气射流扩散火焰进行了研究，测量了其组分的分布(按化学当量比反应)，研究结论如下(见图7-2):
(1)火焰前锋处:燃料和氧化剂的浓度接近零，燃烧产物的浓度在此最大。
(2)火焰外侧:只有氧化剂气体，没有燃料气体。
(3)火焰内侧:只有燃料气体，而无氧化剂气体。
可见，火焰面就像一面隔板，将燃料和氧化剂截然分开。实际上火焰区并不是一个数学上的面，它总有一个厚度。
在径向，由于组分浓度有较大变化，因而形成各自的径向扩散流动。这种由扩散形成的整体流动叫Stefan流动。当多组分反应流体流过惰性表面时，在表面处，各个组分都会有一定的浓度梯度，形成各自的分子扩散流，但这些同时存在的扩散流不可能相互无关，其间必然有一定的联系。同时，相分界面上的物理过程或反应动力学过程要求产生或消耗一定的质量流。于是在扩散的相互干涉和物理化学过程作用下，表面处产生一个法向总物质流。这个物质流不是外部因素造成的，而是由表面本身的特点形成的，这一现象是Stefan首先发现的。Stefan流发生的充分及必要条件是:表面有物理或化学的过程存在，同时表面附近有扩散的相互影响。

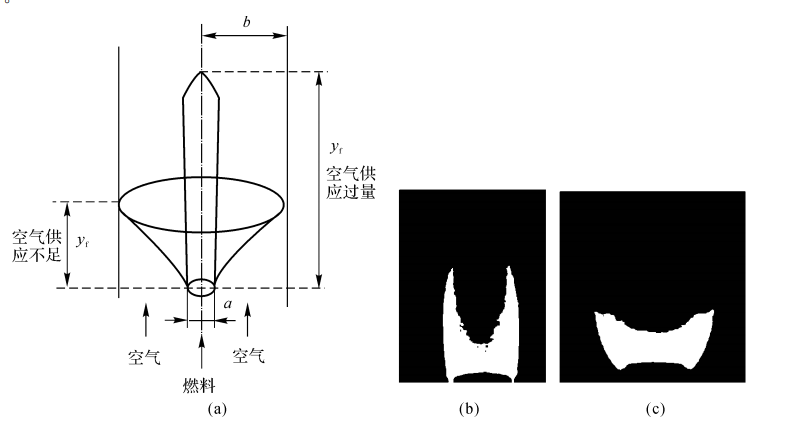
图7-1燃料射流火焰的外形
(a)火焰外形;(b)空气过量火焰照片;(c)燃料过量火焰照片

图7-2射流扩散火焰的组分浓度分布
运用Stefan流概念对分析液面和固面的分界面边界条件(例如推进剂燃烧表面的边界条件)非常重要。
7.1.2描述射流燃烧的基本方程
首先作如下假设:
(1)流动是定常的。
(2)流动Ma数远小于1，流动为低速层流，压强为常数。
(3)Ma低，故黏性力和体积力可忽略不计。
(4)组分间扩散遵守Fick定律，各组分的扩散系数相同。
(5)化学反应为一步反应。
总体连续方程:
\(\nabla \rho u=0\) (7-1)
i组分连续方程:
\(\nabla (\rho {{V}_{i}}(v+{{V}_{i}}))={{\omega }_{i}}\) (7-2)
能量方程:
\(\rho v\nabla \sum\limits_{i=1}^{N}{{{Y}_{i}}{{h}_{i}}=\nabla \lambda \nabla T-\nabla }(\rho \sum\limits_{i=1}^{N}{{{Y}_{i}}{{h}_{i}}}{{V}_{i}})\) (7-3)
利用式(7-1)，式(7-3)变成
\(\nabla (\rho \sum\limits_{i=1}^{N}{{{Y}_{i}}{{h}_{i}}(v+{{V}_{i}})-\lambda \nabla T)=0}\) (7-4)
将式(7-2)及h，hi，的表达式代入式(7-4)可得
\(\nabla (\rho v(\int_{{{T}_{0}}}^{T}{{{C}_{p}}dT)+\rho }\sum\limits_{i=1}^{N}{{{Y}_{i}}{{V}_{i}}(\int_{{{T}_{0}}}^{T}{{{C}_{pi}}dT)}-\lambda \nabla }T)=-\sum\limits_{i=1}^{N}{h_{i}^{0}{{\omega }_{i}}}\) (7-5)
假定路易斯数为1，即
\({{L}_{e}}=\frac{\lambda }{\rho {{C}_{p}}D}=1\) (7-6)
由Fick定律
\({{Y}_{i}}{{V}_{i}}=-D\nabla {{Y}_{i}}\) (7-7)
故式(7-5)化为
\(\nabla \cdot \left\{ \rho v(\int_{{{T}_{0}}}^{T}{{{C}_{p}}dT)-\rho D(\sum\limits_{i=1}^{N}{\nabla {{Y}_{i}}(\int_{{{T}_{0}}}^{T}{{{C}_{pi}}dT)}+{{C}_{p}}\nabla T)}} \right\}=-\sum\limits_{i=1}^{N}{h_{i}^{0}{{\omega }_{i}}}\) (7-8)
根据混合气体比热定义:
\(\int_{{{T}_{0}}}^{T}{{{C}_{p}}dT=}\sum\limits_{i=1}^{N}{{{Y}_{i}}\int_{{{T}_{0}}}^{T}{{{C}_{pi}}dT}}\) (7-9)
根据式(7-9)，可得
\(\nabla \int_{{{T}_{0}}}^{T}{{{C}_{p}}dT=}\sum\limits_{i=1}^{N}{\nabla {{Y}_{i}}(\int_{{{T}_{0}}}^{T}{{{C}_{pi}}dT)+\sum\limits_{i=1}^{N}{{{Y}_{i}}\nabla \int_{{{T}_{0}}}^{T}{{{C}_{p}}dT=}\sum\limits_{i=1}^{N}{{{Y}_{i}}\nabla (\int_{{{T}_{0}}}^{T}{{{C}_{pi}}dT)}}+{{C}_{p}}\nabla T}}}\) (7-10)
将式(7-10)代入式(7-8)，可得能量方程:
\(\nabla \left( \rho v(\int_{{{T}_{0}}}^{T}{{{C}_{p}}dT)}-\frac{\lambda }{{{C}_{p}}}\nabla \int_{{{T}_{0}}}^{T}{{{C}_{p}}dT} \right)=-\sum\limits_{i=1}^{N}{h_{i}^{0}{{\omega }_{i}}}\) (7-11)
i组分方程式(7-2)可化为
\(\nabla (\rho v{{Y}_{i}}-\rho D\nabla {{Y}_{i}})={{\omega }_{i}}\)  (7-12)
方程式(7-11)和式(7-12)称为Shvab-Zeldovich-能量方程及组分连续方程。
假定反应为一步反应，有
\(\omega =\frac{{{\omega }_{i}}}{{{M}_{i}}({{v}_{i}}-{{v}_{i}})}\)
这样，i组分的连续方程式(7-12)化为
\(\nabla \left( \rho v\frac{{{Y}_{i}}}{{{M}_{i}}({{v}_{i}}-{{v}_{i}})}-\rho D\nabla \frac{{{Y}_{i}}}{{{M}_{i}}({{v}_{i}}-{{v}_{i}})} \right)=\omega \)  (7-13)
能量守恒方程化为
\(\nabla \left( \rho v\frac{\int_{{{T}_{0}}}^{T}{{{C}_{p}}dT}}{\sum{{{M}_{i}}({{{{v}’}}_{i}}-{{{{v}”}}_{i}})h_{i}^{0}}}-\frac{\lambda }{{{C}_{p}}}\nabla \frac{\int_{{{T}_{0}}}^{T}{{{C}_{p}}dT}}{\sum{{{M}_{i}}({{{{v}’}}_{i}}-{{{{v}”}}_{i}})h_{i}^{0}}} \right)=\omega \)  (7-14)
假设
\({{a}_{i}}=\frac{{{Y}_{i}}}{{{M}_{i}}({{{{v}”}}_{i}}-{{{{v}’}}_{i}})}\( (7-15)
\({{a}_{T}}=\frac{\int_{{{T}_{0}}}^{T}{{{C}_{p}}dT}}{\sum{{{M}_{i}}({{{{v}’}}_{i}}-{{{{v}”}}_{i}})h_{i}^{0}}}\)  (7-16)
引入线性算子:
\(L(a)=\nabla \left( \rho va-\rho D\nabla a \right)\)
则i组分连续方程式(7-13)为
\(L({{a}_{i}})=\omega \) (7-17)
能量方程式(7-14)为
\(L({{a}_{i}})=\omega \) (7-18)
若令
\(\Omega ={{a}_{T}}-{{a}_{i}}={{\Omega }_{T}}\)
\(\Omega ={{a}_{i}}-{{a}_{1}}={{\Omega }_{i}}(i\ne 1)\)
则有
\(L({{a}_{1}})=\omega \) (7-19)
\(L(\Omega )=\omega \) (7-20)
可见，原来的N+1个含有非线性项w的组分连续方程和能量方程化成了N个线性方程式(7-20)和一个非线性方程式(7-19)
这些方程组的求解，分析如下:
(1)只要解出非线性方程式(7-19)，其他参数可由线性方程式(7-20)确定
(2)有时候，只求解线性方程，也可得到一些满意的结论。

7.2 BurkeSchumann-对限制性射流燃烧的求解
Burke和 Schuman在1928年研究用图如图7-3所示。
基本假设如下:
(1)出口处燃料气体与空气流速相同，燃料-空气的摩尔比值为\(\frac{{{a}^{2}}}{{{b}^{2}}-{{a}^{2}}}\)。
(2)在火焰内它们的流速为常数;燃料气体与空气流之间的扩散系数为常量。由于燃烧反应，T增加，流速v和扩散系数D都增加，它们对火焰形状和尺寸的影响可以相互抵消。
(3)与径向扩散相比，轴向扩散可忽略不计。可认为\(\rho D\frac{\partial {{Y}_{i}}}{\partial y}\approx 0\)。
(4)质量平均速度v只有轴向分量而无径向分量;
(5)燃烧是按化学计量比进行的。

图7-3 Burke-Schumann-问题简图
在这个系统中，参加反应的只有燃料F，氧气O和产物P。如果认为反应是一步的，则有
fF+O=(1+f)P (7-21)
根据 Burke和 Schu ann描述受限制射流燃烧的方程可得
\({{a}_{O}}=\frac{{{Y}_{O}}}{{{M}_{O}}({{{{v}”}}_{O}}-{{{{v}’}}_{O}})}=-{{Y}_{O}}\)
\({{a}_{F}}=\frac{{{Y}_{F}}}{{{M}_{F}}({{{{v}”}}_{F}}-{{{{v}’}}_{F}})}=\frac{{{Y}_{F}}}{f}\)
则 \(\Omega ={{a}_{O}}-{{a}_{F}}=\frac{{{Y}_{F}}}{f}-{{Y}_{O}}\)  (7-22)
式(7-20)变为
\(L(\Omega )=\nabla \left( \rho v\Omega -\rho D\nabla \Omega \right)=0\)  (7-23)
将式(7-23)中散度算子和梯度算子应用到柱坐标系 ，变为
\(\frac{v}{D}\frac{\partial \Omega }{\partial y}-\frac{1}{r}\frac{\partial }{\partial r}(r\frac{\partial \Omega }{\partial r})=0\)  (7-24)
边界条件为
当y=0，0≤r<a时
\(\Omega =\frac{{{Y}_{F,0}}}{f}\)
当y=0，a≤r<b时
\(\Omega =-{{Y}_{O,0}}\)
当y>0，r=b时
\(\frac{\partial \Omega }{\partial r}=0\)  (7-25)
方程式(7-24)和边界条件式(7-25)是BurkeSchum- ann描述受限制射流燃烧的方程。从物理意义上讲， BurkeSchumann-分析认为扩散火焰只牵涉F和O的浓度分布，将化学反应速率看作无穷大，不再考虑温度分布对化学反应速率的影响，而温度对浓度分布的影响通过对 的影响表现出来。假定T对D的影响正好和对v的影响相互抵消，则只需考虑F，O的浓度分布，不必求解能量方程。
假设认为，F只向外扩散，O向内扩散，两者以化学计量比相遇发生化学反应，将扩散来的质量正好消耗掉，形成火焰前锋。因此在火焰处有
\({{Y}_{F}}=0,{{Y}_{O}}=0\)  (7-26)
\(\left( -\frac{\rho D}{f}\frac{\partial {{Y}_{F}}}{\partial r} \right)=\rho D\frac{\partial {{Y}_{O}}}{\partial r}\)  (7-27)
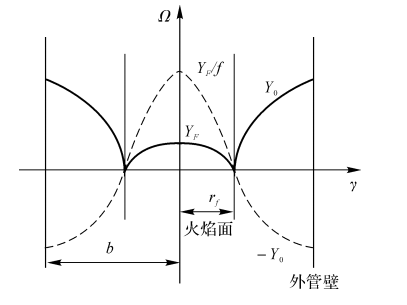
显然，\(\frac{{{Y}_{F}}}{f}\) 和-YO构成一条光滑连续的曲线，这条曲线就是\(\Omega (y,r)\)(见图7-4)。其中，火焰面(YF=YO=0)的半径为r1
当r<rf，时
\(\Omega =\frac{{{Y}_{F}}}{f}\)
当r>rf，时
\(\Omega =-{{Y}_{O}}\)
当r=rf时
\(\Omega ={{(\frac{{{Y}_{F}}}{f})}_{f}}-{{({{Y}_{O}})}_{f}}=0\)  (7-28)
为了便于方程求解，引入无量纲坐标
\(\xi =\frac{r}{b},\eta =\frac{Dy}{{{b}^{2}}v}\)  (7-29)
\(\gamma =\frac{f\Omega }{{{Y}_{F,O}}}=\frac{{{Y}_{F}}-f{{Y}_{O}}}{{{Y}_{F,O}}}\)  (7-30)
则方程式(7-24)化为
\(\frac{\partial \gamma }{\partial \eta }=\frac{1}{\xi }\frac{\partial }{\partial \xi }(\xi \frac{\partial \gamma }{\partial \xi })\) (7-31)

图7-4垂直于y轴截面上的浓度分布
利用分离变量法，求解方程式(7-31)，可得方程解为

有了浓度分布 后，可求解火焰形状方程。方程 在柱坐标系中所描述的曲面就是火焰面，因此可根据 求出火焰形状方程为

其中
\(\xi =\frac{r}{b},\eta =\frac{Dy}{{{b}^{2}}v}\)
J为贝塞尔函数; 为贝塞尔函数\({{J}_{1}}\left( \mu \right)=0\)的一连串正根;\(c=\frac{a}{b}\);v为内管管口处与通风情况有关的参数，通风不足，v小，反之，则大。
当通风不足时，\(\xi =1\)(开口扇形火焰)。
\(\eta =\frac{1}{\mu _{1}^{2}}\ln \left\{ \frac{2(1+v)c{{J}_{1}}(c{{\mu }_{1}})}{(v-(1+v){{c}^{2}}){{\mu }_{1}}{{J}_{0}}({{\mu }_{1}})} \right\}\)  (7-34)
当通风过量时，\(\xi =0\((封闭长火焰)。
\(\eta =\frac{1}{\mu _{1}^{2}}\ln \left\{ \frac{2(1+v)c{{J}_{1}}(c{{\mu }_{1}})}{(v-(1+v){{c}^{2}}){{\mu }_{1}}{{({{J}_{0}}({{\mu }_{1}}))}^{2}}} \right\}\) (7-35)
式中\({{\mu }_{1}}=3.831,c=\frac{a}{b},v=\frac{f{{Y}_{O,0}}}{{{Y}_{F,0}}}\)
图7-5所示为c=0.5时，不同v值计算的限制性射流扩散火焰的形状。
Burke和Schumann对几种情况进行了求解计算，计算结果与试验结果相当一致。 Burke和Schumann根据理论分析得出如下结论:
(1)如果F和O的流率不变，圆柱形火焰的高度不受管子尺寸的影响。
(2)只要其他所有因素不变，则火焰高度和扩散系数成反比。
(3)火焰的垂直尺寸与流速v成正比。
(4)因为D/v与压力无关，所以当总流率不变时，火焰高度与压力无关。
(5)提高燃料和氧化剂的初温对D，v的影响可以相互抵消，从而对火焰形状没有影响。

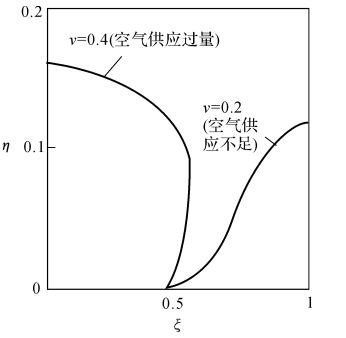
图7-5 Burke-Schuman-问题的火焰形状(c=0.5)
(6)如果在燃料中加惰性气体，使得F的净流率降低(总流率不变)，则火焰向内移动，使通风过量的火焰高度下降，通风不足的火焰高度上升。
(7)当化学计量比f增加时，火焰向内移动使通风过量的火焰高度减少，通风不足的火焰高度上升。

7.3自由射流火焰的表象分析
假定燃烧过程不影响燃料射流与氧气之间的扩散混合速率。在圆柱射流问题中，氧气从射流边界扩散到火焰中心处，燃料就全部烧完，就是说，在这点上，火焰结束。这就变成了一个层流射流的扩散混合问题。通过计算射流边界上O扩散到中心线的时间，可求出火焰高度。
分子运动论指出，在分子扩散中一个分子的平均位移，可由下式求出:
\(\frac{1}{2}\frac{d\overset{\_}{\mathop{{{x}^{2}}}}\,}{dt}=D\) (7-36)
\({{\xi }^{2}}\text{=2}Dt\)  (7-37)
式中，D为扩散系数。\(\overset{\_}{\mathop{{{x}^{2}}}}\,\)为时间t内，在规定的方向上质点位移均方值为指时间t内由于扩散分子离开某一位置位移的均方值。

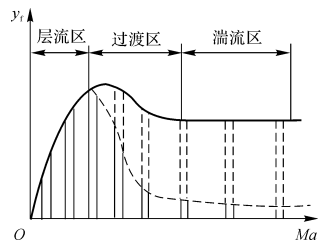
图7-6火焰高度随射流速度的变化
对于圆柱射流，管子半径为a，空气达到火焰顶点需穿过平均距离为a所需扩散时间和燃料微团从管口流向火焰顶点所需时间，假定流率v为常量:
\(t=\frac{{{y}_{f}}}{v}\) (7-38)
\({{\xi }^{2}}={{a}^{2}}=2Dt\) (7-39)
\({{y}_{f}}=vt=\frac{v{{a}^{2}}}{2D}=\frac{Q}{2\pi D}\) (7-40)
式中，\(Q=\pi {{a}^{2}}v\)为体积流率;yf为层流射流扩散火焰的高度。
根据Burke-Schumann理论分析所得火焰高度为
\({{y}_{f}}=\eta \frac{v{{b}^{2}}}{D}=\frac{\eta Q}{\pi D}\) (7-41)
因此，表象分析获得的火焰高度和Burke-Schuman理论分析获得的火焰高度是一致的，即高度与体积流率成正比。
类似的表象分析方法可用于自由湍流射流火焰。不同的是，需用湍流的涡团扩散系数Dt取代分子扩散系数:

由湍流的Prandtl混合长度理论:
\({{D}_{t}}\propto l{v}’\propto av\) (7-43)
式中，Dt为涡团扩散系数;a为管子半径yf;l为湍流混合长度;\({v}’\)表征湍流强度。
由式(7-42)和式(7-43)可得
\({{y}_{f}}\propto a\) (7-44)
这表明，湍流扩散火焰的高度正比于管道半径，而与射流速度无关。

7.4燃料液滴的蒸发与燃烧
燃料液滴的蒸发与燃烧是柴油机、空气喷气发动机和液体火箭发动机燃烧室工作过程的一个基本环节，它的蒸发或燃烧速度直接影响燃烧室尺寸和发动性能液滴燃烧是一个典型的凝相燃烧问题，它所涉及的凝相气化过程具有更加普遍的意义
有关液体燃料在气态氧化剂中的燃烧机理，有如下看法:
(1)早前:认为燃烧发生在液体表面，即液相表面的燃料分子与气相中氧分子反应。
(2)现在:发现燃烧时液体燃料表面温度很低，远低于着火所需温度，且液体气化所需能量(蒸发热)远低于反应活化能，故认为液相表面无燃烧反应。液体燃料先蒸发，后在气相中燃烧。
在一般条件下，由于燃料气和氧气从两个方向朝火焰区扩散在压强和温度都不太低的环境，化学反应时间远小于扩散时间，因而液体燃料燃烧属于扩散燃烧。燃料液滴的燃烧机理与液面燃烧基本相同，也属于扩散燃烧。
当然，某些参数在特殊条件(挥发性高、雾化细、相对速度高、气流进口温度高等)下，只有纯液滴蒸发，直到全部液滴蒸发完才发生燃烧反应，这种情况下，接近预混气燃烧。
7.4.1基本方程
只要压力不太低，燃料液滴在氧化剂气体中的燃烧都属于扩散燃烧。先是液滴表面受热蒸发(或分解)气化，燃料气体向周围扩散，化剂气体则向滴面扩散，两者相遇，在离滴面一定距离的地方形成球形或近似球形的扩散火焰。随着燃料的消耗，液滴的直径逐步缩小，火焰的位置也向里移动，因此整个过程是与时间有关的非定常过程。
由于液体燃料的密度比周围气体的密度大得多，液面向里推进的速度比周围气体运动的速度要小得多，因此在分析液滴的燃烧过程时，可以把液面和扩散火焰看作是相对不动的，把整个过程当作准定常过程。可以把射流燃烧所做的全部假设照搬，射流燃烧的基本方程也完全适用于液滴燃烧。
唯一不同的是把液滴看作是一个半径为R的球，在任何一个半径为r的球面上各参数相同，也就是说球对称。
总体质量守恒
\(4\pi {{r}^{2}}\rho v=4\pi {{R}^{2}}{{(\rho v)}_{s}}\) (7-45)
组分连续方程
\(\rho {{D}_{i}}\frac{d}{dr}({{r}^{2}}\frac{d{{Y}_{i}}}{dr})-(\frac{d({{r}^{2}}\rho v{{Y}_{i}})}{dr})+{{r}^{2}}{{\omega }_{i}}=0\) (7-46)
能量方程
\(\lambda \frac{d}{dr}({{r}^{2}}\frac{dT}{dr})-{{C}_{p}}(\frac{d(\rho v{{r}^{2}}T)}{dr})+{{r}^{2}}\sum\limits_{i=1}^{N}{h_{i}^{0}}{{\omega }_{i}}=0\) (7-47)
7.4.2液滴表面的边界条件 –
液滴的蒸发和燃烧是从燃料表面开始，一直延续到整个空间。其边界条件发生在两处:一是液滴的凝相表面，一是离表面甚远的自由空间。
液滴的燃烧速度是指凝相表面蒸发气化的速度。
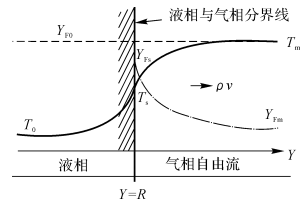
如图7-7所示为液滴表面附近温度浓度分布。

图7-7液滴表面附近温度浓度分布
坐标:液滴中心处r=0，液面处r=R。
1.液面处能量平衡方程(不考虑热辐射)
\({{(\rho v)}_{s}}Q={{\lambda }_{g}}{{(\frac{dT}{dr})}_{s}}\)
考虑热扩散率
\(a=\frac{\lambda }{\rho {{C}_{p}}}\)
引入无因次温度
\({{b}_{T}}=\frac{{{C}_{p}}(T-{{T}_{\infty }})}{Q}\)
则能量方程变为
\({{(\rho v)}_{s}}=\rho a{{(\frac{d{{b}_{T}}}{dr})}_{s}}\) (7-49)
2.液面处质量平衡方程
\({{(\rho v)}_{s}}=\rho {{D}_{F}}{{\left( \frac{d}{dr}(\frac{{{Y}_{F}}}{{{Y}_{Fs}}-{{Y}_{F0}}}) \right)}_{s}}\)  (7-50)
其中，DF为燃料气体扩散系数。
引入系数
\({{b}_{D}}=\frac{{{Y}_{F}}-{{Y}_{F\infty }}}{{{Y}_{FS}}-{{Y}_{F0}}}\)
则质量平衡方程变为
\({{(\rho v)}_{s}}=\rho {{D}_{F}}{{(\frac{d{{b}_{D}}}{dr})}_{s}}\) (7-51)
从上两式可以看出:表面上温度梯度和浓度梯度越大，气化速率越快。
7.5液滴单纯稳态蒸发
液滴的蒸发是一种比较简单的情况，没有化学反应，基本方程可简化。
能量方程:
\(\lambda \frac{d}{dr}({{r}^{2}}\frac{dT}{dr})-{{C}_{p}}\frac{d}{dr}(\rho v{{r}^{2}}T)=0\) (7-52)
组分连续方程(只有液滴蒸发，i=1，Y=Y):
\(\rho {{D}_{F}}\frac{d}{dr}({{r}^{2}}\frac{d{{Y}_{F}}}{dr})-\frac{d}{dr}({{r}^{2}}\rho v{{Y}_{F}})=0\) (7-53)
总体质量守恒方程:
\(4\pi {{r}^{2}}\rho v=4\pi {{R}^{2}}{{(\rho v)}_{s}}\) (7-54)
引入无因次温度bT和系数bD:

能量方程变为
\(\rho a\frac{d}{dr}({{r}^{2}}\frac{d{{b}_{T}}}{dr})-({{(\rho v)}_{s}}{{R}^{2}})\frac{d{{b}_{T}}}{dr}=0\) (7-56)
组分守恒方程变为
\(\rho {{D}_{F}}\frac{d}{dr}({{r}^{2}}\frac{d{{b}_{D}}}{dr})-({{(\rho v)}_{s}}{{R}^{2}})\frac{d{{b}_{D}}}{dr}=0\) (7-57)
方程的边界条件:
r=R处

r=∞处

假定路易斯数 ，即a=DF，则能量方程与组分连续方程的解相同，即bT=bD，因此可以省去下标T和D，再将能量方程积分可得

\(\rho a{{r}^{2}}\frac{db}{dr}-({{(\rho v)}_{s}}{{R}^{2}})b={{C}_{1}}\) (7-61)
利用边界条件，且当r=R和b=bs，时，质量蒸发速度为
\({{\left( \rho v \right)}_{s}}=\frac{\rho a}{R}\ln ({{b}_{\infty }}-{{b}_{s}}+1)\) (7-62)
由此方程可以看出，较小的液滴比较大的液滴蒸发速度更快。
如果消去\({{\left( \rho v \right)}_{s}}\)，可求得另一个b的表达式
\(\left( b-b+1 \right)={{(({{b}_{\infty }}-{{b}_{s}})+1)}^{1-\frac{R}{r}}}\)
自由流和液体表面间的b值之差，从其本身的含义来看是自由流和液体表面之间的温度差或者浓度差，它是传热传质的驱动力，称之为传递数(传热数或传质数)，用B来标记，表达式如下:
\(B={{b}_{\infty }}-{{b}_{s}}\)
假定L为蒸发热，则
\(B=\frac{{{C}_{p}}({{T}_{\infty }}-{{T}_{s}})}{L+{{C}_{L}}({{T}_{s}}-{{T}_{0}})}=\frac{{{Y}_{F\infty }}-{{Y}_{Fs}}}{{{Y}_{Fs}}-{{Y}_{F0}}}\)
对于一个直径为d的小液滴悬浮于热气体介质中，它的热交换问题是通过努赛尔数Nu、雷诺数Re和普朗特数Pr表示的。若v是介质的流动速度(相对于液滴的流动速度)，介质的导热系数、运动黏度和热扩散系数分别由 和a表示，则有
\(\bar{N}u=\frac{{{{\bar{h}}}^{}}d}{\lambda }=2+0.6{{(\frac{vd}{\gamma })}^{\frac{1}{2}}}{{(\frac{\gamma }{a})}^{\frac{1}{3}}}\)  (7-63)
若液滴尺寸很小，由于受到气流的携带，则两者相对运动速度v就很小，雷诺数Re近似为零，因此式(7-63)可简化为
\(\bar{N}u=\frac{{{{\bar{h}}}^{}}d}{\lambda }\text{=2}\) (7-64)
其中，对流换热系数\({{\bar{h}}^{}}\(可由下式求出(l为蒸发体的特征尺寸):
\({{\bar{h}}^{}}\text{=}\frac{\rho {{C}_{p}}a}{l}\bar{N}u\) (7-65)
根据热扩散系数的定义，式(7-65)可变为
\(\frac{{{{\bar{h}}}^{}}}{{{C}_{p}}}\text{=}\frac{2\rho a}{d}\) (7-66)
考虑d=2R，将式(7-66)代入式(7-62)得
\({{(\rho v)}_{s}}=\frac{{{{\bar{h}}}^{}}}{{{C}_{p}}}\ln (B+1)\) (7-67)
式中，B为热力学因数，从能量角度考虑，\({{B}_{T}}=\frac{{{C}_{p}}({{T}_{\infty }}-{{T}_{s}})}{L+{{C}_{l}}({{T}_{s}}-{{T}_{0}})}\)，其中L为蒸发热;从质量角度考虑，\({{B}_{D}}=\frac{{{Y}_{F\infty }}-{{Y}_{Fs}}}{{{Y}_{Fs}}-{{Y}_{F0}}}\)。
从式(7-67)可以看出，蒸发问题被分为两个独立的部分，一部分是\(\frac{{{{\bar{h}}}^{}}}{{{C}_{p}}}\)，由液体表面与环境自由流之间的换热决定;一部分是ln(B+1)，由热力学的相平衡决定。
7.6液滴燃烧蒸发过程及扩散火焰
燃烧时，液滴蒸发过程主要依靠火焰区与液滴表面之间的温度差和浓度差作为传热传质的驱动力。一般情况下液滴燃烧的扩散火焰是在离开表面一定距离处形成的。在扩散火焰中，认为燃料和氧化剂的化学反应速度比扩散混合的速度快得多。
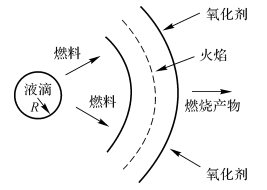
如图7-8所示，火焰区是一个球形薄壳，它将燃料气体和氧化性气体隔开。在火焰面上，燃料和氧化剂的浓度为零(梯度不为零)燃烧产物的浓度和温度在这里为最大值。进行液滴燃烧研究的目的是:
(1)确定蒸发速率。
(2)确定火焰相对液体燃料表面的位置。
(3)在给定几何形状和流动条件下，确定浓度和液滴燃料燃烧产物温度的分布。根据方程可对液滴的燃烧速度、火焰位置、温度、浓度进行计算。
如果液滴和环境的相对速度不大(自然对流和强迫对流很小)，则液滴的蒸发与燃烧可认为在相对静止的环境中进行，它是球对称的。

图7-8燃料液滴燃烧模型
一般工作过程中液滴与氧化性气流间有较大的相对速度，这对燃料液滴的蒸发与燃烧将产生影响，此时液滴周围不再是球对称的Stefan流，包围液滴的火焰不再呈球形，而呈卵形，球对称模型不再适用。
假定液滴燃烧是一步反应，并且在反应系统中，参加反应的只有燃料F、氧化剂O和产物P，令反应的化学计量比为f，则按质量为单位写成的化学式为
fF+O=(1+f)P (7-68)
反应速度为
\(\frac{{{\omega }_{F}}}{-f}=\frac{{{\omega }_{o}}}{-1}=\frac{{{\omega }_{p}}}{1+f}=\omega \) (7-69)
能量方程
\(\lambda \frac{d}{dr}({{r}^{2}}\frac{dT}{dr})-{{C}_{p}}\frac{d}{dr}(\rho v{{r}^{2}}T)+{{r}^{2}}q=0\) (7-70)
式中，q代表燃烧反应所释放的热，也可用燃料的燃烧热来表示q:
\(q=-\sum{h_{i}^{0}{{\omega }_{i}}=-{{\omega }_{F}}\Delta H}\) (7-71)
总体连续方程:
\(\rho v{{r}^{2}}={{(\rho v)}_{s}}{{R}^{2}}\) (7-72)
引入其中B热力学因数，从能量角度考虑，\({{B}_{T}}=\frac{{{C}_{p}}({{T}_{\infty }}-{{T}_{s}})}{L+{{C}_{l}}({{T}_{s}}-{{T}_{0}})}\)，其中L为蒸发热;从质量角度考虑，\({{B}_{D}}=\frac{{{Y}_{F\infty }}-{{Y}_{Fs}}}{{{Y}_{Fs}}-{{Y}_{F0}}}\)。
1.燃烧速度
液滴的燃烧速度计算公式为
\({{\left( \rho v \right)}_{s}}=\frac{\rho a}{R}\ln (B+1)\) (7-73)
2.燃烧时间
液滴直径随燃烧时间的变化关系可由下式确定:
\({{d}^{2}}=d_{0}^{2}-{{\beta }_{b}}t\) (7-74)
\({{\beta }_{b}}=\frac{8\rho a}{{{\rho }_{t}}}\ln (B+1)\) (7-75)
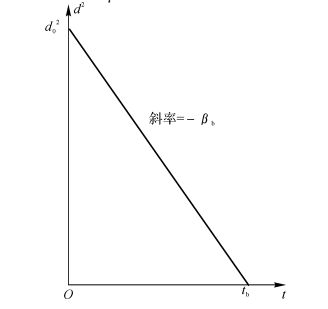
液滴的燃烧时间(也是蒸发时间)(见图7-9):
\({{t}_{b}}=\frac{d_{0}^{2}}{{{\beta }_{b}}}\) (7-76)
碳氢燃料在空气中燃烧，燃烧常数B的数量级为10-2cm/s。

图7-9 液滴蒸发的d2律
3.火焰位置
在火焰处，燃料和氧化剂的浓度为零，用下标f表示火焰的位置，则r=rf处
\({{Y}_{Ff}}=f{{Y}_{Of}}=0\)
火焰位置的表达式如下:
\(\frac{{{r}_{f}}}{R}=\frac{\ln (B+1)}{\ln (\frac{f{{Y}_{O\infty }}}{{{Y}_{F0}}}+1)}=\frac{{{(\rho v)}_{s}}R}{\rho a}\frac{1}{\ln (\frac{f{{Y}_{O\infty }}}{{{Y}_{F0}}}+1)}\)  (7-77)
式(7-77)说明，如果燃烧速度快，火焰将离燃烧表面比较远。因为\(B>\frac{f{{Y}_{O\infty }}}{{{Y}_{F0}}}\)，所以液体燃料扩散火焰永远不会达到液体表面，即rf>R
许多碳氢燃料对氧的化学计量比为0.32，如果纯液体燃料(YF0=1)在标准空气(\({{Y}_{O\infty }}=0.232\))中燃烧，式(7-73)可变为
\(\frac{{{r}_{f}}}{R}=14\ln (B+1)\) (7-78)
对于固体燃料，\({{r}_{f}}\to R\)，火焰位于燃料表面附近
4.温度、浓度分布
火焰区是一个无限薄的面，在火焰内侧不存在氧化剂气体，在火焰外侧不存在燃料。液滴燃烧时的浓度、温度分布如图7-10所示。

图7-10液滴燃烧时的浓度、温度分布
火焰内侧温度分布如下:
\({{C}_{p}}(T-{{T}_{s}})=Q\left\{ (B+1)\exp (-\frac{R}{r}\ln (B+1))-1 \right\}=Q({{(B+1)}^{1-\frac{R}{r}}}-1)\) (7-79)
火焰外侧温度分布如下:
\({{C}_{p}}(T-{{T}_{s}})=(Q+\Delta H({{Y}_{Fs}}-{{Y}_{F0}}))({{(B+1)}^{1-\frac{R}{r}}}-1)+\Delta H{{Y}_{Fs}}\) (7-80)
火焰温度计算公式如下:
\({{C}_{p}}({{T}_{\infty }}-{{T}_{s}})=\frac{{{C}_{p}}({{T}_{\infty }}-{{T}_{s}})+f{{Y}_{o\infty }}(\Delta H-\frac{Q}{{{Y}_{F0}}})}{1+\frac{f{{Y}_{O\infty }}}{{{Y}_{F0}}}}\) (7-81)
燃料浓度分布(R<r<rf)如下:
\({{Y}_{F}}(r)=({{Y}_{F0}}+f{{Y}_{O\infty }})\left\{ 1-\exp (-\frac{{{(\rho v)}_{s}}{{R}^{2}}}{\rho ar}) \right\}-f{{Y}_{O\infty }}\) (7-82)
氧化剂浓度分布(rf<r<∞)如下:
\({{Y}_{O}}(r)=-\frac{({{Y}_{F0}}+f{{Y}_{O\infty }})}{f}\left\{ 1-\exp (-\frac{{{(\rho v)}_{s}}{{R}^{2}}}{\rho ar}) \right\}+{{Y}_{O\infty }}\) (7-83)
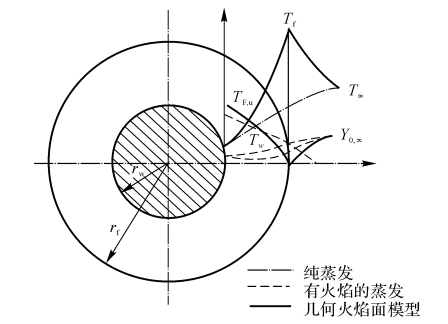
7.7相对静止高温环境中液滴的蒸发与燃烧
如图7-11所示，液滴和环境相对静止，是球对称径向一维流动。

图7-11相对静止高温环境中液滴的蒸发与燃烧
作如下假定:
(1)没有热辐射和热解离。
(2)燃料气由液滴表面向周围扩散，氧和惰性气体由四周向液滴表面扩散。
(3)燃烧产物由火焰区分别向液滴表面和环境两侧扩散。
(4)火焰为球对称。
(5)燃烧区放出的热量一部分传给液滴用于蒸发，大部分释放于环境中。
(6)不考虑边界内移效应，过程为准定常。
列出该体系方程如下:
连续方程:
\(4\pi {{r}^{2}}\rho v=4\pi {{({{r}^{2}}\rho v)}_{\omega }}=const\) (7-84)
动量方程:
\(P=const\) (7-85)
扩散方程:
\(\rho v\frac{dY}{dr}=\frac{1}{{{r}^{2}}}\frac{d}{dr}({{r}^{2}}D\rho \frac{d{{Y}_{s}}}{dr})+{{\dot{\omega }}_{s}}\) (7-86)
能量方程:
\(\rho v{{C}_{p}}\frac{dT}{dr}=\frac{1}{{{r}^{2}}}\frac{d}{dr}({{r}^{2}}\lambda \frac{dT}{dr})+{{\dot{\omega }}_{s}}{{Q}_{s}}\) (7-87)
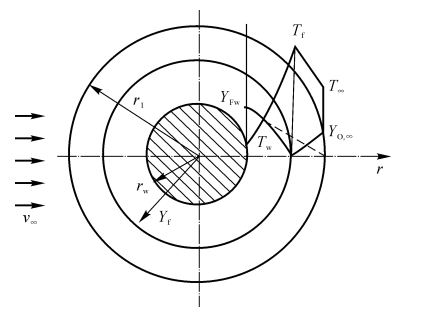
7.8强迫气流中液滴的蒸发与燃烧
在实际的液雾两相流中，当燃料离开喷嘴或当气流湍流脉动较强时，液滴与气流之间存在较大的相对速度，这对燃料液滴的蒸发与燃烧产生较大影响，此时，包围液滴的火焰不再呈圆形、卵形，球对称模型不再适用。

图7-12强迫气流中液滴的蒸发与燃烧
为此，工程上提出一种近似方法“折算薄膜”理论。其基本思想如下:把一个真实的轴对称对流传热、传质问题折算成一个假想的等值球对称分子导热与扩散问题，并把问题人为地分成以下两步:
(1)暂不考虑蒸发与燃烧，把液滴看作是只和气流有对流换热的固球，并把这一对流换热转换成为假想的等值固球导热问题。
(2)不考虑对流的存在，只研究该假想的有分子导热和扩散的球层内的蒸发和燃烧，从而确定蒸发和燃烧速率。
经过大量试验，获得“折算薄膜”半径的经验公式为
\({{r}_{1}}=\frac{{{r}_{\omega }}}{1-\frac{2}{Nu_{T}^{*}}}\) (7-88)
式中 \(Nu_{T}^{*}=\frac{{{h}^{*}}{{d}_{\omega }}}{\lambda }=2+0.6{{\operatorname{Re}}^{0.5}}{{\Pr }^{0.38}}\)
这样的话，很容易将前述球对称理论得到的公式推广到有强迫气流的情况，只需将原来的外边界r=∞换成r=r1。

7.9 碳粒的燃烧
固体燃料包括煤、金属燃料(Al、Mg)、非金属燃料(C、B)和固体推进剂
固体燃料燃烧方式主要包括:
(1)表面燃烧。推进剂燃烧、飞行器头部防护层燃烧。
(2)粉状燃烧。煤粉、金属粉燃烧。
(3)浆状燃烧。
(4)流态化燃烧。
(5)层燃烧。
对于固态碳来说，由于碳沸点很高(接近5000K)，在固体表面上的碳分子只能和吸附的O2，CO，CO2等气体分子发生多相反应碳的燃烧常常是扩散-动力燃烧，受气体组分扩散和表面的反应动力学两类因素的共同制约。
固态碳表面上多相反应机理与气相反应机理不同。碳表面及其附近气层中同时进行下列几种反应：

碳表面反应动力学与吸附过程有关，仍服从Arrhenius定律反应级数一般可按供应不足的组分(如O2，CO2)的表面浓度的一级反应来考虑。
动力学数据表明，一般情况下，E1<E2<E3在温度较低(800℃以下)时，以反应(1)(2)为主;温度较高时，反应(3)起主要作用。

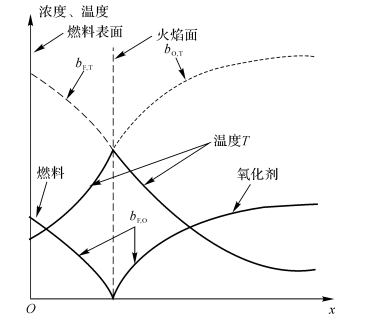
图7-13一般情况下碳表面附近的温度分布附近的温度分布和组分浓度分布

图7-14只存在表面氧化反应时碳表面分布附近的温度和组分浓度
两种情况下碳表面附近的温度及组分浓度分布情况如图7-13和图7-14所示。图7-13中CO2的浓度存在一“驼峰”，说明碳表面存在CO的容积燃烧;温度“驼峰”形状也说明这一现象。碳表面温度高于气相温度，而且碳表面黑度系数大，故辐射效应显著，这一特点往往影响碳的着火特性等。
碳粒燃烧的基本方程，可用类似描述液滴燃烧的基本方程组来描述:
连续方程:
\(4\pi {{r}^{2}}\rho v=4\pi {{r}_{p}}^{2}{{(\rho v)}_{\omega }}=const\) (7-89)
动量方程:
P=const (7-90)
扩散方程:
\(\rho v\frac{d{{Y}_{s}}}{dr}=\frac{1}{{{r}^{2}}}\frac{d}{dr}({{r}^{2}}D\rho \frac{d{{Y}_{s}}}{dr})+{{\dot{\omega }}_{s}}\) (7-91)
能量方程:
\(\rho v{{C}_{p}}\frac{dT}{dr}=\frac{1}{{{r}^{2}}}\frac{d}{dr}({{r}^{2}}\lambda \frac{dT}{dr})+{{\dot{\omega }}_{s}}{{Q}_{s}}\) (7-92)
式中，rp为碳粒半径;，为反应率。
习 题
7.1写出描述射流燃烧的基本方程。
7.2简述和 Schumann对射流燃烧的基本观点
7.3写出液滴单纯蒸发的基本方程。
7.4写出强迫气流中液滴燃烧模型和基本方程
7.5写出碳粒燃烧特点和基本方程。
7.6分析液滴燃烧模型，给出燃烧速度、火焰位置温度分布、燃烧时间的计算公式