高速水下推进的创新概念

摘要

本文主要对高速射流水下推进的概念和研究进展进行了综述。研究表明，某些水推进概念采用了与航空领域类似的原理，同时用水来代替空气作为周围环境和主要工作介质。所分析的推进器类型包括固体火箭发动机、两相气泡冲压发动机和吸水式管道冲压火箭。它们是通过能量性能（比冲、密度比冲和比燃料消耗率），以及反映助推和高速能力的比推力来表征的，后者是指单位横截面推力和推阻比。结果表明，两相冲压发动机的比推力基本上克服了推进器阻力，可用于中高速巡航。但是，如果空气由外部压缩机提供，则其会表现出最高的能量性能；在这种情况下，它需要通过通气管吸入空气，并且不可用于深水水下推进。它的改进型使用船上储存的液化气，完全可以在水下工作，但它的能量性能显示出比火箭更优越的性能。火箭虽具有与速度无关的最小比冲，但却具有随速度降低的高推阻比。海洋管道式火箭可以产生比固体火箭大两倍或三倍的理论比冲，而它们的推阻比值可能超过固体火箭在高速末端的推阻比值。原始图显示了不同推进方法在较宽速度范围内的性能特征。

专用术语

A	横截面积（M2）
Cp	比热[J/（kg·K）]
D	阻力(N)
F	推力（N）
Isp	比冲(s)
Kr	回收系数
	质量流速（kg/s）
P	压力（Pa）
R	比气体常数
r	压缩率
s	熵[J /（kg·K）]
T	温度（K）
U,u	速度（m / s）
V	体积
W	功(J)
ω	比功（J/kg）
X	进出速度比
希腊符号   α         空气体积分数
γ	比热比
η	效率
μ	空气/水质量比
ρ	密度（kg / m3）
a	下标 环境; 初始条件
air	空气
comp	压缩; 压缩空气
exp	膨胀
f	燃料
mix	混合室
opt	最佳
p	推进; 推进剂
T, t	总的
trans	动力传输
w	水

1 引言

本文综述了用于高速水下推进器的喷气推进研究。不涉及通过轴传输机械动力的设备，如螺旋桨和泵驱动的喷水器，而是采用不同的射流产生原理进行水下推进。

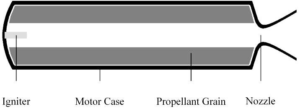
原则上，某些海洋推进概念与航空推进概念是极相似的。区别在于，航空飞行器在气体（空气）介质中运动并经常将空气用作工作介质，而船舶在水中工作，可以将水用作工作液体。火箭发动机可以像航空飞行器一样推动高速水下推进器，不依赖于速度和环境介质；它们可提供很高的推力，且操作时不需要空气，因此，可以适应水下推进器。但是由于其燃料（推进剂）消耗量非常高（意味着比冲相对较低），因而只能够在有限的范围内实现。根据上述原因，已经考虑采用的推进原理是利用周围的水作为工作液体及化学反应物（通常是氧化剂）。 固体推进剂火箭发动机（SRM）的示意图如图1所示。

图1 SRM示意图

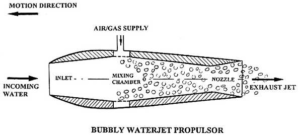
水冲压发动机是一个术语，通常适用于推进器由于其运动而吸水，并通过分流进口减缓进水速度来增加内部压力，将动压力转化为静压的增加。然后将压缩气泡引入水流中，形成一个高速两相排气射流，由于膨胀的气泡对水所做的功，因压力下降而在喷嘴内运动，从而产生推力。在航空冲压喷气发动机中，飞行速度必须达到2马赫以上（约700 m/s）的量级，可在冲压式喷气发动机燃烧室内产生足够的压力，从而实现有效的动力循环。另一方面，水冲压式喷气发动机中，由于水的密度比空气的大得多（大约为1000倍），每秒几米或几十米的运动速度可能就足够了。航空冲压发动机的工作是基于燃烧产生的能量，燃烧产生的能量将工作工质（空气）加热，而水冲压发动机中的工作液体（水）则通过引入压缩空气吸收能量。图2中给出了一种两相水冲压发动机（气泡水冲压发动机）的示意图。

20世纪40年代，两相冲压喷气发动机已经受到了一些关注。关于可压缩气泡流动的早期研究之一是Tangren等人的研究（1949）。他们报道了关于压力和推力测量的理论分析和一系列的实验。在20世纪60年代和70年代，人们对这一主题的关注度与日俱增。Mottard和Shoemaker（1961）在NASA兰利研究中心（Hampton，VA）进行了一项理论和实验研究，他只进行了推力测量。Pierson（1965）研究了采用两相冲压式喷气推进器的水翼设计。 Witte（1969）提出了关于大型水冲压发动机的详细理论研究。在Greiner（1967）编辑的 “水下导弹推进”合集中可以找到一系列概念和技术工作。Muench和Garrett（1972）发表了一篇关于两相海洋推进的综述，讨论了包括喷雾在内的不同工作模式，Muench和Ford（1970）也对此进行了分析。与此同时，前苏联也进行了两相水冲压式发动机研究（Cherney，1977年）。

图2  两相水冲压发动机示意图

20世纪90年代和21世纪，以色列理工学院Gany小组进行了综合研究，推动了两相水冲压式喷气发动机推进领域的重大进展，首先是Albagli和Gany的初步分析（1990,1992）和 Gany（1993）的概念性演讲。Varshay和Gany（1997a，b）取得了与该主题相关的两项美国专利（以及全球多项专利）。此外，Albagli和Gany（2003年）以及Mor和Gany（2004年）对两相气泡流的特性和发展进行了广泛的基础研究，这些研究有助于推进系统的设计和预测。Gany（2004）提出了两相冲压式喷气推进器热力循环的基本考虑，同时，Mor和Gany（2007）还介绍了该系统的性能制定。Koren（2005）和Valensi（2005）的硕士研究课题分别对装有25 mm进气道推进器的水箱进行了实验研究，并使用4 m船进行了海上试验。Gany等（2008）对空气增强水射流进行了研究，后来Gany和Gofer（2014）再次对该问题进行了研究。Haustein等人（2009年，2011年，2013年）多次研究了船载液化气体作为气体储存装置，用于水下海洋冲压发动机中形成气泡喷射。后面将对Gany小组的研究基础进行更详细地阐述。

过去十年中，Chahine及其合作者（例如，Chahine等人，2008年；Singh等人，2014年；Wu等人，2015年）在DynaFlow对空气增强水射流推进进行了广泛的研究，包括气泡流动力学研究。Gowing等人研究了两相水射流喷管（2010年）。 最近，中国的Zhang等人（2018a,b）对两相冲压式喷气发动机进行了研究。

水冲压发动机的另一种形式是冲压式喷气发动机装置，在该装置中，由于注入水与反应燃料之间的化学反应，使进入的水转换成蒸汽。这种反应可以基于碱金属[例如，锂（Li）、钠（Na）和钾（K）]或其他反应性化学品，如三乙基铝（TEA）（例如，参见Schoeffl，1988）。这种类型的推进器如图3所示。虽然为水下推进提供了一种显而易见的解决方案，但要处理这种与空气或水接触时可以点燃的活性燃料，则是一项具有挑战性的任务。

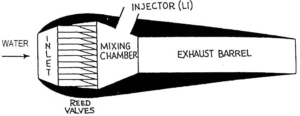
另一种与水冲压发动机有关的推进概念是水脉冲射流或液压脉冲射流。该系统由一个管道组成，该管道的入口配备有簧片阀。由于船舶运动使水进入并充满管道。和前面的概念一样，这里也将反应燃料注入水中，并与管道内的部分水发生反应。放热反应会产生气体（通常是氢）和水蒸气，这些气体和水蒸气导致内部压力升高，意味着入口阀关闭，管道中剩余的水排出，形成高速排气射流和高推力。循环结束后，当压力下降时，进口阀再次打开，同时开始了新的循环。Gongwer（1960）进行了脉冲喷射研究，并考虑用液态碱金属（Li）作为燃料，后来该研究由Payne（1983）与Bohachewsky和Torrey（1985）进行；概念图见图4。液压脉冲喷射器的主要缺点是巨大的循环推力变化会引起强烈的振动和大的机械应力。

还有一种受到关注的水冲压发动机变型是海洋吸水式管道式冲压火箭，它可以提供一种实用而有效的水下推进方法。在运动时，水下管道式火箭通过一个入口吸水。它包括一个由固体推进剂组成的气体发生器，固体推进剂产生热量将进入的水蒸发成蒸汽。常规且平衡的固体推进剂产生的燃烧产物，不会与水发生化学反应。当使用含有大量活性金属（如镁（Mg）或铝（Al））的富含燃料推进剂时，固体推进剂的部分燃烧产物将继续与水发生放热反应，并大幅提高能量性能（图 5）。Hacker和Lieberman（1969）描述了这种使用铝热剂燃料的概念。最近，我们看到有人（Yang和He，2012年；Huang等人，2014年）对这个概念重新产生了兴趣，尽管还没有在实际条件下进行测试。作为目前研究工作的一部分，本文随后将对水下管道式火箭进行讨论。

图3 水下冲压发动机概念是基于将反应燃料（TEA）

注入到进水中的放热反应，从而将水转化为蒸汽

图4 水下脉冲喷射概念

2两相水冲压发动机的理论分析

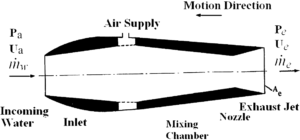
接下来将对两相水冲压发动机（气泡水冲压发动机）进行理想的热力循环分析。为了深入了解所涉及的过程，下面将详细介绍Gany（2004）给出的分析。在图6中给出了推进单元的不同部分和符号。

推进器的一般推力方程是：

\(F={{\overset{\bullet }{\mathop{m}}\,}_{w}}\left( {{U}_{we}}-{{U}_{wa}} \right)+{{\overset{\bullet }{\mathop{m}}\,}_{air}}{{U}_{air,e}}+\left[ \left( 1-{{\alpha }_{e}} \right)\left( {{P}_{we}}-{{P}_{wa}} \right)+{{\alpha }_{e}}\left( {{P}_{air,e}}-{{P}_{a}} \right) \right]A_{e}^{{}}\)   （1）

方程（1）说明了液相和气相中的不同压力和速度值。在理想情况下呈现最佳工作条件和性能，假设两相处于平衡状态，即它们具有相同的速度、温度和压力。此外，假设采用具有P_e=P_a的适配喷管。还可以记住，气体（空气）的质量流量比水流量小两个数量级或更多，\({{\overset{\bullet }{\mathop{m}}\,}_{a}}\langle \langle \overset{\bullet }{\mathop{{{m}_{w}}}}\,\)产生了一个简单的推力方程的近似值， 其中U_a是船的速度，U_e是排气速度：

\(F=\overset{\bullet }{\mathop{{{m}_{w}}}}\,\left( {{U}_{e}}-{{U}_{a}} \right)\)         （2）

图5 水下管道式火箭，通过固体推进剂（或铝热剂）气体/热发生器将水转化为蒸汽

图6两相气泡水冲压式喷气发动机的符号和主要部分

图7理想的两相冲压发动机热力循环（Gany，2004）

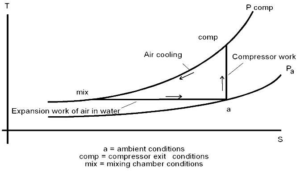
图7描述了（在Gany的研究之后，2004）单位质量空气中两相冲压发动机的理想功率循环：环境温度T_a和P_a（测点a）下的空气由压缩机压缩至压力P_comp（压缩测点）。压缩空气被引导到水下推力单元中，将压缩气体注入并与混合室内分散气泡形式的水流混合。在理想情况下，压缩空气的压力等于混合室压力P_comp = P_mix，其实这是由于扩散器内的水流减慢而导致的冲压力（实际上，它可能略高）。在混合过程中（大约在恒定压力下），气泡迅速失去其热能。该过程在图7中的热力学图表中由压缩测点和混合测点之间的线表示。这种快速冷却得到了Albagli和Gany（2003）的支持，这表明在这种动力循环中几乎不能有效地利用气体热能。它们从混合室运动到喷嘴出口的过程中（回到测点a的情况），气泡等温膨胀，同时它们的压力从P_mix下降到环境压力P_a。在膨胀过程中，气泡吸收周围水的热能，同时将其膨胀功传递给水。在此分析中，假设水的温度和压力等于空气初始状态下的温度和压力，即T_w = T_a和P_w = P_a 。

2.1 理想空气循环效率

每单位质量空气的理想（等熵）压缩功为:

\({{w}_{comp}}={{C}_{p}}{{T}_{a}}\left( {{r}^{\left( \gamma -1 \right)/\gamma }}-1 \right)\)                               (3)

其中r是压缩比：

\(r={{P}_{comp}}/{{P}_{a}}\)                                         (4)

在压缩过程中，空气温度升高：

\({{T}_{comp}}={{T}_{a}}{{r}^{\left( \gamma -1 \right)/\gamma }}\)                                       (5)

对于理想气体，比热C_p是:

\({{C}_{p}}=\frac{\gamma R}{\gamma -1}\)                                           (6)

其中R是特定的气体常数。因此，

\({{w}_{comp}}=\frac{\gamma R{{T}_{a}}}{\gamma -1}\left( {{r}^{\left( \gamma -1 \right)/\gamma }}-1 \right)\)                                 (7)

对于空气，у= 1.4和R = 287 J /（kg·K）。

如前所述，压缩空气的热能在没有做有效功的情况下被转移到水中。由于水的总热容量与空气相比存在巨大差异，因此水温几乎不会改变。通过空气膨胀功将动力传输到水中：

\(W=\int{PdV}\)                                      （8）

在P_comp到P_a的等温膨胀期间，每单位质量空气的功为：

\(w=R{{T}_{a}}\ln r\)                                   （9）

功率循环效率定义为传输到水的等温膨胀功与输送到压缩机的等温膨胀功之比（等于理想循环的等熵压缩功）：

\({{\eta }_{cycle}}=\frac{{{w}_{\exp }}}{{{w}_{comp}}}=\frac{\ln r}{\left[ \gamma /\left( \gamma -1 \right)\cdot \left( {{r}^{\left( \gamma -1 \right)/\gamma }}-1 \right) \right]}\)                   （10）

当压缩比大于1时，等温膨胀功小于等熵压缩功。我们将循环效率视为动力传输效率（从气体到水）：

\({{\eta }_{trans}}={{\eta }_{cycle}}\)                                     (11)

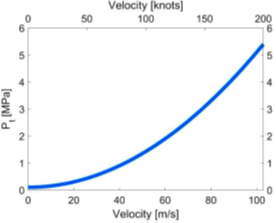
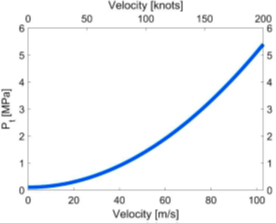
冲压发动机推进中的压力增大是由动态压力（冲压压力）转换为静态压力的结果。可达到的最大压力是获得的停滞压力（总压力，P_t），此时流体速度减慢至零速度。停滞压力与水中巡航速度的关系如图8所示。压力比P_t/P_a是任何巡航速度下的最大压缩比P_comp/P_a：

\({{P}_{comp,\max }}={{P}_{a}}+\frac{1}{2}{{\rho }_{w}}U_{a}^{2}={{P}_{t}}\)                           (12)

在实际应用中，循环效率计算假设：被注入到混合室内的空气流速等于进水速度U_a的50％。那么，混合室中产生的压力P_mix低于总压力P_t。和在理想循环中所假设的一样，压缩空气以混合室中存在的压力注入推进单元，即P_comp = P_mix，因此,

\({{P}_{comp}}={{P}_{a}}+\frac{3}{4}\left( \frac{1}{2}{{\rho }_{w}}U_{a}^{2} \right)={{P}_{t}}-\frac{1}{8}{{\rho }_{w}}U_{a}^{2}\)                     (13)

根据方程式（10），利用方程式（13）中的P_comp，在图9中给出了循环效率或动力传输效率η_trans与巡航速度的关系。可以看出，在理想情况下，η_trans从零速度下的单位值逐渐减小：15 m/s（30节）时约为90%，25 m/s（50节）时约为83%，100 m/s（200节）时约为56%。

图8 停滞压力与水中的巡航速度

图9 理想循环时的循环效率（=动力传输效率）与巡航速度

推进效率η_p定义为推力功率与压缩机输送功率之比。推力是:

\(F{{U}_{a}}={{\overset{\bullet }{\mathop{m}}\,}_{w}}\left( {{U}_{e}}-{{U}_{a}} \right){{U}_{a}}\)                           (14)

喷射推进装置的能量平衡（每单位质量的水）是

\(\frac{U_{e}^{2}}{2}={{K}_{r}}\frac{U_{a}^{2}}{2}+{{\eta }_{trans}}\mu {{w}_{comp}}\)                           (15)

式中，K_r是进水流的动能回收率（由于水是不可压缩流体，K_r也代表推进装置内的动态进水压力回收率），μ是根据两相的质量流量比定义的空气/水质量比：

\(\mu ={{\overset{\bullet }{\mathop{m}}\,}_{a}}/\overset{\bullet }{\mathop{{{m}_{w}}}}\,\)                                 (16)

推进效率可表示如下：

\({{\eta }_{p}}=\frac{\left( {{U}_{e}}-{{U}_{a}} \right){{U}_{a}}}{\left( 1/{{\eta }_{trans}} \right)\cdot \left\{ \left( U_{e}^{2}/2 \right)-\left[ {{K}_{r}}\left( U_{a}^{2}/2 \right) \right]\left. {} \right\} \right.}\)                       (17)

在速度比方面，X = U_e / U_a：

\({{\eta }_{p}}=\frac{2{{\eta }_{trans}}(X-1)}{{{X}^{2}}-{{K}_{r}}}\)                                   (18)

可以表明，对于最高的推进效率，最佳的喷射速度比是：

\({{\left( \frac{{{U}_{e}}}{{{U}_{a}}} \right)}_{opt}}=1+\sqrt{1-{{K}_{r}}}\)                               (19)

然而，如果入口压力回收率K_r接近于1（非常好），则推进效率的最佳值[方程式（19）]意味着推力非常低。实际速度比可以是约1.3~1.4。

空气/水质量比α（近似于空气质量分数）与均质空气/水混合物中空气体积分数之间的关系为:

\(\mu =\frac{{{\rho }_{a}}}{{{\rho }_{w}}}\left( \frac{\alpha }{1-\alpha } \right)\)                               （20）

其中ρ_a和ρ_w分别表示空气和水的密度。这个表达式表明，即使是高体积分数的空气也归因于非常低的质量分数，例如，对于α=50%，那么在大气压力下μ≌0.1%。理想情况下，喷管出口处的压力等于环境压力，P_e=P_a。如果存在单分散气泡，则离散气泡体积分数的最大理论填充量不能超过74％，这相当于质量比μ= 0.35％。更现实地说，它可能是μ=0.25%，这涉及到空气体积分数约为67%。这意味着为了在整个推进器中保持气泡流动，空气-水质量比应该保持较低水平。这是气泡式冲压喷气发动机的固有特征，将其推力限制在不能使船达到高加速度的水平，这与发动机的“高速档”操作类似。还应注意，当推进器速度增大时，空气-水质量比也应该增加，以便克服阻力并超出气泡流动状态。这是因为每单位质量空气的压缩机输出的功率对巡航速度的依赖性[通过压力比；见公式（7）和（9）]较弱于推力功率 [方程式(14）]，这对于该推进方法的有效运行设定了速度限制，使巡航速度达到中高（但不是很高）。然而，如实验结果中所示，推进器产生的推力也随着较高的空气-水质量比而增加，尽管效率低于均匀的气泡流动方程的预测。

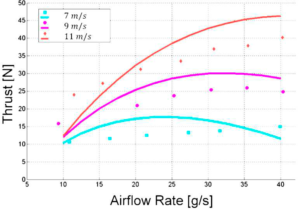
考虑到内部和外部阻力损失，Mor和Gany（2007）绘制了作为巡航速度函数的运行参数的性能图。我们采用这种概念方法预测拖拽池实验（入口直径25 mm和喷管出口直径39.6 mm）中测试的实际推进器的推力与船的速度和注入气流速率。结果如图10所示。穿过推力线并标记为0.67的线表示在大气压下空气的体积分数为67％（质量分数为0.25％）。

图10 测试推进器的理论推力图（N），其入口直径为25mm，喷嘴出口直径为39.6mm，作为运动速度和空气质量流量的函数[基于Mor和Gany的预测方法（2007）]。

两相气泡水冲压发动机通常采用由压缩机产生的压缩空气气泡。因此，它最适合用于水面船舰的推进。如果空气可以通过延伸到水面以上的通气管吸入，它可能对下潜稍微浅的航行器也有用。但是，对于下潜较深的水下航行器，航行器上应该存在气泡源。在我们的实验室中，Haustein等人研究了以浓缩形式储存气体（即液化气体）的创新思想。（2009年，2011年，2013年）。利用自增压液化气，可以将小液滴注入到水下推进装置混合室部分的水流中。与液化气罐内的压力相比，混合室内的压力较低（低于液化气体在水温下的平衡蒸气压），因此，注入的液滴处于过热状态并在水中沸腾，形成的气泡比原来的液滴要大得多。

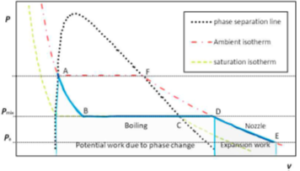
图11 以液化气体沸腾作为气泡源的两相冲压发动机的简化理想热力循环P-V图（ABCD线下的区域反映了由于沸腾和加热可能产生的理想额外功；DE下的区域是喷嘴的膨胀功）

与压缩空气气泡的情况一样，液化气液滴沸腾形成的气泡在通过喷嘴时会膨胀，喷嘴内的压力从混合室下降到出口平面的环境压力。图11给出了液化的过热气体从注入到其相变，以及最后在喷嘴内膨胀的理想简化热力学描述。与注入气泡不同的是，液化气滴在水中沸腾意味着气泡沿着混合室移动时会增长。由于相变引起的气泡体积增加，有可能对水做进一步的膨胀功。然而，气泡形成（以及内部流动中气体体积的增长）是通过闪蒸过程发生的; 因此，作者认为，它对流体膨胀功的利用效率不高。

液化气储存在一个船载储罐中。在环境温度下对蒸汽压力进行自加压。液体压力在注入时降低到混合室压力（图11，A到B线，在恒定焓下）；它通过吸收水中的热量在混合室中沸腾（图11，B线到C线，在恒定压力和温度下的相变）; 然后，形成的气体（蒸汽）在混合室中以恒定压力加热至水温（图11，C线到D线）；最后，它从混合室压力等温度地膨胀到环境压力，同时沿着喷嘴移动（图11，线D到E）。如前所述，可以假设水温恒定。在这种理想化循环中，可用的最大功近似于式（21），并在图11中表示为“相变潜在功”+“膨胀功”，分别指由于喷嘴中的相变（沸腾）和压力梯度而产生的理想气体功：

\({{w}_{T}}\approx R{{T}_{a}}\left[ 1+\ln \left( \frac{{{P}_{mix}}}{{{P}_{a}}} \right) \right]\)                           （21）

理论上，相位变化产生的功可能高于喷嘴中因P_mix/P_a<e的气体膨胀功，因为在前一种情况下，气体体积从很小值（如液体）增加到最大值（如在混合室压力和温度下的气体）。然而，如前所述，相变过程对液体膨胀功的作用可能比较低，这主要归功于喷管中的压力梯度引起的气体膨胀。

3. 吸水式冲压火箭

我们的实验室已对吸水式冲压火箭概念进行了分析，并打算在静态发射设施和水箱中进行测试。Eisen（2018年）的博士研究计划总结了其中一部分工作。水下管道冲压火箭的概念图如图12所示。

图12吸水式管道冲压火箭概念图

     吸水式管道冲压火箭不依赖于大气，因此可以在水下完全深入地操作。与固体火箭发动机（SRM）类似，固体推进剂药柱也可以在不添加水的情况下提供高推力。然而，仅仅是水进入—由于推进器运动而通过入口进入，并且由于固体推进剂的高热释放而进一步转化为蒸汽—即使在没有化学作用的情况下，也可提高推力和比冲。海洋管道冲压火箭的膛压由巡航速度决定，在给定速度下，其最大值等于进入水流的停滞（总）压力。固体推进剂可以设计成在燃烧室压力下燃烧，不需要一个带有节流喷管的单独燃烧室。如图8所示，滞止压力随着运动速度而增加（例如，它在25 m / s的速度下约等于4 bar，在100m / s时等于50 bar）。通过收敛-扩散喷管（推进剂燃烧产物+蒸汽）的气流被阻塞。由于燃烧室压力的增加和热能对排气射流动能的转换增强，能量性能随速度的增加而增加。值得注意的是，由于相对较低的船速，进水的动量远低于排气喷射的动量（与航空冲压发动机相比，航空冲压发动机在飞行速度大于一个数量级时获得类似的停滞压力）。在热化学程序CEA（Gordon和McBride，1994）的辅助下，根据方程(22)–(25)对不同水/推进剂质量比的固体火箭进行了推力计算，得出了平衡流动条件和喷射性能（调整后的喷管）：

\(F={{\overset{\bullet }{\mathop{m}}\,}_{e}}{{u}_{e}}-{{\overset{\bullet }{\mathop{m}}\,}_{w}}{{u}_{a}}\)                                   (22)

出口（喷射）流速等于推进剂+水流速：

\({{\overset{\bullet }{\mathop{m}}\,}_{e}}={{\overset{\bullet }{\mathop{m}}\,}_{p}}+{{\overset{\bullet }{\mathop{m}}\,}_{w}}\)                                     （23）

定义

\(\frac{w}{p}={{\overset{\bullet }{\mathop{m}}\,}_{w}}/{{\overset{\bullet }{\mathop{m}}\,}_{p}}\)                                       （24）

得到：

\(F={{\overset{\bullet }{\mathop{m}}\,}_{p}}\left[ 1+\left( \frac{w}{p} \right) \right]{{U}_{e}}-{{\overset{\bullet }{\mathop{m}}\,}_{w}}{{U}_{a}}\)                               （25）

比冲根据下式计算：

\({{I}_{sp}}=\frac{F}{{{\overset{\bullet }{\mathop{m}}\,}_{p}}{{g}_{0}}}\)                                       （26）

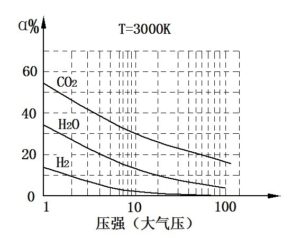
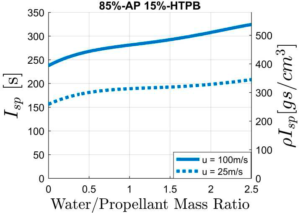
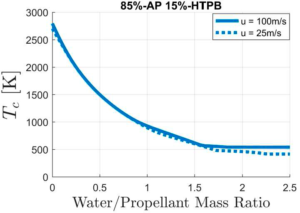
我们首先估计了将水引入燃烧室的效果，在燃烧室中，水在没有与燃烧推进剂发生化学反应的情况下，会发生相变，变成蒸汽。图13给出了这种水增强火箭发动机的计算比冲和密度比冲（对于容积受限系统很重要），以及两种巡航速度下的水-推进剂质量比，25 m/s（意味着燃烧室压力为4 bar）和100 m/s（意味着燃烧室压力为50 bar）。在这两种情况下，假设出口喷管适应环境压力（1巴）。零水/推进剂（w/p）比值表示纯火箭的比冲量（不加水）。采用85%高氯酸铵（AP）和15%端羟基聚丁二烯（HTPB）的固体推进剂配方。通常，w/p比会受到整个燃烧室温度降低到水的平衡沸腾（冷凝）温度的限制（图14）。在较低的燃烧室温度下工作意味着对绝热层、壳体和喷管材料的条件很宽松，以及通过柔性喷管更容易控制推力矢量。很明显，水的添加会提高比冲（高达约30％）。然而，由于喷管膨胀较大，在较高的燃烧室压力下其性能明显高于较低压力下的性能。因此，在低巡航速度（随后是较低的冲压压力）下，与受到相对较低的冲压压力的限制(这意味着性能较低)相比，人们更愿意采用在高燃烧室压力下、不加水的纯火箭工作。

如果使用水反应性推进剂，则可以显着提高吸水式管道冲压火箭的性能。这种推进剂的潜力在于某些金属燃料。这种燃料与水反应时会产生非常大的热量，并产生氢气和大量的蒸汽。一般来说，使用由100%纯金属组成的气体发生器是不切实际的。在实践中，考虑在高度金属化的推进剂中使用最少量的氧化剂，以维持燃烧。然后，将金属和氧化剂颗粒填充在聚合物粘合剂中。为了证明水对金属化燃料的性能上限，对纯金属进行了热化学计算（Gordon和McBride，2004）。 金属与水的一般化学计量反应是：

xMe+yH₂O=Me_xO_y+yH₂                             (27)

其中Me表示金属。表1列出了所选金属与水的重量热、体积热和产氢量。

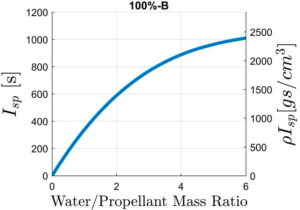
铍（Be）在每个参数中表现出最佳的能量性能，但由于其毒性和反应产物，在实际应用中则不予考虑。在碱金属中，锂与水的反应热很高，但其密度非常低。钠的能量性能较低。锂和钠都是水反应性很强的金属，很难处理并包在固体推进剂中。在其他金属中，硼（B）的理论性能最好（图15）。我们的经验表明，它可以与蒸汽发生反应（Rosenband等人，1998）。然而，在实际应用中，由于硼的副反应和不完全反应，很难获得较高的燃烧效率，而且硼的价格相对较高。

图13采用加水固体推进剂（85%AP+15%HTPB）的水下火箭的计算比冲和密度比冲与水/推进剂质量比的关系曲线

图14采用加水固体推进剂（85％AP + 15％HTPB）的水下火箭的计算燃烧室温度与水/推进剂质量比的曲线关系

表1选定的金属与液态水反应的最大理论重量热和体积热以及产氢量

燃料	密度 g/cm3	比反应能 kJ/g	比能量密度 kJ/cm3	化学计量水/金属质量比	比H2摩尔产量 (mol/g)	比体积H2摩尔产量 (mol/cm3)
Li	0.54	25.5	13.8	1.30	0.072	0.039
Be	1.85	36.1	66.7	2.00	0.111	0.21
B	2.35	26.7	62.7	2.50	0.139	0.34
Na	0.97	2.8	2.7	0.39	0.022	0.021
Mg	1.74	13.0	22.6	0.74	0.041	0.072
Al	2.70	15.2	40.9	1.00	0.055	0.15
Zr	6.49	5.7	37.2	0.39	0.022	0.14

图15采用加水硼燃料的水下管道式冲压火箭的理论比冲和密度比冲与水/硼质量比的关系曲线

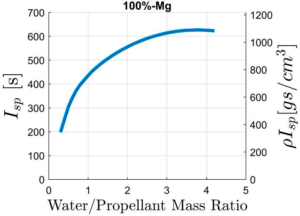
在实际应用中，我们会检验镁和铝，因为它们的使用有效性、低成本和性能都非常好。镁的能量性能比铝低一些，但它与水的反应性更强。图16显示了镁在吸水式管道冲压火箭中的能量性能。 此处更详细地显示了铝作为吸水式管道冲压火箭燃料的性能。 它与水的反应是：

2Al+3H₂O→Al₂O₃+3H₂+818.5 kJ/mol                     (28)

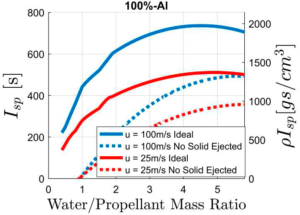
当反应温度低于480℃时，可能会得到其他凝聚相产物[Al(OH)₃，ALOOH]。为了描述铝作为吸水式管道冲压火箭中实际金属化燃料的最高理论性能，针对不同的水/燃料质量比计算了比冲和密度比冲（图17）。结果表明，I_SP和ρI_SP的理论值分别超过700 s和2000 gs/cm³，几乎是传统固体推进剂的三倍。考虑到铝与水的反应产物含有大量的冷凝材料[Al₂O₃或Al(OH)₃]，对冷凝材料留在反应室内、不流出喷管的情况进行重复计算。即使在这种情况下，与固体火箭相比，发动机性能也可能提高一倍或更多。应该注意的是，当使用铝作为反应燃料时，与不与水反应的固体推进剂相比，可能会引入大量的水。而且，如前所述，在实际应用中，使用富燃高金属化固体推进剂气体发生器，其中金属化燃料以细颗粒的形式引入推进剂药柱。也可以使用常规氧化剂如AP。然而，可考虑含氟氧化剂（例如聚四氟乙烯），它可作为与金属反应性很强的粘合剂。

图16采用加水镁燃料的水下管道式冲压火箭的理论比冲和密度比冲与水/镁质量比的关系曲线

（有冷凝产物喷射和没有冷凝产物喷射）与水/推进剂质量比的关系曲线

4 实验步骤

用于水下推进研究的主要测试设施是一个直径为10m的圆形水池（称为水箱或拖水池，图18），配有一个中央电动机，它可以使一个臂旋转，在该旋转臂的顶端装有水下推进器。这种布置可以用作具有连续（圆形）运动的牵引罐，因此它可以实现相对长的测试持续时间。在现有的装置中（使用7.5 kW的中央电动机），可得到高达17 m/s（约34节）的转速。目前正在建造的升级电动机（31 kW）预计可以使牵引速度达到25-30 m/s（约50-60节）。当旋转臂的轴与电动机断开时，也可以测试独立的自推进器。电动机可以测量转速和力矩（和间接力），从而表明安装的推进器的性能。水池设施如图18所示。

图18 用于水下推进研究的直径为10米的水池设施

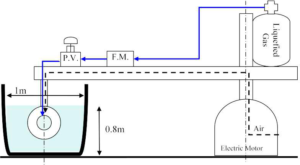
水下两相冲压喷气推进器是一个长390 mm，机身最大直径75 mm，进口直径25 mm，出口喷管直径可在32至40 mm之间变化（图19）。配有压力表，指示推进器的内部压力。加压空气和液化气体的管道安装在臂中，可以提供在测试中使用的液体的测量流速和压力调节流速（图20）。

图19 水下两相气泡水冲压式喷气推进装置

图20两相冲压发动机试验用拖曳池装置的示意截面图，包括空气和液化气体供应装置（P.V=气动阀；F.M=涡轮流量计）

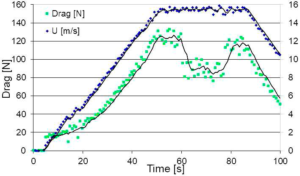
实验以预定的推进器速度模式进行，由中央电动机控制。由于整体系统阻力与推进器机身和支撑支柱阻力导致的阻力超过了推进器产生的推力，因此，试验实际上是拖池试验，推力是根据推进器空气（或气体）关闭和打开时的整体阻力差分别推导出来的。实验顺序是先打开电机，达到所需的速度，然后打开进入推进器的气流，保持稳定运行约10 s，最后，在此阶段之后，关闭气流，关闭电机。通过壅塞式喷管测量气流速度。典型的实验如图19所示[来自Haustein等人获得的数据(2011)]。这里的“阻力”代表系统的整体阻力，包括推进器、支柱阻力和旋转臂阻力。如前所述，实验以不同的预定速度进行。试验结果（Koren，2005年）和模型预测（Mor和Gany，2004年）之间的推力与气流速度对比如图20所示（Koren，2005年之后）。实验结果与理论线的偏差是由于在较高的气流速率范围内，实际的气水质量比超过了实际气泡流的范围。此外，实际的外部和内部阻力可能都高于假设值。然而，值得注意的是，尽管在纯气泡流状态之外运行，但增加气流速率可以增加推力。

图21典型的水下两相推进器拖池式试验

[预定速度是由水箱设施的中央电机得到的；采用自Haustein等人的数据。（2011）]

图22  2-mm过热丁烷液滴在温度为300 K的水柱中沸腾，在约30 ms内显示出约200倍的体积增加[采用自Haustein等人获得的数据(2009)]

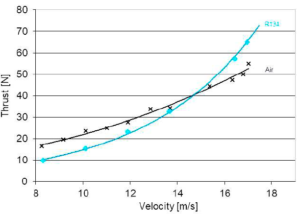
将不同的气体与空气进行比较时，必须基于空气当量进行比较，即，由于气体的推进作用是由其体积分数决定的，所以在相似的条件下，比较的数量具有相同体积。图23 [采用自Haustein等人获得的数据 (2011)]给出了推力测试数据与采用空气或液化气体R134在空气当量流速为17g/s时的速度关系曲线。用水下冲压式喷气推进器进行了试验，推进器的喷管出口直径为39.6 mm。从图22可以得出两个重要结论：（1）总的来说，液化气体和空气的效应相当; （2）在高速范围内，与空气相比，液化气体获得的推力更大，这可以表明由于相变会对膨胀产生一些积极的利用，尽管在低速范围内并不明显。当使用液化丁烷时，观察到类似的液化气体效应。

图23空气和R134液化气体在空气等效流速为17 g / s时的推力与船速关系曲线 [采用自Haustein等人获得的数据。（2011）]

水下火箭推进器

作为吸水式气体发生器管道式火箭推进器的基准，研究了由固体推进剂火箭推进的长360 mm，直径50 mm的机身。该弹体用于两个试验系列：（1）静态点火试验，用于研究发动机性能；（2）水下操作，用于演示和评估使用不同剂量推进剂获得的速度。使用了重量在118到265 g之间的内燃固体推进剂药柱（75%AP和25%聚酯），有一个圆形端口提供渐进推力。发动机和推进剂配置如图23所示。

图24 用于水下火箭推进器的发动机和推进剂配置

1-推进器头部; 2-压力头; 3-固体推进剂药柱; 4-衬层; 5-发动机壳体; 6-出口喷管; 7-喷管支架

静态点火试验显示了稳定燃烧约3 s，最大室压为30 bar，推力约为200 N（20 kgf）。在具有相同火箭发动机的水箱中的水下自推进动态测试使得推进器速度高达20 m/s（40节）。使用了不同的前端头锥配置。推进器被淹没在水面下约7 cm处。