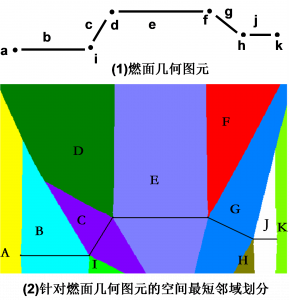
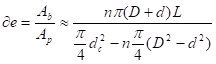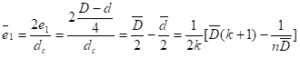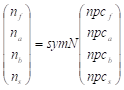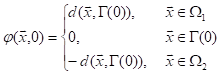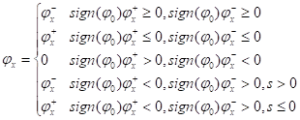第二章  药柱设计

2.1  概述

药柱（grain）是具有特定几何形状和尺寸的固体推进剂，它是发动机的能源和工质源。药柱的几何形状和尺寸决定了发动机的燃气生成率及其变化规律，因此也就决定了燃烧室的压强和发动机推力随时间变化的关系。药柱设计水平的高低在很大程度上影响发动机的性能好坏。

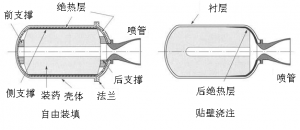
因为现代固体火箭发动机大多采取贴壁浇铸法制造药柱，绝热层（insulation）、衬层（liner）和药柱形成整体，所以就将这种整体结构统称做装药。而浇铸推进剂的过程也有人称之为“装药”。

这里注意药柱和装药的区别，药柱仅是推进剂部分，而装药则是包含绝热层部分。在英语中统称为“GRAIN”。

在发动机设计中药形（grain configuration）的选择和结构的调整以适应发动机和飞行器任务的特殊需要是发动机设计的重要工作之一。通常发动机性能要求和推进剂燃速是决定药形选择来适应期望的推力时间曲线的主要因素。加工能力和制造成本也是很有影响的。尤其是药形必须满足推力、燃烧时间、燃烧室压强、总冲、质心移动、结构强度、储存寿命、温度限制和制造成本的要求。

过去几十年发动机研制结果可提供多种药型。目前，设计集中在相对较少的几种构型，由于大量的固体火箭发动机应用，可以通过组合几种已知的构型或稍微改变一下传统的构型来满足。装药设计的趋势是不再使用会导致裂纹的较弱的结构、产生较高拖尾（sliver）的结构、较低的体积装填分数（volumetric loading fraction）或制造昂贵的结构。

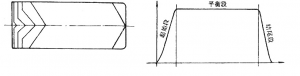
装药在发动机中通常有两种装填方式，即自由装填式（free standing）和贴壁浇铸(case bonded)装填式（图2-1）。

图2-1  装药装填方式

自由装填装药通常适用于小型战术弹和中等尺寸的发动机，其成本低容易检测。贴壁浇铸发动机性能较好，因其省略了支撑装置，绝热层也较少，可以提高体积装填分数。但其制造成本高、应力集中高。然而今天几乎所有大发动机和部分战术发动机都采用贴壁浇铸装药。

推进剂表面燃烧的影响对于柱形、管形、楔形和槽形这样的结构是很明显的。外燃柱形－减面、内燃管形－增面、外燃楔形－减面、内外燃管形－等面。

大部分推进剂装药组合了两种或更多的这些基本的型面来获得期望的燃烧特性。例如：星形组合了楔形和内燃管形。术语“锥柱”是由锥形和柱形缩写而成。

端面燃烧装药（像香烟一样燃烧）是特别的，它仅仅沿轴向燃烧，并且在一个给定的发动机圆柱形壳体中可以装填最多的推进剂。在大型的发动机中（直径在2～3英尺）由于粘接面的燃烧导致的不平行燃面退移会是一个问题，会产生不期望的增面。

为了用于初始加速，期望有一个较高的推力，但是随着推进剂的消耗和飞行器质量的减小，就期望减小推力，这样可以限制火箭推进的飞行器的加速度或敏感的有效载荷。因此，采用较高推力的初始助推段接着较低推力的有动力的续航段（常常是助推的10～30％）可以在飞行器结构重量、飞行器性能和飞行器成本等方面获益。因此，火箭为动力的飞行器常常需要两级或三级推力来满足任务的需要和高效利用可用的总冲。

在单推进剂双推力的固体火箭发动机中，涉及到续航段的因素决定着推进剂类型和药形的选择，由于火箭发动机的大部分是在续航阶段使用的。

在进行下一步的讨论前，先介绍一些基本术语：

药型：装药的初始形状，按照维数来分可以分为一维、二维和三维；按照燃面位置来分可以分为端燃、侧燃和端侧燃；按照推力数量来分可以分为单推力、双推力、多推力和脉冲式；按照推进剂类型来分可以分为复合推进剂、双基推进剂和改性双基推进剂；按照推进剂数量来分可以分为单燃速、双燃速和多燃速；按照特定特征来分可以分为星形、车轮形、翼柱形、锥柱形等多种类型。

柱形药：装药横截面沿轴向保持不变。

等面燃烧：发动机推力、压强和燃烧面积随时间近似为常数。

内孔燃烧：发动机工作过程中，燃烧发生在装药内表面。这种装药能够有效保护发动机壳体。

增面燃烧：发动机推力、压强和燃烧面积随时间是递增的。

减面燃烧：发动机推力、压强和燃烧面积随时间是递减的。

拖尾：在发动机主燃烧过程结束后剩余的部分，一般是作为损失而排出喷管。

震荡燃烧极限：维持稳定燃烧的最小压力，低于此压力会出现熄火或断续燃烧。

包覆层：在装药表面的一个涂层或阻燃材料，防止装药暴露在燃气中。一般是聚合橡胶附加些填料，采用粘、涂、喷等工艺。

衬层：在推进剂未浇铸之前，在壳体或绝热层表面粘贴的一层粘性的、不自燃的聚合物材料，一方面增强装药与壳体之间的粘接性能，另一方面起缓冲作用。

内绝热层：在壳体内部粘贴的一层导热系数较小的隔热材料，防止高温燃气加热壳体，有效保护壳体。

肉厚W：装药的初始表面到绝热壳体内表面或其它装药的交界面间的最大距离，对于端燃装药肉厚近似等于装药的长度。

肉厚分数W_f：装药肉厚与装药外半径之比R_p，W_f=W/R_p。

模数m：装药外半径R_p与内表面半径R_i之比，m=R_p/R_i。

体积装填分数V_f：推进剂的体积V_p与燃烧室容积V_c之比，V_f=V_p/V_c，V_c中不包括喷管，但是包括了推进剂、绝热层、包覆层、自由容积等体积。

药柱设计主要是设计药柱的结构，即确定几何形状和尺寸，使之满足发动机内弹道性能要求和自身结构完整性。

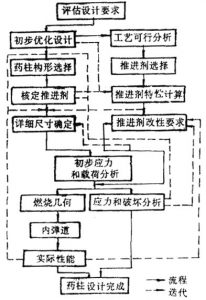
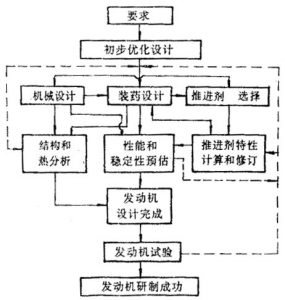
药柱的结构，牵动着发动机总体结构、性能和可靠性等各个方面。所以从某种意义上说，药柱设计是在众多相互制约条件下实现巧妙协调的一种艺术。药柱设计工作大体包含评估设计要求、初步优化设计以及药柱详细设计等主要步骤。图2-2（a）给出典型设计流程。

药柱设计和发动机其他部件设计有密切的关联性，也有交叉性工作；如图2-2框图所（b）所示。

下面重点说明药柱设计的几个主要步骤。

2.1.1  评估设计要求

设计要求主要指以下几个方面，是决定推进剂选择和药柱几何构形的基础。

1．飞行任务决定发动机的战术技术性能要求。在装药设计前就要确定，通常由飞行器总体来定。通常包括：总冲、期望的推力时间曲线及其偏差，发动机质量，储存及工作环境的温度限制，飞行包线，发动机力（震动、弯曲和气动载荷）产生的加速度。外径，长度，质量，喷管潜入长度和入口直径等的要求。

2．选择合适的装药构型来满足这一需求。所选择的装药应当是结构紧凑，体积利用效率高，有足够的燃面来满足推力的需要，尽量避免或适当利用侵蚀燃烧。装药的余药或拖尾尽量小，在燃烧过程质心位置变化尽量小。

3．选择合适的推进剂，主要是性能特性（如特征速度）、机械性能、弹道性能、加工制造特性、羽流特性以及老化性能。若有必要推进剂的配方可作适当的改变或调整，使其精确满足燃烧时间和装药几何要求。

4．装药结构完整性，对绝热层和（或）衬层进行详细应力分析，确保在各种载荷下不被破坏，例如加速度和热应力。可以改变装药几何构型来消除过分的应力集中。

5．随燃烧时间装药的内腔将变得越来越复杂，例如：开槽、翼型和孔型。这些应当仔细检查其对响应、阻尼和不稳定燃烧的影响。

6．装药的加工和推进剂的制造尽量力求简单和低成本。

2.1.2  描述装药的几个重要参数

在发动机总体初步设计阶段，可以认为装药是一理想装药，即装药是等燃面的。这里只关心装药量、燃烧面积、燃烧肉厚和体积等参数。而详细装药的结构型式和参数由装药设计专门程序完成。在总体参数选择中，我们把装药分成单燃速单推力、单燃速双推力和双燃速双推力三种，在总体参数选择的情况下可以进行装药设计。装药设计参数的确定依赖于其它参数的确定，如燃烧室压强、喷管参数等，因此装药的设计和其它部件的设计是一个迭代的过程。

在确保既定的设计要求和满足选定的优化准则（最大总冲、最小药柱质量或最小长度等）前提下，选择推进剂，并协调确定各相关参数的影响，最后定下来几组药柱结构的优选方案。这个工作目前已经形成各种计算机程序，能快速准确地完成。

药柱设计的重要相关参数有如下一些：

（1）药柱质量和体积

推进剂选定以后，根据总冲要求即可估出其质量和体积。

\({{m}_{p}}=\frac{fI}{{{I}_{s}}}=\frac{f\int{_{0}^{t}Fdt}}{{{I}_{s}}}\)                          （2-1）

\(f=1.01\tilde{\ }1.05\)是考虑制造误差和性能偏差的增加量。如果采用的药柱构形有余药，则在\({{m}_{p}}\)中还应加上余药量。

体积     \({{V}_{p}}={{m}_{p}}/{{\rho }_{p}}\)                                              （2-2）

比冲Is应当根据给出的原始参数，估算各种损失后，尽可能采用接近实际情况的实际比冲。下面所引用的推力系数C_F和特征速度C*等也应如此。

（a）

（b）

图2-2  固体火箭发动机及药柱设计流程

（2）喷喉面积及燃面

通过给定的推力和压强，容易算出喷喉面积At

\({{A}_{t}}=\frac{F}{{{C}_{F}}P}\)

压强和推力可采用最大值或最小值。可以根据给出的最大压强估算平均压强，也可以根据燃烧时间t_b或工作时间t_a估算平均压强\(\overline{P}\)

\(\bar{P}=\frac{1}{{{t}_{a}}}\int{_{0}^{{{t}_{a}}}Pdt}\)  或  \(\bar{P}=\frac{1}{{{t}_{b}}}\int{_{0}^{{{t}_{b}}}Pdt}\)

但这种估算都只能是粗略的。在具体药柱设计的性能估算出来之前，只能用相似发动机的比较法或直观判断法去估算压强曲线的变化及初始压强峰。

根据估算出的平均压强去求At，然后按公式

\(P={{(\frac{{{C}^{*}}{{\rho }_{p}}a}{At})}^{\frac{1}{1-n}}}A_{b}^{\frac{1}{1-n}}\)

    或\(F={{C}_{F}}{{A}_{t}}P={{C}_{F}}{{(A_{t}^{-n}{{C}^{*}}{{\rho }_{p}}a)}^{\frac{1}{1-n}}}A_{b}^{\frac{1}{1-n}}\)

找出燃面Ab与F或P的对应关系。

（3）肉厚分数与燃烧时间

肉厚分数\({{\overline{e}}_{1}}\)又称弧厚分数，它是选择药形的最重要的参数之一。一般定义为

\({{\bar{e}}_{1}}=\frac{2{{e}_{1}}}{D}=\frac{2r{{t}_{b}}}{D}\)                          （2-3）

其中e₁为药柱肉厚，D为药柱外径（对管形药柱使用燃烧室内径d_c），为平均燃速。一般可取燃烧时间\({{t}_{b}}=0.95{{t}_{a}}\)。

由de=rdt，和\(r=a{{P}^{n}}\)，得

\({{t}_{b}}=\int{_{0}^{{{e}_{1}}}\frac{de}{a{{P}^{n}}}}\)

（4）装填分数与通气参数（J或\(\partial \text{e}$\)

单位燃烧室容积内装入推进剂的量是药柱设计的质量指标之一。它表示燃烧室容积的利用率。这个指标称为装填密度，以△表示

\(\Delta =\frac{{{m}_{p}}}{{{V}_{c}}}=\frac{{{A}_{T}}{{\rho }_{p}}L}{{{A}_{c}}{{L}_{c}}}\)                    （2-4）

在许多情况下药柱长度与燃烧室长度相差不多，即\({{L}_{c}}\approx L\)

这样

\(\Delta \approx \frac{{{A}_{T}}}{{{A}_{c}}}{{\rho }_{p}}\)

其中，A_T为药柱的横截面积；A_c为燃烧室的横截面积。

称/为装填分数，又称为截面装填因子，以表示。即

\(\eta \text{=}\frac{{{A}_{T}}}{{{A}_{c}}}\)                      （2-5）

可以看出，当\({{\rho }_{p}}\)一定时，η即可代表Δ，反映了药柱设计的质量指标。η的值总是小于1的，但在药柱设计中，应尽可能地增大η值，即尽可能充分利用燃烧室容积。但η的增大会受到通气参量J（或\(\partial \text{e}\)）的限制。否则会引起侵蚀燃烧而产生初始压强峰。

对于药柱截面变化的情况以及球形封头等复杂构形的药柱，有时用体积装填分数η_V表示

\({{\eta }_{\text{v}}}=\frac{{{V}_{p}}}{{{V}_{c}}}=\frac{{{m}_{p}}}{{{\rho }_{p}}{{V}_{c}}}=\frac{I}{{{I}_{s}}{{\rho }_{p}}{{V}_{c}}}\)                       （2-6）

通气参数J或\(\partial \text{e}\)为

\(J=\frac{{{A}_{t}}}{{{A}_{p}}}=\frac{{{A}_{t}}}{{{A}_{c}}-{{A}_{T}}}=\frac{{{A}_{t}}}{{{A}_{c}}(1-\eta )}\)                    （2-7）

                    \(\partial e=\frac{{{A}_{b}}}{{{A}_{p}}}=\frac{{{A}_{b}}}{{{A}_{c}}(1-\eta )}\)                             （2-8）

可以看出，装填分数η地增大会使J、\(\partial \text{e}\)值增大，从而引起侵蚀燃烧。因此，在药柱设计时，一般要通过已知的发动机外径来估算燃烧室的内径d_c，进一步算出Ac，然后用对J或\(\partial \text{e}\)的限制来确定药柱几何尺寸及估算η值。

（5）长径比

药柱的长径比即其长度L与直径D之比。它是由规定的壳体尺寸计算出的。长径比在下列三个方面对药柱设计有影响。

1）药柱端面对燃面变化的影响随L/D的减小而增大。因此在要求等面燃烧的情况下，L/D对选择药形有较大影响；

2）侵蚀燃烧以及对其他参数的敏感性随L/D的增大而增强；

3）高的L/D值有增加不稳定燃烧的趋向。

应当指出，在这些设计参数中，它们经常是互相制约的，如药柱质量与装填分数有一定关系。装填分数增加又受到通气参量的限制。肉厚与燃面亦有一定的函数关系等等。设计时必须综合考虑。

2.1.3  几种典型装药总体参数的确定

（1）单推力装药设计

不同的总体参数选择，有不同的装药设计数据对应，下面讨论参数选择注意的问题：

1）计算条件

燃烧室压强P_c：总体参数用户选择数据（MPa）；

工作时间t：战术技术性能要求规定的设计状态下的工作时间（s）；

喉部半径R_t：喷管设计确定的参数（mm）；

装药外半径R_p：\({{R}_{p}}={{R}_{c}}\text{-}{{\delta }_{c}}-{{\delta }_{i}}\)

R_c-壳体外半径；

δ_c-壳体厚度；

δ_i-绝热层厚度；

忽略衬层厚度。

肉厚分数W_f：W_f=W/R_p.，W为装药肉厚。

推进剂参数：

推进剂压强指数n、特征速度C*、密度ρ_P、比热比k、燃烧温度Tg、气体常数等含义明确，此不赘述。

对于内孔燃烧：

推进剂燃速系数a是根据推进剂装药所需要的燃烧确定的。

\({{r}_{b}}=a{{p}^{n}}=\frac{W}{t}=\frac{{{W}_{f}}{{R}_{p}}}{t}\)

\(a={}^{\frac{{{W}_{f}}{{R}_{p}}}{t}}/{}_{P_{c}^{n}}\)                           （2-9）

该参数主要考虑推进剂能够达到的燃速、成本等，在压强肉厚等参数的相互作用下作适当的调整。装药然面积A_b：

\({{A}_{b}}=\frac{P_{c}^{1-n}{{A}_{t}}}{a{{\rho }_{p}}{{C}^{*}}}\times {{10}^{6}}\)                       （2-10）

对于端面燃烧：

如果装药是端面燃烧，由于端面面积较小，可以采用铅金属丝或燃面开槽等措施增大燃面面积，需要确定一个端面放大系数C，缺省情况下C=1，对于嵌金属丝装药

\(C={1}/{\cos \left( \alpha  \right)}\;\)                            （2-11）

\(Ab=C\pi R_{p}^{2}\)                             （2-12）

α为燃烧锥孔半锥角。

此时推进剂燃速系数a：

\(a=\frac{P_{c}^{1-n}At}{{{A}_{b}}{{\rho }_{p}}{{C}^{*}}}\times {{10}^{6}}\)                        （2-13）

2）装药估算结果

装药的平均燃面积Ab：对于内孔燃烧采用（2-10）式，对于端面装药采用（2-13）式；

装药肉厚W：对于内孔装药采用\({{W}_{f}}={W}/{{{R}_{p}}}\;\)，对于端面装药采用\(W=a{{P}_{c}}^{n}t\)；

装药体积Vp：\({{V}_{p}}=W\cdot {{A}_{b}}\)；

装药质量Mp：\({{M}_{P}}={{V}_{P}}{{\rho }_{P}}+{{M}_{r}}\)，M_r为余药，缺省为0。

（2）单燃速双推力装药设计

采用同一种推进剂，两种不同级别的燃面，来达到两级推力。推进剂的参数同单推力推进剂。与单推力相比多出了第二级参数。

在总体参数选择中介绍，一级压强作为重要总体参数，按照：

\(\frac{{{F}_{1}}}{{{F}_{2}}}=\frac{{{C}_{F1}}{{P}_{c1}}{{A}_{t}}}{{{C}_{F2}}{{P}_{c2}}{{A}_{t}}}=\frac{{{C}_{F1}}{{P}_{c1}}}{{{C}_{F2}}{{P}_{c2}}}={{\varepsilon }_{F}}\)                  （2-14）

ε_F为两级推力比，对于给定的喷管参数、选定的推进剂，通过（2-14）式迭代可以计算出二级燃烧室压强

对于内孔燃烧：

两级总的肉厚W

W=R_pW_f                            （2-15）

推进剂燃速系数可用下式求：

\(a=\frac{W}{{{t}_{1}}P_{C1}^{n}+{{t}_{2}}P_{C2}^{n}}\)                          （2-16）

两级平均燃面积：

\({{A}_{b1}}=\frac{P_{C1}^{1-n}{{A}_{t}}}{a{{\rho }_{p}}{{C}^{*}}}\times {{10}^{6}}\)                       （2-17）

\({{A}_{b2}}=\frac{P_{C2}^{1-n}{{A}_{t}}}{a{{\rho }_{p}}{{C}^{*}}}\times {{10}^{6}}\)                        （2-18）

对于二级端面燃烧：

\({{A}_{b2}}=\pi R_{p}^{2}C\)                            （2-19）

推进剂燃速系数a用（2-18）式计算

\(a=\frac{P_{C2}^{1-n}{{A}_{t}}}{{{A}_{b2}}{{\rho }_{p}}{{C}^{*}}}\times {{10}^{6}}\)                        （2-20）

一级燃面积A_b1用（2-17）式计算。

对于两级都是端面的这种情况很少，此不作讨论。

装药其他参数计算：

一级装药肉厚W₁：\({{W}_{1}}=aP_{c1}^{n}{{t}_{1}}\).；

二级装药肉厚W₂：\({{W}_{2}}=aP_{c2}^{n}{{t}_{2}}\). .

装药体积V_p：\({{V}_{p}}={{W}_{1}}{{A}_{b1}}+{{W}_{2}}{{A}_{b2}}\).；

装药质量M_p：\({{M}_{P}}={{V}_{P}}{{\rho }_{P}}+{{M}_{r}}\)，Mr为余药，缺省为0。

（3）双燃速双推力装药设计

由两种不同燃速的推进剂组成的装药通常是形成两级推力，这里认为缓燃药为装药1，速燃药为装药2，且认为装药1和装药2是等燃面的。此处分为两种情况，一是在第一级缓燃药和速燃药同时燃烧，在第二级速燃药烧完，只剩下缓燃药燃烧。二是一级烧完以后再烧第二级。

推进剂分为两组，含义与前面介绍的一致，计算条件与单燃速双推力相同。与上述两种相比，此种装药较为复杂，也常用，目前多为两级串装。

这里需要考虑两种燃气形成的混合燃气的参数的确定，本文采用重量成分法。假设装药1的质量生成率为m₁，装药2为m₂，则其各自的重量成分为：

\({{q}_{1}}=\frac{{{m}_{1}}}{{{m}_{1}}+{{m}_{2}}}\)

 \({{q}_{2}}=\frac{{{m}_{2}}}{{{m}_{1}}+{{m}_{2}}}\)                                                     （2-21）

则混合气体的参数为：

\({{R}_{g}}={{R}_{g1}}{{q}_{1}}+{{R}_{g2}}{{q}_{2}}\)                                           （2-22）

\({{C}_{p}}={{C}_{p1}}{{q}_{1}}+{{C}_{p2}}{{q}_{2}}\)                                                     （2-23）

\({{C}_{v}}={{C}_{v1}}{{q}_{1}}+{{C}_{v2}}{{q}_{2}}\)                                           （2-24）

\(k={{{C}_{p}}}/{{{C}_{v}}}\;\)                                          （2-25）

\({{T}_{g}}=\frac{{{C}_{p1}}{{T}_{g1}}{{q}_{1}}+{{C}_{p2}}{{T}_{g2}}{{q}_{2}}}{{{C}_{p1}}{{q}_{1}}+{{C}_{p2}}{{q}_{2}}}\)                                            （2-26）

\(C*=\sqrt{C_{1}^{*2}{{q}_{1}}+C_{2}^{*2}{{q}_{2}}}\)                       （2-27）

流经喷管的是两种气体混合产物，这里未考虑化学变化。

通常二级燃烧室压强较低，为了保证效率，往往是保证第二级必要的压强P_c2，然后再设计第一级。

这里分两种情况分别讨论：

1）两级同时燃烧

装药一跨越两级，计算从第二级开始。根据给定的喷管参数、总冲、工作时间及其它一些参数，可以计算缓燃药在第二级的燃面，同时根据燃烧室在第二级的压强P_c2，确定推进剂及装药二级参数。

两级都是内孔燃烧：

两级肉厚：

\({{e}_{1}}={{W}_{f1}}{{R}_{p}}\)                                            （2-28）

          \({{e}_{2}}={{W}_{f2}}{{R}_{p}}\)                                  （2-29）

根据两级推力比计算一级压强P_c1：

\(\frac{{{F}_{1}}}{{{F}_{2}}}=\frac{{{C}_{F1}}{{P}_{c1}}{{A}_{t}}}{{{C}_{F2}}{{P}_{c2}}{{A}_{t}}}=\frac{{{C}_{F1}}{{P}_{c1}}}{{{C}_{F2}}{{P}_{c2}}}={{\varepsilon }_{F}}\)（2-30）

计算C_F2   时用的是装药1的推进剂参数，计算C_F1时用的是混合气体的热力学参数，

根据两级的推力比，利用（2-30）式迭代即可求出第一级的燃烧室压强。讨论：由于装药未设计出来，两种燃气的质量生成不能确定，因此，混合气体的热力参数也不能确定，可近似取装药1的热力学参数。实际上，混合装药之间的热力参数本身相差不大，只是燃速差异较大，这种近似不会产生太大的误差。

计算推进剂1的燃速系数：

\({{a}_{1}}=\frac{e1}{{{t}_{1}}P_{c1}^{n1}+{{t}_{2}}P_{c2}^{n2}}\)                        （2-31）

推进剂2的燃速系数：

  \({{a}_{2}}=\frac{{{e}_{2}}}{{{t}_{1}}P_{c1}^{n2}}\)                       （2-32）

装药1的第一级燃烧肉厚：

\({{e}_{11}}={{a}_{1}}P_{c1}^{n1}{{t}_{1}}\)

第二级燃烧肉厚：

\({{e}_{12}}={{a}_{1}}P_{c2}^{n1}{{t}_{2}}\)

装药1的燃面积：

\({{A}_{b1}}=\frac{P_{c2}^{1-{{n}_{1}}}{{A}_{t}}}{{{a}_{1}}{{\rho }_{p1}}C_{1}^{*}}\times {{10}^{6}}\)

装药2的燃烧面积A_b2可由下式迭代求出：

 \({{a}_{1}}P_{c1}^{n1}{{\rho }_{p1}}{{A}_{b1}}+{{a}_{2}}P_{c1}^{n2}{{\rho }_{p2}}{{A}_{b2}}=\frac{{{P}_{c1}}{{A}_{t}}}{{{C}^{*}}}\)              （2-33）

式中C*为混合燃气的特征速度。

二级为端面燃烧

装药1二级，此时燃面积A_b1计算用下式：

\({{A}_{b1}}=\pi R_{p}^{2}C\)                               

    推进剂1燃速系数a₁用（3-34）式计算

\({{a}_{1}}=\frac{P_{c2}^{1-n1}{{A}_{t}}}{{{A}_{b1}}{{\rho }_{p1}}C_{1}^{*}}\times {{10}^{6}}\)                 （2-34）

推进剂2燃速系数a₂用（2-32）式计算。

其它参数计算同内孔燃烧。

2）两级先后燃烧

装药2烧完以后装药1再燃烧，而且此种情况下，相当于两个独立的装药，互不影响，也分为内孔燃烧和端面燃烧。

后燃的装药1计算总的肉厚e₁                                      

\({{e}_{2}}={{W}_{f2}}{{R}_{p}}\)                                （2-35）

先燃的装药2的肉厚W₁

\({{e}_{1}}={{W}_{f1}}{{R}_{p}}\)                          （2-36）

计算推进剂的燃速系数

两药都为侧面燃烧

装药1的燃速系数a₁

\({{a}_{1}}=\frac{{{e}_{1}}}{P_{c2}^{n1}{{t}_{2}}}\)                        （2-37）

装药2的燃速系数a₂

\({{a}_{2}}=\frac{{{e}_{2}}}{P_{c1}^{n2}{{t}_{1}}}\)                      （2-38）

装药1的燃面积：

\({{A}_{b1}}=\frac{P_{c2}^{1-{{n}_{1}}}{{A}_{t}}}{{{a}_{1}}{{\rho }_{p1}}C_{1}^{*}}\times {{10}^{6}}\)                    （2-39）

装药2的燃面积：

\({{A}_{b2}}=\frac{P_{c1}^{1-{{n}_{1}}}{{A}_{t}}}{{{a}_{2}}{{\rho }_{p2}}C_{2}^{*}}\times {{10}^{6}}\)                    （2-40）

二级药为端面燃烧

装药1二级，此时燃面积A_b1计算用下式：

   \({{A}_{b1}}=\pi R_{p}^{2}C\)                          （2-41）

推进剂1燃速系数a₁用（2-39）式计算

   \({{a}_{1}}=\frac{P_{c2}^{1-{{n}_{1}}}{{A}_{t}}}{{{A}_{b1}}{{\rho }_{p1}}C_{1}^{*}}\times {{10}^{6}}\)                     （2-42）

装药2仍为侧面燃烧，推进剂2燃速系数a₂用（2-42）式计算。

其它参数计算同内孔燃烧。

这里的装药设计仅是为了适应发动机总体设计而定制的，实际装药设计考虑的因素更多。在此，只考虑内弹道性能要求。主要考虑装药的肉厚分数。实际装药设计还应考虑结构完整性、燃烧特性、安全性、成本、工艺、可靠性、存储，与其它粘接材料的相容性等。使用本模块设计的装药为理想的等面燃烧，实际上这样的装药是难以实现的，在总体设计后将进一步对装药的等面性、拖尾、燃面波动等提出进一步的要求。

2.1.4  选择推进剂

选择推进剂主要考虑能量特性（比冲、密度等）弹道特性（燃速、温度敏感系数等），对于其他性质（机械性能、热及贮存稳定性，排出物、价格等）也必须重视。根据具体要求，可以预选出几种推进剂，列出表格，提供进一步分析裁决。有时已有的各种推进剂都不理想，这就要选出几种性能相近（要求改动最小）的推进剂。与厂方协商，请厂方针对某种推进剂进行改性研制（如调节燃速或某些机械性能），进一步提供符合设计要求的推进剂。

2.1.5  药柱构形选择和设计

药柱构形及其分数已在总体设计中讲过。具体药柱的构形应以下面一些条件作为选定的基础。

（1）初步优化设计的结果（弹道限制、质量、容积、长径比等）；

（2）推力——时间曲线；

（3）工艺技术状况；

（4）结构完整性分析。

应该明确，装药结构中包括衬层、限燃层和绝热层，所以要同时考虑。所选择的药型应尽量满足这些要求，但是有时是互相矛盾的，应该选择最重要的满足。例如推力必须满足，应该有足够的燃面。对于相互影响的因素应当进行折中。

2.1.6  药柱详细设计

根据优化设计的结果和药柱的主要几何参数，便可以初步确定药柱的几何尺寸，接着通过迭代计算，定出药柱的详细尺寸，在满足结构完整性要求的前提下，同时满足内弹道特性的要求。

这些工作一般可由计算机程序进行优化。变换几何参数关系，反复对比以确定最佳方案。

对于复杂结构的药形，一般要进行模型吹风试验。检验药柱通道内槽、翼、孔中气动力干扰情况，后底部回流区的流动情况，以及其他易造成旋涡、突扩、复回流区等处的流动状态，杜绝各种可能造成不正常燃烧的因素。

2.1.7  药柱结构分析

上面诸步骤完成后，已为结构的详细分析提供了充分的条件；这个阶段可以最终确定药柱的详细尺寸和结构。主要包含三个方面的工作，即燃烧几何分析、内弹道验算和结构分析。

（1）燃烧几何分析

主要是计算燃面随肉厚（燃烧过程）的变化。这个计算是药柱设计的核心工作，也是最复杂的部分。复杂型面的药柱计算工作量较大。目前有二维、三维通用计算程序。

作为燃烧几何分析的前提，是药柱的平行层燃烧规律（或称几何燃烧规律）。即认为药柱燃烧表面上各点的燃速均沿该点的法线方向；并且整个燃面同时点燃，燃面上各点的燃速处处相等。

（2）内弹道验算

根据药柱燃面的变化规律，可以进行内弹道计算。药柱通道内的流动状况很复杂，属变通道、加质、二相、多维、非稳态流动；再考虑喷管的烧蚀、推力系数的变化等等，计算就非常复杂。可以根据设计要求采取各种简化。

（3）结构分析

初步应力和载荷分析中，只解决装药浇铸后的初始应力以及点火建压过程的载荷状态。固体推进剂药柱属粘弹性物质；贮存使用期内，由于环境温度和各种外载荷的作用，不断产生应力积累和变形叠加，所以对装药发动机要进行使用可靠性和破坏分析。有关内容在后面第九章中介绍。

2.2  二维药柱设计

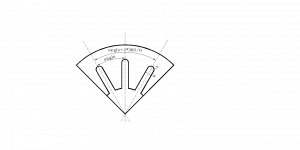
二维药柱的特点是在药柱上作出一个剖面，即可以完全表示清楚燃面变化的规律。药柱的燃烧几何仅限于平面关系；所以比较简单。下面以等截面星形内孔药柱为例，说明一般设计方法。

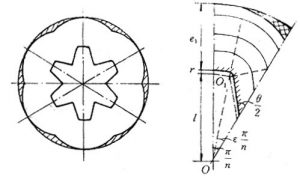
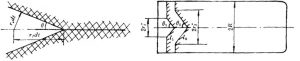
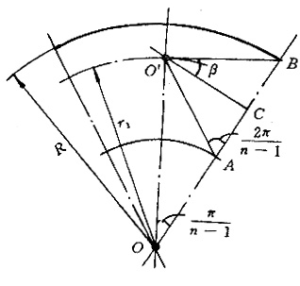
（1）主要几何参数

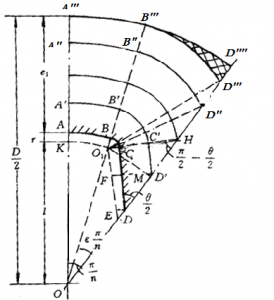
如图2-3，星形内孔药柱的主要几何参数有：

药柱外径D=2R，药柱长度L

药柱肉厚e₁       特征尺寸l

星角数n，       星槽圆弧半径r

星边夹角θ       星角系数ε

显然  \(l+{{e}_{1}}+r=D/2\)

图2-3  半个星角的几何参数

（2）几何参数与设计参数间的关系

图2-4  星孔药柱燃面变化

药柱的主要设计参数一般包括燃烧面积Ab，通道截面积Ap，理论余药面积Af等。

设星角数为\(n,{s}’\)为半个星角的燃烧边长，则有如下关系

\({{A}_{b}}=2n{s}’L\)

药柱长为定值（不考虑药柱端面燃烧），所以与几何参数间的关系可以用与几何参数间的关系来代替。

从图2-4上可以看出，燃面变化分为两个阶段，即星角直边\(\overline{CD}\)消失前与消失后的两个阶段。第一阶段的燃烧边长由两个不断增长的圆弧\({A}'{B}’\)及\({B}'{C}’\)和一个减小的直边\(\overline{{C}'{D}’}\)组成。所以改变星形的几何参数可以使第一阶段的燃面呈增面、恒面或减面变化。而第二阶段只是由圆弧\({A}”{B}”\)和\({B}”{D}”\)组成，它们在燃烧后期不可避免的是增面的。

肉厚\(\overline{CH}\)是划分两个阶段的数值，从图2-4中可以看出，在\(\Delta {{O}_{1}}OH\)中

\(\frac{\overline{{{O}_{1}}H}}{\sin \varepsilon \frac{\pi }{n}}=\frac{\overline{{{O}_{1}}O}}{\sin (\frac{\pi }{2}-\frac{\theta }{2})}\)                        （2-43）

所以     \(\overline{CH}+r=l\frac{\sin \varepsilon \frac{\pi }{n}}{\cos \frac{\theta }{2}}\)

下面我们分别研究这两个阶段的燃烧面变化情况。

第一阶段                     \(e+r\)≤\(l\frac{\sin \varepsilon \frac{\pi }{n}}{\cos \frac{\theta }{2}}\)                      （2-44）

半个星角的燃烧边长为

\({s}’={A}'{B}’+{B}'{C}’+\overline{{C}'{D}’}\)

其中                \({A}'{B}’=(l+e+r)(1-\varepsilon )\frac{\pi }{n}\)

\({B}'{C}’=(e+r)\angle {B}'{{O}_{1}}{C}’=(e+r)(\varepsilon \frac{\pi }{n}+\frac{\pi }{2}-\frac{\theta }{2})\)

\(\overline{{C}'{D}’}=\overline{{{O}_{1}}E}-\overline{EF}=\frac{l\sin \varepsilon \frac{\pi }{n}}{\sin \frac{\theta }{2}}-(e+r)ctg\frac{\theta }{2}\)

整理后得到

\({s}’=\frac{l\sin \varepsilon \frac{\pi }{n}}{\sin \frac{\theta }{2}}+l(1-\varepsilon )\frac{\pi }{n}+(e+r)(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-ctg\frac{\theta }{2})\)

从上述关系式中可以看出：

\({s}’=\frac{l\sin \varepsilon \frac{\pi }{n}}{\sin \frac{\theta }{2}}+l(1-\varepsilon )\frac{\pi }{n}+(e+r)(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-ctg\frac{\theta }{2})\)

从上述关系式中可以看出：

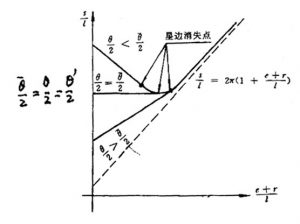
（1）燃烧边长（即燃烧面）在燃烧过程的第一阶段是按线性规律变化的；

（2）(e+r)项的系数决定燃烧面的变化，当

\(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-ctg\frac{\theta }{2}>0\)    增面

\(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-ctg\frac{\theta }{2}=0\)    恒面

\(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-ctg\frac{\theta }{2}<0\)    减面

                  （2-45）

我们把符合恒面燃烧的θ值用\(\overline{\theta }\)表示，可以看出\(\overline{\theta }\)仅与星角数n有关。见表2-1.

表2-1  n与\({{\bar{\theta }}}/{2}\;\)关系

	3	4	5	6	7	8	9	10	11	12
\(\overline{\theta }/2\)	24.55°	28.22°	31.13°	33.53°	35.56°	37.31°	38.84°	40.20°	41.41°	42.52°

第二阶段              \(e+r\)＞\(l\frac{\sin \varepsilon \frac{\pi }{n}}{\cos \frac{\theta }{2}}\)                              （2-46）

\({s}’={A}”{B}”+{B}”{D}”\)

\({A}”{D}”=(l+e+r)(1-\varepsilon )\frac{\pi }{n}\)

\({B}”{D}”=(e+r)\angle {B}”{{O}_{1}}{D}”\)

\(\angle {B}”{{O}_{1}}{D}”=\varepsilon \frac{\pi }{n}+\angle {{O}_{1}}{D}”O\)

\(\angle {{O}_{1}}{D}”O={{\sin }^{-1}}\frac{l\sin \varepsilon \frac{\pi }{n}}{e+r}\)

于是：\({s}’=(l+e+r)(1-\varepsilon )\frac{\pi }{n}+(e+r)\left[ \varepsilon \frac{\pi }{n}+{{\sin }^{-1}}\frac{l\sin \varepsilon \frac{\pi }{n}}{e+r} \right]\)

\(=l(1-\varepsilon )\frac{\pi }{n}+(e+r)[\frac{\pi }{n}+{{\sin }^{-1}}\left( \frac{1}{e+r}\sin \varepsilon \frac{\pi }{n} \right)]\)

总的燃烧面\({{A}_{b}}=2n{s}’L\)

图2-5表示了星形药柱的燃面变化规律。

图2-5  星形药柱周边长变化规律

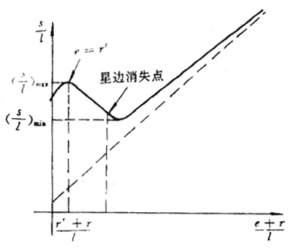
已知两个阶段分界点的肉厚公式\({{e}_{d}}=l\frac{\sin \varepsilon \frac{\pi }{n}}{\cos \frac{\theta }{2}}-r\)，可以看出：当\(\theta /2\)增加，第一阶段的燃面从减面至恒面至增面变化，而e_d则逐渐增加。通常为了使发动机在整个的工作过程中获得基本平稳的推力、压强曲线，提高装填密度，设计星形药柱时第一阶段多采用减面即\(\theta /2\)＜\(\overline{\theta }/2\)。此时第二阶段的燃面在开始时先减，以后再增加。所以最小燃面在第二阶段开始不久处，即

\(e=\frac{l\sin \left( \varepsilon \frac{\pi }{n} \right)}{\cos \left( \frac{{\bar{\theta }}}{2} \right)}-r\)

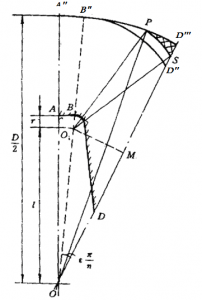
最后，当然至e=e₁时第二阶段结束，通常认为燃烧结束，留下的药块称为余药。然而在某些情况下，余药往往部分地或全部燃完，因此为了准确地预估发动机工作后期的推力、压强曲线，我们给出了余药的燃面变化规律。见图2-6。

图2-6  余药燃面变化

当        \({{e}_{f}}\ge e>{{e}_{1}}\)时

\({{e}_{f}}=\overline{{{O}_{1}}{{D}^{”’}}}-r=\sqrt{{{R}^{2}}+{{l}^{2}}-2Rl\cos \varepsilon \frac{\pi }{2}}-r\)

\({s}’=PS=(e+r)\angle P{{O}_{1}}S\)

\(\angle P{{O}_{1}}S=\angle P{{O}_{1}}O-\angle S{{O}_{1}}O\)

\(\angle P{{O}_{1}}O={{\cos }^{-1}}\frac{{{(e+r)}^{2}}+{{l}^{2}}-{{R}^{2}}}{2(e+r)l}\)

          \(\angle S{{O}_{1}}O=\frac{\pi }{2}-\varepsilon \frac{\pi }{n}+\angle M{{O}_{1}}S\)

\(\angle M{{O}_{1}}S={{\cos }^{-1}}(\frac{1}{e+r}\sin \varepsilon \frac{\pi }{n})\)

\({s}’=(e+r)\{{{\cos }^{-1}}\frac{{{(e+r)}^{2}}+{{l}^{2}}-{{R}^{2}}}{2(e+r)l}-\frac{\pi }{2}+\frac{\varepsilon \pi }{n}-{{\cos }^{-1}}(\frac{l}{e+r}\sin \varepsilon \frac{\pi }{n})\}\)

所以余药燃面变化为

\({{A}_{b}}=2n{s}’L\)

（3）通道截面积\({{A}_{p}}\)

星型药柱的通道截面积随烧去的肉厚e的增大而增大。这里研究的是初始通道截面积A_pi和刚刚开始燃烧不久处的通道截面积。因为它们和发动机的装填密度和侵蚀压强峰有密切关系。

设半个星角的通道截面积为\({{{A}’}_{p}}\)。参看图2-3

(A_{p}^{‘}=\nabla KO{{O}_{1}}+\Delta O{{O}_{1}}E+\int{_{0}^{e+r}{s}’d(e+r)}\)

扇形面积      \(KO{{O}_{1}}=\frac{1}{2}{{l}^{2}}(1-\varepsilon )\frac{\pi }{n}\nabla \)

三角形面积\(\Delta O{{O}_{1}}E=\frac{1}{2}\overline{OE}\cdot \overline{{{O}_{1}}M}=\frac{1}{2}(\overline{OM}-\overline{EM})\cdot \overline{{{O}_{1}}M}\)

                  \(=\frac{1}{2}(l\cos \varepsilon \frac{\pi }{n}-l\sin \varepsilon \frac{\pi }{n}ctg\frac{\theta }{2})\cdot l\sin \varepsilon \frac{\pi }{n}\)

积分

\(\int{_{0}^{e+r}{s}’d(e+r)=\int{_{0}^{e+r}}}\) \(\int_{0}^{e+r}{{s}’d(e+r)=\int_{0}^{e+r}{[\frac{l\sin \varepsilon \frac{\pi }{n}}{\sin \theta /2}+l(1-\varepsilon )\frac{\pi }{n}+(e+r)(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-ctg\frac{\theta }{2})]d(e+r)}}\)

             \(=l(e+r)[\frac{\sin \varepsilon \frac{\pi }{n}}{\sin \theta /2}+(1-\varepsilon )\frac{\pi }{n}]+\frac{1}{2}{{(e+r)}^{2}}(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-ctg\frac{\theta }{2})\)

所以    \({{{A}’}_{p}}=\frac{1}{2}{{l}^{2}}(1-\varepsilon )\frac{\pi }{n}+\frac{1}{2}(\cos \varepsilon \frac{\pi }{n}-\sin \varepsilon \frac{\pi }{n}ctg\frac{\theta }{2}){{l}^{2}}\sin \varepsilon \frac{\pi }{n}\)

             \(+(e+r)\)[\(\frac{\sin \varepsilon \frac{\pi }{n}}{\sin \theta /2}+(1-\varepsilon )\frac{\pi }{n}\)]+\(\frac{1}{2}{{(e+r)}^{2}}(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-ctg\frac{\theta }{2})\)

总的通道截面积      \({{A}_{p}}=3n{{{A}’}_{p}}\)

为了工艺的需要，在星根角处往往制有圆弧\({r}’\)。考虑\({r}’\)的第一阶段半个星角的燃烧边长\({s}’\)和通道截面积\({{{A}’}_{p}}\)为

\({s}’=\frac{l\sin \varepsilon \frac{\pi }{n}}{\sin \theta /2}+l(1-\varepsilon )\frac{\pi }{n}+(e+r)(\frac{\pi }{2}+\frac{\theta }{2}-\frac{\theta }{2}-ctg\frac{\theta }{2})-({r}’-e)(ctg\frac{\theta }{2}+\frac{\theta }{2}-\frac{\pi }{2})\)

\({{{A}’}_{p}}=\frac{1}{2}{{l}^{2}}(1-\varepsilon )\frac{\pi }{n}+\frac{1}{2}(\cos \varepsilon \frac{\pi }{n}-\sin \varepsilon \frac{\pi }{n}ctg\frac{\theta }{2}){{l}^{2}}\sin \varepsilon \frac{\pi }{n}+l(e+r)\)

.[\(\frac{\sin \varepsilon \frac{\pi }{n}}{\sin \theta /2}+(1-\varepsilon )\frac{\pi }{n}\)] + \(\frac{1}{2}{{(e+r)}^{2}}(\frac{\pi }{2}+\frac{\pi }{n}-\frac{\theta }{2}-ctg\frac{\theta }{2})+\frac{1}{2}{{({r}’-e)}^{2}}(ctg\frac{\theta }{2}+\frac{\theta }{2}-\frac{\pi }{2})\)

当e＞r’时，s’和\({{{A}’}_{p}}\)式中均无最后一项，即与前式相同。

对于的第一阶段减面燃烧的星型药柱，由于r’的出现，使e从0-r’之间又出现了增面燃烧。如图2-7。这样把第一阶段的燃面最大值从e=0推迟到e=r’时，同时数值上也降低了，这显然对降低初始压强峰和提高装填分数有利。

图2-7  减面性药柱周边的变化规律

（4）余药截面积A_f

往往当然至e=e₁时发动机工 作结束，剩下未然尽的药称为余药。从图2-4看即、（{B}”'{D}”{D}”’\)部分。余药造成能量损失，设计时应尽可能减小余药量。

半个星角的余药为\({{{A}’}_{f}}\)

\({{{A}’}_{f}}=\Delta {B}”’O{D}”-\Delta {B}”'{{O}_{1}}{D}”’-\Delta {D}”'{{O}_{1}}O\Delta {B}”’O{D}”=\frac{1}{2}{{(l+{{e}_{1}}+r)}^{2}}\varepsilon \frac{\pi }{n}\)

\(\Delta {B}”'{{O}_{1}}{D}”’=\frac{1}{2}\overline{O{D}”’}\overline{{{O}_{1}}M}=\frac{1}{2}\)[\(l\cos \varepsilon \frac{\pi }{n}+{{\sin }^{-1}}(\frac{1}{{{e}_{1}}+r}\sin \iota e\frac{\pi }{n})\)]

\(\Delta {D}”'{{O}_{1}}O=\frac{1}{2}\overline{O{D}”’}\overline{{{O}_{1}}M}=\frac{1}{2}\))\(l\cos \varepsilon \frac{\pi }{n}+\sqrt{{{({{e}_{1}}+r)}^{2}}-{{l}^{2}}{{\sin }^{2}}\varepsilon \frac{\pi }{n}}\)]×\(\left( l\sin \varepsilon \frac{\pi }{n} \right)\)

所以\({{{A}’}_{f}}=\frac{1}{2}{{(l+{{e}_{1}}+r)}^{2}}\varepsilon e\frac{\pi }{n}-\frac{1}{2}{{({{e}_{1}}+r)}^{2}}\)[\(\varepsilon \frac{\pi }{n}+{{\sin }^{-1}}(\frac{l}{{{e}_{1}}+r}\sin \varepsilon \frac{\pi }{n})\)]

         \(-\frac{1}{2}\)[\(l\cos \varepsilon \frac{\pi }{n}+\sqrt{{{({{e}_{1}}+r)}^{2}}-{{l}^{2}}{{\sin }^{2}}\varepsilon \frac{\pi }{n}}\)]\((l\sin \varepsilon \frac{\pi }{n})\)

总的余药截面积\({{A}_{F}}=2n{{{A}’}_{f}}\)

（5）药柱几何参数的确定

按照2.1中介绍的建立相关参数的思路，建立起一组相关参数，以及与药柱几何参数的关系。由于参数间关系复杂，一般不可能用数字解析办法一次求出定解；要靠多次反复试算，求得最佳几何方案。目前发展了计算机程序，大大节约了人力，提高了设计质量。

另外，还有一些几何参数一般要靠经验或工艺条件确定。如药柱m值，定义为\(m=1+\frac{{{e}_{1}}}{l+r}\)，可以参考肉厚分数（\({{\overline{e}}_{1}}=\frac{2e{}_{1}}{D}=\frac{2r{{t}_{b}}}{D}\)）综合考虑；一般取3~4。星槽圆弧半径\(r=(0.015\tilde{\ }0.03)D\)；星根小圆弧半径r’＜r 。

2.3 三维药柱设计 

2.3.1 三维药柱燃面计算的解析法

为了提高发动机的质量比，增加推进剂的体积装填分数；同时也是为了调整药柱的燃面，通常在燃烧室的前后封头部位都充填推进剂，且药柱尾端一般不阻燃。这就构成典型的三维药柱。在计算机发明之前，用图解法几何作图计算燃面。在计算机发明之后，在图形学技术出现以前，采用离散的通用坐标方法计算，目前这两种方法均被图形技术计算方法所取代。

2.3.2 基于计算机图形学的装药设计

前面介绍了几种基于解析方法的装药设计和计算方法，然而大部分装药结构是给不出解析公式的，因此限制了这种方法的应用。随着计算机图形学技术的发展和大量商业化绘图软件的应用，给装药设计提供了一种全新的快速的解决方案。在2.5节中将有详细介绍。

2.3.3 基于离散方法装药数值计算

在现代计算机图形学中尚存在一些未解决的问题，如特征消失问题、奇异点处理问题。装药在燃烧时内腔形体在逐渐扩张，带来大量复杂的交并差计算，有些形体被烧完至消失，例如反圆弧面，这时基于边界表达的造型系统就会出错，计算不能进行，这种现象经常出现，为了避免这种问题的出现设计人员要做大量的手动计算绕过关键点。另外燃烧过程再生的形体（往往难以预测）必须预置，对设计人员要求过高。对于局部包覆的装药几乎是不能计算。为了彻底解决此类问题，采用离散方法基于GPU并行处理技术发展了一套装药计算方法。在2.6节中将有详细介绍。

2.4 几种小型发动机用的药柱

本节介绍两种战术导弹发动机用的药柱。管形药柱和金属丝端燃药柱。前者按两端面是否限燃。而分属于二维和三维药柱；后者系一维药柱的改进，以增大燃面。它们均可应用通用坐标法进行设计计算。本节介绍其解析算法。

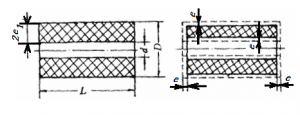
2.4.1 管形药柱设计

（1）单根管形药柱设计

管形药柱的几何参数有外径D、内径d、药柱长L和根数n。通常的标志方法为D/d-L×n，当n=1时，则仅写D/d-L。图2-12所示为单根管形药柱两端面阻燃的管形药柱的肉厚为  

图2-12 管形药柱

\({{e}_{1}}=\frac{1}{4}(D-d)\)

显见，当L＜\(\frac{1}{2}(D-d),{{e}_{1}}=\frac{1}{2}L\)，这时基本是一药饼，很少应用。

两端阻燃的药柱，呈恒面燃烧，其燃烧面积为

\(A{}_{b}=n\pi (D+d)L\)

两端不阻燃的药柱，呈减面燃烧，其燃烧面积为

\({{A}_{b}}=n\pi [(D-2e)+(d+2e)](L-2e)+\frac{n\pi }{2}[{{(D-2e)}^{2}}-{{(d+2e)}^{2}}]\)

当\(e=0\)时，初始燃面

\({{A}_{{{b}_{i}}}}=n\pi (D+d)L+\frac{n\pi }{2}({{D}^{2}}-{{d}^{2}})\)

因此，燃面可写成

\({{A}_{b}}={{A}_{bi}}-4n\pi (D+d)e\)

当燃烧结束时，\(e={{e}_{1}}=\frac{1}{4}(D-d)\)，此时燃面

\({{A}_{{{b}_{f}}=}}={{A}_{b}}_{i}-n\pi ({{D}^{2}}-{{d}^{2}})=n\pi (D+d)L-\frac{n\pi }{2}({{D}^{2}}-{{d}^{2}})\)

（1）单根管形药柱尺寸的确定

1）根据总冲确定药柱体积

\({{V}_{p}}=\frac{I}{{{I}_{s}}{{\rho }_{p}}}=\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})L\)                   （2-47）

2）根据给定的工作压强、推力来确定喷喉面积A_t，从而确定其与燃面的关系。

对两端阻燃的管形药柱，有下列关系

\( {{p}_{c}}={{({{c}^{*}}{{\rho }_{p}}a\frac{{{A}_{b}}}{{{A}_{t}}})}^{\frac{1}{1-n}}} \)

\(F={{c}_{F}}{{p}_{c}}{{A}_{t}}={{c}_{F}}{{p}_{c}}\frac{{{A}_{b}}}{K}={{c}_{F}}{{p}_{c}}\frac{L}{K}\pi (D+d) \)

式中 \(K={{A}_{b}}/{{A}_{t}}\)。

对于两端不阻燃的情况，因为减面性而导致压强、推力逐渐降低。这种情况A_bi对应于P_max和F_max，A_bf对应于p_min和F_min

3）根据发动机的燃烧时间确定肉厚

\({{t}_{b}}=\int{_{0}^{{{e}_{1}}}\frac{\text{d}e}{r}}\)

已知

\({{A}_{b}}={{A}_{bi}}-4\pi (D+d)e \)

\( de=-\frac{d{{A}_{b}}}{4\pi (D+d)} \)

\( r=ap_{c}^{n}=a{{(\frac{{{c}^{*}}{{\rho }_{p}}a}{{{A}_{t}}})}^{\frac{n}{1-n}}}{{A}_{b}}^{\frac{n}{1-n}} \)

代入上式得

\({{t}_{b}}=\int_{{{A}_{bi}}}^{{{A}_{bf}}}{-\frac{1}{a}{{(\frac{{{c}^{*}}{{\rho }_{p}}a}{{{A}_{t}}})}^{-\frac{n}{1-n}}}\frac{1}{4\pi (D+d)}{{A}_{b}}^{-\frac{n}{1-n}}\text{d}{{A}_{b}}}\)

\(\left. =-\frac{1}{a}{{(\frac{{{c}^{*}}{{\rho }_{p}}a}{{{A}_{t}}})}^{-\frac{n}{1-n}}}\frac{1}{4\pi (D+d)}\frac{A{{_{b}^{-}}^{\frac{n}{1-n}}}\text{d}{{A}_{b}}}{-\frac{n}{1-n}+1} \right|_{{{A}_{bi}}}^{{{A}_{bf}}}\)

∴                \({{t}_{b}}=\frac{1}{a}\frac{1-n}{1-2n}\frac{1}{4\pi (D+d)}{{(\frac{{{c}^{*}}{{\rho }_{p}}a}{{{A}_{t}}})}^{-\frac{n}{1-n}}}(A_{bi}^{\frac{1-2n}{1-n}}-A_{bf}^{\frac{1-2n}{1-n}})\)

上式适用于\(n\ne 0.5\)的情况，当\(n=0.5\)时

\({{t}_{b}}=\frac{1}{a}\frac{1}{4\pi (D+d)}{{(\frac{{{c}^{*}}{{\rho }_{p}}a}{{{A}_{t}}})}^{-1}}\ln \frac{{{A}_{bi}}}{{{A}_{bf}}}\)

将\({{A}_{bi}},{{A}_{bf}}\)的关系式代入，即可得D、d、L与t_b的关系式。

往往燃面变化复杂，很难进行严格的积分，此时可采用近似的数值积分方法。即

\({{t}_{b}}=\sum\limits_{j=1}^{m}{\frac{\Delta {{e}_{j}}}{aP_{j}^{n}}}\)

4）根据已知的燃烧室外径及通气参量的限制来确定药柱的外径D及内径d

通常给定导弹外径或燃烧室外径D_c的限制及压强等参数，可以估算出发动机燃烧室的内径d_c。若已知燃烧室壳体壁厚δ，及隔热涂层厚δ_涂。

则                    \({{d}_{c}}={{D}_{c}}-2\delta -2{{\delta }_{}}\)

然后考虑通气参量的条件

\({{A}_{p}}=\frac{\pi }{4}d_{c}^{2}-\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})\)

\(J=\frac{{{A}_{t}}}{{{A}_{p}}}=\frac{{{A}_{t}}}{\frac{\pi }{4}d_{c}^{2}-\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})}\)≤J_允许

由于\({{m}_{p}}={{A}_{b}}{{e}_{1}}{{\rho }_{p}}\)，所以当确定m_p之后，A_b与e₁的条件只能选用一个。通过上述限制性条件计算出的D、d和L，还需要进行修正（尺寸圆整化及考虑内弹道计算和结构上的因素所做的修正）。然后再进行检验，合格后才能最后确定所需的D、d和L。

【例】试求单根管形药柱的几何尺寸D、d和L，已知某发动机的原始参数为

总冲I≥36000·s

最大推力F_max≤（17520-4500\(\frac{t}{{{t}_{b}}}\)）

工作时间t_a≤7s

比冲   I_s=1863.3N.s/kg.

密度   ρ_p=1.615×10³kg/m³.        

特征速度C*=1280m/s

燃速r=6.351×10^-8P^0.75     （e≤1.8cm时）  m/s(-50℃)

燃速r=6.351×10^-6P^0.75     （1.8≤e≤e₁时） m/s(-50℃)

r=5.228×10^-6P^0.35    m/s （+40℃）

燃烧室外径     D_c=200mm

最大工作压强   P_max≤（135×10⁵-37×10⁵t/t_b） Pa

初温范围       \(T=-50\tilde{\ }+40\)℃

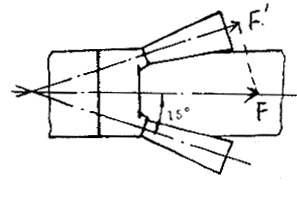
根据导弹总体要求，发动机需采用二个喷管，其轴线与弹的轴线夹角为15°。

图2-13 发动机与喷管的结构示意图

【解】

（1）根据总冲计算药柱体积

           \({{V}_{p}}=\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})L=\frac{1.1I}{{{I}_{s}}{{\rho }_{p}}}=\frac{1.1\times 36000}{1863.3\times 1.615\times {{10}^{3}}}=1.316\)×10^-2（m³）

（2）根据A_t计算A_b

由于给出的是最大推力和压强，而管形药柱是减面燃烧，所以要用高温+40℃下开始燃烧时（即e=0）的情况来计算A_b。通常推力公式表示为\(F={{C}_{F}}{{A}_{t}}P\)，因导弹总体要求发动机采用二个喷管，如图2-13所示。

所以

\(\frac{F}{\cos {{15}^{\circ }}}={{C}_{F}}{{A}_{t}}P\)

选推力系数\({{c}_{F}}=1.44\)

所以

\({{A}_{t}}=\frac{F}{{{c}_{F}}P\cos {{15}^{\circ }}}=\frac{17520}{1.44\times 135\times {{10}^{5}}\times 0.966}=93.3\times {{10}^{-5}}({{m}^{2}})\)

再由压强公式

\(P={{({{c}^{*}}{{\rho }_{p}}aK)}^{\frac{1}{1-n}}}\)

135×10⁵=（1280×1.615×10³×5.228×10^-5×K）\(^{\frac{1}{1-0.35}}\)

得出   K=399

所以   \({{A}_{bi}}=K{{A}_{t}}=399\times 93.3\times {{10}^{-5}}=0.373({{m}^{2}})\)

得     \(2\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})+\pi (D+d)L=0.373({{m}^{2}})\)

（3）通气参量的限制

已知发动机外径D_c=200mm，最大压强为13.5MPa，采用30CrMnSi钢，经强度计算壁厚为2.5mm。另外内壁尚有1.2mm的隔热涂层。

所以发动机燃烧室的内径为

\({{d}_{c}}={{D}_{c}}-2\delta -2{{\delta }_{}}=192.6mm\)

取               J_允许=0.4

则               \(J=\frac{{{A}_{t}}}{{{A}_{p}}}=\frac{{{A}_{t}}}{\frac{\pi }{4}d_{c}^{2}-\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})}=0.4\)

解出           \(\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})=26.8\times {{10}^{-3}}{{m}^{2}}\)

到此共得出三个方程

\(\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})L=13160\times {{10}^{3}}m{{m}^{3}} \)

\(2\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})+\pi (D+d)L=373\times {{10}^{3}}m{{m}^{2}} \)

\( \frac{\pi }{4}({{D}^{2}}-{{d}^{2}})=26.8\times {{10}^{3}}m{{m}^{2}} \)

从而可解出：D=185.6mm;d=20.5mm;L=491mm再综合结构等因素，选用尺寸为

D=180mm;d=25mm;L=500mm

（4）验算总冲、推力、压强和时间等参数。

总冲：     \(I=\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})L{{\rho }_{p}}{{I}_{s}}\)

\(=\frac{\pi }{4}({{0.18}^{2}}-{{0.025}^{2}})\times 0.5\times 1.615\times {{10}^{3}}\times 1863.3 \)

\(=37549(N\cdot s) \)

压强：   \({{A}_{bi}}=2\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})+\pi (D+d)L\)

\=\frac{\pi }{2}({{180}^{2}}-{{25}^{2}})+\pi (180+25)\times 500 \\

\( =371.9\times {{10}^{3}}(m{{m}^{2}}) \)

       \({{A}_{bf}}=\pi (D+d)L-2\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})\)

\( =\pi (180+25)\times 500-\frac{\pi }{2}({{180}^{2}}-{{25}^{2}}) \)

\( =272.1\times {{10}^{3}}(m{{m}^{2}}) \)

检验+40℃时的压强，用公式

\({{P}_{i}}={{({{c}^{*}}{{\rho }_{p}}a\frac{{{A}_{bi}}}{{{A}_{t}}})}^{\frac{1}{1-n}}}\)

\(K=\frac{{{A}_{bi}}}{{{A}_{t}}}=\frac{371.9\times {{10}^{3}}}{933}=398.6\)＜399

可见K值与前面计算的相差甚少，故最大压强（开始时）接近于13.5MPa。

用     \(P={{({{c}^{*}}{{\rho }_{p}}a\frac{{{A}_{b}}}{{{A}_{t}}})}^{\frac{1}{1-n}}}={{({{c}^{*}}{{\rho }_{p}}a\frac{{{A}_{bi}}}{{{A}_{t}}}\frac{{{A}_{b}}}{{{A}_{bi}}})}^{\frac{1}{1-n}}}{{P}_{i}}{{(\frac{{{A}_{b}}}{{{A}_{bi}}})}^{\frac{1}{1-n}}}\)

所以 \({{P}_{f}}={{P}_{i}}{{(\frac{{{A}_{bf}}}{{{A}_{bi}}})}^{\frac{1}{1-n}}}=135\times {{10}^{5}}{{(\frac{272.1\times {{10}^{3}}}{371.9\times {{10}^{3}}})}^{\frac{1}{1-0.35}}}=8.35MPa\)

由于\(\frac{1}{1-n}\)大于1，压力曲线是呈凹形，所以只要\({{P}_{i}},{{P}_{f}}\)满足要求即可。

推力：    \(F={{C}_{F}}{{A}_{t}}P\cos {{15}^{\circ }}=1.44\times 93.9\times {{10}^{-5}}\times 0.966\times P\)

\(=129.8\times {{10}^{-5}}P\)

所以       \({{F}_{i}}=129.8\times {{10}^{-5}}\times 135\times {{10}^{5}}=17519(N) \)

\({{F}_{f}}=129.8\times {{10}^{-5}}\times 83.5\times {{10}^{5}}=10836(N) \)

故满足要求。

时间：由于主要技术要求其工作时间不大于7s，所以应按低温-50℃来验算时间。

\(P={{({{c}^{*}}{{\rho }_{p}}a\frac{{{A}_{b}}}{{{A}_{t}}})}^{\frac{1}{1-n}}}={{\{{{c}^{*}}{{\rho }_{p}}a\frac{{{A}_{bi}}}{{{A}_{t}}}[1-\frac{4\pi (D+d)}{{{A}_{bi}}}e]\}}^{\frac{1}{1-n}}}\)

当≤1.8cm时，燃速规律为\(r=6.351\times {{10}^{-8}}{{P}^{0.75}}(m/s)\)

所以

   \(P={{(1280\times 1.615\times {{10}^{3}}\times 6.351\times {{10}^{-8}}\times \frac{37190\times {{10}^{-5}}}{93.3\times {{10}^{-5}}})}^{\frac{1}{1-0.75}}}{{[1-\frac{4\pi (0.18+0.025)}{37190\times {{10}^{-5}}}e]}^{\frac{1}{1-0.75}}}\)

\(=75.3\times {{10}^{5}}{{(1-6.93e)}^{4}}(N/{{m}^{2}})\)

当1.8cm≤e＜e₁时，燃速规律为\(r=3.0\times {{10}^{-6}}{{P}^{0.5}}\)，代入压强关系式得

\(P=61.23\times {{10}^{5}}{{(1-6.93e)}^{2}}(N/{{m}^{2}})\)

所以，时间为：

\(t=\int{_{0}^{0.018}\frac{de}{a{{P}^{n}}}+\int{_{0.018}^{0.03875}\frac{de}{a{{P}^{n}}}}}\)

\(=\int{_{0}^{0.018}}\)\(=\int_{0}^{0.018}{\frac{de}{6.351\times {{10}^{-8}}{{[75.3\times {{10}^{5}}{{(1-6.93e)}^{4}}]}^{0.75}}}}\)

\(+\int{_{0.018}^{0.03875}}\)\(+\int_{0.018}^{0.03875}{\frac{de}{3\times {{10}^{-6}}{{[61.23\times {{10}^{5}}{{(1-6.93e)}^{2}}]}^{0.5}}}}\)

\(=2.41+3.49=5.9(s)\)

故满足要求。

（2）多根管形药柱尺寸的确定

设计多根管形药柱需要确定的参数有D、d、L和n。它们与上述限制性条件的关系是：

1）药柱的装填与其几何尺寸及根数的关系

药柱在燃烧室内必须按某些特定的规律排列，才能保证药柱可以装入燃烧室。即药柱的外径D与燃烧室的内径d_c之间必须满足一定的关系。如图2-14所示。

设\(\overline{D}=D/{{d}_{c}}\)，显然不同n对应不同的\(\overline{D}\)值见表2-4。

考虑到药柱尺寸和燃烧室尺寸制造上的偏差，实际上采用的\({{\overline{D}}_{\text{exp}}}\)要比\({{\overline{D}}_{\text{th}}}\)小2~3%。同时在确定尺寸D时，还应考虑装填方式和药柱的制造工艺水平。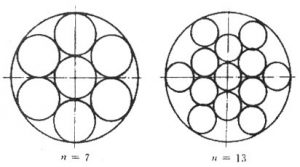

图2-14 多根管形药柱的装填图

表2-4 \(\overline{D}=D(n)\)

	1	2	3	4	5	6	7	11	13	14	19
	1.00	0.500	0.464	0.414	0.370	0.333	0.333	0.247	0.224	0.228	0.200
	＜1.00	0.490	0.455	0.406	0.363	0.327	0.327	0.242	0.220	0.219	0.196

2）通气参量与药柱几何尺寸及根数的关系

对于管形药柱忽略其端面积，其值为

对于管形药柱忽略其端面积，其值为

           （2-48）

由于管形药柱是多通道的药形，所以还需区别药柱内、外通道的值。

\(\partial {{e}_{}}=\frac{n\pi dL}{n\frac{\pi }{4}{{d}^{2}}}=\frac{4L}{d}\)                        （2-49）

\(\partial {{e}_{}}=\frac{n\pi DL}{\frac{\pi }{4}(d_{c}^{2}-n{{D}^{2}})}=\frac{4nDL}{d_{c}^{2}-n{{D}^{2}}}\)                   （2-50）

令   \(k=\frac{\partial {{e}_{in}}}{\partial {{e}_{out}}}\)，即\(\partial {{e}_{in}}=k\partial {{e}_{out}}\)

所以

\(\frac{4L}{d}=k\frac{4nDL}{d_{c}^{2}-n{{D}^{2}}}\)                       （2-51）

得                             \(d=\frac{{{d}_{c}}}{kn\overline{D}}-\frac{D}{k}\)                         （2-52）

\(\overline{d}=\frac{d}{{{d}_{c}}}=\frac{1}{kn\overline{D}}-\frac{\overline{D}}{k}\)                         （2-53）

根据上式知n、k即可求出d，见表2-5。表中\(\overline{D}\)是n的函数，采用\({{\overline{D}}_{\text{exp}}}\)。

表2-5 \(\overline{d}=\overline{d}(n,k)\)

n k	3	4	5	6	7	11	13	14	19
1	0.2776	0.2098	0.1880	0.1827	0.1099	0.1337	0.1297	0.1072	0.0725
1.2	0.2313	0.1748	0.1566	0.1522	0.0916	0.1114	0.1080	0.0893	0.0604
1.4	0.1983	0.1498	0.1343	0.1305	0.0785	0.0955	0.0926	0.0765	0.0518
1.6	0.1735	0.1311	0.1175	0.1142	0.0687	0.0835	0.0810	0.0670	0.0453
1.8	0.1542	0.1165	0.1044	0.1015	0.0610	0.0734	0.0720	0.0595	0.0403
2	0.1388	0.1049	0.0940	0.0913	0.0549	0.0668	0.0648	0.0536	0.0363
3	0.0925	0.0699	0.0627	0.0609	0.0366	0.0446	0.0432	0.0357	0.0242

3）装填分数与药柱几何尺寸及根数的关系

\(\eta =\frac{\frac{n\pi }{4}({{D}^{2}}-{{d}^{2}})}{\frac{\pi d_{c}^{2}}{4}}=\frac{n({{D}^{2}}-{{d}^{2}})}{d_{c}^{2}}=n{{\overline{D}}^{2}}-n{{\overline{d}}^{2}}\)

\(=n{{\overline{D}}^{2}}-n{{(\frac{1}{kn\overline{D}}-\frac{\overline{D}}{k})}^{2}}=\frac{{{k}^{2}}-1}{{{k}^{2}}}n{{\overline{D}}^{2}}-\frac{1}{{{k}^{2}}n{{\overline{D}}^{2}}}+\frac{2}{{{k}^{2}}}\)               （2-54）

同样知n、k可得η，见表2-6。

表2-6 \(\eta =\eta (n,k)\)

n k	3	4	5	6	7	11	13	14	19
1	0.3899	0.4833	0.4822	0.4413	0.6640	0.4476	0.4105	0.5106	0.6300
1.2	0.4606	0.5371	0.5362	0.5026	0.6898	0.5077	0.4776	0.5598	0.6606
1.4	0.5031	0.5696	0.5687	0.5394	0.7054	0.5439	0.5177	0.5895	0.6789
1.6	0.5308	0.5906	0.5898	0.5633	0.7155	0.5675	0.5439	0.6086	0.6909
1.8	0.5497	0.6051	0.6043	0.5798	0.7225	0.5835	0.5618	0.6219	0.6990
2	0.5633	0.6153	0.6147	0.5916	0.7274	0.5951	0.5746	0.6312	0.7049
3	0.5954	0.6398	0.6392	0.6193	0.7391	0.6223	0.6049	0.6336	0.7188

实验表明，k值的大小对燃烧的稳定性和初始压强峰有一定影响。同时从表2-6中可以看出，当k从1增加到2时，装填分数增加较多，而k在2以上变化时，装填分数增加较慢，故一般取k=1~2。

4）肉厚分数\({{\bar{e}}_{1}}\)与n、k的关系

对两端阻燃的管形药柱

  （2-55）

\({{\overline{e}}_{1}}={{\overline{e}}_{1}}(n\)、k)之关系见表2-7。

表2-7 \({{\overline{e}}_{1}}={{\overline{e}}_{1}}(n\)、k)

n k	3	4	5	6	7	11	13	14	19
1	0.0887	0.0981	0.0875	0.0722	0.1086	0.0542	0.0452	0.0559	0.0618
1.2	0.1119	0.1156	0.1032	0.0874	0.1177	0.0653	0.056	0.0649	0.0678
1.4	0.1284	0.1281	0.1144	0.0983	0.1243	0.0733	0.0637	0.0713	0.0721
1.6	0.1408	0.1375	0.1228	0.1034	0.1292	0.0793	0.0695	0.076	0.0751
1.8	0.1504	0.1448	0.1293	0.1128	0.1330	0.0839	0.074	0.0798	0.0779
2	0.1581	0.1506	0.1345	0.1179	0.1361	0.0876	0.0776	0.0827	0.0799
3	0.1813	0.1681	0.1502	0.1331	0.1452	0.0987	0.0884	0.0917	0.0859

5）药柱质量m_p、通气参量∂e与n、k的关系

\({{m}_{P}}=n\frac{\pi }{4}({{D}^{2}}-{{d}^{2}})L{{\rho }_{p}}\)

\(\partial e=\frac{4n(D+d)L}{d_{c}^{2}-n({{D}^{2}}-{{d}^{2}})}\)

消去L，得

          （2-56）

将前面的\(\bar{d}=\frac{d}{{{d}_{c}}}=\frac{1}{kn\bar{D}}-\frac{{\bar{D}}}{k}\)的关系代入即可得到\({{m}_{p}}/{{\rho }_{p}}\partial ed_{c}^{3}\)与n、k的关系，见表2-8。

当\(\partial e=\partial {{e}_{cr}}\)时，即得到极限装药量\({{m}_{P.cr}}\)与几何参数之间的关系，当装填分数愈高时，极限装药量可能愈小，因此，选高装填分数的药柱会受到装药量的约束。

表2-8 \(\Omega ={{m}_{P}}/{{\rho }_{p}}\partial ed_{c}^{3}=\Omega (n\)、k)

n k	3	4	5	6	7	11	13	14	19
1	0.0213	0.0199	0.0178	0.0158	0.0143	0.0118	0.0105	0.0107	0.0090
1.2	0.0237	0.0210	0.0188	0.0171	0.0143	0.0126	0.0115	0.0112	0.0090
1.4	0.0250	0.0217	0.0194	0.0178	0.0144	0.0131	0.0121	0.0115	0.0091
1.6	0.0259	0.0221	0.0198	0.0183	0.0144	0.0135	0.0124	0.0117	0.0092
1.8	0.0266	0.0225	0.0201	0.0186	0.0145	0.0137	0.0127	0.0118	0.0092
2	0.0271	0.0227	0.0204	0.0189	0.0146	0.0139	0.0130	0.0120	0.0093
3	0.0288	0.0238	0.0213	0.0199	0.0149	0.0146	0.0137	0.0125	0.0095

多根管形药柱的几何参数共有4个，而关系式共有5个。因此在确定药柱的参数时必须满足药柱的装填要求、装药量（总冲）的要求和通气参量的要求。而装填分数要求和肉厚分数的要求则只能保证一个。对导弹用发动机如空-空导弹用固体火箭发动机、地-空导弹用的起飞助推器等，为了保证导弹能尽快地达到规定的飞行速度，以利于尽快地接近目标和进入控制飞行，则往往需要保证规定的推力要求，为此应首先保证肉厚分数的要求。对于某些火箭用发动机如野战火箭弹等，则上述技术要求不突出，而应按最大装填分数要求来设计药柱。

对保证技术要求及按肉厚分数确定药柱几何尺寸的情况，首先计算出\({{\overline{e}}_{1}}\)，然后查表2-7，找出几组相近的n、k值。再从表2-6选出对应这几组k、n值的η，找出η较大的一组，再找出相应的\({{m}_{p}}/{{\rho }_{p}}\partial ed_{c}^{3}\)值，代入已知m_p、ρ_p和d_c，计算∂e，看是否满足要求，如不满足可再选η较小的一组n、k来进行计算。

2.4.2 含金属丝端燃药柱

（1）概述

端面燃烧具有药形简单、装填分数高、无侵蚀燃烧、药柱强度好及工作时间可以比较长的优点。但是由于这种药柱的燃面小，因而推力也小，使用受到限制。为了提高这种药柱的推力。一种简单可行的方法是在推进剂中加入金属丝，利用金属丝导热性能高的特点（其导热系数为推进剂的300~500倍），提高了金属丝附近推进剂的温度，从而极大地提高了该处的燃速，造成新的燃面变化规律，燃烧面积增大，推力得到提高。

加入金属丝的方式有两种：一是通常采用的加定向排列的长金属丝。由于利用炽热的金属丝来增加向推进剂的传热以提高燃速，所以只有垂直于燃面方向的金属丝才起作用。二是随机地加入短金属丝纤维，优点是可以用于任何药型，但由于纤维方向任意排列，所以燃速提高小于定向排列的长金属丝。

下面介绍端面燃烧嵌入长金属丝药柱设计的问题

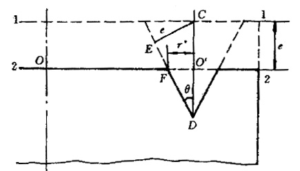
（2）燃烧规律

1). 药柱燃烧阶段划分

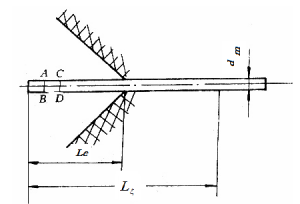
药柱燃烧分三个阶段：起始段、平衡段、结尾段。设药柱的半径为R，初始端面为πR²，推进剂的燃速为r₀。见图2-15。

图2-15 嵌金属丝端面燃烧药柱

（a）起始段：点火后开始时药柱以燃速r₀燃烧，然面向右推进。暴露在高温燃气中的金属丝不断地被高温燃气加热，同时又不断地把热量传入紧密接触金属丝的推进剂。当这部分推进剂的温度升高到某个临界值后即被点燃。并以r_f＞r₀的燃速燃烧，从而形成以金属丝为轴心的圆锥孔。随着燃烧的延续，锥孔不断扩大，燃面也不断增加，一直燃到药柱的外边缘，起始段终止。

（b）平衡段：锥面以不变的θ角向前推进，燃面不变。

（c）结尾段：为减面燃烧。如图2-15所示形状。

2) 燃速及燃面变化规律

如图2-16所示。设r₀为药柱基体的燃速，r_f为沿金属丝的燃速。K为燃速增大倍数。

（a）起始段

锥角θ变化规律：

\(\sin \theta =\frac{{{r}_{0}}\text{d}t}{{{r}_{f}}\text{d}t}=\frac{{{r}_{0}}}{{{r}_{f}}}=\frac{1}{K}\)                       （2-57）

由于                     \({{r}_{0}}={{a}_{0}}{{P}^{{{n}_{0}}}}\)

                         \({{r}_{f}}={{a}_{f}}{{P}^{{{n}_{f}}}}\)

所以                       \(\sin \theta =\frac{{{r}_{0}}}{{{r}_{f}}}=\frac{{{a}_{0}}}{{{a}_{f}}}{{P}^{{{n}_{0}}-{{n}_{f}}}}\)                   （2-58）

当             n_f＜n₀时，θ角随压强上升而增加；

n_f>n₀时，θ角随压强上升而减小；

n_f=n₀时，θ角不随压强变化。

燃面A_b的变化规律：起始段的燃面由锥的侧面与部分端平面所组成。如图2-17所示。

图2-16 燃速与锥角的关系             图2-17 含金属丝药柱燃面变化规律

\({{A}_{b1}}=\pi {{R}^{2}}-\pi r_{1}^{*2}+\pi r_{1}^{*}l=\pi {{R}^{2}}+\pi r_{1}^{*2}(\frac{1}{\sin {{\theta }_{1}}}-1)\)

\({{r}_{1}}^{*}\)、l₁、θ₁分别为“1”时刻的圆锥底圆半径、圆锥母线长及锥顶角。同样在“2”时刻：

\({{A}_{b2}}=\pi {{R}^{2}}+\pi r_{2}^{*2}(\frac{1}{\sin {{\theta }_{2}}}-1)\)

以上我们仅以一根金属丝的情况为例说明问题。对于嵌多根金属丝的药柱，其起始段的燃面变化规律较复杂，可用近似的数值积分法来计算。

（b）平衡段

a.平衡段的燃面

不含金属丝的燃面       \({{A}_{b0}}=\pi {{R}^{2}}\)

含金属丝的燃面         A_bf=πRl

                       \(\frac{{{A}_{b0}}}{{{A}_{bf}}}=\frac{\pi {{R}^{2}}}{\pi Rl}=\frac{R}{l}=\sin \theta =\frac{1}{K}\)

即A_bf相当于A_b0的K倍。由于燃面A_bf是圆锥的侧面积，所以当θ角已知后，它的大小仅取决于底面积的大小。即对于同一直径嵌多根金属丝的药柱，尽管多根金属丝会形成多个交错的圆锥，但由于底面积未改变，所以燃面也与单根金属丝的相等。读者可自行证明之。

b.平衡段的压强

根据压强公式\(P={{({{c}^{*}}{{\rho }_{p}}{{a}_{0}}\frac{{{A}_{b0}}}{{{A}_{t}}})}^{\frac{1}{1-{{n}_{0}}}}}\)

加入金属丝后，燃面变成\({{A}_{bf}}=K{{A}_{b0}}\)

\({{P}_{f}}={{({{c}^{*}}{{\rho }_{p}}{{a}_{0}}\frac{{{A}_{bf}}}{{{A}_{t}}})}^{\frac{1}{1-{{n}_{0}}}}}={{({{c}^{*}}{{\rho }_{p}}{{a}_{0}}\frac{K{{A}_{b0}}}{{{A}_{t}}})}^{\frac{1}{1-{{n}_{0}}}}}\)

知         \(K=\frac{{{a}_{f}}}{{{a}_{0}}}{{P}^{{{n}_{f}}-{{n}_{0}}}}\)

将K代入得：   \({{P}_{f}}={{({{c}^{*}}{{\rho }_{p}}{{a}_{f}}\frac{{{A}_{b0}}}{{{A}_{t}}})}^{\frac{1}{1-{{n}_{f}}}}}\)

当已知a_f、n_f，可由此式计算压强。

c.平衡段推力

\(F={{I}_{s}}{{\rho }_{P}}r{{A}_{b}}\)

将燃面换成A_bf，则

\(F={{I}_{s}}{{\rho }_{p}}r{{A}_{bf}}={{I}_{s}}{{\rho }_{p}}r{{A}_{b0}}K\)                         （2-59）

可以看出，加入金属丝后，燃面、燃速和推力均增加K倍。压强变化取决于n_f、a_f。

（3）燃烧机理

在设计此种药柱时，一个重要的参数r_f必须知道。下面我们简要介绍一种计算r_f的方法。为此需要计算出稳态下沿金属丝长度方向上的温度分布。

图2-18

从上述可知，在起始段及结尾段，燃烧是不稳定过程。即r_f不是常数。而在平衡段r_f是常数。并且等于燃面推进速度或金属丝端面的不断烧蚀速度。

在计算中，由于金属丝的长度比其直径大得多，故可以假定：

1）金属丝看成是无限长的。因此在稳态下金属丝内的温度分布保持定常。

2）温度分布是一维的。即认为同一                  

金属丝截面上温度相等。

基本方程：把坐标原点固定在金属丝的烧蚀端面上。认为此坐标系统固定不动。从而整个金属丝和推进剂将以r_f的速度自右向左移动。这样就可以把不稳定的温度场转化为稳定的温度场求解。以图2-18所示，取出一小段控制体，列出计算方程组。我们把金属丝分为三个部分。

第一部分：暴露在燃气中的金属丝

\({{a}_{m}}\frac{{{\partial }^{2}}{{T}_{1}}}{\partial {{x}^{2}}}+{{r}_{f}}\frac{\partial {{T}_{1}}}{\partial x}+\frac{4{{q}_{1}}}{{{d}_{m}}{{\rho }_{m}}{{C}_{m}}}=0\)       0＜x＜L_e

边界条件：         x=0,       T₁=T_熔

                 x=L_e       T₁=T_燃

式中，T₁：暴露在高温燃气中金属丝的温度，

     T_熔：金属丝的熔点，

     T_燃：推进剂的点燃温度，

     ρ_m、d_m、C_m：分别为金属丝的密度、直径、比热，a_m：导温系数。

     q₁：燃气向金属丝的传热。可以分成对流与辐射传热两部分。可通过金属丝附近的流场计算出。

第二部分：假定一个长度L_ξ，当x＞L_ξ以后认为可以忽略由金属向推进剂的传热q₂。T₂为此段内金属丝内的温度分布。

\({{a}_{m}}\frac{{{\partial }^{2}}{{T}_{2}}}{\partial {{x}^{2}}}+{{r}_{f}}\frac{\partial {{T}_{2}}}{\partial x}+\frac{4{{q}_{2}}}{{{d}_{m}}{{\rho }_{m}}{{C}_{m}}}=0\)       L_e＜x＜L_ξ

边界条件：       x=L_e       T₂=T_燃

                 x=L_ξ       T₃=T_ξ（推进剂初温）

在解上述方程计算T₁、T₂和T₃时，r_f、L_e和L_ξ实际上都是未知数。因此还必须给出三个补充方程。可以用下面三个截面的能量方程来表达：

x=0         \({{\left. {{Q}_{0}}=-{{\lambda }_{m}}\frac{\partial {{T}_{1}}}{\partial x} \right|}_{x=0}}+{{\rho }_{m}}{{r}_{f}}{{q}_{m}}\)

Q₀为在端部燃气通过对流与辐射传给金属丝的热（可以计算出）。方程右边第一项为从端部传入金属丝内部的热，第二项为熔化所吸收的热。

\(\left. x={{L}_{e}}:\frac{\partial {{T}_{1}}}{\partial x} \right|{{\left. _{x={{L}_{e}}}=\frac{\partial {{T}_{2}}}{\partial x} \right|}_{x={{L}_{e}}}} \)

\(x={{L}_{\xi }}:{{\left. \frac{\partial {{T}_{2}}}{\partial x} \right|}_{x={{L}_{\xi }}}}{{\left. =\frac{\partial {{T}_{3}}}{\partial x} \right|}_{x={{L}_{\xi }}}} \)

（4）影响r_f的因素

1）金属丝的材料

使用不同材料的金属丝，可以得到不同的r_f。由于r_f与燃气通过金属丝向推进剂的传热有密切关系，所以材料的热扩散系数a（或称导温系数，\(a=\frac{\lambda }{{{C}_{P}}\rho }\)）对r_f有较大的影响。表2-9中给出某复合推进剂中嵌入不同的金属丝所得到的r_f值。（推进剂的基本燃速r₀=12.7mm/s，可以看出a大的r_f就大。同时在a相关不多的情况下，熔点高的r_f就大。这是因为熔点高，暴露在火焰中的金属丝的长度就长，金属丝端头的温度就高（相当于熔点），故向推进剂中传热就多，r_f就大。

表 2-9

金属丝材料	650℃以下热扩散系数 a（cm2/S）	导热系数 λ（W/（m·K））	熔点（℃）	rf （mm/s）	燃速增大倍数 K
银	1.23	458.9	960	67.3	5.3
紫铜	0.90	393.1	1083	58.9	4.6
钨	0.67	160.4	3370	46.2	3.6
铂	0.35		1755	37.1	2.9
铝	0.94	203.5	660	29.5	2.3
镁	0.66	158.2	651	24.4	1.9
钢	0.064	46.5	1460	20.3	1.6

2）金属丝的直径d_m：开始r_f随d_m增加而增加，到一定值后，再增加r_f下降。见表2-10。同时可以看到随d_m增加，压强指数也下降，这对改善燃烧性能也是有好处的。

表 2-10

金属丝材料	金属丝直径〔或厚度〕 （mm）	燃速rf （mm/s）	燃速增长量 （%）	压强指数 n
铜	无	11.68	—	0.43
	0.0254	28.44	143	0.75
	0.0508	45.74	291	0.58
	0.0762	59.60	411	0.35
	0.1270	55.88	378	0.31
	0.1778	53.34	357	0.21
	0.2540	45.21	287	0.20
银	无	11.18	—	0.45
	0.0254	20.57	84	0.87
	0.0762	45.72	309	0.80
	0.1270	55.88	400	0.40
	0.1778	47.24	323	0.45
	0.2540	52.83	370	0.15
钨	无	11.68	—	0.46
	0.0254	27.94	140	0.73
	0.0762	41.40	254	0.40
	0.1270	39.37	237	0.33
钼	无	11.43	—	0.43
	0.0762	33.02	189	0.40
	0.1270	38.10	234	0.32
	0.2540	32.51	184	0.19

3）压强的影响：提高压强使通过金属丝传入推进剂的热量有所增加，故r_f略有增加。

4）推进剂：显然，不同的推进剂有不同的能量特性、燃速、点燃温度以及热性能（λ、C_p、ρ等）。这些因素都会对r_f有影响。

5）双金属丝问题：前面已论述了金属丝的导温系数a及熔点对r_f的影响。实际上很难找到导温系数a大而又熔点高的金属。因此不少研究人员提出使用双金属丝。即把一层高熔点的金属包在a值高的金属之上。例如用铝丝外包一层钯（Pd），容积比为Pd:Al=54:47。参阅表2-11。

表 2-11

金属丝直径及材料	燃速（mm/s） （P=7.03MPa）	燃速增加倍数 K
无   丝	15.00	—
0.127mm银丝	69.80	3.66
0.178mm银丝	68.60	3.57
0.102mmPd—Al丝	132	7.81
0.127mmPd—Al丝	142	8.49
0.152mmPd—Al丝	117	6.80
0.508mmPd—Al丝	83.8	4.59

6）化学涂层：采用此方法，在工艺上比双金属的办法简单可行。即在金属丝外涂一层化学涂层来改变r_f。一般的化学涂层分两大类：一是“惰性物质涂层”。此涂层起一定的隔热作用，所以目的不是提高r_f而是为了调节r_f。另一类是“氧化物质涂层”。它本身有氧化剂，燃速比推进剂要高。金属丝从燃气中吸收的热量先促使“氧化涂层”分解，进而促使基本推进剂分解。这使物理化学作用结合起来，可以更大地提高燃速。同时也可以降低压强指数，是一个较现实的方案。

（5）含金属丝的药柱设计

• 根据推力的要求，计算所需的r_f；
• 选择金属丝的材料和直径；
• 确定金属丝的根数及排列位置。

尽管含单根与多根金属丝所产生的燃面相同，但采用适当排列的多根金属丝可以较快地缩短起始段及结尾段的延续时间，改善内弹道性能。也就是说，影响起始段及结尾段时间长短的因素是金属丝的根数及其排列方式。

1）关于金属丝排列位置。取半径为R的端面燃烧药柱，其中嵌入n根金属丝。药柱轴心为O，金属丝的圆心为O₁。假设金属丝均匀分布在半径为r的圆上。见图2-19。在一根丝影响的扇形\(\overline{OAB}\)内，显然必须由O₁烧到A、B、O之后，起始段才结束。而且要使起始段最短必须同时燃到A、B、O三点才成。

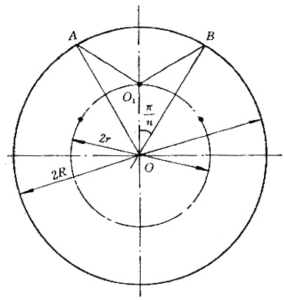
即         \({{O}_{1}}A={{O}_{1}}B={{O}_{1}}O\)

所以O₁点必须是OA与OB的中垂线的交点。       

\(r=O{{O}_{1}}=\frac{R}{2\cos \frac{\pi }{n}}\)

  图2-19 金属丝的排列位置

由此得出均匀分布在一个圆周上的金属丝的情况下，半径r与根数n的关系。见表2-12。

表 2-12

n	4	5	6	7	8	9	10	11	12
r/R	0.707	0.618	0.577	0.555	0.541	0.532	0.526	0.521	0.518

若嵌入金属丝的数目较多时，可以在药柱中心即O点布置一根，其他仍均匀分布在同一圆周上。如图2-20所示。显然要满足起始段最短的要求，必须：

图2-20

\(OA={O}’A={O}’B \)

\({{r}_{1}}=O{O}’=2OA\cos \frac{\pi }{n-1} \)

\(R=OB=OA+2AC \)

\(AC={O}’A\sin \beta =OA\sin \beta \)

\(\beta =\frac{\pi }{2}-\frac{2\pi }{n-1} \)

所以

\(\sin \beta =\sin (\frac{\pi }{2}-\frac{2\pi }{n-1})=\cos \frac{2\pi }{n-1} \)

\(AC=OA\cos \frac{2\pi }{n-1} \)

\(R=OA(1+2\cos \frac{2\pi }{n-1}) \)

所以

\(\frac{r}{R}=\frac{2\cos \frac{\pi }{n-1}}{1+2\cos \frac{2\pi }{n-1}}\)见表2-13

表 2-13

n	7	8	9	10	11	12
r/R	0.866	0.802	0.765	0.742	0.722	0.715

2）关于金属丝根数的选择，一般金属丝的根数越多，起始段结束的时间越短。但根数太多会给工艺上带来困难。通常选根数n＞5有利。

图2-21

为了看清楚排列根数对于起始段延续时间的影响，首先推导起始段烧去的肉厚e与圆锥底圆半径r*的关系式。见图2-21。开始燃烧在1-1截面，当燃至截面2-2时烧去肉厚e，此时圆锥底圆半径为\({{r}^{*}}={O}’F\)

从\(\Delta {O}’FD\) 中 \(\frac{{{r}^{*}}}{{O}’D}=\frac{\sin \theta }{\cos \theta }=tg\theta \)                     

\(\Delta ECD\)中   \(\frac{e}{e+{O}’D}=\sin \theta \)

消去\({O}’D\)，可得

\({{r}^{*}}=\frac{e(1-\sin \theta )}{\cos \theta }\)

对于沿r均匀分布的情况

\({{r}^{*}}={O}’A=\frac{R}{2\cos \frac{\pi }{n}}\)（中心无丝）

\({{r}^{*}}={O}’A=\frac{2R\cos \frac{\pi }{n-1}}{1+2\cos \frac{2\pi }{n-1}}\)（中心有丝见图2-20）

将\({{r}^{*}}=\frac{e(1-\sin \theta )}{\cos \theta }\)代入，即可得起始段结束时烧去的肉厚。即

\(e=\frac{R\cos \theta }{2\cos \frac{\pi }{n}(1-\sin \theta )}\)（中心无丝）

\(e=\frac{2R\cos \theta \cos \frac{\pi }{n-1}}{(1+2\cos \frac{2\pi }{n-1})(1-\sin \theta )}\)（中心有丝）

已知基础燃速r₀，可以从\(t=\frac{e}{{{r}_{0}}}\)得出起始段的燃烧时间，这样即可得出根数n与起始段燃烧时间的关系式

\(t=\frac{e}{{{r}_{0}}}=\frac{R\cos \theta }{{{r}_{0}}2\cos \frac{\pi }{n}\left( 1-\sin \theta \right)}\)（中心无丝）

\(t=\frac{e}{{{r}_{0}}}=\frac{2R\cos \theta \cos \frac{\pi }{n-1}}{{{r}_{0}}(1+2\cos \frac{2\pi }{n-1})(1-\sin \theta )}\)（中心有丝） 

2.5 基于计算机图形学的装药设计

前面介绍了几种基于解析方法的装药设计和计算方法，然而大部分装药结构是给不出解析公式的，因此限制了这种方法的应用。随着计算机图形学技术的发展和大量商业化绘图软件的应用，给装药设计提供了一种全新的快速的解决方案。以下简要介绍这种方法的基本原理和应用。

2.5.1 三维几何造型技术

三维几何造型技术涉及到三维几何造型的计算机存储模型和三维几何模型的表示方法。前者是研究形体在计算机中存储时采用的数据结构模型，有线框模型、表面模型和实体模型，这三种模型各有优缺点，因此目前采用以实体模型为基础，将三种模型统一起来，融合成一体；后者是研究如何表达以及如何构造一个实体模型，当前用的最多的是实体几何造型法、扫描表示法以及边界表示法。关于这部分的基础知识请参考有关图形学的文献，这里只介绍与装药设计相关的图形学内容。

（1）属性信息

属性的用途是为三维实体附件系统或者用户信息，属性可以是简单数据、指向其他实体的指针或者是与应用程序定义的变长度数据（数组、链表等）的连接。由此可以将三维实体的属性分为三类：

• 简单属性，它只包含简单数据，可以表示实体的材料或颜色之类的属性信息。
• 复杂属性，它可以含有指向其他实体的指针，可以表示一些如尺寸、约束或者特征等属性信息。
• 连接属性，它像桥梁一样用来将实体和一些应用程序定义的变长度数据连接在一起。

属性是附加在三维实体对象上，因此要求属性具有对自身行为的控制能力，这个能力体现在，当其所在的实体被施加了分割、融合或者变换等操作后，该实体的属性依然保持其合理性。因此，需要研究属性在实体分割、融合或者变换操作时控制其自身性质的机制。

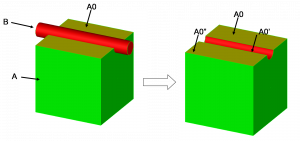
以颜色属性为例，如图2-22所示，立方体A为浅色，其上表面A0为浅色，圆柱体B的表面为深色，经布尔差操作A-B，可以发现面A0被分割为面A0和A0″，均保持原有的浅色，来源于圆柱体B面A’是新生成的面，因此保留B的深色，这种颜色机制是合理的，也就是说实体分割时，应用程序保留原有的属性，不对属性进行更改。装药设计就是利用这一属性特征提取出燃面的。

在几何造型器ACIS中提供了类ATTRIB，该属性类含有控制分割、融合以及变换的方法。

图2-22 实体分割时的颜色属性变化机制

（2）质量特性计算

质量、质心、转动惯量等质量特性参数是固体发动机动力学特性仿真的重要基础数据。为了能够计算任意结构形式的三维实体模型的质量特性，需要从质量、质心、转动惯量的定义出发，根据三维实体模型的表示方法发展相关的算法。对于一个密度均一的三维几何实体V，其质量M、质心\({{M}_{c}}={{({{x}_{c}},{{y}_{c}},{{z}_{c}})}^{T}}\)和转动惯量J的积分表达式如下：

\(M=\iiint\limits_{V}{\rho dV}\)                          （2-60）

\({{M}_{c}}=\frac{1}{M}{{(\iiint\limits_{V}{\rho xdV},\iiint\limits_{V}{\rho ydV},\iiint\limits_{V}{\rho zdV})}^{T}}\)               （2-61）

转动惯量张量，其中：

\[{{I}_{xx}}=\iiint\limits_{V}{\rho ({{y}^{2}}+{{z}^{2}})dV-M(y_{c}^{2}+z_{c}^{2})}\]                 （2-62）

\[{{I}_{yy}}=\iiint\limits_{V}{\rho ({{z}^{2}}+{{x}^{2}})dV}-M(z_{c}^{2}+x_{c}^{2})\]                   （2-63）

\({{I}_{zz}}=\iiint\limits_{V}{\rho ({{x}^{2}}+{{y}^{2}})dV}-M(x_{c}^{2}+y_{c}^{2})\)                  （2-64）

\({{I}_{xy}}={{I}_{yx}}=\iiint\limits_{V}{\rho xydV}-M{{x}_{c}}{{y}_{c}}\)                         （2-65）

\({{I}_{yz}}={{I}_{zy}}=\iiint\limits_{V}{\rho yzdV}-M{{y}_{c}}{{z}_{c}}\)                         （2-66）

\({{I}_{xz}}={{I}_{zx}}=\iiint\limits_{V}{\rho xzdV}-M{{x}_{c}}{{z}_{c}}\)                           （2-67）

质量的计算与坐标系无关，式（2-61）质心的计算在任意一个坐标系xyzo中进行，式（2-62）~（2-67）的计算在以质心为原点的坐标系中进行，可以利用理论力学中的平行轴定理将其转换到任意坐标系中。一般图形引擎中都有获取体积和转动惯量的属性值，用户不必再开发相应的质量和惯量的计算程序。

（3）三维几何造型系统选型

本文在固体发动机的计算机辅助设计和分析研究过程中先后对多种造型平台进行了论证，包括：在Pro/E, UG, Catia 等商用CAD造型平台上二次开发，在OpenGL、Open Inventor、ACIS、Open CASCADE等底层通用几何造型引擎上自行订制。

在高端CAD软件的基础上进行二次开发，这种开发方式避免了对复杂的CAD底层设计理论与设计技术的纠缠，使得系统开发人员可以专注于开发火箭动力系统的专业辅助设计模块。实际上，由于三维几何造型平台过高的技术门槛导致了都采用了二次开发这条技术路线。

但是，这种开发方式是以牺牲自主知识产权与软件设计灵活性为代价的，带来了一系列严重的后果。首先，国外CAD软件开放的开发接口是有限的，二次开发程序不可能随意操纵CAD软件的底层技术，很多固体发动机设计人员迫切需要的设计功能都没有办法通过二次开发的方式来实现。

其次，二次开发受限于某一种CAD平台，限制了用户单位在软件选择和系统集成方面的自由度。在面向产品全生命周期设计（Product Lifecycle Management, PLM）的今天，设计软件的选择更加强调各个设计模块在整体的集成性和最优性。然而，设计单位或许为了与某个小小的二次开发模块相匹配，不得不放弃更多其他的优秀设计软件，甚至重新选择PLM产品集成框架。

再次，大量优秀的计算机辅助设计理念、方法、技术在不断的涌现。这也促使了高端商用CAD厂家不断地在他们的系统中融入这些新技术，升级软件版本。而二次开发模块并不掌握这些核心的技术和理念，因此很多时候二次开发模块在其宿主软件进行了版本升级之后完全无法使用，只能推倒重来。这阻碍了先进设计理念在固体发动机领域的应用。

2.5.2 药柱的变量化设计方法原理

在推进剂选定及喷管尺寸确定后，推力曲线（F~t）与药柱燃面面积的变化趋势一致，因此，设计人员通过不断调整药柱的几何构型来合理设计燃面随肉厚推移的变化关系，获得满足战术性能要求的推力方案；另外，由于固体发动机内部边界几何形状随药柱结构的不同而千变万化，因此，与药柱几何形状有关的计算网格生成、边界条件的确定都比较困难，且复杂的三维几何边界形状必然导致流场及结构场的三维化，建立药柱的三维几何模型及得到药柱在不同燃面推移阶段的几何模型是发动机内流场以及结构完整性分析的基础。

由此可见，药柱燃面推移过程中几何模型的构建，燃面面积、质量、质心和转动惯量的变化规律的计算，是药柱设计的核心内容。

（1）推进剂几何燃烧定律

本章的研究基于下面几何燃烧定律的假设情况:

• 药柱的组分及其物理化学性能处处均匀一致。
• 全部燃烧表面同时点燃。
• 燃烧表面上各点处于相同的燃烧条件。

全部燃烧表面将沿其法向方向，以相同的速度向药柱内部推移。称这种燃烧规律为几何燃烧定律，采用这一定律使得计算大为简化。

几何燃烧规律忽略了压强，初温，燃气流冲刷等因素的影响，是一种在理想假设前提下得到的燃烧定律，与实际的燃烧过程不可能完全相符，但是实践证明，这种规律基本上是正确的，它在宏观上反映了药柱稳定燃烧的基本规律。由于几何燃烧定律可以按纯几何关系导得各种结构的药柱在整个燃烧过程中燃面的变化规律，这为设计人员在药柱设计和发动机性能预估中提供了方便。目前，一些常用药柱燃面的理论燃烧公式也都是使用这种方式得到的。因此本章即以几何燃烧定律为基础开展燃面推移仿真的研究。

（2）实体造型方法

将实体造型技术应用于固体发动机药柱的设计、燃面推移仿真和燃面计算,是一种比较新的方法，称之为实体造型方法。其基本思想是:用基本几何体构成代表药柱外形的实心体和代表药柱空腔的芯模,实心体“减去”芯模就得到药柱的初始形状。模拟燃面推移时,带有空腔的几何体通过改变参数使得变化后的各表面与初始表面等距,实心体“减去”变化后的芯模,就得到新的药柱形状,然后计算出燃烧面积和药柱的形体特征和质量特征,得到燃面面积、质心、惯量、形状等变化规律。

然而，对于一般的边界表达（B-Rep）三维实体，目前还没有稳定的包络面推移求解算法可以处理可能出现的凹面消失问题。事实上，目前主流的边界造型系统一般只能稳定地对三维凸体进行任意厚度的包络面推移造型。

在这种情况下，考虑到对药柱燃面（通常为凹面）直接进行向内的推移造型极容易出现推移面消失和形体自相交。因此本文采用间接造型法，将药柱外轮廓与药柱内腔芯模进行实体布尔差运算，得到药柱的几何实体，如式（2-68）所示。

\({{S}_{grain}}={{S}_{out}}-{{S}_{in}}\)                         （2-68）

式中，S_in构造了药柱的燃面。在燃面推移过程中，依据几何燃烧定律，S_in需要根据肉厚不断向外扩张。同样的，为了避免S_in实体在扩张过程中出现形面消失和形体自相交等问题，本文经过对药型的总结归纳，将芯模分解为一系列可以快速进行燃面推移的特征形体的组合，如翼形特征、楔形特性、星形特征等，如式（2-69）所示。

\({{S}_{in}}=\sum\limits_{i=1}^{n}{S{{F}_{i}}}\)                            （2-69）

在实际的造型过程中，由于布尔差运算比布尔并运算效率更高。因此，采用逐个求差的方式得到药柱实体，如式（2-70）所示。

\({{S}_{grain}}={{S}_{out}}-S{{F}_{1}}-S{{F}_{2}}-…-S{{F}_{n}}\)                 （2-70）

由于对任意的平面二维连通区域，目前已经有健壮而快速的算法，可以精确的计算其二维包络区域。因此，本文采用“二维约束草图+药柱特征生成算法”的方式对SF_i进行造型。设计人员只需要在第三章构建的变量化设计环境中交互构建二维约束草图，并将不同的连通区域定义为相应的药柱特征，即可得到药柱在任意燃烧肉厚下的几何实体与燃面面积和质量特性信息。

（3）药柱变量化设计与燃面推移仿真流程

• 实体造型的方法包括三部分内容：特征形体的定义和描述；特征形体之间的拼合运算（并、交、差）；特性形体按照几何燃烧定律进行推移变化的计算。
• 在变量化设计环境中交互绘制药柱截面草图的几何图元；
• 在约束好的二维草图上选取相应的连通区域定义药柱特征，同发动机零部件的三维造型相似，以扫描表示法将这些具有一定语义的二维参数化的截面，加上特定的操作，拉伸、旋转、扫掠形成三维几何实体，以实体几何构造法将建模过程以及建模数据组织管理起来，三维几何实体内部以边界表示法表达，方便计算质量特性和设置属性信息；
• 所有药柱特征拼合，构成药柱三维芯模；
• 对于贴壁浇铸的药柱，药柱外轮廓实体是基于壳体（绝热层）内表面成形的；对于自由装填的药柱，其外轮廓截面需要设计人员交互创建，回转成形；外轮廓实体与药柱芯模特征依次进行布尔差运算，得到药柱的初始实体，再根据2.5中介绍的基于边界表示法的质量特性算法计算药柱初始质量特性；
• 燃面推移仿真时，首先根据给定肉厚，根据几何燃烧定律对特征截面的连通区域进行offset操作，求得其燃烧平行推移后的二维包络区域；
• 根据不同特征形体的定义算法，按照（2）的方法基于燃烧包络区域进行三维几何造型，得到给定肉厚条件下的特征实体；
• 燃烧后的特征实体相互拼合，构成给定肉厚条件下的药柱三维芯模；
• 将药柱外轮廓实体与燃烧之后的药柱三维芯模特证实体依次进行布尔差运算，得到给定肉厚条件下的药柱实体，并计算该燃烧肉厚下的药柱质量特性。                

（4）药柱燃面面积统计算法

1）布尔运算法

利用药柱外轮廓和芯模的布尔运算来得到的形体来计算药柱的燃面面积，该方法如图所示意，（a）是（b）中外轮廓S_out减去芯模S_in得到的药柱实体S_grain，粗实线表示燃面；（c）是体1：芯模S_in，假设其表面面积为A₁；（d）是体2：外轮廓与芯模求交得到的结果，即\({{S}_{out}}\bigcap {{S}_{in}}\)，假设其表面面积为A₂；（e）是体3：芯模减去外轮廓得到的实体，即\({{S}_{in}}-{{S}_{out}}\)，假设其表面面积为A₃。显然，燃面面积A为：

\(A=({{A}_{1}}+{{A}_{2}}-{{A}_{3}})/2\)                         （2-71）

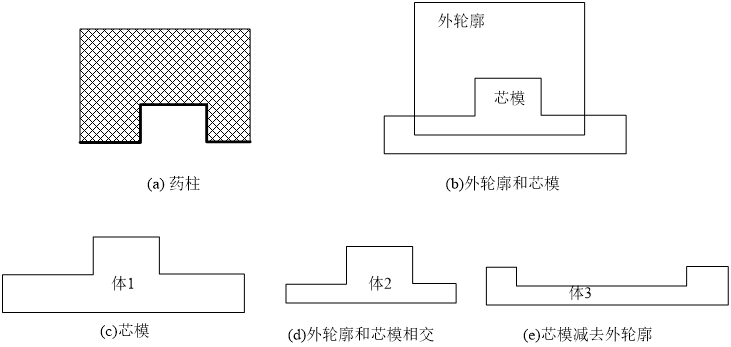
布尔运算方法简单易于理解，不需要辨识药柱的燃面和非燃面。但是这种算法效率较低，从图2-23的计算过程可知，每次计算燃面都需要额外进行一次布尔交和一次布尔差运算，三维几何实体的布尔运算本身相当费时，当药柱芯模比较复杂，特征形体较多时，这种算法显得更加笨拙。

2）基于颜色标识的燃面面积统计算法

基于颜色标识的燃面面积统计算法利用2.5.1节实体分割、融合时颜色属性的变化机制，由于药柱实体S_grain的表面来源于两部分：由外轮廓实体S_out的几何模型表面分裂而成，记为SF_a；由内腔特征实体S_core的几何表面分裂而成，记为SF_b 。

用不同的颜色标记燃面和非燃面，具体过程以图2-25中翼柱形药柱的设计过程为例来介绍：

• 外轮廓实体所有表面标识为蓝色，内腔特征实体表面标识为深色，因此所有的SF_a为蓝色，所有的SF_b为深色；
• 按照（2-70）式进行布尔差运算，得到的药柱实体的表面中，源自外轮廓实体的为蓝色，源自内腔特征实体的为深色，显然，深色的面即为翼柱形药柱的燃面，统计所有深色面的面积即为药柱的初始燃面面积；
• 内腔特征实体扩张以后仍然保持所有表面为深色，同理，与不发生变化的外轮廓实体进行布尔差运算之后，统计得到的扩张后药柱实体的深色表面面积，即为推移后的燃面面积。

这样，只需在初始造型时进行一次颜色标识，造型过程中颜色的变化会自动进行，不需要额外进行记录，并且可以保证燃面统计不发生疏漏，得到精确的计算结果。与基于造型历史追溯的算法相比，由于颜色是作为属性附加在实体的拓扑结构上，所需要的存储空间也比较小。因此，基于颜色标识的燃面面积统计算法是计算效率和存储开销最优的算法。

3）药柱通气面积和燃烧周长的计算

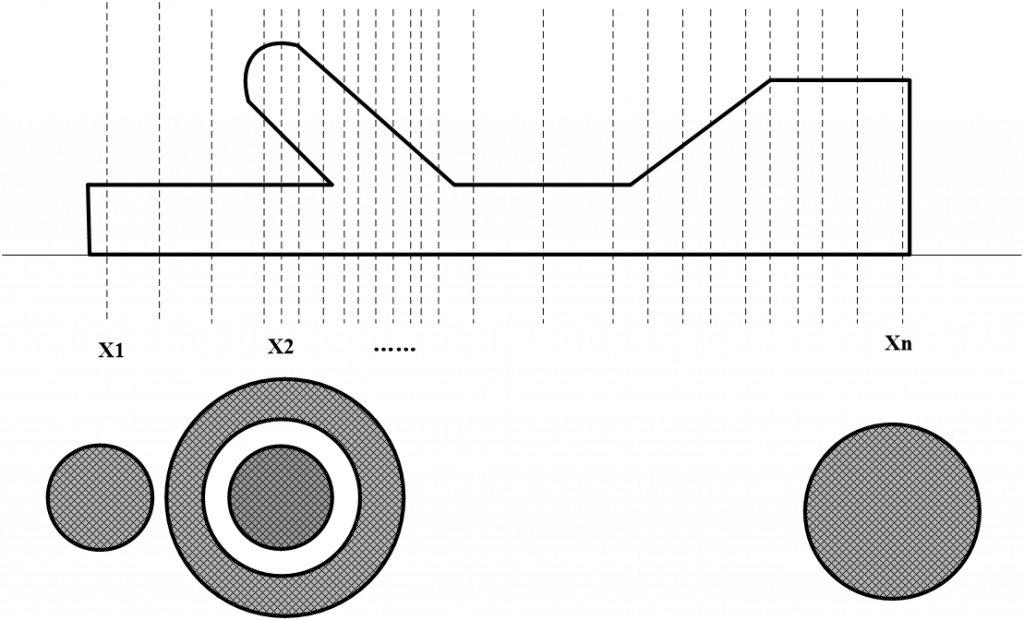
由于一维内弹道计算时需要药柱沿轴向一系列节点X₁,X₂,…X_n处的通气面积A_P和燃烧周长П，这些数据的计算如图2-26所示，取药柱芯模在相应节点处的截面，截面的面积即是通气面积，组成截面的所有边框线即为药柱的燃烧周长。节点的取值一般是在型面变化剧烈处加密，在等直段处间隔较大。

计算完成后，保存所有随节点和肉厚变化的通气面积\({{A}_{p}}({{X}_{i}},{{W}_{i}})\)和燃烧周长\(\Pi ({{X}_{i}},{{W}_{i}})\)，为内弹道计算作准备。

（5）药柱设计规则

为了避免设计过程中出现一些奇异的结构，降低燃面推移仿真效率。在药柱设计过程中，必须要通过一定的设计规则约束设计人员的设计行为，降低设计的随意性，使得设计人员能够设计出可以快速进行燃面推移的药柱形体。为此，本文定义如下药柱设计规则：

规则1：为保证药柱特征形体的可推移特性，药柱特征形体只采用旋转、拉伸、倒角三种特征造型方法的组合进行特征形体的实体生成。

规则2：考虑到二维封闭区域的包络区域运算算法远比三维包络区运运算算法健壮而迅速，因此本文在特征形体三维包络区域运算中，优先考虑“二维特征截面包络区域运算+特征造型”的方式进行特征形体三维包络区域造型。

规则3：药柱实体通常是围绕其中心轴旋转对称的。假设对称数目计为SymN，则本文只沿轴向设计药柱实体的1/SymN，然后对设计结果绕药柱中心轴进行N份圆周阵列，得到药柱实体的全貌。以此来减少实体造型布尔运算的次数。

规则4：在二维截面设计和三维特征造型过程中，应当尽量使得二维截面区域和三维实体为凸体，使得燃面推移算法更加稳定而迅速。

规则5：在进行实体布尔运算时，优先考虑使用“二维布尔运算+实体造型”的方式得到三维布尔运算结果，以减少布尔运算时间。

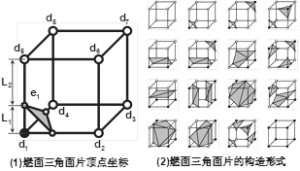
2.5.3 几种常见药柱特征形体定义

为了能够在变量化设计环境中实现任意类型药柱的交互设计，本文定义了以下药柱的特征形体的特征参数和造型过程，同时按照索引键值—标签—属性形式设计了这些特征形体的树形数据结构，以使其能够被变量化设计环境统一管理，实现药柱数据的保存和恢复以及支持设计的撤销、反撤销操作。

（1）药柱外轮廓

对于贴壁浇铸药柱，绝热层的内表面就是药柱的外轮廓型面曲线，取为回转体，是一条在XOY平面上的封闭曲线，绕X轴旋转而成；对于自由装填药柱，可以直接绘制药柱外形的截面草图，然后施加约束。

药柱外轮廓的数据模型见图2-27：

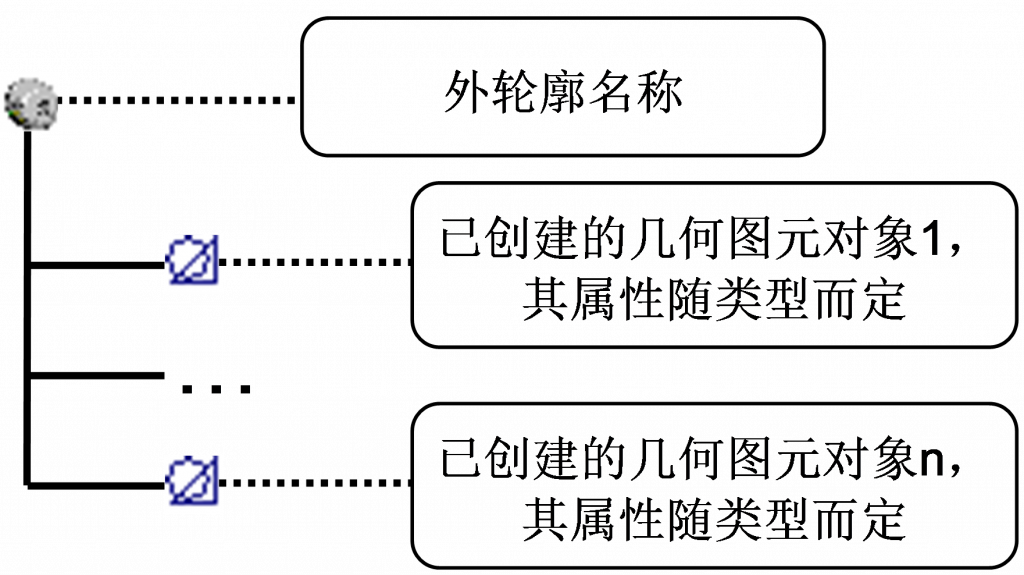
药柱外轮廓特征函数定义为：

F_outline（Section）

其中，Section是由设计人员交互创建的几何图元构成的封闭线框形成的截面。以下特征形体的Section含义相同，不再一一赘述。在燃面推移过程中，药柱外轮廓保持不变。

（2）药柱芯模特征形体

药柱的芯模特征形体在构造过程中应该按照药柱设计规则来定义，这些形体的公用参数有：

SymN-对称数，根据药柱设计规则3，由于药柱的结构一般是回转对称的，为提高求解速度，只构造1/SymN的药柱，然后环形阵列SymN份。

针对目前药柱设计的习惯与药柱的几何特点，本文将药柱芯模特征分为以下6类：

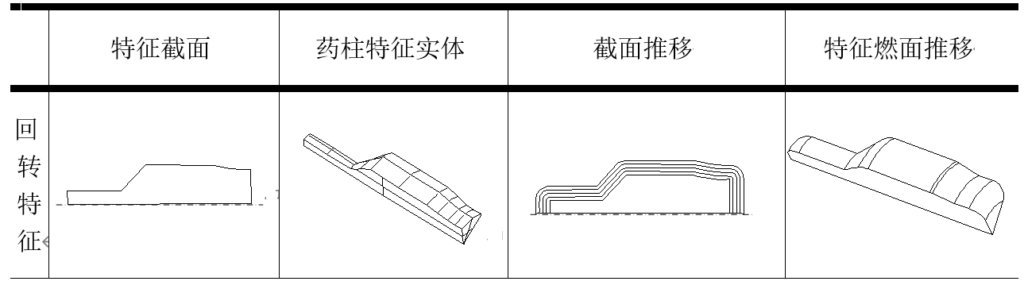
回转形特征：该特征由位于XOY平面上的特征截面绕轴线直接回转成型，轴线可以是X轴，也可以是指定的任意轴。在燃面推移过程中，首先对特征截面进行扩张，然后回转。

图2-28 药柱回转形特征的数据模型

用如下特征函数进行定义：

F_rev（Section,IsBS,Axis）

其中，IsBS是表示该特征形体是否为燃面，Axis是选择回转轴线。

表2-15 回转体

翼形特征：该特征截面位于XOY平面上，首先将截面沿Z轴拉伸，距离为w；然后对于形成的三维实体各个棱边倒角，倒角半径为r。燃面推移时，二维特征截面先扩张e、然后拉伸（w+2e）并倒角（r+e）。

在翼形药柱的实际应用过程中，采用在药柱前段增加一组轴向前翼或者在后段周向增加另一组小翼的方法来增大初始燃面，从而为助推段提供更大的推力，前者称为前后翼，后者称为大小翼。根据设计规则3，在从药柱二维截面生成三维特征形体以及燃面退移时，为了简便，通常只处理循环对称药柱的一个对称单元，然而前后两组翼通常不在同一对称平面内，大小两组翼是周向阵列而成，因此需要采取措施确保所有翼形体都处在一份对称单元中，从而得到合理的布尔运算结果。

图2-29 药柱翼形特征的数据模型

翼形体特征函数定义如下：

F_Wing(Section,w,r,angle,npc)

其中： w––翼形体厚度，r––翼形体顶端倒角半径，angle––该组翼形体起始角度， npc––每个外轮廓对称单元中该组翼的个数。

设药柱的循环对称数目SymN是前后两组翼个数（n_f,n_a）或者大小两组翼个数(n_b,n_s)的最大公约数，则翼形体的个数n与相应npc之间的关系为：

          （2-72）

翼形体在外轮廓对称单元中的周向排列如所示，翼形体起始角度angle表示第一个翼距外轮廓对称单元中心线的角度，其余翼的角度为：

\(angl{{e}_{i}}=angle+i\cdot 2\pi /n\) (i=1,2,…,npc-1)             （2-73）

图2-30 外轮廓对称单元中多个翼的角度分布

表2-16 翼形体

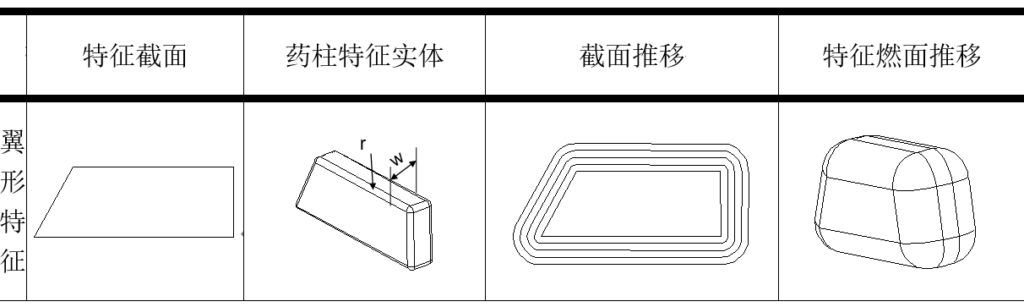
楔形特征：该特征与翼形特征类似，先将位于XOY平面上的特征截面沿Z轴

图2-31 楔形特征形体的数据模型

拉伸w；然后对形成的实体两个侧面拔模，角度为θ；最后倒角r成形。燃面推移过程中，二维截面扩张，再执行拉伸、拔模并倒角操作。对于多组楔形特征形体的处理与多组翼形特征形体一样。

楔形特征函数定义如下：

F_wedge（Section , w , r ,,angle,npc）

表2-17 楔形体

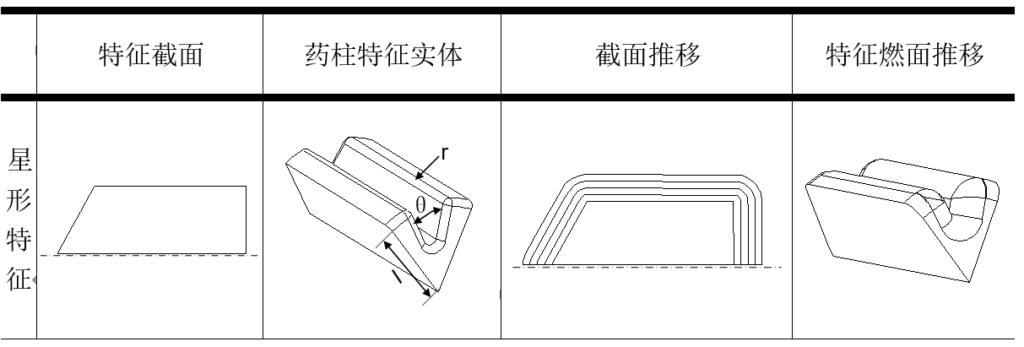
星形特征：星形特征的创建比较复杂，需要用两个截面来表示，一个是星形轮廓截面，一个是楔形星角截面。两个截面均绘制在XOY平面上。构造时，先将XOY平面上的星形轮廓截面绕X轴旋转360°/SymN得到星形轮廓实体，再将楔形星角截面旋转90度到YOZ平面上，沿X轴拉伸l形成楔形星角实体，星形轮廓实体与楔形星角实体求差后倒角r成形。

燃面推移时，二维星形轮廓截面扩张、回转，与向上平移之后的楔形星角求差、倒角成形。

图2-32 星形特征形体的数据模型

星形特征可用如下函数定义：

F_star（Section , r , l）

表2-18 星形体

等截面拉伸特征：该特征用来构造任意径向截面相同的药柱形体，如树枝形、车轮形等。

该特征截面并不在通常特征定义的XOY平面内，而是位于与YOZ平面平行的平面内，因此截面应先绕其中轴线旋转90度，然后再拉伸成形。燃面推移时，截面扩张之后仍绕中轴线旋转，然后拉伸成形。

图2-33 等截面拉伸特征形体的数据模型

等截面拉伸特征函数定义如下：

F_prism（Section ,w,r,IsBS）

表2-19 等截面拉伸体

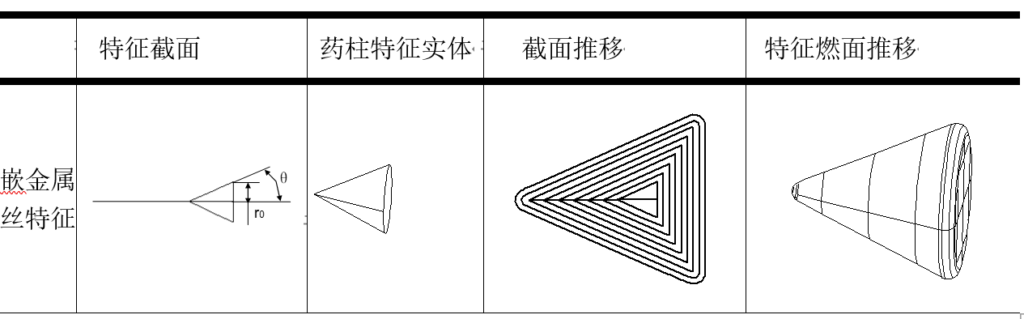
嵌金属丝特征：本文采用一根水平线段描述嵌金属丝的位置和长度。因此首先应根据水平线段的位置和特征参数得到初始的三角形截面，并绕水平线段旋转形成初始的锥形形体。燃面推移过程中，三角形截面扩张，然后绕水平线段旋转成形。

图2-34 嵌金属丝特征形体数据模型

采用如下函数定义该特征：

F_mental（Segment,α, r0，IsMetal）

表2-20 嵌金属丝

以上六种形体的组合可以构成很多药型，足以满足工程需求。图2-36为构建的部分药型示例。

2.6 基于离散方法装药数值计算

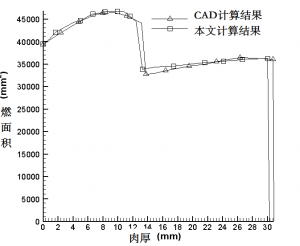
基于计算机二维/三维图形处理技术的装药燃烧几何分析技术，在商业化计算机图形处理系统的支持下可以获得很高的计算精度（燃面计算相对误差一般<0.01%）。然而，现代计算机图形学中尚存在一些未解决的三维图形运算问题，如特征消失问题、三维造型奇异点处理问题等等。装药在燃烧时内腔形体在逐渐扩张，带来大量复杂的三维实体交、并、差计算，有些形体被烧完至消失，例如反圆弧面，这时基于边界表达的三维造型系统往往会出现大量的造型错误，导致计算不能进行。由于这种造型错误经常发生，为了避免这种问题的出现，设计人员要在遵循一定设计规则的条件下，做大量的手动的干预，绕过一些无法计算的关键点。另外燃烧过程再生的形体（往往难以预测）必须预置，这对设计人员的要求是非常高的。因此，对于某些局部包覆的三维复杂装药几乎是无法采用图形学的方法进行计算的。

为了彻底解决装药燃烧几何分析的通用化问题，国内外研究人员提出了各种离散化的装药设计方法。而且，随着高度并行化计算机体系架构的成本不断降低，这些离散化的装药设计方法已经可以快速而准确的应用于工程设计领域。以下简单介绍这一类方法的基本原理和应用。

2.6.1 基于最短距离场的装药燃烧几何分析方法

基于最短距离场（Minimum Distance Fields，MDF）的燃烧几何分析方法最初由美国伊利诺伊州立大学Willcox博士提出。根据平行层燃烧定律，该方法认为，在装药燃烧至某一特定的肉厚（δ）时，此时的燃烧表面应该是：药柱内部到初始燃烧表面之间的最短距离为δ的所有空间点的集合。

从几何学的角度来看，当装药非初始燃烧表面为凸几何面，且装药实体内部无孔洞时，该设想完全成立。正常装药的结构特点一般都满足这些几何条件，因此该方法完全可以用于指导工程设计。

然而，一般情况下，与初始燃烧表面之间的最短距离为δ的空间点的个数是无穷多的。在初始燃烧表面较为复杂的情况下，该无穷点集合组成的燃烧表面是很难用某种解析的方法进行精确描述的。将装药所在的几何空间进行离散，并在这些离散的微小空间单元内进行燃烧表面的近似提取，是一种相对比较可行的做法。

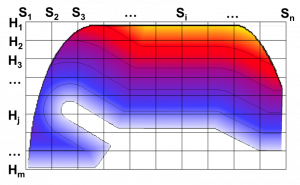
（1）二维无端面燃烧装药的燃烧几何分析

我们首先以一个二维轴对称回转成型，并且端面包覆的装药作为实例，来简单的了解这种离散化的处理方法。如图2-36所示，在二维的条件下，我们可以用矩形网格线将装药所在的空间包围盒离散成一系列微小单元。为了方便描述，我们将垂直于装药中轴线的竖线记为S_i（1≤i≤n），将平行于装药中轴线的横线记为H_j（1≤j≤m），而S_i与H_j的交点记作P_i ,j（1≤i≤n，1≤j≤m）对于网格线上的每一个交点，我们都需要计算其相对于初始燃烧表面的最短距离，记作δ（P_i ,j）。

图2-36 二维回转成型装药计算网格

接下来，针对给定的燃烧肉厚δ，我们都需要对所有的网格线进行搜索，确定网格线上与初始燃面最短距离为δ的几何点。并利用这些几何点进行近似的燃烧曲面反求，从而获得各种燃烧几何分析数据。

由于固体火箭发动机设计过程中比较关心沿轴向的一维流动参数。因此，我们首先沿着发动机的轴向方向，获取燃烧肉厚为δ时，每一个通气截面的燃烧周长和通气面积。然后对燃烧周长进行积分即可得到燃烧面积，而通气面积则是流动分析的几何约束条件。

具体的实现步骤如下：

1、对于S_i截面，依次搜索该截面上的所有网格点，如果存在网格点P_i,j，使得δ（P_i,j）>δ并且δ（P_i,j+1）<δ，则在P_i,j和P_i,j+1之间必然存在一个与初始燃烧表面之间的最短距离为δ的点，记作P_i,δ。

2、在网格足够密的条件下，我们可以通过线性插值获取P_i,δ，如下式：

\({{P}_{i,\delta }}={{P}_{i,j}}+\frac{\left[ \delta -\delta ({{P}_{i,j}}) \right]}{\delta ({{P}_{i,j+1}})-\delta ({{P}_{i,j}})}\cdot ({{P}_{i,j+1}}-{{P}_{i,j}})\)             （2-74）

3、这样一来，在燃烧肉厚为δ时，第i个截面上正好燃烧至P_i,δ点。此时第i个截面的燃烧周长为2πy（P_i,δ），通气面积为πy²（P_i,δ）。

4、从第1个通气截面依次搜索至第n个通气截面，获得在δ肉厚下，每一个通气截面的燃烧周长和通气面积。并对燃烧周长进行积分即可得到燃烧肉厚为δ时的燃烧面积。

\(A(\delta )=2\pi \int{y(}{{P}_{i,\delta }})dx\)

5、将燃烧肉厚按一定的间隔依次从0取到装药燃烧的最大肉厚，重复步骤1-4，可以依次获取每一个肉厚条件下的燃烧面积。就可以最终获得内弹道计算所需要的燃面-肉厚曲线。

（2）三维无端面燃烧装药的燃烧几何分析

对于三维无端面燃烧装药而言，其燃烧几何分析的过程仍然可以首先获取每一个通气截面内的燃烧周长和通气面积，然后通过燃烧周长的积分获取燃烧面积。与二维回转成型装药相比，三维装药每一个通气截面上的燃烧几何结构并不是简单的回转圆，而是复杂的等值线连接而成的不规则区域，如图2-37所示。

a. 二维回转药柱

b. 三维翼柱形药柱

图1-37 通气截面上最短距离云图

对于指定的燃烧肉厚δ，为了在每一个通气截面上获取与初始燃烧表面之间的距离为δ的等值线区域，可以继续用二维矩形网格对装药截面所在的二维区域进行分割。

对于每一个矩形网格，我们将其每一个顶点都标注为“已经参与燃烧（δ_P<δ）”和“未参与燃烧（δ_P>δ）”两种状态。这样一来，每一个矩形网格存在2⁴（16）种状态，而这16种状态可以分为6类，如图2-38所示。

图2-39 各类计算网格内的燃烧曲线提取

在网格足够密的条件下，对于图2-39中的a类和f类网格，其内部是不会存在燃烧曲线的；而对于其他四类网格，我们通过线性插值，可以近似的用直线段拟合其网格内部的燃烧曲线。例如对于b型网格的P₁P₂边，我们可以通过如下公式获取燃烧曲线的顶点坐标：

   \({{L}_{1}}=\frac{({{\delta }_{1}}-\delta )\cdot L}{{{\delta }_{1}}-{{\delta }_{2}}} \)

   \({{L}_{2}}=\frac{(\delta -{{\delta }_{2}})\cdot L}{{{\delta }_{1}}-{{\delta }_{2}}} \)

                     （2-75）

在遍历了通气截面中的每一个网格之后，我们就可以获得所有的燃烧曲线首尾相连而得到的燃烧几何区域。与二维轴对称装药计算类似，对各个截面上的二维燃烧几何区域进行积分，即可得到三维的燃烧几何分析结果。

图2-39 二维燃烧区域的叠加

（3）三维带端面燃烧装药的燃烧几何分析

在有端面燃烧的条件下，不能简单的对燃烧周长进行积分获取燃烧表面积。事实上，在最为简单的纯端面燃烧条件下，是不存在燃烧周长的概念的。我们只有通过对三维空间的搜索来获取装药的燃烧几何数据。而三维空间搜索算法的缺点是计算量十分巨大，例如将药柱离散成1024×1024×1024个网格的条件下，每一步燃面计算都需要处理超过10亿个网格点，即使在大型计算机上也需要耗费大量的机时才能完成计算。为了解决这个难题，使得设计人员在通常的桌面PC系统上也能使用这一类通用的药柱设计方法。我们基于高度并行化的GPU计算构架，充分利用GPU超过上千个并行处理单元，每秒万亿次浮点计算能力的特点，提出了一种高度并行化的体素离散化燃面推移算法，对具有任意初始燃面的任意复杂药型进行实时的燃面计算。

该算法在药柱所在的空间包围盒内均匀的选取N×M×K个空间体素点。如图2-36所示，首先将边界表达的药柱G进行空间离散，确定哪些体素点处于药柱G内，以便对这些体素点进行后续的计算。对于药柱G之外的体素点，为了提高计算效率，并不需要在后续的燃面计算过程中参与计算。

对于处于药柱实体G之内的体素点，该算法利用GPU多核计算架构，通过高度并行化的燃烧状态填充算法，计算出这些体素点到燃面之间的距离场，存放在三维距离矩阵L[N, M, K]内。

对于给定的肉厚δ，只需要在三维距离矩阵空间（L[N, M, K]）内并行的插值抽取出所有肉厚为δ时的燃烧表面面片，然后对这些燃烧表面面片进行面积积分，就可以得到每一个燃烧肉厚条件下的燃烧面积信息。逐步增加肉厚，则可以依次计算出药柱的燃面-肉厚曲线。

该算法的三个关键流程如下所示：

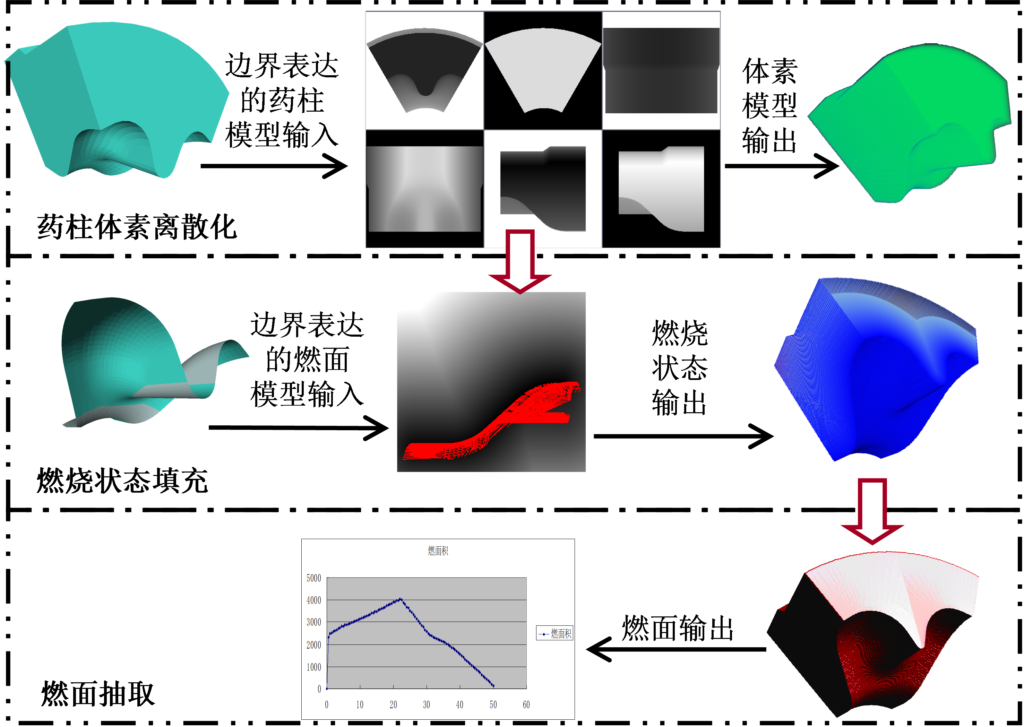
1）边界表达药柱形体的体素离散

为了获得所有在药柱实体内部的体素点，本算法利用GPU渲染引擎，并行的将药柱实体的边界表达模型向X、Y、Z坐标平面的正、负方向进行分辨率为N×M×K的Z-Buffer投影，分别得到Z-Buffer矩阵x₁、x₂、y₁、y₂、z₁、z₂，如图所示。

图2-41 药柱实体的Z-Buffer投影

对于每一个体素点( i, j, k),如满足公式4，则该体素点在药柱实体之内，否则该体素点在药柱实体之外。

\({{\text{x}}_{\text{1}}}\text{ }\!\![\!\!\text{ j, k }\!\!]\!\!\text{ }<\text{ i }<\text{ }{{\text{x}}_{\text{2}}}\text{ }\!\![\!\!\text{ j, k }\!\!]\!\!\text{ } \)

   \({{\text{y}}_{\text{1}}}\text{ }\!\![\!\!\text{ k, i }\!\!]\!\!\text{ }<\text{ j }<\text{ }{{\text{y}}_{\text{2}}}\text{ }\!\![\!\!\text{ k, i }\!\!]\!\!\text{ } \)

   \({{\text{z}}_{\text{1}}}\text{ }\!\![\!\!\text{ i, j }\!\!]\!\!\text{ }<\text{ k}<\text{ }{{\text{z}}_{\text{2}}}\text{ }\!\![\!\!\text{ I, j }\!\!]\!\!\text{ } \)                    （2-76）

2）燃烧状态填充

在计算每一个体素点与初始燃面之间的距离关系时，若燃面由P个三角面片组成，则直接计算需要进行N×M×K×P次点到三角面片之间的距离测试。例如，对于1024×256×256个体素点和包含3万个三角面片的燃面，则需要进行超过2万亿次距离测试，这样的计算量是十分巨大的。

为了大幅度减少距离测试，本算法首先采用Delaunay三角剖分算法得到燃面几何图元的最近邻域图。如图2-42所示，对于燃面的所有几何图元（a, b, …, k），空间剖分算法将获得与之相对应的区域（A, B, …, K）。其中，任何区域中的每一个体素点到对应几何图元的距离最近。

这样一来，1024×256×256个体素点只需要进行约6400万次距离计算即可得到所有体素点与燃面之间的距离关系。而3万个三角面片的空间剖分计算时间相对于6400万次距离计算而言完全可以忽略不计。

图2-42 空间剖分

由于每一次距离计算之间相对独立，因此完全可以将6400万次距离计算均匀的分配到GPU多达上千个并行处理单元之中，每一个处理单元只需要独立的处理几万次距离计算，即可得到最终计算结果。

结合体素离散化计算，图2-44给出了药柱内部每一个体素点的燃烧状态填充结果。

图2-43 填充结果

3）燃面提取与统计

N×M×K个空间体素点将药柱所在包围盒空间均匀的分割成了(N-1)×(M-1)×(K-1)个空间小立方体，其中每一个立方体均以空间体素点作为顶点，且立方体内部不包含任何其它体素点。

燃面抽取算法并行的对每一个空间立方体进行计算。在燃烧肉厚为w时，立方体每一个顶点都存在两种位置关系：1、当顶点与燃面之间的距离d>w时，该顶点处于燃面B(G, w)的正侧；2、当d≤w时，该顶点处于燃面B(G, w)的反侧。只有当立方体每一条边的两个顶点分别处于燃面不同的两侧时，燃面才与该边相交。如图2-45(1)所示，对于一个顶点距离燃面距离为d₁（d₁>w），另一个顶点距离燃面距离为d₅(d₅≤w)的边e₁（边长为L），燃面与e₁的交点与e₁两端点之间的距离如公式（2-77）所示：

\({{L}_{1}}=\frac{({{d}_{1}}-w)\cdot L}{{{d}_{1}}-{{d}_{5}}} \)

   \({{L}_{2}}=\frac{(w-{{d}_{5}})\cdot L}{{{d}_{1}}-{{d}_{5}}} \)          （2-77）

这样一来，燃面与每一个立方体存在2⁸（256）种相交状态。由于立方体的对称性，这256种相交状态可以归纳为16种类型。图2-44(2)给出了每一种类型下燃烧三角面片的构造方式。遍历所有的立方体，并将抽取出来的三角面片的面积求和，就可以求得肉厚为w条件下的燃面积。需要注意的是，若立方体有顶点处于药柱之外，则与该顶点相关的三角面片都应被剔除。

图2-44 燃面提取

在抽取燃烧三角面片时，立方体之间相互没有任何关系，这十分有利于GPU并行算法的实现。

2.6.2 Level Set方法

这里介绍一种基于界面追踪方法的Level Set方法的燃面算法，这种算法适于处理复杂装药构形的燃面变化，能够自动处理拓扑变化，由于是数值计算方法，能够与流场计算进行耦合，实现装药结构变化与流动的耦合计算分析。

Level Set方法把区域Ω中两种介质随时间运动的物质界面看做某个函数\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)的零等值面，\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)满足一定的方程。在每个时刻t，只要求出函数\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)的值，就可获得其等值面的位置，即运动界面的位置。\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)的构造需要满足在任意时刻，运动界面Γ(t)是\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)的零等值面，即满足下式

\(\Gamma \left( t \right)=\left\{ \overset{\scriptscriptstyle\rightharpoonup}{x}\in \Omega :\varphi \left( \overset{\scriptscriptstyle\rightharpoonup}{x},t \right)=0 \right\}\)                     （2-78）

φ的初值满足在Γ(0)附近为法向单调，在Γ(t)上为零。可取\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},0)\)为\(\overset{\scriptscriptstyle\rightharpoonup}{x}\)点到界面Γ(0)的符号距离

  (2-79)

其中\(d(\overset{\scriptscriptstyle\rightharpoonup}{x},\Gamma (0))\)表示\(\overset{\scriptscriptstyle\rightharpoonup}{x}\)到Γ(0)的距离。

为了确保在任意时刻函数φ的零等值面就是活动界面，φ要满足一定的控制方程。在任

意时刻t，对于活动界面Γ(t)上的任意点都有\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)=0\)，因此有

\(\frac{d\phi }{dt}=\frac{\partial \phi }{\partial t}+\vec{V}\cdot \nabla \phi =0\)                       （2-80）

Level Set函数的单位外法向和活动界面在法向上的运动速度分别为

\(\overset{\scriptscriptstyle\rightharpoonup}{n}=\frac{\nabla \phi }{\left| \nabla \phi \right|}\)

\(F={{V}_{n}}=\frac{d\overset{\scriptscriptstyle\rightharpoonup}{x}}{dt}\cdot \overset{\scriptscriptstyle\rightharpoonup}{n}=\frac{d\overset{\scriptscriptstyle\rightharpoonup}{x}}{dt}\cdot \frac{\nabla \phi }{\left| \nabla \phi \right|}=\bar{V}\cdot \frac{\nabla \phi }{\left| \nabla \phi \right|}\)                           （2-81）

将（2-81）代入（2-80），得到φ的控制方程

\({{\phi }_{t}}+F\left| \nabla \phi \right|=0\) \(x\in \Omega\)                （2-82）

此方程就是初值型的Level Set方法的控制方程，并通过其定义计算区域内任意点到界面的符号距离，距离为0的点即为界面上的点。

由于数值方法的内在效应，在进行了几个时间步的求解后，\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)就不再满足式（2-82）定义的符号距离了。为了使函数\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)一直保持为到界面的带有符号的距离函数，消除在计算过程中\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)与界面的符号距离产生的偏离，需要采用一种被称作重新初始化（Re-initialization）的方法使Level Set函数一直满足（2-82）式。Sussman引入了一种通过求解Hamilton- Jacobi方程来得到\(\tilde{\phi }(\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)的较好方法。

\({{d}_{\tau }}+sign({{d}_{0}})(\left| \nabla d \right|-1)=0 \)

   \(d(\overset{\scriptscriptstyle\rightharpoonup}{x},0)={{d}_{0}}(\overset{\scriptscriptstyle\rightharpoonup}{x})=\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},0) \)                 （2-83）

方程（2-83）的解就是到界面的最佳符号距离。实际计算中，在界面附近的单元计算时收敛很快，采用了以下定义在方程（2-83）中的符号函数\(sign(\tilde{\phi })\)进化光滑化：

\(sig{{n}_{\delta }}(d)=\frac{d}{\sqrt{{{d}^{2}}+{{\delta }^{2}}}}\)                       （2-84）

其中δ为计算中的空间步长∆x。

用Level Set方法求解两相介质问题的一般步骤是：

（1）初始化。初始化所要求的物理量及函数\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},t)\)。

（2）求解Level Set方程。求解方程（2-80）的具体形式，得到下一时刻的Level Set函数\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},{{t}_{n+1}})\)在整个求解域中的值。此时的新运动界面\(\Gamma ({{t}_{n+1}})\)就是\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},{{t}_{n+1}})\)的零等值面，即

\(\Gamma ({{t}_{n+1}})=\left\{ \overset{\scriptscriptstyle\rightharpoonup}{x}\in \Omega :\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},{{t}_{n+1}})=0 \right\}\)，但此时的\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},{{t}_{n+1}})\)不再是符号距离函数。

（3）重新初始化。将\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},{{t}_{n+1}})\)代替（2-83）中的\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},0)\)，迭代求解方程（2-80）至稳定解，仍记为\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},{{t}_{n+1}})\)。

（4）求解物理量的控制方程。结合\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},{{t}_{n+1}})\)的值，求解主场的物理量的控制方程，得到t_n+1时刻的物理量的值。在\(\phi (\overset{\scriptscriptstyle\rightharpoonup}{x},{{t}_{n+1}})\)变号处（即界面）进行特殊处理。

（5）重复（2）~（4）步，进入下一时间步的计算。

对重新初始化方程（2-81）的离散采用了修正的Godunov方法。将（2-81）的离散成以下形式（以二维为例）：

\({{\phi }_{t}}+\left( \frac{sign({{\phi }_{0}}){{\phi }_{x}}}{\sqrt{\phi _{x}^{2}+\phi _{y}^{2}}} \right){{\phi }_{x}}+\left( \frac{sign({{\phi }_{0}}){{\phi }_{y}}}{\sqrt{\phi _{x}^{2}+\phi _{y}^{2}}} \right){{\phi }_{y}}=sign({{\phi }_{0}})\)

采用了（2-84）式的方法对\(sign\left( {{d}_{0}} \right)\)进行了光滑化。

\({{\phi }_{x}}\)的离散格式如下（\({{\phi }_{y}}\)的处理方法相同）：

其中，\(s=\frac{sign({{\phi }_{0}})\left( \left| \phi _{x}^{+} \right|-\left| \phi _{x}^{-} \right| \right)}{\phi _{x}^{+}-\phi _{x}^{-}}\)

对空间离散算子\(\phi _{x}^{\pm }\)和\(\phi _{y}^{\pm }\)可采用针对Hamilton-Jacobi方程的五阶的WENO（weighted essentially nonoscillatory）格式。

在获得了燃面的空间位置后，可用以下公式获得燃面面积和装药体积。

燃面面积计算公式：

\(\left| \Gamma (t) \right|=\int{\delta (\varphi )}\left| \nabla \varphi \right|dx\)                       （2-85）

装药体积计算公式：

\(\left| \Omega (t) \right|=\int{H(-\varphi )}dx\)                        （2-86）

使用Level Set方法对一些特殊装药进行了计算得到了较好的精度。图2-46为装药的三维示意图，图中深色部分为装药包覆层。装药前端被切削掉两部分，从而具有很强的三维特性，不具有常见装药的轴对称属性。图2-47为燃烧过程中推进剂燃面的变化过程，计算捕捉到了燃面复杂的变化过程。图2-48为燃面面积变化曲线。

图2-45 特殊装药结构

图2-46 特殊装药燃面变化过程

图2-47 特殊装药燃面变化曲线

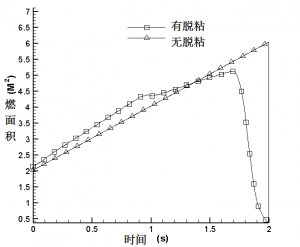
脱粘是一种常见的装药缺陷形式。对含有脱粘等缺陷的装药进行接近实际工作条件下的燃面计算，能够为建立故障诊断模式提供帮助。图2-48，装药构形示意图，图中深色部分为包覆。装药外侧和两端面包覆只有内孔燃烧，并假设药柱一端外侧有部分脱粘。从燃面曲线上可以看出含缺陷的装药燃面与正常情况相比存在较大差异，严重影响内弹道和发动机性能及工作安全。本文的燃面算法可以较好地计算含缺陷的装药燃面，为发动机装药缺陷分析和发动机质量评判提供了参考依据。

图2-48 脱粘结构示意图

图2-49 燃面变化过程

图2-50 燃面变化曲线对比

2.7 药柱的制造与验收技术要求

（1）推进剂配制要求

用于浇铸药柱的推进剂，应严格遵守所规定的配方和工艺进行配料和混合；各组分的原材料牌号、规格、等级应符合有关标准的规定。

投料前对推进剂的各种组分应进行质量检查，各项技术指标均满足要求后方可投料。

（2）性能要求

推进剂的各项性能指标应符合其配方的设计要求。

1）燃速

以药条和标准发动机测推进剂燃速。药条由按规定制做的方坯中切取，用水下声发射测定法，在环境温度为20±2℃和相对湿度低于60%、压强为发动机设计压强的平均值条件下测出药条燃速。并给出3~8MPa范围内的压强指数n和燃速系数a，以及温度敏感系数\({{({{a}_{r}})}_{T}}\)。

标准发动机测燃速，用改变喷喉尺寸的方法得到所需压强；在药柱温度为20±2℃条件下进行热试车，根据记录的p-t曲线求出标准发动机的燃速。

2）密度

对按规定制做的方坯逐个测定其密度，而后求平均值。

3）比冲和特征速度

用标准发动机（药柱温度20±2℃）进行地面热试车，测定其比冲和特征速度。

\({{I}_{s}}=\frac{\int{_{0}^{{{t}_{b}}}F(t)dt}}{{{m}_{p}}} \)

\({{c}^{*}}=\frac{\left[ \int{_{{}}^{{{t}_{b}}}{{p}_{c}}(t)dt{{A}_{t}}} \right]}{{{m}_{p}}} \)

对应每一压强（推力）测点，至少进行三台试车测试，以求其平均值。

4）力学性能

按规定由方坯切取试样，进行拉伸试验；给出抗拉强度σ_m及其相应的伸长率ε_m，和断裂时的伸长率ε_b。

测出伸长率主曲线\(({{\varepsilon }_{m}}-\lg \frac{1}{R{{a}_{T}}})\)、抗拉主曲线（\({{\sigma }_{m}}-\lg \frac{1}{R{{a}_{T}}}\)）和松弛模量主曲线（lg\(E\frac{{{T}_{s}}}{T}-\lg \frac{t}{{{a}_{T}}}\)）。R为应变速率；a_T为移位因子；T_s为参考温度。

5）物理参数

测定下列物理参数：

• 玻璃化温度T_g；
• 线膨胀系数（温度范围：T_g~50℃）；
• 导热率；
• 比热容；
• 初始热分解温度；
• 爆炸威力（N.T.当量）

（3）制造和验收要求

根据发动机装药量的多少，将其组批进行药柱浇铸；每3~5台为一批，每批抽1台进行地面试车（药柱温度20±2℃），测得的燃速及内弹道参数应满足设计要求。

药柱在浇铸过程中，应注意保护燃烧室内的绝热层和衬层；推进剂原材料和料浆在加工和工序转运过程中，应注意防尘和防潮。

浇铸完毕后的药柱按规定固化、拔模后，应进行无损检验，并应严格按设计图纸进行整形。整形后的表面应平滑，不得划伤。所有药柱表面都不得有孔隙、划伤、裂纹和海绵状疏松组织。药柱内部不得有孔隙、夹渣和海绵状组织。药柱与燃烧室前、后封头间的粘结界面不得脱粘。

整形后的药柱应进行几何尺寸测量和质量称量。一般尺寸测量误差不大于尺寸公差的10%；称量误差不大于实际质量的1%。

对每批药柱，需提供粘接界面的扯离强度和抗剪强度。

药柱在规定的服役期内，其结构完整性和弹道性能应满足设计要求。

 

思 考 题

 

1．列出单根管形药柱（自由装填，内外侧面燃烧）的几何参数；导出相关参数的关系。

2．分析开槽管形药柱主要几何参数对燃面变化的影响关系；分析开槽位置（前或后部）对内弹道性能的影响。

3．画图分析说明单根金属丝和多根金属丝药柱的燃面变化规律；比较其异同。

4．分析说明哪些构形的药柱适于高肉厚分数；哪些适于高装填密度。

5．双燃速推进剂组合药柱设计上有何特点？举例说明。

6．比较说明自由装填药柱和贴壁浇铸药柱受外载荷的状况；有何异同？