第四章 喷管和推力控制装置设计
4.1 概述
固体火箭发动机的喷管位于燃烧室的尾部,通常为拉瓦尔喷管,由收敛段(入口段)、喉部和扩散段(出口锥)三部分组成。喷管设计主要依据发动机研制任务书、喷管设计任务书、喷管与发动机对接的关系图、喷管外形尺寸协调图等。
一、喷管的主要作用
(1)根据药柱的燃烧面积,通过控制喷管喉部面积的大小来保证燃烧室具有一定的工作压强,使药柱正常燃烧;
(2)将药柱燃烧生成的燃气的热能转化为动能,燃气流经喷管时不断膨胀加速,最后以高速从喷管出口面排出,产生推进火箭前进的反作用力—推力;
(3)改变推力方向,控制导弹的飞行姿态;
固体火箭发动机的喷管是一种非冷却结构或消融冷却结构的喷管。根据喷管收敛段及其相邻部分是在燃烧室内还是在燃烧室外而分为潜入和非潜入两种喷管。根据推力向量控制方法而分为固定和可动两类喷管。
二、喷管设计
喷管设计一般分为三部分
(1)气动设计,确定与燃气流接触的喷管内表面(型面)形状,使气流无阻碍地加速运动,以便使热能以最大可能转化为动能;
(2)热防护设计,选择烧蚀和绝热材料,确定其厚度和结构,以便在工作过程中保持喷管型面,并使喷管的支撑结构的温度控制在允许的范围内。
(3)结构设计,即喷管支撑结构的设计,将喷管各部分和推力向量控制装置的有关部分组装成整体,并与燃烧室连接,承受除热载荷以外的全部载荷,如内压引起的接触载荷、外载荷和局部作动载荷等。
三、固体火箭发动机的推力控制
推力控制包括推力向量控制和推力终止。
通常所说的固体火箭发动机的推力向量控制仅为推力方向控制,并不包括推力大小控制。由于固体火箭发动机燃烧室内装有推进剂,不可能像液体火箭发动机那样用摆动发动机的方法来改变推力方向,因此,只有通过喷管来实现推力向量控制。固体火箭发动机的推力向量控制装置与喷管结构密切相关。
推力终止装置,用来当火箭达到预定飞行速度后及时终止发动机推力,并使之与弹头脱离。实现推力终止的方法很多,最常用的是反喷管推力终止装置。
四、喷管及其推力向量控制装置的设计要求
喷管设计技术要求主要有结构要求、工作条件、性能要求、环境条件、可靠性和维修性要求等。
(1)喷管结构要求
- 喷管结构类型:潜入、非潜入、或特种喷管;
- 喉径、扩张比、长度、外形及配合结构尺寸等。
(2)喷管工作条件
- 设计最大压强和平均压强,估算的压强时间曲线;
- 推进剂类型,燃烧产物主要成分及物质的量,燃气温度,气体常数,燃气比热比,凝聚相粒子摩尔数等。
(3)性能要求
- 效率高,选择适当的喷管扩张比,尽量减少各种损失,如磨擦、散热、气流扩张、气流分离和二相流损失;能提供所需侧向力,并尽可能减少轴向推力损失。
- 工作可靠,在高温、高压燃气作用下,其结构具有足够的强度和良好的气密性,烧蚀量满足预定要求。
- 结构质量轻,以保证喷管(含推力向量控制装置)有较高的冲量质量比(质量比冲)和发动机有较高的质量比。
- 推力向量控制装置具有良好的频率响应特性和比较小的驱动功率。
- 结构合理,各组合零部件间的间隙适中、同轴性好,可动部分运动灵活,且气密性好,易加工,制造成本低。
- 喷管外壁面温度小于规定值。
- 候补烧蚀率低。
(4)环境条件
- 喷管工作的环境温度;
- 喷管工作高度;
- 贮存的环境及要求;
- 振动及过载条件等。
(5)可靠性和维修性要求
- 可靠性指标及验证方法;
- 维修性要求。
五 喷管设计程序
固定喷管设计程序如图4-1所示:
图4-1 喷管设计程序框图
4.2 喷管的气动设计
喷管的气动设计包括型面设计,流场计算及其它有关参数的计算。流场及其它有关参数,如燃气温度、压强、密度、速度、质量流量等均已在《固体火箭发动机原理》课程中讲过,因此这里只介绍喷管型面设计。
喷管的型面设计是合理地选择收敛段、喉部和扩散段三部分的形状参数,以便使所设计的喷管具有最高的效率。
型面设计包括收敛段、喉部和扩散段气动型面的设计。收敛段的作用是把燃气逐渐加速到声速,由于收敛段的形状不同,燃气加速的程度不同。由此造成喉部声速分布的不同,从而使喷管出口面上燃气参数分布的不均匀,造成一部分性能损失。从工程的观点分析,只要选择一个造型简单,而且能获得声速分布较均匀的形状既可。收敛段主要分为潜入喷管收敛段和非潜入喷管收敛段。收敛段的设计既要使气流均匀加速,又要使喷管的长度尽可能短。与收敛段设计相关的参数有:
接头半径R:应等于后封头接头半径。
收敛半角β:β太小会增加喷管的长度,太大会增加气流的总压损失,β=30°~60°。
入口段椭圆的长半轴和短半轴Ra,Ru:对于潜入和半潜入喷管,入口段型面通常设计成椭圆形,其长短轴之比为3:2,椭圆中心取在喉部截面上,长轴一般为1~2Rt。有时因结构需要,入口段可以做成几段圆弧光滑连接连接而形成的型面入口段的长度不宜过长,通常取1~2Rt。详细型面数据可由专门的喷管设计软件设计。
喷管喉部包括上游一部分、喉部药柱段和下游初始膨胀段。
喉段长度Lt:喉径处设计一圆柱段一方面可提高喉部的加工精度另一方面喉部的上下游可以连续过渡。一般地Lt≤(01~0.3)Rt。
喉部半径Rt:在总体方案设计中已做讨论。
喉部下游半径Rd:为了改善喉部的气动特性,加一圆弧段是非常必要的以减小喷管下游的烧蚀。Rd太小燃气急剧加速,初始扩张区下游烧蚀严重。但Rd太大会增加喷管的长度。因此需按要求和所选材料来合理选取Rd。
扩散段型面设计主要是设计锥形喷管和钟型喷管,钟型喷管喷管可以分为抛物线形、三次多项式型、双圆弧形和离散数据点形,描述扩散段内型面的主要参数有:
初始膨胀半角αm和出口膨胀半角αe:特型喷管的初始扩张半角αm对喷管的长度和燃气流动影响很大。喉部下游的超声速气流随喷管截面积的增大而不断膨胀加速,速度方向指向壁面,在惯性作用下使气流偏离轴线,常造成靠近壁面气流的密度大于中心气流密度。以至壁面压强高于轴心压强。Αm增大,喷管长度缩短,严重影响气流膨胀,加大喷管损失,且会引起初始膨胀区及其下游壁面严重烧蚀。通常特型喷管的初始膨胀半角αm=20~26°,最大可取32°。初始膨胀半角和出口扩张半角之差对喷管性能有较大的影响。试验表明,当\({{\alpha }_{e}}-{{\alpha }_{m}}>{{12}^{\circ }}\)时,实际比冲会有较大的影响。
特型喷管的的损失系数可由下式计算:
\(\eta \text{=}\frac{1}{2}\left[ 1\text{+}\cos \left( \frac{{{\alpha }_{m}}+{{\alpha }_{e}}}{2} \right) \right]\) (4-1)
由于一些复合推进剂中含有铝粉,其燃烧时会生成Al2O3颗粒,形成凝聚相,它随燃气一道流经喷管,形成所谓的两相流。两相流不仅使流场变得非常复杂,使气流速度减小,并造成发动机比冲损失约1.5~2.5%。
膨胀比:在发动机总体方案阶段已经讨论过。在通常情况下扩张比是由总体给出的。在总体没有给出喷管的扩张比时,应根据发动机总体限定的结构尺寸及质量等条件下,选取扩张比使得发动机的比冲最大。扩张比和压强比是互相依赖的,即知道压强比可以求出膨胀比,知道膨胀比可以求出压强比。
出口型面设计:这里将根据膨胀比、出口膨胀半角和出口膨胀半角设计型面。
4.2.1 收敛段和喉部
(1)非潜入喷管
非潜入喷管的收敛段型面一般采用圆锥形(图4-2),其收敛(入口)半角β在30~60°范围内选择。β值选得太小,会增加收敛段长度,使质量和散热损失增大;β值太大,会发生颈缩现象,造成流量损失,同时会加重烧蚀。通常取β=45°。
图4-2 非潜入喷管的收敛段和喉部
图4-3 潜入喷管的入口段形状
喷管喉部包括喷喉的上游与收敛段相切的部分和下游的初始扩散段。喉部形状设计不合理,会造成2~3%的比冲损失,实验结果表明,喉部曲率半径rc越小,喷管效率越低,比冲损失越大。当rc等于或大于喉径(2rt)时,损失最小。但太大也会造成喷管长度增加。所以设计时一般取rc=1~2re(图4-2a)。
为适应结构布局需要,喉部上、下游设计成两个不相等的曲率半径,如图4-2b所示。或将喉径处设计成圆柱段,如图4-2c所示。对于喉径rt≥10cm的喉部,取圆柱段宽Lt≤0.5rt喉部下游半径re2对喷管下游壁面烧蚀有明显影响,re2大,燃气加速缓慢,使初始扩张区下游烧蚀减轻;rc2燃气加速急剧,初始扩张区下游烧蚀严重。但rc2大会使喷管加长,增加消极质量。因此需按要求和所选用材料来合理选取rc2。
(2)潜入喷管
喷管的一部分(收敛段或收敛段加喉部)或绝大部分伸进燃烧室中的叫做潜入喷管。潜入喷管的收敛段和喉部往往构成一个整体。收敛段处于两面或三面受热状态。因此其造型不同于非潜入喷管,把它叫作入口段更确切些。
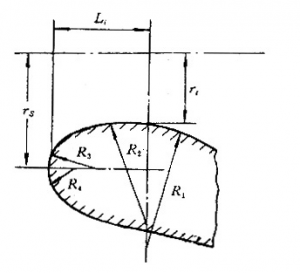
入口段型面通常设计成椭圆形,其长短轴之比为3:2,椭圆中心取在喉部截面上,长轴一般为1~2rt。有时因结构需要,入口段可以做成由几段圆弧光滑连接而成的型面。入口段长度不宜过长,通常取Li=1~2rt。图4-3所示为一种入口段的喉部的形状,图中Li=1~2rt 。图4-3所示为一种入口段的喉部的形状,图中Li为入口段长度,rs为头缘半径,各弧段半径R1、R2、R3和R4于具体结构设计时确定。
(3)长尾喷管
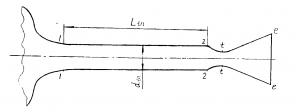
图4-4 长尾管结构参数
图4-4 为亚音速长尾喷管结构特征及参数,选择原则如下:
1)圆筒段内径的确定是以允许的的最大喷管外径,考虑到烧蚀、传热等所有上限值,使外壁温度和结构质量满足要求,通常情况下,尾管内径\({{d}_{itn}}=\left( 1.3\tilde{\ }2.0 \right){{d}_{t}}\)。
2)尾管内径在满足质量要求的情况下尽量能取上限;
3)尾管入口处的速度系数\({{\lambda }_{1}}\le 0.4\);
4)不允许圆筒内出现气流阻塞,即圆筒段长度Ltn与内径ditn之比应满足:
\(\frac{{{L}_{tn}}}{{{d}_{itn}}}\le \left( \frac{1}{\lambda _{1}^{2}}+\ln \lambda _{1}^{2}-1 \right)\frac{k+1}{2k{{f}_{w}}}\) (4-2)
式中fw为壁面摩擦系数,建议取fw=0.00925,k-燃气的比热比。
5)尾喷管设计与其他常规喷管类似。
4.2.2 扩散段
扩散段的设计重要参数的选择是扩张比,喷管面积扩张比与压强比关系如下:
\(\frac{{{A}_{e}}}{{{A}_{t}}}=\frac{\sqrt{k}{{\left( \frac{2}{1+k} \right)}^{\frac{k+1}{2\left( k-1 \right)}}}}{{{\left( \frac{{{P}_{e}}}{{{P}_{c}}} \right)}^{\frac{1}{k}}}\sqrt{\frac{2k}{k-1}\left[ 1-{{\left( \frac{{{P}_{e}}}{{{P}_{c}}} \right)}^{\frac{k-1}{k}}} \right]}}\) (4-3)
通常情况下,喷管扩张比是由发动机总体给出的;
在总体没有给出扩张比时,应根据发动机总体限定的结构尺寸及质量等条件,选取扩张比使发动机获得比冲最大。
非潜入和潜入喷管的扩散段型面设计是一样的,通常有锥形和特形(钟形)两种。特型喷管的扩散段型面设计可分两种:变分原理法和直接优化法。
变分原理法是与喷管超音速段的特征线解法相联系的。特征线法是步进差分法中比较简便又最为精确的数值计算法。特征线法的基本思想是在流场中找到一些特征线,把原来的双曲型偏微分方程化为沿这些特征线成立的全微分方程,然后用差分法在特征线上或特征线的交点上对这些全微分方程求解。从物理观点上来看,特征线是物理扰动传播的路径。
直接优化法的基本思想是假设几种型面曲线,在不同初始膨胀角下进行计算,从而选出相对最佳的型面曲线和初始膨胀角。
(1)锥形扩散段
锥面母线与喉部圆弧相切,半锥角(扩张半角)一般取15°最佳;为使扩散段不致过长,目前一般取=18°。扩张半角引起的扩张损失系数可由下式计算
\({{\eta }_{div}}=\frac{1+\cos {{\alpha }_{e}}}{2}\) (4-4)
决定锥形喷管型面的参数有:喉部半径Rt、喉部下游半径RtD、面积膨胀比εA、出口膨胀半角αe锥形喷管由于其较长的长度在大型高性能的发动机中很少采用。其型面参数采用下面公式确定:
出口内半径:\({{{R}}_{e}}={{R}_{t}}\sqrt{{{\varepsilon }_{A}}}\) (4-5)
扩散段长度:\(Le=\frac{{{R}_{e}}-\left( {{R}_{t}}+{{R}_{tD}}-{{R}_{tD}}\cos {{\alpha }_{e}} \right)}{tg{{\alpha }_{e}}}+{{R}_{tD}}\sin {{\alpha }_{e}}\) (4-6)
(2)特形扩散段
扩散段的母线为曲线所形成的扩散段叫做特形或钟形扩散段。特形扩散段比锥形扩散段造型复杂,需用空气动力学特征线原理造型,其性能也比锥形扩散段优越。
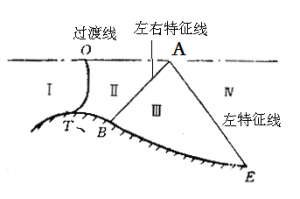
特形喷管的流场如图4-5所示,分为4个区:Ⅰ区为亚声速区,OT为声速过渡线;Ⅱ区为超声速初始膨胀区,AB叫右特征线,气流在该区内急剧膨胀加速,速度方向不断变化,在特征线AB上的各点速度方向与喷管轴线倾角最大。Ⅲ区为均衡区,AE叫左特征线,气流速度在该区内继续增大,其方向也在不断变化。从特征线AB开始倾角逐渐变小,在AE上的各点速度方向与轴线倾角最小;Ⅳ区为均匀气流区,气流通过特征线AE后,速度趋向均匀,等于A点的速度VA。
特形扩散段的造型有两种方法:一是特征线方法;一是印度科学家饶(Rao)提出的饶氏方法,用以求定长喷管的最大推力的扩散段型面。这两种方法都比较麻烦,通常用取代的近似法,前者用双圆弧法近似,后者用抛物线法近似。
图4-5 特型喷管流场划分图
图4-6 双圆弧型面
1)双圆弧法
所谓双圆弧是指喷管扩散段内型面由两个圆弧组成,如图4-6所示。第一个圆弧为喉部区的型面,其中心位于喉部临界截面上,其半径R=dt。第二个圆弧为超声速区型面,其半径R0的大小正好与第一个圆弧切于点B,并与图4-5中用特征线法求得的型面BE相吻合。
双圆弧法是基于径向流动条件提出的,实践证明这种喷管的内型面不会产生激波,因为它与精确解求得的型面比较接近。但是,双圆弧喷管比较短,会造成部分欠膨胀损失和扩张损失。
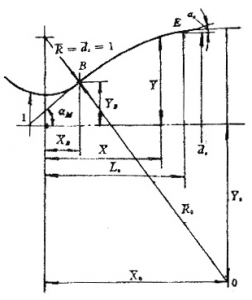
双圆弧型面作图法如下(参见图4-6):
- 给定参数:喉径dt,扩张比ε,出口半角ae ;
- 由ε和2ae ,从图4-5中查得\({{\bar{L}}_{n}}={{L}_{n}}/{{d}_{t}}\);
- 求大圆弧R0的相对值\({{\bar{R}}_{0}}={{R}_{0}}/{{d}_{t}}\);
- \({{\bar{R}}_{0}}=\frac{\bar{L}_{n}^{2}+{{\left( 1.5-de/2{{d}_{t}} \right)}^{2}}-1}{2\left[ 1-{{{\bar{L}}}_{n}}\sin {{\alpha }_{e}}-\left( 1.5-de/2{{d}_{t}} \right)\cos {{\alpha }_{e}} \right]}\)
- 求二圆弧切点B上的气流最大倾角aM
\({{\alpha }_{M}}={{\sin }^{-1}}\frac{{{{\bar{L}}}_{n}}+{{{\bar{R}}}_{0}}\sin {{\alpha }_{\varepsilon }}}{{{{\bar{R}}}_{0}}+1}\)
- 求大圆弧圆心的相对坐标
\({{\bar{X}}_{0}}={{\bar{L}}_{n}}+{{\bar{R}}_{0}}\sin {{\alpha }_{\varepsilon }}\)
\({{\bar{Y}}_{0}}={{\bar{R}}_{0}}\cos {{\alpha }_{\varepsilon }}-\frac{{{d}_{e}}}{2{{d}_{t}}}\)
- 求点B的相对坐标
\({{{\bar{X}}}_{B}}=\sin {{\alpha }_{M}}\)
\({{{\bar{Y}}}_{B}}=1.5-\cos {{\alpha }_{M}}\)
- 给定\(\bar{X}=X/{{d}_{t}}\),且\({{\bar{X}}_{B}}<\bar{X}<{{\bar{L}}_{n}}\),求大圆弧上对应.的\(\bar{Y}=Y/{{d}_{t}}\)
- \(\bar{Y}=\sqrt{\left( {{{\bar{R}}}_{0}}-{{{\bar{X}}}_{0}}+\bar{X} \right)\left( {{{\bar{R}}}_{0}}+{{{\bar{X}}}_{0}}-\bar{X} \right)}-{{\bar{Y}}_{0}}\)
图4-7
2)抛物线法
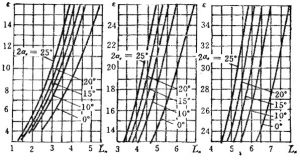
抛物线型面作图顺序如下(参见图4-8):
- 给定参数:喉部半径rt,扩张比ε,出口半角ae 或喷管长度Ln;
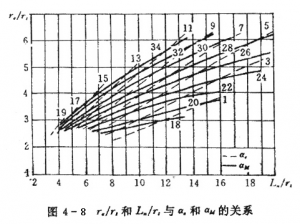
- 由\({{{r}_{e}}}/{{{r}_{t}}}\;=\sqrt{\varepsilon }\)和ae (或Ln/rt)和图4-6查得Ln/rt(或aε )和初始扩张半角am ;
- 取喉部上游曲率半径为 .,下游曲率半径rc2=4rt,作rc2圆弧的切线,使与轴线夹角为am ;
- 由Ln(或ae )和ε求出出口面的端点N,过点N作直线QN,使与轴线夹角为ae ,并与直线MQ交于点Q;
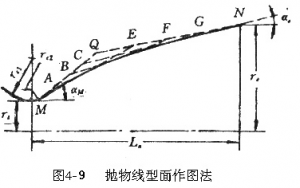
- 将直线MQ和QN分成相同的等分,连接对应的点,作它们的包络线,即得扩散段的抛物线型面;连同rc1和rc2两段圆弧即为整个特形喷管型面,见图4-9。
特形喷管的初始扩张半角am 对喷管长度和燃气流动影响很大。喉部下游的超声速气流随喷管截面积加大而不断膨胀加速,速度方向指向壁面,在惯性的作用下使气流偏离轴线,造成靠近壁面的气流密度大于轴心部分的,以致壁面压强高于轴心压强。am 增大,喷管长度缩短,下游壁面附近压强急剧升高,严重影响气流膨胀,加大喷管损失,且会引起初始膨胀区及其下游壁面严重烧蚀。
通常取特形喷管的初始扩张半角am =20~26°,最大可取am =32°。初始扩张半角am 与出口半角ae 之差值对喷管性能也有重大影响,试验表明,当am–ae>12°时,实际比冲会有较大损失。
特形喷管的扩散损失系数可由(4-1)式计算。
考虑两相流的喷管造型非常复杂,有许多从理论上探求两相流喷管型面的计算方法。都因计算十分复杂,且有许多未知因素,因此很不实用。工程上,在给定收敛段和喉部形状后,用下列幂函数求解扩散段型面
\(y=a+\sqrt{b(x-c)}\) (4-7)
式中 \(a=(y_{e}^{2}-R_{a}^{2}-2L{{R}_{a}}tg{{a}_{a}})/2({{y}_{e}}-{{R}_{a}}-Ltg{{a}_{a}})\)
\(b=2({{y}_{a}}-a)tg{{a}_{a}}\)
\(c={{x}_{a}}-{{({{y}_{a}}-a)}^{2}}/b\)
x为喷管轴线方向,y为半径方向,式中常数a和系数b、c可根据给定的喉径、喉面到出口面的长度、出口直径和出口半角求得。借用图4-5,请读者自行求出a、b和c。
3)三次多项式优化曲面
三次多项式的形式为: y = a + bx + cx2 + dx 3 (4-8)
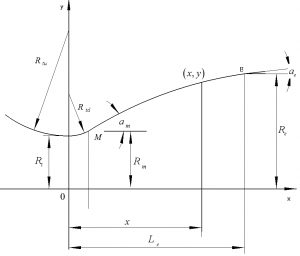
已知条件是(图4-10):
am 扩散段初始膨胀半角
ae 出口膨胀半角
\(\overline{{{R}_{t2}}}\) =Rt2/Rt 喉部下游过渡圆弧无因次半径;
εA面积膨胀比,
图4-10 三次多项式最优型面结构示意图
经过优化的三次多项式曲面的曲线方程为:
\(\overline{y}=\frac{y}{{{R}_{t}}}=1+\overline{{{R}_{td}}}\left( 1-\cos {{\alpha }_{e}} \right)+\text{tg}{{\alpha }_{e}}\overline{x}-\frac{\left( \text{tg}{{\alpha }_{e}}-tg{{\alpha }_{m}} \right){{\left( 2\text{tg}{{\alpha }_{e}}+\text{tg}{{\alpha }_{\text{m}}} \right)}^{2}}}{27{{\left[ \sqrt{{{\varepsilon }_{A}}}-1-\overline{{{R}_{t2}}}\left( 1-\cos {{\alpha }_{e}} \right) \right]}^{2}}}{{\left( \overline{x} \right)}^{3}}\)
(4-9)
扩散段的最佳长度为:
\(L=\frac{3}{2\text{tg}{{\alpha }_{e}}+\text{tg}{{\alpha }_{m}}}\left( {{r}_{e}}-{{r}_{m}} \right)\) (4-10)
对于用户自行输入的型面难以保证在变参数设计过程中满足膨胀比、初始膨胀半角和出口膨胀半角的要求。
4.3 喷管的热防护设计
喷管热防护是指构成喷管气动内型面在发动机工作期间,起到绝热耐烧蚀的作用,保证气动内型面的连续、完整及控制外壁面温度的要求。喷管的热防护设计在于尽可能使喷管型面在工作过程中不改变或少改变,并使其支撑结构的温度控制在许可的范围内。主要工作是选择热防护材料(烧蚀和绝热材料),进行传热、烧蚀和热应力分析,确定热防护结构形状和尺寸。
4.3.1 喷管的热环境
燃气在喷管中流动,会对喷管壁面产生对流、颗粒辐射和碰撞传热。
利用巴兹(Bartz)公式来计算燃气在拉瓦尔喷管中的局部对流换热系数\({{\alpha }_{c}}\)
\({{\alpha }_{c}}=\frac{0.026}{d_{t}^{0.2}}{{\left( \frac{{{\mu }^{0.2}}{{C}_{p}}}{P_{r}^{0.6}} \right)}_{T_{g}^{*}}}{{\left( \frac{{{P}^{*}}}{{{C}^{*}}} \right)}^{0.8}}{{\left( \frac{{{d}_{t}}}{{{r}_{\pi }}} \right)}^{0.1}}{{\left( \frac{{{A}_{t}}}{A} \right)}^{0.9\sigma }}\)
(4-11)
式中,Tg*——表示以燃气在喷管进口处的总温作为定性温度;
dt——喷管喉部直径(m);
rn——喷管喉部的曲率半径(m);
P*——喷管进口处燃气的总压(N/m2);
C*——燃气的特征速度(m/s);
At——喷管喉部的截面积(m2);
б——考虑附面层内物性参数变化影响的修正系数,该值用喷管燃气总温Tg*,燃气侧壁面的局部温度Tω和局部马赫数Ma来表示
\(\sigma \text{=}\frac{1}{{{\left[ \frac{1}{2}\times \frac{{{T}_{\varpi }}}{T_{g}^{*}}\left( 1+\frac{k-1}{2}M_{a}^{2} \right)+\frac{1}{2} \right]}^{0.68}}{{\left[ 1+\frac{k+1}{2}M_{a}^{2} \right]}^{0.12}}}\)
(4-12)
k——比热比
对某种特殊燃气没有资料可查时,则式中的Pr数和粘性系数μ可按下式计算
\(\Pr =\frac{4k}{9k-5}\)
\(\mu \text{=}\left( 1.187\times {{10}^{\text{-}7}} \right)M_{\mu g}^{0.5}{{T}^{9.6}}\) kg/m.s
式中\({{M}_{\varpi g}}\)为燃气的分子量;T为燃气绝对温度。
已知对流换热系数\({{\alpha }_{c}}\)之后,喷管内初始的对流换热的热流密度则可按下式求得
\(q={{\alpha }_{c}}{{\left( \frac{{{h}_{r}}}{{{h}_{e}}} \right)}^{0.5}}{{T}_{r}}\) (W/m2) (4-13)
或按一般高速气流加热的情况进行计算
\(q={{\alpha }_{c}}\left( {{T}_{r}}-{{T}_{\omega }} \right)\) (W/m2)
式中hr为燃气恢复比焓(J/kg);he为燃气静比焓;Tω为壁面温度。随着加热时间的增大,Tω将不断升高;Tr为燃气恢复温度,可按下式计算
\({{T}_{r}}={{T}_{g}}\left( 1+r\frac{k-1}{2}M_{a}^{2} \right)\) 或\({{T}_{r}}={{T}_{g}}\text{+}r\frac{u_{s}^{2}}{2{{C}_{p}}}\) (K)
式中r为恢复系数,对于层流\(r\approx \sqrt{\Pr }\);对于湍流\(r\approx \sqrt[3]{\Pr }\);us为燃气流速;Tg为燃气温度。
关于颗粒辐射和碰撞的传热现在还很难估算,只有借助于实验来确定。
4.3.2 热防护层厚度估算
通过估算的烧蚀厚度,乘上安全裕度f,再加上估算的炭化厚度和原始材料的适当厚度,即为所设计的热防护层厚度。安全裕度定义如下
(4-14)
式中δa和δe分别为允许烧蚀的和估算的烧蚀厚度。
根据所选用的热防护材料,采用不同的计算方法来计算热防护材料的烧蚀和炭化厚度,因为燃气对热防护材料伴有化学反应。现有的几种计算方法都不太成熟,而且非常繁杂,需借助专用程序进行计算。这里介绍几种经验方法。
在设计时,可对每一种已知烧蚀材料的烧蚀数据进行外推,估算出其烧蚀率。利用类似的试验得到每一烧蚀材料的烧蚀数据,用来进行新发动机喷管的烧蚀层设计。
利用巴兹方法换算热防护材料的烧蚀率
式中δa和δe分别为允许烧蚀的和估算的烧蚀厚度。
\({{r}_{a}}={{r}_{am}}{{\left( \frac{{{P}_{c}}}{{{P}_{cm}}} \right)}^{0.8}}{{\left( \frac{{{d}_{tm}}}{{{d}_{t}}} \right)}^{0.2}}\) (4-15)
式中Pc和dt为新设计的发动机的燃烧室压强和喷管喉径;Pcm和dtm为测量烧蚀率的发动机的燃烧室压强和喷管喉径。ram是烧蚀率测量值。
烧蚀厚度可由下式确定
\({{\delta }_{a}}={{r}_{a}}t\) (4-16)
热防护层的炭化厚度可由下面的经验公式估算
\({{\delta }_{c}}=A{{t}^{m}}\exp \left( \frac{-B}{q} \right)\) (cm) (4-17)
式中q为热流密度(W/m2),由式(4-13)计算;A、B和m为经验常数,在给定的热防护材料和条件下用实验方法来确定。
对于碳布/酚醛
A=0.09144 B=7.5˟105 m=0.68
对于高硅氧/酚醛
A=0.07874 B=1.02663˟106 m=0.68
考虑0.2~0.5的烧蚀和碳化安全裕度,因此热防护层的总厚度为
\(\delta \text{=}\left( 1.2\text{ }\!\!\tilde{\ }\!\!\text{ }1.5 \right)\left( {{\delta }_{a}}+{{\delta }_{c}} \right)\)
\(=\left( 1.2\tilde{\ }1.5 \right)\left[ {{r}_{a}}t+A{{t}^{m}}\exp \left( -\frac{B}{q} \right) \right]\) (4-18)
4.3.3 热防护材料
一般热防护材料分为两种:(耐)烧蚀材料和绝热材料。喉衬主要采用耐烧蚀材料,如石墨(多晶石墨、热解石墨)、难熔金属(钨及钨合金)、碳/碳复合材料、陶瓷和陶瓷复合材料。除喉衬外,烧蚀材料用作收敛段和扩散段接触燃气的边界层——烧蚀层。绝热材料用作喉衬的背壁和烧蚀层背壁的绝热层。有些材料既可作烧蚀层也可作绝热层。
通常用烧蚀热效率选择收敛段和扩散段材料,烧蚀热效率越大,材料的吸热能力和绝热性能越好。烧蚀热效率是指一定背壁温升时总热量与材料初始质量min之比:
\({{E}_{ef}}=\frac{{{q}_{cv}}{{t}_{a}}}{{{{m}}_{in}}}\) (4-19)
ta工作时间。
通常用有效烧蚀热选择喉衬材料,有效烧蚀率数值越大,材料热容量越大耗散热量能力强。有效烧蚀热是指总热量与材料耗损量之比:
\({{H}_{ef}}=\frac{{{q}_{cv}}{{t}_{a}}}{\Delta {{{m}}_{in}}}\) (4-20)
(1)喉衬
发动机工作时间较短(小于5s),喉径较小(100mm以下),可采用高强高密度石墨,如石墨T704,石墨T705等;
工作时间在十几到二十几秒的发动机,喉径在150mm以下的发动机可采用石墨渗铜作喉衬。当结构尺寸有非常严格的限制,壁厚很薄时,也可采用碳/碳复合材料;
喉径有严格控制时,可以采用钨渗铜材料;
工作时间较长,一般在30s以上,喉径尺寸大,喷管流量大,工作热环境条件恶劣的喷管,可采用毡基碳/碳复合材料或多向编织碳/碳复合材料。
1)多晶石墨
多晶石墨多用于工作时间不长的小喷管喉衬、多为人工制品。由表4-1可见,顺晶面与垂直晶面间的性能相差较大。多晶石墨强度低,随着温度升高,石墨喉衬径向和轴向逐渐膨胀,如图4-11(a)所示喉衬与背壁绝热层结构会使喉衬的下游部分产生环向裂纹,严重时会碎裂。所以通常石墨喉衬与背壁绝热层采用图4-11(b)所示的锥面配合,并留有适当间隙。当石墨喉衬受热膨胀时,背壁绝热层对喉衬产生挤压压强p,压强在轴向产生分量px,迫使喉衬顺锥面产生轴向位移,使热应力松弛。配合面的半锥角a一般取5~10°。
表4-1 几种喉衬材料性能①
|
材 料 性 能 |
多晶石墨② |
热解石墨② |
碳/碳复合 材料② |
钨 |
|
|
锻造或挤压 |
模压烧结 |
||||
|
密度(g/cm2) |
1.75 |
2.2 |
1.45 |
19.0 |
17.4 |
|
熔化或升华温度(℃) |
3 649 |
3 649 |
3 649 |
3 410 |
3 410 |
|
比热(J/kg·K) |
1 047(2 512) |
921(2 093) |
1 298(2261) |
140(197) |
140(197) |
|
导热系数 (W/(m·K)) 顺晶(层)面 垂直晶(层)面 |
— |
— |
— |
166(104) |
94(57) |
|
121(28) |
346(69) |
31 |
— |
— |
|
|
69(26) |
2.1(0.05) |
14 |
— |
— |
|
|
线膨胀系数 (1/℃) 顺昌(层)面 垂直晶(层)面 |
— |
— |
— |
4.5×10-6 |
4.1×10-6 |
|
2.7×10-6 |
2.4×10-6 |
0.9×10-6(3.1×10-6) |
— |
— |
|
|
4.0×10-6 |
36×10-6 |
2.5×10-6(5.0×10-6) |
— |
— |
|
|
拉伸极限强度 (MPa) 顺晶(层)面 垂直晶(层)面 |
— |
— |
— |
1 103(69) |
379(69) |
|
31(48) |
69(103) |
93(110) |
— |
— |
|
|
21(35) |
2.8 |
4.8(9.0) |
— |
— |
|
|
拉伸模量(MPa) 顺晶(层)面 垂直晶(层)面 |
— |
— |
— |
407×103 |
276 |
|
5.2×103(5.5×103) |
27.6×103(17.2×103) |
15.9×103(14.5×103) |
— |
— |
|
|
6.2×103(8.6×103) |
11.7×103(6.9×103) |
11.0×103(12.4×103) |
— |
— |
|
|
拉压强度(MPa) 顺晶(层)面 垂直晶(层)面 |
— |
— |
— |
— |
— |
|
62.1(75.8) |
69.0 |
93.1(93.1) |
— |
— |
|
|
69(82.7) |
310 |
44.8(62.1) |
— |
— |
|
|
压缩模量(MPa) 顺晶(层)面 垂直晶(层)面 |
— |
— |
— |
— |
— |
|
6.2×103(7.6×103) |
33.1×103 |
17.2×103(15.2×103) |
— |
— |
|
|
5.5×103(6.9×103) |
13.1×103 |
10.3×103(4.5×103) |
— |
— |
|
|
烧蚀率③(mm/s) |
0.059~0.087 |
0.013~0.015 |
0.15 |
— |
— |
① 所示性能为室温下的数据,括号内为2 200℃下的数据。
② 所示材料的密度、强度和模量随加工方法不同,有较大的变化范围。
③ 所示烧蚀率是用聚氨脂推进剂(3 350K)在dt=54mm和=30s的发动机上测得的。
图4-11 石墨喉衬组件的配合
(a)柱面配合 (b)锥面配合
1—喉衬 2—背壁绝热层 3—壳体
2)热解石墨
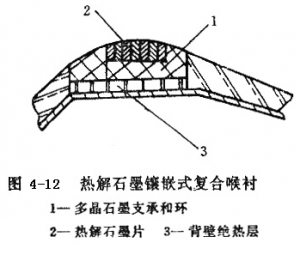
热解石墨是一种高密度、耐烧蚀材料,由气相碳沉积在基体上制成。它在高温下垂直于沉积层方向的膨胀系数很大,给设计带来困难。因成型工艺决定,热解石墨只能制成片状,因此热解石墨喉衬只能设计成镶嵌式结构。为预防轴向膨胀,在间隙里充填耐烧蚀的弹性材料。在发动机工作期间,充填的弹性材料先被烧蚀,热解石墨膨胀后恰好填补间隙。
通常,热解石墨喉衬要用多晶石墨作支承,并在其上、下游装上多晶石墨环,以起热沉作用。在石墨支承和石墨环外边再加背壁绝热层(图4-12)。这种喉衬结构加工复杂,造价高,可靠性低,很少采用。
3)碳/碳复合材料
碳/碳复合材料是一种新型热防护材料,由碳纤维作增强体,沉积碳作基体复合而成。根据增强体的结构,分为碳毡类碳/碳和多向编织碳/碳。前者又分为平板碳毡层叠和整体碳毡两种,后者分为两向、三向、四向和多向数种。
碳/碳复合材料具有良好的耐烧蚀、抗热震、耐机械冲击等性能,且有较高的强度,高温下膨胀系数小,是目前用作喉衬的最佳材料,同时也是用作其余部位的最好热防护材料。喉衬材料一般用三向或四向编织碳/碳复合材料制作。
4)难熔金属
在早期研制的喷管中,曾用钨、钼等难熔金属作喉衬。图4-13所示的钨-石墨复合喉衬,是用钨板旋压成钨衬,再与石墨复合成喉衬。这种结构工艺复杂,成本贵。采用粉末冶金法经模压烧结而成的喉衬,耐烧蚀性稍差,但易加工、价廉。在多孔烧结钨中渗铜,目的是想以渗入的铜作发汗剂,在高温下起发汗冷却作用,事实上喉部的热焓尚不足以使铜熔化蒸发,而只能起到改善烧结钨机加性能的作用。
图4-13 钨-石墨复合喉衬
1- 2-钨衬 3-石墨 4-喷管堵盖
5)陶瓷和陶瓷复合材料
陶瓷具有较高的熔点,在高温下有良好的抗氧化性能;但抗热震性能差,受高温冲击易发生脆裂。近来研制成功的以碳化硅纤维、三氧化二铝纤维增强的陶瓷基复合材料,具有耐磨、耐腐蚀、绝热等优异性能,有可能用作喉衬材料或喷管与燃烧室的热结构连接件。
(2)收敛段和扩散段
通常,工作时间较短,小于5~7s,所在区域内燃气流速低,结构尺寸相对较小,结构质量要求不严格时,收敛段绝热层采用模压高硅氧/酚醛材料结构;
通常,工作时间长,所在区域内燃气流速高,结构尺寸较大,结构质量要求严格时,采用高硅氧/酚醛和碳/酚醛复合模压或高硅氧布/酚醛和碳布/酚醛复合缠绕材料结构;
通常,工作时间ta小于5~7s,扩张比较小,小于9,结构质量要求不严格时,扩散段绝热层采用模压高硅氧、酚醛或高硅氧布/酚醛缠绕材料结构;
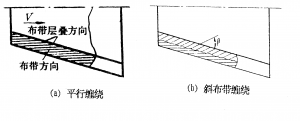
通常工作时间长,扩张比大,采用高硅氧布、酚醛和碳布/酚醛复合缠绕材料结构。缠绕方式有两种:第一种,内层的碳布/酚醛和外层的高硅氧布/酚醛均采用平行缠绕结构;第二种,内层碳布/酚醛采用斜布带缠绕结构,而外层高硅氧布/酚醛仍是平行缠绕结构。通常,斜布带缠绕角为10°~20°。
喷管收敛段和扩散段常用的热防护材料有石棉-酚醛树脂、高硅氧-酚醛树脂和碳-酚醛树脂等。石棉-酚醛只有模压制品,高硅氧-酚醛和碳-酚醛既有模压制品,也有缠绕制品。一般石棉-酚醛只作喉衬背壁和绝热层,不能用作烧蚀层。高硅氧-酚醛和碳-酚醛既可作烧蚀层,也可作绝热层。表4-2列出这三种材料的性能参数。
表4-2 收敛段和扩散段热防护材料性能
|
材 料 性 能 |
石棉-酚醛 |
高硅氧-酚醛 |
碳-酚醛 |
||
|
模压 |
缠绕 |
模压 |
缠绕 |
||
|
密度(g/cm2) |
≤1.85 |
2.0 |
1.70 |
1.50 |
|
|
抗拉强度(MPa) |
>19.6 |
58.8 |
>29.4 |
44.1 |
|
|
抗压强度(MPa) |
>88.3 |
92.0 |
|||
|
抗弯强度(MPa) |
>78.5 |
98.1 |
>68.6 |
||
|
弹性模量(MPa) |
1.07×104 |
1.75 |
0.83 |
||
|
导热系数(W/(m·K)) |
0.84 |
0.47 |
0.36~0.41 |
0.28~0.32 |
|
|
比热(J/kg·K) |
1172.3 |
1 046.6 |
1 004.8 |
1 126.2~1 323.0 |
|
|
线膨胀系数(1/℃) |
(9.3~14.8)×10-6 |
(5.5~8.6)×10-6 |
|||
石棉-酚醛含有大量结晶水,随温度、湿度变化会吸收或失去水份,从而出现膨胀或收缩。因此其制品需存放于有温度、湿度要求的库房内。石棉-酚醛受热后会放出热解气体,设计时必须设置逸气通道。一般逸气通道孔径为1.8~2.5mm,相邻通道中心距为25mm,通道深度为估算的最大碳化层厚度。
高硅氧-酚醛和碳-酚醛是收敛段和扩散段常用材料。尺寸小的零件用模压制品,尺寸大的用缠绕制品。模压制品的纤维方向性差,分布不均匀,对烧蚀性能有影响。缠绕制品按布带卷轴与模具轴线是平行还是有夹角而分为平行缠绕和斜缠绕两种,后者较前者为好。
碳-酚醛的烧蚀性能优于高硅氧-酚醛,但价格较贵。因此,常采用图4-14所示的复合缠绕结构,即在扩散段前段(或收敛段)先缠绕部分碳-酚醛,然后再缠高硅氧-酚醛。试验证明这种结构较合理,扩散段上游较下游烧蚀严重,所以靠上游部分用耐烧蚀的碳-酚醛制做。
图4-14 扩散段缠绕结构
收敛段和扩散段的热防护层与喷管壳体都有胶粘连接,一般为常温固化胶,这种胶粘接工艺简单,粘接的剪切强度高。
(3)尾管材料
通常,对于喷管流量小,工作时间短,推进剂不含铝粉,可采用模压高硅氧/酚醛材料结构、模压碳/酚醛和高硅氧/酚醛复合材料结构或碳布/酚醛和高硅氧布/酚醛层压结构;
对于喷管流量大,工作时间长,应采用镶嵌石墨、碳布/酚醛和高硅氧布/酚醛复合缠绕结构。
通常,镶嵌的材料有高强高密石墨、商强石墨渗铜等:
通常,镶嵌长度有两种。第一种是只在入口区域镶嵌一定长度;第二种是整个尾管长度上镶嵌
镶嵌的石墨应分若干段,长度与厚度之比小于3~4;
直筒段内层缠绕碳布/酚醛时,应采用斜布带缠绕材料结构,外层则采用高硅氧布/酚醛平行缠绕材料结构。
4.4 喷管的结构设计
喷管的有些参数是由发动机总体依据发动机其它部件和整体性能要求而确定的,例如喷管与壳体的接头尺寸、喷管的喉径、面积扩张比及扩张半角;有些参数是考虑到热防护而确定的,例如收敛段绝热层厚度、喉衬厚度、扩散段材料厚度;有些是结构强度的要求,如金属结构件的厚度。设计的顺序是由内型面向外部进行,同时也通过适当地调整内型面,来保证外表面的温度和形状的限制。由于实际的喷管设计有大量的是经验性的,难以总结出一种通用的设计方法,这里只能分别介绍喷管各个部件设计应注意的问题。
通常在发动机长度没有限制和特殊要求时采用非潜入喷管,它由收敛段绝热层、喉衬组件、扩散段绝热层及挡环、喷管壳体等几部分组成。
当在发动机长度受到严格限制的条件下,为保证装药量,喷管前端潜入燃烧室尾部后,且能使喷管在规定的外露长度下保证有足够的扩张比。
长尾管是为了减小装药燃烧时,导致导弹质心前移,将部分仪器放在喷管周围,通常是在收敛段至喉部上游位置之间增加一圆柱段,采用亚音速长尾喷管。
4.4.1 支撑结构
支撑结构主要是将各个部分连接成一个整体,它主要是受强度载荷的作用,常用的材料有钢、钛合金及铝合金等。常用的钢材有30CrMnSiA、45号钢及低碳钢、D406A超高强度钢;常用的钛合金有TC-5、TC-6及高强度钛合金;常用的铝合金有LF6、LD10及LC9高强铝合金等。某些类型的复合材料也可以作为结构材料,如纤维、布带浸渍酚醛或环氧树脂做成的材料,主要用作扩散段的结构材料(既作烧蚀、绝热材料,又作结构材料)。
收敛段圆筒段厚度δ的计算可采用第一强度理论:
\(\delta \frac{\text{2}{{\text{P}}_{\text{c}}}\text{ }{{\text{R}}_{\text{2}}}}{\text{(2}\text{.0}{{\sigma }_{\text{b}}}\text{ }\varphi \text{/ }{{\text{k}}_{\text{n}}}+{{\text{P}}_{\text{c}}}\text{)cos}\theta }+\text{ }\Delta \) (4-21)
或第四强度理论:
\(\delta \frac{\text{2}{{\text{P}}_{\text{c}}}\text{ }{{\text{R}}_{\text{2}}}}{\text{(2}\text{.3}{{\sigma }_{\text{b}}}\text{ }\varphi \text{/ }{{\text{k}}_{\text{n}}}+{{\text{P}}_{\text{c}}}\text{)cos}\theta }+\text{ }\Delta \) (4-22)
式中:θ-收敛段圆台体锥半角;
φ-焊缝系数,无焊缝φ=1;
σb-材料的强度极限(MPa);
Δ-热处理、材料及加工过程的厚度附加量;
R2-收敛段大端的半径;
k n-结构安全系数;
Pc-燃烧室压强(MPa)。
在喉部,结构件的设计应防止内部的绝热部件在高压下吹出,一般应设计一个凸台,或加止动螺钉。厚度可以比收敛段小一些。
在扩散段由于燃气压力较小、燃气温度也有所降低,所以扩散段金属结构件的厚度可以设计得较薄些。为了防止扩散段绝热层被燃气吹掉,可以在结构件的出口加挡环,或在结构件与扩散段绝热层之间加止动螺钉。
结构件与燃烧室的连接,应遵守发动机总体所规定的连接方式和尺寸。
对于有推力向量控制的喷管,还应考虑到一套附加的连接装置。
收敛段绝热层的实际形状是较为复杂的,为研究问题方便,这里假设收敛段是具有厚度为δ的规则形状。
4.4.2 连接结构
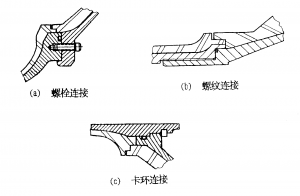
喷管与燃烧室连接常用的方式有法兰、螺纹、卡环等。
图4-15 连接结构
(1)法兰连接计算
通常在结构尺寸没有限制时,常采用法兰-螺栓连接结构。法兰厚度的初步确定可由经验公式初步来计算。
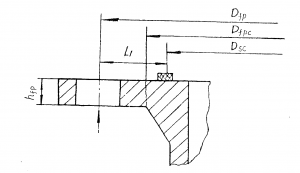
图4-16 法兰连接计算参数
将实际法兰作适当的简化,构成如图4-16所示的简化计算模型,可得到法兰厚度的初步计算公式:
\({{h}_{fp}}=\sqrt{\frac{3F\left( {{D}_{fp}}-{{D}_{fpc}} \right)}{\pi {{D}_{fpc}}\left[ \sigma \right]}}\) (4-23)
式中:F——连接螺栓承受的总拉力,是压强载荷与剩余锁紧力之和:
\(F=\left( 3\tilde{\ }3.2 \right){{P}_{c\max }}\frac{\pi D_{sc}^{2}}{4}\) (4-24)
(2)螺纹连接计算
通常在结构尺寸有严格限制而结构尺寸不太大时(通常直径小于350mm),常采用螺纹连接结构。
螺纹扣数:
\({{n}_{W}}=1.71\frac{F}{S\cdot {{d}_{iw}}\left[ \sigma \right]}\) (4-25)
螺纹长度:
\({{L}_{N}}=(1.5\tilde{\ }2){{n}_{W}}\cdot S\) (4-26)
4.4.3 密封结构
固定喷管密封常采用“O”形橡胶密封圈端面密封,“O”形横截面直径Dsi可参照表4-3表4-4选取,并且尽量取上限。
表4-3 密封圈尺寸参数选择
|
Dsd(mm) |
<50 |
50~150 |
150~300 |
300~700 |
700~1100 |
|
Dsi(mm) |
2~2.5 |
2.5~3 |
3~5 |
5~7 |
7~9 |
Dsd——“O”形圈直径
Dsi ——“O”形圈截面直径
表4-4 密封圈材料性质
|
密封材料 |
常态性质 |
使用温度范围(℃) |
应用 |
|
|
肖氏硬度 Hs |
扯断强度 MPa |
|||
|
丁晴橡胶 |
90 |
23.5 |
-40~+120 |
耐热、固定或动密封 |
|
硅橡胶 |
69 |
7.0 |
-70~+230 |
耐热、耐寒,固定密封 |
|
氟橡胶 |
90 |
21.4 |
-30~+200 |
耐热,动密封 |
“O”形橡胶密封圈的横截面积:
\({{A}_{1}}=\frac{\pi D_{si}^{2}}{4}\)
密封槽的结构形式有矩形和梯形,其横截面积Az可按下式计算:
\({{A}_{z}}={{B}_{g}}\cdot {{H}_{g}}\)
密封槽的横截面积Az与密封圈的横截面积A1之比应满足下式:
\(\frac{{{A}_{z}}}{{{A}_{1}}}=1.10\tilde{\ }1.15\)
“O”形橡胶密封圈的径向压缩量应满足:
\({{\varepsilon }_{SW}}=\frac{{{D}_{si}}-{{H}_{g}}}{{{D}_{si}}}=0.20\tilde{\ }0.33\) (4-27)
对于侧面密封结构,密封槽的横截面积与密封圈的横截面积之比以及压缩量密闭端面密封小一些,可参照上述计算公式,并结合具体结构确定。
4.4.4 喷管堵盖结构
通常采用的喷管堵盖有金属纯铝堵盖和非金属夹布(丝绸)橡胶软堵盖。
4.4.5 粘接剂和密封剂
粘接剂是指将复合喷管中的各零部件粘接在一起所用的材料,通常使用的粘接剂为环氧聚酰胺胶,如941~944胶、JP-1胶、CJ-9胶等。
密封剂是指为组织燃气通过零件间隙而采用的一种固液混合物,通常在堵盖以前的内型面均匀涂抹一层,如环氧HM-1胶。而在较大的间隙配合部位涂抹密封腻子进行密封。
4.4.6 热防护结构
热防护结构是根据对构成喷管的各种热防护材料进行传热、烧蚀计算,确定喷管各部分热防护材料的合理的几何外形及尺寸,并预示喷管在发动机工作过程中的状态。
(1)喉衬结构
- 结构设计
喉衬位于热环境最为恶劣的部位,通常喉衬内型面尺寸在气动设计中就已经确定,喉衬下游的长度应达到扩张比为1.4~1.6,喉衬上游长度应达到收敛比为2.0以上;
通常,对于石墨喉衬、石墨渗铜喉衬和毡基碳/碳喉衬,当其壁厚较薄,长度较长,即长厚比较大时,喉衬应分段,分段位置取在喉部直线段下游10~30mm之间,分界处采用台阶搭接结构;
通常,喉衬与背壁之间的配合采用锥、柱面配合;锥面配合的角度不宜过大,一般取5°~10°,喉衬与背壁组粘后组成喉衬件,再与喷管壳体采用锥、柱面配合;
钨渗铜喉衬通常要求有石墨背壁,结构设计较为复杂;
喉衬背壁通常采用模压石棉/酚醛材料,具有良好的绝热性能。在结构质量和外部尺寸没有严格限制的条件下,也可采用模压高硅氧、酚醛材料,其绝热性能比模压石棉/酚醛稍差,同样条件下其碳化速率比石棉酚醛大三分之一。
- 烧蚀率估算
通常可利用实际工程试验得到的经验公式估算烧蚀率:
烧蚀量与燃气中的CO2和H2O摩尔分数nCO2和nH2O、燃烧室压强、喉衬材料密度、喉半径以及燃烧室的自由容积的长度等有关,单边径向烧蚀量:
\({{\delta }_{tl}}=0.5946{{\left( {{n}_{C{{O}_{2}}}}+{{n}_{{{H}_{2}}O}} \right)}^{1.02}}{{\rho }_{it}}^{-1}P_{c}^{0.876}L_{i}^{-0.243}R_{t}^{0.076}{{t}_{a}}\) (4-28)
当喉径较大时,喉衬单边径向线烧蚀量
\({{\delta }_{t2}}=1.18{{\left( \frac{{{q}_{m}}}{{{A}_{t}}} \right)}^{2.58}}\rho _{it}^{0.19}{{t}_{a}}\) (4-29)
- 碳/碳喉衬烧蚀计算
含有Al2O3粒子的燃气流过碳/碳喉衬表面时产生烧蚀,烧蚀后的喉衬表面粗糙,高低不平,其烧蚀由两部分组成,一部分是由燃气中含有CO2和H2O氧化组分,在高温下与碳发生化学反应,消融表面的碳造成质量耗损,设定下述量反应方程为一级反应且不可逆:
C+CO2→2CO (4-30)
C+H2O→CO+H2 (4-31)
另一部分是由燃气中含有Al2O3粒子,在运动过程中对喉衬壁面撞击摩擦而引起表面质量耗损。
喉衬轴对称热传导方程:
\({{\rho }_{it}}{{C}_{pt}}\frac{\partial T}{\partial {{t}_{a}}}=\frac{1}{r}\frac{\partial }{\partial r}\left( {{k}_{r}}r\frac{\partial T}{\partial r} \right)+\frac{1}{r}\frac{\partial }{\partial z}\left( {{k}_{z}}r\frac{\partial T}{\partial z} \right)\) (4-32)
下标:r-径向;
z-轴向;
t-喉部。
变量:k-导热系数。
扩散控制的碳无因次质量损耗率方程和碳质量损耗率方程:
\({{B}_{W}}=\frac{{{M}_{C}}}{{{M}_{C{{O}_{2}}}}}{{y}_{_{C{{O}_{2}}}}}+\frac{{{M}_{C}}}{{{M}_{{{H}_{2}}O}}}{{y}_{_{{{H}_{2}}O}}}\) (4-33)
\({{m}_{W}}={{B}_{W}}\frac{\psi {{q}_{or}}}{{{h}_{r}}}\) (4-34)
动力学控制的碳无因次质量损耗率方程和碳质量损耗率方程:
\({{B}_{W1}}=\frac{{{M}_{W1}}}{{\psi {{q}_{or}}}/{{{h}_{r}}}\;}=\frac{{\frac{{{M}_{C}}}{{{M}_{C{{O}_{2}}}}}\frac{{\bar{M}}}{{{M}_{C{{O}_{2}}}}}{{k}_{1}}{{P}_{e}}{{n}_{C{{O}_{2}}}}}/{\left[ \frac{\psi {{q}_{or}}\left( 1+{{B}_{W}} \right)}{{{h}_{r}}} \right]}\;}{1+{{k}_{1}}{{P}_{e}}\frac{{\bar{M}}}{{{M}_{C{{O}_{2}}}}\left( \frac{\psi {{q}_{or}}}{{{h}_{r}}} \right)\left( 1+{{W}_{W}} \right)}}\) (4-35)
\({{B}_{W2}}=\frac{{{M}_{W2}}}{{\psi {{q}_{or}}}/{{{h}_{r}}}\;}=\frac{{\frac{{{M}_{C}}}{{{M}_{{{H}_{2}}O}}}\frac{{\bar{M}}}{{{M}_{{{H}_{2}}O}}}{{k}_{1}}{{P}_{e}}{{n}_{{{H}_{2}}O}}}/{\left[ \frac{\psi {{q}_{or}}\left( 1+{{B}_{W}} \right)}{{{h}_{r}}} \right]}\;}{1+{{k}_{1}}{{P}_{e}}\frac{{\bar{M}}}{{{M}_{{{H}_{2}}O}}\left( \frac{\psi {{q}_{or}}}{{{h}_{r}}} \right)\left( 1+{{W}_{W}} \right)}}\) (4-36)
\({{B}_{W}}={{B}_{W1}}+{{B}_{W2}}\) (4-37)
式中:
M-分子量;
qor-对流换热系数;
k1-反应系数,用Arrhenius式\({{k}_{1}}={{k}_{e}}\exp \left( {-E}/{RT}\; \right)\)计算;
粒子侵蚀方程
比质量侵蚀系数方程:
\({{G}_{P}}=2.988\times {{10}^{-5}}{{D}_{P}}V_{P}^{1.296}{{\left( \sin \alpha \right)}^{1.2}}\) (4-38)
粒子侵蚀质量耗散方程:
(4-39)
Vp—粒子运动速度。
喉衬壁面能量平衡方程,进入壁面净热流:
\({{q}_{nw}}={{q}_{gw}}+{{m}_{s}}\left( {{h}_{sw}}-{{h}_{gw}} \right)+{{m}_{ep}}\left( {{h}_{sW}}-{{h}_{swe}}-\frac{1}{2}u_{swe}^{2} \right)\)
\(+{{\rho }_{P}}{{V}_{P}}\left( {{h}_{pw}}+\frac{1}{2}u_{pw}^{2}-{{h}_{pwl}}-\frac{1}{2}{{u}_{pwl}} \right) \) (4-40)
式中下标:l-Al2O3凝相;
s-固相;
w-壁面;
p-粒子;
g-气相;
变量
h-比焓;
q-热流密度;
u-离开或撞击壁面速度。
由两相流数值模拟给出喷管壁面离散点的粒子和燃气参数,粒子冲击角及质量流率,然后进行对流、辐射热流及粒子热增量计算,首先确定壁面化学烧蚀,其次进行粒子侵蚀计算,根据壁面能量守恒方程,计算喉衬内部温度分布及相应的热应力。
(2)烧蚀层和绝热层的厚度
通常高硅氧/酚醛材料用在低热流、高剪切流部位。高温燃气对壁面进行对流传热,壁面在受热后,一部分热量作为热容吸热,提高壁面材料的温度,一部分热量向材料内部传去,还有一部分热量被壁面辐射给燃气。燃气继续向壁面传递热量时,壁面温度继续升高,当壁面温度达到300℃~800℃时,酚醛树脂热解,热解层转变为碳化层,当碳化层厚度不断增大达到极限厚度后,再增加的壁厚就会被剥蚀掉,而碳化层的厚度保持不变,热解面逐渐后移,原始材料层逐渐减薄。
碳化层厚度可用下式计算:
\({{\delta }_{C}}=\int{_{0}^{t}\frac{{{m}_{hd}}}{{{\rho }_{i}}-{{\rho }_{an}}}dt}\) (4-41)
式中:mhd-材料的热解率,kg/s;
ρi-绝热层材料密度;
ρan-碳化层密度kg/m3。
剥蚀厚度计算用:
\({{\delta }_{d}}=\int{_{{{t}_{n}}}^{t}\frac{{{m}_{hd}}}{{{\rho }_{i}}-{{\rho }_{an}}}dt}\) (4-42)
式中:tn-达到极限碳化厚度时间。
烧蚀层和绝热层厚度可以通过经验算法初步确定。经验算法是指通过对经验数据的估算预测烧蚀深度,加上安全裕度和估算炭化层的的厚度,并加上足够的原始材料厚度来确定烧蚀层和绝热层厚度,从而把温度控制在所规定的结构温度之内。
a 烧蚀率
在设计时将每一种将要选择的材料的烧蚀数据类推后估算出烧蚀率,每一种材料的烧蚀数据是通过最为类似的试验得到的,用于新的条件下,预估的烧蚀率能从下面的经验公式中得到:
\({{r}_{est}}={{r}_{rea}}{{\left( \frac{{{P}_{c}}}{{{P}_{cm}}} \right)}^{0.8}}{{\left( \frac{{{R}_{tm}}}{{{R}_{t}}} \right)}^{0.2}}\) (4-43)
b 烧蚀层和绝热层厚度
预估炭化层厚度
\({{\delta }_{ic}}=a\cdot t_{a}^{b}\exp \left( \frac{c}{{{q}_{0r}}} \right)\) (4-44)
对于碳布/酚醛:a=0.9144,b=0.68,c=-754728.66
对于高硅氧布/酚醛:a=0.7874,b=0.68,c=-1025977.01
冷壁热流由Bartz公式计算可以得到:
\({{q}_{or}}={{\alpha }_{1}}\left( {{T}_{r}}-{{T}_{w}} \right)\) (4-45)
对流换热系数
\({{a}_{1}}=\frac{0.026}{{{({{d}_{t}}\cdot {{10}^{-3}})}^{0.2}}}\left( \frac{{{\mu }^{0.2}}{{C}_{pg}}}{{{\Pr }^{0.6}}} \right){{\left( \frac{{{P}_{c}}{{10}^{6}}}{C*} \right)}^{0.8}}{{\left( \frac{{{d}_{t}}}{Rc} \right)}^{0.1}}{{\left( \frac{{{A}_{t}}}{A} \right)}^{0.9}}\)
\(\frac{1}{{{\left[ \frac{{{T}_{W}}}{2{{T}_{c}}}\left( 1+\frac{k-1}{2}M_{a}^{2} \right)+0.5 \right]}^{0.68}}{{\left[ 1+\frac{k-1}{2}M_{a}^{2} \right]}^{0.12}}}\) (4-46)
恢复温度
\({{T}_{r}}={{T}_{g}}+\sqrt[3]{\Pr }\frac{V_{g}^{2}}{2{{C}_{pg}}}\) (4-47)
c 预估烧蚀厚度
\({{\delta }_{ie}}={{r}_{est}}{{t}_{a}}\) (4-48)
d 安全裕度
烧蚀厚度的安全裕度定义为设计的烧蚀厚度与预估的烧蚀层的厚度之差和预估的烧蚀厚度之比。
\({{f}_{a}}=\frac{{{\delta }_{id}}-{{\delta }_{ie}}}{{{\delta }_{ie}}}\) (4-49)
对于不载人的飞行器发动机喷管,烧蚀深度的安全裕度在喉部、入口段和扩散段小端选择0.2~0.5,在扩散段喉部则选择0.1~0.5;而载人飞行器发动机喷管,各个部位的烧蚀安全裕度均选1。
通常,对于不载人飞行器的发动机喷管,炭化深度不加安全裕度,或加一个很小的安全裕度;而载人飞行器的发动机喷管,炭化的深度的安全裕度选择0.25。
e 绝热层设计总厚度
\({{\delta }_{id}}=\left( 1.2\tilde{\ }2.0 \right){{\delta }_{ic}}+\left( 1.0\tilde{\ }1.25 \right){{\delta }_{ie}}\) (4-50)
4.5 喷管分析
4.5.1 气动热分析
(1)喷管热力学参数计算
按照有关标准热力学参数计算程序可分别计算出冻结流条件下的热力学参数,喷管临界截面和出口截面上的静温、静压,喷管的理论特征速度,理论比冲,理论推力系数,喷管临界截面和出口面凝聚相组分的质量分数、气相燃烧产物的平均摩尔质量、平均相对分子质量、单位质量气相燃烧产物的平均气体常数、定熵指数、比热比、定压比热容、平均的定熵指数等。
(2)喷管效率的分析计算
1)喷管两相流流场计算
喷管两相流流场的分析计算,可采用商业用流动分析软件,从而计算出两相流损失,并可以对喷管多种方案计算,然后优化选择最佳喷管型面参数。
2)喷管效率计算
在固体火箭发动机原理及本书的内弹道计算部分均给出了喷管效率的评定方法,目前多采用SPP经验分析方法,计算的损失应包括:扩散损失,边界层损失,化学动力学损失,潜入损失,两相流损失及喉径的烧蚀引起的损失。
3)喷管温度场分析计算
利用喷管流场计算结果,得出喷管表面温度分布,利用Bartz公式计算壁面个点的对流换热系数,在商业化分析软件中对喷管进行建模,把喷管上述计算的温度边界条件,然后进行网格划分从而进行温度场进行分析。如果表面烧蚀不严重,可以当做固定边界进行温度场计算,计算结果可以得到发动机工作时间各典型时刻喷管壁面的温度场。
4)喷管热应力场分析
将温度计算的结果叠加到强度分析中,同时将流场计算的压强分布的结果施加到边界上,可以得到各个典型时刻的节点应力。
4.5.2 结构件分析
在喷管结构方案完成后,对喷管质量、质量分布曲线、质心和转动惯量进行计算,以确保任务书中的要求,如果没有达到还需要重新设计。现代商业化图形软件均具有质量特性计算功能。
4.6 典型结构设计介绍
本节所讨论的喷管结构设计,主要为支承结构设计,前面讲的热防护设计,也有人把它叫做热结构设计。通俗的说法,支承结构就是喷管壳体。喷管型面设计和热防护设计完成后,喷管的外形就基本确定了,再加上推力向量控制装置,喷管壳体的结构和尺寸也就能确定了。
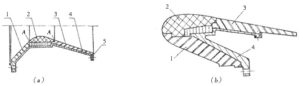
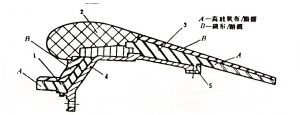
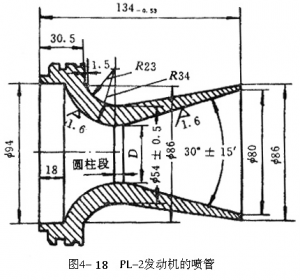
喷管壳体结构常用高强钢、铝合金和复合材料制造,小尺寸喷管的壳体结构包括从连接件到扩散段的全部外壳;大尺寸喷管的壳体结构只到扩散段上游部分的外壳(图4-17)。工作仅几秒钟的小型喷管,可由金属材料制成整体件,如图4-18所示的PL-2喷管。
图4-17 典型喷管结构示意图
(a)非潜入的小型喷管 (b)大型潜入喷管 (c)半潜入喷管
1—收敛段(入口段锥壁)烧蚀绝热层 2—喷衬组件
3—扩散段烧蚀绝热层 4—喷管壳体 5—挡环
关于具有推力向量控制装置的喷管支承结构设计,应按推力向量控制装置的结构和尺寸,连同前面讲的型面计算和热防护设计,具体进行布局,确定结构形状和几何尺寸,典型结构图见§4-6的图4-21~4-23,4-28。
关于喷管壳体壁厚应根据其所受载荷进行计算。喷管壳体所受载荷有:①燃气压强;②热防护层膨胀引起的附加压强;③推力向量控制装置所施加的载荷;④惯性载荷等。
喷管与燃烧室的连接、小型发动机采用螺纹和卡环连接,大型发动机采用法兰螺栓和卡环连接。下面介绍几种特殊喷管结构。
4.6.1 调节喷管
调节喷管是指喷喉面积可进行调节的喷管,多用于全天侯战术导弹发动机。关于喷喉面积调节原理见文献【1】。当调节级数不多时,可采用可换喷管,即按需要更换喉衬,方法较简单,不再赘述。当调节级数较多,甚至需要连续调节时,则
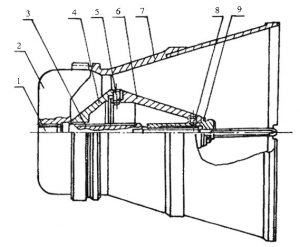
需要采用可调喷管。图4-19所示为一种带调节锥体的可调喷管。
由图4-19可见,可调喷管的收敛段、喉部和扩散段由喷管壳体内壁和调节锥体的外壁组成,二者所形成的最小环形面积就是喷管的临界截面积(喷喉面积)At。调节锥体可沿支承轴前后移动,借以改变喷管临界截面积。
设计时,首先需知喷管的最大和最小喉面积Amax和Amin;选择扩张半角a;通过设计计算确定;颈口半径R1,调节锥体的最大半径R2和调节锥体的支承轴半径r(图4-15)。
图4-19 典型的可调喷管结构
1—支承轴 2—弓形板 3—键 4—前锥体 5—固定螺钉
6—后锥体 7—喷管体 8—螺钉 9—调整螺母
支承轴半径r由强度计算确定。
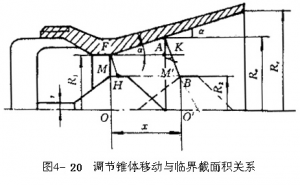
由图4-20可知,调节锥体由里向外移动,临界截面积由小变大。当调节锥体圆柱段移至喷管壳体颈口内时,即调节锥体上M点位于FO截面时,得最小临界截面积
\({A}_{tmin} =\pi \left( R_{1}^{2}-R_{2}^{2} \right)\)
当调节锥体外移至At不能再增时,则此时最小截面积为R1与r所形成的环形面积,亦即喷喉的最大面积
\({A}_{tmin} =\pi \left( R_{1}^{2}-r^{2} \right)\) (4-52)
由调节原理计算出Atmin和Atmax后,即可由式(4-51)和(4-52)确定R1和R2
\({{R}_{1}}=\sqrt{\frac{1}{\pi }{{A}_{t\min }}+{{r}^{2}}}\) (4-53)
\({{R}_{2}}=\sqrt{\frac{1}{\pi }\left( {{A}_{t\max }}-{{A}_{t\min }} \right)+{{r}^{2}}}\) (4-54)
当调节锥体上M点移至M’,此时位移为,由几何关系可推得
\(x=\left( {{R}_{1}}-{{R}_{2}} \right)tg\alpha +\frac{{{R}_{n}}-{{R}_{1}}}{\sin \alpha \cos \alpha }=\left( {{R}_{1}}-{{R}_{2}} \right)tg\alpha +\frac{2\left( {{R}_{n}}-{{R}_{1}} \right)}{\sin 2\alpha }\) (4-55)
若M’点处的临界截面积为At,则
\(x=\left( {{R}_{1}}-{{R}_{2}} \right)tg\alpha +\frac{2\sqrt{R_{2}^{2}+\frac{{{A}_{t}}}{\pi }\cos \alpha -R_{1}^{2}}}{\sin 2\alpha }\) (4-56)
由上式可知,在确定后,即知调节锥体移动距离。反之。由调节锥体的移动距离可知值。因此可于调节锥体的支承轴上刻上刻度,标出相应的临界截面积值。
调节锥体的前锥角,实际上是喷管的收敛角,因此设计时应取得大一些(大于扩张半角a),一般取45°左右;后锥角是形成扩散段的一部分,可取得小一些(接近a值)。由图4-19可见,调节喷管结构复杂,质量大。但是可以连续调节临界截面,使发动机性能更加稳定。
尽管这种结构今天已很少使用,作为HQ-2也已退役,但是这种分析方法在可调发动机中仍然适用。
4.6.2 可延伸喷管
所谓可延伸喷管,是指喷管的扩散段(出口锥)可以向外延伸,增加面积比,提高喷管效益。可延伸出口锥技术是近十多年发展起来的一项新技术,用于上面级发动机可以大幅度提高比冲。一些先进的固体弹道导弹的第二、三级发动机都采用了可延伸出口锥。
固体弹道导弹,尤其是陆基发动发射和潜射导弹,其长度均有限制,因此对各级发动机长度必须加以限制,从而也限制了喷管的扩张比。这样,上面级发动机在高空下工作的性能将得不到充分发挥。为了提高上面级发动机的喷管扩张比,而又不致增加发动机长度,于是提出了可延伸出口锥技术的研究问题 。
所谓可延伸出口锥是将大扩张比的出口锥分成2~3节,最小的一节像普通喷管一样与收敛段和喉衬部分固接在一起,叫做固定出口锥;其余的收藏在固定出口锥的周围,叫做可延伸出口锥。使用时,通过打开机构于发动机点火后(前一级发动机脱开)的某瞬间迅速延伸出去,使喷管扩张比迅速加大。
图4-21所示为MX导弹第三级发动机的可延伸喷管。可延伸出口锥为套筒锥式,平时收缩在固定出口锥的外面,延伸时,靠可延伸作动器将其沿喷管轴向伸展出去,与固定出口锥构成一个完整的扩散段,从而提高扩张比。这种可延伸出口锥的用碳/碳复合材料制成,以减轻质量,提高发动机性能净增益。
图4-21 套筒锥式可延伸出口锥
此外,可延伸出口锥还有多种形式。如气体展开裙式,可延伸出口锥由铌合金箔制成,平时收折于固定出口锥出口处;当发动机工作时靠燃气压强将折叠收藏的裙展开,使喷管扩张比增加。这种裙式可延伸出口锥结构简单、质量轻,但只能延伸一节(图4-22)。图4-23所示为花瓣(折叠板)式出口锥,它由多块(通常为12块)相同弧形板组成,通过铰链将其与固定出口锥后端相连。平时收叠在固定出口锥周围,环向用气动作动环将弧形板串联在一起,延伸时由作动器推动气动作动环,使弧形板只作翻转运动,从而构成一个完整的出口锥。这种可延伸出口锥结构复杂,质量大,比冲净增益小。
图4-22 裙式可延伸出口锥
图4-23 花瓣式可延伸出口锥
4.7 推力向量控制装置的要求和类型
固体火箭发动机的推力向量控制装置与喷管结构密切相关,是导弹控制系统的重要组成部分。它在导弹主动段飞行过程中主要完成三项任务:一是按预定程序提供一定的侧向力,使导弹按预定弹道飞行;二是在导弹姿态或稳定性受干扰时提供一定的侧向力来纠正导弹的姿态,使之稳定地飞行;三是根据指令要求改变飞行轨道。由推力偏斜形成的侧向力使导弹产生控制力矩,用以控制导弹的俯仰、偏航和滚转三个方向的运动。
4.7.1 推力向量控制装置的基本要求
不同用途和射程的导弹对推力向量控制装置的要求不尽相同,但是基于完成控制和稳定任务的一些基本要求是相同的。
(一)最大侧向力应满足导弹要求
推力向量控制装置应满足导弹根据控制和稳定的需要计算出的最大侧向力或推力最大偏斜角的要求。有时还应留有10~20%的余量来确保最大侧向力的要求。通常可动喷管的最大偏斜角为4~8°。
(二)作动力矩要小
推力向量控制装置的作动力矩直接影响伺服机构的功率大小、质量轻重、尺寸大小。所以作动力矩应尽可能地小。
(三)动态特性要好
与伺服机构一起作为控制系统执行机构的推力向量控制装置应具有较好的动态响应特性,控制指令信号与控制力之间应有良好的线性关系,滞后小,响应快。
(四)推力损失应小
大多数推力向量控制装置都会造成轴向推力损失,从而减小导弹射程。为此应尽量减小推力向量控制装置所造成的推力损失。
(五)工作可靠,质量轻,结构紧凑,维护使用方便,易于制造,成本低廉。
4.7.2 推力向量控制装置的分类
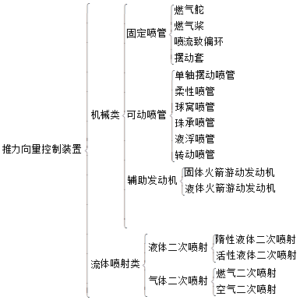
按喷管是否活动,分为固定喷管和可动喷管两类。按工作原理和相应的伺服或供应系统,分为机械和流体喷射类(表4-5)。
表4-5 推力向量控制装置分类
4.7.3 推力向量控制装置的类型选择
由表4-5可见,推力向量控制装置种类很多,如何正确选择。需要导弹总体、控制系统和发动机三方面的设计者密切配合,共同协商确定。选择前应对各种推力向量控制装置性能特点有所了解,这些性能是致偏能力(即侧向力),频率响应,伺服机构的功率及尺寸,轴向推力损失、喷管效率和可靠性等。
(1)致偏能力
是指推力向量控制装置在一定效率下所能达到的最大侧向力或推力最大偏斜角。对于各种可动喷管而言,喷管的摆角基本上就是推力偏斜角;对于流体二次喷射和其它造成部分排气流偏转的推力向量控制装置(如燃气舵、致偏环等)可将侧向力与主推力之比的正弦角作为等效角。尽管有些装置可以达到很大偏斜角,但其效率太低或推力损失太大,装置本身质量大,致使火箭起飞质量大,使用不合理。因此必须强调一定效率下的致偏能力。
(2)频率响应
指推力向量控制装置对控制信号响应的快慢,它直接影响飞行恣态控制的频率。这对于需要快速控制的空-空导弹尤为重要。
(3)伺服机构的功率和尺寸
它反映了推力向量控制装置的作动力矩的大小。作动力矩大,相应的伺服机构功率大,其结构尺寸和质量也大,这关系到发动机的空间布局和发动机的质量比,同时也关系到发动机后封头(或裙)和喷管扩散段的局部承载问题。
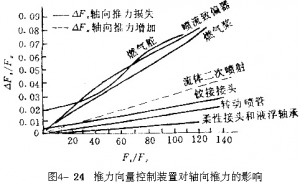
(4)轴向推力的影响
指推力向量控制装置工作时,发动机推力是增还是减。除流体二次喷射装置能使发动机轴向推力有所增加外,其余装置都使轴向推力减少。轴向推力损失会造成发动机总冲降低。为了弥补总冲的损失,势必增加装药量,增加导弹总质量。因此,某些轴向推力损失大的推力向量控制装置不宜用于对质量要求较严的火箭。图4-24比较了几种推力向量控制装置的轴向推力损失,早期使用的燃气舵、燃气桨和致偏环造成的轴向推力损失很大。尤其是燃气舵,即使在舵偏角为零时,也会因舵面阻力造成轴向推力损失。可动喷管中的单摆铰链喷管,除有推力偏斜损失外,还有因分离线处烧蚀及摆动造成的型面不连续而产生的推力损失。
表4-6列举了几种主要推力向量控制装置的性能,它们在一定条件下的性能数据反映了当前技术水平。随着科技发展,某些性能会有提高,尤其是目前广为使用的柔性喷管和具有很大潜力的球窝喷管的性能将会大大提高。燃气桨只做过地面试验。燃气舵和致偏环曾用于某些战术导弹,现在除一些低性能战术导弹还偶尔采用燃气舵外,其它导弹几乎不再使用这两种装置。单轴摆动铰链喷管和转动喷管曾用于四喷管的发动机,但单喷管发动机不再使用。液体二次喷射曾用于北极星、民兵导弹的第二、三级发动机,现在已很少使用。燃气二次喷射在阀门和针栓材料得到解决,并且燃气中不含凝聚相时,也可能得到应用和发展。
表4-6 推力向量控制装置性能比较
|
性 能 装 置 |
推力最大偏斜角 (°) |
最大频率响应(Hz) |
伺服机构功率和尺寸 |
对发动机轴向推力的影响① |
|
单轴铰链摆动喷管 |
15 |
2~5 |
较大 |
—\(\frac{1}{2}F{{\delta }^{2}}\) |
|
柔性喷管 |
15 |
2~5 |
大 |
—\(\frac{1}{2}F{{\delta }^{2}}\) |
|
液浮喷管 |
15 |
10 |
中 |
—\(\frac{1}{2}F{{\delta }^{2}}\) |
|
转动喷管 |
10 |
2 |
较大 |
—2\(F\sin \phi {{\sin }^{2}}\frac{\delta }{2}\) |
|
球窝喷管 |
20 |
2 |
较大 |
—\(\frac{1}{2}F{{\delta }^{2}}\) |
|
燃气舵 |
10 |
10~15 |
小 |
\(-\frac{4{{q}_{a}}{{A}_{ta}}}{{{M}^{2}}-1}[{{\delta }^{2}}+{{(\frac{{{t}_{b}}}{{{B}_{d}}})}^{2}}]\) |
|
燃气桨 |
13 |
小 |
—0.010F |
|
|
喷流致偏环 |
18 |
中 |
\(-\delta R_{i}^{2}\left[ \frac{4}{3}\left( {{p}_{1}}-{{p}_{2}} \right)-\frac{\pi }{2}\left( {{p}_{H}}-{{p}_{a}} \right) \right]\sin \delta \) |
|
|
液体二次喷射 |
6 |
12 |
小 |
+0.3F |
|
气体二次喷射 |
10 |
15 |
小 |
+0.3F |
①只计及推力偏斜损失,均指一个喷管或一对舵面,“+”表示推力增加,“—”表示推力减小。δ及φ角单位为rad,δ是喷管或燃气舵偏转角,φr是转动喷管中心线与旋转轴之夹角。Qa为燃气舵装置的喷管出口面处排气流动压,
- 只计及推力偏斜损失,均指一个喷管或一对舵面,“+”表示推力增加,“—”表示推力减小。δ及φ角单位为rad,δ是喷管或燃气舵偏转角,φr是转动喷管中心线与旋转轴之夹角。Qa为燃气舵装置的喷管出口面处排气流动压,qa=\({{\rho }_{a}}u_{a}^{2},{{A}_{ta}}\)为燃气舵面积,tb为燃气舵翼面厚度,Bd为燃气舵根弦长,ρa和υa 为排气流密度和速度。
本书仅简单介绍单轴摆动喷管、柔性喷管、珠承喷管、液浮喷管和二次喷射推力向量控制装置的设计。
4.8 摆动喷管
表4-5中所示可动喷管中,除转动喷管外,其余都是摆动喷管,这是目前应用较多的一类推力向量控制装置。摆动喷管中除铰链喷管为单轴摆动外,其余均为全轴摆动喷管。所谓单轴摆动,顾名思义,喷管活动体仅能绕某一轴摆动,因此只能提供一个方向的侧向控制力。全轴摆动是指喷管活动体可以绕喷管轴线在360°(圆周)方向上进行摆动,从而可在360°任一方向上提供侧向控制力。
4.8.1 单轴摆动喷管
(1)结构特点
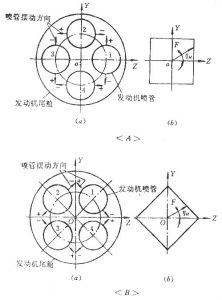
单轴摆动喷管只能提供一个方向的控制力,如需其完成俯仰、偏航和滚转三个方向的运动控制,就必须采用多喷管布置方案。通常采用四喷管布置方案,有“+”形布局和“×”形布局两种布置方案(图4-25)。
图4-25 四喷管布置和摆动情况
A “+”形布局 B “×”形布局
图中Y和Z轴与导弹纵轴X构成直角坐标系。设δ1、δ2、δ3和δ4分别为四个单轴摆动喷管的偏斜角,并规定以逆时针摆动为正,顺时针摆动为负,则对于“+”形布局提供的侧向控制力为
\({{F}_{y}}=\frac{F}{4}\left( \sin {{\delta }_{1}}-\sin {{\delta }_{3}} \right)\). (4-57)
\({{F}_{z}}=\frac{F}{4}\left( \sin {{\delta }_{4}}-\sin {{\delta }_{2}} \right)\) (4-58)
“×”形布局提供的侧向控制力为
\({{F}_{y}}=\frac{F}{4}\left( \sin {{\delta }_{1}}-\sin {{\delta }_{2}}-\sin {{\delta }_{3}}+\sin {{\delta }_{4}} \right)\cos {{45}^{\circ }}\) (4-59)
\({{F}_{\text{z}}}=\frac{F}{4}\left( \sin {{\delta }_{3}}-\sin {{\delta }_{2}}-\sin {{\delta }_{1}}+\sin {{\delta }_{4}} \right)\sin {{45}^{\circ }}\) (4-60)
合成后的侧向控制力和方向角分别为
\({{F}_{s}}=\sqrt{F_{y}^{2}+F_{z}^{2}}\) (4-61)
\({{\eta }_{H}}=t{{g}^{-1}}\left( \frac{{{F}_{y}}}{{{F}_{z}}} \right)\) (4-62)
每个单轴摆动喷管引起的轴向推力损失为
\(\Delta {{F}_{{{x}_{i}}}}=\frac{F}{n}\left( 1-\cos {{\delta }_{i}} \right)=\frac{2F}{n}{{\sin }^{2}}\frac{{{\delta }_{i}}}{2}\). (4-63)
式中n=4,i=1,2,…,4。因此总的轴向推力损失为
\(\Delta {{F}_{x}}=\frac{F}{2}\left( {{\sin }^{2}}\frac{{{\delta }_{1}}}{2}\text{+}{{\sin }^{2}}\frac{{{\delta }_{2}}}{2}\text{+}{{\sin }^{2}}\frac{{{\delta }_{3}}}{2}\text{+}{{\sin }^{2}}\frac{{{\delta }_{4}}}{2} \right)\) (4-64)
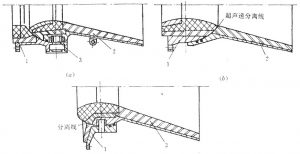
单轴摆动喷管的典型结构如图4-26(a)所示,由固定体、活动体和铰链接头三部分组成。
图4-26 铰链接头单轴摆动喷管结构
(a)亚声速分离线 (b)超声速分离线 (c)潜入式
1—固定体 2—活动体 3—铰链接头
固定体一般以金属法兰与喷管座连接,以凹球台与活动体的凸球台相连。在凹球台的最大直径上,有两个安装转轴的对称孔。
活动体通常以凸球台与固定体凹球台相连,见图4-26(a),(c)。在凸球台最大直径上对称地开有两个安装轴承的孔。活动体的凸球台上一般安装有两道O形密封圈,以防燃气泄漏。活动体上有作动器的铰接支耳。
铰链接头由转轴、轴承、凹球台、凸球台、O形密封圈组成。铰链接头的凹、凸球台的分界线通称分离线,根据分离线的位置不同,将单轴摆动喷管分为亚声速分离线(图4-21(a))、超声速分离线(图4-26(b))和潜入式摆动喷管(图4-26(c))。亚声速分离线虽然密封压强高,易烧蚀,但推力损失小,结构简单,因此早期研制的单轴摆动喷管都为亚声速分离线喷管。潜入喷管的分离线处于气流滞止区,推力损失小,工作可靠性高。
(2)一些关键零、部件的选择
1)轴承
轴承应根据活动体所承受的轴向喷射载荷(活动体内型面上燃气压强所形成的轴向合力)选用,并满足下列要求:
- 体积小,承载能力大;
- 能自动调心,以补偿加工中误差的影响;
- 转动灵活,摩擦力小。
为满足上述要求,通常选用关节轴承。
2)O形密封圈
O形密封圈的截面形状多为“O”形,也可选用“×”形和八角形,以防扭曲变形。O形圈材料有硅橡胶和氟橡胶。在氟橡胶外表面喷涂一层四氟乙烯薄膜,可大幅度降低摩擦系数。
4.8.2 柔性喷管
(1)基本结构和工作原理
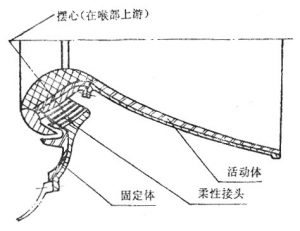
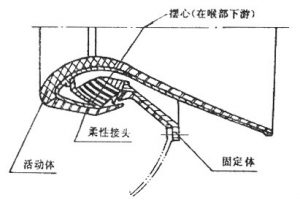
柔性喷管是一种全轴摆动喷管,由固定体、活动体和柔性接头组成,见图4-27和4-28。
柔性喷管的固定体,一端与柔性接头相连,另一端与燃烧室壳体连接。也可以省去固定体与柔性接头的连接,使之成为一个整体,以减轻质量。活动体是由收敛段、喉衬和扩散段组成的完整喷管,其有一法兰与柔性接头相连。由于柔性喷管一般是潜入式喷管因此必须采取热防护措施。例如,在柔性接头受热面安置波纹管式防热套或直接缠绕一层防热套,或者用具有消融烧蚀的碳/碳复合材料做增强件,并在受热面伸出弹性件外一段距离,形成防热栅,以隔绝燃气。
柔性接头的结构是轴对称的,在互成90°的俯仰和偏航平面内安装作动器,可实现喷管的全轴摆动。
图4-27 前摆心柔性喷管
图4-28 后摆心柔性喷管
(2)柔性接头的结构参数
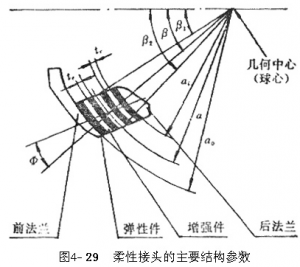
柔性接头的主要结构参数见图4-29。图中a为接头球半径,a1和a0分别为接头球面内径和外径;β为接头角,β1和β2分别为接头内角和外角;φ为锥角;te为弹性件每层厚度,tr为增强件每层厚度,弹性件共有n层,增强件共n-1层。
根据发动机总体设计要求和喷管工作条件选择上述参数并进行接头设计。主要设计条件有:喷管喉径、扩张比、喷管潜入深度、摆心位置、燃烧室压强、喷管外 图4-29 柔性接头的主要结构参数
形轮廓、最大偏斜角、偏斜角速度和角加速度、作动力矩、环境温度和轴向过载等。
接头球半径应尽可能小,通常靠近喉部。
接头角β根据喷管总体布局确定,并受接头强度限制。β的选取范围为45°~70°,β1的选取范围为40°~50°,β2为45°~55°,通常β2-β1=8°~16°。
锥角φ变小,可明显降低增强件和弹性件的应力。当φ>30°时,弹性件应力明显增加。但φ小会增加接头尺寸,通常0<φ<β,一般φ取值为10°~30°。
弹性件的层数和每层厚度根据最大作动力矩和材料的抗剪强度确定。燃烧室压强pc和摆角δ引起的弹性件剪切应力为:
\({{\tau }_{e}}=\frac{\zeta {{p}_{c}}{{t}_{e}}{{k}_{e}}\sin \beta }{a\left( {{\beta }_{2}}-{{\beta }_{1}} \right)}+\frac{0.01745{{G}_{0}}a\delta }{n{{t}_{e}}}\).(kPa) (4-65)
式中ζ=700~1000,对于钢增强件;ζ=1700~2300,对于复合增强件。pc、G0单位为kPa,a、te单位为cm,δ和β为度,而锥角修正系数ke为:
ke=0.528-7×10-3φ+3.26×10-4φ2 (4-66)
材料许用应力为[τ],由式(4-65)有
τe≤[τ] (4-67)
而 nte关系到弹性力矩大小。
增强件每层厚度主要由内圈环向压缩应力来确定。燃烧室压强pc和摆角引起的增强件环向压缩应力为
\({{\sigma }_{r}}=\frac{7150{{p}_{c}}{{k}_{r}}\Omega }{n-1}+\frac{900\delta {{p}_{c}}{{k}_{r}}\Omega }{n-1}\) (4-68)
\({{k}_{r}}=0.1038+0.024\varphi -0.000123{{\varphi }^{2}}\) (4-69)
\(\Omega =\frac{{{\eta }^{0.4}}}{{{t}_{r}}\cos \beta {{\left( {{\beta }_{2}}-{{\beta }_{1}} \right)}^{2}}}\) (4-70)
增强件的材料许用应力为[σ],则由式(4-68)有
\({{\sigma }_{r}}\)≤[σ] (4-71)
(3)柔性喷管的侧向力和作动力矩
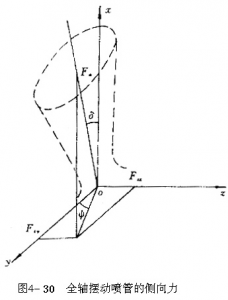
柔性喷管作全轴摆动时的轴线可由空间偏斜角δ和方位角φ二角度参数来确定,如图4-30所示。图中x轴为导弹的纵轴方向,y轴为俯仰轴,z轴为偏航轴,因此可得下列侧向力
\({{F}_{sy}}={{F}_{a}}\sin \delta \sin \varphi \) (4-72)
\({{F}_{sz}}={{F}_{a}}\sin \delta \cos \varphi \) (4-73)
柔性喷管摆动所需的作动力矩包括很多因素,主要的是弹性力矩Msp和摩擦力矩Mf。
弹性力矩是摆动力矩中最大的一项,是弹性件受剪切变形产生的一种反抗力矩。弹性力矩的比力矩为
\(\frac{{{M}_{sp}}}{\delta }=\frac{2.1\times {{10}^{-4}}{{G}_{0}}\rho _{0}^{3}\rho _{i}^{3}}{\rho _{0}^{3}-\rho _{i}^{3}}\left[ I\left( {{\beta }_{2}} \right)-I\left( {{\beta }_{1}} \right) \right]\)(N·m/(°)) (4-74)
式中G0为弹性材料在工作温度下的剪切模量(kPa),由试验确定
\({{\rho }_{0}}=a+\frac{n{{t}_{e}}}{2}\) (cm)
\({{\rho }_{i}}=a\text{-}\frac{n{{t}_{e}}}{2}\) (cm)
I(β1)和I(β2)是与接头内角β1和外角β2相对应的积分值,见表4-5,也可用下式计算
\(I\left( {{\beta }_{i}} \right)=\frac{\pi }{3}-\frac{\pi }{4}\left( \cos {{\beta }_{i}}+\frac{1}{3}{{\cos }^{3}}{{\beta }_{i}} \right)\) i=1,2 (4-75)
由式(4-74)可知,弹性力矩近似与接头球半径a的三次方成正比,所以a应选得小一些。在其它参数一定情况下,增加nte值可减小弹性力矩。
由于弹性件的橡胶材料具有粘滞特性,试验表明柔性接头具有粘滞摩擦力矩和库仑摩擦力矩,其经验公式为
\(\frac{{{M}_{f}}}{\delta }=\left( 4\times {{10}^{-3}}+2.4\times {{10}^{-6}}{{p}_{1}} \right)\left( 1+7.5\times {{10}^{-3}}\frac{d\delta }{dt} \right){{a}^{3}}{{\sin }^{3}}\beta ,\left[ \frac{N.m}{\left( {}^\circ \right)} \right]\) (4-76)
式中p1为试验压强(kPa)。
表4-7 β角的积分值I(β)
|
β(°) |
I(β) |
β(°) |
I(β) |
β(°) |
I(β) |
β(°) |
I(β) |
|
20 |
0.0906 |
31 |
0.2067 |
42 |
0.3531 |
53 |
0.5148 |
|
21 |
0.0995 |
32 |
0.2189 |
43 |
0.3674 |
54 |
0.5298 |
|
22 |
0.1088 |
33 |
0.2315 |
44 |
0.3818 |
55 |
0.5448 |
|
23 |
0.1184 |
34 |
0.2442 |
45 |
0.3963 |
56 |
0.5599 |
|
24 |
0.1283 |
35 |
0.2572 |
46 |
0.4109 |
57 |
0.5749 |
|
25 |
0.1386 |
36 |
0.2704 |
47 |
0.4256 |
58 |
0.5899 |
|
26 |
0.1492 |
37 |
0.2838 |
48 |
0.4403 |
59 |
0.6048 |
|
27 |
0.1601 |
38 |
0.2973 |
49 |
0.4551 |
60 |
0.6198 |
|
28 |
0.1713 |
39 |
0.3110 |
50 |
0.4700 |
61 |
0.6348 |
|
29 |
0.1828 |
40 |
0.3249 |
51 |
0.4849 |
62 |
0.6499 |
|
30 |
0.1946 |
41 |
0.3389 |
52 |
0.4999 |
63 |
0.6649 |
正常设计工作压强下,弹性力矩占总力矩50%以上,摩擦力矩占15~30%
柔性接头总力矩的比力矩经验式为
\(\frac{M}{\delta }=A\frac{{{M}_{sp}}}{\delta }+B\frac{{{M}_{f}}}{\delta }\) (4-77)
式中A和B由试验确定的大于1的两个经验系数。
(4)柔性喷管的特点及应用
柔性喷管具有以下特点:无分离线,偏转能力大,推力损失小,密封性好,响应快,可靠性高。因此,柔性喷管从海神导弹第一、二级发动机采用以来,已迅速推广用于各种导弹发动机,如MX、三叉戟等导弹发动机均采用柔性喷管。
4.8.3 液浮喷管
(1)工作原理
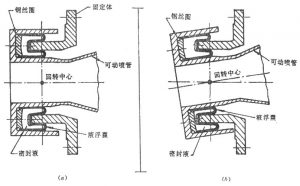
液浮喷管的固定体和活动体是用液浮轴承连接的,这种充满液体(硅油)的轴承在受到喷射载荷作用时,轴承内的液体压强上升到高于燃烧室压强,从而起到对活动体的支撑和对燃气的密封作用。其结构原理如图4-31所示。
液浮轴承是一个容积不变的、由织物增强的胶囊和金属构件组成的密封内腔、囊内充满硅油之类的不可压缩液体,依靠囊的卷边滚动,可使喷管作全轴摆动。当喷管活动体受到燃烧室压强引起的喷射载荷作用时,囊内液体压强上升,产生作用于活动体上的力与喷射载荷平衡。此时活动体犹如借助液浮囊浮在平衡位置上,液浮喷管亦因此而得名。
液浮喷管摆动时,液体在液浮轴承内腔流动,保持密封内腔容积不变,只是囊的卷边发生滚动和剪切变形。喷管摆动时,囊内液体流动和囊的卷边滚动会产生反抗力矩,这种力矩就是液浮喷管摆动时所需要的作动力矩。
(2)液浮轴承的基本结构形式
液浮轴承的囊是在人造橡胶(如氯丁橡胶中间夹一层或多层尼龙布或其它强力织物,通过加热模压而成的,增强织物用来增加囊的承压能力,橡胶起密封作用)。囊的有卷边的一侧用沿圆周方向均布的若干螺钉安装在固定体上;囊的另一侧两个端头用两个钢丝圈加强压边,并用压板压紧,压板用螺钉与活动体连接。
图4-31 液浮喷管的结构原理图
(a)未偏摆时 (b)偏摆后
液浮囊的形状除图4-31所示的柱形囊(侧壁为柱面)外,还有锥形囊(侧壁为锥面)和球形囊(侧壁为球面)。
图4-32 整体囊和局部囊
(a)整体囊 (b)局部囊
根据液浮轴承总体结构和囊的成型工艺,可将囊设计成整体囊和局部囊(图4-32)。前者工艺简单,只需一套成型模具。后者可将内、外囊分开,选用不同材料制造,以满足强度要求;但需要两套模具,还增加了囊的密封部位。
液浮喷管的优点是:①作动力矩小;②液浮轴承既是支撑件,又是密封件,它不受燃气直接冲刷,热防护比较简单。其缺点是:摆心飘移较大,囊内液体易渗漏,尤其是长期贮存后,胶囊老化,更易产生渗漏现象。
液浮喷管的侧向力计算与其它全轴摆动喷管一样。
4.8.4 珠承喷管
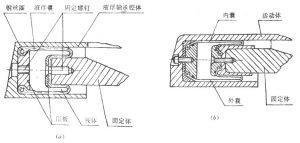
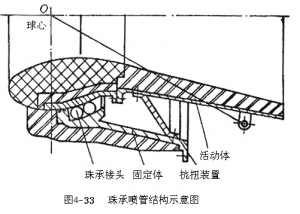
球承喷管是一种以一排或多排滚珠支承喷射载荷、用一道或两道密封圈档住燃气、能够在360°方向上提供侧向控制力的全轴摆动喷管。该喷管的典型结构如图4-33所示,由固定体、活动体和珠承接头构成。
固定体一般以金属法兰与燃烧室后接座相连接,多采用倒锥结构,以便使喷管部分地潜入燃烧室内。连接活动体的部分是凹球台结构,在球窝内装有两道O形密封圈。活动体与固定体连接部分为凸球台结构,在扩张 段有两个互成90°的支耳与伺服机构作动器连接,可在360°方向上作全轴摆动。
球承接头由固定体的凹球台、活动体的凸球台、滚珠和滚珠保持架组成。球台金属表面应有很高的硬度,以承受滚珠传递的接触载荷;应有较高光洁度,以减小摆动时的摩擦;尺寸精度应高,以保持承载均匀。
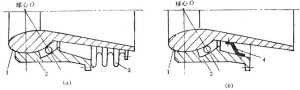
珠承喷管不具有抗扭转的能力,因此需专门设计一抗扭装置,常用抗扭装置有金属筒波纹管和防扭夹布胶囊等(图4-34)。
图4-34 防扭装置示意图
(a)波纹管 (b)夹布胶囊
珠承喷管多为潜入式喷管,固定体与活动体之间的分离线通常设计在气流滞止区。这样既减小烧蚀,还减少了氧化铝粒子进入球台间隙引起摩擦力矩激增的可能性。根据接头球心(摆动中心)位于喷喉的前或后,而分为前支点和后支点珠承喷管。关于珠承喷管的具体设计和计算,详见文献[2]。
4.9 流体二次喷射装置
在喷管扩散段上某一位置向喷管中的超声速燃气流(主流)横向射入另一股流体(二次流),从而产生控制火箭飞行所需要的侧向力。流体二次喷射推力向量控制装置具有频率响应快、效率高、喷管结构简单(固定的)和发动机比冲损失小等优点。
4.9.1 液体二次喷射
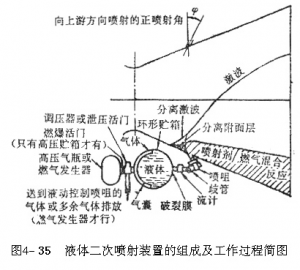
二次流为液体的叫做液体二次喷射,其装置由喷射器、伺服机构、贮箱及增压系统组成,具体组成和工作原理如图4-35所示。
液体二次喷射装置的工作过程如下:当高压气瓶或燃气发生器所产生的高压气体,通过调压器降压,并在进入工质贮箱时等于所要求的压强;通过气囊或直接将液体工质挤压出贮箱,经由导管进入喷射器。当伺服机构接到指令时,喷射器的针栓在伺服机构作动器作用下打开喷射器的喷嘴,使工质经过喷嘴进入喷管扩散段。喷射出的液体工质微滴碎裂、蒸发、并与主气流混合或发生反应,从而使主气流受阻,产生分离激波或冲击波,激波后流速降低压强升高,在扩散段壁面上形成不对称压强分布。因此液体二次喷射产生的侧向力基本上由两部分组成:一是液体在垂直喷管轴线上的反作用力Fs1,一是分离区、激波区上压强在垂直喷管轴线上的合力Fs2,总的侧向力
F=Fs1+Fs2 (4-78)
借助于总的侧向力F即可实现火箭的俯仰和偏航控制。如果采用四喷管,相对二喷管差动喷射,还可实现滚控。
液体二次喷射装置除具有流体二次喷射的共同优点外,还具有:①液体工质在环境温度下贮存和使用,管路和喷射器不受高温燃气烧蚀,所用材料只要满足工质要求即可;②液体工质密度大,且便于贮存。
液体二次喷射装置的不足处是:①所能提供的侧向力有限,一般小于发动机主推力的10%,当要求大侧向力时,需加大喷射流量,这不仅增加工质的携带量,而且降低喷射效率。②装置结构复杂,勤务处理不便。
液体二次喷射的常用工质为氟里昂-114B2和含62%过氯酸锶的水溶液,二者性能见表4-8。
表4-8 两种常用液体喷射工质性能
|
工 质 性 能 |
氟里昂-114B2 |
62%过氯酸锶水溶液 |
|
侧向比冲(N·s/kg) |
680~1 570 |
1 470~2 600 |
|
密度(kg/cm3) |
2.15 |
1.79 |
|
冰点(℃) |
-112 |
-63 |
|
贮存稳定性 |
稳定 |
密封贮存稳定 |
|
与金属相容性 |
无水贮存时无腐蚀 |
仅对不锈钢、铝合金无腐蚀 |
|
与非金属相容性 |
除聚四氟乙烯外,对其它非金属材料均有渗透,溶涨现象 |
好 |
|
毒 性 |
低、微毒 |
低,微毒 |
4.9.2 气体二次喷射
二次流为气体的叫做气体二次喷射,气体二次喷射比液体二次喷射的侧向比冲高,尤其是从燃烧室引入的燃气流,其侧向比冲更高。
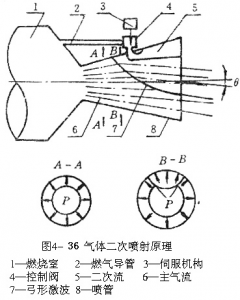
在喷管扩散段射入第二股气流后,这股二次气流迅速膨胀,并转折附壁面流动,对靠近喷射口一侧的主气流形成障碍,在喷射口上游产生一弓形激波,如图4-36所示。经过弓形激波后的那部分主气流发生方向偏斜,导致如图所示的整个喷管排气流离开喷管出口面时不再通过喷管中心线而是偏斜δ角,造成推力偏斜,其横向分力即为侧向控制力。
在喷管扩散段适当位置喷射二次气流,可以得到所需侧向力。调整二次流某些参数,如流量,可以改变激波强度和角度,改变主气流偏斜程度,达到控制侧向力大小的目的。只要在固定喷管的4个象限内各配置一套气体二次喷射装置,即可实现俯仰和偏航所需要的控制力,甚至可以提供滚控所需侧向力。
根据二次气流的来源,气体二次喷射装置可分为:
(1)燃气二次喷射装置
该装置喷射的二次气流取自发动机燃烧室中的高温燃气。其优点是该装置的零、部件少,质量轻,效率高。缺点是管路和阀门必须能承受高温燃气烧蚀,而燃气中的氧化铝沉积可能堵死管道和阀门,引出的燃气既受燃烧室压强波动影响,反过来又影响燃烧室压强。
(2)低温燃气二次喷射装置
该装置用的二次气流来自专门设置的燃气发生器,这种燃气发生器中的推进剂燃烧温度较低,约800~1 300K,仅及发动机燃气温度的1/3~1/2;且燃气中不含金属氧化物,无沉积现象;燃气压强无波动。但是由于二次气流的温度低于主气流当地温度,与主气流进行热交换时会发生吸热反应,因此该装置效率略低一些。
(3)空气二次喷射装置
该装置的二次气流取自发动机周围的空气,由安装于喷管外围的倒锥形集气罩、喷射器和伺服机构组成。装置的结构简单、质量轻、造价低。但只适用于在大气层中飞行的固体火箭发动机,并且随火箭速度加快,空气密度下降,而不能提供足够的侧向力。
气体二次喷射装置尚未见用于正式型号的发动机。
4.10 推力终止装置设计
固体火箭发动机的推力终止是其推力控制的内容之一。当弹道导弹达到所需主动段终点速度,或者航天飞行器完成入轨飞行时,过去大多采用准确地终止发动机的推力(目前,有的已采用末速度修正的办法来解决),以保证导弹或飞行器按预定的弹道或轨道飞行,确定弹着点精度或轨道精度。
固体火箭发动机的推力终止通常是由打开燃烧室前封头上的反喷管,以产生反推力,使发动机的轴向推力降为零或为负值来实现的。本节只介绍反喷管推力终止装置。
4.10.1 反喷管推力终止装置设计要求
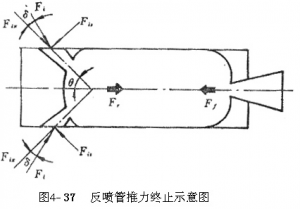
图4-37给出反喷管推力终止示意图,图中Ff为发动机主喷管产生的推力;Fi为单个反喷管产生的推力;设发动机头部有N个反喷管,则所有反喷管产生的轴自反推力
\({{F}_{r}}=N{{F}_{i}}\cos \left( \theta +\delta \right)\)
θ为反喷管轴线与发动机轴线夹角,δ为Fi与反喷管轴线的夹角。推力终止时,发动机的负推力:
\({{F}_{n}}={{F}_{r}}-{{F}_{f}}=N{{F}_{i}}\cos \left( \theta +\delta \right)-{{F}_{f}}\) (4-79)
当Fn≥0时,就会实现发动机推力终止。
通常导弹总体对反喷管推力终止装置提出以下设计要求:
(1)接到推力终止指令后应能及时解锁并打开反喷管通气道;
(2)反喷管产生的轴向反推力必须瞬时建立,并在得到负推力后持续一定时间;
(3)反喷管解锁和打开的同步性要好;
(4)结构简单、易于加工、可靠性高、安全性好。
4.10.2 确定反喷管的喉径
反推力的大小除与反喷管的数量和在发动机头部的布局、推进剂性能、反喷管面积比等因素有关外,主要由反喷管的喉径决定。
(1)燃烧室平衡压强
反喷管打开后,假设推进剂燃速仍服从指数方程,且流动在反喷管喉部壅塞,此时燃烧室中的质量连续方程为
\(\dot{m}={{\rho }_{P}}{{A}_{b}}a{{P}_{c}}^{n}-\frac{{{P}_{c}}}{{{C}^{*}}}\left( {{A}_{t}}+N{{C}_{d}}{{A}_{rt}} \right)\) (kg/s) (4-80)
式中ρp为推进剂密度(kg/m3);Ab为药柱燃面(m2);a为燃速系数;n为压强指数;Pc为燃烧室压强(Pa);At为主喷管喉面积(m2);Art为单个反喷管喉面积(m2);Cd为反喷管喉面收缩系数;C*为特征速度(m/s)。
假设燃气为理想气体,且反喷管打开过程中C*=const,则式(4-80)可改写为
\(\frac{d{{P}_{c}}}{dt}\frac{{{V}_{c}}}{{{\Gamma }^{2}}{{C}^{*2}}}={{\rho }_{P}}{{A}_{b}}a{{P}_{c}}^{n}-\frac{{{P}_{c}}}{{{C}^{*}}}\left( {{A}_{t}}+N{{C}_{d}}{{A}_{rt}} \right)\) (4-81)
式中Vc为反喷管打开时刻的燃烧室自由容积(m3);Γ为比热比k的函数。在反喷管打开的短时间内,n、C*、a、Ab、Vc均不随压强Pc变化,则积分上式可得反喷管打开后燃烧室压强的衰减方程:
\({{p}_{c}}={{\left\{ \frac{{{A}_{t}}}{{{A}_{t}}+N{{C}_{d}}{{A}_{rt}}}+\frac{1-\frac{{{A}_{t}}}{{{A}_{t}}+N{{C}_{d}}{{A}_{rt}}}}{\exp \left[ t{{C}^{*}}{{\Gamma }^{2}}\left( 1-n \right)\left( {{A}_{t}}+N{{C}_{d}}{{A}_{rt}}/{{V}_{c}} \right) \right]} \right\}}^{\frac{1}{1-n}}}{{p}_{0}}\) (4-82)
式中t为自反喷管打开时燃烧室压强开始下降算起的时间(s);P0为反喷管打开时的燃烧室压强。
由式(4-82)可见,随t增长,右式中大括号内第二项趋近于零,事实上,这一过程是很短的。反喷管打开后第二工作状态下的燃烧室平衡压强为
\({{p}_{c2}}={{\left( \frac{{{A}_{t}}}{{{A}_{t}}+N{{C}_{d}}{{A}_{rt}}} \right)}^{\frac{1}{1-n}}}{{p}_{0}}\) (4-83)
(2)斜切口喷管的推力系数
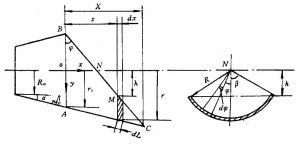
为使导弹具有良好的气动外形,反喷管出口端面常被切成平行于发动机轴线的所谓斜切口喷管(参见图4-38)。为便于反喷管的密封和打开,通常反喷管无收敛段,且喉部有一段较长的圆柱段,有时就是一个圆筒。由于喷管斜切,上游压强p到达图4-38所示斜切口B点处突然降至环境压强Pa,其超声速气流在出口处便发生膨胀偏转,推力方向也将产生δ角的偏转,并产生侧向力Fis(参见图4-37)。因此,斜切口喷管的推力系数的计算不同于普通轴对称喷管的推力系数计算。
计算斜切口喷管推力系数的方法很多。当斜切角较小时,一般采用压强数值积分法;当面积比较小,甚至为斜切口圆筒时,采用二元膨胀波法。本节只介绍压强积分法。
如图4-38所示,当B点发出的膨胀波达不到斜切喷管壁面AC上时,斜切口内的气流参数与相应的普通喷管的参数相同。此时斜切段所产生的推力可由作用于斜切段上的压强积分得到。在斜切口壁面(x,φ)处取一微元面积
\(dA=r\cdot d\varphi \cdot dL=\frac{rd\varphi dx}{\cos \alpha }\)
式中为斜切口喷管的扩张半角,r为x处的圆弧半径。设x处气流压强为p,环境压强为pa,压强合力为\(\left( p-{{p}_{a}} \right)dA\),其在x轴上的分量即为轴向微元推力:
\(d{{F}_{x}}=\left( p-{{p}_{a}} \right)dA\sin \alpha \)
在y轴的分量即为侧向微元推力
\(d{{F}_{y}}=\left( p-{{p}_{a}} \right)dA\cos \alpha \)
dFy=(P0-Pa)dAcos cosψ
因此,斜切部分的轴向和侧向推力为
\(\Delta {{F}_{x}}=2\iint\limits_{A}{(p-{{p}_{a}})\sin a\mathop{{}}^{{}}dA=2\int{_{0}^{X}\overset{{}}{\mathop{{}}}\,\int{_{0}^{\beta }(p-{{p}_{a}})rtgadxd\phi }}}\)
\(\Delta {{F}_{x}}=2\iint\limits_{A}{(p-{{p}_{a}})\sin a\mathop{{}}^{{}}dA=2\int{_{0}^{X}\overset{{}}{\mathop{{}}}\,\int{_{0}^{\beta }(p-{{p}_{a}})rtgadxd\phi }}}\)
\(\text{=}2tg\int_{0}^{X}{\left( p-{{p}_{a}} \right)r\beta dx}\)
\(\Delta {{F}_{y}}=2\iint\limits_{A}{\left( p-{{p}_{a}} \right)}\cos \alpha \cos \varphi dA\)
\(=2\int{_{0}^{X}\int{_{0}^{\beta }}(p-{{p}_{a}})rdx}\cos \phi d\phi \)
\( =2\int{_{0}^{X}}(p-{{p}_{a}})r\sin \beta dx \) (4-84)
因此,斜切口喷管的轴向推力系数CFx为
斜切喷管多侧自推力系数
\({{C}_{Fx}}=\frac{{{F}_{x}}}{{{A}_{rt}}{{p}_{c}}}=\frac{{{F}_{0}}+\Delta {{F}_{2c}}}{{{A}_{rt}}{{p}_{c}}}\)
=\(\frac{{{F}_{0}}+2tag\int{_{0}^{x}(P-{{P}_{0}})rPda}}{\pi r_{rt}^{2}{{P}_{c}}}\)
即
\({{C}_{Fx}}={{C}_{F0}}+\frac{2tg\partial }{\pi }\int{_{0}^{\frac{\lambda }{{{R}_{rt}}}}}(\frac{P}{{{P}_{c}}}-\frac{{{P}_{a}}}{{{P}_{c}}})\frac{r}{{{r}_{rt}}}\beta d(\frac{\lambda }{{{r}_{rt}}})\) (4-85)
推力偏斜角
\(\delta \text{=}t{{g}^{-1}}\frac{{{C}_{{{F}_{y}}}}}{{{C}_{{{F}_{x}}}}}\) (4-86)
为了计算CFx和CFy需知p/pc及β。
p/pc为x截面处气流压强p与燃烧室压强pc之比。因为斜切口内的气流参数与相应的普通喷管的气流参数相同,所以p/pc应满足相应的普通喷管的压强比和面积比的关系,即满足

显见,当0≤x≤X时,0≤β≤π。
注意,对于反喷管,需考虑喉面收缩系数Cd,因此式(4-87)~(4-89)中Art应为CdArt。Cd是小于1的系数,海神导弹飞行试验数据表明Cd≈0.9,对于不同的发动机,其值波动较大。
反喷管打开后,发动机的轴向反推力为
\({{F}_{r}}=N{{C}_{d}}{{A}_{rt}}{{p}_{c2}}\frac{{{C}_{Fx}}}{\cos \delta }\cos \left( \theta +\delta \right)\) (4-90)
由式(4-79)和(4-90)确定反喷管喉径。
4.10.3 反喷管的打开机构
反喷管的打开方法主要有两种,一是滚珠锁紧爆炸螺栓打开机构,一是聚能切割打开机构。
图4-39所示为滚珠锁紧爆炸螺栓打开机构构成的反喷管推力终止装置。这种装置的结构比较简单,动作迅速、可靠。它用挡板、滚珠和压紧螺母锁紧,通过爆炸螺栓起爆解锁,打开反喷管。
图4-40所示为聚能切割打开机构组成的反喷管推力终止装置,该装置尤适用于纤维缠绕壳体,利用聚能药条直接切割反喷管堵盖或燃烧室前封头,以打开反喷管。这种装置具有质量轻、打开时间短、同步性好、安全可靠等优点。
上述两种打开机构的反喷管推力终止装置均已用于型号发动机,如北极星末级发动机和潘兴-2末级发动机。

1-斜切口套筒 2-起爆管 3-反喷管 4-滚珠5-挡板 6-压紧螺母 7-反喷管座 8-绝热套 9-滑板 10-充填塑料11-药柱 12-绝热层
图4-40 聚能切割推力终止装置
1-护套压紧件 2-药条护套 3-聚能药条4-弹性反喷管 5-缠绕壳体 6-绝热层
4.11 喷管分离流动计算
喷管在过膨胀状态下会出现分离流动,目前,一般将流体力学的研究和分析手段分为理论分析、实验研究及数值计算三种。本节对喷管分离流动的理论基础进行了综述,并给出传统喷管的设计方法。
4.11.1 喷管的工作状态
一定面积比的喷管要得到一定马赫数的超音速气流,还要由气流的总压和外界外压Pb来决定。一个设计好了的喷管,不能始终在设计压强下工作。火箭发动机从海平面一直工作到环境压力很低的高空。这个过程中,无论是燃烧室压力还是外界外压都是在不断变化的。
在以下假定条件下,气流总压不变,外界外压改变时,分析喷管内的工作状态。
- 流动是一维定常的。
- 与外界无热量,流量和功的交换,并不计摩擦作用。
- 气体的化学成分不变,相应的气体常数也不变。
当面积比\({{\text{A}}_{\text{e}}}\text{/}{{\text{A}}_{\text{t}}}\)给定后
由\(q({{\lambda }_{e}})={{(\frac{k+1}{2})}^{\frac{1}{k-1}}}{{\lambda }_{e}}{{(1-\frac{k-1}{k+1}{{\lambda }_{e}}^{2})}^{\frac{1}{k-1}}}=\frac{{{A}_{t}}}{{{A}_{e}}}\) (4-91)
可以求出,式中为燃气的绝热指数;(此时求出两个,对应的为超音速流,对应的为亚音速流)
\({{M}_{e}}={{\left( \frac{\frac{2}{k+1}\lambda _{e}^{2}}{1-\frac{k-1}{k+1}\lambda _{e}^{2}} \right)}^{\frac{1}{2}}}\) (4-92)
\(\pi ({{\lambda }_{e}})={{\left( 1-\frac{k-1}{k+1}\lambda _{e}^{2} \right)}^{\frac{1}{k-1}}}\) (4-93)
从而 \({{p}_{e}}={{p}^{*}}\pi ({{\lambda }_{e}})\),记这样求得的压强为\({{p}_{1}}\),则\({{p}_{1}}={{p}^{*}}\pi ({{\lambda }_{e}})\)。
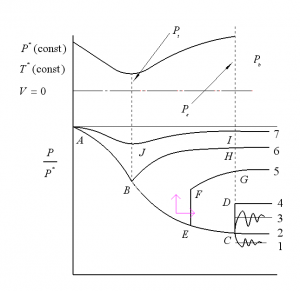
随着反压的增大,喷管的工作状态分为四种情况,如下图4-41所示:
图4-41 喷管的工作状态[34]
(1)欠膨胀及完全膨胀状态\({{p}_{b}}\le {{p}_{1}}\)
当\({{\text{p}}_{\text{b}}}\text{}{{\text{p}}_{\text{1}}}\)时,气流在喷管内没有得到完全膨胀,在出口截面上气流压强高于外界反压,气流流出喷管后,继续膨胀,其压强分布如图中曲线1所示,C点对应的压强就是p1此时外界反压不能影响管内流动,因为外界反压使气流膨胀,膨胀波所造成的扰动是以音速传播的,而气流是超音速的,所以管内流动不受外界扰动的影响。
当pb=p1时,气流到喷管出口截面刚好得到完全膨胀,此时叫做完全膨胀状态,又称设计状态。如图中曲线2所示。
(2)喷管出口外激波\({{\text{p}}_{\text{1}}}\text{}{{\text{p}}_{\text{b}}}\le {{\text{p}}_{\text{2}}}\)
当反压pb>p1时,出口界面气流压强小于外界反压,因此,气流在出口处产生激波。如图中曲线3所示,气流通过激波把压强提高到与反压相等。此时激波的强度由压强比pb/p1决定,当外界反压pb比p1大得不多时,喷管在出口产生弱的斜激波。随着压强比pb/p1的增大,激波强度不断增强,激波角β不断增大。当pb达到p2时,激波角β等于,激波便变成贴在喷管出口的正激波,对应的是图中曲线4。由于正激波刚好贴在出口,波前马赫数为Me,由正激波关系式可求得
\({{p}_{2}}={{p}_{1}}(\frac{2k}{k+1}M_{e}^{2}-\frac{k-1}{k+1})\) (4-94)
可以看出,p2的数值由p1和Me确定,但p1和Me是与膨胀比\({{A}_{e}}/{{A}_{t}}\)有关的,所以压强p2也是一个与\({{A}_{e}}/{{A}_{t}}\)有关的数据。
在\({{p}_{1}}<{{p}_{b}}\le {{p}_{2}}\)这个范围内,超音速气流通过出口外激波提高压强达到与反压相平衡,这个过程发生在喷管出口截面以外,同样对管内流动不能造成影响。
(3)喷管内部激波\({{p}_{2}}<{{p}_{b}}\le {{p}_{3}}\)
当反压大于气流在喷口处产生的正激波所达到的压强p2,高的反压迫使气流在喷管出口之前产生激波以提高压强。如果气流在管内产生激波,这种激波可近似地看作正激波,波后是亚音速气流。通过这种降速增压的过程,使得气流到喷管出口截面上的压强与反压相等。管内的压强如图中曲线5所示。随着反压得继续提高,使得激波位置向喉部推进,当反压提高到p3,管内激波恰好移动到喉部。
此时压强如图曲线6所示,喷管内是亚音速气流在收敛段加速,到喉部为音速,进入扩散段又减速,直到出口截面上气流压强等于反压p3,\({{p}_{3}}={{p}^{*}}\pi ({{\lambda }_{esub}})\)。
当反压在p2和p3之间变化时,管内流动只在最小截面之后有一段超音速流,然后经激波变为亚音速流。因而,反压变化产生的扰动可进入管内亚音速流区域,从而改变激波之后喷管的流动。
(4)管内全亚音速流\({{p}_{b}}>{{p}_{3}}\)
若反压高于p3,则整个喷管内部都是亚音速流,最小截面不再是临界截面,该截面上的气流不是音速,变成亚音速流动。出口截面上的速度不再与面积比有关,而是由压强比\({{p}_{b}}/{{p}^{*}}\)决定,此时,外界的扰动可以影响整个喷管内的流动。压强分布如图曲线7所示。
4.11.2 流动分离状态
以上的讨论都是理想气体在几何管道中的流动情况,实际流动的气体都是有粘性的。粘性不仅会减少通过喷管的流量,影响气流参数的变化,还会影响喷管的气流结构。
边界层是靠近物体表面有很大速度梯度的流体层。在此薄层中,气流速度从物面上的零迅速增大到接近无粘流动计算的速度。
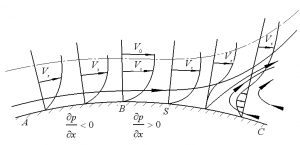
参看图4-42,设气流绕曲壁为平面运动,在截面B前,边界层外边界上的压强梯度\(\frac{\partial p}{\partial x}<0\)即沿X方向压强是减小的,由于在边界层内沿着壁面的法线方向压强是不变的,即\(\frac{\partial p}{\partial y}=0\)。因此,在边界层内部,截面B之前,流体微团为减压加速流动。尽管为了克服摩擦阻力要消耗一部分动能,但因为是加速流动,故不会发生气流从壁面的分离。在截面B之后,边界层外边界上的压强梯度\(\frac{\partial p}{\partial x}>0\),即沿X方向压强是增大的。因而在边界层内部,截面B之后,流体微团为扩压减速流动。在靠近壁面处的流体微团由于克服相当大的摩擦阻力而消耗掉的动能较多。因此,在截面B之后的一段距离内,靠近壁面处的流体微团的速度由于双重的阻滞作用而很快地减小。到了S截面,靠近壁面的流体速度为零,S点称为分离点。S点以后,在逆压梯度的作用下,壁面附近的流体微团作逆向运动,构成倒流,因而形成了流动与边界分离的现象。
参看图4-43:
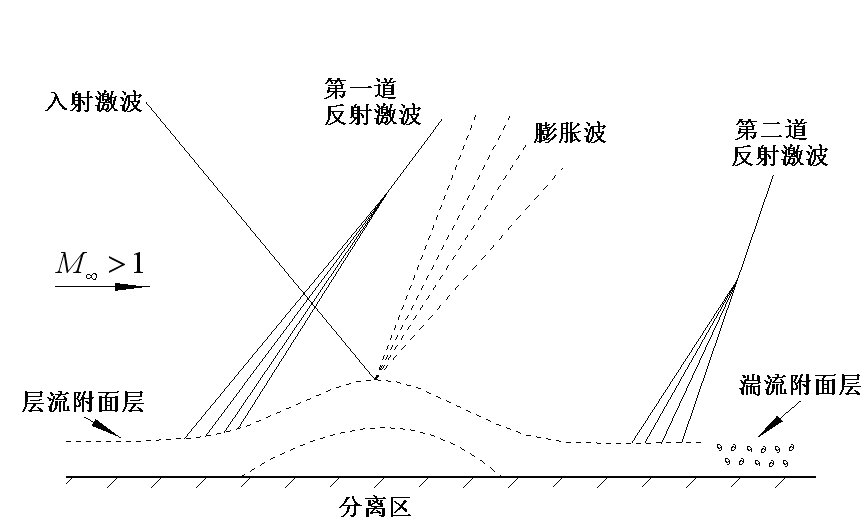
在激波射到层流边界层上的一些实验中,所观察到的典型特征示意地表示在图4-43当斜激波射进平板上的层流边界层时,波后的高压通过边界层中的亚音速层往上传播,使边界层增厚,由此而引起的流线外产生一些斜的弱压缩波,这些弱压缩波合并成一道“反射激波”,其“起点”位于入射激波投射点的上游,由于激波造成的逆压梯度很大,必定引起边界层分离。因为分离区里的运动速度相对很小,所以可以近似地看成是一个等压区。因此,入射激波由此处反射相当于在等压自由边界上的反射,即反射成一束膨胀波,气流经膨胀波折回壁面,使边界层又重新贴到壁面上,经过这一束膨胀波以后,气流折角很大,势必要调整方向,内折并产生第二道“反射激波”。层流边界层在紧靠第二道反射激波的下游,变为湍流。
通过大量的实验发现,喷管中出现两种不同的分离现象。自由激波分离和受限激波分离。在图4-41中,当反压pb的大小达到曲线3所示的状态时,喷管的出口边缘上应有斜激波产生;当反压pb达到曲线4所示的状态,喷管出口处应有正激波产生;反压pb继续增大,喷管内部出现激波。实际上,由于边界层的存在,管内外的气流结构要复杂一些。激波后的产生的高压可通过边界层内的亚音速层逆流向上传播,其结果是上游边界层内压强提高,速度降低,边界层增厚。边界层增厚,迫使边界层边界线向层外折转,超音速气流折转方向必产生斜激波。斜激波朝中心线方向传播可能产生三种形式的激波:直至中心线的斜激波,马赫盘,帽状激波。激波进入喷管内部同时伴随着边界层的分离,这样的流动状态叫做分离流动。通常情况下一旦产生气流分离,气流就不再附着在壁面,这样的流动状态叫做自由激波分离。70年代初,在J-2S发动机的冷流试验中,在极度膨胀的条件下观察到了一种不同类型的气流分离形式。仅在某一压比下才会出现的流动状态下,分离点下游的压力出现不规则性,并比环境压力要高。气流分离后又再附着在喷管上。这样的流动状态称为受限激波分离。图4-44给出了两种分离流场的压力分布及流场。
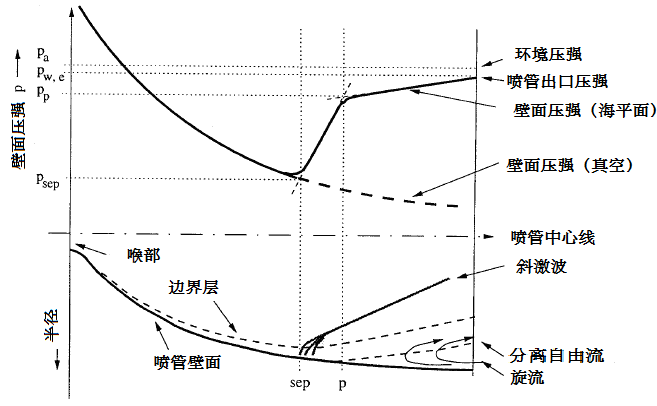
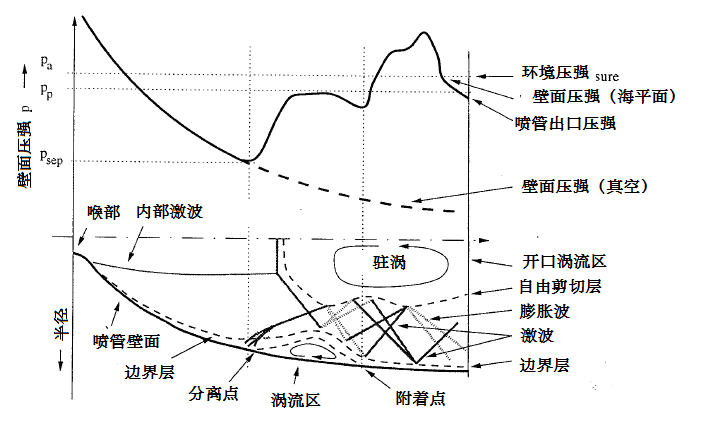
图4-44两种不同的喷管分离现象
4.11.3 分离点参数计算
喷管内气流分离面可通过理论计算或现有的经验公式确定,也可通过下章数值模拟的方法进行计算。本节通过前两种方法来进行分离点参数计算。
a 正激波气流分离面
由于存在气流分离Me<1,并且pe=pa。喷管出口的流量为:
\({{q}_{e}}=\frac{\Gamma {{A}_{e}}{{p}_{e}}}{\sqrt{\frac{R}{M}{{T}_{e}}}}y({{M}_{e}})\) (4-95)
式中,\(\Gamma =\sqrt{k}{{(\frac{2}{k+1})}^{\frac{k+1}{2(k-1)}}}\) (4-96)
\(y\left( {{M}_{e}} \right)={{\left( \frac{k+1}{2} \right)}^{\frac{k+1}{[2(k-1)]}}}{{M}_{e}}{{\left( 1+\frac{k-1}{2}M_{e}^{2} \right)}^{\frac{1}{2}}}\) (4-97)
对于喉部截面有
\({{q}_{t}}=\frac{\Gamma {{A}_{t}}p_{t}^{*}}{\sqrt{\frac{R}{M}T_{e}^{*}}}\) (4-98)
不考虑壁面传热和摩擦,则\(T_{e}^{*}=T_{t}^{*}\),\(p_{c}^{*}=p_{t}^{*}\)。由公式(4-95)和(4-98)联立得
\(y\left( {{M}_{e}} \right)=\frac{p_{c}^{*}{{A}_{t}}}{{{p}_{a}}{{A}_{e}}}=\frac{p_{c}^{*}}{{{p}_{a}}\varepsilon }\) (4-99)
式中ε为面积比。
这样由4-97和4-99联立就可以求出气流分离后在喷管出口的亚音速马赫数Me。
根据连续方程
\(\frac{\Gamma {{A}_{t}}p_{t}^{*}}{\sqrt{\frac{R}{M}T_{t}^{*}}}=\frac{\Gamma {{A}_{e}}p_{e}^{*}}{\sqrt{\frac{R}{M}T_{e}^{*}}}q\left( {{M}_{e}} \right)\) (4-100)
可求得通过激波的总压损失系数
\({{\sigma }_{sep}}=\frac{p_{e}^{*}}{p_{t}^{*}}=\frac{1}{\varepsilon q({{M}_{e}})}\) (4-101)
式中 \(q({{M}_{sep}})={{M}_{sep}}{{\left[ \frac{2}{k+1}\left( 1+\frac{k-1}{2}{{M}_{sep}}^{2} \right) \right]}^{-\frac{k+1}{2(k-1)}}}\) (4-102)
一种近似的一元激波理论认为,通过激波的总压损失系数可表示为激波前的马赫数即分离马赫数Msep的函数,公式如下:
\({{\sigma }_{sep}}=\frac{{{\left[ \frac{\left( k+1 \right)M_{sep}^{2}}{2+(k-1)M_{sep}^{2}} \right]}^{\frac{k}{k-1}}}}{{{\left[ \frac{2k}{k+1}M_{sep}^{2}-\frac{k-1}{k+1} \right]}^{\frac{1}{k-1}}}}\) (4-103)
这样求解方程可以求得分离马赫数Msep。
气流分离面位置所对应的面积比为
\({{\varepsilon }_{sep}}=\frac{{{A}_{sep}}}{{{A}_{t}}}=\frac{1}{M{{a}_{sep}}}{{\left[ \frac{2}{k+1}\left( 1+\frac{k-1}{2}Ma_{sep}^{2} \right) \right]}^{\frac{1+k}{2(k-1)}}}\) (4-104)
b 非正激波气流分离面
喷管中的气流大都属于非正激波气流分离,只有在\({{\text{M}}_{\text{sep}}}\le \text{1}\text{.5}\),边界层才能维持正激波。此外,靠近壁面以及在分离面附近还存在局部超声速区,因此出现 “λ”形斜激波与桥形正激波相交的三叉点。喷管出口马赫数Me仍按上面使用的公式进行求解,但此时分离面的计算较为复杂,需使用现有的经验公式。
Summerfield提出,只要喷管出口壁面压力低于40%的环境压力, 在喷管内就会观察到气流分离。此后, 相应的计算公式被称为“Summerfield准则”。
通常因为把两种独立的物理过程,气流分离和回流放在一个方程考虑,因此采用环境压力pa的分离准则是不准确的。1967年Lawrence提出采用稳态压力pp而不是环境压力来建立分离准则,以便区分两种独立的物理现象。随后他提出分离部分psep/pp应当考虑马赫数壁面冷却和比热比k,回流项pp/pa应当考虑分离点下游型面的影响。
Schmucker在马歇尔航天中心提出了一种新的分离准则。它包含了在分离点处的无粘马赫数, 台阶流动试验已经证明该参数对分离点的影响。然而他忽视了Lawrence的意见, 用一个公式来考虑两种不同的物理现象。尽管存在缺陷,但这个公式仍然被欧洲航天工业广泛使用。不同研究机构提出的分离流动经验公式请参考文献[16]。
影响分离流动的因素有喷管型面,压强比,气流参数,壁面的冷却,以及表面粗糙度等等。
当喷管内出现气流分离时,分离面位置确定后,比冲可按下式计算:
\({I}_{s}={{V}_{sep}}+\frac{{{A}_{sep}}}{q}({{p}_{sep}}-{{p}_{a}})\) (4-105)
推力:
\(F=q{{V}_{sep}}+{{A}_{sep}}({{p}_{sep}}-{{p}_{a}})\) (4-106)
思考题
1.简述固体火箭发动机喷管设计的三部分内容。
2.已知dt=20cm,de=66cm,喉径到出口面距离L=65cm,出口半角ac=180°,试求此喷管的二次曲线型内型面。
3.试讨论喷管各部分用热防护材料的性能及其优缺点。在什么条件下选用碳/碳复合材料?
4.试按图4-20推导公式(4-55)和(4-56)。
5.论述可延伸出口锥的作用,比较各种可延伸出口锥的优缺点,设计可延伸出口锥需注意什么?
6.比较各种推力向量控制装置的特点,你认为哪一种装置最好,为什么?
7.设计反喷管推力终止装置应注意什么?
8.已知反喷管的斜切部分进口截面的面积比\(\frac{{{A}_{1}}}{{{A}_{t}}}=1.1682\),斜切角φ=45°,扩张半角a=15°,pa/pc=0.0133,燃气的比热比k=1.25,反喷管收缩系数Cd=0.9。求推力系数CFx和CFy及推力偏斜角δ。