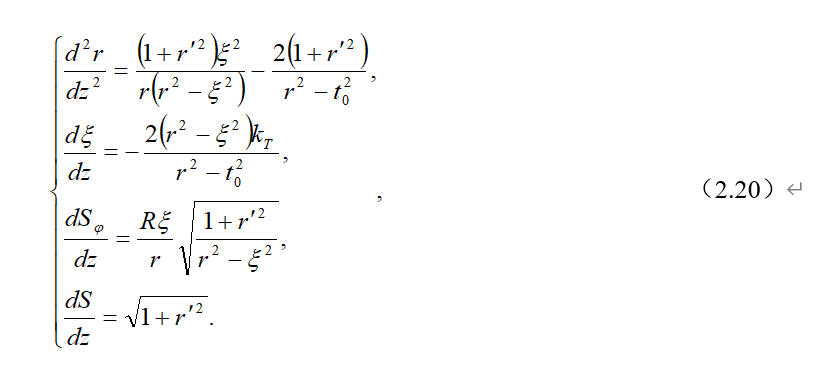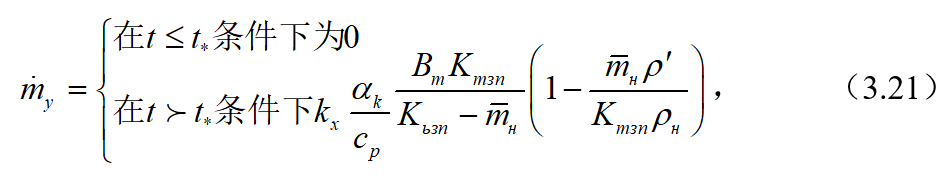固体火箭发动机复合材料的壳体设计和计算

发表于： 2021年7月31日 2021年8月6日
分类：固发设计教材

被阅次数： 6,434

书评：莫斯科鲍曼高等技术大学”航空航天复合材料结构”教研室，技术科学博士，教授И.М.布拉诺夫；技术科学副博士А.Э.德沃列茨基

本书列出了缠绕制作的固体火箭发动机壳体的主要计算方法，这些方法使有可能确定出壳体的结构参数和工艺参数。在”设计发动机壳体所需的初始数据”一章中计算了推进剂几何形状和壳体内压强随时间的变化，以及测定了燃气绕流壳体内表面的速度。对于具体的结构来说，列出了承力壳体的设计和计算（强度、刚度、缠绕工艺参数的计算）和内绝热层的计算和设计。研究了一般的带有局部孔的壳体封头设计问题和壳体连接部件的设计。描述了各结构件生产的综合工艺过程。

目　　录
引言
第一章：设计发动机壳体所需的初始数据
1.1、计算推进剂几何形状和壳体内压强随时间的变化
1.2、测定燃气绕流壳体内表面的速度
第二章：承力壳体的设计和计算（强度、刚度、缠绕工艺参数的计算）
2.1、封头和外形最佳缠绕角的计算方法
2.2、承力壳体强度和刚度的计算方法
2.3、进行计算和对计算结果处理
第三章：壳体内绝热层的计算和设计
3.1、所需的绝热层厚度的计算算法
3.2、内绝热层的非定常加热和质量烧蚀问题的提出
3.2.1、明显考虑内部质量烧蚀和表面质量烧蚀情况的带边界条件的非定常导热系数方程
3.2.2、计算绝热层碳化层的表面质量烧蚀速度
3.2.3、利用分解经验系数不明显考虑内部质量烧蚀和表面质量烧蚀情况的带边界条件的非定常导热系数方程
3.3、测定燃气流与内绝热层表面之间的热质交换参数
3.4、进行计算和对计算结果处理
第四章：带局部孔的壳体封头设计
4.1、孔区补强的壳体试验计算根据
4.2、孔区增强的结构工艺参数和部件结构综合方案
第五章：壳体连接部件的计算和设计
5.1、铆接金属箔连接的计算和设计
5.2、金属箔螺栓柱销连接的计算和设计
5.3、连接舱段的缠绕结构工艺流程图
第六章：壳体各结构件的生产工艺过程
6.1、壳体的生产工艺过程结构
6.2、缠绕壳体所用的原材料准备
6.3、缠绕壳体所用的芯模制作
6.4、缠绕的工艺制度
6.5、缠绕的结构工艺参数确定
6.6、内绝热层的制作工艺
6.7、壳体的热处理
索引目录

引言

在火箭发动机结构件中，使用了大量的复合材料、各种不同种类的热防护材料和特种涂层（表01）。

表01、火箭发动机结构件中的复合材料

发动机结构件的名称

制作结构所采用的复合材料

固体推进剂发动机承力壳体

承力环、连接《裙》

壳体的嵌入法兰、连接舱端框

有机纤维增强塑料、碳纤维增强塑料、玻璃纤维增强塑料。

玻璃纤维碳纤维增强塑料、硼纤维增强塑料、碳纤维增强塑料、有机纤维增强塑料。

易熔基体金属复合材料（AlB、MgB、AlC、MgC）。

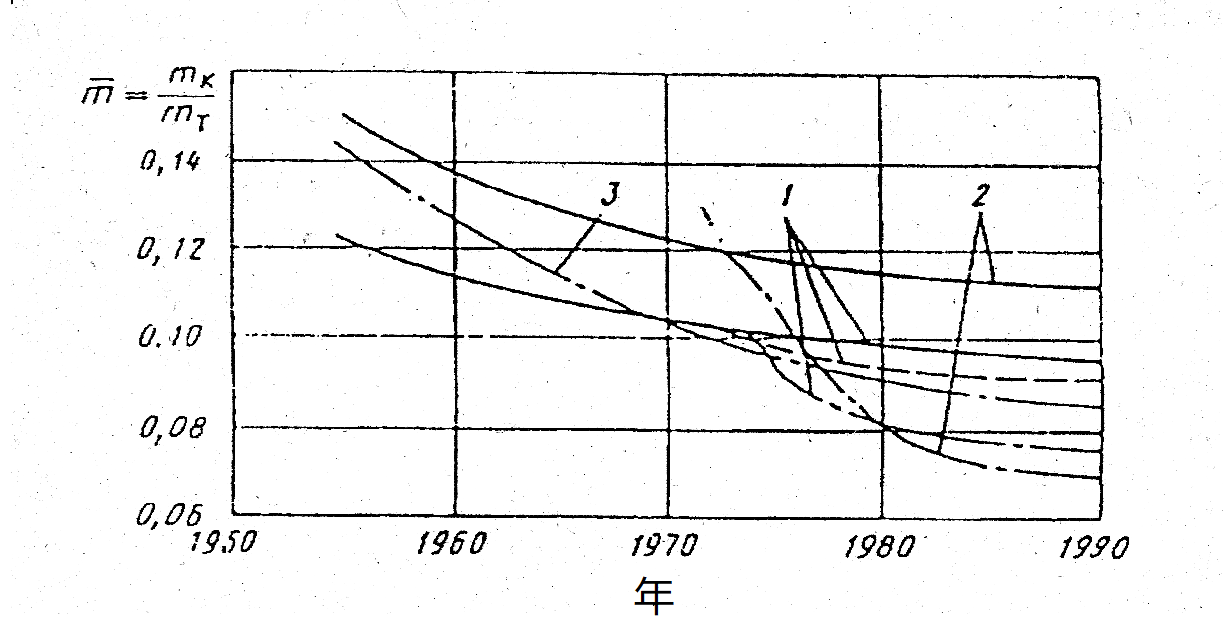
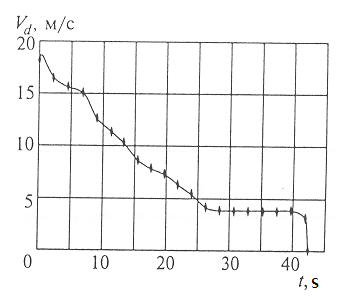
图0.1所示为依靠采用新材料和新制作工艺“民兵”三级固体火箭发动机壳体质量特性比的变化。

图0.1、“民兵”弹道导弹固体火箭发动机壳体质量比的变化：1、2、3、-第一级、第二级、第三级；—钢壳体；- -玻璃纤维增强塑料；- .-有机纤维增强塑料。m_k，m_T分别为壳体质量和发动机总质量。

在固体火箭发动机整体缠绕的带极孔的壳体标准结构中，壳体的主要构件是作为发动机燃烧室承力构件的承力壳体。内绝热层防止承力壳体受推进剂燃烧产物的作用。前法兰将壳体与点火装置连接在一起，后法兰用于连接喷管装置与固体火箭发动机壳体。借助对接部件将发动机壳体与火箭各级间连接。

壳体的承力壳体、对接部件和热防护按构件布置是标准的结构方案。

第一章：设计发动机壳体所需的初始数据

发动机的主要参数：

—药柱的质量 6200kg;

—海拔比冲213.5s;

—最大压强5.5MPa；

—喷管喉部直径190mm;

—喷管出口截面直径900mm。

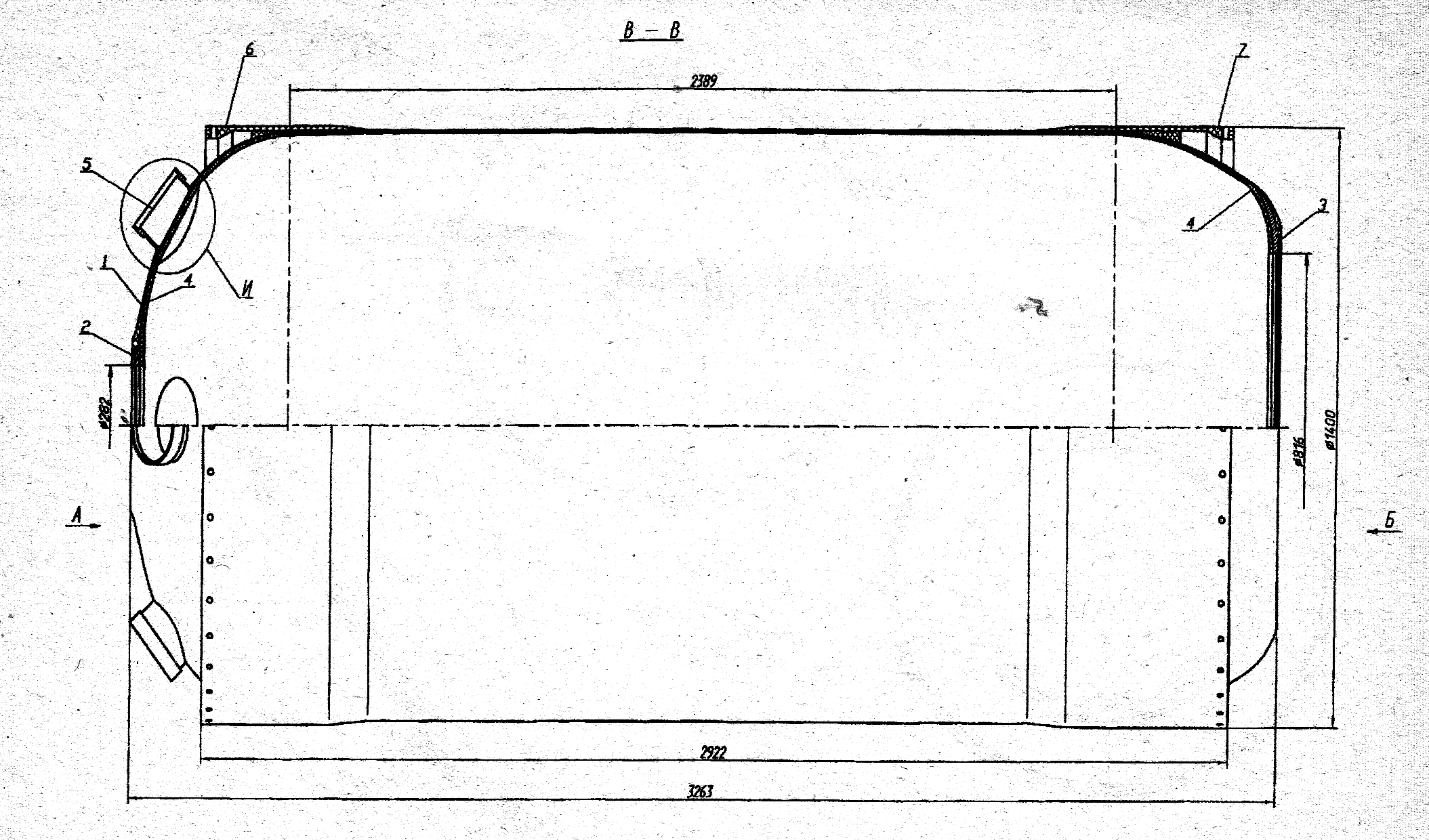
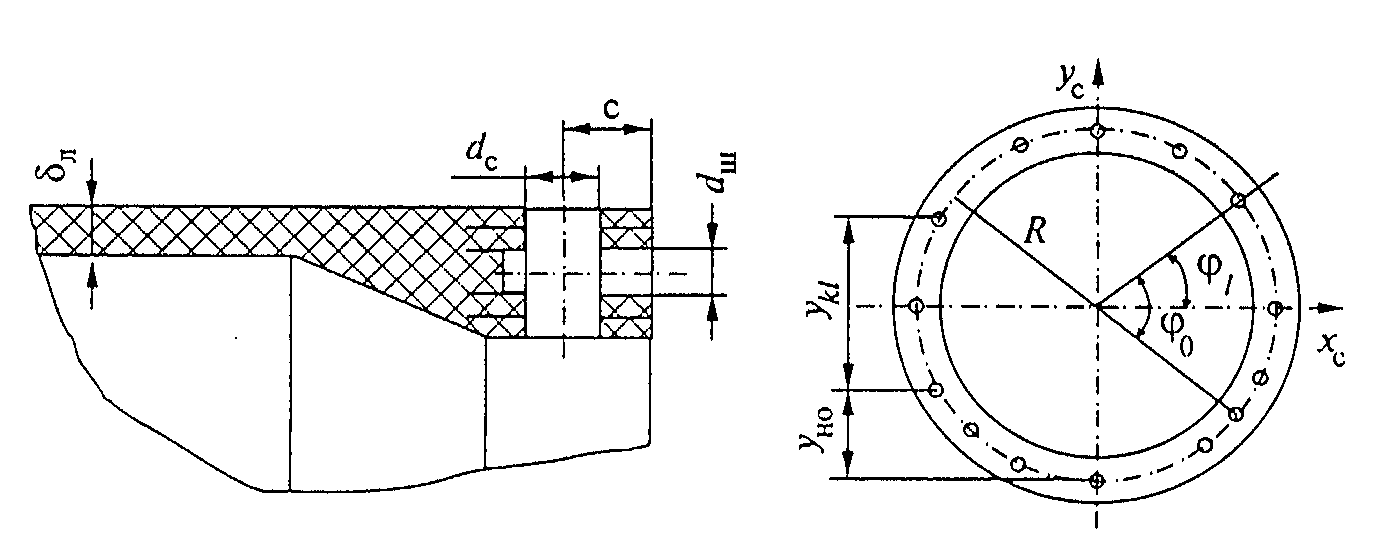
带标明基本外形尺寸的壳体图（图0.1和1.1）。

图1.1、壳体的基本限界尺寸

图位	标记	名称	数量	材料	补充说明
		新研制的制品
1		承力壳体	1	有机纤维增强塑料
2		前法兰	1	钛合金
3		后法兰	1	钛合金
4		绝热层	1	橡胶，卡普隆布
5		舱段对接法兰	4	钛合金
6		前对接部件	1	有机纤维增强塑料/铝合金
7		后对接部件	1	有机纤维增强塑料/铝合金

为了确定对绝热层的热作用参数，选择了药柱的形状和成分，并对药柱几何形状在工作过程中的变化进行了计算，同时对压强和燃烧产物流经壳体内表面的速度也进行了计算。

1.1、计算药柱几何形状和壳体内压强随时间的变化

计算药柱烧蚀的原始数据是在t=0（t—时间）时-燃烧开始时刻的壳体内表面的几何形状和药柱几何形状。所选的ANB-3066牌号药柱的基本特性在表1.1—1.3中列出。药柱的几何参数在所附的草图上列出。

表1.1、 ANB-3066牌号的药柱成分和弹道特性

药柱的成分和特性	值（%）
高氯酸铵	66
聚丁二烯酸	12
环氧树脂	3
铝粉	19
燃烧速度关系（T3=20℃）	2.9（p/98100）^0.3
\(\partial \ln /\partial {{T}_{g}}\)，1/℃	0.002
密度，g/cm³	1.77
稳定燃烧的最小压强，MPa	0.01
真空比冲，m/s	2720*
燃烧温度，K	3420
特征速度C*，m/s	1590

*在P₀=7MPa; Pa=0.1MPa条件下。

表1.2 ANB-3066牌号药柱的热物理特性

特性

值

比热，J/（kg·K）

导热系数，W/(m·K)

线性膨胀系数，l/K

使用温度范围，℃

存放的最高温度,℃

1377

0.24

2×10^-4

-55~+55

表1.3、 4.0MPa压强条件下ANB-3066牌号药柱燃烧产物的特性和平衡成分

特性

值

温度，T,（K）

分子量，μ，g/mol

比热，Cp，J/（kg·K）

粘度，η·10⁴，H·c/m²

导热系数，λ，W/（m·K）

绝热指数，k

组分含量（克分子分率）

H₂

H₂O

HCI

N₂

CO₂

Al₂O₃

3415

27.9

3.76

0.91

1.28

1.16

0.0454

0.3511

0.0947

0.1157

0.0793

0.2656

0.0086

0.3204

表1.4 药柱燃面面积与肉厚的关系

Ab, m²

e, mm

Ab, m²

e, mm

7.44

7.85

8.01

7.98

8.88

9.36

9.83

10.28

9.82

9.51

100

120

140

160

180

9.22

5.99

8.93

8.91

8.90

8.88

8.83

8.81

8.72

8.68

200

220

240

260

280

300

320

340

360

380

为了确定药柱燃面与时间的关系，在药柱的纵向截面图纸上标出与给定时刻的燃烧肉厚相应的燃面中间位置线。此外，将药柱肉厚分成简单的几何形状图。根据相应几何计算就得到用表1.4所燃面（Ab）与肉厚（e）的关系。

药柱燃烧过程中容器中的压强根据用来自燃烧表面气体注入量\(\dot m_b\)与气体通过喷喉截面流量\(\dot m_t\)等式形式表示的质量平衡方程来计算:

\(\dot m_b\left( t \right)=\dot m_t\left( t \right)\) （1.1）

来自燃烧表面的气体注入量用如下关系式计算：

\(\dot m_b\left( t \right)=r\left( t \right){{\rho }_{p}}{{A}_{b}}\left( t \right)\) (1.2)

采用下公式来计算气体流量：

\(\dot m_t\left( t \right)=\frac{{{A}_{t}}p\left( t \right)}{{{C}^{*}}}\) （1.3）

在公式（1.2）和（1.3）中采用下列表示法：

\(r\left( t \right)\)—药柱燃烧速度当前值；

\({{\rho }_{p}}\)—给定的药柱密度，\({{\rho }_{p}}\)=1770kg/m³;

\({{A}_{t}}\)–喷喉截面面积，\({{A}_{t}}\)=3.1416R_t²; \({{R}_{t}}\)—喷喉半径，在计算时\({{R}_{t}}\)=0.128m;\(p\left( t \right)\)—压强；C*—特征速度。

药柱燃烧速度当前值根据下形式的公式计算：

\(r\left( t \right)={a}{{\left[ p\left( t \right) \right]}^{n}}\)， (1.4)

式中\({a},{n}\)—燃速系数和压力指数。

在将药柱燃速与压强关系式（1.4）代入关系式（1.2）并根据公式（1.1）和（1.3）简单变换后，壳体中的压强与时间的关系式就变成下形式：

\(p\left( t \right)={{\left[ \frac{{a}{{\rho }_{p}}{{A}_{b }}\left( t \right)C* }{{{A}_{t}}} \right]}^{1/\left( 1-n \right)}}\) （1.5）

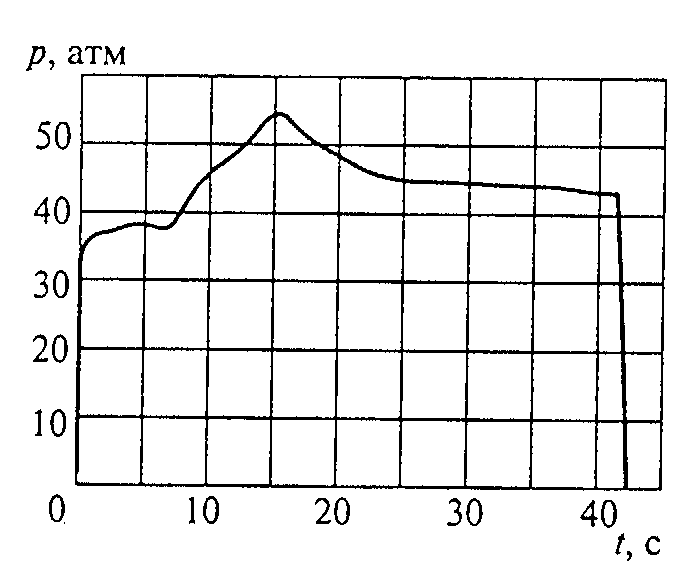
压强时间关系曲线图用图1.2 所示。

图1.2 壳体内压强时间关系曲线

1.2、计算气体绕流壳体内表面的速度

壳体前封头的内表面绕流速度用如下公式计算

\({{V}_{1}}\left( t \right)={{V}_{0}}\left( t \right){{A}_{b1}}\left( t \right)/{{A}_{1}}\left( t \right)\) （1.6）

式中\({{V}_{0}}\left( t \right)\)—气体从燃烧表面的流出速度；\({{A}_{b}}\left( t \right)\)—前封头区的燃烧表面面积；\({{A}_{1}}\left( t \right)\)—气体通过其流入中心通道的锥面当前面积*。

在\({{V}_{1}}\left( t \right)\)值降低到气体从药柱燃面流出速度\({{V}_{0}}\left( t \right)\)级时，给\({{V}_{1}}\left( t \right)\)值赋予用下公式计算的\({{V}_{0}}\left( t \right)\)值

\({{V}_{0}}\left( t \right)=r\left( t \right){{\rho }_{p}}/{{\rho }_{g}}\left( t \right),\ {{\rho }_{g}}=p\left( t \right)/\left( {{R}_{g}}{{T}_{g}} \right)\)，（1.7）

式中\({{R}_{g}}\)—燃烧产物气体常数；\({{T}_{g}}\)—燃烧产物的温度。

壳体后封头内表面的绕流速度用下公式求算

\({{V}_{3}}\left( t \right)={{V}_{0}}\left( t \right){{A}_{b3}}\left( t \right)/{{A}_{3}}\left( t \right)\), （1.8）

式中\({{A}_{3}}\left( t \right)\)—气体通过其流入喷喉的锥面实时面积**；\({{A}_{b3}}\left( t \right)\)—后封头区的燃面面积。

在\({{V}_{3}}\left( t \right)\)值降低到气体从药柱燃面流出速度\({{V}_{0}}\left( t \right)\)级时，(象上次情况中那样)给\({{V}_{3}}\left( t \right)\)值赋予\({{V}_{0}}\left( t \right)\)值。根据上述算法计算出的前、后封头燃烧产物的绕流速度与时间图形关系曲线用图1.3和1.4表示。

图1.3.前封头的绕流速度与时间关系曲线

图1.4.后封头的绕流速度与时间关系曲线

*这个锥面的母线是连接药柱中心通道当前入口边缘上的点与前封头表面打开时刻其表面上当前点的直线段（根据几何学计算取）。

**这个锥面的母线是连接药柱中心通道当前出口边缘上的点与喷喉前缘上当前点的直线段（采用几何计算数据用解析方法计算）。

第二章：承力壳体的设计和计算（强度、刚度、缠绕工艺参数的计算）

用连续缠绕方法制作的复合材料压力壳体设计计算简化为确定保障满足下列条件的结构设计参数：

1）保障所设计结构的质量最小；

2）保持在计算载荷作用下所需的强度（刚度）；

3）工艺的可实现性。

设计过程中所确定的压力壳体主要参数是：

1）压力壳体的封头外形；

2）缠绕角（增强纤维相对于壳体表面子午线的定向角）的分配；

3）构成承力壳体的增强材料层数。

2.1、封头和外形最佳缠绕角的计算方法

在用连续缠绕方法制作压力壳体承力壳体时，按表面测地线在芯模表面铺放增强纱是最合理的。同时，缠绕轨迹用已知的克勒罗理论关系式确定：

\(r\sin \varphi =const\) (2.1)

式中r—壳体的半径；φ—缠绕角。

这种增强方式的合理性由下列情形所决定：

1、在测地线增强条件下，甚至在芯模与纱之间随便怎样小的摩擦系数时，铺放在芯模上的纱都是处在平衡状态，因为在这种情况下，在横向方向没有作用于纱的切线力。

2、在内压作用于壳体的条件下，按测地线铺放的纱中的力在长度上是不变的，这就使得有可能设计出等强度承力结构。

等式（2.1）可按下列形式重写：

\(r\sin \varphi ={{r}_{0}}=const\) (2.2)

式中\({{r}_{0}}\)—极孔半径，根据缠绕的连续性条件， \(\varphi ={{90}^{\circ }}\)。通过分析最新的关系式，就不难看出，只有在极孔半径相同的情况下，可实现测地线缠绕。即使这些半径不同（图2.1），克勒罗函数值\(r\sin \varphi \)仍在\({{r}_{01}}\)—\({{r}_{02}}\)范围内，在这里\({{r}_{01}}\)<\({{r}_{02}}\)—前极孔和后极孔的相应半径。在这种情况下，条件（2.2）显然不会被完成，而且在壳体上的增强纱铺放轨迹将与测地线轨迹不同。通常将这种缠绕称为非测地线缠绕。

既然在非测地线缠绕时，增强纱由于摩擦力不会从芯模表面上滑落，显然在纱与芯模表面之间存在着保障纱静态平衡的最小摩擦系数值。这个条件在数学上以下列方式形成：

\(\left| tg\theta \right|\le {{k}_{fr}}\)，（2.3）

式中\({{k}_{fr}}\)—摩擦系数；\(\theta \)—芯模表面法线\(\vec{n}\)与纱铺放轨迹法线\(\vec{v}\)之间的夹角，它被称为测地线偏差角。

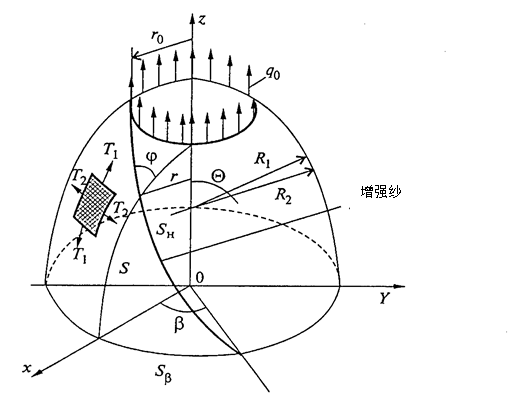
图2.1、壳体示意图

根据确定测地线偏差角并利用微分几何学算法，就不难得到适合于在曲线r=r(z)绕z轴旋转形成的表面上铺放纱的测地线偏差角正切的表达式：

\(tg\theta =-\frac{{\xi }'{{r}^{2}}}{{{\xi }^{2}}-\frac{r{r}”}{1+{{{{r}’}}^{2}}}\left( {{r}^{2}}-{{\xi }^{2}} \right)}\)，（2.4）

式中和后面 \(\xi =r\sin \varphi \)—克勒罗函数表示法，而上分划线表示坐标的微分运算。

显然，（从芯模上纱的稳定性观点来看）按给定的定律\(\xi =\xi \left( z \right)\)，在给定的形状母线\(r\left( z \right)\)旋转面上非测地缠绕轨迹的可实现性，可在按公式（2.4）计算出测地线偏差角正切后根据判据（2.3）来评定。

应指出，通常将符合\(\left| tg\theta \right|=const\)的增强纱铺放轨迹称为恒定偏差线。显然，符合\(\left| tg\theta \right|={{k}_{fr}}\)情况的是由摩擦系数\({{k}_{fr}}\)所决定的最大程度偏离测地线缠绕轨迹的轨迹。

我们来具体地说明在本部分开始大抵上形成的主要设计要求。

设计的最优化性用下公式计算的复合壳体质量值来评定：

\(m=nf{{S}_{1}}\rho \)，（2.5）

式中n—构成承力壳体的纱数量；f—考虑到粘合剂的纱截面换算面积；S₁—两极之间的纱长度；ρ—承力壳体材料的密度。

工艺限制被简化为条件（2.3）和缠绕时纱的连续性条件（通过壳体任意截面的纱数恒定）），其数学表示变成以下形式：

\(nf=const\)。 (2.6)

强度守恒条件以下列方式表达：

\({{\sigma }_{\max }}\left( p \right)\le \bar{\sigma }\) ，（2.7）

式中\({{\sigma }_{\max }}\left( p \right)\)—在内压p作用下增强纱中所产生的最大应力；\(\bar{\sigma }\)—所允许的应力。

这种情况下，设计参数是单值确定结构缠绕轨迹的克勒罗函数与纵坐标的关系\(\xi \left( z \right)=r\left( z \right)\sin \varphi \left( z \right)\)。

在设计用单向带缠绕制作的壳体时，我们将忽略连接纱带中单独纱的聚合粘合剂的承载能力，用仅在增强方向承受载荷的纱线系统替代纱带。这种简化是允许的，因为横向增强的单向纱带强度要比增强方向的小1-2级。此外，在接近破坏载荷条件下的结构工作物理现象图通常与纱线系统相符，因为粘合剂的破坏实质上比壳体承载能力的丧失要早得多。

对于轴对称变形情况来说，加载内压p的无力矩回转壳体平衡方程具有如下形式：

\(\frac{d}{d\theta }\left( r{{T}_{1}} \right)-{{T}_{2}}{{R}_{1}}\cos \theta =0\)

\(\frac{{{T}_{1}}}{{{R}_{1}}}+\frac{{{T}_{2}}}{{{R}_{2}}}=0 \) （2.8）

式中\({{T}_{1}},\ {{T}_{2}}\)—壳体中产生的子午线力强度和环向力强度；R₁，R₂—回转面曲率主半径（图2.2）。利用已知的关系式^[11]

\({{R}_{1}}\cos \theta d\theta =dr\)

就可将（2.8）方程组的第一个平衡方程用较简单形式记作：

\(\frac{d}{dr}\left( r{{T}_{1}} \right)-{{T}_{2}}=0\)。（2.9）

图2.2、压力壳体封头上的增强纱排列和封头的几何特性

壳体中子午线力\({{\sigma }_{1}}\)和环向应力\({{\sigma }_{2}}\)通过增强纱中的应力s以下列方式表示^[8]：

\({{\sigma }_{1}}=\sigma {{\cos }^{2}}\varphi ,\ {{\sigma }_{2}}=\sigma {{\sin }^{2}}\varphi \)。（2.10）

子午线力和环向延伸力的相应表达式就变成以下形式：

\({{T}_{1}}={{\sigma }_{1}}h=h\sigma {{\cos }^{2}}\varphi ,\ {{T}_{2}}={{\sigma }_{2}}h=h\sigma {{\sin }^{2}}\varphi \)。（2.11）

式中h—根据缠绕连续性条件（2.6）按下公式所计算的壳体厚度

\(h\left( r \right)=\frac{nf}{2\pi r\cos \varphi }\)。（2.12）

应指出，正式使用关系式（2.12）来（在\(\phi \to 90{}^\circ \)条件下）测定极孔区的壳体厚度，会得到无限大的值。这种情形的原因是公式（2.12）未考虑到缠绕是用有限宽度的纱带实施的这种情况。因此，在\(\phi \to 90{}^\circ \)条件下的理论结果h→∞在实践中是不会被实现的，在远离极孔边缘超过纱带宽的距离时可以认为公式（2.12）是正确的。

考虑到（2.12），关系式（2.11）可重写成如下形式

\({{T}_{1}}=\frac{nf}{2\pi f}\sigma \cos \varphi ,\ \ {{T}_{2}}=\frac{nf}{2\pi r}\sigma tg\varphi \sin \varphi \)。（2.13）

由（2.13）直接得

\(\frac{{{T}_{2}}}{{{T}_{1}}}=t{{g}^{2}}\phi .\) （2.14）

我们来想象用垂直于回转轴的平面将封头截开。所截开部分的平衡方程以下列方式表示：

\(q={{q}_{0}}\frac{{{r}_{0}}}{r}+p\frac{{{r}^{2}}-r_{0}^{2}}{2r}\) （2.15）

式中—轴向延伸力；—极孔外形上的延伸轴向作用力（见图2.2）。这个轴向力靠增强纱中的应力平衡

\(q=\frac{nf\sigma }{2\pi r}\cos \phi \sin \theta =\frac{nf\sigma }{2\pi {{R}_{2}}}\cos \phi \)。（2.16）

通过联立分析（2.8）的第二个平衡方程，方程（2.14）和（2.16），就不难得到下列关系式：

\(\frac{{{R}_{2}}}{{{R}_{1}}}-\frac{2{{r}^{2}}}{{{r}^{2}}-t_{0}^{2}}=-t{{g}^{2}}\phi \)，（2.17）

式中\(t_{0}^{2}=r_{0}^{2}-\frac{2{{q}_{0}}{{r}_{0}}}{p}\)—由极孔外形承力边界条件所决定的参数。对于顶部密闭或用堵盖封闭的封头来说，\({{q}_{0}}=\frac{p{{r}_{0}}}{2},t_{0}^{{}}=0\)，对于无载荷的外形来说，\({{t}_{0}}={{r}_{0}}\)^[7]。

关系式(2.17) 被称为由柔韧纱系统构成的回转壳体存在的条件。在未完成这个条件时，壳体就变成一种机构，也就是说，不承受纱系统假设范围内的外部载荷。

用克勒罗函数表示（2.17）方程右边的被加数，我们就会记下描述封头母线型面的方程：

\(\frac{{{R}_{2}}}{{{R}_{1}}}-\frac{2{{r}^{2}}}{{{r}^{2}}-t_{0}^{2}}=\frac{{{\xi }^{2}}}{{{r}^{2}}-{{\xi }^{2}}}\)。（2.18）

利用测地线偏差角正切表达式（2.4）和关系式（2.18），我们就记下关于克勒罗函数的缠绕轨迹解析方程：

\({\xi }’=-\frac{2\left( {{r}^{2}}-{{\xi }^{2}} \right)tg\theta }{{{r}^{3}}-r_{0}^{2}}\)。（2.19）

应指出，在\(tg\theta =0\)的情况下，方程（2.19）就变成测地线轨迹方程。

关于计算缠绕最佳轨迹和平衡封头形状的问题在论文中已用变分法解决。确定最佳封头型面和增强纱最佳轨迹的完全解析方程组具有下列形式：

式中\({{S}_{\varphi }},\ S\)—缠绕轨迹的曲线坐标（见图2.2），用来便于实际实现的缠绕轨迹。

（2.20）解析方程组解的边界条件看起来有下列形式：

z=0:

\( {r}’=0;r=R;\xi ={{r}_{02;}} \)

\({{S}_{\beta }}=S=0. \)

式中R—赤道半径。

（2.20）方程组不能用求积分完成，因此，用数值法来解它。

2.2、承力壳体强度和刚度的计算方法

承力壳体的设计厚度按照下列公式测定。

1、封头赤道上的螺旋层厚度根据如下公式计算：

\({{h}_{a}}=\frac{p\left( {{a}^{2}}-r_{0}^{2} \right)+2{{q}_{0}}{{r}_{0}}}{2a\bar{\sigma }{{\cos }^{2}}{{\phi }_{a}}}\) ，（2.21）

式中a—封头的赤道半径；p—内压强；q₀—沿极孔外形分布的轴向力；r₀—极孔半径；\(\bar{\sigma }\)—所允许的纱拉伸应力；\({{\varphi }_{a}}\) —封头赤道上的增强角。在极孔封闭的条件下，假定\({{q}_{0}}=0.5p{{r}_{0}}\), 在极孔开口的条件下，\({{q}_{0}}=0\)。

2、壳体筒体段上环向层的厚度根据如下公式计算：

\({{h}_{k}}=\frac{pa\left( 2-t{{g}^{2}}{{\varphi }_{a}} \right)}{2\bar{\sigma }}\) 。（2.22）

根据单层厚度h_e计算螺旋层层数n_cn和环向层层数n_k：

\({{n}_{cn}}=\frac{{{h}_{a}}}{{{h}_{e}}},\ \ {{n}_{k}}=\frac{{{h}_{k}}}{{{h}_{e}}}\)。（2.23）

如果所得到的n_cn和n_k不是整数，应向增大方向将它们化成整数。同时，螺旋层层数应为偶数。计算封头赤道上螺旋层和壳体筒体段上环向层的实际厚度：

\(h_{a}^{\varphi }={{n}_{cn}}{{h}_{e}},\ \ h_{k}^{\varphi }={{n}_{k}}{{h}_{e}}\)。

在完成设计计算后，应完成对所选实际厚度的应力验算。封头子午线任意点螺旋层中的应力根据如下公式计算：

\({{\sigma }_{cn}}=\frac{pr}{2{{h}_{cn}}{{\cos }^{2}}\varphi }\)，（2.24）

式中h_cn—当前截面中的螺旋层厚度。正如已经指出的那样，这个值是一个变量，并根据缠绕连续性条件（2.12）计算。因为对于所有截面来说，nf值是恒定的，可以通过赤道上的壳体厚度来表示它，也就是说，根据等式（2.12）我们就有

\(nf=2\pi ah_{a}^{\varphi }\cos {{\varphi }_{a}}\)。（2.25）

根据（2.25），封头当前截面中的壳体厚度计算公式可记作成如下形式：

\(h\left( r \right)=h_{a}^{\varphi }\frac{a\cos {{\varphi }_{a}}}{r\cos \varphi }\)。（2.26）

壳体筒体段上的材料环向层中的应力按如下公式计算：

\({{\sigma }_{k}}=\frac{pa-{{\sigma }_{cn}}h_{a}^{\varphi }{{\sin }^{2}}{{\varphi }_{a}}}{h_{k}^{\varphi }}\)。（2.27）

在刚度计算范围内计算气瓶筒体段的变形和位移，筒体段的变形性实质超过封头的变形性。首先按如下公式计算筒体段的刚度：

\( {{B}_{11}}=Eh_{a}^{\varphi}{{\cos }^{4}}{{\varphi }_{a}}, \)

\( {{B}_{12}}=Eh_{a}^{\varphi}{{\cos }^{2}}{{\varphi }_{a}}{{\sin }^{2}}{{\varphi }_{a}}, \)

\( {{B}_{22}}=Eh_{a}^{\varphi}{{\sin }^{4}}{{\varphi }_{a}}+Eh_{k}^{\varphi }. \)

筒体段的轴向和环向相对变形ε₁和ε₂按下测定计算

\({{\varepsilon }_{1}}=pa\frac{0.5{{B}_{22}}-{{B}_{12}}}{{{B}_{11}}{{B}_{22}}-B_{12}^{2}}, \)

\({{\varepsilon }_{2}}=pa\frac{{{B}_{11}}-0.5{{B}_{12}}}{{{B}_{11}}{{B}_{22}}-B_{12}^{2}}. \)

（2.29）

气瓶的最大径向位移w和其长度为l的筒体段轴向延伸率u按如下公式计算：

\(w={{\varepsilon }_{2}}a,\ \ u={{\varepsilon }_{1}}l\)。（2.30）

2.3、计算及其结果处理

设计和计算用的原始数据。

根据订货方所发给的原始数据，气瓶的最大使用压强为5.6MPa。根据可靠性要求，采用的计算压强等于9.0MPa。气瓶材料（单向有机环氧复合材料）的物理力学性能为以下：

—增强方向中的弹性模量E=86.5MPa;

—增强方向中的拉伸破坏应力，\(bar{\sigma }=1800MPa\)。

封头型面设计和螺旋层增强角计算。

在计算型面坐标和纱的增强角度时，采用了下列原始数据：

a=684mm—壳体筒体段的半径；

r₀₁=178mm—前封头的极孔半径；

r₀₂=463mm—后封头的极孔半径。

假定气瓶封头可用测地线缠绕制作，我们就会计算出其赤道上的增强角。根据公式（2.2）中的克勒罗关系式，我们就有

\(\varphi _{01}^{a}=\arcsin \frac{{{r}_{01}}}{a}=\arcsin \frac{178}{684}=15.1{}^\circ \)，

\(\varphi _{02}^{a}=\arcsin \frac{{{r}_{02}}}{a}=\arcsin \frac{463}{684}=42.6{}^\circ \)。

根据壳体筒体段上恒定偏差线我们来评定完成非测地缠绕的可能性。一般形式的恒定偏差线方程在论文^[6]中列出。对于筒体表面的特殊情况来说，可得到：

\(\frac{1}{\xi }=-\frac{tg\theta }{{{a}^{2}}}z+const\)。（2.31）

将坐标轴z的原点放在前封头的赤道面中我们就会用赤道上的增强角表示方程（2.31）中的常数：

\(\frac{1}{\sin \varphi }=\frac{1}{\sin {{\varphi }_{01}}}-tg\theta \cdot \frac{z}{a}\)。（2.32）

由方程（2.32）得到壳体筒体段上增强角从\({{\varphi }_{01}}\)过渡到\({{\varphi }_{02}}\)可实现性条件是很简单的：

\(\frac{\sin {{\varphi }_{02}}-\sin {{\varphi }_{01}}}{\sin {{\varphi }_{01}}\cdot \sin {{\varphi }_{02}}}\cdot \frac{a}{L}\le {{k}_{mp}}\)。（2.33）

对于所研究的情况来说

\({{k}_{mp}}\ge \frac{\sin 42.6-\sin 15.1}{\sin 42.6\cdot \sin 15.1}\cdot \frac{684}{2622}=0.616\)。

所需要的摩擦系数值是不允许高的，因而所研究结构的封头不可能用测地缠绕制作。

根据实现2.1节中所叙述方法的程序进行的计算表明，唯一可能的缠绕轨迹是沿壳体整个长度的恒定偏差线。以两个封头的母线点坐标和纤维角形式的计算结果用表2.1和2.2列出。轴坐标z从极孔方向的封头赤道平面算起。

表2.1 前封头型面点坐标和纤维角

Z,mm	0.0	2.63	5.25	7.88	10.52	13.15	15.80	18.46	21.12	23.18
r,mm	684.0	684.0	684.0	683.9	683.9	683.8	683.7	683.6	683.5	683.4
φ°	34.92	34.99	35.07	35.14	35.22	35.29	35.37	35.45	35.53	35.61
Z,mm	26.51	29.22	31.95	34.70	37.48	40.27	43.09	45.95	48.84	51.74
r,mm	683.2	683.0	682.8	682.6	682.4	682.2	681.9	681.6	681.3	681.0
φ°	35.70	35.78	35.87	35.95	36.04	36.13	36.23	36.32	36.42	36.52
Z,mm	54.68	57.67	60.69	63.74	66.85	70.01	73.20	76.44	79.75	83.11
r,mm	680.6	680.2	679.8	679.4	678.9	678.5	678.0	677.4	676.8	676.2
φ°	36.62	36.73	36.83	36.94	37.06	37.17	37.29	37.42	37.54	37.67
Z,mm	86.51	90.00	93.56	97.16	100.8	104.6	108.4	112.4	116.4	120.5
r,mm	675.5	674.9	674.1	673.4	672.5	671.7	670.7	669.8	668.7	667.6
φ°	37.81	37.94	38.09	38.24	38.39	38.55	38.72	38.89	39.07	39.25
Z,mm	124.7	129.0	133.4	138.0	142.6	147.4	152.2	157.2	162.4	167.7
r,mm	666.5	665.3	664.0	662.6	661.1	659.6	658.0	656.2	654.4	652.4
φ°	39.45	39.65	39.86	40.08	40.31	40.55	40.80	41.06	41.34	41.63
Z,mm	173.1	178.7	184.5	190.4	196.5	202.8	209.3	216.0	222.8	230.0
r,mm	650.4	648.2	645.8	643.4	640.7	638.0	635.0	631.8	628.5	624.9
φ°	41.94	42.26	42.60	42.96	43.34	43.74	44.17	44.62	45.10	45.62
Z,mm	237.3	244.9	252.8	260.9	269.3	278.1	287.1	296.6	306.5	317.0
r,mm	621.1	617.1	612.8	608.3	603.4	598.2	592.7	586.9	580.6	574.0
φ°	46.17	46.75	47.38	48.06	48.79	49.58	50.43	51.37	52.39	53.53
Z,mm	327.2	333.5	338.9	343.9	348.5	352.8	356.9	360.6	364.1	367.5
r,mm	567.2	563.2	559.2	555.2	551.2	547.2	543.1	539.1	535.1	531.1
φ°	54.73	55.31	55.91	56.52	57.16	57.82	58.49	59.19	59.92	60.68
Z,mm	370.6	373.5	376.2	378.8	381.2	383.4	385.5	387.4	389.2	390.8
r,mm	527.1	523.1	519.1	515.1	511.1	507.1	503.1	499.0	495.0	491.0
φ°	61.46	62.28	63.13	64.02	64.96	65.95	66.99	68.10	69.28	70.56
Z,mm	392.3	393.6	394.8	395.8	396.7	397.3	397.7
r,mm	487.0	483.0	479.0	475.0	471.0	467.0	463.0
φ°	71.94	73.46	75.15	77.10	79.44	82.52	89.81

封头厚度的设计选择采用关系式（2.21）—（2.23）进行。

前封头赤道点中的设计厚度按照封闭极孔的（2.21）公式计算，为

\({{h}_{a}}=\frac{pa}{2\bar{\sigma }{{\cos }^{2}}{{\varphi }_{a}}}=\frac{0.9\cdot 684}{2\cdot 180\cdot {{\cos }^{2}}27.6}=2.18\)mm。

假定小纤维角的单层厚度等于\({{h}_{e}}=0.3mm\)，按照公式（2.23）计算前封头赤道点中的螺旋单层的数量：

\({{h}_{cn}}=\frac{2.18}{0.3}=7.3\)。

将所得到的值化成更接近的偶数整数，结果就得到h_cn=8。

按照公式（2.22）计算前封头赤道附近筒体段上环向层的厚度：

\({{h}_{k}}=\frac{0.9\cdot 684\left( 2-t{{g}^{2}}27.6 \right)}{2\cdot 180}=2.95mm\)。

根据公式（2.23）计算前封头赤道附近的筒体段上环向单层层数：

\({{n}_{k}}=\frac{2.95}{0.3}=9.8\)。

将所得到的值四舍五入到更精确的整数，因而就得到n_k=10。

对于后封头也进行类似的计算，不同的地方是开口的极孔采用公式（2.21），而与子午线成34.9°角定向的基本单层厚度按公式（2.26）重新计算，为h_e=0.325mm。结果我们就有

\({{n}_{}}=6,\ \ {{n}_{k}}=9\)。

根据缠绕的连续性，两个封头上的层数应是相同的。从所得到的值中选择适合前封头的最大值。封头赤道上的螺旋层实际厚度为：

—对于前封头\(h_{a}^{\varphi }=8\times 0.3=2.4\) mm

—对于后封头\(h_{a}^{\varphi }=8\times 0.325=2.6\) mm。

承力壳体筒体段上的环向层总厚度等于\(h_{k}^{\varphi }=3\) mm。

采用公式（2.26）找出封头厚度沿子午线的分布，而对所选层数的验算根据公式（2.24）和（2.27）进行。

环向层中的作用应力等于：

—在前封头赤道邻域—1773MPa;

—在后封头邻域—1781MPa。

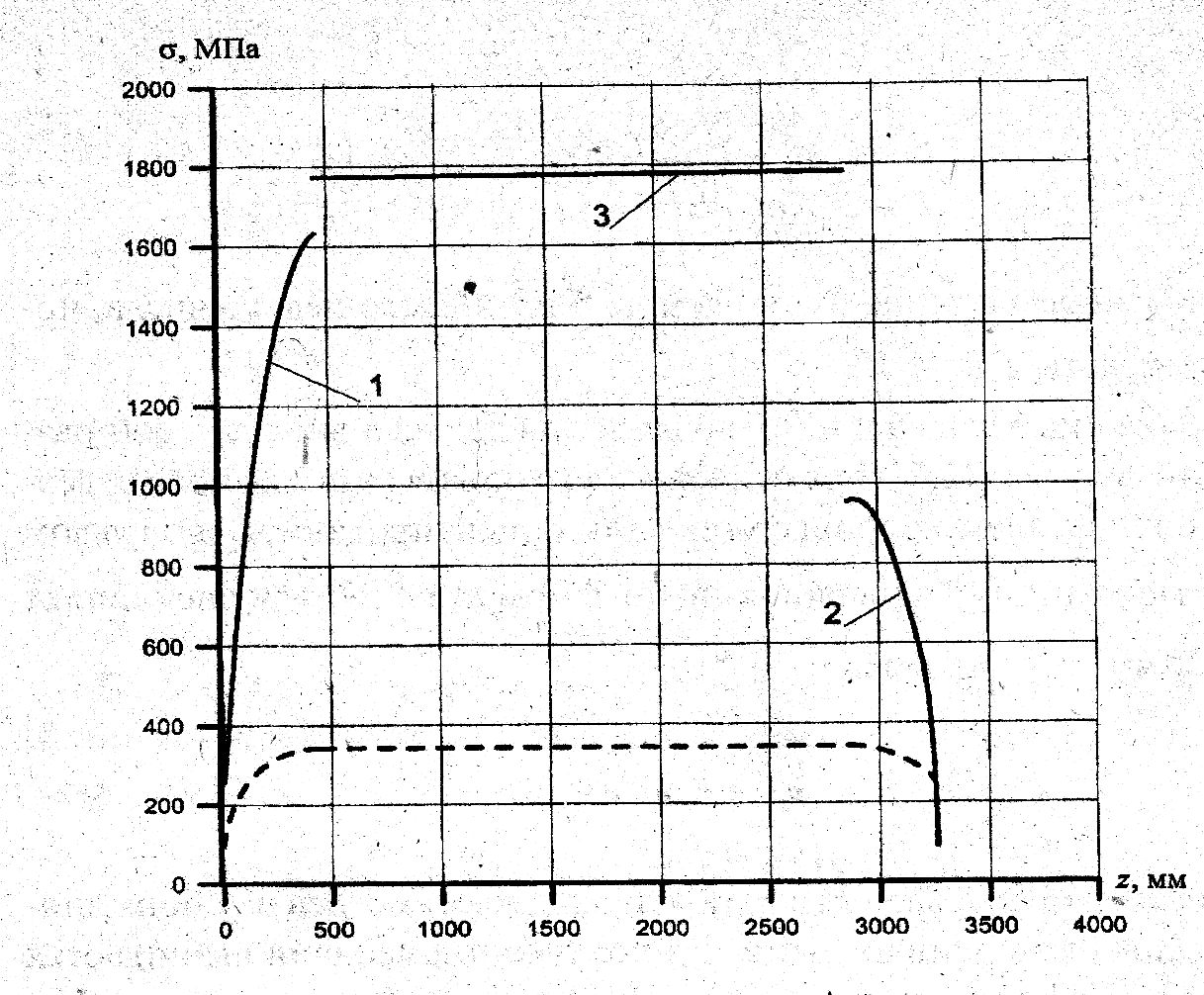
两个封头中的应力计算结果在表2.3和2.4中列出。应力沿结构子午线的分布用图2.3曲线图所示。曲线图上的虚线表示承力壳体的母线。曲线1和2表示结构螺旋层中的应力分布，而曲线3表示环向层中的应力分布。

图2.3 纤维纱中的作用应力沿回转轴的分布

1—前封头螺旋层中的应力分布；2—后封头螺旋层中应力分布；3—筒体段上环向层中的应力分布。

可以看出，螺旋层中的纤维纱应力最大值是在前封头赤道邻域实现（曲线1），为1632MPa,而后封头赤道邻域的应力要小30%，达到954MPa。图上未标出分布的承力壳体筒体段上螺旋层中的纤维材料应力在954—1632MPa范围内变化。环向纤维层中的应力按线性规律从1773MPa变化到1781MPa。

这样一来，我们就有下列计算载荷的最小安全系数值：

—前封头螺旋层中n_p=1800/1632=1.1；

—后封头螺旋层中n_p=1800/954=1.9；

—环向层中n_p=1800/1781=1.01。

表2.3 前封头的厚度和封头中的作用应力沿回转轴的分布

z,mm	0	10.46	20.90	31.33	41.74	52.12	62.45	72.73	82.96	93.12
h,mm	2.4	2.4	2.4	2.4	2.4	2.4	2.4	2.4	2.4	2.4
σ,MPa	1632	1627	1621	1614	1605	1596	1586	1574	1561	1548
z,mm	103.2	113.2	123.1	133.0	142.7	152.3	161.8	171.2	180.4	189.5
h,mm	2.4	2.4	2.4	2.4	2.4	2.4	2.5	2.5	2.5	2.5
σ,MPa	1534	1518	1502	1484	1466	1447	1428	1406	1386	1363
z,mm	198.5	207.3	216.0	224.5	232.8	241.0	249.1	256.9	264.6	272.1
h,mm	2.5	2.5	2.6	2.6	2.6	2.6	2.7	2.7	2.7	2.8
σ,MPa	1341	1317	1294	1269	1245	1220	1194	1168	1142	1116
z,mm	279.5	286.6	293.6	300.4	307.0	313.4	319.7	325.8	331.7	337.4
h,mm	2.8	2.8	2.9	2.9	3.0	3.0	3.0	3.1	3.1	3.2
σ,MPa	1089	1063	1036	1009	982	955	928	902	875	849
z,mm	342.9	348.3	353.5	358.5	363.4	368.0	372.6	376.9	381.1	385.2
h,mm	3.3	3.3	3.4	3.5	3.5	3.6	3.7	3.8	3.9	4.0
σ,MPa	823	796	771	745	720	695	670	646	622	599
z,mm	389.0	392.8	396.4	399.8	403.2	406.4	409.4	412.3	415.1	417.8
h,mm	4.1	4.2	4.3	4.4	4.6	4.7	4.9	5.1	5.3	5.5
σ,MPa	576	554	532	510	489	468	448	429	410	392
z,mm	420.4	422.9	425.2	427.5	429.7	431.8	433.8	435.7	437.6	439.4
h,mm	5.7	6.0	6.3	6.6	7.0	7.4	7.9	8.5	9.3	10.3
σ,MPa	374	357	341	326	311	297	285	274	265	258
z,mm	441.2	441.4	441.7	442.0	442.2	442.5	442.7	442.9	443.2	443.4
h,mm	11.6	11.8	12.1	12.4	12.7	13.0	13.3	13.7	14.1	14.5
σ,MPa	255	255	255	255	256	257	258	259	261	263
z,mm	443.6	443.8	444.0	444.1	444.3	444.5	444.6	444.8	444.9	445.0
h,mm	15.0	15.5	16.1	16.8	17.5	18.3	19.2	20.3	21.6	23.1
σ,MPa	266	269	272	276	282	288	296	305	316	331
z,mm	445.1	445.3	445.3	445.4	445.5	445.6	445.6
h,mm	25.0	27.5	30.7	35.6	43.6	61.4
σ,MPa	349	373	408	460	550	756

表2.4 后封头的厚度和封头中的作用应力沿回转轴的分布

z,mm	0.0	2.63	5.25	7.88	10.52	13.15	15.80	18.46	21.12	23.18
h,mm	2.6	2.6	2.6	2.6	2.6	2.6	2.6	2.6	2.6	2.6
σ,MPa	954	955	956	956	957	957	958	958	959	959
z,mm	26.51	29.22	31.95	34.70	37.48	40.27	43.09	45.95	48.84	51.74
h,mm	2.6	2.6	2.6	2.6	2.6	2.6	2.7	2.7	2.7	2.7
σ,MPa	959	959	959	959	959	959	959	958	958	958
z,mm	54.68	57.67	60.69	63.74	66.85	70.01	73.20	76.44	79.75	83.11
h,mm	2.7	2.7	2.7	2.7	2.7	2.7	2.7	2.7	2.7	2.7
σ,MPa	957	956	955	955	954	953	951	950	949	947
z,mm	86.51	90.00	93.56	97.16	100.8	104.6	108.4	112.4	116.4	120.5
h,mm	2.7	2.7	2.7	2.8	2.8	2.8	2.8	2.8	2.8	2.8
σ,MPa	945	943	941	939	937	934	932	929	925	922
z,mm	124.7	129.0	133.4	138.0	142.6	147.4	152.2	157.2	162.4	167.7
h,mm	2.8	2.8	2.9	2.9	2.9	2.9	2.9	2.9	3.0	3.0
σ,MPa	919	915	911	906	901	897	891	885	879	872
z,mm	173.1	178.7	184.5	190.4	196.5	202.8	209.3	216.0	222.8	230.0
h,mm	3.0	3.0	3.1	3.1	3.1	3.2	3.2	3.2	3.3	3.3
σ,MPa	866	858	850	842	832	823	813	801	790	777
z,mm	237.3	244.9	252.8	260.9	269.3	278.1	287.1	296.6	306.5	317.0
h,mm	3.4	3.4	3.5	3.6	3.7	3.8	3.9	4.0	4.1	4.3
σ,MPa	764	750	735	719	701	683	663	643	621	598
z,mm	327.6	333.5	338.9	343.9	348.5	352.8	356.9	360.6	364.1	367.5
h,mm	4.5	4.5	4.7	4.8	4.9	5.0	5.1	5.3	5.4	5.6
σ,MPa	574	558	542	525	509	493	476	460	443	427
z,mm	370.6	373.5	376.2	378.8	381.2	383.4	385.5	387.4	389.2	390.8
h,mm	5.8	6.0	6.2	6.5	6.7	7.1	7.4	7.8	8.3	8.9
σ,MPa	410	393	376	359	342	324	306	287	267	248
z,mm	392.3	393.6	394.8	395.8	396.7	397.3
h,mm	9.7	10.6	11.9	13.8	16.9	24.0
σ,MPa	227	20.5	182	156	126	88

最后，我们来评定所设计结构的刚度特性。假定纤维角沿长度是不变的，并等于后封头赤道上的纤维角，我们根据公式（2.28）就会计算出结构筒体段的刚度：

\({{B}_{11}}=8650\times 2.6\times {{\cos }^{4}}34.94{}^\circ =10165.8\)，

\({{B}_{12}}=8650\times 2.6\times {{\cos }^{4}}34.94{}^\circ {{\sin }^{2}}34.92{}^\circ =4954.7\)，

\({{B}_{22}}=8650\times 2.6\times {{\sin }^{4}}34.92{}^\circ +8650.3=28364.8\)。

在使用压强Р_ca=5.6MPa条件下，筒体段的轴向和环向相对变形\({{\varepsilon }_{1}}\)和\({{\varepsilon }_{2}}\)根据公式（.29）测定：

\({{\varepsilon }_{1}}=0.56\times 684\times \frac{0.5\times 28364.8-4954.7}{10165.8\times 28364.8-{{4954.7}^{2}}}=0.013\)，

\({{\varepsilon }_{2}}=0.56\times 684\times \frac{10165.8-0.5\times 4954.7}{10165.8\times 28364.8-{{4954.7}^{2}}}=0.011\)。

壳体的最大径向位移w和其长度\({{l}_{c}}=2420mm\)筒体段的轴向延伸率u根据公式（2.30）测定：

w=0.011·684=7.5mm, u=0.013·2420=31.46mm。

第三章壳体内热防护的计算和设计

3.1．所需的热防护层厚度的计算算法

所需的（带有密封层和防扩散层）热防护层厚度是根据在规定时间内所防护的承力壳体表面温度不超过所允许值，并具有给定可靠性的条件来测定的。

对于位于热防护层相对变形大的区域外的截面来说*，按下列公式计算所需的热防护层厚度：

\({{\delta }_{ins}}={{k}_{n}}\left[ {{k }_{g}}{{\delta }_{d}}\left( {{t}_{b}} \right)+{{\delta }_{np}}\left( {{t}_{b}} \right) \right]\)，（3.1）

式中k_g—惯性过载对热防护层破坏深度影响的经验系数；\({{\delta }_{d}}\)—破坏厚度；\({{\delta }_{np}}\)—加热到其内表面所允许温度的热防护层厚度；t_b—计算截面中燃烧产物对热防护层表面的作用持续时间；k_n—热防护层厚度余量系数（安全系数）。

过载对热防护层破坏深度的影响系数是用安置在离心机上的气体发生器按专用方法试验测定的。

热防护层的破坏深度用两种方法计算：

a)根据壳体热防护层和壁中的非定常热传导边界值问题的数值解，并以明显形式考虑到质量的表面和内部烧蚀；

b)利用以不明显形式考虑到质量表面和内部烧蚀的热防护层破坏经验系数。

在第二种情况中，利用如下公式来计算热防护层破坏厚度：

在\(t\ge {{t}_{k}}\)条件下， \({{\delta }_{d}}={{\xi }_{d}}\left( \sqrt{t}-\sqrt{{{t}_{k}}} \right)\) （3.2）

式中\({{\xi }_{d}}\)—热防护层的破坏系数；t—当前时间值；t_k—热防护层表面加热到碳化温度的时间。

升华型的热防护层质量烧蚀线性速度用如下公式计算：

\(v=\frac{q}{\rho H}\)，（3.3）

式中q—进入热防护层表面的热流密度；ρ—热防护层材料密度；H—热防护层有效热焓。

所有情况中的热防护层热透层厚度用数值解壳体壁中非定常热传导方程来计算。

对于位于热防护层相对高变形区的计算截面来说，所要求的热防护层厚度计算公式具有以下形式：

\({{\delta }_{ins}}=\delta _{ins}^{d}/\left( 1+{{\varepsilon }_{y}} \right)\) （3.4）

式中\({{\varepsilon }_{y}}\)—热防护层的横向变形。

热防护层的横向变形根据如下关系式计算

\({{\varepsilon }_{y}}=-{{\varepsilon }_{x}}-{{\varepsilon }_{z}}\)，（3.5）

式中\({{\varepsilon }_{x}},{{\varepsilon }_{z}}\)—热防护层的子午线方向变形和环向变形。

关系式（3.5）是在热防护层材料泊松系数值等于0.5条件下得到的。热防护层所包括的子午线方向变形和环向变形是根据“非金属壳体—金属法兰—热防护层”系统的应力变形状态计算而测定的。例如，在\({{\varepsilon }_{x}}=0.25,{{\varepsilon }_{z}}=0.02\)条件下，我们就得到\({{\varepsilon }_{y}}\)=-0.27。那么\[{{\delta }_{np}}=1.3\delta _{np}^{d}\]。

　　在计算已变形的热防护层热透层厚度时，采用考虑到变形对其影响所测定的热物理特性。

　　在计算“药柱-壳体”系统脱粘区（人工脱粘层外腔）中的热防护层厚度时，应考虑进入到人工脱粘层外腔的凝凝相附聚物的可能影响。

　　热防护层厚度余量系数值是用这个随机值的正态分布定律的假定来计算，这个正态分布定律是用统计处理一系列设计原型制品热防护层厚度的测量结果所得到的。应采用统计分析用实验规划所得到的实验数据的结果来计算余量系数。同时考虑到象下列这样一些因素的影响：

—材料中的组分含量；

—材料结构的不均匀性；

—热防护层、壳体、整个制品的热处理制度。

热防护层厚度的余量系数用如下关系式计算：

\({{k}_{n}}=1+\frac{\Delta \delta }{{{\delta }_{rated}}}\)，（3.6）

式中\(\Delta \delta \)—给定的热防护层无故障工作概率条件下的热防护层厚度偏差；\({{\delta }_{rated}}\)—热防护层特性额定值条件下所测定的热防护层所需厚度。

既然热防护层厚度是一个随机值，并取决于大量的原始独立因素，这个随机值的正态分布定律假定就是合理的，这一点被实物制品热防护层厚度测量结果的统计处理所证实。

在这种情况下，标准安全系数表达式可记作下形式：

\({{k}_{\delta }}=1+{{U}_{p}}{{\bar{s}}_{\delta }}\)，（3.7）

式中U_p—正态分布的分位数；\({{\bar{s}}_{\delta }}\)—热防护层厚度的离散差。

在具备热防护层厚度（或用于其计算的原始数据）与影响因素数学关系式条件下，安全系数值可根据相应因素离散程度用统计模拟（蒙特卡尔洛）方法，或用统计分析用实验规划所得到的试验数据的方法计算。

按照独立因素分组进行这个分析是很方便的：

\({{k}_{\delta }}=1+{{U}_{p}}{{\left[ \sum\limits_{i=1}^{I}{{{\left( {{s}_{\delta i}}/{{\delta }_{rated}} \right)}^{2}}} \right]}^{0.5}}\)，（3.8）

式中\({{s}_{\delta i}}\)—在i组独立因素离散影响下的热防护层厚度均方差。

其离散影响热防护层厚度离散的因素有下列因素：

1、基本工作因素：

—燃烧产物的温度；

—发动机燃烧室中的压强；

—燃烧产物流的速度；

—发动机工作时间；

—燃烧产物化学势；

—热防护层的变形。

2、工艺因素：

—压制的压力；

—加热速度；

—加热温度；

—保持时间；

—冷却速度。

3、半成品因素：

—原料性质；

—组分含量；

—结构的不均匀度。

除了这些因素外，应考虑热防护层制作精度及其厚度的测量精度。

3.2、内热防护层的非定常加热和烧蚀问题的提出

3.2.1、明显考虑内部烧蚀和表面烧蚀情况的带边界条件的非定常热传导方程

为了解决带热防护层的壁非定常加热问题，采用坐标系OY记作的非定常热传导一维方程，坐标系的原点与热防护层工作面的初始位置相连接，而轴与其垂直（与壁横向）方向定向。方程含有计算热防护层材料热分解时吸热和气态分解产物渗透对热防护层加热影响的项：

\(\left( 1-\varphi \right){\rho }'{{{c}’}_{p}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial y}\left( {{\lambda }_{\Sigma }}\frac{\partial T}{\partial t} \right)-{\dot{m}}”{{{c}”}_{p}}\frac{\partial T}{\partial t}-\omega \)。（3.9）

式中φ—热防护层的当前气孔率；\({\rho }’\)—孔状材料基体的密度；\({{{c}’}_{p}}\)—基体的比热；T—温度；t—时间；y—坐标；\({{\lambda }_{\Sigma }}\)—考虑基体碳化和气孔中辐射热迁移的材料有效导热系数；\({\dot{m}}”\)—热解气体的渗透质量速度；\({{{c}”}_{p}}\) —热解气体的比热；\(\omega ={{Q}_{\Sigma }}{{R}_{\Sigma }}\)—热解时的体积吸热速度；\({{Q}_{\Sigma }}\)—热解过程的总热效应；\({{R}_{\Sigma }}\)—热解过程的体积速度。

可将其右边的热传导项和渗透项合并来简化热传导方程（3.9）。为此目的，渗透项用如下形式表示：

\({\dot{m}}”{{\bar{c}}_{p}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial y}\left( {{\lambda }^{m}}\frac{\partial T}{\partial t} \right)\)，（3.10）

式中\({{\lambda }^{m}}={\dot{m}}”{{\bar{c}}_{p}}\delta \left( t \right)\)— “对流”导热系数；—温度范围内填充气孔的气体（蒸汽）比热平均积分值；—等温线\({{T}_{hp}}\)和\({{T}_{n}}\left( t \right)\)之间沿坐标y的距离；hp—热防护层材料热分解开始；n—热防护层表面。

“对流”导热系数公式中包含的热解气体渗透质量速度根据如下关系式计算：

\({\dot{m}}”={{\rho }_{0}}\left( 1-K \right){{\dot{\delta }}_{d}}\)，（3.11）

式中\({{\dot{\delta }}_{d}}\)—热分解（破坏）前缘向热防护层深处的移动速度。

将公式（3.10）代入方程（3.9）中后，方程（3.9）就被变换成如下形式：

\(\left( 1-\varphi \right){\rho }'{{{c}’}_{p}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial y}\left( \lambda _{\Sigma }^{m}\frac{\partial T}{\partial t} \right)-\omega \) （3.12）

式中\(\lambda _{\Sigma }^{m}={{\lambda }_{\Sigma }}-{{\lambda }^{m}}\)—考虑到材料热分解气态产物渗透的有效导热系数。

方程（3.12）源项中包含的热解过程体积速度表达式具有如下形式：

\({{\dot{R}}_{\Sigma }}={{\rho }_{0}}\left( 1-K \right)\frac{\partial X}{\partial }\)，（3.13）

式中\({{\rho }_{0}}\)—材料初始密度值；K—焦炭数；X—材料热分解过程的完成程度。

在将（3.13）表达式代入（3.12）中后，它就具有如下形式：

\({{C}_{ef}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial y}\left( \lambda _{\Sigma }^{m}\frac{\partial T}{\partial t} \right)\)，（3.14）

式中\({{C}_{ef}}=\left( 1-\varphi \right){\rho }'{{{c}’}_{p}}+{{\rho }_{0}}\left( 1-K \right){{Q}_{\Sigma }}\frac{\partial X}{\partial }\)—考虑到材料热分解过程热效应的材料体积比热。

非定常热传导方程（3.14）形式与实践中最广泛采用的无右边渗透项和源项热传导方程相似。这种形式的方程用于未被加热到热分解开始温度的壳体壁：

\({{\rho }_{0}}{{c}_{0}}\frac{\partial T}{\partial t}=\frac{\partial }{\partial y}\left( {{\lambda }_{0}}\frac{\partial T}{\partial t} \right)\)，（3.15）

式中\({{\rho }_{0}},\ {{c}_{0}},\ {{\lambda }_{0}}\)—初始状态的壁材料密度、比热和导热系数。

方程（3.14）和（3.15）的边界条件用下形式记作。

初始条件：

\(T\left( y,0 \right)={{T}_{0}}\left( y \right)\)。（3.16）

内热防护层表面上的边界条件：

\(-{{\lambda }_{\Sigma }}\frac{\partial T}{\partial y}\left| _{y={{y}_{n}}-0} \right.=\left( \frac{{{\alpha }_{k}}}{{{c}_{p}}}-{{\eta }_{q}}{{{{\dot{m}}”}}_{n}} \right)\left( {{I}_{s}}-{{I}_{n}} \right)+{{A}_{cp}}\sigma \left( _{Ts}^{4}-_{Tn}^{4} \right)+{{\dot{m}}_{y}}{{Q}_{y}}\) （3.17）

或 \(-{{\lambda }_{\Sigma }}\frac{\partial T}{\partial y}\left| _{y={{y}_{n}}-0} \right.={{\alpha }_{\Sigma }}\left( {{T}_{}}-{{}_{}} \right)+{{\dot{m}}_{y}}{{Q}_{y}}\)。

式中—气流与热防护层表面之间的对流热交换系数；\({{\alpha }_{\Sigma }}={{f}_{\alpha }}\left( \bar{x},t \right)\)—包含辐射分量的“总”热交换系数；\({{T}_{s}}={{f}_{T}}\left( \bar{x},t \right)\)—冲刷工作面的气流中心温度；\(\bar{x}=x/d\)—从封头圆周中心量起的相对弧坐标；d—壳体的直径；\({{\eta }_{q}}\)—逸出系数（对于涡流气流\({{\eta }_{q}}\)=0.2）；\({{A}_{cp}}\)—气流附壁层和表面的辐射参数计算或经验函数；σ—斯蒂芬-玻耳兹曼常数；\({{\dot{m}}_{y}},{{Q}_{y}}\)—表面烧蚀的质量速度和热效应。

层之间的边界条件：

\(\lambda \left( \frac{\partial T}{\partial y} \right)\left| _{y={{y}_{m}}-0} \right.=\lambda \left( \frac{\partial T}{\partial y} \right)\left| _{y={{y}_{m}}+0} \right.\)；（3.18）

\(T\left| _{y={{y}_{m}}-0} \right.=T\left| _{y={{y}_{m}}+0} \right.\)，（3.19）

式中\({{y}_{m}}\)—层之间m-边界的坐标。

壁外表面上的条件*：

\(\lambda \left( \frac{\partial T}{\partial y} \right)\left| _{y=y_{n}^{H}-0} \right.=0\)。（3.20）

对于容器筒体段来说，非定常热传导方程用如下形式表示：

\( C\left( T \right)\frac{\partial T}{\partial t}=\frac{1}{r}\left( r\lambda \left( T \right)\frac{\partial T}{\partial r} \right),\)

\( \quad r\in \left( {{R}_{0}},{{R}_{m}} \right);t>0 \) （3.14´）

式中在\(T<{{T}_{Hp}}\)条件下\(C\left( T \right)={{\rho }_{0}}{{c}_{0}},\ \lambda \left( t \right)={{\lambda }_{0}}\);在\(T<{{T}_{Hp}}\)条件下\(C\left( T \right)={{C}_{ef}}\left( T \right),\ \lambda \left( T \right)=\lambda _{\Sigma }^{m}\left( T \right)\); \({{R}_{0}},\ {{R}_{m}}\)—内表面和壳体层之间m-界面的半径值；\({{T}_{Hp}}\)—材料热分解开始的温度。

*由于壁是“热厚的”，在其内部可分出带\(y_{n}^{H}\)坐标的假定边界，在热作用结束时该边界上温度升高不超过3K。该边界被看作是计算区域的外（绝热）边界。

在壳体厚度与其曲率半径比值小的条件下，方程（3.14´）就变成与方程（3.14）和（3.15）等值方程。既然（3.14´）形式是比较普通的，我们下面就针对它的这种表示形式分析非定常热传导方程的有限差解。

3.2.2、热防护层碳化层表面质量烧蚀速度的计算

在所研究的情况中，热防护层碳化层的表面质量烧蚀是由碳与O, O₂, CO₂, H₂O气体的化学反应所造成的。当反应速度不取决于碳化层表面温度并由表面与气流热交换强度所决定时，这些反应以扩散方式进行。在假定药柱粒子随着碳化层的碳烧尽而均匀化学烧蚀条件下，可采用如下形式的公式来计算碳化层的化学烧蚀质量速度：

式中\(\frac{{{\alpha }_{k}}}{{{c}_{p}}}\)—燃烧产物流与热防护层表面之间的热交换系数；\({{B}_{m}}\)—燃烧产物的化学势；\({{K}_{m3n}}\)—热防护层的焦炭值；\({{\bar{m}}_{H}}\)—热防护层中的药柱质量分率；\({\rho }’,\ {{\rho }_{H}}\)—碳化层基体和药柱的密度；\({{t}_{*}}\)—碳化层烧蚀开始的时间；\({{k}_{x}}\)—所采用的化学烧蚀模型与试验的匹配系数。

对于碳与上面所列举的燃烧产物化学活性组分反应来说，它们的化学势可按如下公式计算：

\({{B}_{m}}=\frac{{{M}_{c}}}{{{M}_{s}}}\left( {{\mu }_{O}}+{{\mu }_{{{O}_{2}}}}+{{\mu }_{{{H}_{2}}O}}+{{\mu }_{C{{O}_{2}}}} \right)\)，（3.22）

式中\({{M}_{c}},\ {{M}_{s}}\)—碳和燃烧产物的分子量；\({{\mu }_{i}}\)—i组分克分子分率（i=O, O₂, H₂O, CO₂）。

碳化层化学烧蚀开始的时间根据下列条件计算：

a) 在逸出质量速度降低到相应级的条件下，质量交换系数大于零值：

\(\left( \frac{{{\alpha }_{k}}}{{{c}_{p}}} \right)\left| _{t={{t}_{*}}} \right.\ge 0\)；（3.23）

b）热解气体逸出质量速度在其进一步降低时，等于临界值*：

\({{{\dot{m}}”}_{n}}\left( t \right)\left| _{t={{t}_{*}}} \right.\le {{\dot{m}}_{*}}\)。（3.24）

*由于热防护层破坏速度的降低，热解气体逸出的质量速度也随着时间降低。因此碳化层表面的燃烧产物流附面层被挤开的物理效应开始不产生，然后不产生热解气体与燃烧产物活性组分相互作用的化学效应。

根据近似分析热防护层表面所形成的附面层中热质转移过程，假定化学反应对气体混合物扩散和热传递影响小，以及假定普朗特数、施密特数、刘易斯数相等，就可得到计算\({{\dot{m}}_{*}}\)的公式，由此得出相似的假物质浓度和焓的相对（换算）分布图：

\(\frac{\tilde{C}-{{{\tilde{C}}}_{n}}}{{{{\tilde{C}}}_{r}}-{{{\overset{\scriptscriptstyle\frown}{C}}}_{n}}}=\frac{I-{{I}_{n}}}{{{I}_{r}}-{{I}_{n}}}\)，（3.25）

式中\(\tilde{C}={{C}^{0}}-v{{C}^{a}}\)—假物质的浓度；\({{C}^{0}},{{C}^{a}}\)—热解产物中的氧化组分和化学活性组分的浓度；\(v\)—化学计算关系；I—热焓。

根据关系式（3.25），由防热层表面上的质量和热焓平衡条件就得到这个表面上假物质浓度的表达式

\({{\tilde{C}}_{n}}=\frac{{{{\tilde{C}}}_{r}}+B{{{{\tilde{C}}”}}_{n}}}{1+B}\)，（3.26）

式中\(B=\frac{{{{\dot{{m}”}}}_{n}}}{{{\alpha }_{k}}/{{c}_{p}}}\)—逸出的参数。

由于在\(\bar{t}*\)时刻热解气体与燃烧产物的相互作用前缘达到表面，\({{\tilde{C}}_{n}}\)变得等于零，由（3.26）表达式得

\({B}”{{{\tilde{C}}”}_{n}}={{{\tilde{C}}”}_{r}}=C_{r}^{0}\)。（3.27）

由此在\({{{\tilde{C}}”}_{n}}=-v{{\tilde{C}}_{\alpha }}\)条件下，从浓度转换到克分子分率我们就会得到热解气体排出质量速度临界值的如下形式未知公式：

\({{\dot{m}}_{*}}={{k}_{vm}}\frac{{{\alpha }_{k}}}{{{c}_{p}}}\) （3.28）

其中所包含的系数\({{k}_{vm}}\)根据如下关系式计算

\({{k}_{vm}}=\frac{1}{{{M}_{r}}}\sum\limits_{i}{{}}\sum\limits_{\beta }{{}}\frac{{{\mu }_{i}}{{{{M}”}}_{\beta }}}{{{v}_{i\beta }}{{{{\mu }”}}_{\beta }}}\)，

式中\({{\mu }_{i}}\)—燃烧产物流中i氧化组分的克分子分率；\({{{\mu }”}_{\beta }}\) —热解气体中化学活性组分的克分子分率（β=H₂, CH₄, C₂H₂诸如此类）；\({{M}_{s}},\ {{{M}”}_{\beta }}\)—燃烧产物和热解气体β组分的分子量；\({{v}_{i\beta }}\)—燃烧产物i氧化组分与热解气体β组分化学反应中的化学计算系数。

碳化层的线性烧蚀速度根据如下公式计算：

\({{v}_{y}}={{\dot{m}}_{y}}/{\rho }’\left( 1-\phi \right)\)。

根据这些数据确定热防护层工作表面的当前坐标

\({{y}_{n}}\left( t \right)=\int\limits_{{{t}_{*}}}^{t}{{{v}_{y}}dt}\)。（3.29）

包含在热防护层工作表面边界条件中的化学烧蚀热量按如下公式计算：

\({{Q}_{x}}=\left( \sum\limits_{i=1}^{4}{{{\mu }_{i}}{{Q}_{i}}} \right)/\left( \sum\limits_{i=1}^{4}{{{\mu }_{i}}} \right)\)，kJ/kg （3.30）

式中\({{\mu }_{i}}\)—燃烧产物组成中i化学活性组分的克分子分率；\({{Q}_{i}}\)—i组分与碳化学反应的热效应，kJ/kg。

燃烧产物活性组分与碳化学反应的热效应根据原始物质和相应反应产物生成的热量用赫斯定律计算：

\({{Q}_{i}}=\sum\limits_{\alpha }{{{v}_{\alpha }}\Delta {{H}_{\alpha }}-\sum\limits_{\beta }{{{v}_{\beta }}\Delta {{H}_{\beta }}}}\)，（3.31）

式中\(\Delta {{H}_{\alpha }},\Delta {{H}_{\beta }}\)—反应α产物和β原始物质生成的热量；\({{v}_{\alpha }},\ {{v}_{\beta }}\)—化学计算系数。

在高温下参加与碳化层碳化学反应的物质生成的热量在表3.1列出。

表3.1 参加与碳化层碳化学反应的物质生成的热量

物质的化学式	分子量，kg/mol	生成的热量，kJ/mol
CO	0.028	―110.53
CO₂	0.044	―393.51
H₂O	0.018	―286.03

燃烧产物化学活性组分与碳化层碳反应的热效应计算结果用表3.2给出。

表3.2 碳与燃烧产物活性组分反应的热效应

序号	反应	热效应
序号	反应	\({{Q}_{i}}\)kJ/mol_c	\({{Q}_{i}}\)kJ/kg_c
1	C + O →CO	―110.53	―9210
2	C + O₂ → CO₂	―393.51	―32792
3	C + CO₂ → 2CO	+172.54	+14371
4	C + H₂O → CO+H₂	+175.50	+14625

说明：符号《－》表示释放热量，《+》表示吸收热量。

用与现有的碳燃烧热量试验数据比较方法检验所得到的结果证实了所进行计算的正确性。

利用表3.2的数据，按公式（3.30）进行计算在药柱燃烧流中工作的热防护层表面碳化学烧蚀总热效应

\(\sum\limits_{i=1}^{4}{{{\mu }_{i}}}=0.647\)

\({{Q}_{x}}=+14474\)kJ/kg_c

所得到的碳化层材料化学烧蚀参数数值在计算内热防护层时使用。

3.2.3、利用破坏经验系数不明显考虑内部烧蚀和表面烧蚀情况的带边界条件的非定常热传导方程。

为了计算这种情况下的壳体壁中的非定常温度场，采用下列形式的用坐标系OY记作的热传导方程：

\(\rho c=\frac{\partial T}{\partial t}=\frac{\partial }{\partial y}\left( \lambda \frac{\partial T}{\partial y} \right)\)，（3.32）

式中\(\rho ,\ c,\ \lambda \)—取决于温度的壁材料密度、比热和导热系数。

方程（3.32）的边界条件具有下列形式。

初始条件：

\(T\left( y,0 \right)={{T}_{0}}\left( y \right)\)。（3.33）

内热防护层表面上的边界条件：

a) 在\(0<t\le { t }_{k}\)条件下

\({{\left. -\lambda \left( \frac{\partial T}{\partial y} \right) \right|}_{y={{y}_{n}}-0}}={{\alpha }_{\Gamma }}\left( {{T}_{\Gamma }}-{{T}_{\Pi }} \right)-{{A}_{EF}}\sigma \left( {{T}_{\Gamma }}^{4}-{{T}_{\Pi }}^{4} \right)\)

（3.34）

或

\({{\left. -\lambda \left( \frac{\partial T}{\partial y} \right) \right|}_{y={{y}_{n}}-0}}={{\alpha }_{\Sigma }}\left( {{T}_{\Gamma }}-{{T}_{\Pi }} \right)\)

（3.34´）

b) 在\(t\ge {{t}_{k}}\)条件下

\(T={{T}_{k}}=const\), (3.35)

式中\({{\alpha }_{s}}\)—气流与壳体内表面之间的对流热交换系数；\({{\alpha }_{\sum{{}}}}={{f}_{\alpha }}\left( \bar{x},t \right)\)—包含辐射分量的“总”热交换系数；\({{T}_{\Gamma }}={{f}_{T}}\left( \bar{x},t \right)\)—冲刷热防护层工作表面的气流中心温度；—从封头圆周中心量起的相对弧坐标；d—壳体的直径；\({{A}_{EF}}\)—气流附壁层和表面的辐射参数计算函数或经验函数；\(\sigma \)—斯忒藩-玻耳兹曼常数；\({{T}_{k}}\)—热防护层的碳化温度。

层间的边界条件：

\({{\left. \lambda \left( \frac{\partial T}{\partial y} \right) \right|}_{y={{y}_{m}}-0}}={{\left. \lambda \left( \frac{\partial T}{\partial y} \right) \right|}_{y={{y}_{m}}\text{+}0}}\) （3.36）

\({{\left. T \right|}_{y={{y}_{m}}-0}}={{\left. T \right|}_{y={{y}_{m}}\text{+}0}}\) （3.37）

式中\({{y}_{m}}\)—层间m边界的坐标。

在壁的外表面上采用条件（3.20）。

在所研究的情况中，在数值解将内热防护层加热到碳化温度时刻起的热传导方程时，要考虑内热防护层表面按（3.2）定律的位移。

3.3、气流和内热防护层表面之间热质交换参数的确定。

药柱燃烧前缘移到所研究的（带内热防护层）壳体壁截面邻域时刻起就开始从内部对壳体加热。从这个时刻起成分中含有凝聚相粒子和使碳氧化的组分的燃烧产物流就作用于壳体内表面。燃烧产物的温度在时间上是恒定的。压强是按照计算的曲线图随时间而发生变化。

对燃烧产物两相流与用烧蚀护面层防护的壳体表面之间的对流热交换强度进行计算，并考虑到下列因素:*

—气流含凝聚相粒子量；

—速度沿表面的变化性，表面曲率和粗糙度；

—从表面逸出气体。

*与已充分研究过的无梯度“纯”气流绕流光滑不透气薄板上的热质交换计算相比较，这些因素会使计算相当复杂。

所进行的理论和试验研究表明，对于工程实际应用来说，在某些简单的条件下，对流热交换近似计算方法会保障足够的准确性，这种近似计算方法是建立在利用关于所列举复杂因素叠加原理基础之上的。

按照这个方法，对于不含凝聚相粒子的气流所绕流的光滑不透气薄板上的斯坦顿数，采用众所周知的阿弗杜耶夫斯基判据公式作为基本计算关系式：

\(S{{t}_{0}}=0.0296{\text{Re}}_{x}^{-0.2}{{\Pr }^{-0.6}}{{\left( \frac{{{I}_{n}}}{{{I}_{r}}} \right)}^{0.39}}{{\left( 1+\frac{k-1}{2}r{{M}^{2}} \right)}^{0.11}}\)，（3.38）

式中 \(S{{t}_{0}}=\left( \frac{{{\alpha }_{k}}}{{{c}_{p}}} \right)/{{\rho }_{r}}{{u}_{r}}\)—斯坦顿数；

\({{\left( \frac{{{\alpha }_{k}}}{{{c}_{p}}} \right)}_{0}}\)—光滑不透气薄板上的热质交换系数；

\({{\rho }_{r}}\)—表面附近的气体密度；

\({{u}_{r}}\)—气流中心的速度；

\({{{\text{Re}}}_{x}}=\frac{{{\rho }_{r}}{{u}_{r}}x}{{{\mu }_{r}}}\)—雷诺数；

x—特性尺寸；

\({{\mu }_{r}}\)—在表面温度条件下的气体粘度；

Pr—在表面温度条件下的普朗特数；

\({{I}_{n}},\ {{I}_{r}}\)—表面附近和气流中心的气体热焓；

M—马赫数；

k,r—绝热指数和恢复系数。

由此，对流热质交换系数的计算公式就变成如下形式

\(\left( \frac{{{\alpha }_{k}}}{{{c}_{p}}} \right)=S{{t}_{0}}{{\rho }_{r}}{{u}_{r}}\)。

热交换定律对气流沿薄板表面的速度变化性的影响是保守的。如果将平静气流的参数局部值引入判据Re_x中，这个结果就使有可能在气体速度沿薄板表面变化的任何定律条件下有根据地采用（3.38）公式来计算热交换系数。

如果采用薄板有效长度(x_EF)作为特性尺寸，在计算任意形状物体表面上的对流热交换时也可采用这个公式。在这个有效长度的薄板上，附面层以与任意形状表面上相同的冲量损失厚度增大。薄板的有效长度根据如下公式计算

\({{x}_{EF}}=\frac{\int\limits_{0}^{x}{{{\rho }_{r}}{{u}_{r}}{{\left[ r\left( x \right) \right]}^{5/4}}dx}}{{{\rho }_{r}}{{u}_{r}}{{r}^{5/4}}}\)，（3.39）

式中x—从附面层开始形成的点（线）（例如，气体与表面接合线）算起的计算截面弧坐标；r(x)—表面到对称轴线的距离。

对于具有相对小曲率的表面来说，可以实际足够的准确性假定\({{x}_{EF}}=x\)。

通过将下列形式的相应修正值引入计算的途径来考虑复杂因素对热交换系数的影响：

\({{K}_{i}}={{\left( \frac{{{\alpha }_{k}}}{{{c}_{p}}} \right)}_{i}}/{{\left( \frac{{{\alpha }_{k}}}{{{c}_{p}}} \right)}_{0}}\)，（3.40）

式中\({{\left( \frac{{{\alpha }_{k}}}{{{c}_{p}}} \right)}_{i}}\)—考虑i复杂因素影响所计算的热值交换系数。

修正值K_i通常用能再现相应因素对热交换影响的气体动力或液压模拟装置实验测定。实验数据用K_i与说明该因素对热质交换定量影响的参数关系式的形式归纳。燃烧室条件中的热质交换系数总值按如下形式的公式计算：

\(\frac{{{\alpha }_{k}}}{{{c}_{p}}}={{\left( \frac{{{\alpha }_{k}}}{{{c}_{p}}} \right)}_{0}}\prod\limits_{i=1}^{I}{{{K}_{i}}}\)，

式中I—使热交换复杂化的因素数量。

气流的两相性对对流热交换系数的影响用如下形式的修正值考虑：

\({{K}_{\varphi }}={{\left( 1+\frac{{{{\bar{m}}}_{k\varphi }}{{{{c}’}}_{k\varphi }}}{1-{{{\bar{m}}}_{k\varphi }}{{c}_{r}}} \right)}^{0.45}}\)，（3.41）

式中\({{\bar{m}}_{k\varphi }}\)—气流中的凝聚相质量分率。

燃烧产物中所含的凝聚相对辐射热交换的影响在计算燃烧产物的有效辐射能力(ε_EF)时考虑。

气体从热防护层表面进入（逸出）附面层会使摩擦力和对流热交换减小。逸出对对流热交换的影响按如下公式计算：

\({{K}_{ED}}=1-0,19{{\left( \frac{{{M}_{r}}}{{{M}_{n}}} \right)}^{m}}B\)，（3.42）

式中\(B=\frac{{{\rho }_{n}}{{v}_{n}}}{{{\left( {{\alpha }_{k}}/{{c}_{p}} \right)}_{0}}}\)—逸出参数；\({{\rho }_{n}}{{v}_{}}\equiv {{{\dot{m}}”}_{n}}\)—逸出的质量速度；\({{M}_{s}},{{M}_{n}}\)—气流中心和表面附近的气体分子量。

这个公式中的指数m取决于\(\frac{{{M}_{s}}}{{{M}_{n}}}\)的值：

在\(0.2\prec {{M}_{s}}/{{M}_{n}}\prec 1\)条件下，m=0.35;

在\(1\prec {{M}_{s}}/{{M}_{n}}\prec 8\)条件下, m=0.7;

在\({{M}_{s}}/{{M}_{n}}=41.5\)条件下， m=1.0。

在\(0.1\le {{K}_{ED}}\le 5\)条件下，这个公式是适用的。随着气流逸出强度的增大，表面对流热流渐近达到零。

壳体内表面燃烧产物辐射热流按如下公式计算：

\({{q}_{L}}={{A}_{EF}}\sigma \left( T_{s}^{4}-T_{n}^{4} \right)\)， (3.43)

式中A_EF—温度T_S的燃烧产物所含的凝聚相粉尘粒子和温度T_n的表面之间的辐射热交换系数；σ—斯忒藩-玻耳兹曼常数。

假定燃烧产物流和壳体壁是带相应黑度ε_г和ε_п的灰色体，辐射热交换系数的表达式就变成如下形式

\({{A}_{EF}}=1/\left( \frac{1}{{{\varepsilon }_{s}}}+\frac{1}{{{\varepsilon }_{n}}}-1 \right)\)。（3.44）

对于药柱燃烧产物来说，值ε_г在相当窄的范围内变化：ε_г=0.6—0.85。因此，可采用回归关系式计算它。

ε_г=0.0229+0.0616d₃₂+0.00011T_г―0.3684\({{\bar{m}}_{c}}\)+ 0.00502p_г―0.00338L (3.45)

式中d₃₂—凝聚相粒子平均光学直径；\({{\bar{m}}_{c}}\)—燃烧产物中凝聚相质量分率；p_г—壳体中的压强；L—壳体截面的特性尺寸。

3.4、进行计算并对其结果处理

计算所需的热防护层厚度所采用的原始数据

为了计算壳体截面中所需的热防护层厚度，采用了下列原始数据。

1、根据承力壳体强度的保持条件所允许的承力壳体外表面温度—373K.

2．燃烧产物的温度—3415K。

3、壳体工作时间42.4秒。

4、壳体封头内表面绕流速度与时间的关系*。

5、初始状态的热防护层和承力壳体材料的相应热物理特性为：

—密度—1060和1300kg/m³;

—比热—985和1140J/(kg ·K) ;

—导热系数—0.233和0.184W/(m·K) 。

6、碳化温度—773K。

7、根据几何学计算结果所得到的壳体截面暴露时间*。

8、计算截面的工作时间*。

9、在20—4m/s速度范围内线性变化的热防护层破坏系数0.0012—0.0008m/s^0.5。

10、将热防护层表面加热到碳化温度的时间—1s。

11．考虑到惯性过载影响的系数—1.2。

12．安全系数—1.4。

13．计算截面的承力壳体厚度。

14．初始温度—293K。

*根据第1项的计算结果。

基本计算结果。

在计算内热防护层厚度时，针对利用破坏经验系数未明显考虑内部烧蚀和表面质量烧蚀情形，使用了数值解带有边界条件的多层板非定常热传导方程（见3.2部分）。

为了计算每一个截面中的内热防护层厚度，给定了承力壳体的厚度和相应边界条件下的内热防护层的假定厚度。根据计算结果分析了内热防护层—承力壳体界面上的温度。在该温度超过所允许值的情况下，就增大内热防护层厚度，否则，就减小热防护层厚度。在几次逼近后，选择了内热防护层的厚度，在该厚度条件下，内热防护层—承力壳体界面上就达到了所允许的温度。然后按公式（3.1）确定该截面中的内热防护层计算厚度。

壳体前封头及其邻接的筒体段计算截面的热防护层厚度计算结果在表3.3列出。在表中也列出了计算截面的内半径和热防护层的设计厚度。

表3.3 壳体前封头和筒体段的热防护层厚度，mm

半径,mm	141	160	180	200	220	240	262	289	320	357
计算的厚度,mm	12.4	12.1	11.8	11.3	10.9	10.6	10.1	9.7	9.2	8.8
半径/距赤道的距离,mm	399	463	501	552	610	660	678	711	735
计算的厚度,mm	8.3	8.3	8.7	8.8	9.1	8.3	7.8	7.1	6.6
半径/距赤道的距离,mm	70	101	132	159	187	215	244	273
计算的厚度,mm	6.2	5.6	5.2	4.6	4.1	3.5	2.8	2.0

壳体后封头及其邻接的筒体段计算截面的热防护层厚度计算结果在表3.4列出。在表中也给出了计算截面的内半径和热防护层的设计厚度。

表3.4 壳体后封头和筒体段的热防护层厚度，mm

半径,mm	408	428	448	468	488	508	528	548	568	558
计算的厚度,mm	11.6	11.2	10.6	10.2	9.8	9.2	8.8	8.4	8.0	7.6
半径/距赤道的距离,mm	608	628	648	662	671	678	682	-/21	-/11	-/41
计算的厚度,mm	7.1	6.6	6.2	5.7	5.2	4.6	4.1	3.5	2.8	2.0

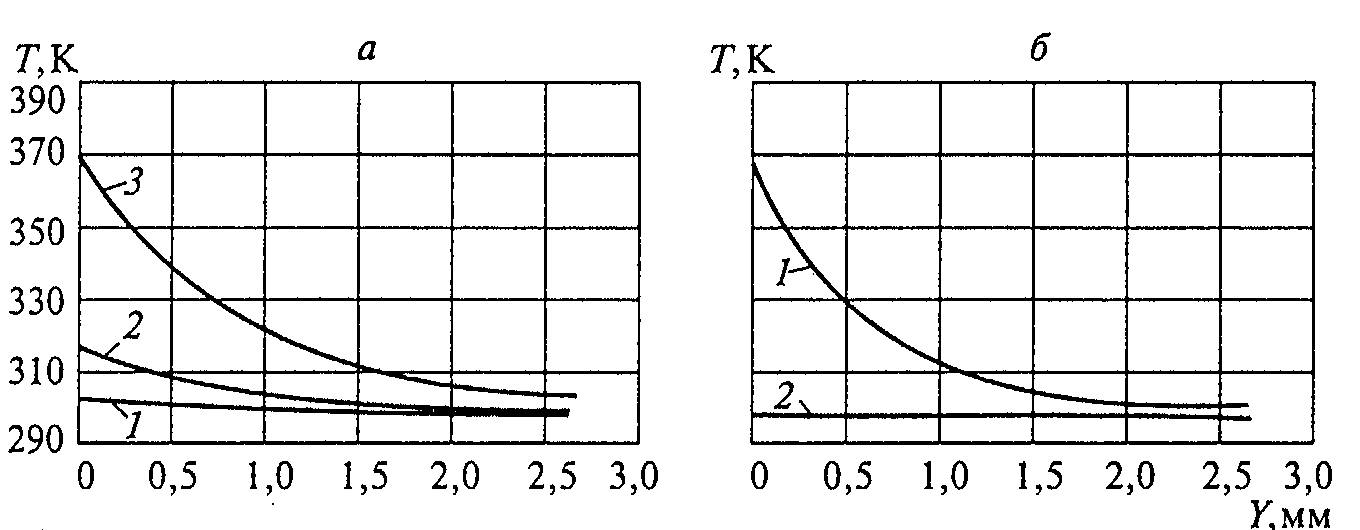
前、后封头特性截面的承力壳体中温度场计算结果用图3.1所示。

图3.1 沿前封头（a）和后封头（b）承力壳体厚度的温度分布图R=678mm。

1—t=42s; 2—t=35s; 3—t=30s。

第四章带局部孔的壳体封头设计

4.1、孔区补强的壳体强度试验计算根据

复合材料结构的设计实践提出了理论和试验研究带局部孔的层状壳体应力状态的迫切问题。壳体中偏心孔的存在会导致产生局部特征应力集中区域，这些区域在决定结构承载能力方面起着主要作用。孔区中增强纤维承载能力的丧失就决定了对孔边缘区域相应加强和补强的必要性。一系列有重大价值的专著对这些问题进行了理论研究。发表了一些研究纱带缠绕壳体中局部切口增强的专著，这些专著主要带有工艺特性并总结了国内外的经验。

我们来研究一下与试验测定用宽正交各向异性衬片补强的圆形孔区中层状壳体应力-变形状态相关的问题。

试验研究是用螺旋缠绕浸有ЭДТ-10粘合剂的ВМПС6,玻璃布所制作的壳体进行的。用单向试件所得到的材料物理力学特性具有下列值：

\({{E}_{1}}=5500Pa;{{E}_{2}}=1000Pa;G=365Pa;{{v}_{1}}=0.038;{{v}_{2}}=0.2;\sigma =130Pa\)。

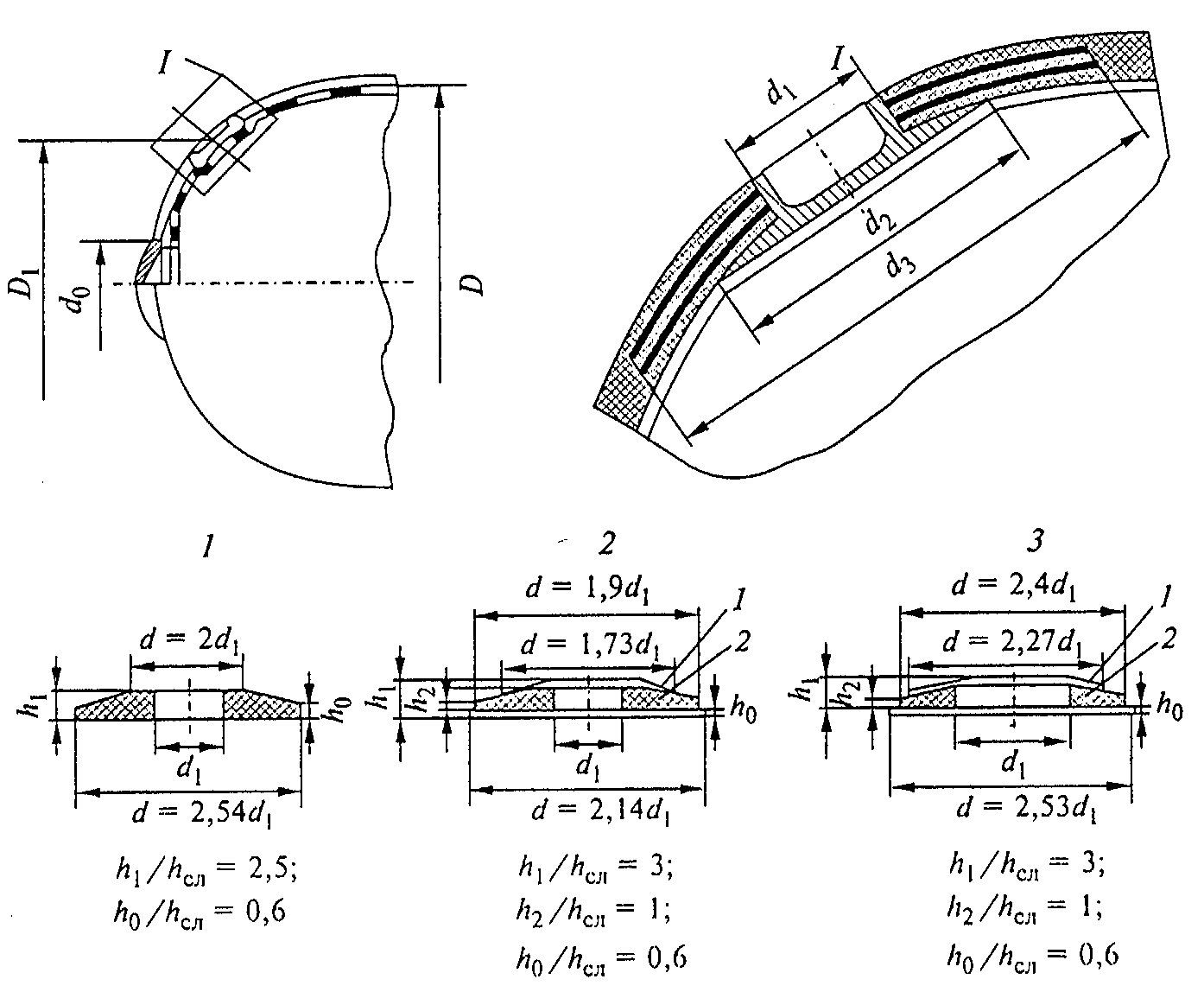
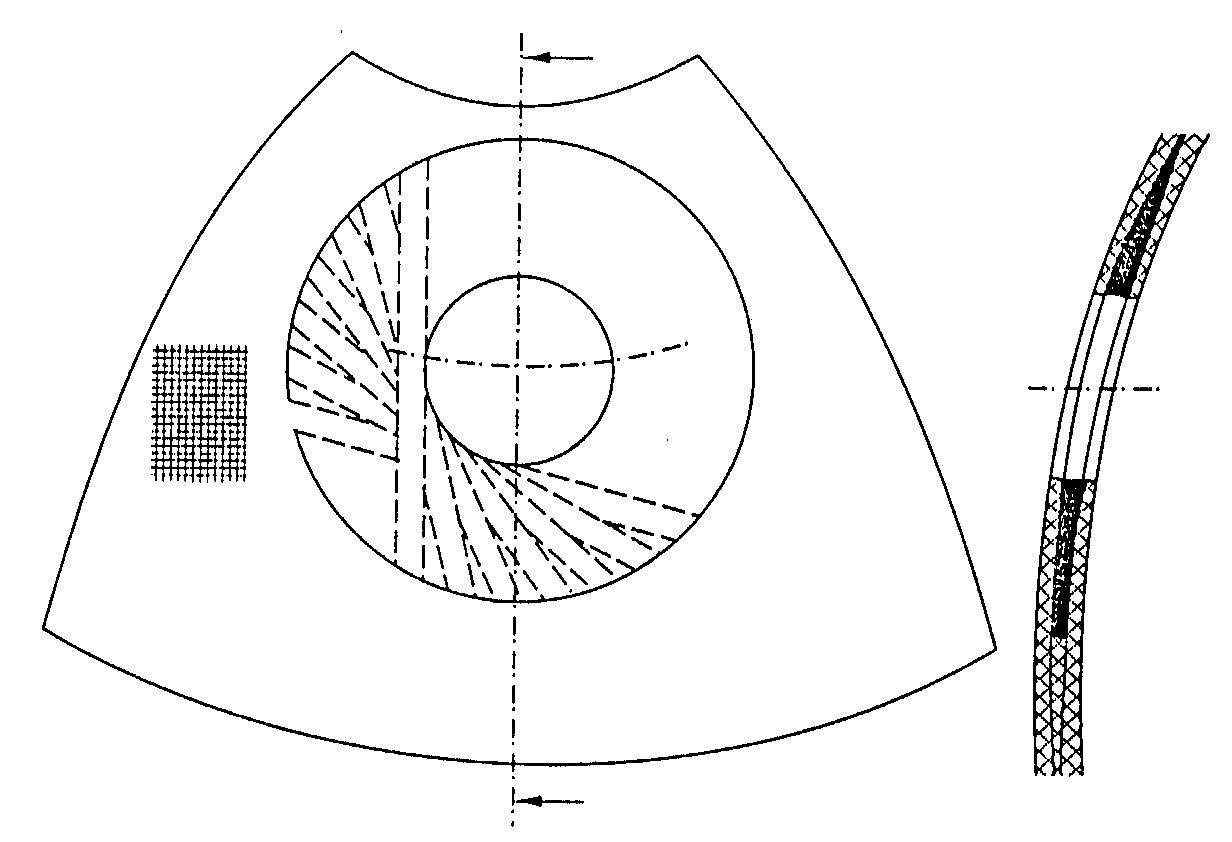
壳体结构型式用图4.1所示，主要几何参数具有下列关系式：

\({{d}_{0}}/D=0.242;\ {{d}_{1}}/D=0.1;\ {{D}_{1}}/D=0.77;\ {{d}_{2}}/{{d}_{1}}=1.3;\ {{d}_{3}}/{{d}_{1}}=\operatorname{var}\)

壳体的内表面是用下列方程给定的曲线绕轴线旋转形成的：

\(y=R\left[ \frac{1-{{k}_{2}}}{\sqrt{{{k}_{2}}}}F\left( k,\theta \right)+\sqrt{{{k}_{2}}}E\left( k,\theta \right) \right],r=R\sqrt{1-{{k}_{2}}{{\sin }^{2}}\theta }\)。

壳体厚度在子午线方向根据如下公式变化

\({{h}_{2}}=\frac{{{h}_{0}}R\cos {{\phi }_{0}}}{r\cos \phi }\)，

式中符号与论著^[5]中所采用的一致。

图4.1. 壳体的结构型式

研究是用三种类型的壳体进行的，这三种类型的相互区别只是衬片的补强类型不同，其结构和子午线截面用图4.1所示。壳体2和3的衬片是用ТСУ玻璃布制作。在衬片之间沿圆周和所切孔切线均匀铺放16根预浸的ВМПС玻璃纤维带，同时，补强层所用的单向玻璃纤维增强塑料（带）的力学性能具有下列值：

\({{E}_{1}}=5500Pa;{{E}_{2}}=1000Pa;{{G}_{12}}=365Pa;{{v}_{1}}=0.02;{{v}_{2}}=0.2\)。

在壳体l中仅仅用恒定厚度的布块实施补强，厚度比为

\({{h}_{1}}/{{h}_{0}}=2.5\)（\({{E}_{r}}=3200Pa;{{E}_{\phi }}=2100Pa;G=320Pa;{{v}_{1}}=0.14;{{v}_{2}}=0.19\)。

壳体是用ВМПС-6缠绕6层螺旋层和在筒体段附加缠绕15层环向层成型的。在缠绕螺旋层后逐层铺放增强衬片，采用下列工艺来制作衬片：a) 铺放增强带；b) 在110—115℃温度和50—60Pa压力条件下预压3—5秒。

为了保障壳体各层与补强衬片之间的粘附力，在放置补强衬片前给接触表面附加涂上BK-32型胶。借助光学敏感涂层和（所测量变形极限达3%）的КБП-10-200型应变仪对应变状态进行了研究。用聚乙烯聚胺固化的K-153混合物作为光学敏感涂层。分阶段地对壳体进行了加载，直至破坏。同时，在每一个加载阶段，在孔区测量了子午线方向和环向方向中的壳体外表面相对变形（坐标系的中心与非极孔的中心重合）。根据研究的结果，建立了变形分布图，并计算出了壳体外层的圆周应力值。

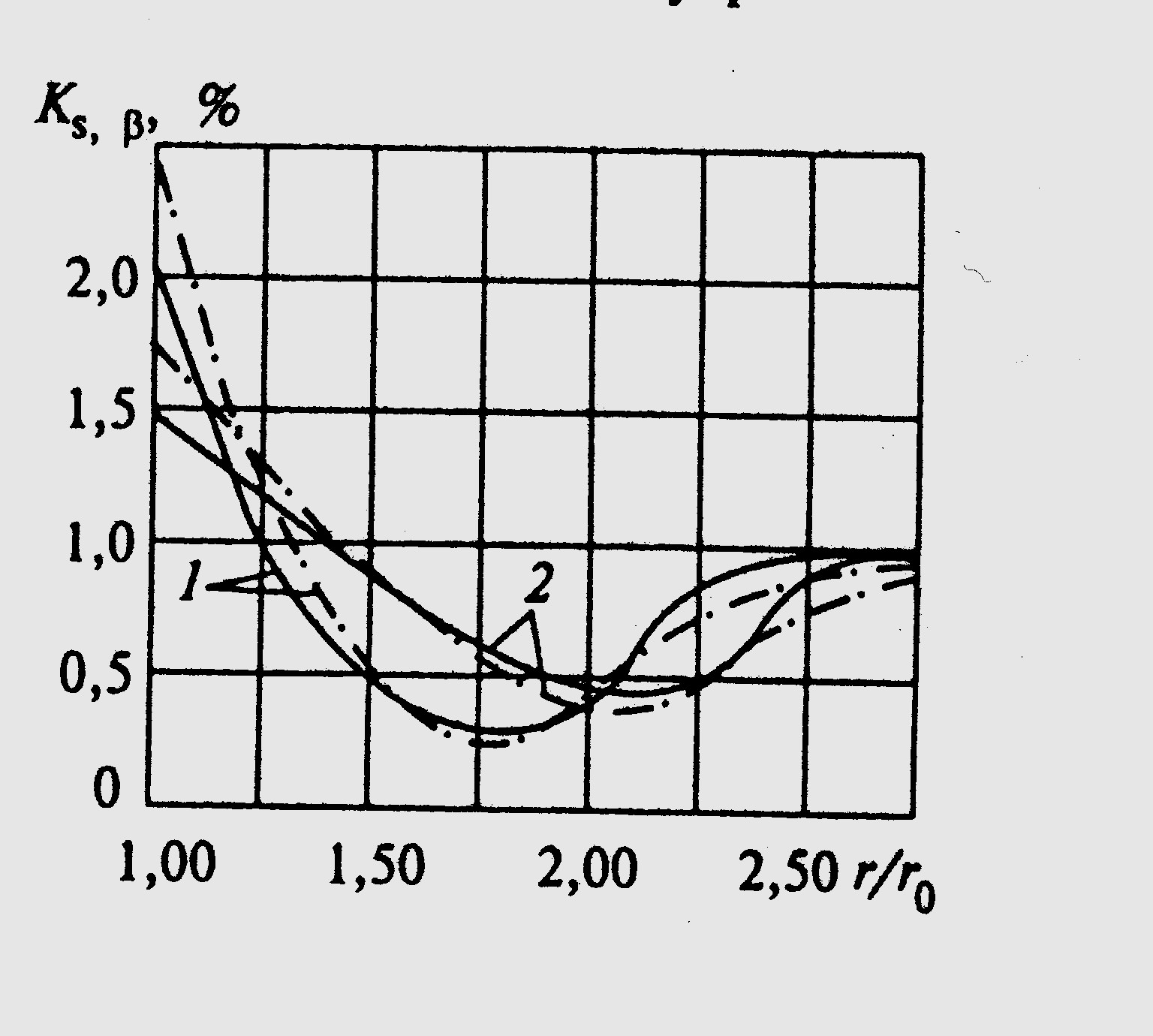
图4.2.а和4.2.b所示的是在加载强度条件下所得到的对三种类型补强（见图4.1）壳体外表面的变形测量结果用。在图4.2.а上曲线与壳体1、2、3 的β=0截面中的切线方向变形变化相对应；曲线4和5与壳体1，2的β=0截面中子午线方向变形变化相对应。在图4.2.b上曲线1，2与最大切线方向变形沿壳体1、2孔周边的变化相对应；曲线3与子午线方向变形沿第一种类型壳体的孔周边的变化相对应。

（a)

(b)

图4.2.针对三种类型补强所得到的壳体外表面变形测量结果

对沿补强区宽度变形的变化分析表明，变形视补强的类型而明显降低。例如，对于壳体第一和第三类型的壳体来说，最大变形的差为大致0.5%。在圆周方向变形的变化关系曲线中，可观察到反映该方向中壳体各层的物理-力学和几何性能变化的某些不对称。

应当注意到，实际上不用改变结构的重量，只改变补强衬片的增强方式就可将壳体的承载能力提高50%。

通过分析壳体破坏的结果，就会得出结论：对于所有类型的壳体来说，破坏发生在与等于1.92—2.16º角相一致的截面中的孔周边上，而且，对于所有壳体类型来说，在补强区会出现壳体分层。

下列计算方式用作为理论计算的基础：用可变几何和刚度参数的圆形层状板代替孔区的壳体；由孔和补强衬片所引起的扰动具有局部特性。

根据所采用的假定，将问题简化成测定带已知边缘载荷的薄板

（试片）的应力变形状态。同时，载荷变化规律和载荷值应根据距孔周边和补强衬片外边缘足够远的某一周边上的扰动条件来确定。扰动衰减界限根据试验结果确定。

由于外部边缘载荷分量的周期性，在所研究的问题中，可将说明应力变形状态（应力、变形、位移）的函数展成傅里叶圆周坐标级数，并分离出初始方程中的变量，结果就可得到如下形式的普通微分方程

\(\frac{dT}{dr}=A\left( r \right)T\) \(\left( {{r}_{0}}\le r\le c \right)\)，

式中\(T=\left( {{T}_{i}}{{S}_{i}}{{u}_{i}}{{v}_{i}} \right)\left( i=1,2,…,2n \right);A\left( r \right)=\left\| {{a}_{ij}} \right\|\left( ij=1,2,…,8n \right);T,{{S}_{i}}\)—i层中的径向力和剪切力；\({{u}_{i}},\ {{\upsilon }_{i}}\)—i层中的点径向位移和切向位移。

矩阵元是层和粘合剂夹层几何和刚度特性的函数。由于补强区和未补强区中的层刚度参数和层的本身数量不同，偶数矩阵元\(A\left( r \right)\)的最后矩阵是零值。在一般情况下，所研究的方程组由\(4n.k\)方程组成。当层的特性不按圆周坐标变化时，方程组分解成两个独立的\(4.n\)阶方程组（n—薄板的层数）。

所建议的应力变形状态计算方法是建立在数值解薄板每一部分的算题并自动满足其共轭条件的基础之上的。所得到的解是在对薄板轴对称加载（k=0）和二次谐波作用下的薄板应力变形状态因素幅度值。对于所研究的薄板给定点中的谐波号来说，解题算法设置有自动求和。

在所阐述的方法基础上，研究了孔区补强和处于恒定内压作用下的壳体应力状态定性图。

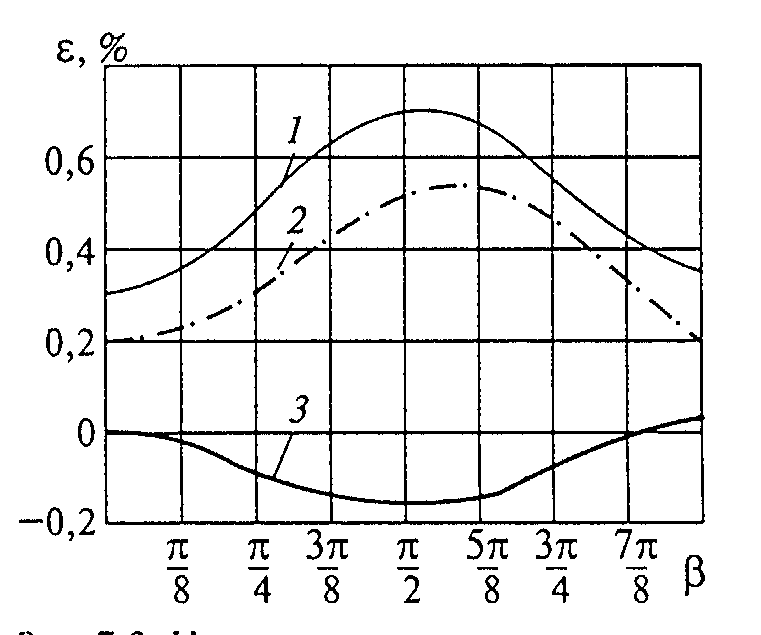
图4.3所示为圆周应力沿半径变化的试验和理论关系曲线，这些圆周应力与截面β=0中未扰动周边上的应力类似，曲线1，2与第一种和第三种类型壳体相对应；实线相对应的是试验值，点划线相对应的是数值分析结果。由所列出的关系式得出结论：对于所有研究的补强类型来说，壳体外层中的变形分布总特征是相似的。

图4.3. 壳体外层变形分布特性

1、2—对于第一种和第三种类型壳体（实线—试验值，点划线—数值分析结果）

计算和试验方法得到的结果比较表明，壳体应力状态的定性图重合是良好的。这证明根据所建议方法，以实际应用足够精度来计算相同类型壳体应力变形状态的可能性，其中包括在设计工作阶段通过采用某些经验得到的修正系数来评定所选补强方案效率并确定其合理参数的可能性。

4.2、孔区的增强结构工艺参数和部件的结构综合示意图。

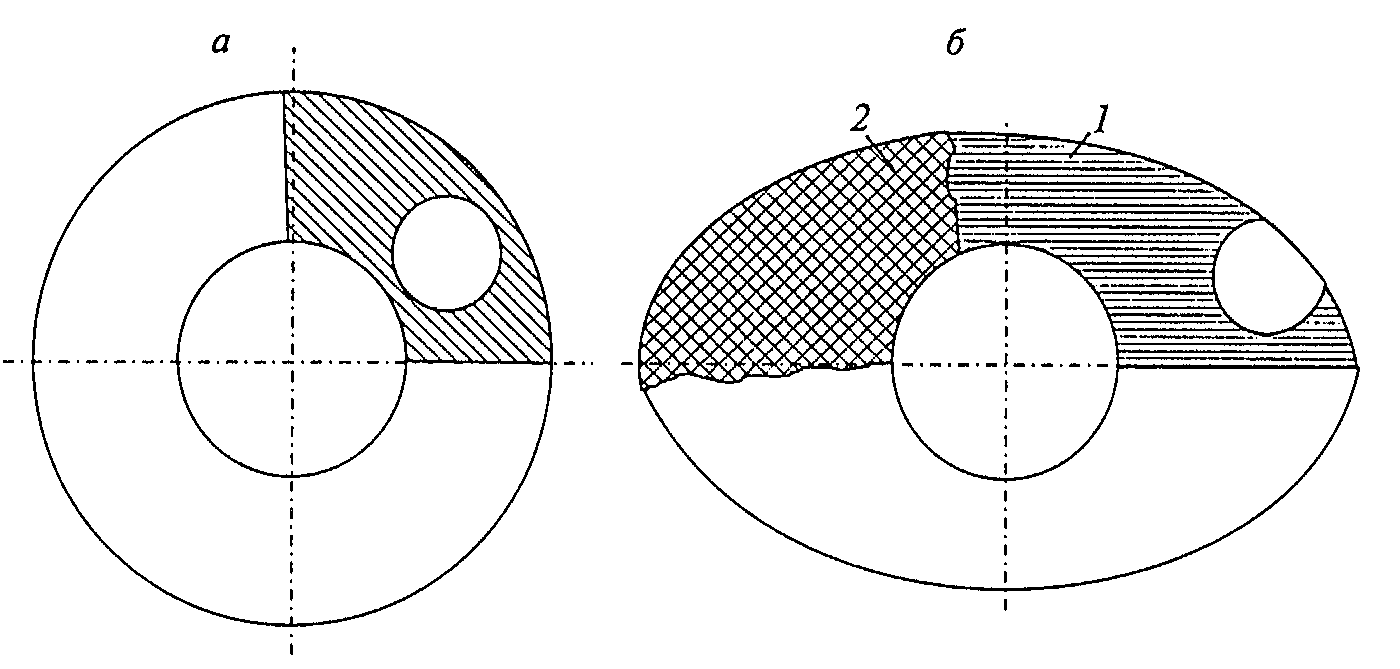
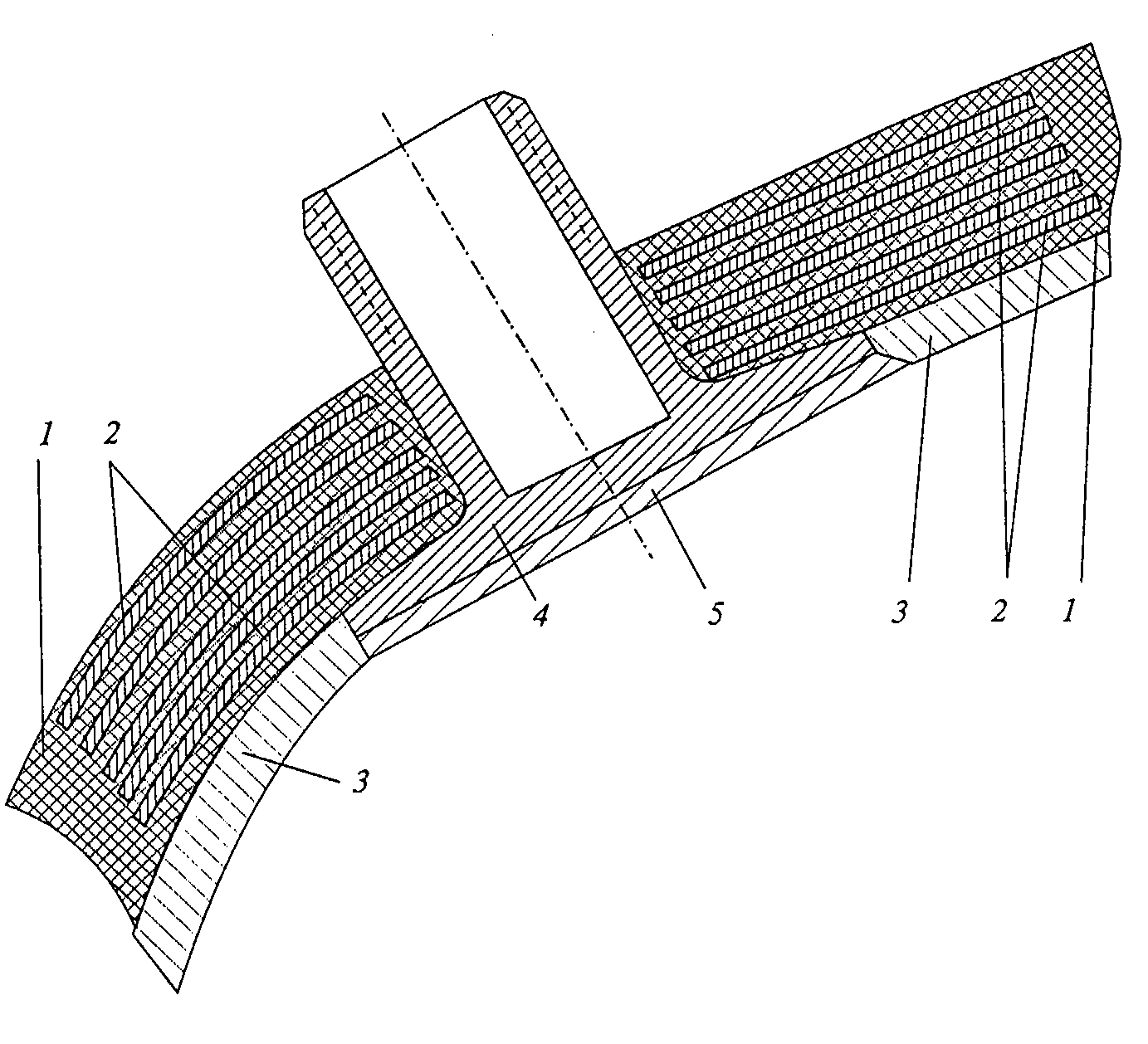
以现代工艺条件为基础的结构优化经验表明，在实践中可实现下列能基本符合对其所提出的要求并能保障壳体所需承载能力的主要类型补强结构件：布块、缠绕的衬片、补强垫。

在用缠绕方法制作结构时，这些补强件放置在材料主要层之间（见图4.4）。

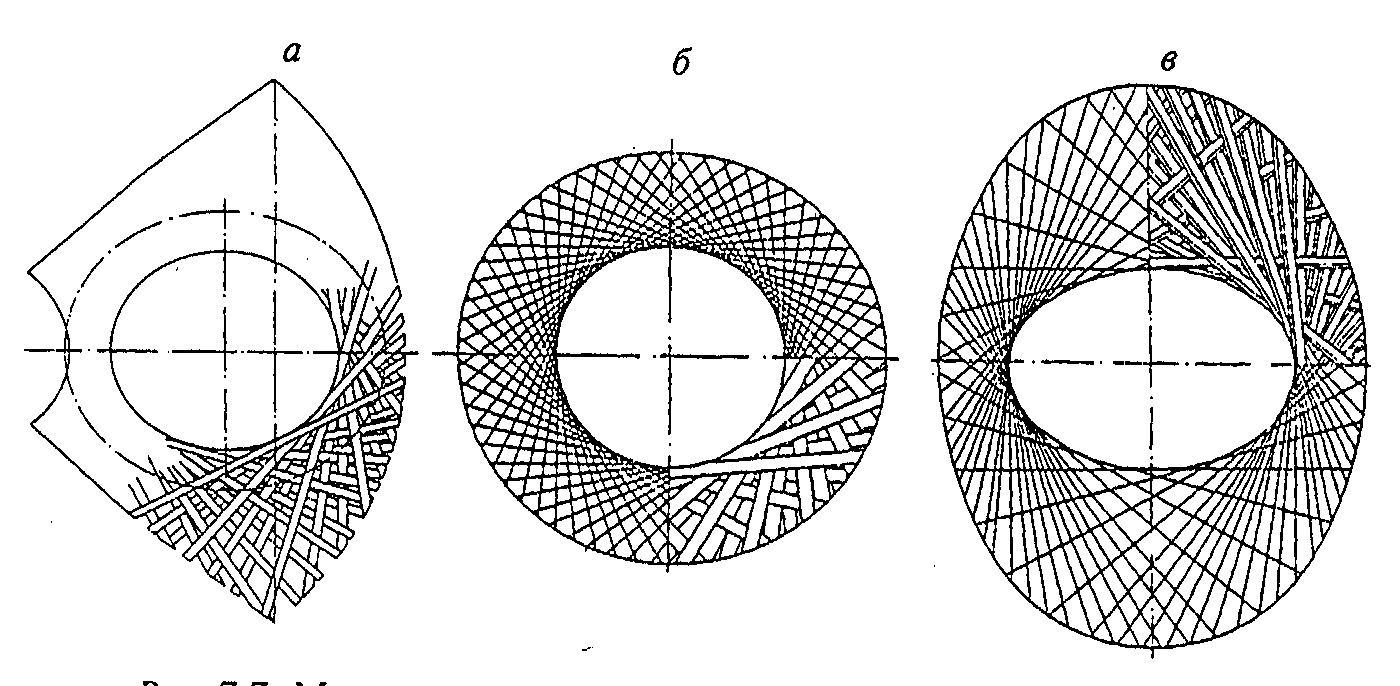
布块（见图4.5. a和b）是几层相互相对位移某一角度（或无位移）的布，或特种编织布，例如，径向-正切编织的布制作。

与布块相比，缠绕的纱衬片（见图4.6. а，b，в）具有很高的强

度和刚度性能。这些性能根据缠绕方式和衬片制作工艺而变化。在大多数情况下，这种衬片沿补强区宽度具有本质的不均匀性。此外，由于它们的制作特点，很难保障其内边缘足够的厚度。

在组合垫中（图4.7）所需的性能用一组横截面不同的、形状不同的各向异性和各向同性材料制作的单独构件来保障。

图4.4、孔区补强的壳体

图4.5、布块

a—径向正切编织布块，b—带层1和2位移的布块

图4.6. 壳体孔上缠绕好的纱垫衬片：

a—缠绕好的扇形纱垫；б—缠绕好的环形纱垫；в—缠绕好的椭圆形纱垫

图4.7、用于壳体孔补强的组合垫

图4.8.带胶合法兰的结构综合示意图

1—承力壳体；2—切口区的增强衬片；3—壳体的热防护；4—特种法兰；5—法兰的热防护

由于孔区的应力分布沿孔周边具有不均匀的特性，补强构件平面形状就可有多种多样的。在所研究的壳体结构中，非极孔的直径与筒体段的直径之比为:

\({{d}_{1}}/D\cong 0.1,\), 而\({{D}_{1}}/D\cong 0.77\)。

考虑到4.1部分所提交的研究结果，并按4.1部分所阐述的方法的精确计算，在所研制的结构中采用恒定厚度圆形布块增强四个偏心孔的方式，布块安置在承力壳体螺旋层之间的切口区中。作为材料使用的是厚度0.25—0.3mm的有机聚对芳酰胺苯并咪唑纤维（CBM）基布，其性能在表1.2节中列出。布块的直径280mm,厚度0.5—0.55mm (由两层布制作)。

在承力壳体缠绕过程中，安置布块的精度用专用工装来保障。为了保障壳体的层与补强布块（衬片）之间的粘附力，在安置前给布巾接触表面上涂抹BK型胶。

在壳体缠绕、固化和除去芯模后，在壳体封头划孔的位置线并进行切孔工序。为了制作孔，或采用普通的金属切削设备，或采用激光切割器。

最后的阶段是将法兰安置（胶合）在孔中。法兰的结构和材料由用途（推力中止、推力反向装置等）所决定。这种结构的综合示意图用图4.8所示。

第五章壳体连接部件的计算和设计

5.1、铆接金属箔连接的计算和设计

抗剪切和抗挤压强度差的复合材料特点使得必须在力学连接区域中采用在质量增加不大的条件下能提高其工作能力的加强构件。

连接的挤压破坏载荷可用下关系式测定

\({{P}_{CM}}=id\left( \sum\limits_{i=1}^{n}{{{\delta }_{i}}{{\sigma }_{CM}}+\sum\limits_{i=1}^{k}{{{\delta }_{i}}{{\sigma }_{CMF}}}} \right)\)，

式中i—铆钉数量；d—承力点的直径；\(\sum\limits_{i=1}^{n}{{{\delta }_{i}}},\sum\limits_{i=1}^{k}{{{\delta }_{if}}}\) —相应壳体和加强

构件的总厚度；n,k—复合材料和金属箔的层数。

用如下表达式类似测定连接的剪切破坏载荷

\({{P}_{cp.L}}=2i\left( c-d/2 \right)\left( \sum\limits_{i=1}^{n}{{{\delta }_{i}}{{\tau }_{cp}}+\sum\limits_{i=1}^{k}{{{\delta }_{i\varphi }}{{\tau }_{cp.\varphi }}}} \right)\)，

式中c—距片边缘的距离；τ_cp,τ_cpф—基材和加强构件的剪切破坏应力。

用如下公式计算强度受损截面的连接破坏载荷

\({{P}_{F}}=\frac{\psi }{{{K}_{a}}}\sum\limits_{i=1}^{n}{{{\sigma }_{Bi}}\left( t-d \right){{\delta }_{i}}}+\frac{1}{{{K}_{\varphi }}}\sum\limits_{i=1}^{k}{{{\sigma }_{B\varphi }}\left( t-d \right){{\delta }_{i\varphi }}}\)，

式中\(\psi \)—考虑复合材料强度增大的系数；\({{K}_{a}},{{K}_{\varphi }}\)—复合材料和加强件孔周围的应力集中有效系数；t—承力点之间的间距；σ_Bi ,σ_Bф—给定方向中的i层复合材料和加强件的强度极限。

复合材料结构设计和试验的经验表明，从得到最小质量观点来看，在许多情况下铆接金属塑料对接连接是最受欢迎的（图5.1）。

图5.1. 用高强金属箔增强的铆接金属塑料连接

1—端框；2—承力壳体；3—弹性楔；4—端框补缠绕层；5—胶合层；6—铆钉；7—金属箔。

为了增大复合材料的抗拉、抗剪、抗挤压强度，提高连接的工作能力，在铆接区采用高强各向同性材料加强金属箔。由于明显的复杂

性，应根据等强度和质量函数最小值条件来解决金属箔连接的设计的

问题。下面举出连接段—壳体的铆接设计方法。

用如下形式记下连接的等强度性条件：

\({{P}_{0}}={{P}_{CM}}={{P}_{cp.L}}={{P}_{cp.m}}={{P}_{F}}\). （5.1）

或通过应力表示这个条件，

\(\sum\limits_{i=1}^{n}{{{\sigma }_{B\alpha }}t{{\delta }_{icL}}=\frac{\psi }{{{K}_{a}}}\sum\limits_{i=1}^{n}{{{\sigma }_{B\alpha i}}}\left( t-d \right){{\delta }_{icc.\varphi}}=id\left( \sum\limits_{i=1}^{n}{{{\delta }_{icL}}{{\sigma }_{CM}}}+\sum\limits_{i=1}^{k}{{{\sigma }_{CM.\varphi}}{{\delta }_{i\varphi}}} \right)}= \)

\(=2i\left( \text{c-}\frac{d}{2} \right)\left( \sum\limits_{i=1}^{n}{{{\delta }_{icL}}{{\tau }_{cp.a}}}+\sum\limits_{i=1}^{k}{{{\delta }_{i\varphi }}{{\tau }_{cp. \varphi }}} \right)=ji\frac{\pi {{d}^{2}}}{4}{{\tau }_{cp.m}} \)

式中\({{P}_{0}},\ {{P}_{F}},{{P}_{CM}},{{P}_{cp.L}},{{P}_{cp.m}}\)–连接整个截面，强度受损截面相应的片挤压、片剪切、承力点剪切破坏载荷；τ_cp.т—承力点的剪切破坏应力；j—对于单或双剪铆钉连接来说，相应等于一或二。

显然，当连接区的强度系数\(\psi =1\)时，连接是有效的。对此，我们通过联立解方程来测定连接的所有参数\(c,d,i,t,{{\delta }_{IcL}},\sum{{{\delta }_{i\varphi }}}\)，

\(G=I\left\{ \frac{\pi {{d}^{2}}}{4}\left( L-S \right){{\gamma }_{3}}+2t\left( c-\frac{d}{2} \right)\left[ \sum\limits_{i=1}^{n}{{{\delta }_{ikk}}{{\gamma }_{k}}} + \sum\limits_{i=1}^{k}{{{\delta }_{ikk}}{{\omega }_{\lambda \varphi }}} \right] \right\}\).，

\(\frac{d}{\sum\limits_{i=1}^{n}{{{\delta }_{icc}}}}=\frac{1}{\gamma }\frac{4}{\pi }\left( \frac{{{\sigma }_{CM\alpha }} + {{\omega }_{\max }}{{\sigma }_{CM.\varphi}}}{{{\tau }_{cp.m}}} \right)\)；

\(\frac{c}{d}=\frac{{{\sigma }_{CM.\alpha}} + {{\tau }_{cp.\alpha}} + {{\omega }_{m\alpha \alpha}}\left( {{\sigma }_{CM.\varphi}} + {{\tau }_{cp.\varphi}} \right)}{2\left( {{\tau }_{cp.\alpha}} + {{\omega }_{\max }}{{\tau }_{cp.\varphi}} \right)}\)，

\({{\omega }_{1}}=\frac{\sum\limits_{1}^{n}{{{\delta }_{m\varphi}}}}{\sum\limits_{1}^{n}{{{d}_{icc}}}}=\frac{{{\sigma }_{B\alpha }}}{{{\sigma }_{B\varphi}}}\left( \frac{{{K}_{\varphi}}}{1-\lambda }-\frac{\psi {{K}_{\varphi}}}{{{K}_{\alpha }}} \right)\)；

\({{\omega }_{2}}=\frac{\sum\limits_{1}^{k}{{{\delta }_{i\varphi}}}}{\sum\limits_{1}^{n}{{{d}_{icc}}}}=\frac{{{\sigma }_{CM.\alpha }}}{{{\sigma }_{CM.\varphi}}}\left( \frac{{{\sigma }_{CM.\alpha }}\psi }{{{\sigma }_{CM.L}}} \right)\)；

\({{\omega }_{3}}=\frac{\sum\limits_{1}^{k}{{{\delta }_{i\varphi}}}}{\sum\limits_{1}^{n}{{{d}_{icc}}}}=\frac{{{\tau }_{cp.\alpha }}}{{{\tau }_{cp.\varphi}}}\left( \frac{\psi }{i}\frac{{{\sigma }_{B\alpha }}}{{{\tau }_{cp.\alpha }}}\frac{1}{\frac{2}{t}-\lambda }-1 \right)\)；

\(i=\frac{1}{j}\frac{4}{\pi }\psi \frac{{{\xi }_{B\alpha}}}{{{\tau }_{cp.m}}}\frac{1}{\lambda }\frac{\sum\limits_{1}^{n}{{{\delta }_{icc}}}}{d}\)。（5.2）

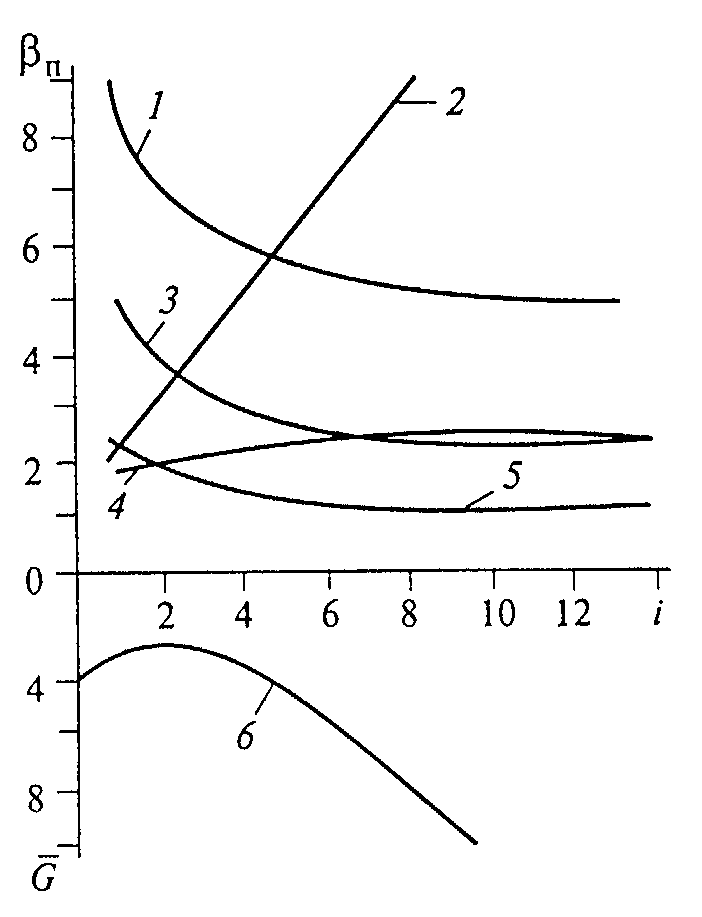
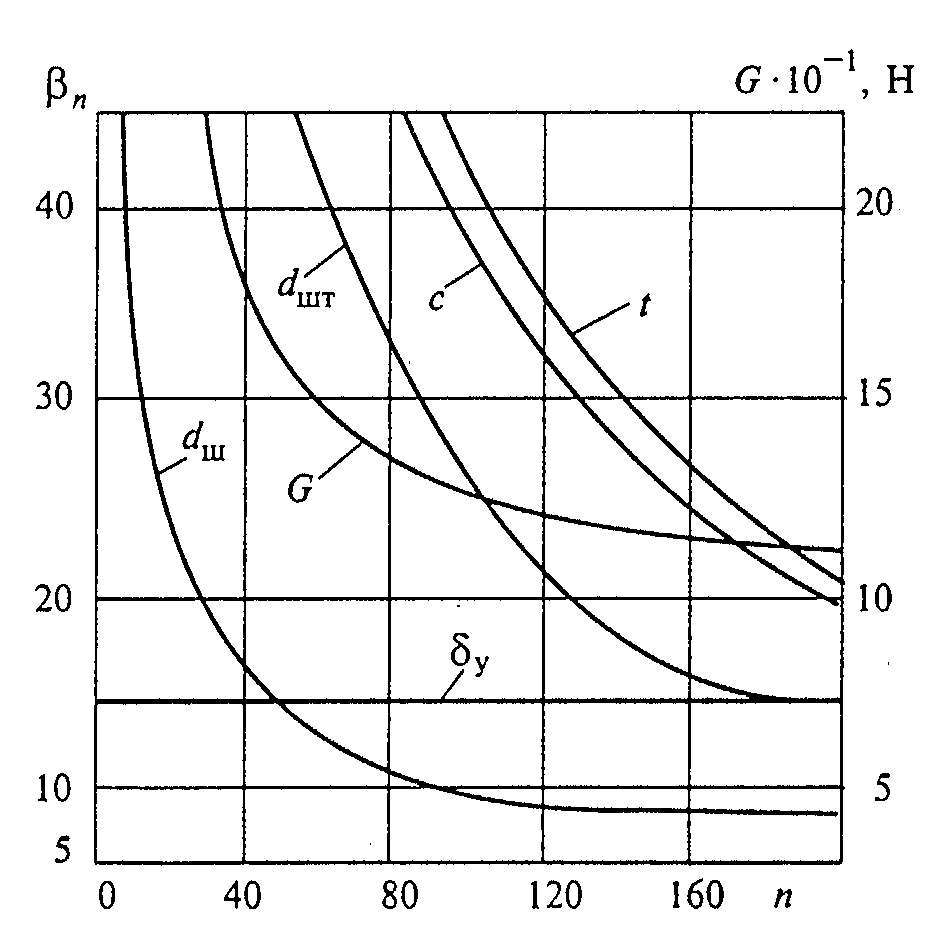
在所列的关系式中\(\omega \)—用金属箔增强对接区的系数，而且\(d/t=\lambda \)。针对ЭДТ-10基玻璃纤维增强塑料、1X18H9T牌号钢箔和钢铆钉制作的壳体而选择铆接最佳参数（\(c,d,i,t,\omega \)）的计算图用图5.2所示。

图5.2.用金属箔增强的铆接最佳参数β_п选择计算图

1—增强系数（\(\omega \)）；2—t/d; 3—\(d/\delta \left( j=1 \right)\);

4—c/d； 5—\(d/\delta \left( j=2 \right)\); 6—\(G\left( j=1 \right)\) 。

初始力学性能如下：\({{\sigma }_{CM\alpha }}\)=500MPa; \({{\sigma }_{B.\alpha }}\)=550MPa; τ_cp.α=80MPa; σ_вф=1300MPa; σ_см.ф=1690MPa; τ_ср.ф=900MPa; τ_ср.т=380MPa; \(\psi \)=1.05; \({{K}_{\alpha }}\)=1.1; \({{K}_{\varphi}}\)=1.05; 玻璃纤维增强塑料密度γ_км=1.8·10⁴kg/m³, 金属箔的密度γ_ф=7.8·10⁴kg/m³，铆钉密度γ_з=7.8·10⁴kg/m³。连接的最佳参数

根据质量函数最小值条件确定，为 \(c/d=2.05;\ t/d=3.15;\ \)\(\ d/\delta =1.8;\)

\(\ \omega =0.29;i=2\)

5.2、金属箔柱销–螺栓连接的计算和设计

根据上面所列举的关系式，我们来研究柱销-螺栓连接的设计。我们来对柱销-螺栓连接类型的法兰对接件的作用载荷进行分析（图5.3）。如果拉紧螺栓（双头螺栓）沿对接圆周等距离配置，在中心拉伸条件下，它们就均匀传递对接截面中的法向力。

拉紧螺栓（双头螺栓Ш）中的应力

\({{\sigma }_{Ш}}=4N/\left( {{n}_{Ш}}\pi d_{Ш}^{2} \right)\)，（5.3）

式中\({{n}_{Ш}}\)—拉紧螺栓（双头螺栓）的数量。

在中心压缩条件下，只是法兰传递法向力，而且压缩应力是沿接触面积均匀分布并用下公式测定

\(\sigma =N/{{F}_{\varphi}}\), (5.4)

式中\({{F}_{\varphi }}\)—法兰的接触面积，不考虑拉紧螺栓孔的面积。

在弯曲条件下，中性轴的位置和双头螺栓及法兰中的应力取决于法兰和拉紧螺栓的刚度比（图5.3）：

\({{\sigma }_{pacm}}={{E}_{Ш}}\frac{{{y}_{H.O}}}{\rho },\) \({{\sigma }_{CHC}}={{E}_{\varphi}}\frac{{{y}_{HO}}}{\rho }\)，（5.5）

式中\({{y}_{HO}}\)—从中性轴到所研究对接点的距离；\({{E}_{bt}},{{E}_{\varphi}}\)—螺栓和（壳体）法兰的弹性模量。

图5.3.用金属箔增强的柱销螺栓连接结构和几何参数。

在纯弯曲条件下

\(N=\int\limits_{F}{\sigma dF=0,}\) \({{M}_{u3s}}=\int\limits_{F}{\sigma ydF}\)。

代入σ值并不考虑拉紧螺栓孔的面积求压缩区法兰接触面积积分后，得

\(\left( {{E}_{Ш}}+{{E}_{\varphi}} \right)S_{x}^{k}-{{E}_{Ф}}S_{x}^{{{n}_{Ш}}}+{{E}_{Ф}}{{S}_{x}}=0\)；（5.6）

\(\frac{1}{p}\left[ \left( {{E}_{Ш}}+{{E}_{Ф}} \right) \right]_{x}^{K}-E_{Ф}^{{{n}_{Ш}}}+{{E}_{Ф}}{{J}_{x}}={{M}_{u3s}}\)，（5.7）

式中\(S_{x}^{k},S_{x}^{{{n}_{Ш}}},{{S}_{x}},{{J}_{x}}\)—拉伸区中的螺栓、所有螺栓\[{{n}_{Ш}}\]和（不考虑拉紧螺栓孔面积）的法兰压缩区面积的相应静力矩和惯性矩。

将静力矩和惯性矩值代入表达式（5.7）中，得

\(\frac{{{E}_{Ф}}\pi Dh}{{{E}_{Ш}}{{F}_{Ш}}{{n}_{Ш}}}=\frac{\pi \left( 1+{{E}_{Ф}}/{{E}_{{}}} \right)\left( \frac{\sin \pi k/{{n}_{Ш}}}{\sin \pi /{{n}_{Ш}}}-\cos {{\phi }_{0}} \right)+\frac{{{E}_{Ф}}}{{{E}_{Ш}}}\pi {{n}_{Ш}}\cos {{\phi }_{0}}}{{{n}_{Ш}}\left( \pi -{{\phi }_{i}} \right)\cos {{\phi }_{0}}+{{n}_{Ш}}\sin {{\phi }_{0}}}\) （5.8）

式中\(D=2R;p=\left( c-{{d}_{r}}/2 \right)\)。

在拉紧螺栓数量足够大\({{n}_{Ш}}\ge 10\)的条件下，可假定\(\frac{\pi }{{{n}_{Ш}}}\approx {{\phi }_{0}};\sin \frac{\pi }{{{n}_{Ш}}}\approx \sin {{\phi }_{0}};\sin \frac{\pi }{{{n}_{Ш}}}\approx \frac{\pi }{{{n}_{Ш}}}\)。那么，表达式（5.8）就变成下形式

\(\frac{{{E}_{Ф}}(\pi Dh-{{F}_{Ш}}{{n}_{Ш}}}{{{E}_{Ш}}{{F}_{Ш}}{{n}_{Ш}}}=1-\frac{\pi }{\pi +tg{{\phi }_{0}}-{{\phi }_{0}}}\)。

表达式（5.8）根据法兰和拉紧螺栓（双头螺栓）的刚度和尺寸比确定对接中性轴的位置。将方程（5.7）代入方程（5.5）中并考虑到（5.8）表达式，得

\({{\sigma }_{pacm}}=\frac{8{{M}_{u3s}}\left( \cos {{\phi }_{i}}-\cos {{\phi }_{0}} \right)}{D{{F}_{Ш}}{{n}_{Ш}}\left( 2tg{{\phi }_{0}}-\sin 2{{\phi }_{0}} \right)/\left( \pi -{{\phi }_{0}}+tg{{\phi }_{0}} \right)}\)，

\({{\sigma }_{CHC}}=\frac{8{{F}_{Ф}}{{M}_{u3s}}}{{{E}_{Ш}}{{F}_{Ш}}D{{n}_{Ш}}}\frac{\cos \phi -\cos {{\phi }_{0}}}{\left( 2tg{{\phi }_{0}}-\sin 2{{\phi }_{0}} \right)/\left( \pi -{{\phi }_{0}}+tg{{\phi }_{0}} \right)}\)。

这样一来，法兰对接的拉紧螺栓（双头螺栓）力的分布用方程给出

\({{p}_{i}}=\frac{8{{M}_{u3s}}}{D{{n}_{Ш}}}\frac{\cos \phi -\cos {{\phi }_{0}}}{\left( 2tg{{\phi }_{0}}-\sin 2{{\phi }_{0}} \right)/\left( \pi -{{\phi }_{0}}+tg{{\phi }_{0}} \right)}\)。

我们来测定法兰型拉紧螺栓（双头螺栓）的初始拉紧力。我们认为，拉紧螺栓的应力是相同的并等于\({{\sigma }_{Ш}}={{P}_{0}}/{{F}_{Ш}}\)，那么，法兰接触表面上的平均挤压应力\({{\sigma }_{Ф}}=\frac{{{F}_{Ш}}}{F}{{\sigma }_{Ш}}\)，式中\(F=\frac{\pi }{4}\left[ {{\left( {{S}_{Г}}+2\delta \right)}^{2}}-d_{Ш}^{2} \right]\)—在拉紧螺栓配置稀疏条件下（\({{S}_{s}}\)—螺帽的支撑面；δ—法兰的厚度）；\(F={{F}_{Ф}}/{{n}_{Ш}}\)—在拉紧螺栓配置稠密条件下。

螺栓（双头螺栓）杆被扭矩\({{M}_{kp}}=\alpha {{P}_{0}}{{d}_{Ш}}\)，扭转,式中α=0.12—在螺纹平均摩擦系数\(\mu =0.2\)条件下。

那么，螺栓的扭转切向应力\({{\tau }_{\max }}=16{{M}_{kp}}/\pi d_{Ш}^{3}\)。

在沿无间隙安置的螺栓均匀分布的切断力\({{Q}_{1}}\)和扭矩\({{M}_{kp}}\)作用于法兰对接处时，我们就会有\(\tau =Q/{{F}_{Ш}}k+2{{M}_{kp}}/D{{F}_{Ш}}k\)。在拉紧螺栓预拉紧时，螺栓被延伸，而法兰压缩量

\(\Delta \delta ={{P}_{0}}/{{C}_{Ш}};\ \Delta \phi ={{P}_{0}}/{{C}_{\phi }}\)，

式中\({{C}_{Ш}},{{C}_{Ф}}\)—螺栓和法兰的相应刚度。由于拉伸力和弯曲力矩的作用，作用于负载最大螺栓的力

\(P=\frac{N}{{{n}_{Ш}}}+\frac{8{{M}_{u3s}}}{D{{n}_{Ш}}}\left( 1-\cos {{\phi }_{0}} \right)/\frac{2tg{{\phi }_{0}}-\sin 2{{\phi }_{0}}}{\pi +tg{{\phi }_{0}}-{{\phi }_{0}}}\)。

螺栓也相应得到附加延伸，法兰预压缩也减小同样的量，也就是说，在对接裂开前螺栓延伸和法兰加速的总量不发生变化，

\({{P}_{Ш}}/{{C}_{Ш}}+{{P}_{Ф}}/{{C}_{Ф}}={{P}_{0}}/{{C}_{Ш}}+{{P}_{0}}/{{C}_{Ф}}\)，式中\({{P}_{Ш}}=P+{{P}_{Ф}}\)—根据螺栓的平衡条件；\({{P}_{Ф}}\)—作用于法兰的力。

这样一来，作用于螺栓的力等于

\({{P}_{Ш}}={{P}_{0}}+\frac{1}{1+{{C}_{Ф}}/{{C}_{Ш}}}={{P}_{0}}+\frac{1}{1+{{C}_{Ф}}/{{C}_{Ш}}}\left[ \frac{N}{{{n}_{Ш}}}+\frac{8{{M}_{u3s}}}{D{{n}_{Ш}}}\frac{\left( 1-\cos {{\phi }_{0}} \right)\left( \pi +tg{{\phi }_{0}}-{{\phi }_{0}} \right)}{2tg2{{\phi }_{0}}-\sin 2{{\phi }_{0}}} \right]\)

（5.9）

测定出作用于拉紧螺栓（双头螺栓）的载荷后，就可计算它们的强度。

在螺栓预拧紧条件下，螺栓中的应力

\({{\sigma }_{Ш}}=4{{P}_{0}}/\left( \pi d_{Ш}^{2} \right);\tau =16{{M}_{kp}}/\left( \pi d_{Ш}^{3} \right)\)。

承受断裂和剪切的拧紧螺栓中的应力，可借助强度条件并考虑拉紧力测定

\({{\sigma }_{EKB}}=\sqrt{{{\sigma }^{2}}}+3{{\tau }^{2}}\le \left[ {{\sigma }_{B}} \right]\)，

式中\({{\sigma }_{Ш}}={{P}_{Ш}}/{{F}_{Ш}}\)；\(\tau =Q/\left( {{F}_{Ш}}k \right)+2{{M}_{kp}}/\left( d{{F}_{Ш}}K \right)\)。

根据等强度条件，我们来测定连接和螺栓材料的最终几何参数

\( \frac{{{d}_{Ш}}}{{{d}_{Г}}}=\frac{{{\sigma }_{CM.\alpha}}+\omega {{\sigma }_{CM.Ф}}}{{{\sigma }_{EKB}}}\frac{4\delta }{\pi {{d}_{Г}}}, \)

\(\frac{c}{{{d}_{Г}}}=\frac{{{\sigma }_{CM.M}}+{{\tau }_{cp.\alpha}}+\omega \left( {{\sigma }_{CM.Ф}}+{{\tau }_{cp.Ф}} \right)}{2\left( {{\tau }_{cp.\alpha}}+\omega {{\tau }_{cp.Ф}} \right)}, \)

\( \frac{t}{{{d}_{Г}}}=1+\frac{{{\sigma }_{CM.Ф}}+\omega {{\sigma }_{ CM.Ф}}}{{{\sigma }_{B\alpha}}\psi /{{K}_{a}}+{{\sigma }_{BФ}}\omega /{{K}_{Ф}}}, \)

\( \omega =\frac{\sum\limits_{i=1}^{n}{{{\delta }_{iФ}}}}{\sum\limits_{i=1}^{n}{{{\delta }_{ikk}}}}=\frac{{{\tau }_{cp.a}}}{{{\tau }_{cp.Ф}}}\left( \frac{\psi {{\sigma }_{Ba}}}{{{\tau }_{cp.a}}2c/\left( t-1 \right)}-1 \right) \)

（5.10）

参数\({{d}_{Ш}},{{d}_{s}},t,\omega \)dш ,dГ, t, c, ω的最佳值（图5.4）。

连接质量的最小值根据下列条件测定：

\(G=n\sum\limits_{i=1}^{n\left( 5.11 \right)}{{{\delta }_{ikm}}\left\{ 2tc\left( {{\gamma }_{a}}+\omega {{\gamma }_{\phi }} \right)/d_{Г}^{2}-\pi \left[ {{\gamma }_{a}}+\omega {{\gamma }_{\phi }}-{{\gamma }_{Г}}\left( 1+\omega \right) \right]/4 \right\}+}c\pi d_{Ш}^{2}n\left( {{\gamma }_{Ш}}-{{\gamma }_{\alpha }} \right)/4\to \min \) （5.11）

图5.4.柱销螺栓连接最佳参数

柱销—30XГCA；双头螺栓—BT-14;

t—柱销之间的间距；

c—距边缘的距离；

d_Ш_m—柱销（螺帽）的直径；

G—连接的质量；

d_Ш—双头螺栓的直径；

δ_y—加厚量；

n—双头螺栓的数量。

5.3、连接段的结构缠绕工艺方式

连接段结构本身也是按图5.5和5.6所列的其中一种缠绕方法成型的。

图5.5给出了带布连接件的壳体一般简图，而图5.6.给出了连接件用螺旋-环向缠绕第二个壳体构成的“双茧”式连接件简图。

图5.5. 带布连接件的壳体示意图

图5.6. “双茧”式连接构件的壳体简图图

图5.7 壳体相对重量与延伸的一般关系特征

图5.8承力壳体质量与壳体相对延伸率的关系曲线

选择其中任何一种方式主要是取决于轴向压缩和拉伸载荷级和连接段的工作条件（内外压强）。

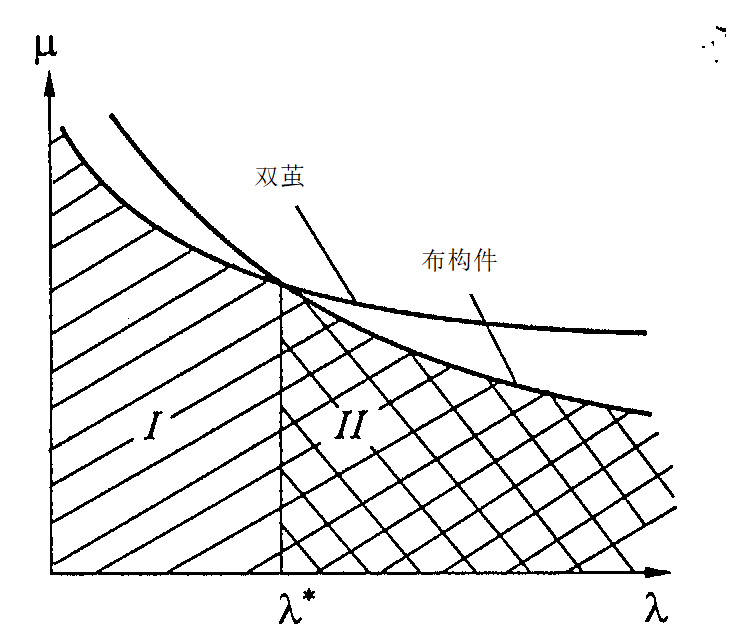
所研究的连接件缠绕方式（I,II）的壳体相对重量与壳体延伸率的一般关系曲线特征用图5.7所示，而承力壳体质量与壳体相对延伸率的关系曲线用图5.8所示。由这些关系曲线得出结论：无论是承力壳体的缠绕方式，还是连接段的缠绕方式都必须使它们最佳化。

连接段对接部件的结构样式在前几节中已表述。尽管所采用的结构可能有差别，在实践中最广泛采用两种形式—带金属段的连接段和全塑料结构。

第六章：壳体结构件的生产工艺过程

6.1、壳体生产工艺过程结构

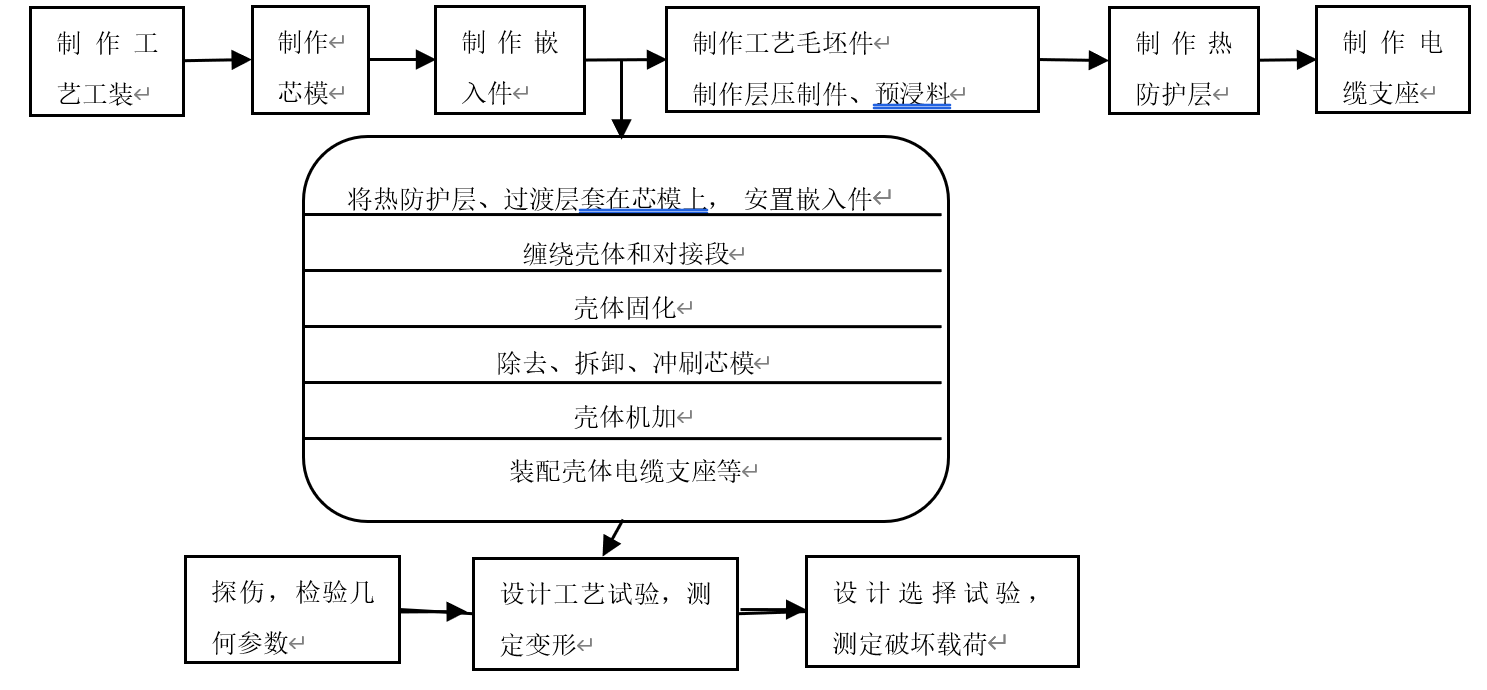
图6.1所示为壳体的生产工艺过程结构图。主要阶段的清单列下。

图6.1、生产工艺流程结构

工艺过程主要阶段包括：

—制作工艺工装和检验测量工装；

—制作聚合砂芯模；

—制作嵌入件（极孔的主要法兰，前封头四个非极孔用的嵌入装

置，制作连接段的金属端框）；

—制作工艺毛坯件、层压制件、预浸料（局部切口处、热防护层和迁移防护层所用的加强布块）；

—制作内热防护层；

—将迁移防护层、热防护层套在芯模上，安置嵌入件；

—缠绕承力壳体和带对接部件的连接段；

—固化壳体；

—除去、拆卸、冲刷聚合砂芯模；

—机加壳体（制作前封头的非极孔，在使用与柱销螺栓连接对接结构情况下，加工连接段的对接处）；

—缺陷检验、几何参数检验；

—设计工艺试验，测定变形特性；

—设计选择试验，测定破坏载荷。

6.2、缠绕壳体用的原始材料准备

配制粘合剂混合物。在固体火箭发动机复合材料壳体生产中主要采用环氧粘合剂混合物。其中最广泛用于“湿”法缠绕的有100%浓度的ЭДТ-10,УП-612M, ЭХД-М, ЭЦА-ЭМ, ЭЦ-М，ЦАТ粘合剂,而用于“干”法缠绕的有 ЦЭДТ-10П, ЭФБ-33, ЭЦТ-1,ЭЦТ-20, ПА等粘合剂（表3.1）。

说明：“秒”—是生产中所采用的非制式粘度测量单位。

表6.1. 粘合剂的成分和工艺特性

粘合剂牌号

成分

组分含量，质量分率

根据B3-1测定的粘度，在T℃条件下，秒

再处理温度，℃

УП-612М

УП-612

ЭД-20

И-МТГФА

110

—

4.5

—

30-35

УП-612М

УП-606/2

ЭХД

0.5-69

100

—

7.0

—

35-40

ЭХД-М

И-МТГФА

ЭЦ-М

ЭА

108

112

—

5.0

—

30-35

—

ЭДТ

ЭД-10

ДЭГ-1

ТЭАТ

100

10-12

—

576

—

252

—

17.0

—

60-62

—

我们通过ЭДТ-10和ЭДТ-10П粘合剂的例子来研究粘合剂混合物配制的一般工艺说明和配制方法。这些粘合剂是环氧树脂、固化剂和促进剂基混合物。粘合剂混合物配方中的组分应通过符合技术条件和国标的入厂检验。在材料进入工区时，用其制作工艺试样来测定粘合剂的初始粘度和溶液的均匀度。用容积50-100L带锚式搅拌器、水加热和冷却的搪瓷装置配制粘合剂。在工作开始前和工作结束后用比例为1：2的酒精-丙酮混合液仔细清洗装置。按照工艺说明实施配制粘合剂，工艺说明规定所必需的原始组分分率、组分的混合程序和混合过程的工艺参数。在50±5℃温度条件下，（根据喷嘴直径为5.4mm的粘度计B3-1）所得到的粘合剂粘度应不小于45秒。针对具体的纤维半成品，用试验方法选择粘度。将准备好的粘合剂用密封容器转到主生产，随附有标明配制日期和粘合剂批号的证明书。

在配制ЭДТ-10П粘合剂的情况下，按照配方，将ЭДТ-10粘合剂用添加有AДЭ-3产品的酒精-丙酮混合液溶解到所需的浓度。为了配制所需浓度的粘合剂，在使用前按照“十字”规则加入酒精-丙酮混合液或粘合剂溶液。所配制好的粘合剂用密封容器存放：在25℃温度条件下ЭДТ-10存放不超过5昼夜，而ЭДТ-10П存放从配制时刻起不超过3昼夜。

为了保障所缠绕壳体中所要求的粘合剂粘度（不超过15-25秒）及其最佳的含胶量，将配制好的胶放入缠绕机的浸胶槽中。应当记住，在下列时间内必须对其再处理：ЭЦА-ЭМ—3小时, ЭХД-М和ЭДТ-10 –4—5小时，УП-612М—10-15小时。

准备半成品纱带。为了提高壳体成型过程生产率，原始纤维材料应绕成单向（平行）纱束、丝束、粗纱束。通常将单向纤维半成品束形成工艺纱带（毛坯带），然后将纱带浸胶，烘干，或在湿状态下最终形成半成品纱带，赋予纱带给定的宽度和厚度尺寸、微结构特性和工艺特性（粘合剂含量、半成品中的可溶组分和挥发物含量、一定的工艺粘性）。缠绕成型壳体用的半成品纱带生产过程由下列工序结合而成：

—原始半成品纤维符合技术条件及其生产标准所规定标准的入厂检验；

—粘合剂成分工艺性能的入厂检验，并使其达到所要求的值；

—由原始半成品纤维形成毛坯带；

—对毛坯带浸渍粘合剂；

—对浸好粘合剂的毛坯带工艺固化；

—形成半成品纱带。

6.3、缠绕壳体用的芯模制作。

复制发动机壳体内腔形状和尺寸的成型工艺芯模的制作过程是壳体生产的最重要部分，通常将芯模的生产分为可破坏芯模或可拆卸芯模的单独生产。

在固体火箭发动机壳体生产中采用组合芯模，其承力结构用高强金属（钢、铝合金）制作成可拆卸的，而其具有复杂和精确型面的工作成型部分用脆性、易熔和可溶金属制作成可破坏的。根据所成型壳体的外形尺寸和生产类型（成批性），可采用不同的工艺芯模。

可拆卸的整体金属芯模制作复杂、价格高、使用困难，它们用在大批量生产直径不超过1—1.5m壳体中。由轻材料制作的可熔芯模在缠绕时易发生蠕变，它们用来制作直径不超过300mm的壳体和小尺寸压力壳体。

可溶解芯模用溶解温度不高的各种可溶解涂料和共晶体盐混合物制作，用这类材料制作直径约600mm的芯模。

脆性或易碎涂料的芯模用来生产带可破坏小拱顶的大尺寸制品，采用石膏、纯白生石膏诸如此类作为脆性材料。充气和充液体的芯模具有可充填的（由弹性材料或柔韧的薄片材料制作）的密封壳体。为了提高芯模刚度、抗扭强度和抗压强度，可用砂子或空心微球充填这类芯模。

在发动机壳体生产中，最常采用成型部分为可冲刷的砂-树脂和砂混合物芯模。缠绕承力壳体用的聚合砂芯模多件结构用图6.2所示，芯模的主要承力构件是轴10，在轴上安置有经过专门成型的单独构件、分段件4，5，7，在轴上装配时，用端面胶合方法将这些构件连接成一个整体。所采用胶的特性、性能和类型在表6.2列出。

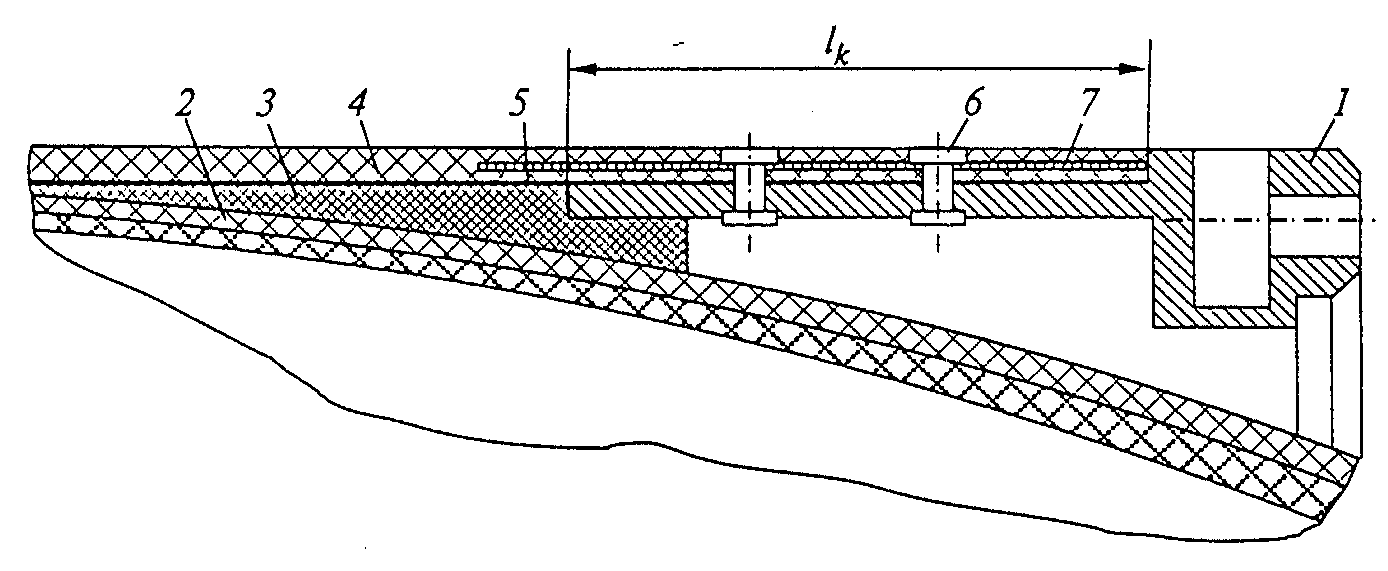
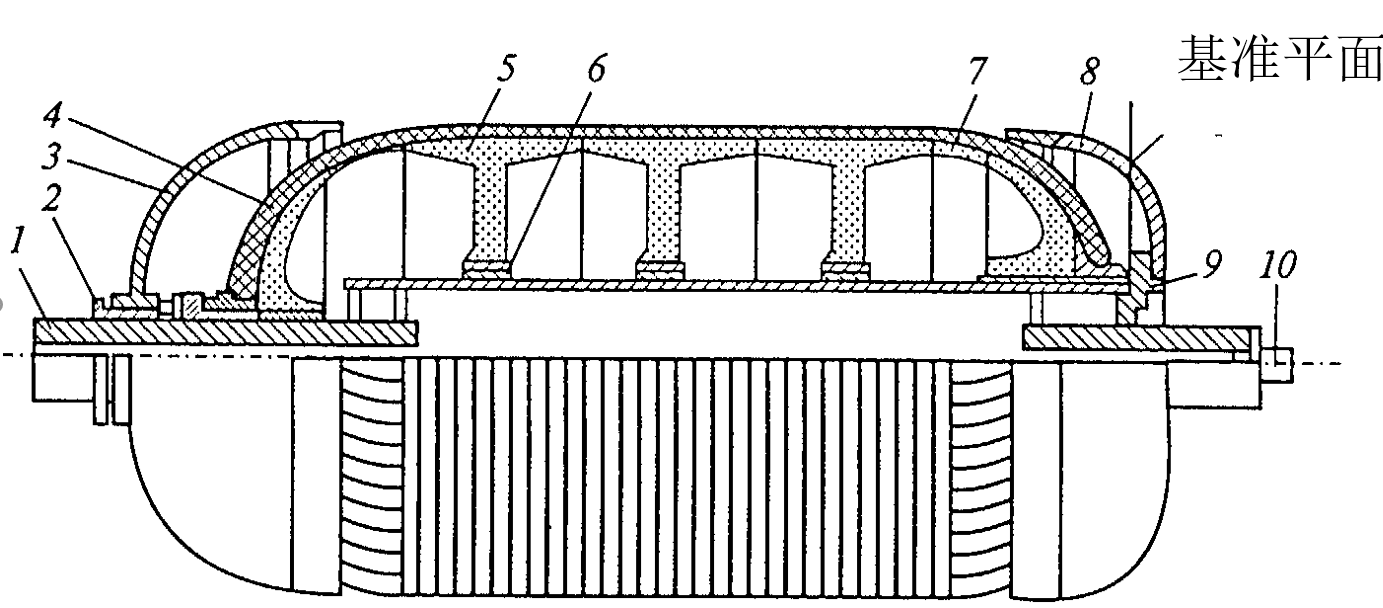
图6.2. 用来缠绕“裙”式固体火箭发动机承力壳体的芯模结构

1—将旋转从轴传递到芯模的键；2，6—套管；3，8—缠绕第二个蚕茧式壳体用的分段件；4，7—聚合砂封头；5—聚合砂筒体构件；9—定位构件；10—轴。

表6.2. 胶合芯模构件的胶和胶接的特性

指标

K-153

环氧三烷树脂基水溶性胶

寿命，小时（份数约3公斤）

固化时间，小时（在不低于15-35℃温度下）

已固化胶的压缩强度，不小于,MPa

芯模材料胶合分离强度,MPa

芯模用热水的可冲刷性

芯模的破坏特性

0.5

5-8

不被冲刷。

芯模材料破坏。

0.5

5-7

可冲刷。

芯模材料破坏。

根据在轴上安装芯模结构件的原则，采用端表面或径向定基准面，这就消除了壳体法兰、封头、筒体构件端表面相互偏扭。

为了消除筒体段构件的间隙，采用将它们与焊接在轴上的套管6楔形连接。

芯模结构（图6.2）包括构件3和8，它们保障在同一个工艺过程中同时制作带对接部件的连接段。在缠绕完主承力壳体后，用布补强螺旋-环向缠绕的方法制作第二个蚕茧式壳体（“假”封头）这些部件，在固化后截去“假”封头，从而形成所要求的连接结构。

为了保障所要求的芯模几何尺寸，在最终装配完后必须对其机加。

在缠绕好的承力壳体固化后，在专用立式台上喷蒸汽（T=90-100℃）4-5小时，或加压喷温度大于80℃的水1-2小时冲刷芯模的聚合砂部分。芯模的制作工艺示意图用图6.3所示。

芯模构件的成型和热处理

图6.3. 芯模制作工艺设备配置简图

在选择芯模种类时，出发点是，缠绕时所允许的半成品纱带工艺张力的径向压力不应超过发动机壳体工作压力的20%，而且缠绕时所允许的径向变形应为0.5mm。用来制作可冲刷芯模的复合组分在表6.3列出。图6.4所示芯模的全视图。

表6.3. 砂-树脂芯模的配方和物理力学性能

性能

芯模材料

可冲刷芯模的含量，质量分率

热处理制度：温度，℃

时间，小时

抗压强度，MPa

在T=20℃

在T=15℃

弹性模量，GPa

压缩弹性模量

拉伸弹性模量

尺寸为1.5x1x1cm2试件的水力破坏时间，在T=100℃下,分

ПВС（聚乙烯醇），2-3

砂子，100

90-120

8.5

10.1

ЭТС，15

УП-605，3

砂子，100

硼砂-3

110-150

100-130

25-26

20-22

18.8

图 6.4. 缠绕固体火箭发动机壳体用的芯模全视图

6.4、缠绕工艺制度

成型的工艺制度取决于一系列参数，这些参数决定着所生产壳体的质量。属于这些参数的有：缠绕时半成品纱带的工艺张力、成型接触压力（所缠绕表面的接触压力）、半成品纱带的温度、半成品纱带的缠绕速度、生产厂房的温度-湿度特性、含尘量和有害气体含有量。

工艺张力用来形成所成型壳体柔韧的纱索系统中的张力，以便使壳体具有结构刚度和强度，以及用来形成缠绕机-装备-芯模-半成品纱带系统中的工艺张力，没有这个张力就不能保障将增强材料按给定的轨迹缠绕到芯模上的运动学和动力学条件，就不能保障达到缠绕结果的稳定性和重现性。工艺张力由成型方法、所成型表面的曲率、半成品纱带的类型、设备的特点和其它因素所决定。对于每一个具体的情况来说，工艺张力取决于材料的类型，用计算确定张力并试验对其精确。例如，对于玻璃纤维增强塑料来说，实际所使用的张力值T₀在T_p < T₀<0.2T_p范围, 式中T₀—张力，而T_p—半成品纱带的断裂力。

成型的接触压力用来在壳体-芯模工艺系统中，也就是说，在所缠绕的半成品纱带和所成型的芯模表面接触界面上（然后是在以前所形成的壳体壁层界面上）形成张力。接触压力保障密实所缠绕的结构、保障给定的密度、（在“湿”法成型时）保障挤出余胶和冲刷气泡，（在“干”法成型时）保障粘合剂的粘合和粘附力。接触压力取决于和T₀一样的因素，而且不应低于0.049MPa，它的最大值只限于压坏脆性增强纤维和破坏工艺芯模的危险性而已。

为了形成工艺张力并对其控制，采用不同的工艺方法和装置：借助可调节制动装置对半成品纱带制动，借助可张开式芯模、充气芯模等在纤维中形成张力。可借助专用滚压装置，通过压紧套、外套（绳索，带子）、外部液体静力压力等形成接触压力并控制它。如果是小直径和中等直径的壳体，可借助所形成的工艺张力保障接触压力所需值

\(q=\frac{N-{{T}_{0}}}{R}\)， (6.1)

式中R—曲线表面的半径。

随着所成型制品直径的增大，T₀最佳值条件下的接触压力值会降低，这就需要有必须的附加装置来将其保持在所要求的水平上。在用有机纤维增强塑料缠绕大型壳体时，采用滚轮能将承力壳体壁强度提高5-8%，将弹性模量提高4-5%。

成型温度T_Ф是成型制度的参数，借助其在壳体缠绕过程中控制半成品纱带的性能，通过变化T_Ф就可改变粘合剂的聚合状态和粘度，调节粘合剂的粘附和自粘附性能，减少气孔率并增大所制作结构的密度。借助接触加热辊子、气动加热器和辐射（红外线）加热器等对半成品纱带实施加热。在每一个具体情况下，成型的最佳温度取决于所采用的粘合剂配方、粘合剂的工艺状态、成型制度的动力参数和缠绕速度。

缠绕速度用所采用的成型方法、缠绕运动示意图、半成品纱带成型工序和制品毛坯件缠绕工序的吻合性、缠绕设备的能力来表征，对于俄国产设备来说，“湿”法缠绕壳体时，半成品纱带的最大输送速度为24米/分。

6.5、缠绕的结构工艺参数确定

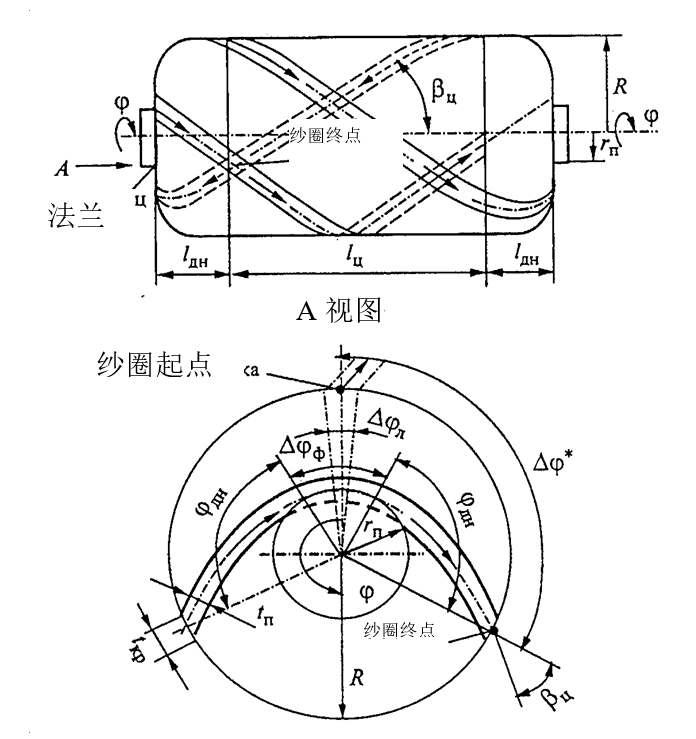
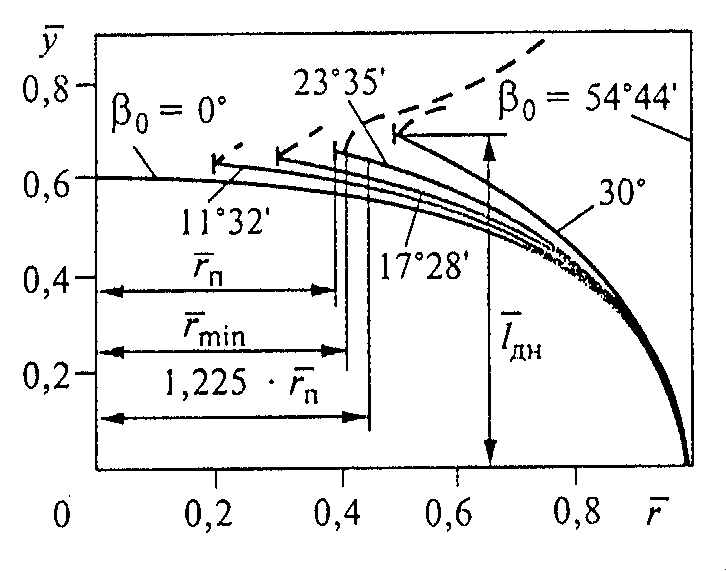
我们来研究一下束丝或宽度为t_л的预浸纱带在旋转芯模表面的铺放方式（图6.5.），在布纱器一个往复行程或在芯模上缠绕一个行程T内，将铺放一个整圈纱（一个螺旋线）。在这种情况下，轨迹的起点和终点只有在芯模在一个缠绕行程内转动整数转数Z_T时才叠合。在Z_T不为整数的其它所有情况下，纱圈的起点和终点以缠绕角距ΔФ错开。

图6.5.带封头的圆筒壳体缠绕示意图

为了保证密实（无间隙）地铺放所缠绕的纱带，必须使ΔФ角是2π（或360°）角的倍数，也就是说，是芯模转动一整圈的倍数，2π/ΔФ之比为整数1，2，3，4，5，6等的角度都将是倍数，与这些数相应的是缠绕角距值ΔФ*，它们等于360，180，120，90，72，60，45°等。最简单的是在壳体法兰处附加一个\(\Delta {{\varphi }_{\Phi }}\)转角就会达到角距的倍数。此外，在每一个缠绕行程或铺放一圈纱带后，应将芯模转动一个纱带的角幅\(\Delta {{\varphi }_{л}}\)，该纱带位置应是角距ΔФ*的整数倍。

这样一来，在每缠绕完一层后，壳体一层中将铺放2π/\(\Delta {{\varphi }_{л}}\)纱带，因为在一个缠绕行程内一圈纱带将两次与壳体的任意圆交叉，那么，在行程数T=2π/\(\Delta {{\varphi }_{л}}\)时，就会形成在每一点成±角度铺放的两个全螺旋层。同时，在Z=Z_TT时，芯模回到初始位置，并移动一个纱带角幅\(\Delta {{\varphi }_{л}}\)。

对于给定的几何尺寸来说，缠绕的工艺参数按下列顺序确定。

1、确定壳体筒体段上的缠绕角度，

\({{\beta }_{0}}={{\beta }_{ч}}=\arcsin \left( {{r}_{n}}/R \right)\) （6.2）

式中R和r_n—壳体筒体段和极孔的相应半径；β_ч—筒体段上的缠绕角度。

2、计算芯模在一个缠绕行程内在壳体筒体段上铺放纱带时的转动角度，

\({{\Phi }_{ч}}=2{{ц}_{ч}}=2\frac{{{l}_{ч}}}{R}tg{{\beta }_{ч}}\) （6.3）

式中l_ч—压力容器筒体段的长度；ц_ч—纱带的旋转角度。

3、确定芯模在每个封头上铺放纱带时的转动角度（图6.5.）

\({{\Phi }_{bH}}=2{{\varphi }_{bH}}=2\int\limits_{r={{r}_{n}}}^{R}{\frac{tg\beta r}{r}ds=2\int\limits_{r={{r}_{n}}}^{R}{\sqrt{1+{{y}^{2}}\left( r \right)}dr}}\) （6.4）

式中r—壳体封头的旋转半径当前值；\(\beta r\)—封头上的缠绕角度；\({{y}^{2}}\left( r \right)\)—封头外形母线导数：

\(y=\int\limits_{r={{R}_{n}}}^{r}{\frac{{{r}^{3}}dr}{\sqrt{\left( {{R}^{2}}-{{r}^{2}} \right)\left[ {{r}^{2}}-{{R}^{2}}\left( {{k}_{1}}-2 \right) \right]\left[ {{r}^{2}}-{{R}^{2}}\left( {{k}_{2}}-2 \right) \right]}}+{{C}_{2}}}\)，（6.5）

式中 \({{k}_{1,2}}=\frac{1}{2}\left( 3\pm \sqrt{1+4t{{g}^{2}}{{\beta }_{0}}} \right)\)，（6.6）

\({{\beta }_{0}}\)—缠绕的初始角度。

在这种情况下，旋转的最大半径\({{r}_{\max }}=R\), 而最小的旋转半径

\({{r}_{\min }}=\pm \frac{R}{\sqrt{2}}\sqrt{\sqrt{1+4tg{{\beta }_{0}}-1}}\)。 (6.7)

在更换变量后（6.5）积分最终形式

\(r=R\sqrt{1-{{k}_{1}}{{\sin }^{0}}\theta }\) （6.8）

通过第一类和第二类椭圆积分来表示：

\(y=R\left[ \frac{1-{{k}_{2}}}{\sqrt{{{k}_{2}}}}F\left( x,\theta \right)+\sqrt{{{k}_{2}}}E\left( x,{{\theta }_{2}} \right) \right]\)，（6.9）

式中\(F\left( x,\theta \right),F\left( x,{{\theta }_{2}} \right)\)—第一类和第二类椭圆积分表值；\(x=\sqrt{{{k}_{1}}/{{k}_{2}}}\)—椭圆积分模数。

根据公式（6.8）和（6.9），用相对坐标\(\left( y=y/R,\bar{r}=r/R \right)\)建立的不同\({{\beta }_{0}}\)值的封头母线形状用图6.6所示。在\({{\beta }_{0}}\)≠0条件下，在壳体的顶部形成孔，并且假定，在内压作用下孔是用盖封闭的；子午线曲线\(y\left( r \right)\)被确定在\({{r}_{\min }}\le r\le R\)范围内。

图6.6 在壳体赤道上不同缠绕角度时圆筒壳体等应力封头子午线的形状

4、求芯模在一个缠绕行程或在铺放一个螺旋线时的旋转角度

\(\varphi _{T}^{P}={{\varphi }_{ч}}+2{{\varphi }_{bH}}\)。（6.10）

5、确定计算的缠绕角距

\(\Delta {{\varphi }_{P}}=\varphi _{T}^{P}-\left[ \frac{\varphi _{T}^{P}}{2\pi } \right]2\pi \)，（6.11）

式中\(\varphi _{T}^{P}/2\pi\)—一个缠绕行程中的芯模整数转数。

6、确定壳体法兰处芯模的附加转动

\(\Delta {{\phi }_{\varphi }}=\frac{\left( \Delta \varphi *-\Delta {{\varphi }_{P}} \right)}{2}\)，（6.12）

式中\(\Delta \phi *\)—所采用的等于最接近角倍数的缠绕角距。

建议选择\(\Delta \phi *\ge {{60}^{\circ }}\)（60º，72º，90º，120º和180º）作为角距。如果\(\Delta {{\phi }_{p}}>{{180}^{\circ }}\),那么,应将芯模转动2\(\Delta {{\varphi }_{\phi }}\)到最接近的附加角度（240º，270º，288º和360°）。

7、计算下一个螺旋线（纱带圈）相对于以前所铺放的螺旋线的位移，也就是说，确定将芯模转动一个纱带角幅

\(\Delta {{\phi }_{л}}=\frac{{{t}_{kp}}}{R}=\frac{{{t}_{л}}}{R\cos {{\beta }_{ч}}}\)，（6.13）

式中t_кр和t_л—所缠绕纱带的相应覆盖宽度和标准宽度。在这种情况下，\(\Delta {{\phi }_{л}}\)应为\(\Delta \phi *\)角的倍数，对于上述\(\Delta \phi *\)值来说，完成这一点是不复杂的，\(\Delta \phi *\)的最大值不超过束丝与芯模表面或所缠绕层表面的摩擦系数f_TP。

在此种情况下，可假设tg（\(\Delta {{\phi }_{л}}\)/2）<f_TP，就是说所缠绕纱带的最大宽度\(t_{л}^{\max }<2R\cos {{\beta }_{ч}}arctg{{f}_{TP}}\)，纱带的最小宽度取决于缠绕过程的速度V_нам。

8、在选择纱带的角幅\(\Delta {{\phi }_{}}\)后，确定芯模在一个缠绕行程内的实际转动角度

\(\varphi _{r}^{*}=\varphi *={{\varphi }_{H}}+2{{\varphi }_{дн}}+2\Delta {{\phi }_{\varphi }}+\Delta {{\phi }_{л}}\)。（6.14）

9、确定芯模在一个缠绕行程内的转数

\({{Z}_{r}}=\frac{\varphi *}{2\pi }\)。（6.15）

10、求出双螺旋层缠绕时纱带的圈数或行程数

\(T=\frac{2\pi }{\Delta {{\phi }_{л}}}=\frac{2\pi R\cos {{\beta }_{л}}}{{{t}_{л}}}\)。（6.16）

11、求出缠绕双螺旋层所需的芯模全部转数

\({{Z}_{ОП}}={{Z}_{r}}T=\frac{\varphi *}{\Delta {{\phi }_{л}}}=\varphi *\frac{R\cos {{\beta }_{ч}}}{{{t}_{л}}}\)。（6.17）

12、根据缠绕的最大速度确定所允许的芯模旋转频率

\({{n}_{ОП}}=\frac{V_{\min }^{\max }\sin {{\beta }_{ч}}}{2\pi R}\)。（6.18）

13、求出一个缠绕行程的时间

\({{\tau }_{r}}=\frac{{{Z}_{r}}}{{{n}_{ОП}}}=\frac{R\varphi *}{{{V}_{ham}}\sin {{\beta }_{ч}}}\)。（6.19）

14、计算双螺旋层最可能少的缠绕时间

\({{\tau }_{Cл}}={{\tau }_{r}}. T=\frac{{{Z}_{ОП}}}{{{n}_{ОП}}}=\frac{2\pi {{R}^{2}}\phi *}{t{{V}_{ham}}tg{{\beta }_{ч}}}\)。（6.20）

6.6、内绝热层的制作工艺

复合材料壳体的高变形性使得其内绝热层的结构工艺方案也具有相应的特点。

为了保障在发动机各构件位移整个范围内的结构整体性，采用类似橡胶的弹性热防护材料作为内绝热层的基材，此外，在位于金属法兰与有机纤维增强塑料壳体连接处的绝热层高变形区，设置有变形补偿片，绝热层、法兰和封头塑料之间氟塑料薄膜的环向层起着补偿片的作用。

为了减轻孔区中药柱成型过程用，在热防护层中制作有脱粘层结构。

除了用三元乙丙橡胶加硅胶填料基的橡胶类材料制作的内绝热层主层外，在绝热层结构中采用了固定防护层，固定防护层首先由阻碍药柱组分向绝热层迁移的防护底层和具有提高药柱与绝热层粘附力的扩展面的固定层组成。

制作半成品热防护材料

半成品绝热层材料是在专门工厂用压延方法制作的。压延的半成品制作工艺过程有下列主要阶段组成：

—用橡胶浑炼机制作组分的橡胶混合物；

—将混合物压延成厚度为10-20mm的片；

—压延片（将材料挤压入圆柱辊之间的间隙，直到得到给定的厚度）。

生产压延好的片厚度一般为0.5—2mm。

半成品热防护材料存放期有限，这是由橡胶混合物的自动硫化过程和脆变过程所决定的。

用球磨机磨碎粉末状填料和工艺添加剂，并随后借助一定尺寸筛孔的筛子分出大粒级。

用热烘箱或真空干燥机烘干除去材料组分中的水分，烘干的时间用实验确定，并取决于所允许的组分水分、烘干的温度和设备的特点。绝热层材料组成中的主要组分烘干制度在表6.4列出。

用天平或定量器确定组分的剂量。在某些情况下（对于液体和颗粒体材料来说），采用定容配料。

给定的半成品质量是靠材料组分在片体积内的均匀分布，以及根据橡胶粘度、温度和所采用的设备实验所确定的混合时间的控制来保障。

表6.4 绝热层组分的烘干制度 .

材料

烘干温度，℃

所允许的水分，%

硅胶

工业碳

氧化锌

酚醛微球

150

110

100

1.0

0.2

3.0

内绝热层的制作

已经指出，内绝热层是带补偿片、脱粘层等形式嵌入件的多层结构，因此，绝热层的毛坯件根据工艺规程单独制作，随后将毛坯件安置在芯模上并在其上缠绕承力壳体。

显然，由于封头的复杂空间形状，其绝热层的制作过程就具有最大复杂性，制作壳体封头绝热层的压模结构示意图用图6.7所示。

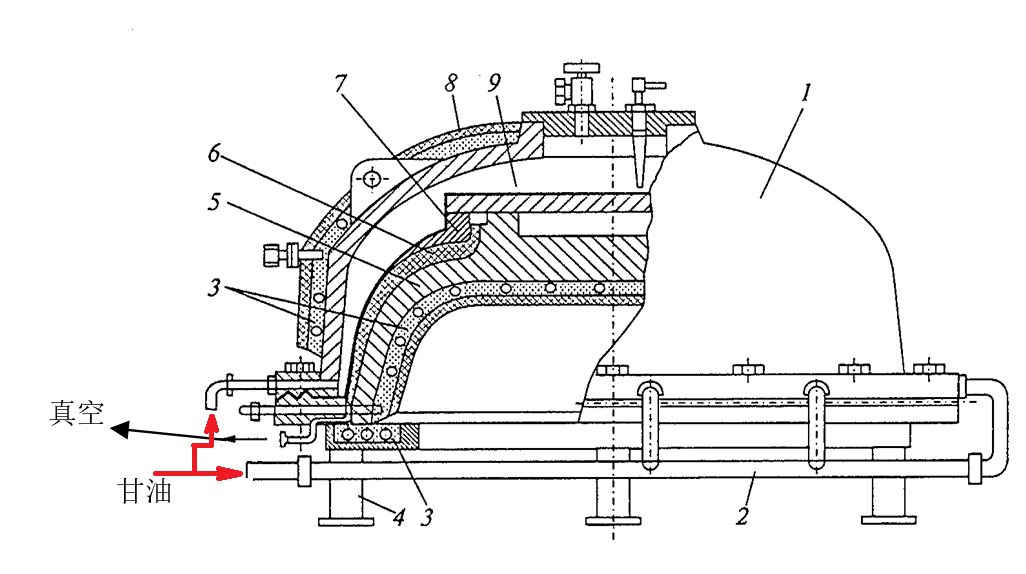
图6.7. 制作固体火箭发动机壳体封头热防护层的压模

1—液压釜模盖；2—甘油供给管道；3—加热器；4—加热支座；5—阴模； 6—封头热防护层毛坯件；7—法兰；8—绝热物；9—真空袋。

封头绝热层的制作过程如下。

在阴模5（封头模具）（见图3.7）上开始铺放绝热层的防护底层和固定底层，然后逐层铺放不同裁切的半成品绝热层材料片，直到得到给定的热防护层厚度。在模具上铺放绝热层过程中，在相应区域安置预先成型（但未固化的）人工脱粘层锁、变形补偿片零件，然后安置壳体的法兰。

在胶合前，将表面脱脂—用溶剂浸湿的擦布擦干净，并随后在车间条件下干燥。橡胶和建议用来胶合橡胶和金属的胶合剂在表6.5列出。

表6.5. 所胶合材料和胶混合物的种类

所胶合的表面	胶成分	胶合强度，MPa
乙丙橡胶与氟橡胶	聚三氯丁二烯和氟橡胶溶液基胶系。	–
乙丙橡胶与金属（钛合金）	聚三氯丁二烯和酚醛橡胶胶基胶系。	抗剥离强度不小于0.2MPa。
乙丙橡胶与有机纤维增强塑料	聚三氯丁二烯基胶	–
未硫化的乙丙橡胶与硫化的乙丙橡胶	丁基橡胶胶	–
未硫化的乙丙橡胶彼此	汽油	–

在上面进行铺放绝热层的模具确定与缠绕承力壳体芯模型面相符的壳体（热防护）内型面。模具的结构能够将法兰安置在未压制的橡胶上，并在硫化过程中保障法兰下面的给定厚度之前限制其位移。

在铺放好的绝热层叠外面铺放排水层，安置真空袋和液压釜的盖，将给定温度的载热体（甘油）加压送到真空袋与液压釜盖之间的空腔中，通过排水层对真空袋与绝热层之间的空腔进行抽真空，以便除去挥发物。

用螺栓或卡口栓将液压釜的盖与液压釜模具连接起来，同时，夹紧工艺橡皮袋的凸边，厚度4-8mm的工艺橡皮袋凸边同时作为密封垫使用。

液压釜的盖装备有对用甘油作载热体的自备加热系统，加热可为蒸汽加热，也可为电加热。为了保障温度场的均匀性，加热系统的工作件制作成分段结构，并能够以不同组合接通其工作。为了减少热损失，液压釜模具和盖用泡沫塑料或矿物棉绝热。

为了保障工艺过程给定的参数，设置有载热体强制循环，将加热到120—130℃温度的甘油用低压高效泵按照管路泵入液压釜。在变化压力时，按确定的制度将热的载热体通过调节到所需压力的排流阀压送并排到加热箱中。

为了除去硫化时所释放出的挥发物，从安置橡皮袋时刻起在整个热处理过程中对橡皮袋和毛坯件之间的空腔进行抽真空，真空深度保持在0.8—0.9大气压级上。为了排除抽真空时的气泡和挥发物的啪的声，在绝热层外表面铺有多孔玻璃布排水层。

在铺放排水层前，在绝热层外表面涂抹防止绝热层与排水层或真空袋粘合的分离层—聚异丁烯树脂溶液。为此目的，采用聚异丁烯溶液，但是，这就会造成在以后的壳体制作工艺过程中仔细用砂纸打磨绝热层表面的必要性，以便保障其与承力壳体牢固粘接。

真空袋在硫化过程中起着重要作用，真空袋在液压釜中破裂会伴随着液体载热体进入绝热层，导致绝热层无法修复的报废，因此，在工艺过程中采用增压和加肥皂水方法检验真空袋完整性（其中有无气

孔、分层、变薄等）的工序。

为了将工艺过程的参数（压力、温度、真空度、保持时间）保持在所要求的范围内，给液压釜装置装备相应的综合测量和调节设备。

重要的应指出，在制作绝热层时应对绝热层进行未完全硫化，因为所要求的绝热层性能是在随后与承力壳体一起热处理时达到的。

在硫化后，清理热防护层毛坯件外表面上的分离层残留物，对热防护层壁进行探伤并测量其厚度。

6.7、壳体的热处理

选择能保障最大物理力学性能、耐热性、所有截面完全固化、剩余应力最小的热处理制度的所有试验研究是用直径140-300mm的薄壁环向试件进行的。显然，对于用缠绕方法在又重又大的结构复杂的聚合砂芯模上制作壁厚20-40mm，而在法兰加厚处达70-80mm、直径2500mm以上的制品来说，将用试件调试好的聚合制度结果直接搬用是不合理的。在制品结构中有已固化的绝热层、有必需自己热处理制度的未固化材料、胶和其它材料，这就使得情况变得复杂。所说的这一切都说明，选择、确定和实现热处理制度问题是一个需要系统解决的综合问题。粘合剂的种类、增强材料的类型和粘合剂与增强材料在高温下相互作用的特性决定着解决这些问题的方法。

在现实条件下，必须考虑到芯模质量、制品材料的导热性、芯模上的绝热层、纤维增强塑料的厚度、热交换条件来计算和修正制度。热交换因数是非常重要的，因为热传递主要是通过在外部加热条件下的对流热交换实现的，实质上它不仅取决于热处理炉的功率，而且还取决于载热体流速度及其方向，对于不同类型的炉子来说，由这些因素所决定的加热动力学实质上是不同的，应该必须考虑到这一点。

必须注意到，对于瞬间加热的试件来说，载热体的温度制度与最佳制度实际上没有区别。对于实际制品来说，炉中的温度明显超过制品壁表面和壁内的实际温度，这种因芯模结构的温度和上面所列因素的差别可能是相当大的，可达到20—40 ℃。

在热处理时，制品最终成型，除了得到重复加热时膨胀的芯模几何尺寸外，也成型制品轴。正如已经研究的那样，轴的结构取决于制品的结构，并具有不同的刚性，因此，选择热处理时轴支架位置的选择是相当重要的因素，在任何情况下，必须注意使支架的固定位置彼此配置在不大距离上，同时，芯模应必须架在轴的支架上或架在与轴刚性连接的零件的支架上。为了避免破坏制品的几何尺寸，不允许将支架安置在夹具、活动套管和其它零件下面。在加热时，粘合剂很快失去自己的粘度，其流动性增大，特别是在增强材料叠层不密实的条件下，在重力作用下就产生某些胶瘤，对于小尺寸制品来说，在粘合剂还未失去流动性阶段上最好是缓慢旋转芯模（1-2转/分）。

制品构件和芯模在轴上的固定方式在热处理过程中起着重要作用，钢轴、聚合砂芯模和制品的线性膨胀系数是不同的，由于质量、导温性和导热性不同，在加热-冷却过程中随时间的变形速度也就不相同，这个最重要的情况决定了必须避免芯模毁坏、避免制品不可逆的变形，避免甚至制品毁坏并与芯模和轴分离。如果法兰和端框的其中一个夹架与轴刚性连接在一起，那么，必须保障相对的法兰和端框自由轴向位移的可能性。轴、芯模、法兰和端框刚性固定成一个系统会导致出现法兰与壳体分层、端框分离、“裙”—承力壳体界面整体性破坏诸如此类的缺陷，甚至在刚性固定条件下制品完整性未被破坏的罕见情况下，剩余应力将很大，就是说，保障制品给定的几何尺寸并保持其不随时间而变化是实际上无法解决的问题。虽然复合材料的不同固化方式已发展到辐射方式，用对流热交换炉热处理的方式还是得到了最广泛的应用。

近来，在实践中采用较经济的空气动力加热炉，采用自动化系统（或根据制品表面上的传感器）来控制和调节炉内的温度。

在完成热处理过程和从炉中取出制品后，不应立即拆卸芯模，应结束内应力的均衡和重新分配的松弛过程。

这个过程持续得相当长，但是用试验方法查明，在从炉中取出制品后1—1.5昼夜拆卸和取出芯模会可靠保障制品几何参数的再现性和材料中最低的剩余应力。

参考书目

1、古济A.H.：薄壳体孔周围的应力集中。-应用力学，1969年5月，第三期，第1-18页。

2、叶尔帕季耶夫斯基 A.H.，瓦西里耶夫，B.B.：增强材料圆筒壳体的强度。-莫斯科，机械制造出版社，1972年。

3、复合材料手册/B.B.瓦西里耶夫，В.Д.普罗塔索夫，B.B.博罗京等；B.B.瓦西里耶夫，Ю.М.塔尔诺波里斯基主编。-莫斯科：机械制造出版社，1990年。

4、米特克维奇А.Б.，普罗塔索夫В.Д.：在非测地缠绕条件下最小质量的玻璃纤维增强塑料平衡压力壳体。聚合物力学，1975年第六期，第983-987页。

5、奥布拉措夫И.Ф.，瓦西里耶夫B.B.，布纳科夫B.A.：复合材料回转壳体的优化增强。-莫斯科：机械制造出版社，1977年。

6、萨温Г.Н.：板和壳体中孔附近的应力分布：全苏壳体和板理论学术会议丛刊。巴库，1966年。-莫斯科：科学出版社，1966年，第904-913页。

7、B.B.瓦西里耶夫，图里奇В.И.：组成环和弹性垫板增强的薄板。-基辅：科学思维出版社，1971年。

8、飞行器结构力学：高等学校航空专业教材/И.Ф奥布拉措夫，Л.А.布雷切夫，B.B.瓦西里耶夫等。И.Ф奥布拉措夫主编。-莫斯科：机械制造出版社，1986年。

9、Parode Y.G. Secondary reinforeicing sestems for spiralloy structures. – J. Spacecraft and Rocrets. 1964.1№3.P. 264-269.

10、沃罗别依B.B.：复合材料结构生产工艺：教学参考书。-莫斯科：莫斯科航空学院出版社，1996年。

11、布拉诺夫И.М.，沃罗别依B.B.火箭和航空航天复合材料结构工艺：高等学校教材。-莫斯科：国立莫斯科Н.Э.鲍曼技术大学出版社，1998年。

系统

347

2025 年 3 月
一	二	三	四	五	六	日
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30
31

引言