第九章不可压缩流体的平面势流
流场中各点的流速平行于某一固定平面,并且各流动参数在此平面的法向没有变化,这种流动称为平面流动。本章研究的是不可压缩流体的平面无旋流动,即不可压平面势流。在平面势流的条件下,将流动基本方程简化为(速度)势函数方程,在给定的边界条件下求解势函数方程,然后根据势函数的性质和伯努利方程,就可以求得所研究流场的速度分布和压强分布。
本章从描述不可压平面势流的势函数方程和流函数方程出发,介绍平面势流的叠加原理,然后介绍几种重要的简单平面势流,最后介绍利用势流叠加原理得到的不可压势流圆柱绕流等问题。
9.1 不可压势流的势函数方程和流函数方程
在平面定常无旋不可压流动中,同时存在势函数φ和流函数ψ。由第八章的式(8.48)和式(8.62)己经导出势函数方程和流函数方程分别为
\[\begin{align}& {{\nabla }^{2}}\varphi =0 \\& \left( 9.1 \right) \\& {{\nabla }^{2}}\psi =0 \\& \left( 9.2 \right) \\\end{align}\]
它们都满足拉普拉斯方程。说明平面不可压势流的流函数和势函数都是调和数。式(9.1)的使用条件是不可压无旋流动,而式(9.2)的使用条件是平面定常不可压无旋流动。因此,流函数方程和势函数方程共同存在的流场是平面定常不可压无旋流动。如果平面流是有旋的,那么该流动也有流函数存在,但是此时流函数并不满足拉普拉斯方程。从上面的讨论可以知道,平面定常不可压势流的势函数和流函数均满足拉普拉斯方程,因此,只要知道了其中之一,就可以用速度为媒介很方便地求出另一个来。
例9.1 已知不可压平面流动的速度分布为
(1)Vx=y,Vy=-x;(2)Vx=x-y,Vy=x+y。
判断是否满足势函数φ及流函数ψ存在条件,并求出φ和ψ。
解:(1)由Vx=y,Vy=-x,得到
∂Vx/∂x=0,∂Vy/∂y=0
满足连续方程,故有流函数,即
\[\begin{align}& \psi \left( x,y \right)=\int{\left( \frac{\partial \psi }{\partial x}dx+\frac{\partial \psi }{\partial y}dy \right)}=\int{\left( -{{V}_{y}}dx+{{V}_{x}}dy \right)}= \\& \int{\left( xdx+ydy \right)}=\frac{1}{2}\left( {{x}^{2}}+{{y}^{2}} \right)=\frac{{{r}^{2}}}{2} \\\end{align}\]
流线族为同心圆。下面再来看看是否存在势函数。为此,用无旋条件来判断:
∂Vx/∂y=1,∂Vy/∂x=-1
显然,旋度
\[{{\omega }_{z}}=\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}-\frac{\partial {{V}_{x}}}{\partial y} \right)\ne 0\]
该流动不是有势流动,因此,不存在函势数。
(2)由 Vx=x-y,Vy=x+y
可得
∂Vx/∂x=1,∂Vy/∂y=1,∂Vx/∂x+∂Vy/∂y=2≠0
流动不连续,故无流函数。又
∂Vx/∂y=-1,∂Vy/∂x=1
因为 ∂Vx/∂y≠∂Vy/∂x
不能满足无旋条件,故不存在势函数。
9.2 平面势流叠加原理和几种简单的平面定常势流
9.2.1 势流叠加原理
平面不可压势流的势函数方程和流函数方程均是拉普拉斯方程,而拉普拉斯方程是线性方程,线性方程有一个重要的特特征,即方程解的可叠加性。两个或数个拉普拉斯方程解的和或差是拉普拉斯方程的解。这样,就可以用一些简单的势函数叠加来获得一个复杂势流的势函数,从而获得复杂势流的解。
考虑势数分别为φ1和φ2的两个有势流动,根据势函数的性质,它们都满足拉普拉斯方程,即
\[{{\nabla }^{2}}{{\varphi }_{1}}=0,{{\nabla }^{2}}{{\varphi }_{2}}=0\]
将这两个方程相加,得到
\[\frac{{{\partial }^{2}}\left( {{\varphi }_{1}}+{{\varphi }_{2}} \right)}{\partial {{x}^{2}}}+\frac{{{\partial }^{2}}\left( {{\varphi }_{1}}+{{\varphi }_{2}} \right)}{\partial {{y}^{2}}}=0\]
或写为
\[{{\nabla }^{2}}\left( {{\varphi }_{1}}+{{\varphi }_{2}} \right)=0\]
上式表明,两个势流叠加,得到一个速度势为φ=φ1+φ2的新的复合流动,它的速度势仍然满足拉普拉斯方程,因此还是势流。由此可以得到一个推论,新的复合势流的速度场也可以直接将各简单势流速度场叠加而得,即
\[\begin{align}& {{V}_{x}}=\frac{\partial \varphi }{\partial x}=\frac{\partial \left( {{\varphi }_{1}}+{{\varphi }_{2}} \right)}{\partial x}=\frac{\partial {{\varphi }_{1}}}{\partial x}+\frac{\partial {{\varphi }_{2}}}{\partial x}={{V}_{x1}}+{{V}_{x2}} \\& {{V}_{y}}=\frac{\partial \varphi }{\partial y}=\frac{\partial \left( {{\varphi }_{1}}+{{\varphi }_{2}} \right)}{\partial y}=\frac{\partial {{\varphi }_{1}}}{\partial y}+\frac{\partial {{\varphi }_{2}}}{\partial y}={{V}_{y1}}+{{V}_{y2}} \\\end{align}\]
类似地,新的复合势流的流函数ψ=ψ1+ψ2,等于两个原来的简单流动流函数之和。为了利用势流叠加原理求解一些复杂的势流,下面将研究几种最简单的平面势流。
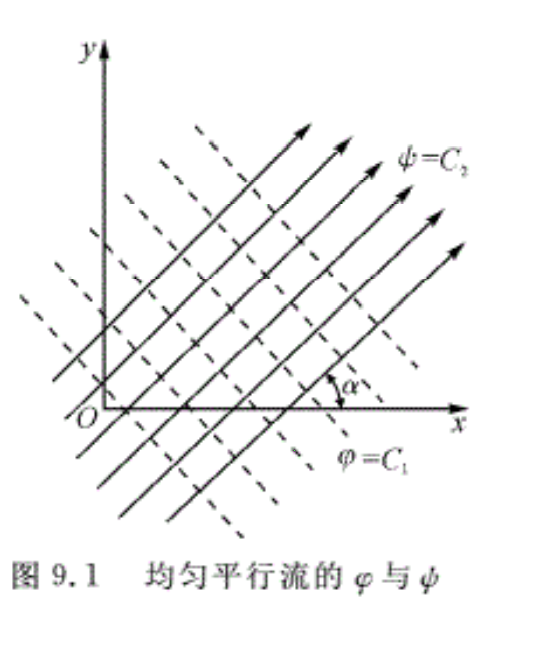
9.2.2 均匀直线流动
设一平面流动的速度V∞在全场处处相同,它与x方向的夹角为α,它的两个分速分别为
\(\left. \begin{align}& {{V}_{x}}={{V}_{\infty }}\cos \alpha =a \\& {{V}_{y}}={{V}_{\infty }}\sin \alpha =b \\\end{align} \right\}\) (9.3)
式中,a,b为常数。这是一个无旋流动,同时又满足连续方程,因此存在势函数φ(x,y)和流函数ψ(x,y)到,利用势函数和流函数的性质,有
\[\begin{align}& d\varphi =\frac{\partial \varphi }{\partial x}dx+\frac{\partial \varphi }{\partial y}dy={{V}_{x}}dx+{{V}_{y}}dy=adx+bdy \\& d\psi =\frac{\partial \psi }{\partial x}dx+\frac{\partial \psi }{\partial y}dy=-{{V}_{y}}dx+{{V}_{x}}dy=-bdx+ady \\\end{align}\]
积分这两式,得到
\[\left\{ \begin{align}& \varphi =ax+by+{{C}_{1}} \\& \psi =ay-bx+{{C}_{2}} \\\end{align} \right.\]
如果取点(0,0)的φ=0,ψ=0,则有C1=C2=0,即
\[\left\{ \begin{align}& \varphi =ax+by \\& \psi =ay-bx \\\end{align} \right.\]
于是,有等势线和流线方程分别为
\[\left\{ \begin{align}& ax+by=const \\& ay-bx=const \\\end{align} \right.\]
可见流线是一族与x轴夹角α的平行线,等势线是一族与y轴夹角为α的平行线,如图9.1所示。图中等势线用虚线表示。
9.2.3 点源和点汇
设在无限大平面上,流体以一恒定的体积流量qv,源源不断地从一个点沿径向向些周均匀地流出,这种流动称为点源,这个点称为源点。qv称为点源强度;若qv为负值,则意味着流体沿径向均匀地从四周流入一点,这种流动称为点汇,这个点称为汇点。若将坐标原点作为源点或汇点,以半径为r的圆作底边的单位高度圆柱面为讨论对象,那么,流过此圆柱面的体积流量qv=2πrVr,即为源(汇)的体积流量,故
\({{V}_{r}}=\frac{{{q}_{v}}}{2\pi r}=\frac{{{q}_{v}}}{2\pi \sqrt{{{x}^{2}}+{{y}^{2}}}}\)
周向速度 \({{V}_{\theta }}=0\)
上式说明,点源或点汇的径向速度与半径成反比,半径越大,流速越低。其分速度为
\[\begin{align}& {{V}_{x}}={{V}_{r}}\cos \theta =\frac{{{q}_{v}}}{2\pi r}\frac{x}{r}=\frac{{{q}_{v}}x}{2\pi \left( {{x}^{2}}+{{y}^{2}} \right)} \\& {{V}_{y}}={{V}_{r}}\sin \theta =\frac{{{q}_{v}}}{2\pi r}\frac{y}{r}=\frac{{{q}_{v}}y}{2\pi \left( {{x}^{2}}+{{y}^{2}} \right)} \\\end{align}\]
根据以上速度分布,就可以容易地求出点源(点汇)的势函数φ和流函数ψ来,即
\[\begin{align}& d\varphi ={{V}_{x}}dx+{{V}_{y}}dy=\frac{{{q}_{v}}\left( xdx+ydy \right)}{2\pi \left( {{x}^{2}}+{{y}^{2}} \right)} \\& d\psi =-{{V}_{y}}dx+{{V}_{x}}dy=\frac{{{q}_{v}}\left( xdy-ydx \right)}{2\pi \left( {{x}^{2}}+{{y}^{2}} \right)}=\frac{{{q}_{v}}d\left( y/x \right)}{2\pi \left[ 1+{{\left( y/x \right)}^{2}} \right]} \\\end{align}\]
积分之,得到
\(\varphi =\frac{{{q}_{v}}}{4\pi }\ln \left( {{x}^{2}}+{{y}^{2}} \right)=\frac{{{q}_{v}}}{2\pi }\ln r\) (9.4)
\(\psi =\frac{{{q}_{v}}}{2\pi }\arctan \frac{y}{x}=\frac{{{q}_{v}}}{2\pi }\theta \) (9.5)
由式(9.4)和式(9.5)可知,点源的等势线是一族同心圆,如图9.2(a)所示,而等流函数线则是从源点发出的射线,如图9.2(b)所示。
当r→0时,Vr→∞,φ→∞因此源点和汇点是奇点,所以径向速度和速度势的表达式只有在源汇点以外才有意义。
将势函数式(9.4)和流函数式(9.5)分别代入拉普拉斯方程,可得\({{\nabla }^{2}}\varphi =0,{{\nabla }^{2}}\psi =0\)说明点源和点汇都是无旋流动,即势流。
9.2.4 点涡(有势涡)
点涡是一种特殊的旋涡流动。形式上,流体在作旋转运动,但是除了原点以外,本质上这是一种无旋流动,故我们称这种涡流为有势涡。与点源或点汇不同,点涡的径向速度为零,而周向速度与半径成反比,它的流线是同心圆,等势线是射线,因此,它的两个分速可以表示为
\[\left. \begin{align}& {{V}_{\theta }}=\frac{\Gamma }{2\pi r} \\& {{V}_{r}}=0 \\\end{align} \right\}\] (9.6)
式中, Γ称为点涡强度。Γ取正值表示流动为逆时针方向转动,负值表示顺时针方向转动。式(9.6)表明,其周向速度与半径成反比,离圆心越远,流速越小。可以证明,点涡是一种和点源的等流函数线及等势函数线恰好互换的流动。位于坐标原点的点涡的势函数和流函数分别为
\[\begin{align}& \varphi =\frac{\Gamma }{2\pi }\theta =\frac{\Gamma }{2\pi }\arctan \left( \frac{y}{x} \right) \\& \left( 9.7 \right) \\& \psi =\frac{\Gamma }{2\pi }\ln r=\frac{\Gamma }{2\pi }\ln \sqrt{{{x}^{2}}+{{y}^{2}}} \\& \left( 9.8 \right) \\\end{align}\]
由此可见,点涡运动的等势线方程为Γ/(2π)× θ=C,即θ=C,为原点出发的射线。点涡运动的流线方程为Γ/(2π) x lnr=C,或r=C,显然,流线是一族同心圆。
根据速度势的性质,由速度势即可求得直角坐标下的各分速Vx,Vy,或极坐标下的各分速Vθ,Vr分别为
\[\begin{align}& {{V}_{x}}=\frac{\partial \varphi }{\partial x}=-\frac{\Gamma }{2\pi }\frac{y}{{{x}^{2}}+{{y}^{2}}},{{V}_{y}}=\frac{\partial \varphi }{\partial y}=\frac{\Gamma }{2\pi }\frac{x}{{{x}^{2}}+{{y}^{2}}} \\& {{V}_{\theta }}=\frac{\partial \varphi }{r\partial \theta }=\frac{\Gamma }{2\pi r},{{V}_{r}}=\frac{\partial \varphi }{\partial r}=\frac{\partial }{\partial r}\left( \frac{\Gamma }{2\pi }\theta \right)=0 \\\end{align}\]
点涡运动是无旋运动即有势运动,除原点以外的流场旋转角速度为零,即
\[{{\omega }_{z}}=\frac{1}{2}\left( \frac{\partial {{V}_{y}}}{\partial x}-\frac{\partial {{V}_{x}}}{\partial y} \right)=\frac{1}{2}\left[ \frac{\partial }{\partial x}\left( \frac{\Gamma }{2\pi }\frac{x}{{{x}^{2}}+{{y}^{2}}} \right)-\frac{\partial }{\partial y}\left( -\frac{\Gamma }{2\pi }\frac{y}{{{x}^{2}}+{{y}^{2}}} \right) \right]=0\]
或者采用极坐标,即
\[{{\omega }_{z}}=\frac{1}{2}\left( \frac{\partial {{V}_{\theta }}}{\partial r}-\frac{\partial {{V}_{r}}}{r\partial \theta }+\frac{{{V}_{\theta }}}{r} \right)=\frac{1}{2}\left[ \frac{\Gamma }{2\pi }\left( \frac{-1}{{{r}^{2}}} \right)+\frac{\Gamma }{2\pi }\left( \frac{1}{{{r}^{2}}} \right) \right]=0\]
在原点,r→0,Vθ→∞,因此在原点附近的流动是有旋的,其旋涡强度为Γ。
9.3 几种简单平面势流的叠加势流
9.3.1 螺旋流(点源或点汇+点涡)
将平面势流点源(或点汇)流动和平面势流点涡流动叠加便得到一种新的平面势流,称为螺旋流或源环流(汇环流)。在螺旋流中流体既作旋转运动,同时又作径向运动,它的轨迹呈螺旋状,故称螺旋流。根据势流叠加原理,螺旋流的势函数和流函数分别为
\[\begin{align}& \varphi =\frac{{{q}_{v}}}{2\pi }\ln r+\frac{\Gamma }{2\pi }\theta \\& \left( 9.9 \right) \\& \psi =\frac{{{q}_{v}}}{2\pi }\theta -\frac{\Gamma }{2\pi }\ln r \\& \left( 9.10 \right) \\\end{align}\]
由流函数便可得到流线方程
\[{{q}_{v}}\theta -\Gamma \ln r=C\]
该式可以写为 \(r={{e}^{\frac{{{q}_{v}}\theta -C}{\Gamma }}}\) (9.11)
是一族对数螺线,它的速度分布为
\[\left. \begin{align}& {{V}_{r}}=\frac{\partial \varphi }{\partial r}=\frac{{{q}_{v}}}{2\pi r} \\& {{V}_{\theta }}=\frac{\partial \varphi }{r\partial \theta }=\frac{\Gamma }{2\pi r} \\\end{align} \right\}\] (9.12)
流体一面在作径向运动,一面又在作旋转运动,二者的合成运动即为螺旋运动。工业上,离心泵内流体的运动,以及旋风燃烧室、旋风除尘器内旋转气流的运动就是属于这种运动。为了减少流体在这类流体机械内的流动损失,避免流体与导叶发生碰撞,离心泵内导叶通常用式(9.11) 所示的对数螺线来设计。
9.3.2 偶极流(点源+点汇)
将强度为qv和-qv的点源和点汇无限地靠近并叠加起来,得到一种新的有势流动,这种流动称为偶极流。
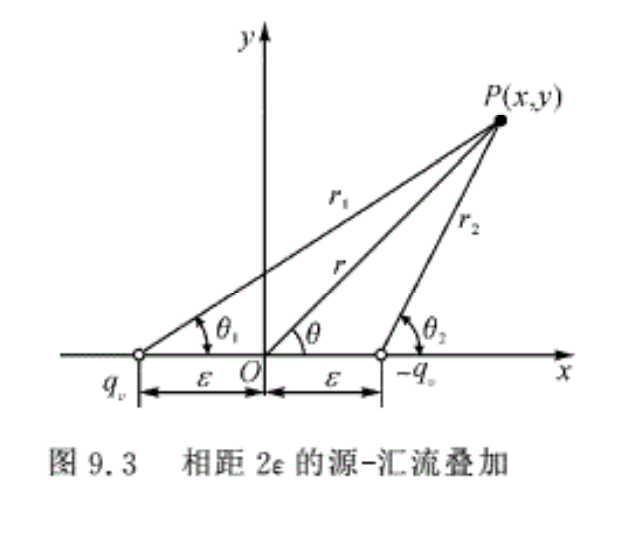
为了研究叠加以后的流场,首先研究图9.3所示的源一汇叠加问题。此时源点和汇点相距2ε,则在流场中任意点P(x,y)处的势函数为点源和点汇的势函数之和,即
\[\varphi ={{\varphi }_{1}}+{{\varphi }_{2}}=\frac{{{q}_{v}}}{2\pi }\left( \ln {{r}_{1}}-\ln {{r}_{2}} \right)=\frac{{{q}_{v}}}{2\pi }\ln \frac{{{r}_{1}}}{{{r}_{2}}}\]
式中,r1和r2为点P至源点和汇点的距离。由图9.3可知
\[\left\{ \begin{align}& {{r}_{1}}=\sqrt{{{\left( x+\varepsilon \right)}^{2}}+{{y}^{2}}} \\& {{r}_{1}}=\sqrt{{{\left( x-\varepsilon \right)}^{2}}+{{y}^{2}}} \\\end{align} \right.\]
代入上述势函数表达式中,有
\[\varphi =\frac{{{q}_{v}}}{2\pi }\ln \sqrt{\frac{{{\left( x+\varepsilon \right)}^{2}}+{{y}^{2}}}{{{\left( x-\varepsilon \right)}^{2}}+{{y}^{2}}}}=\frac{{{q}_{v}}}{4\pi }\ln \frac{{{\left( x+\varepsilon \right)}^{2}}+{{y}^{2}}}{{{\left( x-\varepsilon \right)}^{2}}+{{y}^{2}}}=\frac{{{q}_{v}}}{4\pi }\ln \left[ 1+\frac{4x\varepsilon }{{{\left( x-\varepsilon \right)}^{2}}+{{y}^{2}}} \right]\]
若使源点和汇点无限地接近,即ε→0,并将上式按级数In(1+z)=z-z²/2+z³/3…….展开,并近似取第一项,可得
\[\varphi =\frac{{{q}_{v}}}{4\pi }\frac{4x\varepsilon }{{{\left( x-\varepsilon \right)}^{2}}+{{y}^{2}}}\]
当点源和点汇无限靠近时,令源、汇的强度qv不断增大,即当ε→0时qv→∞,但二者乘积的极限趋于某一常值,保持2εqv=M=常数。M称为偶极流的偶极矩,或称为偶极子的强度。于是有
\[\varphi =\frac{M}{2\pi }\frac{x}{{{x}^{2}}+{{y}^{2}}}\] (9.13)
这就是偶极流的势函数表达式。
偶极流的流函数也可用类似的方法求得,即
\[\psi ={{\psi }_{1}}+{{\psi }_{2}}=\frac{{{q}_{v}}}{2\pi }\left( {{\theta }_{1}}-{{\theta }_{2}} \right)\]
由于
\[\begin{align}& \tan {{\theta }_{1}}=\frac{y}{x+\varepsilon },\tan {{\theta }_{2}}=\frac{y}{x-\varepsilon } \\& \tan \left( {{\theta }_{1}}-{{\theta }_{2}} \right)=\frac{\tan {{\theta }_{1}}-\tan {{\theta }_{2}}}{1+\tan {{\theta }_{1}}\tan {{\theta }_{2}}}=\frac{y\left( x-\varepsilon \right)-y\left( x+\varepsilon \right)}{{{x}^{2}}-{{\varepsilon }^{2}}+{{y}^{2}}}=\frac{2y\varepsilon }{{{x}^{2}}-{{\varepsilon }^{2}}+{{y}^{2}}} \\\end{align}\]
代入流函数表达式,并用级数展开,保留第一项,得到
\[\psi =\frac{{{q}_{v}}}{2\pi }\arctan \frac{-2y\varepsilon }{{{x}^{2}}-{{\varepsilon }^{2}}+{{y}^{2}}}=-\frac{{{q}_{v}}}{2\pi }\frac{2y\varepsilon }{{{x}^{2}}-{{\varepsilon }^{2}}+{{y}^{2}}}\]
与势函数处理方法相同,当点源和点汇无限靠近时,令源、汇的强度qv不断增大,即当ε→0时,qv→∞,但二者乘积的极限趋于某一常值,保持2εqv=M=常数。于是得到偶极流的流函数为
\[\psi =-\frac{M}{2\pi }\frac{y}{{{x}^{2}}+{{y}^{2}}}\] (9.14)
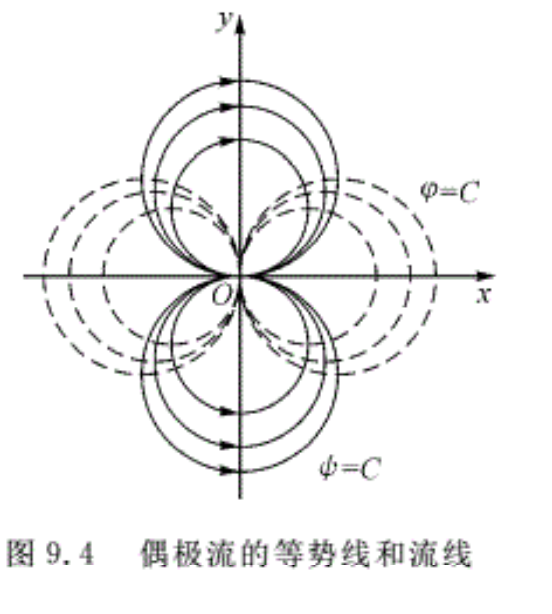
从偶极流的势函数表达式(式(9.13))和流函数表达式(式(9.14))可以看出,等势线和流线都是圆。
流线方程为
\[\frac{y}{{{x}^{2}}+{{y}^{2}}}=C\]
或者
\[{{x}^{2}}+{{\left[ y-1/\left( 2C \right) \right]}^{2}}=1/\left( 4{{C}^{2}} \right)\]
这是圆心在Oy轴上的一族圆方程,在坐标原点与Ox轴相切。因此流体是沿着上述圆周由位于原点的点源流出,重新流入位于原点的点汇,如图9.4所示
等势线方程为
\[\frac{x}{{{x}^{2}}+{{y}^{2}}}={{C}_{1}}\]
或者
\[{{y}^{2}}+{{\left[ x-1/\left( 2{{C}_{1}} \right) \right]}^{2}}=1/\left( 4C_{1}^{2} \right)\]
这是圆心在Ox轴上的一族圆方程,与流线正交,在坐标原点与Oy轴相切。
如果将势函数方程式(9.13)分别对x和y求偏导数,就得到图9.4 偶极流的等势线和流线偶极流的两个速度分量分别为
\[\left\{ \begin{align}& {{V}_{x}}=\frac{\partial \varphi }{\partial x}=\frac{M\left( {{y}^{2}}-{{x}^{2}} \right)}{2\pi {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{2}}} \\& {{V}_{y}}=\frac{\partial \varphi }{\partial y}=-\frac{M\left( 2xy \right)}{2\pi {{\left( {{x}^{2}}+{{y}^{2}} \right)}^{2}}} \\\end{align} \right.\]
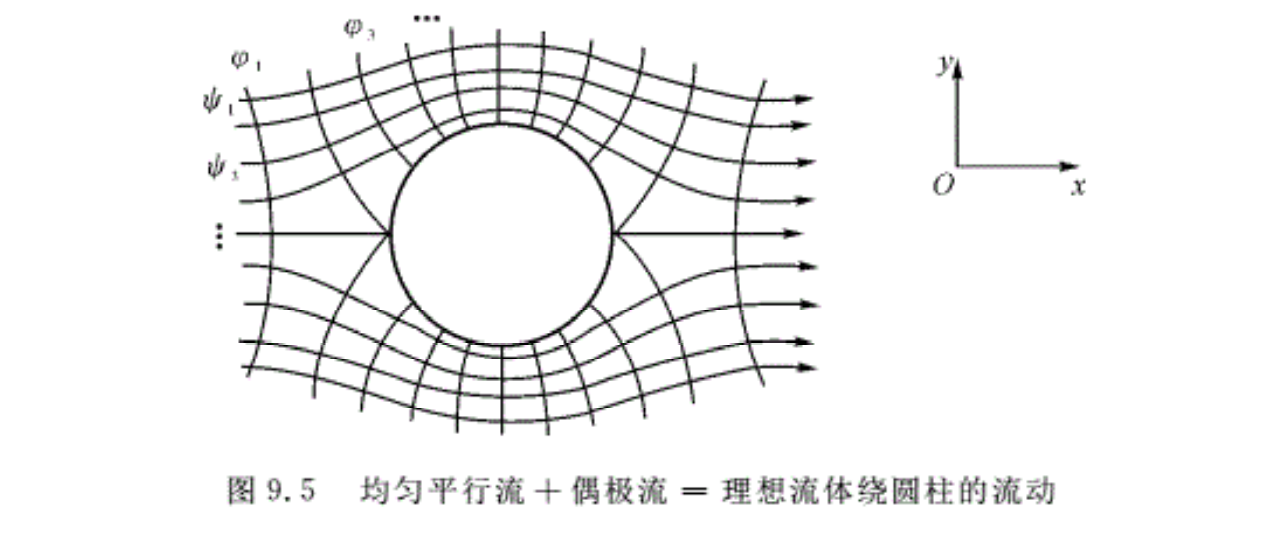
9.4 不带环量的圆柱绕流(均匀直线流+偶极流)
研究表明,如果将一个均匀平行流和偶极流叠加,就可以得到理想流体绕圆柱的平面有势流动。图9.5绘出了这两个势流叠加后流动的示意图。
对于一个流动平行于x方向的流速为V∞的均匀平行流,其流函数和势函数分别为
\[{{\psi }_{1}}={{V}_{\infty }}y,{{\varphi }_{1}}={{V}_{\infty }}x\]
对于偶极流,它的流函数和势函数则分别为
\[{{\psi }_{2}}=-\frac{M}{2\pi }\frac{y}{{{x}^{2}}+{{y}^{2}}},{{\varphi }_{2}}=\frac{M}{2\pi }\frac{x}{{{x}^{2}}+{{y}^{2}}}\]
根据势流叠加原理,新构成的势流的流函数、势函数分别为上述势流的流函数、势函数的代数和,即
\[\begin{align}& \psi ={{\psi }_{1}}+{{\psi }_{2}}={{V}_{\infty }}y-\frac{M}{2\pi }\frac{y}{{{x}^{2}}+{{y}^{2}}}={{V}_{\infty }}y\left( 1-\frac{M}{2\pi {{V}_{\infty }}\left( {{x}^{2}}+{{y}^{2}} \right)} \right) \\& \varphi ={{\varphi }_{1}}+{{\varphi }_{2}}={{V}_{\infty }}x-\frac{M}{2\pi }\frac{x}{{{x}^{2}}+{{y}^{2}}}={{V}_{\infty }}x\left( 1+\frac{M}{2\pi {{V}_{\infty }}\left( {{x}^{2}}+{{y}^{2}} \right)} \right) \\\end{align}\]
由上述流函数公式可知,在y=0及半径为R的圆柱上,流函数ψ等于零,这是一条零流线。由此得到
\[M=2\pi {{V}_{\infty }}{{R}^{2}}\]
代入上述流函数和势函数公式,得
\[\begin{align}& \psi ={{V}_{\infty }}y\left( 1-\frac{{{R}^{2}}}{{{r}^{2}}} \right)={{V}_{\infty }}\sin \theta \left( r-\frac{{{R}^{2}}}{r} \right) \\& \left( 9.15 \right) \\& \varphi ={{V}_{\infty }}x\left( 1-\frac{{{R}^{2}}}{{{r}^{2}}} \right)={{V}_{\infty }}\cos \theta \left( r+\frac{{{R}^{2}}}{r} \right) \\& \left( 9.16 \right) \\\end{align}\]
这就是复合流动的流函数和势函数表达式。
下面进一步分析这一新的复合流动的主要特点。
1.零流线
令式(9.15)为零,即ψ=0,有y=0及r=R两个解,显然零流线是平行于x方向的直线和半径为R的圆柱面,即零流线是一条从负无穷远沿x正方向来的流线,在圆柱的前驻点与圆柱相撞,分为上、下两条流线,沿圆柱的上表面和下表面流动,然后在圆柱的后驻点又汇合成一条流线,再沿 x正向朝止无穷远流去。可见这条流线的特征与理想流体绕圆柱流动的特征是相吻合的,如图 9.6所示。
2.远场流动
将势函数表达式(式(9.16))分别对x,y求偏导数,可得这两个方向的分速分别为
\[\begin{align}& {{V}_{x}}=\frac{\partial \varphi }{\partial x}={{V}_{\infty }}-{{V}_{\infty }}{{R}^{2}}\frac{{{x}^{2}}-{{y}^{2}}}{{{\left( {{x}^{2}}+{{y}^{2}} \right)}^{2}}}={{V}_{\infty }}\left[ 1-{{R}^{2}}\frac{{{\cos }^{2}}\theta -{{\sin }^{2}}\theta }{{{r}^{2}}} \right] \\& {{V}_{y}}=\frac{\partial \varphi }{\partial y}=-{{V}_{\infty }}{{R}^{2}}\frac{2xy}{{{\left( {{x}^{2}}+{{y}^{2}} \right)}^{2}}}=-{{V}_{\infty }}{{R}^{2}}\frac{2\cos \theta \sin \theta }{{{r}^{2}}} \\\end{align}\]
由上两式可知,当r→∞时,Vx=V∞,Vy=0,这表明,在离圆柱体无穷远处,流体速度是平行于 x方向的流动,且等于均匀、平行的来流速度。这有力地说明,复合速度势代表了圆柱绕流问题。
3.圆柱表面流动
将速度势对径向和周向求偏导数,得到复合流动的径向和周向分速分别为
\[\begin{align}& {{V}_{\theta }}=\frac{\partial \varphi }{r\partial \theta }=-{{V}_{\infty }}\sin \theta \left( 1+\frac{{{R}^{2}}}{{{r}^{2}}} \right) \\& {{V}_{r}}=\frac{\partial \varphi }{\partial r}={{V}_{\infty }}\cos \theta \left( 1-\frac{{{R}^{2}}}{{{r}^{2}}} \right) \\\end{align}\]
在圆柱表面上,r=R,根据以上两式,可得Vr=0,Vθ=-2V∞sinθ,这表明在圆柱表面上,新的复合流动是紧紧贴着圆柱表面的,各处的流动速度与圆柱表面相切。在前驻点θ=π,Vθ=0,在后驻点θ=0,Vθ=0,圆柱表面各点的绝对速度为Vθ=2V∞丨sinθ丨,当θ=±π/2时,Vθ=2V∞,圆柱表面的速度大小只与角度θ有关。这又一次证明复合流动是理想流体绕圆柱的流动。
4.圆柱表面压强分布
因为复合流动是有势流,故伯努利方程全场满足。若建立无穷远处与圆柱表面的伯努利方程,则可以导出圆柱表面的压强分布规律来,即
\[{{p}_{\infty }}+\frac{1}{2}\rho V_{\infty }^{2}={{p}_{s}}+\frac{1}{2}\rho V_{\theta }^{2}={{p}_{s}}+\frac{1}{2}\rho \left( 4V_{\infty }^{2}{{\sin }^{2}}\theta \right)\]
由此得到圆柱表面的压强为
\[{{p}_{s}}={{p}_{\infty }}+\frac{1}{2}\rho V_{\infty }^{2}-\frac{1}{2}\rho \left( 4V_{\infty }^{2}{{\sin }^{2}}\theta \right)={{p}_{\infty }}+\frac{1}{2}\rho V_{\infty }^{2}\left( 1-4{{\sin }^{2}}\theta \right)\]
圆柱表面的压强因数
\[{{C}_{p}}=\left( {{p}_{s}}-{{p}_{\infty }} \right)/\left( \frac{1}{2}\rho V_{\infty }^{2} \right)=1-4{{\sin }^{2}}\theta \]
上式表明,在圆柱表面上,前、后驻点的压强因数Cp=1,而在±π/2处,压强因数达最小值Cp=-3。
当θ=π/ 6,θ=5π/6,θ=-π/6,θ=-5π/6时,Cp=0。
在流体力学中,常利用圆柱表面压强分布的规律来制成圆柱形测压管,用来测量流动速度的大小、方向及静压强。
9.5 带环量的圆柱绕流和儒科夫斯基升力定理
在第9.4节讨论的圆柱绕流中,如果半径为R的圆柱体本身在作等速旋转,那么,由于黏性作用,旋转的圆柱会带动紧貼在圆柱表面的流体旋转,同时,又带动周围的流体旋转,其旋转速度与半径成反比。这种流动形态可以用带环量的圆柱绕流来描述,它是由点涡与一个均匀平行流、偶极流叠加而成的,即
均匀平行流+偶极流+环量为-Γ的有势涡→带环量的圆柱绕流
这样,根据势流叠加原理,就可以写出这种流动的势函数和流函数分别为
\[\begin{align}& \varphi ={{V}_{\infty }}\cos \theta \left( r+\frac{{{R}^{2}}}{r} \right)-\frac{\Gamma }{2\pi }\theta \\& \left( 9.17 \right) \\& \psi ={{V}_{\infty }}\sin \theta \left( r-\frac{{{R}^{2}}}{r} \right)+\frac{\Gamma }{2\pi }\ln r \\& \left( 9.18 \right) \\\end{align}\]
而对应的速度分布为
\[\begin{align}& {{V}_{r}}=\frac{\partial \varphi }{\partial r}={{V}_{\infty }}\cos \theta \left( 1-\frac{{{R}^{2}}}{{{r}^{2}}} \right) \\& {{V}_{\theta }}=\frac{\partial \varphi }{r\partial \theta }=-{{V}_{\infty }}\sin \theta \left( 1+\frac{{{R}^{2}}}{{{r}^{2}}} \right)-\frac{\Gamma }{2\pi r} \\\end{align}\]
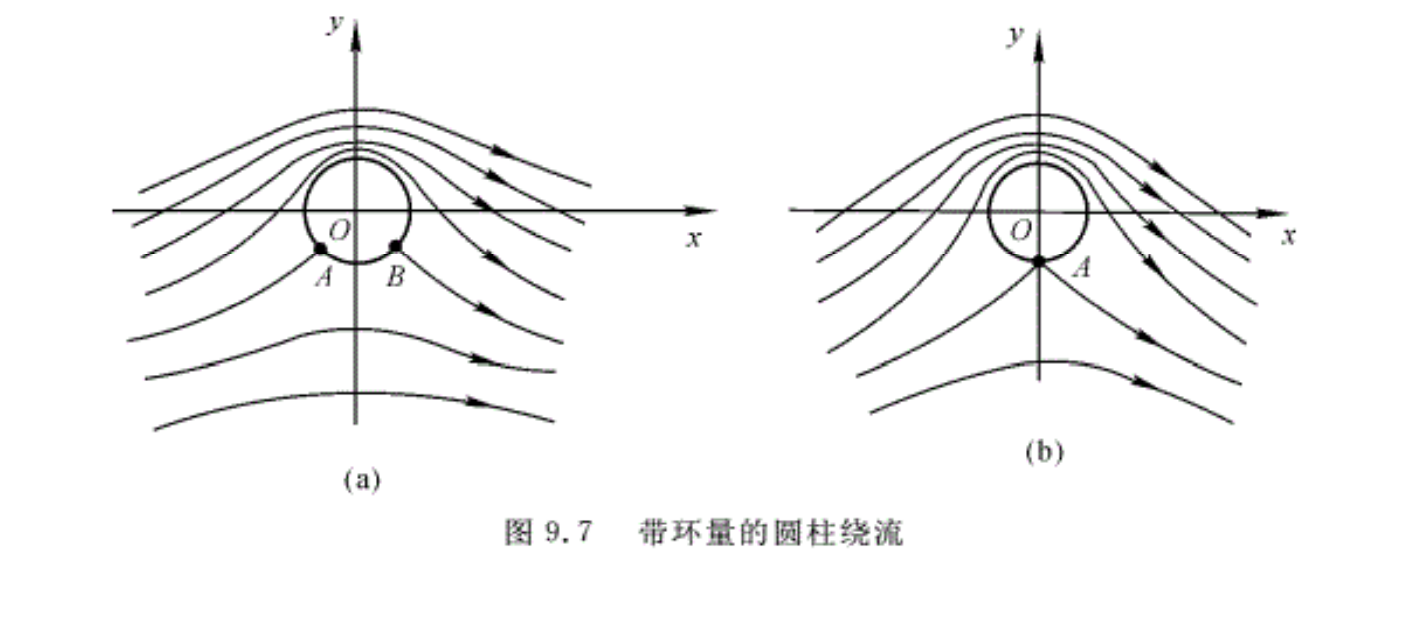
流动如图9.7(a)所示。
在圆柱表面 r=R,Vr=0
\[{{V}_{\theta }}=-2{{V}_{\infty }}\sin \theta -\frac{\Gamma }{2\pi R}\]
在滞止点, Vr=0,Vθ=0,θ=α,
\[\sin \alpha =-\frac{\Gamma }{4\pi R{{V}_{\infty }}}\]
若\(\Gamma =4\pi {{V}_{\infty }}R\),则sinα=-1,α=-π/2,流动如图9.7(b)中的驻点A所示。若Γ<4πV∞R,则丨sinα丨< 1,在圆柱上有两个驻点,如图9.7(a)中的点A和B所示。若Γ>4πV∞R,则在圆柱表面上无滞止点,一般在流体内部有一滞止点。
利用速度分布和伯努利方程,可得到圆柱表面的压强分布规律为
\[\begin{align}& {{p}_{s}}={{p}_{\infty }}+\frac{1}{2}\rho V_{\infty }^{2}-\frac{1}{2}\rho {{\left( -2V_{\infty }^{{}}\sin \theta -\frac{\Gamma }{2\pi R} \right)}^{2}} \\& \left( 9.19 \right) \\& {{p}_{s}}-{{p}_{\infty }}=\frac{1}{2}\rho V_{\infty }^{2}\left[ 1-{{\left( 2\sin \theta +\frac{\Gamma }{2\pi R{{V}_{\infty }}} \right)}^{2}} \right] \\& \left( 9.20 \right) \\\end{align}\]
圆柱表面的压强因数
\[{{C}_{p}}=\left( {{p}_{s}}-{{p}_{\infty }} \right)/\left( \frac{1}{2}\rho V_{\infty }^{2} \right)=1-{{\left( 2\sin \theta +\frac{\Gamma }{2\pi R{{V}_{\infty }}} \right)}^{2}}\]
由此可见,圆柱表面压强分布对称于Oy轴,而不对称于Ox轴;在轴下半圆柱表面上的压强均大于Ox轴上半圆柱表面上的压强。这样,流体流经带环量的圆柱体时就产生了一个向上的升力。通过对圆柱表面的压强进行积分,就可以得到理想流体流经带环量的圆柱体时的升力Y和阻力X,即
\[\begin{align}& Y={{F}_{y}}=\int_{0}^{2\pi }{-pR\sin \theta d\theta } \\& X={{F}_{x}}=\int_{0}^{2\pi }{-pR\cos \theta d\theta } \\\end{align}\]
将式(9.19)代入上式,积分并简化,可以得到
\[\begin{align}& Y={{F}_{y}}=\int_{0}^{2\pi }{-pR\sin \theta d\theta }=\rho {{V}_{\infty }}\Gamma \\& \left( 9.21 \right) \\& X={{F}_{x}}=\int_{0}^{2\pi }{-pR\cos \theta d\theta }=0 \\\end{align}\]
式(9.21)说明,在理想流体流经带环量(顺时针为止)的圆柱体时,流体作用在单位长度圆柱体上的升力大小等于流体密度、远前方来流速度和速度环量的乘积,其阻力为零。
这就是著名的库塔一儒科夫斯基升力定理,它广泛地应用于理论空气动力学中求解翼型的升力。
小结
本章主要讨论不可压缩流体的平面势流的特点。
(1)在不可压缩平面势流中,同时存在流函数和势函数,且它们都满足拉普拉斯方程。拉普拉斯方程是线性方程,线性方程可以叠加。
(2)讨论了几种简单的平面势流,例如均匀直线流动;点源和总汇;点涡等。
(3)将几种简单的平面势流叠加可以获得较为复杂流动的流场。
(4)讨论了不带环量、带环量的圆柱绕流和儒科夫斯基升力定理。
本章内容表示低速流动中,某些绕流流场的求解方法。在流体力学实验中,测量流动速度的大小和方向,以及静压强等流动参数,就是利用本章第9.4节介绍的原理。
思考与练习题
9.1 势流叠加原理是什么?
9.2 己知二维定常流动的流函数为ψ=lnr+2θ,r,θ为极坐标变量。试求其速度分布;并问是否为不可压流动?
9.3 二维不可压定常流动的流函数为ψ=3x²y-y³,问是否为无旋流动?求流场中任意点的速度大小与这点到坐标原点距离的关系。
9.4 己知一流场的势函数为φ=2x²-3y²。求该流场的流函数。
9.5 一平面流场,其速度分布为Vx=x²,Vy=xy。求流函数。
9.6 一直匀流其速度等于常数,沿水平方向流动。问势函数是否存在?若存在,则求势函数的表达式。
9.7 假设一平面流动的势函数为φ=-√3x+y+t,求该流动的速度分布,并求通过点 M(1,0)和点N(2,√3)之间的体积流量。
9.8 一定常不可压平面流动,其速度分布为Vx=x,Vy=-y。求流线方程,并判别流动是否存在势函数,若存在,求势函数方程。
9.9 己知一不可压缩流体流动的速度分量为Vx=∂f/∂y,f=f(x,y),且沿x方向有一条流线,试证明另一速度分量\({{V}_{y}}=-\frac{\partial f}{\partial x}+{{\left( \frac{\partial f}{\partial x} \right)}_{y=0}}\)。
9.10 假设一平面连续流动的速度分布为Vx=x²-y²+x,Vy=-(2xy+y)。问是否为无旋流动?求经过点(1,2)的流线方程。
9.11 如图9.8所示的大容器,盛有深度为H的水,底部有一个半径为r2的小孔,在容器底部的上方有一个半径为r1的圆形平板,且r1>>r2,圆板距容器底部的距离为h(h<<H)。假设正对泄孔的那部分板面上方的表压强为零,板与底部之间的流动可视为点汇,试证明圆板所受的作用力为
\[F=\pi \rho g\left[ \left( H-h \right)r_{1}^{2}+{{Q}^{2}}\ln \frac{{{r}_{1}}/{{r}_{2}}}{4{{\pi }^{2}}g{{h}^{2}}} \right]\]