第三章喷管理论和热力学关系式
火箭发动机喷管和燃烧室内部过程的热力学关系式是计算火箭推进系统性能和确定若干关健设计参数所需的数学工具。这些关系式可用于评定和比较各种火箭推进系统的性能、预测任何利用气体热力学膨胀原理的火箭发动机装包的工作性能、针对给定的性能要求确定一些必要的设计参数(如喷管尺寸和大致形状)。该理论适用于化学火箭推进系统(液体和固体推进剂)、核火箭发动机、太阳能加热推进系统、电阻或电弧加热的电火箭系统以及任何利用气体膨胀作为高速喷射物质的推进机理的推进系统。
本章介绍和阐述一些对火箭发动机装置的分析和设计很重要的基本热力学关系式。利用这些公式,读者可基本了解火箭发动机气体的特性和膨胀所涉及的力学过程。读者需具备基本的热力学和流体力学知识(参见文献1-1、3-1、3-2和3-3)。本章还描述了各种喷管构型、非最佳性能、能量损失、喷管对中、变推力以及四类不同的喷管性能参数的确定方法。
3.1理想火箭发动机
理想火箭推进系统这个概念是很有用的,因为在这种条件下有关的热力学基本原理可以用简单的数学关系式表示,这些关系式将在本章各节中给出。这些公式是准一维喷管流动的理论描述,这种准一维公式是完全两维或三维公式以及实际气动热化学特性的 一种理想化的、简化的形式。但是,通过下面陈述的假设和简化,它们对许多火箭推进系统都足以得到有用的解。对于化学火箭推进,实际测量的性能通常比理论计算值低 1%~6%。在设计新火箭发动机时,当前普遍认可的做法是利用理想火箭发动机参数,然后加以适当的修正,如本章第5节讨论的那样。理想火箭发动机装置应满足以下假设:
- 工质(或化学反应产物)是均相的。
- 工质的所有成分都是气态的。总质量中任何凝聚相(液态或固态)所占的量都可忽略。
- 工质服从完全气体定律。
- 没有穿过发动机室壁的传热,因此流动是绝热的。
- 没有明显的摩擦,忽略所有的边界层效应。
- 喷管流动无激波或不连续性。
- 推进剂流动是定常的。工质的膨胀均匀而稳定,没有振动。瞬变效应(即启动和关机)的时间非常短,可忽略。
- 离开发动机喷管的排气只有轴向速度。
- 在与喷管轴线垂直的任何截面上气体的速度、压力、温度和密度都是均匀的。
- 在发动机燃烧室内气体达到化学平衡,气体成分在喷管内不变(冻结流动)。
- 所贮存的推进剂处于室温,低温推进剤处于沸点温度。
有了这些假设,就可对下面几节将要阐述的简单的准一维理论进行推导,本章后面部分将介绍更复杂的理论,或对列出的一些项目引入修正系数,它们可以使简化分析更加精确。下面一段将解释为什么这些假设只引入了很小的误差。
对于液体火箭发动机,理想化的理论假设喷射系统使燃料和氧化剂完全均匀混合,产生均相的工质。好的发动机喷注器能达到与此非常接近的状态。对于固体火箭发动机装置,推进剂必须基本上是均相和均匀的,燃烧速率必须是稳定的。对下核热、太阳能加热或电弧加热火箭发动机,假设任何横截面上热气的温度都是均匀的,气流是稳定的。由于燃烧室温度一般来说很髙(对于常用推进剤为2500-3600K),远在各种气体相应的饱和状态之上。实际上与完全气体非常接近。上面的假设(4)、(5)和(6)使得火箭发动机喷管内的过程可以采用等熵彫胀关系,由此描述热量向射流动能的最大限度的转化。此外这还意味着喷管流动为可逆热力学过程。壁面摩擦损失难以精确确定,但这在喷管中通常是很小的。除了很小的推力室外,发动机室壁传热造成的能量损失通常小于总能量的1% (偶尔达2%),因此可以忽略。稳态时推进剂流量和压力的短期波动通常小于额定值的5%,它们对火箭性能的影响是很小的,也可以忽略。在精心设计的超声速喷管中,热能向排气定向动能的转变是平稳进行的,没有正激波或不连续性,因此流动膨胀损失总的来说也是很小的。
某些公司和某些作者提出的理想发动机的定义中的假设并不一定包括上述全部11项或与此完全相同。例如,某些作者采用15°半角的锥形喷管作为理想喷管的基本构型而不采用假设(8)(噴管出口速度全为轴向的),以考虑速度扩张损失,这将在本章后面叙述。
3.2热力学关系式概述
本节简要回顾一些推导喷管流动公式所需的基本关系式。这些关系式的严格推导过程和讨论可参见许多热力学和流体力学教科书,如文献3-1和3-2。
能量守恒原理可以直接应用于喷管内的无轴功绝热过程。此外,没有激波和摩擦,流动的熵变为零。焓这个概念在流动系统中是很有用的。焓为内能加流动功(或气体以速度v越过边界所做的功)。对于理想气体,焓可以很方便地表示为比热Cp与绝对温度T之积(定压比热形式上定义为定压下焓对温度的偏导数)。在上述假设下,单位质量的总焓或滞止焓h0为常数,即
\({{h}_{0}}=h+{{v}^{2}}/2J=\)常数 (3-1)
上式中J为热功当量,只有当热量单位(即Blu和Cal)与力学单位(即ft・lbf和J)混合使用时才引入J。在SI单位(kg、m、s)中J为1。在英制单位中J为另一常数 (參见附录1),因为质量单位(即lb)不同。任意两截面x和y之间等熵流动的能量是守恒的。而势能的变化可以忽略,因此流动的焓降伴随有动能的増加。
\({{h}_{x}}={{h}_{y}}=\frac{1}{2}\left( v_{y}^{2}-v_{x}^{2} \right)/J=cp\left( {{T}_{x}}-{{T}_{y}} \right)\) (3-2)
在只有一个进口和一个出口的稳态流动中,质量守恒原理表示为任意截面x 与y上的质量流量\(\dot {m}\)相等,其数学形式就是众所周知的连续方程。设横截面积为A、速度为v、比容为V,则有:
\({{\dot{m}}_{x}}={{\dot{m}}_{y}}=\dot{m}=Av/V\) (3-3)
完全气体定律可以写为
\({{p}_{x}}{{V}_{x}}=R{{T}_{x}}\) (3-4)
式中气体常数R为通用气体常数R’除以流动气体混合物的分子量m。标准状态下分子容积为22.41 m3/ (kg-mol),与此相关R’= 8314.3 J/ (kg.mol.K)。读者经常会发现用密度ρ表示的公式(3–3), ρ为比容V的倒数。对于完全气体,定压比热cp、定容 比热cv及其比值k在很宽的温度范围内都是常数.三者是相关的。
k = cp/cv (3-5a)
cp-cv = R/J (3-5b)
cp = kR/(k – 1)J (3-6)
对于等熵流动过程,任点两点x和y之间存在以下关系:
\({{{{{T}_{x}}}/{{{T}_{y}}=\left( {{{p}_{x}}}/{{{p}_{y}}}\; \right)}\;}^{\frac{k-1}{k}}}={{\left( {{{V}_{y}}}/{{{V}_{x}}}\; \right)}^{k-1}}\) (3-7)
在喷管等熵膨胀过程中,压力显著下降,绝对温度的下降稍微小一些,比容増大。当流动以等熵过程停止时,得到的状态称为滞止状态,用下标“0”表示。有时用“总”字代替“滞止”。从公式(3-1)可以看岀,滞止焓为静止焓(或当地焓)和流体动能之和。根据能量公式可以得到滞止温度T0为
\({{T}_{0}}=T+{{{v}^{2}}}/{2{{c}_{p}}J}\;\) (3-8)
式中T为流体的绝对静温。在绝热流动中,滞止温度为常数。滞止压力与流动中当地压力的关系可以根据前面两个公式得到:
\(\frac{{{p}_{0}}}{p}={{\left[ 1+\frac{{{v}_{2}}}{2{{c}_{p}}JT} \right]}^{\frac{k}{k-1}}}={{\left( \frac{V}{{{V}_{0}}} \right)}^{k}}\) (3-9)
在当地速度接近零时,当地温度和当地压力接近滞止温度和滞止压力。在燃烧室中气体速度很小,燃烧室压力基本上等于滞止压力。理想气体的声速a与压力无关,它定义为
\(a=\sqrt{kRT}\) (3-10)
若用英制(EE)单位,R值必须修正,要増加常数g0,公式(3-10)成为\(\sqrt{{{g}_{0}}kRT}\)。 在EE制中凡是有R的地方都必须使用该修正系数。马赫数M是一无量纲流动参数, 定义为流动速度v与当地声速a之比。
M = v/a =v/ \(\sqrt{kRT}\) (3-11)
马赫数小于1相应于亚声速,马赫数大于1则相应于超声速。当马赫数等于1时,流动速度正好为声速。后面将要指出,所有超声速喷管的喉部马赫数都等于1。现在可以根 据公式(3-2)、(3-7)和(3-10)写出滞止温度和马赫数之间的关系。
\({{T}_{0}}=T\left[ 1+\frac{1}{2}\left( k-1 \right){{M}^{2}} \right]\) (3-12)
或
\(M=\sqrt{\frac{2}{k-1}\left( \frac{T}{{{T}_{0}}}-1 \right)}\)
T0和P0表示温度和压力的滞止值。与温度不同,滞止压力在喷管绝热膨胀中只对等熵流动才保持不变,它可以用下式计算:
\({{p}_{0}}=p{{\left[ 1+\frac{1}{2}\left( k-1 \right){{M}^{2}} \right]}^{\frac{k}{k-1}}}\) (3-13)
等熵流动中喷管内任意两点x和y的喷管面积比可用马赫数表示。其公式为
\(\frac{{{A}_{y}}}{{{A}_{x}}}=\frac{{{M}_{x}}}{{{M}_{y}}}\sqrt{{{\left\{ \frac{1+\frac{1}{2}\left( k-1 \right)M_{y}^{2}}{1+\frac{1}{2}\left( k-1 \right)M_{x}^{2}} \right\}}^{\frac{k+1}{k-1}}}}\) (3-14)
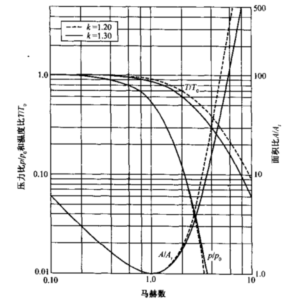
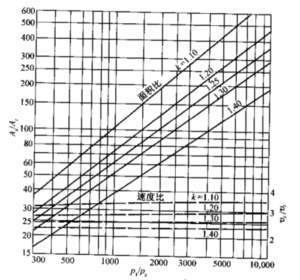
图3-1画岀了上式以及T/T0和P/P0的关系,图中Ax取为At, Mx为1.0。从图3-1可以看出,亚声速流动状态下燃烧室收缩比A1/At,可很小,其值为3〜6,流动通道为收敛形。从该图还可发现k的变化带来的影响几乎看不出来。在固体火箭发动机中, 燃烧室面积A1指初始药柱中的流动通道或空腔的面积。对于超声速流动,喷管截面扩张,面积比増长很快,k值对面积比有显著影响。在M=4时面积比A2/At为15~30, 视k值面定。从另一方面讲,k对压力比的影响很小,对温度比的影响较大。
混合气体的平均分子量 M为所有组分的摩尔分数门ni与其分子量之积(nimi)之和除以所有组分的摩尔分数之和。第五章将对此作进一歩叙述。采用符号m是为了避免与马赫数M混淆。在许多火箭发动机文献中m称为分子重量。
图3-1亚声速和超声速状态下拉伐尔喷管中面积比、压力比和温度比与马赫数的关系
例题3-1 一理想火箭发功机燃烧室在海平面工作,采用燃烧产物的比热比k为1.30的推进剂。求所需燃烧室压力及噴管喉部和出口截面的面积比,假定喷管出口马赫数 M为2.4。噴管进口马赫数很小,可以忽略。
[解] 对于最佳膨胀,喷管出口压力应等于大气压0.1013MPa。若燃烧室气流速度很小,则燃烧室压力等于总压或滞止压力,根据公式(3.13)得
\({{p}_{0}}=p{{\left[ 1+\frac{1}{2}\left( k-1 \right){{M}^{2}} \right]}^{\frac{k}{k-1}}}\)
=0.1013[1 +0.5 ×0.30 ×2.402]2.3/0.3, = 1.50 (MPa)
设喉部Mt = 1.0,根据公式(3-14)确定面积比(同时参见图3-1)为
\(\frac{{{A}_{2}}}{{{A}_{1}}}=\frac{1.0}{2.40}=\sqrt{{{\left( \frac{1+0.15\times {{2.4}^{2}}}{1+0.15} \right)}^{\frac{2.3}{0.3}}}}=2.64\)
3.3喷管内部等熵流动
在收敛-扩张喷管中,燃烧室燃气的大部分热能转变为动能。如后面将阐述的,气体的压力和温度显著下降,而气体速度可超过每秒3km。这是一个基本上是等熵的可逆流动过程,其分析方法将在下面叙述。若喷管内壁有一流动障碍或凸起(如一块焊接飞濺物或残渣),则气体的局部动能转变回热能,局部参数基本上等于燃烧室内的总温和总压。由于这会导致局部壁面很快过热和破坏,喷管内壁必须平滑,不得有任何凸起。滞止状态还会在燃气舵前缘(将在第十六章叙述)或伸入气流中的气体取样管端头出现。
3.3.1速度
根据公式(3-2)可得到喷管出口速度v2:
\({{v}_{2}}=\sqrt{2J\left( h1-h2 \right)+v_{1}^{2}}\) (3- 15a)
上式在理想和非理想火箭发动机中都适用。对于k为常数的情况,利用公式(3-6)和(3-7)可改写上式。下式中下标1和2分别表示喷管进口和出口状态:
\({{v}_{2}}=\sqrt{\frac{2k}{k-1}R{{T}_{1}}\left[ 1-{{\left( \frac{p2}{p1} \right)}^{\frac{k-1}{k}}} \right]+v_{1}^{2}}\) (3-15b)
上式也适用于喷管内任意两点。当燃烧室截面相对喷管喉部截面很大时,燃烧室速度或喷管进口速度相对很小,v12项可忽略。燃烧室温度T1即为喷管进口温度,在等熵条件下它与滞止温度或(对于化学火箭)燃烧温度差别很小。这样就导出了排气速度v2的简化表达式,该表达式很重要,在分析中经常用到。
\({{v}_{2}}=\sqrt{\frac{2k}{k-1}R{{T}_{1}}\left[ 1-{{\left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)}^{\frac{k-1}{k}}} \right]+v_{1}^{2}}\text{=}\sqrt{\frac{2k}{k-1}\frac{{{R}_{0}}{{T}_{0}}}{m}\left[ 1-{{\left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)}^{\frac{k-1}{k}}} \right]}\) (3-16)
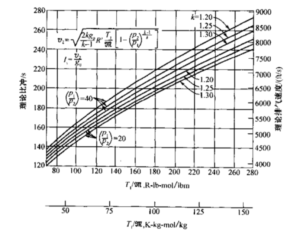
从上式可以看出,喷管排气速度为压比p1/p2、比热比k,喷管进口绝对温度T1以及 气体常数R的函数。由于任何特定气体的气体常数都与分子量m成反比,故排气速度或比冲是喷管进口绝对温度与分子量之比的函数,如图3-2所示。该比值在优化化学火箭发动机混合比时很重要。
图3-2在喷管最佳膨胀时,不同的k和p1/p2值的理想火箭发动机的比冲、排气速度与燃烧室绝对温度t1和分子量m之间的关系
公式2-14和2-15给岀了速度v2、推力F和比冲Is之间的关系,图3-2画出了在2种压比、3种k值下的比冲值。公式(3-16)表明,増加燃气温度(通常通过提高能量释放值达到)或降低推进剂分子量(通常利用氢含量高的低分子量气体来达到)都能改进火箭发动机性能,即提高比冲Is或排气速度v2或c,从而提高飞行器性能。喷管压比p1/p2和比热比的影响不太显著。从图3-2可以看到,性能随压比的増加而增加,该压比随着室压p1的增加或出口压力p2的降低(相应于高空用的设计方案)而増加。k值的影响(比较小)则有点不规则,因为双原子或单原子气体的分子量比较低,但它们的k值却比较高。
为了比较一火箭推进系统与另一火箭推进系统的比冲值,或评估各种设计参数的影响,压比值必须标准化。目前一般采用的标准状态是1000psi(6.894 MPa)的室压和 1 atm (0.1013 MPa)的出口压力。
对于最佳膨胀,p3=p2、等效排气速度c [公式(2-16)]和理想发动机排气速度相等,即
v2=(c2)opt
因此在公式(3-15)和(3-16)中v2可以用c来代替。对于固定的喷管出口面积比和恒定的室压,这种最佳状态只在外界压力p3等于喷管排气压力p2的特定高度出现。 在其他所有高度,\(c\ne {{v}_{2}}\)。
当压比无限大(排入真空)时,喷管出口速度达到理论最大值:
\({{\left( {{v}_{2}} \right)}_{\max }}=\sqrt{2kR{{T}_{0}}/\left( k-1 \right)}\) (3-18)
虽然压力比为无限大,但该理论最大排气速度是一有限值,因为它代表了有限的流体热能。这样的膨胀实际上是不会发生的,因为在这种情况下,至少,许多工质組分的温度会降至液化温度或冰点以下,它们不再是气体,不能再进行气体膨胀。
例题3-2 一台在海平面(p = 0.1013 MPa)工作的火箭发动机,室压p1=2.068 MPa 或300 psi,燃烧室温度t1= 2222 K,推进剂耗量\(\dot {m}\)= 1 kg/s,设为k= 1.30, R = 345.7 J/ (kg.K)o试用图表示参数A、v, V和M随喷管圧力的变化,并计算理论推力和理论比冲。
【解】 选择一系列压力值,并计算各压力相应的A、v和V值。下面给岀了一个计算示 例。跟据完全气体状态方程(3-4)计算初始比容Vl:
V1 = RT1/p1= 345.7×2222/(2.068×106) = 0.3714 (m3/kg)
根据公式(3-7),等熵流动中间压力点处(如px = 1.379 MPa或200psi处)的比容和 温度为
Vx=V1(p1/px) 1/k=0.3714(2.068/1.379)1/1.3 = 0.5072 (m3/kg)
Tx=T1(px/p1)(k-1)/k=2222(1.379/2.068)0.38/1.3= 2053 (K)
根据公式(3-16)可计算出速度:
\({{v}_{x}}=\sqrt{\frac{2k}{k-1}R{{T}_{1}}\left[ 1-{{\left( \frac{{{p}_{x}}}{{{p}_{1}}} \right)}^{\frac{k-1}{k}}} \right]}\)
\(=\sqrt{\frac{2\times 1.30}{1.30-1}345.7\times 2222\left[ 1-{{\left( \frac{1.379}{2.068} \right)}^{0.2307}} \right]}\text{=}771\)(m/s)
根据公式(3-3)计算横截面积:
\({{A}_{x}}={{\dot{m}}_{x}}{{V}_{x}}/{{v}_{x}}\) = 1 × 0.5072/771 = 658 (cm2)
根据公式(3–11)得到马赫数M:
M = v/ \(\sqrt{kRT}\) = 771\(\sqrt {1.30 ×345.7 × 2222}\) = 0.772
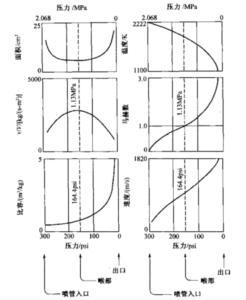
国3-3画出了速度、比容、面积和马赫数随该喷管内压力的变化。在最佳膨胀条件下理想排气速度v2等于等效排气速度c,根据公式(3-16)可计算出该速度为1827 m/s。 进而根据公式(2-6)和(2-14)确定推力F和比冲Is:
F=\(\dot{m}\)v2 = 1 × 1827 = 1827 (N)
Is= c/g0=1827/9.80 = 186 (s)
从上面的例题可以得到一些有趣的推论。在火箭发动机喷管中可以得到很高的气体 速度(lkm/s以上)。燃气流经火箭发动机喷管的温降是很可观的。上例中温度在较短的距离内变化了 1117℃。这是不足为奇的,因为燃气动能的増加是由焓降得到的,而焓降与温降成正比。由于排气在离开喷管时仍然很热(1105 K),故它们还有相当一部 分热能无法转变为气流的动能。
图3-3横截面积、温度、比容和速度随喷管内压力的典型变化曲线
3.3.2 喷管流动和喉部条件
为了使喷管出口气体速度达到很高,要求喷管面积先是减小到一个最小值(上例中相应压力为1.130 MPa或164 psi),然后再増加。这类喷管(以其发明者的名字命名为 拉伐尔喷管)由一收敛段和一扩张段组成。根据连续方程,喷管截面积与v/V成反 比,v/V的值也在图3-3中画出了。在v/V曲线中有一最大值。因为一开始速度増加的速率大于比容増加的速率,然而在扩张段则比容增加的速率更大。
喷管最小面积称为喉部面积。喷管出口面积A2与喉部面积At之比称为噴管面积膨胀比,用希腊字母𝛆表示,这是一个很重要的喷管设计参数。
ε = A2/At (3-19)
单位面积的气体流量在喉部达到最大值。喉部气体压比是唯一的,只与比热比k有关。 在公式3–13中设M = l,可得到该压比为
\({{{{{p}_{t}}}/{{{p}_{1}}=\left[ 2/\left( k+1 \right) \right]}\;}^{{}^{k}/{}_{k-1}}}\) (3-20)
使等熵质量流量达到最大值的喉部压力pt称为临界压力。临界压力比的典型值在 0.53-0.57之间。若压比大于公式(3-20)得出的值,则在给定进口条件下通过特定火箭发动机喷管的流量将小于最大。但是,应注意该压比不是通过整个喷管的压 比,最大流量或塞塞条件(后面将解释)总是在喉部建立,而不是在岀口平面。喷管进口压力与燃烧室总压非常接近,除非是在从喷注器到喷管进口有明显的压降的细长燃烧室中(这将在3.5节讨论)。在临界压力点即喉部处,马赫数为1,比容和温度可以根 据公式(3-7)和(3-12)得到
Vt= V1[(k + l)/2]1/(k-1) (3-21)
Tt= 2T1/(k + 1) (3-22)
公式(3-22)中的喷管进口温度T1非常接近于燃烧温度,因此也接近于喷管流动滞止温度T0。在临界点处这些待性仅有轻微的变化。以k = 1.2的气体为例,临界压比约为 0.56(这意味着Pt约等于室压P0的一半),温度只是稍有降低(Tt=0.91T1),而比 容的膨胀超过了 60% (Vt= 1.61V1)。根据公式(3-15)、(3-20)和(3-22),临界或喉部速度vt为
\({{v}_{t}}=\sqrt{\frac{2k}{k+1}R{{T}_{1}}}={{a}_{t}}=\sqrt{kRT}\) (3-23)
上式中的第一种形式可根据喷管进口条件直接计算喉部速度而不需要知道任何喉部条件。喷管喉部处的临界速度显然就是当地声速。喷管扩张段在超声速状态下压力进一 步降低,而速度进一步増加。若喷管在喉部截面截断,则出口气体速度为声速,而流量依然是最大的。只要喉部达到临界压力,即p2/pl等于或小于公式(3-20)所确定的量,喷管就可以达到声速或超声速流动状态。因此,存在三种喷管类型:亚声速、声速和超声速。表3-1对它们进行了描述。
火箭发动机用的是超声速喷管,这种喷管可以将焓最大程度地转变为动能。所有火 箭发动机喷管进口压力与出口压力之比都是很大的,足以产生超声速流动。在海平面工
作时,只有当燃烧室绝对压力降到约1.78 atm以下时,喷管扩张段才会产生亚声速流 动。这种状态会在起动和关机瞬变阶段的很短时间内出现。
声速等于弹性压力波在介质中的传播速度,声音是无限小的压力波。因此,只要稳态流动系统中任何一处达到声速,压力扰动就不可能穿过声速流或超声速流的位置。故达到声速流的喷管喉部下游的任何小障碍或扰动都不会对喉部或喉部上游的流动产生影 响,只要扰动不把下游压力提高到其临界值以上。进一步降低出口压力甚至将排气段抽 其空也不可能再増加喉部速度或流量了。这种重要状态常称为流动的壅塞,它总建立在 喉部,而不是在喷管出口平面。超声速喷管临界截面的壅塞流量可以根据公式(3–3)、 (3-21)和(3-23)导出,它等于喷管内任何截面上的质量流量。
\(\dot{m}=\frac{{{A}_{t}}{{v}_{1}}}{{{V}_{t}}}={{A}_{t}}{{p}_{1}}k\frac{\sqrt{{{\left[ {2}/{\left( k+1 \right)}\; \right]}^{\frac{k+1}{k-1}}}}}{\sqrt{kR{{T}_{1}}}}\) (3-24)
因此,通过火箭发动机喷管的质量流量与喉部面积At和燃烧室(滞止)压力p1成正比,与T/m的平方根成反比,同时也与气体物性有关。根据公式(3-4)、(3-16)、 (3-21)和(3-23),超声速喷管的喉部面积与下游面积之比可表示为压力和比热的函数,即(下游压力为px)
\(\frac{{{A}_{t}}}{{{A}_{x}}}=\frac{{{V}_{t}}{{v}_{x}}}{{{V}_{1}}{{v}_{t}}}={{\left( \frac{k+1}{2} \right)}^{\frac{1}{k-1}}}{{\left( \frac{{{p}_{x}}}{{{p}_{1}}} \right)}^{\frac{1}{k}}}\sqrt{\frac{k+1}{k-1}\left[ 1-{{\left( \frac{{{p}_{x}}}{{{p}_{1}}} \right)}^{\frac{k-1}{k}}} \right]}\) (3-25)
公式(3-25)中当px=p2时,Ax/At=A2/At,对于低空(海平而到约10 km) 工作的喷管,面积比一般在3~25之间,视燃烧室压力、推进剤组合和飞行器对发动机的 尺寸要求而定。对于高空(100 km以上)工作的喷管,面积比一般在40 – 200之间, 但有些高达400。同样,根据公式(3-15)和(3-23),喷管喉部下游速度(压力为px处)与喉部速度之比为
\(\frac{{{v}_{x}}}{{{v}_{1}}}=\sqrt{\frac{k+1}{k-1}\left[ 1-{{\left( \frac{{{p}_{x}}}{{{p}_{1}}} \right)}^{\frac{k-1}{k}}} \right]}\)
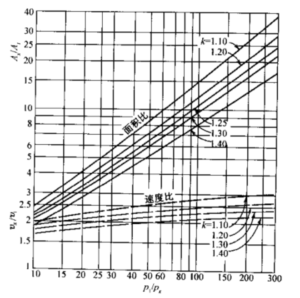
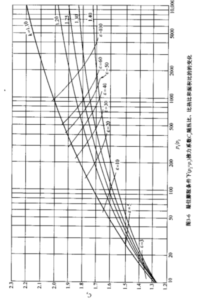
通过这些公式,可根据给定的压比直接确定理想火箭发动机喷管的速度比或面积比, 反之亦然。图3-4和3-5画出了它们之间的关系,由此可根据面积比或速度比确定压力 比。当px=p2时,公式(3-26)给出了喷管出口截面与喉部截面的速度比。当喷管出 口压力等于大气压力时(如p2=p3,參见图2-1),这些公式适用于最佳膨胀状态的喷管。 对于高空工作的火箭发动机喷管,将面积比提高到一定值以后再増加(如达到1000以 上)已无法使排气速度增加很多了。此外,大面积比带来设计上的困难和很重的喷管质量,故实际应用中极限面积比为350左右。
附录2为标准地球大气特性表,它给出了各种高度的大气压力。例如,200 km和 3000 km高度的大气密度相差一个量级以上,它影响卫星的阻力。这些特性每天可能有些不同(主要是由于太阳活动),在南北半球之间也会有所变化。
例 3-3试设计一理想火箭发动机喷管管,工作高度为25 km,作力为5000 N,室压为 2.068 MPa,燃烧室温度为 2000 Ko 假定k = 1.30、R = 355.4 J/ (kg.K)试确定喉部面积、出口面积、喉部速度和出口温度。
【解】25 km高度的大气压力为0.002549 MPa (附录2中比值0.025158乘以海平面压力0.1013 MPa)o
图3-4 超音速喷管扩张面积比、速度比与压力比的关系
图3-5 前图的延续,在更高的压比范围
压力比为p2/p1=p3/p1= 0.002549/2.068 = 0.001232 = 1/811.3
根据公式(3-20)求得临界压力为:
pt= 0.546 ×2.068 = 1.129 (MPa)
根据公式(3-23)求将喉部速度为:
\({{v}_{t}}=\sqrt{\frac{2k}{k+1}R{{T}_{1}}}=\sqrt{\frac{2\times 1.30}{1.30+1}\times 355.4\times {{2800}_{1}}}\text{=}1060\) (m/s)
根据公式(3-15)和图3-2,利用压力比811.3,得到理论出口速度为:
\({{v}_{2}}=\sqrt{\frac{2k}{k-1}R{{T}_{1}}\left[ 1-{{\left( \frac{p2}{p1} \right)}^{\frac{k-1}{k}}} \right]}\) 一
=\(\sqrt{7130\times 355.4\times 2800\times 0.7869}\)= 2605 (m/s)
根据喉部速度和图3-4也可以得到该速度的近似值。最佳膨胀条件下的理论推进剂消耗 率为:
\(\dot{m}\)= F/v2 = 5000/2605 = 1.919 (kg/s)
喷管进口的气体比容为:
V1 = RT1/p1 = 355.4 × 2800/(2.068 × 106) = 0.481 (m3/kg)
喉部和出口截面的气体比容可根据公式(3-21)和(3-6)将到
\({{V}_{t}}={{V}_{1}}{{\left( \frac{k+1}{2} \right)}^{{1}/{\left( k-1 \right)}\;}}=0.481{{\left( \frac{2.3}{2} \right)}^{1/0.3}}\)= 0.766(m3/kg)
V2 =V1(p2/p1)1/k= 0.481(2.068/0.002549)0.7692 = 83.15 (m3/kg)
喉部和出口截面的面积以及喷管面积比A2/At为
At=\(\dot{m}\)Vt/vt = 1.919 x 0.766/1060 = 13.87 (cm2)
A2= \(\dot{m}\)V2/v2 = 1.919 x 83.15/2605 = 612.5 (cm2)
𝜀= A2/At= 612.5/13.87 = 44.16
根据k= 1.30和p1/p2 = 811.2,从图3-5也可直接得到该面积比的近似值。出口温度为
T2 = T1(p2/p1)(k-1)/k=2800(0.002549/2.068)0 .2307 = 597 (K)
3.3.3推力和推力系数
推进剂燃气射流或流出的动量在火箭发动机结构上产生推力或反作用力。由于流动为超声速,喷管岀口压力可能与外界压力不同,这时在动量推力外还要加上压力推力分量,如公式(2-14)表示的:
\(F=\dot{m}{{v}_{2}}+\left( {{p}_{2}}-{{p}_{3}} \right){{A}_{2}}\) (2-14)
任何给定的喷管的最大工作推力都是在真空(p3 = 0)下得到的。利用附录2列出的大 气特性和公式(2-14),可计算在海平面和宇宙真空之间推力随高度的变化。图2-2示 出了推力随高度变化的典型曲线。要把最佳工况下(p2=p3)的计算值修改为给定p1、
k和a2/at下的值。可使用下面的公式。推力修正公式为
\(F={{F}_{opt}}+{{p}_{1}}{{A}_{t}}\left( \frac{{{p}_{2}}}{{{p}_{1}}}+\frac{{{p}_{3}}}{{{p}_{1}}} \right)\frac{{{A}_{2}}}{{{A}_{1}}}\) (3-27)
利用公式(2-5)、(2-18)和(2-14)可得到比冲修正公式为
\({{I}_{s}}={{\left( {{I}_{s}} \right)}_{opt}}+\frac{{{c}^{*}}\varepsilon }{{{g}_{0}}}\left( \frac{{{p}_{2}}}{{{p}_{1}}}+\frac{{{p}_{3}}}{{{p}_{1}}} \right)\) 328〉
例如,若要计算新面积比A2/At、新出口压力p2下的比冲值,就可使用上述关系。
用公式(3-16)、(3-21)和(3-23)的v2、vt和Vt,代入式(2-14)并作整理后可 得
\(F=\frac{{{A}_{t}}{{v}_{t}}{{v}_{2}}}{{{V}_{t}}}+\left( {{p}_{2}}-{{p}_{3}} \right){{A}_{2}}\)
=\({{A}_{t}}{{p}_{1}}\sqrt{\frac{2{{k}^{2}}}{k-1}{{\left( \frac{2}{k+1} \right)}^{\frac{k+1}{k-1}}}\left[ 1-{{\left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)}^{\frac{k-1}{k}}} \right]}+\left( {{p}_{2}}-{{p}_{3}} \right){{A}_{2}}\)
上式的第一种形式为通用形式,适用于所有火箭发动机,而第二种形式只适用羊整个膨 胀过程中k为常数的理想发动机。该公式表明推力与喉部面积At、室压(或喷管进口 压力)p1成正比,并与喷管压比p1/p2,如、比熱比k和压力推力有关。该公式称为理想 推力方程。推力系数CF定义为推力除以室压力和喉部面积At ,由公式(2-14)、 (3-21)和(3-16)可得
\({{C}_{F}}=\frac{{{A}_{2}}v_{2}^{2}}{{{p}_{1}}{{A}_{t}}{{v}_{2}}}+\left( \frac{{{p}_{2}}}{{{p}_{1}}}-\frac{{{p}_{3}}}{{{p}_{1}}} \right)\frac{{{A}_{2}}}{{{A}_{t}}}\)
=\(\sqrt{\frac{2{{k}^{2}}}{k-1}{{\left( \frac{2}{k+1} \right)}^{\frac{k+1}{k-1}}}\left[ 1-{{\left( \frac{{{p}_{2}}}{{{p}_{1}}} \right)}^{\frac{k-1}{k}}} \right]}+\frac{\left( {{p}_{2}}-{{p}_{3}} \right)}{{{p}_{1}}}\frac{{{A}_{2}}}{{{A}_{t}}}\)
推力系数CF为气体特性k、喷管面积比𝛆和喷管压比pl/p2的函数。与燃烧室温度无关。对于任何给定的压比p1/p3,当p2=p3时推力系数Cf和推力F达到最大值。这 个最大值称为最隹推力系数,它是喷管设计中考虑的一个重要准则。利用推力系数可对公式(3-29)进行简化:
F = CFAtp1 (3-31)
公式(3-31)可用于求解Cf,此外它还提供了根据室压、喉部直径和推力的实验测量 值确定推力系数的关系式。从公式(3-30)可以看出,尽管推力系数是室压的函数,但 它与p1并不是简单关联的。然而它与喉部面积却是直接关联的。推力系数可视为与燃 烧室压力只作用于喉部面积所产生的推力相比,由于气体通过超音速喷管的膨胀而产生 的推力的放大系数。推力系数的值约在0.8到1.9之间。该参数方便了观察室压或高度变化对给定的喷管构型带来的影响,或把海平面结果修正到飞行高度条件下的值。
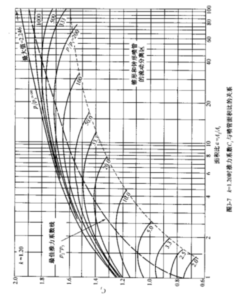
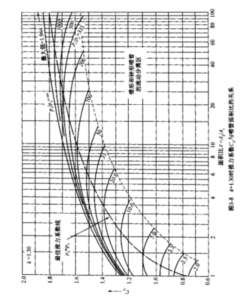
图3-6画出了最隹膨胀条件下(p2=p3)推力系数随压比p1/p2、k值和面积比𝛆 的变化。图3-7和3-8分别画出了k=1.20和1.30时不同压比p1/p3,不同面积比𝛆 的完整的推力系数曲线。这两组曲线可用于计算欠膨胀和过膨胀喷管的工作,有助于解决各种喷管问题,这将在下面解释。这些图中给出的数据是理想值,未考虑诸如喷管扩 散、摩擦以及内部膨胀波等造成的损失。
当p1/p3非常大(例如膨胀到接近真空)时,推力系数接近图3-7和3-8所示的渐近线的最大值。这些图中还给出了非设计状态(\({{p}_{2}}\ne {{p}_{3}}\))下的Cf值,只要喷管在任 何时候都是満流的,即工质没有与喷管壁面分离。流动分离问题将在本节后面讨论。
3.3.4特征速度和比冲
特征速度c*由公式(2-18)定义。根据公式(3-24)和(3-31),特征速度c *可 表示为
\(c*=\frac{{{p}_{1}}{{A}_{t}}}{{\dot{m}}}=\frac{{{I}_{s}}{{g}_{0}}}{{{C}_{F}}}=\frac{c}{{{C}_{F}}}=\frac{\sqrt{kR{{T}_{1}}}}{k\sqrt{{{\left[ \frac{2}{k+1} \right]}^{\frac{k+1}{k-1}}}}}\) (3-32)
它基本上是推进削特性和燃烧室设计的函数,与喷管待性无关。因此,它可以作为一个 评价推进剂组合和燃烧室设计的指标。上式的第一种形式是通用形式,据此可由\(\dot{m}\)、p1和At的实验数据确定c*。最后一种形式以气体特性(即k)、燃烧室温度和分子最m的函数形式给出了c*的最大值,可根据第五章的理论确定。表5-4和5-5列出了一 些推进剂的c*值。文献中有时会使用术语特征速度效率,它表示能量释放的完全程度 和在燃烧室中产生高温、高压气体的完善程度,它为c*的实验测量值和理论值[公式 (3-32)的最后部分]之比,一般在92%-99.5%之间。
利用公式(3-31)和(3-32),推力现在可表示为质量流量、表征燃烧室功能的c* 以及表征喷管膨胀功能的Cf的乘积:
\(F={{C}_{F}}\dot{m}c*\) (3-33)
一些作者使用术语流量系數Cd,它就是c *的倒数。Cd和特征排气速度c*都主要用于化学火箭推进系统。
比热比的变化对各个参数(如c、c*、A2/At、 v2/vt或Is)的影响不如燃烧室温度、压力比或分子比的变化那么大。尽管如此,它还是一个有影响的因素,这可以从图 3-2和3–4〜3-8中看出。单原子气体(如氮气和氩气)的k值为1.67,低温双原子气 体(如氢气、氧气和氮气)的k值为1.4,三个原子以上的气体的k值在1.1-1,3范 围内变化(甲烷为1.11,氨和二氧化碳为1.33)。总的来说分子越复杂,k值就越小° 对于振动能级已被激发的高温分子也是如此。对于典型的多组分火箭发动机排气,k和 m的平均值与燃烧产物的组成(化学组分和浓度)有很大关系,这将在第五章解釋。 表5-4、5-5和5-6给出k和m的值。
例3-4 一火箭发动机室压为20atm,面积比为6,设k = 1.30。试问海平面和25km 高度的推力变化百分數为多少?
【解】在海平面:p1/p3= 20/1.0 = 20;在 25km: p1/p3= 20/0.0251 = 754 (参见附录2)。
利用公式3-30或图3-8确定推力系数(提示:利用囲3-8中相应于A2/At=6.0 的垂直线)。在海平面:CF = 1.33;在25 km髙空处:CF= 1.64。
推力增加百分数为(1.64-1.33)/1.33 = 23%。
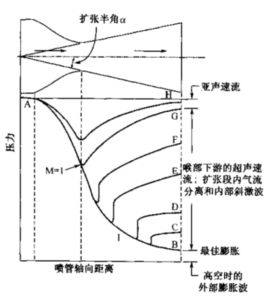
3.3.5欠膨胀和过膨胀噴管
欠膨胀喷管的岀口面积相对最佳面积比而言太小了,流体排出时出口压力大子外界
压力。流体在喷管内的膨胀不完全,在喷管外继续膨胀。喷管出口压力高于当地大气 压。
过膨胀噴管的出口面积相对最佳面积而言太大了,流体出口压力比外界压力低。图 3-9画出了超声速喷管的过膨胀现象,图中沿喷管轴线给出了过热蒸气在不同的反压或压比下典型的压力测量值。曲线AB为相应于最佳反压的面积比下的压力变化。曲线 AC和AD相应于外界压力越来越高时压力沿轴线的变化。喷管上游段内膨胀正常进 行。在曲线AD上的,处,压力低于出口压力,尔后压力突然上升,伴随有气流与喷管 壁面的分离(分离现象在后面叙述)。
图3-9不同流动条件下收敛-扩张喷管的压力分布。进口压力相同,岀口压力不同。基于A.Stodala的实验数据
喷管扩张段内压缩波或激波(它是一种强烈的突跃压缩波,只存在于超声速流动中)的存在对喷管的非理想待性有强烈的影响。曲线ID中的压力突升就是这种用编 波。膨胀波(严格来说也是超声速现象)使喷管出口流动与较低的外界压力相匹配。第十八章将描述压缩波和膨胀波。
超声速喷管中存在以下几种流动状态:
(1) 当外界压力p3低于喷管出口压力p2时,喷管満流,但在岀口处存在外膨胀 波(即欠膨胀)。气体在喷管内的膨胀是不完全的,Cf和Is将小于最佳膨胀下的值。
(2) 当外界压力p3稍高于喷管出口压力p2时,喷管继续满流,直到p2达到p3 的25%~40%左右。膨胀效率稍低,Cf和Is低于最佳喷管的值。喷管岀口截面外存在 激波。
(3)当外界压力更高时,喷管扩张段内将发生流动分离。超声速气流的直径将小于 喷管出口直径。在稳态流动情况下,分离一般是軸对称的,图3-10和3-11画出了分离 流的图形。分离平面的轴向位置取决于当地压力和喷管壁型面。随着外界压力的降低,分离点向下游移动。喷管出口处中心部分的流动仍然是超声速的,但被一环形的亚声速 流动区包围。在分离位置处存在突变,与在分离平面截断的喷管相比推力降低。在喷管 外面的羽流场中存在激波。
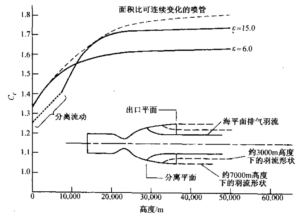
图3.10两个面积比不同的喷管的推力系数。
一个喷管在7000 m以下的高度发生气流分离。图中未示出充分膨胀的排气羽流
(4)对于出口压力稍低于进口压力的喷管,压力比低于临界压力[由式(3-20)定 义],整个喷管内均为亜声速流。火箭发动机喷管在起动和关机瞬变过程中的短时间内 通常会出现这种情况。
估算超声速喷管扩张段内分离平面处的压力的方法通常是经验性的。文献3-4给出 了基于收集到的几十个实际锥形和钟形喷管的分离数据作出的分离区域范围。文献3-5 描述了各种喷管、它们的特性以及估算分离点位置和压力的方法。上述过膨胀和欠膨胀状态的实际压力值是比热比和面积比的函数(参见文献3-1)。
軸向推力的方向通常不因分离而改变,因为对于常规的火箭发动机设计,稳态流动情况下喷管扩张段的某个横截面上的分离通常是均匀的。在瞬变过程(如启动和关机) 中,分离可能不是轴对称的,因此可能对喷管造成短暂的、较大的侧向力。大型火箭发动机喷管在正常的海平面瞬变过程(室压达到满流前)中,在过膨胀流动情况下气流可 能出现一些短暂的流动振荡和非对称分离。文献3-4指出瞬变侧向力的大小和方向会发 生迅速而无规则地变化。所产生的侧向力可能很大,并可能损坏喷管出口锥结构和推力矢量控制常平架作动器。文献3-5和3-6讨论了侧向力的计算方法。
图3-11三级运载火箭中三种典型的火箭发动机喷管排气特性简图。第一级发动机的推力室力室和推力量大,但喷管面积比最小,面顶级或第三级发动机通常推力量小但喷管面积比最大
当出现流动分离时(如在一严重过膨胀喷管中),只要知道喷管中的分离点,就能 计算岀推力系数Cf。因此就可确定一等效小喷管(其出口面积等于分离点处的面积) 的Cf。与不发生分离相比,分离效应使推力和推力系数增大。因此,对于高空用的喷管(ε很大),在有气流分离的情况下海平面推力可能比预计值高,但没有最隹喷管那 么高,在这种情况下实际上可能希望发生分离。在有分离流动时,喷管的很大部分(通 常也是很重的一部分)没有被利用,喷管比实际需要的更大、更长,由此増加的发动机 重量和尺寸降低了飞行性能。因此设计师应选择不会引起分离的面积比。
由于不规则的流动分离和可能造成破坏的侧向载荷,通常具有大面积比过膨胀喷管 的上面级或空间推进系统不要进行海平面静态试脸,海平面试验用面积比小得多的喷管 来代替。然而,实际高空试验和高空模拟试验(高空试验设备类似于第二十章中描述 的)则要用一比一的大面积比喷管进行。避免在低空发生流动分离、在高空具有高Cf 值的理想方法是使用能在飞行中改变喷管面积比的喷管,这将在本节末尾讨论。
在大多数应用中,火箭推进系统必须在一定的高度范围内工作。对于固定的燃骁室压力,这意味着压力比有一定的变化范围。最佳膨胀状态(p2=p3)只在一个高度上 出现.因此面积比固定的喷管绝大多数时间是工作在过膨胀或欠膨胀状态。对于这样的 应用,最好的喷管不一定是能使气体产生最佳膨胀的喷管,而是能使飞行器得到最高飞 行性能(也就是说总冲、或比冲、或射程、或载荷)的喷管,这往往牵涉到对整个动力 飞行弾道作时间平均。
例 3-5 利用例題3-4的數据(p1=20atm,𝛆= 6.0, k =1.30),但面枳比为15。 试比较𝛆不同的两种喷管的高空性能,画出其Cf与高度的关系。假设喷管内无激波。
【解】对于𝛆 = 15的情况,最佳压力比p1/p3=p1/p2,根据图3-6或3-8该值约为180; p3 = 20/180 = 0.111 atm,相当于约1400 m高度,低于此高度喷管为过膨胀。在海平面p1/p3 = 20, p3=1 atm,根据图3-10,会出现分离。根据其他类似喷管的估算, 分离将岀现在总压约为p3的40%或0.4 atm的横截面上。在喷管面枳比为6-7的截面 以下的喷管部分不满流,高速气流只在出口面积的中央才有。弱激波和气流收缩将使排岀气流的压力与1个大气压的外界压力相适应。如果气流不分离,岀口压力达 0.11 atm.但这种状态是不稳定的,无法在海平面维持。随着飞行器高度的增加,分离平面逐渐向喷管下游移动,直到约7000 m髙度,排气将充満整个噴管面积。
对应于不同高度(不同压比)的CF值可根据图3-8中取ε = 15和ε=6的垂直线得到。若为了得到更高的精度,也可利用公式(3-30)计算。结果与图3-10中画出的曲线相似。低空时低面积比6的Cf值较高,但它在高空时性能较低。高空时大面机比喷管的Cf值较高。
图3-11比较了典型三级运载火箭的三种发动机喷管的高空和海平面特性以及不同 面积比时羽流的形状。在海平面条件下点火时,面积比最大的三级喷管将产生流动分离,并蒙受较大的性能损失;第二级喷管将满流,但外部羽流将收缩;由于p2<p3, 因此Is和F有些损失。对第一级喷管没有影响。
例题3–6某火箭发动机试验數据如下:推力F= 53000 lb,推进剂流量\(\dot{m}\)= 208 lb/s,喷管出口面枳比A2/At=10.0,试验台大气压(噴管满流)p3=13.8 psi, 燃烧室压力 p1= 620psi。试验人员还知道,在p1 = 1000psi和p3 = 14.7 psi的标準難率条件下理论 比冲为289s, k = 1.20。试将推力修正到海平面值,并将比冲修正到标准值。假设燃烧温度和k、值随燃烧室压力的变化不大,这对于某些推进剂是合理的。
【解】实际压比p1/p3 = 620/13.8 = 44.9;在标准状态下的理论压比等于1000/14.7 = 68.0,膨胀到海平面的实际压比为620/14.7 = 42.1。根据图3-7或公式(3-30)得到 试验条件下的推力系数CF = 15.1 (对p1/p3 = 44.9、ε = 10和k = 1.20)。用类似方法 得到海平面条件的推力系数为1.49。海平面推力F = 53000 (1.49/1.51) =52300 lb 在试验时测得的比冲为
Is = F/\(\dot{w}\) = 53000/208 = 255 s
因为k、T还有c*都不随p1变化,比冲可以按推力系数成比例地进行修正。若\(\dot{m}\)保持不変,则Is与c成正比。理论比冲是针对最佳膨胀的,即喷管面积比不为10。根据图3-6我3-7,在p1/p2 = 68.0时推力系数为1.60,最佳面积比约为9.0。修正后的比 冲相应为255 (1.60/1.51) =270 so 与289 s的理论比冲相比,该火箭发动机达到了其 最大性能的270/289 = 93.5%。
图3-10和3-11表明,对于一上升飞行的火箭飞行器,理想的设计方案希望具有可 延伸的“橡皮型”扩张段,随着外界压力的降低喷管出口面积可以变大。这种设计方案 能使飞行器在上升过程中的任何高度都达到其最大性能。然而到目前为止,我们还无法 设计出所有高度都能补偿的、类似于“伸縮橡皮”的简单机械装置。然而,有一些实际 喷管构型可隨高度改变流动形状,并得到最大性能。这些喷管构型将在下一节讨论。
3.3.6 燃烧室几何形状的影响
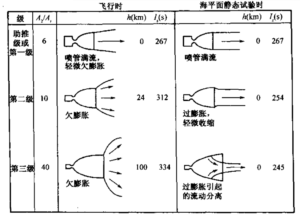
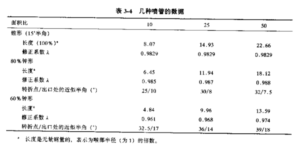
如在解释公式(3-15)和(3-16)时提到的,当燃烧室横截面积比喉部面积大四倍 以上时(A1/At>4),燃烧室速度v1可以忽略。但是.飞行器空间或重量的限制,往往要求液体推进剤发动机具有较小的推力室面积,而固体推进剂发动机则因药柱设计的考虑而导致空腔容积或药孔面积较小。这时对性能影响而言v1已不能忽略。燃烧室内的气体随着热量的加入而膨胀。加速燃烧室内这些膨胀气体所需的能量也会引起压降和附加的能量损失。燃烧室内的这种加速过程是绝热的(无热交换),但不是等熵的。当燃烧室直径等于喷管直径时,即没有喷管收敛段时,这种损失达到最大。这种发动机称为 无喉部火箭发动机,它已用于少量几种战术导弾助推器,这些应用非常强调干质量小、 长度短。由于于质量减轻而得到的飞行性能改进认为超过了无喉部发动机的喷管性能损 失。表3-2针对三种燃烧室面积比(又称收缩比)列出了一些性能的损失。
由于狭长燃烧室内存在这种压降,喷管进口处的压力要比A1/At,较大的燃烧室压 力低。这就造成了推力和比冲的少量损失。文献3.7叙述了有关这种损失的理论。
3.4喷管构型
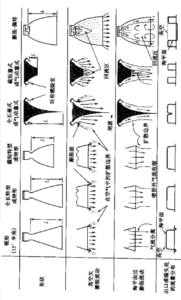
目前有多种成熟的喷管构型。本节叙述这些喷管的几何形状和性能。另外几章(第 六、八、十一、十四和十六章)将讨论喷管的材料、传熱或用途,并叙述它们的要求、 设计、结构和推力矢量控制。质管和燃烧室的截面通常为圆形,有收敛段、最窄位置处 的喉部(最小横截面)以及扩张段。在图1-4、 1-5、1-8、2-1、3-11〜3-13、3-15, 10-2~10-5、 10-16, 11-1 ~ 11-3和14-6〜14-8中可以看到各种喷管。文献3-5和3-8叙述了多种喷管构型。
燃烧室和喷管喉部之间的喷管收敛段从来不是达到高性能的关键部件。该段的亚声速流动在很低压降下就能转弯,因而随便什么半径、锥角、壁面型线或质管进口形状都能令人满意。有些小推力姿态控制推力室的喷管与燃烧室轴线成90°而没有任何性能损 失。喉部型面对性能来说也不是很关键的,采用任意的半径或其他曲线一般都可以。在 这两个区中压力梯度较高,流动紧贴壁面。不同喷管构型的主要差别在于超声速流动的 扩张段,下面将要叙述。整个喷管的壁面应平坦而光滑,使表面粗糙造成的摩擦、辐射吸收和对流传热降到最小。壁面上不得有裂缝、孔、锐边或凸起。
图3-12画出了六种喷管构型,下面将分别进行讨论。前三个简图给出了锥形和钟形喷管。后三个为内部有中心体的喷管,它们有极好的高空补偿特性,虽然它们均经过了地面试睑,但至今都未曾参与过运载火箭的飞行。图3-13比较了几种喷管的长度, 良好的喷管构型的目标是得到最高的实际Is、最小的喷管质量和最短的长度(短喷管可以减小飞行器长度、飞行器结构件和飞行器死重)。
3.4.1锥形和钟形喷管
锥形喷管构型是最古老或许也是最简单的,它比校容易制造,因此目前许多小发动 机中仍在使用。锥形喷管理想发动机的出口排气动量可用一理论修正系数λ修正。该 修正系数为具有有限喷管扩张角2a的喷管气体动量与气流全为軸向的理想喷管气体动量之比:
\(\lambda \text{=}\frac{1}{2}\left( 1+\cos \alpha \right)\) (3-34)
表3-3给出了单位出口面积质量流量均匀的喷管的λ值随α值的变化。对于理想发动 机,λ= 1.0。对扩张锥角为30°(半角α = 15°)的发动机喷管,出口动量(也即排气速 度)为根据公式(3-15b)计算的速度的98.3%。应注意,修正系数λ只能用于公式 (2-14)、(3-29)和(3-30)中的第一项(动量推力),不能用于第二项(压力推力)。
小的喷管扩张角使绝大多数动量沿轴向,于是得到较高的比冲,但长喷管増加,火箭推进系统的干质量、飞行器的千质量以及设计的复杂性。采用大的扩张角能得到短而轻的设计方案,但性能较低。因此锥形喷管的形状和长度有一最佳值(半角一般为 12°〜18°),通常要根据具体用途和飞行轨道进行折衷。
图3-12 几种喷管构型及流动效应简图
图3-13几种喷管长度的比较(部分取自文献3-9)
钟形喷管或特型喷管(参见图3-12和3-13)大概是目前最常用的喷管形状,它在 紧接喷管喉部之后有一大角度的膨胀段(20°到50°),随后喷管型面的斜率逐渐变平, 最终使喷管出口处扩张角很小,其半角通常小于10°。紧接喉部之后使用大的扩张角 (20~50°)是可以接受的,因为这个区域内相对压力较高、压力梯度很大、工质迅速膨胀,不会引起气流分离,除非喷管型面有不连续性。超声速钟形喷管中的膨胀比同样面 积比和长度的简单锥形直喷管更有效,因为其型面设计为使损失最小的曲线,这将在本 节后面解释。过去几十年里大多数喷管是钟形的。
扩张形壁面中超声速气流只能通过膨胀波来改变方向。膨胀波面很簿,在该面上波 动速度増加、流动方向稍有改变,而压力和温度下降。这些波面与流动方向成一斜角。 气体在流过喉部的过程中经历了一系列基本上没有能最损失的膨胀波。在图3-14所示 的钟形喷管中,这些膨胀出现在喉部和转折位置I之间的气流中,气流面积平稳増加, 就像喇叭口。在转折处型面角θi达到最大值。在转折点I和喷管出口点E之间,流动面积仍然在増加,但増加速率不断降低,气体进一步膨胀,膨胀波继续产生。但是,喷管壁型面已经不同了,单位长度内横裁面积的变化率降低。特型喷管这最后一段的目的是让气体离开喷管出口平面时的扩张损失小一些。出口处张角θe较小,一般小于10°,θi与θe之差称为回折角。当气流反向偏转时(点I和E之间)将出现斜压缩波。这些压缩波面也很薄,波面上气流经受微弱冲击,流动偏转,速度实际上稍有降低。每一道压缩波都造成少量的能量损失。精心确定喷管型面(采用一种称为特征线法的数学工具进行分析设计)可以平衡斜膨胀波与斜压缩波,使能量损失降到最低。文献3-3的20.33节以及文献3-8~3-11介绍了喷管型面设计分析方法,这些方法基于超声速气 流、将征线法(文献3-1)和膨胀气体的待性。大多数火箭发动机研制单位都有这种分 析方法的计算机程序。喉部的曲率半径或型面的形状对钟形喷管扩张段的型面是有影响的。
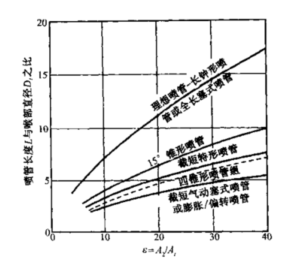
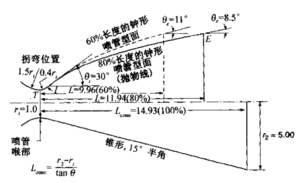
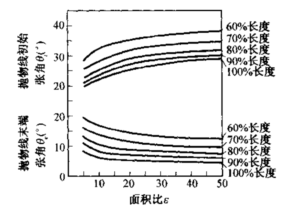
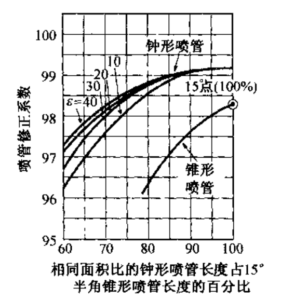
钟形喷管的长度通常用半角为15°的基准锥形喷管长度的分数来表示。80%钟形喷管的长度(喉部截面和出口截面间的距离)比同样面积比的15°锥形喷管短20%。Rao 最早在文献9中介绍了应用于较短的钟形喷管的特征线法。他还提出了拋物线能很好地 近似代表钟形型面曲线(文献3-3的20.33节),而某些喷管设计实际上已经采用了拋 物线。图3-14中最上面的图表明,拋物线在点I处与喉部曲线相切(θi),而其点E处 的张角(θe)和长度L必须根据曲线TI修正。有了这些条件,就可以用简单的几何分 析法或几何作图确定拋物线。通常喉部入口半径采用1.5rt,喉部膨胀半径采用0.4rt。 如果半径采用其他稍微不同的值,结果差别不大。图3–14中间部分的曲线给出了喷管 长度、面积比和两个钟形型面角度之间的关系。图3-14最下面的曲线给出了喷管的修正系数,相当于锥形喷管的λ,可用于修正推力系数或排气速度,只要喷管处于最佳膨胀状态(即p2=p3)
表3-4列出了根据上图得到的儿种型面的数据,以帮助读者应用该方法及检验结 果。该表给出了两个较短的钟形喷管和一个锥形喷管在三种面积比下的数据。可以看 出,随着喷管长度的减小,损失越来越大,而且面积比较小的喷管的损失要更大一些。 修正系数提高1%,比冲(或推力)约提高1%以上,在许多应用中这个差别可能是值 得注意的。缩短长度有明显的好处,通常反映为飞行器质量比的提高。该表和图3-4表 明,在同样面积比下,钟形喷管(75%〜85%长度)的效率与较长的15°锥形喷管 (100%长度)相同甚至要稍高一些。对于更短的喷管(70%等效长度以下),内部斜激波引起的能量损失就比较大了,因此这种短喷管目前不常用。
对于含少量固体颗粒(通常为氧化铝)的固体火箭发动机排气,以及对了某些胶体推进剂的排气,这些固体颗粒会撞击图3-14中I和E之间的反曲率段喷管壁面。在气体由于斜压缩波的作用而偏转、使扩张减小时,颗粒(特别是较大的顆粒)却保持直线 运动的倾向。并高速撞击壁面,由此引起的喷管壁面的磨损和侵蚀可能会很严重,尤其对于通常使用的烧蚀和石墨材料。这种由灼热颗粒造成的磨损随回折角的増大而増加。 如果减小回折角(同时也减小了张角θi),则侵蚀可以减小到可以接受的程度。目前典型的固体火箭发动机的张角为20°〜26°,回折角为10°~15°。相比之下,目前无颗粒的液体火箭发动机的张角为27°~50°。,回折角为15°-30°o因此,排气中有固体颗粒的固体火箭发动机因采用钟形喷管(喷管修正系数高)而得到的性能増长稍微低一些。
图3-14上面对面积比都为25的15°锥形喷管、80%长度钟形喷管、60%长度钟形喷管的内型面进行了比较。长度表示为喉部率径rt(图中为1)的倍数。中间一组曲线给出了初始张角θi和出口张角θe与喷管面积比和百分比长度的关系。最下面的曲线以修正系数的形式给出了喷管损失。
理想的钟形喷管(损失最小)很长,相当于10°–12°左右的锥形喷管,如图3-12 所示。这种喷管的长度差不多等于全长度塞式喷管的长度。通常这种喷管对于合理的飞 行器质量比来说太长了。
两级喷管
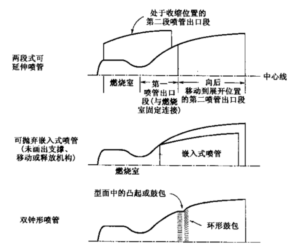
现已研究出了几种改进型钟形喷管,它们具有全程或几乎完整的高空补偿特性,即 它们可以在多种高度下达到最高性能。图3-15画出了三种两级喷管方案,它们在地面或地面附近工作时釆用较低的初始面积比A2/At,而在高空时采用较大的第二个面积 比以提高性能。
图3-15 三种具有高度补偿功能的两级喷管方案简图
可延伸噴管需要作动器、动力源、飞行中将延伸段移动到位的机构、固定和密封装置。它已成功地参加了几种固体火箭发动机和液体火箭发动机的飞行,在这些飞行中它们在点火前展开。图中虽然只画出了两级,但还有三级的方案,图11-3画出了其中一 种。迄今为止还没有在火箭发动机工作时改变面积比的做法。主要冋题在于将延伸段可靠移动到位的坚固的机构、喷管各段之间的热燃气密封,另外它増加了重量。
可抛弃嵌入喷管方案不需要移动机构和燃气密封,但在连接处可能存在滞止温度问题。它要有可靠的释放机构,另外它抛出的嵌入体会产生飞行碎片。到目前为止这种方 案只进行了很少的实际试验。这种方案可参见文献3-12。
双钟形管方案采用了两个缩短钟形喷管,组合成一个带拐点或转折点的喷管,如图3-15所示。在上升段一开始是面积比较低的喷管起作用,转折点处出现分离。随着 高度的増加和气体的进一步膨胀,该点下游的流动逐步向喷管贴紧,直至气流充满整个喷管出口截面,此时喷管在高面积比下工作,得到较高的性能。这种具有环形鼓包的折哀的钟形喷管型面有少量的性能损失。迄今为止这种方案几乎没有实际使用经验。
3.4.2只有气动边界的喷管
前面叙述的两级喷管方案的性能相当于图3-10中两条固定面积比喷管性能曲线中 较高的那部分。该图中虚线表示具有全高度补偿功能、面积比能连续改变的喷管的性能。当对整个飞行时间积分时,额外的性能对于速度増量要求很高的任务(例如单级入 轨用途)是很重要的。图3-12 右边的三种喷管具有全高度补偿功能,这将在下面讨论。 文献3-5和3-8对此作了更多的叙述。
塞式喷管或气动塞式噴管有一个环形燃烧室与一个环形缝隙喷管。这种方案的另一 种形式是把许多独立的小燃烧室(每个燃烧室都有小面积比的短喷管、圆形喉部和矩形 出口)环形排列在公用的塞锥或气动塞周围。它没有锥形喷管或钟形喷管那样的外壁, 在喷管扩张段中热燃气和周围空气之间的分界面成为气流的气动外边界。在上升飞行 时,随着外界压力的降低,这个气体边界向外膨胀,引起中心塞上压力分布的变化,从而自动实现了连续的高度补偿。流动损失最小的气动塞型面是很长的,类似于图3-12 和3-13所示的最佳钟形喷管的长度。整个横截面上单位出口面积的质最流量相对比较均匀,扩张损失达到最低值。
若中心塞尾部截去一段,对壁的型面稍作改变,则喷管就变得很短,如图3-13所示。流场内会有一些内部超声速波,与全长度中心塞喷管相比,推力会有少量损失。压力分布和传热强度沿特型壁表面变化。图8-14画出了在低空和高空条件下典型的特型塞表面压力分布。
底板下面的亚声速区回流气体的压力也产生一部分推力。由于塞子截短造成的损失 能通过把少量气体(约总流量的1%)从底板喷入回流区(提高了底板的背压)所产生 的推力而大大得到弥补。截短气动塞的优点是长度短(有助于减小飞行器的长度和质量)、全高度补偿功能、低空时壁面无流动分离,另外对于某些构型的飞行器面言它易 于装配和布局。
直排式气动塞式喷管是环形轴对称气动塞式喷管的一个变种。它基本上是环形构型的展开形式,8.2节将对此作逬一步解释。
在膨胀偏转喷管中(图3-12),从燃烧室出来的气流沿径向离开啧管軸线。流动在 一扩张的特型喷管外壁面上偏转。这种喷管的长度要短一些,但存在一些内部斜激波损失。离开燃烧室的热气流围绕中心塞膨胀。外界空气和气流之间的气动分界面形成了喷管扩张段中气流的内边界。随着外界压力的降低,越来越多的喷管扩张段被热气流充满。流动边界的这种变化和喷管外壁内部压力分布的变化达到了高空补偿的效果。
多喷管
如果固体发动机上用一簇较小的喷管代替单个大喷管(推力总和相等),喷管长度 就能减小。同样,如果液体火箭发动机单个大推力室用几个较小的推力室代替,喷管及 飞行器的长度将缩短,从而减小了飞行器结构以及死重。俄罗斯首先采用了四个一组的 推力室,每个推力为总推力的25%,相互并列装配在一起,推进剂由同一个供应系统供应。这种四推力室布局已有效地用于俄罗斯的许多大型运载火箭和导弹。由图3-13 可知,这种簇式推力室的长度比单个大推力室缩短了约30%。然而,采用簇式喷管后, 喷管出口处飞行器直径可能会稍微大一些,因此飞行器阻力也会稍微高一些。此外它増 加了发动机的复杂性和发动机质量。
3.5实际喷管
在实际喷管中,流动确实是两维的,但它是轴对称的。对于简单形状的单个喷管, 任何一个截面上的温度和速度都是不均匀的,通常中心区较高,周边附近较低。例如, 对于理想喷管,马赫数为1的面是喉部平面;但对于两维流,它一般是一个在喉部稍微 下游一点的有点弯曲的面。若巳知速度分布,则轴对称喷管的v2的平均值可根据半径 r计算。
\({{\left( {{v}_{2}} \right)}_{average}}=\frac{2\pi }{{{A}_{2}}}\int\limits_{0}^{{{r}_{2}}}{{{v}_{2}}dr}\) (3-35)
本章第1节列出的11条假设和简化仅仅是为了可以用比较简单的算法和数学解去分析实际火箭现象而提出的近似假设。其中大多数假设都可以通过两种途径进行完善:①采用经验修正系数(基于实验数据);②开发或使用更精确的算法,对能量损失、物理或化学现象进行更详细的研究和模拟,通常要进行更复杂的理论分析和数学处理。本节将 对其中一些途径作简要叙述。
与理想喷管相比,实际喷管有能量损失,而且有些能量无法转变为排气动能。下面列出主要的能量损失,其中一些将详细讨论。
(1) 喷管出口截面流动扩散造成的损失,对于锥形喷管它为扩张角余弦的函数,如 公式(3-34)和表3-3所示。采用钟形喷管型面可以减小这种损失。
(2) 与喉部面积相比较小的燃烧室面积或药孔横截面积,换言之小的喷管收缩比 A1/At引起的燃烧室压力损失,它会稍微降低推力和排气速度。参见表3-2。
(3) 边界房中较低的流动速度或壁面摩擦会使等效排气速度降低0.5%~1.5%。
(4) 气体中的固体颗粒或液滴会引起多达5%的损失,如下面将叙述的。
(5) 非稳态燃烧和流动振荡会引起少量的损失。
(6) 喷管流化学反应改变了燃气的特性和温度所造成的损失,一般为0.5%。参见 第五章。
(7) 在瞬变压力工作时性能较低,例如启动、关机或眛冲。
(8) 对于不冷却的喷管材料,例如纤维増强合成树脂或碳,工作时喉部区域的逐渐侵蚀会使喉部直径増加约1 %~6%。这样,当工作接近结束时室压和推力将降低1%~ 6%,并使比冲有所降低(降低0.7%以下)
(9) 气体成分不均匀会降低性能(由不完全混合、湍流或不完全燃烧引起)。
(10) 采用真实气体特性有时会改变气体成分,k和m值,引起少量的性能损失, 比方说0.2%〜0.7%。
(11) 在非最佳喷管面积比下工作会降低推力和比冲。如果飞行器始终在最佳喷管 膨胀的高度(p2=p3)下飞行,就没有损失。如果飞行器的喷管面积比固定、在偏高或偏低的高度飞行,则与有高空补偿功能的喷管相比推力损失可高达15% (在部分飞行段),这可从图3-7和3-8中看出。它还会使性能降低1 %~5%。
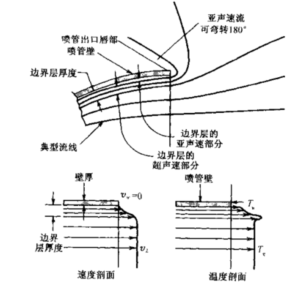
3.5.1边界层
实际喷管在紧貼壁面附近存在粘性边界层,那里的气体速度比无粘流区域中的自由 流速度要低得多。图3-16画出了放大的边界层简图。直接貼着壁面的气流速度为零, 这样边界层可以视为由许多连续的环形薄层叠加而成,各层的速度逐步增加,直到达到自由流速度为止。壁面附近的低速流动为层流、亜声速的,但在边界层内的高速区流动是超声速的,并会转变为湍流状态。随着当地速度的减小以及粘性摩擦,边界层内局部动能会转变为热能,故边界层内局部温度会显著高于自由流温度。紧贴壁面的那一层由于向室壁传热而温度要低一些。气态边界层对喷管和燃烧室壁面上总的传热,有很大的 影响。此外它对火箭发动机性能也有影响,特别是大面积比的较长的喷管,在这种情况 下总质量流量中可能有相当大的比例(2%~25%)在边界层的低速区。压力、温度或密度的高梯度和当地速度的变化(方向和大小)都会影响边界层。对于边界层现象,比例法则一向不可靠。
图3-16高空条件下喷管出口唇部的流动状态,用中面出 流线、边界层、速度和温度分布
文献3-1的第26~28章和文献1-1中描述了计算边界层对性能的影响的理论方法。 对于火箭发动机喷管,真正令人满意的边界层理论分析至今还没有建立起来。所幸的是 边界层对发动机性能的总体影响是很小的,大多数发动机喷管的比冲损失很少超过 1%。
3.5.2多相流
某些火箭发动机的气态工质中包含了许多小液滴和/或固体颗粒,它们必须由气体加速。当在喷管中膨胀时它们将热量传给气体。例如,固体推进剤(参见第十二章)或 某些胶体推进剂(第七章)就会出现这种情况,这些推进剤中含有铝粉,它们会在排气 中形成氧化物小颗粒。离子氧化催化剤或含铍、硼或鋯的推进剂也会出现这种情况。
一般来说,如果颗粒很小(如直径在0.005 mm以下),则它们的速度几乎与气体相同,并与喷管气流处于热平衡。于是,气体消耗动能加速颗粒,同时又从颗粒得到热能。随着颗粒直径的増大,颗粒的质量(以及惯性)随直径的立方増加,然而气动力只随直径的平方増加。因此较大的颗粒其运动不会与气体一样快,而且对气体的传热也不 会像小颗粒那样快。大颗粒的动量要比质量相同的小颗粒低,它们到达喷管出口时的温 度比小颗粒高,因此传出的热量较小。
可以推导出一种用于修正性能(Is、c或c*)的简单的理论方法,如下面将描述的 (文献3-13和3–14中也有)。这种方法基于以下假设:气体和颗粒的比热在整个喷管内为常数;颗粒足够小以致运动速度与气体相同并与气体处于热平衡;颗粒与气体之间无质量交换(无蒸发或凝结)。此外还假设;只有气体有膨胀和加速;颗粒占据的容积与气体容积相比很小,可忽略;如果颗粒数量很少,加速颗粒所需的能量可以忽略;没有 化学反应。
焓h、比容V、气体常数R可以表示为颗粒分数𝛃的函数,β为所有颗粒(液体 和/或固体)的质量除以总质量。存在以下关系(下标g和s分别表示气态和固态):
\(h=\left( 1-\beta \right){{\left( {{c}_{p}} \right)}_{g}}T+\beta {{c}_{s}}T\) (3-36)
\(V={{V}_{g}}\left( 1-\beta \right)\) (3-37)
\(p={{R}_{g}}T/{{V}_{g}}\) (3-38)
\(R=\left( 1-\beta \right){{R}_{g}}\) (3-39)
\(k=\frac{\left( 1-\beta \right){{c}_{p}}+\beta {{c}_{s}}}{\left( 1-\beta \right){{c}_{v}}+\beta {{c}_{s}}}\) (3-40)
把这些关系式用于简单一维喷管流公式,如式(2-16)、(3-15)或(3-32)。比冲或特征速度值将随顆粒分数𝛃的増加而减小。对于很小的颗粒(直径小于0.01 mm)和小的𝛃值(小于6%),比冲损失一般小于2%。对于较大的颗粒(直径在0.015 mm以 上)和较大的β值,这个理论没有用,比冲可以比没有流动滞后的Is值小10%~20%。
实际的颗粒尺寸和分布取决于具体的推进剂、燃烧、特定的颗粒物质以及具体的火箭推 进系统,通常要通过测量才能知道(参见第十二章和十八章)。因此,若要在固体推进剤上添加金属(例如铝)时,只有因额外释热而使燃烧温度T1提高到足以超过排气颗粒带来的性能损失时,添加金属才会提高性能。
在质管面积比很高、喷管出口压力很低(高空或宇宙真空)的情况下,通常为气态 的某些推进剤成分可能会凝结。随着喷管中温度的急剧降低,气相组分如H2O、CO2或 NH3可能疑结并形成液滴。这会造成单位面积气体流量的降低,并且汽化潜熱会转移到其余气体。如果液滴尺寸很小、凝结气体的质量百分數不大,则凝结对性能的总影响 很小。在气体膨胀过程中还可能形成固相颗粒和微小雪颗粒(H2O)或其他成分的冻雾。
3.5.3其他现象和损失
燃烧过程实际上不是完全稳定的。通常若低频和高频室压振荡幅值在额定室压的 5%以下,就认为燃烧是平稳的、流动是比较稳定的。气体特性(k、m、cp)和流动 参数(v、V、T、p等)也会随时间振荡,且不一定沿流动通道均匀分布。因此,这些参数仅仅是“平均”值,但未必总是知道它们是哪一类平均值。理论上很难评估由不均匀的非稳态燃烧引起的能量损失。对于平稳燃烧的火箭发动机,这种损失很小,可以 忽略,但在振荡幅值较大时损失就很显著了。
气体组分在喷管内有些变化,气流中存在化学反应,均匀的或“冻结”气体组分的 假设不完全有效。第五章叙述了更复杂的变组分、变物性情况下的性能分析方法。如图 2-3所示,喷管排出的热能(\(\dot{m}{{c}_{p}}{{T}_{2}}\))无法转变为有用的推进能量(动能)。为降低这种损失,唯一的方法是降低喷管出口温度T2 (采用更大的喷管面积比),但即使这样该损 失仍然较大。
当工作时间较短时(例如反坦克火箭或反复启动和关机的脉冲姿态控制发动机), 启动和关机瞬变过程占了总工作时间的很大部分。在启动和关机的瞬变阶段,平均推 力、室压或比冲要比稳态全工况时的值低。这可以一步步进行分析。例如,启动阶段在燃烧室中反应的推进剤量必须等于通过喷管的气体流量加上把燃烧室充填到较高压力所需的气体量。此外,也可以利用室压与时间关系的经验曲线进行这种计算。在小推力推进系统中,过渡时间非常短,或许只要几毫秒,但对于大型推进系统这个时间可能比较 长(数秒钟)。
3.5.4性能修正系數
本节将讨论半经验修正系数,这些修正系數已经用于根据理论计算性能值估算性能试验数据。掌握一些理论基础有助于建立一些修正系数之间的关系,以及估计一些参数 (如压力、温度或比热比)的影响。
能量转换效率定义为离开喷管的气流的单位流量实际动能与理想排气气流的单位流量动能之比,假设两者的工质、初始状态和初始速度相同,并膨胀到与实际喷管相同的出口压力。该定义可用公式表示为
\(e=\frac{\left( {{v}_{2}} \right)_{a}^{2}}{\left( {{v}_{2}} \right)_{i}^{2}}=\frac{\left( {{v}_{2}} \right)_{a}^{2}}{\left( {{v}_{2}} \right)_{a}^{2}+{{c}_{p}}\left( {{T}_{1}}-{{T}_{2}} \right)}\) (3-41)
式中e表示能员转换效率,v1和v2为喷管进口速度和出口速度,cpT1和。cpT2分别是理想等熵膨胀时喷管进口和出口的焓。下标a和i分别指实际状态和理想状态。在许多 实际应用中v1→0,分子采用公式3-16给出的表达式的平方。
速度修正系數ζv定义为能量转换效率的平方根\(\sqrt{e}\) 。其值在0.85和0.99之间,平均值为0.92左右。该系數也近似等于实际比冲与理想(或理论)比冲之比。
流量修正系数ζd定义为实际发动机质量流量与理想发动机质量流量之比,假设两 者工质相同、从相同的初始状态膨胀到相同的出口压力[公式(2-17)]o
\({{\ zeta }_{d}}=\left( {{{{\dot{m}}}_{a}}}/{{{{\dot{m}}}_{i}}}\; \right)={{\dot{m}}_{a}}\left( {c}/{{{F}_{i}}}\; \right)\) (3-42)
根据公式(3–24)可得
\({{\zeta }_{d}}=\frac{{{{\dot{m}}}_{a}}\sqrt{kR{{T}_{1}}}}{{{A}_{t}}{{p}_{1}}k\sqrt{{{\left( \frac{2}{k+1} \right)}^{\frac{k+1}{k-1}}}}}\)
该流微修正系數的值通常大于1(1.0~1.15)。实际流量大于理论流量的原因如下:
- 气体通过喷管时分子量一般稍有增加,从而改变了气体密度。
- 部分热量传到喷管壁上。这样就降低了喷管内的温度,稍微提高了密度和质量。
- 实际喷管中比热和其他气体待性的变化方式是使流量修正系效稍微増加的。
- 不完全燃烧会提高排气密度。
实际推力一般低于理想发动机的计算推力,实际推力可以用經验性的推力修正系数ζF计算:
\({{F}_{a}}={{\zeta }_{F}}{{F}_{i}}={{\zeta }_{F}}{{C}_{F}}{{p}_{1}}{{A}_{t}}={{\zeta }_{F}}{{c}_{i}}{{\dot{m}}_{i}}\) (3-43)
式中
\({{\zeta }_{F}}={{\zeta }_{v}}{{\zeta }_{d}}={{{F}_{a}}}/{{{F}_{i}}}\;\) (3-44)
ζF值落在0.92和1.00之间[参见公式(2-6)和(3-31)]。因为推力修正系数等于流 量修正系数和速度修正系数的积,故只要知道任何两个修正系数,就可以确定另一个修 正系数。
例题3-7 按以下条件设计一火箭发动机喷管:
燃烧室压力 20.4 atm = 2.068 MPa
大气压力 1.0 atm
燃烧室温度 2861 K
气体平均分子量 21.87 kg/ (kg.mol)
理论比冲 230s (在工作状态下)
比热比 1.229
要求推力 1300 N
试确定:噴管喉部面枳和出口面枳、相应的直径、实际排气速度和实际比冲。
【解】根据公式(3-30)求得理论推力系数。对于最佳状态p2=p3。代入k = 1.229和p1/p2 = 20.4,推力系数CF=1.405。该值可以用图3-7和3-8中的Cf值的内插来检验。取ζF=0.96 (该值根据试验数据得到)。求得喉部面积为
At = F/(ζFCfp1)= 1300/(0.96 × 1.405 ×2.068 ×106) = 4.66 (cm2)
因此,喉部直径为2.43cm。面积比可根据图3-5或公式(3-25)确定ε = 3.42。出口面积为
A2 = 4.66× 3.42 = 15.9 (cm2)
因此出口直径为4.50 cmo理论排气速度为
v2=Isg0 = 230×9.80 = 2254 (m/s)
选择经验速度修正系数ζv为0.92 (根据以前的有关玆验),实际推气速废等于
(v2)a = 2252 ×0.92 = 2074 (m/s)
因为比冲与排气速度成正比,故其实际值可以用理论值乘以速度修正系数ζv来计算:
(Is)a = 230 ×0.92 = 212 (s)
3.6四类性能参数
在利用推力、比冲、推进剂流量和其他性能参数值时,必须仔细确定或检验产生特定数据的具体条件。性能参数至少有四类,它们在概念和数值上往往是不同的,即使针对同一火箭推进系统也是如此。毎类性能参数,如F、Is、c、v2和/或\(\dot{m}\)都应附带明确的适用条件,即
- 燃焼室压力;对于细长燃烧室,要规定室压的位置(例如在喷管进口处);
- 外界压力,或髙度,或真空度;
- 喷管面积比,不管是否最佳值;
- 喷管形状和岀口张角(参见表3-3);
- 推进剂,它们的组成或混合比;
- 理论性能计算中所作的主要假设和修正。例如,分析中使用冻结流还是平衡流 (这将在第五章描述);
- 推进剤的初始温度。
- 第二、三、五章定义的理论性能值,通常适用丁理想火箭发动机,应用于实际火箭发动机时一般要作一些修正。大多数喷管设计单位都有自己的计算机程序,通常不同的喷管构型、不同的推力水平或不同的工作时间采用不同的程序。大多数程序是两维的,采用真实气体特性对喷管内的化学反应作修正,并对流动扩张作修正。许多程序还 对前面提到其他损失作了修正。例如,用于固体推进剤发动机喷管的程序可能考虑了喉部侵蚀和多相流的损失;用于液体推进剂发动机的程序可能考虑了两个以上的同心管区域,各区域可有不同的混合比,因此可有不同的气体特性。考虑膨胀波和压缩波的喷管型面分析可采用有限元分析和/或特征线方法。一些更复杂的程序考虑了粘性边界层效应和喷管壁传热。一般来说,这些计算机模拟程序基于计算流体力学有限元分析和基本的Navier-Stokes方程。大多数单位还有较简单的、可能考虑了一个或多个前面提到的 修正的一维计算机程序,在初步设计或编写建议节时经常使用这些程序。
- 交付性能值即实測性能值是根据全尺寸推进系统的静态试验或飞行试验得到的。 它也应注明状态(例如p1、A2/At、T1等),而且要根据仪表偏差、误差或校正常数对测量值作修正。飞行试验数据需要根据气动效应(例如阻力)作修正。经验系数(例如推力修正系数、速度修正系数和流量修正系数)常用于将上面第①项的理论值转换为近似实际值,该值对于初步估算一般已足够了。在研制新发动机的过程中,有时使用缩 比推进系统,然后采用比例系数把测量值修正到全尺寸数据。
- 标准状态性能值为上述①和②项的修正值。标准状态通常由用户严格规定。通常标准状态指易于评定或易于与基准值比较的状态,也常常指易于测量和/或修正的状态。 例如,为了合理地比较几种推进剂和火箭推进系统的比冲,常把数据修正到以下标准状态(参见例题3-4和3-5):
- p1= 1000 psi 或 894×106 Pa;
- p2=p3=69 psi (海平面)或 1.0132 x 105 或0.10132 MPa;
- 面积比为最佳状态.。p2=p3;
- 锥形喷管的扩张半角α=15°或其他约定值;
- 特定的推进剂,采用设计混含比和/或特定的推进剂组成;
- 推进剂初始温度:21℃(有时为20℃或25℃),或沸点(低温推进剂)。
火箭推进系统通常是根据预定的要求或规范设计、建造、试验和交付的,这些技术要求一般要形成正式的文本,称为火箭发动机技术规范。规范中规定了上面所列的性能和其他一些要求。第十七章在叙述推进系统选择过程时对这些技术条件作了更详细的讨 论。
- 用户通常要求发动机研制单位交付的火箭推进系统满足最低保证性能,如满足最 低的F或Is同时满足两者。该值可通过在额定值(上面的项目①和②)上减去各种可能的损失而确定,如因喷注器或管路压降变化引起的室压变化、喷管表而粗糙、推进剂初始温度、产品之间的制造偏差(如装药容积、喷管尺寸、泵叶轮尺寸等)等造成 的损失。该最低值可通过对这些损失作统计计算而确定,然后由实际全尺寸静态试车或 飞行试验来验证。
3.7喷管对准
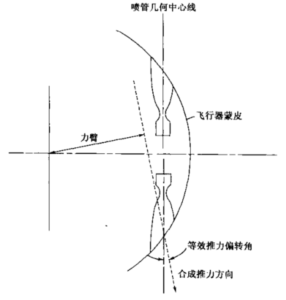
当推力线或推力方向与飞行器的质心不相交时,就会产生一个使飞行中的飞行器旋转的翻转力矩。对于飞行器的受控旋转成姿态控制,转矩是希望有的和必需的,一般它是由推力矢量偏转、空气舵或独立的姿态控制发动机产生的。但是,大小或方向不明的这种转动是不希望有的,当主推进系统的固定喷管的推力轴线偏斜时就会发生这种转动。大推力助推火箭发动机系统即使有很小角度(小于0.5°)的偏斜,也会在工作期间引起很大的翻转力矩。若不进行校正或补偿,这样小的偏斜也会造成飞行器滾动和/ 或偏离预定飞行轨道。为了使该力矩不超过飞行器姿态控制的补偿能力,推进系统所有的固定(无常平架)喷管的轴线都必须非常精确地对准。一般来说,推力轴线取为喷管扩张段内表面的几何轴线。通常需用专门的对准夹具将喷管轴线定位,使之与飞行器重心线的偏斜在±0.25°以内,并使大喷管喉部中心位于飞行器中心线上,误差在1到2mm之内。详细情况可参见文献3-15。
此外还存在其他几种偏斜:①喷管儿何形状不规则(不圆、凸起、表面粗糙度不均匀);②启动和关机瞬时的推力偏斜;③推进系统或飞行器结构在载荷作用下产生的不规则变形;④气流中的不规则性(喷注器缺陷、固体推进剂燃烧速率的不规则)。对于 简単的无制导火箭飞行器,通常使飞行器绕飞行轴旋转起来,以防止只在一个方向有偏 斜,換言之在动力飞行时把偏斜均匀化。
图3-17飞行器局部简图。为与圆住形飞行器的外表面相适应.
采用了两个斜切喷管状态控制推力室
在航天器或运载火箭上面级的有限空间内,有时无法在飞行器可用空间内把大面积比喷管全部容纳进去。在这种情况下,为了能紧凑安装,通常沿飞行器外表面以一定角度把喷管切掉一部分。图3-17画出了两个(四个之二)滾动控制推力室,其喷管出口 截面与飞行器外形一致。斜切喷管的推力方向不再像完全对你喷管那样沿喷管轴的中心 线了,喷管出口流动不再是軸对称的。文献3-16给出了计算斜切喷管的性能和推力方向的方法。
3.8变推力
只有少数应用需要在飞行时改变推力。公式(3-24)、(3-30)和(3-31)表明推力正比于喉部面积At、室压p1或质量流率\(\dot{m}\),但与CF关系不强,而Cf本身又取决于k、高度、压比和A2/At。这些公式表明了改变推力的途径,并表明了其他性能参数如何受这种变化的影响。液体火箭发动机可以在不改变燃烧室形状和喷管喉部面积的情况 下减小进入燃烧室的质量流量(通过推进剂供应系统中的节流阀)。质重流量的减小引起p1以及F几乎线性地降低。燃烧温度稍有变化,但不影响上述关系。此外比冲可能会稍微降低,因此推力调节会有少量性能损失。在液体火箭发动机中,采用节流阀调节推力曾达到了 2比1的推力比。第八章的8.5节将讨论液体火箭发动机的推力随意调节 和它们的设计待点。
另一种改变推力的方法是在调节流量的同时改变喉部面积(通过在喷管中插入可移动的特型枢轴或锥形塞),在这种情况下燃烧室压力p1可适当保持恒定。这种变推力方法已用于液体火箭发动机(如登月发动机,达到了10比1 的变推比)和少数实验固 体推进剂发动机。
随意推力控制需要采用控制系统和待殊部件,第十章10.5节将讨论这方面的一个实例。迄今为止实际飞行的固定推进剂发动机还没有能够随意变推力的。可重复的、程序变推力的固体推进剂发动机是可以实现的,它将在第十一章11.3节讨论。通过巧妙的药型设计,固体推进剂已经实现了质量流量可按预定规律变化,这种设计能改变不同工作阶段的燃烧速率。这对于许多空射军用火箭是很有用的:若需随意变推力的火箭发动机,采用液体火箭发动机是最合适的选择,这已在登月任务中充分得到了验证。