第四章飞行性能
本章叙述采用火箭发动机推进的飞行器(如导弹、航天器、运载火箭或射弹)的性能,目的是从火箭发动机的角度向读者介绍这方面的知识。火箭推进系统对飞行器施加一个力,使其加速(或减速)、克服阻力或改变飞行方向。火箭发动机应用的飞行领域有多种:①大气层内飞行(空面导弹或探空火箭);②近地空间飞行(地球卫星);③月球和行星飞行;④逃逸太阳。这几种情况都将在下面进行讨论。文献4-1 ~4-4中介紹了这些飞行的背景知识。本书附录中给出了转换系数、大气特性以及主要公式汇总。本章先分析简化的理想飞行轨道,然后处理更复杂的飞行路线,描述各种飞行器。
4.1无重力、无阻力空间飞行
这种简单的火箭飞行分析适用于外层空间,那里没有空气(故没有阻力),并且基本上没有显著的地球引力。飞行器的飞行方向与推力方向(沿喷管轴统)相同,即飞行軌迹是一条一维直线加速路径。在发动机工作时间tp内,推进剂流量\(\dot{m}\)与推力F保持不变。对于恒定的推进剂流动,推进剂流量为mp/tp,其中mp为可用推进剂总质量。 根据牛顿第二定律,对于瞬时质量为m、速度为v的飞行器,有
F=mdu/dt (4-1)
对于推进剂流量恒定的发动机.飞行器瞬时质量m可以表示为飞行器初始总质量m0、mp、tp与时间t的函数:
\(m={{m}_{0}}-\frac{{{m}_{p}}}{{{t}_{p}}}t={{m}_{0}}\left( 1-\frac{{{m}_{p}}}{{{m}_{0}}}\frac{t}{{{t}_{p}}} \right)\) (4-2)
\(={{m}_{0}}\left( 1-\zeta \frac{t}{{{t}_{p}}} \right)\text{=}{{m}_{0}}\left( 1-\left( 1-MR \right)\frac{t}{{{t}_{p}}} \right)\) (4-3)
式(4-3)以适用于弾道计算的形式给出了飞行器质量。飞行器质董比MR与推进剂质量分数ζ已在式(2-7)、(2-8)中定义,其关系为
ζ=(1 – MR) (4-4)
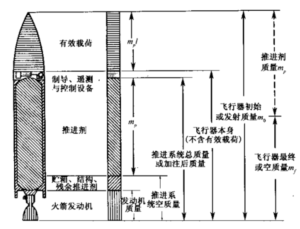
图4-1给出了各种质量的定义。起飞时的初始质量m0等于可用推进剂质量mp加上飞 行器干质量或最终质量mf,而mf等于推进系统死重(如喷管、贮箱、壳体、未耗尽 的残余推进剂)加上制导、控制、电子等有关设备和有效载荷的质量。
对于恒定的推进剂流量\(\dot{m}\)和有限的推进剂燃烧时间,推进剂总质量mp为\(\dot{m}\)t,飞行器瞬时质量m= m0–\(\dot{m}\)to式(4-1)可写为
\(du=\left( F/m \right)dt=\left( c\dot{m}/m \right)dt\)
\(\text{=}\frac{\left( c\dot{m} \right)dt}{{{m}_{0}}-{{m}_{p}}t/{{t}_{p}}}=\frac{c\left( {{{m}_{p}}}/{{{t}_{p}}}\; \right)dt}{{{m}_{0}}\left( 1-{{m}_{p}}t/{{m}_{0}}{{t}_{p}} \right)}=\frac{c\zeta /{{t}_{p}}}{1-\zeta t/{{t}_{p}}}dt\)
图4.1各种飞行器质量的定义
对上式积分,可得到无重力真空条件下飞行器在推进剂耗尽时能达到的最大速度up。 当\({{u}_{0}}\ne 0\)时通常称之为速度増量△u
\(\Delta u={{u}_{p}}=-c\ln \left( 1-\zeta \right)+{{u}_{0}}=c\ln \left( {{{m}_{0}}}/{{{m}_{f}}}\; \right)+{{u}_{0}}\) (4-5)
若假设初始速度u0为零,则
\({{u}_{p}}=\Delta u=-c\ln \left( 1-\zeta \right)=c\ln \left[ {{{m}_{0}}}/{\left( {{m}_{0}}-{{m}_{p}} \right)}\; \right]\)
\(=-c\ln \left( MR \right)=c\ln \left( \frac{1}{MR} \right)=c\ln \left( \frac{{{m}_{0}}}{{{m}_{f}}} \right)\) (4-6)
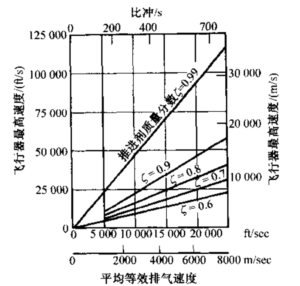
这就是在无重力真空条件下,从u0= O的静止状态起飞的、推进剂流量恒定的飞行器 所能达到的最大速度増量△u。图4-2给出了 c、Is和ζ的变化对速度增量的影响。采用自然对数的底e,式(4-6)可写为另一种形式:
\({{e}^{{\Delta u}/{c}\;}}=1/MR={{m}_{0}}/{{m}_{f}}\) (4-7)
无重力真空条件下可获得的最大飞行速度増量Δu这个概念有助于理解飞行器基本参数的影响。它可用于比较不同的推进系统、飞行器、飞行任务或改进设计方案。
由式(4-6)可知,推进剂质量分数对飞行器速度的影响是对数关系。该值从0.80 提高到0.90,无重力真空中的行星际飞行器最大速度可提高43%。0.80的质量分数意味着结构、蒙皮、有效载荷、推进系统硬件、电子设备、制导系统、气动升力面等的质量只能占飞行器总质量的20%,剩余的80%为可用推进剂。质量分数要超过0.85,必须对飞行器精心设计。根据目前所采用的材料,0.95左右的质量分数看起来可能是实际単级飞行器的极限了。当质量分数为0.90时,MR = 0.1, 1/MR=10.0。并不是只有真空中的星际飞船的质量分数或质量比对关闭动力时飞行器的速度(也包括射程)有强烈影响,几乎所有火箭动力的飞行器都是这样的。为此,设计的一个重点是减少每个飞行器组件的死重,包括推进系统。
图4-2无重力、无阻力空间中,质量比、比冲不同的飞行器的最大速度[式(4-6)的曲线],单级飞行器的1/MR最高可达20,多级飞行器可超过200
改变式(4-6)的形式,可解出在一定的飞行器初始起飞质量或最终质量下、要达到某速度増量所需的有效推进剂质量mp。最终质量包括有效载荷、飞行器结构质量、 推进系统干质量(含残余推进剤)和一小部分制导、通讯、控制设备的质量。本文中
\({{m}_{p}}={{m}_{0}}-{{m}_{f}}\)
\({{m}_{p}}={{m}_{f}}\left( {{e}^{{\Delta u}/{c}\;}}-1 \right)={{m}_{0}}\left( 1-{{e}^{{-\Delta u}/{c}\;}} \right)\) (4-8)
飞行速度増量up与等效排气速度c成正比,故与比冲也成正比。这样,比冲的任何提高(如果用更好的推进剂、更佳的喷管面积比或更高的室压)都会反映为飞行器性能的改进,只要在提高比冲的同时不过多地増加推进系统死重(它会降低有效推进剂质量分数)。
4.2作用在大气层内飞行器上的力
作用在地球大气层内飞行器上的外力通常有推力、气动力和重力。其他一些力如风力、太阳光压等是很小的,在简单计算中通常忽略。
推力是由动力装置(如螺旋桨或火箭发动机)产生的力。它一般作用在动力装置轴线方向,即沿螺旋桨轴线或火箭发动机喷管轴线。式(2-6)已给出了火箭发动机在恒定流量下的推力,它与等效排气速度c和推进剂\(\dot{m}\)有关。在许多火箭发动机中, 推进剂质量消耗率\(\dot{m}\)基本上是恒定的,而启动及关机瞬变过程往往很短,可以忽略。 因此,推力为
F =c\(\dot{m}\)= cmp/tp (4-9)
如第三章所解释的,对于给定的推进剤,等效排气速度c或比冲的值取决于喷管面积比和飞行高度。随着高度的增加,c值会有少量提高,其比例为1.2〜1.6。
阻力D是由流体对运动物体的阻碍所产生的与飞行方向相反的气动力。升力L是垂直于飞行方向的气动力。它们是飞行速度u、飞行器周围流体的密度ρ和飞行器某表面积A的函数。
\(L={{C}_{L}}\frac{1}{2}\rho A{{u}^{2}}\) (4-10)
\(D={{C}_{D}}\frac{1}{2}\rho A{{u}^{2}}\) (4-11)
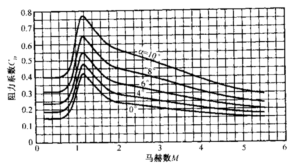
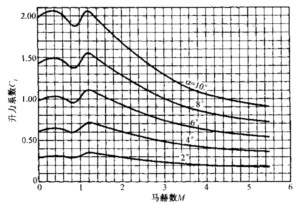
CL、CD分别为升力系数和阻力系数。对于飞机和有翼导弹,面积A指机翼面积。对于无翼导弾或运载火箭,它指与导弹轴线垂直的最大横截面积。升力系数、阻力系数主要与飞行器外型、飞行马赫数、攻角(飞行器轴线或翼平面与飞行方向的夹角)有关。 在低速飞行时,马赫数的影响可忽略,阻力系数、升力系数主要与攻角有关。图4-3给出了典型超声速导弹的阻力系数与升力系数的变化情况。这些系数在马赫数为1附近达到最大值。对于无翼飞行器,攻角α通常很小(0<α<1°)。附录2列出了大气的密度与其他一些特性。地球大气的密度会随太阳活动与昼夜温度的变化而变化,最大可相差 2倍(300~ 1200km之间).这给阻力计算带来了最大的不定因素。气动力还受发动机排气流动及压力分布的影响,这将在第十八章解释。
对于运载火箭和弹道导弹,阻力损失用∆u来表示,一般为飞行器最终速度增量的 5%〜10%。该值相对较低是因为在飞行器速度高的高空,空气密度低,而在空气密度高的低空,飞行器速度低,因此动压较低。
星球引力是月球、太阳及所有行星和恒星施加在飞行器上的引力。引力沿指向吸引体质位中心的方向拉飞行器。在很靠近地球的区域,其他星体的引力与地球引力相比可忽略。由地球产生的引力称为重力。
若忽略地球地理特征和非球形对重力的影响,则重力加速度与物体-地心距离的平方成反比。令R0为地表半径,g0为半径为R0的地表处的加速度,则星球引力g为
g = g0(R0/R)2 = g0[R0/(R0 + h)]2 (4-12)
式中h为高度。在赤道处地球半径为6378.388 km。g0的标准值为9.80665 m/s2。在月球那么远的地方,地球重力加速度只有3.3×104 g0左右。
图4-3 德国V2导弹的阻力系数、升力系数在多种攻角条件下随马赫数的变化。系数基于弹体横截面积,不考虑排气羽流效应
4.3基本运动关系式
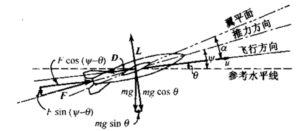
对于在地球附近飞行的飞行器,其他所有天体对它的引力通常可忽略不计。现假设飞行器作直线平衡飞行,所有控制力、侧向力、使飞行器转动的力矩均为零。弹道是两维的,并保持在一个固定平面内。飞行器有机翼,机翼与飞行方向倾斜,其攻角为𝛼,
机翼为飞行器提供了一个与飞行方向垂直的升力。飞行方向与推力方向不一致。图4-4 画出了上述情况。
图4-4两维帯翼飞行器受力图
令θ为飞行航迹与水平面的夹角,φ为推力方向与水平面的夹角。沿飞行方向,质量与加速度的乘积必定等于所有力的合力,即推力、气动力与重力之和。
\(m\frac{du}{dt}=F\cos \left( \psi -\theta \right)-D-mg\sin \left( \theta \right)\) (4-13)
垂直于飞行方向的加速度为u(dθ/dt)。对于常数u和飞行航迹瞬时半径R,该加速度为u2/R。垂直于行速度方向的运动方程为
\(mu\frac{d\theta }{dt}=F\sin \left( \psi -\theta \right)+L-mg\cos \left( \theta \right)\) (4-14)
把式(4-10)、(4-11)代入,就可以从以上两个方程求得加速度为
\(\frac{du}{dt}=\frac{F}{m}\cos \left( \psi -\theta \right)-\frac{{{C}_{D}}}{2m}\rho {{u}^{2}}A-g\sin \left( \theta \right)\) (4-15)
\(u\frac{d\theta }{dt}=\frac{F}{m}\sin \left( \psi -\theta \right)+\frac{{{C}_{L}}}{2m}\rho {{u}^{2}}A-g\cos \left( \theta \right)\) (4-16)
由于上tp、u、Cd、Cl、𝜌、θ和Ψ随时间、任务特点或高度而独立变化,上两式无法得到通解。此外,Cd、CL是速度或马赫数的函数。在更详细的分析中,还可能考虑其他一些因素,如不用于主推进的推进剂(例如用于姿态或飞行稳定性控制的推进剂)。文献4-1〜4.5给出了某些飞行状态下飞行性能的背景知识。对于不同的火箭飞行任务或飞行状态,所要最大化或优化的飞行性能参数是不同的,如△u、射程、击中目标的时间或高度等。火箭推进系统通常为满足具体飞行任务的需要进行设计。
如下面的章节将要叙述的,式(4-15)和(4-16)是通用方程,它在各种特定应用情况下可作进一步的简化。对于粗略的设计估算,根据上面两个基本方程送代计算出的速度、高度或射程一般已能满足需要。对于实际弹道分析、导航计算、空间飞行测轨或 导弹射表制定,该两维简化理论计算结果的精度是不够的。在这种情况下,除了阻力和 重力外还必须考虑各种扰动的影响(如本章第6节所列的),必须采用数字计算机计算复杂的方程。通常把弹道任意划分为很多小段,采用步进法或数值积分法得岀整个弾道。更加通用的三体理论考虑了三个质量(如地球、月球和航天器)相互之间的星球引力。很多空间飞行问题需要采用三体理论研究(参见文献4-2, 4-3)。当推进剂流量和推力不为常数时,前面公式的形式和解更为夏杂。
式(4-15)、(4-16)还可用于根据精确的弹道测量数据(如光学测量或雷达测量数据)确定飞行器飞行期间的实际推力或实际比冲。飞行器加速度(du/dt)是与净推力成正比的,因此,根据推进剂流量(通常知道其变化规律)的估算值或实测值、气动力分析就可以求得火箭推进系统在飞行情况下的实际推力。
对式(4-15)、(4-16)积分,就可求得实际速度和飞行距离的变化历程,于是便得 到了整个弹道。更加通用的情况需要六个方程,三个为三轴平动方程,另三个为三轴转 动方程。通过选择合适的坐标系和原点,可以简化数学求解(参见文献4–2、4-4)o
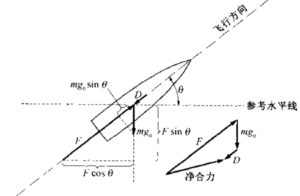
对于推力与推进剂流量恒定的无翼火箭弹、运裁火箭或导弹,这些方程可以简化。 这样,在图4-5中,飞行方向与推力方向相同,且无翼、对称、稳定飞行的飞行器在零攻角时其升力可假设为零。对于相对地球的单平面两维弹道(无风力),飞行方向加速度为
\(\frac{du}{dt}=\frac{c\zeta /{{t}_{p}}}{1-\zeta t/{{t}_{p}}}-g\sin \theta -\frac{{{C}_{D}}\frac{1}{2}\rho {{u}^{2}}A/{{m}_{0}}}{1-\zeta t/{{t}_{p}}}\) (4-17)
图4-5中的力矢量图画出的总净力(把推力、阻力和重力矢量相加)与飞行方向成一角度(航迹将弯曲)。这种图是弹道迭代数值求解的基础.
图4-5无翼飞行器白由体简化受力图。力关量图画出了总净力
本节中的关系式是针对单平面中两维飞行路线的。若发生向该平面外的机动(如因太阳引力、推力偏斜或风造成的),则飞行路线要变成三维的,需要用另一组方程来描述这种飞行。文献4-1给出了大气层内火箭弹的三维运动方程。把飞行器推离其飞行平面需要能量和力。为了达到飞行目标,必须精确计算弹道,如今几乎所有计算都有赖于计算机。现在许多航天企业或政府机关拥有很多用于飞行弹道分析的计算机程序。有些是两维的,相对简单,主要用于各种备选的飞行弹道、飞行器方案或推进系统方案的初步计算及比较。有些程序采用了静止平面地球模型,另外有些采用了旋转曲面地球模型。三维程序也有,用下更加精确的飞行弹道分析,考虑了部分或全部的扰动、轨道面变化或有攻角的飞行情况。如文献4-3中介绍的,它们要比两维程序复杂得多。 若飞行弹道是垂直的(如探空火箭),则式4-17中sin𝛉= 1.0,即
\(\frac{du}{dt}=\frac{c\zeta /{{t}_{p}}}{1-\zeta t/{{t}_{p}}}-g-\frac{{{C}_{D}}\frac{1}{2}\rho {{u}^{2}}A/{{m}_{0}}}{1-\zeta t/{{t}_{p}}}\)
发动机工作结束时飞行器的速度可通过积分得到,积分限为t=0到t=tp,对应的速 度为u=u0和u=up。式(4-18)右侧前两项很容易积分,最后一项仅在飞行器大部分时间都在大气层内飞行的情况下才起明显作用,它可采用图表法或数值法积分,其值可记为BCDA/m0,其中
\(B=\int\limits_{0}^{tp}{\frac{\frac{1}{2}\rho {{u}^{2}}}{1-\zeta t/{{t}_{p}}}}dt\)
这样,飞行器关机速度或推进剂耗尽速度up为
\({{u}_{p}}=-\bar{c}\ln \left( 1-\zeta \right)-\bar{g}{{t}_{p}}-\frac{B{{C}_{D}}A}{{{m}_{0}}}+{{u}_{0}}\) (4-19)
式中u0为初始速度,如由助推器提供的速度,\(\bar{g}\)为考虑时间和高度平均后(据式4-12)的星球引力。\(\bar{c}\)为时间平均等效排气速度,它与高度有关。
在选择火箭彈的最佳弹道时,总要作很多的权衡。例如,在工作时间、阻力、有效载荷、最大速度、最大高度(或射程)之间需进行权衡。文献4-6描述了一探空火箭对有效载荷、最大高度、飞行稳定性之间的权衡。
若忽略地球大气层外的气动力(真空中工作),也没有助推器或其他获得初速度的方法(u0 = 0),则垂直上升弹道的末速度为
\({{u}_{p}}=-\bar{c}\ln \left( 1-\zeta \right)-\bar{g}{{t}_{p}}\text{=}-\bar{c}\ln \text{MR}-\bar{g}{{t}_{p}}\text{=}\bar{c}\ln \left( 1-\text{MR} \right)-\bar{g}{{t}_{p}}\) (4-20)
通常第一项的值最大,其值等于式(4-6)。它与发动机等效排气速度直接成正比. 对质量比的变化很敏感。第二项在上升弾道中急是负的,但若发动机工作时间tp较短、 在高轨飞行或在g相对较小的空间飞行的话,该项的值很小。
对于非垂直飞行弹道,重力损失是飞行方向与当地水平面的夹角的函数。说得更具体一点,重力损失是式(4-15)给出的gsin𝛉dt的积分值。
在简化的两维情况下,海平面垂直起飞的净加速度为
\(a=\left( {{F}_{0}}{{g}_{0}}/{{w}_{0}} \right)-{{g}_{0}}\) (4-21)
\(\frac{a}{{{g}_{0}}}=\left( {{F}_{0}}/{{w}_{0}} \right)-1\) (4 22)
式中a/g0是以海平面重力加速度的倍数表示的初始起飞加速度,F0/w0为起飞推 重比。对于大型的地面或海面发射飞行器,该初始推重比的值大致在1.2到2.2之间。 对于小型导弹(空空、空面、面空型),该值通常较大,有时可高达50甚至100。垂直上升飞行器的最终加速度或末加速度af通常指在火箭发动机临关机前、推进刑完全耗尽前的加速度。
\(\frac{{{a}_{f}}}{{{g}_{0}}}=\left( {{F}_{f}}/{{w}_{f}} \right)-1\) (4-23)
在无重力环境中,上式变为af/g0=Ff/wf-1。对于推进剂流量恒定的飞行器,因为飞行器总质量在推进荆耗尽前达到最小值。且对于上升的飞行器其发动机推力随高度増加,故飞行器最终加速度通常也是最大加速度。若该末加速度太大(导致结构超載、需増加结构质量),则可考虑在发动机工作后期把推力降低到较小的值。
例题4-1 一简单的单机救生信号弹的飞行弹道参数符号如图所示,其特征参數如下。
发射重量 4.0 lbf
可用推进剂质量 0.4 lb
等效比冲 120 s
发射仰角(和对水平面) 80°
发动机工作时间(常推力) 1.0 s
因为飞行速度较低,故忽略阻力。假设没有风,当地重力加速度等于海平面加速度g0并在飞行过程中保持不变。求:动力飞行的初始加速度和最终加速度、最大弹道高度、达到最高点的时间、落点射程、发动机关机时的飞行角度及落地时的角度。
【解】把飞行蛋刀分为三段:1s的动力飞行段、关机后的无动力上升段和自由降落段。 根据式(2-5)可得到推力
F = IsW/tp = 120×0.4/1 = 48 (lbf)
根据式(4-22)可得x、y方向的初始加速度:
(a0)y= g0[(Fsinθ/w)-1] = 32.2[(48/4)sin80°-1] = 348 (ft/s2)
(a0)x= g0(F/w)cosθ = 32.2(48/4)cos80°=67.1 (ft/s2) 飞行方佝初始加速度为
\({{a}_{0}}=\sqrt{\left( {{a}_{0}} \right)_{x}^{2}+\left( {{a}_{0}} \right)_{y}^{2}}\) = 354.4 (ft/s2)
推力方向与飞行方向是一致的。根据式(4-20)可得到动力飞行未速度up的垂直分量与水平分量。飞行器质量因推进剂的消耗而减少。
(up)y= cln(w0/wf)sinθ –g0t=32.2×120 ln(4/3.6)0.984-32.2= 375 (ft/s) (up)x= cln(w0/wf)cosθ= 32.2×120 1n(4/3.6)0.1736=70.7 (ft/s)
无阻力飞行条件下,发动机关机时弹道与水平方向的夹角为
arctan( 375/70.7) = 79.3°
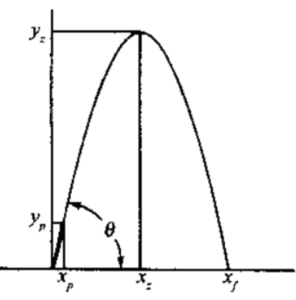
最终加速度为af=Fg0/w= 48×32.2/3.6 = 429 (ft/s2)。在短期动力飞行段,关机点的坐标yp和xp,可通过动力飞行平均速度(最大速度的50%)近似计算。
yp=0.5(up)ytp=0.5×375×1.0=187.5 (ft)
xp= 0.5(up)xtp=0.5×70.7×1.0×35.3 (ft)
无动力弹道段頂点的垂直速度为0。这段抛物綫弾道的初始的速度、x、y坐标值为发动机关机点的值(F=0,u=up,x=xp,y=yp)。在项点(uy)z=0。
(uy)x=0=-g0(tx-tp)+ (up)ysinθ。
在该頂点sinθ=1.0。解tz
tz=tp+(up)y/g0=1+375/32.2=12.6 (s)
可得弹道最大高度为
yz=yp+(up)y(tx-tp)-0.5g0(tx-tp)2
= 187.5+375(11.6)-0.5×32.2(11.6)2=2370 (ft)
从上升点到项点的射程为
xz=(up)x(tz-tp)+xp= 70.7×11.6+35.3=855 (ft)
利用yz=0.5g0t2可得下降的时间为
\(t=\sqrt{2{{y}_{z}}/{{g}_{0}}}=\sqrt{2\times 2370/32.2}=\)12.1 (s)
已知頂点初始水平速度(uz)x与关机点水平速度(up)x相等,可得最终射程或落点距离x为
Xf = (up)x(tdescent)=70.7×12.1 = 855 (ft)
上升段加下降段的总射程为855+855=1710 (ft)。落地时间为12.6+12.1 = 24.7 (s)o 最终速度的垂直分量uf为
uf= g0(tf-tz)=32.2×12.1=389.6 (ft/s)
落地角度θf为
θf= arctan(389.6/70.7)=79.7°
若考虑阻力,则需采用有限元迭代求解飞行弹道,所有速度和距离量的值会稍微小一些。文献4-5给出了一组探空火箭的飞行弹道。
4.4推进系统对飞行器性能的影响
本节叙述一些改进飞行器性能的方法。下面将要叙述的大多数改进方法都要受推进系统选择或设计的直接影响。只有少量的飞行器性能改进与推进系统无关。下面所述的多数方法适用于所有飞行任务,但其中有些只能针对某些任务。
- 等效排气速度c或比冲Is,通常对飞行器飞行性能有直接影响。例如,高的比冲能提高飞行器最终速度增量∆u。高比冲可通过使用能量更高的推进荆(见第七、十二章)、采用更高的燃烧室压力以及采用更大的喷管面积比(对于高空工作的上面级)来实现。
- 质量比 m0/mf对飞行器性能的影响是对数关系。有好几种方法可提高质量比。一种方法是减少最终质量mf,该质量由硬件死重和不可用残余推进剂质量组成。 要减少死重意味着需采用更轻的结构、更小的有效载荷、更轻的制导控制设备或减少不可用残余推进剂。这就需要采用强度更高的结构材料、效率更高的电源设备或更小的电子设备。在实际设计过程中,设计师总是会强调减少所有硬件的质量、把残余推进剂量降低到其实际极限值。另一种方法是提高初始质量,即加大推力、增加推进剂量,同时 把结构质量或推进系统硬件质量的增加控制在最低值。此外,采用两级或多级飞行器能大大提高等效质最比,这将在本章下一节中解释。
- 减少工作时间(即增大推力)能减少重力损失。不过,加速度增大通常会引起结构与推进系统质量的增加,反过来对质量比不利。
- 至少有四神方法可减少阻力(其可视为一种负推力)。阻力可划分为多种形式: (a)形状阻力(形阻)与气动外形有关。细长头锥、尖薄前缘的机翼的阻力要比短粗饨 头外形的小。(b)横截面积小的飞行常所受的阻力小。因此推进系统最好能设计成细长包络形状。(c)阻力与飞行器横裁面积或迎风面积成正比。采用高密度的推进荆可减少 推进剂容积,从而减少飞行器横截面积。(d)摩擦阻力(摩阻)是由空气流过飞行器外 表面时产生的摩擦造成的。流畅的轮廓和光滑的外表面通常能减少摩阻。推进剂密度对摩阻也有影响,因为高密度导致体积小,从面减小了飞行器表面积。(e)底部阻力(压阻)是另一种形式的阻力,它是作用在飞行器底面上的局部气压的函数,与喷管出口设 计(出口压力)和飞行器底部形状有关。第十八章将作进一步讨论。
- 发动机喷管长度一般对飞行器总长度或级长度有明显的影响。如第三章所述, 存在一个最佳喷管型面与最佳长度,它们可通过综合分析得出。缩短喷管能稍微减少飞行器长度,在某些情况下这能减轻一些飞行器结构重量,稍微提高飞行器质量比。
- 增加初始速度u0能增加发动机关机时的飞行器最终速度。向东发射卫星时, 地球自转速度也成了卫星入轨速度的一部分。地球自转切向速度在赤道处为464 m/s, 在肯尼迪空间中心(北纬28.5°)向东发射时该速度为408 m/s。反之,向西发射卫星 时初速度为负,需要更多的速度增量。增加速度u的另一种方法是从飞机或卫星上发射航天器(增加航天器初速度,并使之能向所需的方向发射),或者从飞机上发射空面导弹。
- 对于大气层内的飞行器,可利用气动升力抵消重力,以减少重力损失,增加射程。采用机翼或以一定攻角飞行可增加升力,但同时也增加了阻力。升力还可用于增加 机动性和弹道的灵活性。
- 当飞行速度u接近发动机等效排气速度c时,推进效率达到最高值【式(2- 23)】,发动机排气能量最大程度地转化为飞行器飞行能量。若在很大部分飞行弹道中u 接近c,所需的推进剂最就较少。
这些影响因素中有些可以进行优化。因此,对各种飞行任务都存在一个最佳的推进系统方案,至于那些发动机参数要作为优化目标则与飞行器参数或飞行参数有关。
4.5空间飞行
牛顿引力定律定义空间两体之间的引力Fg如下:
Fg = Gm1m2/R2 = μm2/R2 (4-24)
式中G为万有引力常数[G=6.670×10-11m3/(kg.s2)],m1和m2为两个相互吸引 的天体(如地球和月球、地球与航天器、太阳与行星)的质量,R为两者质心的距离。 地球引力常数μ为牛顿万有引力常数G与地球质量m1(5.974×1024 kg)的积,它等于 3.98600×1014m3/s2
火箭提供了一种逃逸地球去进行月球和行星际旅行、离开我们的太阳系、在空间制造静止或运动空间站的工具。忽略地球自转和其他星体的引力,逃逸地球所需的飞行速度可根据运动体的动能等于其克服重力所需做的功求得。
\(\frac{1}{2}m{{u}^{2}}=m\int{gdR}\)
把式(4-12〉代入g,忽略空气摩擦,得地球逃逸速度公式如下:
\({{u}_{e}}={{R}_{0}}\sqrt{\frac{2{{g}_{0}}}{{{R}_{0}}+h}=\sqrt{\frac{2\mu }{R}}}\) (4-25)
式中R0为地球等效半径(6374.2 km), h为海平面軌道高度,g为地面重力加速度 (9.806 m/s2)。以地球为中心的航天器半径R为R = R0+H。如图4-6所示,地表处逃逸速度为11.179 km/s,在地球大气层范围内各处的逃逸速度与此相差不大。表4-1给出了太阳、各大行星和月球的表面逃逸速度。从地球表面以逃逸速度发射飞行器是没有实际意义的。当飞行器上升穿过大气层时,它要受到严重的气动加热和气动压力。实际运载火箭必須以相对较低的速度穿越太气层,在稠密大气层外加速到较髙的速度。例如,在航天飞机上升段,主发动机推力实际上控制在较小的水平以避免过压和过热。此外,逃逸飞行器也可从空间站或在軌航天飞机上发射。
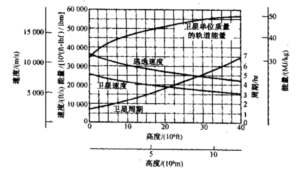
图4-6航天器轨道能量、轨道速度、环绕周期和地球逃逸速度与圆轨道卫星轨道高度的关系。假设地球为球形,忽略地球自转、大气阻力
火箭动力飞船可以成为地球的卫星,象月球那样环绕地球。卫星轨道一般是椭圆形的,有些是圆形的。低地轨道(高度一般低于500 km)记为LEO。卫星可用于广播电视的通讯中继、气象观测以及侦察。卫星轨道一般要高于地球大气层,因为这样能减少克眼阻力(阻力会使飞行器离地球越来越近)所需的能量消耗。考虑到范艾伦帯对航天员和敏感仪器的辐射效应,有时也选择较低的地球轨道。
对于圆轨道,卫星的速度必须高到其离心力能与地球引力平衡
Mus2/R = mg
由式(4–42)可得圆轨道卫星的速度
\({{u}_{s}}={{R}_{0}}\sqrt{{{g}_{0}}/\left( {{R}_{0}}+h \right)}=\sqrt{\mu R}\) (4-26)
该速度小于逃逸速度,两者之比为\(\sqrt{2}\)。以秒为单位的圆轨道相对静止地球环绕一圈的周期𝛕为
\(\tau \text{=}2\pi \left( {{R}_{0}}+h \right)/{{u}_{s}}=2\pi {{\left( {{R}_{0}}+h \right)}^{{3}/{2}\;}}\left( {{R}_{0}}\sqrt{{{g}_{0}}} \right)\) (4-27)
忽略阻力,把单位质量发射到卫星圆轨道所需的能量由动能与势能组成,即
\(E=\frac{1}{2}u_{s}^{2}+\int_{{{R}_{0}}}^{R}{gdR=\frac{1}{2}R_{0}^{2}\frac{{{g}_{0}}}{{{R}_{0}}+h}+}\int_{{{R}_{0}}}^{R}{{{g}_{0}}\frac{R_{0}^{2}}{{{R}^{2}}}dR}\)
\(\text{=}\frac{1}{2}{{R}_{0}}{{g}_{0}}\frac{{{R}_{0}}+2h}{{{R}_{0}}+h}\) (4-28)
图4-6给出了逃逸速度、卫星速度、卫星周期及卫星轨道能量与高度的关系。
高度为482.8 km的地球园轨道卫星的速度约为7375 m/s,环绕静止地球一圈需 1.63 hr,理论上每公斤质量的发射能量为3.35×107 J。半径为6.611倍地球半径 (42 200km)的赤道上空圆轨道卫星的环繞周期为24hr,它相对于地球上的观察者似乎是静止的,这种卫星称为地球同歩轨道上的同步卫星,通當编写为GEO。这种轨道广泛用于通讯卫星。在4.7节介绍运载火箭时我们将描述航天器有效载荷是怎样随着圆轨道高度的增加及轨道倾角(轨道面与地球赤道面的夹角)的变化而减少的。
4.5.1 椭圆轨道
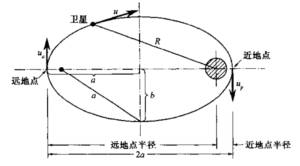
上述圆轨道是图4–7所示的一般椭圈轨道的一个特例。对于一般椭圆轨道.地球 (或任一天体,另一物体围绕其运动)位于椭圆的一个焦点处。运动方程可根据开普勒定律推导。椭圆轨道可以用极坐标描述如下:
\(u={{\left[ \mu \left( \frac{2}{R}-\frac{1}{a} \right) \right]}^{\frac{1}{2}}}\) (4.29)
式中u是椭圆轨道上物体的速度,R是物体与天体中心的瞬时半径(矢量,大小与方 向都有变化),a是椭圆长轴长度,μ是地球引力常数,其值为3.986 ×lO14m3/s2。各 符号巳在图4-7中标明。从上式可知,当运动物体在高焦点最近的位置时即轨道近地点时达到其最大速度up,在轨道远地点时达到其最小速度ua。把R代入式(4.29),定义椭圆偏心率e为\(\sqrt{{{a}^{2}}\text{-}{{b}^{2}}}/a\),得远地点速度和近地点速度为
\({{u}_{a}}=\sqrt{\frac{\mu \left( 1-e \right)}{a\left( 1+e \right)}}\) (4-30)
\({{u}_{\text{p}}}=\sqrt{\frac{\mu \left( 1+e \right)}{a\left( 1-e \right)}}\) (3-31)
图4.7椭圆轨道。中心天体位于椭圆的一个焦点上
楠圖轨道的另一个特性是:对于任何a、b,椭圆任何位置处的速度与瞬时半径之积都为常数,即uaRa=ubRb-uR。卫星的精确轨道路线与它进入轨道时的速度(大小、方向)有关。
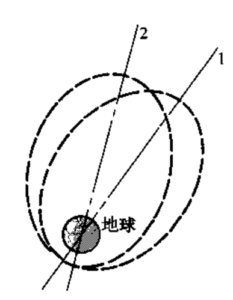
对于行星际转移,利用霍曼最早提出的一种简单的转移椭圆(参见文献4-6)可用最小能量实现理想的转移任务。假设围绕太阳的行星轨道为圆轨道且与初始轨道共面,可以证明,向行星轨道转移的最小能量路径是图4-8所示的一条与行星轨道相切的楠圆线。这种转移需要在转移起点产生一个速度增量(推力相对较高),在转移终点产生另一个速度增量,两个速度增量均为各圆轨道速度与相应的转移椭圆的近地点速度或远地点速度之差。霍曼转移起点和终点的机动推力必须足够大,以缩短发动机工作时间,其产生的加速度至少要O.Olg0,最好更大。若采用电推进,其加速度约为10-5g0。,工作时间可能要数周或数月,其最佳转移轨道将与霍曼椭圆有很大不同。第十九章将叙述电推进的情况。
发射日期或发射点与目标的相对位置对于行星际转移任务是很关键的,因为航天器必须在到达目标轨道后与目标相遇。从地球到月球的霍曼转移时间(t2-t1)约为116小时,从地球到火星约为259天。若采用更怏的转移轨道(更短的转移时间,见图4-8中的虚线),则需要消耗比霍曼转移更多的能量。这意味着要使用更大的航天器、更大的推进系统(有更大的总冲)。对需要进行空间交会的航天器的发射还存在一个发射窗口问题。从地球发射的火星任务航天器可能有两个月以上的发射窗口。霍曼转移椭圆和快速转移路径不仅适用于行星际飞行.也适用于地球卫星从一圆轨道到另一圆轨道(共面)的飞行。此外,若航天器要与另一轨道上的航天器交会,在转移前两个航天器必须
在合适的预定位置,以实现同时到达交会点。若初始轨道(或行星)与目标轨道不共面,则需要更多的能量用于在与初始轨道面垂直的方向施加推力。
例题4-2某卫星从高度为160 km的赤道圆停泊圆轨道利用霍尔椭圆转移到共面同步圆轨道。假设地球为半径6374km的均匀球休。求进入转移轨道所需的速度增量和进入42200km高度的同步轨道所需的速度增量。轨道术语参见图4-8。
组小的反作用控制推力器来执行的,推力器按所需方向发出预定的冲量。航天器整个寿命期间(1~20年)都需要进行这种校正,以克服扰动的影响,维持預定飞行状态。
摄动可分为短周期和长周期两类。以天或轨道周期为振荡周期的摄动力称为昼夜摄动力,长周斯的摄动力称为永年摄动力。
高轨卫星(36000 km以上)所受的摄动力主要是太阳和月球的引力,其方向随卫 星绕地球飞行而变化(卫星坐标)。该三体效应会增加或减小飞行速度并改变飞行方向。 在极端情况下卫星会飞近第三体(如月球),产生所谓的双曲线机动,这种机动会严重改变轨道。这种现象反过来也可用于改变卫星能量,从而有意地改变速度和轨道形状。
中低轨卫星(500 – 35000 km)的摄动力主要来自于地球的非球形。地球形状在赤 道附近凸出,通过两极的横截面也不完全是圆的。按照轨道面与地球赤道面的夹角以及 卫星轨道高度的不同。存在两种摄动:①交点漂移;②拱线(长半轴)漂移。图4-11 以轨道面旋转的形式画出了交点漂移现象,它在轨道高度较低时最大可达每天9°。理论上,赤道面轨道没有交点漂移现象。
图4-11轨道交点漂移(以轨道面旋转的形式画出)。 旋转方向与卫星东西运动方向相反
图4-12 地球非球形引起的椭圆轨道拱线漂移(由1到2)
图4-12画出了拱线漂移(放大示意),地球中心依然是焦点。这种摄动可看作是椭圆轨道在固定平面上的运动。显然,远地点和近地点的位置都要发生变化。变化的速率 是卫星高度和轨道倾角的函数。对于远地点高度为1000海里、近地点高度为100海里的赤道面轨道,供线漂移大概为每天10°。
现代卫星设计(因伸出的天线、太阳电池阵或其他不对称的设备造成了形状的不規 则)在其寿命期内会受到各种干扰卫星位置、轨道的力和力矩。主要的力矩和力来自于以下因素:
- 气动阻力。这种因素在轨道高度为500km以下时很重要,而到800km以上时 一般认为可忽略。文献4-7对气动阻力进行了详细的论述,该阻力除了影响不对称航天器的姿态外还会造成椭圆轨道的变化,即所知的轴线漂移、长轴变短以及轨道偏心率的降低。
- 太阳辐射。这种因素在高轨道(800km以上)时成为主要因素,它是由太阳辐射光子对卫星表面的冲击引起的。对于地球附近的卫星,暴露在阳光下的表面上的太阳光压p (N/m2)为
p = 4.5 ×10–6cosθ[(1 – ks)cos𝜽 + 0.67kd] (4-32)
式中θ为入射阳光与表面法向的夹角,ks和kd为镜面反射系数和漫反射系数。对于卫星星体表面和天线表面,ks和kd的典型值分别为0.9和0.5,对于太阳电池阵表面,ks和kd的典型值分别为0.25和0.01。太阳辐射强度随距离的平方变化(参见文献4-8)。施加在航天器上的力矩T为T=pAl,其中A为投影面积,l为太阳光压压心与航天器质心的距离。
- 重力梯度。航天器上的引力力矩是由分布在航天器各处的质量上的引力差异造成的。确定该力矩需要知道引力场和航天器的质量分布。该力矩随轨道半径的增加而减小,随航天器质量分布(包括伸展物和附件)的不均匀性面增加。重力梯度的影响在运行轨道较低的大型航天器或空间站上最为显著。
- 磁场。地球磁场与卫星内部的磁矩相互作用产生力矩。地球磁场绕地轴进动, 强度很弱(极点和赤道处的磁强分别为63和0.31高斯)。由于磁暴和其他因素,该磁场在方向与强度上是连续波动的。磁场强度与R3成反比,随轨道高度的增加而减小。地磁力干扰在卫星初步设计阶段通常忽略。
- 内部加速度。太阳电池阵展开、推进剂晃动、航天员或航天器内其他质量的运动、反作用飞轮的“卸载”等会产生干扰力矩或干扰力。
卫星推进需求可按表4-2所列的功能分类,该表给出了适用于典型的高轨椭圆轨道卫星的总冲“預算”。控制系统设计师通常把保持同步卫星的位置所需的轨道修正工作分为两种。东西修正指沿东西方向移动卫星轨道面与地球赤道面的交点,它通常修正主要由地球扁率引起的干扰。南北修正一般用于抵消太阳与月球的三体效应干扰。
许多卫星任务不担心摄动力引起的轨道的缓慢变化。但是,在某些任务中必须抵消这些扰动力,把卫星保持在特定轨道和轨道的特定位量上。例如,GEO上的地球同步通信卫星就需要保持其位置与轨道,这样它就能:①一直覆盖地球特定区域或在它的视线范围内一直与地球上某一基站保持联系;②不会对在这条拥挤的赤道面间步轨道上的其他卫星造成威胁。另一个例子是LEO上多个协同工作的卫星组成的通信卫星系统, 这种情况下至少有一颗卫星需在特定位置与地球上某处进行接收与发送射频信号的工作。它们的轨道及卫星之间的相对位置需进行控制与保持(参见文献4-11~4-13)。
轨道保持意味着周期性地施加一个小的修正力或力矩。GEO卫星通常是数月一次。 地球同步卫星轨道保持所需的速度增量△u 一般为每年10〜50 m/s。若卫星质量为 2000 kg、寿命为10年,每年50m/s的修正量需要的总冲约100000 Ns,若采用小推力单元或双元发动机的话相当于需要400 ~ 500kg的推进剂(差不多整星质量的四分之一)。若釆用电推进的话所需的推进剂量可大大减少,但对于某些航天器来说电源设备的质量会增加。
4.5.4任务速度
描述空间任务所需能量的大小的一种简便方法是使用任务速度这个概念,它是达到任务目的所需的全部速度增量的和。在图4-10画出的行星着陆任务简图中,它是弹道中所有粗实线(火箭动力飞行段)所表示的速度增量的和。尽管有些速度增量是通过反推(用于减小飞行速度的负推力)获得的,但这些机动也需要能量,它们的绝对值也应计入任务速度。由地球自转带来的初速度(赤道处为464m/s, 28.5°纬度的发射点为 408m/s)不需要由飞行器推进系统提供。在肯尼迪发射中心把航天器发射到110km轨道、停留一段时间、然后作离轨机动所需的任务速度及各△u组成部分列于表4-3。
飞行器所需的任务速度是任务飞行期间所有平动(力通过飞行器质心,包括转弯) 速度增量绝对值的和。它是假设飞行器各级上所有用于增加飞行器动量的推力室的推进 能量均施加在同一方向上时,飞行器在无重力真空中能达到的理论速度。七可用于比较 不间的飞行器设计方案,并表示任务能量需求的大小。
飞行器所需的任务速度必须等于“能提供的”任务速度,即飞行器各级上的推进系统能提供的速度增量之和。航天飞机推进系统(捆绑固体火箭助推器、主发动机,对于轨道切入还要包括轨道机动系统,这些都在图1-12中面出了)为前面叙述的航天飞机任务“能提供的”总速度增量必须等于或大于9621m/s。对于单级化学推进系统,视有效载荷、飞行器设计方案及推进剂的不同,其能提供的空间任务速度为4000-13000 m/s。若有两级,则或许可达12000~22000m/s。
后面将要叙述的旋转机动不改变飞行器速度,通常不计入任务速度需求。此外,针对长期摄动力(见前面的节)的卫星轨道保持通常也不算在任务速度内。然而,设计师需要考虑为这些情况提供额外的推进能力与推进剂。这些通常由另一称为反作用控制系统的独立推进系统来完成。
表4-4给出了各种行星际任务所需的飞行器速度的典型估算值。若从一空间卫星基地开始行星际旅行,则所需飞行器速度可大大減小,即减掉了卫星环绕地球所需的速度。随着空间飞行目标的扩大,任务速度变得越来越大。对于一给定的单级或多级飞行器,有办法提高其最终速度,但一般只能靠减少有效载荷。表4-5以相对简单的地球轨道有效载荷的百分比的形式给岀了同一飞行器在不同任务下的有效载荷的典型值。由表可知,一飞行器能把很大载荷送入近地轨道,但只能携带该载荷的一小部分在月球上着陆,因为月球着陆需要增加上面级而吃掉了有效载荷质量。因此,在相同有效载荷的情况下,任务速度高的空间飞行需要的飞行器比任务速度低的飞行器要大很多。表4-4、4-5中的数据仅仅是近似值,因为它们与飞行器具体设计待点、所用推进剂、准确的轨道-时间关系以及其他一些超岀了这里的简短讨论范围的因素有关。更详细的空间飞行 知択可•阅文献4-2~4-4、4-11~4-13。
例如,对于共面地月飞行并返回,需按次序完成下面的步骤,每步都需适当的速度增量,其方案与图4-10所示的行星际飞行类似。从地面起飞、进入地球卫星轨道,理论上飞行器需加速到约7300m/s;转入转移轨道约再需2900m/s;减速(反推)、飞向月球、进入月球轨道约需1000m/s;在月球上着陆又制约1600m/s。从月球起飞进入返回地球的轨道还需要2400m/s。在地球大气层内,可利用气动阻力减小飞行器再入速度,该机动无需消耗推进剂。把以上数据相加,再考虑300m/s的速度增量用于各种轨道调整,得总速度增量为14500m/s,这就是该任务所需的累计速度增量近似值。表 4-3、4-4对几种空间任务的任务速度和有效载荷进行了粗略的比较。
4.6机动飞行
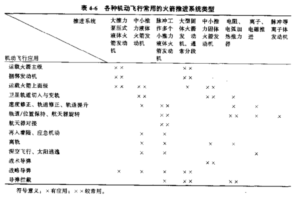
本节叙述各种机动飞行.并把它与具体类型的推进系统联系起来。机动的三种类型是:
(1) 平移机动,火箭发动机推力矢量通过飞行器质心。飞行器动量在飞行速度方向改变。图4-10简要地面岀了复杂飞行弾道中的几种动力飞行段(平移机动)和无动力飞行段(滑行)。迄今为止大部分机动飞行采用化学推进系统。
(2) 纯旋转机动,飞行器上没有净推力,只有纯力偶形成的力矩。要使飞行器绕某轴进行正反方向的转动,需要四个推力器(两个方向相反、推力不在同一条线上的推力器同时点火)。这种机动通常由反作用控制系统完成。大多数反作用控制系统采用了多个液体火箭发动机,但近些年许多空间任务使用了电推进。
(3) 第(1)类与第(2)类的组合,如在一不正好通过飞行器质心的、较大的偏心推力矢量作用下所产生的运动。推力偏移可通过在动力飞行段改变主发动机推力方向 (推力矢量控制)或由一独立的反作用控制系统同时施加一个补偿力矩来校正。
下述类型的空间机动飞行与飞行器加速采用了火箭推进系统。推进系统的所有工作均由飞行器制导与控制系统控制(启动、监视和关机)。
a. 第一级或其上面级推进系统在发射与上升段增加飞行器的动量。它们需要大推力或中推力、工作时间较短(一般为7-8min)的火箭发动机。迄今为止这类推进系统全部采用化学推进系统。它们占了飞行器质量的主要都分,下一节将进一步对其讨论。
b 轨道切入或从一轨道向另一轨道的转移需要精确预定的总冲。它可由运载火箭 顶级主推进系统来完成,但更多的是由一套推力比a项中的上面级小的、独立的推进系统来完成。轨道切入可能只需发动机在飞行器由地面起飞上升到一定位置后工作一次。 若飞行路径是霍曼转移椭圆(最小能量)或快速转移轨道,则需要两段推力作用过程, 一段在转移路径的起点,另一段在终点。对于地球轨道切入,视有效载荷质量、转移时间和具体轨道而定,推力一般为200~45000N。若要转移到更高的轨道,则在飞行方向施加推力;若要转移到更低的轨道,则要在飞行方向的反方向施加推力。转移轨道也可采用推力很小的电推进系统(0.001~1N)来达到,但其飞行路径将有很大不同 (多圈螺旋形),转移时间将会长很多。这将在第十九章解释。在月球任务或行星际任务中也有类似的机动,如图4-10简要画出的行星着陆任务。
c. 速度矢量调整和微小飞行校正机动通常采用带多个小型液体火箭发动机的反作用控制系统进行小推力、短时间、间歇性(脉冲)的工作来完成,不管是转动还是平动。彈道导弹的微调发动机用于精确校正末速度矢量,以提高目标精度。运载火箭上的 姿态控制发动机系统用于在另一精度稍差的推进系统把末级送入轨道后对其进行精确的轨道切入修正机动。深空探测器轨道的中途制导修正机动也属于这一类。轨道保持机动或称为位置保持机动(克服扰动力)推进系统用于把航天器保持在预定轨道和预定位置上,它也可归为这一类。
d. 再入机动和着陆机动有多种形式。若在有大气层的行星上着陆,大气阻力会降低再入飞行器的速度。对于椭圆轨道,阻力会越来越快地降低任何轨道的近地点高度和近地点速度。若要在預定地点精确着陆,则需在預定的高度和离着陆点一定距离处施加一个特定的速度矢量。为了正确使用热防护层,飞行器必须旋转到正确的位置和方向。 为了尽量减少传热(一般对热防护层而言)、准确降落在预定着陆点或准确击中預定目标(弹道导弹),飞行器进入稠密大气层时速度大小和方向的精度是很关键的。这通常 需要进行相对较小的机动(总冲很低)。若大气层很稀薄或没有大气层(如在月球或水星上着陆),则在下降和着陆过程中必须施加一个反推力。火箭推进系统通常可调节推力大小,以保证实现软着陆、适应飞行器在下降过程中其质量随推进剂消耗的减小。例如,登月火箭发动机的推力变化范围为10比1。
e.交会对接同时涉及小推力反作用控制推力器的旋转机动与平移机动。交会与它的时间窗口问题在4.5.1节讨论。对接(有时称为锁定)是两个航天器的连接,互相之间需要平稳地逐步接近(小推力推力器脉冲工作)以防損坏航天器。
f.改变飞行轨道需要在与初始飞行轨道面垂直的方向上施加一个推力(通过飞行器质心)。通常是把推进系统转到合适的方向(由反作用控制系统完成转动)后执行。这种机动用于改变卫星的轨道面,或在行星际(如火星)飞行时从地球轨道面转向与之不共面的行星际飞行轨道。
g.纯旋转机动是把飞行器按指令旋转到某个待定角度,用于对准望远镜、有关仪器、太阳电池阵或天线的指向,以进行观测、导航、通讯或接收太阳能。这种机动也用于把卫星的姿态指向保持在特定方向。例如,若卫星的天线需一直指向地心,则卫星在绕地球一圈中需自转一圈。旋转机动还用于在主推进系统工作前把喷管指向调整到所需的方向。它还可用于保持飞行稳定性或校正姿态角振荡(姿态角振荡会增加阻力、引起飞行器翻滾)。飞行器旋转能提高飞行稳定性,并能消除推力矢量的偏心。若需要快速起旋,则可采用多个推力器的化学反作用控制系统。若允许完成旋转机动的时间较长,则通常可采用多个推力器的电推进系统。
h 如今需要离轨机动与废弃航天器机动以消除空间碎片。废弃航天器不许对其他航天器造成危害。对航天器施加一个较小的推力,使其降到足够低的楠圆轨道,然后大气阻力使其继续减速。废弃航天器通常在再入稠密大气层过程中解体或烧毁。
i 应急机动或变任务机动。若航天器出现故障,决定中断任务(如放弃原定任务, 提前快速返回地球),则一些发动机将用于完成应急任务。例如,阿波罗登月飞船服务舱主发动机通常用于反推进入绕月執道以及从月球轨道返回地球,但它也可用于有效裁荷与运载火箭的应急分离和跨月滑行期间的非正常中途修正,以完成应急返回地球。
表4-6列出了上述机动类型与另外一些机动类型,并给出了已用于这些机动的各种火箭推进系统(如第一章所提到的)。表中略去了几种推进系统,如太阳热推进和核火箭推进。因为这些推进系统尚未真正用于空间任务。电推进系统具有很高的比冲(见表 2-1),这对深空飞行任务非常有吸引力。但电推进系统只能用于哪些允许推力作用时间足够长、以在很小的加速度下达到所需的飞行器速度的任务。表中带–××–符号的项目是近些年来常用的。
4.6.1反作用控制系统
反作用控制系统的功能已在前面讨论机动飞行的节中介绍了。它们用于c、e和g 段的机动控制。在某些飞行器方案中,若飞行器主推力较小,反作用控制系统还用于b 段、d段的一部分和f段的任务。
反作用控制系统(RCS)通常祢为辅助火箭推进系统。几乎所有的航天器和主要的运载火箭都需要该系统,以用于轨道修正(小速度增量)以及姿态修正。若只进行姿态机动,它也称为姿态控制系统。这些术语在工业界和文献中尚未统一。
RCS可在有效载荷级以及多级飞行器的任何一级中采用。在某些任务方案中,RCS 只在最上面一级中采用。在整个飞行过程中它一宜工作,为所有子级提供控制力矩和控制力。几乎所有的运载火箭和大部分航天器都使用了有多个推力器的液体火箭推进系统。早期的航天器方案中曾使用了冷气系统。最近十来年电推进开始用得越来越多,主要用于航天器,这将在第十九章叙述。RCS的工作寿命可能很短(当用于飞行器单独一级时),也可能覆盖整个任务周期(用于在轨航天器时,也许有10年)。
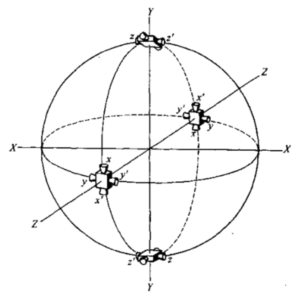
飞行器绕三个相互垂直的軸的姿态必须进行控制,各轴都有两个由度(逆时针与順时针转动),总共有六个转动自由度。俯仰力矩控制飞行器前缘的上升或下降,偏航力矩控制飞行器向左或向右运动,滚动力矩使飞行器绕飞行軸线作顺时针或逆时针转动。为产生一个纯力矩,需要采用两台推力完全相同、同歩工作(启动、关机)、离质心距离相同的推力器。图4-13给出了一筒单球形航天器的姿态控制系统示意图。推力器x-x或x’-x’产生绕X轴的转动力矩。该系统用了12台推力器,这是最少配置。有些航天器因推力器位置布局或其他限制、推力器冗余的考虑,推力器实际上不止12台。 利用不同的喷管组合,该姿态控制系统也能提供平动力。例如,某机组中的x和另一机组的x’同时工作的话,产生的力将推动航天器沿Y轴运动。釆用巧妙的设计方案可减少推力器数目。
图4-13航天器简化姿态控制系统图。产生三轴纯力矩需16 台推力器,图中它分为四个机组
RCS通常包括以下主要子系统:①敏感器件,用于确定航天器在任何时刻相对参考方向的姿态、速度和位置,如陀螺、星敏感器和无线信标机;②控制-指令系统,对实际位置、姿态与所需或预定的位置、姿态进行比较,发出控制指令,在所需时间内改变飞行器的姿态;③用于改变飞行器姿态的装置,如一组高速飞轮、一组姿态控制推力器装置。参见文献4-12和4-14o
姿态的精确校正可采用惯性轮或高速旋转的反作用飞轮,当飞轮的转速增加或降低时它会产生一个力矩。这些飞轮非常简单有效,但它们能提供的角动量变化量一般很小。若增加一套与之相配的姿态控制推力器装置,就可对每个飞轮进行卸载或起旋转,于是飞轮可以不断地在需要时提供小的姿态修正。
一对推力为F、推力线距离为Z的推力器产生的方矩T作用在转动慣量为Ma的航天器上,产生的角如速度为𝛼:
T=Fl=Maα (4-33)
对于质量均布的圆柱体,Ma=0.5mr2,对于均匀球体,Ma=0.4mr2。力臂l采用最 大实际值可使推力和推进剂耗量减到最小。若在时间t内角加速度保持不变,飞行器以角速度ω转动、转过角度θ,有
𝜔= 𝛼t, 𝜃 = 0.5αt2 (4-34)
通常,控制系统检测到–个小的姿态干扰后发岀一个合适的修正指令。在精密的敏感器检测姿态变化后,飞行器实际上已经转动了一个小角度。故必须采取措施,以免飞行器姿态或控制系统产生过调和振荡。为此,许多飞行器需要采用很多极短的脉冲(0.010- 0.030 s)和很小的推力(0.01-100 N),参见文献4-13、4-14。
反作用控制系统的主要特征量有总冲大小、推力器数目、推力大小、推力方向、工作占空特性等。工作占空特性(duty cycle)指推力脉冲的次数、脉冲工作时间、推力间隔时间以及任务工作过程推力器累计工作时间。对一特定的推力器,30%的工作占空特性是指该推力器的累计平均工作时间占推进系统工作时间的30%。推进系统的这些工作参数可通过任务、制导控制方式、所需精度、飞行稳定性、主发动机大致的推力偏心量、三维飞行轨道的变化、弾道摄动和其他一些因素确定。但有些参数一般很难确定。
4.7飞行器
如前面提到的,火箭动力飞行器中的绝大部分是采用固体火箭发动机的简单的单级飞行器。其中大多数用于军事,如下一节将要介绍的。本节叙述较复杂的多级运载火箭和其他一些飞行器,如大型弾道导弹(通常称为战略导弹)和一些探空火箭。它们的导航制导系统都有一定的智能化。最近几年全世界多级火箭飞行器毎年的总产量约为 140 〜220 发。
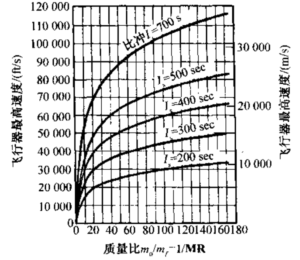
LEO单级入轨飞行器能携带的有效载荷是很有限的。图4-2表明推进剂质量分数为 0.95、平均比冲为400 s的高性能单级飞行器在不帯有效载荷时能达到的理论最终速度 约12000 m/s。若分析中再考虑阻力和重力、比冲再稍高一点、轨道机动和姿态控制系统,则视具体方案不同,有效载荷量约为飞行器起飞质量的0.2% ~1.4%。为了提高有效载荷比、完成要求更高的任务,需采用下面要叙述的两级或多级飞行器。
4.7.1多级飞行器
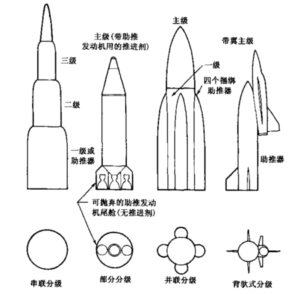
多级火箭飞行器能达到更高的飞行速度、携带更多的有效载荷(对于运载火箭)、 提高近程弹道导弹的性能。当某一级的可用推进剂完全耗尽后,把该级剩下的干质量从飞行器上抛掉,然后下一级推进系统开始工作。最后一级(或顶级)携带有效载荷,这一级通常是最小的,把完成任务的飞行器子级干质量从飞行器上分离可以省去对这部分无用质量继续加速所消耗的能量。随着级数的增加,飞行器起飞质量可以减小。当级数很多时,起飞质量下降的好处就不明显了。实际上级数不能选得太多,因为那样会增加 物理机构的数量、复杂性和质量。视任务而定,通常最合适的级数是两到六级。现已成 功使用的多级运载火箭有多种不同的构型,图4-14画出了其中四种。大多数运载火箭是垂直发射的,但也有少地是从飞机上发射的,如“飞马座”三级运载火箭。
图4-14四种构型的运载火箭子级组合方案简图。第一种是最普通的,各级垂 直叠加,如“民兵”远程导弹和“得尔它”运载火箭。早期的“宇宙神”火箭 采用了部分分级方案,发动机在起飞时全部工作,免得在飞行过程中启动。若在起飞前检测到故障,发动机可在发射台上关机。左右两个助推发动机在飞行途中抛掉。第三种方案中,垂直构型的芯级旁边连有两个或多个“捆绑式”独立助推級,以提髙飞行器性能。最有边的駄载式构型方案用于航天飞机。
多级火箭的有效载荷基本上与起飞质量成正比,尽管它只占起飞质量的一小部分。若50 kg的有效载荷需要6000 kg的多级火箭,则500 kg的有效载荷将需要60000 kg的级数相同的火箭。相同构型的火箭其有效载荷比也相同。若下一级关机后上面級紧接着开始工作,则串联多级火箭的总理论速度就是各级速度增量之和。若有n级,则最终速度增域△uf为
\(\Delta {{u}_{f}}=\sum\limits_{1}^{n}{\Delta {{u}_{i}}}=\Delta {{u}_{1}}+\Delta {{u}_{2}}+\Delta {{u}_{3}}+…\)(4-35)
各级的速度增量可根据式(4-6)计算。对于无重力真空飞行这种简化情况,上式可表示为
\(\Delta {{u}_{f}}={{c}_{1}}\ln \left( \frac{1}{M{{R}_{1}}} \right)+{{c}_{2}}\ln \left( \frac{1}{M{{R}_{2}}} \right)+{{c}_{3}}\ln \left( \frac{1}{M{{R}_{3}}} \right)+…\)(4-36)
上式给出了理想多级火箭在无重力真空中能达到的最高速度。对于更加精确的实际弹道,各级速度增量可通过积分式(4-15)、(4-16)得到,这两式考虑了阻力损失和重力 损失。如本章前面所述,其他损失或弹道摄动也可以考虑进去,这种情况下需采用数值解法。
对于两级或三级飞行器,总质量比(起飞质量与末级最终质量之比)可达100以上 (相当于单级飞行器的等效推进剂质量分数ζ为0.99)。图4-2于是可划分为单级飞行器区和多级飞行器区。
对于多级飞行器,各级的质量比、推力大小、工作时间、质心变化范围通常是经过优化的(利用复杂的弹道计算程序)。高比冲的火箭发动机(如氢氧发动机)一般用于运载火箭的上面级,因为比冲增加带来的好处在上面级上更为明显。
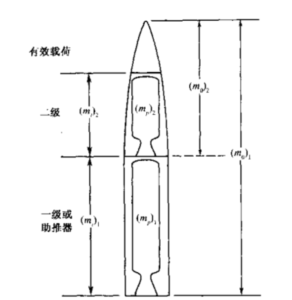
例4-3 —兩级行星探测器(如图)从高轨卫星上发射到真空无重力轨道。图中符号意义如下。
m0为飞行器(ft)发射初始质量;
mp为某级可用推进剂质量;
mi为飞行器某级初始质量;
mf 为飞行器某级最终质量(发动机工作结束后);包括推进系统干质量(含残余推进剂)、飞行器结构质量、控制制导设备质量、有效载荷质量等;
mpl为有效载荷质量;包括控制制导设备、通讯设备、天线、科研设备、电源设备、太阳电池阵、传感器等的质量。
下标1和2表示第一级和第二级。飞行器参数如下:
| 无重力真空中飞行速度增量, | 6200 m/s |
| 比冲Is | 310 s |
| 各级等效排气速度c | 3038 m/s |
| 飞行器初始质量 | 4500 kg |
| 各级推进剂质量分数ζ | 0.88 |
| 各级结构质量分数(1-ζ) | 0.12 |
求 在以下两种情况下的有效载荷量:①两级质量相等;②两级质量比相等。
若例题4-3中采用三级飞行器而不是两级,则有效载荷量更大。然而,有效载荷增加,理论上只有8%~10%。若再增加第四级,则有效载荷增加量更小,只有3%~ 5%。性能改进的潜力随着级数的增加而减小。实际飞行器每增加一级就意味着带来更 多的复杂性(如可靠的分离机构、级间段结构、导管接头、电缆接插件等),需要额外的死重(增加质量比MR),并降低了总体可靠性。因此,通常选择能满足有效载荷要求和速度增量要求的最少的级数。
例題4-3中两种情况下飞行器的飞行弹道是不一样的,因为飞行时间和加速历程不同。从该例题得出的一个结论适用于所有多级火箭飞行器:对每种任务都存在一个最佳级教、最佳级间质量分布,此外通常对各种设计方案还存在一条最佳飞行弹道,使飞行器关健参数如有效载荷量、速度增量或射程等达到最大。
若例题4-3中采用三级飞行器而不是两级,则有效载荷量更大。然而,有效载荷增加,理论上只有8%~10%。若再增加第四级,则有效载荷增加量更小,只有3%~ 5%。性能改进的潜力随着级数的增加而减小。实际飞行器每增加一级就意味着带来更 多的复杂性(如可靠的分离机构、级间段结构、导管接头、电缆接插件等),需要额外的死重(增加质量比MR),并降低了总体可靠性。因此,通常选择能满足有效载荷要求和速度增量要求的最少的级数。
例題4-3中两种情况下飞行器的飞行弹道是不一样的,因为飞行时间和加速历程不同。从该例题得出的一个结论适用于所有多级火箭飞行器:对每种任务都存在一个最佳级教、最佳级间质量分布,此外通常对各种设计方案还存在一条最佳飞行弹道,使飞行器关健参数如有效载荷量、速度增量或射程等达到最大。
4.7.2运载火箭
通常第一级或基础级(常称为助推級)是最大的,需要最大的推力与总冲。所有子级都需要采用化学推进以达到所需的推重比。一般后面的几级(也称为上面级或主级) 推力越来越小。推力大小与飞行器质量有关,反过来又与有效载荷质量及任务有关。图 4-14中的简图给出了典型的实际运载火箭构型方案。在多级火箭中,各级都存在一个最佳的尺寸和推力值,确定该值的分析过程是相当繁琐的。
许多重型运载火箭有两至六个捆绑固体火箭助推器,这些助推器共同形成了捆绑或 连接在运载火箭第一级上的额外的一级(航天飞机、“大力神”、“德尔它”、“宇宙神”、 “阿里安”),这种情况为图4-14的第三种构型。俄罗斯在几种运载火箭上使用了液体推进剂捆绑助推器,因为液体发动机的性能更高。助推器与第一级同时开始工作,工作结束后通常在一级发动机工作结束前与主级分离并抛掉。这种助推器也称为半级或零級。如表3-1所列。
现有很多类型的运载火箭。最小的用于小型有效载荷和低轨道。较大的一般级數较 多、质量较大、成本较高、有效载荷更大或任务速度更高。飞行器的成本随着级数和初 始发射质量的增加而增加。一旦某种运载火箭已被证明是可靠的,通常就对它进行改进。以提高它的性能或任务适应性。运载火箭的各级可能有多种火箭发动机,各用于专门的任务或机动。航天飞机上有67台火箭发动机,它们已在图1-13中面出。多数情况下各发动机用于某种专门的机动任务,但也有许多情况下同一发动机用于一种以上的任 务。例如,航天飞机上的小型反作用控制推力器在轨道切入和再入时用于姿态控制(俯仰,偏航和滚动),另外还可用于平衡内部质量漂移(航天员运动、可伸展臂的运动)、 小的轨道修正、小的飞行路径调整、交会对接以及科学仪器的精确指向。
航天器是运载火箭中携带有效载荷的那部分。它是运载火箭中唯一进入轨道或深空 的部分(有些设计成能返回地球的)。最终的主要空间机动(如轨道切入或行星着陆) 一般需要较大的速度增量。为此提供推力的推进系统可能与航天器结合在一起,也可能裝在紧靠航天器下面的可分离的子级上。4-6节介绍的几种机动通常可由装在多级飞行 器的两个不同子级上的推进系统来完成。选择最佳的推进系统、决定由多个推进系统中的哪一个来完成特定的机动任务将取决于对性能、成本、可掌性、计划进度、任务灵活 性的优化,如第十七章将要叙述的。
在运载火箭从地面发射入轨过程中,它要经历三种不同的弹道飞行。①大多敏火箭 是垂直发射的,随后进行转弯机动,在火箭发动机推力作用下把飞行速度矢量方向指向 预定方向;②火箭随后进行无动力自由弹道滑行(通常是椭圆弾道),直到最高点。③ 最后,卫星需要由化学推进系统提供额外的推动,增加足够的总冲或能量,把它加速到 轨道速度。这最后一次机动也称为轨道切入。在初始动力飞行段,制导系统把弾道角和 末级关机速度控制到关机后火箭空间飞行速度矢量正好使得火箭在所需的轨道高度达到椭圆滑行轨道的远地点。如图4-9所示,多级弹道导弹前面两个上升飞行段与刚才介绍 的相同,但其随后继续沿椭圆弹道飞行,直至奔向目标。
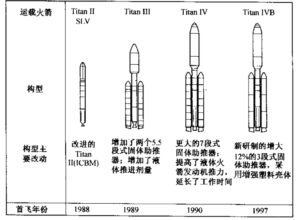
图4-15 “大力神”运载火箭系列的发展过程,由图中四种相关的构型可看出火箭的改进方法(资料来源:洛克希德-马丁公司)
图4-15与表4-7给出了早期“大力神”系列火箭的有效载荷与任务能力的增长以 及轨道对有效载荷的影响。图中画出了四种不同的多级运载火箭构型及其主推进系统的 发展过程。表中给出了这四种火箭构型的有效载荷的增长量,并列出了有效载荷随轨道的变化。若这几种火箭装上第三级,则它可以把相当大的载荷发射到地球逃逸轨道或地 球同步轨道。该表中介绍了这些火箭各级所用的发动机以及相应于几种任选轨道的有效载荷量。
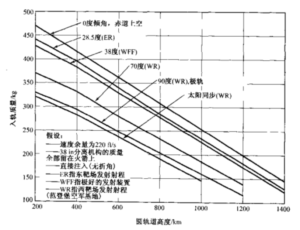
表4-7给出了轨道倾角与高度对有效载荷的影响。轨道倾角是地球赤道面与轨道面 的夹角。赤道面轨道的倾角为零,极地轨道的倾角为90°。因为地球自转为飞行器提供了一个初速度,在赤道上向东发射可获得最大的有效载荷。在轨道高度相同的情况下, 有倾角的轨道其有效载荷要比倾角为零的轨道小。在轨道倾角相同的情况下,有效载荷 随着轨道高度的增加而减小,因为需要更多的能量用于克服地球引力。
航天飞机在佛罗里达的肯尼迪航天中心向东发射进入28.5°轨道时有效载荷最大, 对于185 km高度的轨道其有效载荷约为25455 kgo高度每增加1海里,有效载荷约减少45.4kg。若轨道倾角为57°,有效载荷将减小到约19090 kg。若在西海岸的范登堡空军基地向南发射进入98°倾角的近极地圆轨道,有效裁荷将只有13909kg。
图4-16给出了 “飞马座”火箭的有效载荷与圆轨道高度、倾角的关系,该火箭是一种小型空射运载火箭。当在地球赤道上向东发射,即0°傾角时有效载荷最大。由图可知,当轨道高度超过1200 km后实际有效载荷已经很小。为发射较重的有效载荷或 发射到较高的轨道,需要比“飞马座”更大的火箭。图4-16中的数据基于特定的有效 载荷分离机构(38 in.)和特定的飞行器速度增域余量(220 ft/s),该余量是为大气密度的正常变化(可能使阻力翻倍)、推进系统的质量公差等情况所考虑的。所有运载火箭的制造方都能提供类似的曲线。
图4-16 “飞马座”运载火箭旧效载荷随圆轨道高度及倾角的变化。该火箭是一较简单的空射二级全固体火箭,直径为50 in (Orbital Sciences Corporation提供)
4.8导 弹
目前生产的火箭推进系统大部分用于军事应用。由于导弹及军事任务的种类有很多,因此推进系统也是各种各样的,但全部是化学推进系统。导弹最简单的有小型无制 导尾翼穏定单级火箭弹(用于空面打击和面面轰炸任务),最复杂的有昂贵的远程多级 弹道导弹(用于打击远距离军事或战略目标)。术语“面”指地面(地面发射或地面目 标)、海面(舰上发射)或海平面以下(潜艇发射)。战术导弾用于打击或保护地面部队、近距离武器装备或战略装置、军用飞机或导弹。此外,军队还利用軍用卫星来执行 侦察、来袭预警、保密通讯或导航等任务。
射程在3000km以上的战略导弹一般是两到三级的面-面火箭动力导弹。一些早期的设计采用了液体火箭发动机,有些还在服役。约在50年前,新型战略导弹开始使用 固体火箭发动机。这两种导弹二股都采用液体推进剂反作用控制系统(RCS)以精确调整末级发动机关机时有效栽荷的末速度(大小、方向和空间位置)。使用固体推进剂的 RCS也有。远程导弹的飞行分析和飞行弹道在许多方面与本章中对运载火箭的叙述类似。参见图4-9。
大多数战术导弹使用固体火箭发动机,因为它的勤务工作简单,可快速发射(文献 4-15)o对于飞行高度低、飞行时间长的导弹(如巡航导弹),通常采用吸气式发动机和机翼(提供升力)比采用长时间工作的火箭发动机更好。然而,巡航导弹仍然需要用大型固体火箭发动机发射并把它加速到一定速度。战术导弹有多种类型,不同的规模有不同的推进系统,如文献4-15和本节下面所述。
每种战术导弾都有一个最佳推进系统方案,几乎所有战术导弾都采用了固体火箭发动机。针对每种应用,都存在最佳总冲、最佳推力-时间曲线、最佳喷管构型(单喷管/多喷管、有无推力矢量控制、最佳面积比)、最佳室压、最合适的药柱内孔型面。对于某些战术导弹,排气羽流在可见光、红外或紫外谱段的辐射是否较低以及某些安全特征(使系统对能量刺激不敏感,即低易损性)可能非常重要,这些问题将在第十二章和第十八章讨论。
短程的无控单级火箭动力飞行器,如军用火箭弹(地面发射或空中发射)和救生信号弹,设计方案一般很简单。它们的通用运动方程已在4.3节中导出,文献4-1对其进行了详细分析。
当前无制导火箭动力导弹的产量远远超过其他任何一种火箭动力飞行器。最近几年,美国直径为2.75in的折聲翼无制导固体火箭发动机导弹年产量达25万枚。用于防空、反坦克或步兵支援的制导导弹的年产量为上百枚甚至在千枚以上。表1-6列出了几种制导导弹。
因为这些火箭弹基本上属于无制导导弹,其目标打击精度与初始瞄准以及由不平衡 阻力、风力、振荡和喷管、弹体、机翼的偏置造成的散布有关系。若弾体的初速度较低,则与预定弹道的偏差就更大,因为有翼弾体的气动稳定性在低速时较小。若弹体以相对较高的初速度从飞机上发射,或弹体依靠绕轴旋转提高稳定性,则其目标精度与静止发射的简单翼稳定导弹相比可提高2〜10倍。
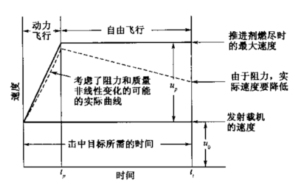
有制导的空空火箭动力导弾或面空火箭动力导弹飞向目标所需的时间通常称为击中目标时间t1,它是一个重要的飞行性能参数。借助于图4-17,认为导弹跨过的距离(称为射程)是速度-时间曲线的积分面积,可以导出其简化计算公式。简化计算假设无 阻力、无重力、飞行方向接近水平、动力飞行段射程相对总射程很小、动力飞行段速度线性增加。
\({{t}_{1}}=\frac{S+\frac{1}{2}{{u}_{p}}{{t}_{p}}}{{{u}_{0}}+{{u}_{p}}}\) (4-37)
式中S为无动力自由飞行射程,up为导弹在动力飞行段关机前所增加的速度,tp为导弹发动机工作时间,u0为导弹发射时的载机速度。为了更加精确,速度增量up可根据 式(4-19)计算。若要得到非常精确的值,只能对考虑了阻力与重力效应的弹道进行详细的一步一步分析。
图4-17无制导、无机动空射火箭弹的简化弹道。实线为无阻力无重 力情况下的飞行速度,虚线为实际飞行速度
对于空中发射的无制导空空或空面火箭弹,对目标的瞄准是速过调整载机的方向而进行的。对于有制导导弹(空空、空地、地空或拦截导弹),发动机推力的方向、大小 和工作时间可由智能制导控制系统控制,以跟踪机动目标。制导系统获取到目标的飞行 轨迹,计算出预定撞击点,然后控制导弹的飞行路径,实现与目标的直接撞击引爆(若采用接近引信,则为接近目标引爆)。地面发射.或轨道发射的反弹道导弹也采用这种方法。无论是无制导火箭弹,还是制导导弹,击中概率都随击中目标时间t1的减小面增加。在一特定的空战情况下,火箭弹的效能大致与击中目标时间的三次方成反比。通常击中目标时间为实际可能的最小值时能得到最好的效果(如击中概率最高)。
对在各种飞行状况下都能达到最小击中目标时间的导弹及推进系统的构型方案进行分析是很复杂的。以下一些火箭发动机特征和参数将有助于减小击中目标时间,但其效果与具体任务、射程、制导控制系统、具体飞行状况有关。
(1)采用高初始推力或高初始加速度,使导弹迅速达到强初始推动的飞行速度。
(2) 增加额外的小推力,用于抵消阻力与重力损失,从而保持高飞行速度。这可由 同一推进系统实现,即采用初始短期推力大、续航阶段推力小(10% ~25%)的推进系统。也可采用能提供离散推力脉冲的系统,在阻力使导弹减速后重新增加导弹速度,从而维持较高的平均飞行速度。
(3) 对于高超声速飞行,两级导弹可能更有效。当第一级的推进剂耗尽后将其拋掉,减小下一级的死重,提高其质量比,从面增加飞行速度。
(4) 若目标为高度机动的,或导弹与目标接近时的相对速度很大,则不仅有必要为 战术导弹提供一个轴向推力,还要为其提供一个较大的侧向推力或侧向加速度。这既可由气动力(升力面或以一定攻角飞行)来完成,也可由可变推力或脉冲工作的多喷管推进系统完成,后一种情况下推进系统有一个轴向推力器、多个侧向推力器。推力器的布局要使其推力基本上穿过导弹质心。提供側向加速度的推力器也称为转向推力器,因为它们使导弹朝与飞行方向垂直的方向转向。
(5)若导弹的L/D比较大(或横截面积较小)、推进剂密度较高(可减小导彈体积),则阻力损失能减小。导弹在低空高速飞行时阻力会很大。
火箭发动机另外还有一种独待的军事应用是火箭助推炮弹,用于增加火炮的射程。 这些炮弹中的小型火箭发动机能在炮筒里承受很高的加速度(通常为5000~10000 g0)目前它们有生产。
4.9排气羽流气动效应
火箭发动机排气射流或羽流对导弹气动特性的影响一般是减小超声速导弹的阻力、 增加亚声速导弹的阻力。对于亚鹿速飞行器,超声速火箭发动机羽流就像是一引射器, 它把附近的空气卷吸进来。它影响发动机装在锥形尾部上的飞行器。火焰的引射作用加 速了附近的空气,因此增加了局部表面摩阻、通常减小了飞行器尾部或邻近喷管出口位置的飞行器底板上的压力。
对于超声速飞行器,其尾都常常是湍流尾迹区,局部压力很低。在发动机羽流的作用下,尾部空间充满发动机燃气,飞行器尾段的压力增加。这样就增加了压差推力,减小了底部阻力。第十八章将讨论排气羽流效应。事实上,一些火炮武器和短程火箭可通 过增加一小型火箭燃气发生器提高射程(提高10%-50%),因为燃气发生器排出的燃 气以一定压力充填在飞行器底部空间,增加了飞行器的底部压力,减小了底部阻力。
4.10飞行稳定性
飞行器的稳定性指其在飞行过程中不旋转、不振荡。飞行中是不希望出现不稳定的,因为俯仰或偏航振荡增加了阻力(大部分时间以一定攻角飞行),并会给仪器设备 和敏感器件(目标捜索器、地平仪、太阳敏感器、雷达)带来问题。不稳定常常会导致飞行器的翻滚(失控翻转),这将引起轨道切入失败、目标丢失、贮箱中液体推进剂晃动。
稳定性可通过合适的设计达到,这样飞行器将具有固有稳定性。稳定性也可通过合适的控制获得,如利用飞机的气动控制面、反作用控制系统或多台摇摆发动机。
当翻转力矩(如由阵风、推力偏心或机翼位置引起的)小于由推力矢量控制或气动 控制面产生的稳定力矩时,飞行将是稳定的。当绕质心的不稳定力矩超过稳定力矩时, 飞行器将转动或翻滚。对于无制导飞行器,如低空火箭弹,直线飞行的稳定性通过使飞 行器具有很大的稳定裕度达到。稳定裕度可通过飞行器尾翼以及使飞行器重心位于气动压心的前面而获得。对于装有主动稳定控制系统的飞行器,希望其固有稳定性接近中 性,这样所需的控制力就比较小,就可采用较小的控制装置、小型RCS推力器、小型 作动机构,从而降低了結构质量。中性稳定性可通过合理的气动面布局和飞行器内部组 件的质量分布使得飞行器重心处于气动压心前面一点点处来获得。因为气动力矩随马赫数变化,压心在飞行器加速飞行过程中并不固定。通常是沿飞行器轴线不断移动的。飞行器重心也会随推进剂的消耗、飞行器质量的减小而改变位置。因此,通常很难使导弹在任何高度、速度和飞行状况下都达到中性稳定性。
稳定性的考虑从多个方面影响火箭推进系统的设计。通过对喷管进行仔细设计,可最大程度地减小推力偏心,从而减小它对飞行器产生的力矩和反作用控制推迸剂耗量。 通过精巧的设计可以控制飞行器重心的移动范围。对于液体火箭发动机,通过采用待殊的设计措施、特殊的贮箱形状、仔细选择贮箱在飞行器中的安装位置可以控制飞行器重心的变化。对于固体火箭发动机,设计师一般在控制重心变化方面自由度就比较小。如图14-6所示,通过在喷管前安装长尾管,已有办法把固体推进剂质量分布在飞行器重心附近。如4.6节和第六章所述,拥有多个推力器的姿态控制液体推进系统已满意地用于产生便飞行器沿多个方向转动的控制力矩。
无制导火箭弹和导弹常常靠倾斜的气动尾翼或倾斜的多个火箭发动机喷管来实现滾动或旋转,以改进飞行稳定性和精度。这与枪膛内的螺旋来福线造成子弹旋转是类似 的。这种旋转稳定性是由陀螺效应带来的,这种情况下旋转轴的偏斜会受到一个力矩的阻碍。但离心效应会引起液体推进剂贮箱的排放问题和固体推进剂药柱的附加应力。在某些情况下,低速旋转不是为了旋转稳定性,而是为了把推力矢量偏心或气动面偏置带来的问题尽量减小或消除掉。