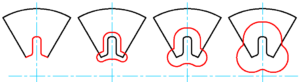
第五章 固体火箭发动机复杂装药及内弹道耦合分析

药柱（grain）是具有特定几何形状和尺寸的固体推进剂，它是发动机的能源和工质源。药柱的几何形状和尺寸决定了发动机的燃气生成率及其变化规律，因此也就决定了燃烧室的压强和发动机推力随时间变化的关系。药柱设计水平的高低在很大程度上影响发动机的性能好坏。

因为现代固体火箭发动机大多采取贴壁浇铸法制造药柱，绝热层（insulation）、衬层（liner）和药柱形成整体，所以就将这种整体结构统称做装药。而浇铸推进剂的过程也有人称之为“装药”。这里注意药柱和装药的区别，药柱仅是推进剂部分，而装药则是包含绝热层部分。在英文文献中一般统称为“grain”。

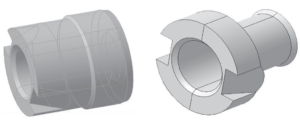
图5- 1 翼柱形药柱实例

在发动机设计中，药形（grain configuration）的选择和结构的调整以适应发动机和飞行器任务的特殊需要是发动机设计的重要工作之一。固体推进剂在被点燃后即开始自持燃烧并释放出作为工质的高温燃气，直至所有推进剂燃烧完毕。在此过程中，固体推进剂的燃烧过程不像液体火箭发动机那样可以通过流量动态调节，而是决定于药柱的形状变化过程。当燃烧表面面积相对较大时，燃气生成率相对更高，则此时的推力相应较大；反之，燃气生成率相对较低，推力也较小。

装药设计的目标是通过对药形和燃烧表面变化趋势的控制，得到完成飞行任务所需的内弹道曲线；同时，保证装药具有足够好的结构完整性，以承受飞行中的过载、内压和震动。一般来说，不会使用会导致裂纹的较弱的结构、产生较高拖尾（sliver）的结构、较低的体积装填分数（volumetric loading fraction）或制造昂贵的结构。通常，发动机性能要求和推进剂燃速是决定药形选择来适应期望的推力时间曲线的主要因素。加工能力和制造成本也是很有影响的。尤其是药形必须满足推力、燃烧时间、燃烧室压强、总冲、质心移动、结构强度、储存寿命、温度限制和制造成本的要求。

在发动机工作过程中，随着燃烧的进行，药柱燃面按一定规律发生退移，被燃面扫过的推进剂则转变为燃气，并流出喷管、产生推力。这一过程中，推力的变化趋势直接取决于燃气生成率的变化趋势，根本上则取决于药柱燃面的运动。执行装药及内弹道耦合分析，可以在进行实际点火试验之前预示发动的推力-时间曲线，为固体火箭发动机装药设计提供有力的参考。

在简单设计中，常基于平行层燃烧定理进行装药及内弹道耦合分析。但是，工程中所实际使用的装药结构较为复杂，不仅难以基于平行层燃烧定理获取燃面-肉厚曲线，实际燃烧过程也未必严格遵照平行层燃烧定理；侵蚀燃烧、粒子冲刷、飞行过载、自旋过载、推进剂成分迁移、多种推进剂的使用等因素都有可能使得药柱装特定区域在同等压强下具有比一般区域更快或更慢的燃速。这些燃速差异的发生机理和分布形式可能十分复杂，包括：

1. 药柱由燃烧特性不同的多种推进剂组成（串装或套装装药）；
2. 药柱中嵌入了用于增强燃烧的金属丝（一般为端燃药柱）；
3. 长细比较大的固体火箭发动机，处在燃气通道狭窄处附近的推进剂受强烈的冲刷作用，当地燃速随之增大；这一效应称为侵蚀燃烧；
4. 高速旋转的固体火箭发动机，其压强在径向上存在显著的不均匀分布；
5. 承受较大横向过载的固体火箭发动机，燃气中的凝相粒子对部分燃面形成显著的冲蚀作用，进而增大当地燃速；
6. 端面燃烧发动机的锥面效应。

图5- 2 串联双燃速装药示例

图5- 3 套装双燃速装药示意图

本章关注当药柱设计、燃烧物理过程较为复杂时，对固体火箭发动机进行装药及内弹道耦合分析的理论与方法。首先，基于平行层燃烧理论，研究复杂装药体素离散化分析方法，解决不考虑非均匀燃烧效应时复杂形式装药的分析问题；随后，进一步讨论非平行层装药燃烧几何分析问题，解决不均匀燃烧效应无法忽略时复杂形式装药的分析问题；最后，讨论将燃面退移与内弹道性能进行耦合分析的理论与方法，完成复杂装药发动机的内弹道性能预示。

5.1  复杂装药最短距离场分析方法

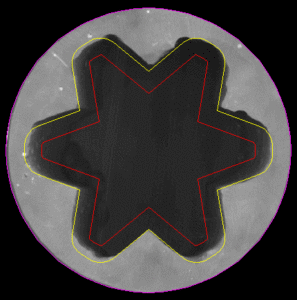
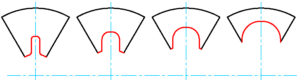
对于几何结构相对简单的药柱，平行层燃烧定理下燃面随退移过程的变化情况可以通过几何分析解算，典型的如端燃药、管状药、不包含椭球段的星形药等。图5- 4展示了某型星形药柱燃面退移几何分析。对于更为复杂的药柱（例如），理论上也可借助几何分析进行燃面-肉厚解算，但几何过程异常繁琐，且推导结果基本不具备通用性，故极少用于工程实践。

图5- 4 典型星形药柱的退移过程

因此，对于结构相对复杂的药柱，燃面退移过程的解算需要借助于计算机软件进行。实际用于发动机燃面退移计算的计算机程序可以分为实体造型法与数值方法两类。实体造型法即用Pro/E、UG、Catia等商业化三维参数化边界造型系统来模拟装药的平行层退移过程，以此来构造每一个肉厚状态下的药柱实体,提取并统计燃面和质量特性。实质上相当于自动构建一系列对应于燃烧不同时刻的CAD模型，这种方法具备较高的精度。然而，迄今为止,边界造型方法并不能稳定高效地处理自由曲面的包络问题。因此，基于实体造型的方法通常要求设计人员严格依照一系列设计规则来进行药柱设计，以此来尽可能地规避燃面自动推移过程中随时可能出现的特征消失和边界造型奇异点等造型错误，并在出现错误时进行人工修正。

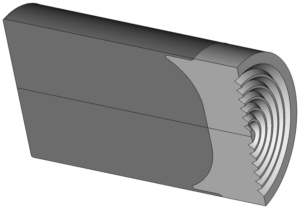
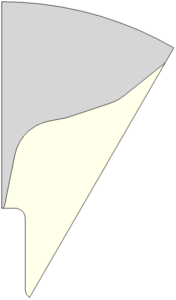
图5- 5 一种难以使用解析方法求解的药柱

（左：药柱    右：初始燃面）

数值方法通过将药柱离散为大量容易处理的基元进行计算。由于每一个基元的退移规律是明确的，算法流程相对简单。但是由于需要大量的基元才能用足够的精度模拟现实中的药柱，这类方法所需的计算量极大。这类方法又可以分为显式方法和隐式方法。显式将复杂几何形状离散为简单图元（如大量三角面片）进行处理，算法直观，但需要在编制算法时明确处理拓扑问题，相对来说算法仍比较复杂；隐式方法将所有几何表面转换为场函数中的等值面，通过操作场函数对等值面进行处理，从算法设计角度来讲最为简单，同时拥有足够的精度，但计算量通常比显式方法更大。目前实用的隐式方法主要指水平集（Level set）方法。

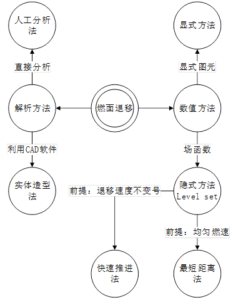
图5- 6 各种燃面退移计算方法的继承关系

水平集方法是处理各类曲面形状变化问题的通用方法，但其所需的计算量和储存空间都较大，为此人们开发了一些在特定前提下适用的快速方法。快速推进法是曲面演化速度恒不变号时可用的一种快速算法，显然药柱退移过程中速度方向不变，故该方法可用于燃面退移计算；但由于算法原理的限制，该方法难以进行并行结算；对于大多数药柱，可以假设燃速在整个燃面上均匀分布，故可以应用另一种快速算法：最短距离场法，该方法的计算量相对于水平集方法大大缩小，且可应用并行计算技术进一步提高计算速度。

本节主要研究使用最短距离场法进行复杂装药分析。我们知道，火焰在推进剂中传播的过程类似于惠更斯原理控制下波的传播过程。

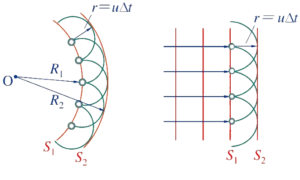
设想当前燃面上每一点都是波源，则下一时刻（时间\(\Delta t\)之后）燃面的形状是以当前燃面上每一点为球心、以\(r\Delta t\)为半径的所有球体的包络面。

图5- 7 火焰与波传播的相似性

反过来，容易知道新的燃面上的任意一点，距离上一时间步中燃面上任一点的距离均不小于\(r\Delta t\)，且上一时间步中燃面上必定有至少一个点与该点的距离恰为.这种场景下，\(r\Delta t\)称为该点到上一时间步中燃面的最短距离。

进一步，我们知道，对于任意药柱，设其初始燃面为B，则燃去肉厚e之后，此时的燃面（设为B’）上任意一点到B的最短距离为e.在药柱内部不存在阻燃材料的前提下，药柱中所有距离B的最短距离为e的点都在B’曲面上。换言之，B’曲面是所有到B的最短距离为e的、处于药柱内部的点的集合。

进一步，在药柱内部定义场函数\(\phi \left( {\vec{x}} \right)\)，使得各点上\(\phi \left( {\vec{x}} \right)\)的值等于点\(\vec{x}\)到B点的最短距离。显然，燃去肉厚e之后，燃烧表面的形状即为场函数\(\phi \left( {\vec{x}} \right)\)的一个等值面：

\(\left\{ \vec{x}|\phi (\vec{x})=e \right\}\)

实际计算中，场函数\(\phi \left( {\vec{x}} \right)\)定义在覆盖药柱的一个网格的所有结点上。这一网格可以是笛卡尔网格或柱坐标网格（如图5- 8）。柱坐标网格在计算回转体药柱时直观上更为自然，但实际上增加了计算复杂度，在精度上也没有特别的优势，故实际计算中更多使用的是笛卡尔网格。

图5- 8 隐式方法计算网格示例

经过以上讨论，计算特定燃烧肉厚下燃面面积的问题被分解为两个子问题：

1. 在每个网格点上计算场函数\(\phi \left( {\vec{x}} \right)\)的取值；
2. 对于给定的肉厚e，利用上述网格点上的\(\phi \left( {\vec{x}} \right)\)的取值构建对应的等值面。

直接计算场函数取值十分简单，仅需穷举组成B的各图元（一般是三角面片）并寻找距离最近的一个。然而, 这类通用的燃面计算方法主要的缺点是计算量十分巨大。例如, 将药柱离散成1024x256x256个体素点的条件下, 每一步燃面计算都需处理超过6700万个体素点, 即使在大型计算机上, 也需耗费大量的机时才能完成计算。为此，需要首先对组成B的各图元构建Voronoi图——这是一种计算机图形学中用于描述最短距离场的数学工具。每个图元在Voronoi图中对应于一片区域，该区域内所有点到本图元的距离小于其他任意图元，如图5- 9。这种方法避免了耗时的穷举测试，可以快速构建最短距离场函数。此外，目前该算法已被成功移植到基于GPU的大规模并行计算架构中，这意味着可以利用GPU提供的强大浮点运算能力，进一步加快距离场构建过程。

图5- 9 基于Voronoi图的空间剖分结果举例

在笛卡尔网格上，计算区域被划分为大量长方体微元。对于任一长方体微元，如果八个节点上\(\phi \left( {\vec{x}} \right)\)的取值同时存在大于e和小于e两种情况，则说明等值面通过该长方体。进而可以使用线性插值法定位燃面所在位置，如图5- 10，该方法称为Marching cubes算法。

图5- 10 构建等值面的Marching cubes算法

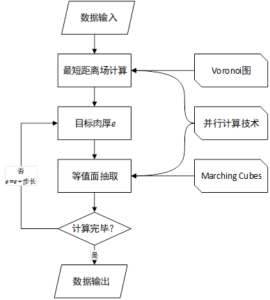
对每一个微元，使用Marching cubes算法进行微元抽取，抽取到的所有燃面微元（三角面片）的集合即为当前时刻的燃面形状，可用于进一步的燃面面积计算。改变计算过程中所用的e的取值并重复以上过程，即可获得整个工作过程中燃面的变化过程。图5- 11概括了使用最短距离场法进行燃面退移分析的一般流程框图。图5- 12展示了使用最短距离场法解算的图5- 5所示的复杂药柱的燃面退移过程。

图5- 11 最短距离场法执行流程

图5- 12 使用最短距离场法解算的复杂药柱燃面退移过程

5.1  非平行层装药燃烧几何分析

5.1.1          基于水平集方法的装药分析

当发动机装药受到强烈的、不可忽略的非均匀燃烧因素影响时，必须使用非平行层退移模型进行燃面推移分析。考虑精度、速度与普适性，这一过程一般基于常规水平集方法进行分析，其优势在于可以准确处理燃速在时间和空间上的不均匀性，能够自动处理拓扑变化，不仅可以用于对上文提到的多种非平行层退移药柱进行模拟，还可以用于对燃烧过程中突发裂缝等故障情形进行模拟。

值得说明的是，在不考虑沉积产物沉积的前提下，固体推进剂的燃速的符号（即燃面移动方向）显然是不变的，由图5- 6，该类情况也可基于快速推进法进行分析。但是，快速推进法本质上是一种串行算法，难以利用并行化技术对其进行加速；因此，虽然快速推进法的绝对运算量较常规水平集方法更低，但其耗时可能更高，在精度方面则不具有优势，因此本书主要讨论基于水平集方法的分析方法。

水平集方法是一种隐式描述移动界面的欧拉方法， 最早由 Osher 和 Sethian 在1988年引入。水平集方法仍然使用等值面思想来描述曲面，图5- 13展示了使用一个定义在二维网格上的距离场函数描述的圆形——即该函数的零等值线。

图5- 13 使用等值线描述的一个圆形

水平集方法相对常见显式方法的突出特征是其利用有向距离场（Signed distance field, SDF）中的零等值面来表达几何曲面。我们用零水平集\(\phi (x,y,t)=0\)来表示移动界面，而且希望界面上的点在移动过程中，始终在这个\(\phi (x,y,t)=0\)的零水平集上，则有：

\(\frac{d}{dt}\phi (x(t),y(t),t)=0\)

由链式法则，可得：

\({{\phi }_{t}}+{{\phi }_{x}}{{x}_{t}}+{{\phi }_{y}}{{y}_{t}}\text{ }=0  \)

\({{\phi }_{t}}+({{x}_{t}},{{y}_{t}})\cdot ({{\phi }_{x}},{{\phi }_{y}})\text{ }=0  \)

\({{\phi }_{t}}+\mathbf{V}\cdot \nabla \phi \text{ }=0  \)

其中\(\mathbf{V}=({{x}_{t}},{{y}_{t}})\)为曲面在每一点的运动速度矢量。该项意味着只有速度场\(\mathbf{V}(x,y,t)\)在水平集的法向方向分量才会影响水平集的移动，因此可以引入下面的法向速度场：

\({{V}_{\mathbf{n}}}=\text{V}(x,y,t)\cdot \frac{\nabla \phi (x,y,t)}{|\nabla \phi (x,y,t)|}.\)

由此将水平集方程的形式改写为：

\({{\phi }_{t}}+{{\mathbf{V}}_{\text{n}}}|\nabla \phi (x,y,t)|=0\)

上述公式中，V_n是推进剂燃速的体现，在不同问题中使用对应的方法对V_n赋值，即可解决多种非等距燃面退移问题。例如：根据推进剂的分布，为处在不同区域的网格节点赋不同的燃速数值，即可求解串装或套装药柱的燃面退移数据；根据流场仿真结果和侵蚀燃烧模型计算各点燃速并赋值给V_n，即可求解侵蚀燃烧环境下的燃面退移问题。

药柱的燃面退移问题中，显然曲面仅沿法向运动，则使用水平集法的方程为：

\({{\phi }_{t}}+r\left( x,y,z \right)|\nabla \phi (x,y,z,t)|=0\)

这是一个标量方程，很容易用数学方法求解。\(\left| \nabla \Phi (x,y,t) \right|\)一项，在标准的有向距离场中应该恒等于1，但非均匀速度场下，每一步之后该特征就会被破坏，需要进行重新初始化操作。重新初始化通过以下方程进行：

\({{\phi }_{t}}=\Delta \tau \ S\left( \phi  \right)\left( 1-\left| \nabla \phi  \right| \right)\)

\(S\left( \phi  \right)=\frac{\phi }{\sqrt{{{\phi }^{2}}+\Delta {{x}^{2}}}}\)

其中\(\Delta \tau \)为按CFL条件选定的不致使计算发散的虚拟时间项。在重新初始化过程中，需要迭代执行上述重新初始化方程，直到计算收敛，或者至少在零等值面附近收敛，才可以认为一次重新初始化完成。

对于速度场中存在强不连续点（面）的情况（如套装或串装药柱），由于每一步退移操作都会严重破坏距离场，故一般每一步退移运算后都需要执行一次重新初始化操作。因此，重新初始化过程经常是整个流程中消耗计算资源最大的步骤。对于退移速度场有弱不连续或者仅仅是不均匀分布的情况，重新初始化的频率可以适当减弱。

如果速度场是均匀的，则方程变为：

\({{\Phi }_{t}}+{{V}_{n}}=0\)

\(\Phi =C+t{{V}_{n}}\)

实际上，此时水平集方法退化为最小距离场方法。

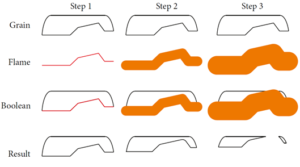
在实际使用中，我们并不直接利用水平集法跟踪燃面的变化，而是首先假定火焰可以向所有方向传播，使用水平集方法跟踪火焰前锋所扫过的“火焰域”的传播，随后通过布尔运算获得实际的药柱曲面，如图5- 14、图5- 15所示。这种做法最大程度地避免了计算过程中出现尖锐的形状（由于数值方法的固有问题，尖锐的形状将在计算中被抹平而产生误差）。

图5- 14 使用“火焰域”与布尔运算获得燃烧后的药柱形状

图5- 15 尖锐形状的出现与规避

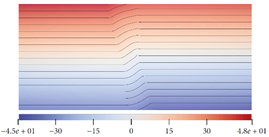
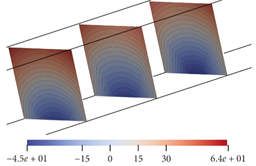
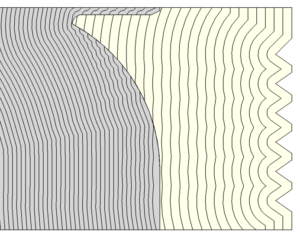
图5- 16展示了一个由两种推进剂组成的管状药柱。使用水平集方法对其燃面退移过程进行模拟，得到如图5- 17所示的结果。可以注意图5- 17右侧的三个距离场截面分别位于慢燃速区、交界面处与快燃速区。

图5- 16 示例双燃速装管状药柱

图5- 17 使用水平集法模拟双燃速管状药柱燃烧过程

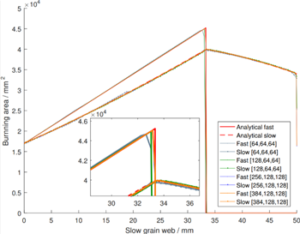
图5- 18 双燃速管状药柱的燃面-肉厚曲线

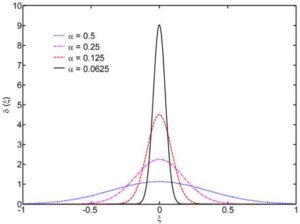
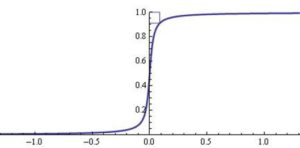
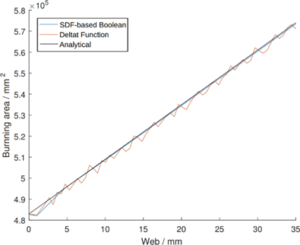
需要注意的是，在大量有关水平集的文献中，分别采用Delta函数（图5- 19）和Heaviside函数（图5- 20）来计算燃面面积和药柱体积是一种普遍现象，这种做法相当于根据每个节点的距离场函数值来决定其处在燃面上和药柱内部的“程度”。但经过实践，这种方法使用在有关固体火箭发动机的燃面抽取中时将引入微小的“波浪状”误差，如图5- 21所示（用Heaviside函数统计药柱体积引入的误差与此类似）。考虑到水平集方法得到的距离场函数与最短距离法得到的函数性质相同，因此仍然可以用上面提到的Marching cubes算法进行燃面抽取，该方法相对解析法的误差很小。

图5- 19 Delta函数

图5- 20 Heaviside函数

图5- 21 使用Delta函数统计燃面引入的误差

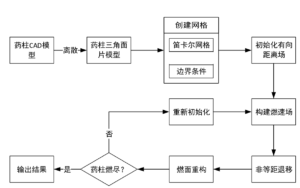
综上，使用水平集方法进行复杂装药燃面退移分析的流程可由图5- 22概括。图中每一步骤的意义如下：

• 使用CAD方法获得需仿真药柱的几何形状；为提高通用性，本文实践中采用离散的三角面片文件（STL格式文件或Wave front OBJ文件）作为输入，因此必须首先将药柱的几何形状离散为三角面片格式；主流的实体造型平台均支持此离散转换操作；
• 依据药柱的形状、大小和包覆形式等进行网格划分以及边界条件的设定；
• 对水平集方法进行初始化，即构建一个初始的有向距离场；
• 循环进行燃速场构建、燃面退移、燃面重构和重新初始化；“燃面重构”指从退移后的有向距离场中构建显式表达的燃面形状，并进行相关统计；
• 检测到药柱燃尽、发动机停止工作后，停止计算并输出结果。

图5- 22 使用水平集方法进行燃面退移仿真的流程框架

上述算法均基于笛卡尔网格构建。但是，如果需要进行燃面退移-有限元（传热、流体等）联合仿真，则笛卡尔网格与有限元计算中常用的贴体网格相比有一些比较明显的劣势，包括：

1. 精确描述复杂的边界条件比较困难；
2. 难以应用不同材料边界上的局部网格加密技术；
3. 难以处理多相材料间的相互作用（因为材料界面与网格界面不对齐）；
4. 在没有材料的位置也必须设置计算网格。

有限元计算中常用的贴体网格可分为结构网格和非结构网格。考虑到结构网格在网格自动划分、动态分割等方面的复杂性显著高于非结构网格，本章基于非结构网格进行燃面退移分析。非结构网格广泛用于各类物理仿真，包括传热、流场、结构仿真等。一般我们说到的非结构网格主要指是四面体（三维）或三角形（二维）网格。其特点是生成和处理都比较简单，多数情况下只需要很少的人工操作，便于实现全自动化的流程；缺点在于计算量大，计算精度相比结构化网格略低。非结构网格的发展相比结构网格略晚，但近些年随着计算能力的飞速提升，非结构网格也得到了长足进步，应用于非结构网格的高精度算法也在迅速发展之中。

传统上，水平集方法运行于笛卡尔网格上。通过一些底层改动，也可以将其运行在非结构网格上。由于任何结构网格都可以分裂为非结构网格，移植到非结构网格也就意味着结构网格可以使用类似的方法移植。

图5- 23 在药柱上划分的非结构网格

图5- 24 在非结构网格计算结构中抽取的燃面

详细讨论向非结构网格的移植涉及到较多关于微分方程数值求解的细节，这里不再详细讨论。有兴趣的读者可以参考《Robust Three-Dimensional Level-Set Method for Evolving Fronts on Complex Unstructured Meshes》和《3D level set methods for evolving fronts on tetrahedral meshes with adaptive mesh refinement》两篇文献。

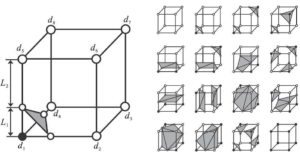
将水平集方法移植到非结构网格的主要目的是便于进行与其它有限元仿真的耦合。随着燃面退移的进行，燃面所在位置是变化的，即物理问题的几何边界发生了变化。为此，每一时间步结束时，需要对仿真网格进行修改，对现有网格的边界部分进行变形、切割、合并等操作，使其适应于新的流场边界。这种方法在程序设计上最为复杂，但计算量较小，大部分网格无需进行修改或插值操作。以四面体网格为例，如图5- 25，被燃面切分的四面体网格可能存在多种情况，可能需要将子网格划分为四面体、三棱柱等，三棱柱中处在燃面上的面可能是底面或侧面，需要对每一种情况进行单独处理。

下图5- 26展示了使用非结构网格上的水平集算法得到的嵌金属丝装药在起始阶段的燃面变化情况。

t=0.05s                 t=0.4s                 t=0.8s

t=1.5s                 t=2.2s                 t=2.5s

图5- 26 嵌金属丝装药燃烧起始阶段的燃面变化

5.1.1          基于二维实体造型法的装药分析

前文介绍了几种用于装药燃面退移计算的数值方法。可以看出，适应能力强的数值算法通常运算量也大，运算量相对较小的算法则适应范围较窄。同时，前文提到了基于CAD的实体造型法难以处理3D药柱的退移，更无法处理非等距退移。然而，对于二维药柱，CAD造型技术已经十分成熟，所以能够通过一些变通方法，利用二维CAD引擎计算2D药柱的等距甚至非等距退移。

图5- 27 复杂二维串装装药举例

图5- 28 复杂二维套装装药举例

基于二维CAD引擎的双燃速推移仿真算法是基于图形学中的偏移(Offset)和布尔运算(Boolean Operation)实现的。其中偏移操作是将一个面的边界（线框）沿着其法线方向向外扩大或向内缩小一定的距离，并形成新的线框与面。 在本算法中，偏移运算主要用于模拟燃面的推移。 布尔运算也被称为集合运算，是以集合论、拓扑学与拓扑流形学为基础，分为交、并、差三种运算，其作用为根据两个输入的几何体（基础几何体和工具几何体）生成一个新的几何体。 在本算法中，布尔运算主要用于计算燃烧对装药几何构型的影响。

假设速燃推进剂与缓燃推进剂的燃速不同， 但两种推进剂的燃速比恒定。同时，仿真推移步长恒定，速燃推进剂的推移步长（简称速燃步长）与缓燃推进剂推移步长（简称缓燃步长）之比等于速燃推进剂与缓燃推进剂的燃速比。对于每一种推进剂，将以下流程作为一个“推移步”：

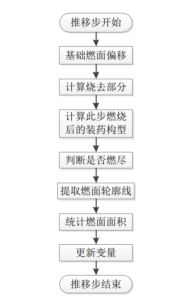
图5- 29 单个推移步的详细流程

图5- 29每个步骤的详细解释如下：

1. 对基础推移截面进行偏移操作：

• 对基础推移截面进行偏移操作，距离为速燃步长，得到速燃偏移截面；
• 对基础推移截面进行偏移操作，距离为缓燃步长，得到缓燃偏移截面；

2. 计算装药在此步烧去的部分，并计算装药在此步燃烧后的构型：

• 将速燃推进剂截面（简称速燃截面）与速燃偏移截面进行布尔交操作，得到速燃切除截面；
• 将速燃截面与速燃偏移截面进行布尔差操作，得到新的速燃截面；
• 将缓燃推进剂截面（简称缓燃截面）与缓燃偏移截面进行布尔交操作，得到缓燃切除截面；
• 将缓燃截面与缓燃偏移截面进行布尔差操作，得到新的缓燃截面；

3. 判断两种推进剂是否燃尽： 通过计算第 2 步得到的速燃和缓燃切除截面的面积分别判断两种推进剂是否已经燃烧完全，并设置算法状态量；
4. 分别提取两种推进剂的燃面轮廓线：

• 提取新速燃截面的线框；
• 将新速燃截面的线框与老速燃截面的线框做布尔差运算，得到速燃燃面轮廓线；
• 提取新缓燃截面的线框；
• 将新缓燃截面的线框与老缓燃截面的线框做布尔差运算，得到缓燃燃面轮廓线；

5. 将此步两种推进剂的燃面模型保存为BRep (Open CASCADE实现)或SAT (ACIS实现)格式，以便仿真后分析结果；
6. 根据第 4 步得到的轮廓线统计燃面面积，详见7 节；
7. 更新计算所用的变量，供下一个计算步使用：

• 将新速燃截面、新缓燃截面、新速燃截面线框、新缓燃截面线框分别赋值给速燃截面、缓燃截面、速燃截面线框和缓燃截面线框；
• 将速燃切除截面和缓燃切除截面的布尔并结果赋值给基础推移截面；

8. 重复第 1 至 7 步，直到第 3 步中判断结果为两种推进剂都燃烧完成。

双燃速装药燃面推移仿真的一大难点在于两种推进剂在燃烧过程中，其交界面会产生复杂的再生燃面，这个再生燃面的仿真是在目前能找到的公开文献中都没能很好解决的。 一种比较常见的简化解决方案是直接将串联双燃速装药的再生燃面当作圆锥面处理，但这种方法仅仅适用于不含复杂初始燃面且两种推进剂的交界线为直线的情况。对于套装双燃速装药，情况更为复杂，林小树提出可以推导出近似的变化规律，但这种方法也仅仅适用于交界面为与装药轴线同轴的圆柱面的情况。

图5- 30 双燃速装药再生燃面示意图

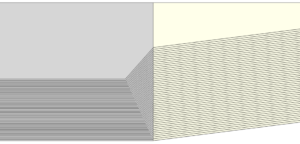
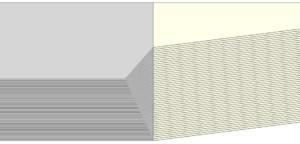
如果在燃面推移仿真中忽略了再生燃面，会导致过渡段及之后的仿真出现较大的误差。在上述退移步机制中，有一个比较核心的几何体——基础推移截面，这个几何体除了在第一次推移前包含的是用户输入的模型外，之后的推移步中此几何体都是由上一步速燃推进剂和缓燃推进剂被切除部分组成的，它实际上包含了两种推进剂最近一次燃烧推移的几何信息（分别由速燃基础推移截面和缓燃基础推移截面表示）。在推移算法中，如果能使速燃基础推移截面和缓燃基础推移截面分别对缓燃截面和速燃截面进行交叉影响，也就能实现速燃推进剂和缓燃推进剂的相互引燃。于是，算法在每一个推移步中都将速燃基础推移截面和缓燃推移基础截面重新合成为一个基础推移截面。 在算法第 2 步， 对缓燃截面与缓燃偏移截面进行布尔差操作时，上一步所产生的速燃基础推移截面会在缓燃偏移截面的几何构型上有所反映，并且通过这些多出的几何信息将缓燃推进剂“点燃”。这种思路解决了不同燃速推进剂相互点燃的过程。算法产生的再生燃面如图5- 31-图5- 32。显然，此算法可以很好地适应各种界面构型。

图5- 31 两种推进剂简单界面再生燃面

图5- 32 两种推进剂复杂界面再生燃面

5.1  燃面退移与内弹道性能耦合分析

固体火箭发动机内弹道性能分析实际上是求解固体火箭发动机内流场的过程。与常规的工程流体力学问题相比，固体火箭发动机内流场问题具备鲜明的“自耦合”特征：流场参数的变动可以直接、显著地影响到流场边界上的燃气生成率（燃速），且该过程的机理处在于流动范畴之外，受控于燃速模型而非流动模型，因此无法在纯流动模拟框架下解决；换言之，求解固体火箭发动机内流场问题的过程必然涉及与燃速模型的耦合计算。

在不关心发动机内部各处流动参数差异时，可以使用零维内弹道模型进行求解；此时，燃速模型与流动模型间的耦合可由解析方法描述，具体求解方法可参考零维内弹道模型的推导过程。当需要发动机内部的流动参数分布时，计算必须采用准一维或三维流动模型，此时燃面上各处的流动参数和燃气生成率均需要单独计算，无法如零维内弹道模型一样通过简单的解析方法得到能使计算稳定的流动参数，而必须使用数值方法进行迭代求解。本节主要以准一维流动模型为例，讨论这种情况下的燃面退移与内弹道性能耦合分析方法。三维流动模型下，耦合分析思路与下文讨论相同，但对求解初始条件的要求更高，收敛过程也更为困难。

首先，建立准一维稳态变截面加质流动模型。选择准一维流动模型的理由主要有两点：

• 工程应用对于计算耗时较为敏感，尤其是在可能涉及参数辨识的场景下；在三维网格上进行流场仿真所消耗的算力一般显著高于一维网格，同时，基于网格的方法所需计算量一般小于无网格法；
• 虽然当前的流场仿真技术技术已经比较成熟，但三维计算模式下仍经常需要手动调节计算设置才能使得计算收敛；相反，在绝大多数情况下，一维方法的整个计算过程不需要人工干预，可全自动进行，且对于参数辨识、优化设计用途而言具备足够的精度；

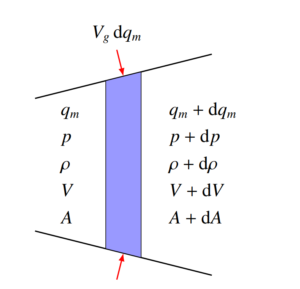
图5- 33 准一维加质流场微元示意图

如图图5- 33，在微元体上游，流入流量、压强、密度、速度和截面面积分别为q_m、p、ρ、V和A，这些物理量的单位均使用国际单位制；在微元体出口处，上述各参数则成为q_m+dq_m、p+dp、ρ+dρ、V+dV和A+dA。微元体侧面上加入的流量为dq_m，燃气离开药柱燃面的速度为V_g。考虑到燃气的密度远小于固体推进剂，在计算V_g时可以忽略燃面退移速度而使用以下公式：

\( {{V}_{g}}\rho {{A}_{b}}=r{{\rho }_{p}}{{A}_{b}} \)

\( {{V}_{g}}=\frac{{{\rho }_{p}}r}{\rho }\)

其中A_b为当前微元体边界上的燃面面积，ρ_p为固体推进剂的密度，r为当前微元体处的推进剂燃速。

对流量公式\({{q}_{m}}=A\rho V\)的两端在一维微元体上取微分，有：

\(\frac{\text{d}{{q}_{m}}}{{{q}_{m}}}=\frac{\text{d}\rho }{\rho }+\frac{\text{d}A}{A}+\frac{\text{d}V}{V}\)

考虑微元体各表面上压力的，略去高阶项，其合力为\(pA\text{ }-\text{ }\left( p+dp \right)\left( A\text{ }+\text{ d}A \right)\)，进而可以列出一维微元体上的动量方程：

\(pA-\left( p+dp \right)\left( A+dA \right)~~=\text{ }\left( {{q}_{m}}+d{{q}_{m}} \right)\left( V+dV \right)-{{q}_{m}}\text{ }V-d{{q}_{m}}{{V}_{\left\{ g|x \right\}}}\)

其中\({{V}_{\left\{ g|x \right\}}}\)为V_g的轴向分量。

令\(y={{v}_{\left\{ g|x \right\}}}/v\)，并将流量公式\({{q}_{m}}=A\rho V\)代入上式，可得：

\(\text{d}p+\rho V\text{d}V+\rho {{V}^{2}}(1-y)\frac{\text{d}{{q}_{m}}}{{{q}_{m}}}=0\)

整理上式，并利用声速公式消去密度项，得到如下动量方程：

\(\frac{\text{d}p}{p}+kM{{a}^{2}}\frac{\text{d}V}{V}+kM{{a}^{2}}(1-y)\frac{\text{d}{{q}_{m}}}{{{q}_{m}}}=0\)

不考虑多燃速药柱的情况时，新加入的燃气与来流具有相同的总焓，即：

\({{h}^{*}}={{c}_{p}}{{T}^{*}}={{c}_{p}}T+{}^{{{V}^{2}}}/{}_{2}={const}\)

对上式两边取微分，再利用\({{c}_{p}}=Rk\text{ }/\text{ }\left( k-1 \right)\)与声速表达式消去c_p，有：

\((k-1)M{{a}^{2}}\frac{\text{d}V}{V}+\frac{\text{d}T}{T}=0\)

状态方程的微分形式为：

\(\frac{\text{d}p}{p}=\frac{\text{d}\rho }{\rho }+\frac{\text{d}T}{T}\)

马赫数定义式的微分形式为：

\(\frac{\text{d}Ma}{Ma}=\frac{\text{d}V}{V}-\frac{1}{2}\frac{\text{d}T}{T}\)

将上述方程联立求解，可以得到如下结果：

\(\frac{\text{d}Ma}{Ma}=\frac{\left[ (k-1)M{{a}^{2}}+2 \right]\left[ \rho V\text{d}A+\text{d}{{q}_{m}}\left( kM{{a}^{2}}(y-1)-1 \right) \right]}{2\left( M{{a}^{2}}-1 \right){{q}_{m}}}\)

\(\frac{\text{d}V}{V}=\frac{\rho V\text{d}A+\text{d}{{q}_{m}}\left[ kM{{a}^{2}}(y-1)-1 \right]}{\left( M{{a}^{2}}-1 \right){{q}_{m}}}\)

\(\frac{\text{d}p}{p}=-\frac{kM{{a}^{2}}\left[ \rho V\text{d}A+\text{d}{{q}_{m}}\left( (k-1)M{{a}^{2}}(y-1)+y-2 \right) \right]}{\left( M{{a}^{2}}-1 \right){{q}_{m}}}\)

\(\frac{\text{d}T}{T}=-\frac{(k-1)M{{a}^{2}}\left[ \rho V\text{d}A+\text{d}{{q}_{m}}\left( kM{{a}^{2}}(y-1)-1 \right) \right]}{\left( M{{a}^{2}}-1 \right){{q}_{m}}}\)

上述结果表达式中的微分项均为沿轴线方向的微分，为无因次量，实际上是沿轴线移动一个微元体厚度后对应参数的变化量。相对于文献中不考虑通道截面积的控制方程组，上述结果表达式的右侧多出了dA项，但该项可以由通道的几何条件直接获得，并未增加数值求解的复杂度。

注意到以上推导结果式的右侧都可以变形为如下形式：

\(\mathbb{X}\frac{\text{d}A}{\left( M{{a}^{2}}-1 \right)A}+\mathbb{Y}\frac{\text{d}{{q}_{m}}}{\left( M{{a}^{2}}-1 \right){{q}_{m}}}\)

其中\(\mathbb{X}\)、\(\mathbb{Y}\)为仅含有k、Ma、y以及常数的表达式。

可以发现，当\(A\to 0\)时（例如燃面前端是嵌金属丝药柱所产生的锥面），以上推导结果式的左端项将具有较大的数值，即各物理参数将具有较大的变化率。测试表明，该情况下求解过程中的误差将更为显著，最终使得计算结果包含显著误差甚至得到物理上显然不合理的结果。必须使用合适的方式、顺序求解，才能得到合理的结果。

以下研究对上述推导结果的数值求解。观察推导结果可以发现，进行求解前，首先需要对上述燃面退移给出的几何数据进行一维离散和分割，并解算发动机中各个截面上的燃面面积与通气面积。此外，进行数值计算所需的一项关键数据dq_m，是未知量，其取值有赖于以当地压强（apⁿ燃速模型）、流速（侵蚀燃烧模型）等参数为输入的燃速模型计算结果。具备dq_m才能沿空间维度进行流动参数求解，但流动参数优势计算dq_m的必要条件。

为解决上述矛盾，前人提出了“尝试-校正”的求解模式，即假定发动机头部压强以计算头部截面状态，进而逐截面计算得到整个发动机内流场；然后，通过据此过程中得到的总流量数据估算发动机尾部压强，检查其是否与逐截面计算所得结果相同，如不同则进行相应的修正；这一过程反复迭代之后，即可得到合理的发动机头部压强的估计值。

考虑上文讨论过的当\(A\to 0\)时计算式左端项将具有较大的数值，进而影响计算精度的问题，本书认为，出于缩小前段误差的目的，应当采用从后端向前求解的路线，参照这一思路，事先假定的物理量应该是后端流量参数。首先假定后端流量，据此算得后端面的所有流动参数，随后逐截面向前计算。计算完成后，检查算得的前端面数据是否速度和流量为零的条件，并对假定的后端面数据进行对应的调整。显然，这一流程经过足够多次迭代后必然收敛。该流程可由图5- 34概括。

图5- 34 固体火箭发动机准一维内流场耦合求解流程

上述流程适用于内孔型装药或自由装填柱状药。对于工程中常见的自由装填管状药，在要求精度不高时，可以视作两个一维流场的组合，并允许求解过程中出现负速度（表征某一流道头部有向前的气流），以两个通道头部截面上质量交换符合质量守恒定律为校验标准，可采用类似上文方法求解。本章对该问题不做详细讨论，读者可自行参考文献《An Approach to Analyse Erosive Characteristics of Two-Channel Combustion Chambers》进行研究。

值得注意的是，在双流道发动机中，发动机工作接近结束时，将有大面积的燃面合并现象，即管形药柱局部或全部成为类似薄壁圆管的结构。本文研究发现，在这一阶段，当两临近燃面之间的间距小于单个网格边长时，燃面的抽取过程将受到干扰，在最终抽取得到的燃面中会存在异常的凹陷甚至破洞，如图5- 35所示。这一现象产生的本质原因是：由于两燃面过于接近，用于抽取某一燃面的部分网格节点中储存的其实是到另一燃面的有向最短距离。该问题是任何基于网格的隐式方法都无法避免的，而显式方法（如动网格技术）在该情况下也会因网格尺度的无限缩减产生类似问题；同时，这一问题仅在药柱即将燃烧完毕时出现，故可以通过一些近似处理手段，避免其干扰正常区域的计算，最终使得这一现象几乎不影响最终计算结果。