第四章 发动机结构分析方法

4.1 药柱结构完整性分析

药柱是固体火箭发动机的重要组成部分。药柱在整个工作期间，将受到诸如环境温度、点火压力、加速度等各种载荷的作用。当固体药柱承受外载荷作用时，因其拉伸模量低，故可能出现结构失效破坏。通常的结构失效破坏形式主要有两种：一种是药柱内部或表面产生裂纹，另一是种药柱—包覆层—绝热层—发动机壳体粘结面脱粘。这二者只要出现其一，就可能导致燃烧面积的突然增大，使燃烧室压力剧增，轻则改变发动机预定的推力特性，重则引起爆炸等灾难性事故。

药柱结构完整性分析就是保证在这些载荷的作用下，避免因大变形造成燃气壅塞，局部压力剧增等现象。而药柱是粘弹性物质，材料又具有近似不可压缩特性，都给有限元模拟带来困难。

4.1.1   药柱粘弹性力学理论

1）药柱粘弹性概述

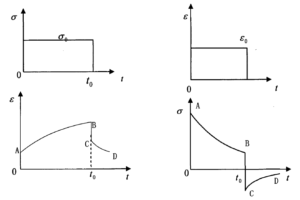
推进剂作为粘弹性材料，其力学性能与时间和温度有着明显的依赖关系。例如，在进行推进剂试件的拉伸试验中，对试件施加阶跃应力σ₀时，其应变响应如图1.1(a)所示。线段OA表示应变的瞬时弹性响应，曲线AB段表示由于推进剂大分子的伸屈和相互移动所引起的延迟弹性响应和流动响应即蠕变。当应力在t₀时突然移去时，应变立即减小BC，线段BC等于线段OA，其后应变沿曲线CD逐渐恢复，并残留少量因流动响应引起的残余应变。

同样，对试件施加阶跃应变ε₀时，其应力响应如图1.1(b)所示。线段OA表示应力的瞬时弹性响应，随后应力沿曲线AB逐渐衰减，即应力松弛。当在t₀时瞬间移去应变，则会有一个瞬时的应力降落BC，随后应力沿曲线CD逐渐松弛。

图 1.1 粘弹性力学模型

粘弹性材料的力学性质可以用一些力学模型来描述，通常,瞬时弹性响应用一个弹性系数为E的弹簧(虎克模型)来模拟，此时

\(\sigma \text{=}E\varepsilon \)

流动响应则用一个粘性系数为η的阻尼器(牛顿模型)来模拟，此时

\(\sigma \text{=}\eta \frac{d\varepsilon }{dt}\)

粘弹性材料的力学性质则可以用这两种元件的各种组合来模拟。

2）线性粘弹性本构关系的积分模型

粘弹性材料的力学行为与时间相关，因此，粘弹性应-应变方程应当描述其应力和应变的演变历程：不仅与当前的应力应变状态相关，而且还应反映出当前应力应变状态在后续时间的演变。

因此，粘弹性本构模型最恰当的表述是遗传积分型式，即Duhamel积分式。既可以应力松弛函数给出，也可以蠕变函数给出，这两种型式完全等价。

小变形情形下的线性粘弹性本构方程，一般以张量形式描述的应力松弛函数关系式给出：

\({{\sigma }_{ij}}\left( t \right)=\int\limits_{0}^{t}{{{G}_{ijkl}}\left( t-\tau  \right)}\frac{\partial {{\varepsilon }_{kl}}\left( \tau  \right)}{\partial \tau }d\tau +{{G}_{ijkl}}\left( t \right){{\varepsilon }_{kl}}\left( 0 \right)\)

上式中，应力松弛函数G_ijkl通常按Prony级数形式给出：

\({{G}_{ijkl}}\left( t \right)=G_{ijkl}^{\infty }+\sum\limits_{n=1}^{N}{G_{ijkl}^{n}}\exp \left( -\frac{t}{{{\lambda }_{n}}} \right)\)

其中，\(G_{ijkl}^{n}\)是第n个级数项的幅值，λ_n是对应第n项松弛时间，是时间常数，约定取正值。\(G_{ijkl}^{\infty }\)对应于无限长时间即完全松弛后的材料模量。

再定义时刻材料的瞬时弹性响应所对应的瞬时弹性模量为：

\(G_{ijkl}^{0}=G_{ijkl}^{{}}\left( 0 \right)\text{=}G_{ijkl}^{\infty }+\sum\limits_{n=1}^{N}{G_{ijkl}^{n}}\)

对应于广义麦克斯韦模型，上述公式可以表示成：

\({{\sigma }_{ij}}\left( t \right)=\sigma _{ij}^{\infty }\left( t \right)+\sum\limits_{n=1}^{N}{\sigma _{ij}^{n}}\left( t \right)\)

\(\sigma _{ij}^{\infty }\left( t \right)=G_{ijkl}^{\infty }{{\varepsilon }_{kl}}\left( t \right)\)

\(\sigma _{ij}^{n}\left( t \right)=\int\limits_{0}^{t}{G_{ijkl}^{n}}\exp \left[ -\frac{t-\tau }{{{\lambda }_{n}}} \right]\frac{\partial {{\varepsilon }_{kl}}\left( \tau  \right)}{\partial \tau }d\tau \)

针对与时间相关的粘弹性有限元分析，时间项按差商离散，设当前时间增量

步为[t_m-1,t_m]，时间增量步长为Δt=t_m-t_m-1，将上述本构模型改写成增量形式：

\({{\sigma }_{ij}}\left( {{t}_{m}} \right)=\left[ G_{ijkl}^{\infty }+\sum\limits_{n=1}^{N}{{{\beta }^{n}}\left( t \right)G_{ijkl}^{n}} \right]{{\varepsilon }_{kl}}-\sum\limits_{n=1}^{N}{{{\alpha }^{n}}\left( t \right)\sigma _{ij}^{n}\left( {{t}_{m}}-t \right)}\)

其中，

\({{\alpha }^{n}}\left( t \right)=1-\exp \left[ -\frac{t}{{{\lambda }_{n}}} \right]\)

\({{\beta }^{n}}\left( t \right)={{\alpha }^{n}}\left( t \right){{{\lambda }_{n}}}/{\left( t \right)}\;\)

还可进一步表示为：

\({{\sigma }_{ij}}\left( {{t}_{m}} \right)=\left[ G_{ijkl}^{0}+\sum\limits_{n=1}^{N}{\left\{ 1\text{-}{{\beta }^{n}}\left( t \right) \right\}G_{ijkl}^{n}} \right]{{\varepsilon }_{kl}}\left( {{t}_{m}} \right)-\sum\limits_{n=1}^{N}{{{\alpha }^{n}}\left( t \right)\sigma _{ij}^{n}\left( {{t}_{m}}-t \right)}\)

对于各向同性线性粘弹性材料而言，独立的材料参数只有两个。因为大多数粘弹性材料一般近乎不可压缩，所以通常取与时间相关的剪切模量G和体积松弛模量K：

\(G\left( t \right)={{G}^{\infty }}+\sum\limits_{n=1}^{N}{{{G}^{n}}\exp \left( -\frac{t}{{{\lambda }_{nd}}} \right)}\)

\(K\left( t \right)={{K}^{\infty }}+\sum\limits_{n=1}^{N}{{{K}^{n}}\exp \left( -\frac{t}{{{\lambda }_{n\nu }}} \right)}\)

对应地，各向同性粘弹性材料的瞬时剪切模量和体积模量分别为：

\({{G}^{0}}={{G}^{\infty }}+\sum\limits_{n=1}^{N}{{{G}^{n}}}\)

\({{K}^{0}}={{K}^{\infty }}+\sum\limits_{n=1}^{N}{{{K}^{n}}}\)

3）时温等效原理

粘弹性材料的材料参数以及力学行为都与温度密切相关。

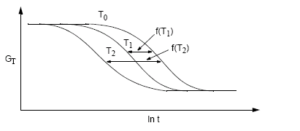
工程上，通常认为粘弹性材料符合热流变简单性假设，即满足时间-温度等效原理：形象地讲，温度升高相当于松弛时间延长，温度降低相当于松弛时间缩短。如图 1.2所示，从不同温度下松弛模量随时间变化的试验曲线上可以清楚看到：不同温度下的松弛曲线沿横轴向参考温度下的松弛曲线平移直至重合，平移距离相对温度呈固定的函数关系式。

图 1.2 不同温度下松弛模量随时间变化的试验曲线

因此，可以定义与温度相关的移位因子a_T，满足：

\(d\xi ={{a}_{T}}\left[ T\left( x,t \right) \right]dt\)

或者写成积分形式：

\(\xi \left( x,t \right)=\int\limits_{0}^{t}{\frac{d\tau }{{{a}_{T}}\left[ T\left( x,\tau  \right) \right]}}\)

从而将当前温度T下的时间t，变换为参考温度T₀下的等效时间x，使得：

\({{G}_{T}}\left( t \right)={{G}_{{{T}_{0}}}}\left( \xi  \right)\)

常用的移位因子函数式是Williams-Landel-Ferry方程，简称WLF方程，即：

\(\lg {{a}_{T}}\left( T \right)=-\frac{{{C}_{1}}\left( T-{{T}_{0}} \right)}{{{C}_{2}}+\left( T-{{T}_{0}} \right)}=-h\left( T \right)\)

于是，

\(\xi \left( t \right)=\int\limits_{0}^{t}{{{10}^{h\left[ T\left( \tau  \right) \right]}}}d\tau \)

这样一来就可以直接换算出不同温度下不同时刻对应的松弛模量。

4.1.1   药柱粘弹性参数获取

1）原理

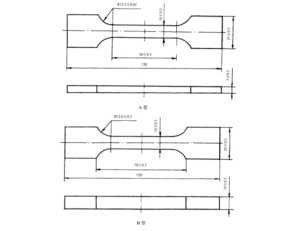
依照国军标GJB 770B-2005，对如图 1.3的试件采用单向拉伸试验法。在定应变下测量试样应力随时间的变化关系，求出应力松弛模量。用折合变量的数据处理方法，把在规定的时间范围和若干温度下得到的模量-时间曲线叠加成某一参比温度下的长时间范围的模量-时间曲线，这一叠加曲线即为应力松弛模量主曲线。

图 1.3 单向拉伸试件示意图

2）试验条件

试样不少于4个，在一般情况下，按以下规定条件进行试验：

1. 拉伸速度：500mm/min
2. 试验温度：70℃，50℃，25℃（或20℃），5℃（或0℃），-20℃，-40℃，特殊情况可增加温度点；
3. 预载荷：最大载荷的2%；
4. 初始恒定应变：5%；
5. 松弛应力测试时间：2s,4s,8s,20s,40s,80s,200s,600s,1000s,10000s(仅50℃时)

3）试验数据处理

表格 1‑1记录了某推进剂的单向拉伸试验数据。根据试验数据求出规定时间点的松弛模量值。

应力松弛模量按如下式子计算

\(E\left( t \right)=\frac{F\left( t \right)\left( 1+{{\varepsilon }_{0}} \right)}{A{{\varepsilon }_{0}}}\)

式中：

E(t)为t时刻的应力松弛模量的数值，单位为兆帕（Mpa）;

F(t)为t时刻的松弛力的数值，单位为牛（N）;

ε₀为松弛试验初始恒定应变；

A为试样工程标距段初始横截面积的数值，单位为平方毫米（mm²）。

表格 1‑1 各个温度下测得的药柱模量散点数据

试验温度（℃）	松弛时间t（s）
	2	4	8	20	40	80	200	600	1000
70	1.41	1.23	1.10	0.908	0.845	0.775	0.690	0.591	0.544
50	1.78	1.59	1.45	1.17	0.979	0.858	0.753	0.651	0.612	0.443
20	2.75	2.39	2.14	1.83	1.74	1.51	1.30	1.00	0.922
0	5.20	4.45	3.94	3.20	2.72	2.27	1.70	1.39	1.27
-20	6.16	5.29	4.73	3.85	3.52	3.10	2.48	1.95	1.84
-40	8.42	6.96	6.15	4.63	4.15	3.27	2.78	2.14	1.92

以表格 1‑1为基础算得的模量对数值见表格 1‑2。

表格 1‑2 药柱各个温度下的模量对数值

	lg(E*Ts/T)
lgt	70	50	20	0	-20	-40
0.30103	0.08083	0.20811	0.43933	0.74669	0.85329	1.02477
0.60206	0.02151	0.15908	0.3784	0.67905	0.78717	0.94206
0.90309	-0.027	0.11905	0.33041	0.62618	0.73857	0.88833
1.30103	-0.11031	0.02587	0.26245	0.53584	0.64917	0.76504
1.60206	-0.14154	-0.05153	0.24055	0.46526	0.61025	0.7175
1.90309	-0.17909	-0.10883	0.17898	0.38671	0.55507	0.614
2.30103	-0.22955	-0.16552	0.11394	0.26114	0.45816	0.5435
2.77815	-0.29681	-0.22873	0	0.1737	0.35375	0.42987
3	-0.3328	-0.25556	-0.03527	0.13449	0.32853	0.38276
4		-0.39591

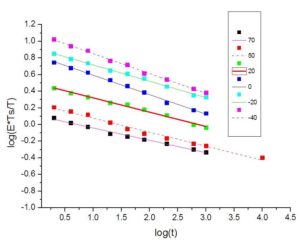
各个温度下的模量对数曲线见图 1.4。

图 1.4 多个温度下前装药新材料模量对数曲线

按照GJB 770B-2005中的方法进一步拟合得到不同温度下的模量对数曲线，由6条模量对数曲线通过作图法可得到6个温度偏移因子的对数值lgaT。以20℃为基准温度Ts，利用lgaT和当前温度与基准温度的差ΔT可以拟合出药柱的时温等效WLF方程。

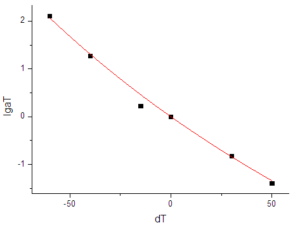
WLF方程的拟合曲线如图 1.5。

图 1.5 药柱的WLF方程拟合曲线

拟合得到的松弛模量prony级数方程相关参数见表格 1‑3。

表格 1‑3 新材料前药柱主曲线prony级数参数

i	0	1	2	3	4	5	6	7	8	9
Ei	0.2859	0.01	3.93705	2.66451	1.64912	1.08181	0.66944	0.43403	0.26984	0.19929
qi		0.00089277	0.35148968	0.23788059	0.14722918	0.09658121	0.05976587	0.03874908	0.0240	0.017792
λi		0.001	0.01	0.1	1	10	100	1000	10000	100000

拟合得到的WLF方程为