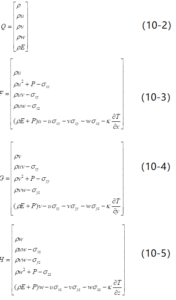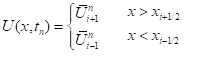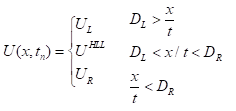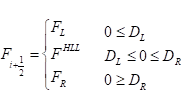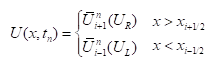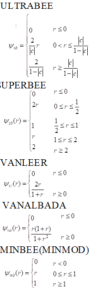第十章 固体火箭发动机数值模拟方法
固体火箭发动机工作过程复杂,涉及不可压流、可压流、多相流、气相与凝聚相燃烧、传质与传热、烧蚀、结构振动与破坏、流动与结构耦合等多个学科方向,是强烈的多学科交叉耦合。
固体火箭发动机研究过程中发动机点火试验是重要的研究手段。但试验周期长,经费多,特别是大型固体火箭发动机试验耗费特别多,在未经充分验证情况下,进行试验,如果失败,难以承受巨大的损失。对于空-空或地-空导弹飞行条件,特殊环境,存在较大的加速度,难以在地面进行真实条件下的试验模拟,需要开展数值模拟工作。同时发动机内工作环境恶劣,发动机内的高温高压燃气、金属颗粒燃烧和两相流运动都难以进行准确的实验测试。仅凭经验、半经验设计方法不能满足现代先进燃烧室的设计要求,因此数值计算已成为先进固体火箭发动机设计的有力工具。
10.1 控制方程
固体火箭发动机内流场可利用守恒型三维Navier-Stokes方程描述:
\(\frac{\partial Q}{\partial t}+\frac{\partial F}{\partial x}+\frac{\partial G}{\partial y}+\frac{\partial H}{\partial z}=S\) (10-1)
其中:
其中S为源相矢量。
10.2 计算方法
固体火箭发动机内流场参数变化剧烈,存在不可压流、可压流和高可压流(高马赫流动区域)。不同的流动区域具有不同的特点,因此其计算模拟方法也存在差异。对于不可压流的低马赫数流动,流体密度基本不变,压力则通过连续和动量方程求解,这种方法被称为基于压力的算法(Pressure-based algorithms)。对于高马赫数的可压流,通过连续方程求解密度,压力则通过状态方程和能量方程获得,这种算法称为基于密度的算法(Density-based algorithms)。
对于低马赫数流动,密度较低幅度的扰动都会导致压力场的较大变化,因此基于密度的算法在这种条件下容易出现不稳定和难以收敛。通过引入人工压缩技术(artificial compressibility technique)可以实现基于密度算法对不可压流的计算,并进一步通过引入矩阵预处理(preconditioning resulting stiff matrices)方法,避免了计算过程中刚性矩阵计算的困难。
流场的数值计算主要方法有有限差分和有限体积两种。有限差分方法将计算区域离散为多个网格点,在网格点上通过泰勒级数展开而得到计算格式。有限体积方法针对积分形式的控制方程,在计算区域上采用控制单元进行离散,这样保证了在每个控制单元上能够保证质量、动量和能量等基本物理量的守恒性。同时积分形式控制方程允许存在间断解,因此适用于流动中出现激波的计算,可以用于高马赫数流场计算。
采用有限体积方法时,当网格尺度有限,特别是计算区域复杂时,其可以比有限差分法更好地满足质量、动量和能量守恒定律。
10.2.1 不可压流计算方法
以二维不可压流的连续和动量方程为例:
\(\frac{\partial }{\partial x}(\rho uu)+\frac{\partial }{\partial y}(\rho \upsilon u)=\frac{\partial }{\partial x}\left( \mu \frac{\partial u}{\partial x} \right)+\frac{\partial }{\partial y}\left( \mu \frac{\partial u}{\partial y} \right)-\frac{\partial p}{\partial x}+{{S}_{u}}\)
\(\frac{\partial }{\partial x}(\rho u\upsilon )+\frac{\partial }{\partial y}(\rho \upsilon \upsilon )=\frac{\partial }{\partial x}\left( \mu \frac{\partial \upsilon }{\partial x} \right)+\frac{\partial }{\partial y}\left( \mu \frac{\partial \upsilon }{\partial y} \right)-\frac{\partial p}{\partial y}+{{S}_{\upsilon }}\)
\(\frac{\partial }{\partial x}(\rho u)+\frac{\partial }{\partial y}(\rho \upsilon )=0\)
方程求解的难度在于对压力的求解,压力梯度出现在了两个动量方程中,而没有单独求解压力的方程。在有限体积法计算中,计算控制容积界面上压力值时,需要采用相邻节点值进行计算。若计算区域离散为均匀网格,压力梯度项在控制容积界面处采用中心差分格式,则有:
\(\frac{\partial p}{\partial x}=\frac{{{p}_{e}}-{{p}_{w}}}{\delta x}=\frac{\left( \frac{{{p}_{E}}+{{p}_{P}}}{2} \right)-\left( \frac{{{p}_{P}}+{{p}_{W}}}{2} \right)}{\delta x}\)
\(\frac{\partial p}{\partial y}=\frac{{{p}_{N}}-{{p}_{S}}}{2\delta y}\)
从上式可以看出,节点P压力梯度与节点P处压力无关。因此,如果所有奇数网格点的压力是一个数值,而所有偶数网格点的压力是另一个值,即奇偶网格点的压力场呈现锯齿形变化,则方程中\(\frac{\partial p}{\partial x}\)和\(\frac{\partial p}{\partial y}\)计算结果处处为零,即压力梯度的影响在计算中不能体现,即“奇偶失连”。同时上述方程求解还存在着速度场与压力场相互耦合,如何实现高效迭代计算的困难。
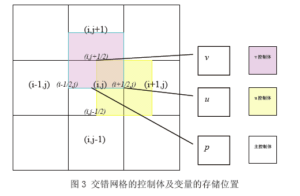
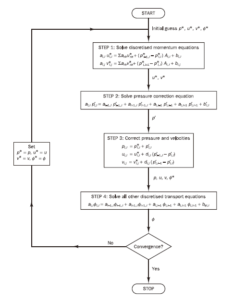
为了解决上述难题,目前常用的算法是在交错网格(图10-1所示)上采用Patankar和Spalding提出的个压力耦合方程的半隐式计算格式(Semi-Implicit Method for Pressure-Linked Equation),即SIMPLE算法,图10-2给出计算流程图。
SIMPLE方法的基本思想是:通过估计的压力场计算速度场的估计值;通过把离散的动量方程带入离散的连续方程计算速度和压力的校正量。
图10-1 交错网格示意图
图10-2 SIMPLE算法计算流程图
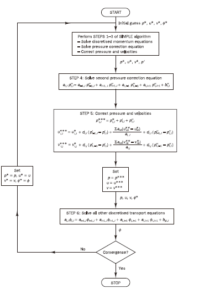
严格地说只适用于定常流动的计算。为了计算非定常流动,一般需要引入内迭代,即:从n时刻的流场出发,执行一次上述求解过程,把计算得到的u,v,p当作n+1时刻的第一次内迭代值,记为\({{u}^{n+1,(1)}},{{v}^{n+1,(1)}},{{p}^{n+1,(1)}}\)。然后把\({{p}^{n+1,(1)}}\)当作n+1时刻压力的改进的估计值,从n时刻的流场出发,再执行一次上述求解过程,把把计算得到的u,v,p当作n+1时刻的第二次内迭代值,记为\({{u}^{n+1,(2)}},{{v}^{n+1,(2)}},{{p}^{n+1,(2)}}\)。重复这个过程k次,直至\(\left\| {{{{p}’}}^{(k)}} \right\|\le \varepsilon \)为止。其中ε是我们给定的压力修正量的收敛指标。
图10-3 PISO算法计算流程图
近年来已有很多学者将SIMPLE算法扩展到适用于在同位网格上计算高速可压流动。
PISO(Pressue Implicit with Splitting of Operators)算法是用于求解非定常速度-压力耦合的可压缩稳定计算方法,后扩展成为求解可压、不可压、定常和非定常的计算方法。PISO算法包括一个预测计算步和两个校正计算步。
10.2.2 可压流计算方法
求解N-S方程计算方法通常是将对流项按Euler方程的离散方法处理,而粘性通量则以中心差分进行离散。解决好Euler方程的计算方法实际上是实现N-S方程计算的基础。求解Euler方程的空间离散数值格式通常分为迎风型和中心型两大类型。迎风型格式早期典型是Lax和Godunov格式,采用特征线构成计算格式。早期迎风格式只有一阶,计算精度较低且存在耗散性,使得激波在几个网格距离内被抹平,但迎风格式解是单调的,不会发生振荡。中心型格式具有二阶精度,能够较好地给出激波位置,但解不具有单调特性,在激波处会出振荡现象。如何建立一个既保持解的单调性,又具有高精度的数值格式成为计算流体力学的发展方向,也是研究的难点。
采用中心型格式计算会在间断处存在振荡,需要添加人工粘性项来消除这种振荡。如何合适地加入人工粘性就成了中心型格式的重要特征。
对于可压缩流动,面临的重要问题是如何处理好计算区域内可能出现的间断,即在流场中可能形成的激波。如何处理好这一问题是这类计算方法和核心。
对于Euler方程:
\(\frac{\partial U}{\partial t}+\frac{\partial F}{\partial x}=0\) (10-6)
我们采用有限体积方法离散上述方程。在任意控制体\([{{x}_{i-1/2}},{{x}_{i+1/2}}]\times [{{t}_{n}},{{t}_{n+1}}]\)上积分上式,有:
\(\int_{{{x}_{i-1/2}}}^{{{x}_{i+1/2}}}{[U}(x,{{t}_{n+1}})-U(x,{{t}_{n}})]dx+\int_{{{t}_{n}}}^{{{t}_{n+1}}}{[F(U({{x}_{i+1/2}},t))-}F(U({{x}_{i-1/2}},t))]dt=0\) (10-7)
令
\(\bar{U}_{i}^{n}=\frac{\int_{{{x}_{i-1/2}}}^{{{x}_{i+1/2}}}{U(x,{{t}_{n}})dx}}{\Delta {{x}_{i}}}\) (10-8)
\(F_{i-1/2}^{n}=\int_{{{t}_{n}}}^{{{t}_{n+1}}}{F(U({{x}_{i-1/2}},t))dt}\) \(F_{i+1/2}^{n}=\int_{{{t}_{n}}}^{{{t}_{n+1}}}{F(U({{x}_{i+1/2}},t))dt}\) (10-9)
其中\(\Delta {{x}_{i}}={{x}_{i+{1}/{2}\;}}-{{x}_{i-{1}/{2}\;}}\),则(10-7)式可以写为:
\(\frac{\bar{U}_{i}^{n+1}-\bar{U}_{i}^{n}}{\Delta t}+\frac{1}{\Delta x\Delta t}[F_{i+1/2}^{n}-[F_{i-1/2}^{n}]=0\) (10-10)
到目前为止整个过程是精确的。
控制体内气体状态平均值的变化是控制体界面上流通量的结果。因此要计算U的演化,关键问题是计算控制体界面上的F。
有限体积方法就是以这个积分关系式出发,把整个流场划分为许多小控制体,每个控制体和周围相邻的某个控制体共享一个界面,通过计算每个界面上的通量来得到相邻控制体之间的影响,一旦每个控制体的变化得到,就能够求解得到整个流场的变化。
假定有某种方法计算出控制体边界\({{x}_{i\pm 1/2}}\)处的通量积分\(F_{i\pm 1/2}^{n}\),则通过(10-10)式可以求解\(\bar{U}_{i}^{n+1}\),即有限体积法计算得到的是控制体内物理量在空间的平均值。即直接求得的只是\(\bar{U}_{i-1}^{1},\bar{U}_{i}^{1},\bar{U}_{i}^{1},\cdots ,\bar{U}_{i-1}^{n},\bar{U}_{i}^{n},\bar{U}_{i+1}^{n}\cdots \)。但是在计算通量时,需要知道U在处的值,即U沿的分布。
因此,在有限体积格式中,要解决的一个重要问题就是如何由\(U\left( x \right)\)在单元内的平均值\(\cdots ,{{\bar{U}}_{i-1}},{{\bar{U}}_{i}},{{\bar{U}}_{i+1}},\cdots \)求出一个函数\(\tilde{U}\left( x \right)\),使得\(\tilde{U}\left( x \right)\)近似\(U\left( x \right)\)到一定精度,并由\(\tilde{U}\left( x \right)\)获得\(U_{i+\frac{1}{2}}^{-}\)和\(U_{i+\frac{1}{2}}^{+}\),进而得到\(F_{i\pm 1/2}^{n}\)。
(1)重构计算
由\(\cdots ,{{\bar{U}}_{i-1}},{{\bar{U}}_{i}},{{\bar{U}}_{i+1}},\cdots \)得到\(U_{i+\frac{1}{2}}^{-}\)和\(U_{i+\frac{1}{2}}^{+}\)的过程称为重构(Reconstruction)。一种重要的常用方法就是假设流动状态在单元界面\({{x}_{i+1/2}}\)是不连续的,先计算出界面\({{x}_{i+1/2}}\)两边U的值,\(U_{i+\frac{1}{2}}^{-}\)和\(U_{i+\frac{1}{2}}^{+}\),再由它们用某种方法计算出\(F_{i+\frac{1}{2}}^{{}}\)。上述方法是非常重要的,是由Godunov在50年代首创的,后来被发展成为通用Godunov方法。最简单的重构是零阶重构:
\({{\left. \tilde{U}\left( x \right) \right|}_{x\in \left[ {{x}_{i-{1}/{2}\;}},{{x}_{i+{1}/{2}\;}} \right]}}\equiv {{\tilde{U}}_{i}}\left( x \right)={{\bar{U}}_{i}}\) (10-11)
即假定\(U\left( x \right)\)的近似值\(\tilde{U}\left( x \right)\)在每个控制体内均为常数,显然此时\(\tilde{U}\left( x \right)-U\left( x \right)=O\left( \Delta x \right)\)。这种重构方法得到的差分格式最多有空间一阶精度。一阶重构可以写为:
\({{\left. \tilde{U}\left( x \right) \right|}_{x\in \left[ {{x}_{i-{1}/{2}\;}},{{x}_{i+{1}/{2}\;}} \right]}}\equiv {{\tilde{U}}_{i}}\left( x \right)={{\bar{U}}_{i}}+{{k}_{i}}\left( x-{{x}_{i}} \right)\) (10-12)
其中ki为系数。采用零阶重构,因此所得到的格式只有一阶精度。在采用零阶重构时,由于认为每个控制体内均为常数,可以得到:
即在\[{{x}_{i\pm 1/2}}\],U(x,tn)存在间断。
Godunov假设的是每个小控制体内是均匀分布,也就是所谓分段常数(piecewise constant),所以后来有分段线性或者分段二次分布,如著名的MUSCL就采用了一次或者二次多项式,如果得到了这个多项式,就可以求出控制体i左右两个界面的一侧的值\(U_{i+\frac{1}{2}}^{-}\)和\(U_{i+\frac{1}{2}}^{+}\)。
求解\(U_{i+\frac{1}{2}}^{-}\)和\(U_{i+\frac{1}{2}}^{+}\)重构过程中,采用多项式的阶数越高,误差就越小。通常分段线性就能得到不错的结果,所以工程计算中大都采用这种方式,商用计算软件Fluent和Fastran以及NASA的CFL3D也采用这种求解方式。
(2)数值通量计算
在解决了数据重构问题后,下一步是进行通量\(\int_{{{t}_{n}}}^{{{t}_{n+1}}}{F(U({{x}_{i+1/2}},t))dt}\)的计算。Godunov采用了激波管问题精确黎曼解来计算\(F_{i\pm 1/2}^{n}\)。但精确解只适用于一维简单问题,为求解复杂流动问题,提出各种近似黎曼解,如Roe求解器、HLL求解器和Osher求解器等。以下对HLL和Roe求解器进行简单介绍。
1)HLL求解器
Harten等人研究后提出,(10-13)式的解可以近似写为下列形式:
(10-14)
其中DL、DR是Riemann问题的解中左波和右波运动速度的近似值。UHLL是与DL、DR有关的常数。(10-14)称为Riemann问题的HLL近似解。该近似认为Riemann问题左右波之间的区域不存在接触间断,为由左右两波分隔开的三个常数区域。
通过将积分关系式(10-7)并考虑(10-14),可以得到HLL近似中中间状态的守恒变量的值:
\({{U}^{HLL}}=\frac{{{D}_{R}}{{U}_{R}}-{{D}_{L}}{{U}_{L}}+{{F}_{L}}-{{F}_{R}}}{{{D}_{R}}-{{D}_{L}}}\) (10-15)
定义:\({{F}_{L}}=F({{U}_{L}}),{{F}_{R}}=F({{U}_{R}})\)
\({{F}^{HLL}}=\frac{1}{2}({{F}_{L}}+{{F}_{R}})-\frac{1}{2}[{{D}_{R}}({{U}_{R}}-{{U}^{HLL}})-{{D}_{L}}({{U}^{HLL}}-{{U}_{L}})]\) (10-16)
从(10-16)式可以看出,\(\frac{1}{2}[{{D}_{R}}({{U}_{R}}-{{U}^{HLL}})-{{D}_{L}}({{U}^{HLL}}-{{U}_{L}})]\)起着格式粘性的作用。因此,根据守恒律直接确定通量,可以更好的体现格式粘性的影响,且通过选取适当的DL、DR也可以对格式粘性进行直接控制。一般而言,在单元界面\({{x}_{i+1/2}}\)处,数值通量为:
(10-17)
这样,就得到了(10-10)式中数值通量的一种基于HLL近似Riemann 解的计算方法。
计算DL, DR 的方法,由下式给出:
\({{D}_{L}}={{u}_{L}}-{{a}_{L}},\ \ \ \ \ {{D}_{R}}={{u}_{R}}+{{a}_{R}}\) (10-18)
一种稳定性更好的取法是:
\({{D}_{L}}=\min ({{u}_{L}}-{{a}_{L}},{{u}_{R}}-{{a}_{R}})\)
\({{D}_{R}}=\min ({{u}_{L}}+{{a}_{L}},{{u}_{R}}+{{a}_{R}})\)
(10-19)
HLL格式具有正定性,满足离散熵条件,其缺点是格式粘性较大,对接触间断的分辨率较低。后续研究者发展了HLLC求解器,进一步提高了计算精度。
2)Roe求解器
考虑扩张一维守恒型Euler 方程 :
\(\frac{\partial U}{\partial t}+\frac{\partial F}{\partial x}=0\) (10-20)
对于Riemann间断问题
(10-21)
对应的拟线性形式为:
\(\frac{\partial U}{\partial t}+A\frac{\partial F}{\partial x}\) \(A(U)=\frac{\partial F}{\partial U}\) (10-22)
Roe方法处理过程是在计算单元中利用左右函数的常数态UL、UR构造一个合理的常矩阵\(\tilde{A}({{U}_{L}},{{U}_{R}})\),用于近似原来的Jacobi矩阵,这样能够将复杂的非线性问题转换为线性问题,将拟线性方程(10-8)转换为线性方程
\(\frac{\partial U}{\partial t}+\tilde{A}({{U}_{L}},{{U}_{R}})\frac{\partial F}{\partial x}\) (10-23)
矩阵\(A(U)\)的左、右特征向量为\(L(U)\)和\(R(U)\),则\(A=R(U)\Lambda L(U)\)。由于\(\tilde{A}({{U}_{L}},{{U}_{R}})\)在形式上与\(A(U)\)相似,则有
\(\tilde{A}=R(\tilde{U})\tilde{\Lambda }L(\tilde{U})\) (10-24)
其中\(\tilde{U}\)可按下式计算得到
\(\overset{\tilde{\ }}{\mathop{u}}\,=\frac{\sqrt{{{\rho }_{L}}}{{u}_{L}}+\sqrt{{{\rho }_{R}}}{{u}_{R}}}{\sqrt{{{\rho }_{L}}}+\sqrt{{{\rho }_{R}}}}\)
\(\overset{\tilde{\ }}{\mathop{v}}\,=\frac{\sqrt{{{\rho }_{L}}}{{v}_{L}}+\sqrt{{{\rho }_{R}}}{{v}_{R}}}{\sqrt{{{\rho }_{L}}}+\sqrt{{{\rho }_{R}}}}\) (10-25)
\(\overset{\tilde{\ }}{\mathop{H}}\,=\frac{\sqrt{{{\rho }_{L}}}{{H}_{L}}+\sqrt{{{\rho }_{R}}}{{H}_{R}}}{\sqrt{{{\rho }_{L}}}+\sqrt{{{\rho }_{R}}}}\)
\({{\overset{\tilde{\ }}{\mathop{a}}\,}^{2}}=(\gamma -1)\left( \overset{\tilde{\ }}{\mathop{H}}\,-\frac{1}{2}({{\overset{\tilde{\ }}{\mathop{u}}\,}^{2}}+{{\overset{\tilde{\ }}{\mathop{v}}\,}^{2}}) \right)\)
Roe格式的数值通量可按下式计算得到:
\({{F}_{i+\frac{1}{2}}}=\frac{1}{2}(F({{U}_{L}})+F({{U}_{R}}))-\frac{1}{2}{{L}^{-1}}\left| {\tilde{\Lambda }} \right|L({{U}_{R}}-{{U}_{L}})\) (10-26)
(3)TVD格式
TVD(Total Variation Diminishing)格式即总变差减小(不增)格式。所谓总变差,是衡量函数的光滑性的一种指标,其定义为:
\(TV=\int_{-\infty }^{\infty }{\left| \frac{\partial u}{\partial x} \right|}dx\) (10-27)
在离散点上,\({{u}^{n}}=\{u_{i}^{n}\}\),有:
\(TV({{u}^{n}})=\sum\limits_{i=-\infty }^{\infty }{\left| u_{i+1}^{n}-u_{i}^{n} \right|}\) (10-28)
如果数值方法可以使得TV不随时间增加,即
\(TV({{U}^{n+1}})\le TV({{U}^{n}})\) (10-29)
那么可以称为是总变差减小TVD格式。
定义:TVD格式
\(u_{i}^{n+1}=H(u_{i-r+1}^{n},…,u_{i+s}^{n})\) (10-30)
TVD格式具有保单调性,所以在间断附近不会出现非物理振荡。
根据这一条件,可以构造精度高于一阶的TVD格式。下面介绍构造TVD格式的思路。
方程\(\frac{\partial u}{\partial t}+\frac{\partial f(u)}{\partial x}=0\),\(f(u)=au\)的差分格式为:
\(u_{i}^{n+1}=u_{i}^{n}+\frac{\Delta t}{\Delta x}\left[ {{f}_{i-\frac{1}{2}}}-{{f}_{i+\frac{1}{2}}} \right]\) (10-31)
如果(10-31)具有TVD性质,记此时的数值通量为\(f_{i+\frac{1}{2}}^{TVD}\)。即
\(u_{i}^{n+1}=u_{i}^{n}+\frac{\Delta t}{\Delta x}\left[ f_{_{i-\frac{1}{2}}}^{TVD}-f_{_{i+\frac{1}{2}}}^{TVD} \right]\) (10-32)
如果要求格式具有高于一阶精度,则\(f_{i+\frac{1}{2}}^{TVD}\)可以写成:
\(f_{i+\frac{1}{2}}^{TVD}=f_{i+\frac{1}{2}}^{LD}+{{\varphi }_{i+\frac{1}{2}}}\left[ f_{i+\frac{1}{2}}^{HI}-f_{i+\frac{1}{2}}^{L0} \right]\) (10-33)
其中\(f_{i+\frac{1}{2}}^{L0}\)是某一阶格式的数值通量,\(f_{i+\frac{1}{2}}^{HI}\)是二阶格式的数值通量。\({{\varphi }_{i+\frac{1}{2}}}\)称为通量限制器。我们希望选择合适的\({{\varphi }_{i+\frac{1}{2}}}\),使格式在光滑区具有二阶精度。当采用三点格式时,\(f_{i+\frac{1}{2}}^{L0}\),\(f_{i+\frac{1}{2}}^{HI}\)可写成如下一般形式:
\(f_{i+1/2}^{L0}={{\alpha }_{0}}au_{i}^{n}+{{\alpha }_{1}}au_{i+1}^{n}\)
\(f_{i+1/2}^{HI}={{\beta }_{0}}au_{i}^{n}+{{\beta }_{1}}au_{i+1}^{n}\) (10-34)
\(f_{i+\frac{1}{2}}^{L0}\)可以有多种取法,如取
\({{\alpha }_{0}}=\frac{1}{2}\left( 1+s \right),{{\alpha }_{1}}=\frac{1}{2}\left( 1-s \right)\) (10-35)
时,\(f_{i+\frac{1}{2}}^{L0}\)为一阶迎风格式的数值通量,其中\(s=sign(a)\)。
当取:
\({{\alpha }_{0}}=\frac{1}{2c}\left( 1+c \right),{{\alpha }_{1}}=-\frac{1}{2c}\left( 1-c \right)\)
时,\(f_{i+\frac{1}{2}}^{L0}\)对应的差分格式为Lax-Friedrichs格式。注意,上式中\(c=\frac{a\Delta t}{\Delta x}\)。
二阶精度的三点格式只有Lax-Wendroff格式,即:
\({{\beta }_{0}}=\frac{1}{2}\left( 1+c \right),{{\beta }_{1}}=\frac{1}{2}\left( 1-c \right)\) (10-36)
把(10-34)式代入(10-33)式,有
\(f_{i+\frac{1}{2}}^{TVD}=[{{\alpha }_{0}}+({{\beta }_{0}}-{{\alpha }_{0}}){{\phi }_{i+\frac{1}{2}}}](au_{i}^{n})+[{{\alpha }_{1}}+({{\beta }_{1}}-{{\alpha }_{1}}){{\phi }_{i+\frac{1}{2}}}](au_{i+1}^{n})\) (10-37)
下面为几种常用的通量限制器\(\psi (r)\):
不同的限制器的性能有一定差别。\(\psi (r)\)越大,格式的耗散越小,对激波的分辨率越高。但是,\(\psi (r)\)过大,数值结果中可能出现一些异常现象。如正弦波可能变为方波的形状,甚至可能导致计算失稳。对于定常流动的计算,使用光滑的限制器容易收敛到较小的残差。
10.2.3 湍流模型
目前处理湍流计算有三种方法:直接数值模拟(DNS)方法,大涡模拟(LES)方法和雷诺平均N-S(RANS)方法。其中RANS方法已广泛应用于工程计算,而LES方法也逐步走进工程实际应用中。
雷诺平均N-S方程的思路是将湍流瞬时运动分解为平均运动和脉动两部分。将脉动运动部分对平均运动的影响通过雷诺应力项来模化,即通过湍流模型来封闭雷诺平均N-S方程能够求解,对雷诺应力做出各种假设,给出各种经验和半经验本构关系。从对模型处理的出发点不同,可以分为雷诺应力模型和涡粘性模型。
雷诺应力模型即所谓二阶矩模型,是从雷诺应力满足方程出发,将方程未知项用平均流动的物理量和湍流特征尺度表示得到。由于保留了雷诺应力所满足的方程,可以较好地反映雷诺应力随空间和时间的变化规律。但此模型保留方程组较多,计算量较大。
另一种类型是粘性涡模型,是由Boussinesq仿照分子粘性的思路提出。根据引入的附加微分方程数量可分为零方程模型、半方程模型、一方程模型和两方程模型。常见的一方程模型为Spalart-Allmaras(SA)模型,两方程模型为K-e和k-w模型。
大涡模拟(LES)的基本思想是通过对湍流运动的过滤将湍流分解为可解尺度湍流(包含大涡脉动)和不可解尺度湍流运动(包含所有小尺度脉动),可解尺度湍流运用数值计算方法直接求解,小尺度湍流脉动的质量、动量和能量输运对大尺度运动的作用采用建立亚格子模型的方法从而使可解尺度运动方程封闭。
湍流大涡模拟的主要理论观点是,将空间几何区域通过网格划分为直接求解部分与建模求解部分,依据是湍流能谱分布、串级理论和涡粘性假设,认为流体的宏观剪切运动形成雷诺应力张量,进而形成大尺度的旋涡,通过湍流能量串级输运,大涡破碎成小涡,小涡呈现出各向同性的趋势,并进行能量的耗散,能量是从大到小单向传递的。大于空间网格尺度的旋涡直接求解,而旋涡尺度小于空间滤波尺度时,LES中称为亚格子尺度(SGS:Sub-grid Scale),被近似认为是各向同性,其湍流运动能量占湍流全部能量的很小部分,可通过类似于RANS中提出的涡粘性假设进行模化求解。从LES提出至今,这种求解观点对于单纯的流动问题,经过多年的实践检验,可行性和通用性已经得到验证。
10.3 数值模拟软件和计算策略介绍
10.3.1 数值模拟软件介绍
1.FLUENT软件
FLUENT软件是由美国FLUENT Inc公司于1983年建立,基于有限体积方法和结构及非结构网格的通用化计算流体软件。计算方法分为基于压力和基于密度两个部分。基于压力的求解器包含SIMPLE、SIMPLEC、PISO和Coupled算法。差分格式包括一阶和二阶迎风、中心差分、三阶MUSCL和QUICK格式等。基于压力的求解器包含Roe和AUSM方法,差分格式包括一阶和二阶迎风和三阶MUSCL格式。湍流模型包括Reynolds应力模型(RSM)、S-A模型、标准k-ε模型、RNGk-ε模型、k-ω模型、k-ωSST模型。多相流模型VOF、Euler-Euler模型和Euler-Lagrange方法,包含粒子蒸发、破碎和聚合过程。燃烧模型包括有限速率模型、Eddy-Dissipation模型、EDC模型、PDF模型预混燃烧模型。辐射模型包括P1、ROSSELAND、DTRM、DO和S2S。2007年FLUENT软件被Ansys公司收购,成为Ansys软件平台的一个产品,可以通过Ansys Workbench平台实现FLUENT和Ansys的流/固耦合分析。
2.CFX软件
CFX软件采用有限体积法,实现在非正交曲线坐标进行离散。在同位网格上采用SIMPLE和SIMPLEC算法,具有QUICK、CONDIF、MUSCL及高阶迎风格式。代数方程求解包括线迭代、多重网格和块隐式方法。湍流模型包括标准k-ε模型、RNGk-ε模型、低Reynolds k-ε模型、k-ω模型、代数应力模型及微分应力模型和大涡模拟等。可计算包括可压缩及不可压缩流动、多相流动、耦合传热与燃烧化学反应、多种气体燃烧和动力学模型。还包括滑移网格等处理涡轮叶片流动的模型。2003年CFX软件被Ansys公司收购,目前与FLUENT一样同为Ansys公司产品。
3.CFD++软件
CFD++是美国Metacomp Technologies 公司的流体力学模拟软件。CFD++可以有效的解决流体力学问题中的可压流(任何马赫数)和不可压流,包括单组分和多组分流动、化学反应流动、多相流、稳流和非稳流、旋转机械、热传导、多孔介质等等。一阶、二阶和三阶的湍流方程,结合经典的壁面方程,可以精确的捕捉壁面附近的流体压缩参数、压力梯度、热传导等各种湍流特性。一方程:Rt模型、SA模型。两方程:Realizable k-ε模型、非线性(cubic)k-ε模型、k-l、q-l模型、SST模型。三方程:Realizable k-ε-Rt模型、k-t-fμ模型。七方程非线性RSTM LES、混合LES/RANS(LNS)和R-γ转捩模型。计算格式包括:三维TVD重构、显式时间格式达到四阶精度、隐式时间格式二阶精度、有限体积法、稳态快速收敛、瞬态快速计算、双时间步长、先进的多重网格技术。
10.3.2 数值计算的基本策略
1.网格生成
网格的质量对数值计算结果有着重要的影响,所以对网格生成应给予重视。
(1)生成网格可采用成熟的网格生成软件,如ICEM、Gridgen、Gambit、Patran等软件。
(2)从CAD软件生成的构型转换到网格生成软件时,需注意格式转换过程中产生的拓扑结构错误,应及时修正。在不影响主要计算区域的前提下,对微小尺寸结构进行优化或忽略。
(3)在计算之前应对网格质量进行检查,如偏斜度(skewness)、宽高比(aspect ratio)、最小表面面积(minimum face area)和网格正交性(grid orthogonality)。这些参数会严重影响计算精度,甚至会使得计算发散,尤其是采用高阶计算格式的条件下。如果存在网格质量问题,需要针对存在的问题重新生成网格。
(4)在物理量变化剧烈的区域应增加网格密度,直到继续增加网格数量对计算结果影响程度在可接受范围之内。
2.初始条件和边界条件
(1)好的初始条件会使得计算更加稳定并具有更好的收敛性,所以初值最好是接近真实的物理结果。
(2)可以利用简单计算和较粗糙网格的计算结果来获得初步计算结果作为计算初值。
(3)例如计算湍流前,可通过层流计算结果作为湍流计算的初值。如果计算燃烧流场,首先将冷态流场计算结果作为燃烧计算初值。计算非稳态问题,如果对初始的瞬间过程不感兴趣,则可以将稳态计算结果作为非稳态计算的初值。
3.计算过程
(1)可以在计算过程中改变差分格式、高阶格式和松弛因子等参数。
(2)计算初始阶段可使用低阶格式保证计算的稳定性,之后再改为高阶格式,提高计算精度。
(3)对于精度较高的非稳态计算CFL数应小于1.0,对于LES计算CFL数应小于0.6左右。
(4)如果对初始阶段的瞬态过程是关注的重点,那么应该选用高阶的离散格式和严格的收敛限。
(5)如果从稳态计算结果开始非稳态计算,那么难以得到初始瞬态的准确计算结果。
(6)不能仅依靠残差来判断计算是否收敛,还应监视计算重点区域的物理量(压力、马赫数、阻力等)是否达到平衡,以及计算区域内进出口流量是否达到平衡。
10.4 固体发动机数值模拟应用
10.4.1 两相流数值模拟和燃烧不稳定大涡模拟
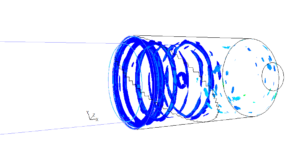
随着对大型分段式固体火箭发动机研究的深入和超细铝粉的使用,低频燃烧不稳定又成为高性能固体发动机研制面临的重要问题。通过国内外研究发现流动不稳定——声学——两相流动——推进剂燃烧反馈的耦合反馈是燃烧不稳定的形成的主要原因。针对燃烧不稳定过程中的障碍涡脱离和转角涡脱离开展了大涡模拟研究。
图10-4 障碍涡脱离计算结果
通过大涡模拟计算获得了障碍下游区域大尺度旋涡脱落、运动和碰撞的详细结构及发展过程。计算结果同时显示压强振荡的振幅随着潜入式喷管背壁区空腔体积的增大而线性增大,且背壁区空腔体积比其入口形状对压强振荡振幅的影响大。
图10-5 转角涡脱离
燃烧室的台阶扩张比、台阶上下游的管流长径比是影响两类旋涡脱落现象形成的重要结构参数。台阶上游长径比主要是对边界层稳定性产生影响,大长径比结构下边界层容易失稳、卷吸,形成近壁面拟序结构。而台阶下游长径比主要对旋涡的发展扩散产生影响,如果下游长径比较大,脱落旋涡经过较长距离的耗散并导致流场湍流强度增加,因此规律的相干涡结构难以发展至下游喷管。
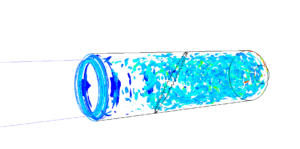
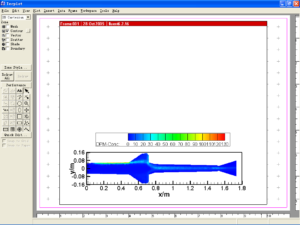
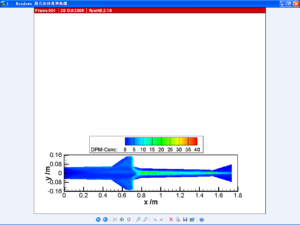
下图为美国Illinois大学开展了多相流大涡模拟计算结果,其中大粒径粒子采用Lagrangian模型计算,小粒径粒子采用Eulerian方法计算。获得了发动机内铝和铝氧化物粒子运动的详细过程及其与气相的耦合关系,为精细化分析燃烧不稳定、传质传热、烧蚀和流固耦合提供了有力的工具。
图10-6 多相流大涡模拟模拟
10.4.2 发动机高过载模拟
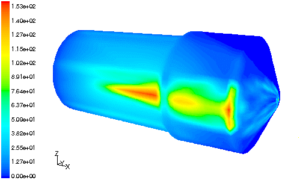
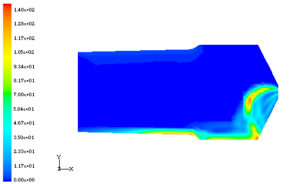
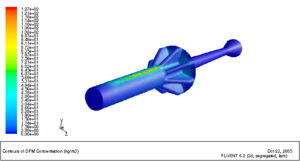
固体火箭发动机在某些工作状态下会在较大的过载下工作。燃烧室内的氧化铝粒子在大过载条件下会形成聚集,粒子浓度大幅度增加形成稠密两相流。这种高温稠密粒子流会对燃烧室内绝热层形成强烈冲刷,破坏发动机热结构。由于发动机内两相流动通过实验测试难度极大,所以数值模拟成为较好的分析手段。图10-7为高过载条件下燃烧室内粒子浓度分布。通过数值模拟获得了粒子浓度的空间分布,在过载方向粒子浓度远大于其他区域,并且部分粒子与壁面碰撞后发生反弹。这些粒子聚集并与壁面碰撞的区域就是烧蚀严重的位置。图10-8为过载条件下长尾管发动机粒子浓度分布,为长尾管发动机设计提供了依据。
图10-7 过载条件下燃烧室内粒子浓度分布
图10-8 过载条件下长尾管发动机粒子浓度分布
10.4.3 点火瞬态过程
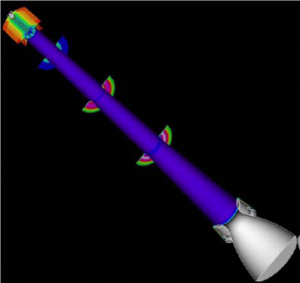
固体火箭发动机点火瞬态过程存在较大的冲击载荷,对发动机工作可靠性存在明显的影响。对于大型发动机的点火瞬态研究虽然开展了大量理论分析和缩比实验,但仍存在一定局限性。随着数值模拟能力的提高,开展大型发动机全尺寸点火瞬态的流固耦合分析成为可能,为发动机设计提供了新手段。图10-9为美国伊利诺斯大学针对航天飞机助推器开展的点火瞬态过程计算。通过全尺寸非稳态流固耦合计算,获得了点火过程中燃气对推进剂的瞬态传热和点火过程,并分析了点火压力冲击对推进剂结构的影响,为点火可靠性评价提供了依据。图10-10为意大利罗马大学针对Zefiro 16发动机开展了点火瞬态分析计算,获得了点火过程中点火燃气在燃烧室内的传播过程,并揭示了在点火过程中出现压力振荡的原因。
图10-9 大型火箭助推器发动机点火过程
图10-10 发动机点火瞬态过程
10.4.4 推进剂燃烧详细计算
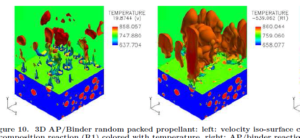
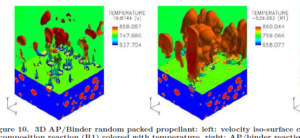
常规的发动机数值计算中假设推进剂燃烧非常迅速,认为进入燃烧室内已是燃烧完成的燃气,忽略了推进剂的详细燃烧过程。近年来随着燃烧不稳定研究中对推进剂动态燃烧过程的关注以及发动机在复合交变载荷下燃烧性能的研究,对推进剂详细燃烧过程的数值模拟逐渐受到重视。图10为美国佐治亚理工大学开展了AP与粘结剂燃烧过程的详细计算结果。获得不同压力下推进剂多尺度燃烧退移过程,并且与实验数据吻合良好,为推进剂细观精细化研究奠定了很好的基础。
图10-11 推进剂燃烧详细计算