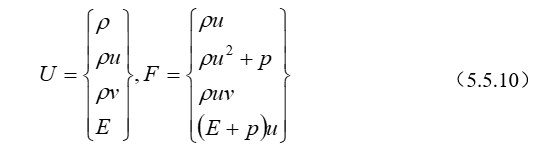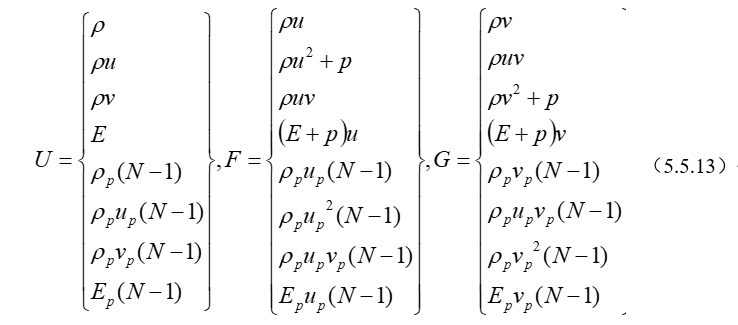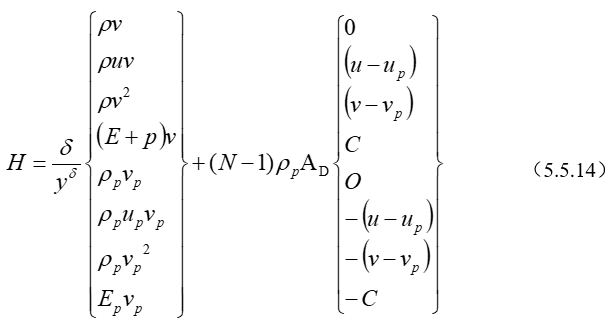第五章 固体火箭发动机的流动方程
5.1 引言
固体火箭发动机的主要部件是燃烧室和喷管。相对于喷管,发动机燃烧室中燃气流动有两方面明显特征,其一,由于固体推进剂的燃烧,燃烧室中的燃气流动是加质流动,而喷管燃气流动一般很少考虑加质,某些喷管的热防护壁面会产生少量挥发气体,但它们对主流的影响是微不足道的;其二,燃烧室内由于装药燃面的退移,燃气通道的形状和截面面积是不断变化的,而喷管中由于烧蚀导致的热防护壁面退移量相对整个喷管截面来说很小,一般可忽略其对流动的影响,除了喷管喉径变化较大时要适当考虑外,一般流动计算不予考虑。因此,对喷管可以采用相对于惯性坐标系的刚性控制体;对燃烧室必须采用边界可变的控制体,而且在控制面上有质量向控制体内渗透。根据这两个不同的特点,喷管和燃烧室中的流动必须用有区别的方程来描述。
固体火箭发动机中的燃气成份与推进剂的种类密切相关。目前,固体火箭发动机广泛采用含铝复合推进剂,含铝推进剂燃烧产物中含有相当数量的Al2O3粒子,使燃气成为气固两相的流动。两相流计算一般还需要用纯气相流动或“两相平衡流动”的计算结果作为其迭代计算的初场。所谓“两相平衡流动”,就是把两相燃气看作为一种拟单相的完全气体,它的比热比和气体常数按气相和粒子相的含量折算。因此必须考虑纯气相流动和两相流动两种控制方程。
本章首先讨论喷管中的纯气相流动方程,然后讨论燃烧室中的纯气相流动方程,再此基础上,再简单讨论两相流动方程。事实上,由于结构和所考虑的因素的不同,不可能将控制方程写得包罗万象或千篇一律,我们只能针对最常用和较简单的状态来建立方程,为研究发动机内多维流动问题奠定一定的基础。
5.2 喷管纯气相流动方程
在气体动力学一维流动理论中,曾经讨论过喷管的一维等熵流动。采用一维假设来研究喷管中的流动,计算简单,物理概念清晰,这对初学者掌握概念和在工程问题中开展定性分析十分有用。然而,当喷管截面变化比较急剧时,流场中的参数就明显偏离一维分布,按一维流动确定的流量、音速面、出口速度、推力等就会出现较大偏差,难以满足现代火箭发动机研制需求。因此,对于计算精度要求较高,特别是要求有各点分布参数的喷管流场,需采用多维流动理论来描述求解。对大多数火箭发动机喷管来说,其流场接近二维轴对称条件。
喷管多维流动的控制方程,可以采用固定形状惯性控制体的控制方程来描述。在符合绝热、无粘、无外功和不考虑体积力的情况下,它们为连续、动量、能量或音速方程、熵方程,并以状态方程作为补充。在均熵流条件下,熵方程恒满足;有时能量方程用音速方程来代替。因此,喷管纯气相流动控制方程的矢量形式为:
连续方程
\(\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \overline{V})=0\)(5.2.1)
动量方程
\(\rho \frac{D\bar{V}}{Dt}+\nabla p=0\) (5.2.2)
能量方程
\(\rho \frac{D}{Dt}(h+\frac{{{V}^{2}}}{2})=0\) (5.2.3)
或音速方程
\(\frac{Dp}{Dt}-{{a}^{2}}\frac{D\rho }{Dt}=0\) (5.2.4)
状态方程
\(p=\rho RT,h={{C}_{p}}T\) (5.2.5)
它在笛卡尔坐标系和圆柱坐标系中的表达式,以及在二维轴对称流下的表达形式,都包括在表3.2中。其中表3.2中的方程是针对定常流动,对于非定常流动,还需要引入\(\frac{\partial ()}{\partial t}\)项。因此,我们将喷管常用的轴对称流动方程列出如下,其余不再赘述。它们为:
连续方程
\(\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x}(\rho u)+\frac{\partial }{\partial x}(\rho v)+\delta \frac{\rho v}{y}=0\) (5.2.6)
对平面流动,δ=0;对轴对称流动,δ=1。
动量方程
\(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\frac{1}{\rho }\frac{\partial p}{\partial x}=0\) (5.2.7)
\(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+\frac{1}{\rho }\frac{\partial p}{\partial y}=0\) (5.2.8)
能量方程
\(\frac{\partial }{\partial t}(h+\frac{{{V}^{2}}}{2})+u\frac{\partial }{\partial x}(h+\frac{{{V}^{2}}}{2})+v\frac{\partial }{\partial y}(h+\frac{{{V}^{2}}}{2})-\frac{1}{\rho }\frac{\partial p}{\partial t}=0\) (5.2.9)
或音速方程
\(\frac{\partial u}{\partial t}+u\frac{\partial p}{\partial x}+v\frac{\partial p}{\partial y}-{{a}^{2}}\left( \frac{\partial \rho }{\partial t}+u\frac{\partial \rho }{\partial x}+v\frac{\partial \rho }{\partial y} \right)=0\) (5.2.10)
状态方程
\(p=\rho RT,h={{C}_{p}}T\) (5.2.11)
以上方程组适用于非定常流动,对于定常流动,方程组中所有\(\frac{\partial ()}{\partial t}\)项等于零。
从数学上看,描述轴对称喷管流动的控制方程组属于一阶拟线性偏微分方程组。所谓“一阶”,是指方程中只含有未知函数的一阶偏导数;所谓“拟线性”,是指方程对未知函数来说是非线性的,而未知函数的偏导数来说是线性的。由于方程本身的性质和复杂的边界条件,求解喷管流场控制方程的解析解十分困难,一般采用数值方法获得数值解。
在定常流情况下,方程组(5.2.6)~(5.2.10)对应于亚音速流动区、跨音速流动区、超音速流动区分别是椭圆型、抛物型、双曲线型。对就不同类型的方程组,数值求解方法也不同。跨音速流动区的偏微分方程组是混合型的,它在一个狭小的流动区域内,顺着流动由亚音速到音速到超音速,方程由椭圆型转变为抛物型,再转变为双曲型,因此增加了求解难度。
对于双曲线型方程,存在两条实特征线,且下游的流动参数不能逆流上传,它的求解方法可以用相对简便和精确的向前步进方法—特征线法求解。对于定常跨音速流的数值计算,目前常采用时间相关法来进行,即取对应非定常流动方程经过足够长时间后的渐近解作为定常跨音速流场的解。而对于非定常跨音速流动,其控制方程是双曲型的,求解时避免了像混合型那样类型的变化。
轴对称定常流控制方程在亚音速流动区是椭圆型的,也可以用非定常流方程(双曲型)来求解。鉴于此,将方程(5.2.6)~(5.2.10)写成非定常的形式。
方程(5.2.6)~(5.2.10)使用的范围是绝热、无粘、无外功和不计体积力的情况,对流动是否有旋无限制。在无旋流动情况下,可以采用更简化的气动方程和无旋流条件,它们的矢量形式为:
\((\bar{V}\cdot \nabla )\left( \frac{{{V}^{2}}}{2} \right)-{{a}^{2}}(\nabla \cdot \bar{V})=0\) (5.2.12)
\(\nabla \times \bar{V}=0\) (5.2.13)
气动方程是在无旋条件下由连续、动量和音速方程合并简化而得,其中只有速度一个变量,音速a在无旋条件下也是速度的单一函数,因此 这一组方程就简单得多。
在轴对称情况下,方程(5.2.12)、(5.2.13)为:
\(({{u}^{2}}-{{a}^{2}})\frac{\partial u}{\partial x}+({{v}^{2}}-{{a}^{2}})\frac{\partial v}{\partial y}+2uv\frac{\partial u}{\partial y}-\delta \frac{{{a}^{2}}v}{\partial y}=0\) (5.2.14)
\(\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}=0\) (5.2.15)
式中,对于轴对称流,\(\delta =1\) ;对于平面流,\(\delta =0\)。音速a对完全气体,有
\({{a}^{{{*}^{2}}}}={{a}^{2}}+\frac{\gamma -1}{2}=const\) (5.2.16)
对于采用端面燃烧装药的固体火箭发动机,喷管中的流动可以看成是无旋流。液体火箭发动机在燃烧室头部喷嘴排列均匀的情况下,比较接近均匀的无旋流场。但靠近壁面处,由于保护室壁的需要,常常偏于富燃料,因此近壁处与中心处的燃烧条件有差别,流线之间存在焓梯度,是有旋流动。
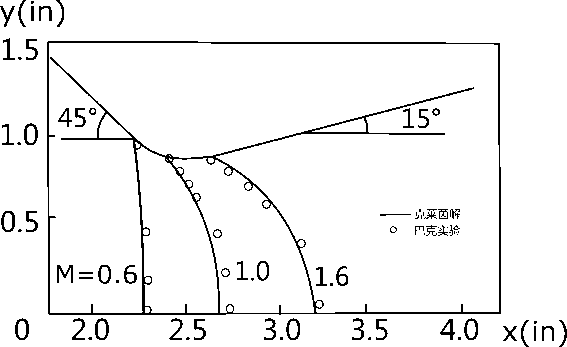
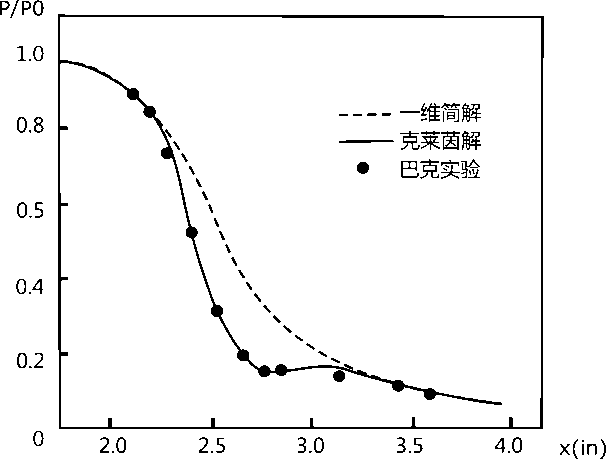
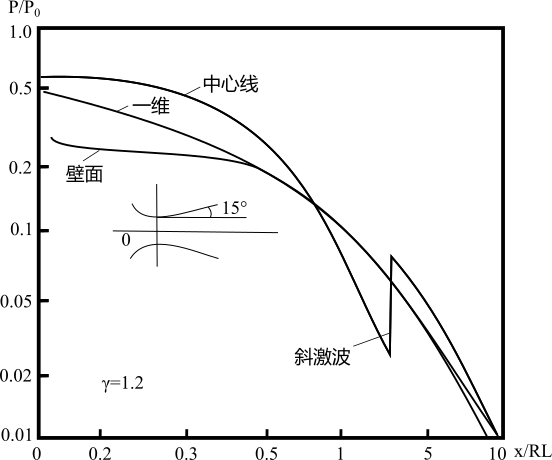
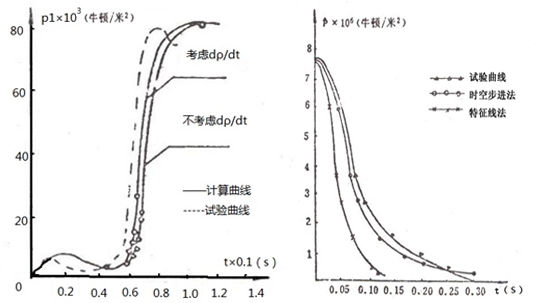
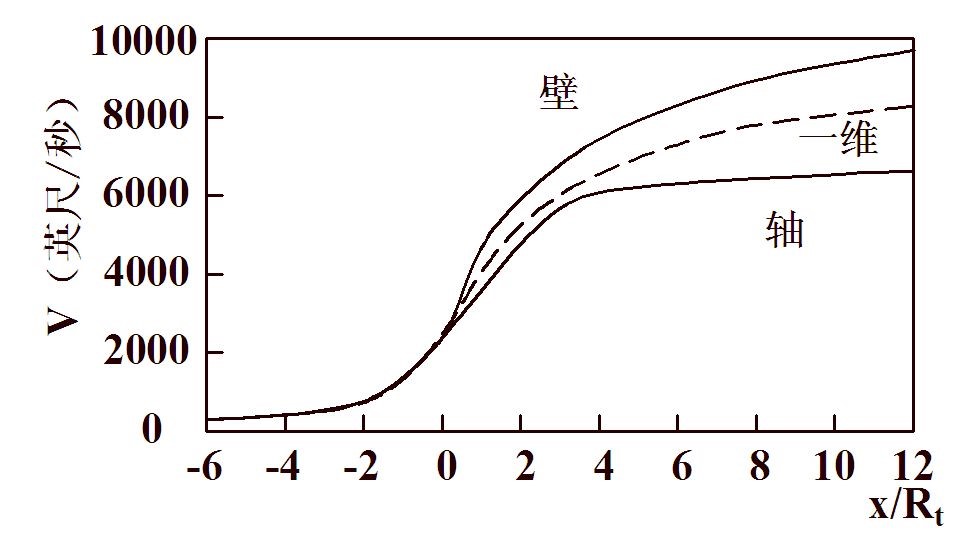
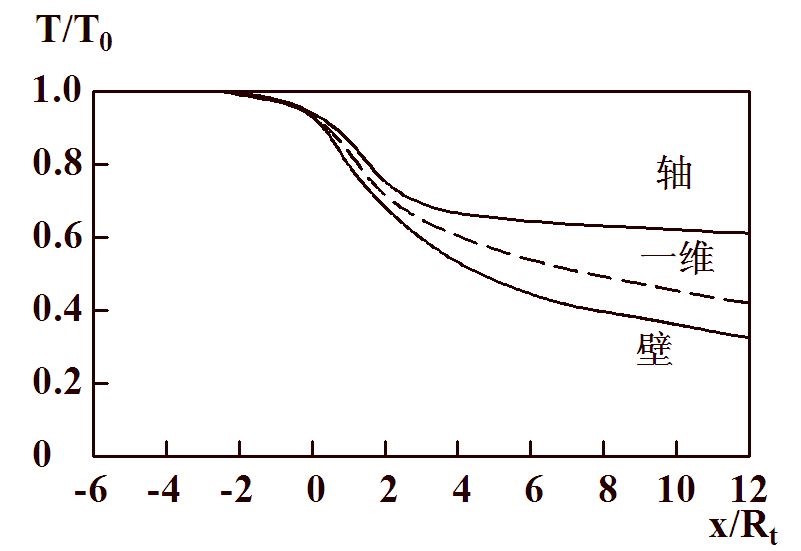
为了说明轴对称流动计算与一维流动计算结果的差别,图5-1给出了部分计算结果。
(a)锥形喷管中的等马赫线分布
(b)壁面压力比分布与一维解的比较
(c)壁面和轴上气流马赫数的分布
(d)壁面和轴上压力比的分布
(e)锥形喷管中的压力分布
图5-1 轴对称喷管的部分计算结果
5.3 燃烧室纯气相流动方程
在固体发动机燃烧室中,由于装药燃面的退移,燃气流通通道的形状是变化的。如果取燃气通道的周界为控制面,由它围成的空间为控制体,则控制面和控制体的形状是变化的。
在第二章,我们推导了任意外延参数N的瞬时时间变化率,方程为:
\(\frac{DN}{Dt}=\frac{\partial }{\partial t}\int_{{{V}_{c}}}{n\rho d{{V}_{c}}}+\int_{A}{n\rho \bar{V}\cdot d\bar{A}}\) (5.3.1)
对于形状固定的惯性控制体,偏导数可移至积分号内,即:
\(\frac{DN}{Dt}=\int_{{{V}_{c}}}{\frac{\partial (n\rho )}{\partial t}d{{V}_{c}}}+\int_{A}{n\rho \bar{V}\cdot d\bar{A}}\) (5.3.2)
而对于形状可变的控制体,对应于方程(5.3.1)等号右边第一项,在△t时间内,容积\({{V}_{c}}\) 中参数的变化量为:
\(\Delta \int_{{{V}_{c}}}{n\rho d{{V}_{c}}=}\int_{{{V}_{c}}}{\frac{\partial (n\rho )}{\partial t}d{{V}_{c}}\Delta t+\int_{A}{n\rho \bar{U}\cdot d\bar{A}\Delta t}}\)
式中,\(\bar{U}\) 为某一瞬时控制面上任一点的运动速度矢量。上式除以△t并取极限,可得:
\(\frac{\partial }{\partial t}\int_{{{V}_{c}}}{n\rho d{{V}_{c}}=}\int_{{{V}_{c}}}{\frac{\partial (n\rho )}{\partial t}d{{V}_{c}}+\int_{A}{n\rho \bar{U}\cdot d\bar{A}}}\) (5.3.3)
对应于方程(5.3.1)等号右边的第二项,考虑到控制面运动速度\(\bar{U}\)总是使气流速度\(\bar{V}\)产生相反的效应,这时应为:
\(\int_{A}{n\rho (\bar{V}-\bar{U})\cdot d\bar{A}}\) (5.3.4)
因此,在控制体形状变化时,结合(5.3.3)和(5.3.4),任意外延参数N的时间变化率为:
\(\frac{DN}{Dt}=\int_{{{V}_{c}}}{\frac{\partial (n\rho )}{\partial t}d{{V}_{c}}}+\int_{A}{n\rho \bar{U}\cdot d\bar{A}}+\int_{A}{n\rho (\bar{V}-\bar{U})\cdot d\bar{A}}\)
进一步得到控制体形状变化时,任意外延参数N的时间变化率为:
\(\frac{DN}{Dt}=\int_{{{V}_{c}}}{\frac{\partial (n\rho )}{\partial t}d{{V}_{c}}}+\int_{A}{n\rho \bar{V}\cdot d\bar{A}}\) (5.3.5)
即对于可变控制体,任意外延参数N的时间变化率与其在刚性控制体时具有相同的表达形式。
(5.3.5)式中的A是全部控制面,在燃烧室中即为通气面AP和装药燃烧侧面积Ab。设\({{\rho }_{mp}}\) 为推进剂密度,r为燃速,\(\rho \)为燃气密度,则垂直于装药燃烧侧面的燃气的注入速度
\({{v}_{B}}=\frac{{{\rho }_{mp}}}{\rho }\) (5.3.6)
将(5.3.5)式应用于发动机燃烧室,为
\(\frac{DN}{Dt}=\int_{{{V}_{c}}}{\frac{\partial (n\rho )}{\partial t}d{{V}_{c}}}+\int_{{{A}_{p}}}{n\rho \bar{V}\cdot d\bar{A}}-\int_{{{A}_{b}}}{n\rho {{v}_{B}}\cdot dA}\) (5.3.7)
利用(5.3.7)便可推导连续、动量和能量方程。
在质量守恒关系中,内涵参数n=1,因此连续方程为:
\(\int_{{{V}_{c}}}{\frac{\partial \rho }{\partial t}d{{V}_{c}}+}\int_{{{A}_{p}}}{\rho \bar{V}\cdot d\bar{A}=\int_{{{A}_{b}}}{\rho {{v}_{B}}dA}}\) (5.3.8)
在动量守恒关系中,\(n=\bar{V}\) ,因此动量方程为:
\(\int_{{{V}_{c}}}{\overline{B}\rho d{{V}_{c}}-}\int_{{{A}_{p}}}{pd\bar{A}-\int_{{{A}_{b}}}{pd\bar{A}}}=\int_{{{V}_{c}}}{\frac{\partial (p\overline{V})}{\partial t}D{{V}_{c}}+\int_{{{A}_{p}}}{\bar{V}(\rho \bar{V}\cdot d\bar{A})}}\)(5.3.9)
需要注意的是,在推导动量方程中,由质量\(-\int_{{{A}_{b}}}{n\rho {{v}_{B}}dA}\) 项产生的动量是可以忽略的,理由如下:
在燃面上由于质量渗透而产生的动量为
\(-\int_{{{A}_{b}}}{n\rho {{v}_{B}}dA}=-\int_{{{A}_{b}}}{\rho ({{v}_{B}}-r){{v}_{B}}dA=-\int_{{{A}_{b}}}{\rho {{v}_{B}}^{2}\left( 1-\frac{\rho }{{{\rho }_{mp}}} \right)dA}}\)
式中,\(\rho /{{\rho }_{mp}}\) 约为百分之一,因此,\(1-\frac{\rho }{{{\rho }_{mp}}}\approx 1\);同时,在装药通道中,\(\rho {{v}_{B}}^{2}\ll p\) ,因此这一项产生的动量可以忽略。
在能量守恒关系中,\(n=e+\frac{{{V}^{2}}}{2}+gz\)。式中内能原用符号为u,为避免与x方向的速度分量u混淆,并考虑到流动控制方程中使用符号的习惯,改用e。对燃气,略去gz,因此能量方程为:
\(\int_{{{V}_{c}}}{\frac{\partial }{\partial t}\left( \rho \left( e+\frac{{{V}^{2}}}{2} \right) \right)}d{{V}_{c}}+\int_{{{A}_{p}}}{\left( e+\frac{{{V}^{2}}}{2} \right)(\rho \bar{V}\cdot d\bar{A})}=\int_{{{A}_{b}}}{\rho {{v}_{B}}\left( e+\frac{{{V}^{2}}}{2} \right)dA}\) (5.3.10)
因为\(e=h-\frac{p}{\rho },\rho {{v}_{B}}={{\rho }_{mp}}r\),因此(5.3.10)还可写成:
\(\int_{{{V}_{c}}}{\frac{\partial }{\partial t}\left( \rho \left( h+\frac{{{V}^{2}}}{2} \right) \right)}d{{V}_{c}}+\int_{{{A}_{p}}}{\left( h+\frac{{{V}^{2}}}{2} \right)(\rho \bar{V}\cdot d\bar{A})}=\int_{{{A}_{b}}}{{{\rho }_{mp}}r\left( h+\frac{{{V}^{2}}}{2} \right)dA}\) (5.3.11)
下面来推导在燃烧室中连续、动量和能量方程的微分方程形式。为了方便起见,仅推导一维非定常形式。
将连续方程(5.3.8)除以△x并取极限,得到
\(\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{1}{\Delta x}\int_{{{V}_{c}}}{\frac{\partial \rho }{\partial t}d{{V}_{c}}+}\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{1}{\Delta x}\int_{{{A}_{b}}}{\rho \bar{V}\cdot dA=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{1}{\Delta x}\int_{{{A}_{b}}}{\rho {{v}_{B}}dA}}\) 或
\(\int_{{}}{\frac{\partial \rho }{\partial t}dA+\frac{\partial }{\partial x}\int_{{{A}_{P}}}{\rho udA}=}\int_{{{A}_{P}}}{{{\rho }_{mp}}rdA}\) (5.3.12)
设在x截面上u均匀,\({{\rho }_{mp}}\) 为均质,燃速r处处相等,则(5.3.12)写成微分形式为:
\(\frac{\partial }{\partial t}(\rho {{A}_{p}})+\frac{\partial }{\partial x}(\rho u{{A}_{p}})={{\rho }_{mp}}r\frac{\partial {{A}_{b}}}{\partial x}\) (5.3.13)
同理,不计体积力,一维动量方程的微分形式,由(5.3.9)为:
\(\frac{\partial }{\partial t}(\rho u{{A}_{p}})+\frac{\partial }{\partial x}(\rho {{u}^{2}}{{A}_{p}})=-{{A}_{p}}\frac{\partial p}{\partial x}\) (5.3.14)
式中,\(-{{A}_{p}}\frac{\partial p}{\partial x}\) 是将方程(5.3.9)中的压力项除以△x并求极限得到的,第一个压力项为:
\(-\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{1}{\Delta x}\int_{{{A}_{p}}}{pd\bar{A}}=-\frac{\partial }{\partial x}(p{{A}_{p}})\)
第二个压力项为:
\(-\underset{\Delta x\to 0}{\mathop{\lim }}\,\int_{{{A}_{b}}}{pd\bar{A}}=-\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{1}{\Delta x}\int_{{{A}_{b}}}{p\bar{n}d\bar{A}}=-\int_{s}{p\bar{n}ds}\)
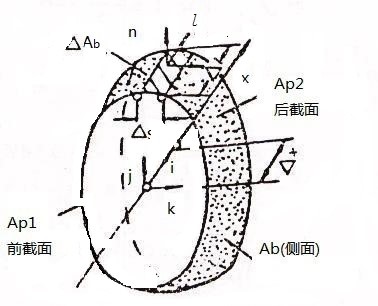
式中,s为燃面周边,参看图5-2。取x方向的动量,有:
\(-\int_{s}{p\cos (\bar{n},\bar{j})ds=}\int_{s}{p\sin (\bar{l},\bar{i})ds}\)
图5-2 控制体
设p沿s分布均匀,则为
\(\int_{s}{p\sin (\bar{l},\bar{i})ds}=p\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{{{A}_{{{p}^{2}}}}-{{A}_{{{p}^{1}}}}}{\Delta x}=p\frac{\partial {{A}_{p}}}{\partial x}\)
这样,方程(5.3.9)中的两个压力项:
\(-\int_{{{A}_{P}}}{pd\bar{A}-}\int_{{{A}_{b}}}{pd\bar{A}}=-\frac{\partial }{\partial x}(p{{A}_{p}})+p\frac{\partial {{A}_{P}}}{\partial x}=-{{A}_{p}}\frac{\partial P}{\partial x}\)
一维能量方程为:
\(\frac{\partial }{\partial t}\left\langle \rho {{A}_{p}}(e+\frac{{{V}^{2}}}{2}) \right\rangle +\frac{\partial }{\partial x}\left\langle \rho v{{A}_{p}}(e+\frac{{{V}^{2}}}{2}) \right\rangle ={{\rho }_{mp}}r{{H}_{f}}\frac{\partial {{A}_{b}}}{\partial x}\) (5.3.15)
式中,Hf是单位质量推进剂的焓,它等于推进剂燃烧时加入通道的单位质量燃烧产物的总焓,即\({{H}_{f}}={{h}^{*}}=h+\frac{{{V}^{2}}}{2}\) 。
图5-3表示燃烧室中典型的一维非定常流动计算结果。
(a)启动过程 (b)排气过程
图5-3 燃烧室中的非定常流动
5.4 燃烧室和喷管中的两相流动方程
5.4.1 两相流的概念
两相流动在流体力学中具有广泛的概念。例如,弹头再入大气层时气层时气体中夹杂雨雪冰,石油管道中有气团、杂志的石油粘流,锅炉中伴有汽团的水流,具有粉尘的煤燃烧气流等。我们这里所说的两相流动,是指固体火箭推进剂中添加铝粉之后,在燃气中含有Al2O3凝相(液相或固相)粒子这种特定的流动。
目前,固体火箭发动机广泛采用添加铝粉的复合推进剂,添加铝粉会提高了推进剂的能量并能抑制高、中频振荡燃烧,但另一方面会造成两相流损失。在许多高能推进剂中常加入10~20%的铝粉。对于加17%铝粉的复合推进剂,燃烧产物中按重量计约含有30%的Al2O3粒子。据统计,在喷管流动中,两相流损失常占总损失的 ,含Al2O3粒子的燃气流动,是气—固两相流动。两相流动的规律和参数与纯气相流动相比有明显的区别,因此受到设计者很大的关注。
人们对含铝推进剂的燃烧产物中的粒子做了细致的收集和分析工作,结果表明,98%以上是Al2O3,形状大体上是球形的。在喷管喉部附近上游,粒子处于高温,呈液相,凝聚力使之呈球形;下游,则随着加速降温而凝固为固相圆球。也就是说,Al2O3粒子在流动中存在相变。
由于推进剂中铝粉的粒度和发动机工作条件不同,粒子的直径分布差异较大。在较简单的计算中,可将粒子看作是均一直径,对于较详细的计算,可将粒子按不同的尺寸分组进行。在喷管流动中,不同直径的粒子,其运动速度是不同的。
我们已经建立了清晰的概念,纯燃气流是连续介质。对火箭发动机中的两相流动来说,一般把其中的凝相粒子群看成一种“拟流体”,把两相燃气看作气相流体和凝相粒子拟流体的一种混合液体。在这个混合流体中,气相流体和凝相拟流体各为组元。对凝相粒子赋以拟流体的概念,实际上就是对它施用连续介质假设。
固体火箭发动机中的两相流动有以下特点:
1)气体燃烧产物在流动中加速时带动着粒子加速,但粒子并不加速到与气体燃烧产物相同的速度,即由速度滞后。这说明气相对粒子相有推动力,或者说粒子相对气相有阻力。
2)气体燃烧产物在加速流动中降温,温度较高的凝相粒子向气相传热,但粒子的温度没有流动燃气降低得那样快,即由温度滞后。这样,粒子带走了更多的热,使热损失加大。
3)粒子对压力没有贡献,粒子在流动中不膨胀做功。
在固体火箭发动机中,气相与凝相间的作用力最主要的是粘性阻力。我们采用一维定常动量方程来看这种阻力。设球形粒子的质量为 ,则牛顿运动第二定律为:
\(\frac{4}{3}\pi r_{p}^{3}{{\rho }_{mp}}\frac{d{{V}_{p}}}{dt}=\delta {{F}_{D}}\) (5.4.1)
q式中,下标p表示粒子的参数。由于粒子对气流的压力没有贡献,因此粒子动量方程中没有压力项。方程(5.4.1)也可以写成:
\(\frac{4}{3}\pi r_{p}^{3}{{\rho }_{mp}}{{V}_{p}}\frac{d{{V}_{p}}}{dx}=\delta {{F}_{D}}\) (5.4.2)
粒子在气流中运动的粘性阻力\(\delta {{F}_{D}}\)常表示为阻力系数CD、迎风面积和相对运动动压头之乘积,即
\(\delta {{F}_{D}}={{C}_{D}}\pi r_{p}^{2}\frac{1}{2}\rho (V-{{V}_{P}})\left| V-{{V}_{P}} \right|\) (5.4.3)
斯托克斯流动区(Re<0.1)的阻力系数CD,S为:
\({{C}_{D,S}}=\frac{24}{{{R}_{e}}}=\frac{24\mu }{2{{r}_{p}}\rho \left| V-{{V}_{p}} \right|}\) (5.4.4)
式中, 为动力粘性系数。将(5.4.4)代入(5.4.3),再代入(5.4.2)得:
\({{V}_{p}}\frac{d{{V}_{p}}}{dx}=\frac{9}{2}\frac{\mu {{C}_{D}}}{{{\rho }_{mp}}{{r}_{p}}^{2}{{C}_{D,S}}}\left( V-{{V}_{p}} \right)\)
令 \({{A}_{D}}=\frac{9}{2}\frac{\mu {{C}_{D}}}{{{\rho }_{mp}}{{r}_{p}}^{2}{{C}_{D,S}}}\) (5.4.5)
则单一颗粒的动量方程为:
\({{V}_{p}}\frac{d{{V}_{p}}}{dx}={{A}_{D}}\left( V-{{V}_{p}} \right)\) (5.4.5)
式中,\({{A}_{D}}(V-{{V}_{P}})\)为气相与凝相间单位质量的阻力。
我们再通过一维能量方程来看粒子与气体间的热交换。假设每一个粒子都是不可压缩的,则粒子与气体间的热交换仅改变粒子的焓。因此单个粒子的能量方程为:
\(\frac{4}{3}\pi r_{p}^{3}{{\rho }_{mp}}\frac{d{{h}_{p}}}{dt}=\delta \overset{\bullet }{\mathop{{{Q}_{P}}}}\,\)
或
\(\frac{4}{3}\pi r_{p}^{3}{{\rho }_{mp}}{{V}_{p}}\frac{d{{h}_{p}}}{dx}=\delta \overset{\bullet }{\mathop{{{Q}_{P}}}}\,\)
设粒子与气流间的热交换为对流传热,对流传热系数为hc,则
\(\delta \overset{\cdot }{\mathop{{{Q}_{p}}}}\,={{h}_{c}}(4\pi {{r}_{p}}^{2})(T-{{T}_{p}})\) (5.4.8)
对流传热系数可以通过努赛尔数Nu来确定:
\({{h}_{c}}=\frac{{{N}_{u}}\lambda }{2{{r}_{p}}}\) (5.4.9)
式中,\(\lambda \(是气体的导热系数,由普朗特数Pr确定:
\(\lambda =\frac{{{C}_{p}}u}{{{P}_{r}}}\) (5.4.10)
将(5.4.9)代入(5.4.8),再代入(5.4.7),再代入(5.4.6),得:
\({{V}_{p}}\frac{d{{h}_{p}}}{dx}=\frac{3}{2}\frac{\mu {{C}_{P}}{{N}_{u}}}{{{\rho }_{mp}}{{r}_{p}}^{2}{{P}_{r}}}(T-{{T}_{p}})\)
令 \({{B}_{D}}=\frac{3}{2}\frac{\mu {{C}_{P}}{{N}_{u}}}{{{\rho }_{mp}}{{r}_{p}}^{2}{{P}_{r}}}\) (5.4.11)
则单一粒子尺寸的能量方程为:
\({{V}_{P}}\frac{d{{h}_{p}}}{dx}={{B}_{D}}(T-{{T}_{P}})\) (5.4.12)
式中,\({{B}_{D}}(T-{{T}_{P}})\)为气相与凝相间单位质量的传热。
早期计算阻力和传热时,认为喷管中的两相流动是斯托克斯流动,且不考虑气流的可压缩性和稀薄效应等因素的影响,因此,可采用斯托克斯流动圆球的阻力系数和努赛尔数,它们分别为:
\({{C}_{D,S}}=\frac{24}{{{R}_{e}}},{{N}_{u,s}}=2\)
实际上,喷管中的流动并不是斯托克斯流动,且影响CD和Nu的因素也很多,需对它们进行修正,经修正的系数为(5.4.4)和(5.4.10)中的CD和Nu。
5.4.2 燃烧室和喷管中的两相流动方程
对于固体发动机燃烧室和喷管中的两相流动,作如下假设:
1)流动绝能、无粘、不计重力作用,气相是完全气体;
2)粒子为只存均一的球体,内部温度均匀,忽略粒子所占的容积,认为粒子是离散的,即粒子间互相没有作用;
3)仅考虑粒子与气体间的阻力和传热作用,粒子对气流压力没有贡献,在流动中不膨胀做功,粒子不起化学反应。
根据两相流的概念,两相流方程与纯气相流方程的主要差别在于:前者除一组气相方程外,还有一组关于粒子的方程。在这两组方程中,都有粒子与气体间的阻力和热交换项。正是这两项,反映出凝相与气相间的相互作用;也正是这两项,将气相与凝相的两组方程联成了相互制约的整体。由于粒子对气流压力没有贡献,因此在粒子动量方程中没有压力项。
(1)燃烧室中的一维非定常两相流动方程
对于燃烧室,仅列出一维非定常两相流动方程。
定义燃烧室中凝相质量比ε为凝相质量与混合气体质量之比:
\(\varepsilon =\frac{{{m}_{p}}}{{{m}_{m}}}\) (5.4.13)
一维气相方程为:
\(\frac{\partial }{\partial t}(\rho {{A}_{p}})+\frac{\partial }{\partial x}(\rho u{{A}_{p}})=(1-\varepsilon ){{\rho }_{mp}}r\frac{\partial {{A}_{b}}}{\partial x}\) (5.4.14)
\(\frac{\partial }{\partial t}(\rho u{{A}_{p}})+\frac{\partial }{\partial x}(\rho {{u}^{2}}{{A}_{p}})=-{{A}_{p}}\frac{\partial p}{\partial x}-{{\rho }_{p}}{{A}_{p}}{{A}_{D}}(u-{{u}_{p}})\) (5.4.15)
\(\frac{\partial }{\partial t}\left\langle \rho {{A}_{p}}(e+\frac{{{u}^{2}}}{2}) \right\rangle +\frac{\partial }{\partial x}\left\langle \rho u{{A}_{p}}(h+\frac{{{u}^{2}}}{2}) \right\rangle =(1-\varepsilon ){{\rho }_{mp}}r{{H}_{f}}\frac{\partial {{A}_{b}}}{\partial x}-{{\rho }_{p}}{{u}_{p}}{{A}_{p}}{{A}_{D}}(u-{{u}_{p}})+{{\rho }_{p}}{{A}_{p}}{{B}_{D}}({{T}_{p}}-T)\)
(5.4.16)
在气相方程中,应计入的是气相质量,因此出现\((1-\varepsilon )\( 。另外,在动量方程中出现粒子阻力项,能量方程中出现由阻力产生的能量项和粒子的传热项。
一维凝相方程为:
\(\frac{\partial }{\partial t}({{\rho }_{p}}{{A}_{p}})+\frac{\partial }{\partial x}({{\rho }_{p}}{{u}_{p}}{{A}_{p}})=\varepsilon {{\rho }_{mp}}r\frac{\partial {{A}_{b}}}{\partial x}\) (5.4.17)
\(\frac{\partial }{\partial t}({{\rho }_{p}}{{u}_{p}}{{A}_{p}})+\frac{\partial }{\partial x}({{\rho }_{p}}{{u}_{p}}^{2}{{A}_{p}})={{\rho }_{p}}{{A}_{P}}{{A}_{D}}(u-{{u}_{p}})\) (5.4.18)
\(\frac{\partial }{\partial t}\left( {{\rho }_{p}}{{A}_{p}}\left( e+\frac{{{u}_{p}}^{2}}{2} \right) \right)+\frac{\partial }{\partial x}\left( {{\rho }_{p}}{{u}_{p}}{{A}_{p}}\left( {{h}_{p}}+\frac{{{u}_{p}}^{2}}{2} \right) \right)=\varepsilon {{\rho }_{mp}}r{{H}_{f}}\frac{\partial {{A}_{b}}}{\partial t}+{{\rho }_{p}}{{u}_{p}}{{A}_{P}}{{A}_{D}}(u-{{u}_{p}})-{{\rho }_{p}}{{u}_{p}}{{B}_{D}}({{T}_{p}}-T)\) (5.4.19)
气相状态方程仍为
\(P=\rho RT\) (5.4.20)
而凝相状态方程,当凝相温度TP离于Al2O3熔点Tmp时,为:
\({{h}_{p}}={{h}_{p,l}}={{C}_{p,l}}({{T}_{p}}-{{T}_{_{mp}}})\) (5.4.21)
式中,Cp,l是液态粒子的比热。当Tp<Tmp时,为:
\({{h}_{p}}={{h}_{p,s}}={{C}_{p,s}}({{T}_{_{mp}}}-T)\) (5.4.22)
式中,Cp,s是固态粒子的比热。
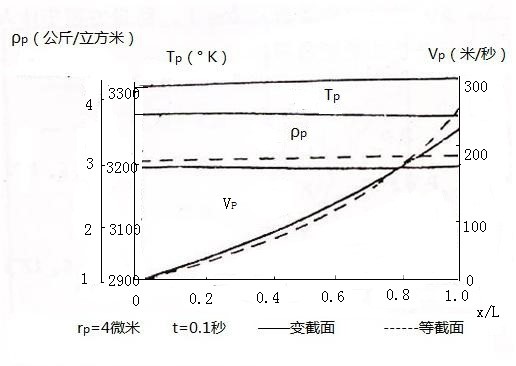
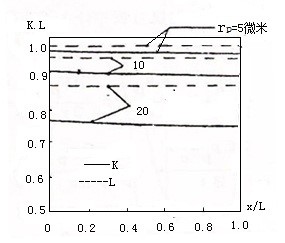
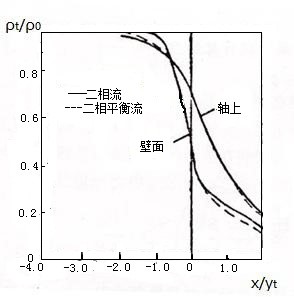
燃烧室中一维两相流动计算的结果表示于图5-4,其中速度滞后数k和温度滞后数L定义为
\(K=\frac{{{V}_{P}}}{V},L=\frac{{{T}^{*}}-{{T}_{p}}}{{{T}^{*}}-T}\) (5.4.23)
(a) 气相参数分布
(b) 粒子相参数分布 (c) 粒子的速度和温度滞后数分布
图5-4 燃烧室中一维二维两相流动的计算结果
(2)喷管中轴对称两相流动方程
我们以较常用的轴对称两相流动方程为例。与燃烧室中的方程相比,喷管中无加质,通道形状不变化,此外,对气相方程来讲,在亚音速区是椭圆型的,在音速面是抛物型的,在超音速区是双曲型的,在跨音速区是混合型的。许多研究者用时间相关法求解跨音速方程,因此我们把气相方程仍写成非定常的。而凝相方程是双曲型的,因此有时也可以写成定常的形式。
气相方程:
\(\frac{\partial \rho }{\partial t}+\rho \frac{\partial u}{\partial x}+\rho \frac{\partial v}{\partial y}+u\frac{\partial \rho }{\partial x}+v\frac{\partial \rho }{\partial x}+\delta \frac{\rho u}{y}=0\) (5.4.24)
\(\frac{\partial (\rho u)}{\partial t}+\rho u\frac{\partial u}{\partial x}+\rho v\frac{\partial u}{\partial y}+\frac{\partial \rho }{\partial x}=-{{\rho }_{p}}{{A}_{D}}(u-{{u}_{p}})\) (5.4.25)
\(\frac{\partial (\rho v)}{\partial t}+\rho u\frac{\partial v}{\partial x}+\rho v\frac{\partial v}{\partial y}+\frac{\partial \rho }{\partial y}=-{{\rho }_{p}}{{A}_{D}}(v-{{v}_{p}})\) (5.4.26)
\(\frac{\partial \left\langle \rho \left( h+\frac{{{V}^{2}}}{2} \right) \right\rangle }{\partial t}+\frac{\partial \left\langle \rho u\left( h+\frac{{{V}^{2}}}{2} \right) \right\rangle }{\partial x}+\frac{\partial \left\langle \rho v\left( h+\frac{{{V}^{2}}}{2} \right) \right\rangle }{\partial y}=\frac{\partial p}{\partial t}+{{\rho }_{p}}{{B}_{p}}({{T}_{P}}-T)-{{\rho }_{p}}{{A}_{p}}\left\langle {{u}_{p}}(u-{{u}_{p}})+{{v}_{p}}(v-{{v}_{p}}) \right\rangle \) (5.4.27)
连续方程中 为算符,对平面流动δ=0;对轴对称流动,δ=1。动量方程中计入了粒子阻力,能量方程中计入了由阻力和传热产生的能量项。
凝相方程为:
\(\frac{\partial {{\rho }_{p}}}{\partial t}+{{\rho }_{p}}\frac{\partial {{u}_{p}}}{\partial x}+{{\rho }_{p}}\frac{\partial {{v}_{p}}}{\partial y}+{{u}_{p}}\frac{\partial {{\rho }_{p}}}{\partial x}+{{v}_{p}}\frac{\partial {{\rho }_{p}}}{\partial y}+\delta \frac{{{\rho }_{p}}{{v}_{p}}}{y}=0\) (5.4.28)
\(\frac{\partial ({{\rho }_{p}}{{u}_{p}})}{\partial t}+{{\rho }_{p}}{{u}_{p}}\frac{\partial {{u}_{p}}}{\partial x}+{{\rho }_{p}}{{v}_{p}}\frac{\partial {{v}_{p}}}{\partial y}={{\rho }_{p}}{{A}_{D}}(u-{{u}_{p}})\) (5.4.29)
\(\frac{\partial ({{\rho }_{p}}{{v}_{p}})}{\partial t}+{{\rho }_{p}}{{u}_{p}}\frac{\partial {{v}_{p}}}{\partial x}+{{\rho }_{p}}{{v}_{p}}\frac{\partial {{v}_{p}}}{\partial y}={{\rho }_{p}}{{A}_{D}}(v-{{v}_{p}})\) (5.4.30)
\(\frac{\partial \left\langle {{\rho }_{p}}\left( {{h}_{p}}+\frac{{{V}_{p}}^{2}}{2} \right) \right\rangle }{\partial t}+\frac{\partial \left\langle {{\rho }_{p}}{{u}_{p}}\left( {{h}_{p}}+\frac{{{V}_{p}}^{2}}{2} \right) \right\rangle }{\partial x}+\frac{\partial \left\langle {{\rho }_{p}}{{v}_{p}}\left( {{h}_{p}}+\frac{{{V}_{p}}^{2}}{2} \right) \right\rangle }{\partial y}=-{{\rho }_{p}}{{B}_{p}}({{T}_{P}}-T)+{{\rho }_{p}}{{A}_{p}}\left\langle {{u}_{p}}(u-{{u}_{p}})+{{v}_{p}}(v-{{v}_{p}}) \right\rangle \)
(5.4.31)
粒子相方程与凝相方程中有关阻力项和传热项的正负是相反的。
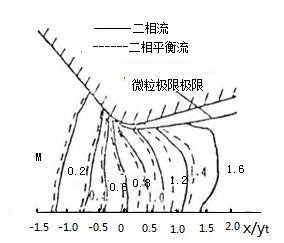
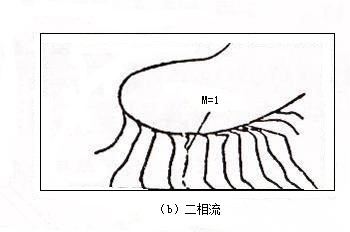
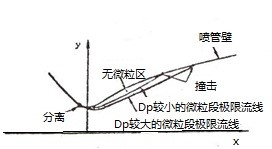
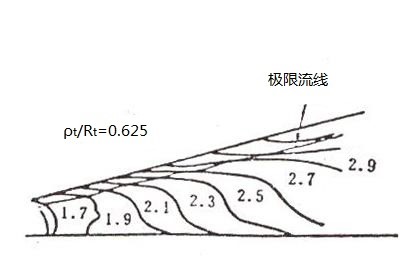
图5-5是喷管跨音速两相流动计算的结果,图5-6是喷管超音速段两相流动计算的结果。两相流动与纯气相流动相比,有明显的区别。除流动参数有较大的差别外,理论计算结果表明,喷管中的两相流动存在极限流线和无粒子区。
(a) 音速线的位置 (b) 等马赫数线
(c) 轴上和壁面上马赫数的比较 (d) 轴上和壁面上无因次压力的比较
(e) 轴上和壁面上无因次密度的比较 (f) 潜入喷管的等马赫数线的分布
图5-5 喷管跨音速两相流动计算结果
(a) 粒子极限流线和无粒子区 (b) 等马赫数线分布
(c) 气流速度分布 (d) 气流温度分布
图5-6 喷管超音速段两相流动的计算结果
5.5 方程的守恒型式
一般来说,把微分运算以外存在未知量的方程称为原始型方程,把未知量都放在微分运算符以内的方程称为守恒型方程,相应地,在微分运算以内的变量称为守恒变量。为了数值计算的方便,通常要将方程化成守恒型,因此,熟悉守恒型方程的表达形式非常重要。
喷管轴对称纯气相流动的方程组(5.2.6)~(5.2.9)为:
\(\frac{\partial \rho }{\partial t}+\frac{\partial }{\partial x}(\rho u)+\frac{\partial }{\partial y}(\rho v)+\delta \frac{\rho v}{y}=0\) (5.5.1)
\(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+\frac{1}{\rho }\frac{\partial p}{\partial x}=0\) (5.5.2)
\(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+\frac{1}{\rho }\frac{\partial p}{\partial y}=0\) (5.5.3)
\(\frac{\partial }{\partial t}(h+\frac{{{V}^{2}}}{2})+u\frac{\partial }{\partial x}(h+\frac{{{V}^{2}}}{2})+v\frac{\partial }{\partial y}(h+\frac{{{V}^{2}}}{2})-\frac{1}{\rho }\frac{\partial p}{\partial t}=0\) (5.5.4)
其中,连续方程已经是守恒型方程,下面将动量和能量方程化为守恒型。
将(5.5.1)式乘u,(5.5.2)式乘ρ,然后相加得:
\(\frac{\partial (\rho u)}{\partial t}=\frac{\partial }{\partial x}(\rho {{u}^{2}}+p)+\frac{\partial }{\partial y}(\rho uv)+\delta \frac{\rho uv}{y}=0\) (5.5.5)
将(5.5.1)式乘以v,(5.5.3)式乘ρ,然后相加得:
\(\frac{\partial (\rho v)}{\partial t}+\frac{\partial (\rho uv)}{\partial x}+\frac{\partial (\rho {{v}^{2}}+p)}{\partial y}+\delta \frac{\rho {{v}^{2}}}{y}=0\) (5.5.6)
(5.5.5)和(5.5.6)式就是动量方程的守恒形式。
将(5.5.1)式乘以\(h+\frac{{{V}^{2}}}{2}\),(5.5.4)式乘ρ,然后相加,并考虑到滞止内能
\(E=\rho \left( e+\frac{{{V}^{2}}}{2} \right),e={{C}_{v}}T=h-\frac{p}{\rho }\) (5.5.7)
有
\(\frac{\partial E}{\partial t}=\frac{\partial }{\partial x}\left\langle (E+p)u \right\rangle +\frac{\partial }{\partial y}\left\langle (E+p)v \right\rangle +\frac{\delta (E+p)v}{y}=0\) (5.5.8)
描述二维无粘气体流动的控制方程可由守恒型式的连续方程(5.5.1),动量方程(5.5.5)、(5.5.6),能量方程(5.5.8)等四个方程和状态方程组成。四个守恒型式的方程与原始方程组是等价的。
在数值计算中,对守恒型方程组常采取如下的缩写形式:
\(\frac{\partial U}{\partial t}+\frac{\partial F}{\partial x}+\frac{\partial G}{\partial y}+H=0\) (5.5.9)
其中,
显然,守恒型缩写形式的方程(5.5.9)实际上包含了连续方程,两个方向的动量方程和能量方程共四个方程。
同理,喷管中二维两相流动方程(5.5.24)~(5.5.31)也能表达为守恒型缩写形式。我们将纯气相和两相的二维流动守恒型方程缩写形式书写成统一的格式:
\(\frac{\partial U}{\partial t}+\frac{\partial F}{\partial x}+\frac{\partial G}{\partial y}+H=0\) (5.5.12)
其中
其中,算符δ对平面流动为0,对轴对称流动为1,两相流指示系数N,对纯气相流动为1,对两相流动为2,而
\(C=\left\langle {{u}_{p}}(u-{{u}_{p}})+{{v}_{p}}(v-{{v}_{p}}) \right\rangle -\frac{{{B}_{D}}}{{{A}_{D}}}({{T}_{p}}-T)\) (5.5.15)
通常采用以上方程的守恒形式作为数值模拟的控制方程,对这些方程进行求解,从而获得固体火箭发动机中的流动规律。