第二章 固体火箭冲压发动机的主要性能参数

发动机的主要作用是产生推力。用与飞行器上的发动机要求在质量轻﹑尺寸小的条件下产生最大的推力，说明这方面性能的参数称为推力特性。此外还要求发动机每产生1千克推力在单位时间内所消耗的燃料尽可能的少。

2.1 发动机的推力和阻力^【1】

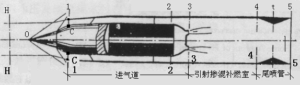
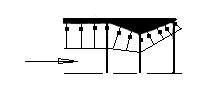
在固体火箭发动机设计书中^{【5】～【7】}，已经介绍了火箭发动机产生推力的公式，火箭—冲压组合发动机产生推力的原理及计算推力的原则基本上也是相同的。然而也有不同之处，因为在火箭——冲压组合发动机中有空气流入发动机。以超音速飞行的组合发动机为例，空气以超音的速度进入进气道时，由于中心锥的作用使超音空气流产生压缩，在中心锥锥顶O处产生斜激波：如图2-1所示，超音气流经过激波后流速降低（但仍为超音速），压力增高，方向也发生转折。在计算推力时应当考虑空气进入发动机时所具有的动量，以及所产生的阻力等现象。

图2－1 发动机典型截面标记（黑体字为对称位置）

2．1．1 推力和阻力的概念及推力的计算

发动机的推力是气流经过发动机时作用于发动机内表面，外壳外表面和露出进气口外的中心锥面上所有气流压力和摩擦力的轴向合力。

所谓发动机内表面是指气流在“1CC1”截面于“55”截面之间于进入发动机内的气流相接触的表面，作用在内表面上所有作用力的轴向合力用表示。

作用在发动机外壳外表面的所有作用力的轴向合力，用表示。

露出进气口外的中心锥外表面为锥面COC,作用在锥面COC的所有作用力的轴向合力用表示。

因此从物理意义上看，发动机的推力为三部分轴向力的总和，即

\(F={{F}_{in}}+{{F}_{out}}+{{F}_{\text{c}}}\)   （2-1）

为了计算方便我们规定：轴向合力的方向与推力方向一致的取为正值，相反的取为负值。

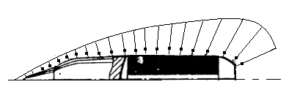
在推导计算推力的公式之前，分析一下组合发动机各个部件气流压力分布情况及轴向合力的方向是有益的。进气道中心锥体表面上的气流压力分布如图2-2（a）所示，显然其轴向合力的方向与推力方向是一致的。进气道外壳上气流压力的轴向合力的方向朝后，发生器内气流压力的轴向合力方向朝前，尾喷管内气流压力的轴向合力方向朝后，如图2-2（b）（d）所示。

(a) 中心体上气流压力的分布

（b） 进气道内外壁面压力分布

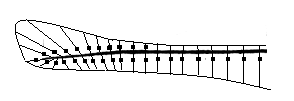
（c）燃气发生器内部压力分布

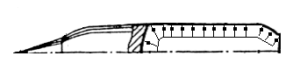
（d）尾喷管内部压力的分布

图2－2 发动机各部分压力分布

下面推导三个轴向合力F_in﹑F_out﹑F_c的计算公式：

 1．内表面上轴向合力的计算：

根据F_in的物理意义，F_in可由下式计算：

\({{F}_{in}}=\int_{A}{\text{p}dA}\)                                （2-2）

始终A表示面积，此处代表发动机内表面的轴向投影面积。

显然，在积分（2-2）式时，必须知道气流压力p沿内表面分布的情况。当然，这是可以用测量或理论计算的方法而获得，但是因组合发动机的工作过程相当复杂，精确的测量或计算内表面上气流压力分布的情况是困难的。因此F_in的计算一般并不直接按照（2-2）式进行，而是利用动量定理进行计算。

为了应用动量定理，取截面1CC1及55作为控制面（图2-1），控制面内所包含的燃气当作一个整体作为研究对象。为了简化计算假定发动机内的气流是一维定常流动，即同一界面的气流参数认为是均匀的，而且不随时间而变化。

沿着发动机轴向，按照动量定理，控制体内气体所获得的动量变化率应等于气体所受到的外力。这部分气体所受的外力（不计重力）有三方面：一是发动机内表面对气流的作用力，此力与F_in大小相等，方向相反（与推力方向也相反），此力用F_in表示。二是发动机进口环形缝隙截面上所受到的空气的压力，方向与推力方向相反，其大小为\({{p}_{cir}}{{A}_{cir}}\cos {{\delta }_{avg}}\)，此处\({{p}_{cir}},{{A}_{cir}}\)代表进口环形缝隙截面的气体压力和界面积。三是喷管出口截面上所受到的燃气的反压，方向与推力方向相同，其大小为\({{p}_{5}}{{A}_{5}}\)。因此可得：

\(-{{F}_{in}}-{{p}_{cir}}{{A}_{cir}}\cos {{\delta }_{avg}}+{{p}_{5}}{{A}_{5}}=\frac{dM}{dt}\)                 （2-3）

式中\(\frac{dM}{dt}\)为气体的动量M对时间t的变化率，每秒内进入控制体的空气质量为\({{\dot{m}}_{K}}\)，流速为\({{V}_{cir}}\)，方向与推力方向相反。燃气发生器的固体推进剂相对于发动机的速度为零。每秒内离开喷管出口界面的燃气质量为\({{\dot{m}}_{5}}\)，流速为\({{V}_{5}}\)，方向与推力方向相反。因此控制体内气体沿轴向的动量变化率为：

\(\frac{dM}{dt}={{{\dot{m}}}_{5}}(-{{V}_{5}})-{{{\dot{m}}}_{K}}(-{{V}_{cir}})\cos {{\delta }_{avg}} \)

\(=-{{\left[ \rho {{V}^{2}}A \right]}_{5}}+{{\left[ \rho {{V}^{2}}A \right]}_{cir}}\cos {{\delta }_{avg}} \)

注脚5表示5截面上的参数， cir表示进口环形缝隙截面上的参数。将此式带入（2-3）式中，得

\({{F}_{in}}={{\left[ \rho {{V}^{2}}A \right]}_{5}}-{{\left[ \rho {{V}^{2}}A \right]}_{cir}}\cos {{\delta }_{avg}}-{{p}_{cir}}{{A}_{cir}}\cos {{\delta }_{avg}}+{{p}_{5}}{{A}_{5}}\)

\({{F}_{in}}={{\left[ \left( p+\rho {{V}^{2}} \right)A \right]}_{5}}-{{\left[ \left( p+\rho {{V}^{2}} \right)A\cos {{\delta }_{avg}} \right]}_{cir}}\)             （2-4）

2.外壳在发动机外壳外表面的作用力有二部分组成：一是空气压力而产生的轴向合力，其值为\(\int_{{{A}_{1}}}^{{{A}_{5}}}{pdA}\)，因为一般说来\({{A}_{5}}>{{A}_{1}}\)，其轴向合力的方向是朝后的（与推力方向相反）。二是空气与外壳外表面的摩擦阻力，用\({{X}_{fri}}\)表示，其方向总是与推力方向相反。因此

\({{F}_{out}}=-\int_{{{A}_{1}}}^{{{A}_{5}}}{pdA-{{X}_{fri}}}\)

\({{F}_{out}}=-\int_{{{A}_{1}}}^{{{A}_{5}}}{{{p}_{H}}dA}-\int_{{{A}_{1}}}^{{{A}_{5}}}{\left( p-{{p}_{H}} \right)dA}-{{X}_{fri}}\)

在上式右方加﹑减\(\int_{{{A}_{1}}}^{{{A}_{5}}}{{{p}_{H}}dA}\)得

令\(\int_{{{A}_{1}}}^{{{A}_{5}}}{\left( p-{{p}_{H}} \right)dA}={{X}_{sw}}\)                                           （2-5）

并称\({{X}_{sw}}\)为前缘波阻。将（2-5）式代入上式，得

\({{F}_{out}}=-\int_{{{A}_{1}}}^{{{A}_{5}}}{{{p}_{H}}dA}-{{X}_{sw}}-{{X}_{fri}}\)                                 （2-6）

3.锥体COC表面上轴向合力也是由二部分组成。一是作用在锥体表面上空气压力的轴向合力。用\({{\overline{p}}_{\text{c}}}\)表示空气作用在锥体表面上的平均静压力，则此轴向合力为\({{\overline{p}}_{\text{c}}}{{A}_{\text{c}}}\)。二是空气与锥体表面的摩擦力，其轴向合力用表示X_c。X_c和\({{\overline{p}}_{\text{c}}}{{A}_{\text{c}}}\)的方向与推力方向相反。因此

\({{F}_{\text{c}}}=-{{\overline{p}}_{\text{c}}}{{A}_{\text{c}}}-{{X}_{\text{c}}}\)                                      （2-7）

   4.推力F的计算

将（2-4）﹑（2-6）﹑（2-7）式代入（2-1）式，得

\( F={{\left[ \left( p+\rho {{V}^{2}} \right)A \right]}_{5}}-{{\left[ \left( p+\rho {{V}^{2}} \right)A\cos {{\delta }_{avg}} \right]}_{cir}}-\int_{{{A}_{1}}}^{{{A}_{5}}}{{{p}_{H}}dA} \)

\( -{{X}_{sw}}-{{X}_{fri}}-{{\overline{p}}_{c}}{{A}_{c}}-{{X}_{c}} \)         （2-8）

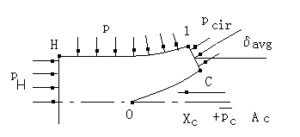
利用（2-8）式计算推力还是有困难的。因为缝隙截面上气流参数已经受到中心锥的干扰，因而\({{\left[ \left( p+\rho {{V}^{2}} \right){{A}_{cir}}\cos {{\delta }_{avg}} \right]}_{cir}}\)这一项得值计算较为复杂。最好能通过未受干扰的HH截面上的气流参数来计算推力。这是可以做到的。为此取HH和1COC1表面为控制面（图2-3），应用动量定理得

图2－3 前嘴部气流受力图

\({{\left[ pA\cos {{\delta }_{avg}} \right]}_{cir}}+{{X}_{c}}+{{\overline{p}}_{c}}{{A}_{c}}-{{\overline{p}}_{H}}{{A}_{H}}-\int_{{{A}_{H}}}^{{{A}_{1}}}{pdA} \)

\(={{{\dot{m}}}_{K}}{{\left( -V\cos {{\delta }_{avg}} \right)}_{cir}}-{{{\dot{m}}}_{K}}\left( -{{V}_{H}} \right) \)

即      \({{\left[ \left( p+\rho {{V}^{2}} \right)A\cos {{\delta }_{avg}} \right]}_{cir}}={{\left[ pA\cos {{\delta }_{avg}}+{{{\dot{m}}}_{K}}V\cos {{\delta }_{avg}} \right]}_{cir}} \)

\( ={{\left[ \left( p+\rho {{V}^{2}} \right)A \right]}_{H}}+\int_{{{A}_{H}}}^{{{A}_{1}}}{pdA}-{{X}_{c}}-{{\overline{p}}_{c}}{{A}_{c}}\)              （2-9）

将式（2-9）代入（2-8）式，得

\(F={{\left[ \left( p+\rho {{V}^{2}} \right)A \right]}_{5}}-{{\left[ \left( p+\rho {{V}^{2}} \right)A \right]}_{H}}-\int_{{{A}_{1}}}^{{{A}_{5}}}{{{p}_{H}}dA} \)

\( -\int_{{{A}_{H}}}^{{{A}_{1}}}{pdA}-{{X}_{fri}}-{{X}_{sw}} \)            （2-10）

此式可以进一步简化。因为对于封闭体H1551H来说（图2-1）,若外表面作用有p_H的均匀压力，其合力为零，即

\({{p}_{H}}{{A}_{H}}+\int_{{{A}_{H}}}^{{{A}_{1}}}{{{p}_{H}}dA}+\int_{{{A}_{1}}}^{{{A}_{5}}}{{{p}_{H}}dA}-{{p}_{H}}{{A}_{5}}=0\)

将此式加在（2-10）式右方，得

\(F=\left[ \left( {{p}_{5}}-{{p}_{H}} \right){{A}_{5}}+{{\rho }_{5}}{{V}_{5}}^{2}{{A}_{5}} \right]-\left[ \left( {{p}_{5}}-{{p}_{H}} \right){{A}_{H}}+{{\rho }_{H}}{{V}_{H}}^{2}{{A}_{H}} \right] \)

\( -\int_{{{A}_{H}}}^{{{A}_{1}}}{\left( p-{{p}_{H}} \right)dA}-\int_{{{A}_{1}}}^{{{A}_{5}}}{\left( {{p}_{H}}-{{p}_{H}} \right)dA}-{{X}_{fri}}-{{X}_{sw}} \)      （2-11）

令   \(\int_{{{A}_{H}}}^{{{A}_{1}}}{\left( p-{{p}_{H}} \right)dA}={{X}_{ad}}\)                                         （2-12）

我们称X_ad为附加阻力。上式可写为

\(F={{\rho }_{5}}{{V}_{5}}^{2}{{A}_{5}}-{{\rho }_{H}}{{V}_{H}}^{2}{{A}_{H}}+\left( {{p}_{5}}-{{p}_{H}} \right){{A}_{5}}-{{X}_{ad}}-{{X}_{sw}}-{{X}_{fri}}\)         （2-13）

或者可写为

\(F={{\dot{m}}_{5}}{{V}_{5}}-{{\dot{m}}_{K}}{{V}_{H}}+\left( {{p}_{5}}-{{p}_{H}} \right){{A}_{5}}-{{X}_{ad}}-{{X}_{sw}}-{{X}_{fri}}\)               （2-14）

由上式可见，推力F是\(\left\{ {{{\dot{m}}}_{5}}{{V}_{5}}-{{{\dot{m}}}_{K}}{{V}_{H}}+\left( {{p}_{5}}-{{p}_{H}} \right){{A}_{5}} \right\}\)相减去三种阻力X_ad﹑X_sw﹑X_fri而得。为了以后讨论问题方便，给出如下不同定义的推力。

   5.不同定义的推力

下面给出名义推力(额定推力)﹑有效推力﹑净推力的概念。

（1）名义推力F_m

以未受干扰气流的HH界面与发动机出口55截面为基准而计算的推力。这里不考虑摩擦阻力并认为发动机外表面作用的是均匀的大气压力P_H。显然

\({{F}_{m}}={{\dot{m}}_{5}}{{V}_{5}}-{{\dot{m}}_{K}}{{V}_{H}}+\left( {{p}_{5}}-{{p}_{H}} \right){{A}_{5}}\)                              （2-15）

名义推力F_m是式（2-14）的前三项。

这里，我们引入截面冲量和富裕冲量的概念，分别用I和I_ex表示。

冲量：在所论截面上的冲量等于

\(I=\dot{m}V+\left( p-{{p}_{H}} \right)A\)                                       （2-16）

\(\dot{m}\)为该截面的质量流量。

富裕冲量：在所论截面上的富裕冲量等于

\({{I}_{ex}}=\dot{m}V+\left( p-{{p}_{H}} \right)A\)                                   （2-17）

有了冲量和富裕冲量的概念，可以简化推力公式，例如

\({{F}_{m}}={{I}_{ex5}}-{{I}_{exH}}\)                                           （2-18）

所以名义推力就是而基准面HH和55的富裕冲量之差。

为了以后计算和分析问题方便，将冲量公式表示为λ的函数形式：

\(I=\dot{m}V+pA=\left( \rho {{V}^{2}}+p \right)A= \)

\(\left[ \rho {{V}^{2}}+p \right]\frac{{\dot{m}}}{\rho V}=\dot{m}\left[ V+\frac{p}{\rho V} \right] \)

因为\(\frac{p}{\rho }=RT=R{{T}^{*}}\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)=\frac{k-1}{2k}{{a}_{cr}}^{2}\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)\)

而   \({{a}_{cr}}=\sqrt{\frac{2kR{{T}^{*}}}{k+1}}\)   ———临界速度

代入后，得

\( I=\dot{m}\left[ \frac{k+1}{2k}{{a}_{cr}}^{2}\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)\frac{1}{V}+V \right] \)

\(=\dot{m}{{a}_{cr}}\left[ \frac{k+1}{2k}\frac{1}{\lambda }\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)+\lambda \right] \)

\(=\frac{k+1}{2k}\dot{m}{{a}_{cr}}\left[ \frac{1}{\lambda }\left( 1-\frac{k-1}{k+1}{{\lambda }^{2}} \right)+\frac{k+1}{2k}\lambda \right] \)

\( =\frac{k+1}{2k}\dot{m}{{a}_{cr}}\left[ \frac{1}{\lambda }+\lambda \right] \)

\( =\frac{k+1}{2k}\dot{m}{{a}_{cr}}Z\left( \lambda \right) \)                      （2-19）

因而，名义推力F_m可以表示为λ等参数的函数，这是从推力公式中就更加明显的反映出发动机内﹑外部工作状态对推力的影响。关于这个问题将在以后有关文章节中详细讨论。

（2）有效推力F_e

这是以11截面和55截面为基准而计算的推力。采用富裕冲量的概念后可得

\({{F}_{e}}={{I}_{ex5}}-{{I}_{ex1}}\)                                              （2-20）

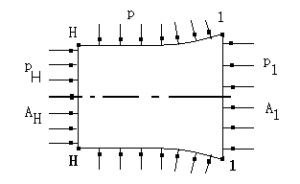
式中I_ex1是整个11截面上气流的富裕冲量。应用动量定理，可以求出11截面和HH截面上富裕冲量的关系。由图2-4可见

图2－4 HH截面和11截面间气流受力图

\({{p}_{1}}{{A}_{1}}-{{p}_{H}}{{A}_{H}}-\int_{{{A}_{H}}}^{{{A}_{1}}}{pdA=\dot{m}}\left[ \left( -{{V}_{1}} \right)-\left( -{{V}_{H}} \right) \right]\)

\({{\rho }_{1}}{{V}_{1}}^{2}{{A}_{1}}+{{\rho }_{H}}{{V}_{H}}^{2}{{A}_{H}}-{{p}_{H}}{{A}_{H}}=\int_{{{A}_{H}}}^{{{A}_{1}}}{pdA}\)

\(\left[ {{\rho }_{1}}{{V}_{1}}^{2}{{A}_{1}}+\left( p-{{p}_{H}} \right){{A}_{1}} \right]-\left[ {{\rho }_{H}}{{V}_{H}}^{2}{{A}_{H}}+\left( {{p}_{H}}-{{p}_{H}} \right){{A}_{H}} \right]=\int_{{{A}_{H}}}^{{{A}_{1}}}{\left( p-{{p}_{H}} \right)dA}\)

即： \({{I}_{ex1}}-{{I}_{exH}}={{X}_{ad}}\)                                           （2-21）

就是说，11截面与HH截面富裕冲量之差就是附加阻力。将（2-21）式代入（2-20）式，得

\({{F}_{e}}={{I}_{ex5}}-{{I}_{exH}}-{{X}_{ad}}\)

利用（2-18）式的关系，得

\({{F}_{e}}={{F}_{m}}-{{X}_{ad}}\)                                           （2-22）

因此，有效推力就等于名义推力减去附加阻力。

（3）净推力F_n

从名义推力中减去附加阻力X_ad前缘波阻X_sw﹑外壳摩擦阻力X_fri，净剩的推力称为净推力。因此

\({{F}_{n}}={{F}_{m}}-{{X}_{ad}}-{{X}_{sw}}-{{X}_{fri}}\)                                    （2-23）

以上三种不同的推力概念有其不同的用途。名义推力F_m比较容易计算的，在分析发动机的内流参数对推力的影响，采用名义推力也是比较方便的。有效推力的概念与一般喷气发动机的推力概念是一致的。从有效推力中扣去发动机本身的外部阻力（X_sw和X_fri），才是为飞行器所获得的推力，这个推力就是净推力。因此当需要综合衡量发动机设计的推力性能时，就要用到净推力的概念。因为冲压发动机和火箭——冲压组合发动机与飞行器的关系十分密切，目前已出现这样的布局，发动机和飞行器从结构上以结合成为一体，有些结构部件既属于飞行器的，也是属于发动机的。因此在设计发动机时，不仅要考虑发动机的有效推力，而且应考虑外部流动状况以及阻力的大小，只有把发动机的性能与飞行器的性能综合考虑并协调起来，才能得到合理的设计。

2．1．2 阻力的计算

前缘波阻X_sw与外壳摩擦阻力X_fri之和称为发动机的外阻力，这是气流在发动机外部造成的阻力。进入发动机内部的气流，因为摩擦﹑附面层分离以及加热等原因也产生阻力，称为内阻力。在计算推力时，内阻力的影响通过总压损失系数已反映在出口截面气流速度V₅上了。在计算推力的公式中没有明显的内阻力项，但已经把内阻力的作用考虑在内了。

（1）前缘波阻

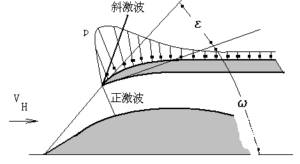
在超音速飞行时，在组合发动机进气道的前缘必然产生激波，如图2-5所示。气流通过波后，压力升高。波后压力作用在外壳外表面上形成向后方向的阻力，这就是前缘阻波的本质。

图2－5前缘波阻压力分布

知道了波后压力分布情况，可由下式计算波阻

\({{X}_{sw}}=\int_{{{A}_{1}}}^{{{A}_{5}}}{\left( p-{{p}_{H}} \right)}dA\)                                 （2-5）

式中P为波后气流的压力

若令\(\frac{p-{{p}_{H}}}{{{q}_{H}}}={{C}_{sw}}\)，而\({{q}_{H}}=\frac{1}{2}{{\rho }_{H}}{{V}_{H}}^{2}\)

并称C_sw为升压系数

即（2-5）可改为：

\({{X}_{sw}}=\int_{{{A}_{1}}}^{{{A}_{5}}}{{{C}_{sw}}{{q}_{H}}}dA=\overline{{{C}_{sw}}}{{q}_{H}}\left( {{A}_{5}}-{{A}_{1}} \right)\)                     （2-4）

式中\(\overline{{{C}_{sw}}}\)称为平均升压系数，使整个外壳外表面上C_sw的平均值。

前缘波后压力分布可由计算或实验确定。波后压力分布的计算方法有好几种，例如：

特征线法：利用超音速流动中气流参数沿着特征线的变化规律，作出特征线网络，逐点计算波后外壳表面的压力。

小干扰理论：这个理论假定气流沿外壳流动时所产生的参数变化是一种小干扰，在此基础上推导简化的压力计算公式，利用这个公式逐点计算波后外壳表面上的压力。

激波膨胀波理论：利用超音速气流通过激波﹑膨胀波后气流参数变化的规律，计算出压力分布情况。因为马赫数为M_H的气流是通过进口斜激波之后沿着外壳外表面流动的，而气流沿外壳流动是一个膨胀过程，又可利用膨胀波的关系式计算压力的变化。

所有这些方法都涉及比较深入的气流动力学的知识，这里不再详述。

当有跨音区存在时，压力P很难计算，只有依靠实验。

通过以上说明，可以看到波阻的大小与\(\overline{{{C}_{sw}}}\)和\(\left( {{A}_{5}}-{{A}_{1}} \right)\)成正比。\(\overline{{{C}_{sw}}}\)又与前缘斜激波的强度有关。当角度\(\left( \omega +\varepsilon \right)\)越大，前缘斜激波越强，\(\overline{{{C}_{sw}}}\)也越大。如果\(\left( \omega +\varepsilon \right)\)减小时，不仅\(\overline{{{C}_{sw}}}\)可以减小（即波后升压可以减小），而且轴向投影面积\(\left( {{A}_{5}}-{{A}_{1}} \right)\)也可以减小。但是ω角是由气流的进气角决定的，ε角取决于进气道前缘的结构强度，因此\(\left( \omega +\varepsilon \right)\)角度不能任意减小，因而波阻X_sw也不能任意减小。在进行进气道设计时，波阻是应该考虑的一个因素。

（2）外壳摩擦阻力

由于空气具有黏性，当发动机在空气中飞行时，气流与外壳表面之间存在相对运动，在紧贴外壳表面的一层气流中产生了速度梯度，因而存在剪切应力形成了摩擦阻力。计算外皮摩擦阻力的公式如下：

\({{\overline{X}}_{fri}}={{C}_{fri}}\cdot \frac{1}{2}{{\rho }_{H}}{{V}_{H}}^{2}{{A}_{fri}}\)                             （2-25）

式中   C_fri——摩擦阻力系数

A_fri——发动机外壳与外部气流发生摩擦阻力的表面，也即发动机外壳的

侧表面面积

根据气体动力学的知识可以知道，摩擦阻力系数C_fri是Re（雷诺数）的函数。对于紊流来说，C_fri可以用经验公式表示：

当\({{R}_{e}}\le {{10}^{6}}\)       \({{C}_{fri}}=\frac{0.074}{{{R}_{e}}^{\frac{1}{5}}}\)                             （2-26）

\({{R}_{e}}>{{10}^{6}}\)      \({{C}_{fri}}={{\left( \frac{0.242}{{{R}_{e}}gl} \right)}^{2}}\)                         （2-27）

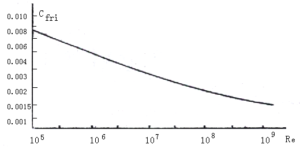
摩擦阻力系数C_fri与雷诺数Re的函数关系也可以用实验曲线表示，如图2-6所示。

图2－6 摩擦阻力系数C_fri与雷诺数Re的关系曲线

图中雷诺数\({{R}_{e}}=\frac{{{V}_{H}}\cdot d}{v}\)，式中d为外壳外表面直径，ν为空气的运动黏性系数。

外壳摩擦阻力与前缘波阻之和称为外部阻力，用X_out表示。

\({{X}_{out}}={{X}_{fri}}+{{X}_{sw}}\)

（3）附加阻力

前面已经叙述了附加阻力是名义推力与有效推力之差，是11截面与HH截面的富裕冲量之差，现在进一步讨论一下附加阻力是怎样形成的，它的物理本质是什么？

我们已经知道，在应用动量定理计算推力时，是在确定的气流流入截面与确定的气流流出截面之间进行的。气流流出截面一般取55截面，即喷管出口截面。气流流入截面的取法可以不同，在计算名义推力时取HH截面为气流流入截面，在计算有效推力时取11截面。由于HH截面上的富裕冲量可能小于11截面的富裕冲量，因此取HH截面为流入截面而计算的推力就必然大与实际有效的推力值。也就是说，为了计算上的方便，在计算名义推力时（它是用HH截面为流入截面的）就比发动机能发出的有效推力多计算了一部分似乎存在的推力。实际上这部分推力对发动机来说是不存在的。既然名义推力中多计算了一部分推力，就应该将这部分推力从名义推力中减去。为了与外阻力的名称统一起来，我们把从名义推力中应减去的部分\(\left( {{I}_{ex1}}-{{I}_{exH}} \right)\)就成为附加阻力。

对于进气道安装有中心锥的发动机，进气截面A₁是一个假想的界面，真实的进气截面是环形缝隙界面A_cir。可以证明，关系式

\({{X}_{ad}}=\int_{{{A}_{H}}}^{{{A}_{1}}}{\left( p-{{p}_{H}} \right)}dA={{F}_{m}}-{{F}_{e}}\)

仍然是适用的。

这里再强调说明一下，引入附加阻力的概念其目的是。为了便于计算推力，为了便于分析影响推力的各个因素。因为HH截面的气流未受中心锥的干扰，气流参数均匀。但是用HH截面为计算基准面也带来了矛盾，即多计算了一部分推力。采用了附加阻力的概念后就完满的解决了这个矛盾。

附加阻力与进气道前气流的流态密切有关，这是由（2-12）式可以明显的看出来的。带中心锥的超音速进气道，气流在进口前有三种流态，如图2-7所示。

当飞行马赫数正好等于额定马赫数（即M_H=M_rd）时，锥顶产生的斜激波正好交于进气道前缘，因此进口空气流柱的流线H-1没有通过斜激波,因而没有发生转折，它平行于发动机的X轴，如图2-7（b）所示。在此情况下A_H=A₁。

图2－7 超音速进气道的三种工况

所以   \({{X}_{ad}}=\int_{{{A}_{H}}}^{{{A}_{1}}}{\left( p-{{p}_{H}} \right)}dA=0\)

面积A_H对A₁的比值，也是一个重要的参数，用Ф_H表示，并称为流量系数，利用流量系数Ф_H可以表征进口气流的流态。关于它的物理意义以后进一步阐明。根据定义

\({{\Phi }_{H}}=\frac{{{A}_{H}}}{{{A}_{1}}}\)                                    （2-28）

因此，当M_H=M_rd时，

\({{\Phi }_{H}}=1,{{X}_{ad}}=0\)

当M_H<M_rd时，斜激波在进气道前缘之前通过，如图2-7（a）所示。空柱的流线H-1经过斜激波时发生转折，因此不再平行X轴,这时A_H<A₁,因此

\({{\Phi }_{H}}<1,p\ge {{p}_{H}}\)

即： \({{X}_{ad}}=\int_{{{A}_{H}}}^{{{A}_{1}}}{\left( P-{{P}_{H}} \right)}dA>0\)

也就是说，当φ_H<1时，就出现附加阻力。

当M_H>M_rd时，斜激波进入进气道口内，空气柱流线H-1也不发生转折，因此

\({{\Phi }_{H}}=1\)     \({{X}_{ad}}=0\)

对于超音速飞行的进气道来说，Ф_H不可能大于1。因为超音速气流是不能自然拐弯的，只有通过激波或膨胀波时超音速气流才会发生转折。气流在进口前没有变化，当然也没有冲量变化，也就不出现附加阻力。

附加阻力与动力q_H乘最大迎风面截面A_max之比，可以取A_max=A₁叫做附加阻力系数C_xad

\({{C}_{xad}}=\frac{{{X}_{ad}}}{{{q}_{H}}{{A}_{\max }}}=\frac{{{X}_{ad}}}{{{q}_{H}}{{A}_{1}}}\)                                 （3-29）

附加阻力系数C_xad随Ф_H的变化，如图2-8所示。由图可见，随着Ф_H的下降（进气道越偏离额定工作状态），附加阻力系数不断增大。

图2－8 附加阻力系数与流量系数的关系曲线

对于不同的进气道，流量系数Ф_H相同条件下， 附加阻力系数也是可以不同的，从减小附加阻力的角度来看，进气道在超临界状况是可取的。关于进气道的亚临界或超临界等工况，将在第三章（进气道）中讨论。

由以上情况可以看到，附加阻力与内流的设计（例如进口气流的流态﹑气流在进口前的激波形式等）有关。为了减小附加阻力，使流量系数Ф_H尽量接近于1是有利的。

知道了HH截面和环形缝隙截面1CC1的气流参数以后，可以设计附加阻力。HH截面上的气流参数由飞行状态决定，至于环形截面上的气流参数如何确定将在第三章中阐述。

如前所述，附加阻力是在流量系数Ф_H<1的情况下产生的，我们以图2-7（a）的流态进行计算。利用图2-3所示的受力图，由（2-9）式得

\(\int_{{{A}_{H}}}^{{{A}_{1}}}{p}dA={{\left[ \left( p+\rho {{V}^{2}} \right)A\cos {{\delta }_{avg}} \right]}_{cir}}-{{\left[ \left( p+\rho {{V}^{2}} \right)A \right]}_{H}}+{{X}_{\text{con}}}+{{p}_{c}}{{A}_{c}}\)

\({{X}_{ad}}=\int_{{{A}_{H}}}^{{{A}_{1}}}{\left( p-{{p}_{H}} \right)}dA={{\left[ \left( p+\rho {{V}^{2}} \right)A\cos {{\delta }_{avg}} \right]}_{cir}}- \)

\({{\left[ \left( p+\rho {{V}^{2}} \right)A \right]}_{H}}+{{X}_{\text{c}}}+{{p}_{\text{c}}}{{A}_{\text{c}}}-{{p}_{H}}\left( {{A}_{1}}-{{A}_{H}} \right) \)

因为  \( \rho {{V}^{2}}A=\frac{p}{RT}{{V}^{2}}A=\frac{1}{kRT}kp{{V}^{2}}A \)

\( =kpA\frac{{{V}^{2}}}{{{a}^{2}}}=k{{M}^{2}}pA \)

代入上式，得

\({{X}_{ad}}=k{{M}_{cir}}^{2}{{p}_{cir}}{{A}_{cir}}\cos {{\delta }_{avg}}+{{p}_{cir}}{{A}_{cir}}\cos {{\delta }_{avg}}-k{{M}_{H}}^{2}{{p}_{H}}{{A}_{H}} \)

\( +{{p}_{\text{c}}}{{A}_{\text{c}}}+{{X}_{\text{c}}}-{{p}_{H}}{{A}_{1}} \)

所以 \( {{X}_{ad}}={{p}_{cir}}{{A}_{cir}}\cos {{\delta }_{avg}}\left( 1+k{{M}_{cir}}^{2} \right)-k{{M}_{H}}^{2}{{p}_{H}}{{A}_{H}}-{{p}_{H}}{{A}_{1}} \)

\( +{{\overline{p}}_{\text{c}}}{{A}_{\text{c}}}+{{X}_{\text{c}}} \)

（2-31）

因为 \({{q}_{H}}=\frac{1}{2}{{\rho }_{H}}{{V}_{H}}^{2}=\frac{1}{2}\frac{{{p}_{H}}}{R{{T}_{H}}}{{V}_{H}}^{2}=\frac{1}{2}k{{p}_{H}}{{M}_{H}}^{2}\)                 （2-32）

\({{C}_{xad}}=\frac{{{X}_{ad}}}{{{q}_{H}}{{A}_{1}}}\)

因此  \({{C}_{xad}}=\frac{2}{k{{M}_{H}}^{2}}\left\{ \frac{{{p}_{cir}}}{{{p}_{H}}}\frac{{{A}_{cir}}}{{{A}_{1}}}\left( 1+k{{M}_{cir}}^{2} \right)\cos {{\delta }_{avg}}-{{\Phi }_{H}}k{{M}_{H}}^{2}-1+\frac{\overline{{{p}_{c}}}{{A}_{c}}}{{{p}_{H}}{{A}_{1}}} \right\} \)

\(+{{C}_{\text{xc}}} \)       （2-33）

式中 \({{C}_{\text{xc}}}=\frac{{{X}_{\text{c}}}}{{{q}_{H}}{{A}_{1}}}\)，并称为中心锥摩擦阻力系数。

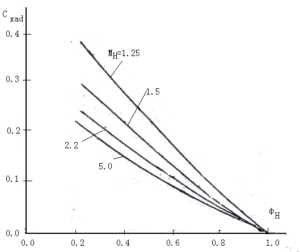
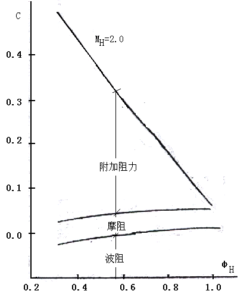
由（2-33）式可以看出C_xad与M_H﹑Ф_H等参数的关系，图2-9就表示了这种关系式。

为了尽可能的增加提供飞行器使用的净推力，必须努力减小各种阻力。当流量系数接近于1时，附加阻力越来越小，但外阻却在增大。然而附加阻力减小的量大，外阻增加的量小，所以总的阻力随Ф_H接近于1而下降，如图2－9所示。从降低阻力的角度来看，在外壳设计要尽可能降低外阻，在内流设计时使流量系数接近于1以降低附加阻力。

图2－9 阻力系数随变化的关系

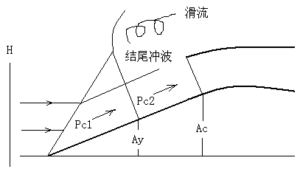
图2－10 亚临界流动情况

当外压式超音速扩压器为亚临界溢流情况时，进口气流状态如图2-10所示。在此情况下，结尾激波吐出口外，使得中心锥面上的净压必须分段计算。因此（2-33）中的\[\frac{\overline{{{p}_{\text{c}}}}{{A}_{\text{c}}}}{{{p}_{H}}{{A}_{1}}}\]项用下式代替。

\[\frac{\overline{{{p}_{\text{c}}}}{{A}_{\text{c}}}}{{{p}_{H}}{{A}_{1}}}=\frac{\overline{{{p}_{c1}}}{{A}_{y}}}{{{p}_{H}}{{A}_{1}}}+\frac{\overline{{{p}_{c2}}}\left( {{A}_{c}}-{{A}_{y}} \right)}{{{p}_{H}}{{A}_{1}}}\]                   （2-34）

计算上式，关键在于封口激波前移的位置不好确定，即截面积A_y不好确定。关于这个问题可参阅资料ARC-RM3035。

2．2发动机的推力特性

可以说明发动机推力特性的性能参数有：

（1）推力：不同定义的推力和计算方法已在上面一节阐述。

（2）推力系数：在分析冲压发动机和固体火箭冲压发动机性能时，常把推力系数作为发动机的推力特性参数，所谓推力系数就是单位迎面推力与迎面气流动压头q_H的比值，即

\({{C}_{F}}=\frac{{{F}_{m}}}{{{q}_{H}}\times {{A}_{\max }}}\)

一般常采用名义推力F_m，并取发动机最大横截面积A_max为特性截面，因而

\({{C}_{F}}=\frac{{{F}_{m}}}{\frac{1}{2}{{\rho }_{H}}{{V}_{H}}^{2}\cdot {{A}_{\max }}}\)                               （2-35）

应当注意，这里的推力系数与火箭发动机中的推力系数的概念是不相同的。

当然，特性截面可以不取为最大截面A_max，例如也可以取为进口截面A₁或进口流束界面A_H，究竟取哪个截面视分析问题是方便而定。

为什么把推力系数作为发动机的推力特性参数常常是方便的呢？因为推力系数与阻力系数很相似，采用推力系数后易于将发动机与飞行器联系起来进行分析。特别在研究可用推力和飞行器的需要推力时，使用推力系数的概念就特别方便。此外，C_F值与飞行高度的关系较小（在第八章中详细讨论），因此C_F仅与一个外界参数——飞行数M有关，而不是与两个外界参数M_H﹑H有关。

（3） 单位迎面推力与单位质量推力：因为组合发动机用于导弹等飞行器上，因而发动机的质量﹑外廓尺寸等因素具有很大意义，一般来说，要求在发动机质量和外廓尺寸最小的情况下产生需要的推力。

但是对于发动机质量和外廓尺寸的要求程度，在很大程度上取决于安装发动机的飞行器。对于重型飞行器来说，发动机的质量和外廓尺寸并不像工作时间短的较轻型的飞行器那样重要，然而在有些情况下发动机的质量和外廓尺寸甚至是确定采用发动机形式的主要因素。

说明发动机质量和外廓尺寸的性能指标，往往与发动机的推力特性结合在一起。发动机的单位迎面推力F_A是发动机推力和最大横截面积之比，

\({{F}_{A}}=\frac{{{F}_{m}}}{{{A}_{max}}}\)                                   （2-36）

而推力系数也是单位迎面推力与迎面气流动压头的比值，即

\({{C}_{F}}=\frac{{{F}_{A}}}{{{q}_{H}}}\)                                     （2-37）

因而推力系数C_F完全可以用来评价发动机的单位迎面推力。

发动机的单位质量推力是发动机推力和发动机总重的比值，

\({{F}_{G}}=\frac{{{F}_{m}}}{{{m}_{m}}}\)                                    (2-38)

发动机单位质量推力F_G的倒数，称为发动机的比重γ_G

\({{\gamma }_{G}}=\frac{{{C}_{F}}}{{{F}_{m}}}\)                                    （2-39）