第三章 流场模拟计算
流场模拟计算是运用计算流体动力学(Computational Fluid Dynamics简称CFD)技术,利用计算机对流体相关问题进行数值仿真,利用图像的形式显示仿真计算结果,对包含有流动、传热等相关物理问题的系统所进行的数值计算和仿真分析。CFD技术是伴随计算机迅猛发展而诞生的新学科,其计算原理主要建立在经典流体力学和数值分析的基础上而形成的。CFD技术通过把时间上和空间上的连续物理量进行离散化处理,通过数值分析的插值方法求解出场变量的近似值。随着时间的推移,CFD技术计算结果更加符合实际。
3.1 通用流场模拟计算
经过几十年的发展,CFD技术进步很大,CFD分析技术已经广泛应用于取代一些经典力学中的近似计算方法和图解的方法,并得到了不错的分析结果。目前,CFD计算方法已经完全可以解决绝大多数与流体和传热相关的问题,只要有流体存在,就会涉及流体分析的各行各业,如水利工程、航空航天、流体机械、土木工程等领域,一些典型的应用场合如下:
- 航空航天飞行器的设计研发
- 风机、水泵和轮机等流体机械的流动分析
- 汽车行驶流场、噪声、阻力及内燃机燃烧、冷却分析等
- 建筑通风性和稳定性分析
- 电池、电子器件的热管理分析
- 室内环境温度及内流场状态分析
- 细菌在食品中的运移分析
CFD技术已经深入到社会的各行各业,是产品研发中重要的辅助手段,对减少产品研发周期和减少研发成本具有重要的意义。
3.1.1计算流体力学三个控制方程及离散化方法
流体动力学的基本控制方程主要有三个,即:质量守恒方程,动量守恒方程和能量守恒方程。面对特殊问题的求解还需要其他的控制方程,如要分析含有多种成分的流体问题时,会用到组分质量守恒方程;如涉及流体系统流动紊乱,处于湍流流动状态,还需要湍流控制方程。本小节只对流体分析中的三大基本控制方程进行介绍。
- 质量守恒方程
质量守恒方程是基本控制方程之一,所有流动问题都必须满足质量守恒方程,该方程的含义为:在单位时间内,流体微元质量的增加等于同一时间段内流入该微元的净质量。
\(\frac{\partial \rho }{\partial t}\text{+}\frac{\partial \left( \rho u \right)}{\partial x}\text{+}\frac{\partial \left( \rho v \right)}{\partial y}\text{+}\frac{\partial \left( \rho w \right)}{\partial z}=0\) (3-1)
通过引入矢量符号
\(\text{div}\left( a \right)={\partial {{a}_{x}}}/{\partial x}\;+{\partial {{a}_{y}}}/{\partial y}\;+{\partial {{a}_{z}}}/{\partial z}\;\) (3-2)
可将式3-1写成以下形式
\(\frac{\partial \rho }{\partial t}\text{+div}\left( \rho U \right)=0\) (3-3)
在上式中,ρ是流体密度,单位kg/m3;t是时间,单位s;U是速度矢量,u、v、w分别为U在x、y、z三个方向上的分量,单位m/s。
式3-1所列公式为瞬态三维可压缩的质量守恒方程,如果流体不可压缩,即流体密度ρ为常数,可以得到:
\(\text{div}\left( U \right)=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0\) (3-4)
- 动量守恒方程
动量守恒方程也是所有流动问题必须遵循的三个基本方程之一,该方程可以描述为:在流体微元中,动量的变化率等于所有作用在该微元上的外力之和,即俗称的第二牛顿定律。通常,动量守恒方程还被称为Navier-Stokes方程,具体表达式如下:
\(\frac{\partial \left( \rho u \right)}{\partial t}+\text{div}\left( \rho uU \right)=\text{div}\left( \mu \text{grad}u \right)-\frac{\partial p}{\partial x}+{{S}_{u}}\) (3-5)
\(\frac{\partial \left( \rho v \right)}{\partial t}+\text{div}\left( \rho vU \right)=\text{div}\left( \mu \text{grad}v \right)-\frac{\partial p}{\partial y}+{{S}_{v}}\) (3-6)
\(\frac{\partial \left( \rho w \right)}{\partial t}+\text{div}\left( \rho wU \right)=\text{div}\left( \mu \text{grad}w \right)-\frac{\partial p}{\partial z}+{{S}_{w}}\) (3-7)
式中,\(\text{grad}u\left( {} \right)\text{=}{\partial \left( {} \right)}/{\partial x}\;+{\partial \left( {} \right)}/{\partial y}\;+{\partial \left( {} \right)}/{\partial z}\;\),是梯度计算公式,Su、Sv、Sw是动量方程的广义源项,表达式如下:
\({{S}_{u}}\text{=}\frac{\partial }{\partial x}\left( \mu \frac{\partial u}{\partial x} \right)+\frac{\partial }{\partial y}\left( \mu \frac{\partial v}{\partial x} \right)+\frac{\partial }{\partial z}\left( \mu \frac{\partial w}{\partial x} \right)+\frac{\partial }{\partial x}\left( \lambda \text{div}U \right)+{{F}_{x}}\) (3-8)
\({{S}_{v}}\text{=}\frac{\partial }{\partial x}\left( \mu \frac{\partial u}{\partial y} \right)+\frac{\partial }{\partial y}\left( \mu \frac{\partial v}{\partial y} \right)+\frac{\partial }{\partial z}\left( \mu \frac{\partial w}{\partial y} \right)+\frac{\partial }{\partial y}\left( \lambda \text{div}U \right)+{{F}_{y}}\) (3-9)
\({{S}_{w}}\text{=}\frac{\partial }{\partial x}\left( \mu \frac{\partial u}{\partial z} \right)+\frac{\partial }{\partial y}\left( \mu \frac{\partial v}{\partial z} \right)+\frac{\partial }{\partial z}\left( \mu \frac{\partial w}{\partial z} \right)+\frac{\partial }{\partial z}\left( \lambda \text{div}U \right)+{{F}_{z}}\) (3-10)
- 能量守恒方程
如果问题涉及到温度场分析,往往需要能量守恒方程,该方程的含义为:在流体微元中能量增加率为进入该流体单元的净热流量和外力对该微元做功之和,方程表达式如下:
\(\frac{\partial \left( \rho T \right)}{\partial t}+\text{div}\left( \rho UT \right)=\text{div}\left( \frac{k}{{{C}_{p}}}\text{grad}T \right)+{{S}_{T}}\) (3-11)
将上式展开后可得:
\(\frac{\partial \left( \rho T \right)}{\partial t}+\frac{\partial \left( \rho uT \right)}{\partial x}+\frac{\partial \left( \rho vT \right)}{\partial y}+\frac{\partial \left( \rho wT \right)}{\partial z}= \)
\(\frac{\partial }{\partial x}\left( \frac{k}{{{C}_{p}}}\frac{\partial T}{\partial x} \right)+\frac{\partial }{\partial y}\left( \frac{k}{{{C}_{p}}}\frac{\partial T}{\partial y} \right)+\frac{\partial }{\partial z}\left( \frac{k}{{{C}_{p}}}\frac{\partial T}{\partial z} \right)+{{S}_{T}} \)
(3-12)
在式中,T为温度,单位K;Cp为比热容,单位J/kg.K;k为传热系数,单位W/m2.K;ST为流体的粘性耗散项。
流体的能量守恒方程虽然是基本控制方程之一,但若流体的换热量非常小,甚至是可以忽略时,一般不会引用能量方程。
由于理论推导的不同,离散化方法较多,常用的有有限差分法、有限体积法和有限元法,具体介绍如下:
- 有限差分法
有限差分法(Finite Difference Method,FDM)是比较经典的数值计算方法,这种方法计算简便,应用的场合较多。有限差分法将求解区域划分为差分网格,并将信息储存于网格节点之中,然后利用差商去替代偏微分方程的导数,推导出离散点上未知数的差分方程组,求解这些代数方程组的解,也就可以获得偏微分方程组的数值近似解,这是将偏微分方程转化为代数方程组进行求解的数值分析方法。
- 有限体积法
有限体积法(Finite Volume Method,FVM),也被称为控制体积法(Control Volume Method,CVM),这种方法发展较晚,近几年应用较多,这种离散方法的计算效率非常高,被广泛应用于各个CFD数值分析领域。有限体积法的基本思想是将计算区域划分为不同的控制体积,每一个控制体积都包含有一个节点,并将待求解变量储存在控制体积的节点之上,然后将待求解的微分方程对每个控制体积进行积分,这样就得到了一组离散方程。有限体积法的基本思想是因变量在控制体积中的守恒,思想原理较为简单,理解起来方便,可以从思想原理中得到直接的物理意义。
一般来说有限体积法的精确性要高于有限差分法,即使网格质量不佳,也可以得到较为理想的结果。因此,有限体积法被广泛应用于各大流体计算软件当中,如Fluent和STAR-CCM+等。
- 有限元法
有限元法(Finite Element Method,FEM)在流体动力学领域应用较少,其发展较早,由于它的基本思想是极值原理和划分差值,同时又采用了变分计算中的选择逼近函数对求解区域进行积分的方法,所以有限元法具有很强的适应性。但其求解速度比有限体积法和有限差分法都要慢,因此,一般的CFD分析软件使用有限元法较少。
3.1.2 CFD分析软件及求解流程
CFD软件种类繁多,但真正实现商业化应用的并不是很多,目前市场上通用的CFD软件主要有Fluent、STAR-CD、CFX、PHOENICS。
- Fluent
Fluent最早由美国流体技术服务软件creature推出,后来被ANSYS收购并推出许多新的版本和增加新的功能。该软件是较早进入市场的商用流体力学计算软件。Fluent是基于有限体积法的商用计算软件,功能强大且计算可靠性高。在目前计算流体力学软件中,Fluent的应用最为广泛,在美国的市场占有率可达60%左右,在国内市场同样成为了许多研发机构采用的首选计算流体力学软件,得到了广泛的认可。
Fluent主要优点之一体现在网格特性方面,Fluent提供了非常多样化的网格类型,支持三角形、四边形面网格和四面体、六面体、金字塔形体网格,以及混合型非结构网格,用以复杂问题的求解。同时,Fluent还提供了强大网格处理功能,使用者可以根据所要求解的具体问题对网格进行加密和细化,保证计算精度,得到更可靠的计算结果。
Fluent的另外一个优点是可以求解不同类型的问题,如可以解决二维平面问题、三维流动问题、轴对称问题分析等,也可以完成不可压流分析、可压缩流分析、湍流分析、层流分析、定常分析、非定常分析、传热分析、多孔介质分析以及化学反应分析等,在计算湍流问题时,可根据实际情况和需要选择不同的湍流模型,Fluent可选择的湍流模型有: 模型、雷诺应力模型(Renolds)、标准壁面函数、大涡模型(LES)以及双层近壁模型等。但也有其不完善的地方,如工作界面不友好。
- STAR-CD
STAR-CD由CD-adapco公司开发。该软件同样具有强大的功能,不仅可以计算常规的流体问题,还可以进行超音速计算、多相流计算、热舒适性分析等,同时软件自带网格划分功能,软件具有良好的用户界面,它将建模、求解、后处理和所有数学模型、物理模型以及算法全部都整合到一个软件包中,操作流程化,使用方便。STAR-CD同样具有多种求解器和不同的湍流模型,以及大量的差分格式,计算功能强大。
STAR-CCM+是CD-adapco公司生产的新一代产品,STAR-CCM+采用了领先于其他软件的连续介质数值分析技术,在汽车行业领域应用最为广泛,可用于汽车外流场分析、空气动力学分析、电动汽车的电池散热分析、乘员舱热舒适性分析、传统汽车发动机舱散热分析以及空调除霜除雾性能分析等。STAR-CCM+将建模、前处理、网格生成与处理、数值分析以及后处理集中于统一的工作界面,操作方便。
- CFX
CFX是由英国AEA Technology公司开发的一款为解决其遇到的工业实际问题而开发的一款专业CFD分析软件,其计算可靠性高,物理模型丰富,该软件所解决的实际案例丰富,应用较广。该软件采用了基于有限元的有限体积法,兼顾了有限体积法和有限元法的优点,保证了计算的准确性,但求解速度缓慢。对于旋转机械,该软件还提供了一体化的专业解决方案,功能强大。
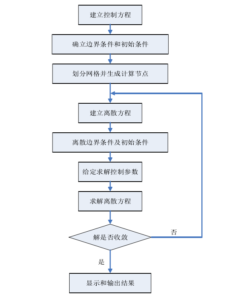
只要涉及到流体问题,无论是气体流动、液体流动、还是燃烧反应、传热问题等,都拥有一套相同的计算流程,都需要建立三维模型,对模型进行前处理、网格划分、模型设置、参数选择与设置、求解计算、后处理。如在进行工程分析是一般使用专业的CFD软件,针对所要分析的问题,选择合适的控制方程、离散格式、湍流模型、边界条件和初始条件,并根据实际需要设定其他的一些边界条件。划分网格时,对于二维问题,一般采用三角形或者四边形网格;对于三维问题,一般采用四面体、六面体或者三棱体网格。对于曲率较大的拐角或其他一些重要的区域,网格需要加密,在边界处要绘制出一定厚度的边界层,便于对小尺度的层流进行分析。在进行流体分析时,一般采用有限体积法的离散化方法。给定初始条件和边界条件,并将其赋予到已划分好的网格或者节点上,再设定求解收敛条件便可进行计算,并对计算结果进行后处理,通过流线图、矢量图、标量图以及X-Y曲线图加以显示,根据结果图和相关数据对流体问题进行评价。CFD通用的求解流程如图3.1所示。
图3.1 CFD分析求解流程
3.2 计算实例
CFD软件种类繁多,但真正实现商业化应用的并不是很多,目前市场上通用的CFD软件主要有Fluent、STAR-CD、CFX、PHOENICS。
3.2.1 固体火箭发动机点火瞬态流场模拟计算
点火过程是固体火箭发动机开始工作的起始阶段,也是固体火箭发动机工作过程的重要组成部分,点火过程的完善程度直接影响固体火箭发动机的性能、工作效率以及可靠性和安全性,正确认识点火过程对固体火箭分析、设计、改进等意义重大。
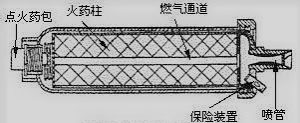
在固体火箭发动机的点火过程中,点火讯号的能量输出经过发货系统和能量释放系统的传递和放大后,点火器产生高温的燃烧产物,喷射到推进剂装药表面和装药通道中,随后经历一系列复杂的物理化学过程,才完成点火。
图3.2 固体火箭发动机
固体火箭发动机点火瞬态过程是一个机理复杂的非定常过程,包括药柱加热、局部点燃、火焰沿药柱表面传播和燃烧室增压等过程。正常点火条件下应保证固体推进剂全部表面在整个使用温度范围内都能可靠的点燃,并在较短的时间内进入预定的稳定燃烧状态,建立起正常的点火压力。如果点火瞬态过程发生异常,可能会导致发动机点火失败。
根据点火过程在时间过程上的不同阶段进行分析讨论,点火过程可以分为:点火药引燃和燃烧;点火药燃烧产物向装药表面传热;装药的局部点燃;火焰沿整个装药表面的传播等环节。
(1) 点火机理
点火药燃烧产生的热量是点燃推进剂的主要能源。点火药的基本特点是火焰温度高、燃速快、本身容易点燃。在点火装置中,点火药的点燃常用桥丝式发火管,通电后使发火系统启动工作,发火系统再点燃点火药,这个过程很短,由点火装置确定。
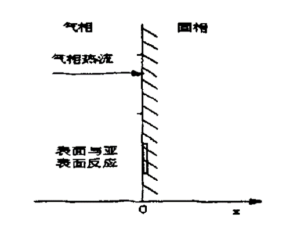
固相着火理论认为着火过程是由固体推进剂内部的温度来控制的。该理论不考虑气相的放热和质量扩散以及非均相化学反应的作用。由于不考虑气相控制方程,故数学表达式大为简化,但也正因为如此,该理论不能预示环境氛围的影响。固相点火理论的示意图如下:
图3.2 固相点火机理
固相点火理论所涉及的控制方程、初始和边界条件如下:
控制方程:
\({{\rho }_{P}}{{c}_{gr}}\frac{\partial {{T}_{P}}}{\partial t}={{\lambda }_{P}}\left( \frac{{{\partial }^{2}}{{T}_{P}}}{\partial {{x}^{2}}} \right)+{{\rho }_{P}}{{Q}_{P}}Z\exp \left( -\frac{E}{R{{T}_{P}}} \right)\) (3-13)
式中,ρP推进剂药柱密度,t时间,Cgr推进剂药柱比热容,QP反应热,TP推进剂药柱温度,x到气/固界面距离,λP推进剂药柱导热系数,E活化能,R气体摩尔常数,Z指前因子。
初始条件:
x=0 \({{\dot{q}}_{n}}+{{\rho }_{P}}{{r}_{b}}{{Q}_{P}}=-{{\lambda }_{P}}\left( \frac{\partial {{T}_{P}}}{\partial x} \right)\)
边界条件:
t=0 TP=T0
\(x=\infty \) \(T={{T}_{0}}={{T}_{\infty }}\)
式中,\({{\dot{q}}_{n}}\)温度梯度所引起的环境与推进剂表面间的能量传输;T0推进剂初始温度。
即认为:
- 主装药点燃前,不发生相变和化学反应;
- 主装药表面温度达到点火温度Tig时,推进剂立即被点燃。
(2) 数学模型
对模型均采用以下假设条件:
- 点火瞬态忽略两相流,涉及到三种气体,分别为空气、点火燃气和固体推进剂燃气。对应本小节给定相应算例,假定这三种气体具有同样得物性参数。至于点火燃气和推进剂燃气的密度和比热,通过换算分别应用到其所使用的UDF(用户自定义,编译写入fluent)源项的质量和能量项中;
- 在点火瞬态过程的计算过程中,假定固体推进剂具有恒定的热传导系数;
- 计算过程中,认为推进剂的化学反应在推进剂源项加质的一薄层内进行完全,在燃烧室内各种气体组分的成分不再发生变化;
- 由于点火滞后时间相对发动机工作过程,时间相当短暂,本节计算过程中不考虑燃烧室体积的变化,认为燃烧室体积是恒定的;
- 忽略侵蚀燃烧的影响;
- 忽略点火器的点火延迟时间。
从而对三维模型燃气的控制方程、药柱能量守恒方程做简化。
三维模型燃气的控制方程:
1)质量守恒方程:
\(\frac{\partial \rho }{\partial t}+\frac{\partial \left( \rho u \right)}{\partial x}+\frac{\partial \left( \rho v \right)}{\partial y}+\frac{\partial \left( \rho w \right)}{\partial z}=0\) (3-14)
2)x方向动量守恒方程:
\( \frac{\partial \left( \rho u \right)}{\partial t}+\frac{\partial \left( \rho uu \right)}{\partial x}+\frac{\partial \left( \rho uv \right)}{\partial y}+\frac{\partial \left( \rho uw \right)}{\partial z}+\frac{\partial P}{\partial x} \)
\(=\frac{1}{Re}\left( \frac{\partial {{\tau }_{xx}}}{\partial x}+\frac{\partial {{\tau }_{xy}}}{\partial y}+\frac{\partial {{\tau }_{xz}}}{\partial z} \right) \)
(3-15)
- y方向动量守恒方程:
\( \frac{\partial \left( \rho v \right)}{\partial t}+\frac{\partial \left( \rho vu \right)}{\partial x}+\frac{\partial \left( \rho vv \right)}{\partial y}+\frac{\partial \left( \rho vw \right)}{\partial z}+\frac{\partial P}{\partial y} \)
\( =\frac{1}{Re}\left( \frac{\partial {{\tau }_{yx}}}{\partial x}+\frac{\partial {{\tau }_{yy}}}{\partial y}+\frac{\partial {{\tau }_{yz}}}{\partial z} \right) \)
(3-16)
- z方向动量守恒方程:
\( \frac{\partial \left( \rho w \right)}{\partial t}+\frac{\partial \left( \rho wu \right)}{\partial x}+\frac{\partial \left( \rho wv \right)}{\partial y}+\frac{\partial \left( \rho ww \right)}{\partial z}+\frac{\partial P}{\partial z} \)
\(=\frac{1}{Re}\left( \frac{\partial {{\tau }_{zx}}}{\partial x}+\frac{\partial {{\tau }_{zy}}}{\partial y}+\frac{\partial {{\tau }_{zz}}}{\partial z} \right) \)
(3-17)
- 能量守恒方程:
\( \frac{\partial \left( \rho e \right)}{\partial t}+\frac{\partial \left( \rho ue \right)}{\partial x}+\frac{\partial \left( \rho ve \right)}{\partial y}+\frac{\partial \left( \rho we \right)}{\partial z}+\frac{\partial \left( Pu \right)}{\partial x}+\frac{\partial \left( Pv \right)}{\partial y}+\frac{\partial \left( Pw \right)}{\partial z} \)
\( =\frac{1}{Re}\frac{\partial \left( {{\tau }_{xx}}u+{{\tau }_{xy}}v+{{\tau }_{xz}}w+{{q}_{x}} \right)}{\partial x}+\frac{1}{Re}\frac{\partial \left( {{\tau }_{yx}}u+{{\tau }_{yy}}v+{{\tau }_{yz}}w+{{q}_{y}} \right)}{\partial y} \)
\( +\frac{1}{Re}\frac{\partial \left( {{\tau }_{zx}}u+{{\tau }_{zy}}v+{{\tau }_{zz}}w+{{q}_{z}} \right)}{\partial z} \)
(3-18)
- 状态方程:
\(P=\rho RT\) (3-19)
在上述基本方程中,内能\(e=\frac{RT}{\gamma -1}+\frac{1}{2}\left( {{u}^{2}}+{{v}^{2}}+{{w}^{2}} \right)\);
\({{\tau }_{xx}}=-\frac{2}{3}\mu \left( \nabla \cdot \vec{V} \right)+2\mu \frac{\partial u}{\partial x}\);
\({{\tau }_{yy}}=-\frac{2}{3}\mu \left( \nabla \cdot \vec{V} \right)+2\mu \frac{\partial v}{\partial y}\);
\({{\tau }_{zz}}=-\frac{2}{3}\mu \left( \nabla \cdot \vec{V} \right)+2\mu \frac{\partial w}{\partial z}\);
\(\nabla \cdot \vec{V}\text{=}\frac{\partial u}{\partial x}\text{+}\frac{\partial v}{\partial y}\text{+}\frac{\partial w}{\partial z}\);
\({{\tau }_{xy}}=\mu \left( \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y} \right)\);
\({{\tau }_{xz}}=\mu \left( \frac{\partial w}{\partial x}+\frac{\partial u}{\partial z} \right)\);
\({{\tau }_{yz}}=\mu \left( \frac{\partial v}{\partial z}+\frac{\partial w}{\partial y} \right)\);
\({{q}_{x}}=K\frac{\partial T}{\partial x}\);
\({{q}_{y}}=K\frac{\partial T}{\partial y}\);
\({{q}_{z}}=K\frac{\partial T}{\partial z}\)。
而u、v、w分别为笛卡尔坐标系下各个方向的速度分量。ρ、T、P、μ、K分别为气体的密度、温度、压强、动力粘性系数和热传导率。R为气体常数,γ为比热比,Re为雷诺数。
药柱能量守恒方程:
假定药柱内无热源,固体推进剂与气相点火燃气的能量守恒方程为:
\(\frac{d}{dn}\left[ {{\lambda }_{P}}\frac{d{{T}_{P}}}{dn} \right]-{{\rho }_{P}}{{C}_{P}}r\frac{d{{T}_{P}}}{dn}+{{Q}_{P}}=0\) (3-20)
式中,λP为推进剂导热系数,本节认为是常数;TP为推进剂温度;ρP为推进剂密度;
CP为推进剂比热容;r为推进剂燃速;QP为单位体积推进剂在单位时间内固相反应所放出的能量;n为推进剂外法线方向。
药柱未点燃前,质量源项\(\dot{m}\)和动量源项\(\dot{m}h\)均为零;
药柱点燃后:
质量源项 \(\dot{m}={{\rho }_{P}}rA\) (3-21)
能量源项 \(\dot{m}h={{\rho }_{P}}rA{{c}_{P}}{{T}_{g}}\) (3-22)
式中,ρP为推进剂密度;A为推进剂点燃面积;P为燃烧室压力;燃速\(r=a{{P}^{n}}\),其中a为常数,n为推进剂燃速压力指数;cP为燃气定压比热;Tg为燃气温度。
湍流模型选用针对湍流发展非常充分,适应于各向同性湍流的标准\(-\varepsilon \)湍流模型。
(3) 内孔形装药发动机三维数值分析
在总结已有研究成果的基础上,对一内孔形装药发动机的点火瞬态过程作3.2.2节中所述简化,考虑了点火瞬态过程中燃气与固体推进剂之间的对流与导热,建立了点火瞬态过程的数学模型,对其进行数值模拟从而得到点火瞬态过程的压强-时间曲线及各时刻的流场以及推进剂表面温度变化情况。
流域几何模型:
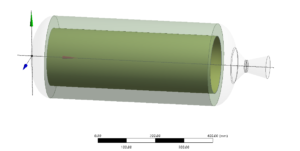
发动机几何模型被分内流域、源相区、固相域。在流场数值计算时,考虑内流域和源相区为一个整体,点火燃气从内流域前点火入口流入,接触到源相区,当其温度达到发火温度时,从中往内流域添加质量、动量、能量源项。药柱逐渐被点燃,药柱燃气不断与点火燃气混合,流出,可近似模拟药柱被点燃。本算例为内表面燃烧,故源相区取药柱内表面上厚度1mm的层。
图3.3 内流域几何模型
图3.4 源相区几何模型
图3.5 内流域网格
边界条件设置:
点火入口:质量流率入口,编写UDF,对边界赋予实际点火流量曲线和实际按热力学计算软件计算成分得到的点火燃气温度;
点火盒壁面:绝热无滑移壁面;
燃烧室壁面:绝热无滑移壁面;
加质区壁面:绝热无滑移壁面;
加质区-主流域接触面:内接触面,编写UDF,对加质域赋予判断达到发火温度后瞬间反应完全的实际点火燃气物性,从内接触面流入主流域,添加质量、动量和能量;
喷管壁面:绝热无滑移壁面;
出口:压强出口,严格按地面点火实验环境计算,101325Pa,300k。
计算结果:
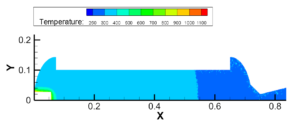
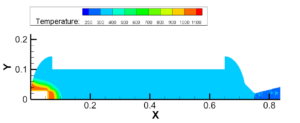
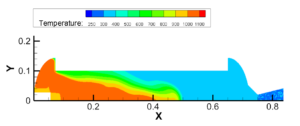
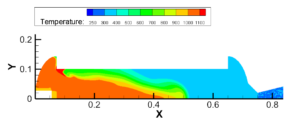
发火过程:点火燃气从点火入口法线方向流入,在主流域中扩散,在加质区对流传热;认为加质区内离散点上温度达到发火温度时控制单元中的材料被瞬间点燃反应完全成推进剂燃气,加质流入主流域,和点火燃气混合,扩散;同时加质区内对流传热,推进剂最终完全点燃,在点火燃气流尽后完全填充整个一体化流域。
图3.6 点火燃气扩散过程
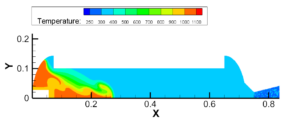
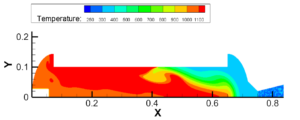
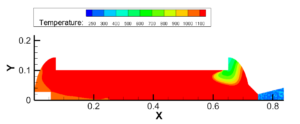
图3.7 推进剂被引燃及推进剂燃气扩散过程
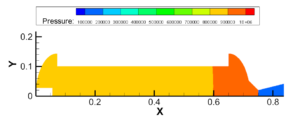
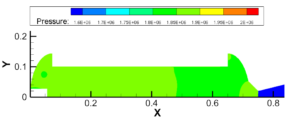
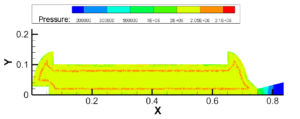
建压过程:在喷管喉部设置堵盖,认为其在内压达到2MPa时打开;堵盖未打开时,燃烧室内压强分布前后存在压强差,震荡建压;堵盖打开后,燃烧室内整体均匀建压,壳体各向受压一致。
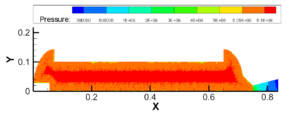
图3.8 0.9~1MPa建压过程
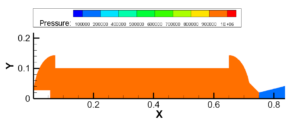
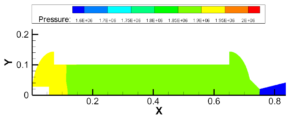
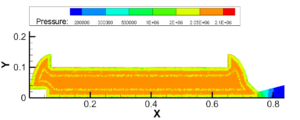
图3.9 1.8~1.95MPa建压过程
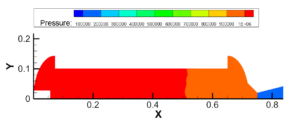
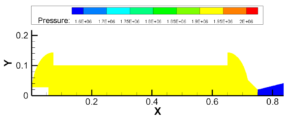
图3.10 堵盖打开前后
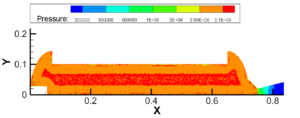
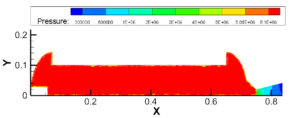
图3.11 2.05~2.15MPa建压过程
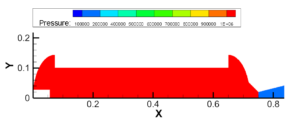
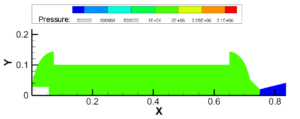
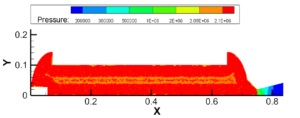
图3.12 5.05~5.15MPa建压过程
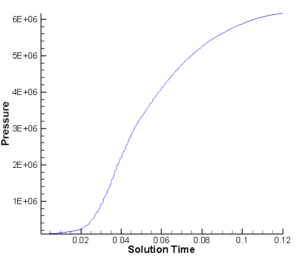
图3.13 燃烧室建压曲线
3.2.2 固体火箭发动机内流场烧蚀模拟计算
固体火箭发动机作为火箭和导弹的动力装置,具有高比冲、高可靠性、结构简单、机动性能好、成本低等特点,在各领域得到越来越广泛的应用。发动机长时间在高温高压的恶劣环境下工作,为保证发动机能够正常运行,通常会在发动机壳体内部附上一层绝热层。在绝热层的设计中,其厚度直接影响着发动机结构的稳定性,因其长时间暴露在燃气中,绝热层被烧蚀破坏必将成为一大安全隐患。
喉衬作为固体火箭发动机中的核心部件,其烧蚀条件最为苛刻,喉衬材料不仅要承受热负荷、机械负荷和热冲击,还要经受化学侵蚀,机械剥削,并且需具有较好的形状和及尺寸稳定性。随着更大载荷、更大推力和更高燃气温度、更远射程固体火箭发动机的发展,其对喉衬材料的烧蚀性能提出了更高要求。
通过数值仿真得到烧蚀严重的位置,大大减少预算。
3.3.1 烧蚀机理
热防护是固体火箭发动机设计中一项重要的任务,也因此,绝热层的烧蚀研究具有十分重要的意义。通常在气流速度大的部位与接触火焰时间长的部位将绝热层设计厚一些。
将绝热层厚度设置得太薄或者太厚都不合理。厚度太小,可能导致壳体烧穿,从而使发动机工作失效。而厚度取得太大时,一方面会增加固体火箭发动机的消极重量,另一方面会减小推进剂药柱的有效体积,缩短其工作时间。
3.3.2 物理模型
除了求解连续相的输运方程,Fluent也可以在拉氏坐标下模拟流场中离散的第二相。由球形颗粒构成的第二相分布在连续相中,近似模拟固体火箭发动机推进剂中金属成分在燃烧中被剥离氧化得到的颗粒相。Fluent可以近似计算这些颗粒的轨道以及由颗粒引起的热量/质量传递。相间耦合及耦合结果对离散相轨道、连续相流动的的影响均可以考虑进去。
Fluent提供的离散相模型选择如下:
- 对稳态和非稳态流动,可用拉氏公式考虑离散相的惯性、曳力、重力
- 预报连续相中,由于湍流涡旋作用而对颗粒造成的影响
- 离散相的加热/冷却
- 液滴的蒸发与沸腾
- 颗粒燃烧模型,包括挥发成分析出和焦炭燃烧模型
- 连续相与离散相的耦合
- 液滴的迸裂与合并
基于固体火箭发动机的两相流模型(DPM)采取以下简化:
3.3.3 计算实例-拉伐尔喷管稳定烧蚀三维数值分析
对拉伐尔喷管作三维旋转。
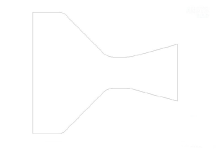
图3.14 几何模型
考虑到仿真结果中最具有表征性的烧蚀位置分布与网格离散分布息息相关,将网格严格按ICEM CFD划分。
图3.15 离散网格
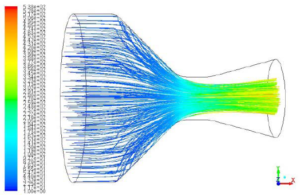
图3.16 粒子轨迹云图
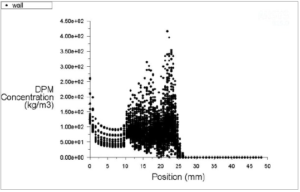
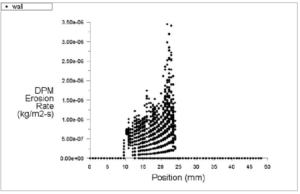
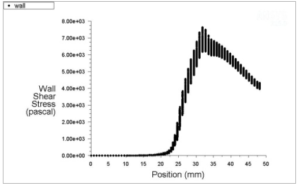
图3.17 壁面烧蚀位置
图3.9 壁面