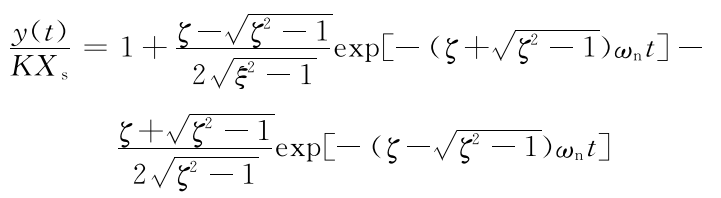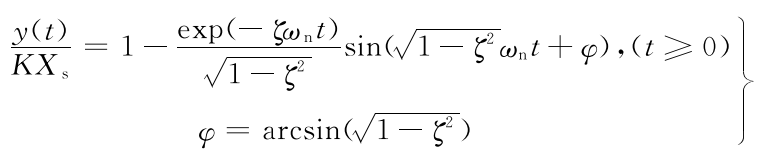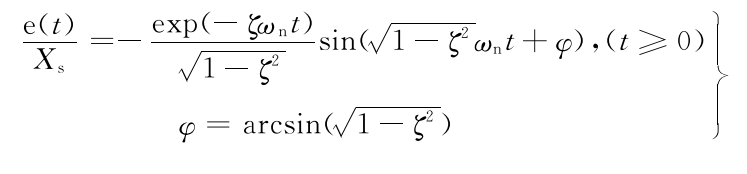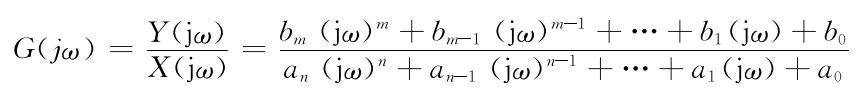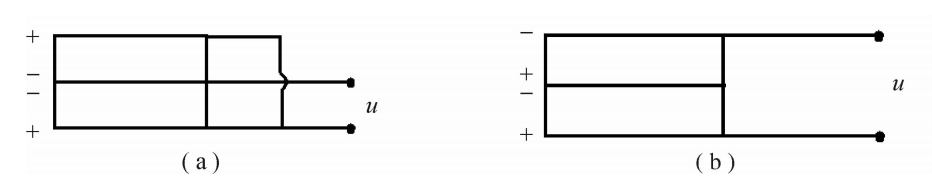目 录

 第1章 绪论

第2章测量系统的特性

第3章传感器

第4章火箭发动机试验技术

第5章温度测量

第6章流量测量

第7章数据采集系统

第8章测量系统的干扰及其抑制方法

第9章数据处理与不确定度评估

第10章非接触式测量技术概论

第1章绪论

1.1测试技术的地位与作用

测试(MeasurementandTest)是测量与试验的概括，是人们借助于一定的装置，获取被测对象相关信息的过程。测试技术包含了两部分的含义：一是测量，指的是使用测试仪器获取被测参数的量值；二是试验，指让被测试对象能够真实呈现所预期的参数或规律的技术和过程。以火箭发动机地面试车为例，发动机推力是主要测量参数之一，目前大多采用推力传感器和计算机数据采集系统来进行测量。但是，光有这些是不够的。火箭发动机工作时会产生推力，如果不将其可靠固定，发动机就会飞出去，产生危险，且无法完成测量；但是如果将发动机刚性固定，推力就无法传递给传感器，也不能准确进行测量。这就需要设计一种特殊的装置，既能将发动机可靠地约束在试车台上，同时又能保证发动机推力不失真地传递给推力传感器。这种装置就是试车架，在后面的章节会详细介绍。可见，试车架属于试验技术，推力传感器和数据采集系统属于测量技术。在很多情况下，试验和测量是很难完全区分的。一般来说，试验技术与测试对象有很大关系，而测量技术则具有一定的通用型，例如火箭发动机与汽车发动机的试验内容很多是不同的，但采用的传感器和数据采集系统等可能是类似的。

火箭发动机试验一般都要测量哪些参数呢?这与试验的任务有关。通常型号发动机研制过程是按照设计指标要求开展的，那么生产出来的发动机是否能够正常工作、性能是否达到设计指标要求，就需要在地面通过试车来进行检验。一般地面试验中最主要的两个参数是发动机推力和工作压强。如果是液体发动机还要测量燃料的流量等参数。为了检测发动机的状态有时候还需要测量壳体表面的温度、应变等参数。对于一些新型发动机的预先研究或者发动机基础研究，测试的内容可能更加丰富，除了上述参数外，有时候还需要测量压强的分布、燃气的温度、速度和组分等。

火箭发动机的发展过程也是与测试工作息息相关的。固体火箭发动机虽然结构简单，但是它在工作中的物理化学过程却十分复杂，因此对它的研究也是非常困难的，至今也没有完全清楚地掌握它的规律。当然也就不能单以理论计算来设计制造一个性能优良的发动机。一个新型发动机的研制，几乎毫无例外地都必须经过反复的试验，通过实验取得数据用以改进设计，并以实验作为技术鉴定的手段。对大量测试工作取得的数据资料进行统计、总结，从中寻求规律性的东西，不仅可以改进提高发动机的性能，还可以完善和发展发动机的理论。比如，早期在使用双基推进剂的固体火箭发动机中出现反常燃烧的现象，当时由于测试手段比较落后，只能用铜柱测压器测量燃烧过程中燃烧室内的最大压力值，而不能测出燃烧全过程的压力

变化规律，因此无法揭露反常燃烧现象的本质。后来，由于测量技术的发展，能够记录燃烧室压力随时间的变化规律后，发现双基推进剂要维持正常的燃烧必须使燃烧室内的工作压力超过推进剂的临界压力值，因而得出了极限压力这一概念。发动机的工作是否正常只取决于极限压力是否高于推进剂的临界压力值，而与最大压力无关。从而确定了保证发动机正常工作的设计原则。又如，随着高能推进剂被广泛采用，不稳定燃烧的现象也越来越突出，要研究不稳定燃烧，没有动态测量的技术，就不能揭露它的本质。随着动态参数测量技术的发展，也就逐步揭示了不稳定燃烧的机理。

随着火箭技术的发展，实验科学也在不断进步，研究的对象和内容也愈加广泛和深入，因此对测试技术提出了越来越高的要求。测试技术是一门涉及学科领域很广泛的科学技术，它涉及到力学、电子学、光学、机械学以及近代理论和边缘交叉的综合科学，而且又往往与被研究的对象紧密地结合在一起。

本书将介绍测试系统的原理、组成与特性；火箭发动机试验中推力、压强、应变、温度和流量等主要参数的测量原理和测试技术；数据采集系统的原理与使用方法；介绍测试系统设计与使用过程中抗干扰技术；试验结果分析和数据处理方法等内容。

1.2火箭发动机试验的特点

测试技术的应用很广泛，但火箭发动机试验和测试有其特殊性，只有充分了解火箭发动机试验的特点，才能有针对性的设计试验系统，开展测试工作。

火箭发动机在研制过程中和在交付使用前，必须经历一系列试验，主要有以下几种。

1)部件试验，如燃烧室壳体静力试验、喷管摆动试验、点火装置发火试验等。

2)发动机地面点火试验。

3)使用性试验，即模拟发动机使用时所处环境条件的试验，例如振动试验、冲击试验、运输试验、环境条件试验、贮存试验等。

4)遥测飞行试验，发动机作为全弹(箭)动力装置参与飞行试验。火箭发动机地面点火试验又称试车，其特点可以归纳为以下几点。

(1)工作时间短且测量环境恶劣。固体火箭发动机工作时间短，只有零点数秒到数十秒，最长不过百余秒，在很短的时间内，燃烧室中推进剂燃烧要释放出巨大的能量，产生高温(2000～4000K)、高压(3～25MPa)的燃气，通过喷管喷出，流速可达到2000m·s-¹,同时伴随着强烈的振动和产生巨大的噪声，这样就形成了非常恶劣的测量环境。

同时，由于工作时间短，各种参数变化快，对各参数的测量传感器和仪器要求具有快速测量能力和防高温、耐高压、抗冲击及抗干扰的能力，因此对测量技术的要求是很高的。

(2)技术领域广，工作系统多。试验与测量集中了许多现代科学技术(包括管理科学),是一项系统工程。

固体火箭发动机是利用现代科学技术中若干最新成就所研制的尖端产品，对它进行试验要涉及许多技术领域，如现代测量技术、机械设计技术、电子技术、真空低温技术、精确的计量技术、自动控制技术、计算机技术，对结果的分析还要用到现代数理统计及可靠性技术等。只有把这多种技术、多种系统、分系统及分散在各岗位的技术人员组织起来使之有计划、有步骤地协同工作，试验才能完成。因此，只有采用系统管理科学，才能组织好地面点火试验。

(3)试验费用高，次数少。大型固体发动机造价昂贵，每次试验耗资达数十万元甚至数百万元，而且一台发动机只能试验一次。昂贵的造价决定了用于点火试验的发动机数量不能太多。这就要求精心组织每次试验，做到稳妥可靠、万无一失，并尽可能多地获得一些测量数据。

(4)不安全因素多，危险性大。研制初期的发动机容易发生故障，甚至发生爆炸，因此试验中的安全技术措施非常重要，要做好各种防范措施。

(5)环境污染较严重。固体火箭发动机点火试验时，排出的大量燃气中，含有一定量的有害气体和氧化铝微粒，扩散到空气中，会造成大气污染；一旦试验失败，要动用消防水灭火，产生的污染水流入周围地区和河流，也会造成环境污染，必须进行监测和治理。

由于点火试验具有上述特点，因此，对试车台的建立、试验设备的配置、发动机参数的测量系统等提出了特殊的要求，这些要求将在以后的各章中分别叙述。

1.3试验技术的发展与展望

火箭发动机试验与测量技术是根据火箭发动机技术发展的需要，随着科学技术水平的提高而发展起来的。由于现代科学技术的发展，新型的高强度、低密度材料的出现，高能推进剂的研制成功，新的设计理论的突破，计算机辅助设计的应用，火箭发动机的性能有了很大的提高。此外，冲压发动机、组合发动机等新型发动机和新概念发动机技术的发展，也大大拓宽了传统火箭发动机研究的领域。这些对发动机试验技术与测量技术就提出了更高的要求。目前，火箭发动机试验技术发展趋势大致可归纳为下述几点。

(1)试验能力将会进一步提高。用于航天助推器的固体火箭发动机通常是非常大的，如美

国的“大力神-C3”火箭有两个直径3m的发动机，总推力达9000kN,美国还研制了直径4m

和6.6m的固体助推器，推力达数十兆牛。为试验这种巨型火箭发动机必须建造巨型试车台。首先遇到的是巨型试车架的设计与制造问题，运输、起吊问题，还有数十兆牛力值的传感器计量与校准，建立数十兆牛力值的标准等等，都需要突破一系列技术难关。

(2)符合测量系统的特殊要求。一些具有特殊用途的发动机，如多次启动的发动机、宇宙飞船上弹射救生的逃逸发动机，有的工作时间极短，推力却非常大。这些发动机试验对测量系统要求非常苛刻。要求测量系统有很好的动态特性，能不失真地测量推力脉动，这些都是尚待解决的技术难点。

(3)测量方法的新突破。固体火箭发动机地面点火试验中瞬时燃速的测量、瞬时质量流量测量、喷管摆动的瞬时中心的测量、内外流场测量等，随着高能直线加速器、X射线CT技术及激光全息技术等在火箭发动机试验中的应用，可望有新的突破。

(4)高空模拟试验的要求更高，范围更大。随着发动机技术性能提高，高空模拟试验领域内，不仅要提高模拟高度(到120km以上),还要模拟温度环境(气动加热)、宇宙射线辐射环境及微重力环境，甚至还要模拟宇宙间的“冷”“黑”等环境，这无疑又将提出新的技术课题。

(5)计算机辅助试验与仿真技术的应用。为减少试验次数，节省费用开支，可通过少量试验，获得一定量试验数据，建立数学模型，利用计算机辅助试验或仿真来解决部分试验问题。当然计算机仿真技术不能完全代替发动机点火试验，最终还得靠热试车来检验、评定发动机的性能参数。

第2章测量系统的特性

对于不同的测试对象和任务，其测量参数的特性不同，对测量系统的要求也不同。例如，特别微弱的信号就需要灵敏度高的传感器，快速变化的参数就要求测量系统各个环节的响应要快。因此有必要先来了解测量系统的特性。

2.1测量系统的基本概念

2.1.1测量系统的组成

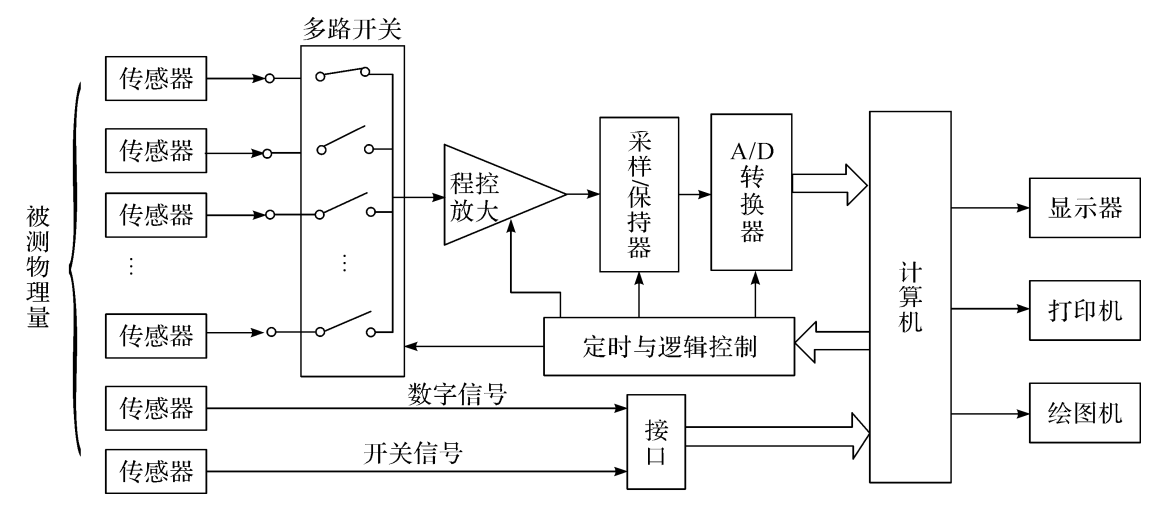
测量系统是指能完成一定测量任务的、若干元部件和仪器的组合。对于诸如推力、压力和应变等各种非电量参数，通常将其转换为电压和电流等电量进行测量，这种方法称为非电量电测法，是目前广泛采用的一种测量方法。用非电量电测法组成的测量系统，一般由传感器、中间调节部分、显示记录仪器和采集处理仪器等构成，如图2.1所示。

图2.1测量系统组成

为了叙述方便，将传感器、测量与记录仪器或测量系统称为测量装置，将被测量(如压力、推力和温度等)统称为输入，将测量装置的指示值或记录称为输出或响应。

1.传感器

将被测物理量直接转换为相应电量的装置称为传感器。国标GB7665—1987对传感器的定义是能感受规定的被测量并按照一定规律转换成可用输出信号的器件和装置。

一般来讲，传感器主要由敏感元件和变换器两部分组成。

(1)敏感元件：直接感受被测量并将其转换为另一种形式的物理量。

(2)变换器：将敏感元件输出量转换为适于传输和测量的电信号。

例如，用电阻应变式测力传感器测量发动机推力时，传感器中的应变筒是敏感元件，将力转换成应变，而贴在应变筒上的电阻应变片是变换器，将应变转换为电阻值的变化。但要注意，并不是所有传感器都能明显的分清敏感元件和变换器两个部分，例如用来测温的热电偶，它既直接感受温度，又将温度转换为电势。

2.中间调节部分

中间调节部分的作用是将传感器输出的信号调整为合适的电压、电流等形式，然后传输到下一个环节，通常包括电桥、调制、放大、解调、积分、微分及模/数转换等电路。例如，应变式压力或推力传感器输出的电压很小，需要用应变放大器进行放大，应变放大器就属于中间调节部分。

3.显示和记录仪器

显示和记录仪器的作用是将信号直观地进行显示和记录，常用的显示和记录仪器有：指针式仪表、电子示波器、磁带记录仪、瞬态波形记录仪和高速摄影(摄像)等。

4.采集和处理仪器

通过测量系统把被测参数记录下来，就测量过程本身来说已经结束。但所记录下来的只是一些原始数据，它往往还不能作为最终结果提供使用。为此还必须把这些数据经过判读、整理、计算，以符合试验任务所要求的形式呈现，通常把这一过程称为数据处理。在过去的模拟测试系统中，数据处理是人工完成的。计算机及带有微处理机的数据处理仪器的出现与应用，使得数据采集及处理的工作完全可由计算机或专门仪器自动完成，并以人工处理无法比拟的速度直接给出高精度的最终试验结果，节省了大量时间。计算机作为测量系统的一个环节其作用还不仅如此，在整个测量过程中它还可以按照人们的意志控制过程的进行，成为整个测量系统的指挥中心，从而使测量系统的功能不再限于完成试验数据采集这一传统功能，还将对试验过程进行实时控制。因而，在有些场合下会出现测控系统的说法，即测试系统与控制系统的统称。

2.1.2模拟测量系统和数字测量系统

根据测量系统的输出形式，可将测量系统分为模拟测量系统和数字测量系统。通常被测的物理量都是随时间连续变化的量，这些被测量经过测量系统的各种变换与处理之后，输出的是连续变化的量(如电压或电流),这种测量系统称为模拟测量系统，如光线示波器、纸带式记录仪等。若被测量经过测量系统以后是以数字形式输出的，则叫做数字测量系统，如各种数字式测试仪表。

模拟测量系统的优点是价格便宜，形象直观，但突出的缺点是精度低。数字测量系统精度高，可以方便的实现多路测量、试验过程的自动控制以及数据处理的自动化，因此得到越来越广泛的应用。

2.1.3静态和动态参数测量

测量装置能否胜任预定的任务，是由它们的特性决定的。为了正确选择和使用测量装置，达到技术上合理，经济上节约，需要了解被测参数物理量的性质。通常根据被测物理量变化的快慢可以分为静态参数和动态参数，相应的测量系统称为静态参数测量系统和动态参数测量系统。

(1)静态参数：被测物理量不随时间变化或变化很缓慢，用代数方程表示输入和输出量之间的关系，静态参数表征测量装置的静态特性。

(2)动态参数：被测物理量随时间迅速变化，需要用运动微分方程来描述其输入和输出之间的关系，动态参数表征测量装置的动态特性。

例如，气瓶内的压力，保温箱内的温度等参数通常变化都比较缓慢，可以作为静态参数处理；而火箭发动机点火瞬态过程，火箭发动机出现的不稳定燃烧等，其压力参数变化比较快，一般作为动态参数处理。

这里需要注意的是，由于快和慢本身就是相对的，因此动态参数与静态参数的概念也是相对的，两者并没有截然的分界线。这就需要掌握测量装置的特性，根据实际测试任务的要求和特点来合理选择测试装置。

2.2测量系统的静态特性

当测量静态的物理参数时，测量的质量主要受测量系统以下几方面性质的影响。

2.2.1量程

(1)测量上限：测量系统所能测量的最大被测量的值。

(2)测量下限：测量系统所能测量的最小被测量的值。

(3)量程：用测量上限和下限表示的被测量的区间。

如果一个测量系统包括多个测量装置，则该测量系统的测量上限应该由各测量装置的测量上限的最小值决定，而该测量系统的测量下限应该由各测量装置的测量下限的最大值决定。例如，一个压强测量系统包括了压强传感器和数据采集仪器，压强传感器测量范围是0～5MPa、输出电压是0～10V,而数据采集仪器的输入电压是—5～5V。那么该系统的压强测量下限是0MPa(0V和—5V中最大值所决定),测量上限是2.5MPa(由10V和5V中最小值决定，假定传感器的输出与输入之间是严格线性)。

通常情况下压强传感器是测量相对于环境气压的相对压强(工程上习惯称之为表压),即所测压强与环境气压的差值。例如，表压传感器量程为0～0.5MPa,表示所测压强的量程相对于环境气压是0～0.5MPa,若环境气压是0.995×10⁵Pa,则所测压强的绝对值是0.995×10⁵～5.995×10⁵Pa,若环境气压为1.008×10⁵Pa,则所测压强的绝对值变为1.008×10⁵～6.008×10⁵Pa。对于量程是一0.05～0.5MPa的表压传感器，若环境气压是0.995×10⁵Pa,则所测压强的绝对值是0.495×10⁵～5.995×10⁵Pa。也有的传感器是测量绝对压强(称之为绝压传感器),则所测量压强与环境气压是没有关系的。

2.2.2精度

1.精密度τ

表示测量装置指示值的分散性，对某一稳定的被测量用同一测量装置在短时间内连续重复测量多次，其测量结果的分散程度，分散程度越小，精密度越高。但精密度高并不一定符合被测数据的真值。

2.准确度ε

表示测量装置示值误差的大小，即示值有规律偏离真实值的程度。准确度反应了系统误差的大小。

3.精确度δ

它是精密度和准确度两者综合的结果，表示测量结果与真实值之间的差别。在最简单的

情况下可取两者的代数和，即

δ*=τ+ε

通常都是以精度来表示测量装置的优劣，而精度最终往往又是以测量误差的相对值来表示。

在工程应用中，为了简单地表示测量装置测量结果的可靠程度，引入一个测量装置精度等级的概念，其精度等级用引用相对误差的数值表示为

\(\gamma=\pm \frac{{\delta}_{max}}{{M}_{max}-{M}_{min}}\times 100%\)                         (2.1)

式中

_δmax——测量范围内的最大绝对误差；

M_max,M_min——上限和下限。

测量装置的精度等级是对y_m的一系列标准百分比数值进行分档，精度等级有0.001,

0.005,…,2.5,5级，它们的容许引用相对误差的最大值分别为±0.001%,±0.005%,…,±2.5%,±5%。

绝对误差δ是指被测量的真值与仪表示值之差，在实际工作中，真值无法求得，通常是用上一级或更高精度等级的标准仪器的测量结果作为真值。虽然这两者并不相等，但上一级或更高精度等级的标准仪器的示值要比工作仪器的结果更接近于真值。

注意：由于测量装置的精度与相对误差有关，因此在使用以引用相对误差表示精度的仪器仪表时，应尽量避免在接近测量下限的三分之一的量程范围内工作，以免产生较大的误差。

2.2.3重复性

由于测量装置中的某些随机性变动、周期性变动、漂移、环境条件(如室温、气压、振动等)或工作条件(如电源电压、频率等)的变化，使得在一定测量条件下对同一数值的被测量进行重复测量时的结果不完全相同。重复性误差定义为

\({R}_{n}= \frac{{\delta {R}}_{max}}{{M}_{max}-{M}_{min}}\times 100%\)      (2.2)

式中

_ΔRmax——全量程范围内最大的重复性差值。

重复性和稳定性具有同样的含义，用来表示在一段相当长的时间内测量装置维持其输出特性恒定不变的性能。

2.2.4分辨力

指测量装置可能检测到的输入信号的最小变化量的能力。也可以说，输出量产生变化时，输入量的最小变化量。

2.2.5灵敏度

灵敏度是指测量装置在稳态下输出变化对输入变化的比值，用S表示，即S=dy/dx它是测量装置静态参数。

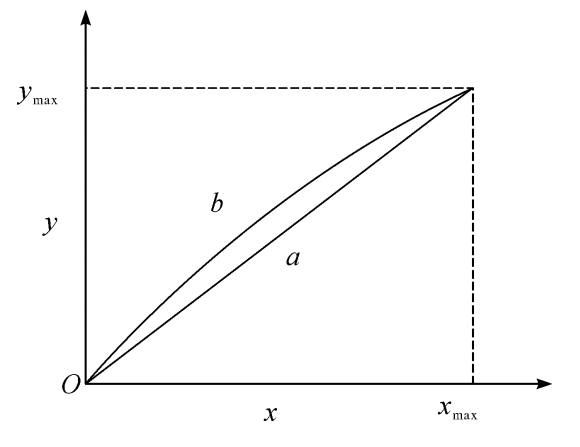
静态特性曲线是指测量装置在稳态下输入输出的关系，灵敏度相当于静态特性曲线上各点的斜率。如图2.2所示，具有线性特性(见图2.2中a线)的测量装置的灵敏度是常数；具有非线性特性(见图2.2中b线)的测量装置的灵敏度在整个量程内不是常数。

图2.2静态特性曲线

测定灵敏度的方法称为标定或校准。首先用人为的方法产生数值不同的被测参数x₁,x2,…,然后由测量装置输出相应的输出量y₁,y2,…,制成表格或绘成曲线，该曲线称为标定曲线，曲线上各点的斜率就是各点的灵敏度系数。通过标定还可以消除测量装置的系统误差。

2.2.6滞后量

(1)滞后效应：在输入量增加和减少的过程中，同一输入量将得到不同的输出值，减少过程的输出量要比增加过程的输出值大一些，这种现象称为滞后效应，如图2.3所示。

图2.3滞后效应曲线

(2)滞后量：在测量范围，这种差别的最大值称为滞后量，用△Hmax表示。

(3)迟滞误差：滞后量与测量范围之比称为迟滞误差，可表示为

\({H}_{r}= \frac{{\delta {H}}_{max}}{{M}_{max}-{M}_{min}}\times 100%\)      (2.3)

滞后效应的原因如下。

1)运动部件的外摩擦。

2)变形材料的内摩擦。

为了减少滞后效应，应尽量减少摩擦面，并对变形零件进行热处理和多次反复加载的老化处理。

2.2.7线性度(非线性误差)

测量装置的静态特性曲线，往往不是严格服从直线关系，在实际工作中，为了简化起见，对于与直线关系偏差不大的特性曲线，可以用一条参考直线来代替，两者之间的偏差程度可用非线性误差来表示，有

\({L}_{n}= \frac{{\delta {L}}_{max}}{{M}_{max}-{M}_{min}}\times 100%\)  (2.4)

式中

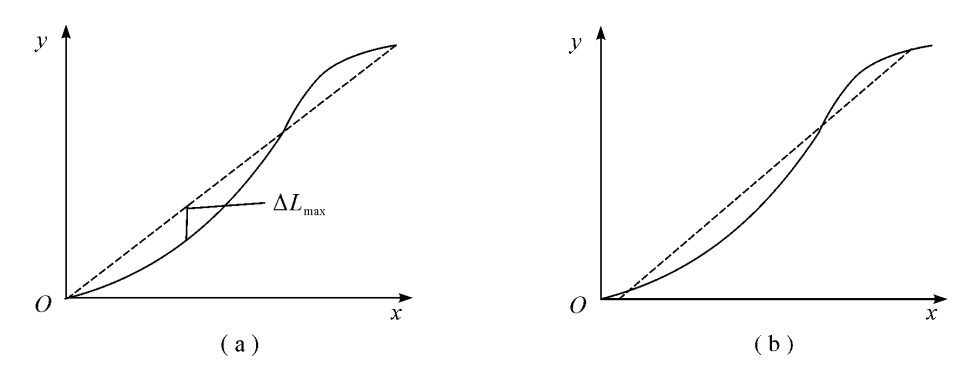
ΔLmax——在测量范围内实际特性曲线与参考直线之间的最大偏差，如图2.4(a)所示。注意：参考直线与处理方法有关，常见的处理方法是最小二乘法(见图2.4(b))。

图2.4线性度特性曲线

(a)起点和终点连线；(b)最小二乘法

2.2.8漂移

(1)漂移：它指输入量不变时输出量的变化，它是由于温度变化或测量装置内部元件的不稳定所引起的，也是衡量测量装置静态稳定性的重要指标，一般分为温度漂移和时间漂移。

(2)温度漂移：由温度变化引起的漂移。

(3)时间漂移：由其他原因造成的漂移。

2.2.9实例

BLR-1型拉压力传感器是火箭发动机推力测量常用的传感器，其产品系列有16种规格，量程从100kg到10t,主要静态特性指标如下。

(1)额定载荷下的电压灵敏度S₀=1.0～1.5mV·v-¹。

(2)分辨力为额定载荷的0.1%。

(3)非线性误差小于0.5%。

(4)滞后性及重复性误差小于0.5%。

需要注意的是，这里的灵敏度是指传感器承受额定载荷条件下，其输出的电压与所输入的激励电压之间的灵敏关系。即，在额定载荷下，给传感器输入的每伏激励电压所输出的毫伏数。例如，某传感器的额定载荷是500kg,额定灵敏度是1.013mV·v-1,它表示该传感器在承受500kg载荷时，输入电压变化1V时其输出电压变化1.013mV。说明书标明该传感器的建议工作电压是10V,那么在500kg载荷、施加10V激励电压时，传感器的输出电压应为10.13mV。

2.3测量装置的动态特性

2.3.1基本概念

1.动态参数测量

当被测量的物理量随时间变化比较快，由于测量装置各个环节的惯性(电的、机械的、磁的和热的等),测量装置输出量的变化不能及时地反映被测物理量的变化，因而它们之间的数值关系和测量静态参数时的测量过程不同。这种参数的测量称为动态参数测量。

2.信号

(1)信号的定义。通常将反映被测物理量变化的连续模拟量称为信号。为了正确地选择测量装置及估计动态误差，保证测量装置的精度，需要对模拟信号的分类及其在时域或者频域中的特性有所了解。

(2)信号的分类。模拟信号可以分为确定性信号和随机信号两大类。

1)确定性信号：如果在每一瞬时，信号都有一个完全确定的数值，即能用明确的数学关系式描述，这种信号称为确定性信号，如周期信号、振动过程产生的信号。

2)随机信号：如果信号不是一个确定的时间函数，即不能确切地求出某一瞬时信号的大小，这种信号称为随机信号。

(3)信号的表示法。

1)时间域表示法：用时间坐标来描述。

2)频率域表示法：用频率坐标来描述。

3.频谱

用频域表示法描述信号能更有效地了解信号的性质。实际的信号波形都不是简单的简谐波形，按照傅里叶分析法，可以将信号分解为许多个谐波分量，由其振幅和相位来表示，各个谐波可以按照频率高低排列起来成为谱状。按照这样排列的各次谐波的全体称为频谱。各次谐波振幅的全体称为振幅频谱(或称为幅值谱);各次谐波相位的全体称为相位频谱；而各次谐波能量的全体称为能量频谱。通常如不加以说明，频谱一词指的是幅值谱。

(1)周期信号的频谱。我们知道，周期信号可以用傅里叶级数展开，看成许多正弦和余弦波叠加的结果，即

x(t)=A₀+A₁sin(at+φ_i)+A₂sin(2at+φ_₂)十…+A,sin(not+φ_n)十…

这些正弦(余弦)波的频率为一个基本频率的整数倍，这个具有基本频率的正弦(余弦)波称为基波；等于基波频率整数倍频率的正弦(余弦)波称为谐波。用频谱来描述周期信号的几个例

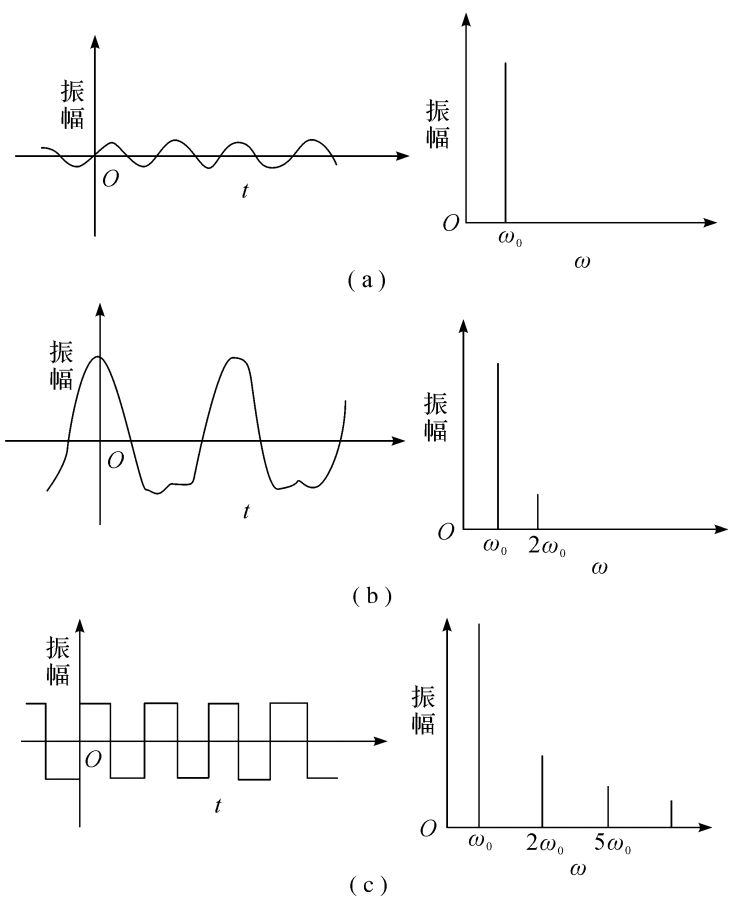
子，如图2.5所示。周期性波形的谱线称为线谱，又称离散谱。

图2.5周期信号频谱曲线

 (a)正弦波，在ao处有一条谱线；(b)简单复合波，有两条不同振幅的谱线； (c)周期方波，由许多不同振幅的谱线组成

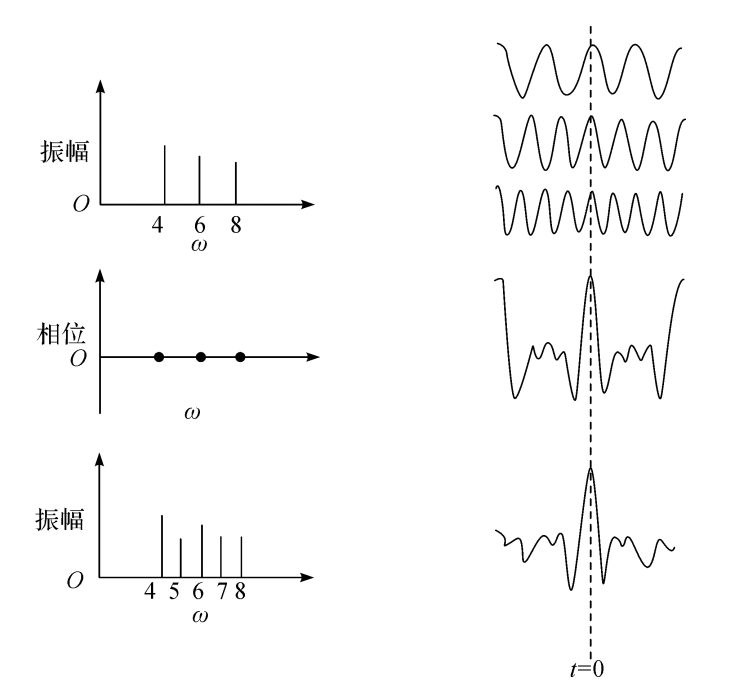
(2)非周期信号的频谱。对于非周期信号，包括瞬变信号和冲击信号，它们的频谱是不能用线谱来表示的，必须用连续谱来表示它们，即需要采用傅里叶积分的形式，其道理可以通过图2.6所示直观地看出。

图2.6傅里叶级数向积分过渡的示意图

图2.6(a)表示有频率为4Hz、6Hz、8Hz的三个波形，在t=0时其相位相同，合成波形的高峰每秒出现两次，因为4、6、8的最高公因子为2。而图2.6(b)中，又加进了频率为5Hz、7Hz的波形，因此，最高公因子变成1,所以每秒出现一次高峰，如果在4～8Hz之间，加进相差1/1000Hz的频率分量，所合成波形的频率(指高峰的频率)就变成1/1000Hz,即在第1000s才重新出现。同样，如果分量在无限小的频率间隔上出现，则合成波就在无穷大的时间之间才重复出现，这样振幅-频率曲线就逐步逼近了傅里叶积分曲线。

因此，任意一个仅出现一次的瞬态波形，也就是不重复出现的波形，都可以看成是频率间隔为无限小的无数谐波分量的叠加。

2.3.2测量系统的动态特性

1.测量系统一般动态数学模型

测量系统的动态特性是指在动态测量时测量系统输出量与输入量之间的关系，其数学表 示式称为系统的动态数学模型，由系统本身的物理结构所决定，可以通过支配具体系统的物理 定律来获得。研究测量系统的动态特性，广泛采用的数学模型是常系数线性微分方程。在忽 略测量系统的某些固有物理特性(如非线性因素等)并进行适当简化处理后，一般测量系统输 入量x(t)与输出量y(t)之间的关系可以表示成如下形式：

\({a}_{n}\frac{{d}^{n}y(t)}{{dt}^{n}}+{a}_{n-1}\frac{{d}^{n-1}y(t)}{{dt}^{n-1}}+…+{a}_{1}\frac{{d}y(t)}{{dt}}+{a}_{0}y(t)=\)

\({b}_{m}\frac{{d}^{m}x(t)}{{dt}^{m}}+{b}_{m-1}\frac{{d}^{m-1}x(t)}{{dt}^{m-1}}+…+{b}_{1}\frac{{d}x(t)}{{dt}}+{b}_{0}x(t) \)        (2.5)

式中

a_o,a₁,…,a_n及b_o,b₁,…,b_m——与测量系统物理参数有关的常系数。

式(2.5)描述的系统是一个线性系统。应该指出，一些实际测量系统不可能在相当大的工 作范围内都保持线性。例如，有些系统在大信号作用下，测量系统的输出可能出现饱和；在小 信号作用时，系统可能存在死区。在低速工作时可以看成是线性的系统，在高速工作时却是非 线性的(如阻尼器)。为了避免由于非线性因素而造成数学分析上的困难，人们总是忽略某些 影响较小的物理特性，通过适当的假设，把一般测量系统当作线性定常系统来处理。尽管这样 的处理可能会使测量系统分析结果的准确性受到一定影响，但研究这种理想测量系统的动态 特性，仍然是最基本的方法。

式(2.5)的解，就是测量系统对一定输入量的响应。对此类方程的求解，已有成熟的方法。 其中，拉普拉斯变换方法在测量系统动态特性分析中应用广泛。所谓拉普拉斯变换，是将时域 函数f(t)(定义t≥0)转换成s域函数F(s)的一种变换，定义为

L[f(t)]=F(s)=\(\int\limits_{0}^{\infty }{f(t){e}^{-st}{dt} }\)     (2.6)

式中

s——拉普拉斯算子； L——拉普拉斯变换运算符号。

运用拉普拉斯变换，线性微分方程可以转换成复变数的代数方程。微分方程的解则可以 通过求因变量的拉普拉斯反变换来求得。

对于式(2.5)所示的常系数线性微分方程，如果所有初始条件均为零(描述测量系统动态 特性的微分方程，一般都可以满足这一条件),那么,微分方程的拉普拉斯变换可以简单地用s 代替d/dt,s²代替d²/dt²等后得到，即

\({a}_{n}{s}^{n}Y(s)+ {a}_{n-1}{s}^{n-1}Y(s)+…+{a}_{1}{s}Y(s)+ {a}_{0}Y(s)=\)

\({b}_{m}{s}^{m}Y(s)+ {b}_{m-1}{s}^{m-1}Y(s)+…+{b}_{1}{s}Y(s)+ {b}_{0}Y(s) \)    (2.7)

式中

X(s),Y(s)——是测量系统输入量x(t)和输出量y(t)的拉普拉斯变换。

式(2.7)是一个代数方程，解这个代数方程可以得到Y(s),而微分方程的时间解y(t)可以 由Y(s)进行拉普拉斯反变换求得。拉普拉斯反变换定义为：若时域函数f(t)的拉普拉斯变换 是F(s),则F(s)的拉普拉斯反变换

\({L}^{-1}[F(s)]=f(t)=\frac{1}{2\pi {j}}\int\limits_{c-j\infty}^{c+j\infty}{F(s){e}^{st}ds}\)   (2.8)

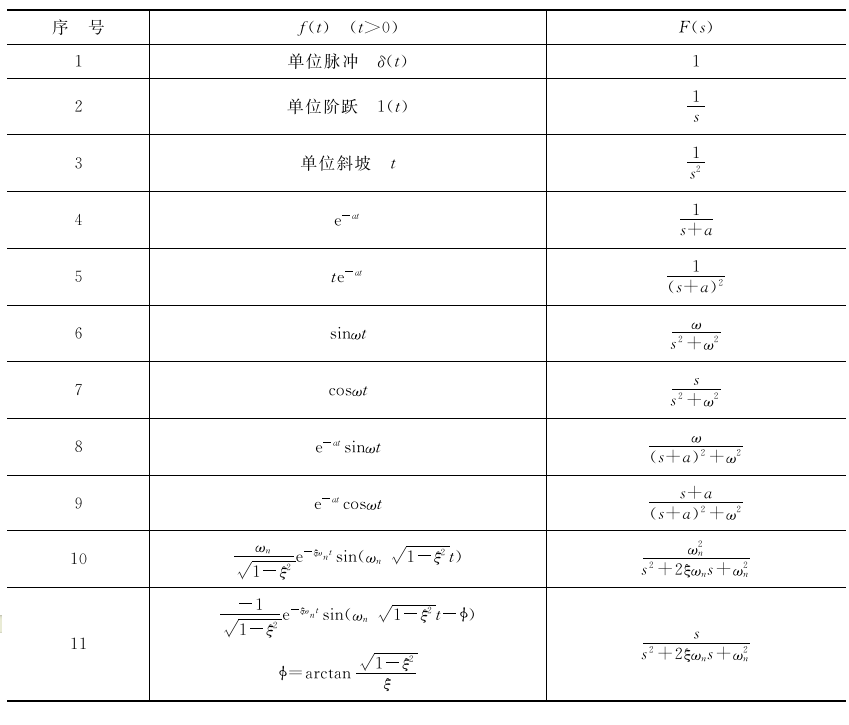
由式(2.6)、式(2.8)给出的拉普拉斯变换与反变换的积分运算很复杂。实际使用时，不必 进行复杂的积分运算，可以直接运用拉普拉斯变换表。表2.1中给出了测量系统动态特性分 析中常用到的拉普拉斯变换对照。利用拉普拉斯变换表求F(s)的反变换时，若F(s)不能直接 在表中找到，须将它展开成部分分式，写成已知拉普拉斯反变换的s的简单函数。

 2.传递函数

在全部初始条件为零时，系统输出量的拉普拉斯变换与输入量的拉普拉斯变换之比称为 线性定常系统的传递函数。传递函数表达了线性定常系统的输入量与输出量之间的关系。对

式(2.5)所描述的系统，若全部初始条件为零，则对方程两边进行拉普拉斯变换可得到该系统 的传递函数G(s)为

\(G(s)=\frac{Y(s)}{X(s)}=\frac{{b}_{m}{s}^{m}+{b}_{m-1}{s}^{m-1}+…+{b}_{1}{s}+{b}_{0}}{{a}_{n}{s}^{n}+{a}_{n-1}{s}^{n-1}+…+{a}_{1}{s}+{a}_{0}}\)  (2.9)

传递函数分母中s的最高阶数等于测量系统输出量最高阶导数的阶数。若s的最高阶数

为n,则称该系统为n阶测量系统。传递函数表达了测量系统本身的特性，而与输入量无关。 传递函数反映了系统的响应特性，但它不能表明测量系统的物理结构。物理结构完全不同的 两个系统，可以有相同的传递函数，具有相似的传递特性。

  表2.1测量系统的常用拉普拉斯变换对照表

例如，水银温度计与RC低通滤波器同属一阶系统；动圈式指示仪表与弹簧测力计都是二 阶系统。尽管它们的物理特性相差悬殊，但却有相似的传递函数。

利用传递函数有助于确定测量系统总的动态特性。测量系统总是由若干测量环节组成 的，如果已知各组成环节的传递函数，那么,通过适当的综合，很容易得到整个测量系统的传递 函数，亦即获得测量系统的动态特性。

测量环节组合的基本方式主要有串联、并联和反馈。串联测量系统传递函数G(s)是各测 量环节传递函数G(s)之乘积，即

\(G\left( s \right)=\prod\limits_{i=1}^{n}{{{G}_{i}}}\left( s \right)\)            (2.10)

并联测量系统的传递函数是各测量环节传递函数之和，即

\(G(s)=\sum\limits_{i=1}^{n}{{G}_{i}(s)}\)    (2.11)

反馈测量系统的传递函数(闭环传递函数)为

\(G(s)=\frac{{G}_{1}(s)}{1+{G}_{1}(s) {G}_{2}(s)}\)

(2.12)

式中

G₁(s)——正向回路传递函数； G₂(s)——反馈回路传递函数。

3.基本测量系统的动态特性

大多数测量系统的动态特性可归属于零阶系统、一阶系统和二阶系统3种基本类型。尽 管实际上还存在着更复杂的高阶测量系统，但在一定条件下，它们都可以用这3种基本系统动 态特性的某种适当的组合形式来逼近。例如，对于用式(2.5)描述的测量系统，其传递函数一 般总可以按部分分式法而改写成以下形式：

\(G(s)=\sum\limits_{i=1}^{q}{\left(\frac{{\alpha}_{i}}{s+{p}_{i}}\right)}+\)\(\sum\limits_{j=1}^{r}{  \left(\frac{{\alpha}_{j}s+{\beta}_{j}}{{s}^{2}+2{xi}_{j}\omega_{ nj }s+{\omega }_{nj}^{2}}   \right)}\),(q+2r=n)     (2.13)

这表明，一般的测量系统，描述其动态特性的传递函数总可以由若干低阶系统的传递函数的并 联来求得。所以，研究基本测量系统的动态特性具有重要的意义。

(1)零阶测量系统。在式(2.5)所描述的测量系统中，若方程诸常系数中，除a₀、b₀之外其 余全为零，那么微分方程就变成了简单的代数方程

y(t)=Kx(t)             (2.14)

式中

K=b₀/a₀——测量系统的稳态灵敏度(或静态灵敏度)。

用式(2.14)来描述动态特性的测量系统称为零阶测量系统。

零阶测量系统具有理想的动态特性。不论被测物理量x(t)如何随时间而变化，零阶测量系统的输出都不会失真，输出在时间上也没有任何滞后。

(2)一阶测量系统。若式(2.5)中除a₁,a₀和b₀外，其余系数均为零，可得

a₁dy(t)/dt+a_oy(t)=b_ox(t)             (2.15)

用上述方程来描述动态特性的系统，称为一阶测量系统。

式(2.15)中的三个系数a₁,a₀和b。可以合并成两个基本系数。若用a₀除方程两边并进行拉普拉斯变换，则

TsY(s)+Y(s)=KX(s)                (2.16)

式中

T=a₁/a₀——时间常数；K=b₀/a_o——稳态灵敏度。

时间常数T具有时间的量纲，而稳态灵敏度K则具有输出量/输入量的量纲。实际上，对任意阶测量系统，K总是被定义为K=b₀/a₀,并总是具有同样的物理意义。

一阶测量系统的传递函数为

G(s)=Y(s)/X(s)=K/(Ts+1)                (2.17)

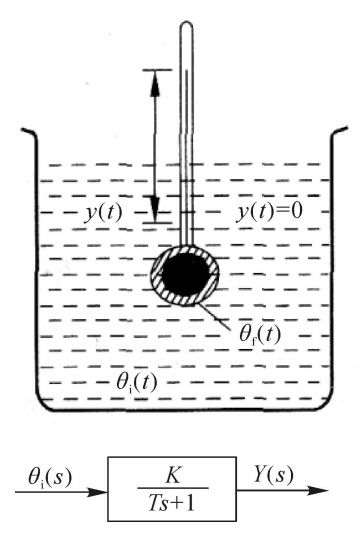
图2.7一阶测量系统

如图2.7所示的水银温度计测温系统，可近似为一阶测量系统。系统输入量是温度计温包周围被测流体的温度θ_i(t)输出量是温度计中水银柱上部表面的位移y(t)。假设θ_i(t)只是时间t的函数，那么,根据传热学的有关知识，可以建立起如下的微分方程

aA[0_i(t)-0_f(t)]= \(\rho (c)V\frac{d{\theta}_{f}(t)}{dt}\)

式中

α——被测流体与温度计温包之间的换热系数，单位：W/(m²·℃);

A——温包壁换热面积，单位：m²;

V——温包容积，单位：m³;

ρ——水银密度，单位：kg·m-³;

c——水银比热容，单位：J·(kg·℃)-¹;

θ_f(t)——温度计温包中水银温度，单位：℃。

温度计输出量y(t)与温包中水银温度θf(t)之间的关系可由代数方程来描述为

\(y(t)=\frac{\beta V}{{A}_{c}}{\theta}_{f}t\)             (2.18)

式中

β——水银体膨胀系数，单位：1/℃;

A_c——毛细管横截面积，单位：m²。

整理上述两方程得其传递函数为

\(\frac{\rho c V}{\alpha A}\frac{dy(t)}{dt}+y(t)=\frac{{\beta}V}{{A}_{c}}{\theta}_{i}(t)\)

其传递函数可写为

\(G(s)=\frac{K}{{Ts}+1}\)

式中

T——测量系统的时间常数，单位：s,\(T=\rho V/(\alpha A)\);

K——测量系统稳态灵敏度，单位：m/℃,K=βV/A_c。

显然，这是一个一阶测量系统。

(3)二阶测量系统。二阶测量系统可以用微分方程来描述为

\({a}_{2}\frac{{d}^{2}y}{{dt}^{2}}+{a}_{1}\frac{dy}{dt}+{a}_{0}y(t)={b}_{0}x(t)\)     (2.19)

两边同时除以a_。,并引入以下新的参数：

K=b₀/a₀——系统稳态灵敏度；

\({\omega}_{n}=\sqrt{\frac{{a}_{0}}{{a}_{2}}}\)——系统固有频率，或称系统无阻尼自然频率；

\(\zeta ={a}_{1}/(2\sqrt{{a}_{0}{a}_{2}})\)——系统阻尼比，无量纲。

则描述二阶测量系统的微分方程可写为

\(\frac{1}{{\omega}_{n}^{2}}\frac{{d}^{2}y(t)}{{dt}^{2}}+\frac{2\zeta}{{\omega}_{n}}\frac{dy(t)}{dt}+y(t)=Kx(t)\)     (2.20)

由方程(2.20)可以给出二阶测量系统的传递函数为应为方程(2.21)

\(G(s)=\frac{Y(s)}{X(s)}=\frac{K}{\frac{1}{{\omega}_{n}^{2}}{s}^{2}+\frac{2\zeta s}{{\omega}_{n}}+1}\)  (2.21)

或

\(G(s)=\frac{Y(s)}{X(s)}=\frac{K{\omega}_{n}^{2}}  {{s}^{2}+2\zeta {s}{\omega}_{n}+{\omega}_{n}^{2}}\)  (2.22)

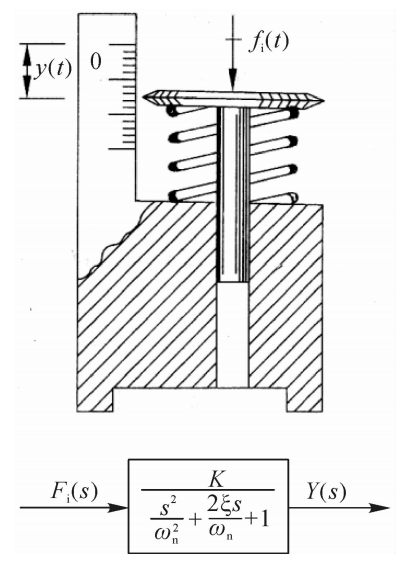
如图2.8所示的测力弹簧秤是二阶测量系统的一个典型实例。假设弹簧的特性是线性的，且具有恒定的劲度系数K_s; 系统具有良好的润滑作用，黏性阻尼系数恒为B;运动系统的 总质量为M。若调整测力弹簧秤，在初始状态使被测力f_i(t)= 0,输出量y(t)=0,则有下述微分方程：

\(M\frac{{d}^{2}y(t)}{{dt}^{2}}+B\frac{dy(t)}{dt}+{K}_{s}y(t)={f}_{t}(t)\)

此式与二阶测量系统的微分方程相吻合。若定义

\(K=\frac{1}{K},{\omega}_{n}=\sqrt{{K}_{s}/M},\zeta=\frac{B}{2\sqrt{M{K}_{s}}}\)

图2.8二阶测量系统

则测力弹簧秤的传递函数与典型二阶测量系统的传递函数相同。

2.4测量系统的动态响应

 动态测量的任务在于定量地确定被测物理量的变化规律，由测量系统的输出量去推断被 测物理量。因此，一个测量系统的输出信号能否正确地重现输入信号，这是动态测量中的一个 重要问题，需要通过研究测量系统的响应特性来解答。

 测量系统的响应是系统保真度的一种反映，可以用来评价测量系统正确传递并显示输入 信号全部信息的能力。实际上，被测量通常并不遵从某一简单的函数关系，在许多情况下也难 以用解析的方法表示，且其具有随机性。因此，用真实的输入信号作用于测量系统来研究系统 的响应特性是困难的。通常，在分析、设计和试验测量系统时，总是用某些典型输入信号，通过 研究测量系统对这些典型信号的响应来了解系统的动态性能。

 研究测量系统的动态性能，可以从时域和频域两方面来讨论。在低阶系统中或输入简单 的瞬态信号时，测量系统的性能指标多以时域量值的形式给出；而在高阶系统中和输入周期性 的、复杂的信号时，以频域量值的形式给出测量系统的性能指标则更为方便。

 2.4.1测量系统对阶跃输入的响应

 测量系统的时域性能指标通常是以系统对阶跃输入量的瞬态响应形式给出的。那么把一 个阶跃函数作用于测量系统时可假设测量系统初始处于静止状态，输入量x(t)、输出量y(t) 以及y(t)的各阶导数均为零，在时间t=0+时，输入量x(t)立刻增加到Xg,即

x(t)=0      t<0

x(t)=X      t≥0

 阶跃函数的拉普拉斯变换为X_s/s。

 1.一阶测量系统对阶跃输入的响应

 典型一阶测量系统的传递函数由式(2.17)给出。对阶跃输入，测量系统输出量的拉普拉 斯变换为

\(Y(s)=\frac{K}{{T}_{s}+1}\frac{{X}_{s}}{s}\)

 取上式的拉普拉斯反变换，得到一阶测量系统对阶跃输入的响应为

\(y(t)=K{X}_{s}\left[1-exp(-\frac{t}{T})\right],(t\ge 0)\)          (2.23)

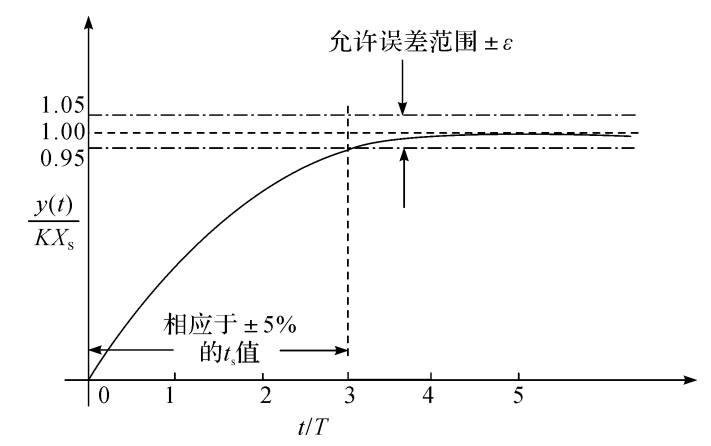
式(2.23)表明，输出量y(t)的初始值等于零，而稳态值为KXg,当t=T时，系统输出量 y(t)的数值等于稳态输出值的63.2%。这里，T为一阶测量系统的时间常数。T值愈小，系 统响应愈快。为了进行可靠的动态测量，应使测量系统的时间常数尽量的小。图2.9(a)给出 了一阶测量系统对阶跃输入的响应曲线。

 在研究动态测量时，动态测量误差是人们关注的主要问题。动态测量误差e(t)定义为

 \(e(t)=\frac{y(t)}{K}-x(t)\)              (2.24)

 在阶跃输入条件下，一阶测量系统的动态测量误差为

 e(t)=-X_sexp(-t/T)    (2.25)

 无量纲化后，得到相对动态测量误差图2.12(b)给出了无量纲化动态测量误差e(t)/Xs与t/T关系曲线。

图2.9一阶测量系统对阶跃输入的响应曲线

 (a)响应曲线；(b)相对动态测量误差

 描述测量系统响应速度的主要性能指标是稳定时间。稳定时间是指测量系统的响应曲线 到达并保持在其最终值周围的某一允许误差范围之内时所需要的时间，记为t_s。稳定时间愈 小，测量系统对阶跃输入的响应愈快。对于一阶测量系统，有

\({t}_{s}=T ln\frac{1}{\varepsilon}\)   (2.26)

 式中

 ε——允许误差。

 显然，稳定时间ts不仅与测量系统的时间常数T有关，而且还取决于所选择的允许误差ε。 通常允许误差范围多取为±2%或±5%。如图2.10所示为一阶测量系统的稳定时间的意义。

图2.10一阶测量系统稳定时间

 2.二阶测量系统对阶跃输入的响应

典型二阶测量系统的传递函数由式(2.21)给出，即

\(G(s)=\frac{Y(s)}{X(s)}=\frac{K}{\frac{1}{{\omega}_{n}^{2}}{s}^{2}+\frac{2\zeta}{{\omega}_{n}}s+1}\)

对于幅值为X的阶跃输入，系统输出量的拉普拉斯变换为

\({Y(s)} =\frac{K{{X}_{s}}}{\frac{1}{{\omega}_{n}^{2}}{s}^{2}+\frac{2\zeta}{{\omega}_{n}}s+1}\)

(2.27)

 对Y(s)进行拉普拉斯反变换，可得到二阶测量系统对于阶跃输入的时间响应。响应的具 体形式取决于测量系统本身的参数ζ和ω_n。

 (1)若ζ>1(过阻尼情况),二阶测量系统对阶跃输入的响应函数为

 (2.28)

 此响应函数包括着两个衰减的指数项，且以指数规律随时间的增大而逼近稳态输出值。当 ω_n一定时，ζ愈大，系统对阶跃输入的响应愈慢；当ζ》1时，二阶测量系统的阶跃响应与一阶测 量系统类似。

 (2) ζ=1(临界阻尼情况)时，测量系统对阶跃输入的时间响应为

 \(\frac{y(t)}{K{X}_{s}}=1-(1+{\omega}_{n}t)\exp{-{\omega}_{n}t }\),(t≥0) (2.29)

 此时，二阶测量系统对阶跃输入的响应也以指数规律随时间的增大而逼近稳态输出值，但已处 于临界状态，ζ稍有减小，系统就会产生振荡而进入欠阻尼状态。

 (3)0<ζ<1(欠阻尼情况)时，测量系统对阶跃输入的时间响应为

    (2.30)

 式(2.30)表明，在欠阻尼情况下，二阶测量系统对阶跃输入的响应是衰减的正弦振荡，它 随时间增大而趋向稳态输出值KX_s。,振荡频率为\({\omega}_{d}={\omega}_{n}\sqrt{1-{\zeta}^{2}}\)。在ω_n一定时，ω_d随阻尼 比ζ而变化。如果ζ=0,二阶测量系统对阶跃输入的响应变为无阻尼等幅振荡的形式。

 二阶测量系统在不同阻尼比时对阶跃输入的无量纲响应曲线如图2.11所示。图中，横坐 标是以ζ与ω_n的乘积形式给出的，因此，曲线只是ζ的函数。这表明，ω_n是系统响应速度的直 接标志。对于一定的阻尼比ζ，ζ增大一倍，将使系统的响应时间减半。另外，ζ增大使得振 荡减小，系统稳定性增加，但响应曲线第一次穿越稳态输出值的时间却被延迟下来。

 在阶跃输入条件下，当0<ζ<1时，二阶测量系统的动态测量误差为

     (2.31)

这一动态误差信号是衰减的正弦振荡。当t→∞时，动态误差趋于零。

 图2.11二阶测量装置对阶跃输入的响应曲线

 描述二阶测量系统瞬态响应速度的主要性能指标是稳定时间t_s。在欠阻尼二阶测量系 统中，很难写出稳定时间的精确表达式。但由式(2.31)可知，欠阻尼二阶测量系统的相对动态 测量误差可由下式来限定，即

 \(\left| \frac{e\left( t \right)}{{{X}_{s}}} \right|\le \frac{\exp \left( -\zeta {{\omega }_{n}}t \right)}{\sqrt{1-{{\zeta }^{2}}}}\)   t≥0      (2.32)

 由式(2.32)可求得在一定的允许误差下稳定时间的近似表达式。当0<ζ≤0.8并取允 许误差范围为±2%时，稳定时间可近似地按下式来求得，即

 t≈4.5/(ζω_n)          (2.33)

 若取允许误差范围为±5%,则

 t≈3.5/(ζω_n)     (2.34)

 描述二阶测量系统相对稳定性的主要指标是最大过冲量。在阻尼比ζ<1时，系统的阶 跃响应会在稳态输出值上下产生衰减的正弦振荡。响应曲线达到过冲量第一个峰值所需要的 时间，称为峰值时间，以t_p表示为

\({{t}_{p}}=\frac{\pi }{{{\omega }_{n}}\sqrt{1-{{\zeta }^{2}}}}=\frac{\pi }{{{\omega }_{d}}}\)   (2.35)

 第一个过冲峰值超过稳态输出值的数量称为最大过冲量，以M_p表示为

\({{M}_{p}}=\frac{y({{t}_{p}})}{K{{X}_{s}}}-1=\exp \left( -\frac{\zeta \pi }{\sqrt{1-{{\zeta }^{2}}}} \right)\times 100%\)         (2.36)

 由式(2.36)可知，M_p与ζ有关。ζ愈小，M_p愈大，测量系统的相对稳定性愈差。

 应该指出，一个测量系统的瞬态响应，既应该有足够的快速性，又应该有充分的稳定性，而 表征测量系统瞬态响应特性的主要时域性能指标都与阻尼比ζ有关。为了获得满意的瞬态响 应特性，ζ必须选择在0.4～0.8之间，小的ζ值(ζ<0.4)会造成系统瞬态响应的严重过冲，

而大的ζ值(ζ>0.8)将使系统的响应变得缓慢。许多实际的二阶测量系统(或测量仪表)都

 取ζ=0.6～0.7作为阻尼比的最佳值范围。

 2.4.2测量系统的频率响应

 频率响应是测量系统对正弦输入的稳态响应。当测量系统的输入量是形式为Xsinωt的 正弦波时，在全部瞬态效应消失之后，系统的输出量将是一个与输入量同频率的正弦波。不 过，输出量的幅值通常不等于输入量的幅值，同时两者间也存在着相位差。由于频率相同，测 量系统输出正弦波与输入正弦波之间的关系，完全可以由两者之间的幅值比和相位差来决定。 实际上，当输入信号频率w变化时，测量系统输出量与输入量之间的幅值比和相位差都会随之 发生变化。通常把输出量与输入量的幅值比随输入信号频率的变化关系称为测量系统的幅频 特性，相位差随频率的变化关系称为测量系统的相频特性。幅频特性和相频特性共同表达了 测量系统的频率响应特性。在实际遇到的测量问题中，任何输入信号都可以表示成不同频率 的正弦信号之和。对线性测量系统，如果已知系统的频率响应特性，就可以利用叠加原理求得 测量系统对任意输入信号的响应。

 测量系统的频率响应可以利用正弦传递函数来求得。测量系统的正弦传递函数可以直接 用jω代替传递函数中的s得到。对式(2.9)所描述的系统，其正弦传递函数可方便地表达为

      (2.37)

 式中，\(j=\sqrt{-1}\),ω为信号的角频率。

 正弦传递函数G(jω)是以ω为参数的复变函数。对任意给定的角频率ω,G(jω)是一个 复数，它可以表示成极坐标形式为

 G(jω)=|G(jω)|∠G(jω)

 其中|G(jω)|是复数G(jω)的模，∠G(jω)是它的相角。可以证明|G(jω)|就是测量系 统输出量与输入量的幅值比，而∠G(jω)是输出量与输入量的相位差。当输入频率变化时，幅 值比|G(jω)|就是测量系统的幅频特性，常记为(Y/X)ω或A(ω) ,∠G(jω)是系统的相频特性，以φ(ω)表示。为了在频率域中对测量系统的动态性能进行全面的描述，必须指出系统的 幅频特性和相频特性。

 幅频特性和相频特性常以曲线形式绘出。实际作图时，用对数坐标来绘制特性曲线更为 方便。在对数坐标中幅值比用分贝(dB)表示，横坐标可用角频率ω或其相对应的对数表示， 以提高低频范围的分辨能力。

1.一阶测量系统的频率响应

 典型一阶测量系统的正弦传递函数G(jω)可表示为

 \(G\left( j\omega  \right)=\frac{K}{jT\omega +1}=\frac{K}{\sqrt{{{T}^{2}}{{\omega }^{2}}+1}}\angle \arctan \left( -\omega T \right) \)       (2.38)

 由式(2.37)可知，一阶测量系统的幅频特性和相频特性分别为

\(\frac{Y}{X}\left( \omega  \right)=\left| G\left( j\omega  \right) \right|=\frac{K}{\sqrt{{{T}^{2}}{{\omega }^{2}}+1}}\)          (2.39)

 \( \varphi \left( \omega  \right)=\angle G\left( j\omega  \right)=\angle \arctan \left( -\omega T \right) \)          (2.40)

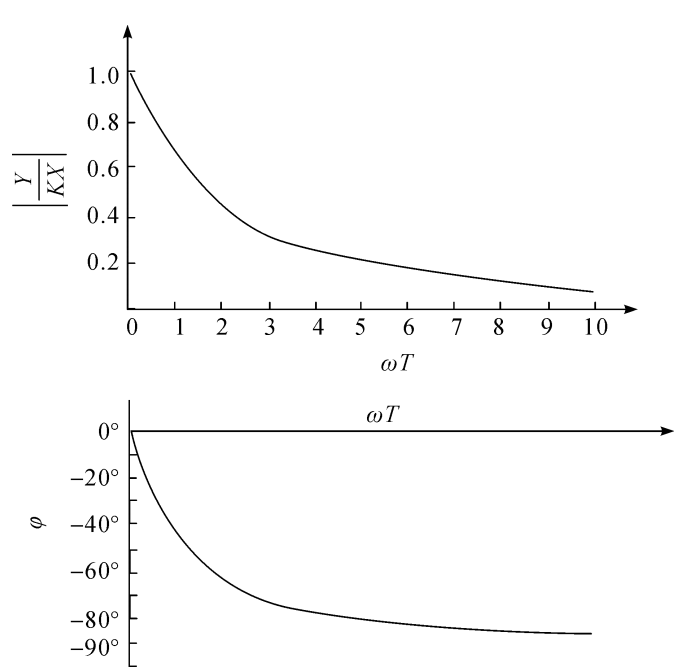
图2.12给出了一阶测量系统的幅频 特性曲线和相频特性曲线。曲线的纵坐 标分别以相对幅值比|Y/(KX)|和相角 φ表示，横坐标以角频率与时间常数乘积 ωT表示。

 图2.12一阶测量系统的频率特性

 理想测量系统(零阶系统)的频率特 性可由其正弦传递函数表示如下：

  G(jω)=K∠0°

 如果式(2.38)近似零阶系统的频率特性， 一阶测量系统就接近于理想系统。这种 情况只有当ωT足够小时才会出现，否则， 一阶测量系统就会存在着不可忽视的测 量误差。

  一阶测量系统频率响应的幅值误差为

 \(\left( \frac{Y}{K}-X \right)=\frac{X}{\sqrt{{{T}^{2}}{{\omega }^{2}}+1}}-X\)(2.41)

 将式(2.41)无量纲化之后，可得到系统频率响应的相对幅值误差为

 \(\left( \frac{Y}{KX}-1 \right)=\frac{1}{\sqrt{{{T}^{2}}{{\omega }^{2}}+1}}-1\)   (2. 42)

 对于给定的相对幅值允许误差ε,若被测信号频率为ω,则满足测量要求的系统时间常数 应为

 \(T=\frac{1}{\omega }\frac{\sqrt{2\varepsilon -{{\varepsilon }^{2}}}}{1-\varepsilon }\)   (2.43)

 而对同样的ε,时间常数为T的一阶测量系统所能精确测量的被测信号频率应为

\(\omega =\frac{1}{T }\frac{\sqrt{2\varepsilon -{{\varepsilon }^{2}}}}{1-\varepsilon }\)  (2. 4)

 可见，对一阶测量系统，相应于一定的时间常数T,总存在着某一输入频率ω,当低于这一频率 时，可以认为测量是足够精确的。或者说，如果需要足够精确地测量某一高频信号，一阶测量 系统必须有足够小的时间常数。

 2.二阶测量系统的频率响应

典型二阶测量系统的正弦传递函数可以表示为

 \(G\left( j\omega  \right)=\frac{K}{{{\left( \frac{j\omega }{{{\omega }_{n}}} \right)}^{2}}+\frac{2j\zeta \omega }{{{\omega }_{n}}}+1}\)    (2.45)

 其幅频特性和相频特性分别为

 \(\frac{Y}{X}\left( \omega  \right)=\left| G\left( j\omega  \right) \right|=\frac{K}{\sqrt{{{\left[ 1-{{\left( \frac{\omega }{{{\omega }_{n}}} \right)}^{2}} \right]}^{2}}+{{\left( \frac{2\zeta \omega }{{{\omega }_{n}}} \right)}^{2}}}}\)   (2.46)

\(\varphi \left( \omega  \right)=\angle G\left( j\omega  \right)=\arctan \frac{2\zeta {\omega }/{{{\omega }_{n}}}\;}{{{\left( \frac{\omega }{{{\omega }_{n}}} \right)}^{2}}-1}\)  (2.47)

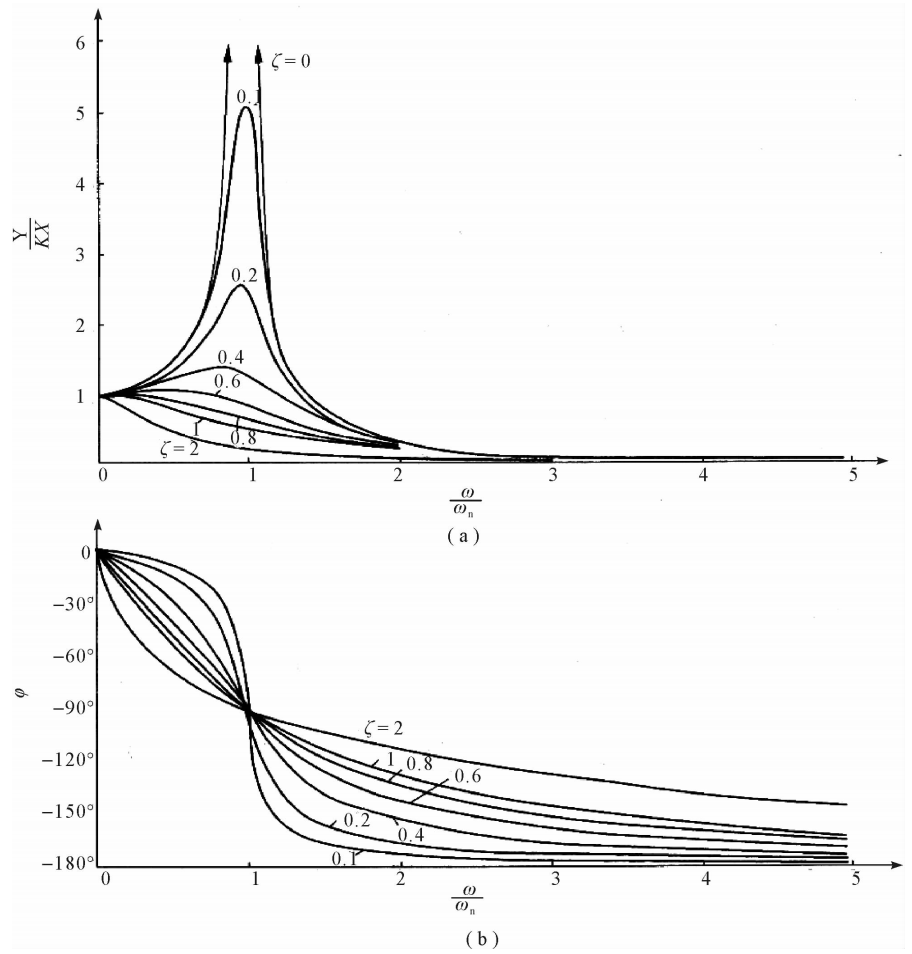
 图2.13给出了二阶测量系统的幅频特性曲线和相频特性曲线。图中，幅值比以相对值 Y/(KX)|表示，横坐标以ω/ω_n表示此图，还以阻尼比ζ为参变量。由图2.13中可以看出， 当ζ小于某一值时，幅频特性曲线有峰值(产生谐振的情况)。出现峰值的条件可以由幅频特 性|G(jω)|的分母部分为最小值时求得。由式(2.46)的分母表达式，当

\(g\left( \omega  \right)={{\left[ 1-{{\left( \frac{\omega }{{{\omega }_{n}}} \right)}^{2}} \right]}^{2}}+{{\left( \frac{2\zeta \omega }{{{\omega }_{n}}} \right)}^{2}}\)

为最小时，不难得到出现峰值时的频率，即谐振频率

\({{\omega }_{r}}={{\omega }_{n}}\sqrt{1-2{{\zeta }^{2}}}\),(0≤ζ≤0.707)

图2.13二阶测量系统的幅频特性和相频特性

 (a)幅频特性；(b)相频特性

谐振峰值为

\({{M}_{r}}={{\left| \frac{Y}{KX} \right|}_{\max }}=\frac{1}{2\zeta \sqrt{1-{{\zeta }^{2}}}}\)       (2.48)

 当阻尼比ζ>0.707时，不产生谐振，幅值比|G(jω)|将随角频率ω的增大而单调减小。 很明显，增大ω_n,会增大使幅频特性曲线相对平坦的频率范围。要精确测量高频信号，测量系 统必须具有足够高的ω_n,否则，就会产生动态幅值误差。

 对于测量系统的阻尼比ζ,其最佳值范围是由幅频特性和相频特性共同决定的。从幅频 特性曲线来看，使曲线相对平坦的最大频率范围出现在ζ值约为0.6～0.7之间。对动态测量 来说，尽管系统输出量与输入量之间的相位差等于零是最理想的，但从二阶测量系统的相频特 性曲线来看，实现这一点几乎是不可能的，甚至接近零相位差的频率范围也是极为有限的。在 实际问题中，如果测量的目的在于正确地复现输入信号的波形，而不重视在输出信号与输入信 号之间存在的时间延迟，那么,二阶测量系统的相频特性并不需要始终具有零值相位差，而要 求其具有良好的线性特性，使相位差随角频率ω的变化呈线性。这样，系统对于不同频率正弦 波的延迟时间相同，不会引起输出波形的失真。由相频特性曲线可以看出，阻尼比ζ=0.6～ 0.7时，相频特性曲线在很宽的频率范围内几乎都是直线。上述两方面的原因，使得一般二阶 测量系统都选择ζ=0.6～0.7作为系统阻尼比最佳值范围。在这个最佳5值范围内，二阶测 量系统具有最大的不失真输出频率范围。

第3章传感器

在固体火箭发动机试验中，需要测量的参数很多。目前经常测量的有发动机推力、侧向分力、燃烧室压力、发动机壁温分布、壳体的应变等等。在第1章概论中曾介绍了发动机试验的特点，根据这些特点，发动机试验的参数测量需要采用非电量的电测法，也就是要把发动机在试验过程中表现出来的各种不同质的物理量转变为电量，然后再进行处理、传输和记录。测量向我们提出的第一个问题是如何将各种被测物理量变换成与之相应的电量。这就是测量系统的第一个环节——传感器所要完成的任务。在此先举一个例子来说明传感器工作的一般过程和原理。

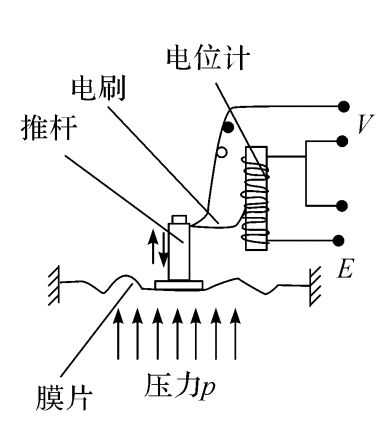
如图3.1所示为一种压力传感器的原理图。它由膜片、推杆、电刷和电位计等组成。电位计上供以直流电源E。当压力p作用在膜片上时，膜片的中间部分因变形而产生位移，这个位移由推杆带动电刷在电位计上滑动，使电刷与电位计一端的电阻值产生变化，从而使输出电压V也发生变化，这样就把压力的变化转换为电阻或电压的变化。其中直接感受压力的弹性元件——膜片，称为敏感元件，带有电刷的电位计叫做变换器。

图3.1压力传感器原理图

由此可知，传感器的作用是将被测量(这里是压力)转换成与其相应的容易检测、放大和传输的电量(这里是电压)。敏感元件的作用是将被测量变为另一种形式的物理量(这里是把压力变为位移)。而变换器的作用则是将敏感元件变成的物理量转变为电量(这里是将位移转变为电阻)。传感器的核心是变换器，变换器可以是传感器的一部分，也可以作传感器独立使用。

通常，构成一个完整的传感器，它还将包括把敏感元件、变换器组成一个整体的壳体，连接固定件和其他补偿、放大等元器件。

变换器的种类很多，本章只介绍在发动机参数测量及一般工程测量中常用的几种变换器和由这些变换器所构成的传感器。

3.1电阻应变式变换器

电阻式变换元件广泛地应用于工程测量中，它们的共同特点是把被测参数转化为电阻值的变化。可以构成电阻的材料有多种，如金属、非金属、半导体材料等。因此，电阻式变换元件也有多种类型。能引起电阻材料发生阻值变化的原因也很多，在测量中常用的物理现象主要有导体长度的变化、导体内应力的变化、温度变化等等。应用上述原理构成了电位器式电阻变换器(见图3.1所示)、应变式变换器和热电阻式变换器等等。可用来测量位移、转角、力、压力、应力及温度等物理参数。本节只讨论应用最广的应变式变换器。热电阻式变换器将在第5章中做介绍。

3.1.1金属应变片

金属电阻应变式变换器是一种能将机械构件的应变转换为电阻值变化的变换元件。一般都做成片状。应用时将其贴在变形构件的表面。通常称为电阻应变片或电阻应变计，简称应变片。

1.工作原理

电阻应变片的工作原理是基于它的应变效应。我们知道，金属丝的电阻值与其长度、截面积及该金属材料的电阻率有关，可用公式表示为

\(R=\rho\frac{l}{S}\)      (3.1)

式中

R——电阻，单位：Ω;

ρ——电阻率，单位：Ω·m;

l——长度，单位：m;

S——截面积，单位：m²。

实验证明，当金属丝在受力状态下，其长度、截面积及电阻率都发生变化，从而金属丝的电阻也随之改变。它们之间数量上的关系可对式(3.1)做一些简单的数学处理求得。

对式(3.1)两边先取对数，再进行微分，有

\(\ln R=\ln \rho +\ln l-\ln S \)

\(\frac{dR}{R}=\frac{d\rho }{\rho }+\frac{dl}{l}-\frac{dS}{S} \)    (3.2)

设金属丝截面为圆形，半径为r,则圆形截面积S=πr²,dS=2πrdr,所以\(\frac{dS}{S}=2\frac{2dr}{r}\),代入式(3.2),有

\(\frac{dR}{R}=\frac{d\rho }{\rho }+\frac{dl}{l}-2\frac{dr}{r} \)   (3.3)

由材料力学知，\(\frac{dl}{l}=\varepsilon \),\(\frac{dr}{r}=\nu \varepsilon \)其中μ是泊松比(对于一般金属μ=0.3～0.5),代入式(3.3),有

\(\frac{dR}{R}=\frac{d\rho }{\rho }+(1+2\mu)\varepsilon\)    (3.4)

对于金属材料很小，可略去，则

\(\frac{dR}{R}=\frac{d\rho }{\rho }+(1+2\mu)\varepsilon={K}_{0}\varepsilon\)    (3.5)

式中K₀=1+2μ,称为金属材料的灵敏度系数(在弹性限度内K₀=1.9～3.0)。ε的单位是长度/长度，为无因次量，但习惯上仍给以单位，这个单位叫“应变”。即把相对变形量100%(即ε=1)称为一个应变，用符号ε表示。它的10-6称为一个微应变，记作jε。

 用钢材料制成的构件，在弹性范围内，相对变形ε<2.5×10-³,电阻变化率△R/R< 0.75%,在实际使用时，为可靠起见，材料不会用到弹性上限，因此△R/R的数值往往是千分之 几或万分之几，这样，用一般的仪表及简单的线路无法进行测量，必须经过放大，通常把与应变 测量配套使用的专用放大器称为应变放大器(电阻应变仪)。

 2.金属应变片的类型和结构

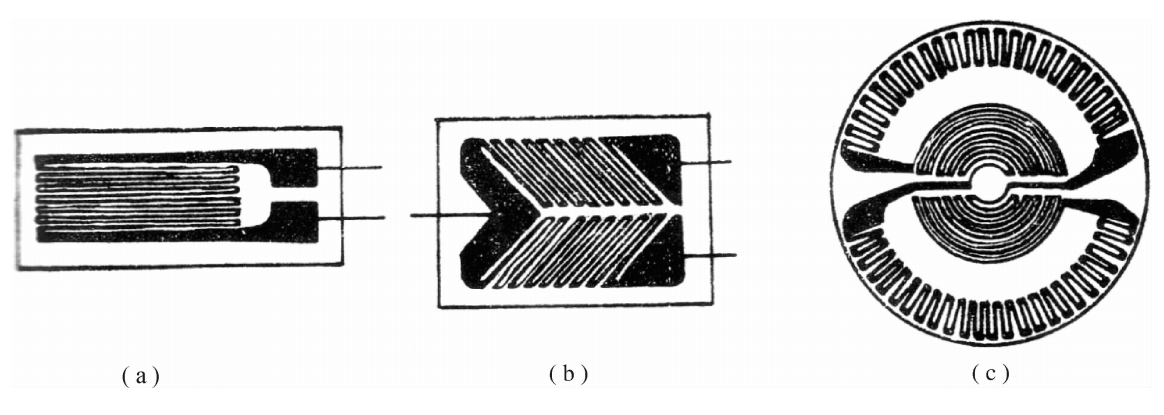
 为了获得高的电阻值，金属丝需要长一些，但点测量需要面积小一些，因此要将金属丝绕 成栅状。根据金属材料的形式和制造方法的不同，金属电阻应变片分为丝式、箔式和薄膜式三 种结构形式。

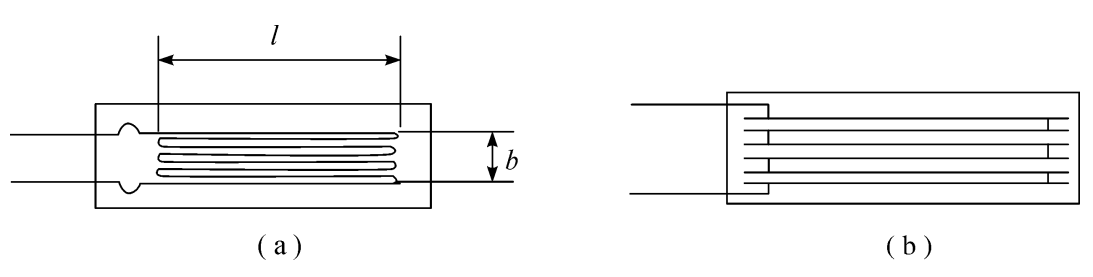
 (1)丝式应变片。金属丝式应变片是用直径为0.02～0.04 mm的高电阻率金属丝制成 的，常用的材料包括康铜(Cu55%、Ni45%)、卡玛合金(Ni74%、Cr20%、Al3%、Fe3%)和镍铬 合金(Ni80%、Cr20%)等。为了获得高的电阻值，将电阻丝绕成栅网状，称为敏感栅。将敏感 栅贴在两层绝缘材料之间，引线多使用0.15～0.3 mm的镀锡铜线或铜带，用钎焊或点焊与敏 感栅相连接，这种应变片又分为圆角线栅式和直角线栅式两种，分别叫做丝绕式和短接式，如

 图3.2所示。图3.2(a)中1称为标距或基长，b称为基宽，I×b称为应变片的使用面积。应变 片的规格一般是以使用面积、灵敏度系数和电阻值来表示的。应用时将应变片牢固地贴在被 测构件的表面上，当构件受力变形时，应变片的敏感栅也随之变形，同时电阻也发生相应地变 化，通过测量电路，最终可将其转换为电压或电流的变化。

 图3.2金属丝式应变片

 (a)圆角线栅式；(b)直角线栅式

圆角线栅式应变片制造简单，但横向灵敏度较大。直角线栅式应变片的横线采用粗导线， 电阻很小，横向灵敏度小，因而测量误差也小。应变片的敏感栅被粘贴在基底上，基底材料有 纸和有机聚合物两大类。前者称为纸基应变片，后者称为胶基应变片。纸基应变片纸的厚度 为0.05 mm左右，工作温度一般为70℃以下。为了提高应变片的耐热和防潮性能，使用浸含 有酚醛树脂的纸作为基底，工作温度可达180℃,并且长时间工作稳定性较好。胶基应变片使 用酚醛、环氧树脂和聚酰亚胺等有机聚合物作基底材料。聚酰亚胺的工作温度范围是-269～ 400℃,绝缘电阻达22000 MQ以上，这种基底的厚度通常为0.025 mm,这就使得应变片具有 良好的柔韧性，适于贴在曲面上。

 (2)箔式应变片。金属箔式电阻应变片的基本原理与丝式应变片相同，但它的敏感栅是由 很薄的金属箔片用照相制版、化学腐蚀的光刻技术制成的，在制造工艺方面便于大量生产，电 阻值的分散度很小。箔片的材料为康铜、镍铬合金等，厚度多在0.001～0.01 mm之间，最薄 0.00035 mm。它的基底由环氧树脂、聚脂塑料、聚酰胺塑料等材料制成，厚度为0.025 mm 左右。如图3.3(a)所示为普通形式的箔式应变片，它的横向部分特别宽，以减小横向灵敏度。

为适应不同场合下的应变测量，其敏感栅可以做成不同的形状，如图3.3(b)所示是测量扭矩 用的应变片。图3.3(c)是贴在承受流体压力的圆膜片上的应变片。因为它很薄，能够与被测 表面紧密地贴合，正确地反应变形；由于它的表面积与横截面积之比较大，散热性好，允许通过 较大的电流；此外，箔式应变片还有承受交变载荷时疲劳寿命长、长时间测量蠕变小等优点。 目前所采用的应变片大多数都是箔式的。

 对于泵用机械加工和化学腐蚀等方法制成的应变片，称之为体型应变片。可以看出丝式 应变片和箔式应变片均属于体型应变片。

图3.3箔式应变片

 (a)普通形式；(b)测扭矩用；(c)贴片式

  (3)薄膜式应变片。薄膜应变片一般是采用真空蒸发、溅射、化学气相淀积及等离子化学 气相淀积等方法，把金属、合金、半导体材料或氧化物淀积在基片(或弹性体)上制成的。薄膜 应变片与体型应变片相比，由于其导电机理不同，其应变灵敏系数是它的显微结构和厚度的函 数。薄膜应变片的厚度仅是通常箔式应变片厚度的1/10,其与传统箔式应变片相比，具有一 系列明显的优点。

1.  容易制作高阻值的微型应变片：一般箔式应变片的最高阻值为1 kΩ左右，而对于同样 尺寸的薄膜应变片阻值可达2～10 kΩ,这样可以施加更高的桥压，获得高的输出信号。
2.  由于其厚度极薄、质量轻、约束力小，因而对基片(或弹性体)应变部位的变形没有附加 效应。
3.  由于薄膜应变片不用黏合剂，相互之间连接呈无机质化，因而几乎没有蠕变和滞后，长 期稳定性好。
4.  具有优良的耐湿性、耐热性及耐热冲击性，便于制成高精度、高可靠性的元件。
5.  便于规模生产，适于生产低成本、高精度传感元件。

薄膜应变片与传统箔式应变片相比，有以下缺点。

1.  生产设备比较复杂，价格昂贵。
2.  生产工艺过程比较复杂，对产品质量难于控制。
3.  薄膜应变片的应用受弹性体的形状、尺寸大小等因素的限制。
4.  金属应变片的主要特性

 (1)应变片的灵敏度。金属电阻丝的电阻相对变化与它所感受的应变之间具有线性关系， 并用它的灵敏度系数K₀来表示。但用金属丝绕成电阻应变片之后，电阻-应变特性就与金属 单丝时有所不同。应变片的电阻-应变特性须用实验的方法测定。

 实验证明，电阻应变片的电阻相对变化△R/R与应变ε的关系在很大范围内是线性的，即

 \(\frac {\Delta R}{R}=K\varepsilon\)

\(K=\frac{{\Delta R}/R}{\varepsilon}\)      (3.6)

 式中

 K——电阻应变片的灵敏度。

 实验表明，应变片的灵敏度K恒小于线材的灵敏度系数K。。究其原因，除了胶体传递变 形失真之外，就是存在着横向效应。

 所谓横向效应是指当应变片贴在构件上，当构件承受拉力变形时，应变片栅丝的直线部感 受的是纵向拉应变，而栅丝的圆角端部却感受的是压应变。因此，在测量纵向应变时，栅丝的 圆角端部不仅不产生正的电阻变化，反而横截面积变大，产生负的电阻变化，即横向部分将纵 向部分的电阻变化抵消了一部分，从而降低了整个应变片的灵敏度。

 (2)应变片的稳定性。在使用应变片进行测量时，常常发生滞后、零点飘移和蠕变现象。 这些现象都会影响到测量的精度。

 所谓滞后是指在恒定温度下，循环加载时，加载特性曲线和卸载特性曲线的不重合程度， 以加载曲线和卸载曲线中最大差异值来表示。实践表明，多次加卸载后，这种不重合程度将 减小。

 零点飘移是在试件不受力且温度恒定的情况下，应变的指示值随时间变化的特性。一般 以三小时内指示应变的最大值与时间之比，称为零点飘值。

 蠕变是在温度恒定，试件承受某种恒定的机械应变的条件下，贴在试件上的应变片的指示 应变值随时间变化的特性。

 上述这些特性都是用来衡量应变片的稳定性的。

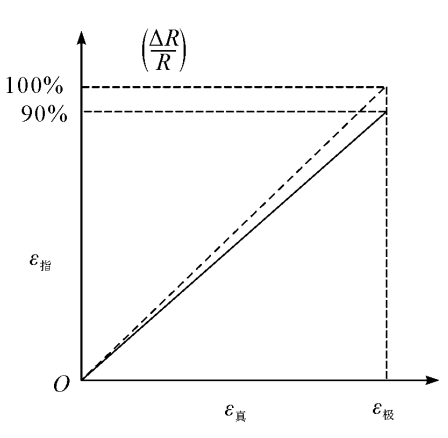
 (3)线性度和应变极限。应变片的线性表明应变片电 阻变化率和应变变化之间的关系。严格地讲，它们之间总 是不成线性的。但实践表明它的非线性误差很小，而且在 多次反复加卸载后将获得改善。应变片的线性度一般要求 在0.05%或1%以内。

 应变片的应变极限是指当温度一定时，指示应变和真 实应变的相对差值不超过一定数值时的最大真实应变数 值。一般差值规定为10%,则指示应变数值为真实应变的90% 时的真实应变值称为应变片的应变极限，如图3.4所 真 8极 示。真实应变是由于温度变化或施加机械载荷在试件上产生应力所引起的单位变形。指示应变是指经过校准的应变仪的应变读数，它是与应变片的电 阻相对变化相对应的。

图3.4应变片的应变极限图

 (4)应变片的工作电流。在利用应变片进行测量时，通常把电阻丝接入桥式电路。为了提 高灵敏度，应适当增加流过电阻丝的电流。但电流太大将使应变片的温升过高。应变片因温 度升高阻值增大而产生误差，甚至将应变丝烧断，或者使黏结剂软化，不能正确传递应变，这也 会带来测量误差。

应变片的温升除与电流有关外，还与许多因素有关，如应变片尺寸、线栅的材料、黏合剂的传热性能、试件材料及尺寸以及散热情况等有关，应根据具体情况而定。—般按经验在静态测量时，允许电流密度为50A·mm-²,短期使用允许电流密度达100A·mm-²。

(5)应变片的动态特性。用应变片进行动态测量时，应该考虑它的动态响应特性。应变片的敏感栅有一定的长度，它所反映出的应变实际上是该长度的平均应变。在动态测量时，应变是以应变波的形式在构件中传播的，其传播速度与声波相同。测量静态应变或变化频率较低的应变时，它能正确反映构件内各点的应变。当被测应变的变化频率较高时，构件内各点的应变在某一瞬间有较大的差别(设应变波沿应变片基长方向传播),应变片反映的平均应变相差很大，产生了失真。

设动态应变以正弦波的形式变化，经理论分析，当应变测量的相对误差小于2%时，可得以下近似关系式：

\(f=\left(\frac{1}{10}-\frac{1}{20}\right)\frac{v}{l}\)   (3.7)

式中

f——动态应变的频率，单位：Hz;

v——应变波的传播速度，单位：m·s-¹;

l——应变片基长，单位：mm。

应变波在钢内的传播速度为5000mm·s-¹,若取1/10,l和f的关系见表3.1。

表3.1应变片基长与最高应变频率的关系

3.1.2桥式测量电路

应变片因形变而产生的电阻变化量往往很小，应用起来很不方便。在测量中往往把应变片连接成桥式电路，使之产生一个相对变化的电压(电流),然后输到放大器或直接输到记录仪器中去。

1.单臂电桥

如图3.5所示为由四片阻值相等的应变片组成的电桥，其中每片应变片R称为电桥的一个桥臂，设电桥供以直流电源，其电压为E.;并设电桥的输出负载为无穷大；电路中的电容、电感均可以不考虑。

当四个桥臂的电阻均未发生变化时，电桥上1,2两个顶点的电位相等，输出端没有信号输出，即U=0。

若电桥的一个桥臂发生电阻变化，其值为△R,则1,3两点间的电压为

\({U}_{13}=\frac{1}{2}{E}_{c}\)

图3.5单臂电桥

而2,3两点间的电压降为

\({U}_{23}=\frac{R}{2R+\Delta R}{E}_{e}\)

 输出端1,2两点间输出的不平衡电压为

\(U={U}_{13}-{U}_{23}={E}_{e}\left(\frac{1}{2}-\frac{R}{2R+\Delta R}\right)=\frac{1}{2}{E}_{e}\frac{\delta R}{2R+\Delta R}\)    (3.8)

 已经知道，在实际应用中应变片的应变量很小，—般电阻的相对变化△R/R<0.75%,上 式分母中的△R/R可以忽略，因此式(3.8)可以写作

\(U=\frac{1}{4}{E}_{e}\frac{\Delta R}{R}=\frac{1}{4}{E}_{e}{K}{\varepsilon}\)   (3.9)

 由式(3.9)可见，当供桥电源电压保持不变时，电桥输出端的电压和应变片的应变成正比； 要增大输出电压信号，在应变片最大允许电流范围内，可适当提高供桥电压。

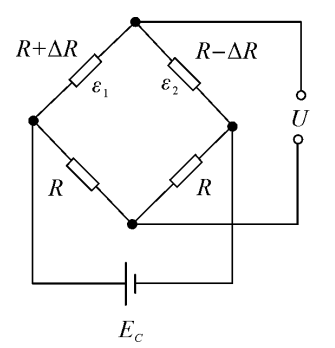
 2.差动电桥

 若电桥两个相邻的桥臂产生电阻变化，且变化的性质相反，即一片受拉产生正应变ε₁,一 片受压产生负应变ε₂,如图3.6所示，称为半桥差动电桥，则输出电压为

 \(U=\frac{1}{4}{E}_{e}K({\varepsilon}_{1}-{\varepsilon}_{2})\)    (3.10)

 若ε₁=-ε₂=ε,则

 \(U=\frac{1}{2}{E}_{e}K{\varepsilon}\)    (3.10)

 当电桥的四个桥臂均发生电阻变化，且相邻桥臂的变化性质相反，如图3.7所示，这时输 出电压为

  \(U=\frac{1}{4}{E}_{e}K({\varepsilon}_{1}-{\varepsilon}_{2}+{\varepsilon}_{3}-{\varepsilon}_{4})\)    (3.11)

 若ε₁=-ε₂=ε₃=-ε₄=ε,则

 \(U={E}_{e}K{\varepsilon}\)  

这时，电桥的输出电压是单臂工作时的四倍。 差动电桥的好处是可以消除非线性误差，提高灵敏度，此外还具有温度补偿的功能。

 图3.6半桥接线图

图3.7全桥接线图

 3.1.3应变片的温度补偿

 1.温度影响

 由于应变引起应变片的电阻变化很小，而温度的变化也使应变片的电阻值发生改变，从而影响到应变的测量结果，这种温度误差称为应变片的温漂。温度变化引起电阻变化有两方面的原因。

(1)电阻温度效应。当温度变化时，金属导体的电阻值随温度的变化而变化。通常用电阻温度系数α表示。若温度变化为△T,应变片电阻R的变化量△R₁t为

△R₁t=Rα△T

式中

α——应变电阻丝的电阻温度系数，单位：℃-¹。

(2)线膨胀系数不同而产生的电阻变化。由于应变电阻丝的材料与被测试件材料的线膨胀系数不同，当环境温度变化△T时被测试件的长度由L变到L+△L₁,而应变电阻丝由L变到L+△L₂,试件及电阻丝的长度相对变化分别为

\(\frac{\Delta{L}_{1}}{L}={\beta}_{1}\Delta T,\frac{\Delta{L}_{2}}{L}={\beta}_{2}\Delta T\)

式中

β₁——被测试件的线膨胀系数，单位：℃^-1;β₂——应变片的线膨胀系数，单位：℃^-1。

由于线膨胀系数不同，长度产生的相对变化△L=△L₁—△L₂应变电阻丝的相对变形为

\(\varepsilon=\frac{\Delta L}{L}=\frac{{\Delta L}_{1}-{\Delta L}_{2}}{L}=({\beta}_{1}-{\beta}_{2})\Delta T\)

相应的电阻变化为

AR=K(β-B₂)△T

因此，环境温度变化△T后，应变电阻丝总的电阻变化为

\(\frac{\Delta R}{R}=\frac{{\Delta R}_{1t}+{\Delta}_{2t}}{R}=\left[\alpha+K({\beta}_{1}-{\beta}_{2})\right]\Delta T\)    (3.12)

由上式可知，温漂除与△T有关外，还与应变片本身的性能参数α,K,β₂以及被测材料的线膨胀系数β₁有关。

2.温度补偿方法

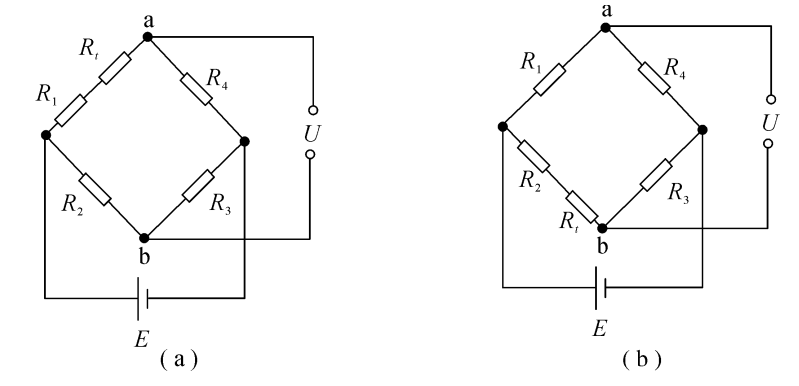
(1)电路补偿法。为了消除上述温度误差的影响，—般均采用温度补偿的办法。对于单臂电桥来说，具体方法是用与测量应变片R₁完全相同的—片应变片R₂(称为补偿片),贴在一块与待测构件相同且不产生应变的材料上，并放在与测量片相同的温度场内，在连接电路时，补偿片接在与测量片相邻的桥臂上，如图3.8所示(暂不考虑电阻R),其中R₃=R₄。由于应变片R₁和R₂相同，并贴在相同的材料上，又置于同一温度场内，所以两片应变片因温度变化所引起的电阻变化完全相同，温度变化对电桥的输出没有影响，从而达到了温度补偿的作用。这种方法的缺点是很多情况下补偿件不容易找。

实际上情况是复杂的，加上补偿片后，可能还不能满足要求，往往在桥臂中串接温度补偿

电阻R,如图3.8所示。温度补偿电阻是用电阻值较小并有正温度系数(α>0)的金属丝绕制而成的，当温度升高时，R的值增大。

若温度升高时，电桥输出电压的偏移相当于R₁减小的结果，这时可将温度补偿电阻R.串接在R₁的桥臂中，如图3.8(a)所示。

若温度升高时，电桥输出电压的偏移相当于R₂减小的结果，这时则将温度补偿电阻Rt接在R₂的桥臂中，如图3.8(b)所示。

图3.8温度补偿电阻接线图

采用电路补偿，方法简便，能在较大的温度范围内进行有效的补偿。这种补偿方法在各种应变式传感器中得到广泛地应用。

前面也提到采用差动电桥本身就具有温度补偿的功能。

(2)自补偿法。这种补偿方法的出发点是使应变片的总温度系数为零。即当温度变化时，应变片的总电阻值不变化。这种具有自身补偿作用的应变片称为自补偿应变片。这种方法又分为两种。

1)对敏感栅材料进行处理法。由式(3.12)可知，由温度引起的电阻变化为

\(\Delta R=R\left[\alpha+K({\beta}_{1}-{\beta}_{2})\right]\Delta T\)  

若要求应变片的电阻变化与温度无关，应使

α+K(β₁-β₂)=0或α=-K(β₁-β₂)     (3.13)

对一定的试件材料，其线膨胀系数β₁为常数。若能选择电阻丝的温度系数α和线膨胀系

数β₂使式(3.13)成立，则实现了补偿。目前采用的方法是控制康铜丝的合金成分和退火温度，使电阻丝具有不同的α和β₂值。由试验可知，随着电阻丝退火温度的增加，其电阻温度系

数变化较大，如图3.9所示，可从负值变为正值，并在某一温度下为零。

图3.9电阻温度系数曲线

一些常用材料的线膨胀系数见表3.2。若康铜丝的线膨胀系数β₂=15×10^–⁶℃^–¹,则粘贴在材料上的应变片得到完全补偿的条件可由式(3.13)、表3.2及图3.9求出。表3.2是K为2时求出的。例如：贴在硬铝上的康铜丝应变片为补偿温度的影响，就需要采用电阻温度系数α=-14×10^-6的康铜丝。为此，电阻丝应在340℃温度下退火。但使用表3.2时应注意，都是假设α和β为常数时进行计算的，一般在25～100℃时是正确的。

表3.2常用材料的线膨胀系数

这种自补偿应变片加工容易、成本低，缺点是只适用于特定的材料，补偿温度范围也较窄。

 2)双金属栅法。减小应变片电阻温度系数的另一 种方法是采用两种金属丝制成的组合式自补偿应变片。 这种应变片的敏感栅由两种电阻温度系数不同的电阻

 丝串接而成，如图3.10所示。两种材料的电阻温度系 数符号相反，适当调整二者之间的长度比，在温度变化 时，就有可能使敏感栅总的电阻变化为零或不超过规定的数值，实现自补偿。组合式自补偿应变片使用方便。值得注意的是这种方法只能消除电阻 温度系数，不能消除由线膨胀系数不同产生的变化。

 图3.10组合式自补偿应变片

 实际应用中可以将上述几种补偿方法进行组合使用。

 3.2压阻式变换器

 上述介绍的金属电阻应变片是利用金属丝的形变所引起电阻值的改变，由于金属丝的形 变很小，因此灵敏度较低。而半导体应变片则具有很高的灵敏度。半导体应变片的原理是利 用半导体材料的压阻效应，也就是应力引起电阻率的变化，其灵敏度可达到金属应变片的几十 甚至上百倍。半导体应变片可以叫做压阻式变换器，用其制成的传感器叫做压阻式传感器，具 有灵敏度高，易小型化，动态响应频率高等特点。

 3.2.1半导体应变片

 金属丝式和箔式应变片性能稳定，精度较高，至今仍在不断改进和发展，并在一些高精度 应变式传感器中广泛地应用着。这类应变片的主要缺点是应变灵敏度系数较低。20世纪50 年代末出现了高灵敏度的半导体应变片，它是把P型或N型半导体晶体沿一定的晶向切取出 细薄丝，经加工处理制成的。

 1.半导体应变片的原理

 金属电阻应变片是由于金属形状发生变化所引起电阻值的改变，而半导体应变片是根据 半导体单晶的压阻效应及半导体晶向异性的原理制成的。压阻效应是一种应力引起电阻率的 改变而导致它的电阻值也随之变化的现象。

 由式(3.4)已得出电阻值变化的一般表达式为

 \(\frac{dR}{R}=(1+2\mu)\varepsilon +\frac{d\rho}{\rho}\)

 可见，电阻的变化是由应力而引起电阻率和形状变化的综合结果。

 对大多数金属来说dρ/ρ«1,主要是形状效应。但对半导体应变片情况则完全不同，形 状效应几乎可以忽略，主要是压阻效应起作用，并且dρ/ρ具有很大的数值。

 半导体应变片和金属电阻应变片一样，都是以灵敏度系数K这一参数来表征其特性的。 由于电阻率的变化是由压阻效应引起的，若以σ表示应力，则可表示为

\(\frac{d\rho}{\rho}={\pi}_{1}\sigma\)    (3.14)

 式中

 π₁——压阻系数，与半导体种类以及应力方向和晶轴方向之间的夹角有关。 根据胡克定律，有

 σ=Eε

 式中

 E——某一晶轴方向的弹性模量。 可得

 \(\frac{d \rho}{rho}={\pi}_{1}E\varepsilon\)      (3.15)

 再将式(3.15)代入式(3.4),得

 dR/R=(1+2μ+π₁E) ε    (3.16)

 对于半导体π₁E»1+2μ,因此

 dR/R=Kε=π₁Eε    (3.17)

 式中

 K——半导体应变片的灵敏度系数。

 2.半导体应变片的特点

 制造半导体应变片的材料有锗、硅、锑化铟、磷化镓、磷化铟与砷化镓等。一般常用锗和 硅，因为它们能获得比较大而稳定的压阻效应。半导体应变片主要有以下优点。

 (1)半导体应变片的灵敏度系数比金属丝式应变片高得多，通常是金属应变片的数十到上 百倍。高灵敏度排除了测量微小信号的困难，有时可不用放大器而直接采用指示或记录仪表 就可以进行测量。

 (2)N型半导体与P型半导体的灵敏度系数的符号相反。这样可以在同一应力方向上各 贴一片P型和N型半导体应变片，组成电桥的相邻两臂，不但可以增大输出信号，而且有一定 的温度补偿作用。

 (3)可制作小型和超小型应变片(如长1 mm,宽0.08 mm),频率响应很高，响应时间为 10-¹¹s数量级，可用来做高频传感器。

 半导体主要有以下缺点。

 (1)电阻温度系数大，而且各片间的电阻温度系数也不尽相同，温度稳定性不及金属应 变片。

 (2)温度灵敏度系数大(随温度升高，K的绝对值下降)。

 (3)应变-电阻变化的非线性比较大。

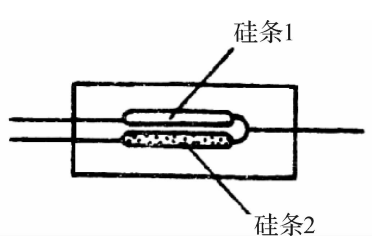
 针对这些缺点，已经研究出了许多新的品种和补偿方法， 使半导体应变片得到越来越广泛的应用。图3.11所示是将 具有正灵敏度系数的P型硅条1和负灵敏度系数的N型硅 条2并列布置在同一基底上的温度自补偿半导体应变片。若 将1和2接在电桥的相邻两臂，即可起到温度补偿作用。

图3.11温度自补偿半导体应变片

 半导体应变片除做成单片黏结在变形元件上使用以外， 随着集成电路技术的发展，已经可以做到用扩散的方法在单晶硅膜片上制成多个半导体应变

计并组成电桥，称为集成应变片。

3.2.2压阻式传感器

用集成应变片可以做成小尺寸传感器的敏感元件及变换器，这种传感器叫做压阻式传感器。根据不同的结构，可以用来测量力、压力、压差及加速度等。

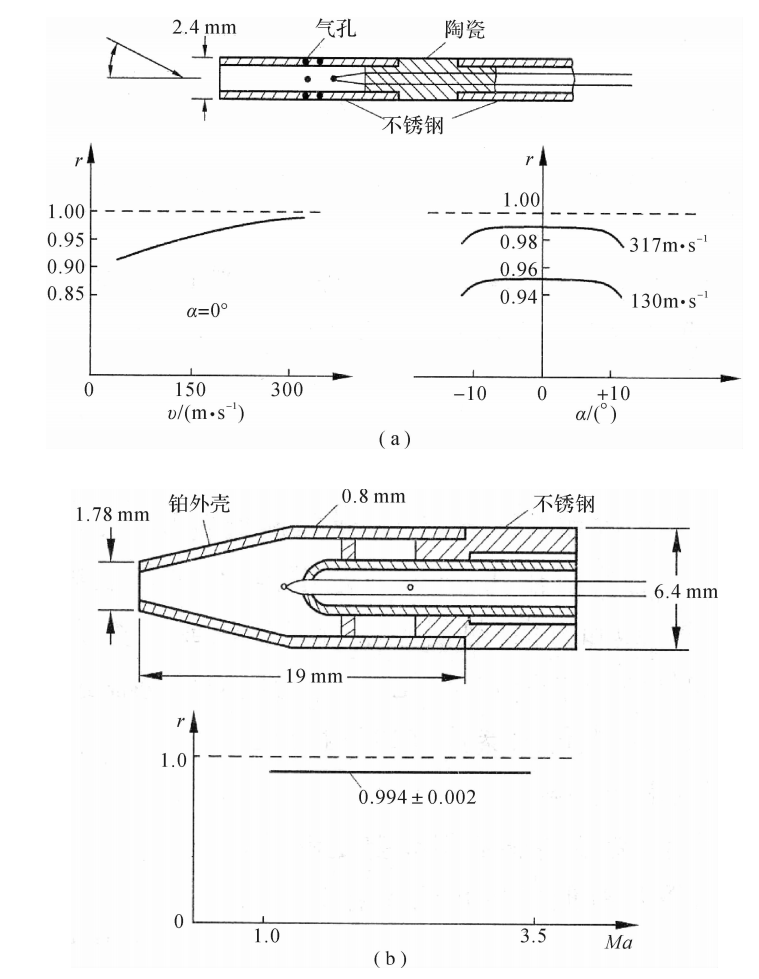
压阻式传感器的硅膜片本身就是敏感元件。由于应变片不用黏合剂黏结，扩散的应变片与硅膜片间是分子接触，同此其线性误差和滞后误差都很小，也不会出现用胶接法产生的绝缘不良、脱胶、蠕变和老化等现象，精确度优于0.1%。压阻式传感器具有很高的固有频率。如国产CYG-Ⅱ型压阻式传感器的固有频率大于17kHz;DYC动态压阻传感器的固有频率为100kHz～2MHz,可用来测量爆炸冲击波。此外，这类传感器的结构简单，可微型化。如可

制成直径为0.8mm、量程为0.69MPa,输出40mV的压力传感器。微型传感器可以广泛地用于宇航、医学等领域的测量中。

压阻式传感器目前尚存在的问题是受温度影响大。一般应用在100℃或150℃以下。如采用好材料、先进工艺、温度补偿、水冷却等措施，工作温度可达480℃。

3.3压电式变换器

上述介绍的变换器都需要外来电源供电才能产生输出，而压电式变换器则很独特，它利用了晶体的压电效应，自身可以产生电荷，因此无需电源供电。压电式变换器的固有频率很高，常用于动态参数的测量。下面就对其工作原理和特点进行介绍。

3.3.1工作原理

有许多物理量，如冲击、振动及一些瞬变过程，可以采用压电式传感器进行测量。压电式传感器的核心是压电变换器。一些晶体，如石英、钛酸钡等，受到外力作用时，几何形状发生变化，使晶体内部产生极化现象，表面上有电荷出现，形成电场。在外力去除后，表面又重新回到不带电的状态。这种现象称为压电效应。具有这种性质的材料，叫做压电材料。如果将压电材料置于电场中，其几何尺寸也会发生变化，这种由于外电场的作用，导致压电材料变形的现象，称为逆压电效应，或电致伸缩效应。压电材料可分为两大类：即压电单晶体——石英，酒石酸钾钠等；多晶压电陶瓷——钛酸钡，锆钛酸铅等。

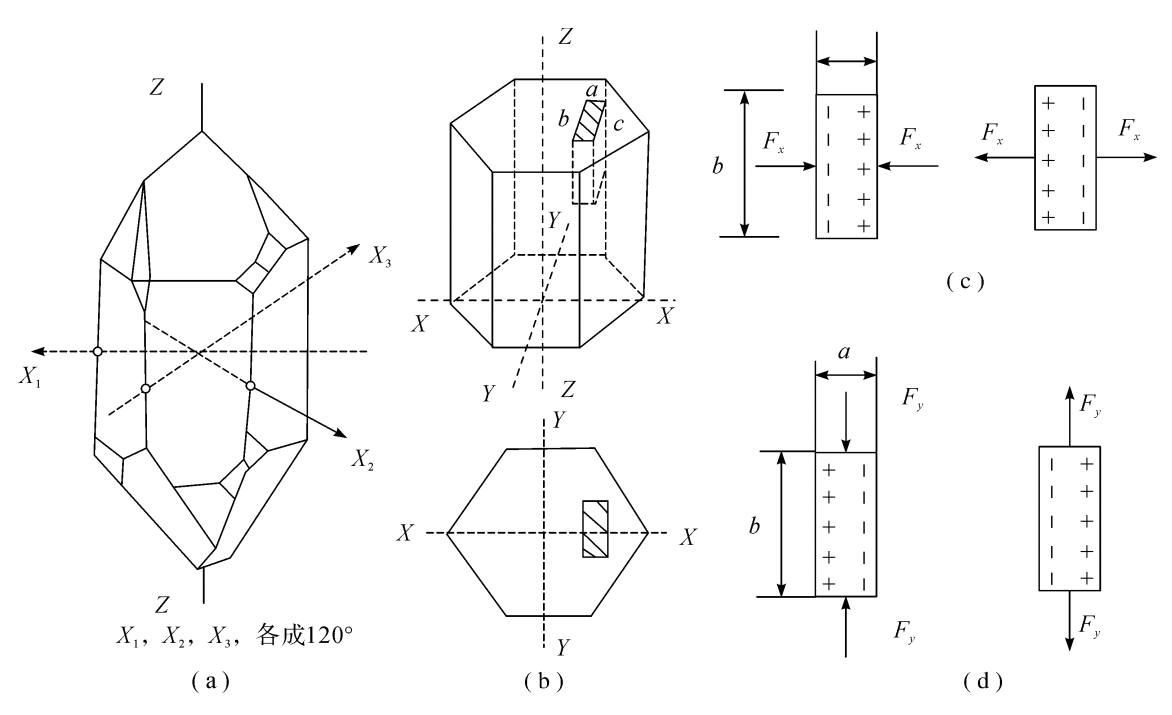
以下以石英为例说明压电现象。石英(SiO₂)晶体的结晶形状为六角形晶柱，如图3.12

(a)所示，两端为一对应的棱锥，六棱柱体是它的基本组织，见图3.12(b)。纵轴线Z—Z叫做光轴，穿过六角棱线而垂直于光轴的轴线X—X叫做电轴，垂直于棱面的轴线Y—Y称为机械轴。

如果从石英晶体中切割出一块平行六面体，使它的晶面分别平行于电轴、光轴和机械轴。当沿X轴方向加力时，受力表面产生电荷，电荷的极性与加力的方向有关。反向加力时，电荷的极性也相反，这种现象称为纵向压电效应，如图3.12(c)所示。当沿Y轴方向加力时，仍在与X轴垂直的面上产生电荷，电荷的极性同样与作用力的方向有关，这种现象称为横向压电效应，见图3.12(d)。当沿Z轴方向加力时，不论力的大小与方向如何均不产生电荷。

图3.12石英晶体

(a)石英晶体外形；(b)石英晶体基体及切片；(c)纵向压电效应；(d)横向压电效应

在外力作用下，晶面上产生电荷的多少常用极化强度J表示。极化强度是指压电晶体片表面上的电荷密度。极化强度与晶体的变形大小成正比，在弹性限度内与压强pa成正比，因此纵向极化强度为

\(J=K{p}_{x}=K\frac{{F}_{x}}{{A}_{x}}\)     (3.18)

式中

K——纵向压电系数；

A_x——垂直于X轴的晶面面积，单位：mm²;

F_x——作用在面积A₂上的外力，单位：N。

根据极化强度的定义，在表面A_x上所产生的电荷为

\({q}_{x}=J{A}_{x}=K{F}_{x}\)   (3.19)

可见，纵向压电效应使晶面上产生的电荷量与外力成正比，而与晶体的尺寸无关。沿Y轴方向施加外力Fy,则极化强度为

\(J’=K’{p}_{y}=K’\frac{{F}_{y}}{{A}_{y}}\)        (3.20)

式中

K′——横向压电系数；

A_y——垂直于y轴的晶面面积，单位：mm²;

F_y——作用在面积A_y上的外力，单位：N。

在A_x面上产生的电荷为

\({q}_{y}=J’{A}_{x}=K’\frac{{F}_{y}}{{A}_{y}}{A}_{x}=K’{F}_{y}\frac{b}{a}\)   (3.21)

式中

a,b——晶体片的尺寸，见图3.12(b),单位：mm。

此时的电荷量不仅与作用力的大小有关，而且与尺寸有关。当晶体的尺寸确定后，电荷量也与外力成正比。

比较式(3.19)与式(3.21)可以看出，对于同样尺寸的晶片，用同样大小的力，当作用力的方向不同时，其电荷值的大小也不同，因而它们的输出灵敏度也不一样。

在用压电晶体制成的传感器中，晶片常制成圆形，晶片的两个圆平面上各放有一个金属片或蒸镀一层金属膜所构成的极板。受力后两个极板上分别聚集正负电荷。由于晶体是绝缘材料，因而它相当于一个平板电容器，在两极板之间呈现出电压，其大小为

\(u=\frac{q}{C}=\frac{{KF}_{x}}{{\varepsilon A}_{x}/d}=\frac{Kd}{{\varepsilon A}_{x}}{F}_{x}\)

式中

C——两极板间的电容，单位：F;

ε——晶体片的介电常数；

d——晶体片的厚度，单位：mm。

当压电晶体确定之后，K,d,ε和Ax均为定值，极板间的电压也和外力成正比。这样，用压电晶体制作的传感器就可以有电荷和电压两种输出形式，放大器也相应地分为电压放大器和电荷放大器两种。传感器的灵敏度也因此有单位力的电荷输出和单位力的电压输出两种表示形式，即

\({S}_{q}=\frac{q}{{F}_{x}}\)和\({S}_{u}=\frac{u}{{F}_{x}}\)

分别称为电荷灵敏度和电压灵敏度。两者的关系可以通过电容联系起来，即

\({S}_{u}=\frac{u}{{F}_{x}}=\frac{q}{{CF}_{x}}=\frac{{S}_{q}}{C}\)

为了提高传感器的输出灵敏度，通常由两片以上的晶体片叠合起来。根据输出的要求，晶体片的连接有并联(见图3.13(a))和串联(见图3.13(b))两种。对于并联接法，输出的总电压U,总电荷量Q,总电容量C与单片晶体的电压u,电荷q、电容量c的关系为

Q=nq,U=u,C=nc

式中

n——晶体总片数。

图3.13两片晶体片电路的连接方式

(a)并联连接法；(b)串联连接法

对于串联接法，则有

Q=q,U=mu,C=c/n          (3.22)

并联连接法的输出电荷量增大，常以电荷输出。由于电容量也随之增大，时间常数也将增大，适用于测量缓变信号。串联接法的输出电压量增大，常以电压输出。因其电容量小，时间常数小，适用于测量迅变信号。

3.3.2特点

利用压电式变换器可以制成体积小、重量轻而且频率响应很高的各种传感器，广泛地用于测量爆炸压力，发动机内的动态压力、振动、冲击及各种动态力的传感器中。

1.优点

(1)固有频率很高。如厚度为d(mm)的压电石英晶体，固有频率fo可近似写作fo=2730/d(Hz)。在振动测量中所应用的压电式加速度传感器，其固有频率一般可达40～50kHz,高者达100kHz,如进一步减小石英晶体和其他零件的质量，并适当增加预紧力，小型压力传感器的固有频率可达200kHz。这是其他类型的变换器无法相比的。

(2)非线性较小。所组装的传感器的非线性误差一般可小于1%。要进一步提高线性度，应保证所有晶体和其他零件的承压面研磨成光学平面，在净化室内装配，因为极小的尘埃进入承压面之间都会使线性降低。在结构合理、制作精细的情况下，压电式传感器的非线性可达到0.2%。

(3)压电变换器属于发电变换器类，因此它不需要有电源供电。

2.缺点

由于电荷很容易泄漏掉，压电式变换器一般不能用来测量静态分量。为了能将电荷保持住，在组成传感器时，要求传感器的有关部分有高的绝缘电阻。选用绝缘性能好的材料，如聚四氟乙烯、聚苯乙烯、陶瓷等。在保持内部零件纯净干燥的条件下，在净化室内组装，严格密封或焊封，可使绝缘电阻达到10¹³～10¹⁴Ω。如果传输导线和二次仪表(如电荷放大器)的绝缘阻抗也很高，则传感器可在静态条件下进行标定。

3.4几种常用传感器

同样一种变换器，采用不同的敏感元件，可以制成不同类型的传感器。例如，应变片式变换器本身可以直接测量应变，也可以做成力(荷重)传感器或者压力传感器。压电式变换器可以做成力传感器或者加速度传感器。下面介绍火箭发动机测试常用的几种传感器。

3.4.1BLR-1型拉压力传感器

BLR-1型拉压力传感器是一种性能较为优良的应变式传感器，它既可以测量推力(压缩力),也可以测量拉伸力。常用来测量发动机主推力及侧向分力。它采用丝式应变片作变换

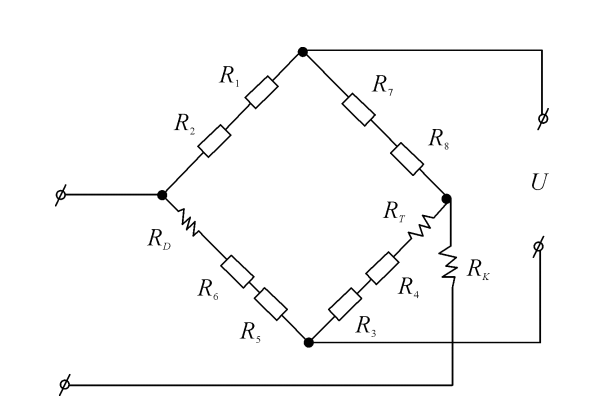
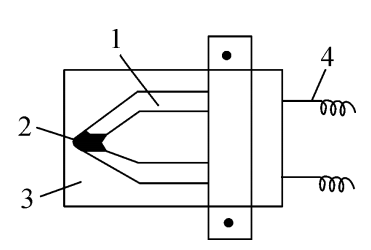
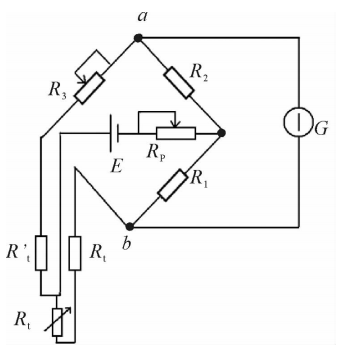
器，其结构如图3.14所示。它的敏感元件为空心圆柱体的应变筒。应变筒的两端通过螺纹与被测物体相连接(如发动机与支架)。在应变筒上共贴有八片阻值为60Ω的应变片，四片竖贴，四片横贴，组成全桥电路，见图3.15。八片应变片组成的电桥，其承受电压的能力比四片应变片组成的电桥高一倍，应变片R₁和R₂、R₃和R₄、R₅和R₆、R₇和R₈分别黏结在应变筒的对称位置，可以消除作用力偏斜造成的非线性误差。

图3.14BLR-1型电阻式拉压力传感器

图3.15BLR-1型拉压力传感器电桥

R₁～R₈—电桥测量应变片；R_D—初始不平衡补偿电阻；R_T—温度零点补偿电阻；R_K—输出灵敏度补偿电阻

由于应变片较多，各片因温度变化引起的电阻变化不完全相等，靠电桥本身不能完全达到温度补偿的目的。因此，在桥路中串入一个用电阻丝绕成的温度补偿电阻R_T,该电阻丝的电阻温度系数的符号与应变片电阻丝的电阻温度系数相反。用改变环境温度(由0℃升至60℃),实测电桥因温度变化的输出，决定R_T的阻值及应该串在哪一个桥臂之中。由于电桥中接入了温度补偿电阻R_T,加之各桥臂的初始电阻值不可能完全相等，造成电桥的初始不平衡。为此，在与R_T相邻的桥臂中串入一个电阻温度系数很小的初始不平衡补偿电阻R_D。R_K是输出灵敏度补偿电阻。传感器的输出灵敏度是指在额定载荷下，单位供桥电压使电桥产生的输出电压值。R_K的作用是消除在同一批传感器中，由于敏感元件、应变片和粘贴工艺等方面的差异，使得同一批规格的传感器具有相同的灵敏度。

被测力通过连接螺纹，直接作用在应变筒上，使应变筒在轴向和圆周方向分别产生相应的应变。此时电桥失去平衡，输出电压正比于作用力的大小。

设应变筒平均直径为D(cm),应变简壁厚为δ(cm),作用力为F(.),R₁、R₂和R₃、R₄贴在轴向，并接在相对的桥臂上，两桥臂的应变分别为ε₁和ε₃;R₅、R₆和R₇、R₈贴在周向，组成电桥另外的一对相对的桥臂，两桥臂的应变分别为ε₂和ε₄,则轴向应变

\({\varepsilon}_{1}={\varepsilon }_{2}=\frac{F}{\pi D \delta E}\)

周向应变\({\varepsilon}_{2}={\varepsilon}_{4}=-\mu{\varepsilon}_{1}=\frac{-\mu F}{\pi D\delta E}\)

式中μ为泊松比(对于钢材μ=1/3);E为弹性模量(钢材E=2×10⁶kg·cm-²),忽略电路中小电阻R_D,R_T,R_K的影响，可求出输出电压U,由式(3.11)可得

\(U=\frac{1}{4}K({\varepsilon}_{1}-{\varepsilon}_{2}+{\varepsilon}_{3}-{\varepsilon}_{4}){E}_{e}=\frac{K(1+\mu)F}{\pi D \delta E}\)  (3.23)

式中

K——应变片灵敏度系数；Ee——供桥电压，单位：V。

当外力F为额定载荷F_n时，可以求出在额定载荷下的灵敏度S₀

\({S}_{0}=\frac{U}{{E}_{e}}=\frac{K(1+\mu){F}_{n}}{\pi D \delta E}\)   (3.24)

S₀是指在额定载荷下，每伏供桥电压所输出的毫伏数。对于BLR-1型拉压力传感器S₀=1.0～1.5mV·V^-1。

这种传感器所采用的应变片允许最大电流为25mA,所以最大供桥电压为6V,而输出电压只有2～4mV,不能直接推动记录仪表，需加以放大，通常与各种型号的放大器配合使用。BLR-1型拉压力传感器的产品系列有十六种规格，量程从100kg到10t,供测量各种力值范围使用。主要性能指标如下:

(1)分辨力为额定载荷的0.1%。

(2)非线性误差小于0.5%。

(3)滞后性及重复性误差小于0.5%。

国内还生产一种与BLR-1型传感器很类似的应变式测力传感器，叫做BHR-4型荷重传感器，其应变筒和电桥的组成以及性能指标与BLR-1传感器相同，主要区别是BHR-4型传感器两端无螺纹连接件，因此只能承受推力。其结构及外形如图3.16所示。

图3.16 BHR-4型荷重传感器

3.4.2 BYY-3型和ZQ-Y型应变式压力传感器

在压力测量中，如果发动机工作比较稳定，一般都喜欢采用结构较简单、坚固耐用、输出较大的传感器。BYY-3型和ZQ-Y型压力传感器就是在发动机的稳态压力测量中经常被选用的传感器。

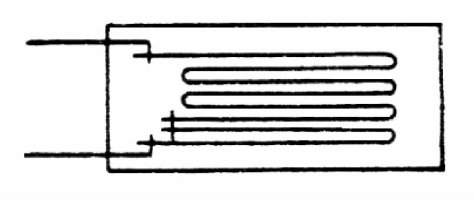
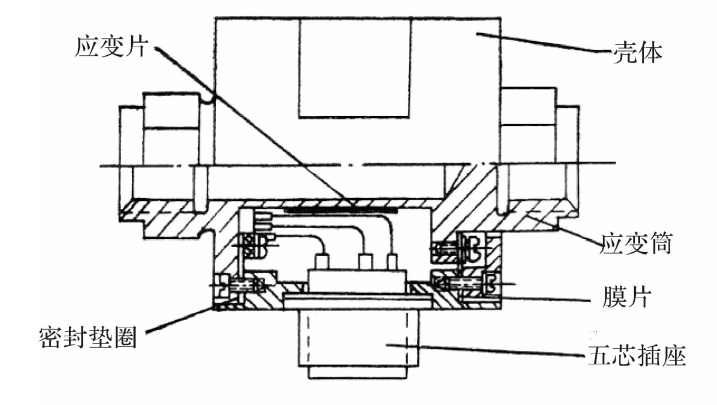
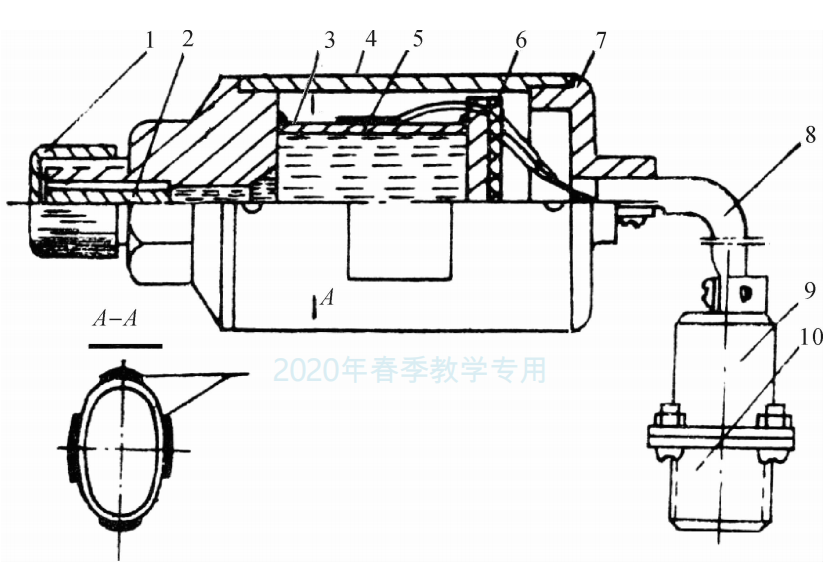
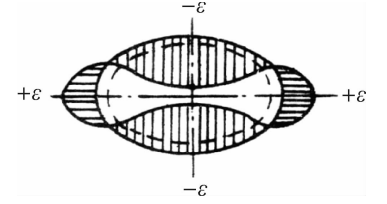
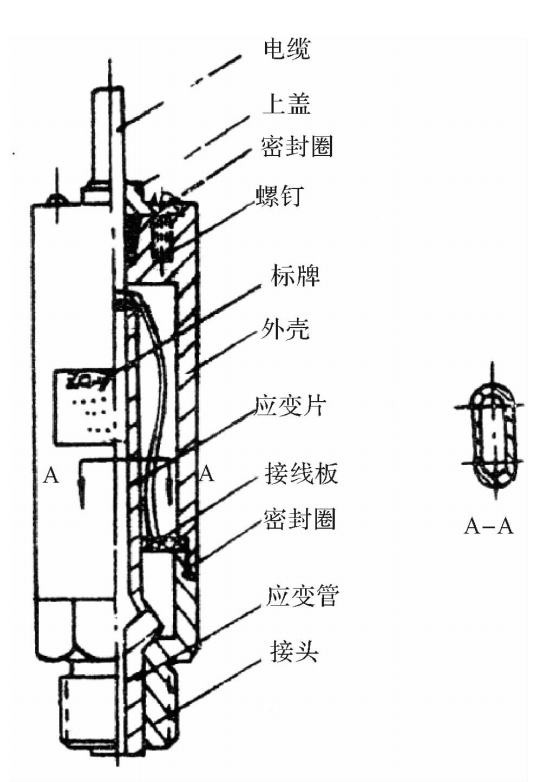
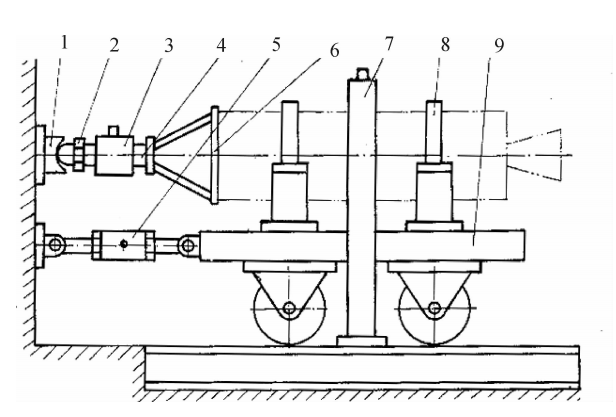
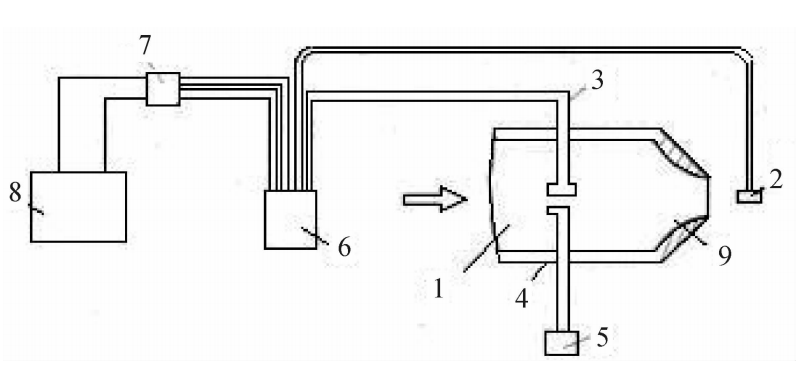
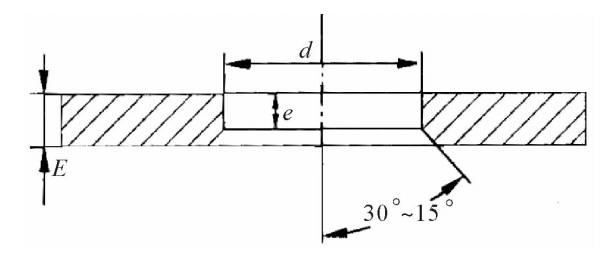
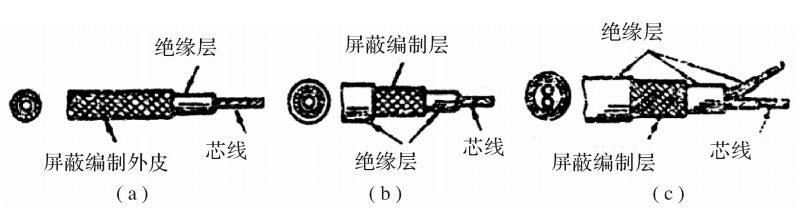
如图3.17所示是BYY-3型扁管应变式压力传感器。传感器的敏感元件是一个截面形状为椭圆的管子，其一端焊在基座上，另一端被封闭，在椭圆管的内外表面对称地贴有四片金属箔应变片，并连接成全桥电路。使用之前，拔下阻油销，向椭圆管内注入油液，用以隔热并传递压力。为防止油液流出，再装上阻油销。工作时压力通过接咀内阻油销外表面的四个沟槽向管内传压力，椭圆管的断面随之有圆形变化的趋势，即长轴缩短，短轴伸长。沿椭圆周向的应变在长轴方向是压应变，在短轴方向为拉应变，如图3.18所示。这样，四片应变片中，对边二片受拉，电阻增大，而另一对边的二片受压，电阻减小。满足本章第3.1节所介绍的全桥接法。

图3.17BYY-3型压力传感器

1一保护帽；2一阻油销；3一应变元件；4一外壳；5一应变片；6一接线板；7一上座；8一电缆；9一插头座；10一四芯电缆插座

图3.18椭圆管的应力分布

BYY-3型压力传感器由于采用椭圆管作为敏感元件，它的变形量较大。又采用了箔式应变片，同时椭圆管内充满了油，改善了应变片的散热条件，应变片允许输入较大的电流(每片可承载300～400mA的直流电流，而丝式应变片允许电流小于30mA),故能得到较大的输出电流，在额定压力下传感器的输出电流约为2mA。

这种传感器的另一特点是，发动机的高温燃气作用在中间介质油上，椭圆管不与燃气接触，因此它可以用于较长时间工作的发动机的压力测量。

椭圆管变形量大带来的不利影响是使传感器的非线性误差和滞后误差增大(非线性误差<4%,滞后误差<1%)。同时这种结构影响了传感器的频率响应特性，使之不宜用来测量高频动态压力。

目前应用较普遍的另一种传感器是ZQ-Y型电阻应变式压力传感器(见图3.19)。结构形式与BYY-3型传感器类似，其敏感元件是一扁平形截面的弹簧管。它与BYY-3型的主要不同点是整个尺寸较为紧凑，相应地频率响应也有所提高。弹簧管外表面粘贴4～8片丝式应变片。该型传感器除输出比BYY-3型小以外，其他性能指标较BYY-3型为高。非线性、迟滞误差及重复性误差按不同的等级可达0.1%～0.5%。

图3.19ZQ-Y型压力传感器

图3.20BPR-3型压力传感器

3.4.3BPR-3型压力传感器

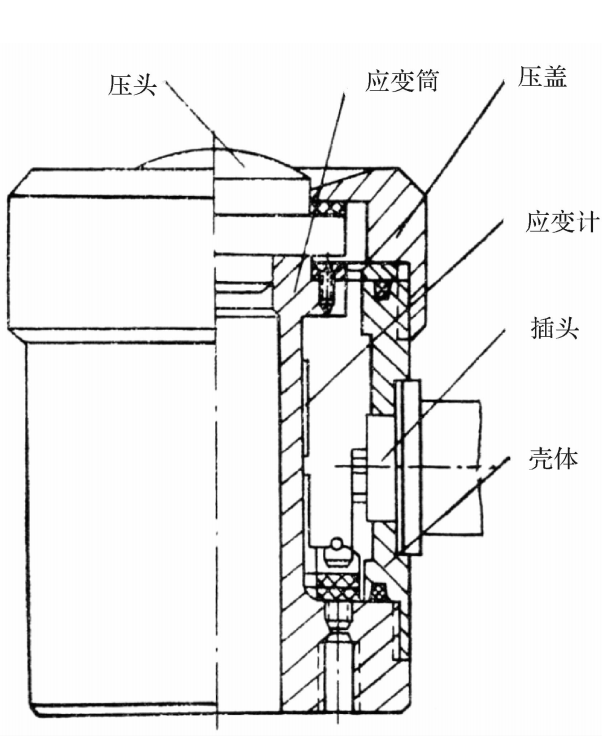
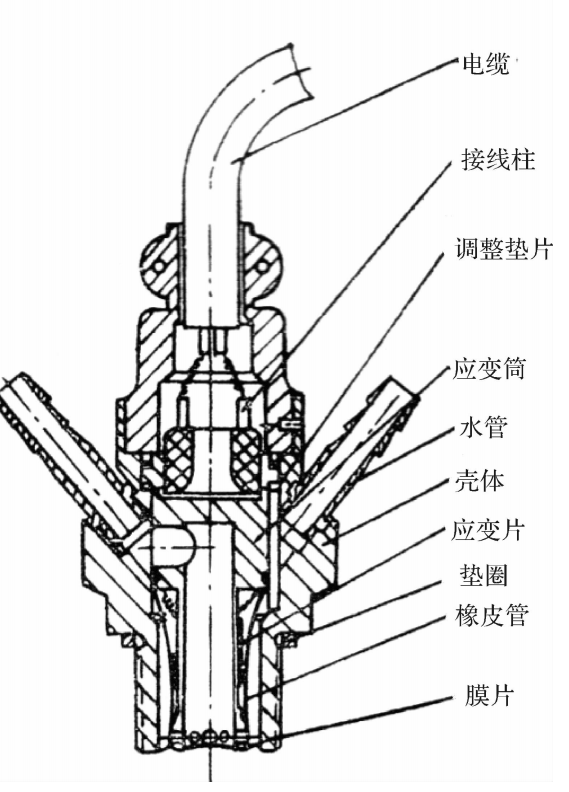
BPR-3型压力传感器是一种水冷式高频压力传感器，适于用来测量动态压力。其变换器是丝式应变片。

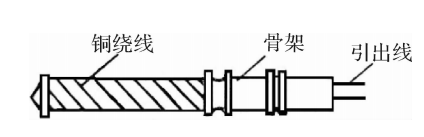
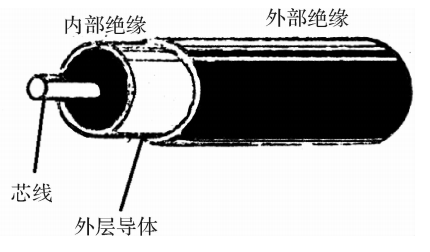
以上所介绍的BYY-3或ZQ-Y型压力传感器，由于管腔很大，降低了传感器的频响特性，BPR-3型压力传感器采用了另—种设计，如图3.20所示。它感受压力的是一个垂链形膜片，并将压力变成集中力作用在应变筒上。应变筒的外表面上，沿轴向和圆周方向各贴有一片阻值为200Ω的应变片，并接成半桥电路。应变筒和膜片靠冷却水强制冷却。应变筒靠膜片的一端开有径向孔，形成冷却水通道。冷却水由应变筒中心流向膜片，经径向孔流向孔腔，由排水管流出，流量约为1.5kg·min-¹(水压约为0.7～1bar)( 1bar=100kPa)。为防止应变片受水浸泡，用一橡皮管粘贴在应变简的两端。

由应力分析可知，垂链形膜片受压后，在它的断面内产生纯拉应力而无弯矩，这与一般平膜片相比具有很高的结构效率。因此，垂链形膜片可以做得很薄(0.2～0.3mm),质量小而且柔软。质量小可以减小膜片对传感器固有频率的影响，使传感器的固有频率主要取决于应变筒。由于它的变形不产生什么弹性力，膜片上受的压力几乎全部传给应变筒，这就保证了应变筒的应变与压力保持线性关系。

应变筒是一端固定，一端自由的轴向振动的空心圆筒。由振动理论可知，它的固有频率取决于材料的性质和筒的尺寸(应变筒的刚性和可动部分的质量)。应变筒用2Cr13合金钢制成。长度为20mm,固有频率可达3×10⁴Hz以上。传感器的灵敏度主要取决于筒的厚度，一般灵敏度为0.5mV·V^-1以上。

这种传感器的量程为3～25MPa,有七种规格。主要性能指标如下。

(1)非线性及滞后误差小于1%。

(2)分辨力为额定压力的0.1%。

(3)固有频率(通水)3000Hz以上。

(4)各向经受25g(频率40～80Hz)振动或100g冲击，引入误差小于1%。

(5)最大桥压10V。

3.4.4DYC型动态压力传感器

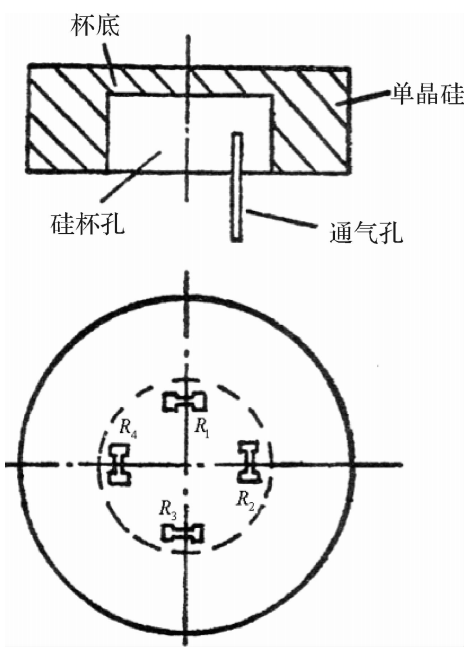
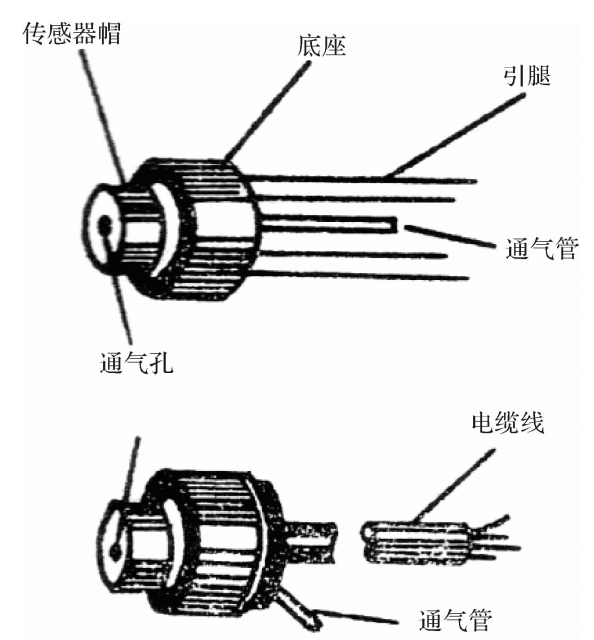
DYC型动态压力传感器是一种压阻式传感器，主要由敏感元件和壳体两部分组成。敏感元件是扩散型硅杯式力敏器件，形状如图3.21所示。

图3.21扩散型硅杯

图3.22DYC型传感器外形

由于整个单晶硅片的形状像一个倒置的杯子，故称为“硅杯”式。硅杯中央(即杯底)是一个周边固定的圆形薄膜，是承受压力的部分。在这片圆形薄膜上制作了四个扩散电阻，它们的阻值都相等，即R₁=R₂=R₃=R₄。但它们在膜片上的方向不同，其中R₁、R₃方向一致，R₂、R₄方向一致，而两者又相互垂直。利用单晶硅具有各向异性的特点，当圆形膜片受到压力时，四个电阻的电阻率都将发生变化，因而它们的电阻值也随之改变。如果R₁、R₃的阻值增加△R,则R₂、R₄的阻值将减小△R。这四个电阻由内部引线接成惠斯登电桥，并由四个桥顶引出四条引线。使用时，将电桥的两个对顶端的引线接恒流电源(恒流电流为2mA),另外两个对顶端的引线作为信号输出端。当没有压力作用时，电桥处于平衡状态，输出为零；当膜片受到压力作用时，因R₁、R₃阻值增加，R₂、R₄阻值减小，使电桥失去平衡，输出端将输出一个与压力相应的电压信号。

壳体由镀金的圆形底座和传感器帽组成。在底座和帽上开有通气小孔，使被测压力与膜片相接触。传感器外形如图3.22所示，其中一种带有专供传感器用的四芯电缆线；另一种直接引出四个引腿，可以插接或焊接使用。

3.4.5DaCY420型压力变送器

DaCY420型压力变送器是一种带信号放大和调理功能的压阻式压力传感器，由压力敏感部件、恒流源供电电路和信号放大处理电路三部分组成。压力敏感部件采用全固态压阻式压力传感器，其包括两个单晶硅片接合在一起，上面硅片通过集成电路工艺和微机械加工工艺构成一个惠斯通应变电桥，该电桥输出电压信号与作用在硅片上的压力差成正比。恒流源供电电路可产生最大2mADC的电流，用于激励压力传感器工作。信号放大处理电路用于将惠斯通电桥产生的电压信号线性放大处理后并转换成DC为0～5V或4～20mA等多种标准化信号。在较宽的供电电压(也称为激励电压)范围内，DaCY420型压力变送器的输出信号与供电电压无关，而传统传感器则对激励电压的精度和稳定性等提出了很高的要求。此外，Da-CY420型压力变送器的稳定性和线性度均要优于传统的传感器，无需在每次试验前都进行标定工作。

表3.3DaCY420型变送器主要性能参数

DaCY420型压力变送器自身带有信号放大和调理功能，输出信号无需中间调节部分，就可以直接输入数据采集系统。此外它的敏感元件还进行了特殊的防热处理，承受高温燃气的能力比一般的非冷却型压力传感器要强。

以上介绍的几种压力传感器都属于相对压力传感器，其输出的压力是被测压力与环境压力的差值，因此在后处理时需要将示值加上环境压力。另外还有一些属于绝对压力传感器，其应变筒内部需要抽真空。目前应用较多的主要是相对压力传感器。

目前市面上传感器种类很多，在实际应用时，需要根据测试任务的性质和要求来选择适合的传感器，一般需要考虑的因素包括量程、精度、响应频率、适用环境(环境温度、冲击、振动及高温燃气等)、可靠性和性价比等。

第4章 火箭发动机试验技术

在发动机的各种试验中，地面点火试验是最主要的，也是最具特色的，因此作为试验技术的主要内容来介绍。绪论中已经阐述过地面点火试验在火箭发动机研制和研究中的重要作用，而要发挥好其作用，则必须有先进可靠的发动机试验技术作为支撑。

通常在产品研制阶段，地面点火试验的目的是检验发动机是否达到设计要求的性能，还有一些试验是为了演示新原理、验证关键技术、为故障分析提供依据以及研究规律等。

火箭发动机地面点火试验技术要解决的问题主要有三个：一是如何测得准确，二是如何保证安全，三是如何模拟得真。模拟得真是指如何在地面模拟飞行的特殊环境或者状态，例如高空的低压环境、飞行过载和旋转等。

随着科学技术的不断发展，火箭发动机测试的内容越来越丰富，但最基本的仍然是推力和压力的测量。

4.1推力和压力测量技术

在固体火箭发动机试验中，推力和压力是两个最主要的被测参数。推力的大小及其随时间的变化规律，表征着固体火箭发动机的性能。它直接影响火箭的射程和飞行特性，并可由试验测量的推力值推算出发动机的其他重要参数，如平均推力、总冲和比冲等。

发动机燃烧室内的燃气压力是另一个重要参数。由于压力测量比推力测量简单而又准确，因此在发动机试验中，若条件允许，均进行压力测量。由试验测得的压力随时间变化的规律，可以清楚地看出发动机的结构设计和装药设计是否合理。并可由此推算出发动机的推力、流量系数、燃烧速度等重要参数。虽然推力和压力是两个互不相同的参数，使用的传感器不同，测量的方法也不同，但就测量系统的设计原则和设计测量系统应注意的问题，却有很多一致的地方。

4.1.1推力的测量

1.如何测量发动机推力

我们可以利用前面学过的测力传感器来测量发动机的推力。对于固体火箭发动机静止试验，我们要有一个承受发动机推力的结构件，一般称为承力墩。推力传感器可以放在承力墩和发动机之间。除了承力墩我们还需要一个构件来承受发动机的重量，并将发动机可靠地“限制”在试车台上，否则发动机一旦偏斜就会发生危险。但是这个构件又不能将发动机固定死了，而要允许发动机在推力方向有一定的自由度，否则推力就不能正确地传递给传感器。如何才能做到这一点，如图4.1所示为一种常用的中心架式的结构，发动机被两个中心架限制，只能沿推力方向移动。这种构件称为试车架，是发动机推力测量中的关键构件。除了传感器我们还需要与之配套的数据采集系统，或者显示记录仪器。

图4.1中心架结构示意图

综上所述，要想测量发动机的推力最少需要以下四部分。

(1)承力墩：承受发动机的推力。

(2)试车架：固定发动机，并将推力正确传递给传感器。

(3)推力传感器。

(4)数据采集系统。

2.推力传感器的安装

固体火箭发动机做静止试验时，一般有水平和垂直两种形式的试验台架。不论哪一种，为了保证推力的测量精度，对推力传感器的安装一般都有如下要求。

(1)推力传感器安装后的轴线与发动机的推力作用线相重合。一般在试车台架上都装有固定推力传感器的支座，要求支座便于固定传感器，也便于调整传感器的轴线。

(2)传感器和发动机之间不要留间隙。这主要是为了防止推力传感器在发动机点火时，由推力峰值造成的发动机与传感器之间的撞击损坏或者影响测量精度。有时为了消除间隙甚至可以给发动机加一个恒定的预紧力，使发动机压紧传感器。如果预紧力已知，在数据处理时可以扣除这部分力；如果未知，可以利用原位标定来消除(原位标定将在4.2.2中介绍)。

(3)尽量减少横向力的干扰。目前测力传感器的精度已经达到较高的水平，综合误差可小

于0.03～0.05%。在实际应用中，往往由于安装位置不准确、台架变形、振动等原因使传感器受到横向干扰力。一般推力传感器抗横向载荷的能力差，在推力测量中造成测量误差。

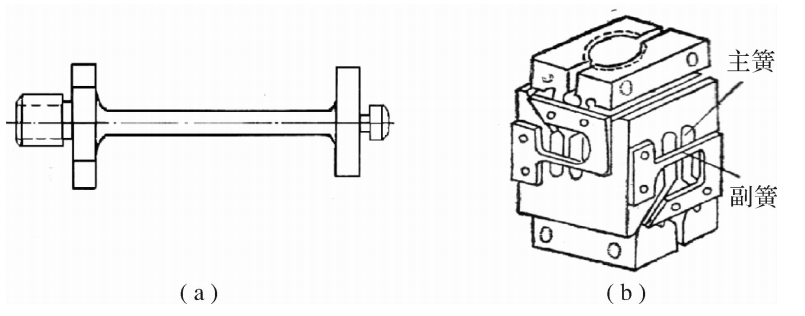
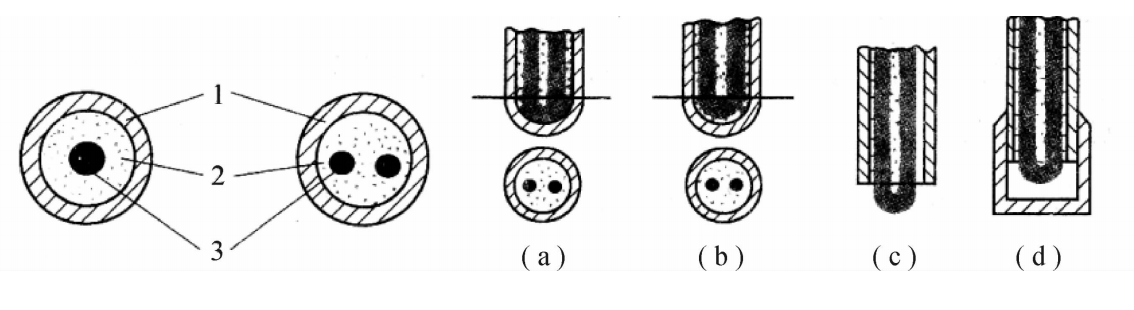
为了改善传感器的使用条件，可以采用纵向刚度大，横向刚度小的挠性传力件。最常用的挠性件有圆杆式挠性件和万向挠性件两种(见图4.2)。使用时将挠性件成对的连接在拉压传感器的两端。圆杆挠性件的设计、加工都比较简单，但在轴向受压情况下，往往是以压杆稳定性作为设计准则。这样设计出的杆式挠性件侧向刚度不理想，随着侧向力的大小不同，其转动中心也在变化，而且轴向尺寸长，固有频率低，使试验台架不紧凑。

万向挠性件是由两片相互垂直并交叉的簧片构成，又叫叉簧式挠性件，如图4.2(b)所示。每个簧片的两侧各有一个副簧片，四面一共有4个副簧片，用它承受横向力(如水平安放时，承受传感器和挠性件自身的重量)。它还可以保护主簧片，并部分地补偿主簧片刚性的变化。这种传力构件的挠曲点固定、尺寸较短、柔性好，但重量大且加工非常困难。

图4.2挠性件

(a)圆杆式挠性件；(b)万向挠性件

4.1.2压力的测量

固体火箭发动机试验测量压力时，必须在发动机外壁上，在需要测量压力的部位开口并焊上传感器连接管嘴。原则上测压口的位置应不改变发动机工作状态，不影响发动机的正常工作。这些测压口在不测压时应当用堵盖加以保护。测压口的位置还应使传感器装拆方便。

在发动机上测量压力时，可以采用充油的压力传感器。试验前先把传感器的空腔内充满油。用油作为介质，使传感器空腔与燃气隔离，防止压力传感器被高温燃气烧坏。加入油以后，通过油传递压力，增加了压力传递的阻尼作用，降低了传感系统的频率响应。油介质的密度愈大，频率愈低，管道愈长频率也愈低。这类传感器只适于对频率要求不高的场合。有时也可以不采用充油测压管方案，而是在传感器测压孔内涂抹一定的硅酯或黄油，以避免高温燃气损坏传感器。

对高频压力的测量，不仅应选用高频压力传感器，而且安装传感器时应使传感器的膜片与发动机的内壁齐平。如果在安装时传感器与内壁之间形成了空腔，那么由于空腔效应，会使系统的幅频特性变坏。传感器与内壁形成的空腔是一个一端封口的圆柱体，发动机的燃气压力就是通过这段气柱传给传感器的膜片。气柱是随着燃气压力变化而被压缩或膨胀。很明显这段气柱就是一个弹性振动系统。如果忽略气柱气体的黏性，它的谐振频率f可由下面公式估算：

f=a/4L

式中

a——在某温度下气柱内声速，单位：m·s^-1;

L——气柱长度，单位：m。

由式(4.1)可见，气柱愈长固有频率愈低。例如，气柱长度L=30m,气柱温度T=400K,气柱的声速可由下式求得

\(a=20.1\sqrt{T}=20.1\sqrt{400}\)=402m·s-

则\(f=\frac{a}{4L}=\frac{402}{4\times 30}\)=3.3kHz

被测信号频率范围应远低于传感器测量系统的固有频率，才能得到满意的频率响应特性。当气柱的直径很小时，气柱的黏性就不可以忽略，它将使压力信号衰减，相位滞后。严重时压力传递系统将变成一个惯性系统，甚至无法传递高频压力。

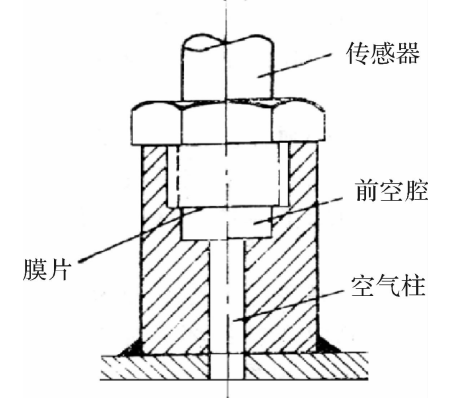
在安装传感器时，传感器在安装座中留有空腔。如图4.3所示，空腔中充满不流动的气体，若把空腔与圆柱段一起加以考虑，将是一个振动系统。系统的振荡频率可用下式估算：

\(f=\frac{2}{2\pi}\sqrt{\frac{S}{V(L+\pi r/2)}}\)

式中

r——空气柱半径，单位：m;

L——空气柱长度，单位：m;

S——空气柱截面积，单位：m²;

V——前空腔容积，单位：m³;

a——声速，单位：m·s^-1。

图4.3安装传感器形成的空腔

由式(4.2)可知，传压管道越长、越细、膜片前的空腔越大，则传压系统的固有频率越低，越不适于传输动态压力。因此，在测量动态压力时，应当尽量使传感器的膜片与发动机内壁齐平，减少空腔效应。

4.2推力和压力测量系统的标定

4.2.1标定的概念

标定是确定测量系统(装置)输入与输出之间对应关系，或者是确定测量系统(装置)灵敏度系数的操作。实际上传感器的说明书上通常会给出输入与输出之间的关系，但一般在发动机试验前还需要进行标定，这是为什么呢?

这是因为试验时的测量系统和环境与传感器出厂标定时的测量系统和环境是不完全相同的，因此为了消除或者减少这种差别带来的误差，试验前有必要进行标定。

为了确定测量系统输入与输出之间的对应关系，应该在量程之内给传感器施加一系列已知的力(压力),记录对应的输出，通过对输入和输出数据的处理，就可以得到其对应的关系。可以看出，要进行标定，除了传感器和数据采集系统外，还需要两个关键的装置：一是力源，用来产生输入；二是标准仪表，用来确定输入量的大小。根据测量参数性质的不同，标定一般分为静态标定和动态标定。

测量系统是由许多环节组成的。测量系统静态标定时，是对整个系统进行综合标定。系统中各个环节的静态特性都综合在一个标定结果中，如果标定是在与实际试验条件完全相同的条件下进行的，就可以提高测量数据的可信赖性，减少误差。一般测量系统的静态标定都是在当日试验前进行的。标定后，测量系统中一切环节都不得变动，包括仪器设备、使用条件、环境条件等。有时为了确保标定的可靠性，在试验后，再以试验时同样条件重新标定一次，检查测量系统在工作过程中是否有变化。

4.2.2推力的标定

在进行推力标定时，常用的力源有砝码、机械加力装置、液压加力装置，其目的是提供稳定、可变的力。机械加力装置通常采用手动加力，通过大传动比的齿轮减速机构来放大力，液压加力装置分为自动和手动两种方式。推力标定的标准仪表主要有测力计和标准传感器等。当用砝码做力源时，砝码的重量是已知的，因此其本身也可以算作标准仪表。

1.测力机

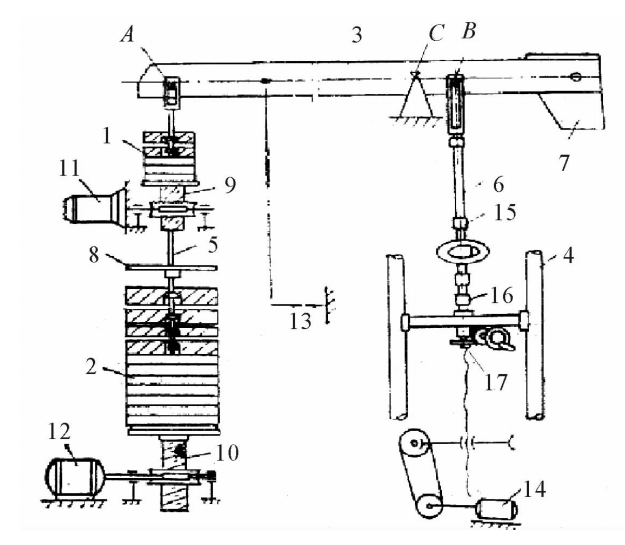
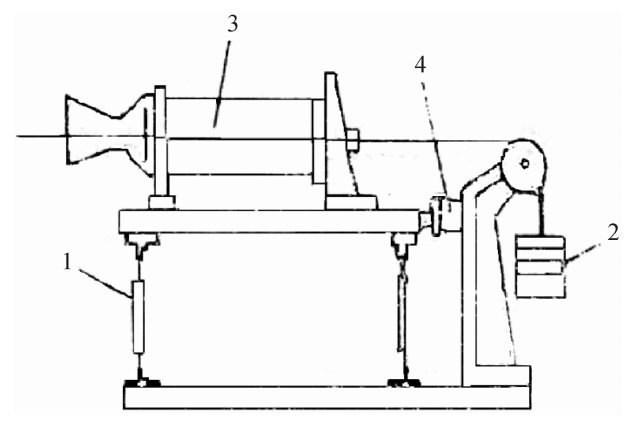
现在介绍一种二等测力机，“二等”指该测力机标定达到的精度级别。这种测力机是杠杆砝码式，量程1～60kN分档可调。其结构原理如图4.4所示。测力机主要由杠杆、主体支座、砝码和电气控制等部分组成。测力机的负荷是由一套小标准砝码和一套大标准砝码组成。小砝码1是五个一组，每个1000N。大砝码2是十一个一组，每个5000N。标准负荷是通过杠杆3加在被校的测力传感器16上。杠杆的力臂比是10:1,由支点刀口C支承在机架上。传感器通过拉杆6挂在刀口B上，根据标定时所需要的力，加上相应的砝码。

图4.4测力机原理图

1一小砝码；2一大砝码；3一杠杆；4一机架；5,8一砝码托盘；6一拉杆；7一配重；9,10一丝杠；11,12,14一电机；13一平衡指示器；15一连接器；16一被校传感器；17一下夹头

当杠杆平衡时，传感器所受的负荷为

F=KW

L=L₂/L₁=10

式中

K——杠杆力臂比；

L₁——刀口B至刀口C的距离，单位：mm;

L₂——刀口A至刀口C的距离，单位：mm;

W_n——砝码重量，单位：N。

杠杆的初始平衡由移动配重7来平衡。大小砝码串连挂在砝码吊杆上，每个砝码之间有活动空隙。当升降丝杠9、10所带动的砝码托盘8、5上升时，托盘逐个分别托起大、小砝码，减少负荷。全部砝码被托起时，负荷为零。托盘下降时，根据需要使砝码逐个加入，增加负荷。标准负荷的大小由加入的砝码数量来调节，分别控制电机11、12,通过蜗杆传动机构升降丝杠来实现。给被标定的传感器16加卸载荷，由电机14通过蜗杆蜗轮带动传感器的下夹头17来实现。平衡状态由平衡指示器13指示。

2.测力计

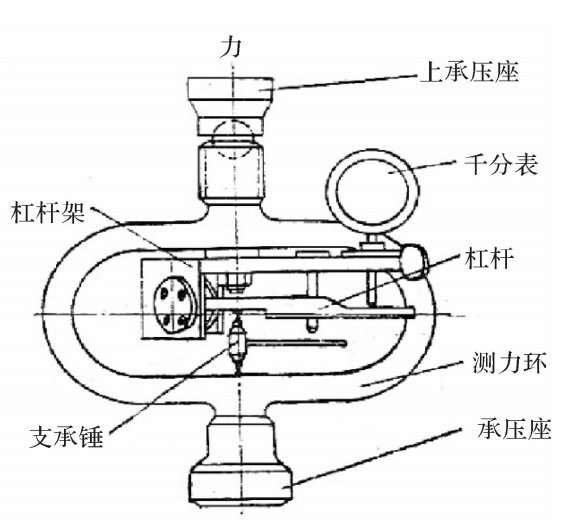
常用的三等测力计的结构如图4.5所示，它是由测力环、杠杆、千分表和支座组成。测力环由弹性好的钢材制成，在外力作用下产生变形。轴向变形量通过杠杆放大机构放大，用千分表指示变形量的大小。根据力与千分表读数对照表查出相应的外力大小。

图4.5环形测力计

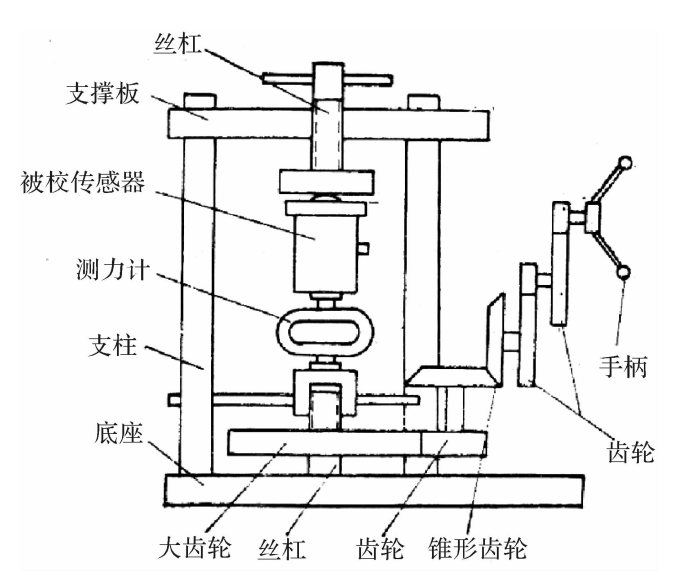
使用环形测力计时，还需配用加力装置。加力装置一般有机械加力和液压加力两种方式。用机械方法加力的齿轮传动机构如图4.6所示。这是一种大传动比的减速装置，被标定的传感器和测力计串连放在加力的轴线方向上。摇动手柄通过一系列传动齿轮和丝杠，把承力盘往上移，将力传递给传感器和测力计。用这种装置可以提供几十吨的力。

图4.6机械加力标定装置

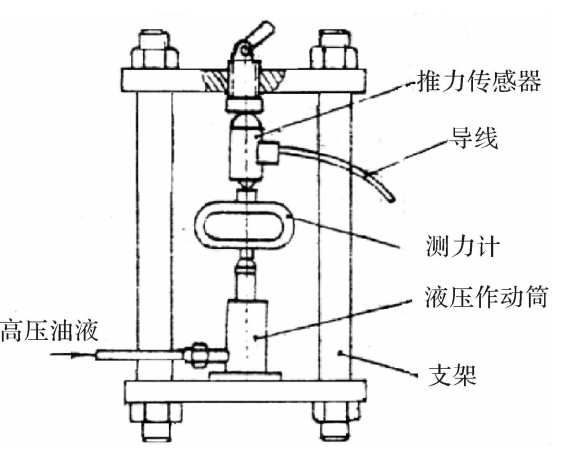
液压加力装置(见图4.7)与机械方法加力装置的区别是，液压作动筒代替机械传动机构。作动筒可用手摇活塞压力计或电动液压系统加压。用液压千斤顶代替作动筒使用更方便，但卸压时不易控制。

图4.7液压加力标定装置

3.原位标定

前面介绍的标定方法，都是非原位标定，也就是将传感器放在标准测力机或液压加力装置上分级加载进行标定。标定工作完成后，再将传感器固定在发动机上。对于推力标定，发动机和支架的影响、传感器安装的影响等都不可忽略。因此，只标定推力传感器本身是不够的，往往要在测量现场进行原位标定(或原位校准)。原位标定是在试验条件下，发动机、推力传感器，试验台架联在一起进行现场标定。这样就需要专门的标定装置。标准力可由活塞式压力计和油缸供给，或用杠杆和砝码加力。用这种装置标定推力，可以消除包括台架、传感器安装等各种因素引入的系统误差。如图4.8所示的原位标定装置采用了校准砝码加力方式。

图4.8砝码式原位测力标定示意图

1一弹性连杆；2—砝码；3一发动机；4一传感器

4.2.3压力的标定

进行静态压力标定最常用的力源是活塞式压力计，也叫油压机，此外还有气压的压力计，其原理类似打气筒。标准仪表有砝码、标准压力表和标准传感器。这些力源和标准仪表组合可以形成多种的标定系统。

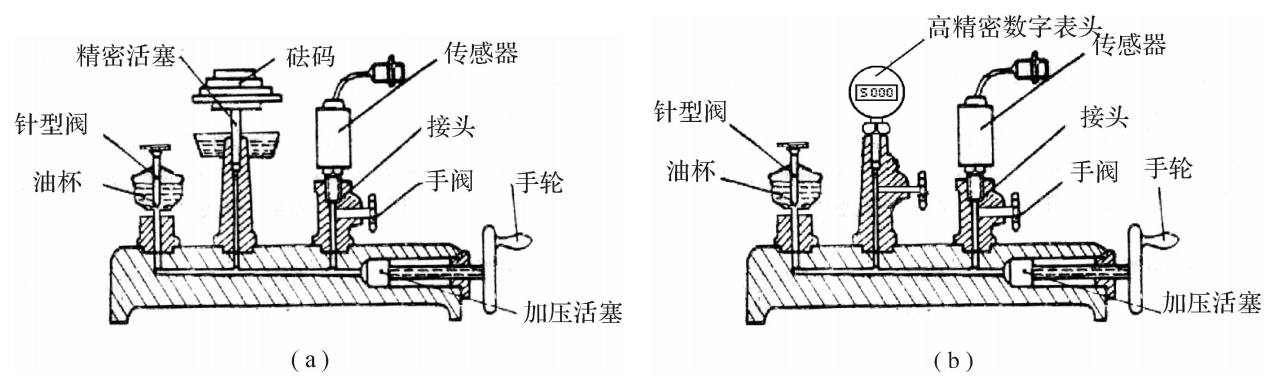
如图4.9(a)所示为用砝码作为标准仪表的活塞式压力计，主要是利用连通器的工作原理，即在一个连通器内加入液体，加压后压力通过液体传递到各个方向，各处的压力均相等。活塞式压力计是由加压活塞、精密活塞、砝码和油杯等组成。压力计的油液由油杯供给，压力由加压活塞挤压油液而产生。油压作用在精密活塞上，产生向上推动的力，将砝码托起。当油压作用在活塞上产生的力与砝码重力平衡时，油液压力等于砝码重量除以活塞有效面积。被标定的传感器装在同一个连通管上，油压同样作用到传感器上。由于精密活塞的有效面积很精确，砝码也是标准的，因此，可以产生精度很高的压力。

图4.9活塞式压力计结构原理图

(a)标准砝码式；(b)高精度数字表头式

精密活塞与活塞筒的配合也很精密，为了减少摩擦力的影响，标定时要转动砝码盘，使静摩擦变为动摩擦。要求砝码盘转速为120r·min-¹。为了减少重力与活塞轴线偏移造成的误差，应当用水准调整底座使之水平。由于各地的重力加速度不同，对于一定质量的砝码，应当做修正，这样才能得到精度较高的压力。

随着传感器技术和电子技术的不断发展，新型的活塞式压力计已不再采用砝码来计量所加的标准力值，而是采用高精度电子式压力传感器表头或者高精度标准传感器来测量。采用高精度电子式压力传感器表头可以直观的显示当前所加载压力值，如图4.9(b)所示，其示值精度一般优于0.1%。高精度标准传感器具有很高的稳定性和输出精度。进行传感器标定时，利用高精度数据采集仪器对标准传感器的输出电压进行采集，根据标准传感器所提供的压力——电压对应关系即可确定出加载至被标定传感器的压力。

压力标定在精度要求不太高的情况下，可以选用弹簧管式压力表作为压力的标准。压力表的精度可根据需要选取。

4.2.4动态标定

进行动态参数测量时，测量系统的频率响应范围直接影响测量的准确性。新建立的动态参数测量系统在投入试验之前，除进行静态标定外，还应对动态测量系统进行动态标定。一个测量系统的动态特性完全用分析的方法来确定是困难的，也不够准确，所以多采用实验的方法标定。

测量系统的动态标定方法，一般是给被标定的系统输入阶跃、斜坡或正弦等典型信号，然后用记录仪表将系统的输出波形记录下来，再分析计算记录的结果，求出系统有关的一些动态参数。因为测量系统的信号源检测部分是非电量测量系统，所以要求输入非电物理量信号。作为标定的信号源应该是具有理想波形的周期或脉动信号源，这种信号的产生比较困难，信号源装置也比较复杂。下述分别介绍几种稳态周期性压力源和非稳态信号源。

1.正弦压力信号发生器

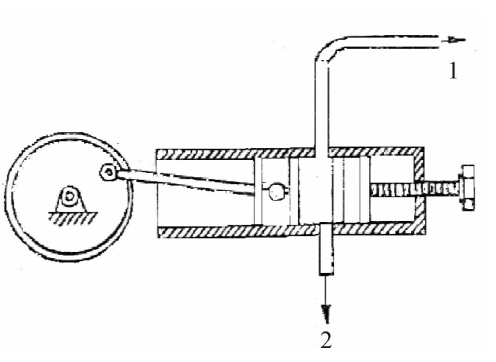
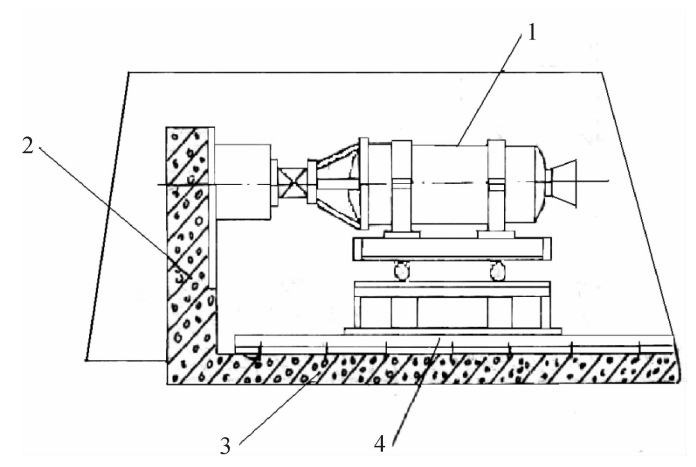
产生正弦压力的发生器有很多种，如图4.10所示是一种标定压力传感器的活塞式正弦压力信号发生器。发生器由电磁振动器和活塞筒体组成。向电磁振动器输入正弦电压后，电磁振动器产生一正弦力，由它带动活塞产生往复运动。活塞筒内充满液体(油),筒体两侧对称位置上连接标准传感器和待标定的压力传感器。如果活塞行程不变，压力振幅可通过调整缸筒体积来改变。对标准传感器的要求是应当在标定频率范围内幅频特性平坦。标定时只要将被标定测量系统与标准传感器之间的幅值比和相位差进行比较计算，就可以得到被标定测量系统的频率特性。

其他的还有转盘式和旋转阀式的正弦压力发生器。这些标定设备都属于稳态周期性压力源，是一种相对标定设备。压力源的实际压力-时间关系，由标准高频压力传感器提供。为取得一个压力传感器或测量系统的幅频特性，需要做不同频率、不同幅值的多次实验，标定工作比较费时。

图4.10活塞式正弦压力信号发生器

1一接待标定的压力传感器；2一接标准压力传感器

2.阶跃压力信号发生器

用稳态的正弦信号校验测量系统的频率特性需要测量许多频率点。如果用某些特殊形式的脉冲信号作为校验信号源，则可从被测系统得到动态特性的全部信息，其测量结果与用稳态正弦信号校验法是一样的，但校验所用的时间却少得多。

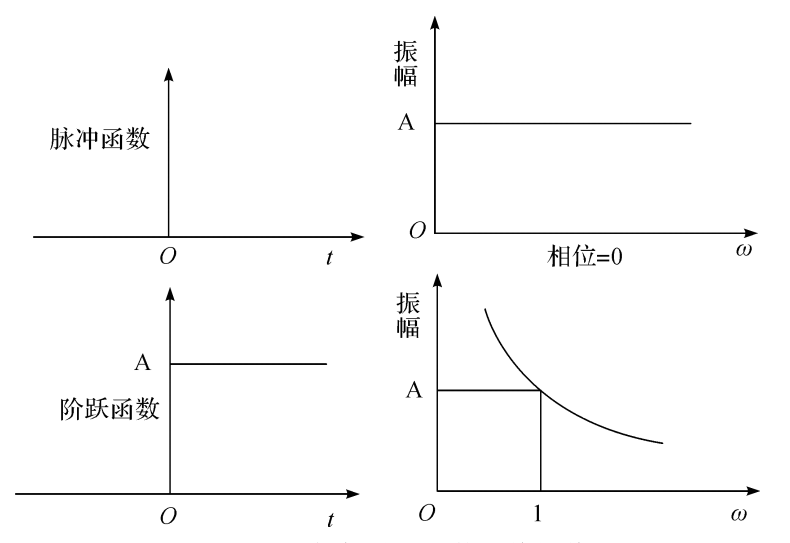
一般常用的脉冲信号是脉冲函数和阶跃函数。这两种函数在0～一的频率范围内具有连续频谱，如图4.11所示表示出这两种函数及其频谱。单位脉冲函数在整个频率范围内幅值都等于1,相位为零。因此，测量系统对它的响应的频谱就等于测量系统的频率特性。如果用实验方法记录下测量系统对脉冲函数的响应，再将其进行傅里叶变换，就可以得到测量系统的频率特性。

图4.11脉冲、阶跃函数及其频谱

阶跃函数是脉冲函数对时间的积分，其频谱的幅值为,而相位等于一2,其中A₈是阶跃函数的幅值。因此，测量系统对阶跃函数的响应函数，进行傅里叶变换乘以jo,即可得出测量系统的频率特性。如果用频谱分析仪或者数据处理软件对测量系统的响应函数进行分析，得到测量系统的频率特性是很方便的。

脉冲函数的强度等于脉冲高度与持续时间的乘积，频谱的幅值决定于强度大小。标定用的脉冲最大高度受到测量系统过载的限制。持续时间则决定于测量系统的最高频率响应。测量系统的频带宽，频谱的幅值就小。信号幅值小，测量精度就低。对于阶跃函数，它的持续时间长，在低频范围能量大。所以阶跃函数特别适用于低频测量系统的标定。

非电测量系统用脉冲信号源标定其动态特性很普遍。产生脉冲信号源的方法也很多。一种是用脉冲膜片法，该装置是由两个空腔组成，中间用膜片隔开，其中一个空腔充有一定压力的空气，被标定的传感器固定在空腔的壳体上，当膜片被突然切断时，可获得压力阶跃。这种用降压方法获得的压力阶跃，更接近理想的阶跃函数。其降压时间约为0.25ms。

另一种阶跃函数压力源是闭式爆炸器。压力源由炸药产生。在爆炸器的压力室中，放置烈性硝甘炸药和雷管，引爆后产生压力阶跃。它的压力峰值由药量和有效容积来控制。这种装置可得到在0.3s内产生压力阶跃高达5MPa的压力信号。

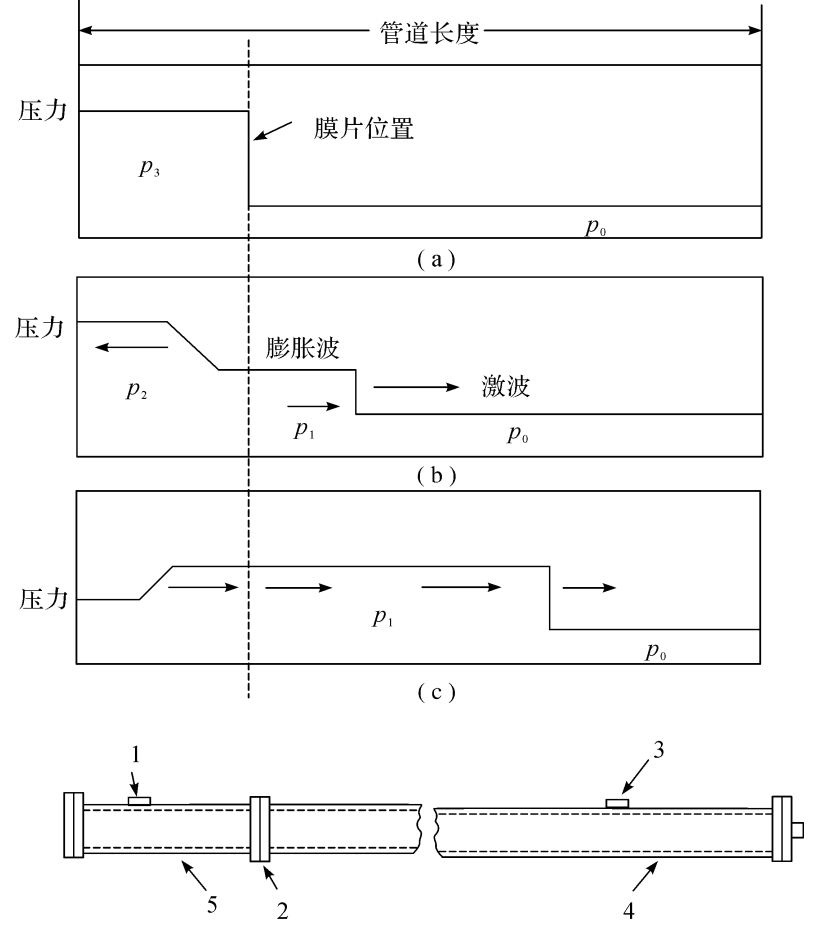
激波管也是一种阶跃信号发生器，激波管的构造如图4.12(d)所示。激波管的构造十分简单，它是一根两端封闭的长管，用膜片分成两个独立的空腔。左边较短的是高压腔，右边较长的是低压腔。把高压气通入高压腔，当高低压腔的压力差达到一定值时，膜片突然破裂。由于压力突变产生一个高速运动的激波，传向低压区，膨胀波传向高压区。当激波传到低压区的管端时，装在管端的被标定的传感器将受到一个上升时间很短的阶跃压力波(约10-⁸s),直到膨胀波的反射波从高压区传到传感器为止。这一阶跃压力波可在短时间内保持不变(约数毫秒)。用这样一个已知波形、已知幅值的阶跃压力波，可以进行压力传感器的动态参数标定(见图4.12)。

图4.12激波管外形和压力波形图

(a)膜片破裂前；(b)膜片破裂后；(c)膨胀波折回后；(d)激波管

1,3一压力传感器；2一膜片；4低压区；5一高压区

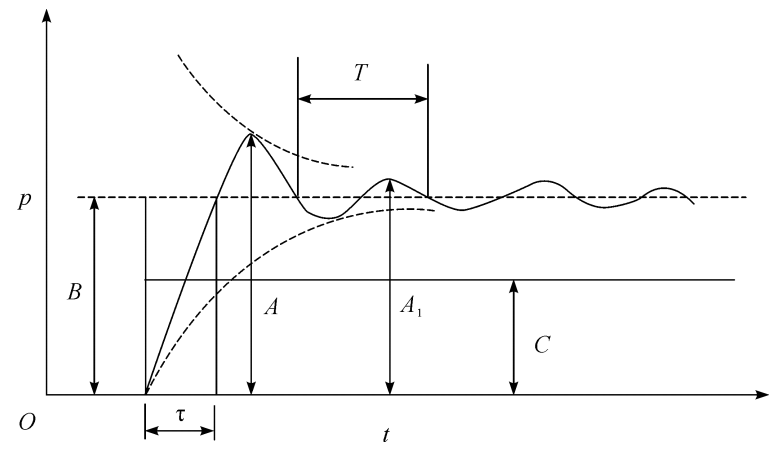
全部动态参数可以从传感器的响应曲线上得到，这些参数包括上升时间t、过冲比A/B,自振频率w、阻尼比ξ和动态灵敏度δ等。由图4.13可知：

图4.13传感器的动态响应曲线

阻尼比为

\(\zeta=\frac{\delta}{\sqrt{{\delta}^{2}+4{\pi}^{2}}}\)

动态灵敏度为

\(\delta=ln\left(\frac{A-B}{{A}_{1}-B}\right)\)

自振频率为

\({\omega}_{0}=\frac{2\pi}{T\sqrt{1-\zeta}}\)

激波管产生的阶跃压力的特点是压力上升快，压力持续时间短，适合于标定自振频率高和阻尼比大的传感器。对于阻尼比不大而自振频率低的传感器，由于阶跃压力反应的过渡时间长(约数十毫秒),就需要激波管的阶跃压力持续时间长。激波管的长度必须做得很长。这样的压力传感器不适于用激波管标定。

对于推力测量系统的动态标定，同样可以用正弦力发生器或爆炸法来标定。

4.3试车台

试车台是发动机地面点火试验专用的场所，通常包含建筑物和设施两部分。试车台的建筑物部分可分为试车台主体、辅助厂房和测控中心(测控间)等几部分。试车台主体通常是指试车间、承力墩和导流槽等三个部分的组合体，是试验的主要场地。辅助厂房通常有装配间、标定间和摄影间等。测控中心是发动机工作时测控人员集中工作的场所，内有时序控制和数据采集等仪器设备。为了保证安全，测控中心要与试车台主体保持足够的安全距离。试车台的设施主要包括试车架、测控系统、供水系统、能源系统及其他一些专用设施等。对试车台的基本要求是安全可靠、操作方便，应保证在发动机正常情况下能安全可靠地工作，在发动机工作出现异常或紧急情况时能及时地进行安全防护。

试车台的建筑规模主要取决于发动机的结构尺寸和工作推力，根据试验发动机的大小，试

车台的承载能力可从数千牛到数万千牛不等，如美国研制“大力神-3C”火箭助推器时就建造了承载能力达33700kN的巨型试车台，最常用的是承载能力为50kN,100kN,500kN,1000kN,2000kN,4000kN的试车台。

4.3.1试车台的类型

按试验时发动机的安装姿态划分，试车台可有水平试车台和垂直试车台两种类型。

1.水平试车台

水平试车台又叫卧式试车台，试验时发动机的轴线(或推力方向)与地面平行。如图4.14所示就是一种敞开式的水平试车台。固体火箭发动工作过程，推进剂不断减少，发动机的质量在不断变化。由于水平试车台发动机的重力方向与轴向推力方向垂直，因此工作过程中发动机质量的变化对推力测量影响小，但同时对侧向力敏感性低。水平试车台的用途很广，它可适用于各种大小和各种结构材料的发动机。

图4.14水平试车台结构简图

1一试验发动机；2一承力墩；3一地基；4一试车架

2.垂直试车台

垂直试车台是发动机轴线(或者推力方向)与地面垂直，又可分为两种：一种是发动机喷管朝下的正立式，另一种是发动机喷管朝上的倒立式。不管是正立式还是倒立式，它们的共同使用特点是便于测量发动机在工作过程中所产生的侧向力，但发动机在工作中质量的变化对推力测量值的影响较大。

正立式试车台的发动机喷口朝下，推力朝上，因此需要解决好燃气排导和承力两大问题。

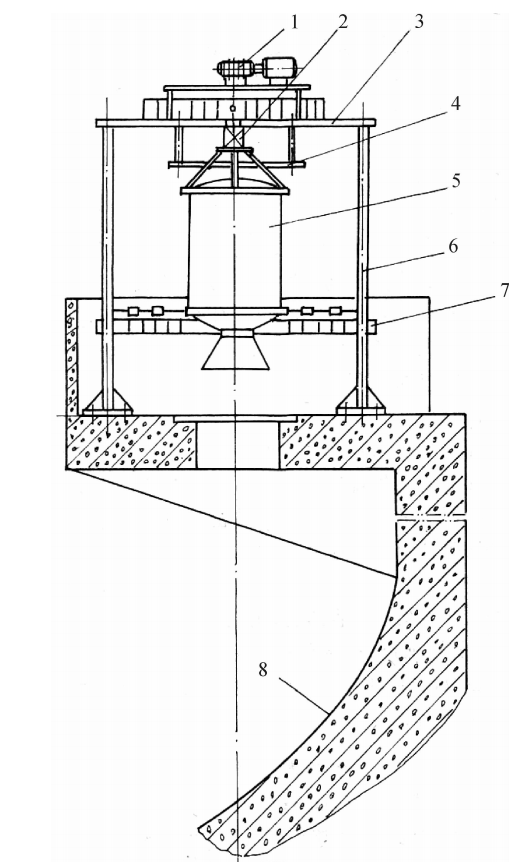
如图4.15所示的正立式试车台是一种钢筋混凝土结构的，由带有排气道(导流槽)的水平基座和带有金属覆板的立柱组成。在这种试车台上进行发动机试验时，发动机的推力由覆板、立柱和地基承受。发动机推力较大时，不仅要求覆板和立柱有足够的强度和刚度，而且对基础也有很高要求。对于竖直发射的火箭来说，正立式试车台发动机的工作姿态与发射时的姿态一致，这可以算作正立式试车台的一个优点。

图4.15正立式试车台结构简图

1一提升机构；2一测力组件；3一覆板(承力平台);4一吊挂；5一试验发动机；6一立柱；7一工作平台；8一导流槽

与正立式的情况相反，在倒立式试车台上试验时，发动机的推力直接作用在地面基础上，燃气直接排放到空中，不存在气流冲刷和反作用力问题。相比之下，这种试车台的结构比较简单，设计和建造也都比较容易，因此应用也比较多。如美国的“大力神-3C”火箭助推器就是在这种试车台上试验的。这种试车台的缺点是发动机工作状态与实际飞行时差别较大，采用含铝推进剂的发动机容易在发动机头部产生氧化铝沉积。

4.3.2试车台的组成

发动机尺寸不同，试验的类型和要求不同，试车台的规模和组成也会有所不同，现在介绍试车台比较常见和重要的组成部分。

1.试车间

试车间是发动机点火试验的工作间，其内部装有发动机、试车架、监测仪器和测试电缆等，是试车台的核心部分。试车间由基础、围墙和屋顶三部分组成，对试车间的要求如下。

(1)必须坚固耐用，具有一定的抗震和防爆能力。

(2)空间足够宽敞，便于发动机的吊运和安装。

(3)室内机构设置齐全，满足发动机与试车架安装、定位与固定的需要。

(4)便于试后的现场处理。

2.承力墩

承力墩的作用是平衡(或承受)发动机工作时所产生的推力，承力墩一般为钢筋混凝土构筑物，其承力面上设置具有一定厚度的钢板，钢板开设一定数量的安装孔。对承力墩有两点要求：一是承载能力要足够大，一般地说，其承载能力应为发动机最大推力的5～10倍；二是承力面要尽量与地平面相垂直。

3.导流槽

水平试车台和正立式垂直试车台上都需建造导流槽。导流槽的主要作用是将发动机排出的燃气导向远离试车间的地方，保护试车台设备和周围建筑物，减少气流冲击波和由此而引起的噪声。导流槽的结构型式可因使用目的和要求而异。在无特殊测量要求，而只起排放燃气作用的情况下，水平试车台的导流槽为一较宽敞的用水泥构筑的直通道，正立式垂直试车台的

导流槽为图4.15所示弧形通道。对导流槽的要求，一是具有足够的抗气流冲刷和烧蚀能力，二是具有一定的长度和宽度。

经验表明，在导流槽的表面上浇灌一层冷却水，不但可以对导流槽起保护作用，延长其使用寿命，而且可以大大地减少导流槽的长度。根据这一特点，立式台的导流槽多采用冷却式结构。

4.测控中心

发动机试验过程点火程序控制、参数测量等都是在测控中心(测控间)内完成的，由于它是发动机工作时测试人员集中工作的场所，其内部装有时序控制台、数据采集系统、计算机、监控与对讲等各种精密仪器和设备，为了保证人身和设备的安全，为了使测试设备长期保持稳定的工作性能，对测控中心提出了比较严格的要求，具体如下。

(1)与试车间之间保持足够的安全距离。

(2)有较宽敞的空间。

(3)有良好的环境条件，如良好的通风、恒定的温度与湿度、随时保持室内清洁、良好的照明等。

(4)远离强动力源，具有抗干扰能力。

(5)与试车间之间要建造维护方便的电缆沟。

5.测控系统

测控系统包括发动机点火程序控制和参数测量两大部分，参数测量又可分为信号变换、信号调节、信号采集与处理等三个环节。起信号变换作用的各种传感器都位于试车间内，而且多数是直接装在发动机的相应部位上；信号调节器多数是放在前置放大间内；点火程序控制、参数测量中的信号采集与处理工作都是在测控中心内完成的。

6.试车架

试车架是发动机试验的重要设施，主要作用是约束发动机并保证推力的测量，在下一节中将会详细介绍。

4.4试车架

试车架是发动机地面点火试验不可缺少的主要设备，试车架的作用是：承受发动机及其附件的全部质量，对发动机加以必要的限位或定位，传递发动机在工作中所产生的推力。试车架的性能对发动机工作的安全可靠性以及推力测量的精确性有直接影响。对试车架的基本要求如下。

(1)保证发动机在装调和工作过程中的安全可靠性。

(2)保证发动机推力测量的精确性。

(3)保证发动机在工作过程中的动态特性稳定。

(4)操作性好。

4.4.1分类

试车架主要按用途分类，也可按连接特点、受力状态、安装特点或通用性分类。

1.按用途分类

(1)常规试车架。它仅测量轴向推力的试车架，它又可分为结构试验试车架和性能试验试车架。前者用于模样试验阶段，特点是结构简单，成本低廉，坚固耐用，容易维修，通用性好，安装方便，操作迅速。后者用于初样、试样和定型试验阶段，提供各种性能数据，特点是试验精度高，其推力测量系统精度优于0.5%。

(2)旋转试车架。能给发动机提供转动力矩和支撑的试车架，用于发动机转动下的内弹道特性、氧化铝沉积量及对热结构影响的试验。要求转速可调，在试验过程中能保持稳定，并能在转动中测量压力、推力、转速及温度等参数，以确定旋转对发动机性能和结构的影响。

(3)多分力试车架。能测出发动机多个方向的力和力矩的试车架。用于测量发动机推力矢量控制装置产生的姿态控制力和力矩，也可用它来确定推力终止机构产生的侧向干扰力和发动机产生的推力偏心值等，一般能测3～6个分量。

(4)推力终止试车架。用于测量推力终止机构打开后发动机所产生的瞬态推力及负推力。要求是要具有良好的动态性能，并能避免反向喷管打开时产生的破坏影响。

2.按连接特点分类

(1)外摩擦副试车架。动架和静架之间采用滚球、滚轮、静压导轨等形式连接的试车架。

(2)内摩擦副试车架。动静架之间采用板簧、圆杆挠性件、万向挠性件等形式连接的试车架。

3.按结构安装特点分类

(1)整体式试车架。试车架主体采用整体结构形式，它的主要安装定位基准和关键尺寸都靠加工精度保证，优点是安装方便，误差小，整体刚度大，常用于小型发动机试车。

(2)组装整体式试车架。加工成几个部分以后固定成整体结构形式，使用中不再拆开，优点是便于运输和加工，用于大型发动机试车。

(3)组装式试车架。利用发动机本身作为中心连接件组成的试车架，适用于特大型发动机试车。

4.按通用性分类

(1)通用试车架。直径和长度在一定范围内可调的试车架，用于模样阶段的结构考核性试验。

(2)专用试车架。针对某一型号发动机试验专门设计的高精度试车架，优点是测量准确、可靠，安装操作简便，用于初样、试样、定型等阶段的性能试验。

此外，还可按动静架之间的连接件的受力状态分为支撑式试车架和吊挂式试车架，前者连接件受压力作用，后者受拉力作用。

4.4.2组成

试车架通常由静架、动架、推力架、测力组件和小位移元件等五个基本部分组成，另外还可根据试车架不同类型要求加上原位校准装置、安全限位装置等部分。对于不同类型的试车架来说，其形式和组成会有所差异，下面以图4.16所示滚轮车式试车架为例来介绍试车架的组成。

图4.16滚轮车式试车架

1一球凹；2一球接头；3一测力组件；4一连接接头；5一预紧装置；6一推力架；7一安全限位装置；8一产品支架；9一滚轮车

1.静架

静架是试车架的承力构件，也称定架，通常安装在试车台的基础上，与动架通过小位移元件相连，对于水平和正立式试车台来说，还要承受发动机和动架的质量。图4.16中滚轮导轨就可以算作静架。

2.动架

动架是定位和固定发动机的结构件，一方面与发动机定位和连接，确保与发动机一起运动；另一方面要提供与测力组件、原位校准装置、小位移元件的定位和连接，以确保准确测量。

图4.16中滚轮车与产品支架就属于动架。

3.推力架

推力架也称为过渡架，它是发动机主推力的传力结构件，使发动机轴线对准主推力测量元件，有些情况下也可以算作动架的一部分。对于中型和大型发动机，推力架一般做成锥台框架形结构，大端与发动机前裙端面连接，小端与测力组件定位连接。发动机推力通过前裙端面传给推力架，然后再通过小端传给测力组件。

4.测力组件

它是试车架感受发动机作用力的测量元件，一般由测力传感器、挠性件(或球面接头)和连接件组成。传感器用来感受作用力，挠性件用来改善传感器的受力状态，消除非轴向力对测量的干扰。

5.小位移元件

它是动静架之间的连接件，用来支撑发动机-动架组合体的质量，并提供沿发动机轴向运动的小位移自由度，使发动机推力全部作用到推力传感器上。常用的元件有滚动元件和弹性元件，如图4.16中所示的滚轮就属于小位移元件。

6.原位校准装置

它用于高精度试车架的静态校准，由校准力源、标准力传感器、传力件、安装连接件等组成。力源是“模拟推力”的力发生器，它可是机械的(如千斤顶、杠杆机构等),也可是液压的。当推力大于100kN时，一般采用液压式，它具有结构紧凑、体积小、质量小、便于在试车架上安装、产生的力值大等优点。要求力源加载、卸载过程稳定。标准力传感器是用来指示力源力值的标准器，要求有好的稳定性和高的精度。

7.安全限位装置

它是试车架的安全防护构件，用来限制试车架可动部件在允许的正常范围内活动，超过允许范围，则起刚性限位作用。它有很高的强度和刚度，分布于试车架的薄弱环节处和关键部位，防止它们出现过大的变形和破坏，也可减小发动机工作失常时造成的破坏。

4.4.3常用试车架

1.滚动元件试车架

常用的滚动元件试车架有滚轮车式、滚球式和中心架式三种。

如图4.16所示是滚轮车式试车架结构简图，滚轮内装有滚动轴承，四个滚轮在两条钢轨上运动。其优点是结构简单，安装操作简便快速，通用性好，应用很普遍。大型发动机，特别是长发动机，滚轮车做成分段式，它可消除发动机工作时轴向延伸影响，亦可适应各种长度。

滚球式试车架的优点是既可沿轴向自由调节，又可沿水平面在一定范围内任意调节；缺点是沿轴向调节距离太小，对试车架安装要求较高，操作较复杂。

中心架式试车架的优点：首先是将动架重量减到最小，以保证试车架具有尽可能高的固有频率，有利于动态力的测量；其次是安装操作简便，通用性好，普遍使用于小型发动机试验。

2.高精度试车架

各类高精度试车架有以下共同特点。

(1)动静架之间采用挠性件(板簧)连接。

(2)选用高精度传感器和万向挠性件。

(3)采用原位校准技术。

(4)使用高精度安装对准工具。

(5)结构上设计成专用的整体式结构。

高精度试车架为什么选择挠性元件而不是滚动元件，原因为挠性件是靠材料本身的弹性变形提供运动自由度的，弹性变形时引起材料的内摩擦，内摩擦与外摩擦相比具有摩擦力小，重复性好的优点。各种外摩擦连接，由于构成运动自由度的两个或多个零件之间存在相对运动(滑动或滚动),接触表面间摩擦力大，影响因素多，很难控制，重复性差，用在精密测量设备上将影响测量精度。加之存在间隙和摩损，用在有强烈冲击、振动的火箭发动机试验中将产生更大的误差。因此，目前在火箭发动机试验中，都普遍采用了各种型式的挠性件。

挠性件按功能分为弯曲挠性件和扭转挠性件。弯曲挠性件的轴向刚度大，侧向刚度小，可传递轴向力，避免侧向力干扰，用于动静架之间、测力组件两端和多分力试车架的连接中；扭转挠性件的轴向刚度大，扭转刚度小，用于主推力测力组件中，有利于滚动力矩测量。这两种挠性件可分开设计，也可合并成一件设计。

挠性件按提供自由度的方式分为单向运动性能挠性件和万向运动性能挠性件，前者如板簧，后者如圆杆和万向挠性件。

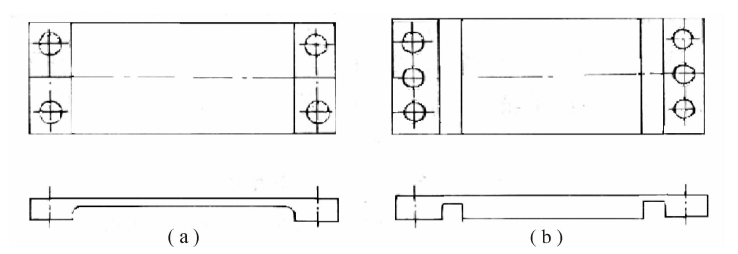
板簧主要有单工作段板簧和双工作段板簧两种(见图4.17)。

图4.17板簧结构示意图

(a)单工作段板簧；(b)双工作段板簧

单工作段板簧如图4.17(a)所示。这种板簧的结构和加工简单，采用薄而宽的矩形截面，厚度方向有大的挠性，宽度方向有较大的刚度，用于常规高精度试车架的动架和静架的连接中。它既可受拉，又可受压，其弹阻力值及其在试车过程中的变化较小，有利于推力测量。缺点是侧向刚度较差，抗侧向干扰能力弱，常用在小吨位试车架中。

双工作段板簧如图4.17(b)所示，其弹阻力值及其变化均较小，加之增加了中部刚性段，大大增加了侧向刚度，一般要增加到100倍以上。这种板簧提高了抗侧向干扰力的能力，适用于大吨位的高精度试车架中。

如图4.18所示是一个直径约1m,推力约200kN的中型发动机试车架结构简图。它采用了单工作段双板簧作为动架和静架之间的连接件，其弹阻力仅为推力的0.075%。原位校准采用液压系统，后支撑采用中心架，并设计了专用后裙定位板作为定位基准。

3.多分力试车架

多分力试车架主要用来测量发动机产生的推力偏心值，推力矢量控制机构产生的姿态控制力和力矩，以及推力终止机构打开时所产生的侧向干扰力等。比较常见的是六分力试车架，它是利用刚体的平衡原理，适当布置约束，以限制发动机的6个自由度(3个移动自由度和3个转动自由度),使之处于静定平衡状态。由于每一约束均由带传感器的测力组件来承担，并通过挠性件把相互间的干扰减到最小。所以，通过试车即可测得配置的六个约束所承受的6个分力。根据6个分力的作用点和方向进行空间向量合成，求出推力向量的大小、方向和作用点。

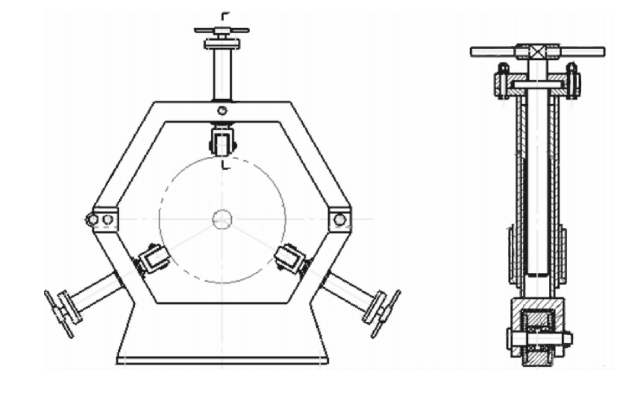
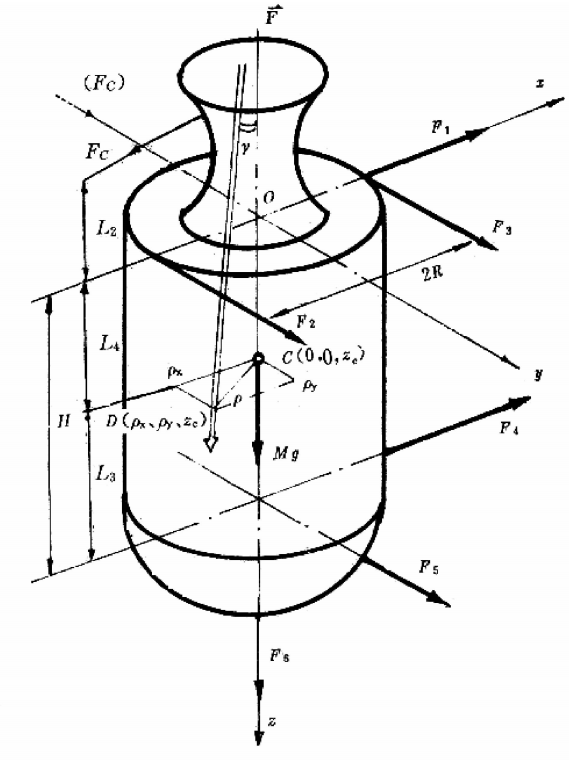
如图4.19所示是测推力偏心的立式六分力试车架测量示意图。选O-XYZ直角坐标系，以F₁和F₆两传感器的理论轴线交点为坐标原点，F₁传感器的理论轴线为X轴，F₆传感器理论轴线为Z轴，通过O点平行于F₂和F₃的轴线为Y轴，安装传感器的方向为各坐标轴的正方向，H、R为台架的结构尺寸，是已知数。

图4.18高精度试车架示意图

1一前横梁；2一悬吊板簧；3一标准力组件；4一校准加力油缸；5—测力组件；6一后横梁；7一法兰接头；8一推力架；9一前裙支撑弧座；10一后支撑中心架；11-后裙定位板；12一动架；13一板簧；14-底座；15一承力架

图4.19立式六分力试车架受力图

选坐标原点为力的简化中心，设主矢量和主矩为F(F_x,F_y,F_z),M(M_x,M_y,M_z)。空间力系的平衡条件是主矢量和主矩分别在3个坐标轴上的投影同时为零，即

\(\sum{F }_{x}=0\)，\(\sum{M }_{x}=0\)

\(\sum{F }_{y}=0\)，\(\sum{M }_{y}=0\)

\(\sum{F }_{z}=0\)，\(\sum{M }_{z}=0\)

由此可得到各分力和分力矩的计算公式为

\({F}_{x}={F}_{1}+{F}_{4}\)

\({F}_{y}={F}_{2}+{F}_{3}+{F}_{5}\)

\({F}_{z}={F}_{6}+{M}{g}\)

\({M}_{x}=-{F}_{5}H\)

\({M}_{y}={F}_{4}H\)

\({M}_{z}=({F}_{3}-{F}_{2})R\)           (4.5)

式中

F₁,F₂,…,F₆——传感器测得的6个分力，单位：N;

F_x,F_y,F_z——主矢量在3个坐标轴上的投影，单位：N;

M_x,M_y,M_z——主矩在3个坐标轴上的投影，单位：N·m;

M——发动机和动架的质量，单位：kg;

g——重力加速度，单位：m·s-²。

主矢量的值为

\(F=\sqrt{{F}_{x}^{2}+{F}_{y}^{2}+{F}_{z}^{2}}\)   (4.6)

主矩的值为

\(M=\sqrt{{M}_{x}^{2}+{M}_{y}^{2}+{M}_{z}^{2}}\)    (4.7)

推力偏心角γ是指发动机实际推力作用线L与发动机几何中心轴线间的夹角(见图4.19),可由下式求出

\(\gamma=arctan\frac{\sqrt{{F}_{x}^{2}+{F}_{y}^{2}}}{{F}_{z}}\)     (4.8)

4.5高空模拟试车台

高空模拟试验是固体火箭发动机在模拟高空低压环境下进行的点火试验(简称高模试验)。进行高空模拟试验的地面试验设施为高空模拟试车台(简称高模试车台)。

4.5.1概述

1.高空模拟试验的目的

(1)考核发动机高空喷管的结构与性能。在高空工作的固体火箭发动机通常均采用大面积比喷管以获得高的比冲，但大面积比喷管在地面试验时，将出现喷管内气流分离，导致轻质喷管的损伤或破坏，以及推力测量失真。

(2)考核与验证发动机在高空工作的结构性能与可靠性，精确测量发动机性能参数。

(3)测量在高空工作条件下，发动机排气流对相邻结构的传热影响，从而确定采取相应的防热措施。

2.高空模拟试车台的主要技术问题及参数

火箭发动机在进行高空模拟试车时，排出大量高温、高速燃气，如何将排出的高温、高速燃气抽吸排入大气，保持试验舱内处于稳定的低压环境是高空模拟试车台要解决的首要技术关键，其次是试验舱及满足试验要求的专用设备的设计。

决定高空模拟试车台规模及排气系统设计的主要技术参数是要求达到的模拟高度和排出燃气的质量流率。要求达到的模拟高度越高，燃气排出的质量流率越大，则高空模拟试车台的规模越大。

3.高空模拟试车台的基本类型

全程持续工作的高模试车台根据其排气系统的排出方式可以分为两大类：一类是“泵-扩压器”型高模试车台，习惯称之为被动引射高模试车台；另一类是“扩压器十外加抽吸系统”型高模试车台，习惯称之为主动引射高模试车台。

被动引射高空模拟试车台在早期的发动机高模试车中被广泛采用，但由于其存在的固有缺陷，已经不能满足先进固体火箭发动机高模试车的要求，在国外已被主动引射高模试车台所取代。

4.5.2被动引射高空模拟试车台

1.工作原理

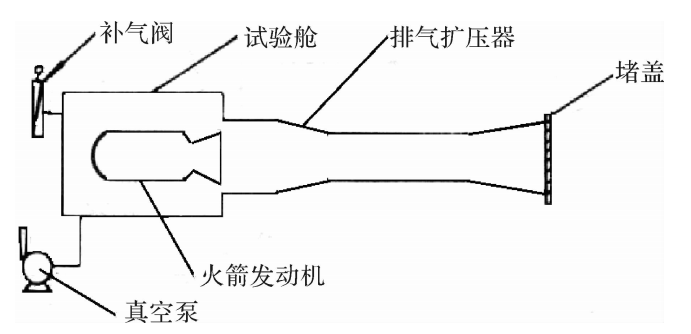
被动引射高空模拟试车台如图4.20所示，主要由试验舱、排气扩压器、扩压器堵盖、机械真空泵、补气系统、冷却系统等组成。

图4.20被动引射高空模拟试车台原理图

被动引射高空模拟试车台在进行高模试车时，试验舱内低压环境是依靠发动机工作时燃气的引射抽吸效应来维持的。发动机工作前，用真空泵将试验舱抽到需要模拟的低压环境。发动机工作时，从喷管中排出的超声速燃气通过扩压器后，流速降低，压力增高而排入大气。在燃气排出的同时会抽吸试验舱内的空气，使试验舱在发动机的稳态工作期间内，维持一定的低压状态。可以看出，扩压器是被动引射高空模拟台的关键设备。在扩压器正常运转期间，试验舱压力大小与发动机燃烧室压力及扩压器几何尺寸有关。

2.工作过程

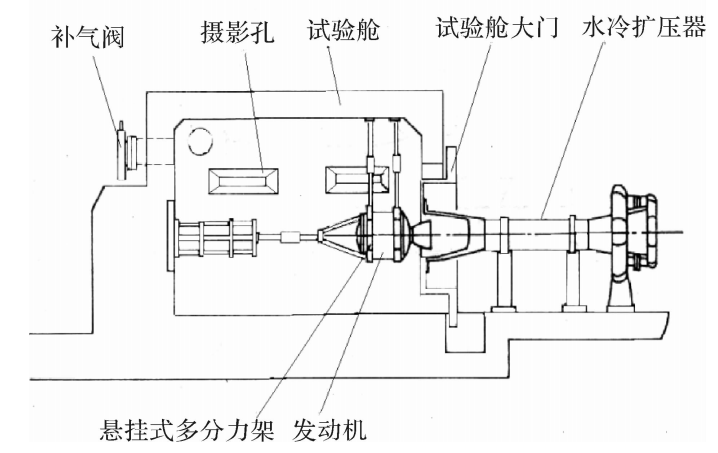
在发动机与扩压器按要求安装后，将扩压器堵盖连接于扩压器出口端面。打开试验舱与真空泵相连的阀门，开启真空泵对试验舱进行抽空直至达到模拟高空点火所需的压力，拧下扩压器堵盖上的连接螺栓，打开扩压器冷却水供给系统，发动机按程序进行点火。点火后发动机 第4章火箭发动机试验技术排出的燃气冲开堵盖排入大气，在发动机工作至推进剂燃烧结束时，由于燃烧室压力下降，扩压器已不能正常运转，燃气将在外压作用下部分回流入试验舱。为了减少燃气回流造成的不利影响，在此时将位于试验舱后端的补气阀门打开，外部的空气迅速进入试验舱，使舱压与外部环境压力平衡。如图4.21所示为一个实际应用的被动引射高空模拟试车台的结构示意图。

图4.21被动引射高空模拟试车台结构示意图

3.模拟能力

此类高空模拟试车台，在发动机稳态工作期间，即使扩压器几何参数按最优设计，其试验舱模拟的压力高度为18～23km。

4.局限性

(1)回流冲击。一般情况下，对不同的发动机进行高模试车时，要配备与之匹配的扩压器，每种扩压器均对应着一个最小启动压力。在发动机点火工作期间，当燃烧室压力大于扩压器最小启动压力时，扩压器能够正常工作，保持试验舱内相应的低压环境；反之，扩压器不能正常工作。因此，在发动机点火过渡阶段的压力建立期间和发动机燃烧结束的压力下降期间，扩压器都处于不能正常启动状态，在这两个阶段都将出现燃气回流进入试验舱的情况并导致回流冲击。大的回流冲击将可能导致喷管的损坏，尤其对软质的大面积比喷管或易碎的可延伸喷管出口锥将导致严重的后果。回流冲击是被动引射高模试车台的严重缺陷。

(2)喷管不能摆动。由于被动引射高模台其扩压器出口直通大气，其出口反压高，为了保证扩压器能够正常启动，扩压器的入口直径受到限制，难以采用允许喷管进行摆动的大面积比扩压器。因此，对采用摆动喷管的发动机，不能在被动引射高模试车台上进行摆动喷管的试车。

(3)不能精确测定发动机的推力与总冲。由于在发动机点火过渡阶段和燃烧结束的压力下降阶段，喷管受不能满流和回流冲击的影响，使得推力和冲量测量会不真实。

(4)不利于试车后的校准。由于被动引射高模台不能在试车后使试验舱仍维持一定时间的低压环境，因此不利于测量系统试车后的校准。

4.5.3主动引射高空模拟试车台

主动引射高空模拟试车台是指发动机进行高空模拟试车时，试验舱内低压环境的建立，除了利用排气扩压器的增压引射作用外，还利用外加的排气抽吸系统(如蒸汽引射器、机械排气机组等)。增加排气抽吸系统后，可使试验舱内的压力模拟高度提高，使试验舱内的低压环境在试车全过程中得到保持，并有效地防止燃气回流。

主动引射高空模拟试车台主要有如图4.22所示的几种组成方案。

图4.22主动引射高空模拟台组成方案

图4.22中，前两种组合方案应用较为普遍，第三种方案一般应用于推力较小、工作时间较长的发动机试验中。下面重点介绍前两种方案。

1.“燃气扩压器十蒸汽引射器”高空模拟台

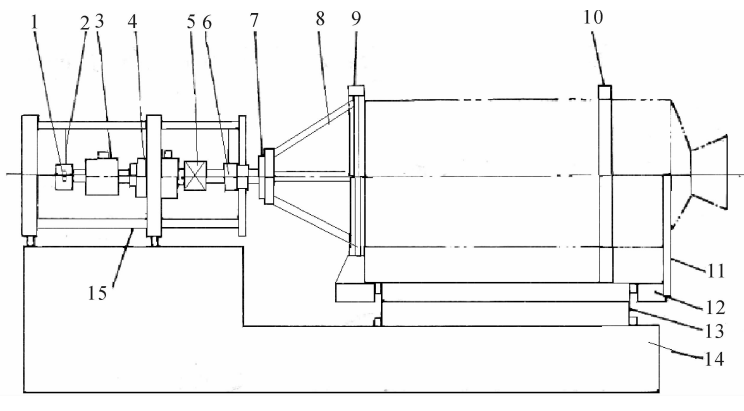
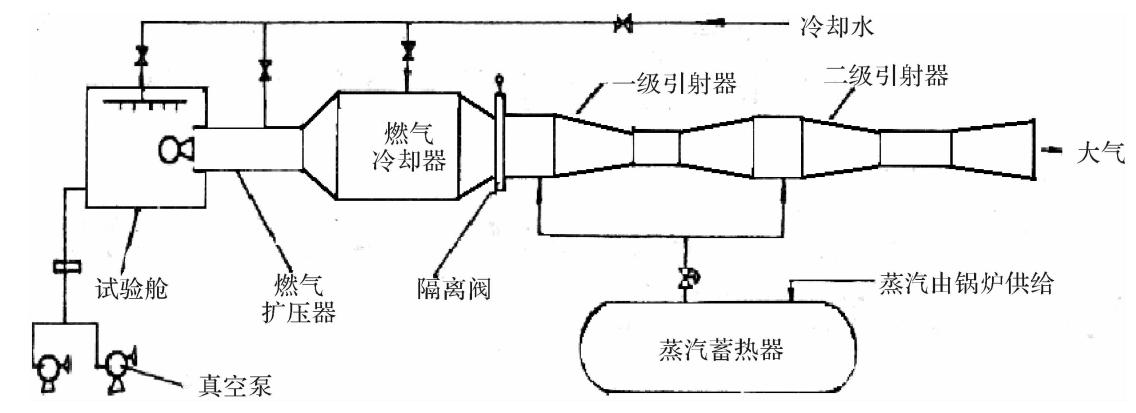
“燃气扩压器十蒸汽引射”高模试车台的示意图如图4.23所示，主要由试验舱、燃气扩压器、燃气冷却室、隔离阀、蒸汽引射器(可以采用多组并联、每组多级串联方案)、蒸汽供给系统、控制测量系统以及冷却水供给系统等组成。

图4.23“燃气扩压器十蒸汽引射器”高空模拟台示意图

在发动机点火前，将系统的隔离阀门关闭，此时从试验舱至燃气冷却室处于密封状态。试验舱内的初始低压环境可以通过与试验舱相连的机械真空泵或辅助蒸汽引射器的抽吸达到。发动机临近点火时，各供水系统按要求供水，启动主蒸汽引射器，打开隔离阀门。在主蒸汽引射器的引射抽吸作用下，维持试验舱的低压状态。发动机点火后，燃气通过喷管进入排气扩压器进行第一次增压，然后进入燃气冷却室与呈雾状喷出的冷却水混合。通过水的汽化吸热，燃气与水蒸气的混合气体温度降至隔离阀门和引射器构件所能承受的温度，进入第一级蒸汽引射器。蒸汽喷嘴中喷出的高速蒸汽流裹挟进入的混合气体，通过蒸汽引射器进行第二次增压。

之后混合气体进入第二级蒸汽引射器再次增压后排入大气。发动机工作结束后，已无燃气排出，可关闭隔离阀门，然后蒸汽引射器停止工作。此时试验舱内应仍保持一段时间的低压状态，以便测量系统进行试车后的校准。

蒸汽供给系统是此类高模台的重要系统。在发动机高空模拟试车时(特别是大推力发动机),在试车的短短数十秒钟内要供给大量具有稳定压力的蒸汽，如直接采用锅炉供汽是难以做到，且不经济。最经济和实用的办法是采用蒸汽蓄热器供汽。蒸汽蓄热器的工作原理是在压力容器中贮存水，将来自锅炉的蒸汽通入水中使水加热，使容器内水的温度和压力升高，形成具有一定压力的饱和水。当容器内压力下降时，饱和水变成过热水，自蒸发产生蒸汽。采用此方法，在有足够的蓄热器条件下可以满足短时间内提供流量大而压力稳定的蒸汽的要求。

2.“扩压器十环状蒸汽引射器十排气机组”主动引射高空模拟台

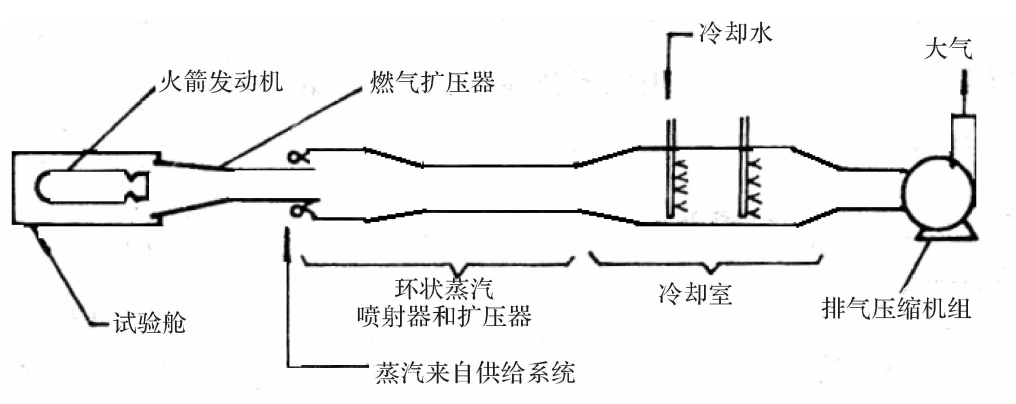
“扩压器十环状蒸汽引射器十排气机组”主动引射高空模拟试车台示意图如图4.24所示，由试验舱、燃气扩压器、环状蒸汽引射器、燃气冷却室、排气压缩机组以及蒸汽供给系统、控制测量系统和冷却水供给系统等组成。

图4.24“扩压器十环状蒸汽引射器十排气机组”高空模拟台示意图

发动机点火前，启动机械排气机组，对试验舱及燃气冷却室进行预先抽空，达到一定低气压条件后，启动环状蒸汽引射器以及辅助排气机组使试验舱迅速达到预定的低气压环境。发动机工作期间，试验舱内的低气压环境主要靠发动机排气扩压器和排气机组的抽吸作用来保持，此时环状蒸汽引射器起辅助作用。为使高温燃气在进入排气机组前能够冷却，在排气机组前设置燃气冷却室，使燃气温度降至排气机组能够承受的温度。燃气冷却室的另一作用是起冷凝器的作用，使部分蒸汽得到冷凝，从而减少排气机组的负荷。发动机接近燃烧结束时，环状蒸汽引射器接替排气扩压器的工作，与排气机组一道继续保持试验舱的低压环境，防止回流造成的影响。

3.主动引射高空模拟试车台的优点

与被动引射式高空模拟试车台相比，主动引射高空模拟台具有以下优点。

(1)模拟高度高。根据试验要求，配备适当能力的抽气系统可获得高于30km的模拟高度，能保证面积比小于100的喷管在试车全过程中处于满流工作状态。

(2)无回流冲击。由于外加排气抽吸系统，可以保证在试验全程(从发动机点火到燃烧结束)中试验舱内压力稳定，回流冲击很小，甚至没有回流冲击，不会造成大面积比喷管或轻质可延伸出口锥结构的损坏，并能精确测量发动机工作全程中的推力和总冲，推力测量的不确定度可以达到0.5%以下。

(3)可进行摆动喷管的推力矢量控制试验。外加排气抽气系统后，排气扩压器的出口反压降低，扩压器的直径可以增大，满足了喷管在全轴摆动(摆角最大可达8°)下进行高模试验的要求。从而能够考核摆动喷管的结构性能和动态性能，精确测量伺服系统的作动力和发动机的侧向分力。

(4)便于试后处理。可根据需要，在发动机工作结束后继续保持试验舱内的低压状态，以利于试验后的校准，提高测量精度。

(5)对环境保护有利。经过喷水冷却后，燃气中有害成分和微粒大部分得以消除，排气得到净化，减少了环境污染。

第5章温度测量

在固体火箭发动机的热试验中，温度测量在总的测量工作中占相当的比例。如试验前需要知道当时的环境温度、装药的初温；试验中需要测量燃气的温度，用其验证计算公式所给予的假设条件和主要数据的正确性；测量发动机及其部件外表面的温度，以判断结构部件是否处在正常的工作条件之下；防热措施是否有效；在某些研究性的试验中，往往需要测量点火药燃烧后所建立的温度及推进剂表面的温度等。可见，温度是火箭发动机试验中需要测量的重要参数之一。

在各个技术领域中，测温的方法及仪表种类甚多。本章着重介绍热电偶的原理及使用方法，另外，对发动机试验中常会遇到的电阻温度计作些简单介绍。

5.1温度的基本概念

5.1.1温度

温度是表征物体冷热程度的物理量。其本质是与物体内部分子的运动相联系的。温度的高低反映了物体内部分子运动剧烈的程度，即反映了分子平均运动动能的大小。

5.1.2温标

用来度量温度高低而规定的标尺称为温度标尺，简称温标。温标规定了温度的读数起点和测量温度的基本单位，它是温度数值的表示方法。各种温度计的分度值均由温标来确定，国际上常用的温标有摄氏温标、华氏温标、热力学温标和国际实用温标等。

1.摄氏温标(℃)

摄氏温标是根据液态水银随温度升高而膨胀的性质建立起来的。它是把在标准大气压下冰的融点定为零摄氏度(0℃),把水的沸点定为100摄氏度(100℃)的一种温标。将一支水银玻璃温度计放在融冰和沸水中，分别在水银面的位置刻线，表示0℃和100℃。并在两条刻线之间等分100份，每一等份为一摄氏度。

2.华氏温标(°F)

华氏温标选用的测温物质也是水银。它规定在标准大气压下冰的融点为32°F,水的沸点定为212°F,两点间划分为180等份，每一等份为一华氏度。华氏温标t_F和摄氏温标t_C之间的换算关系为

/({t}_{F}=\frac{9}{5}{t}_{C}+32/)(5.1)

/({t}_{C}=\frac{5}{9}{t}_{F}-32/)(5.2)

随着生产和科学技术的发展，发现用不同的玻璃和不同纯度的水银制成的水银温度计，尽管在0℃和100℃(或在32°F和212°F)时指示是一致的，但在中间温度的示值则不完全相同，这是由于不同的玻璃和不同纯度水银的膨胀系数有差别而引起的。另外，上述温标只规定了水冰点和水沸点之间的温标，这个温度范围太小，不能满足日益发展的生产和科学研究的要求。需要制定一个统一的更为科学的温标。

3.热力学温标(K)

热力学温标是一种与物质的物理性质无关的科学的温标。它是根据热力学第二定律导出的，已由国际计量大会规定为国际统一的基本温标。目前国内外所用的摄氏和华氏温标实际上是延用了过去的名称，而在内容上都已根据热力学温标赋予了新的概念。热力学温标规定分子停止运动时的温度为绝对零度。这是一种理论温标，可借助于气体温度计来实现。但是气体温度计装置复杂，所测得的结果需要修正，使用很不方便。因此，国际上又采用一种同热力学温标相接近，而且复现精度高，便于应用的协议性国际实用温标。

4.国际实用温标

国际实用温标，是一个国际协议性温标，它与热力学温标相接近，而且复现精度高，使用方便。国际计量委员会在18届国际计量大会第七号决议通过了1990年国际温标ITS-90。在国际温标ITS-90中，热力学温度(符号为T)是基本物理量，它的单位为开尔文(符号为K),定义为水三相点的热力学温度的1/273.16。水的三相点在273.16K(0.01℃)及611.73Pa出现。ITS-90中共定义了17个固定点及其温度值。在ITS-90中规定了不同温区的四种定义方法或内插仪器。0.65～5.0K用氦蒸气压温度方程；3.0～24.5561K温区用内插气体温度计；13K～961.78℃用铂电阻温度计做内插仪器；961.78℃以上温区由普朗克辐射定律定义。

由于以前的温标定义中，使用了与273.15K(冰点)的差值来表示温度，因此现在仍保留这个方法。根据定义，摄氏度的大小等于开尔文，温差亦可以用摄氏度或开尔文来表示。国际温标ITS-90同时定义国际开尔文温度(符号为T90)和国际摄氏温度(符号为t90)。

摄氏温度符号为t,单位为℃,但概念上已按下式重新定义

t=T-273.15     (5.3)

工程上近似取t=T-273。

5.1.3测温仪表

1.按测量方法分

(1)接触式：温度计、热电偶等。

(2)非接触式：红外热像仪等。

2.按工作原理分

(1)利用物质热膨胀与温度的关系(双金属温度计、玻璃水银、压力表式)。

(2)利用金属或半导体电阻与温度的关系(电阻温度计)。

(3)利用热电效应(热电偶)。

(4)利用物体的辐射能与温度的关系(红外辐射温度计)。

5.2热电偶

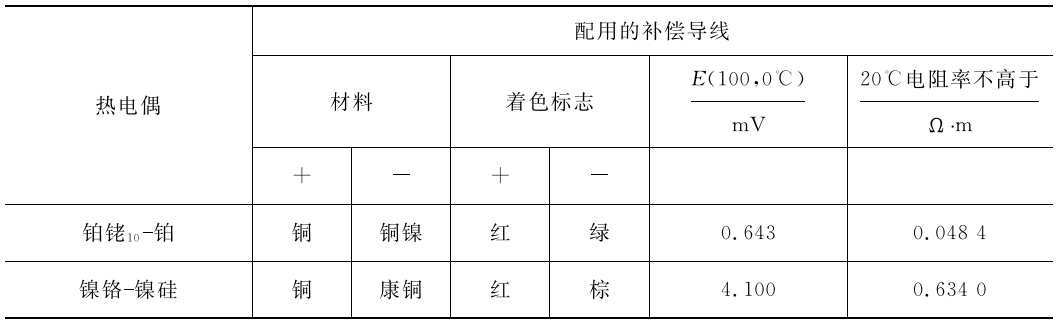
在温度测量中，热电偶是一种应用最广泛的温度传感器。它具有结构简单、制作方便、测量范围宽、热惯性小和输出信号便于远距离传输等优点。可用来测量流体温度，也可以测量固体表面或内部某点的温度。微型热电偶适用于动态快速温度测量。

5.2.1热电偶测温原理

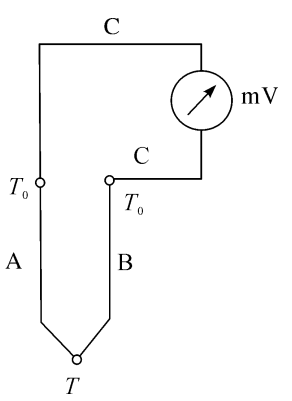
热电偶是由两种不同的均质导体(或半导休)连接成一闭合回路而制成的温度计，如图5.1所示。两导体的连接点1和2简称为结点。用热电偶测温时，节点1置于被测温度T处，称为测量端(工作端、热端);节点2则置于某一恒定温度T₀处，称为参考端(自由端、冷端)。当两个节点的温度不同(T≠T₀)时，回路中就会产生电动势，接在回路中的毫伏计便会发生偏转，而且两节点的温度相差愈大，指针偏转也愈大，这种现象称为热电效应。相应的电动势称为热电势。这种热电势是由两种导体的接触电势和单一导体的温差电势组合而成的。

图5.1热电效应示意图

1.接触电势

它是由于相互接触的两种金属导体内自由电子的密度不同而造成的。当两种不同的金属

A、B接触在一起时，在金属A、B的接触处将会发生电子扩散。电子扩散的速率和自由电子的密度及金属所处的温度成正比。设金属A、B中的自由电子密度分别为NA和Ns,并且NA>

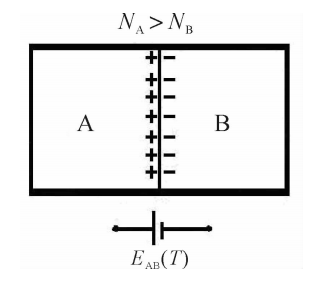
NB,在单位时间内由金属A扩散到金属B的电子数要比从金属B扩散到金属A的电子数多。这样，金属A因失去电子而带正电；金属B因得到电子而带负电。于是在接触处便形成了电位差，即接触电势，如图5.2所示。这个电动势将阻碍电子由金属A进一步向金属B扩散，一直达到动平衡为止。这种由于两种金属的自由电子密度不同而在接触处形成的电动势，称为接触电势。用EAB(T)表示接触电势，其值可表示为

\({E}_{AB}(T)=\frac{kT}{e}ln\frac{{N}_{A}}{{N}_{B}}\)    (5.4)

式中

k——波耳兹曼常数，等于1.38×10^-23J·K-¹;

T——接触处的绝对温度，单位：K;

e——电子电荷量，等于1.602×10^-19C;

NA,NB——金属A,B的自由电子密度。

对于A,B两种金属导体构成的回路(见图5.1),温度T端的接触电势即可由上式计算。同样可计算温度T₀端的接触电势，有

\({E}_{AB}({T}_{0})=\frac{k{T}_{0}}{e}ln\frac{{N}_{A}}{{N}_{B}}\)    (5.5)

在回路中E_AB(T₀)和E_AB(T)的方向相反，所以总的接触电势为

\({E}_{AB}(T)+ {E}_{BA}({T}_{0})={E}_{AB}(T)- {E}_{AB}({T}_{0})=\frac{k}{e}(T-{T}_{0})\ln\frac{{N}_{A}}{{N}_{B}}\)

显然，当两结点的温度相同，即T=T₀时，回路中的总接触电势将等于零。

图5.2接触电势示意图

图5.3温差电势示意图

2.温差电势

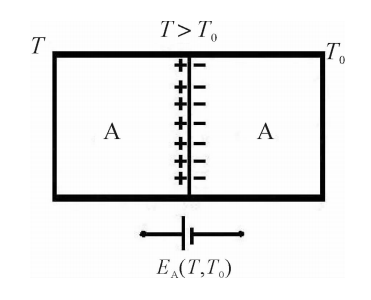
在一根均匀的金属导体中，如果两端的温度不同，则在导体的内部也会产生电势，这种电势称为温差电势，如图5.3所示。温差电势的形成是由于导体内高温端自由电子的动能比低温端自由电子的动能大，这样，高温端自由电子的扩散速率比低温端自由电子的扩散速率大，因此对于导体的某一薄层来说，温度较高的一边因失去电子而带正电，温度较低的一边因得到电子而带负电，从而形成了电位差。当导体两端的温度分别为T和T₀时，温差电势可表示为

\({E}_{A}(T,{T}_{0})=\int\limits_{{T}_{0}}^{T}{{\sigma}_{A}dT}\)    (5.7)

式中

σ_A——导体A的汤姆逊系数，是温度的单值函数。对于由两种金属A,B组成的热电偶回路，温差电势等于它们的代数和，即

\({E}_{A}(T,{T}_{0})+{E}_{B}( {T}_{0}, T)= {E}_{A}(T,{T}_{0})-{E}_{B}(T, {T}_{0})=\int\limits_{{T}_{0}}^{T}{({\sigma}_{A}-{\sigma}_{B})dT}\)   (5.8)

这个电势的大小只与热电极材料A、B和两节点温度T、T₀有关，若T=T。,则温差电势为

零。

综上所述，对于均质导体A、B组成的热电偶，其总电势为接触电势与温差电势之和，即

\({E}_{AB}(T,{T}_{0})={E}_{AB}(T)- {E}_{AB}( {T}_{0})-{E}_{A}(T, {T}_{0})+{E}_{B}(T, {T}_{0})\)

\(=\frac{k}{e}(T-{T}_{0})\ln\frac{{N}_{A}}{{N}_{B}}-\int\limits_{{T}_{0}}^{T}{({\sigma}_{A}-{\sigma}_{B})dT}\)   (5.9)

由于系数σ_A、σ_B是温度的单值函数，式(5.9)可表示为

\({E}_{A}(T,{T}_{0})=f(T)-f({T}_{0})\)    (5.10)

根据式(5.9)或式(5.10)可得出下述结论。

(1)如果热电偶两电极材料相同，即使两端温度不同(T≠T₀),但输出总电势仍为零。因此，热电偶必须由两种不同的材料构成。

(2)若热电偶两节点的温度相同，则回路中的总电势必然等于零。

(3)热电势的大小只与材料和节点的温度有关，而与热电偶的尺寸、形状及沿电极温度分布无关。但应注意，若热电极本身性质不均匀，由于有温度梯度存在将会产生附加电势。

(4)如果保持冷端的温度不变，即使f(T₀)=常数。这样，回路中的热电势E_AB(T,T₀)就只与温度T有关，而且是T的单值函数，这就是利用热电偶测量温度的原理。

5.2.2热电偶的基本定律

利用热电偶测温时，必须在热电偶回路中接入连接导线和测量仪表。这样，在回路中将形成若干结点，这些结点是否也产生热电势，因而影响温度测量结果?下面分为几种情况讨论这一问题。

1.均质导体定律

由式(5.10)得出的结论(1)可知：用一种均质导体(或半导体)组成的闭合回路，两端点温度不同时，不能产生热电势。这一规律称为均质导体定律。

应用这一定律可以检验热电偶电极材料的质量。当只用一种热电极组成的回路受热时，如果有热电势产生，则说明该热电极有变质或不均匀疵病。

2.中间导体定律

在热电偶测温回路中接入的导线和仪表，其导体材料往往与热电偶所用的材料不同。如图5.4所示，若将热电偶的冷端T₀分开，串接入第三种导体(中间导体)C,其总的热电势有什么变化呢?中间导体定律回答了这个问题：在热电偶回路中，只要接入的中间导体两节点的温度相同，这样接入的中间导体对热电偶回路的总热电势没有影响，即

\({E}_{ABC}(T,{T}_{0})={E}_{AB}(T)- {E}_{AB}( {T}_{0})-{E}_{A}(T, {T}_{0})+{E}_{B}(T, {T}_{0})\)  (5.11)

证明：如图5.4所示，从A点出发，沿逆时针方向，可得总的热电势为

\({E}_{ABC}(T,{T}_{0})={E}_{AB}(T)+{E}_{B}( {T}_{0})+{E}_{BC}({T}_{0})+{E}_{C}({T}_{0},{T}_{0})- {E}_{CA}( {T}_{0})-{E}_{A}(T, {T}_{0})\) 

图5.4接入导线原理图

其中Ec(T₀,T₀)=0,而

\({E}_{BC}({T}_{0})+{E}_{CA}({T}_{0})=\frac{k{T}_{0}}{e}\ln\frac{{N}_{B}}{{N}_{C}}+\frac{k{T}_{0}}{e}\ln\frac{{N}_{C}}{{N}_{A}}=\frac{k{T}_{0}}{e}\ln\frac{{N}_{B}}{{N}_{A}}={E}_{BA}({T}_{0})\)

则

\({E}_{ABC}(T,{T}_{0})={E}_{AB}(T)- {E}_{B}( T,{T}_{0})+{E}_{BA}({T}_{0})+{E}_{A}(T, {T}_{0})\)

\(={E}_{AB}(T)- {E}_{AB}( {T}_{0})-{E}_{A}(T, {T}_{0})+{E}_{B}(T, {T}_{0})\)

证毕。

该定律推广下去，在热电偶回路中接入多种导体后，只要每种导体两端的温度相同，对回路的总热电势也无影响。

3.中间温度定律

所谓中间温度定律，是指热电偶在节点温度为T、T。时的热电势等于该热电偶在节点温度为T、T_n和Tn、T₀时相应的热电势的代数和，即

E_AB(T,T₀)=E_AB(T,T_n)+E_AB(T_n,T₀)

(5.12)

证明：E_AB(T,T_n)=f(T)一f(T_n),E_AB(T_n,T₀)=f(T_n)一f(T₀),则

\({E}_{AB}(T,{T}_{n})+{E}_{AB}({T}_{n},{T}_{0})=f(T)-f({T}_{n})+f({T}_{n})-f({T}_{0})=f(T)-f({T}_{0})={E}_{AB}(T, {T}_{0})\)

证毕。

如果T₀=0℃,则

\({E}_{AB}(T,0)={E}_{AB}(T,{T}_{n})+{E}_{AB}({T}_{n}, 0)\)

当利用热电偶进行测温时，应知道热电势与温度的对应关系，以便根据测得的热电势值求出相应的温度。式(5.9)虽然给出了两者关系的数学表达式，但在工程上应用起来还是比较困准的。工程上常用实验的方法得出温度与热电势的关系并制成表格，这种表格被称为分度表。

各种热电偶的分度表都是在冷端为0℃时制成的。如果在实际应用中热电偶的冷端不是0℃而是中间某一温度T,,这时显示仪表测得的热电偶输出电势为E_AB(T,T_n),利用该种热电偶的分度表可查出E_AB(T_n,0)的值，将此值与测量值E_AB(T,T_n)相加，即可算出EAB(T,0),再查该热电偶的分度表可求得工作端的温度。

4.标准电极定律

如果两种导体A和B分别与另一种导体C组成热电偶，当其结点温度均为T、T₀时，其热电势是已知的，则由导体A和B组成的热电偶产生的热电势可由下式求得：

\({E}_{AB}(T,{T}_{0})={E}_{AC}(T,{T}_{0})+{E}_{BC}(T,{T}_{0})\)

这里导体C称为标准电极。在实际应用中，一般都选择纯铂为标准电板，这是因为金属铂易于提纯，而且物理化学性能稳定，熔点较高。只要知道某些金属导体与标准电板相配的热电势，就可以根据式(5.13)求得任何两种导体所配成热电偶的热电势。利用这一定律可以简化热电偶的选配工作。

5.2.3热电偶的材料、种类及结构

1.对热电偶材料的要求

根据以上分析，似乎任意两种不同的导体或半导体都可作为热电极而组成热电偶。但是作为实用的测温元件，为了保证在应用中具有足够的精度和可靠性，对热电极材料有如下一些具体要求。

热电偶的热电势和温度之间的关系称为热电特性，对热电特性的要求：①在测温范围内它的热电特性应当是稳定的，不随时间变化；②热电势和温度之间应是简单的单值函数关系，并尽可能呈线性；③温度变化时，热电势变化应足够大，即灵敏度要高。④复制性要好：用同样成分的材料制成的每只热电偶，其热电特性一致称为复制性好。这样便于大量生产和热电偶的互换。

为了保证上述热电特性的各项要求，热电极材料要具有足够的物理化学稳定性，不易氧化或腐蚀。电阻温度系数要小，导电率要高。

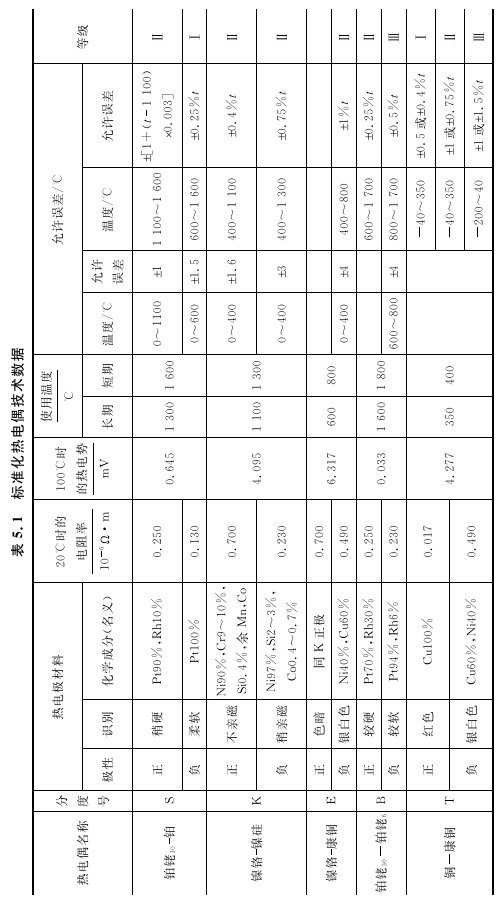
实际上没有一种材料能同时满足上述全部要求，在应用中只能根据具体的使用情况选用不同的材料，以满足各种不同测温条件的要求。目前能配制成的热电偶达百种以上，但常用的为数并不多。这些常用热电偶性能优良稳定，被列入工业标准，故称为标准化热电偶。标准化热电偶是定型产品，成批生产。同一型号的标准化热电偶互换性好，有统一的分度表，并有与其配套的显示仪表，使用很方便。标准化热电偶的技术数据见表5.1。

2.热电偶的种类

热电偶的种类很多，按热电极的材料可分为难熔金属热电偶(如钨铼；-钨铼20等),贵重金

属热电偶(如铂铑3。-铂铑；等),廉价金属热电偶(如镍铬-镍硅等),非金属热电偶(如石墨-碳化硅等)。按使用温度范围可分为高温热电偶(如钨铼₅-钨铢20、铂铑30-铂铑6等),中温热电偶(如镍铬-镍硅等),低温热电偶(如铜-康铜等)。按结构分有普通热电偶、铠装热电偶、簿膜热电偶等。按用途可分为标准热电偶和工业热电偶(如表面热电偶、快速热电偶、多点式热电偶等)。按工业标准化可分为标准化热电偶和非标准化热电偶。非标准化热电偶多用于高温及超高温的测量，表5.2列举了几种铂族和难熔金属所组成的非标准热电偶及其适用的测温上限。

表5.2非标准热电偶

3.常用热电偶

(1)铂铑10-铂热电偶。铂铑10合金和纯铂分别为热电偶的两个正、负热电极。铂铑10合金中铂占90%,铑占10%。长时间测温范围在0～1300℃之间，在良好的使用环境下可短时测量到1600℃。这种热电偶的优点是容易得到比较纯的铂和铂铑合金，所以测量精度高，便于复制；不易氧化和具有较好的化学稳定性。因此，常用于精密测量和作为标准热电偶。其缺点是热电势较小，平均灵敏度为0.009mV·℃-¹左右，而且热电特性是非线性的；铂、铑等属于贵重金属，价格昂贵，所以一般使用的铂铑10-铂热电偶的热电极直径较细，为0.5mm;在还原性气体(H₂和CO等)、金属蒸气和SiO₂中会遭损坏，在这种情况下热电偶需要装在保护管中，与有害物质隔离。

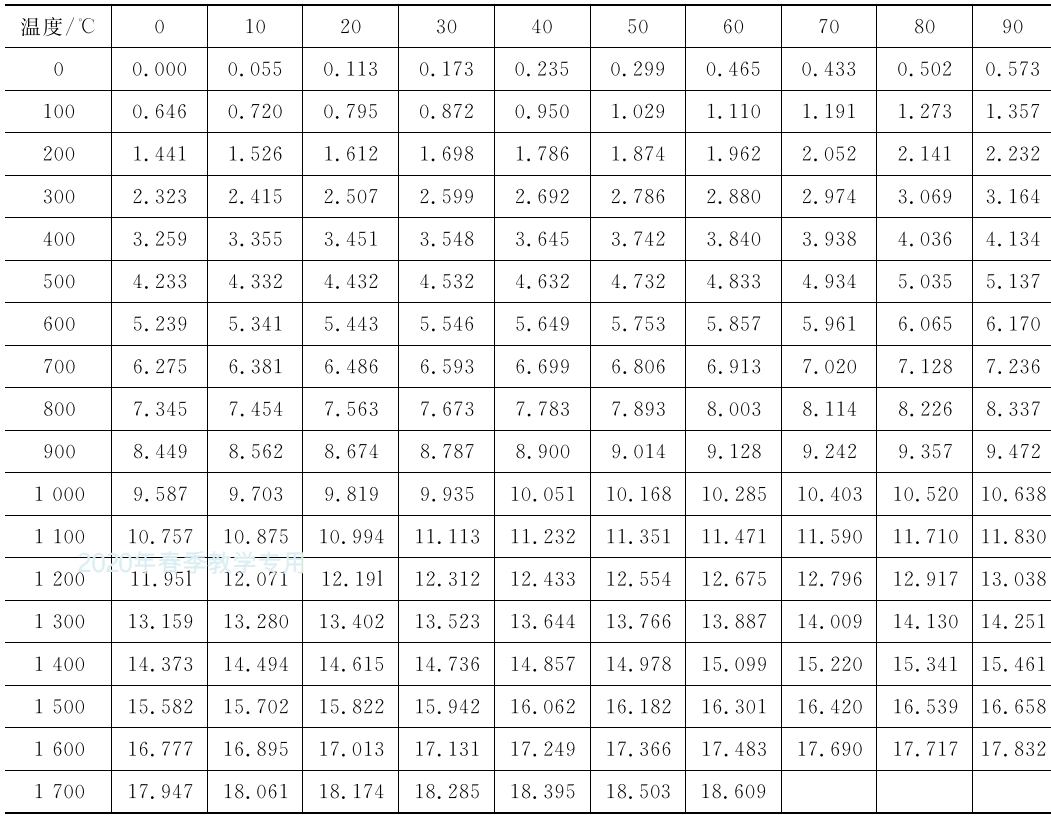
铂铑10-铂热电偶的分度号为S,其分度表见表5.3。本表为粗略的分度表，如需精细的分度表，请查相关手册。

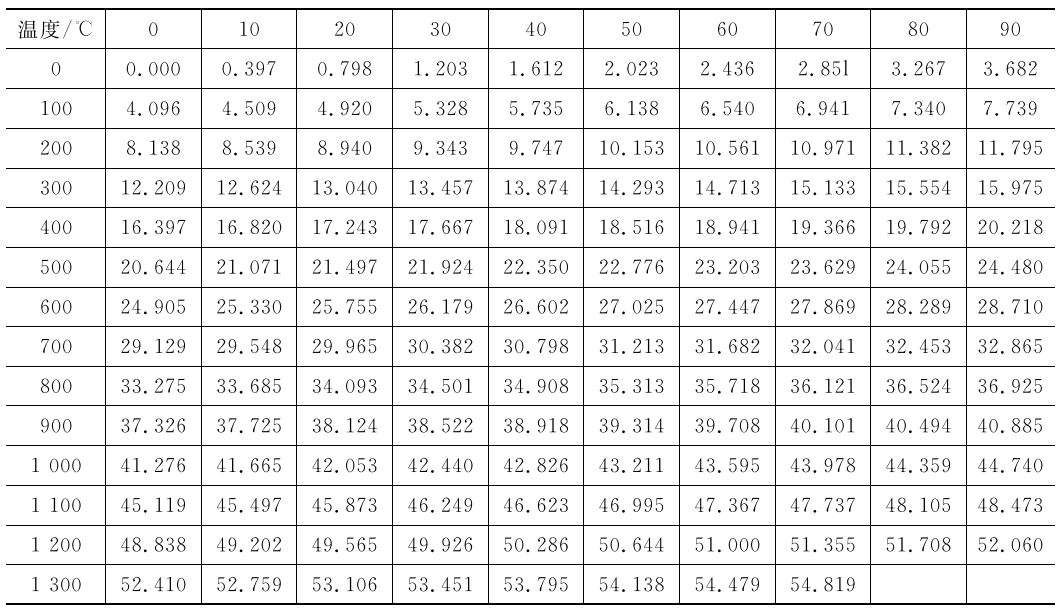
(2)镍铬-镍硅(镍铝)热电偶。这种热电偶的正极为镍铬合金，负极为镍硅合金，其成分见表5.1。因热电极材料中含有大量的镍，所以在高温下抗氧化和抗腐蚀的能力都很强，化学稳定性好。这种热电偶的灵敏度较高(平均灵敏度约为0.04mV·C-¹,约为铂铑10-铂热电偶的4倍左右，热电特性近于线性关系。在还原性气体和含SO₂,H₂S等气体中易被侵蚀，长时间使用温度为1100℃,短期可达1300℃。镍铬镍硅热电偶的分度号为K。其粗略的分度表见表5.4。

表5.3铂铑10-铂热电偶分度表(分度号为S,冷端温度为0℃)

表5.4镍铬-镍硅热电偶分度表(分度号为K,冷端温度为0℃)

(3)铂铑₃₀-铂铑；热电偶。这种热电偶正极的铂铑合金中含铑30%,负极中铑占6%,分度号为B,其测温范围为300～1600℃,短期可达1800℃。它的特点是性能稳定，测量精度高，适用于氧化性和中性介质，在还原性气体中易被侵蚀，灵敏度不高，价格贵。

(4)铜-康铜热电偶。它是一种贱金属热电偶，常用热电偶丝直径为0.2～1.6mm。适用于-200～400℃范围内测温。测量精度高、稳定性好、低温时灵敏度高、价格低廉，其分度号为T,其分度表可查阅相关手册。

(5)镍铬-康铜热电偶。镍铬-康铜热电偶也属于贱金属热电偶，工业用热电偶丝直径一般

为0.5～3mm。实验室用时可根据测量对象的要求采用更细的直径。在常用的几种热电偶中以镍铬一康铜热电偶的灵敏度最高，价格最为便宜，但其抗氧化及抗硫化物介质的能力较差，适于在中性或还原性气氛中使用。它的分度号为E,其分度表可查阅相关手册。

随着现代科学技术的发展，大量的非标准化热电偶也得到迅速发展以满足某些特殊测温要求。例如钨铼₅-钨铼₂₀可以测到2400～2800℃高温，在2000℃时的热电势接近30mV,精度达被测温度的1%,但它在高温下易氧化，只能用于真空和惰性气氛中。铱铑₄₀-铱热电偶可在氧化气氛中测到2000℃高温的热电偶，因此成为宇航火箭技术中的重要测温工具，在2000℃时的热电势为10.753mV。镍铬-金铁是一种较为理想的低温热电偶，可在2～273K范围内使用，热电势率为13～22μV·℃-¹。世界各国使用的热电偶有40～50种，可查阅有关专著。

4.热电偶的结构

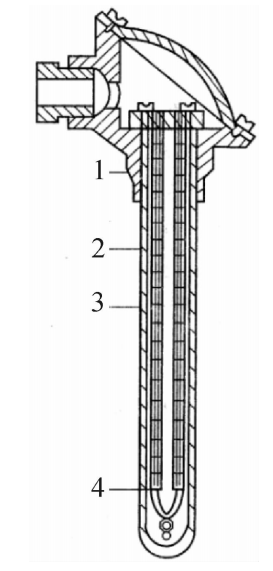
(1)普通热电偶。如图5.5所示是一支典型工业用热电偶结构图。它由热电极、绝缘套管、保护套管以及引线盒等组成。其绝缘套管大多为氧化铝或工业陶瓷管。保护套管则根据测温条件来确定，测量1000℃以下的温度一般用金属套管，测1000℃以上的温度则多用工业陶瓷甚至氧化铝保护套管。

图5.5普通热电偶

1一接线盒；2一保护套管；3一绝缘套管；4一热电偶丝

(2)铠装式热电偶。由于某些实验研究的需要，要求热电偶小型化和灵活，即具有惯性小、性能稳定、结构紧凑、牢固、抗震、可挠等特点。铠装热电偶能较好地满足这些要求。它的结构

形式如图5.6所示。由热电极、耐高温的金属氧化物粉末(如Al₂O₃)、不锈钢套管三者一起经拉细而组成一体，外直径从0.25～12mm不等。其长度则可根据使用需要自由截取。

图5.6铠装热电偶结构

(a)碰底型；(b)不碰底型；(c)露头型；(d)帽型1一金属套管；2一绝缘材料；3一热电极

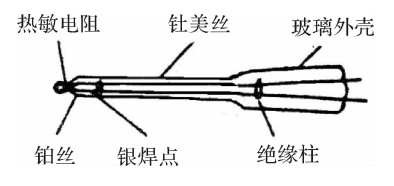
(3)薄膜式热电偶。采用真空蒸镀或化学涂层等制造工艺将两种热电极材料蒸镀到绝缘基板上，形成薄膜状热电偶，其热端接点极薄，约0.01～0.1μm。它适于壁面温度的快速测量，基板由云母或浸渍酚醛塑料片等材料做成，使用时用黏合剂将基片黏结在被测物体表面上，反应时间约为数毫秒。典型的薄膜热电偶形状如图5.7所示。基板尺寸为60mm×6mm×0.2mm。

图5.7薄膜热电偶

1一热电极；2一热接点；3一绝缘基板；4一引出线

5.2.4热电偶的冷端处理

式(5.10)是热电偶测温原理的基本方程式，它说明对于一定的热电偶材料A和B,热电势只与两个连接点的温度t和t₀有关。只有当参比端温度t₀稳定不变且已知时，才能得到热电势和被测温度t的单值函数关系。此外，前面已说明，实际使用的热电偶分度表中热电势和温度的对应值是以t₀=0℃为基础的，但在实际测温中参比端温度t₀往往不稳定，也不一定恰好等于0℃,这就需要对热电偶的参比端温度进行处理。

1.冰点法

这是一种精度最高的处理办法，可以使t₀稳定地维持在0℃。其实施办法是将纯净的白雪或碎冰和纯水的混合物放在保温瓶中，再把细玻璃试管插入冰水混合物中，在试管底部注入适量的油类或水银，热电偶的参比端就插到试管底部，实现了t₀=0℃的要求，如图5.8所示。

图5.8冰点槽

1一冰水混合物；2一保温瓶；3一油类或水银；4-蒸馏水；5一试管；6一盖；7一铜导线；8—热电势测量仪器

2.热电势修正法

在没有条件实现冰点法时，可以设法把参比端置于已知的恒温条件，得到稳定的t₀,根据

中间温度定律式(5.12),有

\(E(t,0)=E(t,{t}_{0})+E({t}_{0},0) \)    (5.14)

式中E(t₀,0)是根据参比端所处的已知稳定温度t₀去查热电偶分度表得到的热电势。然后根据所测得的热电势E(t, t₀)和查到的E(t₀,0)二者之和再去查热电偶分度表，即可得到被测量的实际温度t

3.冷端补偿器法

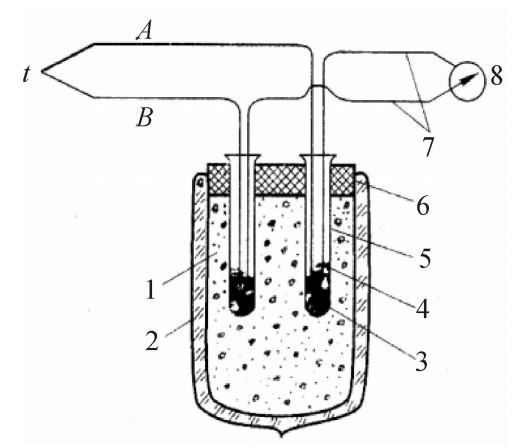
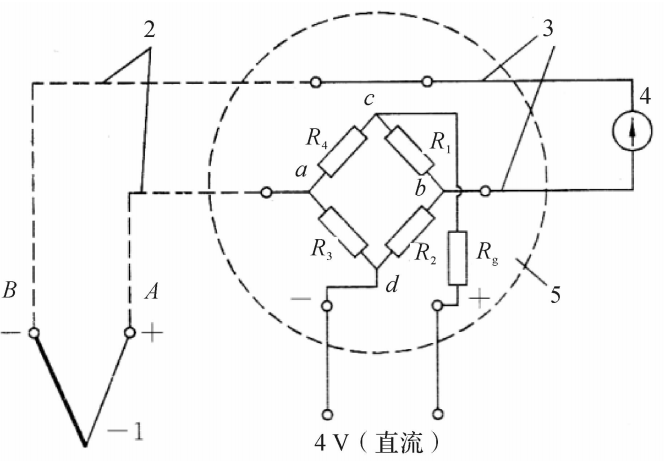
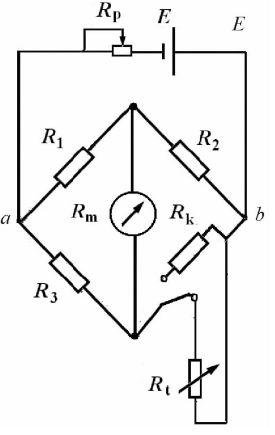
很多工业生产过程既没有长期保持0℃的条件，也没有长期维持参比端恒温的条件，热电偶的参比端温度t₀往往是随时间和所处的环境而变化的。在此情况下可以采用冷端补偿器来自动补偿t₀的变化。如图5.9所示为热电偶回路接入补偿器的示意图。

图5.9冷端补偿器接入热电偶回路1一热电偶；2一补偿导线；3—铜导线；4一指示仪表；5一冷端补偿器

冷端补偿器是一个不平衡电桥，桥臂R₁=R₂=R₃=1Ω,采用锰铜丝无感绕制，其电阻温度系数趋于零。桥臂R₄用铜丝无感绕制，其电阻温度系数约为4.3×10-³/℃,当温度为0℃时R₄=1Ω。Rg为限流电阻，配用不同分度号热电偶时R作为调整补偿器供电电流之用。桥路供电电压为直流电，大小为4V。

当热电偶参比端和补偿器的温度t₀=0℃时，补偿器桥路四臂电阻R₁～R4均为1Q,电桥处于平衡状态，桥路输出端电压U_ba=0,指示仪表所测得的总电势为

\(E=E(t,{t}_{0})+{U}_{ba}=E(t,0)\)        (5.15)

当t₀随环境温度增高时，R₄增大，则a点电位降低，使U_ba增加。同时由于t₀增高，E(t,t₀)将减小。通过合理设计计算桥路的限流电阻R_g使U_ba的增加值恰等于[E(t,0)-E(t,t₀)],那么指示仪表所测得的总电势将不随t₀而变，有

\(E=E(t,{t}_{0})+{U}_{ba}=E(t,{t}_{0})+[ E(t,0)- E(t,{t}_{0})]=E(t,0)\)      (5.16)

式(5.16)说明当热电偶参比端温度t₀发生变化时，由于冷端补偿器的接入，使仪表所指示的总电势仍保持为E(t,0),相当于热电偶参比端自动处于0℃。由于电桥输出电压U_ba.随温度变化的特性为U_ba=Φ(t),与热电偶的热电特性E=f(t)并不完全一致，这就使得具有冷端补偿器的热电偶回路的热电势在任一参比温度下都得到完全补偿是困难的。实际上只有在平衡点温度和计算点温度下可以得到完全补偿。所谓平衡点温度，即上面所提及的R₁～R₄均相等且为1Ω时的温度点；所谓计算点温度是指在设计计算电桥时选定的温度点，在这一温度点上，桥路的输出端电压恰好补偿了该型号热电偶参比端温度偏离平衡点温度而产生的热电势变化量。除了平衡点和计算点温度外，在其他各参比端温度值时只能得到近似的补偿。因此采用冷端补偿器作为参比端温度的处理方法会带来一定的附加误差。不过这个误差是限制在一般工业温度测量所允许的误差范围之内的。我国工业用的冷端补偿器有两种参数：一种是平衡点温度定为0℃;另一种是定为20℃。它们的计算点温度均为40℃。

4.补偿导线法

生产过程用的热电偶一般直径和长度一定，结构固定。而在生产现场又往往需要把热电偶的参比端移到离被测介质较远且温度比较稳定的场合，以免参比端温度受到被测介质的热干扰。于是采用补偿导线代替部分热电偶丝作为热电偶的延长。补偿导线的热电特性在0～100℃范围内应与所取代的热电偶丝的热电特性基本一致，且电阻率低，价格也必须比主热电偶丝便宜。对于贵金属热电偶而言这一点显得更为重要。使用补偿导线法的连接方式如图5.10所示。

图5.10热电偶与补偿导线连接图

由图5.10可知，由于引入补偿导线A’和B′之后，参比温度由t₀变为t₀′,根据连接导线定律，回路总热电势为

\(E={E}_{AB}(t,{t}_{0})+{E}_{A’B’}({t}_{0},{t’}_{0})\)

已经规定补偿导线在0～100℃范围内，有

\({E}_{AB}(t,{t’}_{0})={E}_{A’B’}({t}_{0},{t’}_{0})\)

那么

\(E={E}_{AB}(t,{t’}_{0})\)  (5.17)

这相当于把热电偶的参比端迁移到温度为t’₀处，然后可再接入冷端补偿器或其他所需仪器。表5.5给出了几种常用热电偶的补偿导线特性。

表5.5常用的热电偶补偿导线技术数据

5.2.5热电偶测温系统的误差分析

如果由热电偶、补偿导线、冷端补偿器、动圈式温度指示仪等组成如图5.11所示的测温系统，那么该测量系统会有多大的测量误差呢?

图5.11热电偶与动圈指温仪系统图1一热电偶；2一补偿导线；3一冷端补偿器；4一动圈式温度指示仪

1.分度误差△₁

任何一种热电偶的通用分度表都是统计结果，某一具体热电偶的数据与通用分度表会存在一定偏差△₁参看表5.1。例如铂铑一铂热电偶在600℃以上使用时允许偏差为±0.25%t;镍铬-镍硅热电偶为±0.75%t。

2.补偿导线误差△₂

多数热电偶的补偿导线材料并非热电偶本体材料，因此存在误差。对于铂铑-铂热电偶在0～100℃补偿范围内，误差为±0.023mV;对于镍铬-镍硅热电偶为±0.15mV;镍铬一康铜热电偶为±0.30mV。

3.冷端补偿器误差△₃

除平衡点和计算点两个温度值得以完全补偿外，冷端补偿器在其他各温度值均不能完全得到补偿，其偏差如下：铂铑-铂热电偶为±0.04mV;镍铬-镍硅热电偶为±0.16mV;镍铬一康铜热电偶为±0.18mV。

4.显示仪表误差△₄

该误差由仪表的精度等级所决定。对XCZ-101动圈式温度指示仪为满量程的士1%。例：若采用镍铬-镍硅热电偶按图5.11组成测温系统。XCZ-101的量程为0～1000℃,被测温度在显示仪表上的示值为800℃。根据以上分析，由各项误差组成的总误差为

Δ=±\(\sqrt{{6}^{2}+{3.7}^{2}+{3.9}^{2}+{10}^{2}}\)=±13℃

5.2.6热电偶在发动机壁温测量中的应用

由于热电偶有较宽的测温范围和较小的测量端，具有能测量“点”的温度和较高的测温准确度等特点，在发动机试验中，可用来测量零部件的表面温度。下面介绍利用热电偶进行发动机壁温测量时，有关热电偶的选用、制作及安装方法。

1.热电偶的选用

固体火箭发动机壁面温度的变化率，相对于发动机的其他工作参数要缓慢一些。考虑到热电偶应有较好的动态性能、尽量减小导热误差、又照顾到制作方便并具有一定的强度，一般

可选用直径0.1～0.3mm的热电偶丝。热电偶材料的选择主要根据被测温度的变化范围，镍铬-镍硅热电偶的使用温度较高而且能产生较大的热电势，是常用热电偶之一。其他标准热电偶材料的选用可见表5.1。

2.热电偶的安装

用热电偶测量壁面温度时，由于热电偶和外界有热交换，通过热电偶导线导出热量，因而改变了被测点的温度场。热电偶的指示温度与真实壁温之间的偏差称为热电偶的导热误差。显然，导热误差不仅与热电偶导线的散热能力有关，与被测表面的导热能力有关，而且还与热电偶的安装方式有关。

安装方式一种是壁面敷设法。这种方式比较简单。原则上讲，只要热节点与壁面保持良好的接触，即可进行测温。如采用压紧、黏接、焊接等方法，其中以焊接的接触质量为最好。常采用的焊接方法有：乙炔焊、接触焊、电容储能焊等。热电偶与壁面可采用不同的接触形式，如

图5.12(a)所示为点接触，热量集中从热结点附近的壁面传给热电偶而散失到周围的空气中，因此热结点处的壁温低于它周围的温度。如图5.12(b)所示为片接触方式，先将热电偶的测量端与导热性能良好的集热片(如铜片)焊在一起，然后再与壁面接触，散热量由集热片所接触的那块壁面共同分摊，温度场的改变情况将有所减小。如图5.12(c)所示为等温线接触方式，热电偶的导线从热节点后贴壁面等温区敷设—段距离，然后再离开壁面引出。这样，热电偶导线散失的热量主要是从引出处的壁面传出的，而在热结点处壁面所传出的热量相应地减少，可以有效地减小导热误差。此外，选取直径小、导热系数小的热电偶丝对减小导热误差也是有利的。

图5.12接触形式示意图

(a)点接触；(b)片接触；(c)等温线接触

对于有一定强度余量的发动机，测量壁温时可采用壁面埋设法。即在被测的壁面上开一条细长槽，将热电偶的测量端放在槽的端头，使其与壁接触良好。绝缘的热电偶导线沿槽敷设，然后自壁面引出，沿槽敷设的热电偶用填充物(如耐热水泥、钎焊料等)固定。显然，这种敷设方法产生的导热误差更小。

导热误差通常用安装系数Z来表示。若被测壁面的温度为T_w,周围介质温度为T_g,如图5.12(a)所示。热电偶的指示值为T_j。实际测量误差(T_w-T_j)与最大可能出现的误差(T_w-T_g)的比值Z称为安装系数，即

\(Z=\frac{{T}_{w}-{T}_{j}}{{T}_{w}-{T}_{g}}\)   (5.18)

Z值所给出的误差概念是相对于可能出现的最大误差来说的。Z值愈小，热电偶的测温准确度愈高。对于一定的安装方式，Z值可用理论计算或由实验确定。因计算时往往要作一些简化的假设，难以获得正确的结果，所以通常是通过实验确定。

为了便于热电偶与被测表面连接与折卸，热电偶还可以做成可装卸的形式，如图5.13所示为几种可装卸型的表面热电偶。如图5.13(a)所示为垫圈式，将热电偶测量端牢固地焊在一个垫圈上，测温时用螺钉将其固定在被测位置。图5.13(b)为螺栓式，热电偶测量端装在螺栓内，将其旋在被测位置的螺孔内。图5.13(c)是管夹式，热电偶牢固地焊在一个管夹上，适于测量小直径发动机的壁面温度。

图5.13可装卸型表面热电偶

(a)垫圈式；(b)螺栓式；(c)管夹式

5.3电阻温度计

利用导体或半导体的电阻随温度变化的特性而制成的测温计称为电阻温度计。常用于测量-200～500℃范围内的温度。采用特殊的电阻感温元件，可以把低温范围下延到绝对零度附近(如锗电阻温度计可以测量到15K的温度),高温范围可以扩大到1000℃左右。500℃以下，电阻温度计的输出信号比热电偶大得多，即灵敏度高；此外，用导体制作的电阻温度计，其准确度很高。在固体火箭发动机试验中，通常用电阻温度计测量发动机保温室内的温度，或用于保温室的温度控制系统中。

5.3.1电阻温度计的测温原理及结构

实验证明，大多数金属当温度升高1℃时，其电阻值约增加0.4～0.6%,称它具有正的电阻温度系数。而大多数半导体的电阻值则随着每升高1℃而减小3～6%,称它具有负的电阻温度系数。电阻温度计就是利用电阻随温度变化的特性制成的。作为制造电阻温度计的材料，要求它应能承受一定的温度，具有尽可能大而稳定的电阻温度系数和尽可能大的电阻系数。

1.金属电阻温度计

高电阻合金虽有较大的电阻系数，但电阻温度系数不大而不被采用。纯金属的电阻温度系数比合金大得多，而且纯金属也易于提纯和复制，所以实际上都采用纯金属。通常用纯金属铜、镍和铂作为制作电阻温度计的材料。国产电阻温度计所用的材料有铜和铂两种。

铂电阻具有测温精度高、线性和化学稳定性良好等特点。在“国际实用温标——ITS-90”中规定铂电阻温度计为13.8033K～273.16K范围内的基准器。铂的电阻值与温度的关系由以下两式表示。

(1)在0～630.755℃范围内，电阻值

R,=R₀(1+At+Bt²)

(2)在一200～0℃范围内，电阻值

R_t=R₀[1+At+Bt²+C(t-100)t³]

式中

A,B,C——常数；

R₀——在0℃时的电阻值，单位：Ω。

铂的纯度通常以R₁₀₀/R₀表示，R₁₀₀是100℃时铂电阻的电阻值。基准铂电阻R₁₀₀/R₀不小

于1.3925;工业铂电阻R₁₀₀/R₀不小于1.391。我国工业铂电阻温度计R₀有两种：50Ω和100Ω。因此，相应地就有两种R₁～t的关系表，称为分度表。符号Pt50和Pt100称为分度号。指示温度的显示仪表就是根据分度表来刻度的。标准的实验室用铂电阻R₀=10Ω或30Ω。

铜电阻的分度号有Cu50(R₀=50.00Ω)和Cu100(R₀=100.00Ω)两种，可在一50～+150℃温度范围内使用，其阻值与温度呈线性关系为

R,=R₀(1+αt)

式中

α——电阻温度系数。

铜的电阻温度系数比铂大，而且容易加工和提纯，价格便宣。主要缺点是当温度超过100℃后容易氧化。此外，铜的电阻率小(约为铂电阻率的17%),所以与同阻值的铂热电阻相比时，铜热电阻体积大。

将直径为0.03～0.2mm的铜丝或铂丝按照一定的顺序绕在一定形状(如管状，平板形、十字形等)的耐热性能好，膨胀系数小的绝缘骨架(骨架材料如：云母、陶瓷，塑料等)上。外面罩上钢(或黄铜、玻璃，石英等材料)保护套，接出引线便构成电阻温度计。如图5.14所示为未加保护套的铜电阻温度计，称为铜电阻体。从这样的结构可以看出，金属电阻温度计只适用于测量变化较缓慢的平均温度。

图5.14铜电阻体结构图

图5.15半导体热敏电阻

2.半导体温度计

半导体温度计的感温元件——热敏电阻是利用半导体的电阻随温度增高而减小的特性制成的，它具有很高的灵敏度。其测温范围一般为一100～300℃。热敏电阻的温度-电阻关系可用公式表示为

R(T)=R(T₀)e^k           (5.19)

\(k=\beta\left(\frac{1}{T}+\frac{1}{{T}_{0}}\right)\)     (5.20)

式中

R(T),R(T₀)——温度为T和T₀时的电阻值，单位：Ω;

β——与热敏电阻材料和制造工艺有关的常数。

由式(5.19)可以看出R(T)与温度之间呈非线性关系。

热敏电阻是用各种金属的氧化物(如镁、镍、锰等氧化物)按一定比例混合后，挤压成型。经过烧结成致密的陶瓷体状。可以根据需要做成各种形状，如球形、杆形、垫圈形等。具有较好的化学稳定性。如图5.15所示为与59型半导体温度计配套用的热敏电阻。由于体积小、热容量小，对温度的响应很快(时间常数t≤0.5s),可用于测量物体表面的点温度。

热敏电阻的不足之处是复制性差，即对同一型号的热敏电阻，其电阻温度特性分散性较大；易老化，即电阻值随时间略有变化；其电阻值与温度之间的非线性关系也给热敏电阻的使用造成了困难。

5.3.2电阻温度计的测量线路

用电阻温度计测量温度时，因电阻与温度之间有一定的函数关系，确定了电阻的数值就可以相应地得到温度的数值。测量电阻的方法较多，如电桥法、电位计法和比率计法等。现在我们介绍较为通用的电桥法。

1.不平衡电桥

图5.16所示为不平衡电桥测量电阻的原理图。电桥的三个桥臂为已知固定电阻R₁、R₂和R₃,且均等于电阻温度计R_t在0℃时的电阻值。电源E通过限流电阻R_t供给电桥a,b两顶点一固定电压U。当接在第四个桥臂上的电阻温度计的电阻R_t变化时，在指示仪表R_M中便有电流流过，R_t变化愈大，流过指示仪表的电流也愈大，即电桥愈不平衡。通过指示仪表的电流可按下式计算，有

\({I}_{M}=\frac{E({R}_{1}{R}_{t}-{R}_{2}{R}_{3})}{{R}_{M}({R}_{1}+{R}_{3})({R}_{2}+{R}_{t})+{R}_{1}{R}_{3}(({R}_{2}+{R}_{t})+{R}_{2}{R}_{t}({R}_{1}+{R}_{3})}\)(5.21)

当R₁,R₂,R₃和R_M为定值时，上式可写作

I_M=f(U,R_t)(5.22)

由式(5.22)可以看出，通过指示仪表的电流I_M是电压U和电阻R_t的函数。要使电流I_M只是电阻R_t的函数，则必须在固定的电压U下进行测量。为此，电桥中另有一个检查电阻Rk,把转换开关S扳向Rk,调节电阻Rp将电流I_M调整到规定的数值上，这时电桥的输入电压U即为规定的数值。此时，I_M和R_t之间已成为单值函数关系。知道I_M之后，被测温度R_t的值也就被确定了。

图5.16不平衡电桥原理图

2.平衡电桥

用平衡电桥进行测量的原理如图5.17所示，R₁=R₂为已知电阻，R₃是可变电阻，可由其刻度R读出电阻值，R_t是电阻温度计的电阻值，R₁为连接导线的电阻，G为检流计。测温时R_t发生变化可以通过调节R₃使检流计G中没有电流通过，此时电桥保持平衡。平衡时a,b两点的电位相等，即R₁R₃=R₂(R_t+R₁)

可得电阻温度计的电阻值为

\({R}_{t}=\frac{{R}_{1}}{{R}_{2}{R}_{3}}-{R}_{1}\)

图5.17平衡电桥原理图

对于低阻值的金属电阻温度计，为了消除导线电阻R_t随环境温度变化而引起的误差，在电阻R₃的桥臂一端接上一根与连接导线完全相同的导线，其电阻R₁’=R₁,见图5.18。用另一根导线将电阻温度计直接接在电源上，把三根导线扎在一起以补偿温度的影响。三根导线的连接方法用于不平衡电桥时，也可以部分地消除连接导线因环境温度变化所引起的误差。

图5.18平衡电桥的三根线接法原理图

对于平衡电桥和不平衡电桥都应防止温度计电流过大，在线路中均设有限流电阻Rp,否则电阻R,因电流大而自身发热会引入误差，一般希望电流小于140mA。

如果将图5.18中a和b两点的电位经过电子放大器进行电压放大和功率放大，然后接入一可逆电动机，电动机通过传动系统自动调节电阻R₃,使电桥始终保持平衡，这样便构成了工业用的自动平衡电桥。它能够用来自动、连续地指示记录，而且准确度也比较高。

5.4接触式测温技术及误差分析

根据测温对象的性质，接触式测温一般包括固体测温和流体测温，前文介绍的发动机壁面测温就属于固体测温，以下主要介绍流体测温技术。

5.4.1流体温度测量、导热误差分析

在实验研究和工业生产过程中经常采用接触式测温元件测量管道或容器内流体介质温度。在流体管道或容器保温较好的情况下，管壁温度与流体温度接近，流体将以对流换热方式传热给测温元件，测温元件再通过导热方式沿套管向外部环境导热。如图5.19所示为分析管道内流体温度测量问题的简化模型。

图5.19测量管道内流体温度示意图

根据传热学中沿细长杆导热的原理，测温元件传热误差可用公式表示为

(5.23)

式中

t,——敏感元件温度，单位：℃;

t——流体介质温度，单位：℃;

t₀——测温元件保护套管外露部分周围介质温度，单位：℃;

l₁,l₂——保护套管插入管内和外露部分的长度，单位：mm;

α₁,α₂——管道内、外介质与测温元件保护套管之间的对流换热系数；

λ₁λ₂——管道内、外部分测温元件套管的导热系数，对于均质套管λ₁=λ₂;

C₁,C₂——套管插入和外露部分的外圆周长，单位：mm;

A₁,A₂——套管插入和外露部分的截面积，单位：mm²。

显然，这项误差△t=t_r-t_f主要考虑温度计的枢轴导热，忽略了其他因素影响。为使测温误差减小，提高测量精度可从以下两方面进行。

1.温度计的安装方式

(1)使|t_o—t_f|尽可能地减小。具体办法是把管道和套管外露部分一起进行保温，使套管外露部分温度接近管道温度。

(2)增大l₁,减少l₂,即增大温度计的插入深度、减小外露部分。具体实施办法是利用管道的弯头或斜向插入。若管道过细，不便于斜插或无弯头可利用，那么管道要局部加粗然后斜插。

(3)增加α₁。通常使温度计迎着气流方向插入，敏感元件头部置于管道中心线上，以得到最大的对流换热系数α₁。

2.温度传感器材料和结构

(1)减小温度计套管的导热系数λ,即不宜采用高导热系数的材料作套管。但λ过低将会增加测温动态误差。

(2)增加套管的外圆周长和截面积之比C/A。

\(C/A=\frac{4}{{d}_{1}\left[1-{{d}_{2}/{d}_{1}}^{2}\right]}\)

式中

d₁,d₂——套管外直径和内直径，单位：mm。

因此在强度允许条件下可采用薄壁或小直径的套管。

例：如图5.20所示，压力为3MPa,流速30m·s-¹,温度t_r=386℃的蒸汽流过管道，采用5种不同的安装方法进行测温，各温度计的示值如下。

图5.20温度计安装方式的误差比较

1)采用铂电阻温度计，安装在管道拐弯处，有足够插入深度，温度计迎着气流，管道及套管外露部分保温，此情况下温度计示值为t_r₁=386℃。

2)采用玻璃管水银温度计，垂直气流方向插入，温包处于管道中心线位置，外露部分短，且套管的外露部分保温，此情况下温度计示值为t_r2=385℃。

3)除温度计套管直径更大，管壁更厚外，其他各条件同2),示值t_r3=384℃。

4)与2)基本上一样，只是插入深度较浅，温度计示值t_r₄=371℃。

5)采用铂电阻温度计，垂直于气流方向插入管道中心，外露部分较长且管道及外露部分均未保温，温度计示值t_r5=341℃,其误差达-45℃。

5.4.2高速气流温度测量、速度误差分析

当气流速度的马赫数Ma>0.2～0.3时，速度对于气体温度测量的影响就必须加以考虑了。在高速气流中气体分子同时进行无规则的热运动和有规则的定向运动。这种分子的无规则运动表现为分子运动的平均动能，用“静温”来度量，记作T₀;而定向有规则的运动则用“动温”来度量，记作T_v。T₀和T_v之和称为“总温”,又称为“滞止温度”,记作T^*,则

\({T}^{*}={T}_{0}+{T}_{v}={T}_{0}+{v}^{2}/2{C}_{p}\)         (5.24)

式中

v——气流速度，单位：m·s-¹;

Cp——气体定压比热容，单位：J·(kg·K)-¹。

由式(5.24)可见，以速度v运动的气体，当其滞止后动能会无损失的全部转换成内能，这时气体的静温即是总温。一般情况下，人们需要知道气体的静温T₀,因为气体的物理性质取决于该温度。但如果直接测量静温T。就需使测温传感器随同流体以相同速度流动，这显然是不实际的。

实际上处于高速气流中固定安装的测温传感器，如热电偶或热电阻，对高速气流只有一定的滞止作用，并非完全绝热滞止。因此传感器既不能直接指示静温，也不能简单的测量总温。传感器实际的指示值被称为有效温度，记作T_r。如果不考虑测温元件对外的散热损失，用(T_r-T₀)表示气流被传感器滞止恢复为内能的部分。定义

\(r=\frac{{T}_{r}-{T}_{0}}{{T}^{*}-{T}_{0}}\)         (5.25)

式中

r——恢复系数。

由式(5.24)和式(5.25)可得

\({T}^{*}-{T}_{r}=(1-r){v}^{2}/2{C}_{p}\)      (5.26)

由热力学知道理想气体的定压比热容c_p、定容比热容c_v、气体常数R、比热比k和声速a。有关系式为

c_p—c_v=R，c_p/c_v=k，a_o=\(\sqrt{{\gamma}RT}\)。

于是式(5.24)和式(5.26)分别为

\({T}^{*}={T}_{0}\left(1+\frac{k-1}{2}{M}_{a}^{2}\right)\)            (5,27)

\({T}^{*}-{T}_{r}=(1-r){T}^{*} \left(\frac{k-1}{2}{M}_{a}^{2}\right)/\left(1+\frac{k-1}{2}{M}_{a}^{2}\right)\)    (5.28)

由式(5.27)可见，对于空气，当马赫数Ma<0.22时，T。和T*之偏差不超过1%。如果温度传感器的导热和辐射误差很小，允许忽略，则定义高速气流测温传感器的示值T_r和总温T*之间的差值为速度误差△T_s,根据式(5.28),有

ΔTs=\((r-1) {T}^{*} \left(\frac{k-1}{2}{M}_{a}^{2}\right)/ \left(1+\frac{k-1}{2}{M}_{a}^{2}\right)\)  (5.29)

由式(5.29)可见，传感器的恢复系数越低，马赫数Ma越高，速度误差就越大。实验表明，恢复系数不仅与被测气体性质和Ma数有关，还与测温传感器的结构和安装方式有关。对于裸露热电偶传感器，r的数据在0.6～0.9范围内，具体值取决于热电偶热结点的形式(如对接、铰接或球形焊点)和方向(热偶丝平行于气流或垂直于气流)。为获得高r值并使r值与气流条件(如气流速度和方向)无关，应专门对传感器进行设计和实验研究，以使其接近理想滞止条件，并要求传感器具有以下特点。

(1)传感器热容低，以求快速响应。

(2)为使导热损失最小，温度传感器引线要足够长。

(3)要求其辐射屏蔽罩具有低导热和低辐射率。

(4)通气孔能使滞止室连续的充满流体，以补充导热和辐射热损失，同时气流又应保持足够小，以使滞止条件基本上得到维持。

(5)在超音速气流条件下钝的形状引起的正冲击波能减少非准直的影响，同时也使边界层温度增加并减少传感器的热损失。

如图5.21所示是实验室用的传感器实例二则。

图5.21测量滞止温度传感器

(a)较低Ma时；(b)较高Ma时

应该指出，恢复系数为1的传感器是很难做到的。因此对每个测温传感器的恢复系数应实验测定。测定工作是在校准风洞中进行的，其装置如图5.22所示。气流在稳压箱中的流速很低，热电偶3测出的温度是总温T*,被测定的热电偶2处于绝热喷管出口的高速气流中，测得有效温度Tr,则热电偶2的恢复系数为

\(r=1-\frac{ {T}^{*}-{T}_{r}}{{T}^{*} \left(\frac{k-1}{2}{M}_{a}^{2}\right)/ \left(1+\frac{k-1}{2}{M}_{a}^{2}\right)}\)    (5.30)

由流体力学知

\(Ma=\sqrt{\frac{2}{k-1}\left[{\left(\frac{{p}^{*}}{p}\right)}^{\frac{k-1}{k}}-1\right]}\)

\(r=1-\frac{{T}^{*}-{T}_{r}}{\left[1-{(\frac{p}{{p}^{*}})}^{\frac{k-1}{k}}\right]{T}^{*}}\)    (5.31)

式(5.31)中p和p*分别为静压和总压。对于亚声速气流喷嘴出口处的静压为大气压力，可由当地大气压力计读取。总压可由总压管4和压力指示仪5测出。

图5.22恢复系数r测定装置

1一稳压箱；2一实验热电偶传感器；3一总温热电偶；4一总压管；5一压力计；6—冰点瓶；7一切换开关；8一电位差计；9—喷管

5.4.3动态测温法

当被测气体温度很高以致超过所使用的热电偶测温上限时，以上各种以热平衡法为基础的测量方法已不实用，有时可采用动态测温法。动态测温法的基本原理是热电偶突然接触高温介质，当热电偶尚未到达使用极限温度时就脱离高温介质。热电偶接触与脱离高温介质可以根据被测对象的特点采用插入和拔出热电偶的机械办法，或者用冷却气体保护热电偶不被加热和停止冷却气体使高温气体流过热电偶测量端的办法。

如果忽略热电偶的导热和辐射误差，所用的热电偶为裸露的，其动态数学模型可用一阶微分方程来描述为

\(T\frac{{dt}_{r}}{d\tau}+{t}_{r}={t}_{g}\)     (5.32)

方程解为

\({t}_{r}={t}_{0}+({t}_{g}-{t}_{r0})(1-{e}^{-\frac{\tau}{T}})\)  (5.33)

式中

T——热电偶时间常数；

τ——时间，单位：s;

t_g——被测气体的温度，单位：℃;

t_r——热电偶随时间变化的示值；

t_r0——热电偶尚未与被测介质接触前的指示值。

根据热电偶接触到高温介质的短时间内记录得到的t_r和τ,求解被测介质的温度t_g是很方便的。但是值得注意的是用动态方法所测量出的温度其误差是相当大的。一方面因为时间常数T并非是一个常数而是温度的函数；另一方面在很多情况下辐射误差不能忽略，因此提出以下的修正方程：

\({t}_{g}={t}_{r}+{T}_{0}(1+a {t}_{r}\frac{{dt}_{r}}{d\tau}+\frac{\varepsilon\sigma}{\alpha}[{({t}_{r}+273)}^{4}-{({t}_{s}+273)}^{4}]\)    (5.34)

式中

T₀——0℃时热电偶的时间常数；

a——热电偶比热容修正常数，

c_p=c_po(1+at);

α——被测气体对热电偶的对流传热系数；

σ——玻耳兹曼常数；

ε——辐射率。

第6章流量测量

6.1流量测量的基本概念

在液体火箭发动机试验中，要了解燃料燃烧过程的好坏，就必须测量输送系统中两种燃料组元的流量比。要确定燃烧室的冷却效果，就必须测定冷却系统中冷却液的流量。在某些特殊试验中，还须测定操纵管路中气体的流量和发动机中吹洗用的流体的流量。总之流量和推力一样，在液体火箭发动机试验中是一个必测的参数。其测量范围可以从每秒数克到每秒一百千克以上。流量的测量根据各种不同的情况可以采用不同的方法。但在选择测量方法和仪表时，必须考虑以下几个基本因素。

(1)被测流体的物理化学性质，例如是液体还是气体、密度、黏度和腐蚀性等。

(2)流量的变化范围(量程)。

(3)测量需要的精度。

(4)流体状态变化的允许度。大多数流量测量仪器的引入会改变流体的状态，有些情况下要求这种改变不能太大，因此需要提出对流体状态改变的允许度。

如果我们只需测量试车时的平均流量，则测量方法很简单，只需将试车前后燃料组元贮箱的重量称出，并记录下试车时间，就能方便地确定。但实际试验时往往需要了解试车中流量的变化，即要测出瞬时流量值，这样不仅能了解燃烧组元流量的快速变化的数值大小，而且能够看出流量相对于其他的被测参数如压力、温度等在相位上的偏移，于是就能较全面地评定发动机的工作品质。

6.1.1流量

流量也称流率，是单位时间内流过管道某截面物质的体积或质量数，一般称前者为体积流量，后者为质量流量。测量物质流量的仪器叫流量计。

在某一段时间内流过管道流体总的数量称为物质的总量，因为它是流量在某一段时间内的积分。总量也可以用质量或体积表示。测量总量的仪表—般叫做计量表，目前习惯上有的仍叫做流量计。

流量和总量的单位由它们的定义可知：它们是体积或质量与时间的导出单位，由于体积、质量和时间应用着不同的单位，因此实用流量单位也就很多。例如：m³·s^-1,m³·h^-1,L·s^-1,L·min^-1,kg·s^-1,kg·h^-1及t·h^-1等。当需要由体积流量换算为质量流量时可以应用下式计算，有

\({q}_{m}=\rho {q}_{v}\)     (6.1)

式中

q_m——质量流量，单位：kg·s^-1;

q_v——体积流量，单位：m³·s^-1;

ρ——介质的密度，单位：kg·m-³。

流量测量中经常用到一个重要的关系式：

q_v=vA      (6.2)

式中

A——管道的截面积，单位：m²;

v——流经该截面流体的平均速度，单位：m·s-¹。由这个公式可以看出，流量的测量可以转换为流体速度的测量。

6.1.2流量测量的方法

流体流动的动力学参数，如流速、动量等都直接与流量有关，因此这些参数造成的各种物理效应均可作为流量测量的物理基础。目前，已投入使用的流量计有100多种，从不同的角度出发流量计有不同的分类方法。但一般可归结为容积法、流速法和质量流量法三种。

1.容积法

利用容积法制成的流量计相当于一个具有标准容积的容器，它连续不断地对流体进行度量，在单位时间内，度量的次数越多，即表示流量越大。这种测量方法受流动状态影响较小，因而适用于测量高黏度、低雷诺数的流体。但不宜于测量高温高压以及脏污介质的流量，其流量测量上限较小。椭圆齿轮流量计、腰轮流量计、刮板流量计等都属于容积式流量计。

2.速度法

由流体的一元流动连续方程可知，截面上的平均流速与体积流量成正比，于是与流速有关的各种物理现象都可用来度量流量。如果再有流体密度的参数，便可得到质量流量。

在速度法流量计中，节流式流量计历史悠久，技术最为成熟，是目前工业生产和科学实验中应用最广泛的一种流量计。此外属于速度式流量计的还有转子流量计、涡轮流量计、电磁流量计和超声流量计等。

3.质量流量法

无论是容积法，还是速度法，都必须给出流体的密度才能得到质量流量。而流体的密度受流体的状态参数影响，这就不可避免地给质量流量的测量带来误差。解决这个问题的一种方法是同时测量流体的体积流量和密度或根据测量得到的流体的压力、温度等状态参数对流体密度的变化进行补偿。但更理想的方法是直接测量流体的质量流量，这种方法的物理基础是测量与流体质量流量有关的物理量(如动量、动量矩等),从而直接得到质量流量。这种方法与流体的成分和参数无关，具有明显的优越性。但目前生产的这种流量计都比较复杂，价格昂贵，因而限制了它们的应用。

应当指出，无论哪一种流量计，都有一定的适用范围，对流体的特性以及管道条件都有特定的要求。目前生产的各种容积法和速度法流量计，都要求满足下列条件。

(1)流体必须充满管道内部，并连续流动。

(2)流体在物理上和热力学上是单相的，流经测量元件时不发生相变。

(3)流体的速度一般在声速以下。

众所周知，两相流动是工业过程中广泛存在的流动现象。两相流流量的测量已越来越引起人们的重视，国内外对此已进行了大量的实验研究，但目前尚无成熟的产品出现。

6.2节流式流量测量法

这种测量方法是把节流装置装入被测管道中，使被测介质在管道中造成局部收缩，处在一定压力下的介质，流经这个局部收缩时，其流速(动能)增加，因而静压力(位能)降低，所以在节流装置前后将产生一定大小的压力降，流动介质的流量愈大，在管道直径一定时流速将愈大，因而产生的压力降也愈大。这样，如果用差压计测出相应的压力差大小，就可以判断所流过物质流量的大小。

最常用的节流装置有孔板、喷嘴、文邱利喷嘴和文邱利管等几种型式，如图6.1所示。对于各种型式的节流装置而言，流量的测量方法和基本方程是一样的，不同的是其中的一些系数。

图6.1节流装置的基本形式

(a)孔板；(b)喷嘴；(c)文邱利喷嘴；(d)文邱利管

6.2.1不可压缩流体流量公式

以不可压缩流体流经孔板为例，来分析流体流经节流件的流动情况。图6.2是其示意图。当流体流经孔板时，由于流束断面的变化，流束的速度显著提高，因而动能增加，流体的静压力则随之减少。流体经孔板后，流束的断面逐步扩大而恢复到原来的状态，流速逐渐降低到原来的流速，则静压力也随之逐渐回升，但是由于流体的能量在流动过程中有一部分消耗于摩擦、涡流、撞击等方面，所以压力不能完全恢复，而有一个压力降，此压力降就称为流体流经节流件的压力损失δ_p。

图6.2流体经过孔板时的参数变化情况

为了推导流量公式，在管道上选取两个截面，截面1-1,在节流件上游侧，节流件对此截面上的流速分布没有影响，流体的压力为p’₁,流体的平均流速为v₁,流束截面的直径(即管内径)为D,流体的密度为ρ₁;截面2-2,即流束的最小断面处，它位于孔板出口以后的地方，对于喷嘴和文邱利管则位于其喉管内。此处流体的压力为p‘₂,平均流速为v₂,流体密度为ρ₂流束直径为d′(对孔板，小于孔板的开孔直径d’₂而对喷嘴和文邱利管则等于其开孔直径d)。

截面1-1和截面2-2流体总流的伯努里方程为

\(\frac{{p’}_{1}}{{\rho}_{1}}+\frac{{v}_{1}^{2}}{2}=\frac{{p’}_{2}}{{\rho}_{2}}+\frac{{v}_{2}^{2}}{2}\) (6.3)

流体总流的连续方程为

\({\rho}_{1}{v}_{1}\frac{\pi {D}^{2}}{4}={\rho}_{2}{v}_{2}\frac{\pi {d}^{2}}{4}=\)  (6.4)

联立方程式(6.3)和式(6.4)求解v₂,而且令节流件的开孔直径与管径D之比为β=d/D, 流束的最小断面\(\pi \frac{{d’}^{2}}{4}\)与节流件开孔面积\(\pi \frac{{d}^{2}}{4}\)之比为μ=d’²/d²。μ称之为流束的收缩系数。对于不可压缩流体，ρ₁=ρ₂=ρ,于是

\({v}_{2}=\frac{1}{\sqrt{1-{{\mu }^{2}}{{\beta }^{4}}}}\sqrt{\frac{2}{\rho }\left( p_{1}^{‘}-p_{2}^{‘} \right)}\)    (6.5)

应当指出，在推导这个方程式时：压力p¹和p²取的是截面1-1和2-2处的压力，而在实际中，我们经常取节流装置前后端面处的压力即p1和p₂。其次，在推导这个方程时，假定是理想流体：没有摩擦，截面各点速度相等，即等于平均流速，这也与实际情况有差别。为此将式(6.5)的右边乘以系数ξ,对上述分析的影响因素加以修正。经过这样的修正后，得到的速度应是最小截面d²处真实的平均流速V₂,即

\({{\bar{V}}_{2}}=\frac{\zeta }{\sqrt{1-{{\mu }^{2}}{{\beta }^{4}}}}\sqrt{\frac{2}{\rho }\left( p_{1}^{‘}-p_{2}^{‘} \right)}\) (6.6)

实际测得的压力差(p₁-p₂)是按一定的取压方式在管壁处取得的，与理论上的压力差(p’₁-p’₂)是不同的，它们间的关系为

\(\sqrt{p{{‘}_{1}}-p{{‘}_{2}}}=\sqrt{\psi }\sqrt{{{p}_{1}}-{{p}_{2}}}\)

式中

\(\sqrt{\psi}\)——取压系数，取压方式不同，\(\sqrt{\psi}\)值亦不同。

在实际应用中，用实测压力差(p₁-p₂)替代(p’₁-p’₂),并用节流件的开孔面积πd²/4代πd’²/4,则流量公式为

\({q}_{v}=\frac{\mu\zeta\sqrt{\psi}}{\sqrt{1-{\mu}^{2}{\beta}^{4}}}\frac{\pi}{4}{d}^{2}\sqrt{\frac{2}{\rho}({p}_{1}-{p}_{2})}\)   (6.7)

令

\(a=\frac{\mu\zeta\sqrt{\psi}} {\sqrt{1-{\mu}^{2}{\beta}^{4}} }\) (6.8)

则式(6.7)可写成如下的常见形式：

\({q}_{v}=a\frac{\pi}{4}{d}^{2}\sqrt{\frac{2}{\rho}({p}_{1}-{p}_{2})}\)   (6.9)

式中

a——流量系数，是各种节流装置的重要参数。

流量系数是由实验求得的，其值一般在0.6～1.2之间。质量流量为

\({q}_{m}=a\frac{\pi}{4}{d}^{2}\sqrt{ {2\rho}({p}_{1}-{p}_{2})}\)\)    (6.10)

6.2.2可压缩流体的流量公式

可压缩流体流经节流件时，由于压力的变化，密度随之而变化。如果仍用以不可压缩流体的伯努里方程为基础得出的流量系数a,则算出的流量偏大。

假定流经节流件的热力过程是等熵过程，即可逆绝热过程。则其过程方程为

\({p’}_{1}{v}_{1}^{k}={p’}_{2}{v}_{2}^{k}\)     (6.11)

式中

k——等熵指数，对于理想气体，k=c_p/c_v。

为简化推导，将实际过程按绝热过程处理，并假定流体为理想流体，则截面1-1与2-2间的伯努里方程为

\(\frac{k}{k+1}\frac{{p’}_{1}}{{\rho}_{1}}+\frac{{v}_{1}^{2}}{2}=\frac{k}{k+1}\frac{{p’}_{2}}{{\rho}_{2}}+\frac{{v}_{2}^{2}}{2}\)    (6.12)

联立式(6.4)、式(6.11)和式(6.12),可求解出v₂。将v₂带入式(6.2),经过推导和整理，最终可以得到与不可压缩流量公式相近的形式：

\({q}_{v}=\varepsilon a\frac{\pi}{4}{d}^{2}\sqrt{\frac{2}{\rho}({p}_{1}-{p}_{2})}\)   (6.13)

或

\({q}_{m}=\varepsilon a\frac{\pi}{4}{d}^{2}\sqrt{ {2\rho}({p}_{1}-{p}_{2})}\)\)    (6.14)

式中

ε——膨胀修正系数。为了使用方便，一般各种情况下的ε分别列在图表内，可直接由曲线查出。

前面得到的式(6.9)、式(6.10)和式(6.13)、式(6.14)之差别仅在一个膨胀修正系数ε,因此可以说，不可压缩介质的膨胀修正系数等于1,可以认为式(6.13)和式(6.14)是流量方程的普遍形式。

6.2.3标准节流装置

流量系数a和膨胀修正系数ε受多种因素影响，需由实验求出，不同几何形状的节流元件及不同的取压方式，a和ε各不相同，流量和压差的关系须单独标定才能使用，这样节流装置(包括节流元件及其前后管道、取压方式)使用起来很不方便，因此必须标准化。

标准化的理论基础是：对于一定粗糙度的管道，几何相似的节流装置在流体动力学相似(管内流动雷诺数R_eD相等)的条件下，流量系数a相等。因此，完全可以由试验确定a值。1932年国际上统一了节流元件的标准形式，其后，各国相应地制定了相关的标准。其中内容包括a和ε的实验数据以及保证与试验时几何相似和流体动力学相似的具体条件，如节流元件的结构和尺寸及公差、取压方式、管道条件、流体条件及流量测量误差等。符合国际上规定的条件即可直接使用给出的a和ε值，这种节流装置称为标准节流装置。

我国国家标准GB2624—1981规定的标准节流装置如下：

(1)标准孔板，角接取压。

(2)标准孔板，法兰取压。

(3)ISA1932喷嘴(标准喷嘴),角接取压。国际上还有其他标准化了的节流装置，如长径喷嘴、文丘利喷嘴等。

1.标准节流元件

(1)标准孔板。标准孔板为中间开孔两面平整的薄板，由不锈钢制成，如图6.3所示。标准孔板的加工、安装要求如下。

图6.3标准孔板

1)开孔直径d根据计算得到，但应大于等于12.5mm。d的数值应取4个不同位置测量值的算术平均值，任一实测值与平均值之差不应大于0.05%。d的加工公差与工作温度下的

β值有关，当β<0.67时，公差是±0.001d,当β>0.67时，公差是±0.0005d。

2)图6.3中e的尺寸为

0.005D<e<0.02D

D为管道直径，各处e的测量值不得相差0.001D以上。

3)孔板厚度E满足

e<E<0.05D

当50mm<D<100mm时，允许E=3mm。在各处E的测量值不得相差0.005D以上。

若E<0.02D,则孔板可不作如图6.3所示的圆锥开口。

4)上游边缘应尖锐，严格直角，无可见反光，上游与下游边缘均应无毛刺，无划痕。

5)孔板加工过程中不得用刮刀或破布进行修刮和打磨。

6)孔板安装必须与管道轴线垂直，其偏差不得超过±1°。其中心线和轴线的偏差不得大

于0.015D(1/β-1)。

(2)ISA1932喷嘴(标准喷嘴)。ISA1932喷嘴是一个以管道中心线为对称轴的对称体，如图6.4所示。

ISA1932喷嘴的型线由进口端A、收缩部分第一圆弧面C、第二圆弧面C₂、圆筒形喉部e和圆筒形出口边缘保护槽H等5部分组成。圆筒形喉部长0.3d,其直径即节流元件开孔直

径d。对于ISA1932喷嘴的加工安装要求可见相关标准。

2.取压装置

(1)角接取压装置。角接取压装置有环室取压和单独钻孔取压两种，如图6.5上半部和下半部所示。

环室有均压作用，压差比较稳定，所以被广泛采用。但当管径超过500mm时，环室加工麻烦，一般采用单独钻孔取压。

(2)法兰取压装置。法兰取压装置如图6.6所示。它由一对带有取压孔的法兰组成，两个取压孔的轴线必须垂直于管道的轴线，取压孔直径不大于0.08D,最好取6～12mm。取压孔轴线距节流件端面距离为25.4±1mm。

图6.4标准喷嘴

图6.5环室取压和单独钻孔取压装置

图6.6法兰取压装置

3.标准节流装置的管道条件

标准节流装置针对不同的条件对节流件前后直管段的长度都有要求，具体要求见相关标准。

4.标准节流装置的流体条件

标准节流装置测量的流体除需满足本章第一节提出的要求外，还要求流体必须是在圆管内流动，且密度和黏度已知，流速稳定，不存在漩涡，只允许流量缓慢变化。故不宜测量脉动流的流量。

6.2.4节流式流量计的特点

1.优点

(1)标准孔板结构易于复制，简单，牢固，性能稳定可靠，使用期限长，价格低廉。

(2)节流式流量计应用范围极广泛，至今尚无任何一类流量计可与之相比。全部单相流体，包括液、气、蒸汽皆可测量，部分混相流，如气固、气液和液固等亦可应用，一般生产过程的管径、工作状态(压力，温度)皆有产品。

(3)检测件与差压显示仪表可分开由不同生产厂家生产，便于专业化形成规模经济，它们的结合非常灵活方便。

(4)检测件，特别是标准型的，是全世界通用的，并得到国际标准组织的认可。对标准型检测件进行的试验研究是国际性的，其他流量计一般仅依靠个别厂家或研究群体进行，因此其研究的深度和广度不可同日而语。

正是由于上述原因，标准型节流式流量计无需实流校准，即可投用，在流量计中亦是唯一的。

2.缺点

(1)测量的重复性、精确度在流量计中属于中等水平，由于众多因素的影响错综复杂，精确度难以提高。

(2)测量范围窄，由于流量与差压为平方根关系，一般范围度仅3:1～4:1。

(3)压损大(指孔板，喷嘴)。

(4)现场安装条件要求较高，如需较长的直管段(指孔板，喷嘴),一般难以满足。

(5)检测件与压差显示仪表之间引压管线为薄弱环节，易产生泄漏、堵塞、冻结及信号失真等故障。

为了弥补上述缺点，近年来采取了一些改进措施，有效地提高了节流式流量计的性能。

6.3涡流式流量计

6.3.1工作原理

涡流式流量计利用了一种非常有趣的流动现象——卡门涡街。我们在流动的流体中放置一个圆柱或棱柱形物体，则在这个物体的下游就将看到如图6.7所示的两列漩涡。上下两列漩涡旋转方向相反并交替出现，因此也把这两列漩涡称为“卡门涡街”

实验证明，由于漩涡间的相互影响，漩涡列一般是不稳定的。卡门研究了漩涡稳定的条件，他指出，对于插入流体中一圆柱形物体，当涡列间隔h和漩涡间距l之比h/l=0.281时，涡街是稳定的。此时所产生的单侧漩涡频率f和漩涡发生体两侧流体速度v₁间存在如下关系：

\(f=Sr\frac{{v}_{1}}{d}\)   (6.15)

式中

d——漩涡发生体的迎流最大宽度，单位：m;

Sr——斯特劳哈尔数，无量纲。

图6.7卡门涡街

图6.8斯特劳哈尔数与雷诺数关系曲线

在以d为特征尺寸的雷诺数Re_d的一定范围内，Sr为常数(见图6.8)。因此，当柱体的形状、尺寸决定后，就可以根据式(6.15)通过测定f来测量漩涡发生体两侧的流体速度v₁。

根据流动连续方程

A₁v₁=Av  (6.16)

式中

A₁——漩涡发生体两侧流通面积，单位：m²;

A——管道流通面积，单位：m²;

v——管道截面上流体平均速度，单位：m·s-¹。

定义截面比m=A₁/A,则由式(6.15)和式(6.16)可得\(v=f\frac{dm}{Sr}\),则流量为

\({q}_{v}=Af\frac{dm}{Sr}\)  ,(6.17)

6.3.2涡街流量计的构造

通常涡街流量计由漩涡发生器、检测元件和转换器组成。其中漩涡发生器是核心，其形状、尺寸和构造要能保证产生强烈的稳定涡街，并在较宽的雷诺数范围内，Sr为常数，以使仪表有线性输出。常见的漩涡发生器有圆柱体和三角柱体，对于圆柱体，Sr=0.21,对于三角柱

体，Sr=0.16。

检测元件用来检测涡街的发生，而转换器则将检测元件的信号转换为频率信号。那么如何才能检测涡街的交替发生呢?

常用的做法是利用插入流体的漩涡发生体本身。圆柱的两侧开两排对应的孔，作为导压

孔，如图6.7(a)所示。在实际流动中，当流体即将离开靠近的表面时，如果此时有一部分流体被吸入，则流体与表面分离将变慢。相反，如果表面有流体吐出分离将加快。由于开了两个相对应的孔，有漩涡的一边，一部分流体被吸入，使流体分离变慢，直到这个漩涡完全形成才分开；相反，在无漩涡的一方，所有导压孔将同时吐出流体，加快了流体的分离，妨碍了漩涡的形成。这样的结构即使有外界干扰或流速分布不均匀等影响，涡列也会稳定地产生。

可见，在圆柱中开导压孔可保证产生稳定的涡列，由于形成每一个漩涡都将伴随着在导压孔中有一定方向的流体流动，而且这个流动方向是交替变化的。因此我们只要设法检知导压孔中流体流动或流动方向的变化频率，即可反映出漩涡产生的频率。

检测漩涡频率的方法一般有热丝检测法和力学检测法。热丝检测法在导压孔中间用一个壁隔开，中间留一个小孔，在小孔上装有通电的细铂丝。当有流体流过时，由于铂丝温度的改变，将引起铂丝电阻的变化，每产生一个漩涡，电阻变化一次。显然这种方法测出的频率将是单列漩涡产生频率的两倍。另外值得注意的是用热丝法仅适用于测量气体。

图6.9涡街流量计外形

图6.10一种力学检测法的测量电路

力学检测法将热丝换成带孔的膜片或摆旗，当流体流过时，膜片变形或摆旗摆动，用应变片可测出变形频率或摆旗频率。膜片开孔的目的是要保证流体仍能从导压孔中流过，以保证产生稳定的漩涡。如图6.9所示为一种采用力学检测法的涡街流量计，如图6.10为其测量电路，可以看出作用于检测元件上的应力是通过压电元件来检出。除此之外，还可以用超声波来流量显示检测尾流中的涡街。其原理如图6.11所示。发射电路产生的等幅振荡电信号加到发射换能器上，激励其中的压电晶片产生连续等幅超声波，发射到流体中，透过管壁到达接收换能器。当漩涡通过声束时，使声束产生折射和反射，引起偏转，接收换能器接收到的声能减小，输出的信号幅值也明显减小。当漩涡通过后，接收换能器的输出又恢复到原先的幅值。故漩涡的频率就是超声信号被调制的频率。接收电路则检出和放大此频率信号，然后进行流量显示和累积。

图6.11超声波涡街流量计的结构

6.3.3涡街流量计的安装

如图6.12所示给出了通常情况下对涡街流量计上下游直管段长度的要求，可以看出下游直管段的长度应不小于5D,而上游则有不同的要求。

图6.12涡街流量计上下游直管段

(a)管径收缩；(b)管径扩大；(c)90°弯管；(d)两个同平面的900弯管；(e)两个不同平面的90°弯管；(f)截止阀

6.3.4涡街流量计的特点

1.优点

(1)结构简单牢固，安装维护方便(与节流式差压流量计相比较，无需导压管和三阀组等，

减少泄漏、堵塞和冻结等)。

(2)适用流体种类多，如液体、气体、蒸汽和部分混相流体。

(3)精确度较高(与差压式，浮子式流量计比较),一般为测量值的(±1%～±2%)R。

(4)范围宽，可达10:1或20:1。

(5)压损小(约为孔板流量计1/4～1/2)。

(6)在一定雷诺数范围内，输出频率信号不受流体物性(密度，黏度)和组分的影响，只需在

一种典型介质中校验而适用于各种介质，如图6.13所示。

图6.13不同测量介质的斯特劳哈尔数

2.缺点

(1)不适用于低雷诺数测量(Re_p≤2×10⁴),故在高黏度、低流速、小口径情况下应用受到限制。

(2)漩涡分离的稳定性受流速分布畸变及旋转流的影响，应根据上游侧不同形式的阻流件配置足够长的直管段或装设流动调整器(整流器),一般可借鉴节流式差压流量计的直管段长度要求安装。

(3)力敏检测法对管道机械振动较敏感，不宜用于强振动场所。

6.4流体阻力式流量计

6.4.1靶式流量计

1.工作原理

如图6.14所示，在测量管中心放置一块圆形靶板，当流体冲击靶板时，靶板上会受到阻力，其大小为

 图6.14靶式流量计工作原理

1一靶；2一密封膜；3一导流管

\(F={C}_{D}\frac{\rho {v}^{2}}{2}{A}_{0}\)    (6.18)

式中

F——靶板上受的力，单位：N;

C_D——阻力系数；

ρ——流体密度，单位：kg·m-³;

v——流体流速，单位：m·s-¹;

A₀——靶板受力面积，单位：m²。利用上式可得出速度v的表达式，将v代入流量公式q_v=v(A-A₀),得

\({q}_{m}=1.253\alpha D(\frac{1}{\beta}-\beta)\sqrt{\rho F}\)     (6.19)

式中

A——测量管截面积，单位：m²;

α——流量系数，α=\(1/\sqrt{{C}_{D}}\)；

β——直径比，β=d/D;

D——测量管内径，单位：m;

d——靶板直径，单位：m。

由式(6.19)可以看出，只要测量出作用在靶上的阻力，就可以得到流体的流量。

2.流量系数

当被测介质密度和靶的几何尺寸确定后，流量计的精度取决于流量系数的精度。流量系数与靶的形状、管道直径、直径比及雷诺数等因素有关。实验证明，对于圆盘形靶，当雷诺数大于临界雷诺数，流量系数趋于恒定。国产靶式流量计的临界雷诺数可低至2000左右，比节流元件低的多。

3.特点

(1)优点。

1)可以测量小流量，高黏度、高脏污以及有悬浮固体颗粒等介质。

2)压力损失一般低于节流式流量计，约为孔板压力损失的一半。

(2)缺点。

1)精度不是很高。

2)在很多情况下，压力损失还是偏大。

6.4.2浮子流量计

1.工作原理

浮子流量计也叫转子流量计，它是一个垂直安装的锥管，其中有一个可以上下自由浮动的浮子(转子),它在自下而上流动的流体作用下上下浮动。浮子在锥管中形成一个环形通道面积，它比浮子上下锥管流通面积小而产生节流作用，故在浮子上下形成静压差，产生一个向上的力。这样作用在浮子上的力就有压差力、重力、浮力和粘性摩擦力等，当所有力平衡则浮子稳定在某一高度。如果流量增加，压差增加，浮子上升，流通面积增加，压差减少，重新达到平衡，又稳定在某一高度。这样我们就可以利用浮子的高度来反映流经锥管流体的流量。有兴趣的话读者可以自己推导高度和流量之间的关系式。

2.分类

浮子流量计分为玻璃管浮子流量计和金属管浮子流量计，如图6.15所示。玻璃管浮子流量计结构简单，价格低廉，但易碎；金属管浮子流量计使用温度和压力范围宽，不易碎。

图6.15浮子流量计

(a)玻璃管浮子流量计；(b)金属管浮子流量计

3.特点

浮子流量计具有结构简单，工作可靠，压力损失小而且恒定，可测小流量等优点。

在工业产生和科研工作中，经常遇到比较小的流量测量问题，节流装置在管径小于50mm还未实现标准化，所以对于小管径的流量测量常用浮子流量计。对于比较大的流量测量问题(管径在100mm以上),则很少用浮子流量计，因为这种口径的浮子流量计与其他流量计相比显得太笨重。

6.5速度式流量计

6.5.1涡轮式流量计

1.工作原理

涡轮流量计的结构如图6.16所示，在一个不锈钢壳体的前端固定一个前导流件，它由四片相互垂直的直片组成，用以去掉来流的漩涡，成为流线平行于轴线的流动。中间是叶轮组件，后边是后导流件。叶轮置于被测流体中，受流体的驱动而旋转，以旋转速度快慢来反应流量的大小。

图6.16涡轮流量计

如图6.17所示为涡轮叶片的示意图，α是涡轮叶片与轴线夹角，ro是叶轮平均半径，S₀是叶栅流通面积，n是叶轮转速。则r₀处流体的切向速度为

 图6.17涡轮叶片与轴线夹角示意图

\({v}_{0}=2\pi {r}_{0}n\)    (6.20)

被测流体通过叶片的轴向平均流速为

\({v}_{Z}=Q/{S}_{0}\)     (6.21)

则有

\(\tan alpha=\frac{{v}_{Q}}{{v}_{Z}}=\frac{2\pi{r}_{0}nS}{Q}\)    (6.22)

于是

\(Q=\frac{2\pi{r}_{0}nS}{\tan\alpha} \)  m³·s-¹    (6.23)

式(6.23)中除Q和n外的参数是已知的，只要测量出涡轮的转速n就可以得到流量Q。转速n的测量方法有磁电法、光电法、霍尔效应法等。

2.磁电法原理

如图6.18所示为磁电式涡轮流量计的工作原理。当用磁铁材料制成的叶片旋转通过固定在壳体上的永久磁铁时，磁铁磁路中磁阻发生周期的变化，从而使在永久磁铁外部的线圈感生出交流电脉冲信号。设涡轮叶片数量为Z,则脉冲信号的频率为f=nZ,代入式(6.23),得

\(Q=\frac{2\pi{r}_{0}nS}{\tan\alpha Z} f=\frac{1}{\xi}f\) (6.24)

式中

ξ-涡轮流量计的流量系数

图6.18磁电式涡轮流量计工作原理

1一导流器；2一轴承；3一涡轮；4一壳体；5一前置放大器；6一累计流量计算器；7一瞬时流量指示仪表

3.涡轮流量计的特点

(1)优点。

1)测量精度高，精密可达±(0.1～0.2)%。

2)测量范围宽，可达10:1。

3)响应快，可测脉动测量，可进行瞬时指示和累计计算。

4)线性好，耐压高(16MPa),体积小，压损小。

(2)缺点。

1)对被测流体清洁度要求较高。

2)适用的温度范围小。

3)轴承的磨损使仪表的使用寿命受到影响。

6.5.2超声波流量计

1.分类

根据原理的不同，超声波流量计可以分为以下几类。

(1)传播时间法。

(2)多普勒效应法。

(3)波束偏移法。

(4)相关法。

(5)噪声法。其中传播时间法应用较为广泛，下面主要介绍这种方法。

2.工作原理

声波在流体介质中传播，假如其方向与介质运动方向相同，则传播速度加快，反之则传播速度降低。

图6.19超声波流量计测量原理

如图6.19所示，在管道中分别顺流和逆流安装了两对超声波发射器和接收器，F1和J1为顺流的发射器和接收器，F2和J2为逆流的发射器和接收器，两者与轴线的夹角为α。顺流速度为

\({v}_{1}^{c}=c+v\cos\alpha\)     (6.25)

逆流速度为

\({v}_{2}^{c}=c-v\cos\alpha\)     (6.26)

利用式(6.25)和式(6.26)可以导出流体的速度：

\(v=\frac{{v}_{1}^{c}-{v}_{2}^{c}}{2\cos\alpha}\)     (6.27)

但是通常无法直接测出超声波顺流和逆流传播的速度，因此常用测量时间差、相位差和频率差等方法来获得流体的速度。

(1)时差法。如果超声波发生器发射一短小脉冲，测量顺流和逆流传播的时间差。顺流传播时间为

\({t}_{1}=\frac{L}{c+v\cos\alpha}=\frac{\frac{D}{\sin\alpha}}{ c+v\cos\alpha }\)    (6.28)

逆流传播时间为

\({t}_{2}=\frac{\frac{D}{\sin\alpha}}{ c+v\cos\alpha }\)    (6.29)

时差为

\(\Delta t={t}_{2}-{t}_{1}=\frac{2Dv\cot\alpha}{{c}^{2}-{v}^{2}{\cos}^{2}\alpha}\)   (6.30)

实际中流速一般都远小于声速(即v≤c),此时式(6.30)可写成

\(\Delta t\approx {t}_{2}-{t}_{1}=\frac{2Dv\cot\alpha}{{c}^{2}}\)  (6.31)

流速为

\(v=\frac{1}{2D}{c}^{2}\tan\alpha\Delta t\)     (6.32)

流量方程为

\(Q=\frac{\pi}{4}{D}^{2}v=\frac{\pi}{8}D{c}^{2}\tan\alpha\Delta t\)   (6.33)

由于在一般工业管道中所能产生的时差极小，如1μs左右，在工业中测量这个时差还是比较困难的。

(2)相差法。该法是测量连续振荡超声波在顺流和逆流传播时接收信号之间的相位差，而相位差与速度之间有如下关系：

\(\Delta \phi=\omega\Delta t=\omega\frac{2D\cot\alpha}{{c}^{2}}v\)   (6.34)

流量公式为

\(Q=\frac{D{}^{2}\tan\alpha}{16f}\Delta\phi\)    (6.35)

这里，f=2是超声波的频率。由式(6.35)可以看出，相位差与流量成正比，这里把时差测量变成了相位差测量，可以相应地提高测量精度，比前者有所改进。这里需要指出，上述两种方法的流量方程中都包含有声速的平方一项。由于声速是随介质温度变化而改变，这会给测量带来误差。

(3)频差法。该方法是测量顺流和逆流超声波脉冲的重复频率差。顺流频率为

\({f}_{1}=\frac{c+v\cos\alpha}{\frac{D}{\sin\alpha}}=\frac{(c+v\cos\alpha)\sin\alpha}{D}\) (6.36)

逆流频率为

\({}_{}=\frac{{c-v\cos\alpha}\sin\alpha}{D}\)    (6.37)

频差为

\(\Delta f=\frac{\sin 2\alpha}{D}v\)   (6.38)

流量方程为

\(Q=\frac{\pi}{4}{D}^{3}\frac{\Delta f}{\sin 2\alpha}\)   (6.39)

由式(6.39)可见，最后的流量与频率差成正比，而与超声波传播速度无关，所以可以得到较高的精度。

3.特点

(1)优点。

1)非接触测量，无插入零件，没有流体附加阻力。

2)不受介质的黏度，导电性及腐蚀性的影响。

3)线性好，易实现数字化输出。

(2)缺点。

1)精度不高(1%)

2)不适合温度波动大，介质物理性质变化大的流体(声速影响)。

3)不适合小流速、小管径的测量(相对误差大)。

6.6容积式流量计

6.6.1原理

由计量流体的体积来测量流量是一种古老的方法，如翻斗式流量测量设备就是用一个容器接收液体，等该容器内液体达到一定量时，容器自动翻转而排空容器内的液体，然后重新接受液体而开始一个新循环，通过计量单位时间内容器的翻转次数来测量流量。概括地说，这种方法是用一个固定容积的容器周期性地吸入、排出等量体积的流体，来测量流体流量的。其关键是如何能够连续地测量。由此发展起来的连续计量流体体积的容积流量计，由于直接测量流体的体积，所测流量理论上与流体的黏性、密度和流态无关。

常用的容积式流量计有腰轮流量计、刮板流量计和椭圆齿轮流量计等，下面主要介绍腰轮流量计和刮板流量计的原理。

6.6.2腰轮流量计

腰轮流量计又叫罗茨流量计，其工作原理如图6.20所示。在进出流量计流体的压力差的推动下，两个相同尺寸的腰轮分别绕各自的固定轴反相旋转，它们之间的相位差为90°。它们之间的相位差是由一对相互啮合的齿轮保证的，而两个腰轮不直接接触。两个腰轮在压差力的作用下旋转，交替将流体从流量计入口扫入它们和流量计壳体之间的空间内，再排出到流量计出口。

图6.20腰轮流量计工作原理

不难看出，在理想的情况下，所有流体只有通过腰轮与流量计壳体之间的计量空间才能流过流量计，而一个腰轮旋转一圈排到出口的流体体积是两倍的计量空间容积。因此，通过测量腰轮的旋转数，可知道流过流量计的流体体积；腰轮的单位时间旋转次数乘上四倍的计量空间容积就是体积流量。

6.6.3刮板流量计

刮板流量计的工作原理如图6.21所示，流体在流量计进出口压差作用下，推动流量计的刮板和转子一起转动。刮板在一个固定的凸轮作用下，可以沿径向运动而伸出和收回。当某一刮板转到流量计壳体的计量空间的起始点B时，处于计量空间内的流体随着前一刮板正好转过计量空间的终止点C时，而开始排出到流量计出口；与此同时，流量计入口处的流体开始再次充满计量空间。在流量计转子旋转一周之后，有6倍计量空间容积的流体经过流量计。同样，测量转子的转速，可知流体的体积流量。

图6.21刮板流量计工作原理

1一凸轮；2一壳体；3一刮板；4一滚子；5一转子；6一档块

6.6.4容积式流量计的特点

1.优点

(1)精度高(精密0.1级)。

(2)没有前置直管段要求。

(3)可用于高黏度流体的测量。

(4)范围度宽，一般为10:1到5:1,特殊可达30:1或更大。

(5)直读式仪表，无需外部能源，可直接获得累计总量，操作简便。

2.缺点

(1)结构复杂、体积大，故一般只适用于中小口径。

(2)一般不适用于高低温场合。

(3)大部分只适用洁净单相流体。

(4)安全性差，如检测活动件卡死，流体就无法通过。

6.7流量计的校准

涡轮流量计的校准可以采用定容法、称重法和比较法。

6.7.1定容法

定容法一般是在流量不变的前提下，使流体连续流入容器内，精确测量流体流动的起止时间和流入容器的体积总量，用平均流量代替瞬时流量作为标准。其关键在于：①保证流量高度稳定；②计时和计量都要足够精确。

定容法校准装置如图6.22和图6.23所示，一种是葫芦定容式流量校准装置，一种是管式定容校准装置。

图6.22葫芦定容式流量校准装置

1一加注阀；2,3一断流阀：4一发动机入口阀；5一孔板；6—流量计；7一温度压力则量点8,9一液位计；10一容器；11一上容腔；12一中容腔；13一下容腔

图6.23管式定容校准装置

1一标准体积管入口计数器；2一标准体积管出口计数器；3一持球阀；4一操作器；5一球；6一断流阀；7一发动机入口阀；8一孔板；9,10一容器截止阀；11一容器

6.7.2称重法

在流量稳定的条件下，已知比重的流体通过流量计，记录总工作时间，并称重流过流量计 的介质总重量。

6.7.3比较法

将标准流量计和被校流量计同时串接在流体管路里，用标准流量计校验被校流量计。

第7章数据采集系统

7.1概论

7.1.1数据采集的意义和任务

“数据采集”是指将温度、压力、流量、位移等模拟量采集、转换成计算机能够识别的数字量后，再由计算机进行存储、处理、显示或打印的过程。相应的系统称为数据采集系统。

得益于计算机技术的飞速发展和普及，数据采集系统在工业生产和科学研究中得到广泛应用。在生产过程中，应用这一系统可对生产现场的工艺参数进行采集、监视和记录，为提高产品质量、降低成本提供信息和手段。在科学研究中，应用数据采集系统可获得大量的动态信息，是研究瞬变物理过程的有力工具，也是获取科学奥秘的重要手段之一。

数据采集系统的任务，具体地说，就是采集处理传感器输出的模拟信号并转换成计算机能识别的数字信号，由计算机根据不同的需要进行相应的计算和处理，得出所需的数据。与此同时，将计算得到的数据进行显示或打印，以便实现对某些物理量的监视，其中一部分数据还将被计算机控制系统用来控制某些物理量。

数据采集系统性能的好坏，主要取决于它的分辨能力和速度。在保证分辨能力的条件下，应有尽可能高的采样速度，以满足实时采集、实时处理和实时控制对速度的要求。对于数据采集系统来说，表征分辨能力的指标参数是分辨率，表征速度的指标是采样率。

通常情况下，计算机是无法实现数据采集的全部功能，需要专门进行数据采集的仪器/采集卡与其配合使用。有的采集仪器内置了存储器、计算机/单片机等，可以独立开展数据采集工作。

7.1.2数据采集系统的基本功能

由数据采集系统的任务可以知道，数据采集系统具有以下几方面的功能。

(1)数据采集。计算机按照预先选定的采样周期，对输入到系统的模拟信号进行采样。有时还要对数字信号、开关信号进行采样，这类信号的采样处理方法与模拟信号的有所不同，由专门的采集电路/设备进行处理。

(2)模拟信号处理。模拟信号是指随时间连续变化的信号，这些信号在规定的一段连续时间内，其幅值为连续值，即从一个量变到下一个量时中间没有间断。例如正弦信号。模拟信号有两种类型：一种是由各种传感器获得的低电平信号；另一种是由仪器、变送器输出的电流信号。这些模拟信号经过采样和模/数(即模拟量/数字量，Analog/Digital,A/D)转换输入计算机后，常常要进行数据正确性判断、标度变换、线性化等处理。

模拟信号非常便于传送，但它对干扰信号很敏感，容易使传送中的信号幅值或相位发生畸变。因此，有时还要对模拟信号做零漂修正、数字滤波等处理。

(3)数字信号处理。数字信号是指时间和幅值都离散化的信号。在二进制系统中，数字信号是由有限字长的数字组成，其中每位数字不是0就是1,这可由脉冲的有无来体现。数字信号的特点是，它只代表某个瞬时的量值，是不连续的信号。

数字信号是由某些类型的传感器或仪器输出，它在线路上的传送形式有两种：一种是并行方式传送；另一种是串行方式传送。数字信号对传送线路上的不完善性(畸变、噪声)不敏感，这是因为只需检测脉冲的有无来获取信息，至于信号的精确性(幅值、持续时间)是无关紧要的。

数字信号进入计算机后，常常需要进行码制转换的处理，如BCD码转换ASCII码，以便显示数字信号。

(4)开关信号处理。开关信号主要来自各种开关器件，如按钮开关、行程开关和继电器触点等。开关信号的处理主要是监测开关器件的状态变化。

(5)二次数据计算。把直接由传感器采集到的数据称为一次数据，把通过对一次数据进行某种数学运算而获得的数据称为二次数据。二次数据计算主要有平均、累计、变化率、差值、最大值和最小值等。

(6)屏幕显示。显示装置可把各种数据以方便于操作者观察的方式显示出来，屏幕上显示的内容一般称为画面，常见的画面有相关画面、趋势图、模拟图、一览表等。

(7)数据存储。数据存储就是按照一定的时间间隔，定期将某些重要数据存储在外部存储器上。

(8)打印输出。打印输出就是按照一定的时间间隔或人为控制，定期将各种数据以数据、表格或图形的形式打印出来。

(9)人机交互。人机联系是指操作人员通过键盘或鼠标与数据采集系统对话，完成对系统的运行方式、采样周期等参数的设置。此外，还可以通过它选择系统功能、选择输出需要的画面等。人机联系是通过人机界面实现的，对于一个合格的数据采集系统来说，良好的人机界面是必不可少的。

7.1.3数据采集系统的结构形式

数据采集系统主要由硬件和软件两部分组成。从硬件方面来看，目前数据采集系统的结构形式主要有两种：一种是计算机数据采集系统；另一种是集散型数据采集系统。下面分别介绍这两种系统的结构和特点。

1.计算机数据采集系统

计算机数据采集系统的结构如图7.1所示，是由传感器、多路开关、程控放大器、采样/保持器、A/D转换器、计算机及外设等部分组成。各部分的作用如下：

为了便于理解，可以把计算机数据数据采集系统看成一个加工产品的流水线，被测模拟信号相当于待加工的原料，由若干条传送带传入，程控放大器、采样/保持器和A/D转换器则相当于三个加工环节，都在一条流水线上，这样就需要多路开关控制依次让不同传送带上的原料进入加工流水线。当A/D转换器加工好的产品(数字信号),由专门的小车运送到仓库(计算机中的寄存器)。整个过程由定时与逻辑控制部分来负责控制。而数字信号和开关信号则相当于特殊的成品，由专用通道直接进入仓库。

图7.1计算机数据采集系统框图

(1)传感器。各种待转换的物理量如温度、压力、位移、流量等都是非电量。首先要把这些非电量转换成电信号，然后才能做进一步的处理。把各种物理量转换成电信号的器件称为传感器。传感器的类型有很多。由于传感器的知识在第三章中有详细的论述，这里不再重复。

(2)多路开关。数据采集系统往往要对多路模拟量进行采集。在不要求高速采样的场合，一般采用公共的A/D转换器，分时对各路模拟量进行A/D转换，目的是简化电路，降低成本。可以用多路开关来轮流切换各路模拟量与A/D转换器间的通道，使得在一个特定的时间内，只允许一路模拟信号输入到A/D转换器，从而实现分时转换的目的。(注意：多路开关并非所有的计算机数据采集系统中必需的。在如图7.6所示的多路同步采样A/D电路中就不需要多路开关。)

以如图7.2所示的AD7501为例来说明多路转换模拟开关的原理。该芯片包括8路输入

(S1～S8)、1路输出(OUT)、3路通道选择端(A2～A0)和输出选择EN。当EN有效时，A2～A0选择S1～S8中某路输出。例如，A₂A₁A₀=000时，OUT=S1;A₂A₁A。=111时，OUT=S8。

图7.2多路转换模拟开关AD7501

一般模拟多路开关有2N个模拟输入端，N个通道选择端，由N个选通信号控制选择其中一个开关闭合，使对应的模拟输入端与多路开关的输出端接通，让该路模拟信号通过。有规律地周期性改变N个选通信号，可以按固定的序列周期性闭合各个开关，构成一个周期性分组的分时复用输出信号，由后面的A/D转换器分时复用对各通道模拟信号进行周期性转换。

(3)程控放大器。在数据采集时，来自传感器的模拟信号一般都是比较弱的低电平信号。程控放大器的作用是将微弱的输入信号进行放大，以便充分利用A/D转换器的满量程分辨率。例如，很多传感器的输出信号是毫伏数量级，而A/D转换器的满量程输入电压多是2.5V、5V或10V,且A/D转换器的分辨率是以满量程电压为依据确定的。为了能充分利用A/D转换器的分辨率，就要把模拟输入信号放大到与A/D转换器满量程电压相应的电平值。

一般情况下通用数据采集系统均支持多路模拟通道，而各通道的模拟信号电压可能有较大差异，因此最好是对各通道采用不同的放大倍数进行放大，即放大器的放大倍数可以实时控制改变。程控放大器能够实现这个要求，就在于它的放大倍数可以随时由一组数码控制。这样，在多路开关改变其通道序号时，程控放大器也由相应的一组数码控制改变放大倍数，即为每个模拟通道提供最合适的放大倍数。它的使用大大拓宽了数据采集系统的适应面。

(4)采样/保持器。A/D转换器完成一次转换需要一定的时间，在这段时间内希望A/D转换器输入端的模拟信号电压保持不变，以保证有较高的转换精度。这可以用采样/保持器(S/H)来实现，采样/保持器的加入，大大提高了数据采集系统的采样频率。

(5)A/D转换器。因为计算机只能处理数字信号，所以须把模拟信号转换成数字信号，实现这一转换功能的器件是A/D转换器。A/D转换器是采样通道的核心，因此，A/D转换器是影响数据采集系统采样速率和精度的主要因素之一。

(6)接口电路。该电路用来将传感器输出的数字信号进行整形或电平调整，然后再传送到计算机的总线。

(7)计算机及外部设备。它们负责对数据采集系统的工作进行管理和控制，并对采集到的数据做必要的处理，然后根据需要来显示和打印。

(8)定时与逻辑控制电路。数据采集系统各器件的定时关系是比较严格的，如果定时不合适，就会严重影响系统的精度。例如，多路开关的两个开关切换时间是800ns,在多路开关切换期间，程控放大器同时切换放大倍数，大约是800ns;从程控放大器的一个新放大倍数到产生稳定的输出大约是400ns;那么,从程控放大器倍数开始切换到采样/保持器开始跟踪至少

需要1.2μs。若采样/保持跟踪时间是6μs,A/D转换至少再延迟6μs后才能开始。对于以上所描述的情况，必须遵守如图7.3所示的时序图。

图7.3数据采集系统工作时序图

由图7.3可知，数据采集系统工作时，各个器件必须按照以下过程顺序执行：

1)模拟多路开关开始切换。

2)程控放大器放大倍数开始切换。

3)采样/保持器开始保持。

4)A/D转换器开始转换。

5)A/D转换完成。

定时电路就是按照各个器件的工作次序产生各种时序信号，而逻辑控制电路是依据时序信号产生各种逻辑控制信号。

由于生产和科学研究的需要，使得计算机数据采集系统的结构还有其他方案，如适于高速采样的数据采集系统、无相差并行采样(各路均有采样/保持器、A/D转换器)的数据采集系统

等。如图7.4～图7.6所示，目前最常见的3种采集系统结构分别是多路共用采集电路分时采集、多路同步取样共用A/D分时采集和多通道同步采样A/D。可以看出，图7.1所示的计算机数据采集系统属于多路共用采集电路分时采集。

图7.4多路共用采集电路分时采集

图7.5多路同步取样共用A/D分时采集

图7.6多通道同步采样A/D

计算机数据采集系统有以下特点：

(1)系统结构简单，容易实现，能够满足中、小规模数据采集的要求。

(2)计算机对环境的要求不是很高，能够在比较恶劣的环境下工作。

(3)计算机的价格低廉，可降低数据采集系统的投资。

(4)计算机数据采集系统可作为集散型数据采集系统的一个基本组成部分。

(5)计算机的各种I/O模板及软件都比较齐全，很容易构成系统，便于使用和维修。

这里需要指出的是，在如图7.1所示的计算机数据采集系统中，加上D/A转换器，就构成了计算机数据采集与控制系统。

2.集散型采集系统

集散型数据采集系统的结构如图7.7所示。集散型数据采集系统是计算机网络技术的产物，它由若干个“数据采集站”和一台“上位机”及通信线路组成。

数据采集站一般是由单片机数据采集装置组成，位于生产设备附近，可独立完成数据采集和预处理任务，还可将数据以数字信号的形式传送给上位机。

上位机一般为计算机，配置有打印机和绘图机。上位机用来将各个数据采集站传送来的数据，集中显示在显示器上或用打印机打印成各种报表，或以文件形式储存在磁盘上。此外，还可以将系统的控制参数发送给各个数据采集站，以调整数据采集站的工作状态。

图7.7集散型数据采集系统

数据采集站与上位机之间通常采用网络和异步串行方式传送数据。数据通信通常采用主从方式，由上位机确定与哪一个数据采集站进行数据传送。

集散型数据采集系统主要有以下特点。

(1)系统的适应能力强。无论是大规模的系统，还是中小规模的系统，集散型系统都能够适应，因为可以通过选用适当数量的数据采集站来构成相应规模的系统。

(2)系统的可靠性高。由于采用了多个以单片机为核心的数据采集站，若某个数据采集站出现故障，只会影响某项数据的采集，而不会对系统的其他部分造成任何影响。

(3)系统的实时响应性好。由于系统中各个数据采集站之间是真正“并行”工作的，所以系统的实时响应性较好。这一点对于大型、高速、动态数据采集系统来说，则是一个很突出的优点。

(4)对系统硬件的要求不高。由于集散型数据采集系统采用了多机并行处理方式，每一个单片机仅完成数量十分有限的数据采集和处理任务。因此，它对硬件的要求不高，可以用低档的硬件组成高性能的系统，这是计算机数据采集系统方案所不可比拟的。

另外，这种数据采集系统是用数字信号传输代替模拟信号传输，有利于克服干扰。因此，这种系统特别适合于在恶劣的环境下工作。

由上述介绍可以看出，计算机数据采集系统是基本型系统，由它可组成集散型数据采集系统。

7.2模拟信号的数字化处理

7.2.1概述

数据采集系统中采用计算机作为处理机。众所周知，计算机内部参与运算的信号是二进制的离散数字信号，而被采集的各种物理量一般都是连续模拟信号。因此，在数据采集系统中同时存在着两种不同形式的信号：离散数字信号和连续模拟信号。在研究开发数据采集系统时，首先遇到的问题是传感器所测量到的连续模拟信号如何转换成离散的数字信号。

连续的模拟信号转换成离散的数字信号，经历了以下两个断续过程。

1.时间断续

对连续的模拟信号x(t),按一定的时间间隔T_s,抽取相应的瞬时值(也就是通常所说的离散化),这个过程称为采样。连续的模拟信号x(t)经采样过程后转换为时间上离散的模拟信号x _s (nT _s)(幅值仍是连续的模拟信号),简称为采样信号。

2.数值断续

把采样信号x _s (nT _s)以某个最小数量单位的整倍数来度量，这个过程称为量化。采样信号x _s (nT _s)经量化后变换为量化信号x _q (nT _s),再经过编码，转换为离散的数字信号x(n)(时间和幅值都是离散的信号),简称为数字信号。

以上转换过程见图7.8。

图7.8信号转换过程

对连续的模拟信号离散化时，是否可以随意对连续的模拟信号做离散化处理呢?实践证明，在对连续的模拟信号做离散化处理时，必须遵守一定的原则，而如果随意进行，将会产生如下一些问题。

(1)可能使采样的点增多，导致占用大量的计算机存储单元，严重时将因存储空间不够而无法正常工作。

(2)也可能是采样点太少，使采样点之间相距太远，引起原始数据值的失真，复原时不能原样复现出原来连续变化的模拟量，从而造成误差。为了避免产生上述问题，在对模拟信号离散化时，必须依据采样定理规定的原则进行。

7.2.2采样过程

采样过程如图7.9所示。一个在时间和幅值上连续的模拟信号x(t),通过一个周期性开闭(周期为T_s,开关闭合时间为v)的采样开关K之后，在开关输出端输出一串在时间上离散的脉冲信号x_s(nT_s),把这一过程称为采样过程。

图7.9采样过程

采样后的脉冲信号x_s(nT_s)称为采样信号。0,T_s,2T_s,…各点称为采样时刻，τ称为采样时间，T_s称为采样周期，其倒数f=1/T_s称为采样频率。应该指出，在实际系统中，τ远小于T_s,也就是说，在一个采样周期内，只有很短一段时间采样开关是闭合的。

7.2.3采样定理

采样周期T,决定了采样信号的质量和数量：T_s太小，会使x_s(nT_s)的数量剧增，占用大量的存储单元；T_s太大，会使模拟信号的某些信息被丢失，这样一来，若将采样后的信号恢复成原来的信号，就会出现失真现象，影响数据处理的精度。因此，必须有一个选择采样周期T_s的依据，以确保使x_s(nT_s)不失真地恢复原信号x(t)。这个依据就是采样定理。

设有连续信号x(t),其频谱为X(f),以采样周期T_s采得的离散信号为x_s(nf_s)。采样定理指出，在一般情况下，对一个具有有限频谱X(f)的连续信号x(t)进行采样，只有当采样频率为f≥2f_c(f_c为连续信号x(t)截止频率)时，由采样后得到的采样信号x_s(nT_s)才能无失真地恢复为原来信号x(t)。在这里需要注意两点：

(1)绝大多数情况下，只要满足f_s≥2 f_c就可以实现频率的不失真恢复，即f_s≥2 f_c是充分条件。在个别情况下，可能会出现f_s=2 f_c时无法实现频率不失真恢复。

(2)对于幅值的不失真恢复来说，f_s≥2f_c只是必要条件，而非充分条件。必须先明确给出“不失真”的定义，也即对幅值的误差要求，然后才能确定出合适的取样频率。不同的误差要求，对取样频率的要求是不一样的。例如：假设不失真的误差要求为0.1%时对应f_s=4 f_c，当

误差要求为0.01%时，取样频率f_s必定要大于4 f_c。目前还没有办法给出一个明确的函数来确定f_s与f_c的关系。

在上面的内容中已经指出，在个别情况下可能会出现f_s=2 f_c时无法实现频率不失真恢复。这种情况发生在f_c =1/(2T_s)时。例如，设连续信号为

x(t)=Asin(2πf_ct+φ),0≤φ≤2π

其采样值为

x_s(nT_s)=Asin(2πf_cnT_s+φ)

当f_c=1/(2T_s)时，则有

x_s(nf_s)=Asin(2πnT_s/2T_s +φ)=Asin(πn+φ)=A[sin(πn)cosφ+cos(πn)sinφ]=A[cos(πn)sinφ]

=A(-1)ⁿsinφ

当φ=0时，x_s(nT_s)=0,即采样信号为零，无法恢复原模拟信号。

当0<| sinφ|<1时，x_s(nT_s)的幅值均小于原模拟信号，即x_s(nT_s)没有代表原模拟信号x(t),出现失真。

当| sinφl=1时，x_s(nT_s)=(-1)ⁿA,它与原模拟信号的最大幅值是相同的。但必须对采样的起始点做严格的要求，即保证φ=π/2的条件。

综上所述，当f_c=1/(2T_s)时，只有在采样的起始点严格地控制在φ=π/2时，才能由采样信号不失真地恢复出原模拟信号，然而这是难以做到的。因此，采样定理对于f_c=1/(2T_s)时是不适用的。

7.3模拟信号的放大、采样与保持

7.3.1放大器

在许多场合，传感器输出的信号不仅很微弱，且伴有很大的共模电压(包括干扰电压，关于干扰的相关内容将在第8章进行介绍)。这种信号需要用高共模抑制比、高增益、低噪声、高输入阻抗的放大器来放大，习惯上将此类放大器称为测量放大器，又叫仪表放大器。

目前广泛使用的是由三个运算放大器组成的三运放测量放大器，其电路如图7.10所示。其中A₁和A₂为两个性能一致(主要指输入阻抗，共模抑制比和开环增益)的通用集成运放，以同相放大方式工作，构成平衡对称的差动放大输入级；A₃以差动放大方式工作，用来抑制A₁和A₂的共模信号，并接成单端输入方式，以满足接地负载的需要。

图7.10三运算测量放大电路

由电路结构分析，有

\({U}_{O1}=\left(1+\frac{{R}_{1}}{{R}_{G}}\right){U}_{i1}-\frac{{R}_{1}}{{R}_{G}}{U}_{i2}\)

\({U}_{O2}=\left(1+\frac{{R}_{2}}{{R}_{G}}\right){U}_{i2}-\frac{{R}_{2}}{{R}_{G}}{U}_{i1}\)

\({U}_{O}=-\frac{{R}_{4}}{{R}_{3}}{U}_{O1}+\left(1+\frac{{R}_{4}}{{R}_{5}}\right)\frac{{R}_{6}}{{R}_{6}+{R}_{5}}{U}_{i2}-\frac{{R}_{2}}{{R}_{G}}{U}_{i1}\)

通常R₁=R₂,R₃=R₅,R₄=R₆。对差模输入电压U_i1—U_i2,测量放大器的增益为

\({A}_{vf}=\frac{{U}_{O}}{{U}_{i1}-{U}_{i2}}=-\left(1+\frac{2{R}_{1}}{{R}_{G}}\right)\frac{{R}_{4}}{{R}_{3}}\)

测量放大器的共模抑制比主要取决于输入级运放A₁和A2的对称性、输入级运放A₃的共模抑制比、输入级外接电阻R₃和R₅以及R₄和R₆的匹配精度(±0.1%以内)。其共模抑制比可达120dB以上。

测量放大器电路还具有增益调节功能，通过调节R_G可改变增益而不影响电路的对称性。由于输入级采用了对称的同相放大器，输入电阻可达数百兆欧以上。

隔离放大器是一种特殊的测量放大电路，有输入放大器、输出放大器、隔离器以及隔离电源等部分组成，如图7.11(a)所示。其输入、输出和电源电路之间没有直接的电路耦合，适用于高共模电压环境下的小信号测量。图中，R_iso为隔离电阻，约为10¹²Ω;C_iso。为隔离电容，典型值为20pF;U_D为输入端的差模电压；Uc为对输入端公共地的输入级共模电压，即隔离器两端或输入端与输出端两公共地之间能承受的共模电压，额定的隔离峰值电压通常高达5000V。图7.11(b)为隔离放大器的电路符号。

图7.11隔离放大器的基本组成及符号

 (a)基本组成；(b)电路符号

由于隔离放大器采用浮置式设计(浮置电源、浮置放大器输入端),输入与输出端相互隔离，不存在公共地线的干扰。因此，具有极高的共模抑制能力，能对信号进行安全准确的放大，可有效防止高压信号对低压测试系统造成的破坏。

常采用的隔离方式有电磁(变压器、电容)耦合和光电耦合，如图7.12所示。

图7.12隔离放大器原理框图

(a)变压器耦合；(b)电容耦合；(c)光电耦合

变压器耦合采用载波调制-解调技术，具有较高的线性度和隔离性能，共模抑制比高，技术较成熟；但带宽较窄约千赫兹以下(高性能的变压器耦合隔离放大器带宽可达20kHz左右),且体积大、工艺复杂、成本高。电容耦合采用数字解调技术(电压-频率变换或电压-脉冲占空比变换),将输入信号以数字量的形式由电容耦合到输出侧，可靠性好，带宽较宽，具有良好的频率特性。光电耦合结构简单，成本低廉，器件质量轻，频带宽；但是非线性期间，在信号放大时，将出现较大的非线性误差。

7.3.2采样/保持器

模拟信号进行A/D转换时，从启动转换到转换结束输出数字量，需要一定的转换时间。在这个转换时间内，模拟信号要基本保持不变，否则转换精度没有保证，特别当输入信号频率较高时，会造成很大的转换误差。要防止这种误差的产生，必须在A/D转换开始时将输入信号的电平保持住，而在A/D转换结束后又能跟踪输入信号的变化。能完成这种功能的器件叫采样/保持器。采样/保持器在保持阶段相当于一个“模拟信号存储器”。

采样/保持器是一种具有信号输入、信号输出以及由外部指令控制的模拟门电路。它主要由模拟开关K、电容CH和缓冲放大器A组成，它的一般结构形式如图7.13所示。

图7.13采样/保持器的一般结构形式

采样/保持器的工作原理如图7.14所示。在t₁时刻前，控制电路的驱动信号为高电平时，模拟开关K闭合，模拟输入信号U₁通过模拟开关K加到电容C_H上，使得电容C_H端电压Uc跟随模拟输入信号U₁变化而变化，这个时期称为跟踪(或叫采样)期。在t₁时刻，驱动信号为低电平，模拟开关K断开，此时电容C_H上的电压Uc保持模拟开关断开瞬间的U₁值不变并等待A/D转换器转换，这个时期称为保持期。而在t₂时刻，保持结束，新一个跟踪(采样)时刻到来，此时驱动信号又为高电平，模拟开关K重新闭合，电容C_H端电压Uc又跟随模拟输入信号U₁变化而变化，直到t₃时刻驱动信号为低电平时，模拟开关K断开……。

从以上介绍可知，采样/保持器是一种用逻辑电平控制其工作状态的器件，它具有以下两个稳定的工作状态。

图7.14采样/保持器的工作原理示意图

(1)跟踪状态。在此期间它尽可能快地接收模拟输入信号，并精确地跟踪模拟输入信号的变化，一直到接到保持指令为止。

(2)保持状态。对接收到保持指令前一瞬间的模拟输入信号进行保持。

因此，采样/保持器是在“保持”命令发出的瞬间进行采样，而在“跟踪”命令发出时，采样/保持器跟踪模拟输入量，为下次采样做准备。在数据采集系统中，采样/保持器主要起以下两种作用。

(1)“稳定”快速变化的输入信号，以利于A/D转换器把模拟信号转换成数字信号，减小采样误差。

(2)用来储存模拟多路开关输出的模拟信号，这样可使模拟多路开关继续切换下一个待转换的信号。

从以上采样/保持器的工作原理可知，电容CH对采样/保持的精度有很大的影响，如果电容值过大，则其时间常数大，当模拟信号频率高时，由于电容充放电时间长，将会影响电容对输入信号的跟踪特性，而且在跟踪的瞬间，电容两端的电压会与输入信号电压有一定的误差。而当处于保持状态时，如果电容的漏电流太大，负载的内阻太小，都会引起保持信号电平的变化。

为使采样/保持器有足够的精度，一般在其输入端和输出端均采用缓冲器，以减少信号源的输出阻抗，增加负载的输入阻抗。在选择电容时，容量大小要适宜，以保证其时间常数适中，并选用泄漏小的电容。

7.4量化与编码

7.4.1量化的概念

由上述讨论可知，来自传感器的连续模拟信号经过采样器采样后，变成了时间上离散的采样信号，但其幅值在采样时间t内是连续的，因此，采样信号仍然是模拟信号。为了能用计算机处理信号，须将采样信号转换成数字信号，也就是将采样信号的幅值用二进制代码来表示。由于二进制代码的位数是有限的，只能代表有限个信号的电平，故在编码之前，首先要对采样信号进行“量化”。

量化就是把采样信号的幅值与某个最小数量单位的一系列整倍数比较，以最接近于采样信号幅值的最小数量单位倍数来代替该幅值。这一过程称为量化过程，简称量化。

最小数量单位称为量化单位。量化单位定义为量化器满量程电压FSR(FullScaleRange)与2”的比值，用q表示，因此有

\(q=\frac{FSR}{{2}^{n}}\)

式中

n——量化器的位数。

例如，如果量化器满量程电压为10V,量化器位数为8位，则量化单位

\(q=\frac{10}{{2}^{n}}=0.0391\)V

7.4.2量化方法

大家都知道，日常生活中使用的人民币，其最小单位是分，任何货物的价值都是“分”的整数倍，对不到一分钱的剩余部分，有两种处理方法：一种是一概忽略不计，只舍不入；一种是有舍有入，例如常用的四舍五入。类似地，模/数转换器也有两种量化方法。

1.“只舍不入”的量化

如图7.15所示，为了对采样信号的幅值进行量化，将信号幅值轴分成若干层，各层之间的间隔相等，且等于量化单位q。在“只舍不入”的量化过程中，信号幅值小于量化单位q的部分，一律舍去。

图7.15“只舍不入”的量化过程

2.“有舍有入”的量化

如图7.16所示，在“有舍有入”的量化过程中，采样信号幅值中小于q/2的部分，舍去；大于或等于q/2的部分，计入。

图7.16“有舍有入”的量化过程

7.4.3编码的概念

模/数转换过程的最后阶段是编码。编码是指把量化信号的电平用数字代码来表示，编码有多种形式，最常用的是二进制编码。

如同十进制数，二进制的数码是由多个位组成。数码最左端的位叫做最高有效位，简称最高位，以符号MSB表示；数码最右端的位叫做最低有效位，简称最低位，以符号LSB表示。二进制数码的每一位有两个可能状态：“0”表示这一位没有贡献；“1”表示这一位有贡献。二进制数码的每一位的贡献为其右边一位贡献的2倍。数码作为一个数，代表一个量化信号量值，只有当码制和码制间的相互关系被定义之后，数码才具体代表该量化信号的某一个量值。因此，所谓二进制编码，就是用1和0所组成的n位数码来代表量化电平。

在数据采集中，被采集的模拟信号是存在着极性的，例如单极性信号，电压在0～+10V之间变化；双极性信号，电压在一5～+5V之间变化。因此，二进制码也分成两大组：单极性二进制码和双极性二进制码，在应用时，可根据被采集信号的极性来选择编码形式。

7.4.4 单极性编码

单极性编码的方式有以下两种。

1. 二进制码

二进制码是单极性码中使用最普遍的一种码制。在数据转换中，经常使用的是二进制分数码。在这种码制中，一个(十进制)数D的量化电平可表示为

\(D=\sum\limits_{i=1}^{n}{{a}_{i}{2}^{-n}=\frac{{a}_{1}}{2}+\frac{{a}_{2}}{{2}^{2}}+…+\frac{{a}_{n}}{{2}^{n}}}\)        (7.1)    

由式(7.1)可以看出，第1位(MSB)的权是1/2,第2位的权是1/4,……,第n位(LSB)的权是1/2ⁿ。a_i或为0或为1,n是位数。数D的值就是所有非0位的值与它的权的积累加的和。

2. 二-十进制(BCD)编码

尽管二进制原码是普遍使用的一种码制，但是，在系统的接口中，经常使用另一些码制，以满足特殊的需要。例如，在数字电压表、光栅数显表中，数字总是以十进制形式显示出来，以便于人们读数。在这种情况下，二-十进制码(BCD)有它的优越性。BCD编码中，用一组四位二进制码来表示一位0～9的十进制数字。

7.4.5 双极性编码

在很多情况下，模拟信号是双极性的，即有时是正值，有时为负值。为了区别两个幅值相等而符号相反的信号，就需要采用双极性编码。双极性编码也有多种形式，最常见的有符号一数值码、偏移二进制码、2的补码。

1. 符号-数值码

在这种码制中，最高位为符号位(“0”表示正，“1”表示负),其他各位是数值位。这种码制与其他双极性码制比较，其优点是信号在零的附近变动1LSB时，数值码只有最低位改变，这意味着不会产生严重的瞬态效应。其他双极性码，在零点附近，都会发生主码跃迁，即数值码的所有位全都发生变化，因而可能产生严重的瞬态效应和误差。其缺点是有两个码表示零，

0+为0000,0一为1000。因此，从数据转换角度来看，符号-数值码的转换器电路比其他双极性码复杂，其造价也较昂贵。

2. 偏移二进制码

偏移二进制码是转换器最容易实现的双极性码制。一个模拟输出量Uo,当用偏移二进制码表示时，其代码完全按照二进制码的方式变化，不同之处，只是前者的代码简单地用满量程值加以偏移。以4位二进制码为例，代码的偏移情况如下。

(1)代码为“0000”时，表示模拟负满量程值，即—FSR。

(2)代码为“1000”时，表示模拟零，即模拟零电压对应于2″-¹数。

(3)代码为“1111”时，表示模拟正满量程值减1LSB,即FSR—FSR/2”-1。

偏移二进制码的优点是除了容易实现外，还很容易变换成2的二进制补码。偏移二进制码的缺点是在零点附近发生主码跃迁。

3. 2的补码

2的补码符号位与偏移二进制码的符号位相反，而数值部分则相同。2的补码对于数字的代数运算是十分方便的，因为减法可以用加法代替。2的补码的缺点与偏移二进制码相同。

7.5A/D 转换

由图7.1所示的数据采集系统结构可以看出，模拟信号经过放大、采样与保持之后，进入到A/D转换器。A/D转换器(简写为ADC)的功能是将采样保持后的模拟信号转换为按特定编码规则量化的数字信号。常见的A/D转换器主要有两种，逐次比较型(也称为逐次逼近型)和双积分型。

7.5.1 逐次比较型A/D转换器

逐次比较型转换过程和用天平称物重非常相似。天平称重物过程是，从最重的砝码开始试放，与被称物体行进比较，若物体重于砝码，则该砝码保留，否则移去。再加上第二个次重砝码，由物体的重量是否大于砝码的重量决定第二个砝码是留下还是移去。照此一直加到最小一个砝码为止。将所有留下的砝码重量相加，就得此物体的重量。仿照这一思路，逐次比较型A/D转换器，就是将输入模拟信号与不同的参考电压作多次比较，使转换所得的数字量在数值上逐次逼近输入模拟量对应值。

对如图7.17所示的电路，它由启动脉冲启动后，在第一个时钟脉冲作用下，控制电路使数据寄存器的最高位D_n-1为1,其他位置为0,这样形成数据1000…0(具体的数字位数由A/D转换器位数所决定),这一数值送入D/A转换器后将输出电压V_ref/2(其中V_ref为A/D转换量化处理的满量程电压)。A/D转换器的输入电压将与D/A转换器的输出进行比较，若V₁≥V_ref/2则比较器输出为1,否则输出0,这一比较结果将存于数据寄存器的D_n-1位。然后在第二个时钟脉冲作用下，数据寄存器的次高位D_n-2置1,其他低位设为0,最高位由上一次的比较结果所决定。如果最高位为1,此时D/A转换器的输出将变为3V_ref/4，若V₁≥3V_ref/4则数据寄存器的次高位D_n-2将置为1,否则置为0;如果最高位为0此时D/A转换器的输出将变为V_ref/4，若V₁≥V_ref/4则数据寄存器的次高位D_n-2将置为1,否则置为0。以此类推，逐次比较得到输出数字量。

逐次比较型A/D转换器完成一次转换所需的时间与其位数和时钟脉冲频率有关，位数愈少，时钟频率愈高，转换所需时间越短。这种A/D转换器具有转换速度较快，精度高的特点。

下面以一个具体的实例说明A/D转换过程。设图7.17中A/D转换器的分辨率为8位，A/D转换器的输入模拟量V₁=6.84V,D/A转换器基准电压V_ref=10V。根据逐次比较A/D转换器的工作原理，可画出在转换过程中时钟脉冲、启动脉冲、D7～D0及D/A转换器输出电压Vo的波形，如图7.18所示。

图7.17逐次比较型A/D转换器原理

图7.18逐次比较型A/D转换器波形图

(1)当启动脉冲低电平到来后A/D转换开始，在第一个时钟脉冲CP作用下，数据寄存器将D₇～D₀=10000000送入D/A转换器，其输出电压Vo=5V。由于V₁>Vo,因此D₇设置为1。

(2)第二个时钟脉冲时，寄存器输出D₇～D₀=11000000,Vo=7.5V。由于V₁<Vo,所以D6设置为0。

(3)第三个时钟脉冲时，寄存器输出D₇～D₀=10100000,Vo=6.25V。由于V₁>Vo,所以D₅设置为1。

(4)第四个时钟脉冲时，寄存器输出D₇～D₀=10110000,Vo=6.875V。由于V₁<Vo,所以D₄设置为0。

(5)第五个时钟脉冲时，寄存器输出D₇～D₀=10101000,Vo=6.5625V。由于V₁>Vo,所以D₃设置为1。

(6)第六个时钟脉冲时，寄存器输出D₇～D₀=10101100,Vo=6.71875V。由于V₁>Vo,所以D₂设置为1。

(7)第七个时钟脉冲时，寄存器输出D₇～D₀=10101110,Vo=6.796875V。由于V₁>Vo,所以D₁设置为1。

(8)第八个时钟脉冲时，寄存器输出D₇～D₀=10101111,Vo=6.8359375V。由于V₁>Vo,所以D。设置为1。

当八位均比较完时，得到的最终结果为D₇～D₀=10101111,即为A/D转换后的量化结果。该数字量所对应的模拟电压为6.8359375V,与实际输入的模拟电压6.84V的相对误差仅为0.06%。

7.5.2 双积分型A/D转换器

采用双积分法的A/D转换器由电子开关、积分器、比较器和控制逻辑等部件组成。如图7.19所示。基本原理是将输入电压变换成与其平均值成正比的时间间隔，再把此时间间隔转换成数字量，属于间接转换。双积分法A/D转换的过程是先将开关接通，待转换的模拟量Vi采样输入到积分器，积分器从零开始进行固定时间T的正向积分；积分时间T到后，开关再接通与Vi极性相反的基准电压V_ref将其输入到积分器，进行反向积分，直到输出为0V时停止积分。Vi越大，积分器输出电压越大，反向积分时间也越长。计数器在反向积分时间内所计的数值(脉冲个数),就是输入模拟电压Vi所对应的数字量，从而实现了A/D转换。

图7.19双积分型A/D转换器原理

(a)原理框图；(b)原理波形

由于双积分A/D转换器在转换时间内采集的是输入电压的平均值，因此具有很强的抗工频干扰能力。尤其对周期等于第一个积分周期T(也称为A/D转换的采样时间)或者其几分之一的对称干扰(所谓对称干扰是指整个周期内平均值为零的干扰),从理论上来说，有无穷大的抑制能力。即使当工频干扰幅度大于被测直流信号，使得输入信号正负变化时，仍有良好的抑制能力。由于在工业系统中经常碰到的是工频(50Hz)或工频的倍频干扰，故通常选定采样时间T总是等于工频电源周期的倍数，如20ms或40ms等。另一方面，由于在转换过程中，前后两次积分所采用的同一积分器。因此，在两次积分期间(一般在数十到数百毫秒之间),R,C和脉冲源等元器件参数的变化对转换精度的影响均可忽略。

双积分型A/D转换器主要有以下特点。

(1)计数脉冲个数与RC无关，可以减小由RC积分非线性带来的误差。

(2)对脉冲源要求不变，只要在两个积分时间内稳定即可。

(3)转换精度高。

(4)转换速度慢，不适于高速应用场合。

7.5.3 采集控制方式

A/D转换后的结果，需要交由计算机进行运算和存储等处理。这就涉及到数据采集的控制方式。

依然可以参考流水线的例子，A/D转换器加工好以后的产品(数字信号)要被小车输送到仓库(寄存器)中，由于A/D转换器加工产品需要一定的时间，小车的运送是要预先设定好的，如何协调好A/D转换器与运送小车之间的关系呢?这就是采集控制方式要解决的问题。

1.无条件采集

无条件采集方式最简单，就是让小车按照预先设定好的周期来运送产品，而不管A/D转换器加工产品的状态。

当采集一开始，模拟信号x(t)的第一个采样点的数据就被采集，然后，经过一个采样周期，再采集第二个采样点数据，直到将一段时间内的模拟信号的采样点数据全部采完为止。这种方式主要用于某些A/D转换器可以随时输出数据的情况。CPU认为A/D转换器总是准备好的，只要CPU发出读/写命令，就能采集到数据。CPU采集数据时，不必查询A/D转换器的转换状态，也无须控制信号的介入，只通过取数或存数指令进行数据的读/写操作，其时间完全由程序安排决定。

无条件采集的优点在于模拟信号一到就被采入系统，因此，它适用于采集任何形式的模拟信号，例如，重复的或不重复的。又由于所有采样点是按时间顺序排列，因而易于实现信号波形的显示。

无条件采集的缺点在于每个采样点数据的采样、量化、编码、存储，必须在一个采集时间间隔内完成。若对信号的采集时间间隔要求很短时，那么每个采样点的数据处理就来不及做了。

无条件采集除了通常使用的定时采样(即等间隔采样)外，还常常使用变步长采样(即等点采样)。这种采样方法无论被测信号频率为多少，一个信号周期内均匀采样的点数总共为N个。由于这种采样方法的采样信号周期随被测信号周期变化，故通常称为变步长采样。变步长采样既能满足采样精度要求，又能合理地使用计算机内存单元，还能使数据处理软件的设计大为简化。

应该注意，必须在确信A/D转换器总处于准备好的情况下才能使用该方式。

2.条件采集

这种采集过程是受控制的。常用的控制方式有程序查询方式、中断控制方式。

(1)程序查询方式。当采集系统实时性要求不高时，可以采用程序查询方式进行巡回采集。所谓查询，就是CPU不断地询问A/D转换器的状态，了解A/D转换器是否转换结束。当需要采集时，CPU发出启动A/D转换的命令，等到A/D转换结束后，由第一输入通道将结果取入内存，然后CPU再向A/D转换器发出转换命令，等到A/D转换结束后，由第二通道将结果取入内存……,直至所有通道采集完毕；如果A/D转换未结束，则CPU等待，并在等待中做定时查询，直到A/D转换结束为止。

程序查询方式相当于派管理员(CPU)一直盯着A/D转换器，如果加工好了，就让小车运到仓库，如果没有加工好，就一致盯着。

查询方式的优点在于要求的硬件少，编程也简单。特别是询问与执行程序同步，能确知A/D转换所需的时间。这种方式的缺点是：程序查询常常浪费CPU的时间，使其利用率不高。为了提高CPU的工作效率，可以采用中断控制方式进行数据采集。

(2)中断控制方式。采用中断方式时，CPU首先发出启动A/D转换的命令，然后继续执行主程序。当A/D转换结束时，则通过接口向CPU发出中断请求，请求CPU暂时停止工作，来取转换结果。当CPU响应A/D转换器的请求时，便暂停正在执行的主程序，自动转移到读取转换结果的服务子程序中。在执行完读取转换结果的服务子程序后，CPU又回到原来被中断的主程序继续执行下去。这就大大提高了CPU的效率。

中断控制方式相当于给管理员配了一个呼叫器，A/D转换器工作时不用在现场盯着，如果A/D转换器加工好了，就呼叫管理员，管理员接到呼叫，停下手头的其他工作，然后命令小车将产品运送到仓库，完了以后再接着干手头的工作。

3.直接存储器存取(DMA)方式

利用中断控制方式进行数据采集，可以大大提高CPU的利用率。但是，中断方式仍是由CPU通过程序，把采集的数据从I/O端口传送至CPU的寄存器，然后再由寄存器送至内存。

图7.20中实线部分为中断方式传送数据的示意。在此过程中，CPU的寄存器是数据的必经之路，从而使数据传输需要一定的时间。如果要高速数据采集，采用中断控制方式显然是不合适的。

图7.20DMA传送方式示意图

DMA方式是一种由硬件完成数据传送操作的方式。如图7.20所示，虚线部分表示在DMA控制器控制下，数据直接在外部设备和存储器MEM之间进行传送，而不通过CPU和I/O,因而可以大大提高数据的采集速率。

以上介绍的采样控制方式各有利弊，应根据采样速率的要求、系统工作的特点、模拟信号的数量、计算机的工作任务等方面综合考虑进行选择。

(1)无条件采集。无须控制信号介入，所要求的硬件和软件最简单，但仅适于随时处于准备好状态的A/D转换器，且要求CPU与A/D转换器同时工作，使用时很不方便。

(2)中断方式。具有很强的实时处理能力，可充分发挥CPU的效率。但通常这种方式的软件开发和调试比查询方式要困难些。构成一个高效、可靠的中断系统的费用，可能比查询方式系统要稍高些。如中断源过多时，将造成频繁申请中断，使CPU没有时间处理其他运算，在CPU效率方面和查询方式就没有什么两样了。所以中断方式通常应用于主程序要同时处理其他任务，不宜接受查询的情况下，以及一个或多个模拟信号源要实时采集而不允许错过的场合。

(3)查询方式。与中断方式比较，无须保护现场，软件开发和调试比较容易，所需硬件也少。但查询需浪费CPU的时间，且当实时系统给定时间限制时，软件编制相对要难些。所以当查询方式能满足系统等待时间要求时，或一个系统专门采集几个模拟信号源的特殊情况下，查询方式是令人满意的。

(4)DMA方式。此方式传送每个字节只需一个存储周期，而中断方式一般不少于10个周期，且DMA控制器可进行数据块传送，不花费取指令时间，所以DMA方式传送数据的速度最快。因此，一个数据采集系统是否采用DMA方式，常需在速度、灵活性与价格之间做出折衷考虑。DMA方式常用于高速数据采集系统。

虽然DMA方式的硬件复杂程度和成本比前几种方式相对较高，但总体来说均在可接受的范围内。因此，目前的数据采集系统一般都采用DMA方式。在一些对采集频率和时间精度要求不高的情况下，可能会采用另外几种控制方式，如简单的数显仪表和手持式监测仪等。

7.6 总线技术

所谓总线是指计算机、测量仪器、自动测试系统内部以及相互之间信息传递的公共通路，是计算机和内部测试系统的重要组成部分，其性能在计算机和自动测试系统中具有举足轻重的作用。简单的来说，总线规定了计算机、仪器设备等内部及相互之间进行信息传输的标准规范，在硬件上涉及外形尺寸、安装方式、物理接口标准、电气信号连接等等，在软件上涉及了软件开发与应用接口函数、通讯协议等等。总线是计算机、自动测试系统乃至网络系统的基础。

我们可以把总线想象成一个高速公路网络，信号和数据相当于汽车，为了能让汽车在高速路网上高速、高效和可靠地运行，就需要按照一定的规范建设硬件设施，汽车也要按照交通规则运行，总线技术就是这些规范和规则的总和。现在世界各地的高速公路都很相似，这是为什么呢?因为按照标准化的方式来建设，不仅可以降低成本，而且可以提高运行效率和安全性。

利用总线技术，能够大大简化系统结构，增加系统的兼容性、开放性、可靠性和可维护性，便于实行标准化以及组织规模化的生产，从而显著降低系统成本。总线的类别很多，分类方式多样，典型的分类是仪器总线(如GPIB,VXI和PCI)、计算机总线(如ISA,PCI,USB和IEEE1394)和工业现场总线(如Profi Bus,CAN和Field Bus)等。总线技术包含的内容极为广泛，这里主要介绍目前广泛使用的GPIB,VXI,PCI,PXI和LXI总线技术。

7.6.1 IEEE488总线

IEEE488通用接口总线又称GPIB(General Purpose Interface Bus)总线，是HP公司在20世纪70年代推出的台式仪器接口总线，因此又叫HPIB(HP Interface Bus),1975年IEEE和IEC确认为IEEE488和IEC652标准。该标准总线在仪器、仪表及测控领域得到了最广泛的应用。虽然该总线出现的时间比较久，但目前仍在很多传统仪器中广泛使用，如信号发生器、示波器等。

这种系统是在计算机中插入一块GPIB接口卡，通过24或25线电缆连接到仪器端的GPIB接口。当计算机的总线变化时，例如采用PCI或PCIE等不同总线，接口卡也随之变更，其余部分可保持不变，从而使GPIB系统能适应计算机总线的快速变化。GPIB总线是一种数字式并行总线，最多可以连接15个设备(包括作为主控器的主机),可以采用星形连接或者线性连接的拓扑结构，如图7.21所示。GPIB仪器的接口插头照片如图7.22所示。

图7.21GPIB仪器连接的拓扑结构

（a）星形连接；(b)线性连接

图7.22GPIB接口插头

由于GPIB系统在PC出现的初期问世，所以有一定的局限性。如其数据线只有8根，传输速率最高1Mbps(如果采用高速HS488交互握手协议，传输速率可高到8Mbps),传输距离20m(加驱动器可达500m)等等。尽管如此，目前GPIB仍是仪器、仪表及测控系统与计算机互连的主流并行总线。因为装有GPIB接口的台式仪器的品种和数量都明显超过倍受青睐的VXI仪器，而且在目前应用的VXI系统中，与GPIB混合应用比例很大，还有相当数量采用外主控计算机控制的VXI系统，其计算机通过GPIB电缆和GPIB-VXI接口进行控制。以PCI为基础的PXI系统，也都具有GPIB接口。所以，在相当长的时间内，GPIB系统仍将在实际应用中，特别是中、低速范围内的计算机外设总线应用中占有一定的市场。

7.6.2 VXI总线

VXI(VMEbuse Xtensionfor Instrumentation)总线是VME计算机总线在仪器领域中的扩展，由HP等公司于1987年提出，1992年成为IEEE1155标准。在该系统中围绕机械、电气、控制方式、通信协议、电磁兼容、软面板、驱动程序、I/O控制乃至机箱、印制电路板的VXI总线产品相互兼容。VXI规范定义了3个96针的DIN连接器P1,P2和P3,P1连接器是系统必备的，P2和P3两个连接器可选。从功能上分，VXI总线系统共有以下8种总线。

(1)VME计算机总线。

(2)时钟和同步总线。

(3)模块识别总线。

(4)触发总线。

(5)相加总线。

(6)本地总线。

(7)星形总线。

(8)电源线。

VXI系统综合了计算机技术、GPIB技术、PC仪器技术、接口技术、VME总线和模块化结构技术的成果，1998年修订的VXI2.0版本规范采用了VME总线的最新进展，提供了64位扩展能力，数据传输率最高可达80Mbps。VXI系统最多可包含256个器件(装置),可组成一个或多个子系统，每个子系统最多可包含13个插入式模块，插入一个机箱内，在组建大、中规模自动测量系统以及对速度、精度要求高的场合，具有其他仪器无法比拟的优势，如图7.23和图7.24所示。

VXI规范定义了4种尺寸的VXI模块。较小的尺寸A和B是VMEbus模块定义的尺寸，并且从任何意义上来说，它们都是标准的VEMbus模块。较大的C和D尺寸模块是为高性能仪器所定义的，它们增大了模块间距，以便对包含用于高性能测量场合的敏感电路的模块进行完全屏蔽。A尺寸模块只有P1,P2和P3连接器。目前市场上最常见的是C尺寸的VXIbus系统，这主要是因为C尺寸的VXIbus系统体积较小，成本相对较低，又能够发挥VXIbus作为高性能测试平台的优势。VXI总线支持即插即用，人机界面良好，资源利用率高，容易实现系统集成，大大地缩短了研制周期，且便于升级和扩展。但VXI系统的成本相对较高。

为什么要对机箱尺寸、模块间距这些非常具体的内容设置规范呢?这是因为通过长期的实践，人们发现测试过程和结果受很多环境因素的影响，例如散热、电磁干扰、振动等，只有对这些具体环节进行具体和细致的规范，才能保证测试的系统的可靠工作。

图7.23 VXI模块尺寸与总线分布

图7.24 典型的VXI系统配置

7.6.3PCI和PXI总线

外围设备互连总线(Peripheral Component Interconnect, PCI)由Intel公司于1993年提出后，很快成为PC行业新的事实上的标准，PCI总线是一种同步的、独立于CPU的32/64位局部总线，最高工作频率33MHz(32位)和66MHz(64位),数据传输率为127.2MB·s-(32位)和508.6MB·s^-1(64位),很好地解决了ISA总线(早期的计算机总线)的瓶颈问题，并带来了真正的即插即用(PnP)功能，大大提高了系统的数据采集率。Compact PCI总线由多家厂商于1994年提出，是PCI总线的12种规范之一，也是PCI总线的增强和扩展，在电气上完全与PCI兼容，具有抗振颤和利于散热等优点，更适合于工业测控的应用。其数据宽度同PCI一样，最高传输速率可达528MB·s^-1。在计算机硬件不断发展过程中，PCI总线的带宽逐渐成为显卡的发展瓶颈，因而出现了取代PCI总线的第三代I/O技术PCIExpress(简写为PCI-E或PCIe)规范，2007年推出的PCIExpress2.0规范将传输速度提升为5GB·s^-1。

PXI总线是1997年美国国家仪器公司(NI)发布的一种高性能低价位的开放性、模块化火箭发动机测试技术器总线。PXI是PCI在仪器领域的扩展(PCI eXtensions for Instrumentation),是用于自动测试系统机箱底板总线的规范，在机械结构方面与Compact PCI总线的要求基本相同，不同的是PXI总线规范对机箱和印制电路板的温度、湿度、振动、冲击、电磁兼容性和通风散热等提出了要求，与VXI总线的要求非常相似。在电气方面，PXI总线完全与Compact PCI总线兼容。所不同的是PXI总线为适合于测控仪器、设备或系统的要求，增加了系统参考时钟、触发器总线、星型触发器和局部总线等内容。除了PXI系统具有多达八个扩展槽(一个系统槽和7个仪器模块槽),而绝大多数台式PCI系统仅有三个或四个PCI扩展槽这点差别之外，PXI总线与台式PCI规范具有完全相同的PCI性能。而且，利用PCI-PCI桥技术扩展多台PXI系统，可以使扩展槽的数量理论上最多能扩展到256个。其他的PCI性能还包括以下几种。(1)33MHz和66MHz工作频率。(2)32位和64位数据宽度。(3)127.2MB·s^-1 (32位)和508.6MB·s-¹(64位)的峰值数据吞吐率。(4)通过PCI-PCI桥技术进行系统扩展。(5)即插即用功能。PXI将Windows NT和Windows 95定义为其标准软件框架，并要求所有的仪器模块都必须带有按VISA规范编写的WIN32设备驱动程序，使PXI成为一种系统级规范，保证系统的易于集成与使用，从而进一步降低用户的开发费用，所以在数据采集、工业自动化系统、计算机机械观测系统和图像处理等方面获得了广泛应用。PXI的规格有两种：3U(100mm×160mm)和6U(233.35mm×160mm),如图7.25所示。PXI硬件由3个基本部分组成：机箱、系统控制器和外设模块。PXI保留3UPXI64位PCI和PXIJ132位PCI6UPXIPXI保留PXI保留364位PCI和J2PXIJ132位PCI图7.25PXI规格7.6.4LXI总线LXI(LAN eXtensions for Instrumentation)由安捷伦科技和VXI Technology公司于2004年推出。LXI基于IEEE802.3以太网技术，是以太网在仪器领域的扩展，它利用现有Ethernet标准、Internet工具、LAN协议、IEC物理尺寸和IVI驱动程序的各方优点，从而使测试系统的互连平台转向了具有更高传输速率的PC标准的IO,而不需要机箱和昂贵的电缆，并可使用标准的软件，如图7.26所示。LXI总线速度现在最快达到数千MB·s^-1,未来还将向数万MB·s^-1发展。LXI理论上支持的设备数目不受限制，并且通过使用路由器、交换机—140—火箭发动机测试技术

器总线。PXI是PCI在仪器领域的扩展(PCI eXtensions for Instrumentation),是用于自动测试系统机箱底板总线的规范，在机械结构方面与Compact PCI总线的要求基本相同，不同的是PXI总线规范对机箱和印制电路板的温度、湿度、振动、冲击、电磁兼容性和通风散热等提出了要求，与VXI总线的要求非常相似。在电气方面，PXI总线完全与Compact PCI总线兼容。所不同的是PXI总线为适合于测控仪器、设备或系统的要求，增加了系统参考时钟、触发器总线、星型触发器和局部总线等内容。

除了PXI系统具有多达八个扩展槽(一个系统槽和7个仪器模块槽),而绝大多数台式PCI系统仅有三个或四个PCI扩展槽这点差别之外，PXI总线与台式PCI规范具有完全相同的PCI性能。而且，利用PCI-PCI桥技术扩展多台PXI系统，可以使扩展槽的数量理论上最多能扩展到256个。其他的PCI性能还包括以下几种。

(1)33MHz和66MHz工作频率。

(2)32位和64位数据宽度。

(3)127.2MB·s^-1 (32位)和508.6MB·s^-1 (64位)的峰值数据吞吐率。

(4)通过PCI-PCI桥技术进行系统扩展。

(5)即插即用功能。

PXI将Windows NT和Windows 95定义为其标准软件框架，并要求所有的仪器模块都必须带有按VISA规范编写的WIN32设备驱动程序，使PXI成为一种系统级规范，保证系统的易于集成与使用，从而进一步降低用户的开发费用，所以在数据采集、工业自动化系统、计算机机械观测系统和图像处理等方面获得了广泛应用。

PXI的规格有两种：3U(100mm×160mm)和6U(233.35mm×160mm),如图7.25所

示。PXI硬件由3个基本部分组成：机箱、系统控制器和外设模块。

图7.25 PXI规格

7.6.4 LXI总线

LXI(LAN eXtensions for Instrumentation)由安捷伦科技和VXI Technology公司于2004年推出。LXI基于IEEE802.3以太网技术，是以太网在仪器领域的扩展，它利用现有Ethernet标准、Internet工具、LAN协议、IEC物理尺寸和IVI驱动程序的各方优点，从而使测试系统的互连平台转向了具有更高传输速率的PC标准的IO,而不需要机箱和昂贵的电缆，并可使用标准的软件，如图7.26所示。LXI总线速度现在最快达到数千MB·s^-1,未来还将向数万MB·s^-1发展。LXI理论上支持的设备数目不受限制，并且通过使用路由器、交 换机和中继器，对线缆长度几乎没有限制，还可以使用无线局域网技术。LXI不受地理限制，可以实现远程测量应用。LXI被认为未来将取代GPIB,但与GPIB相比LXI还存在一定的延迟问题。

图7.26 LXI总线仪器

LXI标准围绕四个主要方面：物理要求、Ethernet协议、LXI接口和LXI触发。所有LXI必须实现IEEE 802.3 Ethernet标准接口(推荐RJ—45连接器)。它们必须至少使用TCP/IP协议IPv4版，支持IP(Internet协议)、TCP(传输控制协议)和UDP信息，LXI标准推荐Giga-bit Ethernet。

LXI模块不同于VXI和PXI,因为LXI是自封装的。LXI模块提供自己的电源、冷却、触发、EMI屏蔽和Ethernet通信。它可用世界各地的交流电源供电(100～240Vac和47～66Hz),也可使用隔离48V作直流供电，并且允许Ethernet供电。LXI标准为各附件推荐了特定的物理位置，包括电源线(后板右方)、电源开关(后板右下方)、Ethernet连接器(后板电源左方)、LAN复位开关(后板凹入处)、触发总线电缆(后板最右方)、信号出入模块(前板)和LAN/电源/IEEE1588指示器(前板左方)。对于带前面板的LXI仪器，LAN/电源/IEEE1588指示器可在显示器上示出，对于在前面有键盘的装置，LAN复位开关可由其键盘实现。

在寻址方面，每一个LXI必须有一个不可改变的MAC地址，以及可通过DHCP(动态主机配置协议)、自动IP和手动IP改变的IP地址。LXI装置支持动态主名注册，此时装置IP地址由网络主机映射到多个用户友好名称。这一寻址规则保证了LXI仪器在网络中的共存，而不要求用户做许多工作。

通过融合LAN和IEEE1588时间同步协议，LXI提供多种GPIB、PXI和VXI所不具备的触发模式。三种类型的LXI设备：C类、B类和A类，递增地实现这些能力。

(1)C类是基本类型，它包括对LAN接口和协议的全部要求，LAN查询功能，IVI驱动程序接口，仪器网页，以及推荐的电源、冷却、尺寸、指示灯和复位按钮。所有LXI仪器必须达到C类要求。

(2)B类包括全部C类要求并加上IEEE1588时间同步。因此有可能实现位于网络任何位置LXI设备的亚微秒级同步。B类还增加对等和一对多的LAN信息传送模式(B类和A类要求，C类允许)。

(3)A类包括C类和B类要求，并增加了能使相邻LXI仪器触发的硬件触发总线。该触发总线类似于VXI的背板总线，这是8路的低电压差分总线，对相邻仪器能达到5ns·m^-1的定时精度。预期合成仪器将是符合A类标准的仪器。

每一台符合LXI标准的设备都必须提供自己的网页。网页上要有该设备的各种重要信息，包括制造商、型号、序列号、说明、主名、MAC地址和IP地址。标准还要求这一可从浏览器接入的配置网页要允许使用者改变参数，如主名、说明、IP地址、子网掩码和TCP/IP配置模式。接入这些网页很简单，只需把仪器的IP地址键入任何W3C浏览器的地址行。

7.7 虚拟仪器技术

7.7.1 虚拟仪器的概念

虚拟仪器(Virtual Instrument, VI)概念最早是由美国国家仪器公司(National Instrument, NI)提出的。虚拟仪器是指通过应用程序将通用计算机与功能化硬件结合起来，用户可通过友好的图形界面来操作这台计算机，就像在操作自己定义、自己设计的一台单个仪器一样，从而完成对被测试量的采集、分析、判断、显示、数据存储等。与传统仪器一样，它同样划分为数据采集、数据分析处理、显示结果三大功能模块。

虚拟仪器的实质是利用I/O接口设备完成信号的采集与传输，利用计算机强大的软件功能完成信号的运算、分析与存储，利用计算机显示器模拟传统仪器的控制面板，并以多种形式表达输出测试结果。

虚拟仪器是计算机技术与仪器技术深层次结合产生的全新概念的仪器。它将许多以前由硬件完成的信号处理工作，交由计算机软件进行处理，这种测试仪器的硬件功能软件化，是对传统仪器概念的重大突破，是仪器领域内的一次革命。虚拟仪器是继第一代仪器——模拟式

仪器、第二代仪器——分立元件式仪表、第三代仪器——数字式仪器、第四代仪器——智能化仪器之后的新一代仪器。虚拟仪器代表了当前测试仪器发展的方向之一。

7.7.2 虚拟仪器的组成

虚拟仪器是计算机化的仪器，由计算机、模块化功能硬件和应用软件三大部分组成。一般而言，虚拟仪器所用的计算机是通用的计算机，虚拟仪器根据其模块化功能硬件的不同，而有多种构成方式。例如以数据采集卡、信号调理电路及计算机为仪器硬件平台组成的PC-DAQ测试系统，以GPIB标准总线仪器与计算机为硬件平台组成的GPIB测试系统，以VXI标准总线仪器与计算机为硬件平台组成的VXI测试系统，等等。如图7.27所示显示出了虚拟仪器典型的体系结构。

无论上述哪种形式的虚拟仪器系统，都是通过应用软件将仪器的模块化功能硬件与各类计算机相结合，如图7.28所示显示了采用多种不同总线技术的虚拟仪器系统。PC-DAQ测试系统是虚拟仪器VI最常用的最基本方式，因为一般而言，这种类型的虚拟仪器成本比较低，它能充分利用计算机的计算能力。

图7.27 虚拟仪器典型的体系结构

图7.28 采用多种总线技术的虚拟仪器系统

7.7.3虚拟仪器的特点

在虚拟仪器系统中，强调“软件构成仪器”的概念，硬件仅仅是为了解决信号的输入输出，软件才是整个仪器的关键，用户可以根据自己需要定义仪器的功能，通过修改软件的方法，很方便地改变、增减仪器系统的功能与规模，并可方便地同外设、网络及其他应用连接。从这一角度来看，与传统仪器相比虚拟仪器具有以下三个特点。

1. 不强调物理上的实现形式

虚拟仪器通过软件功能来实现数据采集与控制、数据处理与分析及数据的显示这三部分的物理功能。其充分利用计算机系统强大的数据处理能力，在基本硬件的支持下，利用软件完成数据的采集、控制、数据分析和处理以及测试结果的显示等，通过软、硬件的配合来实现传统仪器的各种功能。

2. 在系统内实现软硬件资源共享

虚拟仪器的最大特点是将计算机资源与仪器硬件、数字信号处理(DSP)技术相结合，在系统内共享软硬件资源。它打破了以往由厂家定义仪器功能的模式，而变成了由用户自己定义仪器功能。使用相同的硬件系统，通过不同的软件编程，就可实现功能完全不同的测量仪器。

3. 图形化的软件面板

虚拟仪器没有常规仪器的控制面板，而是利用计算机强大的图形环境，采用可视化的图形编程语言和平台，以在计算机屏幕上建立图形化的软面板来替代常规的传统仪器面板。软面板上具有与实际仪器相似的旋钮、开关、指示灯及其他控制部件。在操作时，用户通过鼠标或键盘操作软面板，来检验仪器的通信和操作。

除上述特点之外，与传统仪器相比(见表7.1),虚拟仪器还有以下几方面的优势。

(1)虚拟仪器用户可以根据自己的需要灵活地定义仪器的功能，通过不同功能模块的组合可构成多种仪器，而不必受限于仪器厂商提供的特定功能。

(2)虚拟仪器将所有的仪器控制信息均集中在软件模块中，可以采用多种方式显示采集的数据、分析的结果和控制过程，这种对关键部分的转移进一步增加了虚拟仪器的灵活性。

(3)由于虚拟仪器关键在于软件，硬件的局限性较小，因此与其他仪器设备连接比较容易实现，而且虚拟仪器可以方便地与网络、外设及其他应用连接，还可利用网络进行多用户数据共享。

(4)虚拟仪器可实时、直接地对数据进行编辑，也可通过计算机总线将数据传输到存储器或打印机。这样做一方面解决了数据的传输问题，另一方面充分利用了计算机的存储能力，从而使虚拟仪器具有几乎无限的数据记录容量。

(5)虚拟仪器利用计算机强大的图形用户界面(GUI),用计算机直接读数。根据工程的实际需要，使用人员可以通过软件编程或采用现有分析软件，实时、直接地对测试数据进行各种分析与处理。

(6)虚拟仪器价格低，而且其基于软件的体系结构还大大节省了开发和维护费用。

表7.1虚拟仪器与传统仪器对比

7.7.4虚拟仪器的开发环境

当前，各种虚拟仪器开发工具和平台种类比较多，但总体上说，虚拟仪器应用程序的开发 环境主要有两类：

 一类是通用编程软件，常用的有VB,VC++,Visual Studio.net、Delphi和C++Builder 等。用户通过静态/动态连接库调用或者采用COM技术进行虚拟仪器二次开发，将外部硬件 通过驱动程序连接到计算机上，根据需要开发相应的数据分析或仪器控制功能。NI公司的 LabWindows/CVI基于C语言形成了一个独立的虚拟仪器开发平台，将仪器面板(界面)设计 和程序代码开发集于一体。

另一类是基于图形化语言(又称为“G”语言)的软件开发环境，常用的有NI公司的Lab- VIEW、Agilent公司的VEE和HPTIG软件等。

目前最为流行的虚拟仪器开发环境是LabVIEW(Laboratory Virtual Instrument Engi- neering Workbench)。利用LabVIEW进行虚拟仪器开发主要包括两方面的工作：一是用于 图形用户界面的前面板设计(见图7.29);二是进行实现程序功能的框图开发，这一过程与传 统程序开发环境中代码编写类似，最大的不同是利用框图连线代替了代码编写。如图7.30所 示显示了一个简单正弦信号发生器的框图程序。采用LabVIEW可以实现快速、高效的开发 虚拟仪器程序。对虚拟仪器开发感兴趣的读者可以参考相关的教材进行学习。

 图7.29虚拟数字示波器的软面板

图7.30 框图程序

7.8 数据采集系统应用举例

7.8.1 富氧烧蚀实验系统的测控方案

为了模拟固体火箭冲压发动机补燃室内的富氧烧蚀环境，考核绝热材料的烧蚀性能，采用了一种富氧烧蚀实验系统。其工作原理是将一定流量的氧气、氮气和燃气进行混合，使混合气的压强、温度、速度和氧浓度等参数与固冲发动机补燃室的富氧烧蚀环境接近，将绝热材料试件放在该气氛下进行烧蚀实验，测量其烧蚀率。实验中需要测试多种参数项目：氧气和氮气稳压舱的压强、流量、节流孔板前压强、燃气发生器室压、试验段压强和燃气温度等，测试系统还承担了发动机点火、氧气和氮气管路阀门时序控制的任务。

针对该实验任务测控系统采用了“PCI总线十网络”的工作模式，测试软件采用LabVIEW编写。测试系统的服务器端位于实验现场，采用了内置NIPCI-6259多功能数据采集卡的工控机，直接测量被测参数并进行时序控制；客户端位于百米之外的测控室，用户直接操作客户端软件，通过网络实现操作指令与数据的传递。如图7.31所示为测控系统框图，如图7.32所示为测控软件的界面。

7.8.2 组合发动机实验系统的测控方案

火箭基组合循环发动机(RBCC)地面直连实验系统由多个子系统组成：燃料供应系统、氧化剂供应系统、加热火箭、一次火箭和实验发动机等。需要测试的项目众多，包括不同管路上液体/气体的压强、温度和流量，以及实验发动机推力和不同位置的压强分布等，并需要对实验系统多个点火器和数十个管路阀门的工作时序进行精确控制。为了保证实验状态参数调节的重复性和准确性，实验系统还采取了自动控制技术，由控制系统自动调节实验系统中各减压器压强。系统中还配备了液体火箭发动机点火状态监测模块，一旦检测到液体火箭发动机未能正常点火，将给PLC时序控制系统发出紧急关机指令，以保证整个实验过程能够安全中止。

整个测试系统需要测试的参数超过100路，控制参数为30多路。该实验测试系统采用了“VXI总线+PLC”的测控方案，如图7.33所示。

图7.31富氧烧蚀实验测控系统框图

图7.32富氧烧蚀测控软件界面

图7.33 RBCC实验测控系统框图

7.8.3 发动机综合实验室集成测试方案

某研究所建立的发动机综合实验室，包含了固体发动机、固冲发动机、水冲压发动机、高过载试验、热结构试验、火工品装置试验等试车台。出于安全考虑，测控大厅距离各试验现场近百米，需要解决信号的远距离传输问题，因而采用了LXI总线技术。由于测试系统需要为多个试验项目进行服务，为了提高测试系统利用率，并节约建设费用，对测试系统进行了模块化设计，整个集成测试系统结构如图7.34所示。

图7.34 发动机综合实验室集成测试方案框图

测试系统包括2台32通道扫描采集模块(最高采样频率为500kHz)和1台8通道并行采集模块(单通道采样频率100kHz),最大测试能力包括32通道压强和推力等电压信号，16通道温度信号，16通道应变信号，8通道振动信号。传感器输出的信号首先接入信号调理模块(进行信号放大和滤波，并为桥路提供激励),然后再接入位于实验现场的便携式数据采集模块(根据测试需要可接入并采或者串采模块),数据采集模块通过网络与远端测控大厅的主控机相连。实验测试人员可以根据实际需要将测试模块移动至相应的测试现场，从而实现了测试设备的高效重复利用。实验测试时，测试人员在测控大厅操作主控机，通过网络对前端的测试模块发出控制指令，完成测试参数设置、数据采集与存储等功能。

整个测试系统的功能除了数据采集之外，还包括具有5路点火和10路控制的高精度时序点火控制功能，15路闭路监控和10路对讲功能。为了实现实验现场与测控大厅之间大量信号的实时高效传输，测试系统采用了光纤传输技术。

第8章测量系统的干扰及其抑制方法

8.1概论

有经验的测试工作者都知道，为了提高测量系统的精度，必须选用精度高、稳定性和频率特性好的测量仪器组成测量系统。有时，即使选用了质量好、精度高的测量仪表组成测量系统，可是把这个系统投入现场使用时，也会由于受到干扰而使测量精度达不到要求。如果被测信号电平很低时，甚至可能出现信号被干扰信号淹没的现象，以致无法进行正常的测量工作。可见，处理好干扰问题，也是关系到测量结果的精度高低和测量工作成败的重要条件之一。所以说，抗干扰既是测试工作者必须要解决的问题，也是必须要掌握的基本知识。

噪声原来的定义是指不同频率，不同强度的杂乱声音的组合。在电工学、电子学等学科中，把那些不需要的电压和电流，并在一定条件下形成危害电路正常工作的电量信号(干扰电压和干扰电流),也称为“噪声”,或者“干扰”。通常，以干扰电量为对象进行研究时，多使用“噪声”这个词；以干扰电量所造成的危害作用为对象进行研究时，多使用“干扰”这个词。

图8.1给出了6种由于叠加了噪声波形而使原来信号产生畸变的情形。即使是有用的正常信号，如果耦合辐射到其他电路或系统中，也会干扰它们的工作。从定义上讲，也应当把这种耦合辐射到其他电路和系统中的信号看作是一种噪声。

图8.1信号与叠加了噪声的信号波形

(a)整流电流的绞波；(b)方波的振铃；(c)正弦波的尖蜂；(d)脉冲波形失真；(e)寄生振荡；(f)共态噪声

在电磁干扰控制技术领域，信号的传播方式不仅有“路”,而且还有“场”,是一种电磁现象。把设备或系统中除去有用信号以外的所有电磁信号称为电磁噪声(简称噪声)。由电磁噪声引发不期望得到的结果，称为电磁干扰(简称干扰)。如果一个噪声电压使得一个电路产生误动作，它就是一个干扰。噪声是不能被消除的，而只能尽量将其抑制，直到其不能引起不良后果。

人们常常把噪声和干扰混淆，其实两者的区别是十分明显的：噪声是原因，干扰是后果。

通常，测量仪器仪表都要给出它的精度指标，但当使用它进行测量时，由于噪声的影响使测量结果的实际精度有所降低。仪表所能检测的最小信号将取决于噪声的大小，此时所能达到的精度和分辨率称为实际精度和实际分辨率。

一个测量系统的实际分辨率是指在保证系统输出端达到一定的信噪比要求的情况下系统的输入端必需的最小信号电压。不言而喻，系统受到的干扰越大，其实际分辨率就越低，测量结果的精度也就越低。

在测量电路中，总是要程度不同的受到噪声的影响。换句话说，被测信号和噪声干扰总是同时存在于测量电路中，而衡量它们之间相对大小的指标就是信噪比，通常以SNR表示。若信号的功率为P_s,信号电压的有效值为S,噪声功率为P_N,噪声电压的有效值为N,则

\(SNR=10\lg\frac{{P}_{s}}{{P}_{N}}=20\lg\frac{S}{N}=20(\lg S-\lg N)\)    (8.1)

其单位为分贝(dB)。

在测量系统中，SNR值大，表示信号大，相对地噪声较小。从测量的角度来看，总是希望SNR尽可能的大，以使测量结果达到所期望的精度。

8.2干扰的产生及耦合

8.2.1电磁干扰的形成因素

电磁干扰由电磁干扰源发射，经过耦合途径传输到被干扰设备(敏感设备)。因此，形成电磁干扰必须具备下列三个基本要素(称为干扰的三要素)。

(1)电磁干扰源。任何形式的人工电子、电气设备或自然现象所发射出的电磁能量，使处于相同环境的其他设备、人或其他生物受到危害，导致不期望的后果，这种发射电磁能的装置或自然现象即称为电磁干扰源。

(2)传输通道。传输通道又称耦合途径或耦合通道，是指把电磁能量从干扰源传输(或耦合)到敏感设备上，即传送电磁干扰的通路或媒介。

(3)敏感设备。敏感设备又称为被干扰设备，指当在电磁干扰源发射的电磁能量发生电磁危害时，导致性能降低的器件、设备或系统，以及受到伤害的人或其他生物。许多器件、设备或系统，既是电磁干扰源又是敏感设备。

8.2.2干扰源

电子设备在工作时，往往产生一些起副作用的干扰电压。干扰产生于干扰源，干扰源可以划分为以下三类。

(1)由于静电、大功率开关触点断开、电机电刷跳动等引起的放电噪声。

(2)由感应电炉、中高频电源、开关电源、逆变电源、可控硅变流器等产生的中高频振荡以及大功率输电线产生的电气干扰噪声。

(3)由于电机启动电流、大功率用电器合闸电流、开关电路的导通电流等产生的浪涌噪声。

1.放电噪声

在放电噪声中，最常见的类型是火花放电产生的噪声干扰。主要是大自然现象的天电(雷电)干扰，同时还有电气设备、大功率开关触点、点火装置等引起的干扰。雷电作为大自然现象的典型代表，是大气层中产生火花放电噪声的主要原因，可以在低频至高频或更高频率范围内造成干扰，可以传播到很远的距离。

火箭发动机的点火器在点火过程中将产生非常陡峭的冲击电流，从而激励了其附属电路的振荡，并由点火导线等辐射出去，这种干扰波具有很高的频率分量。

电动机的旋转运动因其火花放电而成为噪声源。在有整流子换向装置的电动机中，电刷将相邻的整流子片(存在电位差)短接，于是就在与整流片相连接的电机转子绕组中流过短路电流，而转动一角度后，电刷又很快地转入断开状态，在此瞬间即产生了火花。旋转过程是循环往复进行的，因此形成了频率范围很宽的噪声干扰。在没有整流子的电机中，其转子引出电流是采用滑环和电刷，在运转过程中两者接触状态也要发生上述类似变化，同样也会产生火花放电噪声干扰。

开关设备类由于开关的通断而使电流通断也是形成火花放电噪声干扰的原因之一。设备由运行状态转为停止状态，即当开关断开时，开关两极(触点)间的距离由零过渡到断开状态。触点断开瞬间，电极间距离非常小，触点间电压若在最小点火电压以上时，就产生火花放电。特别是感性负载，当切断流经电感的电流时，由于电感的反电动势，将会在触点间产生很大的感应电压，更容易产生火花放电。在产生火花放电之后，往往还伴随着弧光放电和辉光放电(这两类放电也是产生放电噪声的原因),直至熄灭。

2.振荡噪声

大功率输电线是工业频率的干扰噪声来源。低电平的信号线只要有一段距离与输电线相平行，即使输电线功率不够大，也会使其遭受工频干扰。在电子设备内部，由于工频感应也会产生交流声。如果工频电源的波形失真较大，其所包含的高次谐波分量也就越多，因此而产生的干扰也就越大。

感应电炉、中高频电弧炉、开关电源、直流-交流变换器(变频器)、可控硅变流器等设备在工作时，将会产生振荡噪声干扰。这些运用脉冲波形工作的设备在工作过程中会产生感应噪声。因为脉冲波形的电流、电压上升前沿陡峭，从而包含丰富的高次谐波分量，容易引起感应噪声。

电子开关(固态继电器、可控硅等)的通断可使电流发生急剧变化，从而形成干扰。如果电子开关通断的电路是上述脉冲振荡设备，则由于电子开关的通断会产生阻尼振荡。

开关电源作为一种开关方式控制的直流稳压电源，以其体积小、重量轻、效率高的特点被广泛应用于工作控制系统的各个领域，成为工业发展不可或缺的一种电源方式。开关电源为了实现小型化，要提高开关频率。针对频率较低的开关电源，只有开关脉冲的高次谐波产生噪声干扰，而经过高频化设计后，其基波本身也构成了一种噪声干扰源，产生一种更为强烈的传导干扰波，同时也会产生一种超标准的杂散信号。

3.浪涌噪声

有些用电设备诸如炼钢电弧炉、电弧焊机，由固态继电器控制的大电流设备(如电炉)、电机启动(启动电流通常达到额定电流的4～6倍)等，其工作于频繁通断状态，将会产生很大的电流冲击，周期性地从供电网中获取快速变动的冲击性功率，从而引起电网电压的波动，产生浪涌噪声干扰。由大电流冲击而引起的浪涌噪声往往使得电网电源产生很大波动，干扰公共供电点的其他用电设备不能正常工作，因此这种浪涌噪声须加以抑制，控制其最大值在允许范围之内。

在测量现场中噪声可能来自各方面，有时一些常被人们忽视的因素也可能成为一个严重的噪声源。例如采用扭绞的办法(不焊接)连接信号线，接插件接触不良，传感器的引线似断非断等都可能产生接触噪声。特别是在下述情况下更要引起注意：在发动机试车前的静态情况下检查系统工作正常，但当发动机点火工作时，在强大的燃气流的冲击扰动和试车台架的激烈振动下，使隐患立刻暴露出来造成随机干扰，轻者使测量结果中引入偶然误差，重者可使测量完全失败。又如当测量回路中有不同种类的金属导线时，若导线两端的环境温度不同，就会产生热电势，形成热电噪声。如果两种金属材料导线的接点处受到高温浪涌热源(如受发动机的高温燃气的烘烤与辐射)的作用，也会产生较大的浪涌热电势。

8.2.3电磁干扰的耦合途径

电磁干扰控制技术的任务之一就是采用有效手段阻断各种耦合通道。典型的干扰传播模式为传导耦合、感应耦合和辐射耦合。

1.传导耦合

沿电源线或信号线传输电磁干扰称为传导耦合。电子系统内的各设备之间、电子设备内各单元电路之间存在各种连线，如电源线、信号传递线及公共地线等，这就有可能使一个设备或单元电路的电磁能量沿着导线传输到其他设备和单元电路，形成电磁干扰。

(1)沿电源线的传导耦合。电网中的各种电气、电子和机械设备，在启动、运行、切断时都会向电源网传送频谱相当宽的电磁干扰。此外，在电子系统或电子设备内部也会通过公共电源线形成各部分之间的相互干扰。图8.2说明了干扰源(电动机)的干扰通过电源线直接耦合到敏感器(信号电路)的情形。

图8.2沿电源线的传导耦合

(2)通过公共电源内阻的耦合。当两个或几个设备或单元电路共用一个电源时(见图8.3),由于电源内阻R_s和公共阻抗R的作用，电路2的电源电流发生任何变化都会影响电路1的电源电压。

图8.3公共电源内阻的耦合

(3)通过公共地线阻抗的耦合。在系统或设备内部，通常是几个设备或单元电路共用一条

公共地线，如图8.4所示。各设备或单元的电流在流过地线阻抗R_g时就会产生压降，造成各单元对地电压的相互影响。电路1、电路2的对地电压为V_g=(I₁+I₂)R_g,任何一个电路的电流变化都会影响另一路的对地电压。

图8.4公共地线阻抗的耦合器

(4)漏电耦合。漏电耦合是电阻性耦合方式。当相邻的元件或导线间的绝缘电阻降低时，有些信号便通过这个降低了的绝缘电阻耦合到逻辑元件的输入端而形成干扰。

如图8.5所示为漏电耦合的示意图。其中R_m为电路A与B之间的绝缘电阻，Z_B为B电路的输入阻抗。当绝缘电阻R_m降低时，A上的电压通过R_m与Z_B的分压耦合到电路B上，可在电路B上引起干扰电压。

图8.5漏电耦合

2.感应耦合

感应耦合包括电容性耦合和电感性耦合。

(1)电容性耦合。如图8.6所示为电容耦合通道，当两根导线距离较近时，就形成了一个电容器，会产生电容性耦合。其耦合程度取决于干扰源和敏感器之间的分布电容的大小，以及干扰源和敏感器的阻抗和频率范围。在高阻抗的高频电路中，最易产生电容耦合。

图8.6电容耦合途径

(2)电感性耦合。如图8.7所示为导线间互感产生的电感耦合，在电路B中感应的电压，即

V_B=M(di_A/dt)

式中，M是互感。影响干扰的因素有电流i_A的变化率、两导线间的距离以及两导线的平行走线长度。

图8.7电感耦合途径

3.电磁辐射耦合

电磁辐射耦合是指远场耦合，干扰源发射的电源能量以平面波的形式，通过空间传播作用到敏感器上。

如图8.8所示为电磁辐射对一矩形回路产生耦合的示意图。其中的矩形线圈置于X—Z平面上，其宽度为l,高度为h,辐射源S发射的电磁波从左向右以速度v传播。电磁波的电场和磁场分别以Ei及Hi表示，它们的方向分别沿X轴和Y轴。电磁场通过线圈回路将产生感应电压Vi,则

\({{V}_{i}}=\oint{{{E}_{i}}\text{d}l}\) (电场分量感应电压)

\({{V}_{i}}=-\frac{\partial\varphi}{\partial t}=-\frac{\partial}{\partial t}\int\limits_{A}{{{B}_{i}}dA}\)  (磁场分量感应电压)

图8.8电磁辐射耦合示意图

由此可见，回路面积越大，产生的电磁干扰量就越大。尽可能压缩电流环路面积，是抗干扰技术的重要措施之一。

8.2.4差模干扰与共模干扰

噪声通过各种耦合方式引入到测试系统回路中，形成的干扰分为两种模式：差模干扰和共模干扰。

1.差模干扰

差模干扰又称为串模干扰、常模干扰或对称干扰。

在介绍差模干扰之前，首先介绍差模电压的概念。所谓差模电压，是指一组规定的带电导体中任意两根之间的电压。例如，信号传输过程中的信号输入线与信号返回线之间；电源的相线与中线之间、相线与相线之间等等。

差模干扰指干扰信号为差模电压形式的干扰，是线与线之间的干扰，干扰电流在两线上的方向相反。如图8.9所示，N为干扰源，R为受扰设备，V_N为干扰电压，干扰电流I_N和信号电流I_s的路径往返两条线上是一致的。

图8.9差模干扰

差模干扰源于外来的感应磁通或电磁辐射信号在回路线间环路上所产生的感应电势，并叠加在信号电路中，将直接对系统的工作形成影响。差模干扰还源于同一电源线路中，如同一线路中工作的电机、开关及可控硅等，它们产生的干扰往返于电源线与地线之间，形成差模干扰。

2.共模干扰

共模干扰也称为纵模干扰、不对称干扰或接地干扰。

在介绍共模干扰之前，首先介绍共模电压的概念。所谓共模电压，是指每个导体与规定参考点(通常是地或机壳)之间的电压。例如，信号传输过程中的信号输入线与地之间、信号返回线与地之间；电源中的中线与地之间、任何一相线与地之间等等。

共模干扰，系指干扰信号为共模电压形式的干扰，是线与地之间的干扰，各接地干扰电流(通过接地阻抗)具有相同的方向。如图8.10所示，干扰侵入线路和地之间。干扰电流在两条线上各流过一部分，以地为公共回路，而信号电流只在往返两条线路中流过。

图8.10共模干扰

共模干扰是由辐射或串扰形式耦合到电路里面的。由于来自空间的感应对每条导线的作用是相同的，例如雷电、电弧、电台、大功率辐射装置等，它们在电源线上形成共模干扰。通常，线路上的干扰电压的差模分量和共模分量是同时存在的，而且由于线路的阻抗不平衡，两种分量在传输中会互相转变。如图8.11所示说明了共模干扰转换成差模干扰的原理。

在图8.11中，N为干扰源，L为负载，Z₁和Z₂是导线1和导线2的对地阻抗。如果Z₁=Z₂,则干扰电压V_N1和V_N2相等，从而干扰电流I_N1和I_N2也相等，即干扰电流不流过负载。然而当Z₁≠Z₂时，V_N1≠V_N2, I_N1≠I_N2,于是VN= V_N1一V_N2,V_N/Z₁=I_N(Z为负载阻抗),这就是差模干扰电流。因此，当发现差模干扰时，首先考虑它是否由于线路的不平衡状态而由共模干扰转换来的。通常，输入输出线与大地或机壳之间发生的干扰都是共模干扰；信号线受到静电感应时产生的干扰也多为共模干扰。抑制共模干扰的方法很多，如屏蔽、接地、隔离等。抗干扰技术在很多方面都是围绕共模干扰来研究其有效的抑制措施。

图8.11共模干扰转换成差模干扰

8.3抑制干扰的措施

8.3.1屏蔽

屏蔽技术能有效地抑制通过自由空间传播的电磁干扰。通过应用屏蔽技术，可以限制系统内部的辐射电磁能对外部元件和装置的干扰，同时也防止来自系统外部的辐射干扰进入系统内部。屏蔽按其原理可分为电场屏蔽、磁场屏蔽和电磁场屏蔽。

1.电场屏蔽

电场屏蔽的原理如图8.12所示。将电场感应看成分布电容间的耦合，未加屏蔽时B点的感应电压为

图8.12电场屏蔽原理图

(a)未加屏蔽；(b)加屏蔽

\({{V}_{B}}=\frac{{{C}_{1}}}{{{C}_{1}}+{{C}_{2}}}{{V}_{A}}\)

在A和B之间增加屏蔽板S后，B点的感应电压为

\({{V}_{B0}}=\frac{{{C}_{10}}}{{{C}_{10}}+{{C}_{2}}+{{C}_{4}}}{{V}_{A}}\)

由于C₁。远小于未屏蔽时C₁值，故V_B0值远小于未屏蔽时的V_B值。

在进行电场屏蔽时，屏蔽板尽量靠近受保护的物体，而且屏蔽板的接地必须良好，以增大电容C₄值。屏蔽板的形状对屏蔽效能有显著影响。例如，全封闭的金属罩有最好的屏蔽效果，而开孔或带缝隙的屏蔽罩的屏蔽效能会下降，这主要是剩余电容C10的值受影响。屏蔽板的材料以良导体为好，对厚度无要求，只要满足强度要求即可。

2.磁场屏蔽

磁场屏蔽的目的是消除或抑制直流或低频交流磁场与被干扰回路的磁耦合。如图8.13所示，一根载流导体四周会同时产生电场与磁场。若用一个良好接地的非导磁金属屏蔽体封闭该导线，则电场的电力线终止于该金属屏蔽体，电场得到了有效屏蔽，但对原磁力线没有什么影响。当采用高导磁材料将敏感元件进行屏蔽时(见图8.14),由于屏蔽材料的导磁率很高，为磁场提供了一条磁阻很低的通路，空间的磁场会集中在屏蔽材料中，从而使敏感元件免受磁场干扰。

图8.13载流导体的电场与磁场

图8.14用高导磁材料实现磁屏蔽

3.电磁场屏蔽

对于电磁波来说，电场分量和磁场分量总是同时存在的。所以在屏蔽电磁波时，必须同时对电场和磁场加以屏蔽，故通称为电磁场屏蔽。屏蔽体之所以能阻止电磁波的传播，是因为电磁波在穿越屏蔽体时发生了能量的反射衰减和吸收衰减。如图8.15所示表示屏蔽体的电磁屏蔽机理。

图8.15电磁场屏蔽机理

当电磁波到达屏蔽体表面时，由于空气的波阻抗与屏蔽体(通常是金属材料)的特性阻抗不相等，所以对入射波产生反射，使穿越界面的电磁能量减弱。这种由于反射而造成的入射波减弱现象称为反射衰减(反射损耗)。反射损耗与屏蔽体的厚度没有太大关系。空气波阻抗与屏蔽体特性阻抗相差越大，引起的损耗也愈大。波的反射还与频率有关：频率越低，反射越严重。

上述反射不可能做到全反射，仍有部分电磁波进入屏蔽体，并在体内继续向前传播。电磁波在穿越屏蔽体时，在屏蔽体内会引起感生涡流。感生涡流可产生一个反磁场用以抵消原干扰磁场，同时涡流在屏蔽体内流动时产生热损耗。电磁波频率越高，涡流损耗也就越大。

在屏蔽体内未被吸收的电磁波到达材料的另一面时，又一次遇到屏蔽体特性阻抗与空气阻抗不相等情况，除部分会穿越屏蔽体而进入被屏蔽的空间外，余下大部分电磁波会在屏蔽体表面形成再次反射，再次返回屏蔽体内部。因此电磁波在穿越屏蔽体的过程中会有多次反射，逐渐被屏蔽体吸收，只有极少部分存在于被屏蔽的空间内。

4.屏蔽效能

金属屏蔽体的屏蔽效能是由反射损耗和吸收损耗而得到的。对于电场的屏蔽，屏蔽体必须接地；对于磁场的屏蔽，屏蔽体可不必接地。屏蔽电缆的屏蔽效能，主要不是因反射和吸收衰减而引起的，而是由屏蔽层的接地所产生的，也就是说，屏蔽电缆的屏蔽层只有接地后才能起到屏蔽作用。露出屏蔽层之外的芯线部分越短越好。屏蔽电缆的屏蔽效能与所用材料及其编织密度等因素有关。一般说来，编织层的屏蔽效能随编织密度的上升而增加，随频率的升高而减少。在实际应用中，还需注意电缆的弯曲程度也是影响屏蔽效能的重要因素。在电缆弯曲时，靠近内侧的覆盖率最大，靠近外侧的覆盖率则显著减小。

在实际应用中，最常见的错误是将电缆屏蔽层的末端捻成一根小辫，接到连接器的一根针上，然后再接到机箱内壁或线路板上。这种连接方法对于高频的电磁干扰是没有屏蔽功能的，有时甚至会使电磁干扰更加严重。特别是当屏蔽层连接到线路板上时，往往使电磁干扰现象更加严重。这主要是磁屏蔽依赖于围绕屏蔽层的径向屏蔽电流分布的一致性，“小辫子”的端接方式导致屏蔽层上的电流集中在屏蔽层的一侧。正确的端接方式是保证电缆屏蔽层与屏蔽机箱要在360度范围搭接。

在屏蔽体的屏蔽效能设计当中应当注意的要点包括以下几点：

(1)屏蔽层必须接地，否则起不到屏蔽效果。

(2)所有进入屏蔽箱的电缆、导线、电源线都应当进行滤波。

(3)电缆进出屏蔽箱时，电缆屏蔽层必须接到壳体上。

(4)屏蔽低频磁场的难度要大于屏蔽电场，低频磁场的反射损耗很小，屏蔽低频磁场应使用磁性材料。

(5)屏蔽电场、平面波和高频磁场应使用良导体材料。

(6)在10MHz以上，吸收损耗是最主要的屏蔽机理。

(7)屏蔽体的屏蔽效能通常由开孔、接缝连接处的电磁泄漏决定，而不是由材料本身的屏蔽效能决定。

(8)开孔或不连续的最大尺寸决定了屏蔽体的最大泄漏，而不是它的面积。

(9)屏蔽体上大量小尺寸开孔对屏蔽的影响要小于同样面积的大尺寸的开孔或接缝的影响。

8.3.2 接地

实践证明，测控系统和其他工业用电子设备的干扰与系统的接地方式有很大关系。接地技术往往是抑制噪声的重要手段，良好的接地可以在很大程度上抑制系统内部噪声耦合，防止外部干扰的侵入，提高系统的抗干扰能力。反之，若接地处理得不好，会导致噪声耦合，形成严重干扰。因此，在抗干扰设计中，对接地方式应予以认真考虑。

电气设备中的“地”,通常有两种含义：一种是“大地”,另一种是“工作基准地”。所谓“大地”,这里是指电气设备的金属外壳、线路等通过接地线、接地极与地球大地相连接。这种接地可以保证设备和人身安全，提供静电屏蔽通路，降低电磁感应噪声。“工作基准地”是指信号回路的基准导体(如控制电源的零电位),又称“系统地”。这时的所谓接地是指将各单元、装置各部分电路信号返回线与基准导体之间的连接。这种接地的目的是为各部分提供稳定的基准电位。对这种接地的要求是尽量减小接地回路中的公共阻抗压降，以减小系统中干扰信号公共阻抗耦合。

根据电气设备中回路性质和接地目的，可将接地方式分为以下三类:

(1)安全接地：设备金属外壳等的接地。

(2)工作接地：信号回路接于基准导体或基准电位点。

(3)屏蔽接地：电缆、变压器等屏蔽层的接地。

工作接地通常分为三类：单点接地、多点接地和混合接地。

1.单点接地

单点接地一般分为串联连接和并联连接两种形式(见图8.16)。如图8.16(a)所示的串联单点接地(又称公共接地),由于简单方便，对于要求不高的场合，应用较广。但是这一接地形式不宜用在电源功率有很大差异的电路之间，这是由于高功率电路产生大的地电流会对低功率电路产生很大的影响。

图8.16单点接地

(a)串联连接；(b)并联连接

如图8.16(b)所示的并联单点接地(又称分离接地),是低频电路最适宜的接地方式，因为来自不同电路的地电流之间没有交叉耦合。这种接地形式中任何一个电路的地电位只受这个电路的地电流和它自身地线阻抗的影响。这种接地需要接地线较多，布线显得繁杂。

单点接地系统的地阻抗在高频时变得很大。当地线长度等于1/4波长的奇数倍时，高频地阻抗会非常高。同时，这种地线还类似于天线而辐射噪声。因此，接地导线应保持短于1/20波长，以维持低阻抗和防止辐射。一般在高频时不使用单点接地。

2.多点接地

多点接地系统通常用在高频和数字电路中，在火箭发动机试验的实际使用过程中会出现屏蔽层的多点接地。目前在许多试验间和测控间，特别是新建实验室的各个房间内，都会设有一个等电位地，但是实际上各个等电位很难达到真正意义的等电位，在这种没有完善等电位地却要求获得很好抗干扰效果的情况下，可采用如下方法实施：在测试仪器现场将所有机壳连接在一起，进行等电位基础上的多点接地，而电缆屏蔽层在测控室连接一只10nF左右耐压1500V的隔离电容，然后再接地。如图8.17所示，现场1和现场2的接地点B和C是等电位，但和控制室的接地参考点A不是等电位。

图8.17屏蔽层的多点接地方法

3.混合接地

混合接地是根据不同的频率，采用不同的接地形式。如图8.18所示为一个典型的通用混合接地系统。在低频时，电容等效于断开，它相当于单点接地；在高频时，电容等效与导通，它相当于多点接地。

图8.18混合接地

8.3.3隔离

信号隔离目的之一是从电路上把干扰源和易干扰的部分隔离开来，使测控装置与现场仅保持信号联系，但不直接发生电的联系。隔离的实质是把引进的干扰通道切断，从而达到隔离现场干扰的目的。许多测控系统既包括弱电控制部分，又包括强电控制部分，要让两者之间既保持控制信号联系，又要隔绝电气方面的联系，即实行弱电和强电隔离，这是保证系统工作稳定，设备与操作人员安全的重要措施之一。

测控装置与现场信号之间，弱电和强电之间常用的隔离方式有光电隔离、变压器隔离、继电器隔离等。

1.光电隔离

光电隔离是由光电耦合器件来完成的。光电耦合器是20世纪70年代发展起来的新型电子元件，是以光为媒介传输信号的器件。其输入端配置发光源，输出端配置受光器，因而输入和输出在电气上是完全隔离的。开关量输入电路接入光电耦合器之后，由于光电耦合器的隔离作用，使夹杂在输入开关量中的各种干扰脉冲都被挡在输入回路的一侧。除此之外，还能起到很好的安全保障作用，因为在光电耦合器的输入回路和输出回路之间有很高的耐压值，达0.5～1kV,甚至更高。由于光电耦合器不是将输入侧和输出侧的电信号进行直接耦合，而是以光为媒介进行间接耦合，所以具有较高的电气隔离和抗干扰能力。如图8.19所示给出了常见的两种典型光电隔离应用。

图8.19光电隔离

(a)外部输入信号隔离；(b)控制输出信号隔离

2.继电器隔离

继电器的线圈和触点之间没有电气上的联系，因此，可利用继电器的线圈接受电气信号，利用触点发送和输出信号，从而避免强电和弱电信号之间的直接接触，实现了抗干扰隔离。

如图8.20所示，当A端输入高电平时，晶体三极管T饱和导通，继电器J吸合；当A点为低电平时，T截止，继电器J释放，完成了信号的传送过程。D是保护二极管。当T由导通变为截止时，继电器线圈两端产生很高的反电势，以继续维持电流IL。由于该反电势一般很高，容易造成T的击穿。加入二极管D后，为反电势提供了放电回路，从而保护了三极管T。

图8.20继电器隔离

3.变压器隔离

电源隔离变压器除了能改变电压外，还可以把输入绕组和输出绕组在电气上彼此隔离，原、副边绕组没有电气连接，如图8.21所示。隔离变压器变比n₁/n₂=1时，即变成了分离变压器，这种变压器原、副边匝数相同，并不能实现电压变换，但却能使副边绕组与输入电网完全隔离，即使人站在潮湿地面上触及副边绕组，也不会发生触电危险。这种分离变压器常用在不带电源变压器又需要线路板相对安全的电源装置中，比如某些场合使用的开关电源输入级。

图8.21隔离变压器

另外，分离变压器与供电电源地之间没有电气联系，因而可以抑制由电源引起的共阻抗干扰。需要注意的是这种方法对直流或者低频交流信号不适用。

当多点接地间距很大且被连到交流电源地上时，会在电路中形成一个有害的噪声电压。

如图8.22所示，在两个接地点之间有电位差，地环电路电流形成噪声源。这种情况在很多的火箭发动机试验中会出现。除了可以多点接地变成单点接地以避免形成地环路，还可以采用隔离技术将两个电路隔离。

图8.22两电路之间的地环路问题

(a)地环路；(b)变压器隔离地环路；(c)光电耦合隔离地环路

8.3.4 滤波

滤波技术是抑制电气、电子设备中传导电磁干扰，提高电气、电子设备抗干扰水平的主要手段。滤波的实质是压缩信号回路干扰频谱的一种方法，当干扰噪声频谱成分不同于有用信号的频带时，可以用滤波器将无用的干扰噪声滤除。滤波器将有用信号和干扰噪声的频谱隔离得越完善，它对减小有用信号回路内的干扰的效果就越好。然而完全消除沿导线到设备传输的干扰噪声通常是不可能的。滤波的目的是将干扰噪声减小到一定的程度，使传输到设备的干扰噪声不超过标准给定的规范，从而不至于引起设备的误动作。

根据使用场合，滤波器可分为电源滤波器、信号滤波器和控制线滤波器等。按照工作条件或者结构，滤波器可分为无源滤波器和有源滤波器，此外，还有用软件实现的数字滤波器。

电源滤波器(又称电源线滤波器),主要用于滤除电源线通过传导耦合的电磁噪声。电源滤波器主要由电感和电容组成，由于是无源器件，它在工作时不消耗能量。滤波器的工作原理是利用电容在高频时的低阻抗特性，将火线、中线上的高频干扰导入地线(共模干扰的抑制),或将火线上的高频干扰电流导入中线(差模干扰的抑制);同时利用电感线圈在高频时的高阻抗特性，将高频干扰反射回干扰源。信号滤波器(又称信号线滤波器),主要是为了抑制信号线上的电磁于扰。

滤波器最重要的是频率特性，可用对数幅频特性20lgA来表示，在抗干扰技术中又称为衰减系数，即

衰减系数=\(20\lg\left|\frac{{V}_{o}{j\omega}}{{V}_{i}{j\omega}}\right|\)

式中

V。——滤波器的输出信号；

V₁——滤波器的输入信号；

ω——信号的角频率。

信号通过滤波器，被滤除(或称被衰减)的信号频段称为阻带，被传输的信号频段称为通带。根据阻带和通带的频谱，又可将滤波器分为以下4种：

(1)低通滤波器：允许低频信号通过，但阻止高频信号通过。

(2)高通滤波器：允许高频信号通过，但阻止低频信号通过。

(3)带通滤波器：允许规定的某频段信号通过，但阻止高于和低于该频段的信号通过。

(4)带阻滤波器：只阻止规定的某频段信号通过，但允许高于或低于该频段的信号通过。

在抗干扰技术中，使用最多的是低通滤波器，主要是电容和电感元件组成的无源滤波器。

图8.23给出了电容滤波器的结构与特性。图8.23(a)结构最简单，接在干扰源线间能衰减差模噪声；接在干扰源和地线间能衰减共模噪声；接在印刷电路板中的直流电源线和地线间能抑制电源噪声。图8.23(b)电容器中点接地，能够把噪声电流旁路入地，能消除共模噪声。图8.23(c)的C₃接在电源线间，这种结构能有效地抑制共模(由C,C₂完成)和差模噪声(由C₃完成)。

图8.23电容滤波器的结构与特性

(a)抑制差模干扰；(b)抑制共模干扰；(c)抑制差/共模干扰；(d)输入输出特性

电感线圈有两种，即常模扼流圈和共模扼流圈。如图8.24(a)所示是常用结构，串接在线路中对高频噪声有很大的阻抗，可以抑制高频噪声电流。电源线路中使用的常模扼流圈是把导线绕在磁芯上制成；微弱信号线路中的电感线圈可以自制，其方法是将漆包线缠绕在电阻上，漆包线两头焊在电阻引脚上。如图8.24(b)所示表明共模轭流圈的绕制方向相反，线圈中的负载电流因方向相反，所形成的磁场互相抵消，不会出现磁饱和。同样，当出现差模噪声时，也会因极性相反而使磁通互相抵消，因而基本上不起电感作用。如图8.24(c)所示表明当出现共模噪声时，两个线圈所产生的磁通方向相同，使电感作用加倍，因而对线路与地线间的共模噪声起到很强的抑制作用。

图8.24电感滤波器

(a)常用结构形式；(b)对差模干扰无抑制作用；(c)对共模干扰有抑制作用；(d)输入输出特性

由电阻和电容组成的RC低通滤波器接在电路中，按其结构可分为L形、П形和T形，如

图8.25所示。它具有滤去高频、而让低频信号容易通过的性能。这三种形式的RC滤波器制造简单，价格便宜，体积小，对外界的磁场变化敏感低，广泛应用于信号传输线路中的噪声抑制。

图8.25RC低通滤波器

(a)L形；(b)П形；(c)T形

由电感和电容组成的LC滤波器主要用于低通滤波，按电路结构也可分为L形、Ⅱ形和T形，如图8.26所示。LC低通滤波器比RC低通滤波器具有更好的滤波性能，但是制造电感线圈比较麻烦，不利于大规模生产和不便于集成化和小型化，使其应用范围受到局限。

图8.26LC低通滤波器

(a)L形；(b)П形；(c)T形

8.3.5合理电气布线

1.信号线的类型

测控系统中最常用的线缆类型主要有双绞线、屏蔽线、同轴线等，这些线缆的性能参数有很大区别，应用场合也不同。

(1)双绞线。双绞线是系统布线技术应用中最常用的一种传输介质，使用由来已久。双绞线是由两根具有绝缘保护层的铜导线互相绞在一起组成的。两根导线的电流方向相反、幅度相等。由于两根导线上感应电流的方向相反，一根导线在信号传输过程中辐射的电波会被另一根线上发出的电波抵消，大大降低信号干扰的程度。

双绞线一般由两根22～26号绝缘铜导线相互缠绕而成，如果把一对或多对绞合导线放在一个绝缘套管中便构成了双绞线电缆。两根导线相互扭合，其扭绞节距的长短与该导线的线径有关。线径越细，扭绞节距越短；节距越短，抑制感应噪声效果越明显。但这样所用导线的长度便越长，导致成本增大。从性价比来说，节距为5cm左右较为适宜。

双绞线在信号传输应用中具有以下特点：

1)传输距离远，传输质量高。

2)抗干扰能力强，对共模干扰噪声具有很强的抑制作用。

3)布线方便。

双绞线主要用来传输模拟信号，也适用于数字信号传输，特别是适用于较短距离的数字信号传输。虽然双绞线具有抗干扰能力强、传输距离远、布线容易、造价低廉等优点，但其对信号也存在着较大的衰减，并且产生波形畸变。所以在双绞线上远距离传输信号时，必须采取特殊措施，诸如放大和补偿等。

采用双绞线进行信号传输的可靠程度取决于所用导线的质量、长度及传输技术。只要合理选择和安装双绞线，就可以在有限长的距离内实现很高的可靠传输速率。双绞线分为屏蔽双绞线和非屏蔽双绞线两种。屏蔽双绞线电缆的外层由一层金属箔包裹，从而能抑制双绞线向外辐射电磁波，同时具有很高的信号传输速率。但屏蔽双绞线造价相对较高，安装施工也比非屏蔽双绞线电缆困难。与同轴电缆类似，它还要求配备支持屏蔽功能的专用连接器和相应的连接技术。

(2)屏蔽线。用铜丝编织网或者金属薄膜将绝缘芯线包裹起来，构成的电缆称为屏蔽线(见图8.27)。芯线外面包裹的铜丝编织网或金属薄膜称为屏蔽层。屏蔽层由单层编织网或金属薄膜构成，称为单层编织网线，能提供80%～95%的覆盖率，有效抑制来自电动机控制电路、磁性线圈、动作过程设备和一般用电设备产生的低阻抗干扰噪声。在有些场合，诸如计算机通讯控制、局域网系统等需要抑制更高频率干扰噪声时，就需要选用双层屏蔽线。

屏蔽线的作用有两个：一是防止外界干扰噪声对芯线产生影响；另一个是阻止内部信号向外辐射，干扰其他电路和布线。利用金属屏蔽层对电磁波的反射、吸收和趋肤效应原理，有效地防止外部电磁干扰进入电缆，同时也阻止内部信号产生的电磁波辐射出去(所谓趋肤效应是指电流在导体截面的分布随频率的升高而趋于导体表面分布。频率越高，趋肤深度越小，即电磁波的穿透能力越弱)。

屏蔽线的屏蔽层仅起屏蔽作用，不能将其作为电流回路线使用。屏蔽线作为信号线使用时，屏蔽层要正确接地，一般不采取多点接地方式，应参考以下原则：①信号源端接地时，屏蔽电缆的屏蔽层应在信号源侧实行单点接地；②相反，信号源端悬浮时，应在信号接收侧实行单点接地。

使用屏蔽线时，要注意屏蔽层不能断。如需将两段屏蔽线接起来时，不仅芯线要焊接好。其屏蔽层也要可靠的焊接起来。如果用接插件转接时，屏蔽层也要单用一对插脚保持良好的连接。

图8.27屏蔽线的结构

(3)同轴电缆。同轴电缆也是一种常用的信号传输线，例如家庭的闭路电视信号就是采用同轴电缆传输。同轴电缆的一根导线位于中心，称为芯线；另一根导线是环形截面，称为外层导体，与芯线同轴，因此称为同轴电缆。在芯线与外导电层之间填充聚乙烯等高芯线介电常数的绝缘物，以保持其截面为同心圆，为了防止外导电层接地短路，所以电缆外还包有一层绝缘层，如图8.28所示。在使用时把电缆的外导电层接地，由于它的屏蔽作用可以有效地抑制噪声。因为同轴电缆可以传输宽频带的信号，所以它适合于长距离传输高频或前后沿很陡的脉冲信号，但同轴电缆的价格较高。

图8.28 同轴电缆构造

2.信号传输线的敷设

信号线的敷设直接关系到系统的抗干扰性能。在敷设信号线时应注意以下几点。

(1)信号线在穿入钢管或金属蛇皮管时，管皮要牢固接地。对于相互容易干扰的信号线不要合用一根管子，要分别单独穿管。

(2)信号线一定要远离干扰源。干扰源主要是一些大容量的电气设备，尤其是大电感设备，如大变压器、大电动机等。远离是为了防止漏磁通引起的感应干扰。同时也应注意远离不带屏蔽的大电流电源线。

(3)信号线要分类分层敷设。在计算机测控系统中，一般有三类导线：低电平导线，指0.1V以下的模拟回路，很容易受干扰影响，大多是测量回路，如热电偶测温回路、压力传感器信号电路等；中电平导线，如指示灯电路，各种显示电路等；高电平强导线，如强电按钮、行程开关、接触器等。信号线又可分为模拟信号线和数字信号线，这两种信号线不能合用一组电缆，且应远离。上述各类导线电缆在分层导线支架上放置时，应按信号线、低压线、AC和DC电源线、高压电源线的顺序，从上到下依次分层放置。

图8.29信号线的敷设

(a)设置隔离板；(b)不设置隔离板；(c)电缆架隔离；(d)电源屏蔽罩隔离

(4)对于同一电缆沟内的信号电缆和电源电缆安置时应注意以下几点。

1)电缆沟内要设置金属隔板，将信号电缆与电源电缆用隔板分开，并使金属板接大地，如图8.29(a)所示。

2)若都在电缆沟内自由敷设而不能加隔离板时，可加大两种电缆之间的距离。若电源电缆不带屏蔽层，且电流在10A以上时，彼此间距要在15cm以上，如图8.29(b)所示。

3)若电缆沟内是用电缆架隔离，也应加大两者之间的距离。若电源电缆不带屏蔽，且电流大于10A,其间距也在15cm以上，如图8.29(c)所示。

4)若要缩小间距，可将电源电缆加屏蔽罩，如图8.29(d)所示。

(5)屏蔽线、转接线应注意以下几点。

1)信号线为屏蔽线时应注意屏蔽层的接地问题。

2)远距离传输线一般均是通过接线箱衔接，此时也应注意分类设置接线箱，要注意防止通过接线箱引进各种干扰。

(6)要防止信号线的振动。工业现场杂散磁场较多，若信号线由于敷设时工作不细致，要求不严，则可使信号线随机器或其他物体一起振动，形成切割磁力线的运动。振动速度越高，导线摆幅越大，由切割磁力线而进入信号线的干扰也就越大。因此，信号线除了要远离产生杂散磁场的电器和大电流导体外，还要将信号线固定牢靠，最好将信号线穿于钢管，以防止因信号线抖动而引进更多的磁场干扰。

8.3.6设置远端放大器，提高信噪比

在用长线传输小信号时，尽管已经采取了一些抑制干扰的措施。但在这条长线上仍然还会拾取一些噪声，它与有用信号一起进入系统的输入端，被放大同样的倍数，使输出信号的信噪比降低，由此会带来较大的测量误差。如果把放大器设置在信号源附近，先把有用信号放大成大信号后再传输，而信号传输线上拾取的噪声没有被放大，因此提高了信噪比。近来由于集成电路技术的发展，使得集成运算放大器的体积大为缩小，因而把它藏于传感器的壳体之内，制成了远端放大器。如DaCY系列压力变送器，将传感器输出的毫伏级微弱信号变成了1~5V的信号，信噪比提升了2～3个数量级。

第9章数据处理与不确定度评估

9.1数据处理

固体火箭发动机试验数据处理的内容包括推力、压力曲线上特征点的确定、发动机内弹道特性和能量特性参数的计算、异常数据的判定等。

9.1.1推力-时间曲线与压力-时间曲线

发动机试验中，推力、压力是最重要的测量对象。通过测量系统可以获得推力-时间(F-t)、压力-时间(p-t)数据，通过各种绘图软件(如Origin和Tecplot)可以绘出相应的F-t、p-t曲线。在固体火箭发动机试验中，把p-t曲线定义为基准曲线。典型的p-t,F-t曲线如图9.1所示。

图9.1固体火箭发动机p-t和F-t曲线

图9.1中的符号说明如下。

p_c——燃烧室压力，是发动机工作时燃烧室内燃气的瞬时总压；

p_i——初始压力，发动机点火后，燃烧室压力上升到某一规定数值(通常为300kPa);

\({{\hat{p}}_{i}}\)——初始压力峰值。发动机点火后p-t曲线的上升段向平衡段过渡前出现的压力峰值；

P_bi——燃烧终点压力，是发动机装药肉厚燃烧终了时刻的压力值；

P_max——燃烧室最大压力，在发动机工作过程中除了初始压力峰值及由于不稳定燃烧产生的异常压力值外在p—t曲线上的最大压力值；

P_min——最小压力，在p-t曲线上，在\({\hat p}_{i}\)与p_bf之间的最小压力值；

P_af——工作终点压力，一般把p_c下降到300kPa时的值定为工作终点压力；

t₀——时间零点，指点火信号给出的时刻；

t_i——发动机工作时间起点，即压力升到p_i时对应的时刻；

\({t}_{{\hat p}_{i}}\)——初始压力峰值时刻；

t_noc——堵片打开时间，从t_i为起点到喷管堵片打开时刻的时间间隔；

t_id——点火延时时间，t₀到t_i之间的时间间隔；

t_bf——燃烧终了时刻，发动机装药肉厚燃烧完了的时刻即p_bf的对应时刻；

t_b——燃烧时间，指装药肉厚燃烧时间即t_i与t_bf之间的时间间隔；

t_af——工作终点时刻，是p_af对应的时刻；

t_a——工作时间，在p-t曲线上，t_i与t_af之间的时间间隔；

F——推力，它是作用在发动机内、外表面上所有力的合力。具有推力终止机构的发动机试验时推力亦称为主推力；

F_i——初始推力，与t_i对应的F值；

\({\hat F}_{i}\)——初始推力峰值，发动机点火后在F-t曲线上，上升段向平衡段过渡前的推力峰值；

F_max——最大推力，除初始推力峰值外F-t曲线上的最大值；

F_min——最小推力，在\({\hat F}_{i}\)与F_bf之间出现的最小值；

F_bf——燃烧终点推力，与t_bf对应的推力值；

F_af——工作终点推力，与t_af对应的推力值。

9.1.2 t_bf的确定方法

在p-t曲线上确定t_bf点现在还没有一种统一的规定，下面介绍几种常用的方法。

(1)双切线法。这是最通用的一种方法。在p-t曲线拖尾段画出两条切线，如图9.2所示。用双切线确定装药肉厚燃尽终点的方法又可以分为三种。

图9.2双切线法确定燃烧终止点

1)两切线夹角的角平分线与p-t曲线交点(点A)定义为肉厚燃尽时刻。

2)取DE中线与p-t曲线交点(点B)定义为肉厚燃尽时刻。

3)过两切线交点的t轴的垂线与p-t曲线的交点(点C)定义为肉厚燃尽时刻。数据分析证明，DE中线法与角平分线法取点的敏感度低。

(2)特征值dp/dt法。dp/dt值可能是一预估的常数，也可能为基于试验内弹道曲线某一规定下的变量。该方法可以使用计算机数值计算来确定燃尽时刻点。

(3)二阶导数法。该方法试图确定如dp/dt变化率最大点为燃尽时刻，这是一种计算机方法，它对数值点进行数值处理，用压力对时间的二阶导数d²p/dt²的极值来确定肉厚燃尽时刻。

(4)预定系数法。对于特定的发动机，p—t曲线变化是有规律的，p_max与p_bf之间的比例系数K_b是一个常数，即

\({K}_{b}=\frac{{p}_{bf}}{{p}_{max}}\)    (9.1)

K_b值可以从多次试验统计得到。这样利用预定的系数K_b就可以根据p-t曲线上的p_max计算出p_bf从而找到t_bf,即燃烧终止点。

还可以用燃烧时间压力冲量与工作时间压力冲量之比确定系数K’_b,即

\({K’}_{b}=\frac{\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{b}}{pdt}}{\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{a}}{pdt}}\)  (9.2)

这里的K’_b值也是由多次试验的统计中得到，或由设计理论p-t曲线给出，然后用迭代法可以确定肉厚燃尽点。

(5)燃速公式法。由p-t曲线上看出，不同时间对应的压力值是不同的，而当发动机的装药的燃速符合

r=apⁿ     (9.3)

时，则不同时间的燃速也是不相同的。但当把p-t曲线按时间t分成若干个Δt小区域时，在每一个小区域内，可以认为p值不变。这样一来在Δt内燃速也可视为恒定的了。在Δt内燃烧掉的装药肉厚用Δe表示，则

Δe=rΔt

设某一时间间隔t_m,这里

t_m=Δt₁+Δt₂…十Δt_m=mΔt

则在t_m内燃烧去的肉厚e_m为

e_m=aΔt(p₁＋p₂＋…＋p_m)        (9.4)

当燃烧去的肉厚等于装药肉厚e₀时，即

e_m=e₀

时，则

t_b=mΔt

利用这一思路，可以编程计算t_b,条件如下。

1)燃速公式r=apⁿ,a,n为已知。

2)装药肉厚已知。

3)压力数据采集时间间隔已知。燃速公式可以通过标准试验发动机试验中或用药条声发射技术获得。

9.1.3压力数据处理

利用p-t曲线处理可得到下列内弹道特性参数：

(1)燃烧时间平均压力为

\({\bar p}_{tb}=\frac{\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{b}}{pdt}}{{t}_{b}}\)    (9.5)

式中

\(\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{b}}{pdt}\)—燃烧时间压力冲量。

(2)工作时间平均压力为

\({\bar p}_{ta}=\frac{\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{a}}{pdt}}{{t}_{b}}\)    (9.6)

式中

\(\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{a}}{pdt}\)——工作时间压力冲量。

(3)特征速度。特征速度用c*表示，它是衡量固体火箭发动机推进剂化学能大小和燃烧完全程度的一个特征参数。理论上特征速度是喷管进口燃气总压p_tin和喷管临界截面面积A_t的乘积与燃气质量流量q_m之比，即

\({c}_{th}^{*}=\frac{{p}_{tin}{A}_{t}}{{q}_{m}}\)

通过点火试验，可以按下式计算发动机的实验特征速度：

\({c}^{*}=\frac{{\bar A}_{t}{\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{a}}{pdt}}}{{m}_{gr}}\)    (9.7)

式中

\({\bar A}_{t}\)——点火试验前后喷管临界截面面积的算术平均值，单位：m²;

m_gr——推进剂总质量，单位：kg;

pdt——工作时间压强冲量，单位：Pa·s;

c*——实验特征速度，单位：m·s-¹。

9.1.4推力数据处理

通过推力曲线处理，可以得到总冲、比冲、平均推力和推力系数等数据。

(1)总冲：

\(I=\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{a}}{Fdt}\)    (9.8)

(2)比冲：

\({I}_{s}=\frac{I}{{m}_{gr}}\)(9.9)

(3)工作时间平均推力：

\({\bar F}_{ta}=\frac{T}{{t}_{a}}\)      (9.10)

(4)燃烧时间平均推力：

\(F=\frac{\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{b}}{Fdt}}{{t}_{b}}\)    (9.11)

(5)推力系数。推力系数C_F是固体火箭发动机水平的表征量之一，理论推力系数C_Fth是发动机推力与喷管临界截面面积A_t同喷管进口面燃气总压之比，即

\({C}_{F}=\frac{F}{{A}_{t}{p}_{tin}}\)

而实验推力系数可以用下式计算：

\({C}_{F}=\frac{I}{{\bar A}_{t}{\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{a}}{Fdt}}}\)     (9.12)

式中

\({\int\limits_{{t}_{i}}^{{t}_{i}+{t}_{a}}{Fdt}}\)——工作时间压力冲量，单位：Pa·s。

9.2异常数据的处理

测量数据中出现异常数据时，主要靠工程的、经验的方法判断和剔除。根据工程技术知识从以往掌握的测量数据的比较中，对测量系统性能的分析中找出异常数据。而数理统计方法可以作为判别异常数据的辅助方法。常用的是格拉布斯检验法和培根-德雷珀法。

9.2.1格拉布斯检验法

对某一参数x有n个测量数据x;(i=1,2,…,n),将这n个数据按数值大小顺序排列为

x₁≤x₂≤…≤xn

计算统计量为

\({T}_{n}=\frac{{x}_{n}-{\bar x}}{s}\),   \({T}_{1}=\frac{{\bar x}-{x}_{1}}{s}\)      (9.13)

式中

\({\bar x}=\frac{1}{n}\sum\limits_{i=1}^{n}{{x}_{i}}\)

\(s=\sqrt{\frac{1}{n-1}\sum\limits_{i=1}^{n}{({x}_{i}-{\bar x})}^{2}}\)

取T_n和T₁其中较大者。取显著水平α,查《格拉布斯检验法的临界值T(n,α)表》,见表9.1,得到一个T(n,α)临界值。

若  T≥T(n,α)

则判断x_n(或x₁)为异常数据，应剔除之。余下的n-1个数据重复上述过程直到T<T(n,α)为止。

表9.1格拉布斯检验法的临界值T(n,α)表

9.2.2培根-德雷珀法

对于线性计量测量系统的校准数据，适合用此方法来判定是否有异常数据，方法如下。计算统计量为

\({R}_{kr}={\left|\frac{{e}_{ij}}{{s}_{i}}\right|}_{max}\)    (9.14)

\({e}_{ij}={y}_{ij}-{\hat y}_{i}\)   (9.15)

        (9.16)

式中

y_ij——校准数据，即各校准点传感器输出数据；\({\hat y}_{i}\)——对应于校准点x;,由拟合公式计算出来的数据，或称统计校准数据；

k——校准级数；

r——对应于每一个校准级的测量次数；

x_i——校准加载值；

\({\bar x}\)——校准加载的算术平均值。

取显著水平α,查表9.2《培根-德雷珀检验法的临界值R_br(α)表》取临界值R_br(α)。若R_br≥R_br(α),则相应的那个e_ij所对应的y_ij为异常数据，应重新补正。

表9.2培根-德雷珀检验法的临界值R(x)表

9.3测量数据的不确定度

9.3.1术语

下列名词是在以后的论述中经常出现的。

(1)被测量。受到测量的量。

(2)直接测量。能直接得到被测量的量值的测量，如用力传感器测量火箭发动机的推力属于直接测量。

(3)间接测量。通过与被测量的量有函数关系的其他量的测量得到被测量的量值的测量。比冲的测量是间接测量。

(4)测得值。由测量所得到的被测量的结果，对观测值进行全部适宜平差和修正后的说明或记录值。

(5)测量过程。与给定测量目标有关的全部信息、设备和操作。

(6)真值(TrueValue)。若量与测量过程可以完全确定，且所有测量不完善性可以排除时，由测量得到的一个值。真值是一个理想概念，它是客观存在的，但又无法准确地知道，只能逼近它。

(7)误差(Error)。测得值与被测量真值之差。由于真值不能准确地确定，因而误差也是不能确切地确定的。

(8)不确定度(Uncertainty)。对量的真值缺乏了解的测度，亦即是对误差在某个范围内的估计。它是测量结果质量的表征。

(9)标准不确定度(Standard Uncertainty)。以估计标准差表示的测量不确定度。

(10)A类不确定度〔Type A Evaluation(of Standard Uncertainty)〕。由观测数列的统计分析评定的不确定度，也称统计不确定度。

(11)B类不确定度〔Type B Evaluation(of Standard Uncertainty)〕。不是由统计分析评定的不确定度，亦称非统计不确定度。

(12)合成不确定度(Combined Standard Uncertainty)。受到几个不确定度分量影响的测量结果的标准不确定度，它由其分量的方差、协方差求和开方而得。

(13)范围因子(Coverage Factor)。为增大置信概率，将合成不确定度放大一个倍数时所乘的一个数值因子。典型的取值范围为2≤K≤3。

(14)展伸不确定度(Expanded Uncertainty)。合成不确定度乘以范围因子。

9.3.2不确定评估

如果有一组观测数据x_i=x_true+ε_i,则误差ε_i可以分解为两个分量——一个为偶然分量，具有有限方差和零均值；另一个为偏移，具有有限均值和零方差。如果存在偏移，就无法从重复测量中去确定它的值，偏移的评定要从测量影响因素分析着手，或用与其他测量方法获得的结果相比较，或从测量仪器再现性与性能知识的估计中实现。对偏移做出最佳评估后，测量结果就已被修正，存在的是对偏移评定不确定度相联系的剩余不确定度。这样，这两个分量均构成了测量过程的不确定度：由直接测量和统计分析方法评定的不确定，及由其他间接的非统计方法评定的不确定度。前者称“A类不确定度”,后者称“B类不确定度”。

1.A类不确定度评估

A类不确定度用标准差s_i和自由度ν_i表征，自由度ν_i可用下式计算。有

ν_i=n-t     (9.17)

式中

n——重复测量数据个数；

t——约束个数。

标准差的估计用贝塞尔法和最小二乘法。

贝塞尔法。贝塞尔法适用对某一物理量μ在同一条件下作多次独立的计算，在剔除异常数据后获得n个测量值x₁,x₂,…,x_n,求其标准差，方法如下：

测量值的数学期望为

\(\mu=E\left({{x}_{i}}\right)=\bar{x}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{x}_{i}}}\)   (9.18)

一次测量的标准差为

\({{s}_{i}}=\sqrt{\frac{1}{n-1}{{\sum\limits_{i=1}^{n}{\left({{x}_{i}}-\bar{x}\right)}}^{2}}}\)   (9.19)

测量平均值的估计标准差为

\({{s}_{{\bar{x}}}}=\frac{1}{\sqrt{n}}{{s}_{i}}\)    (9.20)

(2)最小二乘法。此方法适用于线性计测系统的校准数据进行统计计算标准偏差。对应于校准加载值x;(i=1,2,…,k),重复测量r次，得到校准数据y;(i=1,2,…,k; j=1,2,…,r)。计算

\({{\bar{y}}_{i}}=\frac{1}{r}\sum\limits_{j=1}^{r}{{{y}_{ij}}}\)      (9.21)

求样本(x₁,\(\bar y\)₁),(x₂,\(\bar y\)₂),…,(x_k, \(\bar y\)_k)的回归方程，假设\(\bar y\)_i与x_i存在线性关系，即

\(\bar y\)_i=a+bx_i十ε_i

使y的观测值\(\bar y\)_i与(a+bx_i)的偏差的平方和为最小来估计a,b的方法叫“最小二乘法”。于是所求的a,b的估计值为

当x=x₀时，对应的\({\hat y}\)=\({\hat y}\)₀,这里\({\hat y}\)₀就是y对应于x=x₀时的数学期望。\({\hat y}\)₀的标准差按下式计算：

     (9.24)

式中

y_ij——校准数据

\({\hat y}\)_i——对应于x_i的回归值；

n——校准数据总数(n=kr);

k——校准的级数：

r——对应于每一个加载值x_i的测量次数；

x_i——校准加载值；

x₀——被测参数值。

2.B类不确定度估计

B类不确定度不由统计分析方法评定，并不意味它们没有统计评估的信息，以前类似测量的记录、测量仪器的检定资料都是估计的信息。B类不确定度用近似标准差μ_j和等效自由度ν_j表示。B类不确定度可以籍助于试验前信息，如仪器制造质量说明书、检定证书或其他证书提供的数据，使用经验、试验对比数据等。

(1) μ_j按下式计算，有

\({\mu}_{j}=\frac{{\Delta}_{j}}{{K}_{j}}\)   (9.25)

式中

μ_j——第j个因素引起的B类不确定度；

Δ_j——第j个因素引起的误差极限值；

K_j——范围因子；

(2)Δ_j,K_j及ν_j根据下述情况选取。

1)当仪器制造说明书或检定证书给出展伸不确定度及K值时，则K_j为给出值，ν_j也可取给出值，当给出自由度大于30时，ν_j,取30。

2)当说明书或检定证书给出极限误差为Δ_j,并给出置信概率为0.95,自由度ν_j时，则K_j可查t分布表。

3)当仪器说明书或检定证书只给出极限误差Δ_j,未给出对应的标准差倍数时，K_j取2,自由度ν,根据类似检定情况取值，最大不超过30。

4)当通过试验或经验估计Δ_j时，K_j取2,ν_j取2或1。

9.3.3单通道测量结果不确定度评估

固体火箭发动机的推力、压力采用线性测量系统来直接测量。一般来说，对同一个参数要安排几个通道测量。首先讨论单个通道测量过程不确定度的评估。

测量过程不确定度从来源分为以下几种。

(1)校准等级不确定度。

(2)数据取得不确定度。

(3)数据处理不确定度。

各来源的不确定度又可分为A类不确定度和B类不确定度，以下分别评估。

1.校准等级不确定度

校准等级不确定度就是标准传递过程产生的不确定度，用s₁表示校准不确定度的A类分量，u₁表示它的B类分量，ν₁表示等效自由度。如图9.3所示是测量推力的力值标准传递关系。

图9.3力值标准传递关系

固体火箭发动机试验测量用的工作传感器要用二级标准传感器来校准，二级标准传感器又要由更高一级标准器校准，这样一级一级向上追溯到国家基准级标准器。各级标准传递过程中都存在不确定度，表9.3列出了各校准级的不确定度。

表9.3各级校准不确定度

表中的s₁₁、s₁₂、s₁₃、s₁₄可根据各级校准数据，按式(9.24)计算，u₁₁、u₁₂、u₁₃、u₁₄可根据各校准仪器的Δ_j值估计(式(9.25))然后用总方根的办法合成s₁及u₁,即

\({s}_{1}=\sqrt{{s}_{11}^{2}+{s}_{12}^{2}+{s}_{13}^{2}+{s}_{14}^{2}}\)    (9.26)

\({u}_{1}=\sqrt{{u}_{11}^{2}+{u}_{12}^{2}+{u}_{13}^{2}+{u}_{14}^{2}}\)    (9.27)

等效自由度按怀特公式计算，有

\({\nu}_{1}=\frac{{{s}_{11}^{2}+{s}_{12}^{2}+{s}_{13}^{2}+{s}_{14}^{2}}^{2}} {\frac{{s}_{11}^{4}}{{\nu}_{11} }+\frac{{s}_{12}^{4}}{{\nu}_{12} }+\frac{{s}_{13}^{4}}{{\nu}_{13} }+\frac{{s}_{14}^{4}}{{\nu}_{14} }+}\)   (9.28)

实际应用中，只要知道了二级标准传感器的标准差和最大极限误差，分别用s₀和Δ₀表示，再用它校准工作传感器，计算出s₁₄,u₁₄,就可以计算校准不确定度为

\({s}_{1}=\sqrt{{s}_{0}^{2}+{s}_{14}^{2}}\)    (9.29)

\({u}_{1}=\sqrt{{\frac{{\Delta}_{0}}{K}}_{0}^{2}+{u}_{14}^{2}}\)    (9.30)

这里s₀包括了本身的和以上各级校准的A类不确定度，Δ₀也包含了以上各级的B类不确定度。二级标准传感器的s₀与Δ₀由该传感器检定时在检定证书上给出。二级以上的校准时的不确定度都包含在里面了，使用起来就比较方便。关于等效自由度v₁的估算，考虑到各级校准数据一般都在30个以上，因此取ν₁为30是可行的。

2.数据取得不确定度

数据取得不确定度评定，举推力测量为例。表9.4列出了推力测量数据取得不确定度来源。

表9.4数据取得不确定度

数据取得不确定度 s₂,u₂和等效自由度 ν₂计算如下：

 \({s}_{2}=\sqrt{{s}_{21}^{2}+{s}_{22}^{2}+{s}_{23}^{2}+{s}_{24}^{2}}\)    (9.31)

\({u}_{2}=\sqrt{{u}_{21}^{2}+{u}_{22}^{2}+{u}_{23}^{2}+{u}_{24}^{2}}\)    (9.32)

\({\nu}_{2}=\frac{{{s}_{21}^{2}+{s}_{22}^{2}+{s}_{23}^{2}+{s}_{24}^{2}}^{2}} {\frac{{s}_{21}^{4}}{{\nu}_{21} }+\frac{{s}_{22}^{4}}{{\nu}_{22} }+\frac{{s}_{23}^{4}}{{\nu}_{23} }+\frac{{s}_{24}^{4}}{{\nu}_{24} }+}\)   (9.33)

分别找出表9.4中各种不确定度分量往往比较困难，实际工作中，可以通过发动机点火试 验前的加载试验来估计s₂,u₂。推力传感器在原位校准中得到校准系数c₃,加载试验要模拟 发动机推力，加载装置通过标准传感器指示值对工作传感器施加额定推力值，测量系统采集记 录数据，采样时间要满足稳态所必需的最小观测时间，一次采样数据不少于15个，加载次数不 少于12次。

 A类不确定度s₂为

 \({{s}_{2}}={{c}_{3}}\sqrt{\frac{\sum\limits_{i=1}^{n}{{{\left( {{{\bar{y}}}_{i}}-\bar{y} \right)}^{2}}}}{n-1}}\)    (9.34)

 式中

 C₃——推力校准系数；

 \({\bar y}_{i}\)——第i次加载试验采集的数据平均值(mV), \({\bar y}=\frac{1}{n}\sum\limits_{i=1}^{n}{{\bar y}_{i}}\)

 n——加载试验次数。

 3.数据处理不确定度

 数据处理不确定度分别用s3和 u₃表示。用计算机对采样获得的原始电量数据进行处理， 转换为力、压强、温度及速度等工程物理量，该过程的不确定度来源于校准曲线的拟合和计算 机的分辨力。由于计算机的分辨力远远高于测量精度要求，曲线拟合误差在校准与加载试验 中都已经考虑过了，所以这些不确定度通常可以忽略。

第10章非接触式测量技术概论

随着火箭发动机技术的发展，对测试技术也提出了新的要求。除了推力、压力等宏观参数的测量，人们需要了解发动机工作过程中更多、更细的参数，例如流动形态、流动速度、燃气温度和组分分布等。对于冲压发动机和组合发动机等动力来说，其流动和燃烧过程更为复杂，这种需求就更为强烈。

虽然目前数值模拟技术有了很大的进步，但是对于发动机内复杂的流动和燃烧过程，实验测量仍然是无法完全替代的。这是因为，一方面数值模型是否合理、计算结果是否准确都需要实验的校验，另一方面很多数值模型的建立是基于实验研究基础上的。

随着科学技术的进步，非接触式测量技术得到了很大的发展。所谓非接触式测量技术，就是测量过程中与对象不接触，对对象不产生干扰(或者干扰极小)。因此对于一些非常复杂精细的流动和燃烧过程，以及高温等恶劣环境，非接触式测量技术显然具有非常明显的优势，因此在流动和燃烧等领域得到越来越广泛的应用。

在非接触式测量技术中应用最为普遍的是光学诊断测量技术。普通的光学测量技术基于光的折射、反射和散射等现象，激光光谱诊断技术则基于激光与物质复杂的相互作用。当激光与燃烧场中的凝相粒子、分子、自由基等作用时，会由于各种效应产生喇曼散射、瑞利散射、米散射、荧光等信号，这些信号携带了燃烧场的温度、密度、组分浓度等信息。

与传统的接触法测量技术相比，激光光谱诊断技术具有很多优点：对燃烧场几乎没有扰动，可以精确测量真实的燃烧过程；测量信息丰富，可以在线测量瞬态燃烧场的温度、压力、流速、组分等各种信息；空间和时间分辨率高，可以测量瞬时一维、二维及三维燃烧场信息；具有可视性，形象直观。

本章首先简要介绍激光诊断技术的类型，然后主要介绍阴影、纹影、PIV、PDPA和LIF等一些非接触式的诊断测量技术。

10.1激光诊断技术

由于激光诊断技术功能的多样性，激光诊断技术的分类比较复杂。从空间上讲，可以分为点测量、线(一维)测量、面(二维)测量和体(三维)测量；从时间上讲，可以分为连续测量和脉冲测量；从燃烧所关心的主要参数上讲，可以分为温度测量、组分(包括最终产物、自由基和离子)浓度测量、速度测量和两相流粒度测量等；从光的相干性，可以分为相干测量和非相干测量。

从测试的对象来看，系统的燃烧效率是研究者最为关心的，通常用主要生成物的浓度表征燃烧效率。燃烧产物的浓度检测方法包括化学检测法和光谱检测法。化学检测法通常基于采样技术，然后采用气相色谱仪之类的仪器测量。从微观上说，无论主要组分还是微量组分，产物的浓度实际上是分子数密度，分子数密度的不同导致与激光产生相互作用的样本数量的不同，从而导致光强或谱线线型的改变。许多光谱学方法都可以用于组分浓度的检查，包括散射法、激光诱导荧光和吸收光谱技术等。

温度是燃烧场的另一个重要信息，反应能量的释放程度。尽管存在响应速度慢、需要校正等缺点，热电偶还是最常用的温度测量方法。但是，在要求快速响应、高温或者不能被扰动的环境下，需要采用非接触式测量方法。光学和光谱学方法可用于温度的非接触测量，可以将此类方法分为四类。第一类利用辐射原理，从不同波长的辐射强度中获取温度，比如双波长或多波长测量方法；第二类方法基于光的干涉，温度的变化导致气体介质密度的改变，从而影响折射率；第三类为光谱学方法，跃迁强度与跃迁能级的粒子数密度有关，而振动一转动态的粒子数密度服从玻尔兹曼分布，与从而与温度相关，可以从各种谱线中获取温度信息；第四类基于数字图像处理技术，从色彩分布信息中获取温度。这些方式的分类不是绝对的，辐射法中也需要用到一些光谱的运算，数字图像处理方法通过对火焰颜色的处理可以获得组分的一些信息。

燃烧与流动密切相关，但是有些流动现象可以与燃烧无关，比如冲压发动机进气道和隔离段的流动。常用的流动诊断方法多基于光的散射，比如粒子图像速度仪(Particle Image Velocimetry, PIV)和相位多普勒粒子分析仪(Phase Doppler Particle Analyzer, PDPA);纹影法也是研究流动的常用方法，利用的是光的折射现象；利用不同方向光束的多普勒频移也可以探测流场的速度，比如吸收光谱方法。

固体火箭发动机、液体火箭发动机、冲压发动机和航空发动机都存在两相流问题。液滴的雾化、蒸发和燃烧过程决定着燃烧效率，并对燃烧稳定性产生影响。在固体火箭发动机中，金属的燃烧及其产物的两相流特性不仅影响发动机的燃烧效率和稳定性，还会影响熔渣的沉积。碳氢燃料在某些条件下生成的碳烟，其燃烧产物也可以被认为是两相流。两相流的粒度分布是研究者关心的问题，PDPA利用散射效应测量两相流中凝相的粒度，激光诱导白炽光技术用于测量碳烟的粒度，彩虹技术可以测量液滴的粒度和温度。

表10.1显示是几种常用激光诊断技术在燃烧流动方面的测量能力。

表10.1常用的激光诊断方法

10.2阴影和纹影技术

在流动和燃烧研究中，很多时候需要了解流场的结构和细节，例如各种波系(激波、膨胀波)、剪切层/混合层、波系的反射和干扰等等。流动显示技术就是对流场的结构和细节进行呈现的技术。流动显示技术有很多种，这里主要介绍比较常用的阴影和纹影法。

10.2.1阴影法

我们都有这样的生活经验：在炎热的夏天，经常可以看到地面上出现气流扰动的虚影；在飞机发动机喷口也能看见这种情况。这是因为高温热源导致空气密度不均匀，而光线的折射又与密度有关，因此光线经过空气密度不均匀的区域，发生不同的折射，使得光线聚拢和发散，就出现了我们看到的明暗扰动的虚影。这其实就是阴影法的基本原理。

阴影法是光学显示中最简单的一种。如图10.1所示，将一束光(散射或平行光)透过流动试验区投射到屏幕上(或通过透镜),若试验区内流体未受扰动，密度均匀，屏幕上亮度均匀；若流体受扰动，由于密度变化引起光线偏折，投射到屏幕后偏离原来位置，将出现暗纹，一般能定性观察激波、边界层、尾流和漩涡等。通常会出现如下三种情况。

(1)均匀密度：各点光线的折射率相同，平行光透过流场后仍然保持平行。

(2)密度梯度为常数，即二阶导数为零：光线的偏转角正比于密度梯度，偏转角为常数，屏幕上的亮度不会改变。

(3)密度的二阶导数不为零：屏幕上的亮度变化正比于密度的二阶导数，当\(\frac{{\partial}^{2}{\rho}}{{\partial x}^{2}}>0\)\时，即(\frac{{\partial}^{2}{n }}{{\partial x}^{2}}>0\)(式中ρ为密度，n为折射率),光线的偏转有发散的趋势，形成暗区；反之，有聚拢趋势，形成亮区。

图10.1阴影仪原理图

由此可见，阴影图像只能显示出折射率的二次导数的不均匀性。由于对比度的精确测量是很困难的，因此典型的阴影系统很少用作定量研究。

图10.2所示为风洞实验的阴影图。

图10.2风洞实验的阴影图

10.2.2纹影法

我们已经知道阴影法图像的明暗正比于密度的二阶导数。如果某个区域的密度梯度为常数，也就是说密度线性增加或者减小的，此时密度的二阶导数为零，亮度没有任何变化，也就是说这种密度变化是完全显示不出来。如果某个区域密度的二阶导数是非零的常数，例如密度以平方关系变化，此时该区域的明暗是整体变亮或者变暗，虽然与未扰动的区域有区别，但该区域内密度变化是体现不出来的。可见阴影法能够反映的流场细节还是比较有限的。而纹影法则提高了一步，纹影法图像的亮度与流体密度的一阶导数有关，而且在一定的条件下可以进行定量分析。

那么纹影法是如何提高对密度变化的分辨能力的?实际上通过在光路焦点附近增加一个刀口遮挡来实现的。如图10.3所示，由光源发出一束平行光线，在通过气流密度不均匀的测试段时，光线发生偏转(见图10.3中虚线),位于焦点处的刀口切割光源像的程度与流场的折射率梯度有关，这样，由屏上的光强分布与流场中光折射率一阶导数的关系，可以求出流场的密度分布。

图10.3双透镜纹影仪的原理图

若用金属刀口，则在光屏上显示光强的明暗分布。若用一种彩色滤光片取代金属刀口，则在屏上呈现出色彩分明的图像。由于人眼对彩色的分辨率比光强明暗反差更敏感，这样更有利于实验观察和定性分析。

图10.4所示为典型的纹影照片。

图10.4自由射流激光纹影图

10.3粒子图像测速技术

气流速度是空气动力学实验与测量领域的一个重要参数，早期主要采用热线风速仪等接触式方式进行测量，随着技术的发展，粒子图像测速技术(PIV)和相位多普勒粒子分析技术(PDPA)等非接触式测量方法得到了越来越广泛的应用。在火箭发动机和冲压发动机领域，经常会采用冷流模拟实验的方法来研究一些流动问题，PIV技术具有不干扰流场，可以一次获得平面、甚至三维的速度场分布，在冷流实验中具有很大的优势。

很多人都有过用照相机或手机进行连拍的经验，如果我们对一个运动的小球进行等时间间隔的连拍，在连拍图像上，把相邻两幅小球的中心连线，则连线的方向就是小球该时刻运动的方向，连线长度(换算成实际长度)除以时间间隔就是该时刻小球的运动速度。本质上讲PIV和这个原理很相似。

PIV测量的不是流体的速度，而是示踪粒子的速度，也就是说需要在流体中加入微小粒子，如果粒子的随流性很好，则粒子与流体之间的滞后很小，就可以通过测量粒子的运动速度来代替粒子所在位置流体的速度了。

如果在流场中均匀的布撒大量的粒子，然后用片光源照亮需要测量的流动区域，PIV就可以测量一个截面上的二维速度分布。

可以看出，PIV从本质上看是一种图像分析技术，利用粒子对入射光产生米散射的原理，并以此作为示踪粒子，用照相机对含粒子的流场进行瞬时拍照。它可在瞬间冻结流场，给出二维速度分布。通过对粒子影像的查询处理，确定粒子两次成像的位移量Δx, Δy(见图10.5)。由于激光器发生两次脉冲的时间间隔是已知的，这样就可以得到粒子的运动速度矢量。

所测平面内大量粒子的运动矢量，构成了二维平面速度矢量场。两个摄像机成一定角度布置，共同对一个平面成像，采用一定的重构算法，可实现速度场的三维测量。

图10.5确定粒子位移的示意图

在粒子浓度很低时，称此PIV模式为PTV(Particle Tracking Velocimetry),即粒子追踪速度场仪。当粒子浓度高到使映像图在接收区重叠时，称此PIV模式为LSV(Laser Speckle Velocimetry),即激光散斑速度场仪。通常所讲的PIV是指粒子浓度很高但映象在接收区不重叠的情况。

典型的PIV系统包括照明流场的瞬时多次曝光光源系统(双脉冲激光器、光导臂、片光镜头)、粒子图像的记录装置(数字摄像机)、粒子图像的处理判读方法及设备(计算机和数据处理软件)和粒子播放示踪装置等，如图10.6所示。双脉冲激光器发出两束具有很短时间间隔的脉冲光，光通过光导臂传输至实验场所，由片光镜头将束光转换为片光，照明感兴趣的流场区域。数字相机拍摄图像，由图像处理软件处理成速度场。没有杂质的气态流场不能产生足够强度的米散射，因此需要在流场中播撒一定粒度的示踪粒子。PIV获得的流场速度实际是示踪粒子的速度，因此所播撒粒子的随流性非常关键，随流性与粒子的粒度有关。

图10.6典型PIV的组成图

由于激光器和数字摄像机技术水平的限制，传统的PIV时间分辨能力较差，一般最多每秒成像15次，适合于研究稳态的流场。对于随时间变化较为剧烈的流场，例如百赫兹量级的涡脱落，需要高时间分辨能力的PIV技术。近年来，PIV技术向高时间分辨、微观成像、层析成像等方向发展。可获得的商业化产品有以下几种。

(1)层析PIV系统(Tomo-PIV)。采用四台相机摄像，利用层析重构算法和三维互相关分析，可以得到一个控制体内流场速度分布；

(2)显微PIV系统。将显微技术和PIV技术相结合，可以研究细观流动的流场分布，比如血管的血液流动。

(3)高时间分辨PIV(高速PIV)系统。采用高时间分辨的激光器和高速数字相机，可以实现每秒钟千赫兹量级的速度场测量。

层析技术、显微技术、高时间分辨技术可以相互组合，形成强大的非稳态、细观流场的分析能力。采用内窥镜技术，还可以研究装置内部的流场状况。

10.4相位多普勒粒子分析仪

相位多普勒粒子分析仪(PDPA)是激光多普勒测速仪(Laser Doppler Velocimetry, LDV)的扩展，利用运动微粒散射光的多普勒频移测量速度，利用不同接收方向上散射光的相位差测量粒子尺寸，测速精度为1%。

PDPA系统一般包括激光发生器、冷却系统、光纤驱动器、光纤、发射器、接收器、光电倍增管、多普勒信号分析仪和DSA软件等，典型的组成如图10.7所示。其工作过程如下：首先，由激光器产生一束相干光源，这束光经准直器校直后，垂直进入布喇格盒中进一步被分为三色六束光，同色的两束单色光分别被频移0MHz和40MHz后，聚焦于测量区域中。在焦点处示踪粒子接收入射光并向四周散射。接收器接收部分散射光并通过全反射光纤把光信号传递给光电倍增管，光电倍增管将光信号转换为电信号。电信号进入多普勒信号分析仪，经过过滤、放大等处理后输入计算机，最后由计算机显示和处理。

图10.7典型PDPA系统组成

PDPA系统一般采用氩离子激光发生器，它能产生多种谱线的激光，波长范围主要分布在蓝光和绿光区域。若输出激光的功率为0～5W,则绿光的最大输出为2W,蓝光为1.5W,紫

光为0.45W。氩离子激光发生器是大电流器件，放电电流为数十安培，因而电源及放电管发热厉害，工作时必须通水冷却。

一束来自激光器的相干光进入布喇格盒中后进行分色分束处理，首先经过光调制器，生成一系列频移光束。其中一束为零级光，相当于没有加频移的光束，其性质和入射光一样，只是光强占入射光的47%左右，另一束光加了40MHz的频移，其光强占入射光的50%左右，剩余的少数光弃之不用。两束光在色散棱镜中被分色，产生三对不同颜色的光束，波长分别为

514.5nm(绿光)、488.0nm(蓝光)、476.5nm(紫光)。分色分束后的三对光束经耦合器耦合，沿两根光纤通过全反射从两个发生器射出汇交于一点。从发射器出来的光，其强度只有进入光纤前光强的40%,同色光强度大约相等。三色光强度顺序为绿光>蓝光>紫光。

一个二维光发射器和光接受器配合可完成粒度测量和二维速度的测量，增加一个光发射器可完成三维速度的测量。需要说明的是，PDPA的几束光需要对焦至一点，测量的速度是通过该点的粒子的速度。

两束同色光形成间距已知的相关条纹，当粒子通过该区域时散射光强产生变化，这便是速度测量的原理(见图10.8)。多普勒频移与粒子速度的关系中，由于频率没有正负，所以大小相同、方向相反的速度得到的频率是一样的。为了判别流动方向，PDPA采用频移装置使其中一束光产生频移，这样控制体中的干涉条纹就会从高频光束向低频光束一侧移动，基于此原理可获得速度的方向。微粒散射光强与其尺寸有关，微粒越小，散射光越弱，据此原理可获得单个粒子大小的分辨，加上适当的算法可给出粒度分布和不同定义的平均粒径。

图10.8相干条纹示意图

PDPA的功能不算强大，三维测量的难度不小，主要是对焦比较困难。传统的氩粒子激光器产生大量的热，需要大量的冷却水对激光器进行冷却。近年来，PDI(相位多普勒干涉仪)技术逐渐取代PDPA,其速度和颗粒粒度的测量原理与PDPA差别不大，采用半导体泵浦的激光器功率更小，操作更为简便。

10.5激光诱导荧光技术

通过不同的方式使原子、分子或自由基跃迁至受激态，然后自发回迁至较低能级，向外辐射光子，就会产生荧光。电子轰击、化学反应(化学发光)、加热或光子吸收都可以产生荧光，这里只讨论最后一种方式，即光子吸收。荧光应该被视为吸收光子跃迁后自发辐射产生的现象。荧光信号的强弱与分子或自由基的数密度相关，因此可以通过荧光信号的强度获得浓度信息。

激光诱导荧光(Laser Induced fluorescence, LIF)主要用于探测化学反应的中间产物和自由基，例如，OH和CH。由于LIF方法的灵敏度高，它可以在较低浓度下检测到其中特有成分的电子跃迁光谱(紫外段)。

让一束激光通过燃烧火焰，调节激光波长，当激光能量等于分子的某两个特定能级差时，该分子会吸收光子能量跃迁至高能态，处于高能态的分子是不稳定的，当它从高能态回到基态时，就会产生自发辐射而发射荧光，这就是激光诱导荧光。如果使用片状激光束进行激发，就可以对燃烧场某个断面的参量分布进行成像，此时该技术又称为平面激光诱导荧光技术(Plane Laser Induced Fluorescence, PLIF),如图10.9所示。LIF信号强度是温度、压强、摩尔浓度等参数的函数，选取适当的激励能级可以使得荧光强度在一定范围内仅与温度或仅与浓度有关。通过实验参数的设置，即可求得燃烧场的相对浓度或温度分布，此时，只要有一个点的值是确定的，便可以确定整个燃烧场的参数分布。

图10.9典型PLIF实验系统

LIF技术具有很高的信号强度和光谱分辨率，优异的时间和空间分辨率，灵敏度高，测量结果丰富直观。对于燃烧流场，LIF技术可以用来探测众多由C、O、N和H等元素构成的活性分子和基团。例如，利用可调谐染料激光器LIF技术可探测碳氢燃料燃烧的重要的中间产物OH基，从而了解燃料燃烧过程。

LIF荧光信号与激光激励波长和探测波长密切相关，选择过程复杂。主要使用染料激光器，结构和操作较为复杂，并且价格昂贵。对于浓度较低的组分，难于精确测量。LIF测量结果是相对值，荧光强度并非正比于温度和组分浓度，需要进行标定。

由于荧光与能态分布相关，LIF也可用于温度测量。LIF法测温是通过测量荧光强度随激发光波长的变化，从而得到基态转动能级粒子数的分布或者振动能级粒子数的分布，然后根据玻耳兹曼公式计算出体系的温度。在燃烧系统中LIF的应用包括测量温度、测量粒子浓度、燃料分布等方面。目前，LIF已成为燃烧气流的化学与结构研究的重要手段。但是，目前的LIF只是一种定性的测量方法，很难做到定量。