第一章 绪 论

第二章 高压室内弹道理论基础

第三章 高压室内弹道计算

第四章 弹射器低压室内弹道的一般问题

第五章 并联无后坐式弹射器低压室内弹道方程组及解法

第六章  并联无后坐式弹射器内弹道设计

第一章 绪 论

1.1、火箭导弹弹射器的基本组成、基本工作原理及分类

发射技术中利用火箭导弹以外的力源，将火箭导弹发射出去的技术称为弹射技术，采用弹射技术发射火箭导弹的装置称为弹射装置。弹射装置中产生弹射动力并将火箭导弹发射出去的部分称为弹射器。

发射方式

热发射（hot launch）系统

利用导弹本身的发动机或者助推器产生推力将导弹射出发射管，因此系统本身并无动力结构，并拥有排焰排气管道。热发射系统的优点是效率较高，它能够节省发射系统的体积和重量、并降低其维护成本。可是在可靠性方面，热发射系统却比冷发射系统略逊一筹，因系统本身并无动力将有问题的导弹射出，当出现点火卡弹或其他的状况时，难以排出弹体，故其技术要求高，须保证发射失败时系统能承受推进剂在发射管内长时间灼烧与弹头殉爆时不会导致其他发射管内的弹体诱爆。

冷发射（cold launch）系统

使用其它的机构（最常使用的是弹射杆，利用燃气带动一个拉杆将导弹弹出去）将导弹弹射出去，待其离开发射管后，再点燃发动机。此系统的优点是安全，因为它能够有效地将有问题的导弹射离舰艇。苏联的舰载冷弹射防空导弹是陆上的S-300与“道尔”导弹的改型，燃气发射器是整合在储运发射筒内部，不是共用弹射装置。

由于导弹于离开发射管后才点燃发动机，因此冷发射系统不用承受点燃导弹所产生的高热火焰，对导弹气动外形改动较小，有利于保证导弹的飞行性能，可使该系统的使用寿命较长。但是，相较于热发射系统，冷发射系统的发射效率较低，而且难以做到不同导弹共架发射，而且如果发射失败，发射器有可能将导弹弹出去后掉到船上爆炸，造成更大伤亡。因此，垂直发射井实际倾角通常在85度左右，使得导弹出井后会离开舰艇舱面的上空。

共架发射（Concentric Canister Launch）系统

也称作冷-热兼容发射系统，使得同一发射井可以发射多种不同用途的冷发射与热发射的导弹，有同时享有冷、热发射系统的优点以及更强导弹兼容性为优势，但把两种系统合二为一的技术要求很高，目前仅解放军海军的052D型和055型驱逐舰上有使用。

1. 冷发射基本组成

尽管弹射器的种类很多，但仍可概括出它们的基本组成。当然并不是每一种弹射器都具有每一基本组成部分。

(1)发射筒  一般说，弹射装置大多具有发射筒，即其定向器为筒式。这是因为发射筒易于密闭气体，以形成所需要的弹射力；而且发射筒可兼作包装筒，给导弹提供所要求的温度、湿度环境，具有贮存、运输、发射导弹等多种功能，使导弹平时得到良好的保护，简化维修保障工作，战时减少战前检测，战术使用简便，

(2)高压室与低压室 以燃气或压缩空气为工质的弹射器均具有高压，低压两个工作室，其原因是火药必须在高压下才能正常燃烧，而导弹在发射过程中，为了保护弹上仪器，其所受发射加速度不允许过大，为了解决导弹纵向加速度不能过大与火药正常燃烧，或压缩空气贮气设备不能过重过大的矛盾，弹射器分设高压室与低压室。火药在高压室中得到正常燃烧所必需的压力环境，而导弹在低压室中受低压推动向前运动。仅有高压室或低压室的弹射器可看作某些条件下的特例，前者如炮式弹射器，后者如液压式弹射器。

高压室用以形成弹射动力源。对于以燃气为工质者，高压室即半密闭的火药燃烧室，火药燃烧后通过其上不同形式的喷管或管道阀门系统将高压燃气排送到低压室中去。高压室可以固定在发射筒中，也可在弹后随弹一起运动。

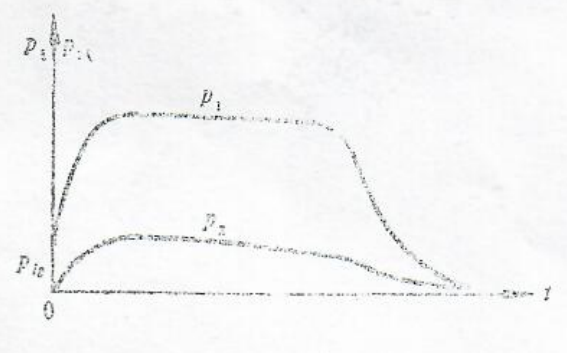
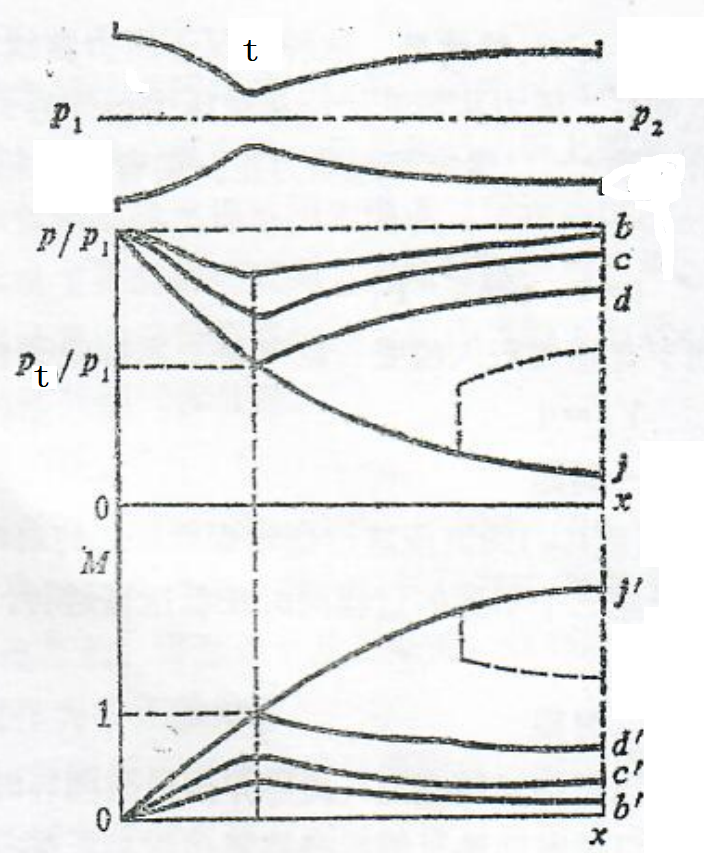
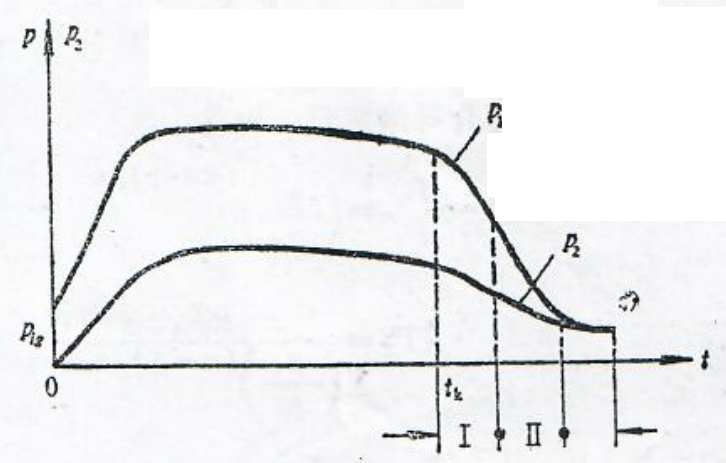
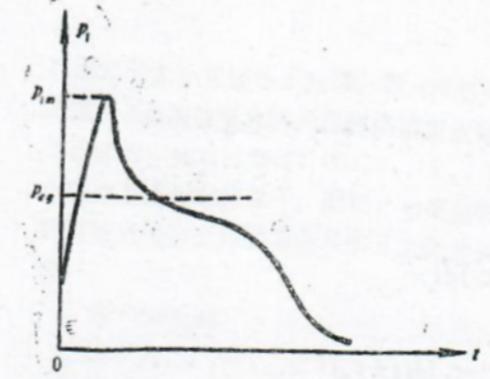
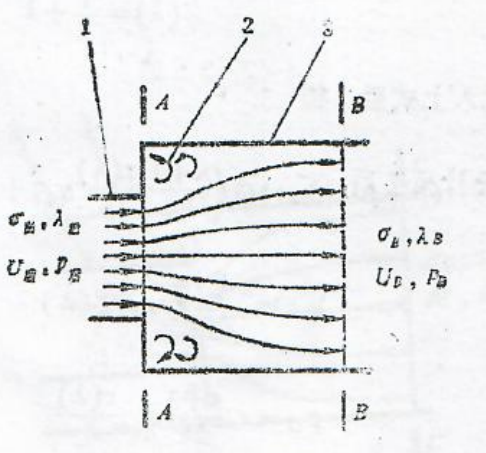
高压室喷管在未点火工作时由喷口膜片密封，当点火工作后，点火药气体在高压室中建立起压力pi。当pi达到使装药点燃的点火压力pig时，一般要求所有喷口膜片亦同时破膜，即点火压力pig等于破膜压力p。此后高压室即成为一个半密闭的燃烧室，燃气顺利进入低压室，低压室开始建立压力p₂,故高、低压室压力曲线的关系如图1.1所示。

图1.1 高、低压室压力曲线

低压室是形成弹射力的密闭或半密闭空间，一般就是发射筒内的导弹后部空间。通过高压窒喷口或管道送来的工质在此建立起低压室压力，作用在导弹承压面上形成弹射力。低压室的压力远低于高压室压力，一般为几个兆帕，随着导弹的运动，低压室容积不断扩大。

(3)反后坐装置 其作用是产生向前的推力以抵消发射筒的后坐力，这样可以改善发射支架的受力情况，保持瞄准精度。倾斜发射的小型战术导弹弹射器常具有反后坐装置，因为对于这类弹射器要求运动机动性好，无论便携使用或车载，均希望重量小；且其跟踪扫描装置常与发射筒安装在一起，发射筒的后坐将影响瞄准精度。

水下垂直发射或地下并弹射哉略导弹以及从飞沉上横向弹射机载导弹，均可不设反后坐装置，因为后坐力对潜艇这样重量很大的载体及高速飞行的载机不会产生很大的影响。

反后坐装置一般为尾喷管式或制动小火箭式。

(4)隔热装置或冷却装置

为防止高温燃气损伤导弹，需要在弹后采用隔热装置或燃气冷却装置。隔热装置即在弹后放置隔热活塞或用尾罩将导弹尾部笼罩起来。活塞或尾罩的作用除隔离高温燃气外，还可通过外圆上的密封措施密时燃气并承受、传递弹射力。弹射过程中，活塞或尾罩随弹运动至发射筒口，而后止于筒口或随弹飞出后，与弹体分离，自行坠落。尾罩的重量比铰大，需用侧向发动机使其在指定的地点坠落。

战略导弹的活动底座(相当于活塞)或尾罩无论止动于筒口或坠落地面，其动能均相当大，处理好这部分能量是一个复杂的问题。为了避免这个问题发生而出现了使燃气降温的办法，即采用冷却装置。当燃气温度降至足够低时就可以不要活动底座或尾罩了。据报导，美国“三叉戟”  潜地导弹及MX陆基机动发射导弹均无尾罩，后者的燃气温度可冷却至204～260℃。常用的冷却剂是水，燃气通过水室后温度大大降低，并使水汽化，燃气与水蒸汽混合后共同作为弹射工质，因而称为燃气蒸汽式弹射器。

除此之外，弹射器的组成还包括筒口止动装置、密封装置等。

2.基本工作原理

尽管弹射装置的型式各异，工作过程也不完全相同，但它们的基本工作原理是相同的。无论哪种弹射装置都有一个形成弹射力的外动力源(高压室)。由于受到导弹纵向发射加速度的限制以及不允许高温气体直接接触导弹，从高压室产生出来的大量高压气体(如压缩空气)或高温高压气体(如燃气)不能直接用来推动导弹运动，而必须经过降温降压环节，如喷管、冷却系统或阀门管路等，然后进入低压室形成弹射力，将导弹弹射出筒。一般情况下。导弹第一级发动机在出筒口或出地面、出水面之后才点火工作。

3.分类

根据不同的准则可对弹射装置进行不同的分类，按照作功工质的不同可将弹射装置分为四大类，燃气式弹射装置、压缩空气式弹射装置、液压式弹射装置、电磁式弹射装置。其中电磁式弹射装置不是靠气压或液压来形成弹射力，而是用完全不同的一种力——电磁力来作为弹射力，因而不存在作功工质的问题。它是一种最新发展起来、尚处于实验室研究阶段的特殊弹射方式。

燃气式弹射装置又含括以下六种型式：

无后坐式：并联式，一串联式

• 燃气式
• 横弹式
• 活动底座式
• 燃气蒸汽式
• 自弹式
• 炮式

这六种型式中的前四种(无后坐式、横弹式、活动底座式、燃气蒸汽式)具有共同的特点，即都具有一个固定在弹射器上的燃气发生器(高压室),所以亦可称为固定高压室式弹射装置；自弹式则不同，它的高压室不是固定在弹射器上，而是随弹一起运动，所以称为运动高压室。运动高压室可以是在弹后附加一个小燃烧室，也可以直接由第一级发动机兼任。由于形成弹射力的燃气工质是由随弹运动的高压室或导弹自身的发动机流出的，故取名为自弹式弹射器。自弹式本质上是自力发射与弹射的结合，因弹射力为其发射动力的主要成分，故亦归为弹射的一种。

无后坐式弹射装置由于具有尾喷管(反后坐装置),故根据高、低压室配置关系的不同又可分为并联无后坐式与串联无后坐式。

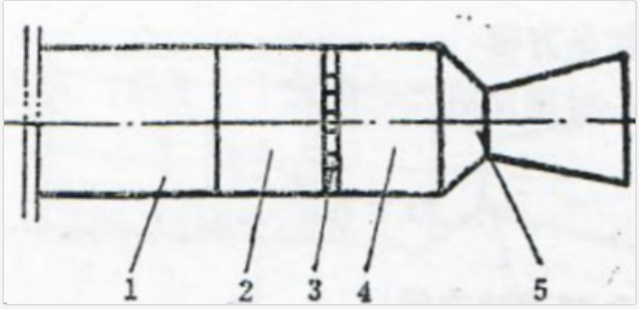
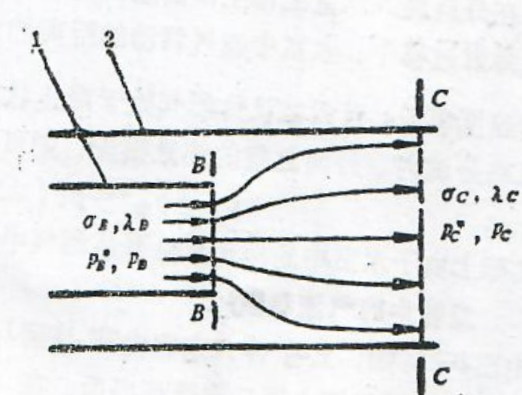
图1.2及图1.3分别为串联无后坐式及并联无后坐式弹射器的原理图。

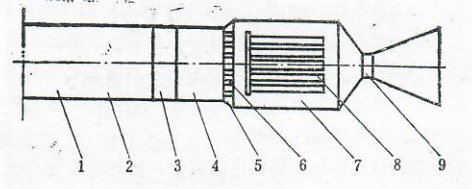
图1.2串联无后坐式弹射器
1一发射筒；2一导弹；3一活塞；4一低压室；5一前隔板；6一前喷口；7一高压室；8一火药；9一尾喷管。

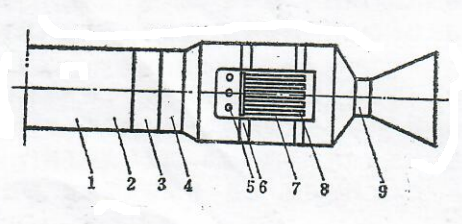
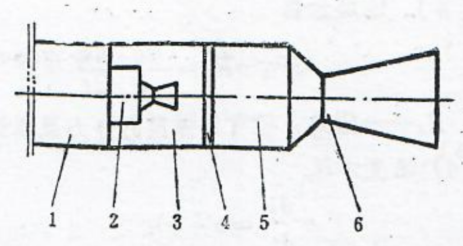
图1.3并联无后坐式弹射器
1一发射筒：2一导弹；3一活塞；4一低压室；5一高压室喷口；6一高压室支腿；7一高压室；8一火药；9一尾喷管。

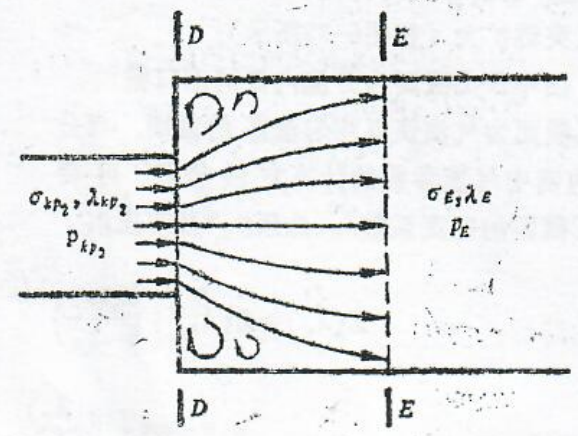
图4为横弹式弹射装置原理图，其弹射力垂直导弹纵轴，常用于空空、空地及空舰等机载导弹的弹射。

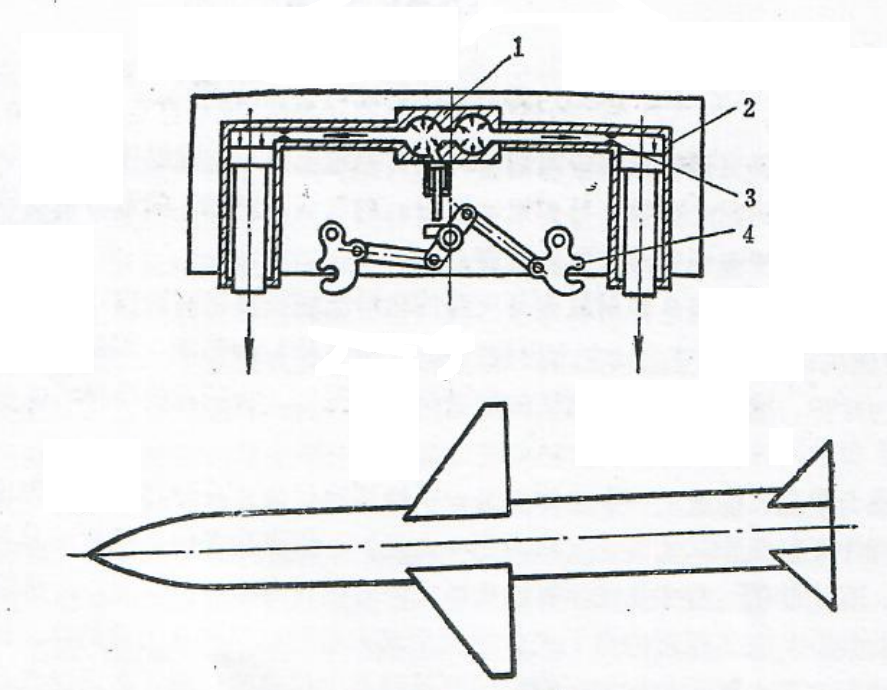
图1.4横弹式弹射装置(提拉杆式的)
1一高压室；2一低压室；3一节流口；4一挂弹钩。
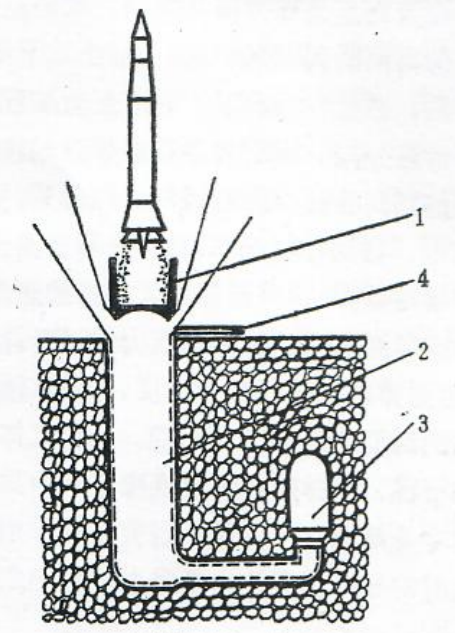
图5为井下发射战略导弹用的活动底座式弹射装置原理图。

图1.5活动底座式弹射装置，井下发射

1一活动底座或者尾罩；2一发射筒；3一高压室；4一筒口顶盖。

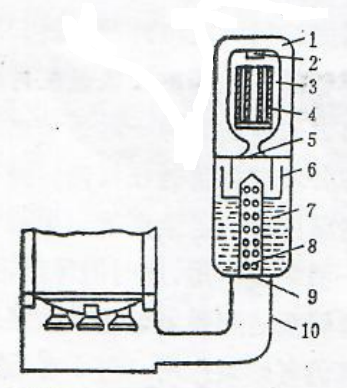
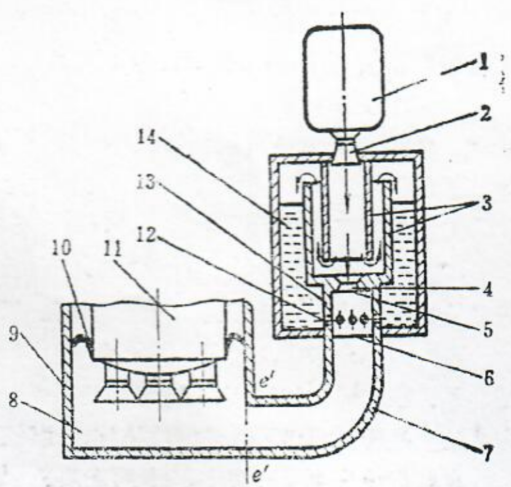
图1.6燃气蒸汽式弹射装置，潜射发射
1一外壳：2一点火器；3一高压室；4一装药；5一喷管；6一分流圆筒；7一水室；8-立管上的小孔；9一隔膜；10一弯管。

图6为燃气蒸汽式弹射装置，水下发射或陆基机动发射战略导弹时常用此类弹射装置。限于篇幅，我们不可能逐一地研究每一种弹射装置的内弹道问题，而是选择最具代表性的并联无后坐式弹射器的内弹道问题作为重点研究对象，在此基础上再结合各自的特点对串联无后坐式、自弹式、燃气蒸汽式弹射器的内弹道问题中带个性的问题兼作一定的叙述。书中有关内弹道基础理论部分及解决问题的方法对于以燃气为动力源的其它弹射器也都是适用的。

1.2、弹射内弹道学的研究对象和任务

弹射内弹道学是研究弹射过程中弹射器内一切弹射现象和过程规律性的科学。它包括火药在弹射器高压室内的燃烧规律，导弹运动规律，燃气流动规律，能量转化规律以及弹射器高、低压室内的压力变化规律等方面的内容。

那么什么是弹射过程呢?弹射过程是火药的化学能在汲短的时间内(百分之几秒或千分之几秒)经过燃烧这种化学变化转变为燃烧产物(火药气体)的热能，然后通过燃烧产物膨胀作功又转变为导弹、燃气以及发射简等的运动动能的过程。火药是使导弹、发射简运动起来的能源。

由工程热力学知，能量从一个物体到另一个物体的传递有两种方式：一为传热，一为作功。传热过程中无能量形式的转化(由内能→内能);借作功来传递能量时总是和物体的宏观位移有关，在作功的过程中往往伴有能量形式的转化(内能→机械能)。从能量传递的观点来看，弹射过程中，在高压室内由于火药燃烧生成大量燃烧产物及大量的热，这些热传逆给燃烧产物而得到高温燃气，故燃烧产物的加热过程漏于传热的过程；高温燃气在低压室膨胀作功推动活塞一导弹一发射筒运动的过程则属于能量传递的另一过程——作功过程，即火药气体的内能转化为机械能的过程。

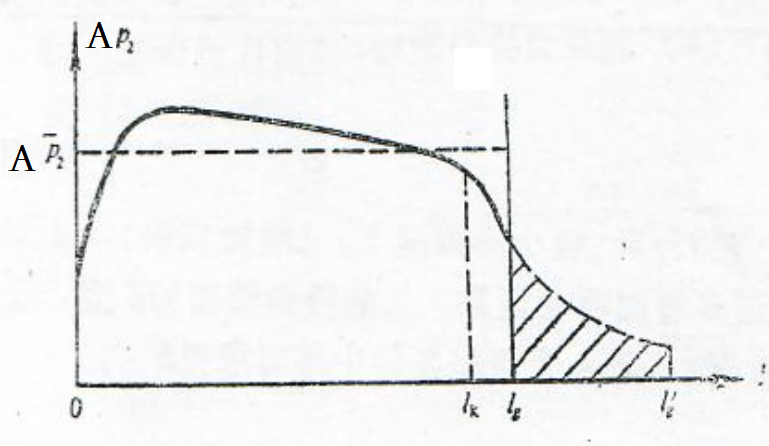
弹射过程的起点亦即点火过程的起点，而其终点是导弹离简瞬间。我们定义导弹运动至发射筒口、弹射力不再起作用的瞬间为导弹的离筒瞬间。根据活寨是否止动于筒口，又可分别出现两种情况。一是活塞止动于筒口的情况，在此种情况下，活塞止动过程开始的瞬间是导弹离筒瞬间，因为从该瞬间以后，导弹与活塞分离，弹射力不再对导弹起作用，导弹速度达到弹射过程的最大速度，该速度称为导弹的离简速度，弹射过程至此结束。二是活塞并不止动于筒口，而是随导弹一起运动出筒的情形，在这种情况下，导弹-活塞离开筒口后，简内火药气体并没有被密封在筒内，弹射力继续对导弹-活塞起作用，导弹的速度继续增加，当导弹到达筒口前一定距离后，火药气体迅速向周围空间扩散，压力迅速下降，火药气体不再对导弹一活塞起作用，此时的导弹速度才达到弹射过程的最大速度。导弹从活塞承压面到达筒口截面瞬间至达到弹射过程最大速度瞬间的时间间隔称为后效期，火药气体在这一期间对导弹一活塞仍有后效作用。对于有后效期的情况，导弹的离筒速度应定义为后效期结束时之导弹速度，弹射过程也应延至后效期结束时才算结束。本课程不研究后效作用，故仍认为活塞承压面到达筒口截面瞬间为离筒瞬间，此时的导弹速度认为是弹射过程中之最大速度(离筒速度),弹射过程至此结束。

综上所述，弹射过程的起点是点火过程的起点，终点则分别有两种情况；当活塞止动于简口时，活塞开始止动瞬间即为离筒瞬间，亦即弹射过程终点；当活塞随弹出简时，由于不考虑后效期，故离简瞬间(弹射过程终点)指的是活塞承压面到达简口截面的瞬间。
离筒瞬间的导弹速度称为离筒速度。

我们研究发射筒内的弹射现象和过程，是为了有效地控制弹射过程，以便改进现有的弹射器和设计更新的弹射器。分析研究弹射过程就是要弄清楚弹射过程中各因素之间的关系，具体说，就是；装填条件(火药种类、形状、尺寸、火药重量、导弹重量等),弹射器内部结构诸元(如发射筒口径d尚，发射筒l断面积A,高、低压室的初始容积\({\bar V}_{10},{\bar V}_{20}\),导弹全行程长\({l}_{g}\)等)与高、低压室的压力变化规律、导弹速度变化规律之间的关系。内弹道学的任务就是从理论和实验两个方面来研究上述因素间的关系，找出它们的规律，而后应用到弹射装置的设计中去。

具体说，内弹道学包含两个基本问题，其一是在已知装填条件和高、低压室内部结构诸元的条件下求得高、低压室的压力变化规律及火箭导弹运动规律

(p₁-t,p₂-t,p₂-l,v-t,v-1)

特别是高，低压室的最大压力及火箭导弹离筒速度这三个重要的弹道诸元。这个问题称为内弹道学的正面河题或弹道解法问题，其二是求得装填条件和弹射装置内部结构诸元的合理和可能的方案，以使规定重量和直径的火箭导弹在不超过允许发射加速度的条件下获得规定的离筒速度。这个问题称为内弹道学的反面问题或弹道设计问题。

在对新的弹射装置进行内弹道设计时，是以弹道解法为基础的，即利用弹道解法所提供的内弹道公式，计算出能满足总体给定条件(火箭导弹重量，火箭导弹直径，离筒速度，发射加速度允许值)的弹射器结构数据和装填条件。应该指出，能满足给定条件的弹道设计方案不是唯一的，而是可以有多个，这就需要在设计过程中对它们进行分析比较，选择其中最合理的方案，然后，还需要对该方案作出正面问题的解，即计算出该方案的压力曲线和速度曲线。正面问题不是多解的，它的解只有一个。这样求得的弹道设计方案以及压力曲线和速度曲线将是进一步设计高压室、发射简、反后坐装置以及弹体，引信等的重要原始数据。

1.3、研究弹射内弹道学的方法

当研究弹射器内错综复杂的物理，化学过程时，将遇到许多常量、变量，在建立这些量之间的相互关系时，必须抓住过程的本质，并将其作必要的简化，在某些有时并非完全正确的假设下建立起一系列方程式，而后再进一步研究积分的方法，把内弹道正面问题解出来。有了正面问题所建立的各种内弹道公式，便可进行反面问题的计算。
正是由于简化和假设的存在，因而所建立的数学模型还不能逼真地描述弹射器内发生的所有物理化学现象。为了验证理论计算的正确性，并对理论计算进行修正，必须发展实验内弹道学。理论内弹道学与实验内弹道学的研究及相互补充，使我们有可能比较合理地解决弹射器的内弹道问题。

第二章 高压室内弹道理论基础

2.1火药的一般知识

目前，除压缩空气式弹射器、液压式弹射器及电磁式弹射器之外，凡以燃气为动力源的弹射器均以火药为其能源。

什么是火药?火药是通过化学或物理的方法，将氧化剂和燃烧剂结合在一起的固体含能材料，它在一定的激发能量作用下，能在没有外界助燃剂(如氧)的参加下，以迅速而有规律的燃烧形式进行爆发变化，生成大量的高温气体。

火药和一般固体燃料如煤的主要不同是：火药本身含有氧，可以在没有外界供氧的条件下燃烧，而一般固体燃料燃烧时必须依靠外界供氧。

火药和炸药都是含有不稳定基团、分子结构较不稳定的物系。火药的燃烧与炸药的爆炸都是激烈的化学反应，反应速度很快，放出的热量足以维持反应持续不断地进行。从这一点上说，它们之间没有本质的差别，火药也可归为炸药的一类。但燃烧和爆炸又是各有特点的两种不同的变化过程，后者的传播速度要比前者迅速得多，燃烧的传播速度一般仅为每秒几毫米到几十毫米，而爆炸则可达每秒数千米，因而燃烧在时间上，约为万分之一秒至几十秒(根据武器的要求而不同),而爆炸却是在几十万分之一秒或更短的时间内完成，其瞬间压力可达1～4万兆帕。

火药的用途十分广泛，不论在军事工业、民用或宇航工业中都得到多方面的应用。在军事上，火药主要用作各种发射武器的发射能源以及各种飞行器的推进能源。前者如枪、炮、弹射装置等的发射药，后者如固体火箭发动机的推进剂。

由于火药具有独特的优点，因此到目前为止，在作为武器系统的能源方面仍占有稳固的地位。首先，火药是一种固态物质，使用比较方便。平时火药不工作时，体积较小，当点燃工作后，可在极短的时间内发生剧烈的化学变化(燃烧反应),一方面放出大量的热提供了能量的来源；另一方面产生大量的火药气体而成为作功的工质来源。此外，火药的另一个优点是可以通过火药成份、形状和尺寸的变化来控制其燃烧规律，从而达到所要求的内弹道性能。

在生产过程中，总是将火药加工成一定的形状和尺寸，我们将具有一定几何形状和尺寸并装填于燃烧室内的火药称为装药。

2.1.1、 火药的分类

火药的分类方法很多，不同的准则可以有不同的分类。比如：按用途分，可分为枪炮发射药、火箭固体推进剂及其它用途火药；按成型工艺分，可分为压制成型火药及浇铸成型火药。枪炮及中小型火箭多采用前者，大塑火箭、导弹多采用后者，弹射装置多采用前者。按火药燃烧时的外部特征可分为有烟药与无烟药。目前最常用的是按火药的结构及基本能量成分进行分类，可分为均质火药、异质火药及复合改性双基火药三大类：

1.均质火药

均质火药的基本成分是硝化纤维素。任何纤维素经脱脂后，用浓硝酸和浓硫酸组成的混酸处理，即经过硝化作用后，就制成了硝化纤维素。一般部是采用棉纤维作原料，故习惯上都称之为硝化棉。如果混酸的组成不同，硝化的程度不同，则制成硝化棉的化学组成也不同。通常以单位重量硝化棉的含氮量百分数表示这种组成。目前均质火药所采用的硝化棉，按含氮量区分，有以下三种：

1号棉，又称强棉，其含氮量为13.0～13.5%;2号棉，也称强棉，其含氮量为12.05～12.4%;3号棉，称为弱棉，或称胶棉，其含氮量为11.5～12.1%。

硝化棉溶解于某些溶剂后，可以形成可塑体，再经过压实、成型等一系列加工过程，就可刷成均质火药。由于所用的溶剂不同，就可制成不同类型的均质火药。观代均质火药主要有以下三类：

(1)单基火药 这类火药的主要成分是硝化棉，一般多用1号棉和2号棉的混合棉，使之溶于乙醇乙醚的混合溶剂中，形成可塑体，然后压制成型，再经过浸泡把乙醇乙醚溶剂排出，最后经烘干而制成，其成分一般含有：硝化纤维素94～98%;挥发性溶剂0.2～5.0%;水分0.8～1.5%;安定剂(常用的是二苯胺)1～2%。

由上述成分可以看出，硝化纤维素是唯一的主要成分，故单基药亦称为硝化棉火药；又由于其溶剂乙醇乙醚属于易挥发性溶剂，故又称为挥发性溶剂火药。硝化棉在其中的作用既是火药唯一的能量来源，又是保证火药强度的成分。

单基火药在制造成形时，为了使得溶剂易于排除，火药厚度不得不受到一定的限制。由于这类火药含有挥发性溶剂和具有吸湿性，因而要求在保存期间具有良好的密封条件。单基火药能量较低，常用于枪及小口径炮。

(2)双基火药 以硝化纤维素和硝化甘油(或其它含能增塑剂)为主要组分的火药称为双基火药。硝化甘油是一种难挥发的液态爆炸性物质，它在双基药中既是主溶剂(增塑剂)又是另一主要能量成分，它可以溶解含氮量铰低的3号硝化棉，形成可塑体。(因为1号和2号硝化棉难溶于硝化甘油)再经压制成型后，即制成双基火药。其成分一般含有：硝化纤维素30～60%;硝化甘油25～40%;中定剂1～5%;水分0.5～0.7%;其它成分1～3%。

图2.1 双基发射药

由上述成分可以看出，其主要成分有硝化纤维素与硝化甘油两种，故双基火药又称作硝化甘油火药。由于硝化甘油是难挥发性溶剂，故又称为难挥发性溶剂火药。

硝化甘油火药在制造过程中一般由于没有挥发性溶剂的排除问题，因而生产周期短，并适于制造厚度较大的火药。由于硝化棉和硝化甘油的比例可以在较大的范围内变化，所以这类火药的能量能满足多种弹道性能的要求。双基火药的吸湿性较小，常温下有良好的物理化学安定性，内弹道性能稳定。但这类火药的燃烧温度较高，容易使发射筒产生烧蚀现象。

双基火药中通常枪炮用的称为双基发射药，而固体火箭发动机用的称为双基推进剂，其组成基本是相同的，但又不完全相同。它们都是以上述硝化纤维素和硝化甘油(或其它含能增塑剂)为基本含能成分。但为了改进内弹道性能或适应火箭发动机、弹射装置等的多种弹道性能要求，还可在基本配方中有选择地添加各种其它成分。如为了降低燃烧温度，可在其中加入一些降温剂，常用的降温剂大部是芳香族化合物，如二硝基甲苯，它们本身是缺氧物质，所以加入双基药溶解于硝化甘油中以后，能降低火药的氧平衡，从而降低了火药的燃烧温度。此外，二硝基甲苯还是增塑剂，对硝化棉有溶解能力，使火药结构更加致密，不易吸湿。它们又称为双芳型火药。

又如，为了改善化学安定性，可加入适量的化学安定剂，如二号中定剂。为了满足火箭发动机改善燃烧稳定性的要求，可加入燃烧稳定剂，如MgO、CaCO₃、TiO₂等；为改善其内弹道性能，可加入多种船盐作为燃烧催化剂，如PbO、苯二甲酸铅、鞣酸铅、水杨酸铅等。这些铅盐的作用是使火药燃烧速度受压力和温度的影响较小，从而有利于内弹道性能的稳定，并在各种使用温度下具有相近的内弹道性能。

由于所含的成分不同，而有不同牌号名称的双基药，如双铅-1(SQ-1)、双芳镁-1(SFM-1)等。

事实上，现在的所谓双基药已不单纯是硝化甘油火药，凡是与硝化甘油性质类似的爆发性物质并能代替硝化甘油而与硝化棉制成溶塑体者，都可以制成双基药。例如以硝化二乙二醇作为硝化棉的溶剂所制成的硝化二乙二醇火药也是双基药。

双基药具有悠久的历史，工艺比较成熟，可压制亦可浇铸成型。

近年来，为了提高双基药的能量，在其中加入了一些炸药成分，如黑索金、吉纳等，还适量地加入了一些铝粉，因而研制成功了一些新的双基药。

但总的说，双基药的能量仍不够高，燃速范围也较窄，还需今后进一步研究解决。

(3)三基火药 三基火药是在双基火药的基础上加入一定数量含能(爆炸性)有机结晶化合物(如硝基胍)而制成的。如硝化二乙二醇火药的燃烧速度比较低，如在其中加入20～30%的硝基胍，制成硝基胍火药，则可克服这一缺点。因为其主要含能成分有三种，即硝化棉、硝化二乙二醇和硝基胍，所以又称三基药。由于硝基胍中含氢和氮比较多，含氧少，所以硝基胍火药的燃烧温度比较低，对发射筒烧蚀作用比较小，因此常称硝基胍火药为“冷火药”。

除硝基胍火药外，还有含其它含能成分(如黑索金等)的三基药及多基药。选用新”基”的一般原则是：能使硝化棉良好塑化，与硝化甘油互溶并起能源的作用。

均质火药为固态胶体。根据成分及厚度的不同呈半透明或不透明状，硝化棉火药一般为灰黄色略带绿色，比较粗糙无光泽，且比较坚硬；硝化甘油火药一般为棕褐色，比较光滑，略有光泽，且较柔软有弹性。总的说，火药的颜色外观随其成分及生产特点而定。

2.异质火药

(1)复合火药 自二次世界大战后开始制造复合火药以来，其品种性能均有了较大发展。由于它具有成本低，使用温度范围宽，发动机构造简单，可浇铸大型药柱等优点，所以应用范围日益扩大。复合火药不是溶塑体，而是由含燃料的高分子粘合剂将金属粉状燃烧剂(如铝粉)、氧化剂粘结成一体后得到的。其特点是结构的不均匀性，即各组分之间存在明显的界面，故又称作异质火药。

复合火药中氧化剂的主要作用是为燃烧过程提供所需要的氧，目前广泛采用的是过氯酸铵(NH₄CIO₄),因为它最易得到，且与其它组分的相容性好，能量亦较高。有时亦采用硝酸铵(NH₄NO₉)或过氯酸钾(KCIO₄)作氧化剂。

粘合剂及燃烧剂由同一种物质来承担，其主要作用是提供然烧元素，同时把氧化剂颗粒和其它添加物颗粒粘合起来成为火药的弹性基体，使火药具有一定的形状和机械性能。 日前，用作复合火药粘合剂的有：聚硫橡胶、聚氮酯、聚丁二烯、聚氟乙烯等。

在复合药中加入一些金属燃烧剂如铝粉、镁粉，可使燃烧温度得到提高，从而增加了火药气体的热能。
一般说，复合药能量高、密度大(可至1.75克/厘米’),临界压力低，但燃速亦低，一般在压力7兆帕下燃速为10—15毫米/秒。

(2)黑火药 实际上是一种最简单的复合药，其成分为75%的硝酸钾(作为氧化剂)15%的木炭(作为燃料)和10%的硫磺(作为粘合剂和燃料)。过去，这种火药曾作为小口径火炮的发射药使用过，但因其能量低，燃烧后有较多的固体残渣而污染炮膛，因而在均质火药出现后，很快就被淘汰。但是由于其着火速度快，燃烧后产生大量高温气体和炽热固体粒子，易于起引燃作用，所以目前被广泛地用作点火药。

3.复合改性双基火药

为了提高双基火药的能量，在双基药中加入过氯酸氨和金属粉末(通常为铝粉)组成复合改性双基火药。这种火药在结构上更接近于异质火药，各固体成分都是以机械混合物的形式加入，但它又是在双基火药的基础上发展起来的一种新型火药，其中硝化纤维素与硝化甘油的作用为粘合剂，过氯酸氨为氧化剂，铝粉为燃烧剂，将经过球化处理的硝化棉和过氯酸氨、铝粉等固体物质与硝化甘油的混合溶剂(二硝基甲苯、中定剂溶解于硝化甘油中)配浆混合，然后浇铸在燃烧室的壳体中或药模中，经固化即成为复合改性双基药。
这种火药能量高(实际比冲为245～255秒，为国内外火药中实测比冲最高的),燃速高(10-30毫米/秒),燃烧温度高(3650～3800K),且由于是在双基药基础上发展起来的，故可利用原有生产基础及原料来源等方便条件，因此发展迅速。但其高、低温力学性能较差，室温下延伸率常大于25%,而低温时(如-57’℃)延伸率则常小于15%,高温时有流动和塌陷现象。

2.1.2、火药的药型与标记

火药都具有一定的形状和尺寸。这是因为火药燃烧时气体的生成速率与火药的表面面积有关，而火药表面积的大小以及它们在燃烧过程中的变化是由火药的尺寸及形状决定的。因此可以通过对火药形状和尺寸的设计来控制弹射过程中然气生成的规律，从而控制弹射器高、低压室的压力变化规律，以保证导弹获得所需要的离简速度。

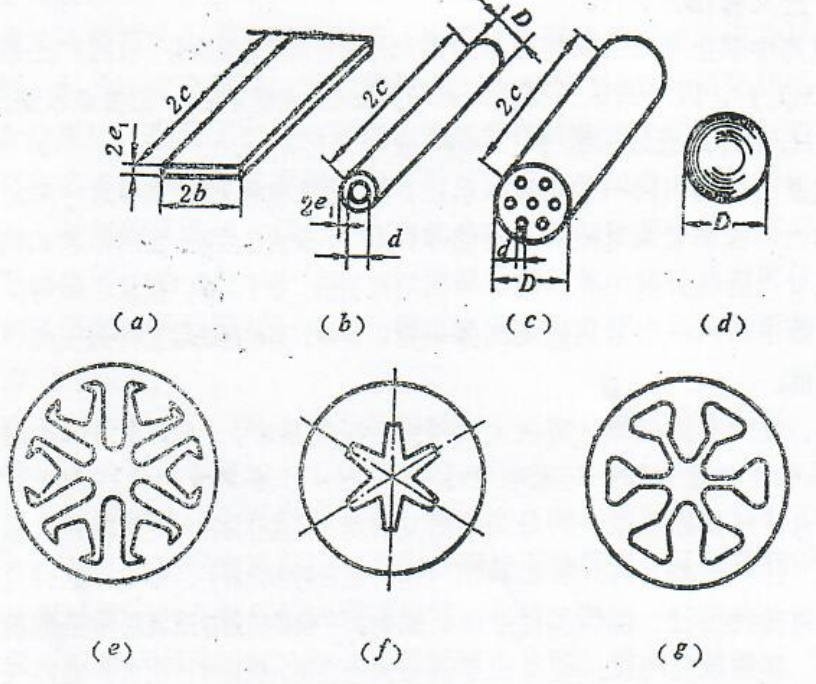
现有的火药形状十分多样。有管状、带状、片状，圆环状、粒状、球状等简单形状以及内孔有七孔、十四孔等多孔管状，还有内孔为星型、车轮型、树枝塑等复杂形状(图2-2)。

火药的形状不同，标记方法也不同。对于火药的基本尺寸，用以下的符号来表示(图2-2):

2e:表示火药的厚度，称为肉厚(或弧厚)。肉厚指的是火药最薄、最先燃完部分的尺寸。火药燃烧只需考虑厚度，厚度部分烧完了，长宽也就不存在了。在管状药中，肉厚即半径之差；

2b表示火药的宽度；2c表示火药的长度；D表示管状药的外径；d 表示管状药的内孔直径。

图2-2 典型火药形状
(a)带状(或片状):(b)单孔管状；(t)多孔管状；(4)球状；()树技型；(J)星型；(g)车轮型。

火药的尺寸大小差别也很大，小的称为药粒，直径可小至0.5毫米，大的称为药柱，重量可达几十吨。前者主要用于枪炮，后者主要用于火箭发动机，弹射装置所用药型随弹射装置种类不同而不同，两者均可选用。

对于复杂形状的火药，还有一些别的符号表示相应部分的尺寸，在此不一一叙述。为了简明地表示出火药的性能、形状、尺寸及有关的生产条件，有的火药已规定了标记方法，通常对每一批火药都注明一定的标记，即火药的脾号。现以一部分炮用双基药为例，将其标记方法介绍如下：

1.管状药的标记

由三部分组成：

火药名称-热量等级；

肉厚(以0.1毫米计)/孔数-长度(以厘米计);

批号/制造年份-制造厂代号。

其中火药名称是以火药的主要成份来表示的；热量等级是按实验测定值将双基药分为2、3、4三个等级，其热量分别为3×10⁶、3.2×10⁶焦/公斤和3.43×10⁶焦/公斤，例如：双芳-3 18/1-26 2/70 – 45:双芳 表示含二硝基甲苯的双基药；
3 表示热量为3.2×10°焦/公斤；
18表示肉厚为18毫米；1 表示单孔；
26 表示长度为26厘米；2/70表示70年第2批；45表示制造厂代号。

2.带状药和片状药的标记

火药名称：
厚度(以0.01毫米计)-宽度(以毫米计)×长度(以毫米计);批号/制造年分-制造厂代号。
例如：双带40-5×1502/60-45,即表示代号为45的工厂60年制造的第二批双基带状
药，其厚度为0.4毫米，宽5毫米，长150毫米。有时宽度和长度也可省略不写。

3.环状药的标记

火药名称：
厚度(以0.01毫米计)-内径(以毫米计)/外径(以毫米计);批号/制造年分-制造厂代号。其中内、外直径皆只取近似平均值的整数，也可省略不写。
例如：双环14-32/659/64-35,即表示代号为35的工厂64年制造的第9批双基环状药，
其厚度为0.14毫米，内径32毫米，外径65毫米。

2.1.3 火药的基本性能

凡以火药为能源的各类武器性能都与火药的性能有关，火药的基本性能可归纳为以下几个方面。

1.能量性能

一般情况下希望火药有尽可能高的能量特性，这样就可减少燃烧室的体积、重量或提高飞行速度，增加武器的射程。

不同的武器选用不同的特征量来表示火药的能量性能。枪炮通常用爆热、比容及火药力来表示；火箭采用比冲和比重；而弹射装置则选择爆热、爆温、标准状态下火药气体的比容为能量特征量。

2.燃烧性能

火药在武器燃烧室内的燃烧过程应进行得比较完全，以使能量充分释放及燃烧有一定的规律性及稳定性。此外，火药对环境的敏感程度愈小愈好，即火药的燃速受温度、压力、气流速度及加速度的影响愈小愈好。

3.力学性能

火药在制造、贮存、运输及使用过程中会受到各种载荷的作用，在这些情况下，火药应能符合要求不致产生变形甚至破裂损伤，否则将会引起不正常燃烧，严重时甚至会发生爆炸事故。大型药柱在这方面的要求比较严格，在整个使用温度范围内均应具有良好的强度及延伸率。

4.物理化学安定性

指的是火药所具有的在一定的时间内保持其物理或化学性能不发生显著变化的性能。根据这个时间的长短，可定出该种火药的贮存期限。为了满足战时的大量需要，希望火药能有较长时间的贮存期限。

物理化学性能的变化如：由于温度的影响，火药中的溶剂会重新分布，如硝化甘油析出到火药的表面，这样就破坏了各组分分布的均匀性，因而影响弹道性能或增加了运输过程中的危险性，这类问题就是物理安定性方面的问题；化学安定性主要是指火药在贮存过程中的自动分解作用。物理化学安定性好，贮存年限可以延长。

5.安全性

指的是火药对外界各种激发能源(如撞击、摩擦、静电火花、热、冲击波等)的敏感程度，亦可称作机械感度。机械感度小，则火药在生产、贮存、运输及使用过程中的安全性增加，反之就可能引起着火或爆炸。
除以上几方面外，火药还应有良好的工艺性和经济性等。

2.1.4、火药的能量特征量

火药的特征量是表征火药性质的量，亦可称为火药的标识量或示性数，它包括成分特征量(如硝化棉的含氮量、挥发物含量等)、能量特征量和弹道特征量。下面介绍能量特征量。

能量特征量即表征火药能量的特征量。火药在高压室内燃烧时，一方面产生大量的火药气体，一方面释放出大量的热能，这些热能使火药气体获得很高的温度，温度愈高，气体作功的能力也愈大。高温燃气流入低压室后膨胀作功，热能转化为导弹的动能，在极短的时间内将导弹加速到所要求的离筒速度。由此可知，火药燃烧后放出的热量、生成燃气的多少和燃气的温度是三种能够表示火药作功能力大小的能量特征量。

1.爆热

爆热的定义为：在298K(或其它标准温度)下的1公斤火药经爆发反应(燃烧)变成相同温度的爆发产物时所放出的热量。也就是说，爆热指的是1公斤标准温度下的火药在没有外界氧的条件下进行爆发反应(燃烧)而产生高温燃烧产物，使燃烧产物的温度又降回到标准温度的过程中所放出的全部热量。

根据爆发过程进行的条件(定压还是定容)及产物最终的聚集状态(主要指其中的水为气态还是液态)可将爆热分为定容爆热Qv及定压爆热Q_p。根据水的状态(液态还是气态),定容爆热又有水为气态的定容爆热Qv_(g)、水为液态的定容爆热Q_v(l)此外还有水为气态的定压爆热Q_p(g)。爆热的单位为kJ/公斤。

我们平时所说的火药的爆热通常指的是水为液态时的定容爆热Q,可用量热计测定其大小，即将火药放在热量弹内于真空下燃烧，所放出之热量由一定量的水来吸收。如水的始温为298K,再根据记录下来的水温，即可算出Q _v(l),应该注意，火药在量热计中燃烧期间所生成的产物中的水是以气态存在的，冷却到298K时则已变成液态了，故所测得的Q_v(l)中尚包含有气态水凝结成液态水并降温至298K时所放出之热量。水的状态不同，热量值也不同，Q_v(l)与Q_v(g)之间有以下关系：

\({Q}_{v(l)}={Q}_{v(g)}-9.927{n}_{{H}_{2}O}\)

式中9.927为定容下一摩尔水的汽化热；n_H2O为一公斤火药燃烧产物中水的摩尔数。

需要说明的是，火药的爆热与火药的完全燃烧热是两个不同的概念，它们在数值上也不相同。由化学热力学可知，燃烧热是一摩尔化合物在过量氧的条件下充分燃烧，使其中的元素生成稳定氧化物时的热效应，简言之，就是一摩尔物质完全氧化时所产生的热效应。火药的完全燃烧热与上述燃烧热同属一个概念。而火药的爆热则是一公斤火药在武器燃烧室中进行的燃烧反应(爆发反应的一种形式)的热效应，是在隔绝外界氧的条件下进行的，不存在过量氧的条件，相反，一般是在氧不足的条件下进行的，故反应产物中含有大量没有完全氧化的成份，如CO,H₂等气体，如遇空气，还可进行二次燃烧，进一步放出热量。综上可知，火药的爆热(易于混淆的是，习惯上常将爆热称作燃烧热)不仅在概念上不同于火药的完全燃烧热，且数值上也小于完全燃烧热。

爆热愈大，火药经燃烧放出的化学能也愈多，火药的作功能力也愈大。

2.爆温

由化学热力学知道，假定燃料在燃烧时所放出的热量并未外传，热损失也略去不计，即假定为绝热燃烧，则燃烧所产生的热量全部用以加热燃烧产物本身，提高其温度。在定容或定压情况下的绝热燃烧可看作是：首先燃料(设温度为T₀——298K或其它标准温度)在燃烧反应中变为燃烧产物(温度为T₀——298K或其它标准温度)并同时放出热量(即爆热);然后这些热量使燃烧产物在定容或定压下被加热，其温度由T₀上升到T_v,它们分别是燃烧产物在定容或定压条件下理论上所能达到的最高温度，称为火药的定容爆温或定压爆温。

综上所述可知，火药在绝热定容条件下燃烧时所能达到的最高温度称为定容爆温，习惯上亦称作定容燃烧温度，以T_v表示。

火药在绝热定压条件下燃烧时所能达到的最高温度称为定压爆温，习惯上亦称作定压燃烧温度，以T_p表示。它们的单位均为K,如以°C表示，则爆温的符号分别为T_v及T_p

若要笼统地给爆温下一个定义，则可定义为：火药在绝热条件下燃烧所能达到的最高温度。

燃烧产物的温度由T₀升高到T_v或T_p,其内能或焓就相应地增大，其内能或焓的增大值就等于温度为T₀的燃料在定容或定压条件下进行燃烧反应时所放出的热l量。由于内能和焓都代表火药燃烧所释放的能量，只不过是在不同条件下释放而已，我们忽略其间的微小差别，将它们看作相等，则得到：

\({H}_{{T}_{0}}={E}_{{T}_{v}}\)

式中\({H}_{{T}_{0}}\)——一公斤火药气体在温度T₀时的焓；

\({E}_{{T}_{v}}\)——一公斤火药气体在温度T_v时的内能。

因

\({H}_{{T}_{0}}={C}_{p}{T}_{0}\)

\({E}_{{T}_{v}}={C}_{v}{T}_{v}\)

所以

\(\frac{{T}_{v}}{{T}_{0}}=\frac{{C}_{p}}{{C}_{v}}\)

式中\({C}_{p},{C}_{v}\)——分别为火药燃烧期间的定压比热及定容比热，近似地将比热看作定值，即

\(\frac{{T}_{v}}{{T}_{0}}=\frac{{C}_{p}}{{C}_{v}}=k\)

上式表明，火药的定压爆温与定容爆温之间存在着简单的比例关系，其比例系数就是比热比k。

由于火药的爆温很高，如T_v≈2500～3500K,且燃烧时间又很短，所以直接测量爆温困难较大，通常是用计算来确定爆温。下面介绍一种计算定容爆温的方法。按照定义，假设燃烧是在定容下进行的一种绝热过程，则火药燃烧所放出的热量只用来加热火药气体分子。根据比热定义，有

\({Q}_{v(T)}=\int\limits_{25}^{{T}_{v}}{C}_{v}dT\)

如已知火药的\({Q}_{v(T)}\)和火药气体的定容比热\({c}_{v}\),则可用上式求得爆温T_v

由于下限25°C和Tv相比可以略去不计，因此将上式写成下式，亦不致产生很大的误差

\({Q}_{v(T)}=\int\limits_{0}^{{T}_{v}}{C}_{v}dT\)

火药气体为混合气体，其中的每一种气体成份的定容比热C_vi;与C_v有如下关系：

\({C}_{v}=\sum\limits_{1}^{K}{{C}_{vi}}\)

式中n_i,c_vi—i成分气体的重量百分数及其定容比热。对于一公斤火药气体

\(\sum\limits_{1}^{K}{{n}_{i}{C}_{vi}}=100%\)

火药气体中每一种气体的定容比热c_vi与温度T的关系通常用直线函数来表示：

c_vi=a_i+b_iT

a_i,b_i为经验常量，不同的气体有不同的值，可由手册或热力学书中查到。所以

\({C}_{v}=\sum\limits_{1}^{K}{{n}_{i}({a}_{i}+{b}_{i}T)}\)

\({Q}_{v(T)}=\int\limits_{0}^{{T}_{v}}{\sum {{{n}_{i}({a}_{i}+{b}_{i}T)}}}\)

积分后得.

\({Q}_{v(T)}={\sum{n}_{i}{a}_{i}{T}_{v}+\frac{1}{2}\sum {n}_{i}{b}_{i}{T}_{v}^{2}}\)

\({T}_{v}=\frac{-\sum {a}_{i}{n}_{i}+\sqrt{{\sum {n}_{i}{a}_{i}}^{2}+2\sum{{n}_{i}{b}_{i}{Q}_{v(g)}}}}{\sum {n}_{i}{b}_{i}}\)

\({T}_{v}={T}_{v}+273\)

火药的燃烧温度愈高，其作功的能力也愈大。不同的火药，即使有相同的爆热，但由于n_i,a_i,b_i不同，实际的燃烧温度也不同。也就是说，火药的燃烧温度不仅与爆热有关，还与火药气体的成份有关。因此爆温是一个独立的能量特征量，不能由爆热包含。

3.标准状态下火药气体的比容v₁

一公斤火药燃烧后所产生的气体在标准状态(温度为273K,压力为1.01325×10⁵帕)下所占的体积(其中水为气态)称为标准状态下火药气体的比容γ₁.

比容通常是在量热计中测量爆热后，将气体引入气量计中测量出气体的体积，然后再通过状态方程换算到标准状态时的体积，即标准状态下的比容γ₁,

显然，气体的比容愈大，则在同样条件下，作功的能力也愈大。火药气体的比容γ₁≈0.8～1.0m³/kg。

2.1.5、火药的弹道特征量

火药的弹道特征量即对弹道有重要影响的火药特征量，包括火药力f与余容α。

1.余容

实际气体只有在高温低压下才近似地服从理想气体状态方程。在弹射器的高压室中，工作压力的取值范围约为20～50MPa，一般说，燃气具有高温高压的性质，应按实际气体的状态方程来表达压力p,温度T和比容γ之间的关系。低压室的情况则为高温低压，可以按理想气体来处理。但有时为了简化计算，或在高压室的工作压力不很高的情况下，也近似地采用理想气体的状态方程，

实际气体的状态方程即范德瓦尔方程：

\(\left(p+\frac{\alpha}{{\gamma}^{2}}\right)(\gamma-\alpha)=RT\)

式中α/γ²项是考虑了分子间作用力所作的修正。对于火药气体来说，由于其温度很高，所以即使其密度很大，分子间的引力也相对很小，α/γ²项可以忽略不计；α项是考虑了气体分子本身所占体积的影响而作的修正，其值不等于每公斤气体分子本身的体积，而是分子本身体积的四倍。高压室中火药气体具有高压的性质，在高压下气体分子体积的四倍对容器的容积占有不可忽略的分量，因此α项不可忽略。在内弹道学中，α称为余容。其单位为dm³/kg。计算火药气体的余容，最常用的是塞劳近似式

α≈10^-3γ₁

范德瓦尔方程简化成

\(p(\gamma-\alpha)=RT\)

式中γ为火药气体的比容，即一公斤火药气体所占的体积，单位是分dm³/kg。

2.火药力

火药力分为定容火药力f与定压火药力f₀,其定义为：

f=RT

f₀=RT₀

可以测得，又简称为火药力，f₀又称为火药力换算值。下面分析其物理意义：

火药力中之R为火药气体的气体常数。它与火药气体的状态无关，只与火药气体的性质有关，正因为在不同状态时R都为常数，我们就可取标准状态时的情况来计算R的数值。

在标准状态下，p=p_a(1大气压=1.01325×10⁵帕),T=273K, γ=γ₁。又由于α仅是γ₁的千分之一，因而在计算R时仍可用理想气体的状态方程，即

\(R=\frac{{p}_{a}{\gamma}_{1}}{273}\)

对上式进行分析，便可知道R的物理意义。由热力学知道；1/273是气体的体膨胀系数(对一切气体都相等),即在压强不变的条件下，当温度升高1°C时，一定质量气体体积的增量等于它在0°C时体积的1/273(盖·吕萨克定律)。根据γ₁的定义知道，一公斤火药气体在0°C、1个大气压下的体积是γ₁,所以1公斤火药气体在1个大气压力下温度升高1°C时气体体积的增量应等于γ₁/273,那末，p_a与γ₁/273的乘积便是1公斤火药气体在1个大气压下，温度升高1°C对外膨胀所作的功。这也就是气体常数R的物理意义。

在国际单位制(SI)中，压力的单位采用Pa(N/m²),比容的单位为m³/kg，温度的单位为K，相应的气体常数的单位为J/kg·K。

现在可以建立火药力的概念，即1公斤火药燃烧后的气体生成物在1个大气压力下，当温度由0K升高到T_vK(或T₀K)时膨胀所作的功称为定容火药力(或定压火药力)。因此，火药力表示每kg火药作功的能力。其单位是kJ/kg

\(f=R{T}_{v}=\frac{{p}_{a}{\gamma}_{1}}{273}{T}_{v}\)

由上式可知，改变火药的性质，使γ₁或T_v增加，火药力就增加。当γ₁及T_v都大时，火药燃烧既放出大量的热又生成大量的气体，火药力就具有较高的数值，火药就具有较大的作功能力

“力”的名称与功的因次不符，但它是历史上遗留下来的名称，延用至今。

余容α和火药力f是与火药性质有关的两个弹道特征量，由它们的表达式可知，它们以一定的形式与火药的能量特征量联系着。

2.2 火药的燃烧

2.2.1火药的燃烧过程

从内弹道学的观点看，高压室内装药的燃烧过程可分为三个阶段：即点火、引燃和燃烧。

点火 由于外界能源的作用，一部分火药表面的温度升高到发火点以上而发生着火的现象称为点火。

引燃 点火后，火焰沿火药表面传播的过程称为引燃。

燃烧 火药表面引燃后，火焰向火药内层传播的过程称为燃烧。

引燃和燃烧并没有化学物理本质上的差别，因此有时也将燃烧过程看作只有点火和燃烧两个阶段。

1.装药的点火

装药点火是否可靠，直接影响装药的正常燃烧，因此控制点火过程是保证高压室正常工作的关键之一。

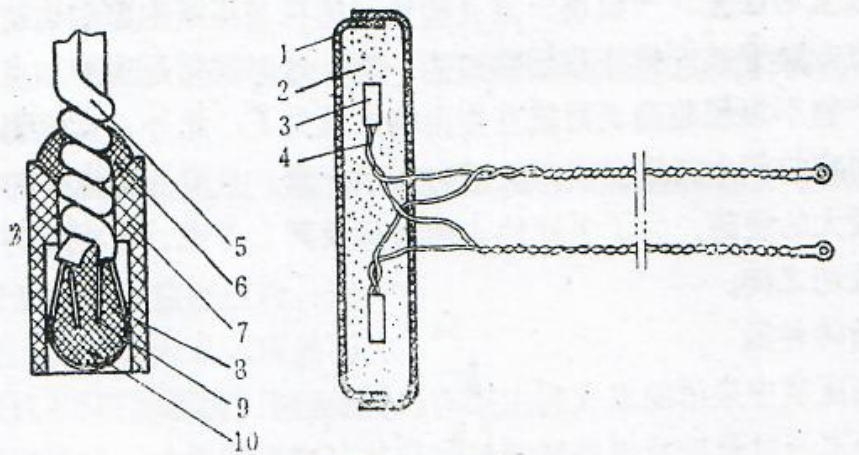
火药的点火过程很复杂。高压室点火一般采用电点火方式，即由发火管点燃点火药而后点燃装药。发火管内有由金属丝制成的电桥，其周围粘结着对热很敏感的引火药，引火药成球状或滴状。当给金属丝通以电流时，金属丝灼热而使引火药着火产生火焰。当引火药与点火药之间有一段距离或引火药产生的火焰能量不足时，还需采用扩焰药，在扩始药(或引火药)火焰的作用下，点火药迅速被点燃，产生一定温度，一定压力的点火药燃烧产物——点火药气体与固体微粒。这些固体与气体的生成物在一定的压力下便以一定的速度沿装药表面流动，并将能量(主要是热能)传递给装药表面，在能量的激发下，局部装药表面温度达到发火点而开始燃烧。图2-2为最简单的电点火装置——点火药盒。

图2-3点火装置

1一点火药盒；2一点火药；3一发火管；4,5一导线；8,10—胶漆；7一套管；8一引火药；9一电桥。

点火过程所对应的时间称为点火延迟期，以t_ig表示，其定义不甚统一，我们采用以下定义：从点火药燃烧产物开始向装药表面传热起，至装药燃烧表面出现第一个火焰为止的时间间隔。在工程上就规定为从发出点火电讯号开始至高压室达到点火压力p_ig为止的时间间隔。

点火压力p_ig的定义也没有统一规定，认识各有不同。我们规定p_ig为高压室装假药柱时点火药燃烧所达到的最大压力。

t_ig是表征点火过程的重要参数之一，也是点火装置设计的重要技术指标，当点火压力在1～10兆帕时，t_ig在10^-2～10^-3秒的范围内。

2.影响点火的因素

火药的点火是否正常，受到多种因素的影响，例如：

(1)火药的性质 不同类型火药被点燃所需要的能量是不一样的。一般说来，均质的双基火药较易点燃；火药表面的发火点温度愈高，建立加热层所需能量愈多，因而愈难点燃；火药的密度大、导热系数大、燃速小都将使点燃困难。

(2)火药的初温  初温高则易于点燃。

(3)点火药的性质 点火药燃烧产物对装药表面的传热形式主要有三种：高温点火药气体的传导与对流；点火药火焰的热辐射以及灼热的固体微粒与装药表面接触时的热传导。其中固体颗粒具有较大的热容和辐射率，其热传导与辐射作用都比较大，对点火能量的传递起到了良好的作用，因此常选用燃烧产物中含固体微粒较多的点火药。

(4)点火药量 点火药量的多少会造成点火药气体压力的高低，而气体压力的高低反映了气体分子对火药表面碰撞动量的大小。碰撞动量大则有利于传热，有利于促使装药表面的热分解，有利于装药的点燃。但点火压力过高则会引起高压室内的压力急升，称为点火引起的初始压力峰，这对高压室设计不利，是应该避免的。点火药量过少，则不能点燃装药，或形成中途熄火、迟发火等现象。

(5)点火药的粒度 装药接受点火药燃烧产物传递来的能量，使表面温度升高到燃点且在燃烧表面内层建立起加热层(这样才能引起剧烈的燃烧反应并使燃烧反应维持下去)是需要一定的时间的，点火药燃烧产物对装药表面的作用时间应大于上述时间，这样才能保证装药被可靠点燃。对于不易点燃的装药，有时采用粒度大的点火药，以适当延长点火药燃烧产物对装药表面的作用时间。

(6)点火装置的位置 一般说，点火装置安排在高压室的前端比较合理，但有时由于结构上的需要，点火装置被安排在靠近喷口的一端，这时就需适当增加点火药量，因为有一部分点火药燃烧产物不流经装药表面就直接由喷口流失了；此外，点火装置靠近喷口一端放置还容易使径向匀布的数个高压室喷口破膜时间不一致，且对火药点火的一致性的影响也不够好。对于长度较大的装药，为了更好地点燃装药及其它考虑，常将装药分为两段，将点火药安排在两段火药之间。

3.点火药的种类

弹射装置高压室中采用的点火药主要有(1)黑火药(简称黑药);(2)烟火剂类型的点火药，如由金属粉末与过氯酸盐或硝酸盐等氧化物制成的混合物；(3)均质火药。这几种点火药可单独使用，亦可组合使用，如黑药与烟火剂的组合，或黑药和均质火药块的组合等。

黑药使用较为广泛，因为它具有以下优点：易于用火焰、电火花和热金属丝点燃；燃速较快、密度与导热系数较小；

燃烧产物中含有一定数量的固体微粒和大量气体。炽热的固体微粒与装药表面直接接触进行热传导；大量气体则能在高压室内建立必要的点火压力，并能迅速包围装药表面，易于使装药点燃；

化学安定性(火药在一定的时间内维持其化学性质不变的能力)较好，生产方便及成本较低等。

其缺点为点火能量不高(爆热为3×10⁶～3.2×10⁶J/kg)以及容易吸湿等。当黑药的湿度大于2%时，其可燃性就大大降低。黑火药通常多用作双基药的点火药。

黑药依其粒度可分为大粒黑药与小粒黑药。前者又分为1,2,3号，后者可分为1,2,

3,4号，具体尺寸可见手册，粒度大者，燃烧时间长，总燃烧面积小，故能量放出速度低，压力升高速度也慢，适于点燃大、中型双基药。

一公斤黑药燃烧后可生成0.564公斤固体微粒和282立方分米的气体(标准状况下的气体体积),爆温为2200～2500°C,火药力约为25×10³～30×10³kJ/kg，发火点为265～320°C。黑火药的真密度为1.60～1.93kg/dm³,假密度(堆积密度)为0.9kg/dm³左右。

烟火剂类型的点火药种类很多，但都是由氧化剂、燃烧剂和粘结剂混合而成的机械混合物，这是它与黑火药类同之处，不同之处是：①能量较黑火药高，燃烧产物温度高，一般在3000K以上，且燃烧产物中大部分为凝相微粒，气体量少，炽热的粒子对点磁装药很有利，而复合药的临界压力较低，这一点与烟火剂点火药的特性正好适应，故此类点火药适用于较难点燃的复合药；②不易产生过高的点火压力。

烟火剂类型的点火药的缺点为：①引燃温度高，如镁的发火点为550℃,过氢酸钾的分解温度为610℃,比黑火药高得多，为此常采用黑火药作引燃药来解决此问题。③大多数烟火剂类型的点火药有较强的吸湿性，稳定性也较差，使用时需很好密封。③骨格高。

4.主要点火参数的确定

(1)点火压力p_ig为了保证可靠点燃装药，要求点火装置在高压室内建立适当的点火压力。双基药常用黑火药作为点火药，点火压力可取为等于火药的临界压力或等于高压室工作压力的30～40%。复合药燃点较高，但可在较低压力下正常燃烧，故选用烟火剂等高能点火药，而点火压力可比双基药低一些。

(2)点火药量w_ig当点火药种类选定后，便需根据高压室的装药情况及结构参数来确定点火药量，以w_ig表示。

点火药量的多少对点火压力有很大影响，点火压力过高或过低都会导致高压室燃气压力的不正常情况(图1-3)。

图2-4点火不正常时的高压室压力曲线

曲线1为点火药量过多或粒度过细，造成了点火初始压力峰。曲线2为点火药量不足(或其它原因)造成在高压室工作的初始阶段压力未能建立起来的情况，称为迟发火现象。曲线3则是由于点火药量过少或点火药受潮等原因引起之极端情况，即点火药燃烧完毕，装药未能点燃。

目前确定点火药量的方法主要是经验法，即参考同类产品，同时利用现有经验或半经验公式进行估算，定出初步点火药量，然后进行高压室的高低温试验，使其内弹道性能满足要求，即低温下要求点火可靠；高温下点火压力峰不超过允许值。通过试验调整确定点火药量。

下面介绍几种经验公式：

由点火压力pig确定点火药量点火时，高压室可视为密闭容器，根据状态方程，有

\({m}_{ig}=\frac{{p}_{ig}{V}_{f}}{(1-\varepsilon){f}_{ig}}\)

式中V_f–高压室的初始自由容积，V_f=V_c-V_p;

V_c—高压室无装药时之容积；V_p—装药体积；

ε—点火药燃烧产物中凝固相微粒的重量百分数，黑火药的ε≈60%;f_ig—-点火药的火药力。黑火药的fig≈3.0×10⁴kJ/kg；

p_ig-—点火压力。可参考装药的临界压力来决定，或取高压室工作压力的30～40%。

②装药为管状双基药的点火药量可由下式进行估算：

\({m}_{ig}=16\sqrt{\frac{{A}_{b0}{A}_{t}}{\Delta}}\)       (g)

\({m}_{ig}=36 \sim 50\sqrt{\frac{{A}_{b0}{A}_{t}{D}_{c}}{\Delta L}}\)             (g)

式中A_t——高压室喷喉面积(dm²);

D_c—高压室内径(dm);

L——装药的长度(dm);

A_b0——装药的起始燃烧面积(dm²);

Δ——高压室装填密度(kg/dm³);\(\Delta=\frac{{m}_{g}}{{V}_{c}}\)

m_g—装药质量(kg);

V_c-—高压室无装药时之容积(dm³)。

(3)点火药燃烧时间 点火药燃烧时间应等于或略长于前述之点火延迟期tis,但点火药燃烧时间亦不应过长，如火焰已传播到整个装药表面，点火药仍在继续燃烧，就可能使点火压力峰和侵蚀压力峰同时出现，产生过高的初始压力峰。点火药燃尧时间过短，则不能在装药表面建立起相应的加热层，并使装药表面达到点燃温度，因而不能可靠点燃装药。

5.装药的引燃

由于点火药燃烧产物对整个装药表面的包围是一个过程，且总是不均匀的，所以总有一部分装药表面先被点燃，而后火焰再传播至整个表面，火焰扩展的过程即称为引燃。实际的过程往往是靠近点火药附近的装药表面先被点燃，被点燃的装药也开始分解、气化，气化后的产物继续进行化学反应，直至生成最后的燃烧产物并释放出热能，热能加热燃烧产物后使之成为高温燃气，它与点火药高温燃气一起使高压室内压力升高并沿装药表面流动，使其余装药表面温度升高，达燃点而着火燃烧，于是火药全面点燃。

6.装药的燃烧

装药表面点燃后，燃烧反应放出的热量就向内层传递，对未燃火药进行加热，形成加热层，其传热方式主要是热传导，由于火药是热的不良导体，所以加热层仅是很薄的一层。如果在单位时间内，加热层吸收的热量大于散出的热量，则该层的温度升高，火药连续不断地分解，内层亦开始燃烧，火焰向内层传播，所产生的热量又加热下一层，整个燃烧过程就这样依靠其本身的作用逐层稳定地进行下去，直至全部装药燃尽为止。

根据燃烧速度是否随时间变化，燃烧过程可分为稳态燃烧过程及非稳态燃烧过程。当外界条件(压力、初温)一定时，燃烧速度不随时间变化的燃烧称为稳态燃烧，反之称为不稳态燃烧，燃烧过程完全的稳态燃烧称为正常燃烧，反之，称为不正常燃烧。

通常所说的正常点火，指的是火药全面点燃及燃烧的最初阶段能正常进行。

在高压下引燃速度显著地超过燃烧速度。一般说，在压力4～5MPa时就可以认为引燃是瞬时的，所以在内弹道学中，为了处理问题方便，往往不专门研究点火过程，而是假设装药瞬时、全面点燃，这是内弹道学中的重要假定。

2.2.2、双基药的稳态燃烧机理

燃烧机理是说明燃烧过程本质的理论。它研究燃烧过程中存在哪些物理化学变化，固体的火药如何变成气态燃烧产物等内容。

从研究内弹道学的观点来看，研究燃烧机理可使我们了解火药燃烧的本质，影响燃烧速度的各种因素，从而建立起描述火药燃速的基本公式，对于从事化学研究的人员来说，研究燃烧机理主要是为了更好地控制、调节和改善火药的燃烧性质，以及指导新火药配方的设计。

对火药燃烧的研究大致是按以下四个步骤进行的：

①根据实验观测，提出燃烧的物理模型。其实验内容包括测定温度分布、邀烧产物的成分、拍摄燃烧区的结构，观察中途熄火后火药表面结构及组成等。

②在某些假设的前提下，建立数学模型，通常表示为燃烧速度及燃烧表面温度的计算公式。

③由实验测定各物理化学常数后，求解数学模型，使燃速与燃烧表面温度最终表示为燃气压力和火药初温的函数。

④用实验来检验理论，即用各种条件下燃速及表面温度的测定值与理论计算值相比较，验证理论的正确性。

由于火药的燃烧是个复杂的物理化学过程，虽然长期以来，很多人对它进行了大量的理论与实验研究，但许多问题至今并未获得一致的认识与结论，因此我们只能对燃烧机理的基本概念作一简单介绍。

双基药和复合药的燃烧机理各有自己的特点，我们主要介绍双基药稳态燃烧机理的基本概念。

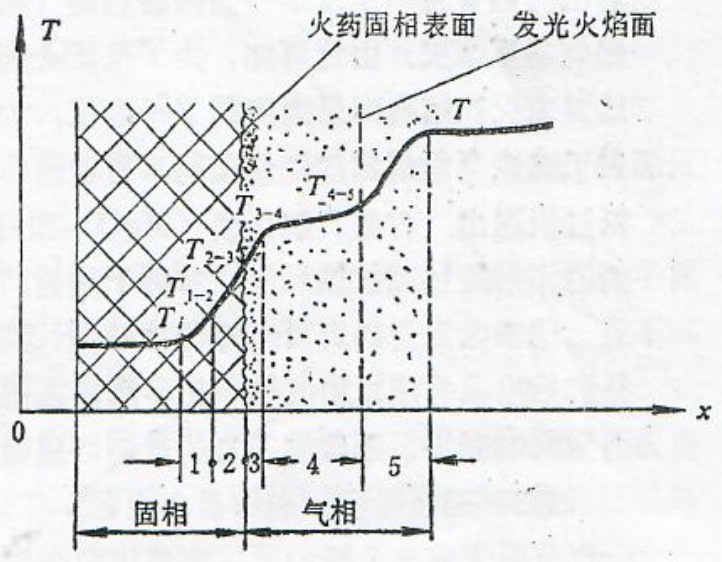
从40年代末以来，许多学者对双基药的燃烧进行了实验研究，并在此基础上提出了多种稳态燃烧模型，其中以近代燃烧理论中的火药多阶段燃烧假说较为完善。这种假说认为：火药燃烧过程是一个多阶段的连续的物理化学变化过程。在实际情况下，这些阶段不能截然分开，而是互相连系、互相渗透的。但为了方便地说明问题的实质，可以各阶段的特点为依据，将燃烧过程划分为五个阶段，每个阶段的大小与火药的性质、压力、初温等条件有关；在不同的条件下，火药的燃烧可以在不同的阶段结束，图1-4表示燃烧的各个阶段(区)和相应的温度分布。

第1区是固相加热区。点火药燃烧后生成的高温燃烧产物(或火药燃烧后所产生的高温燃烧产物)复盖在火药表面上，其热量通过热传导、对流和辐射的形式很快加热了火药表面层并向火药内部传递，使得接近表面的一薄层火药温度升高，形成温度梯度。固相加热区的温度是从火药的初温T_i逐渐增高至第1区与第2区交界处的T_1-2(约为85～90°C)。T_1-2相当于火药中最不稳定的组元(活性成份)开始分解的温度。在这一区中，火药的化学变化还未发生，只是由于温度升高而软化和熔化，完全属于物理变化过程。这一区是燃烧的准备阶段，火药燃烧时如无充分预热的加热层，则上一层火药燃完后，燃烧就会停止。由此也可看出初温T_i的重要。初温高，燃烧过程进行的速度快，燃速也就增加。在压力为10MPa的条件下，双基药固相加热区的厚度约为0.01mm。

图2-5  火药燃烧过程图解

第2区是凝聚相反应区。当火药温度达到T_1-2,即某些组分的熔点、沸点或热分解温度时，火药发生软化、熔化、分解产物的蒸发、升华等物理过程，同时还发生化学反应。这一区的化学反应主要是热分解反应。例如硝化棉、硝酸酯的热分解，其反应如下：

硝化棉大分子的热分解反应：

((C₆H₁O₂(ONO₂)₃)₂→xC₆H₇O₂(ONO₂)₃-q

C₆H₇O₂(ONO₂)₃→2H₂0+3NO₂+C₆H₃O₃-q

硝酸酯溶剂的热分解反应：

R-ONO₂→R′-CHO+NO₂-q

在接近火药表面的一层中，还有：

NO₂+CH₂O→H₂O+CO+NO+q

2NO₂+CH₂O→H₂O+CO₂+2NO+q

-q表示化学反应吸热，+q表示放热。

由反应式可以看出，硝化棉热分解时，首先由大分子变成小分子，小分子再分解生成二氧化氮、水和碳、氢、氧原子团。

二氧化氮还可以进一步和碳、氢、氧原子团以及硝化棉起作用，生成物有NO,CO,H₂,H₂O,CO₂等，是放热反应。

这一区既有吸热反应又有放热反应，但后者超过前者，总的热效应是正值，温度由T_1-2升至T_2-3,T_2-3为火药表面的温度，即火药中基本组元全部分解的温度。双基药的T_2-3约为280～350°C。T_2-3的高低取决于燃烧室压力，它随压力的增加而增加。这就说明燃烧室压力是影响气体对火药表面传热的因素，因此，燃烧室压力增加，燃速也增加。

这一区共放出总放热量的10%。由于它邻近第1区和第3区，所以一方面从第3区传入一部分热量，同时还传出一部分热量到第1区。

火药的固相分解速度主要取决于这一区中的温度和热量。燃烧室压力如太低，则分解出来的二氧化氮很快逸出，来不及与火药及分解的中间产物进一步反应，因此放热反应减少，放出的热量将不足以维持固相加热层(第1区)和本区分解作用的进行，火药便会发生脉冲燃烧甚至熄灭。由此可知，为了保证火药的稳定燃烧，需要在这一区内放出足够的热量，这就要求火药燃烧时压力应高于一定值。为了提高火药在低压下燃烧的稳定性，还在火药中加入了燃烧稳定剂与燃烧催化剂。前者的作用是与这一区的生成物结成一层薄膜，防止二氧化氮过快逸出。石墨、氧化镁(MgO)和白垩(CaCO₃)等均可起燃烧稳定剂的作用。催化剂的作用是加速放热反应，有利于热量的放出。

这一区火药的表面为蜂窝状结构，其固相物质是尚未分解的火药，而凹处则充湍着火药分解后生成的液体和气体，化学反应在凹处内进行。在10MPa压力下，双基药反应区的厚度约为0.09mm，厚度随压力的升高而减薄。

第3区是嘶嘶区，或称混合相区。在这一区内，由于第2区中的气体分解产物逸出时，将一部分尚未完全分解的固体和液体的微粒也一起带出，发出嘶嘶的响声并以烟雾的形式存在，互相混合在一起，形成混合相区。它们之间继续互相作用，除第2区的一些反应继续进行外，其中主要的还进行着二氧化氮还原为一氧化氮的反应以及氢和碳的氧化反应；

NO₂+(CHO)_N→NO+CO+H₂O+H₂+Q

NO₂+CO→NO+CO₂+Q

NO₂+H₂→NO+H₂O+Q

NO+CO→1/2 N₂+CO₂+Q

这一区的厚度在10MPa压力下约为0.002mm，T_3-4约为700～1000℃,火药此时几乎完全气化，所放出之热量约为每千克1.25×10⁶～1.67×10⁶焦，占总放热量的40～50%,这一区在火药燃烧过程中有很重要的意义，它一方面从第4区得到热量。另一方面向第2区传出热量。由于在低压下火焰区距固相表面太远，从第4区传给火药表面的热量很少，而火药燃烧过程的维持主要依靠这一区放出的热量。这一区的温度还不太高，有的反应如氮的氧化物需在1500°C、100大气压以上才能完全还原为分子氮，因此如果压力太低，火药的燃烧经常就在这一区中止，能量因而不能完全释放出来。由此可知，火药对燃烧室压力有一定的要求。

第4区是暗区。这一区内，由于温度不够高，因而气体不发光，故称作暗区。暗区内基本上没有物理变化，化学变化也不明显，主要是中间产物继续反应，如一氧化氮还原为氮等。但由于温度不到1500°C,化学反应的速度很低，放出的热量也少，温度升高主要靠第5区传来的热。这一区的厚度随燃烧条件的不同而有很大的不同。低压时，暗区的厚度很厚；压力升高后，暗区迅速变薄，甚至可能根本消失。在10MPa的压力下，双基药暗区厚度约为

0.2mm。低压下，由于化学反应进行得慢，放出的热量很少，而气体还有散热等因素，因此温度升高不快，这一区的厚度就厚。暗区愈厚，第5区离固相表面的距离就愈远，第5区的热量愈不易传到固相表面上去。当压力低于某一临界压力值时，甚至一氧化氮不再发生反应，燃烧过程中止。这时约有一半的火药能量没有释放出来，这种现象称作不完全燃烧。相反，在高压下，暗区被压缩，气体浓度增加，大量NO还原成N。,放出的热量使温度升高，当温度升至1500°C以上时，反应加速，燃烧过程进入第5区。

第5区是火焰区，这一区是第4区的继续。由于火药气体的温度升高至1500°C时即开始发光，这一区的温度随火药成份不同可达到2000～3200°C,超过了气体发光的温度，因而发出强烈的火焰，故称作火焰区。这一区的化学反应激烈，主要是一氧化氮还原为氮气的放热反应，50%的火药能量在这一区放出。

2NO+CO+H₂→N₂+CO₂+H₂O+Q

这一区是火药完全燃烧的最后一区，在这一区内生成最后的燃烧产物。

高压室压力愈高，火焰区距火药表面愈近。本区内反应放出的热量除提高燃烧产物温度外，甚至还可传入嘶嘶区。

实际燃烧过程中的这5个区域是不能严格分开的，而是一个互相交叉的连续过程。可能在第2区内有第5区的反应，也可能在第5区内有固体颗粒而发生第3区的反应。此外，在不同的压力下，火药的主导反应是不同的，因而有时只有五个区中的几个区。

多阶段燃烧说有助于我们了解燃烧过程的实质，但它没有考虑燃烧过程的热损失，没有考虑火药气体有流出时所产生的流速影响，没有考虑扩散、辐射以及其它物理过程的影响等问题，因而也还需要进一步完善。

2.3火药的几何燃烧定律

具体的火药都是具有一定的几何形状及尺寸的，具有一定形状和尺寸的火药称为装药。装药在燃烧过程中其燃烧面积的几何形状和尺寸按照什么规律变化?这个问题不解决，就无法研究弹射器高压室中的压力变化规律。1880年硝化棉火药的发明者法国学者维也里在对简单药形火药燃烧的观察中发现，从火炮的炮膛里抛出来的带状药残药，只是从各边烧去了某一厚度而仍保持了其原来的形状；同时在密闭爆发器的实验中，他还发现两种性质相同，形状相同，只是燃烧层厚度不同的火药，以相同的装填密度△(=m_g/V_c)在密闭爆发器(内弹道试验用的）

以下关于装药的内容 略。

第三章 高压室内弹道计算

这部分可参阅固体火箭发动机原理或设计，主要是计算高压室怕p~t,\({\dot m}_{p} \sim t\)。

第四章 弹射器低压室内弹道的一般问题

 无坐力炮是发射时利用后喷物质的动量抵消后坐力使炮身不后坐的火炮。一般火炮在发射炮弹的同时，还会产生巨大的后坐力，使火炮后退很远的距离，这既影响射击的准确性和发射速度，又给操作带来不便。 
　　1879年，法国的德维尔将军等人发明了火炮的反后坐复进装置，但它并没有消除开炮时的后坐现象，只是使后坐炮身能够自动回复到原来的位置。并且 它还会使炮架结构复杂，重量增加，机动性降低。 
　　世界上第一门能够消除后坐现象的火炮是由美国海军少校戴维斯研制的。戴维斯的设计思想非常独特，他把两颗弹尾相对的弹丸放在一根两端开口的炮管内发射。射击时，向前射出的是真弹头，另一颗向后抛的是假弹丸──铅油质的配重体，使其作用力相互抵消，从而使炮射不发生后坐。抛射出的配重体散落在炮尾后不远的地方，射手避开了这个危险区就不会受伤害。戴维斯于1914年发明的世界上第一门无坐力炮人称 “戴维斯炮”。 
　　“戴维斯炮”还有许多不完善之处，人们对它进行了改进和发展。1917年，俄国人梁布欣斯基取消了配重体，直接用向后喷出的火药气体来进行平衡。这样，抛射固体配重体的后半截炮管也就没有用了，使无坐力炮的炮管缩短了一半，此后，英国的库克和苏联的特罗菲莫夫、别尔卡洛夫、库尔契夫斯基等人对无坐力炮作了新的发展，在炮管的尾部安上喷管，使流过喷管的气体速度增大，从而减少喷出的气体量。1936年，梁布欣斯基研制出一种75.2毫米无坐力炮，这是世界上正式装备部队的第一种无坐力炮。无坐力炮的第一次实战应用是1941年的苏联─芬兰战争。 
　　在第二次世界大战及战后年代，无坐力炮在各国军队中得到广泛应用，并不断改进。无坐力炮体积小，重量轻、结构简单，操作方便，适于伴随步兵作战。但后喷火焰大，易暴露。它主要用于近距离射击坦克等装甲目标。

     82毫米无后坐力炮于1979年设计定型，1981年批量生产装备部队，该炮是一种营属火炮，装备到步兵营。该炮身管和药室为整体结构，采用横向开关闩机构，为减轻炮重，药室容积较小；炮闩有上、下两个喷孔，利用闩轴和开闩杆完成与炮尾的闭锁；炮闩上还装有长喷管，以减少后喷危险角；该炮配用直瞄和间瞄两用合一光学瞄准镜和微光瞄准镜。

     破甲弹为火箭增程弹，采用双锥药型罩；榴弹内装825颗钢珠（图1）。

图1

不论何种类型的弹射器，其高压室本质上都是一个半密闭的燃烧室，它们的内弹道计算(求得p₁-t曲线)都可按第二章的方法得到解决。第二章的内容对以燃气为动力源的各类弹射器高压室都是适用的，具有普遍意义。因此，无后坐弹射器高压室的内弹道计算问题(正面问题)可以认为已经解决，而低压室内弹道计算问题的解决尚与弹射器的结构类型有关。本章研究与低压室内弹道有关的某些问题，如无后坐式弹射器及自弹式弹射器所具有的反作用力计算问题，无后坐条件问题以及各类弹射器都存在的次要功计算等问题，这些问题是解决低压室正面问题的基础。

4.1弹道特点

各类弹射器中以无后坐式较为典型，我们选择无后坐式作为代表来分析其弹道特点，至于其它型式弹射器的弹道特点可见第四章的有关叙述。

(a)

(b)

图4-1  无后坐式弹射器

(a)并联无后坐式；(b)串系无后坐式

与其它类型的弹射器相比，无后坐式弹射器内弹道的基本特点是：为了抵消后坐，有大量燃气由尾喷管流出。对于并联无后坐式弹射器来说，是低压室燃气经尾喷管流出，对于串联无后坐式弹射器，则是高压室的燃气经尾喷管流出。下面研究这两种型式弹射器由其基本特点带来的其它特点。

①并联式低压室内存在着三个主要的物理过程：从高压室而来的燃气流入，经尾喷管的燃气流出及导弹的向前运动，其中导弹的运动和燃气经尾喷管的流出是在同一个压力——低压室压力的作用下发生的，其特点可概括为低压推弹、低压后喷。

串联式低压室内只有从高压室来的燃气流入及导弹运动，没有燃气的流出。因而特点是低压推弹、高压流出。

②不论是并联式还是串联式，总要有大量燃气流出，所以火药的消耗量大。一般说来，大约只有1/3的燃气用来作功，推动导弹向前运动，2/3的燃气则由尾喷管向后喷出，所产生的推力消除了因导弹运动而产生的发射筒后坐运动。

③由于有大量燃气流出的现象，因此为了维持所需要的低压室压力，在单位时间内必须有足够多的燃气由高压室流入，也就是要求高压室有足够大的每秒燃气生成量，所以无论串联式或并联式弹射器，高压室中的装药一般都具有大燃烧面、高燃速的特点。

④为了充分利用火药能量，提高装药利用系数η_ω(\({\eta}_{\omega}=m{v}_{g}^{2}/2\omega\)),装药应在导弹离筒之前这样一个极短的时间内工作完毕，因而多采用薄肉厚、高能量的火药。

⑤由于高压室破膜压力破等于点火压力p_ig故低压室压力曲线p₂-t的时间起点与高压室压力曲线相同，即t=0时，p₁=p_ig,p₂=0。

⑥在弹射初始条件方面的特点：串联或并联无后坐式低压室在弹射过程开始时均存在两种不同的起始压力，一是导弹开始运动时的低压室压力，称为起动压力p₀。有时由于勤务上的需要(如运输等),用剪切销或其它方式将导弹与发射筒连接在一起，在剪切销被剪断瞬间低压室的压力就是起动压力，起动压力与导弹承压面积的乘积亦可称为牵制力；当导弹没有剪切销而处于自由状态时，起动压力主要用于克服最大静摩擦力。另一个起始压力是尾喷管开始喷气时之压力p_om,称为起喷压力。由于勤务(如防潮等)及内弹道方面的需要，尾喷管常装有一喷管堵盖，起喷压力也就是冲破喷管堵盖时低压室内燃气之压力。根据p₀及p_om值的不同，导弹起动和喷管起喷的时间t₀及t_om可能不一致，而表现出下列三种情况：

(i)p₀>p_om(t₀>t_om)  在这种情况下，尾喷管先开始喷气，导弹后开始运动。低压室压力在由p_om上升到p₀的过程中，低压室相当于一个有气体流出的半密闭定容贮气室，发射筒受前冲力。

(ii) p₀<p_om(t₀<t_om)导弹开始运动之后尾喷管才开始喷气。压力在由po增加到p.的过程中，低压室相当于一个密闭的变容贮气室，此时发射筒受后坐力。

(iii) p₀=p_om(t₀=t_om)导弹的运动与尾喷管的喷气同时开始。这是无后坐的理想情况。

具有两个不同的起始压力p₀及p_om是无后坐弹射器独有的特点。p₀及p_om的大小以及它们的差值不但影响发射筒平衡，而且对压力曲线也有影响。p₀不宜太大，否则将容易引起导弹及发射筒的激振而降低发射精度。

合理地设计剪切销及尾喷管堵盖的强度(包括联接强度)可得到p₀=p_om的理想情况，因而剪切销与喷管堵盖的作用除勤务需要外，还是实现p₀=p_om及在一定范围内调节弹道的手段。

4.2次要功系数

在弹射过程中，高压室向低压室喷入大量高温高压燃气，与此同时，低压室内产生了各种运动形式。当导弹在燃气压力推动下剪断剪切销开始运动后，克服摩擦阻力，一面向前作直线运动，一面又作旋转运动(旋转弹有此运动)。紧随着导弹的运动，燃气在发射筒内也同时运动。所有这些运动形式都是能量转换的具体表现。当然，根据热力学第二定律，任何热机都不可能将取得的热量全部转变为机械功。弹射器实质上也是热机，它也不可能将火药燃烧所放出的热量全部转变为机械功。所以，在弹射过程中，除散热损失外，火药气体的能量只是部分地转换成下列的机械能形式，还有相当部分的热能由于高温燃气排入大气而散失；

• 导弹直线运动的动能E₁=mv²/2,m是导弹的质量，v是导弹的速度；
• 导弹旋转运动的动能E₂;
• 导弹克服摩擦阻力所消耗的能量E₃;
• 燃气运动的能量E₄;
• 导弹剪断剪切销所消耗的能量E₅。

这五种能量消耗都是以作功的形式表现的。五种功中，以导弹的直线运动功E₁最大，一般说约占总功的95%以上，因此称为主要功，其余四种功则称为次要功。其中除剪断剪切销的功E₅以外，其余三种功皆与E₁成一定的比例关系，可直接找出其关系式。假设K₂,K。,K₄分别为E.,E₃,E₄与E;的比例系数，则四项功的总和可表示为：

∑E_i=(1+K₂+K₃+K₄)E₁

令φ=(1+K₂+K₃+K₄)                       (4-1)

则∑E_i =φE₁= φmv²/2                    (4-2)

式中φ称为次要功系数，其物理意义是：如果将导弹质量增加到原来的φ倍，那么新质量

(φm)导弹的直线运动功与质量为m的导弹的主要功、次要功之和相等，即它们在能量消耗方面的效果相同，因此φ也可称为虚拟质量系数，意思就是用将导弹质量放大一个倍数的办法来考虑次要功的影响。

下面计算各次要功，并导出各比例系数K_i

1.导弹的旋转运动功

设Q为导弹沿发射筒内膛线运动时的旋转角速度，I为导弹的转动惯量，则导弹的旋转运动动能为

\({E}_{2}=\frac{1}{2}I{\Omega}^{2}\)

\(I=m{\rho}^{2}\)

式中p——导弹的惯性半径；

m—导弹的质量。

图(4-2)是发射筒的纵向展开图。角α称为膛线缠角。由图(4-2)可知，导弹的直线运动速度为v,旋转运动产生的切线速度为rΩ,r为导弹的半径。则有

图4-2发射筒展

\(\tan \alpha=\frac{r\Omega}{v}\)

故    \(\Omega=\frac{v\tan\alpha}{r}\)

代入E₂式，得

\({E}_{2}=\frac{m{\rho}^{2}{v}^{2}{\tan\alpha}^{2}}{2{r}^{2}}={(\frac{\rho}{r})}^{2}{\tan}^{2}\alpha\frac{m{v}^{2}}{2}\)

\(={K}_{2}\frac{m{v}^{2}}{2}\)

\({K}_{2}={(\frac{\rho}{r})}^{2}\)

可知，对于确定的无后坐弹射器，K₂是个常量，不同弹射器的K₂值浮动也不太，根据实际计算，K₂一般约在0.01左右。

2.导弹的摩擦功

无后坐弹射器的发射筒一般都是滑膛，即便有膛线，其根数也很少，这是由于导弹的转速一般都较低的缘故。因此，导弹在运动过程中虽也克服摩擦阻力作了功，但这部分功比较小，可以忽略不计，即可认为K₃≈0。

3.燃气运动功

由于低压室在弹射过程中不断有燃气从高压室流入，又不断从尾喷管流出，发射筒中的燃气质量是变化的，因此燃气的运动功也是不断变化的，K₄不是定值，而是变量。为了求

出K₄，首先需要研究发射筒内的压力分布问题。我们以并联无后坐式为例来分析问题。

(1)低压室燃气流速分布 压力变化和流速变化是密切相关的，求出流速变化规律将容易地求出压力分布规律。

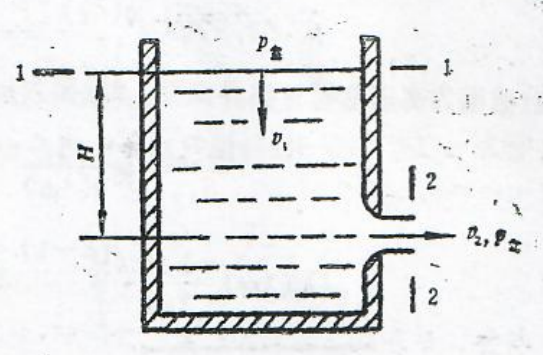
当高压室达到点火压力，装药开始燃烧时，高压室喷口膜片也同时破裂，燃气流入低压室。当低压室压力还未达到起动压力p₀或起喷压力p_om时(假设p₀=p_om),低压室内没有气体轴向流动。在这种情况下，可以近似地认为低压室内压力处处相等。当压力超过p₀(或p_om)以后，导弹的起动与尾喷管的起喷同时开始，低压室内形成了气流。由于导弹的运动，弹后空间的气体也跟着一起向前运动；由于尾喷管的打开，一部分气流又向后运动，因此低压室内形成了两个相反方向的气流。这两股气流之间，必然存在着速度为零而压力最大的滞止点，滞止点的位置随弹射过程的进行不断变化：开始阶段，导弹运动速度很低，滞止点的位置接近弹底。随着导弹速度的增加，气体向前流动的速度也相应地增加，滞止点相对弹底的距离愈来愈大；另一方面，由于弹射过程中低压室压力是不断变化的，所以向后流动的气流速度也是不断变化的。每一瞬间向前和向后的两股气流的速度大小决定了该瞬间滞止点的位置，也就是说，滞止点的位置是随时间变化的。滞止点的移动问题是复杂的气体动力学问题。滞止点处气体速度为零而压力最大，在滞止点两边的气流速度增加，压力下降。在导弹底部，气体流速就等于导弹的运动速度，而弹底压力则小于滞止点压力(图4-3)。

图4-3发射筒内气体速度分布

早在1790年，法国数学家和力学家拉格朗日(Lagrange)就接受法国国民议会的委托从事炮膛中火药气体运动规律的研究。二百年来，许多学者对此作了大量研究。拉格朗日把问题归结为：在一个等截面的、一端封闭的园管中，距底部某距离处放置重量为G的活塞，在火药瞬时燃完，且不考虑活塞与管壁间的縻擦及散热的条件下，研究气体和活塞的运动。这就是火炮内弹道学中著名的拉格朗日问题的内容，作为用气体动力学观点解内弹道学问题的第一次尝试，拉格朗日本人提出了一个筒化假设，称为拉格朗日假设，即把弹后的火药气体和未燃完药粒的两相混合流动看成为单一的火药气体的流动，且认为火药气体沿炮膛是均匀分布的，即火药气体的密度不随炮膛断面而变化(\(\partial p/\partial x=0\))。密度均匀分布的假设本质上是把气流看成不可压缩流体，这看起来是与实际情况相矛盾的，它不能反映膛内的热力学过程。但分析和实验的结果表明，在ω/m<1的情况下，由于弹丸速度较低；气流的速度亦较低，处于亚音速流动的情况，弹后的气流密度、压力梯度亦小，因此把气流看成不可压缩流是可以接受的。应用拉格朗日假设的内弹道近似解接近于精确解。也就是说，在低压低速的情况下，近似解具有一定的精确性。反之，当ω/m>1时，则将带来较大误差，拉格朗日假设不再能应用，应采用两相流气动力模型求得精确解。

以上分析的是一般火炮的膛内气体流动问题，对于弹射器低压室(发射筒内的弹后空间)中的气体流动问题，其工作特点尚与经典的拉格朗日问题有所不同，即弹射器发射筒不一定是一端封闭的圆管，而可能是半封闭的圆管，发射筒中的燃气如前所述是向两端流动的，这种情况类似无坐力炮的情况，故弹射器的拉格湖日问题可用与无坐力炮的拉格朗日问题相同的办法来解决。

由于考虑到低压室中燃气的低压低速特性，我们将仍以拉格朗日假设为前提来求得低压室中的燃气流动规律，并作如下假设：

①忽略燃气的粘性及散热，故可不考虑沿发射筒壁流动时的摩擦及气体的内摩擦，这样弹后空间任一横断面上各点气流速度及压力均是相等的，即忽略同一断面上气流参量的差异，燃气流动视为一维定常等熵流动。

②,忽略低压室截面积与发射筒截面积的差别，认为低压室内径与发射筒内径相等，这样就可忽略由于横截面变化带来的气流参量的变化。

③低压室中燃气密度是均匀分布的。

如图4-3所示，将横座标x的起点取在低压室的后端面(尾喷管的入口截面)处。

设某瞬时t,导弹底部距低压室后端面为L,导弹速度为v,故弹底处燃气流速亦为v,低压室后端面燃气流速为U₂,Z点代表滞止点，L_Z表示滞止点的位置，U_z表示燃气的流速。

对于一元定常等熵流，其质量方程为

\(\frac{\partial}{\partial t}(\rho A)+\frac{\partial}{\partial t}(\rho{U}_{x}A)=0\)

由于假设②,即截面积A为常数，故上式可写为：

\(\frac{\partial \rho}{\partial t}+\frac{\partial}{\partial t}(\rho{U}_{x})=0\)

根据拉格朗日假设

\(\frac{\partial \rho}{\partial x}=0\)

故

\(\frac{\partial \rho}{\partial t}+\rho\frac{\partial {U}_{x}}{\partial t}=0\)

或

\(\frac{\partial {U}_{x}}{\partial t}=\frac{1}{\rho} \frac{\partial \rho}{\partial t} =0\)    (4-3)

上式右边仅是t的函数，与x无关，故上式的解可写为

\({U}_{x}={k}_{1}x+{k}_{2}\)            (4-4)

即低压室中燃气流速为线性分布，这就是由弹后燃气密度均匀分布的拉格朗日假设导致的重要结论，有时亦将燃气流速按线性分布称作拉格朗日假设。

剩下的问题就是确定k₁,k₂,它们都是t的函数。

边界条件：当x=0时，U_x=-U_B;x=L时，U_x=v_x代入(4-4)式当x=0时，-U₂=k₂

k₂=-U_B

当x=L时，

v=k₁L-U_B

k₁=(v+U_B)/L

故(4-4)式为：

\({U}_{x}=\frac{1}{L}(v+{U}_{E})x-{U}_{B}\)

\({U}_{x}=\frac{x}{L}v+(\frac{x}{L}-1){U}_{B}\)           (4-5)

这就是燃气流速按线性分布的公式，其图形如图4-3所示。

(2)低压室压力分布公式 如图4-3所示，在x处取厚为dx的微分单元体，其质量为dμ,气流速度为U_x,作用在x断面上的压力为p_₂x,作用在x+dx断面上的压力为p_2x+dp_2x,又设某瞬时由高压室流入低压室的燃气总质量为M₁由尾喷管流出的燃气总质量为M₂,根据牛顿第二定律，作用在该气体上的外力之和等于该气体的质量乘以外力作用下所获得的加速度，若X方向为气体流动方向，则有

\(A[{p}_{2x}-({p}_{2x}+{dp}_{2x})]=d\mu\frac{{U}_{x}}{dt}\)

无后坐式弹射器多用于倾斜发射，存在导弹本身重量的轴向分力，由于高低射角较小，故此力相对较小，可忽略不计。故上式为

\(A{dp}_{2x}=-d\mu\frac{{L}_{x}}{dt}\)              (4-6)

由假设③,有

\(d\mu=\frac{dx}{L}({M}_{1}-{M}_{2})\)

由(4-5)式得

\(\frac{{U}_{x}}{dt}=\frac{x}{L}\frac{dv}{dt}+\left(\frac{x}{L}-1\right)\frac{d{U}_{B}}{dt}\)

代入(4-6)式，则

\(d{p}_{2x}=-\frac{1}{A}d\mu\frac{d{U}_{x}}{dt}\)

\(=-\frac{1}{A}\frac{dx}{L}({M}_{1}-{M}_{2})\left[\frac{x}{L}\frac{dv}{dt}+\left(\frac{x}{L}-1\right)\frac{{U}_{B}}{dt}\right]\)

\(=-\frac{{M}_{1}-{M}_{2}}{A{L}^{2}}\frac{dv}{dt}xdx-\frac{{M}_{1}-{M}_{2}}{A{L}^{2}}\frac{d{U}_{B}}{dt}xdx\)

\(+\frac{{M}_{1}-{M}_{2}}{AL}\frac{d{U}_{B}}{dt}dx \)

令\(H=\frac{{U}_{B}}{v}\)称为速度比，则

\({dp}_{2x}=-\frac{{M}_{1}-{M}_{2}}{A{L}^{2}}\frac{dv}{dt}xdx-\frac{{M}_{1}-{M}_{2}}{A{L}^{2}}\frac{dv}{dt}xdx\)

\(+\frac{{M}_{1}-{M}_{2}}{AL}H-\frac{dv}{dt}dx \)

导弹在弹底压力作用下获得直线运动动能、克服摩擦力并获得旋转运动动能，因此以弹底压力p₂x表示的导弹运动方程应为：

\(A{}_{}={\varphi}_{1}m\frac{dv}{dt}\)              (4-7)

φ₁是只考虑导弹摩擦功及旋转运动功的次要功系数，  φ₁=1+K₂+K₃。将

\(\frac{dv}{dt}=\frac{A{p}_{2x}}{{\varphi}_{1}m}\)

代入dp_2x式，得

\({dp}_{2x}=-\frac{({M}_{1}-{M}_{2}){p}_{2d}}{m{\varphi}_{1}{L}^{2}}(1+H)xdx+\frac{({M}_{1}-{M}_{2}){p}_{2d}}{m{\varphi}_{1}{L}}Hdx\)

积分上式得

\(\int\limits_{{p}_{2x}}^{{p}_{2d}}{d{p}_{2x}}=-\frac{({M}_{1}-{M}_{2}){p}_{2d}}{m{\varphi}_{1}{L}^{2}}(1+H)\int\limits_{x}^{L}xdx+\frac{({M}_{1}-{M}_{2}){p}_{2d}}{m{\varphi}_{1}{L}}H\int\limits_{x}^{L}dx \)

\({p}_{2x}={p}_{2d}\left\{1+\frac{({M}_{1}-{M}_{2}){p}_{2d}}{m{2\varphi}_{1}{L}^{2}}(1+H)(1-\frac{{x}^{2}}{{L}^{2}})+\frac{({M}_{1}-{M}_{2}){p}_{2d}}{m{\varphi}_{1}{L}}H(1-frac{x}{L}) \right\}\)

此即任意瞬间低压室内压力分布公式。可知，其分布规律为抛物线。当x=0时，得低压室后端面处之压力p_a,则

\({p}_{2x}={p}_{a}={p}_{2d}\left\{ 1+\frac{({M}_{1}-{M}_{2})}{2m{\varphi}_{1}} (1-H)\right\}\)

当x=L时，p_2x即弹底压力p_2d

p_2x=p_2d

当x=Lz,即滞止点处，有Ux=0,由(4-5)式有

\({L}_{z}=\frac{{U}_{B}}{v+{U}_{B}}L\)

或

\({L}_{z}=\frac{H}{1+H}L\)               (4-9)

若已知速度比H及导弹行程L,则由(4-9)式可求得L_z,代入(4-8)式后可得滞止点压力p_z

\({p}_{2}={p}_{2d}\left[1+\frac{({M}_{1}-{M}_{2})}{ {2\varphi}_{1}m} \frac{1}{(1+H)}\right]\)

(3)求K₄ 既然低压室内存在着压力分布，那么在建立内弹道方程时就必须考虑低压室内因压力分布带来的各点压力值的不同，这样内弹道方程将变得复杂，为了使问题简化，我们引进瞬时平均压力的概念，即认为在某瞬时t,低压室压力均匀分布，各点压力相等，其大小等于低压室内压力分布的积分平均值，即

\({p}_{1}=\frac{1}{L}\int\limits_{0}^{L}{{p}_{2x}}dx\)   (4-11)

L.0

式中p₂称为瞬时平均压力，在不同的瞬时有不同的值。

这样一来，给内弹道计算带来很大方便，各内弹道方程中的压力变量就可用统一的瞬时平均压力p₂来表示，换句话说，内弹道方程中的压力p₂是某瞬时简内压力分布的平均压力。

将(4-8)式代入(4-11)式，并积分，求得瞬时平均压力与弹底压力之关系，即

\({p}_{2}={p}_{2d}\left[1+\frac{({M}_{1}-{M}_{2})}{ {3\varphi}_{1}m} {(1-\frac{H}{2})}\right]\)     (4-12)

如果以平均压力p₂来表示导弹运动方程，则次要功系数除包括K₂和K₃外，还应包含K₄,即

\(A{p}_{2}={\varphi}_{1}m\frac{dv}{dt}\)

\(\varphi={\varphi}_{1}+{K}_{4}=1+{K}_{2}+{K}_{3}+{K}_{4}\)

因

\(A{p}_{2}={\varphi}_{1}m\frac{dv}{dt}\)

故  \(\frac{{p}_{2}}{{p}_{2d}}={\varphi}_{1}m\frac{dv}{dt}\)

由(4-12)式

\(\frac{{p}_{2}}{{p}_{2d}}=1+\frac{({M}_{1}-{M}_{2})}{ {3\varphi}_{1}m} {(1-\frac{H}{2})}\)

故  \(\varphi = {\varphi}_{1}+\frac{({M}_{1}-{M}_{2})}{ 3m} {(1-\frac{H}{2})}\)

\({K}_{4}=\frac{({M}_{1}-{M}_{2})}{ 3m} {(1-\frac{H}{2})}\)

实际计算结果表明，K₄的值很小，可以忽略不计，即可以认为K₄≈0。

,因此，对于无后坐弹射器而言，φ的理论值可近似取为1(在旋转弹的情况下可取为1.01)。但在实际应用中，φ常当作符合系数处理，即在理论值附近不大的范圈内取恰当的值(一般是较理论值稍大),以进行对初速的修正，使计算值能较好地符合实测值。

4.3反后坐装置反作用力计算

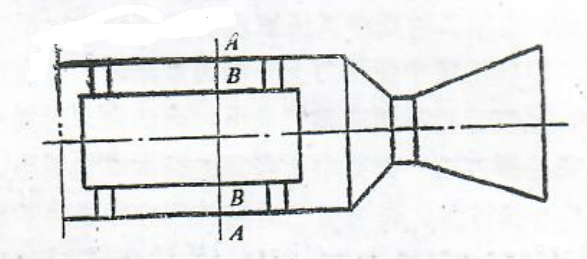
无后坐式弹射器及倾斜发射时之自弹式弹射器均有消除后坐的要求。它们之所以能实现”无后坐”,主要是采用了反后坐装置，其形式一般有尾喷管式或制动小火箭式。前者可以图4-1(a)为典型代表，即在发射筒后端部连接一拉瓦尔喷管；后者为在发射筒后端部固定有两个(或一个)独立的小火箭(图4-4),利用其提供之推力抵消弹射过程中发射筒所受之后坐力。

一般说，制动小火箭的燃烧室(亦称反后坐高压室)与发射筒内的低压室是不相通的，故采用此种反后坐装置的弹射器，其本质上与串联无后坐式可属同一种类，因它亦是低压推弹、高压后喷，只不过其后喷燃气是由另一个燃烧室——反后座高压室喷出的罢了。下面分别讨论这两种反后坐装置提供的反作用力计算。

（a）两个制动小火箭

(b)一个制动小火箭。

图4-4制动小火箭式反后坐装置

1一发射筒；2一制动小火箭。

4.3.1制动小火箭式反后坐装置反作用力计算

当采用制动小火箭式反后坐装置时，其反作用力的计算就是火箭发动机推力的计算，这在固体火箭发动机或气体动力学的教科书中已有现成的结论可以引用。对于经常采用的先收缩后扩张的变截面喷管——拉瓦尔喷管，其推力公式在下述假设下可有(4-13)式的形式。

①燃烧室内的装药完全燃烧，所产生的燃气为完全气体，燃气具有固定不变的物理化学性质；

②燃气具有理想气体的性质；

③燃气在喷管中的流动是一维定常流；

④喷管中的燃气无粘、无导热，因而没有摩蒜及其它消耗性损失，即流动是等熵的；⑤燃气充满整个空间，因而是连续的；

⑥火箭发动机为轴对称体，且燃烧室具有足够大的容积，燃气由大容器流入喷管，因而喷管入口截面气流速度可视为零。

\(F=G{U}_{e}+{A}_{e}({p}_{e}-{p}_{a})\)        (4-13)

式中F—推力；U_e,S_e,p_e——喷管出口截面之燃气流速、截面积及压力；

G——喷管秒流量；

p_a——外界气体压力。

推力F的方向与气流方向相反。由(4-13)式知，F的大小由两项组成，第一项GU_e称为动推力，是由向后高速流动的燃气动量变化所提供的，通常占总推力的90%以上。第二项A_e(p_e-p_a)称为静推力，它是由喷管出口截面的压力p_e与外界气体压力p_a的差值产生的推力。根据p_e与p_a的关系，可出现以下三种情况：

① p_e<p_a,称为过膨胀状态，此时静推力为负值，动推力较大，喷管出口处出现压缩波。

② p_e>p_a,称为欠膨胀状态。此时静推力为正值，动推力较小。

③ p_e=p_a,称为理想膨胀状态，或设计状态，此时静推力为0,推力等于动推力，且达到最大值。

过膨胀状态在自弹式弹射器上有时会出现，设计状态在实际上不可能达到，尾喷管通常都属于第二种状态，即欠膨胀工作状态。

由(4-13)式可知，推力的大小决定于质量流率G,外界气体压力p_a及喷管出口截面上的各参数U_e,p_a,A_e,为了计算某瞬间的推力，必须确定该瞬间的G,U_e,p_c这些量是不易用实验来确定的，故在实际应用时为了便于分析计算，还需将推力公式转化为更简单实用的形式，即用推力系数来表示的推力公式。

由气体动力学知，一元、定常、连续、等熵流的流速公式及流量公式参见有关发动机原理。

如果气体是从象发射简那样的圆柱形管道中流出，则假定发射筒口就是临界断面，即

\(\frac{{A}_{e}}{{A}_{t}}=1\)

且

\(\frac{{p}_{e}}{{p}_{c}}=\frac{{p}_{t}}{{p}_{c}}={\left(\frac{2}{k+1}\right)}^{\frac{1}{k-1}}\)

代入C_F的公式，求出的C_F值用C_F0表示，则

\({C}_{F0}=(k+1){\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}-\frac{{p}_{a}}{{p}_{c}}\)    (4-16)

此时推力公式为

\(F={C}_{F0}{P}_{c}{A}_{t}\)

在实际的喷管流动中，由于散热、摩擦损耗等因素造成流量及流速的损失，而使实际的推力系数总小于理论推力系数，为此可引用流速及流量修正系数对推力公式进行修正；

\(F={A}_{t}{p}_{c}\left\{{\varphi}_{1}{\varphi}_{2}\Gamma\sqrt{\frac{2k}{k-1}\left[1-{\left(\frac{{p}_{e}}{{p}_{c}}\right)}^{\frac{k-1}{k}}\right]}+\frac{{A}_{e}}{{A}_{t}}\left(\frac{{p}_{e}}{{p}_{c}}-\frac{{p}_{a}}{{p}_{c}}\right)\right\}\)

\({C}_{F}={\varphi}_{1}{\varphi}_{2}\Gamma\sqrt{\frac{2k}{k-1}\left[1-{\left(\frac{{p}_{e}}{{p}_{c}}\right)}^{\frac{k-1}{k}}\right]}+\frac{{A}_{e}}{{A}_{t}}\left(\frac{{p}_{e}}{{p}_{c}}-\frac{{p}_{a}}{{p}_{c}}\right)\)

除无后坐式、自弹式弹射器反作用力计算时要用到以上推力公式外，自弹式弹射器运动高压室亦需运用(4-14)(4-15)式对自推力进行计算。

4.3.2尾喷管式反后坐装置反作用力计算

尾喷管式反后坐装置是在发射筒后端部连接一个尾喷管(如图4-5所示),尾喷管大都采用能获得高流速的拉瓦尔喷管。弹射器的尾喷管工作特点与火箭发动机喷管的工作特点不同，因而提供的推力表达式亦不相同，弹射器尾喷管工作特点如下

图 4-5 尾喷管

①火箭发动机燃烧室是一端封闭一端开口的半密闭容器，而弹射器尾喷管则是两端开口的，没有封闭的底部。②火箭发动机燃烧室的燃气认为是由大空间经小孔流出，燃烧室内燃气的流速较喷管内流速小得多，故可假设喷管入口截面的气流速度U_B=0,燃烧室内的压力是均匀分布的，其大小即为总压p_c.弹射器低压室的情形则不同，燃气在低压室内运动较复杂，压力分布是不均匀的，尾喷管入口截面B-B处的流速已有一定大小，即U_B≠0。

1.喷管入口截面B-B处之总压p_B

根据发射简内压力分布公式(4-8),当x=0时，可得喷管入口截面B-B处之静压p_B

\({p}_{B}={p}_{2d}\left[1+\frac{{M}_{1}-{M}_{2}}{2{\varphi}_{1}{m}_{m}}(1-H)\right]\)              (4-18)

B-B截面燃气流速为U_B,故该截面之总压p_OB为：

\({p}_{OB}={p}_{B}+\frac{\rho}{2}{U}_{B}^{2}\)   (4-19)

下面求UB及H:

通过B-B截面流出之燃气秒流量\({\dot m}_{B}\)为

\({\dot m}_{B}=\rho{U}_{B}{A}_{B}\)

故

\({U}_{B}=\frac{{\dot m}_{B}}{\rho{A}_{B}}\)

因

\(\rho=\frac{{M}_{1}-{M}_{2}}{{V}_{20}+Sl}\)     (4-20)

故

\({U}_{B}=\frac{{\dot m}_{B}}{{A}_{B}}\frac{{V}_{20}+Sl }{{M}_{1}-{M}_{2}}\)

式中V₂₀—低压室初始容积；

A_B—B-B截面之截面积；

M₁—在时间t内由高压室流入低压室的燃气总质量；

M₂—在时间t内，低压室流出的燃气总质量；

ρ—低压室燃气密度。

因     \({G}_{2}=\frac{d{M}_{2}}{dt}\)

故     \({U}_{B}= \frac{{V}_{20}+Sl }{{A}_{B} ({M}_{1}-{M}_{2})}\frac{d{M}_{2}}{dt}\)         (4-21)

\(H=\frac{{U}_{B}}{v}=\frac{{V}_{20}+Sl }{{A}_{B}v ({M}_{1}-{M}_{2})}\frac{d{M}_{2}}{dt}\)

将(4-18)、(4-20)式代入(4-19)式，得：

\({p}_{OB}={p}_{2d}\left[1+\frac{{M}_{1}-{M}_{2}}{2{\varphi}_{1}{m}_{m}}(1-H)\right]+ \frac{{M}_{1}-{M}_{2}}{2({V}_{20}+Sl)}{H}^{2}{v}^{2}\)

2.尾喷管反作用力F_p

如忽略外界大气压力的影响,则尾喷管反作用力F_p就是火药气体作用在尾喷管上的轴向力,其大小等于作用在喷管壁上所有压力的积分值,其方向取为与气流方向一致为正。喷管受力如图4-6所示。

设喷管任意截面之面积为A,压力为p,

则  

\({F}_{p}=\int\limits_{t}^{B}{pds}-\int\limits_{t}^{e}{pds} = \int\limits_{e}^{B}{pds}\)

图4-6喷管受力示意图

分部积分得

\({F}_{p}={p}_{B}{A}_{B}-{p}_{e}{A}_{e}-\int\limits_{e}^{B}{sdp}\)

将流量方程

\(\rho=\frac{\dot m}{AU}\)

和动量方程

\(\frac{dp}{\rho}+d\frac{{U}^{2}}{2}=0\)

合并,得

\(\frac{AU}{\dot m}dp+UdU=0\)

\(-Adp={\dot m}dU\)

代入F_p式,则

\({F}_{p}={p}_{B}{A}_{B}-{p}_{e}{A}_{e}-\int\limits_{{U}_{e}}^{{U}_{B}}{\dot m}dU\)

\({F}_{p}={p}_{B}{A}_{B}-{p}_{e}{A}_{e}-{\dot m}({{U}_{B}-{U}_{e}})\)

\(\dot m= {\varphi}_{2}\frac{{K}_{0}}{\sqrt{R{T}_{0}}}{A}_{t}{p}_{OB}\)

故

\({F}_{p}=\left\{\frac{{A}_{B}}{{A}_{t}}\frac{{p}_{B}}{{p}_{OB}}-\frac{{A}_{e}}{{A}_{t}}\frac{{p}_{e}}{{p}_{OB}}+{\varphi}_{1}{\varphi}_{2}{k}_{0}\left[\sqrt{\frac{2k}{k-1}\left[1-{(\frac{{p}_{B}}{{p}_{OB}})}^{\frac{k-1}{k}}\right]}-\sqrt{\frac{2gk}{k-1}\left[1-{(\frac{{p}_{e}}{{p}_{OB}})}^{\frac{k-1}{k}}\right]}\right]\right\}{A}_{t}{p}_{OB}\)

令

\(\pi=\frac{p}{{p}_{OB}}\)   (压力比)

\(\varepsilon =\frac{A}{{A}_{t}}\) (面积比)

\({F}_{u}(\varepsilon)=\sqrt{\frac{2gk}{k-1}\left(1-{\pi}^{\frac{k-1}{k}}\right)}\)

则

\({F}_{p}=\left\{{\varepsilon}_{B}{\pi}_{B}-{\varepsilon}_{e}{\pi}_{e}+{\varphi}_{1}{\varphi}_{2}{K}_{0}\left[{F}_{u}({\varepsilon}_{B})-{F}_{u}({\varepsilon }_{e})\right]\right\}{A}_{t}{p}_{OB}\)   (4-26)

或

\({F}_{p}={C}_{F}{A}_{t}{p}_{OB}\)    (4-27)

其中

\({C}_{F}=\left\{{\varepsilon}_{B}{\pi}_{B}-{\varepsilon}_{e}{\pi}_{e}+{\varphi}_{1}{\varphi}_{2}{K}_{0}\left[{F}_{u}({\varepsilon}_{B})-{F}_{u}({\varepsilon }_{e})\right]\right\}\)           (4-28)

实际计算F_p时，必须知道p_OB的大小，这就需要将p_OB表达式及H表达式、p_2d表达示即(4-23)式、(4-22)式、(4-12)式列入低压室内弹道方程组，与内弹道计算同时进行，解出p_OB及H。此外尚需知道A_t即尾喷管喉部面积的大小，这是下一节无后坐条件所要解决的问题。在下一节中为了能用一个筒便的方法得出喷喉尺寸的估算值，反作用力的计算仍采用发动机推力公式来进行，即仍将低压室一端看成封闭的，且认为U_B=0,这样计算出来的A_t,虽然误差大一点，但可作为A_t的第一次近似值，而后通过修正或实验调整加以解决。修正的具体作法是；将估算出之A_t代入F_p式，可计算出尾喷管反作用力F_p,然后以发射筒为示力对象求出发射筒所受之不平衡力F_R及不平衡冲量I

\(I=\int\limits_{0}^{tg}{F}_{R}dt\)

图4-7平衡摆架示意图

式中tg—导弹在发射筒中加速运动的时间。比较I与I_M(不平衡冲量允许值),看是否有I<I_m,如此式得不到满足，则需调整A_t直至满足I<I_M时为止。这样就得到理论计算的A_t下一步就需将弹射器放在测动平衡的平衡摆架上测实际不平衡冲量I_s,平衡摆架如图4-7所示。当测得的实际不平衡冲量I_s与规定的不平衡冲量允许值I_M有差值时，就需进一步调整A_t以消除这个差值。

调整喷喉面积的近似公式为

\(\Delta {A}_{t}=\frac{\Delta I}{\varphi m {v}_{g}}{A}_{t}\)

式中ψ——次要功系数；

ΔA_t——喷喉面积的调整量；

ΔI—-实验测得的不平衡冲量与其允许值的差值，△I=I_s-I_M

v_g——导弹离筒速度。

此式虽是近似公式，但实际使用中既方便，可信度也足够。

I_m的大小目前尚未制定统一的标准，只能参考相近武器如无坐力炮进行选取。根据现有无坐力炮的数据，一般

\(K=\frac{{I}_{M}}{\varphi m {v}_{g}}\)=0.02～0.025

式中K—动量比。当肩射时，K取小值；当架射时，K取大值。

4.4 无后坐条件

无后坐弹射器利用尾喷管所产生的向前推力来平衡发射筒所受的后坐力，以保持发射筒的平衡无后坐。后坐力的大小与发射筒结构尺寸、装填条件有关，推力的大小也与喷管结构尺寸有关。因此，一定的发射筒结构尺寸，装填条件必然要求一定的尾喷喉尺寸，即尾喷管的结构尺寸与发射筒的结构尺寸、装填条件之间存在着某种关系，满足此种关系，发射筒才能保持平衡，我们将这种关系称为无后坐条件。下面利用动量守恒原理来导出这种关系。

根据弹射过程的特点，可以将其分成两个不同的阶段，一是导弹出发射筒口之前的阶段(t=0～t_g),一是出发射筒之后直到后效期终了的阶段(t=t_g～t_h)。导弹离筒后，进入后效期，在后效期中，燃气不仅对弹继续作用，同时对发射筒亦有作用。

根据动量守恒原理，在合外力为0的情况下，系统的动量守恒。

在第一阶段，我们取发射筒、导弹、燃气为系统的组成，故系统的动量是由发射筒的运动、燃气喷出尾喷管、导弹运动及燃气在发射筒内的运动四部分的动量所组成。

第二阶段，系统组成中去掉了导弹，只剩下发射筒及燃气，故系统的动量是由发射筒运动、发射筒内燃气的运动以及燃气由筒口、尾喷管喷出所产生的动量所组成。

对于燃气在发射筒内的运动状况，细致地研究起来是比较复杂的，因此，不论在第一阶段或第二阶段，均可近似地认为燃气一半向前运动，另一半向后运动，因而动量相互抵消。这样一来，在下面的动量守恒方程中就可不必考虑燃气在发射筒内的运动这一项，这种假设虽是近似的，但仍有一定程度的准确性。

4.4.1并联无后坐式弹射器的无后坐条件

首先分析第一阶段(t=0～t_g)的动量变化，并假定起动压力不等于起喷压力(p_o>p_om,t_o>t_om)。

当t=0时，导弹、发射筒和燃气均没有运动，故系统的初动量为0,系统的末动量也应为0,即发射筒的动量+导弹的动量+后喷燃气的动量=0        (4-29)

第一项发射筒的动量用(\(M\vec V\))I表示，下标I表示第一阶段；\(\vec V\)、M为发射筒的运动速度及质量。

根据动量的变化等于冲量，且取指向筒口的方向为正，再结合并联式低压推弹低压后喷的特点，则整个第一阶段从尾喷口打开瞬间t_om到导弹离笥瞬间t_g,导弹的动量变化应为\(+A\int\limits_{{t}_{0}}^{{t}_{g}}{p}_{2}dt\),由于导弹初动量为0,故(4-29)式中的第二项导弹的动量应为\(+A\int\limits_{{t}_{0}}^{{t}_{g}}{p}_{2}dt\)。

同理，可得第三项后喷燃气动量为\(+{C}_{F} {A}_{t2}\int\limits_{{t}_{om}}^{{t}_{g}} {p}_{2}dt\)。式中A_t2为尾喷管喉部面积，A为发射筒横截面积，C_F为推力系数，p₂为低压室压力。

故

\({\vec {MV}}_{I}={C}_{F}{A}_{t2} \int\limits_{{t}_{om}}^{{t}_{g}}{p}_{2}dt-A\int\limits_{{t}_{0}}^{{t}_{g}}{p}_{2}dt\)

\(={C}_{F}{A}_{t2}\int\limits_{{t}_{om}}^{{t}_{0}}{p}_{2}dt+{C}_{F}{A}_{t2}\int\limits_{{t}_{0}}^{{t}_{0}}{p}_{2}dt -A\int\limits_{{t}_{0}}^{{t}_{g}}{p}_{2}dt \)

\({\vec {MV}}_{I}={C}_{F}{A}_{t2} \int\limits_{{t}_{om}}^{{t}_{0}}{p}_{2}dt+ ({C}_{F}{A}_{t2}-A)\int\limits_{{t}_{0}}^{{t}_{g}}{p}_{2}dt\)             (4-30)

下面再看第二阶段(t=t_g～t_h)的动量变化。

当导弹离筒后，发射筒内的燃气由筒口及尾喷管同时喷出，其相应的反作用力分别为\({C}_{F0}A{p}_{2}\)及\({C}_{F}{A}_{t2}{p}_{2}\),这两个力方向相反，所以第二阶段终了时发射筒的动量为

\({\vec {MV}}_{II}= {C}_{F}{A}_{t2} \int\limits_{{t}_{g}}^{{t}_{h}}{p}_{2}dt –{C}_{F0}A\int\limits_{{t}_{g}}^{{t}_{h}}{p}_{2}dt\)

\({\vec {MV}}_{II}=( {C}_{F}{A}_{t2}–{C}_{F0}A)\int\limits_{{t}_{g}}^{{t}_{h}}{p}_{2}dt\)       (4-31)

式中C_F0——发射筒口处的推力系数；

t_h——后效期作用终了时间。发射筒的总动量为这两个阶段动量之和，即

\({\vec {MV}}={\vec {MV}}_{I}+{\vec {MV}}_{II}\)

无后坐条件中的“无后坐”指的是整个过程(t=0～t_h)无后坐，即只要求MV=0,由此可求得无后坐条件为：

\( {C}_{F}{A}_{t2} \int\limits_{{t}_{om}}^{{t}_{0}}{p}_{2}dt+ ({C}_{F}{A}_{t2}-A)\int\limits_{{t}_{0}}^{{t}_{g}}{p}_{2}dt +( {C}_{F}{A}_{t2}–{C}_{F0}A)\int\limits_{{t}_{g}}^{{t}_{h}}{p}_{2}dt=0\)    (4-32)

上式各项就是各阶段(t_om~t₀,t₀~t_g,t_g~t_h)所受不平衡冲量的大小，其中主要阶段，即导弹在发射筒中运动阶段(t=t₀~t_g)的不平衡冲量为(\(({C}_{F}{A}_{t2}-A)\int\limits_{{t}_{0}}^{{t}_{g}}{p}_{2}dt \))

亦可写为\(({C}_{F}\frac{{A}_{t2}}{A}-1)\varphi m{v}_{k}\)。

由(4-32)式可知，标志喷管结构尺寸的喉部面积A_t2不仅与压力p₂有关(p₂又与发射筒结构尺寸、装填条件有关),而且也与导弹起动时间t₀及喷口打开时间t_om有关。上式是在t₀>t_om的条件下得出的，当t₀<t_om时，上式第一项要变号。总之，在保证发射筒无后坐的条件下，一定的发射筒结构尺寸，装填条件及t₀,t_om值将确定出一定的A_t2值。应该指出，由于无后坐条件只保证了发射筒在整个发射过程中无后坐，即只保证了总动量MV=0,而每一阶段仍可能是有动量的，故所说的发射筒无后坐并不意味着发射筒在每一瞬间都不受后坐力或前冲力的作用。例如，在弹射的初始阶段，由于t₀>t_om或t₀>t_om,发射筒要受到前冲力或后坐力的作用；又如导弹出筒口以后，由于C_FA_t2及C_F0A的不相等，也会使发射筒受不平衡力的作用，只是由于不平衡力的作用时间都很短，而发射筒又具有惯性，在发射筒还没有移动或移动很小时，已为以后阶段产生的相反力所平衡而保持整个弹射过程中的无后坐，所以我们只能称这种弹射器为无后坐弹射器，而不能称为无后坐力弹射器。

在理想情况下，t₀=t_om,则(4-32)式中的第一项为0。

还由于导弹出筒口瞬间的发射筒压力p_g已比较低，C_F0A与C_FA_t2的差值实际上也不大，因

此第三项的值可近似地认为等于0,这样，无后坐条件就变为：

\(({C}_{F}{A}_{t2}-A)\int\limits_{{t}_{0}}^{{t}_{g}}{p}_{2}dt=0\)

即\({A}_{t2}=\frac{1}{{C}_{F}}A\)         (4-33)

由上述分析可知，在理想情况下，在弹射过程的每一瞬间，发射筒都不受不平衡力的作用。因此，这种情况下的无后坐弹射器才又可称作无后坐力弹射器，(4-33)式称作理想的无后坐条件式。

实际的无后坐弹射器虽不完全是理想的情况，但由于t₀、t_om及它们的差值都很小，C_F0A与C_FA_t2的差值也不大，因此采用理想无后坐条件式仍有一定的准确性。为了消除这方面的误差，以及考虑实际喷管的消耗(考虑实际喷管的摩擦及散热),可用修正系数χ₀来对理论推力系数C_F进行修正，最后得到

\({A}_{t2}=\frac{1}{{\chi}_{0}{C}_{F}}A\)

\({\chi}_{0}\)=0.88～0.95                (4-34)

4.4.2 串联无后坐式弹射器的无后坐条件

如果按照理想情况t₀=t_om考虑问题，且考虑到导弹出发射筒口前所产生的后坐不平衡

是主要的，导弹出筒口后，气体从尾喷管和筒口流出的差别可以忽略，即只考虑t₀～t_g的情况，则根据(4-29)式，即发射筒的动量+导弹的动量+后喷燃气的动量=0,再结合串联无后坐式低压推弹、高压后喷的特点，得：

\(\vec {MV}+ A\int\limits_{{t}_{0}}^{{t}_{g}} {{p}_{2}dt}-{C}_{F}{A}_{t2}\int\limits_{{t}_{0}}^{{t}_{g}}{{p}_{1}dt}=0\)

发射筒在整个弹射过程中应平衡无后坐，即

\(\vec {MV}=0\)

故\(A\int\limits_{{t}_{0}}^{{t}_{g}} {{p}_{2}dt}={C}_{F}{A}_{t2}\int\limits_{{t}_{0}}^{{t}_{g}}{{p}_{1}dt}\)

若将积分取平均值，得：

\(A{\bar p}_{2}={C}_{F}{A}_{t2}{\bar p}_{1}\)    

\({A}_{t2}=\frac{A}{{C}_{F}}\frac{{\bar p}_{2}}{{\bar p}_{1}}\)                (4-35)

考虑损失后，上式变为

\({A}_{t2}=\frac{A}{{\chi}_{0}{C}_{F}}\frac{{\bar p}_{2}}{{\bar p}_{1}}\)

此即理想情况下(t₀=t_om)串联无后坐弹射器的无后坐条件。

第五章 并联无后坐式弹射器低压室内弹道方程组及解法

高压室正面问题在第三章中已得到解决，所得到的p-t关系是解析式。本章解决低压室的正面问题。

所谓低压室内弹道正面问题就是指在给定发射筒构造诸元(包括口径d,发射筒断面积A,低压室初始容积V₂₀,导弹行程长l_g等)、喷口条件(主要指喉部面积A_t2)及装填条件(包括导弹重M_m,装药量M_g火药力f₀,余容α,火药比重ρ_p等)的情况下确定出低压室内的压力变化规律和导弹速度变化规律，特别是确定出低压室内最大压力p_m及导弹离筒速度(亦可称初速)v_g这两个重要的内弹道诸元。

弹射过程中，低压室内包含有多种运动形式，在一定的筒内结构及装填条件下，各种运动形式都不是孤立存在的，而是相互依存又相互制约的。低压室的压力变化规律及导弹速度变化规律实际上就是各种矛盾运动综合的结果。为了研究低压室的压力、速度变化规律，首先必须列出能够描述低压室主要弹射现象的方程，组成内弹道方程组，这样的方程组应能够反映出各种运动过程相互依存、相互制约的关系。然后再用一定的数学方法，由方程组解出压力曲线及速度曲线，即p-l,v-l,p-t,v-t曲线，这些曲线反映了发射筒内的压力变化规律及速度变化规律。建立方程组并从中解出压力曲线及速度、加速度等曲线这两方面的内容合在一起就是低压室内弹道正面问题所包含的内容。其中后者称为内弹道解法，有时亦将整个正面问题的解决称为内弹道解法.

5.1 基本假设

为了描述低压室在弹射过程中的各种物理现象以及进行内弹道计算，必须根据无后坐弹射器的特点建立各有关的基本方程。但是由于弹射现象的复杂性，以及我们认识上的局限性或数学处理上的困难，对于所有的弹射现象并非都能准确无误地用内弹道方程表达出来，而.是只能在某些假设的基础上用内弹道方程组表示出主要的物理现象，忽略掉次要的现象。这样，既使内弹道计算保持了一定的准确性，又使计算过程得到简化。为此作出如下假设：

①低压室的燃气状态为高温低压，因而可当作理想气体处理。

②燃气在尾喷管内的流动服从一元定常等熵假设。

③不考虑发射筒中的压力分布，各弹道方程中的压力一律采用瞬时平均压力p₂。

④用φ来考虑各种次要功。应该指出，在所有的次要功中，燃气运动功的计算是非常复杂的。上一章导出的K₄公式建立在多种假设基础之上，因而是十分粗略的，故φ值也是不准确的。在弹道的符合计算中，我们常将φ这个量作为修正量处理。

⑤忽略高压室壁对低压室内燃气的热交换；对因低压室壁热传导而引起的燃气能量损失(热散失)不进行直接计算，而是用降低流入低压室的燃气温度的办法予以考虑。

⑥弹射过程中，绝热指数k看作常量。

5.2内弹道方程组

5.2.1 弹射过程分析

根据低压室内各物理现象的发展规律将弹射过程分为三个时期：前期、第一时期及第二时期。

1. 前期

这一时期定义为由低压室的时间起点(即开始建立压力的瞬间)开始(t=0,p₂=0),到导弹起动或尾喷管打开瞬间(t₀或t_om)为止。低压室压力曲线的时间起点亦即高压室的时间起点，在这一瞬间，装药全面着火，高压室压力达到p_ig,喷口膜片亦同时破膜，低压室开始建立压力，即t=0时，p₁=p_ig=p_b(破膜压力),p₂=0。

(1)t₀=t_om的情况 这种情况下的低压室相当于一个有燃气不断流入的定容贮气室。这一时期压力由零升高到p₀(=p_om),而后导弹起动，尾喷管同时打开。这一时期的特定条件为l=0,v=0,M₂=0

(2)t₀>t_om的情况 在这种情况下压力曲线的变化显然有两个不同阶段。第一个阶段是从时间的起点开始到t_om,即压力从零开始，一直升到喷口打开压力p_om,气体开始流出尾喷管为止。第二个阶段是从t_om到t₀,此阶段的压力是由p_om升高到导弹起动压力p₀,导弹开始运动为止。可以看出，前一阶段，低压室相当一个有气体流入的定容贮气室，后一阶段相当于有气体流出的半密闭定容贮气室。前者的特定条件为

l=0,v=0,M₁=0

后者的特定条件为

l=0,v=0

(3)t_om>t₀的情况 这种情况下压力曲线的变化也分为两个阶段。第一个阶段从时间的零点到t₀,压力从零开始到起动压力p₀即导弹起动为止。第二个阶段是从p₀到p_om,压力从₀升高到psm、尾喷管起喷为止。前者同样相当于有燃气流入的定容贮气室，其特定条件为

l=0,v=0,M₂=0

后者相当于有燃气流入的变容贮气室，其特定条件为

M₂=0

2.第一时期

是从t₀(或t_om)到高压室燃烧结束瞬间t_g的时期，其特点是燃气的流入、导弹的运动及燃气的流出这三个不同的过程同时在低压室进行。这一时期是低压室最主要、最有代表性的工作时期。

3.第二时期

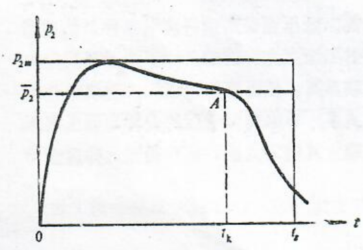
是从高压室燃烧结束点t_b到导弹离筒瞬间t_g时期。这一时期又分为三个阶段。第一阶段是高压室喷口的喉部参量能维持临界值时期。第二阶段是亚音速流动时期，第三阶段是p₁=p₂,高、低压室成为一个统一贮气室阶段(有时只有两个阶段，甚至只有第一阶段)。由于高压室燃烧结束，低压室的燃气流入量迅速下降，低压室压力也下降很快，导弹速度必然增加很慢，这就说明第二时期如太长，对增加初速并没有多少好处。因此，燃烧结束点t_k的选择，总是在保证下列两个前提下尽可能取较大的t_k/t_g值：保证装药在导弹离筒前燃烧结束；保证初速稳定。

由以上分析可知，第一时期最具有代表性，因为它包含了所有三个影响压力变化的因素：导弹运动、燃气流入及流出；而前期与第二时期所包含的只有这些因素的一部分，因此只能算作第一时期的特例。

一般说来，导弹弹离筒口就可认为弹射过程结束了。但是实际上弹射过程并没有完全结束，因为导弹离筒后，发射筒内的火药气体也随之流出，对导弹还继续产生一定的推动作用，导弹的速度还继续有所增加。这样，就又形成了一个时期，通常称为后效期，因此导弹在弹射过程中所获得的最大速度并不在发射筒口处，而是在离筒口一定距离处，该处即后效时期结束点。实际上，燃气除对导弹有后效作用外，对发射筒也有后效作用。导弹离筒后，燃气由尾喷管的继续流出，以及发射筒口燃气的流出，都对发射筒产生后效作用。燃气对导弹和对发射筒的这两种不同的后效作用是同时开始的两个独立过程。导弹的后效作用在导弹离开燃气推动作用之后结束，而发射筒的后效作用则是在低压室压力下降到2个大气压时结束。显然，这两个后效作用时期虽是同时开始，却并不是同时结束的。对后效期我们不作研究。

5.2.2、方程组

我们主要是建立最有代表性的第一时期方程组。与其它类型弹射器的低压室相比，并联无后坐式弹射器低压室的基本特点是有气体流出现象。由于低压室在弹射过程中有气体的流入、流出，因此不仅表现有气体状态的变化、能量的变化，而且还有质量的变化，因而可以建立质量平衡方程、状态方程和能量方程。下面讨论这三个方程以及其它各有关方程。

1.流入方程

低压室的流入方程就是高压室的流出方程。高压室的燃气不是流入压力不变的大气空间，而是流入压力不断变化的低压室，即反压是不断变化的。

根据喷管理论知道，气体在拉瓦尔喷管中流动，除喷管断面积对气体流动状态发生影响外，燃烧室内的压力(即高压室压力p₁)以及喷管外界压力(称为反压，即低压室压力p₂)对气体在喷管中的流动状态也发生显著影响(图5-1)。

图5-1拉瓦尔喷管在反压下的工作情况

只有当反压与燃烧室压力之比p₂/p₁值等于或小于(p_d)₄/p₁值时，喷管喉部截面才能达到音速，喉部才处于临界状态。此时喉部断面的压力p_t与燃烧室压力之比p_t/p₁称为临界压力比，其大小为，

\(\frac{{p}_{t}}{{p}_{1}}={\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\)

由于高压室是薄壁容器，其喷孔大多没有扩张段，即便有也很短，也就是说，“d”状态(参见图5-1)的出口截面压力值(p_e)_d等于或接近p_t值，故可以认为：

\(\frac{{({p}_{e})}_{d}}{{p}_{1}}=\frac{{p}_{t}}{{p}_{1}}={\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\)

而高压室喷孔喉部达到音速的内外压力比p₂/p₁为：

\(\frac{{p}_{2}}{{p}_{1}} \le \frac{{({p}_{e})}_{d}}{{p}_{1}}=\frac{{p}_{t}}{{p}_{1}}\)

故

\(\frac{{p}_{2}}{{p}_{1}} \le {\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\)

注脚”1”代表高压室，注脚”2”代表低压室。根据以上分析，建立低压室流入方程时必须考虑以下两种情况，

\(\frac{{p}_{2}}{{p}_{1}} \le {\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\)

\(\frac{{p}_{2}}{{p}_{1}} \ge {\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\)

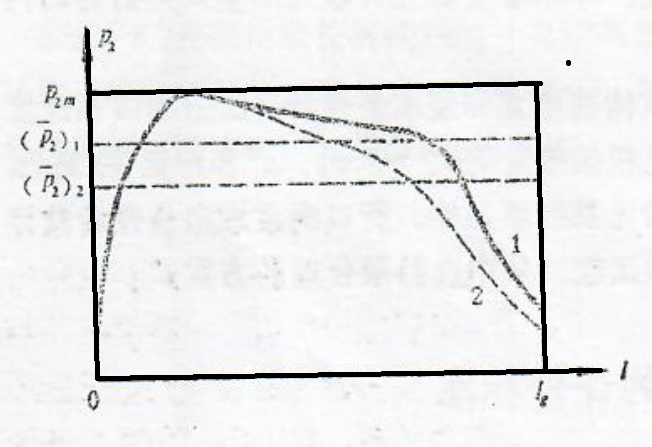
由p₂-t,p₁-t曲线图5-2可知，当t=t_k时，即在高压室的上升段及平衡段，低压室相应的为前期及第一时期，p₂与p₁的关系始终满足\(\frac{{p}_{2}}{{p}_{1}} \le {\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\)的条件；而到t_k~t_g阶段，即高压室的排气段，低压室的第二时期，则又要分为两种情况来考虑：

图5-2压力曲线

第一段：如图中I段，仍能满足\(\frac{{p}_{2}}{{p}_{1}} \le {\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\)的条件；

第二段：如图中Ⅱ段，其p₂与p₁的关系为\(\frac{{p}_{2}}{{p}_{1}} \ge {\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\);

下面分别按各种情况来建立低压室的流入方程。

(1)第一时期(t₀～t_k)这一时期\(\frac{{p}_{2}}{{p}_{1}} \le {\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\),且T₁=χ₁T₀。在这种情况下，高压室喷口喉部的流动状态处于临界状态，它的流量仅与p₁有关，而与p₂无关，这时的流量方程即临界断面的流量方程

\({\dot m}_{1}={C}_{D}{A}_{t1}{p}_{1}\)

\({C}_{D}=\frac{{K}_{0}}{\sqrt{R{T}_{1}}}\)

\({K}_{0}=\sqrt{k}{\left(\frac{2}{k+1}\right)}^{\frac{k+1}{2(k-1)}}\)

式中T₁——高压室燃气温度，T₁=x₁T₀。考虑摩擦损失及热损失后，实用的高压室喷口流量公式应为

\({\dot m}_{1}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}{p}_{1}}{\sqrt{{\chi}_{1}R{T}_{0}}}\)    (5-1)

式中φ₂₁——高压室喷口的流量消耗系数，第二个注脚“1”代表高压室。

上式\({\dot m}_{1}\)为某瞬时t高压室喷孔的秒流量。如果用M₁代表t时间内的总流量，即

\(\frac{{dM}_{1}}{dt}={\dot m}_{1}\)

则上式可写为

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}{p}_{1}}{\sqrt{{\chi}_{1}R{T}_{0}}}\) (5-2)

\({dM}_{1}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}R{T}_{0}}}\int\limits_{0}^{t}{{p}_{1}dt}\)

(2)  第二时期(t_k～t_g)在这一时期\({T}_{1} \ne {\chi}_{1}{T}_{0}\),T₁为变量。

①第I段 因为此时仍保留\(\frac{{p}_{2}}{{p}_{1}} \le {\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\)的条件，只是T₁变为变量了，故流量方程应写为：

\({\dot m}_{1}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}{p}_{1}}{\sqrt{R{T}_{0}}}\)  (5-4)

因为喷管流动符合等熵假设，故有

\(\frac{{T}_{k}}{{T}_{1}}={\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{k}}\)

\({RT}_{1}=\frac{{RT}_{k}}{{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{k}}}\)

故

T=χ₁T₀

代入(5-4)式整理后，得\({\dot m}_{1}\)表达式

\({\dot m}_{1}=\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}{p}_{1}} {\sqrt{R{T}_{k}}}{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{2k}}\)     (5-5)

此式即(5-34)式之不同表达形式。

②第Ⅱ段，\(\frac{{p}_{2}}{{p}_{1}} \le {\left(\frac{2}{k+1}\right)}^{\frac{k}{k-1}}\)此时喷孔喉部已不能维持临界流量，故流量公式应用亚音速流动之\({\dot m}_{1}\)式

\({\dot m}_{1}=\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{A}_{A}{p}_{1}} {\sqrt{R{T}_{k}}}\sqrt{\frac{2k}{k-1} \left[ {\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{2}{k}}-{\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{k+1}{k}}\right] }\)    (5-6)

式中A_A——高压室喷孔出口截面积，如仍将

\({RT}_{1}=\frac{{RT}_{k}}{{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{k}}}\)

代入，整理后得

\({\dot m}_{1}=\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{A}_{A}{p}_{1}} {\sqrt{R{T}_{0}}}\sqrt{\frac{2k}{k-1}{{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{k}}} \left[ {\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{2}{k}}-{\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{k+1}{k}}\right] }\)      (5-7)

\({T}_{k}={\chi}_{1}{T}_{0}\)

1. 流出方程

低压室尾喷管为拉瓦尔喷管，燃气排至大气空间，因此流速为超音速，流量方程为

\({\dot m}_{2}=\frac{{dM}_{2}}{dt}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}{p}_{2}} {\sqrt{R{T}_{2}}}\) (5-8)

式中φ₂₂一低压室喷管流量消耗系数。第二个注脚“2”代表低压室；

T₂一低压室燃气温度。

我们引入符号τ₂代表低压室燃气温度与高压室燃气温度之比，或称低压室相对温度

\({\tau}_{2}=\frac{{T}_{2}}{{T}_{1}}\) (5-9)

(1)第一时期(t₀~t_k)

\({T}_{k}={\chi}_{1}{T}_{0}\)

故

\(\sqrt{{RT}_{2}}=\sqrt{{\chi}_{1}{\tau}_{2}R{T}_{0}}\)

低压室流出方程可写为

\({\dot m}_{2}=\frac{{dM}_{2}}{dt}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}{p}_{2}} {\sqrt{R{T}_{0}{\chi}_{1}{\tau}_{2}}}\)     (5-10)

(2)  第二时期(t_k～t_g)

\({T}_{1}={T}_{k}{\left(\frac{{p}_{1}}{{p}_{k}}\right)}^{\frac{k-1}{k}}\)

故

\({\dot m}_{2}=\frac{{dM}_{2}}{dt}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}{p}_{2}} {\sqrt{R{T}_{k}{\tau}_{2}}}{\left(\frac{{p}_{1}}{{p}_{k}}\right)}^{\frac{k-1}{k}}\)    (5-11)

1. 质量平衡方程

弹射过程中，某瞬时t低压室内所存燃气量N应等于由高压室流入的气体量M₁减去由尾喷管流出的气体量M₂,即

N=M₁-M₂       (5-12)

这就是低压室的质量平衡方程。

1. 状态方程

(1)第一时期 此阶段共同的特点是p₂<p₁。

在发射筒中，由于导弹不断向前运动，低压室容积不断扩大，因而属于变容的情况；又由于有燃气的流入和流出，因而我们只能建立某瞬时t的状态方程。

低压室的燃气状态为高温低压，故可视为理想气体，不考虑余容α的影响。

在导弹起动后某个瞬时，低压室自由容积(火药气体可以自由运动的空间)应为V₂₀+Al。在变容情况下，由于火药气体膨胀作功，使温度不断下降，所以T₂是变量(与定容时情况不同)。故变容下气体状态方程应为：

\({p}_{2}=\frac{NR{T}_{2}}{{V}_{20}+Al}\)

式中N₂-某瞬时低压室中的燃气重量；

A一发射筒横截面积；

l一某瞬时导弹行程。

因

\({T}_{2}={\chi}_{1}{\tau}_{2}{T}_{0}\)

故

\({p}_{2}==\frac{N{\chi}_{1}{\tau}_{2}R{T}_{0}}{{V}_{20}+Al}\)

(2) 第二时期(t_k～t_g)

\({T}_{2}={\tau}_{2}\frac{{T}_{k}}{{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{k}}}\)

故

\({p}_{2}==\frac{N{\chi}_{1}{\tau}_{2}R{T}_{k}}{{V}_{20}+Al}{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{k}}\)

\({T}_{k}={\chi}_{1}{T}_{0}\)

5.导弹运动方程

严格地说，导弹是在弹底压力的作用下向前运动的。上一章在讨论低压室压力分布规律时曾提及，导弹的运动方程除可用某瞬时的弹底压力p₂_d来表示外，也可用某瞬时低压室内的平均压力p₂来表示。只要所取的次要功计算系数与所取的压力相对应，用什么压力来表示运动方程都是可以的

\({Ap}_{2d}={\varphi}_{1}m\frac{dv}{dt}\)

\({Ap}_{2}={\varphi}m\frac{dv}{dt}\)\)

\({\varphi}={\varphi}_{1}+{K}_{4}\)

为了与其它各方程取得一致，采用以瞬时平均压力表示的导弹运动方程

\({Ap}_{2}={\varphi}m\frac{dv}{dt}\)\)

对于倾斜发射(有射角)之情况，等式左面还应增加一项导弹的重力分力，此项力的方向与Ap₂相反。但考虑到一般射角均较小，当射角只在几度的范围内时，此项力可不计算，而用加大φ的办法来考虑。

6.导弹速度方程

\(\frac{dl}{dt}=v\)

1. 能量方程

为了建立低压室能量方程，必须对低压室内各种能量变化情况进行分析。低压室有燃气的流入和流出，属于开口系统。根据热力学第一定律的能量方程式：     

进入系统的能量-离开系统的能量=系统中储存能量的变化    (5-14)

一般说来，对于开口的热力系统，进入系统的能量包括从外界传入的热量、外界对物质流所作的功以及随同物质流带进系统的能量；而离开系统的能量包括向外传出的热量和对外所作的功,以及随同物质流带出系统的能量。

所谓系统，是由固定空间内的工质组成，其边界是包围该空间的表面。

对于低压室来说，我们取低压室内的燃气为研究对象，其边界为包围燃气的表面，亦即低压室壳体及进出口截面，

首先分析进入系统的能量：

①不考虑高压室壁对低压室的热交换，因而认为没有外界热量的传入。

②外界也没有对燃气作功。

③由于高压室燃气的流入，带进低压室的能量为焓H₁。

再分析离开系统的能量：

①认为没有热量向外传出，散热损失用χ₂对高压室流入燃气的温度T₁进行修正的办法予以考虑，即认为流入燃气的温度为χ₂T₁(注意!χ₂T不是低压室燃气温度T₂),χ₂称为低压室散热修正系数，χ₂≈0.9。

②对外所作的功就是推动具有虚拟质量φm的导弹所作之功φmvdv。

③由于燃气经尾喷管的流出，带出系统的能量为焓H₂。

根据(5-14)式可得到低压室能量平衡方程。在dt时间内

\({c}_{p}{\chi}_{2}{T}_{1}{dM}_{1}-({c}_{p}{T}_{2}{dM}_{2}+{\varphi}mvdv)=d[{c}_{v}{T}_{2}({M}_{1}-{M}_{2})]\)   (5-15)

式中C_p-定压比热；c_v-定容比热。

因   \({c}_{v}=\frac{R}{k-1}\)

      \({c}_{p}=\frac{k}{k-1}R\)

故

\(\frac{k}{k-1}R {\chi}_{2}{T}_{1}{dM}_{1}-(\frac{k}{k-1}R {T}_{2}{dM}_{2}+{\varphi}mvdv)=d[\frac{R}{k-1}{T}_{2}({M}_{1}-{M}_{2})]\)     (5-16)

这就是低压室的能量平衡方程。

(1)第一时期(t₀～t_k)

T₁=χ₁T₀

故(5-16)式右边为

\(\frac{1}{{T}_{1}}d[{T}_{2}({M}_{1}-{M}_{2})]=\frac{{T}_{2}}{{T}_{1}}d({M}_{1}-{M}_{2})+({M}_{1}-{M}_{2})d\frac{{T}_{2}}{{T}_{1}}\)

\(={\tau}_{2}d({M}_{1}-{M}_{2})+({M}_{1}-{M}_{2})d{\tau}_{2}\)

故能量方程为

\(({M}_{1}-{M}_{2})d{\tau}_{2}=(k{\chi}_{2}-{\tau}_{2})d{M}_{1}-{\tau}_{2}(k-1)d{M}_{2}-\frac{k-1}{{\chi}_{1}R{T}_{0}}{\varphi}mvdv\)

(2)第二时期(t_k~t_g)

\({T}_{1}\ne {\chi}_{1}{T}_{0}\) (T₁是变量)     (5-16)’

\(\frac{1}{{T}_{1}}d[{T}_{2}({M}_{1}-{M}_{2})] =\frac{{T}_{2}}{{T}_{1}}d({M}_{1}-{M}_{2})+({M}_{1}-{M}_{2})\frac{d{\tau}_{2}}{{T}_{1}}\)

\(={\tau}_{2}d({M}_{1}-{M}_{2})+\frac{{M}_{1}-{M}_{2}}{{T}_{1}}{\tau}_{2}{dT}_{1} +({M}_{1}-{M}_{2}){dT}_{2}\)

故能量方程为

\(({M}_{1}-{M}_{2})d{\tau}_{2}=(k{\chi}_{2}-{\tau}_{2})d{M}_{1}-{\tau}_{2}(k-1)d{M}_{2}-\frac{{M}_{1}-{M}_{2}}{{T}_{1}}{\tau}_{2}{dT}_{1}-\frac{k-1}{{\chi}_{1}R{T}_{1}}{\varphi}mvdv\)     (5-16)’’

式中

\({T}_{1}={T}_{k}{\left(\frac{{p}_{1}}{{p}_{k}}\right)}^{\frac{k-1}{k}}\)

5.3 内弹道解法

前面谈到，由于弹射过程中物理现象的复杂性，我们对于很多现象并没有能完全了解，即便在已了解的基础上抓住主要矛盾，在必要的假设条件下将各种现象综合成内弹道方程组，但在求解的过程中又往往遇到数学上的困难，必须进一步进行某些简化处理而求得近似解。这些压力曲线、速度曲线的近似程度因建立方程组时的假设条件和数学简化程度而异，需要采用修正系数对计算结果进行修正，才能使理论计算结果与实测结果相符合。不同的假设有不同的内弹道方程组，再加上不同的数学处理就有不同的解法和修正方法。因此，只有内弹道实验才是判断各种解法和所取修正系数正确与否的唯一标准。离开了内弹道实验，解法就失去了实际的意义。

内弹道解法可有分析解法和数值解法两种。利用数学解析的方法直接由内弹道方程组解出压力曲线和速度曲线者称为分析解法。所得到的解，称为解析解。通过解析解可以清楚地看到各种因素对压力和速度的影响，但分析解法的计算过程比较复杂，有的方程组甚至无法用分析解法，而必须用数值解法。在电子计算机广泛应用的今天，求解的问题可以不必花很大精力来寻求手解的方法，但为了日常弹道计算实践的需要，某些简化的解法仍不失其实用意义。一般说，如用电子计算机求解，则内弹道方程组可详尽一些，使之能较准确地反映出发射简内的物理过程；如采用手解法，则可将方程组进行较大程度的简化，以获得计算的简便，然后再采用适当的修正系数以修正简化假设所带来的误差，这样才能使简化解法既具有简化的优点，又达到一定准确性的要求。

一、等温解法

1.方程组

(1)低压宝第一时期内弹道方程组

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}R{T}_{0}}}{p}_{1}\)

\(\frac{{dM}_{2}}{dt}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}}{\sqrt{{\chi}_{1}{\tau}_{2}R{T}_{0}}}{p}_{1}\)

\(N={M}_{1}-{M}_{2}\)

\({p}_{2}=\frac{N{\chi}_{1}{\tau}_{2}R{T}_{0}}{{V}_{20}+Al}\)

\({Ap}_{2}={\varphi}m\frac{dv}{dt}\)

\(v=\frac{dl}{dt}\)

\(({M}_{1}-{M}_{2})d{\tau}_{2}=(k{\chi}_{2}-{\tau}_{2})d{M}_{1}-{\tau}_{2}(k-1)d{M}_{2}-\frac{k-1}{{\chi}_{1}R{T}_{0}}{\varphi}mvdv\)        (5-17)

以上方程组共有七个方程八个未知量(M₁,M₂,p₂,t,N,T₂,l,v)。在解方程时，可以其中一个变量作为自变量，其余各变量皆作为它的函数解出。

对这七个方程如用分析解法将会遇到很大困难，因此，必须采用数值解法。除可利用电子计算机求得所须的压力曲线和速度曲线外，再介绍一种便于手解的简化解法——等温解法。

简化解法的中心问题是将低压室相对温度τ₂取平均值，并作为常量处理。为什么τ₂可以当作常量处理呢?我们首先分析变量τ₂随时间的变化规律：

当高压室开始向低压室排气时，低压室壁是冷的，燃气进入低压室后要加热室壁，因此低压室相对温度τ₂起点很低，但此时导弹尚未起动，尾喷管亦未起喷(假设t₀=t_om),因此τ₂很快上升，当低压室压力达到起动压力及起喷压力后，导弹向前运动，尾喷管开始排气。燃气膨胀作功推动导弹向前运动消耗了一部分能量，燃气的流出也带走了一部分能量，通过低压室壁还有一部分热量损失，所有这些因素都使低压室的温度下降，但由于高压室不断有燃气流入低压室进行能量补充，因此低压室温度虽由上升转为下降，但下降得比较缓慢，这种情况一直维持到高压室燃烧结束点t_k为止。当高压室燃烧结束后，低压室燃气流入量迅速降低，低压室的相对温度τ₂也迅速下降，但此时导弹已具有较高的速度，且已运动到接近筒口，因此T₂的下降段很短。由以上分析可知，低压室燃气温度变化规律可分为三个阶段：

①0→t₀(t_₀m):     τ₂急速上升；

②t₀(t_om)→t_k:    τ₂缓慢下降；

③t_k→t_g:        τ₂急速下降。

其中第一阶段和第三阶段时间间隔都很短，第二阶段时间较长，因此可以忽略第一、第三两段时间内τ₂的变化，将τ₂当作常量处理，这样对弹道解的结果不致产生显著的误差。根据经验，可取τ₂≈0.7～0.8

在τ₂当作常量处理时，能量方程就不需要了。方程组由前面6个方程组成，包含7个未知量，减少了τ₂这个变量。

(2)低压室第二时期内弹道方程组

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}{p}_{1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{\left(\frac{{p}_{k}}{{p}{1}}\right)}^{\frac{k-1}{2k}}\)   (第I段)

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{S}_{A}{p}_{1}}{\sqrt{{\chi}_{1}{RT}_{0}}} {\sqrt{\frac{2k}{k-1}{\left(\frac{{p}_{k}}{{p}{1}}\right)}^{\frac{k-1}{2k}}\left[{\left(\frac{{p}_{k}}{{p}{1}}\right)}^{\frac{k-1}{k}}-{\left(\frac{{p}_{2}}{{p}{1}}\right)}^{\frac{k+1}{k}}\right]}}\)    (第Ⅱ段)

\(\frac{{dM}_{2}}{dt}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}{p}_{2}}{\sqrt{{\chi}_{1}{\tau}_{2}{RT}_{0}}}{\left(\frac{{p}_{k}}{{p}{1}}\right)}^{\frac{k-1}{2k}}\)

\({p}_{2}=\frac{({M}_{1}-{M}_{2}){\chi}_{1}{\tau}_{2}{RT}_{0}}{{V}_{20}+Al}{\left(\frac{{p}_{1}}{{p}{k}}\right)}^{\frac{k-1}{k}}\)

\(\frac{dl}{dt}=v\)

\(({M}_{1}-{M}_{2})d{\tau}_{2}=(k{\chi}_{2}-{\tau}_{2}){dM}_{1}-{\tau}_{2}(k-1){dM}_{2}-\frac{{\tau}_{2}({M}_{1}-{M}_{2})}{{T}_{1}}{dT}_{1}-\frac{k-1}{{RT}_{1}}{\varphi}mvdv\)

\({T}_{1}={T}_{k}{\left(\frac{{p}_{1}}{{p}{k}}\right)}^{\frac{k-1}{k}}\)

2. 等温解法

现在说明简化解法的计算方法和步骤。以t₀=t_om的情况为研究对象。

(1)前期 对前期的计算只需算出前期结束瞬间t=t₀各诸元的值，这些数值便是解第一时期方程系的初始条件。

由于前期的结束瞬间t₀就是第一时期的起点，故对于t=t₀瞬间，第一时期的内弹道方程组也是适用的，但需结合前期的特定条件。当t₀=t_om时，特定条件为：l=0,v=0,M₂=0。故前期的内弹道方程组为；

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}{p}_{1}}{\sqrt{{\chi}_{1}{RT}_{0}}}\)

\({p}_{2}=\frac{{M}_{1}{\chi}_{1}{\tau}_{2}{RT}_{0}}{{V}_{20}}\)

对前期结束瞬间(t=t₀时),其相应的值为：

\({p}_{2}={p}_{20}=\frac{{M}_{10}{\chi}_{1}{\tau}_{2}{RT}_{0}}{{V}_{20}}\)   (5-18)

\({M}_{1}={M}_{10}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}{p}_{1}}{\sqrt{{\chi}_{1}{RT}_{0}}}\int\limits_{0}^{{t}_{0}}{{p}_{1}dt}\)    (5-18)’

式中待确定的三个量为M₁₀,p₂₀,t₀。其中p₂₀,M₁₀分别为前期结束瞬间(t=t₀)时的低压室压力及燃气总流入量。

前期结束瞬间，低压室压力达到起动压力，即t=t₀(=t_om)时，p₂₀=p₀(=p_om)。p_o是取定的，故为已知量，将之代入状态方程(5-18)式即可求出该瞬间高压室燃气流出量M₁₀(即低压室的燃气流入量),

\({M}_{10}=\frac{{p}_{0}{V}_{20}}{{\chi}_{1}{\tau}_{2}{RT}_{0}}\)

代入燃气流入方程(4-18)’后得

\(\int\limits_{0}^{{t}_{0}}{{p}_{1}dt}=\frac{{M}_{10}\sqrt{{\chi}_{1}{RT}_{0}}}{{\varphi}_{21}{K}_{0}{A}_{t1}}=\frac{{p}_{0}{V}_{20}}{{\varphi}_{21}{K}_{0}{A}_{t1}{\tau}_{2}\sqrt{{\chi}_{1}{RT}_{0}}}\)

积分\(\int\limits_{0}^{{t}_{0}}{{p}_{1}dt}\)

代表高压室压力曲线中t=0~t₀时的p₁~t曲线下的面积，此时高压室压力曲线正处于上升段，可以近似地认为p₁随t呈直线变化(图5-3),所以有：

\(\int\limits_{0}^{{t}_{0}}{{p}_{1}dt}=\frac{{p}_{ig}+{p}_{10}}{2}{t}_{0}\)

高压室p₁-t是已知的，面积\(\int\limits_{0}^{{t}_{0}}{{p}_{1}dt}\)的大小也是已知的，故必可在p₁-t上找到一点A,OA段所对应的曲线下面积正好等于已知的\(\int\limits_{0}^{{t}_{0}}{{p}_{1}dt}\)值。A点的坐标(t₀,p₁₀)就是前期结束瞬间的时间及高压室压力值。至此，前期结束瞬间各诸元都已求得：

t=t₀,p₁=p₁₀,p₂=p₀(=_pom),\({M}_{10}=\frac{{p}_{0}{V}_{20}}{{\chi}_{1}{\tau}_{2}{RT}_{0}},{M}_{20}=0,v=0,l=0\)

图4-3

(2) 第一时期 前面导出的内弹道方程组(5-17)式就是第一时期的方程组。我们可以将质量平衡方程与状态方程合并而将变量N缩减掉，同时由于τ₂取为常量，故能量方程不需研究，这样，方程组就变为五个方程，六个变量：

\(\frac{{dM}_{1}}{dt}={\dot M}_{1}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}{p}_{1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}\)  

\(\frac{{dM}_{2}}{dt}={\dot M}_{2}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}{p}_{2}}{\sqrt{{\chi}_{1}{\tau}_{2}{RT}_{0}}}{{p}_{2}}\)

\({p}_{2}=\frac{({M}_{1}-{M}_{2}){\chi}_{1}{\tau}_{2}{RT}_{0}}{{V}_{20}+Al}{\left(\frac{{p}_{1}}{{p}{k}}\right)}^{\frac{k-1}{k}}\)

\(\frac{dv}{dt}={\dot v}=\frac{{Ap}_{2}}{{\varphi}m}=\frac{{Ap}_{2}g}{{\varphi}{m}_{m}}\)

\(\frac{dl}{dt}={\dot l}=v\)

\({p}_{2}=\frac{{\chi}_{1}{\tau}_{2}{RT}_{0}({M}_{1}-{M}_{2})}{{V}_{20}+Al}\)                (4-19)

六个变量是：t,p₂,M₁,M₂,v,l。这样的方程组就可利用欧拉法(见本章附录)来求数值解了。

取n及n+1两相邻点的t区间△t,△t称为步长

△t=t_n+1-t_n

整个方法分两个步骤进行，第一步按照欧拉公式由n点的各变量值求n+1点的各变量值，称为n+1点各变量的预测值。按欧拉折线法有：

\({{M}_{1}}_{(n+1)}^{(0)} ={M}_{1(n)}+{\dot M}_{1(n)}{\Delta}t\)

\({{M}_{2}}_{(n+1)}^{(0)} ={M}_{2(n)}+{\dot M}_{2(n)}{\Delta}t\)

\({v}_{(n+1)}^{(0)} ={v}_{n}+{\dot v}_{n}{\Delta}t\)

\({l}_{(n+1)}^{(0)} ={l}_{n}+{\dot l}_{n}{\Delta}t\)

由于初始条件M_1(n),N_2(n),v_n,1_n是已知的，由内弹道方程组(4-19)式可求得它们的微商\({\dot M}_{1(n)}, {\dot M}_{2(n)}, {\dot v}_{n}, {\dot l}_{n}\)这样就可分别求出M_1(n+1),M_2(n+1),v_(n+1),l_(n+1)的预测值，再将它们代入状态方程:

\({p}_{2(n+1)}^{(0)}=\frac{{\chi}_{1}{\tau}_{2}{RT}_{0}\left({M}_{1(n+1)}^{(0)}-{M}_{2(n+1)}^{(0)}\right)}{{V}_{20}+A{l}_{n+1}^{0}}\)

而求得n+1点p₂的预测值\({p}_{2(n+1)}^{(0)}\)。所有各变量的预测值均求得以后，第二步就是按改进的欧拉方法算出M₁_(n+1),M₂_(n+1),V_n+1,l_n+1的校正值，代入状态方程后就可求得p₂_(n+1)的校正值。逐点求下去，就得到所需要的数值解。

按照改进的欧拉公式，有

\({M}_{1(n+1)}^{(k)}=M_{1(n)}+({\dot M}_{1(n)}+{\dot M}_{1(n+1)}^{(k-1)})\frac{\Delta t}{2}\)

\({M}_{2(n+1)}^{(k)}=M_{2(n)}+({\dot M}_{2(n)}+{\dot M}_{2(n+1)}^{(k-1)})\frac{\Delta t}{2}\)

\({v}_{(n+1)}^{(k)}=v_{(n)}+({\dot v}_{(n)}+{\dot v}_{(n+1)}^{(k-1)})\frac{\Delta t}{2}\)

\({l}_{(n+1)}^{(k)}=l_{(n)}+({\dot l}_{(n)}+{\dot l}_{(n+1)}^{(k-1)})\frac{\Delta t}{2}\)

式中 \({\dot M}_{1(n+1)},{\dot M}_{2(n+1)},{\dot v}_{(n+1)},{\dot l}_{(n+1)}\)是将M₁_(n+1),M₂_(n+1),p₂_(n+1),l_n+1的预测值代入方

程组(4-19)式而求得。利用改进的欧拉公式所求得之M₁_(n+1),M₂_(n+1),v_n+1,l_n+1就是校正值，再将它们代入状态方程得到p₂_(n+1)的校正值，对于校正值如不再进行迭代，就可进行下一点的计算。对于每一区间重复同样的计算过程，从起始点t=t₀(=t_om)一直计算到燃烧结束点t_k为止，第一时期的数值解便得到了。

 (3)第二时期 这一时期的微分方程组已如前所述，计算方法同第一时期，即仍采用欧拉数值法一直计算到离筒瞬间t_g为止。

t_g之确定：离筒瞬间的导弹行程长l_g是已知的(弹道设计时确定),当用数值法计算到l=l_g时，对应的t即t_g,离筒瞬间其余各弹道诸元亦随之而得，共包括t_g,p₂_g,v_g,l_g四项。

 (4)几点说明

①当求得整个第一时期的数值解后，还要确定出最大压力点的正确位置。我们知道，最大压力点的条件是\(\frac{d{p}_{2}}{dt}=0\)在这一点的两边\(\frac{d{p}_{2}}{dt}\)有正、负号的变化，因此可以在数值解值计算中根据最近最大压力相邻区间的\(\frac{d{p}_{2}}{dt}\)值计算，再插值求出最大压力点（t_m,p_2m）的正确位置。

②在整个从t=t₀(=t_om)到t=t_g的区间里，究竟取多大的步长Δt才是合适的呢?步长的选取应该考虑截断误差和舍入误差的综合影响，从实际情况出发，作全面的考虑。由于低压室压力曲线在最大压力点以前上升比较迅速，到达最大压力点以后，曲线开始缓慢下降；而到达高压室燃烧结束点后，低压室压力曲线的下降也比较迅速，因此，在t=0～t_m以及t=t_k～t_g期间，步长应适当取小些；而在t=t_m～t_k期间，步长可适当取大些。一般说，总的计算点数取到30～40点就可认为达到手解法准确度的要求。

③当用手算法进行计算时，准确度一般要求不高。如用改进的欧拉公式进行一次迭代就可够用时，则可按下面的格式编表计算：

n    0,1,2,…

t_n     t₀

p_1n    p₁₀

p_2n    p₀

M_1n    M₁₀

\({\dot M}_{1n}\)

M_1(n+1)

M_2n

\({\dot M}_{2n}\)

M_2(n+1)

\({\dot v}_{n}\)  0

\({ v}_{n}\)

\({ v}_{n+1}\)

\({\dot l}_{n}\)  0

\({l}_{n}\)

\({l}_{n+1}\)

P_2(n+1)

\({\dot M}_{1(n+1)}\)

\({ M}_{1(n+1)}^{(1)}\)

\({\dot M}_{2(n+1)}\)

\({v}_{(n+1)}^{(1)}\)

\({\dot v}_{(n+1)}\)

\({\dot l}_{(n+1)}\)

\({l}_{(n+1)}^{(1)}\)

\({p}_{2(n+1)}^{(1)}\)

最后，绘制p₂-t,v-t,p₂-1,v-l曲线。

④误差修正

任何解法都是在一系列假设基础上建立起来的，不同的假设将带来不同的误差，因而也就有不同的修正方法。在解决了弹道解法之后，应根据解法的特点来讨论误差的修正问题。

本解法中，假设低压室的温度是不变的，反映在低压室流出方程中，τ₂作为常量处理。τ₂的大小是根据经验选取的，因此τ₂本身就具有修正系数的性质，可以调整其大小，以使p-t的计算结果与实测结果相符。

用次要功系数φ进行修正也是一种重要的修正方法。在弹道方程中φ虽具有一定的物理意义，但是在实际应用中，将它当作符合系数来处理又常常比其它修正方法来得方便。修正φ的最显著特点是它对最大压力和初速具有相反的弹道效应，即最大压力随φ的增加而增加，初速则随φ的增加而下降。一般为了达到初速的符合，常用φ来进行修正，其大小在理论值附近不大的范围内取适当的值。

上面谈到的是根据假设可以估计到的误差修正，除这些误差外，还可能出现一些其它误差，如由于多次弹射，低压室尾喷管因燃气烧蚀而使喉部面积扩大所产生的误差等，就是在进行弹道解时无法考虑的误差。

只要合理而正确地进行常量的选取，即使是简化的解法也可以得出大致与实际相符合的结果。

二、非等温解法

如果τ₂不作常量处理，仍看作是变量，则解法称为非等温解法。非等温解法的方程组中需加入能量方程，且低压室燃气温度直接用T₂表示，不需引入相对温度τ₂,这样，增加了一个变量T₂,也增加了一个方程，仍可用数值解法获得弹道解。

1. 内弹道方程组

(1)前期 在这一时期M₂,v,l均为0,故有

\({\dot m}_{1}=\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}\)

\({p}_{2}=\frac{{M}_{1}{RT}_{2}}{{V}_{20}}\)

\(\frac{{dT}_{2}}{dt}=\frac{(k{\chi}_{1}{\chi}_{2}{T}_{0}-{T}_{2})}{{M}_{1}}\frac{{M}_{1}}{dt}\)

(2)第一时期

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}\)

\(\frac{{dM}_{2}}{dt}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}}{\sqrt{{RT}_{2}}}{p}_{2}\)

\({p}_{2}=\frac{({M}_{1}-{M}_{2}){RT}_{2}}{{V}_{20}+Al}\)

\(\frac{dv}{dt}=\frac{A{p}_{2}g}{\varphi {m}_{m}}\)

\(\frac{dl}{dt}=v\)

\(({M}_{1}-{M}_{2})\frac{{dT}_{2}}{dt}=(k{\chi}_{1}{\chi}_{2}{T}_{0}-{T}_{2})\frac{{dM}_{1}}{dt}-{T}_{2}(k-1)\frac{{dM}_{2}}{dt}-\frac{k-1}{R}{\varphi}\frac{{m}_{m}}{g}v\frac{dv}{dt}\)

(3)第二时期

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{2k}}\)   (第I阶段)

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{A}_{A}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}\sqrt{\frac{2k}{k-1}{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{k}}\left[{\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{2}{k}}-{\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{k+1}{k}}\right]}\)   (第II阶段)

\(\frac{{dM}_{2}}{dt}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}}{\sqrt{{\chi}_{1}{RT}_{0}{\tau}_{2}}}{p}_{2}{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{2k}}\)

\({p}_{2}=\frac{({M}_{1}-{M}_{2}){RT}_{2}}{{V}_{20}+Al}\)

\(A{p}_{2}={\varphi}m\frac{dv}{dt}\)

\(\frac{dl}{dt}=v\)

\(({M}_{1}-{M}_{2})\frac{{dT}_{2}}{dt}=(k{\chi}_{2}{T}_{1}-{T}_{2})\frac{{dM}_{1}}{dt}-{T}_{2}(k-1)\frac{{dM}_{2}}{dt}-\frac{k-1}{R}{\varphi}mv\frac{dv}{dt}\)

\({T}_{1}={T}_{k}{\left(\frac{{p}_{1}}{{p}_{k}}\right)}^{\frac{k-1}{k}}\)

2. 内弹道解法

为了解以上微分方程组，只能采用数值解法。从实用、精确度以及便于上计算机考虑，用四阶龙格-库塔法较好。关于龙格-库塔法的数学原理，在此不作介绍，仅把解题的公式写出，以便直接应用。

如给定微分方程组

\({\dot y}=f(x,y,z)\)

\({\dot z}={\varphi}(x,y,x)\)

和一初始条件

y(x₀)=y₀

x(x₀)=x₀

用龙格-库塔法求解时，公式如下：

y_n+1=y_n+(K₁+2K₂+2K₃+K₄)/6

z_n+1=z_n+(l₁+2l₂+2l₃+l₄)/6

式中

K₁=hf(x_n,y_n,z_n)

\({K}_{2}=hf({x}_{n}+\frac{h}{2},{y}_{n}+\frac{{K}_{1}}{2},{z}_{n}+\frac{{l}_{1}}{2})\)

\({K}_{3}=hf({x}_{n}+\frac{h}{2},{y}_{n}+\frac{{K}_{2}}{2},{z}_{n}+\frac{{l}_{2}}{2})\)

\({K}_{4}=hf({x}_{n}+h,{y}_{n}+{K}_{3},{z}_{n}+{l}_{3})\)

l₁=hφ(x_n,y_n,z_n)

\({l}_{2}=h{\varphi} ({x}_{n}+\frac{h}{2},{y}_{n}+\frac{{K}_{1}}{2},{z}_{n}+\frac{{l}_{1}}{2})\)

\({l}_{3}=h{\varphi} ({x}_{n}+\frac{h}{2},{y}_{n}+\frac{{K}_{2}}{2},{z}_{n}+\frac{{l}_{2}}{2})\)

\({l}_{4}=h{\varphi} ({x}_{n}+h,{y}_{n}+{K}_{3},{z}_{n}+{l}_{3})\)

按以上公式，将时间取步长为h,则可以从t₀时的M₁,M₂,v,l,T₂,p₂值计算出下一点各量的值。再重复上述过程又可得出再下一点的各值。重复下去，一直计算到各时期完了。

5.4其它形式弹射器的低压室内弹道问题

5.4.1、串联无后坐式弹射器的低压室内弹道方程

串联无后坐式高低压室依次排列，串联在一起，如图5-4所示，其弹道特点为低压推弹高压后喷，低压室只有燃气的流入及导弹的运动两个物理过程。而没有燃气流出的过程。

设：A_t2——尾喷喉面积(高压室后喷管喉部面积);

A_t1——高压室前喷孔喉部面积。

1.流入方程

(1)第一时期(t₀～t_k)

有\(\frac{{p}_{2}}{{p}_{1}}\le{\left(\frac{2}{k+1}\right)}^{k/(k-1)}\)

且\({T}_{1}={\chi}_{1}{T}_{0}\)故

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}\)

\({K}_{0}=\sqrt{k}{\left(\frac{2}{k+1}\right)}^{\frac{k+1}{2(k-1)}}\)

图5-4串联无后坐式弹射器原理图

1一导弹；2一低压室；3一高压室前喷孔：4一高压室：5-尾喷喉。

(2)第二时期(t_k～t_g)

\({T}_{1}\ne{\chi}_{1}{T}_{0}\),T₁为变量。

①第I段(见图4-2)此时仍保留\(\frac{{p}_{2}}{{p}_{1}}\le{\left(\frac{2}{k+1}\right)}^{k/(k-1)}\)的条件，只是T.变为变量了，故流入方程应写为：

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{2k}}\)

②第Ⅱ段\(\frac{{p}_{2}}{{p}_{1}}\ge{\left(\frac{2}{k+1}\right)}^{k/(k-1)}\)此时高压室前喷孔喉部已不能维持临界流量，故流量公式应用亚音速流动之\(\dot m\)式：

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{A}_{A}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}\sqrt{\frac{2k}{k-1}{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{k}}\left[{\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{2}{k}}-{\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{k+1}{k}}\right]}\) 

式中A_A——高压室前喷孔出口截面积。因串联式弹射器高压室前喷孔一般为直喷孔，故A_A=A_t1

2.流出方程

串联式低压室无尾喷管，故流出为0,即

\(\frac{{dM}_{2}}{dt}=0\)

3.质量平衡方程

某瞬时低压室燃气的质量N就是高压室的流入量，故N=M₁;

4.状态方程

对第一时期及第二时期之I,Ⅱ段，其特点为p₂<p₁,故状态方程为

\({p}_{2}=\frac{{NRT}_{2}}{{V}_{20}+Al}\)

5.导弹运动方程

\(A{p}_{2}=\frac{\varphi {m}_{m}}{g}\frac{dv}{dt}\)

\(\frac{dv}{dt}=\frac{A{p}_{2}g}{\varphi {m}_{m}}\)

6.导弹速度方程

\(\frac{dl}{dt}=v\)

7:能量方程

串联无后坐式低压室的特点是M₂=0,故其能量方程应为

\({c}_{p}{T}_{1}{\chi}_{2}{dM}_{1}-{\varphi}mvdv=d({c}_{v}{T}_{2}{M}_{1})\)

上式左方第一项为dt时间内由高压室流入燃气带进来的能量，第二项为dt时间内推动导弹作功消耗的能量，等式右方为低压室内燃气储存能量的变化量。

上式亦可由并联式能量方程求得，只需将Y₂=0代入并联式低压室能量方程即可得与上式相同的结果

\({c}_{p}{T}_{1}{\chi}_{2}{dM}_{1}-{\varphi}mvdv={c}_{v}{T}_{2}{dM}_{1}+{c}_{v}{M}_{1}{dT}_{2}\)

因

\({c}_{p}=\frac{kR}{k-1},{c}_{v}=\frac{R}{k-1}\)

故

\(\frac{kR}{k-1}{T}_{1}{\chi}_{2}{dM}_{1}-{\varphi}mvdv=\frac{R}{k-1}{T}_{2}{dM}_{1}+\frac{R}{k-1}{M}_{1}{dT}_{2}\)

\({M}_{1}{dT}_{2}=(k{\chi}_{2}{T}_{1}-{T}_{2}){dM}_{1}-\frac{k-1}{R}{\varphi}mvdv\)

对第一时期，有\({T}_{1}={\chi}_{1}{T}_{0}\);

对第二时期，有\({T}_{1}={T}_{k}{\left(\frac{{p}_{1}}{{p}_{k}}\right)}^{\frac{k-1}{k}},{T}_{k}={\chi}_{1}{T}_{0}\);。

5.4.2、自弹式弹射器低压室内弹道方程

自弹式弹射器将高压室分为运动高压室与固定高压室，后者亦可称反后坐高压室。运动高压室具有轴向喷管，并随弹一起运动，固定高压室则与发射筒后端连接在一起，起反后坐作用。发射筒后端部为封闭的，隔板既是发射筒的底板又是反后坐高压室的前端盖，故其弹道特点亦为高压后喷、低压推弹。其原理如图5-5所示。

图5-5自弹式弹射器原理图

1一导弹；2一运动高压室；3一低压室；4—隔板；E-反后坐高压室；6一尾喷喉。

设：  A_t1为运动高压室喷喉截面积；A_t2为尾喷管喉部截面积。自弹式弹射器的低压室内弹道方程组如下：

1.流入方程

(1)第一时前(t₀~t_k)此时期有\(\frac{{p}_{2}}{{p}_{1}}\le{\left(\frac{2}{k+1}\right)}^{k/(k-1)}\),且\({T}_{1}={\chi}_{1}{T}_{0}\),故流入方程为

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}\)

\({K}_{0}=\sqrt{k}{\left(\frac{2}{k+1}\right)}^{\frac{k+1}{2(k-1)}}\)

(2)第二时期(t_k～t_g)

\({T}_{1}\ne{\chi}_{1}{T}_{0}\),T₁为变量。

①第I段(见图4-2)此时仍保留\(\frac{{p}_{2}}{{p}_{1}}\le{\left(\frac{2}{k+1}\right)}^{k/(k-1)}\)的条件，只是T.变为变量了，故流入方程应写为：

\(\frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{2k}}\)

②第Ⅱ段\(\frac{{p}_{2}}{{p}_{1}}\ge{\left(\frac{2}{k+1}\right)}^{k/(k-1)}\)此时高压室前喷孔喉部已不能维持临界流量，故流量公式应用亚音速流动之\(\dot m\)式：

\(\dot m = \frac{{dM}_{1}}{dt}=\frac{{\varphi}_{21}{A}_{A}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}\sqrt{\frac{2k}{k-1}{\left(\frac{{p}_{k}}{{p}_{1}}\right)}^{\frac{k-1}{k}}\left[{\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{2}{k}}-{\left(\frac{{p}_{2}}{{p}_{1}}\right)}^{\frac{k+1}{k}}\right]}\) 

式中A_A——运动高压室前喷孔出口截面积。A_A=ε_AA_t1，ε_A-运动高压室面积膨胀比。

2.流出方程

串联式低压室无尾喷管，故流出为0,即

\(\frac{{dM}_{2}}{dt}=0\)

3.质量平衡方程

某瞬时低压室燃气的质量N就是高压室的流入量，故N=M₁;

4.状态方程

对第一时期及第二时期之I,Ⅱ段，其特点为p₂<p₁,故状态方程为

\({p}_{2}=\frac{{NRT}_{2}}{{V}_{20}+Al}\)

5.导弹运动方程

由于高压室是具有轴向喷管的运动高压室，故使导弹运动的发射动力除弹射力外，还包括运动高压室喷管提供的轴向自推力。

设：F₁为弹射力，F₁=(A-ε_AA_t1)p₂;

F₂为自推力，F₂=C_F₁A_t1p₁;

A为发射筒截面积；C_F为运动高压室喷管之推力系数。

总发射动力F=F₁+F₂,故导弹运动方程为；

\({C}_{F1}{A}_{t1}{p}_{1}+(A-{\varepsilon}_{}{A}_{t1}){p}_{2}=\frac{\varphi q}{g}\frac{dv}{dt}\)

\(\frac{dv}{dt}=\frac{[{C}_{F1}{A}_{t1}{p}_{1}+(A-{\varepsilon}_{}{A}_{t1}){p}_{2}]g}{{\varphi}{m}_{m}}\)

需要指出的是，由于运动高压室的燃气不是喷向大气空间，而是喷向有反压p₂的低压室，故当使用F₂=C_F₂A_t1p₁时有一前提条件，即低压室压力p₂的选择应小于等于运动高压室喷管的第二临界压力，即保证冲波不致进入到喷管中去，这样喷管的推力才不致受外界反压(即低压室压力p₂)的影响而变小。

6.导弹速度方程

\(\frac{dl}{dt}=v\)

7:能量方程

自弹式弹射器低压室没有流出，故M₂=0,故其能量方程应为：

\({c}_{p}{T}_{1}{\chi}_{2}{dM}_{1}-{\varphi}mvdv=d({c}_{v}{T}_{2}{M}_{1})\)

上式左方第一项为dt时间内由运动高压室流入燃气带进来的能量，第二项为dt时间内推动导弹作功消耗的能量，等式右方为低压室内燃气储存能量的变化量。

上式与串联式能量方程相同，只需将Y₂=0代入并联式低压室能量方程即可得与上式相同的结果

\({c}_{p}{T}_{1}{\chi}_{2}{dM}_{1}-{\varphi}mvdv={c}_{v}{T}_{2}{dM}_{1}+{c}_{v}{M}_{1}{dT}_{2}\)

因

\({c}_{p}=\frac{kR}{k-1},{c}_{v}=\frac{R}{k-1}\)

故

\({M}_{1}{dT}_{2}=(k{\chi}_{2}{T}_{1}-{T}_{2}){dM}_{1}-\frac{k-1}{R}{\varphi}mvdv\)

对第一时期，有\({T}_{1}={\chi}_{1}{T}_{0}\);

对第二时期，有\({T}_{1}={T}_{k}{\left(\frac{{p}_{1}}{{p}_{k}}\right)}^{\frac{k-1}{k}},{T}_{k}={\chi}_{1}{T}_{0}\);。

5.4.3、燃气蒸汽式弹射器低压室内弹道方程

工作原理

与前述几种弹射器不同，燃气蒸汽式弹射器低压室中作功的工质不是单一的燃气，而是燃气与蒸汽的混合工质，如图5-6所示。

燃气由高压室1的拉瓦尔喷管喷出后，由分流圆筒分成两路流动：一路由立管上部的第二喷管进入立管内腔并给管中水面加压，当压力达预定值后，隔膜6破裂，立管中之水泻入弯管，高温燃气随后也不断经立管喷进弯管，使水汽化。燃气的高速流动使立管喷水孔处形成低压区；与此同时，水室上部空间的另一路燃气经过分流圆简所形成的通道给水室水面加压，因此在立管喷水孔的两面(即立管内、外壁处)产生压差，立管外壁处为高压，内壁处为低压，立管外面的水便自动喷进立管，遇高速流动的高温燃气后汽化成水蒸汽，并与降低了温度的燃气一起混合成所需要的燃气蒸汽，经弯管输送到低压室，将导弹弹射出筒。

图5-6燃气蒸汽式弹射器原理图

1一高压室；2一高压室喷管；3一分流圆筒；4一第二喷管；5—喷口膜片；6—隔膜；7一弯管；8一低压室；9一发射简；10—适配器；11一导弹；12一立管喷水孔；13—立管；14一水室。

2.基本假设

①水室中的水经立管喷水孔射入立管后在弯管中完成加热、汽化、过热三个过程，进入发射筒时是燃气与过热蒸汽的混合工质。

②高压室流出之燃气大部分经立管进入发射筒膨胀作功，只有少量燃气经分流圆筒进

入水室上部空间，故可忽略进入水室空间的燃气量，认为所有燃气均流入立管。

③用温度修正系数χ₂对进入发射筒的混合工质温度Te’进行修正，目的是考虑：水室上部空间的燃气带走的一部分热能；弯管内燃气的摩擦损失；燃气进入发射筒后产生的气流旋涡；适配器漏气；弯管及发射筒的散热所造成的能量损失。χ₂的经验数据约为0.6左右。

④设水药比为η(η=冷却水质量/火药质量),当高压室燃气排空时，水室的水也全部喷射完毕。

3.低压室第一时期内弹道方程组

(1)流入方程

由图4-6知，弯管的出口截面e′-e’即低压室的入口截面，故低压室的流入方程即弯管出口截面e’-e’的流出方程。由e’-e’截面流出的是燃气与蒸汽的混合工质，根据假设④,它们的秒流量有以下关系：

\({\dot m}_{l} ={\eta}{\dot m}_{r}\):

式中\({\dot m}_{l}\)——水蒸汽的秒流量；

\({\dot m}_{r}\)——燃气的秒流量，

\({\dot m}_{r}= \frac{{dM}_{r}}{dt}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{p}_{1}\)

(2)状态方程

低压室的状态方程为燃气、蒸汽及空气的混合气体的状态方程，故

\({p}_{2}=\frac{{M}_{r}{R}_{r}+{M}_{l}{R}_{l}+{M}_{k}{R}_{k}}{{V}_{20}+Al}{T}_{2}\)

式中M_r,M_l——分别为0～t时间间隔内燃气、蒸汽的总流入量；

M_k——发射筒中原有的空气质量；R_r,R_l,R_k——分别为燃气、蒸汽及空气的气体常数。

(3)运动方程

\(A{p}_{2}-{R}_{0}=\frac{{\varphi}{m}_{m}}{g}\frac{dv}{dt}\)

式中R₀——阻力，包含导弹重力分力及摩擦阻力。

(4)速度方程

\(\frac{dl}{dt}=v\)

(5)能量方程

燃气蒸汽式弹射器无流出，故在dt时间内，其能量方程应为，

\(\frac{{k}_{r}{R}_{r}}{{k}_{r}-1}{\chi}_{2}{T}_{e}^{‘}{dM}_{r}+\frac{{k}_{l}{R}_{l}}{{k}_{l}-1}{\chi}_{2}{T}_{e}^{‘}{dM}_{l}-mvdv-{R}_{0}dl\)

\(=d\left(\frac{{R}_{r}}{{k}_{r}-1}{T}_{2}{M}_{r}+\frac{{R}_{l}}{{k}_{l}-1}{T}_{2}{M}_{l}+\frac{{R}_{k}}{{k}_{k}-1}{T}_{2}{M}_{k}\right)\)

式中  T_e‘——发射简入口截面e’-e’处的混合工质温度；

T₂——发射简内(即低压室内)混合工质的温度。

上式左方第一项为dt时间内由弯管流入燃气带进来的能量，第二项为流入蒸汽带进来的能量，第三项为导弹运动消耗的能量，第四项为摩擦阻力作功消耗的能量；等式右方为发射筒中内能的变化，

k_r:,k_l,k_k——分别为燃气、过热水蒸汽及空气的绝热指数。

附录 欧拉方法简介

常微分方程初值问题的数值解法有多种，欧拉法是其中基本的且较简单的一种。设有一阶微分方程

\(\dot y=f(x,y)\)                                (1)

其中函数f(x,y)在xy平面上的某域D上确定、连续(图5-7),且有对y的偏导数。又设

If_x(x,y)|≤M, lf_y(x,y)l≤K,  (x,y)∈D                 (2)

式中M,K均为常数。

现在要求出(1)式在D内通过给定点(x₀,y₀)的解，也就是求在D内满足下列两个条件的连续且有连续导函数的一个函数y(x)

\(\frac{d}{dx}y(x)=f[x,y(x)]\)

\(y({x}_{0})={y}_{0}\)                           (3)

条件(2)可以保证满足(3)式的解存在且唯一，这个条件称为李布其希条件。

所谓满足(3)式的数值解法就是求在一串点x₀,x₁…,x上函数y(x)的近似值y₀,

图5-7

y₁,…,y_n,用以代替精确值y(x₀),y(x₁),…,y(x_n)。

称△x_n=x_n+1-x_n,为求解的步长，通常用h(>0)表示。

(3)式也可写成积分方程的形式

\(y(x)=y({x}_{0})+\int\limits_{{x}_{0}}^{x}{\dot y}{dx}\)            (4)

或写成更一般的公式

\(y({x}_{n+1})=y({x}_{n})+\int\limits_{{x}_{n}}^{{x}_{n+1}}{\dot y}{dx}\)           (5)

数值解法的公式通常是以(4)式为基础计算得到的，用各种不同的近似计算来求(4)式中之积分，便得到不同的解法。

欧拉折线法(5)式中积分的几何意义是导函数y-x图形中由x_n到x_n+1区间曲线下的面积，欧拉法就是用矩形面积\(h{\dot y}_{n}\)来代替此面积。或者说，是用矩形积分公式求(5)式中之积分项。

在D内取足够小的步长及等距离点

x_n=x₀+nh            (n=0,1,2,…)

将矩形公式

\(\int\limits_{{x}_{n}}^{{x}_{n+1}}{\dot y}{dx}\approx h{\dot y}_{n}\)

代入(5)式，则

\({y}_{n+1}={y}_{n}+h{\dot y}^{n}\)                   (6)

由初始条件知y_n(即y_n=y₀),h的大小是可取的，\({\dot y}_{n}=f({x}_{n},{y}_{n})\),将y_n,x_n值代入待解之微分方程\({\dot y}=f({x},{y})\)即得\({\dot y}_{n}\),于是y_n+1可求。这样求出的y _n+1值是近似值，按同样方法逐点求下去，可求得y_n+2,y_n+3,…,于是得到D域中的一个点列(x_n,y_n),(n=0,1,…)。连结这些点便得到一条通过(x₀,y₀)点的折线，称为欧拉折线，这便是所要求的欧拉方法数值解。

由泰勒级数

\({y}_{n+1}={y}_{n}+h{\dot y}_{n}+\frac{{h}^{2}}{2!}{\ddot {y}}_{n}+…={y}_{n}+h{\dot y}_{n}+O({h}^{2})\)

可以看出欧拉方法的截断误差大致与h²成正比。截断误差就是纯粹由于舍去了某些项而引起的误差，它与所取的近似公式有关，而与计算工具无关，如欧拉法的截断误差就是由于舍去了二阶及二阶以上的项所引起的。

除此而外，还有一种误差称为舍入误差，它是由计算过程中四舍五入引起的，如计算机的字长是有限的，字长范围以外的有效数字就被舍去。

改进的欧拉法 误差来源不外乎上述两种，为了减少截断误差就应缩小步长h,但步长缩小了，在相同区间里计算的步数n就加多，从而引起含入误差的积累增大。因此考虑还是方从法上改善，得出了改进的欧拉法，使误差尽可能小，以提高数值解法的精度。

在数值积分中梯形法比矩形法精度高，如果在求(5)式的积分项时不用矩形公式而用梯形公式，亦即不用矩形面积而用梯形面积代替导函数\(\dot y-x\)曲线下的面积：

\(\int\limits_{{x}_{n}}^{{x}_{n+1}}{\dot y}{dx}\approx \frac{1}{2}({\dot y}_{n}+{\dot y}_{n+1})\)  

则由(5)式可得

\({y}_{n+1}={y}_{n}+\frac{1}{2}({\dot y}_{n}+{\dot y}_{n+1})\)

\({\dot y}_{n+1}=f({x}_{n+1},{y}_{n+1})\)              (7)

公式(7)与(6)不同，(6)式右端不包括y_n+1,这种形式的公式称为开型公式。(7)式的右端和左端都有y_n+1,即要用y_n+1;来求y_n+1,这种形式的公式称为闭型公式。计算闭型公式要用迭代法，其迭代过程是：

\({ y}_{n+1}^{0}={y}_{n}+h{\dot y}_{n}\)   

\({y}_{n+1}^{k}={y}_{n}+\frac{1}{2}h[{\dot y}_{nn}+{\dot y}_{n+1}({x}_{n+1},{y}_{n+1}^{(k-1)})]\) (8)

式中(k)代表迭代次数。当相邻两次迭代结果在所要求的位数上全相等时，迭代即可停止，这时将

\({y}_{n+1}^{(k)}={y}_{n+1}^{(k+1)}={y}_{n+1}\)

当作y(x_n+1)的近似值。这样逐点求下去，得到y_n+2,y_n+3,…,就是所求的改进欧拉方法的数值解。

如果迭代三、四次仍达不到要求时，可缩小步长再计算。

公式(8)是利用欧拉折线法的计算结果作为y_n+1⁽⁰⁾,称为初始预测值，将y_n+1⁽⁰⁾代入梯形公式(改进的欧拉法),求出之y_n+1⁽¹⁾,称作y_n+1的修正值。这种把欧拉折线法和改进的欧拉法联合起来使用的方法，称为预测-校正法。

第六章  并联无后坐式弹射器内弹道设计

6．1  内弹道设计的任务

在前面各章里，介绍了火药燃烧的基本知识，并根据有关理论和实验结果建立了内弹道方程组，解决了高、低压室弹道解法这个重要的实际问题，得到了高、低压室压力变化曲线和导弹速度变化曲线，对弹射过程中各种因素之间的关系有了进一步的认识。但是在内弹道学中认识各种规律并不是最后的目的，更重要的是运用这些规律去改进武器、设计出性能更好的武器。本章要解决的问题就是运用对弹射过程中高、低压室内各种矛盾运动规律性的认识来进行新武器的内弹道设计。具体说，就是在给定导弹直径d,离筒速度v_g,导弹发射重量m_m及允许的最大纵向发射加速度a^*的条件下设计出保证发射筒无后坐的高、低压室构造诸元及装填条件。这也就是无后坐弹射器的反面问题。本章着重研究并联无后坐式弹射器的内弹道设计问题。

需要指出，弹道解法是根据已知的高、低压室构造诸元和装填条件解出压力曲线和速度曲线，因而只有一个解；而弹道设计则不同，它是根据给定的d、m_m、v_g、a^*和选定的高压室工作压力及低压室压力设计出高、低压室构造诸元及装填条件，所以满足给定条件的设计方案实际上存在多个，必须在设计过程中进行分析比较，从中选择最合理的方案。

6.2  弹道方案的评价标准

方案选择是一个复杂的问题，在满足战术技术要求的前提下，要尽量使内弹道性能优越。因此，在选择方案时，除可直接比较各种不同方案的构造诸元及装填条件外，还可另外选取一些与弹道性能有关的特征量作为对不同方案内弹道性能评价的标准。

1.装药利用系数η_g

\({\eta}_{g}=\frac{\frac{1}{2}\frac{{m}_{m}}{g}{v}_{g}^{2}}{{m}_{g} }\)    (5-1)

式中

m_m——导弹发射重量；

m_g——高压室装药质量：

v_g——导弹离筒速度。

η_g的大小表示火药能量利用率。弹射器的能源就是火药，因此火药能量是否得到充分利用，显然应当作为评价武器性能的重要标准。η_g愈大，达到同样筒口动能所需的装药愈少，因此，从火药能量利用的角度出发，希望η_g尽量大一些好。

2.装填系数η_v

弹射过程中，低压室压力p₂是变化的，p₂-l曲线下面的面积\(\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}\)表征了弹射力F_p2作功的大小。图6-1中的曲线1和曲线2,假设它们的最大压力p_₂m和导弹全行程l_g均是相同的，但曲线1下降得比曲线2缓慢，因此它们曲线下的面积\(\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}\)是不同的, 如果我们以p_2m和L_g所构成的矩形面积作为基准，那么,它们的压力曲线下面积, 在这个矩形面积中所占的比例也就不同。

若以η_g代表这样的比例，则有

\({{\eta}_{g}}=\frac{\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}}{{p}_{2m}{l}_{g}}\)    (5-2)

η_g装填系数。η_g的大小反映了压力曲线下面积充满p_2ml_g矩形面积的程度，或者说，反映压力曲线平缓或陡直的变化情况。曲线变化的情况与高压室中火药燃烧情况有关，一般说，对于增面燃烧火药，低压室p₂-l曲线比较平缓；对减面性较大的火药，p₂-l曲线下降比较迅速，所以η_g的大小也体现了高压室火药燃烧渐增性的大小。

如果将(5-2)式的分子分母同乘以发射筒横截面积A,则得：

\({{\eta}_{g}}=\frac{A\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}}{A{p}_{2m}{l}_{g}}=\frac{A\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}}{{V}_{g}{l}_{g}}\)    (5-3)

式中Al_g=V_g称为发射筒工作容积，\({A\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}}\)则为弹射力所作之功。从上式可知，η_g也代表了p₂_m一定时的单位发射筒工作容积所能完成的功，因而表示了发射筒工作容积的利用效率，η_g亦称为发射筒工作容积利用系数。

为了能方便地计算出η_g必须对上式进行适当转化。由导弹运动方程可得：

\({A\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}}=\frac{1}{2}{\varphi }m{v }_{g}^{2}\)   (5-4)

代入(5-3)式中，得:

\({{\eta}_{g}}=\frac{\frac{1}{2}{\varphi }m{v }_{g}^{2}}{{V}_{g}{l}_{g}}\)    (5-5)

此处我们引入平均压力\({\bar p}_{2}\)的概念，\({\bar p}_{2}\)就是p₂-1曲线下的面积对于1_g的积分平均值

\({{\bar p}_{2}}=\frac{\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}}{{l}_{g}}\)        (5-6)

所以(5-2)式可写为

\({\eta}_{g}=\frac{{\bar p}_{2} }{{p}_{2m}}\)        (5-7)

即η_g可以表示为平均压力与最大压力之比。

由图5-1可知，\({\bar p}_{2}<{p}_{2m}\),所以η_g<1。无后坐弹射器低压室的η_g一般为0.6～0.85。

3.金属利用系数η_Q

\({\eta}_{Q}=\frac{\frac{1}{2}\frac{{m}_{m}}{{v}_{g}^{2}}}{Q}\)   (5-8)

式中   Q——弹射器重量。

η_Q表示弹射器单位重量所能产生的筒口动能，它是装药和弹射器设计的综合性能指标，在一定程度上表现了武器的机动性能。

一般说，评价内弹道设计方案的这些系数越大，则方案愈好。然而，这些系数之间虽然是互相联系却又是互相矛盾的，如η_g较大时，η_Q往往较小，所以所谓最佳方案只能是在满足主要战术技术要求条件下且综合内弹道性能较好的方案。通常应选η_Q和η_g尽可能大的方案，以保证发射筒有尽可能小的重量和体积。但在某些特殊情况下，其它要求可能成为评选方案的主要依据，如为了满足运载或空降方面的要求，特别规定发射筒长度不得超过某个值，此时，筒长就可能成为评选方案的主要依据。

6.3内弹道设计的基本方程

前已指出，典型的弹道设计问题可以归纳为确定高、低压室采用何种装填条件及构造诸元，才能保证将规定重量和直径的导弹，在不超过最大发射加速度允许值的条件下，加速至规定的离筒速度并保证发射筒无后坐。因此，首先必须建立联系高、低压室构造诸元、装填条件与表征弹道性能的高低压室压力和导弹速度之间的函数关系。导弹离筒速度的获得是低压室压力作用的结果，因此，我们由低压室状态方程出发来建立其间之关系，从而得到内弹道设计的基本方程。

根据某瞬时低压室状态方程：

\({p}_{2}=\frac{{\chi}_{1}{\tau}_{2}{RT}_{0}({M}_{1}-{M}_{2})}{{V}_{20}+Al}\)

其中

\({M}_{1}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}\int\limits_{0}^{t}{{p}_{1}dt}\)

\({M}_{2}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}}{\sqrt{{\chi}_{1}{\tau}_{2}{RT}_{0}}}\int\limits_{0}^{t}{{p}_{2}dt}\)

\(l=\int\limits_{0}^{t}{vdt}\)

可见，状态方程体现了构造诸元、装填条件与压力、速度之间的关系。但式中M₁,M₂,l,p₂都是时间t的函数，它们的变化规律都是未知的，其余各构造诸元也是未知的，所以上式在弹道设计时还不能解决实际问题。考虑到弹道设计时p₂虽不知道，但平均压力\({\bar p}_{2}\)却是已知量，是我们根据发射加速度的允许值选定的；那么在压力曲线上必定存在这样一个点A,在该点处压力的大小正好等于\({\bar p}_{2}\)值，即A点是\({\bar p}_{2}\)与p₂-l曲线的交点(见图6-2)。根据计算结果又知道，A点的位置大体是在燃烧结束点附近，即t≈t_k时，\({p}_{2}={\bar p}_{2}\)。而t_k, \({\bar p}_{2}\)在弹道设计时都是已知的，如将已知的t_k,t代入M₁,M₂,l式，则该瞬时的燃气流入、流出量及导弹行程的大小就也都成为已知量了。所以，如果选择t=t_k瞬间来建立低压室状态方程，就可得到待求的构造诸元与已知的其余各诸元之间的关系，也就得到了可供实际应用的弹道设计基本方程。

当  t=t_k时

\({p}_{2}={\bar p}_{2},{M}_{1}={M}_{1k},{M}_{2}={M}_{2k},l={l}_{k}\)状态方程为

\({\bar p}_{2}=\frac{{\chi}_{1}{\tau}_{2}{RT}_{0}({M}_{1k}-{M}_{2k})}{{V}_{20}+A{l}_{k}}\)  (5-9)

由低压室流入方程，有

\(\int\limits_{0}^{{M}_{1k}}{d{M}_{1}}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}\int\limits_{0}^{{t}_{k}}{{p}_{1}dt}\)

将p₁取积分平均值\({\bar p}_{1}\)即

\({\bar p}_{1}=\frac{\int\limits_{0}^{{t}_{k}}{{p}_{1}dt}}{{t}_{k}}\)

故

\({M}_{1k}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}} {\bar p}_{1}{{t}_{k} }\)

对恒面燃烧，高压室压力p₁可看作常量，等于平衡压力，即\({\bar p}_{1}={p}_{eq}\),则

\({M}_{1k}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}} { p}_{eq}{{t}_{k} }\)   (5-10)

由低压室流出方程，有

\(\int\limits_{0}^{{M}_{2k}}{d{M}_{2}}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}}{\sqrt{{\chi}_{1}{\tau}_{2}{RT}_{0}}\int\limits_{{t}_{om}}^{{t}_{k}}{{p}_{2}}dt}\)

图5-2

将p₂对t_k取积分平均值，该值与\({\bar p}_{2}\)接近，故可近似地认为等于\({\bar p}_{2}\),则上式为：

\({M}_{2k}=\frac{{\varphi}_{22}{K}_{0}{A}_{t2}}{\sqrt{{\chi}_{1}{\tau}_{2}{RT}_{0}}}{\bar p}_{2}({t}_{k}-{t}_{om})\)

由运动方程

\(A{p}_{2}=\frac{{\varphi}{m}_{m}}{g}\frac{dv}{dt}\)

\(\int\limits_{0}^{v}{dv}=\frac{Ag}{{\varphi}{m}_{m}}\int\limits_{{t}_{0}}^{t}{{p}_{2}dt}\)

用\({\bar p}_{2}\)代替p₂,则

\(v=\frac{Ag{\bar p}_{2}}{{\varphi}{m}_{m}}{(t-{t}_{0})}\)

因

\(\int\limits_{0}^{{l}_{g}}{dl}=\int\limits_{{t}_{0}}^{{t}_{k}}{vdt}\)

\(=\frac{Ag{\bar p}_{2}}{{\varphi}{m}_{m}}\int\limits_{{t}_{0}}^{{t}_{k}}{(t-{t}_{0})dt}\)

\(=\frac{Ag{\bar p}_{2}}{{\varphi}{m}_{m}}\int\limits_{{t}_{0}}^{{t}_{k}-{t}_{0}}{(t-{t}_{0})d(t-{t}_{0})}\)

故

\({l}_{k}=\frac{Ag{\bar p}_{2}}{{\varphi}{m}_{m}}{(t-{t}_{0})}^{2} \)

将M₁,M₂k,l₂式代入(6-9)式，得：

\({\bar p}_{2}=\frac{{\chi}_{1}{\tau}_{2}{RT}_{0}}{{V}_{20}+A\frac{Ag{\bar p}_{2}}{{\varphi}{m}_{m}}{({t}_{k}-{t}_{0})}^{2}}\)

\(\left[\frac{{\varphi}_{21}{K}_{0}}{\sqrt{{\chi}_{1}{RT}_{0}}}{A}_{t1}{\bar p}_{1}{t}_{k}-\frac{{\varphi}_{22}{K}_{0}}{\sqrt{{\chi}_{1}{\tau}_{2}{RT}_{0}}} {A}_{t2}{\bar p}_{2}({t}_{k}-{t}_{om})\right]\)

低压室压力一般都不高，故起动压力p_o及起喷压力p_om也很小，相应的t₀及t_om亦小，故可忽略t₀,t_om值，解出\({\bar p}_{1}{A}_{t1}\)表达式：

\({\bar p}_{1}{A}_{t1}=\left[\frac{{V}_{20}+\frac{{A}_{2}g{\bar p}_{2}}{2{\varphi}{m}_{m}}{{t}_{k}}^{2}}{{\chi}_{1}{\tau}_{2}{RT}_{0}}+ \frac{{\varphi}_{22}{K}_{0}}{\sqrt{{\chi}_{1}{\tau}_{2}{RT}_{0}}} {A}_{t2}{\bar p}_{2}{t}_{k}  \right]\frac{\sqrt{{\chi}_{1}{RT}_{0}}}{{\varphi}_{21}{K}_{0}{t}_{k}}\)

取φ₂₁=φ₂₂=φ₂,得

\({\bar p}_{1}{A}_{t1}=\frac{{V}_{20}+\frac{{A}^{2}g{\bar p}_{2}}{2{\varphi}{m}_{m}}{{t}_{k}}^{2}}{\sqrt{{\chi}_{1}{\tau}_{2}{RT}_{0}}{{\varphi}_{21}{\tau}_{2}{K}_{0}{t}_{k}}}+ \frac{ {A}_{t2}{\bar p}_{2}}{\sqrt{{\tau}_{2}}}  \)     (6-11)

这就是内弹道设计的基本方程。方程左端反映了从高压室流入低压室燃气平均秒流量的大小，方程的右端由\({\bar p}_{2}\)及装填条件、构造诸元组成。因此，上式表征了在一定的构造诸元和装填条件下，为了在低压室建立起必要的\({\bar p}_{2}\)而需要的燃气每秒流入量；或者说，上式表示了构造诸元、装填条件与弹道性能的关系。

6.4压峰比及其限制准则

1.压峰比p_r

前已述及，有侵蚀时之压力曲线如图6-3所示，我们将最大压力p_1m(初始压力峰值)与无侵蚀时之平衡压力p_eq的比值定义为压峰比，用符号p_r表示，

\({p}_{r}=\frac{{p}_{1m}}{{p}_{eq}}\)

图6-3

p_1m的大小是需要限制的，否则对高压室强度极为不利。有了p_r后，只需限制p_r就可达到限制p_1m的目的。

下面研究压峰比的计算问题。由前面的分析知，p₁-t曲线在最大压力点处转弯，即t=t₁时，\(\frac{{dp}_{1}}{dt}=0\),代入(2-16)式，则有

\(\frac{{\chi}_{1}{RT}_{0}}{{V}_{\varphi}}\left(\omega\frac{d{\varphi}}{dt}-{\dot m}_{1}\right)=0\)

故

\(\omega\frac{d{\varphi}}{dt}={\dot m}_{1}\)

\({\rho}_{p}{A}_{b}{\varphi}a{p}_{1m}^{n}={C}_{D}{A}_{t1}{p}_{1m}\)

式中

φ——侵蚀燃速系数；

\({p}_{1m}={\left(\frac{{\rho}_{p}{A}_{b}{\varphi}a }{{C}_{D}{A}_{t1}}\right)}^{\frac{1}{1-n}}{\varphi}^{\frac{1}{1-n}}\)

其中

\({\left(\frac{{\rho}_{p}{A}_{b}{\varphi}a }{{C}_{D}{A}_{t1}}\right)}^{\frac{1}{1-n}}\)

就是无侵蚀时的平衡压力。

故

\(\frac{{p}_{1m}}{{p}_{eq}}={\varphi}^{\frac{1}{1-n}}\)    (6-12)

上式表明，压峰比p_r是侵蚀燃速系数中的函数。只要知道φ值，就可求出p_r值，再根据p_r的大小就可求得压力峰值p_1m

\( {{p}_{1m}}={{p}_{eq}}{\varphi}^{\frac{1}{1-n}}\)

2.限制压峰比的准则

侵蚀效应使装药脱离平行层燃烧规律，使高压室压力曲线性能变坏，过高的压力峰值还会造成危险，并给控制高压室压力带来困难。因此，设计高压室时，对压峰比p_r (或最大压力p_1m)要予以限制。限制p_r也就是限制φ。φ与æ有关，æ大φ也大，所以可通过规定æ值的大小来限制压峰比的大小，换句话说，æ值是限定压峰比的一个准则，简称æ准则。

对于管状药，æ准则中还有一个内通气参量æ_内和外通气参量æ_外的问题：

æ_内=A_b内/A_T内

式中 A_b内——管状药内孔表面积；

A_b外——管状药外表面积；

A_T内、A_T外——内孔通气面积和外通气面积。

一般æ_内≠æ_外，在这种情况下，燃气流动情况更复杂一些，通常也是根据经验处理之，一般取λ=æ_内/æ_外=1～3。考虑到弹射器装药一般肉厚都较小，λ选取过大，内外压差就大，容易产生碎药。

限定压峰比的准则除æ准则外，还有J准则，æ₁准则；

J=A_t1/A_p

式中 A_p——高压室通气面积。

J也是通气参量，称为喉通比。它表征燃气在高压室中的流动速度，因而也表征装药侵蚀燃烧的严重程度，所以J也可作为限定压峰比的一个准则。

æ₁= æK_N(A_b/A_T)

K_N=A_b/A_t1,称为面喉比；

式中

A_T–装药末端的端面面积。

æ指的是燃通比的初始值。根据苏制“H”型火药和“HM”型火药的管状装药燃烧室的经验数据：

当æ₁<2×10⁶时，p_m/p_eq=1;

当æ₁>6×10⁶时，产生十分强烈的侵蚀压力峰。

我国的火药手册也介绍了按照æ准则整理的侵蚀压力峰数据，以及按此方式整理出的p_m/p_eq-æ经验关系式，但这些数据和经验公式仍有一定的局限性。

总之，压力峰的大小与通气参量有关，当通气参量大于一定值后，初始压力峰将急剧增高，这个值称为通气参量的界限值æ_cr,J_cr, æ_1cr。

设计高压室装药时应根据允许的p_r值，再按p_r与通气参量J或æ的关系，求出通气参量的临界值J_cr或æ_cr,并使其æ≤æ_cr,或J≤J_cr,以限制压力峰值。

通常峰值比p_r与通气参量J或æ的关系由内弹道实验测出。实验表明，对于一定的火药和高压室，峰值比p_r是通气参量、初温、面喉比K_N等的函数，亦即

p_r=f(J,K_N,T_i)

p_r=f(æ,K_N,λ,T_i)

式中 λ=æ_内/æ_外。

由于目前实验研究不充分，尚缺乏各种不同火药的峰值比与上述参量之间关系的详尽数据。下面仅列出了“171”双基药的一些粗略实验数据。

表6-1 “171”火药(+50°C,Kn=180,λ=1.83)

æ	J	æ1	pmax(105帕)	peq(105帕)	pr=pm/peq
89.3	0.497	0.61×106	113.8	114.2	0.998
111	0.617	0.929×106	141.9	117.0	1.11
130	0.722	1.319X106	196.0	134.1	1.46
140	0.778	1.413×106	258.6	131.3	1.87

已知p_r与J或æ的关系，便可根据压力峰的限制值确定通气参量的临界值J_cr、æ_cr。在装药设计时就要保证其通气参量不得超过此临界值，即J≤J_cr,或æ≤æ_cr。下表列出了几种双基药æ_cr的粗略数据：

表6-2 各种火药的æ_cr值

火药种类	双芳镁一1	双铅—1	双石一2	171	161	PT-12
æcr	155	160	170	130	160	140

6-5低压室内弹道设计

前已述及，弹射器最基本的任务就是要使规定重量的导弹达到规定的vg值，亦即获得规

定的筒口动能\(\frac{1}{2}{\varphi}_{m}{v}_{g}^{2}\)又由\({\bar p}_{2}\)的定义

\({\bar p}_{2}=\frac{\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}}{{l}_{g}}\)

故  \(A{\bar p}_{2}{l}_{g}=A {\int\limits_{0}^{{l}_{g}}{{p}_{2}dl}}=\frac{1}{2}{\varphi}m{{v}_{g}^{2}}\)

可知，导弹在不变的力Ap₂作用下所达到的筒口动能与在实际变化的力Ap₂作用下所获得的筒口动能是相同的。因总体要求的只是保证达到一定的筒口动能，故可用在不变的力Ap₂作用下导弹的匀加速运动来代替导弹的实际运动(在变化的力作用下的非匀加速运动)。

因此，进行低压室设计总的出发点是：假设导弹在低压室平均压力\({\bar p}_{2}\)的作用下作匀加速直线运动。

1. 发射筒内径d_筒的选取

导弹在筒内处于待发状态时的最大直径是已知的，一般说，发射筒的内径只要能将导弹最大直径包含进去就可以了，但在实际情况中往往由于下列两方面的原因而取d_筒略大于导弹最大直径：

一是由于结构上的需要，如某些导弹采用弧形可折叠翼，装入发射筒时，将弹翼折叠，再用弹翼抱环套在其上约束之，弹翼抱环之外径与发射筒配合，因此d_筒比导弹最大直径要大；另一种原因是由于推动导弹向前运动的弹射力等于Ap₂,在方案比较时希望适当增加发射筒断面积A以提高弹射力，或者是在保持弹射力不变的条件下，增加A以获得较低的\({\bar p}_{2}\)从而有利于减轻发射筒重量。

d_筒一般可比导弹最大直径大出5～25毫米。

2. 平均发射加速度允许值a*的计算

由导弹运动方程知

\(\vec{a}=\frac{d\vec{v}}{dt}=\frac{\vec{A{p}_{2}}}{\varphi m}\) (5-13)

式中\(\vec{a}\)——导弹在发射筒内的纵向加速度。

在弹射过程中，由于弹上仪器的要求，导弹所受纵向发射加速度的最大值a_max不能超过某一规定值，该值称为发射加速度允许值，以符号a*表示。a*的大小通常在总体设计时确定，并作为对弹射器设计的战术技术要求提出，因而在低压室设计时应使导弹在任何时候所受发射加速度都不超过a*值。导弹所受发射加速度的最大值发生在高温时的最大压力瞬间，因此a*值限制着高温时导弹所受最大加速度a_max的大小，故a*也可称为高温时的允许过载，a_max≤a*。

通常低压室设计是在常温条件下进行的，并且根据低压室平均压力值p₂来计算其它参量，因此需要的是常温下的平均加速度允许值a*。必须经过下述三个步骤才能由高温发射加速度允许值a*求得常温平均加速度允许值a*。由(6-13)式知，平均加速度允许值a*与平均压力\({\bar p}_{2}\)的允许值成正比。

(1)求常温下的允许加速度值a₀* 由(6-13)式知，在A,m,φ一定的条件下，加速度的大小与低压室压力成正比，所以，

\(\frac{{a}_{max,h}}{{a}_{max,0}}=\frac{{p}_{2m,h}}{{p}_{2m,0}}\)

式中a_max,h,p_2m,h-—高温时导弹所受最大加速度及最大压力值

a_max,0,p_2m,0——常温时导弹所受最大加速度及最大压力值，

若取 a_max,h=a*,  a_max,0=a₀^*

则

\(\frac{{a}_{max,h}}{{a}_{max,0}}=\frac{{a}^{*}}{{p}_{0}^{*}}\)

令 \(\frac{{p}_{2m,h}}{{p}_{2m,0}}={A}_{1}\)

则 \({a}_{0}^{*}=\frac{{a}^{*}}{{A}_{1}}\)

由实验结果知，A₁的大小随所选火药的不同而有不同的值，通常A₁=1.1～1.25。

(2)求常温下的平均加速度允许值西常在求出常温发射加速度允许值\({\bar a}_{0}^{*}\)后，还需求出常温平均加速度允许值\({\bar a}_{0}^{*}\)，根据\({\bar a}_{0}^{*}\)才能确定出\({\bar p}_{2}\)的允许值。

由充满系数的定义

\({\eta}_{g}=\frac{{\bar p}_{2}}{{p}_{2m}}\)

而 \(\frac{{\bar p}_{2}}{{p}_{2m}}=\frac{{bar a}_{0}^{*}} {{a}_{0}^{*}}\)

故  \({\bar a}_{0}^{*}={ a}_{0}^{*}{\eta}_{g}\)

通常 η_g=0.6~0.8

ne=0.6～0.85

(3)求常温下实际的平均加速度允许值\({\bar a}^{*}\)，在实际的弹射器中，由于高、低压室喷喉直径的制造误差及烧蚀作用引起之尺寸变化；发射筒内径的制造误差；火药几何尺寸的制造误差以及不同批号火药之间的性能差别，都将引起低压室实际压力的波动，表现为每发的p₂-t曲线都不是完全重合的，我们将这种不重合现象称为压力跳动\(=\frac{{p}_{2max}-{p}_{2min}}{{p}_{eq}}\),式中p_eq表示各发压力的平均值。一般压力跳动值约为5%),因此实际的平均加速度值也会有相应的跳动。

为了使跳动量最大的那发弹的发射加速度值也不超过\({\bar a}_{0}^{*}\)，应使实际的平均加速度允许值\({\bar a}^{*}\)还要较\({\bar a}_{0}^{*}\)再下降5%,即

\({\bar a}^{*}=\frac{{\bar a}_{0}^{*}}{{A}_{2}}\)

A₂=1.05

综合上述各因素，常温下实际平均加速度的允许值\({\bar a}^{*}\)为

\({\bar a}^{*}={a}^{*}\frac{{\eta}_{g}}{{A}_{1}{A}_{2}}\)

式中   A₁=1.1～1,25:A₂=1.05;η_g=0.6～0.85,

3.低压室平均压力\({\bar p}_{2}\)的选取

由(6-14)式求得\({\bar a}^{*}\)后代入(6-13)式即可求得低压室平均压力的允许值。只要满足下式的\({\bar p}_{2}\)都可选为低压室的平均压力

\({\bar p}_{2}\le{\bar p}_{2}^{*}\)

由(6-4)、(6-6)式可得

\(A{\bar p}_{2}{l}_{g}=\frac{1}{2}\frac{{\varphi}{m}_{m}}{g}{v}_{g}^{2}\)    (6-15)·

即弹射力\(A{\bar p}_{2}\)在l_g的长度上对导弹作功的结果使导弹在筒口获得\(\frac{1}{2}\frac{{\varphi}{m}_{m}}{g}{v}_{g}^{2}\)的筒口动能。筒口动能的大小是既定的，因此\(A{\bar p}_{2}{l}_{g}\)的乖积也不能变，\({\bar p}_{2}\)取值的大小显然与A,l_g有关。分析这三个物理量之间的关系将帮助我们考虑如何选择\({\bar p}_{2}\)值。

从减小发射时声响的观点出发\({\bar p}_{2}\)应取低值。由(6-15)式知，\({\bar p}_{2}\)取低值的结果必须由增大A或增大l_g来弥补，才能保持\(A{\bar p}_{2}{l}_{g}\)乘积不变。但前已提及，A的增加不能是无限的，它受到使用条件的限制，只允许在有限的范围内比导弹最大直径增加一个数值。

增加l_g以降低\({\bar p}_{2}\)的办法只在一定的范围内可行，在燃烧结束点1_g以后再过多地增加l_g反而是不利的。因为实际的p₂-l曲线是逐渐下降的，在接近筒口处压力已比较低，如继续增加l_g至l’_g则图(6-4)中增加出来的阴影部分面积很小，即导弹动能增加很小，而发射筒的重量Q_筒却因为l_g的增加而加大了，因此从能量利用的观点看，用Q_筒的增加换取导弹动能的有限增量是不合算的。当然，l_g的增加也受到使用条件的限制，发射筒长度过大将给发射、行军、维护带来不便，某些情况下，总体设计时也对l_g的大小提出限制。

\({\bar p}_{2}\)的降低必然使发射加速度a^*降低，即加速度允许值a^*没有得到充分利用。

图6-4

总之，在保证\({\bar p}_{2}\le{\bar p}_{2}^{*}\)的条件下，\({\bar p}_{2}\)的选取必须考虑其与A、l_g、a之间的关系，在总的方案合理的前提下确定\({\bar p}_{2}\)的大小，同时也就确定了S及l_g的大小。

\({\bar p}_{2}\)确定后，再根据(6-13)式反算出实际平均加速度\(\bar a\)的大小。

4.导弹在发射筒中运动时间t_g的确定

根据匀加速直线运动的假定有

\({t}_{g}=\frac{{v}_{g}}{\bar a}\)

5. 高压宣装药燃烧结束时间t_k的确定

t_k是低压室第二时期的起始点，在第二时期中高压室没有装药燃烧，压力迅速下降，排入低压室的燃气流量也迅速下降，即低压室中使压力上升的因素减弱，但此时导弹运动速度已较大，低压室容积扩大较快，尾喷管仍不断有燃气流出，因此第二时期中低压室压力下降很快，压力冲量较小，这就使得导弹在这一时期中所获得的速度增量很小，因此高压室装药燃烧不能过早结束，t_k不应比t_g小得过多，否则第二时期的压力冲量将不能使导弹的速度由v_k增加到所需要的v_g。此外，由于压力下降快，发射筒材料的利用率必然低，从减轻发

射筒重量的角度考虑也不宜使t_k与t_g的差值过大。但也不应将燃烧结束点取在发射筒口，因为当t_k=t_g时，燃烧结束点的跳动将不可避免地引起导弹离筒速度v₂的分散，这对无控段的射击精度是不利的，为了兼顾这两方面的要求，取

\({v}_{k}={\eta}{v}_{g}\)

η=0.9～0.95

又因为有导弹作匀加速直线运动的假定，故有

\({t}_{k}={\eta}{t}_{g}\)

6.低压室尾喷管喷喉面积A_t2的确定

根据无后坐条件可求得A_t2

\({A}_{t2}=\frac{1}{{\chi}_{0}{{C}_{F}}}A\)

χ₀=0.88～0.95

推力系数C_F的值可计算亦可查表。k=1.25时之C_F值如下表，

表6-6 k=1.25时之C_F值

Ae/At	1	4	9	16	25
de/dt	1	2	3	4	5
CF	1.323	1,616	1.719	1.776	1.813

表中A_e-—喷管出口截面积；

d_e——喷管出口截面之直径；

d_t——喷管喉部直径。

表中数据表明，C_F随A_e/A_t的增加而增加。在A_e/A_t较小的情况下，C_F增加较快，以后的增加就愈来愈慢，所以在喷管设计时为了不过多增加喷管重量，又能得到较高的C_F值，通常在A_e/A_t略大于4或d_e/d_t=2.0～2.3之间取C_F值，代入无后坐条件中即可求得A_t2

7.低压室初始容积V₂₀的选取

由低压室状态方程

\({p}_{2}=\frac{{\chi}_{1}{\tau}_{2}{RT}_{0}({M}_{1}-{M}_{2})}{{V}_{20}+Al}\)

知，初始容积W₂₀愈小，则p₂愈大，低压室压力曲线上升得快；当导弹开始运动以后，弹后空间Al不断增加，W₂₀相对于Al变为小量，对p₂的影响愈来愈小。但W₂₀的取值不能过小，其大小应能保证图(6-5)中的环形面积ABBA大小尾喷管喉部断面积。可按草图设计结果初步估算出W₂₀值进行低压室设计，在设计过程中再作进一步调整。有资料介绍无后坐弹射器的经验数据为；

\(\frac{{V}_{20}+A{l}_{g}}{{V}_{20}}\)≈2.5~9

图6-5

7.其它形式弹射器的内弹道设计问题

对于串联无后坐式及自弹式弹射器，其内弹道设计步骤基本上与并联无后坐式相同，但必须重新推导它们的无后坐条件及内弹道设计基本方程。串联无后坐式弹射器的无后坐条件

已在第三章中建立了。下面分别解决自弹式的无后坐条件及串联无后坐式及自弹式的内弹道设计基本方程的问题。

一、串联无后坐式弹射器的内弹道设计基本方程

与并联无后坐式弹射器的方法相同，我们仍从低压室状态方程出发来建立联系高、低压室构造诸元、装填条件及表征弹道性能的高、低压室压力和导弹速度之间的函数关系，即内弹道设计的基本方程。

因为串联无后坐式低压室无流出，即M₂=0,故状态方程为：

\({p}_{2}=frac{{M}_{1}{RT}_{2}}{{V}_{20}+Al}\)

其中

\({M}_{1}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}\int\limits_{0}^{t}{{p}_{1}dt}\)

\(l=\int\limits_{{t}_{0}}^{t}{vdt}\)

我们仍采用与并联无后坐式相同的假设，即认为当t=t_g时，p₂=\({\bar p}_{2}\),计算结果表明，这个假设是有一定准确性的。因此我们选择t=t_g瞬间来建立低压室状态方程，这样便可得到待求的构造诸元与已知的其余各诸元的关系，即得到可供实用的内弹道设计基本方程，

当t=t_k时，p₂=\({\bar p}_{2}\);\({M}_{1}={M}_{1k2}\);l=l₂。则

\({\bar p}_{2}=\frac{{M}_{1k}{RT}_{2}}{{V}_{20}+Al}\)

\({M}_{1k}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}\int\limits_{0}^{{t}_{k}}{{p}_{1}dt}\)

\(=\frac{{\varphi}_{21}{K}_{0}}{\sqrt{{\chi}_{1}{RT}_{0}}}{A}_{t1}{\bar p}_{1}{t}_{k}\)

由运动方程

\(A{p}_{2}=\frac{{{\varphi}}{m}_{m}}{g}\frac{dv}{dt}\)

得

\(\int\limits_{0}^{v}{dv}=\frac{{sg}{m}_{m}}{\varphi}(t-{t}_{0})\)

又因

\(\int\limits_{0}^{{t}_{k}}{dl}=\int\limits_{{t}_{0}}^{{t}_{k}}{vdt}=\frac{A{\bar p}_{2}g}{{\varphi}{m}_{m}}\int\limits_{{t}_{k}}^{{t}_{k}}{(t-{t}_{0})dt}\)

\(=\frac{A{\bar p}_{2}g}{{\varphi}{m}_{m}}\int\limits_{0}^{{t}_{k}-{t}_{0}}{(t-{t}_{0})d(t-{t}_{0}) }\)

故

\({l}_{k}=\frac{1}{2}\frac{A{\bar p}_{2}g}{{\varphi}{m}_{m}}{{t}_{k}-{t}_{0}}^{2}\)

将M₁,l₂代\({\bar p}_{2}\)式，则

\({\bar p}_{2}=\frac{{RT}_{2}}{{V}_{20}+A\frac{1}{2}\frac{A{\bar p}_{2}g}{{\varphi}{m}_{m}}{({t}_{k}-{t}_{0})}^{2}}\frac{{\varphi}_{21}{K}_{0}}{\sqrt{{\chi}_{1}{RT}_{0}}}{A}_{t1}{\bar p}_{1}{t}_{k}\)

忽略t₀后解出\({\bar p}_{1}{A}_{t1}\)表达式

\({A}_{t1}{\bar p}_{1}=\frac{{{\bar p}_{2}}{\sqrt{{\chi}_{1}{RT}_{0}}}\left({V}_{20}+ \frac{1}{2}\frac{{A}^{2}{\bar p}_{2}g}{{\varphi}{m}_{m}}{t}_{k}^{2}\right)}{ {\varphi}_{21}{K}_{0}{RT}_{2}{t}_{k}}\)

上式即串联无后坐式弹射器的低压室内弹道设计基本方程。在选定高压室工作压力\({\bar p}_{1}\)后，即可据此设计高压室前喷喉面积A_t1,

二、自弹式弹射器内弹道设计基本方瞿

与并联无后坐式及串联无后坐式弹射器的方法相同，仍由状态方程出发来建立自弹式弹射器的内弹道设计基本方程。

由于自弹式弹射器低压室无流出，故M₂=0,状态方程为：

\({p}_{2}=\frac{{M}_{1}{RT}_{1}}{{V}_{20}+Al}\)

\({M}_{k}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}\int\limits_{0}^{t}{{p}_{1}dt}\)

\(l=\int\limits_{{t}_{0}}^{t}{vdt} \)

同样，假设t=t_k时，p₂=\({\bar p}_{2}\),M₁=M_1k;l=l_k.则

\({M}_{1k}=\frac{{\varphi}_{21}{K}_{0}{A}_{t1}}{\sqrt{{\chi}_{1}{RT}_{0}}}{{\bar p}_{1}{t}_{k}}\)

由运动方程

\({F}_{1}+{F}_{2}=\frac{{\varphi}{m}_{m}}{g}\frac{dv}{dt}\)

式中F₁——弹射力；F₁=(A-ε_AA_t1)p₂;

F₂-—自推力，F₃=C_FA_t₁p₁;

ε_A,C_F—-运动高压室喷管膨胀比及推力系数。

故上式为

\(\frac{{\varphi}{m}_{m}}{g}dv=\int\limits_{{t}_{0}}^{t}{({F}_{1}+{F}_{2})dt}\)

忽略t₀,得

\(v=\frac{{F}_{1}+{F}_{2}} {{\varphi}{m}_{m}}{gt}\)

因\(dl=\int\limits_{0}^{t}{vdt}\)

\({l}_{k}=\frac{{F}_{1}+{F}_{2}} {2{\varphi}{m}_{m}}{g}{t}_{k}^{2}\)

故

将M_1k及l_k式代入p₂式，整理后得:

\({p}_{1}{A}_{t1}=\frac{{\bar p}_{2}\sqrt{{\chi}_{1}{RT}_{0}}\left[{V}_{20}+\frac{{F}_{1}+{F}_{2}} {2{\varphi}{m}_{m}}{A}{g}{t}_{k}^{2}\right]}{{\varphi}_{21}{K}_{0}{RT}_{2}{t}_{k}}\)

此式即自弹式弹射器的内弹道设计基本方程。当选定运动高压室工作压力后，可据此得出运动高压室喷喉面积A_t1。

三、自弹式弹射器无后坐条件

与并、串联无后坐式弹射器相同，我们仍在下述前提下建立自弹式弹射器的无后坐条件：

• 按照t₀=t₀_m的理想情况来考虑问题；

②认为导弹在出发射筒口前的后坐不平衡是主要的，即只考虑t₀～tg的情况

• 动量以指向筒口方向为正。

仍取发射筒、导弹、燃气为系统的组成，根据(4-29)式，即

发射筒的动量十导弹的动量+后喷燃气的动量=0。

根据动量的变化等于冲量，在整个t₀~t_g期间，导弹动量的变化应为+\(\int\limits_{{t}_{0}}^{{t}_{g}}{}\)(F₁+F₂)dt。由于导弹的初动量为0,故上式中第二项导弹的动量应为+\(\int\limits_{{t}_{0}}^{{t}_{g}}{}\)(F₁+F₂)dt。同理可得第三项反后坐高压室后喷燃气的动量为\(-\int\limits_{{t}_{0}}^{{t}_{g}}{{C}_{F3}{A}_{t3}{p}_{3}dt}\)。故

\(MV+\int\limits_{{t}_{0}}^{{t}_{g}}{({F}_{1}+{F}_{2})dt}-\int\limits_{{t}_{0}}^{{t}_{g}}{{C}_{F3}{A}_{t3}{p}_{3}dt}=0\)

式中:

F₁—弹射力，F₁=(A-ε_AA_t1)p₂;

F₂—自推力，F₂=C_F2A_t1p₁;

C_F3,A_t3,p₃——反后坐高压室的喷管推力系数，喉部面积及工作压力；MV——发射筒的动量。

当整个弹射过程无后坐时，MV=0,故

\(\int\limits_{{t}_{0}}^{{t}_{g}}{({F}_{1}+{F}_{2})dt}=\int\limits_{{t}_{0}}^{{t}_{g}}{{C}_{F3}{A}_{t3}{p}_{3}dt}\)

\((A-{\varepsilon}_{A}{A}_{t1}){\bar p}_{2}({t}_{g}-{t}_{0})+{C}_{F2}{A}_{t1}{\bar p}_{1}({t}_{g}-{t}_{0})={C}_{F3}{A}_{t3}{\bar p}_{3}({t}_{g}-{t}_{0})\)

\({A}_{t3}=\frac{(A-{\varepsilon}_{A}{A}_{t1}){\bar p}_{2}+{C}_{F2}{A}_{t1}{\bar p}_{1}}{{C}_{F3}{\bar p}_{3}}\)

上式即自弹式弹射器的无后坐条件，据此可求出反后坐高压室的喷喉面积A_t3

四、燃气蒸汽式弹射装置中的立管喷水孔设计

对于如图5-6所示的燃气蒸汽式弹射装置，在进行内弹道设计时，除高、低压室中的内弹道参量(装填条件、构造诸元)需确定外，还有一个燃气蒸汽式弹射装置所特有的重要构造诸元——立管喷水孔的面积s₂亦需予以确定。

图5-30

水室中的水由喷水孔向立管内喷射的过程可简化为如图6-30所示的模型。

设喷水孔到水面的距离为H,水的密度为ρ_w,水面下降速度为v₁,水面压强为p₀，水由喷水孔流出速度为v₂,孔外压强(即立管内燃气流的静压)为p_H。根据伯努利方程有

\(\frac{{v}_{1}^{2}}{2}+\frac{{p}_{0}}{{\rho}_{w}}+H=\frac{{v}_{2}^{2}}{2}+\frac{{p}_{H}}{{\rho}_{w}}\)

不可压缩定常一维流动连续方程为

\({v}_{1}{s}_{1}={v}_{2}{s}_{2}\)

式中  s₁——水室中水面面积；

s₂——喷水孔总面积。

联立以上两个方程，得

\(\frac{{v}_{2}^{2}}{2}\left[1-{\left(\frac{{s}_{2}}{{s}_{1}}\right)}^{2}\right]=\frac{{p}_{0}-{p}_{H}}{{\rho}_{w}}+H\)    (6-16)

又由5.4知，冷却水质量=ηω。

设水室中的冷却水在t_g时间内全部喷入立管，故有

\({s}_{2}{v}_{2}{\rho}_{w}=\frac{\eta\omega}{{t}_{g}}\)              (6-17)

将(6-17)式代入(6-16)式，得

\(\frac{1}{2}{\left(\frac{\eta\omega }{{s}_{2}{t}_{g}{\rho}_{w}}\right)}^{2}  \left[1-{\left(\frac{{s}_{2}}{{s}_{1}}\right)}^{2}\right]=\frac{{p}_{0}-{p}_{H}}{{\rho}_{w}}+H\)  (6-18)

式中η、ω、t_g、s₁、ρ_w、H为已知数，故只需求出p₀及p_H,s₂便可由(6—18)式求出。

下面的问题转化为求p₀及p_H。

1.高压室喷管出口截面的燃气流参数

设高压室喷管为超音速喷管，且认为燃气在高压室喷管中的流动为一维定常等熵变截面管流。由连续方程可对其任意两个截面写出：

\(C\frac{{p}_{1}^{*}{s}_{1}}{\sqrt{{T}_{1}^{*}}}q({\lambda}_{1})= C\frac{{p}_{2}^{*}{s}_{2}}{\sqrt{{T}_{2}^{*}}}q({\lambda}_{2})\)

式中p₁*、T₁*、λ₁、q(λ₁)——分别为1截面的气流总压、总温、速度系数及流量函数；p₂*、T₂*、λ₂、q(λ₂)——分别为2截面的气流总压、总温、速度系数及流量函数。在定常等熵的条件下

T₁*=T,*,

p₁*=p₂*

故

\(\frac{{s}_{2}}{{s}_{1}}=\frac{q({\lambda}_{1})}{ q({\lambda}_{2})}\)

若取1截面为高压室喷管临界截面，e截面为出口截面，则有

\(\frac{{s}_{e}}{{A}_{t1}}=\frac{1}{ q({\lambda}_{e})}\)

而 \(q({\lambda}_{e})={(\frac{k+1}{2})}^{\frac{1}{k-1}}{\lambda}_{e}{\left(1-\frac{k-1}{k+1}{\lambda}_{e}^{2}\right)}^{\frac{1}{k-1}}\)

高压室设计完毕后，s_e、A_t1即为已知数，故λ_e可求出。因

\({\pi}({\lambda}_{e}）=\frac{{p}_{e}}{{p}_{e}^{*}}={\left(1-\frac{k-1}{k+1}{\lambda}_{e}^{2}\right)}^{\frac{1}{k-1}}\)

故\({{p}_{e}}={{p}_{e}^{*}}{\pi}{\lambda}_{e}\)

\({M}_{e}=\sqrt{\frac{\frac{2}{k+1}{\lambda}_{e}^{2}}{1-\frac{k-1}{k+1}{\lambda}_{e}^{2}}}\)

式中p_e、M_e——分别为高压室喷管出口截面的静压及马赫数。

从高压室喷管流出之超音速燃气流由于受到第二喷管的阻碍，将出现激波，设此激波为正激波。当高压室喷口与第二喷管之间距离足够大时，该激波将产生于高压室喷管出口截面之外，对高压室的正常工作没有影响。为使结构紧凑，第二喷管的位置按下述原则设置：使得正激波正好出现在高压室喷管的出口截面上。这样高压室出口截面的气流参数即激波前的参数，激波后的亚音速气流的参数可由正激波的有关公式计算求得。

2. 激波后的气流参数

由于激波的厚度很薄，其数量级约为10^-8～10^-6毫米，故波后气流的横截面积s₂后仍可认为等于高压室喷管的出口截面积s₁。因

速度系数   \({\lambda}_{1}{\lambda}_{2}=1\)

马赫数 \({M}_{2}=\sqrt{\frac{\frac{2}{k+1}{\lambda}_{2}^{2}}{1-\frac{k-1}{k+1}{\lambda}_{2}^{2}}}\)

故激波前后的总压比

\(\frac{{p}_{2}^{*}}{{p}_{1}^{*}}={\left[\frac{(k+1){M}_{2}^{2}}{2+(k-1){M}_{2}^{*}}\right]}^{\frac{k}{k-1}}{\left[\frac{2k}{k+1}{M}_{2}^{2}-\frac{k-1}{k+1}\right]}^{-\frac{1}{k-1}}\)

激波前后的静压比，\(\frac{{p}_{2}}{{p}_{1}}=\frac{2k}{k+1}{M}_{2}^{2}-\frac{k-1}{k+1}\)

注脚“2”表示激波后。

3.分流内筒中的气流参数

激波后的气流进入分流圆筒中的内筒后，通道突然扩大(参见图5-3及图6-31)。这时在死角区形成旋涡，使机械能发生不可逆损失，总压下降，直到流过6～10倍筒径的距离后(到达B-B截面)才恢复为平行均匀流动。

图6-31

1-高压室喷管；2一死角区；3一分流内筒。

设图6-31中之A-A截面为波后的横截面，其气流参数为波后的气流参数；B-B截面为气流下游恢复均匀流态的截面。

由于死角区内的压强近似为常数，等于中心气流内原来的压强p₂。若忽略气流与筒壁之间的摩擦，则可写出A-A、B-B截面间的动量方程：

\({\dot m}({U}_{B}-{U}_{A})=({p}_{A}-{p}_{B}){s}_{B}={p}_{A}{s}_{e}+{p}_{A}({s}_{B}-{s}_{e})-{p}_{B}{s}_{B}\)

或

\({\rho}_{B}{U}_{B}^{2}{s}_{B}-{\rho}_{A}{U}_{A}{U}_{B}{s}_{e}={p}_{A}{s}_{e}+{p}_{A}{s}_{e}\left(\frac{{s}_{B}}{{s}_{e}}-1\right)-{p}_{B}{s}_{B}\)   (5-19)

式中\(\dot m\)——气流流过A-A、B-B截面的秒流量；

U_A，U_B——气流在A-A、B-B截面上的流速；

s_B——B-B截面的面积；

ρ–燃气的密度。

由（6-19）式可以看到，方程左边出现了\(({\rho}{U}^{2}+p)s\)项，该项可表为速度系数λ的函数，即

\(({\rho}{U}^{2}+p)s=({\rho}{U}^{2}+p)\frac{\dot m}{{\rho}U}={\dot m}\left(\frac{p}{{{\rho}U}+U}\right)\)

\(={\dot m}\left[\frac{{gRT}^{*}{\tau}(\lambda)}{{\lambda}{a}_{cr}}+{\lambda}{a}_{cr}\right]\)

式中 T*——总温

a_cr——临界音速，\({a}_{cr}=\sqrt{\frac{2k}{k+1}{RT}^{*}}\)

\({\tau}(\lambda), {z}(\lambda)\)——气体动力学函数

\({\tau}(\lambda)=\frac{T}{{T}^{*}}=1+\frac{k-1}{k+1}{\lambda}^{2}\)

\({z}(\lambda)=\lambda+\frac{1}{\lambda}\)

将a_cr代入上式，得

\(({\rho}{U}^{2}+p)s={\dot m}\left[\frac{k+1}{2k}\frac{{\tau}(\lambda)}{\lambda}{{\lambda}{a}_{cr}}+{\lambda}{a}_{cr}\right]= {\dot m}\frac{k+1}{2k}{a}_{cr}{z}(\lambda)\)

其中  \(ps= {\dot m}\frac{k+1}{2k}{a}_{cr}\frac{{\tau}(\lambda)}{\lambda}\)

而  \(\frac{{\tau}(\lambda)}{\lambda}={\left(\frac{k+1}{2}\right)}^{\frac{1}{k-1}}\frac{1}{y(\lambda)}\)

故 \(ps= {\dot m}\frac{k+1}{2k}{a}_{cr}{\left(\frac{k+1}{2}\right)}^{\frac{1}{k-1}}\frac{1}{y(\lambda)}\)

式中y(λ)——气体动力学函数

\(y(\lambda)= {\left(\frac{k+1}{2}\right)}^{\frac{1}{k-1}}\lambda{\left(1-\frac{k-1}{k+1}\right){\lambda}^{2}}^{-1}\)

故（6-19）式可写成

\({\dot m}\frac{k+1}{2k}{a}_{cr,B}Z({\lambda}_{B})-{\dot m}\frac{k+1}{2k}{a}_{cr,A}Z({\lambda}_{A})\)

\(={\dot m}\frac{k+1}{2k}{a}_{cr,A}{\left(\frac{k+1}{2}\right)}^{\frac{1}{k-1}}\frac{1}{y({\lambda}_{A})}\left(\frac{{s}_{B}}{{s}_{A}}-1\right)\)

化简得 

\(Z({\lambda}_{B})=Z({\lambda}_{A})+\frac{k+1}{2k}{\left(\frac{k+1}{2}\right)}^{\frac{1}{k-1}}\frac{1}{y({\lambda}_{A})}\left(\frac{{s}_{B}}{{s}_{A}}-1\right)\)

查气体动力学函数表可求得λ_B

由连续方程有

\({\pi}({\lambda}_{B})={\left(1-\frac{k-1}{k+1}{\lambda}_{B}^{2}\right)}^{\frac{k}{k-1}}\)

式中q(λ),π(λ)——气体动力学函数。

若忽略摩擦及气流与筒壁间的热交换，则从B-B截面以后的各截面的燃气流参数均与B-B截面相同，直至分流内筒的出口截面为止。

4. 分流外筒中的气流参敷

燃气流由分流内筒流入分流外筒后，通道又突然扩大(如图6-32所示)。

图中B-B截面为分流内筒的出口截面，C-C截面为气流恢复均匀流态的截面。与分流内筒中气流参数的计算方法相同，可得C-C截面的速度系数λc、总压p_c*及静压p_c,

\(Z({\lambda}_{c})=Z({\lambda}_{B})+\frac{k+1}{2k}{\left(\frac{k+1}{2}\right)}^{\frac{1}{k-1}}\frac{1}{y({\lambda}_{B})}\left(\frac{{s}_{C}}{{s}_{B}}-1\right)\)

\({p}_{C}^{*}={p}_{B}^{*}\frac{{s}_{B}q({\lambda}_{B})}{{s}_{C}q({\lambda}_{C})}\)

\({p}_{C}={p}_{C}^{*}{\pi}({\lambda}_{C})\)

\({\pi}({\lambda}_{B})={\left(1-\frac{k-1}{k+1}{\lambda}_{B}^{2}\right)}^{\frac{k}{k-1}}\)

图6-32

1一分流内筒；  2一分流外筒。

5.第二喷管中的气流参数及出口截面积s_t

分流外筒中的气流经C-C截面后，大部分流入第二喷管，另外少部分通过分流内、外筒的筒间通道流入水室上部空间。下面分析进入第二喷管中的燃气流参数及s_t求法。

第二喷管为音速喷管，其入口截面的气流参数为λ_c、p_c*、p_c,而出口截面为临界截面，故其参数为：

λt2=1

p_t2*=p_c*

p_t2=π(λ_t₂)p_t2*,

注脚t₂表示第二喷管临界截面。

设高压室喷管的秒流量为\({\dot m}_{1}\),第二喷管的秒流量为\({\dot m}_{2}\),流入水室的燃气流量为△\({\dot m}\)。则有

\(\Delta{\dot m}={\dot m}_{1}-{\dot m}_{2}={\dot m}_{1}\left(1-\frac{{\dot m}_{2}}{ {\dot m}_{1}}\right)\)=\({\dot m}_{1}\left(1-\frac{{{t}_{t2}}^{*}}{ {p}_{1}}\frac{{s}_{t2}}{{A}_{t1}}\right)\)

故 \({s}_{t2}=\frac{1-\frac{\Delta{\dot m}}{{\dot m}_{1}}}{\frac{{p}_{t2}^{*}}{{p}_{1}}}{A}_{t1}\)

式中   p₁、A_t1——高压室压力及高压室喷喉面积。

6.水室中的燃气流参数

现在分析流入水室上部空间的燃气所形成的压力。

在弹射过程中，水室中燃气移动的距离约为冷却水面至喷水孔之间的高度差。可见燃气流动的速度很低，可近似认为燃气处于滞止状态，故水室中的燃气静压p₀接近其总压p₀*室。如再忽略分流内、外筒之间的能量损失，则可得：

p₀=p₀*=p_c*

实际上由于水室中的冷却水总要从燃气中吸收一部分热量，故p₀将小于p_c*。

7.立管中的气流参数

由图5-6可知，立管伸入水室内部与第二喷管相连，燃气流由第二喷管流出后，在立管中继续膨胀增速为超音速气流(如图6-33所示)。在E-E截面处气流充满整个立管横截面。下面写出D-D、E-E截面间的动量方程：

图6-33

\({\dot m}({U}_{E}-{U}_{t2})={s}_{t2}({p}_{t2}-{p}_{E})\)

\({\dot m}={s}_{t2}{U}_{t2}{\rho}_{t2}\)

式中ρ₂-—D-D截面上燃气的密度。

\({s}_{t2}{U}_{t2}{\rho}_{t2} ({U}_{E}-{U}_{t2})={s}_{t2}({p}_{t2}-{p}_{E})\)

两边同乘·\(\frac{1}{{U}_{t2}{p}_{t2}}\)

则

\(\left(\frac{{U}_{E}}{{U}_{t2}}-1\right)\frac{{\rho}_{t2}}{{p}_{t2}}=\left(1-\frac{{p}_{E}}{{p}_{t2}}\right)\frac{1}{{U}_{t2}}\)

因

\(\frac{{\rho}_{2}}{{p}_{t2}}=\frac{1}{{RT}_{t2}}=\frac{k}{{a}_{t2}^{2}}\)

故

\(k\left(\frac{{U}_{E}}{{U}_{t2}}-1\right) =\left(1-\frac{{p}_{E}}{{p}_{t2}}\right)\frac{{a}_{t2}^{2}}{{U}_{t2}^{2}}\)

上式中

\(\frac{{a}_{t2}^{2}}{{U}_{t2}^{2}}=1\)

故

\(\frac{{U}_{E}}{{U}_{t2}}=\frac{1}{k}\left(k+1-\frac{{p}_{E}}{{p}_{t2}}\right)\)

将D-D与E-E截面之间的气流视为绝能流动，则这两个截面上的总温相等，因而临界音速亦相等，即

\({a}_{t22}={a}_{tE}={U}_{t2}\)

故

\(\frac{{U}_{E}}{{U}_{t2}}=\frac{{U}_{E}}{{a}_{t2}}={\lambda}_{E}\)

代入上式，得

\({\lambda}_{E}=\frac{1}{k}\left(k+1-\frac{{p}_{E}}{{p}_{t2}}\right)\)

由连续方程，得

\({s}_{t2}{U}_{t2}{\rho}_{t2}={s}_{E}{U}_{E}{\rho}_{E}\)

\(\frac{{U}_{E}}{{U}_{t2}}=\frac{{s}_{t2}{\rho}_{t2}}{{s}_{E}{\rho}_{E}}\)

\({\lambda}_{E}=\frac{{s}_{t2}{\rho}_{t2}}{{s}_{E}{\rho}_{E}}\)

(5-23)

由绝热过程方程式有

\(\frac{{\rho}_{t2}}{{\rho}_{E}}={\left(\frac{{p}_{t2}}{{\rho}_{E}}\right)}^{\frac{1}{k}}\)

代入(6-24)式，得

\({\lambda}_{E}=\frac{{s}_{t2}}{{s}_{E}}{\left(\frac{{p}_{t2}}{{\rho}_{E}}\right)}^{\frac{1}{k}}=\frac{1}{\frac{{s}_{E}}{{s}_{t2}}{\left(\frac{{\rho}_{E}}{{p}_{t2}}\right)}^{\frac{1}{k}}}\)

\({\lambda}_{E}=\frac{1}{{\varepsilon}_{E}{x}_{E}^{1/k}}\)

式中\({\varepsilon}_{E}=\frac{{s}_{E}}{{s}_{t2}},{x}_{E}=\frac{{\rho}_{E}}{{p}_{t2}}\)

若选取适当的ε_E,则联立(5—23)、(5—26)式可解得λ_E及x_E,因而p_E及M_E亦可求得：

\({p}_{E}={x}_{E}{p}_{t2}\)

\({M}_{E}={\lambda}_{E}{\left(\frac{\frac{2}{k+1}}{1-\frac{k-1}{k+1}{\lambda}_{E}}\right)}^{\frac{1}{2}}\)

式中p_E、M_E、λ_E——E-E截面的静压、马赫数及速度系数。

立管中的燃气流经E-E截面后将和立管喷水孔喷入的水柱相遇而受阻，故燃气流在与喷入水柱混合之前又将出现激波(仍按正激波处理)。若忽略燃气流与立管间的热交换及摩擦，则激波前的气流参数应与E-E截面的气流参数相同。

由正激波公式可得波后气流参数；

\({\lambda}_{s}=\frac{1}{{\lambda}_{E}}\)

\({p}_{s}=\left(\frac{2k}{k+1}{M}_{E}^{2}-\frac{k-1}{k+1}\right){p}_{E}\)

式中λ_s、p_s——波后的速度系数及静压.

燃气流穿过激波之后就到达喷水区，故可认为波后的气流参数即燃气流与水柱相遇时的参数。

至此，水室水面的燃气静压p₀及立管喷水孔处燃气流的静压p_s均已可求，代入(5-18)式后，便可求得喷水孔总面积s₂

参 考 文献

(1)工程热力学，沆维道、郑佩芝、蒋淡安合编，人民教育出版社，1965年。

(2)  工程热力学，郑令仪、孙祖国、赵静霞编，国防工业出版社，1983年。

(3)  圆体火箭发动机原理，董师颜、孙思诚、张兆良、徐万赋编，国防工业出版社，1983年。

(4)  固体火箭发动机设计，王元有等编著,国防工业出版社，1984年。

(5)  身管武器和火药火箭内弹道学，〔苏〕M.E.谢列伯梁可夫著,国防工业出版社，1965年。

(6)  无后坐炮设计，杨则尼等编著,国防工业出版社，1983年。

(7)无坐力炮设计手册，张东妍编，国防工业出版社，1978年。

(8)The Internal ballistics of a Recoilless High-low Pressure Gun,Kapur,J.N.,Applied Scientific Research,Section A,Vol6,No.5-6,1957.