第三章 固体推进剂火箭发动机的稳定燃烧

这一节将研究推进剂燃速规律改变的原因，也论述了用来预示火箭发动机稳定工作过程的方法。

3.1与内流空气动力学流场无关的燃速规律的变化

3.1.1 所用材料引起的变化

3.1.1.1发生在推进剂/绝热层界面上的变化

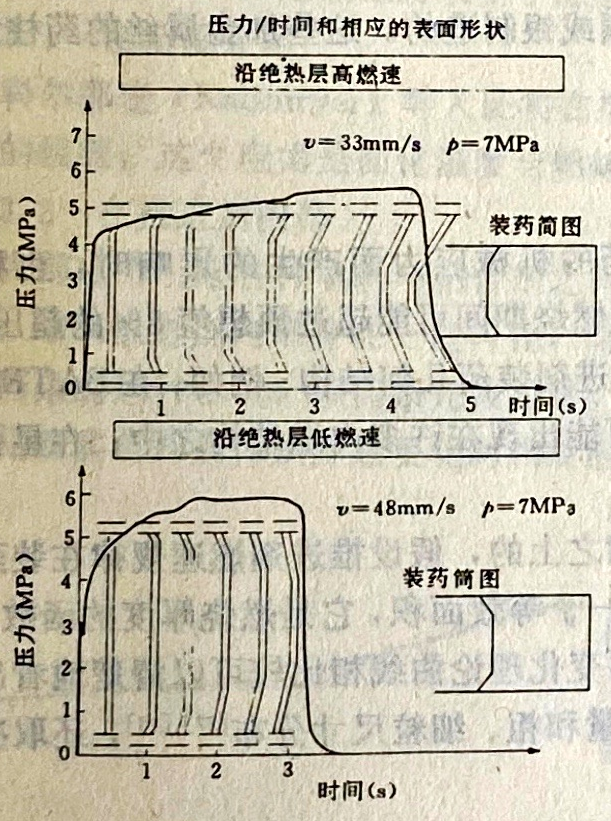
在端面燃烧方式下，固体推进剂装药对这种现象特别敏感。分析中止燃烧后的燃烧表面，常常可以看到表面已变形，这很容易用靠近绝热层的推进剂燃速发生改变来解释(图4.5)。

图4.5端面燃烧装药燃面退移的形象表示

(a)局部燃速变化的原因

·在靠近阻燃层的区域里存在着大浓度的细颗粒，或在那个区域存在着特别的颗粒分布。这些颗粒可能是高氯酸铵、抗不稳定燃烧添加剂、或者固态内弹道催化剂。如果再被细化，所有这些组分都能增加燃速值。迈斯内(Messner)[24]指出，含有铁氧化物的配方可得到70%的燃速激升。史密斯(Smith)[5]对靠近界面AP聚集的试验证明进行了评价。但是，乔利(Jol-ley)等人却认为那种特性不会总是出现。

• 在界面推进剂液体组分迁移

在固化过程中，当推进剂仍为捏塑体，并在硬化中捏塑性趋于降低时，就有可能出现增塑剂或内弹道添加剂的迁移。阻燃层中增塑剂的转移，不仅导致推进剂局部填加剂含量的增加，而且还导致燃速增加。相反，推进剂局部内弹道添加剂含量的减少降低了燃速，但是，火焰前锋以平行层方式前进的趋势抵消了这种作用。

• 界面附近材料的热传导

这种现象，产生于由燃烧室内部气流引起的对发动机壁面的热传递，引起了与加热材料直接接触的推进剂温度的升高。这种状态很有可能出现在自由装填端面燃烧固体装药的燃烧过程中。加热气体在壳体和装药之间间隙内的流动可能引起绝热层和相接触的局部推进剂的加热。

(b)补救方法

• 活性粘合剂推进剂装药情形

这里，我们关心硝化甘油被绝热层吸收这一现象：该处推进剂爆热局部地减少了，但是内弹道添加剂的含量却明显地增加了。推荐应用高度交联阻燃层或硅酮。其中加入多异氰酸酶床层，可以推迟组分的迁移，这使绝热层有足够的时间来保持其机械强度。当加热物质出现在界面附近时，可以证明，加入具有分解放热性能的组分对限制燃速激升是很有用的。

•  惰性粘合剂异质推进剂装药情形

通常的聚氨酯型粘合树脂中，增塑剂的迁移减慢，从而降低燃速激升。这可以利用高交联聚氨酯或多异氰酸酯作为防止物质迁移的屏障。

3.1.1.2控制燃速

(a)采用的技术

有许多研究来评价可以局部控制燃速的端面燃烧推进剂装药的优点。有两种技术可以考虑：

第一种技术是在垂直于燃面加入推进剂药条，这些药条比基体推进剂具有更高的燃速。在两种推进剂之间不产生热交换，因为它们都是良好的热绝缘体，而且在较低燃速推进剂中产生的锥面角度，在特定工作压强]下，取决于两种燃速之间的比率。

另一种技术是在推进剂装药内部加入金属丝来获得超燃速效应。这些金属在相对低温下熔化，导热非常好，它向邻近的推进剂传递着热流，提高了该处的初始温度并因此提高了该处的燃速。所用的有代表性的金属丝是用铜或银制造的。这些加金属丝的药柱设计

在第二章中已经讨论过了。

3.1.2峰值效应

3.1.2.1现 象

峰值效应—-当用来预示由于复合推进剂装药的机械应力而产生的影响时，也称为BARF、BRAF、SBRE或BRINBOW效应——是指在燃烧期间可能超过预想值8%的超压强这个超压强在工作中不是常数。相应的时间取决于推进剂装药几何结构。例如，在BATES装药中，与肉厚烧掉一半的那个点相对应。这种现象可能出现在许多内燃结构之中；在星孔装药中也同样观察到了这种现象。

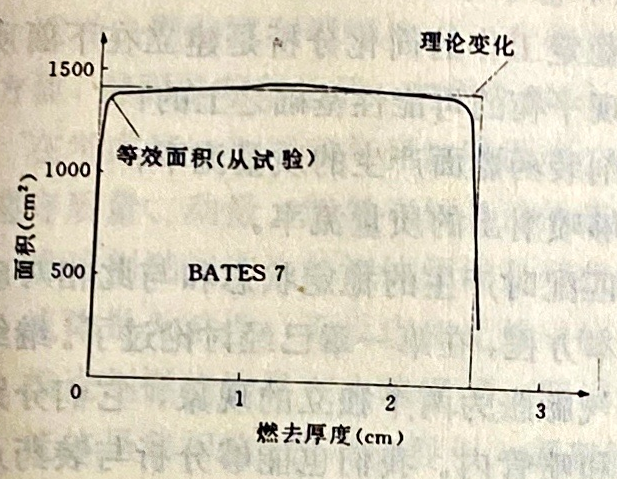
这样一个燃烧分析结果是建立在内弹道规律基础之上的，假设推进剂燃速规律在装药各点都是一样的。然后这种分析提供出燃面变化，成为一个等效面积，它是燃烧厚度的函数。当燃烧过程中出现了峰值效应时，把前面的分析与燃面变化理论曲线相比较可以清楚地看出两者存在的差别(图4.6)。这主要取决于AP,它的含量和粗、细粒尺寸分布[27、[28],还取决于推进剂内是否含有铝。

图4.6 BATES装药燃面变化的比较

3.1.2.2制造方法的影响

分析在超压最大值下BATES推进剂装药中止燃烧后得到的结果，表明峰值效应是由作为推进剂厚度函数的燃速规律变化所引起的。弗莱德兰德(Friedlander)和乔丹(Jordan)给出了相同的解释，即，由制造过程引起了推进剂固体填料的特殊分布。

3.1.2.3考虑峰值效应的内弹道预示

通常，某一推进剂的平均然速与经验规律的偏差仅仅通过从燃烧过程所获得的结果分析而得，它具有如下的形式：

\(\frac{{r}_{r}}{{r}{0}}=f(e)\)

式中r_r—推进剂在燃烧过程中的实际然速，r₀——是已知的推进剂燃速，不包括峰值效应，e——是燃烧厚度。

作为一个规律，r./ro的变化值为5%,在0.95到1.05范围内。对一些径向燃烧为主的装药(管形的，星形的),上述规律在绘图时呈现出一个峰值，对更复杂的具有各种燃烧形式组合(在R、Z和θ)的药型(FINOCYL类型),具有正弦曲线的形状.目前，精确的内弹道预示通常需要大量的试验结果为先决条件，这些分析有助于建立\(\frac{{r}_{r}}{{r}{0}}=f(e)\)规律，这在计算中是必须要考虑到的。

3.1.3机械应力

机械应力出现在与壳体粘接的推进剂药柱内：

在推进剂固化后冷却期间；在工作期间，当燃烧室增压时。

在某些情况下，这些应力改变了燃速规律。

3.1.3.1在粘接界面

科尔耶麦(Kallmryer)等人证实在推进剂阻燃层界面燃速增加了，这个燃速增加是粘接应力的函数；这个应力是固化温度与燃烧温度之差的函数。

3.1.3.2在推进剂内部

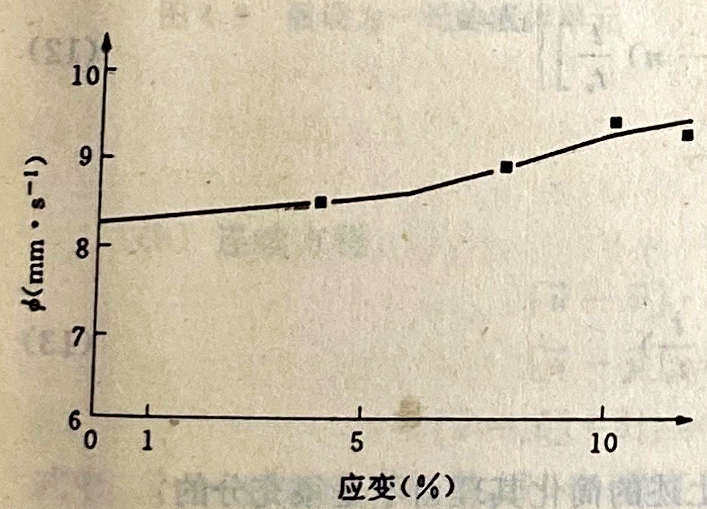
内部应力引起各种填料与粘合剂之间的脱湿过程发生；随着负载强度的提高，脱湿程度增加。结果推进剂内部存在一些内孔，而成为可压缩，于是观察到燃速增加[31]。图4.7演示了对药条的这种影响，该药条先被拉紧，然后用强到足以保持伸长状态的力来加以限制。燃速变化确实与药条体积开始变化时相对应。

图4.7推进剂伸长对燃速规律的影响燃速矢量平行于张应力

3.1.4加速度

在飞行时，由于火箭加速度，可能会改变发动机的工作状态。对含铝推进剂，这种改变尤为明显。

中止燃烧表明，当受到直接指向推进剂表面的垂直加速度作用时，这种类型推进剂燃烧表面出现了大量的圆锥形小坑。它们是由大量的铝液滴引起的，液滴加强了对表面的热传导，结果，在接触点燃速明显地增加了。当铝液滴变得更大(且可能被氧化)时，小坑底部的燃速减小下来(尽管仍然大于没有加速度时的燃速),小坑底部变平了。

基于对这个课题所进行的研究，如图4.8所示，我们注意到，当存在下列情形时这种现象才会出现：

• 加速度超过一个临界值，该临界值是铝颗粒尺寸和燃速的函数(对燃速为5mm/s且含有5μm的铝颗粒的推进剂来说，大约为10g);
• 加速度和燃面之间的角度通常达不到临界值(大约为20°);超过这个值，加速度对燃速的影响可以忽略不计。

3.2流场确定

3.2.1背景和基本原理

发动机稳定工作的简化分析是建立在下面所述两项之间实现平衡的可能性基础之上的：

• 由推进剂装药燃面产生的质量流率；
• 喷管能够喷射出的质量流率。

当两者匹配时产生的稳定状态和与此相对应的单位质量基本方程，在第一章已经讨论过了。继续假设燃烧和燃气膨胀为两个独立的现象，它们分别发生在燃烧室和喷管内。我们也能够分析与装药点火和熄火阶段相对应的瞬态过程。

图4.8加速度对发动机工作的影响

3.2.1.1瞬态状态

当我们不考虑由于燃烧造成的中心通道体积变化(它相当小，因为瞬态阶段很短)时，我们确实包括了表示内部气体质量变化的项，它代表中心通道的填充(或排空),且与燃气的可压缩性相联系。因此，从喷管排出的质量流率与推进剂燃面喷出的质量流率相比少了一项建立项。连续方程写为：

\({t}_{s}\frac{d{p}_{c}}{dt}+{p}_{c}=\frac{\dot m}{{C}_{D}{A}_{t}}\)                (11)

式中 \({t}_{s}=V/(r{T}_{c}{C}_{D}{A}_{t})\)——滞留时间，V-燃烧室容积，pc、Tc——燃烧室压强和温度，

At——喷管喉部截面积，\(\dot m\)——推进剂装药质量流率，\({C}_{D}\)——推进剂流量系数，r——R/M这里R是理想气体常数，M是气体分子量。

(a)增压

如果稳态燃速规律以及推进剂装药整个燃面瞬间点燃这种假设有效，则在这些条件下，压强变化由下式给出：

\({p}_{c}={p}_{\infty}{\left\{1-\exp{\left[1-(1-n)\frac{t}{{t}_{s}}\right]}\right\}}^{1/(1-n)}\)              (12)

这里，p∞是相应于稳定工作时的燃烧室压强。

(b)泄压

假设整个表面突然熄火，我们有：

\({p}_{c}={p}_{\infty}{\left\{1-\exp{\left[1-(1-n)\frac{t}{{t}_{s}}\right]}\right\}}^{1/(1-n)}\)              (13)

3.2.1.2推进剂装药设计的必要条件

由于下面几个原因，证明第一章的稳态假设和上述的简化其理由不是很充分的：

• 仅仅给定了压强平均值，这个压强水平在整个燃烧室是不均匀的。压强变化，它是推进剂厚度的函数，只要利用一系列不连续平衡来合理地近似地工作点就可以知道。
• 燃烧室内的压强变化是不确定的；必须确切地知道药柱的完整性，特别是在燃烧建立阶段。还必须确定与之相联系的局部燃速表达式(例如：方程(1))。
• 假设燃烧室内的燃气速度为零，但未考虑与热传递的增加和侵蚀燃烧相关的问题。
• 没有一个非定常现象的模型：方程(12)和(13)对瞬态结果来说只具有有限的合理性。另外这些假设还不包括推进剂流量系数的变化。

更加完整的模型应该包括非定常过程，因此必须具备准确的内流空气动力学知识。

• 3.2.2 流体力学守恒方程

流场由燃烧室和喷管构成。有些边界是惰性边界，例如：燃烧室和喷管的惰性边界。另一方面，燃面是喷射边界，在整个时间，燃面以r速度(推进剂燃速规律)沿着垂直方向移动。

在考虑流体性能和与壳体壁面热交换的约束假设条件范围之内，SNPE计算机程序求解了遵守质量、动量、能量守恒条件的流体力学方程：

• 推进剂燃烧产生的流体假设是理想的，在高温下加热了的气体。
• 流体是无粘性、无反应和无传导的，与壁面没有热交换。
• 推进剂燃烧边界在火焰根部；假设火焰高度忽略不计。
• 流体是单相的。没有必要引入凝聚相，这是因为并不因为它的出现而改变压强场或燃速。但是，在任何实际性能预估时应该对此加以考虑。

3.2.3求解一维方程

3.2.3.1 微分方程

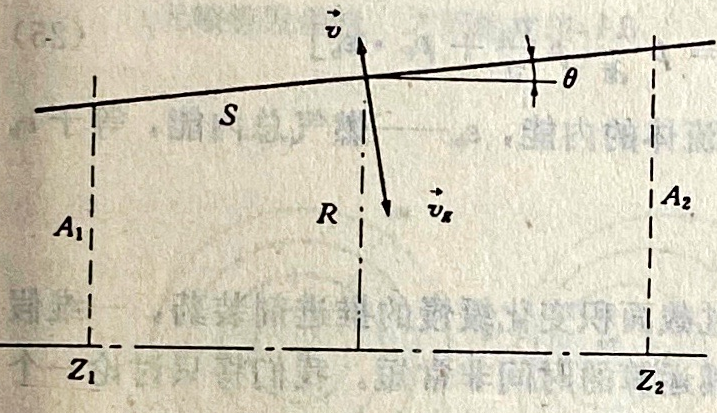
将确定图4.9所示流体段内守恒方程的每一项。这个流体段具有两个静止边界(A1和A2)和一个运动边界S。

图4.9假设为一元的流体单元

(a)燃烧壁面上气体的绝对速度

壁面流体速度假设是壁面释放出的喷射气体的速度，这里，质量守恒方程要求：

\({\rho}{{\vec v}_{r}}={\rho}_{p} {\vec v}\)                       (14)

式中\(\rho,{\rho}_{p}\)——分别是气体和推进剂的密度

\({\vec r}_{v}\)-—燃气相对于壁面的速度，

\({\vec v}\)——壁面绝对速度。

因此：   \({\vec v}_{r}={\vec v}_{g}-{\vec v}\)                         (15)

这里\({\vec v}_{g}\)是壁面上气体的绝对速度。

考虑每个矢量的各自方向，我们发现：

\({v}_{g}=v\left(\frac{{\rho}_{p}}{\rho}-1\right)\)

(b)连续方程

\([{\vec u}-{\vec v}]\bullet {\vec n}{|}_{{A}_{1}}={\vec u}\bullet {\vec n}=-u({Z}_{1})\)      (16)

\([{\vec u}-{\vec v}]\bullet {\vec n}{|}_{{A}_{2}}={\vec u}\bullet {\vec n}=-u({Z}_{2})\)      (17)

\([{\vec u}-{\vec v}]\bullet {\vec n}{|}_{s}={\vec u}_{g}\bullet {\vec n}-{\vec v}\bullet {\vec n}=-({v}_{g}+v\)      (19)

式中\(\vec u\)——流体速度矢量，\(\vec n\)——垂直于表面的矢量。对\({A}_{1},\)A₂和S计算流体流出项(垂直方向指向流场外侧)。

已知：\(dS=2\pi R\frac{dZ}{\cos \theta};\frac{\partial A}{\partial t}=2\pi R\frac{v}{\cos \theta}\)

则对dZ小增量，我们有：

\(\frac{\partial }{\partial t}(\rho A)+\frac{\partial }{\partial t}(\rho \mu A)={\rho}_{p}\frac{\partial A}{\partial  t}\)

(c)动量方程

假设为沿Z轴的单向轴流，必须计算方程的张量乘积在Z上的投影：

\(\frac{\partial}{\partial t} \int\limits_{V{t}}^{}{\rho {\vec u}dV}=-\int\limits_{V(t)}^{}{\rho[{\vec u}\times ({\vec u}-{\vec v}) ]{\vec n}dS}–\int\limits_{S(t)}^{}{(\rho I+T)}{\vec n}dS\)

式中T——二阶偏张量，粘性张力的表示式，I——单位矩阵，V(t)——受面积S(t)的限制的运动的体积我们得到：

Z向投影： \([{\vec u}\times({\vec u}-{\vec v})]{\vec n}{|}_{{A}_{1}}=[{\vec u}\times {\vec u}]{\vec n}{|}_{{A}_{1}}=-{u}^{2}({Z}_{1})\)      (21)

Z向投影：  \([{\vec u}\times({\vec u}-{\vec v})]{\vec n}{|}_{{A}_{2}}=[{\vec u}\times{\vec u}] {\vec n}{|}_{{A}_{2}}={u}^{2}({Z}_{2})\)      (22)

Z向投影：  \([{\vec u}\times({\vec u}-{\vec v})]{\vec n}{|}_{s}=-{v}_{g}({v}_{g}+v)\sin \theta \)    (23)

考虑到\(\partial Z/\partial A=2\pi R \text{tg} \theta\),并让Z1趋近于Z₂,我们得到：

\(\frac{\partial}{\partial t}(\rho uA)+\frac{\partial}{\partial Z}(\rho {u}^{2} A)+A\frac{\partial}{\partial Z}(p)={\rho}_{p}{v}^{2}\frac{{v}_{g}}{v}\frac{\partial A}{\partial Z}  \)     (24)

(d)能量方程

当对整个体积V(t)积分时，当地能量守恒方程为：

\(\frac{\partial}{\partial t}\int\limits_{V(t)}^{}{\rho (e+\frac{{\vec u}^{2}}{2})dV}=-\int\limits_{S(t)}^{}{\rho(e+\frac{{\vec u}^{2}}{2})(\vec u-\vec v){\vec n} dS}-\int\limits_{S(t)}^{}(p\bullet {\vec u}-T\bullet {\vec u}){\vec n}dS-\int\limits_{St()}^{}{{\vec q}\bullet {\vec n}dS}\)

如上处理可以确定各项，则微分表示式为：

\(\frac{\partial}{\partial t}(\rho \varepsilon A)+\frac{\partial}{\partial Z}(\rho \varepsilon {u} A)+\frac{\partial}{\partial Z}(puA)={p}\frac{\partial A}{\partial t}[p\frac{{v}_{g}}{v} +{\rho}_{p}{\varepsilon}_{b}] \)           (25)

式中ε——气体流量的总内能，e=u²/2,这里表示流体的内能， εb——燃气总内能，等于\({e}_{b}+{v}_{g}^{2}/2\),这里eb表示燃气的内能。

3.2.3.2计算一维方程组的计算机程序

因为, 对具有“长度对直径”高比值和燃气流过截面积变化缓慢的推进剂装药，一维假设证明是相当正确的，因此，已开发了几种程序，其运算的时间非常短。我们将只讨论一个例子：PROCNE[34],它在推进剂装药初步设计分析中得到广泛的应用。

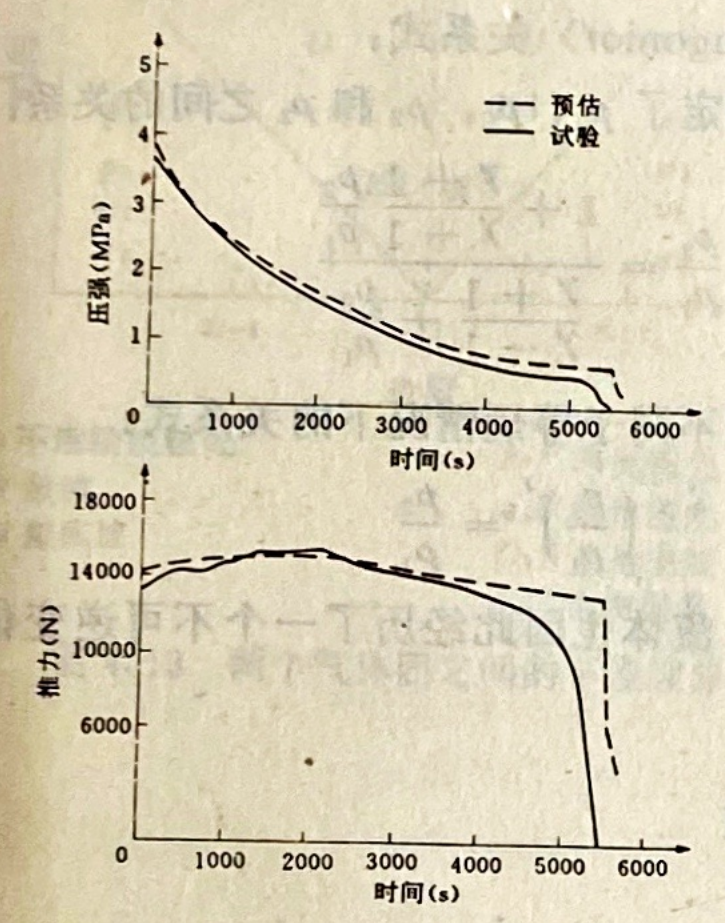
守恒方程中考虑了非定项。沿着推进剂装药轴线方向流场分成不同的区域：它包括燃烧室流场和喷管流场。程序所选择的数字方法是：杨奈恩科(Yanenko)[35]提出部分两步法(fractional two-steps)。PROCNE1程序用来计算内流空气动力学流场的变化，它考虑了作为时间函数的几何变化。图4.10是无喷管发动机的压强、推力预示与试验结果的比较。

图4.10预示(PROCNEN)和试验(无喷管发动机)之间的比较

3.2.4 复杂几何条件的守恒方程计算

通过推进剂装填系数的提高，特别是实现了复杂几何结构的装药设计，从而获得了火箭发动机内弹道性能的提高。这样的结构引起了压强和流动速度的明显变化，也使得推进剂燃速规律和当地气体动力学流场之间的耦合成为可能。因此，必须求解尽可能典型状态时的流体力学方程。

3.2.4.1 二维和三维程序基本原理

戈都诺伍(Godunov)等人建立了求解控制方程的数字程序。在讨论这个程序之前，一些关于激波和不连续分析的提示是必需的。

(a)激波

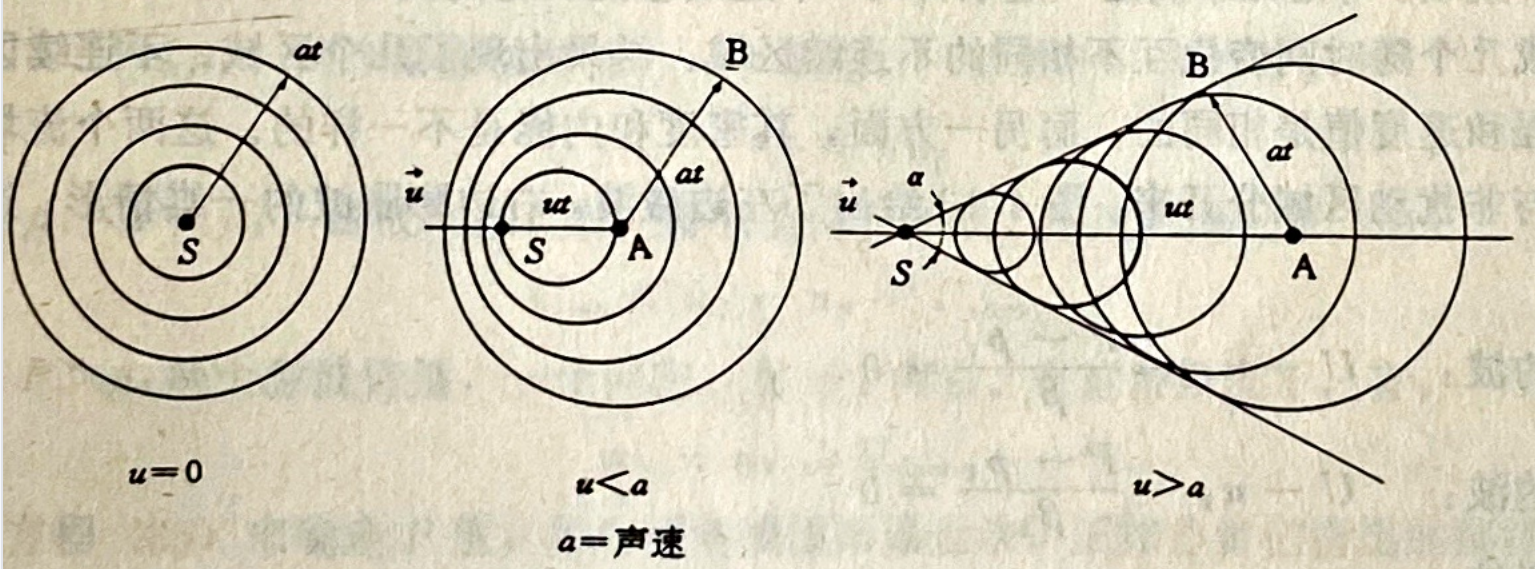
首先是一些流体力学的概念：在无运动流体中或在以均一速度运动的流体中给出一个小扰动源S(图4.11):

图4.11小扰动在均一速度运动流体内的传播

• 无运动流体：u=0

时间t=0时，扰动出现，它在各个方向以声速a扩散，时间t时，占据了一个半径值为at的球面。

• 以均一速度运动的流体；当u<a时

在亚声速流里，扰动球面一个套一个，且包围着扰动源，只要具有足够的时间，扰动就可以达到流场各个点

• 以均一速度运动的流体：当u>a时

在超声速流里，扰动波出现在一包络面里。仅在包络面里的空间才受到扰动的影响。

• 不连续的形成

在受轻微压缩作用的流体里，由于介质温度升高，连续波越来越快地扩散，最后赶在一起形成一道压缩波。相反情况，当流体受到轻微膨胀扰动，由于温度下降，这些波不可能赶在一起，因此在大多数气体中不会出现不连续波，尽管它可能出现在某些计算方法里

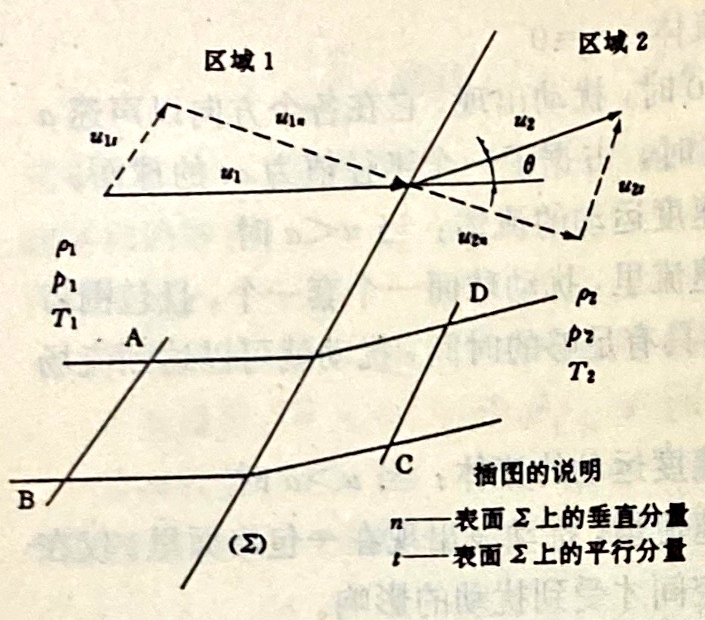
• 通过不连续平板的变化(图4.12)

图4.12 通过不连续平面(S)的流场变化

当经过不连续面时，可压缩流经历了有限的压强温度变化，但是它的速度不仅在方向而且还在数值上发生突变。ABCD体积上的守恒方程写出如下：

• ·质量守恒\({\rho}_{1}{u}_{1n}={\rho}_{2}{u}_{2n}\)                     (26)
• 动量守恒\({p}_{1}+{\rho}_{1}{u}_{1n}^{2}={p}_{2}+{\rho}_{2}{u}_{2n}^{2}\)                     (27)

这里 \({u}_{1n}={u}_{2n}\)

• 假设绝热，则能量守恒为：

\(\frac{{u}_{1n}^{2}}{2}+\frac{\gamma}{\gamma-1}\frac{{p}_{1}}{{\rho}_{1}}=\frac{{u}_{2n}^{2}}{2}+\frac{\gamma}{\gamma-1}\frac{{p}_{2}}{{\rho}_{2}}=\frac{\gamma+1}{2(gamma-1)}\left[ {c}_{2}-\frac{\gamma-1}{\gamma+1}{u}_{1t}^{2}\right]\)

这里\(c=\sqrt{\frac{2(\gamma-1)}{\gamma+1}{c}_{p}{T}_{c}}\)

还要加上理想气体状态方程：

\({p}_{1}={\rho}_{1}\gamma {T}_{1}\)

\({p}_{2}={\rho}_{2}\gamma {T}_{2}\)

这里ϒ=R/M——单位气体常数雨果尼奥特(Hugoniot)关系式：

这个式子确定了\({p}_{1},{\rho}_{1},{p}_{2},{\rho}_{2}\)之间的关系：

\(\frac{{\rho}_{2}}{{\rho}_{1}}=\frac{1+\frac{\gamma+1}{\gamma+1}\frac{{p}_{2}}{{\rho}_{1}}}{\frac{\gamma+1}{\gamma-1}+\frac{{p}_{2}}{{\rho}_{1}}}\)

这个关系明显地不同于等熵情况下的关系式

\({\left(\frac{{\rho}_{2}}{{\rho}_{1}}\right)}^{\gamma}=\frac{{p}_{2}}{{p}_{1}}\)

经过激波，流体也因此经历了一个不可逆变化过程，理想气体的熵为：

\(S={c}_{v}\ln \left(\frac{p}{{\rho}^{\gamma}}\right)\)十常数

雨果尼奥特关系式仅表达了熵增时的实际物理变化。

(b)不连续分析方法

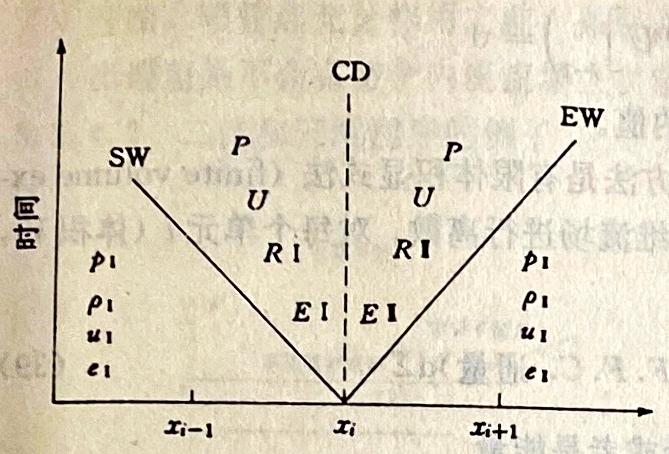
戈都诺伍等人[36]提出了如下的方法：当两团同样气体(假设是不同压强值的理想、可压缩气体)相遇时，在初始压强分布之内，相遇面形成了不连续面。相遇面每边的物理值可能经历了某种跳动。可是如果满足一定条件时，不连续也能以稳定的形式存在。如果不满足，它就会分裂成几个随时间变化互不相同的不连续区域。结果出现了几个区域。不连续区域接触边上的压强和速度值是相同的。而另一方面，其密度和内能是不一样的。这两个流场被激波或膨胀波与非扰动区域分开来。图4.13给出了左边激波，右边膨胀波的一维情形。这些通常表示如下：

CD不连续接触处,     p,P当地压力   u,U当地速度    O,R当地密度   EW膨胀波    e,E当地能量

图4.13 两个气体团之间的不连续分离

左边的波：\(U-{u}_{I}-\frac{P-{p}_{I}}{{\beta}_{I}}=0\)   (31)

右边的波：\(U-{u}_{II}-\frac{P-{p}_{II}}{{\beta}_{II}}=0\)     (32)

对于激波：

\({\beta}_{i}=\sqrt{{\rho}_{i}\frac{\gamma+1}{2}P_\frac{\gamma-2}{2}{p}_{i}}\)

这里i=I或II,取决于波是处于左边的，还是右边的。

对于膨胀波；\({\beta}_{i}=\frac{\gamma-1}{2\gamma}{\rho}_{i}{a}_{i}\frac{1-\frac{P}{{p}_{i}}}{1-{\left(\frac{P}{{p}_{i}}\right)}^{\frac{\gamma-1}{2\gamma}}}\)

式中ai——介质i的声速=,i—i=I或II,取决于膨胀波是处于左边的，还是右边的。

结果，就能确定两股气体相遇出现的区域。消去方程(31)和(32)的U,则P可由下式确定:

\(F(P)={u}_{I}-{u}_{II}=\frac{P-{p}_{I}}{{\beta}_{I}}+\frac{P-{p}_{II}}{{\beta}_{II}}=f(P,{p}_{I},{\rho}_{I})+f(P,{p}_{II},{\rho}_{II})\)                        (35)

与

\(f(P,{p}_{i},{\rho}_{i})=\frac{P-{p}_{i}}{\sqrt{{\rho}_{i}\left(\frac{\gamma+1}{2}P+\frac{\gamma-1}{2}{p}_{i}\right)}}, P \ge {p}_{i}\)

\(f(P,{p}_{i},{\rho}_{i})=\frac{2}{\gamma-1}{a}_{i}\left[{\left(\frac{P}{{p}_{i}}\right)}^{\frac{\gamma-1}{2\gamma}}-1\right], P < {p}_{i}\)                    (36)

分析函数F(P)可以揭示出几个可能性。假设pI<pII则

\(f({p}_{I})={U}_{exp}=\frac{2}{\gamma-1}{a}_{II}\left[{\left(\frac{{p}_{I}}{{p}_{II}}\right)}^{\frac{\gamma-1}{2\gamma}}-1\right]\)         (37)

\(f({p}_{II})={U}_{shock}=\frac{{p}_{I}-{p}_{II}}{\sqrt{{\rho}_{I}\left(\frac{\gamma+1}{2}{p}_{II}+\frac{\gamma-1}{2}{p}_{I}\right)}}\)     (38)

• 如果0<P≤p_I,两个膨胀波传播，一个朝左，一个朝右，我们有：

u_I-u_II≤U_exp

• 如果p_I<P≤p_II,激波向左扩展，膨胀波向右扩展，在这种情况下，有：

U_exp<u_I-u_II<U_shock

• 如果P>p_II两个激波传播，一个向左，另一个向右。在这种情况下，有：

u_I-u_II≥U_shock

求解方程(35)来确定P值，用牛顿切线逐渐逼近法，正如作者们指出的那样，对某一初始值，该方法保证收敛迅速。用收敛时的P值[36]来计算其它参数。

(c)数值方法

由戈都诺伍等人建立的流体动力学一维非定常方程的差分格式，给我们提供了这一方法的简单实例。假设流场每一单元体的密度ρ、冲量ρu、各总能量ρ(e+u²/2)是常数，对流场性能的每一项进行简化，并且在t到t+Δt时间间隔内采用J-1/2网格(对\([{x}_{j-1},{x}_{j}]\)部分),则守恒方程写出如下：

\({\rho}^{j-\frac{1}{2}}-{\rho}_{j-\frac{1}{2}}({x}_{j}-{x}_{j-1})+\Delta t({[RU]}_{j}-{[RU]}_{j-1})=0\)

\(({[\rho u]}^{j-\frac{1}{2}}  -{[\rho u]}_{j-\frac{1}{2}})({x}_{j}-{x}_{j-1})+\Delta t({[P+R{U}^{2}]}_{j}-{[P+R{U}^{2}]}_{j-1})=0\)

\(\left({\left[\rho(e+\frac{{u}^{2}}{2})\right]}^{j-\frac{1}{2}}-{\left[\rho(e+\frac{{u}^{2}}{2})\right]}_{j-\frac{1}{2}}\right)({x}_{j}-{x}_{j-1})\)

\(+\Delta t\left(   {\left[ RU(E+\frac{{U}^{2}}{2})+PU\right]}_{j}-{\left[RU(E+\frac{{U}^{2}}{2})+PU\right]}_{j-1}   \right)=0\)

下标代表t时刻的值，而上标代表t+Δt时刻的值。

这种计算可以扩展到三维结构上去，所采用的方法是有限体积显式法(finite volume ex.plicit method)。这种计算必须以小单元体对整个三维流场进行离散。对每个单元i(体积Vi面积∑i,守恒方程概括为

\(\frac{\partial}{\partial t}\int\limits_{{V}_{i}}^{}{(F.F.C.)dV}=\int\limits_{{\sum}_{i}}^{}{(F.F.C.flux)}d\sum\)          39)

这里F.F.C(指流场特性)是气体质量密度、动量或者是能量。

为了得到(39)式左边的项目，假设每个单元的F.F.C是常数，则可以引出如下的近似：

\(\frac{\partial}{\partial t}\int\limits_{{V}_{i}}^{}{(F.F.C.)}dV=\frac{{V}_{i}}{\Delta t}[{F.F.C.}_{t+\Delta t ,i}-{F.F.C.}_{t ,i}]\)  

这里F.F.C表示t时刻整个单元i的F.F.C值。

为了计算方程(39)第二项，该项与通过单元网格边界F.F.C能量相对应，我们还需应用前一节所述方法来求解每个与单元i相邻的单元的接触处不连续问题。

这些计算是以垂直于单元i每个面的方向进行的。速度的切线分量在通过激波或膨胀波之后并不改变。

这就给出了流体的那个边界上的性能：压强、垂直速度、切线速度、质量密度和能量。然后，在时间t+Δt和在单元i内用下式就能显式地计算各种通量的幅值：

\({F.F.C.}_{t+\Delta t,i}={F.F.C.}_{t ,i}+\frac{\Delta t}{{V}_{i}}\int\limits_{\sum i}^{}(F.F.C.flux)d\sum\)  

用理想气体状态方程加以完善的方程(39),t+Δt时刻的F.F.C值可以显式地计算出，它是建立在已知i时刻的值和从不连续分析中得到的“主值”(maior values)(P、U、R、E)基础之上的：

• 在二维中，相对于四面中的每一个面；
• 在三维中，相对于单元i六面中的每一个面。

在这点计算时，要考虑的uI和uII值是所选择的整个边界上的速度向量的垂直分量。

(d)边界条件

表示式(方程(39))说明需要引入以质量、动量和能量通量形式表示的边界条件，这些通量穿过了位于计算流场边界上的表面。为确定这些通量值，还需要更多的数值，这取决于所遇到的边界类型：

• 在不渗透壁面情况下，气体进入单元的速度在边界上必须是0,如：U=0。确定P值，则需要建立符合上述条件的具有特性值(u_I,p_I,ρ_I)的模型单元。如果(u_II,p_II,ρ_II)是单元边界上的值，则我们看到选择\({u}_{I}^{N}=-{u}_{II}^{N}\)(这里上标N代表速度矢量垂直于表面的分量),p_I=p_II以及ρ_II=ρ_I是问题的一个解。
• 如果边界是推进剂装药的对称面，则计算按不渗透壁面的方式来处理。
• 在喷射壁面情况下，确定各种通量值需要两个步骤。首先，辟面反应按僚性膀而者虑；其次，由于推进剂然烧，使获得的质量、能量通量增加了，与推进剂燃烧有关的动量通量假设为零。
• 如果边界位于喷管超声速喷射区域出口平面上，最简前的微向流场区域外延伸一点，并且指定假想单元与边界单元具有相同F.F.C计算值。计算

开始，喷管起充分作用之前，条件是相同的，因此这也是非常不严格的。必须注意到导出误差是不会在整个内流流场上扩散的。

3.2.4.2二维和三维程序的例子

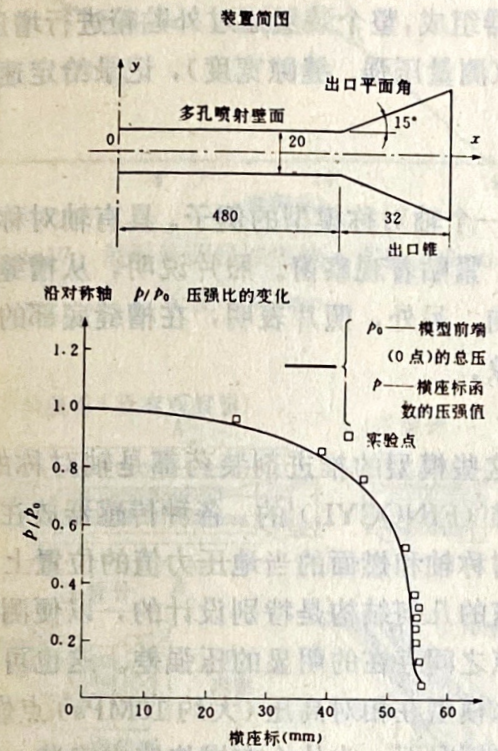
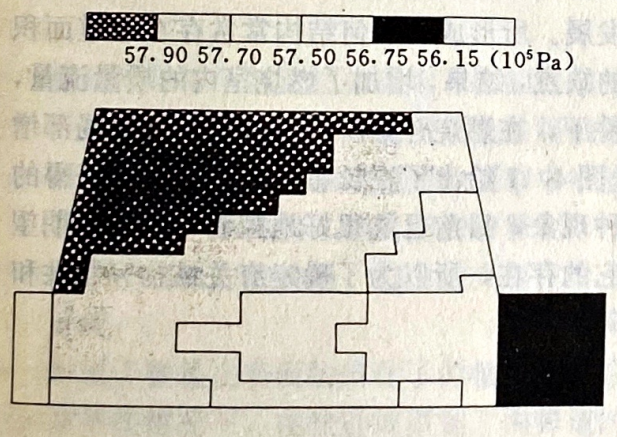
图4.14显示的是二维平面情况计算与实验结果之间的比较。由法国国家航空航天研究局(ONERA)建立的实验装置模拟了类似于无喷管火箭发动机燃烧室的构造形式。冷空气流(260K)提供给多孔壁面，它足以在膨胀区域引起超声速状态。图4.15表示的是FINOCYL型推进剂装药前部的计算结果。

图4.14普诺妮(Procne)程序。预示和实验结果比较。

图4.15 Fin.内压强分布

3.2.5流场的实验测量

要完成的实验是：

• 确定实际几何构造中的流场
• 证实预估所获得的结果。这些模型有时不同于实际的推进剂装药结构形式；然而它们具有易于控制输入参数和不很复杂的边界条件的优点。

3.2.5.1 流场测量

(a)压强测量

定常流动试验不需要使用具有非常宽测量范围的传感器。但是为了准确获得流场各个位置压强的测量值，这些压强传感器必须是精确的，即使对于非常高的压强平均值也应该如此。

(b)速度测量

用以测定速度平均值和它的波动(当要计算雷诺张量分量时所需要的参数)的热线测试技术(hotwire technique)[37]被用来测量”纯净”冷气流(没有粒子)。激光测量方法(ONERA所采用的方法)可以观察到冷气体中当地的速度场，但是这个技术需要给流场提供非常细小的颗粒。

(c)温度测量

响应时间短的热电偶制造技术有了发展，这就提供了在燃烧室热侵蚀气体环境内进行温度测量的可能性。

(d)显像法

为了在试验期间观察流场，显像法需要在实验装置上开一个透明观察窗。这个方法不仅适用于冷气体也适用于热气体。但是，在非常高的温度下，必须确认观察窗的变形使所观察到的现象和过程不致失真。

3.2.5.2用于确定流场的模型

(a)缝隙增压分析模型

对于自由装填的推进剂装药，在绝热金属壁面和推进剂阻燃层之间存在着缝隙。在点火期间，缝隙里的压强与燃烧室里的压强是不平衡的。由于压强差，推进剂装药受压靠住壳体壁面，引起推进剂伸长，以及出现了各向不同性的压缩应力。这些可能影响装药的结构完整性，特别是在冷起动时。

试验模型由放置一圆柱形中心孔推进剂装药的容器组成，整个装置通过外贮箱进行增压。这是一冷气试验。沿着不同母线分布了许多测量仪器(测量压强、缝隙宽度),记录给定速率下承受压强升高的模型性能。

(b)流线显像法模型

能够试验几种类型的几何构造。图4.16表示的是一个轴对称模型的例子。具有轴对称槽的的半圆柱形推进剂装药，模拟实际装药的结构形状，紧贴着观察窗。照片说明，从槽缝中流出的流线，当遇到中心主流时，流线都有明显的偏向。另外，照片表明，在槽缝底部的底流处，存在着燃速比推进剂其它任何地方都要高的现象

图4.16 轴对称试验发动机燃烧工作时的流体流线显像法试验装置简图

(c)压强场分析模型

用于这些模型的推进剂装药都是轴对称的，或者是三维(FINOCYL)的。各种传感器放在可以测得沿对称轴和燃面的当地压力值的位置上。燃烧室的几何结构是特别设计的，以便测到不同测量点之间存在的明显的压强差。这也可以解释为什么模型在相对高压(大约10MPa)点燃，以及在某些情况下，为什么在燃烧室内安装一个用来增加压强盖的由心棒。

3.3 与内部空气劫力学场相关的内弹道修正

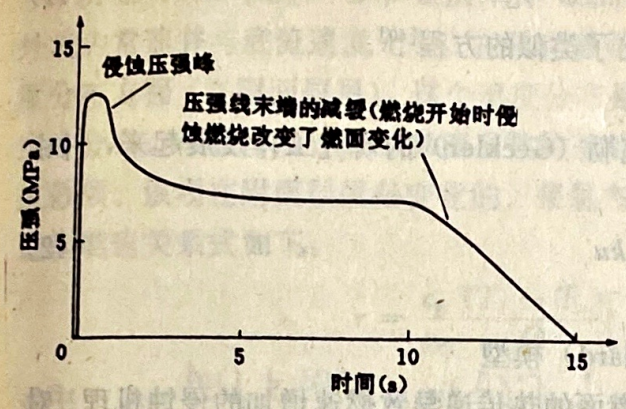
火箭发动机性能的增加引起了高装填系数装药的发展。所形成的几何结构常常存在通道面积减少的缺点，结果，增加了燃烧室内的质量流量，特别是在燃烧开始的时候。试验表明，在这些条件下，在燃烧开始阶段，推进剂燃速局部增加，与装药燃烧表面理论变化值相比存在着偏差。图4.17给出了在长星孔推进剂前端获得的压强变化。它清楚地表明在点火时存着超压。这种现象，目前已能很好地控制，有时还期望用来获得规定的压强变化。考虑到并不总是希望它的存在，所以为了确定有关结构完整性和推进剂燃面变化的结果，必须对此进行精确地计算。

图4.17星形装药侵蚀燃烧 直径203mm长度1000mm

3.3.1 侵蚀燃烧现象

3.3.1.1 确定配方敏感性

大量的研究已建立起来专门的试验装置，以确定受到平行于燃烧表面上的平均热流作用下的推进剂燃烧速度。大部分试件都是小试件，形状象小薄片，放置于由上流气体发生器释放的热气流中。

已用各种方法来确定试件的燃速；X射线照相；通过光电倍增管检测燃烧时间；中止燃烧已便形成未燃尽试件的新表面；通过透明观察窗的高速摄影。

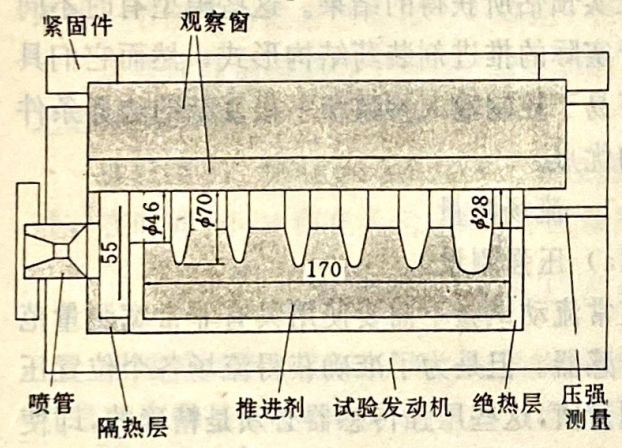
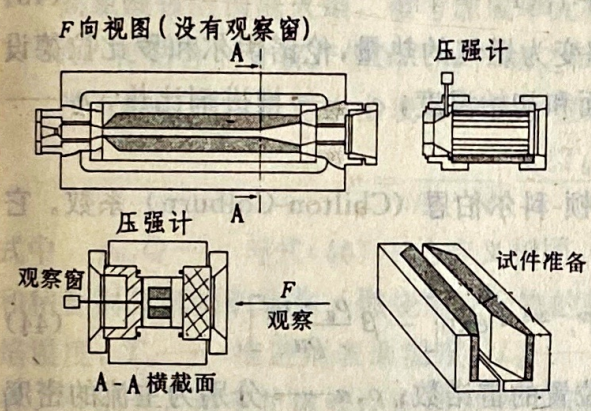
已公布的研究报告介绍了各种装置。拉泽丹(Razdan)和郭(Kou)[38],以及金(King)[39.采用放置在上流的燃气发生器。在法国，ONERA和SNPE,研制了一有趣的试验系统，它建立在超声波方法基础之上。这个方法可以对燃烧位置直接进行当地的测量，因此，通过求导，可以得到没有紊流现象时的推进剂燃速值。这个系统如图4.18所示；它包括一观察窗，以便能够使用超声波发送器，它可以使用大量的推进剂。后一特点提供了更接近于推进剂装药实际燃烧的有利条件，而不必借助于燃气发生器。

图4.18镘蚀燃烧试验分布

3.3.1.2试验结果

最重要的观察结果是[38]:

• 侵蚀现象的出现与主流的临界值有关。对于大量的混合物，就有可能确定某一速度临界值(或单位质量流率)。超过此值，推进剂燃速就会增加。基础燃速越低(没有平均流时所确定的值),对于主流的敏感程度就越大。对于给定的流动速度，推进剂的敏感性取决于压强水平。马克兰德(Marklund)和莱克(Lake)[40]完成的实验表明，对于壁面上同一流速来说，燃速随着压强水平的提高而增加。但是，如果我们考虑单位质量流率而不考虑流动速度，我们仍可以发现以前注意到的趋势，即推进剂基础燃速的变化。压强越高，推进剂基础燃速越大，推进剂对单位质量流率的敏感性也变得越小。

• 一般说，主流温度和化学成分没有影响：

-—当燃气不发生反应时，推进剂敏感性与发生器产生的燃气性质无关；

-—燃速增加似乎与流过推进剂表面的热燃气温度基本无关。

一些配方成分的存在可能引起负的侵蚀效应：这个效应(燃速减小而不是增加)可以从活性粘合剂推进剂基础燃速的观察中很清楚地看到，燃速通过添加内弹道改进剂已经有了增加。下面提供几种可能的解释：

——减少了表面的热传递，它由边界层化学反应物的吹动造成，结果改变了传输系数和反应速度；

——形成了覆盖在表面的熔化了的粘合剂，它由流体中的剪应力引起；——在某些情况下，在推进剂添加了内弹道改进剂，而因此破坏了碳化残渣。

3.3.2现象的模型化

3.3.2.1基本模型

为了把当地的燃速值与燃烧室内气体特性联系起来，已经提出了各种经验或者理论定律。

(a)倍增定律

\(r={r}_{b}(1+ku)\)或\(r={r}_{b}(1+KG)\)                          (40)

式中rb-—\(a{p}^{n}\)。为推进剂参考燃速，k——常数，u-—主流的平均速度，假设是一维的，G——\({\rho}_{g}u\)为主流的单位质量流流率，\({\rho}_{g}\)——燃气密度。

同样地，引入流速临界值G”

\(r={r}_{b}[1+k(G-G”)]\)         (41)

格林(Green)、维里恩诺伍(Vilyunov)提出了类似的方程。

(b)加法定律

这种类型的定律，是从科内(Corner)和杰克勒(Geckler)的研究工作发展起来，并由博伊森(Boisson)提出。

\(r={r}_{b}+ku\)                        (42)

3.3.2.2详细模型

(a)伦诺伊尔(Linoir)和罗比拉德(Robillard)模型

伦诺伊尔和罗比拉德提出了一种从流体到燃面的热传递导致燃速增加的侵蚀机理。对于给定压力的表面流动，通过在基础燃速上加上一个侵蚀部分来计算推进剂新的燃速，它可以从表面的能量平衡中得到：

\(\alpha({T}_{f}-{T}_{s})={\rho}_{p}{r}_{e}[L+{c}_{p}({T}_{s}-{T}_{i})]\)           (43)

式中 re侵蚀燃烧部分，L—-—由于固体分解变为燃气的热量，伦诺伊尔和罗比拉德设此项为零，Tf,Ts,Ti—-分别为推进剂的火焰、表面和初始温度，Cp-—推进剂比热，ρp推进剂密度。

热传导系数α是由兰尼(Rannie)修正的奇尔顿-科尔伯恩(Chilton-Colburn)系数。它考虑了表面喷射因素：

\(\alpha=0.0288{c}_{g}{\rho}{u}{\text{Re}}_{x}^{-0.2}{\text{Pr}}^{-2/3}\exp{\left[-\beta\frac{{\rho}_{g}{v}_{g}}{{\rho}u}\right]}\)     (44)

式中cg 气体的定压比热；Re,x-基于轴向位置的雷诺数；ρ,u——分别为主流的密度和速度；\({\rho}_{g},{v}_{g}\)—分别为主流的密度和速度；β——常数；Pr——普朗特数。

考虑到式(43)和(44),则新燃速隐式表示为：

\(r=a{p}^{n}+{r}_{e}\)                      (45)

一些研究者[38]已对此定律进行了修正：

• 所采用的雷诺数取决于直径而不是轴向位置；
• 引入一表示机械侵蚀的项(奥斯本(Osborn)和伯瑞克(Bruick));
• 对加入催化剂的EDB配方，当存在平台效应(不论在什么压强水平，燃速为常数)时，引入一辅加的分量：乔杰克(Jojic)和布莱戈杰维克(Blagojevic)。

(b)包括燃烧机理的附面层分析模型

莱恩杰利模型[43]

所用的基本燃烧模型是萨默菲尔德的GDF模型，模型描写的是含有高篇酸铵的复合推进剂。该模型仅考虑氧化产物(AP分解)和可燃气体(粘合剂分解)之间的扩散火焰，并假设刘易斯(Lewis)和施密得特(Schmidt)数近似于1,利用该模型，则燃速由下式给出：

\(r=\left[ \frac{{c}_{g}{({T}_{f}-{T}_{s})}^{1/2}}{Q}\right] \bullet \frac{{\rho}_{g}}{{M}_{1/3}}\frac{\mu}{{\rho}_{p}}\left(1+\frac{\rho\varepsilon}{\mu} \right)\)                   (46)

式中Cg气体比热，Tf,Ts—分别为火焰及表面温度，Q———加热推进剂，以及传输给气体所需的热量，\({\rho}_{g},{\rho}_{p}\)—分别为气体和推进剂密度，M—容器内可燃气体质量，μ,ε-分别表示主流的粘性和紊流扩散系数。

式(46)考虑了由于主流的存在而对流体传输性能的修正。因此GDF模型引入了复合推进剂的参考然速，该项与当地的流动形态有关，而不受火焰本身高度的影响。

方程(46)中的ρε/μ是从库特(Couete)流附面层方程积分计算而得来的，其中假设外流为常速并与底流速度无关。在马克斯曼(Marxman)工作基础之上，莱恩杰利给出了速度分布方程(在附面层里),这个速度分布是壁上具有定常喷射速度对平板上的速度分布。在这个分布、动量厚度计算和摩擦系数的基础上，莱恩杰利用普朗特混合长度假设计算了紊流扩散项。该项在附面层里是变化的。菜恩杰利建议用整个火焰高度L的平均值。所提供的推进剂燃速关系式如下：

\(r=\frac{{c}_{g}}{{\rho}_{p}}\frac{({T}_{f}-{T}_{s})}{Q}\left[\frac{\mu}{L}+\frac{8.3}{{10}^{3}}\frac{{\rho}_{e}{\mu}_{e}}{{Re}_{x}^{0.1}}{\left(\frac{L}{\beta}\right)}^{m}\psi\right]\)                (47)

式中\(\psi=\frac{\ln (1+B)}{B}\left[ 1+B{\left( \frac{L}{\delta}\right)}^{\alpha}\right]\frac{1}{\alpha+2}\)

金模型[44]

模型中考虑的机理的是代表含有过氯酸铵复合推进剂的燃烧机理，包括两种火焰：高氯酸铵的预混火焰，

• 被考虑成单元推进剂
• AP和粘合剂分解产生的气体产物之间的扩散火焰

没有外流则可以写出由表面能量守恒确定的燃速:

\(r=\frac{1}{{\rho}_{p}{Q}}\left[\frac{{\lambda}_{1}({T}_{fox}-{T}_{s})}{{L}_{1}}+\frac{{\lambda}_{2}({T}_{f}-{T}_{0})}{{L}_{diff}+{L}_{kin}}\right]\)      (48)

式中ρ_p,Q——与式(46)中的定义相同，λ₁-—HCLO₄/NH₃气相的热传导系数，λ₂AP和粘合剂分解的氧化剂/燃烧剂混合物的热传导系数，T_fox——AP火焰温度，T_f——扩散火焰温度，T_s——推进剂表面温度，L₁——AP火焰高度，L_diff,L_kin——与扩散火焰有关的参数，分别为：由于扩散和反应动力学引起的高度。

当表示出各种高度时，金给出：

\(r={A}_{1}p\left\{1+\frac{{A}_{2}}{1+{A}_{3}{p}^{2}{d}_{AP}^{2}}\right\}\)                           (49)

式中A₁、A₂、A₃——常数，它取决于推进剂和气体热性能以及取决于推进剂表面温度和相应于各种火焰类型的高度，P——压强，d_AP——AP颗粒直径。

在这个模型里，考虑了在流体速度影响下，扩散火焰弯曲的流体作用，方程(48)则成为：

\(r=\frac{1}{{\rho}_{p}{Q}}\left[\frac{{\lambda}_{1}({T}_{fox}-{T}_{s})}{{L}_{1}}+\frac{{\lambda}_{2}({T}_{f}-{T}_{0})}{{L}_{diff}\sin \theta+{L}_{kin}}\right]\)              (50)

这里θ(<π/2)是扩散火焰方向与燃烧表面形成的角度。

方程(50)所采用的各种物理性能在喷射壁面情况下保持同样的值。角度可以用简单迭代过程从附面层速度分布中计算出。建立在米克利(Mickley)和戴维斯(Davis)试验结果基础之上的经验公式使得确定当地流速成为可能，而当地流速是推进剂表面上横截面位置、主流速度和气体喷射速度的函数。

(c)最新模型

这些模型(1976年的斯威瑞登科沃(Sviridenkvo)和耶戈德金(Yagodkin),拉泽丹和郭3],贝德蒂尼(Beddini)[45]求解了简单二维构型(平面、圆柱通道)通道面积不变的守恒方程。在远离壁面，所考虑的简化假设[为：二维流动是等熵的，流体是无粘的，尽管这种假设在文献[4]中并未引用。

接近于壁面的流体性能更加复杂；与粘性有关的项被包括了进来(考虑了雷诺张量)。这些研究者利用了紊流流场，当平均时，是定常的假设：每个物理量由平均定常值和偏离于个时间内平均值的波动项所组成。

3.3.2.3 实际应用

所谓的“标准装药”SNPE方法是为快速确定推进剂侵蚀燃烧敏感性目的而发展起来的，它由在固定压强下星形小装药的燃烧组成。这些试验在不同长度的装药上进行，因此，也就与燃烧表面面积和通道面积之比的变化相对应。当推进剂为含高氯酸铵复合推进剂时，利用金模型,可以得出做过试验(方程(41)中斜率k和临界值G*的复合推进剂侵蚀燃烧参数近似值。这些值以后可以通过与压强变化(图4.19)尽可能地相一致而得到修正。