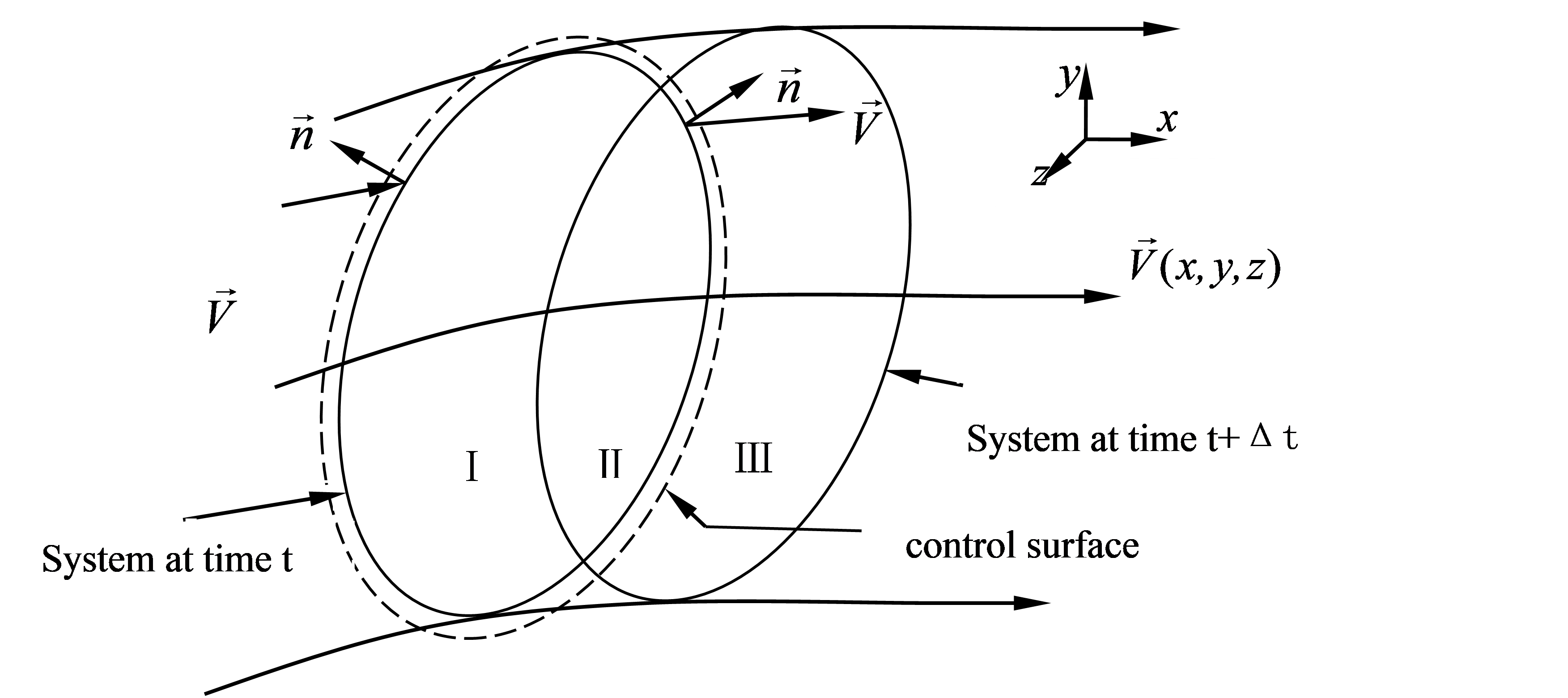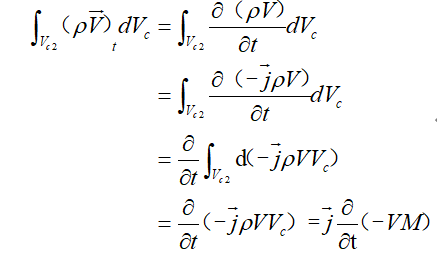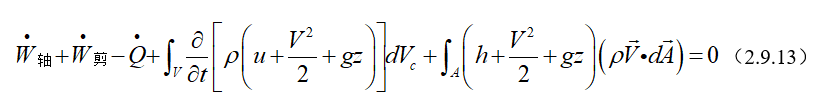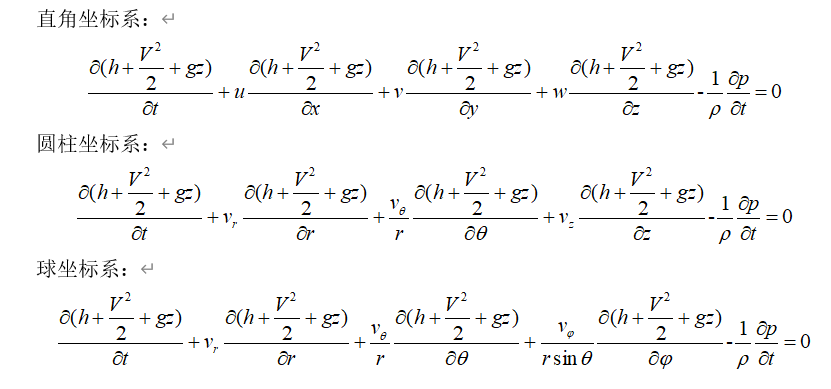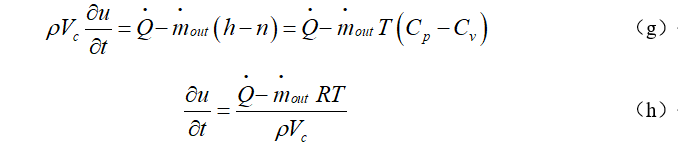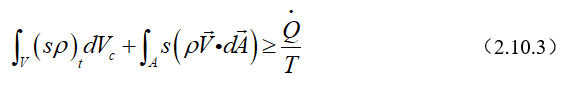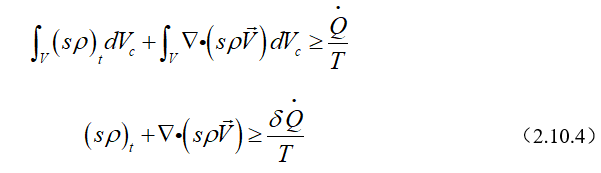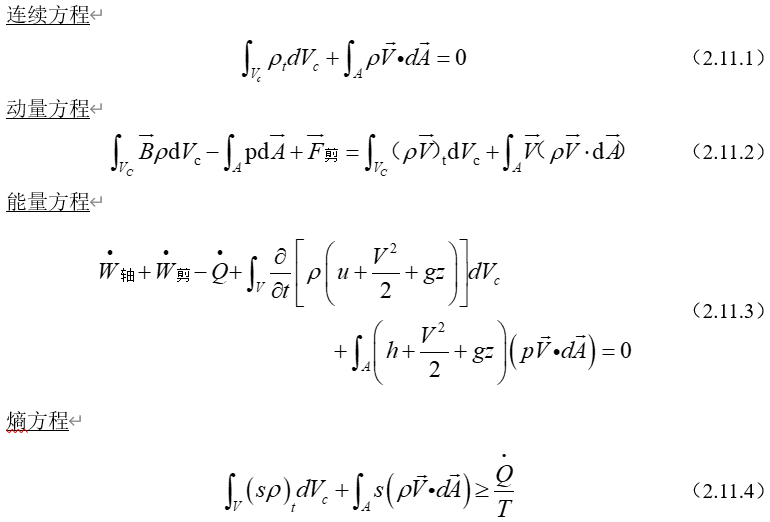第二章 无粘可压缩流体流动的控制方程
2.1 运算符号
δ不精确的微分
∇矢量倒三角符号
\(\frac{\partial }{\partial ()}\)对()的偏微分
\(\frac{D}{Dt}\)实质导数(随流导数),即跟踪流体微团运动的导数
在笛卡尔坐标系中的矢量算子:
\(\vec{A}={{A}_{x}}\vec{i}+{{A}_{y}}\vec{j}+{{A}_{z}}\vec{k}\)
\(\vec{B}={{B}_{x}}\vec{i}+{{B}_{y}}\vec{j}+{{B}_{z}}\vec{k}\)
\(\vec{A}\bullet \vec{B}={{A}_{x}}{{B}_{x}}+{{A}_{y}}{{B}_{y}}+{{A}_{z}}{{B}_{z}}\)\[\vec{A}\times \vec{B}=\left| \begin{matrix}
{\vec{i}} & {\vec{j}} & {\vec{k}} \\
{{A}_{x}} & {{A}_{y}} & {{A}_{z}} \\
{{B}_{x}} & {{B}_{y}} & {{B}_{z}} \\
\end{matrix} \right|=({{A}_{y}}{{B}_{z}}-{{B}_{y}}{{A}_{z}})\vec{i}+({{A}_{z}}{{B}_{x}}-{{A}_{x}}{{B}_{z}})\vec{j}+({{A}_{x}}{{B}_{y}}-{{A}_{y}}{{B}_{x}})\vec{k}\]
\(\nabla =\frac{\partial }{\partial x}\vec{i}+\frac{\partial }{\partial y}\vec{j}+\frac{\partial }{\partial z}\vec{k}\)
\(\nabla \varphi =grad\varphi =\frac{\partial \varphi }{\partial x}\vec{i}+\frac{\partial \varphi }{\partial y}\vec{j}+\frac{\partial \varphi }{\partial z}\vec{k}\)
\(\nabla \bullet \vec{A}=div\vec{A}=\frac{\partial {{A}_{x}}}{\partial x}+\frac{\partial {{A}_{y}}}{\partial y}+\frac{\partial {{A}_{z}}}{\partial z}\)
\[\vec{A}\times \vec{B}=\left| \begin{matrix}
{\vec{i}} & {\vec{j}} & {\vec{k}} \\
{{A}_{x}} & {{A}_{y}} & {{A}_{z}} \\
{{B}_{x}} & {{B}_{y}} & {{B}_{z}} \\
\end{matrix} \right|=({{A}_{y}}{{B}_{z}}-{{B}_{y}}{{A}_{z}})\vec{i}+({{A}_{z}}{{B}_{x}}-{{A}_{x}}{{B}_{z}})\vec{j}+({{A}_{x}}{{B}_{y}}-{{A}_{y}}{{B}_{x}})\vec{k}\]
\(\frac{D\left( {} \right)}{Dt}=\frac{\partial \left( {} \right)}{\partial t}+u\frac{\partial \left( {} \right)}{\partial x}+v\frac{\partial \left( {} \right)}{\partial y}+w\frac{\partial \left( {} \right)}{\partial z}\)
\(\vec{i}\bullet \vec{j}=\vec{i}\bullet \vec{k}=\vec{j}\bullet \vec{k}=0\)
\(\vec{i}\bullet \vec{i}=\vec{j}\bullet \vec{j}=\vec{k}\bullet \vec{k}=1\)
\(\vec{i}\times \vec{i}=\vec{j}\times \vec{j}=\vec{k}\times \vec{k}=0\)
\(\vec{i}\times \vec{j}=\vec{k}\),\(\vec{j}\times \vec{k}=\vec{i}\),\(\vec{k}\times \vec{i}=\vec{j}\)
矢量恒等式:
\(\nabla \left( ab \right)=a\nabla b+b\nabla a\)
\({{\text{x}}_{\text{i}}}\)
\(\nabla \times \left( \phi \vec{A} \right)=\phi \nabla \times \vec{A}+\nabla \phi \times \vec{A}\)
\(\nabla \bullet \left( \vec{A}\times \vec{B} \right)=(\nabla \times \vec{A})\bullet \vec{B}-(\nabla \times \vec{B})\bullet \vec{A}\)
\(\nabla \times \left( \vec{A}\times \vec{B} \right)=(\vec{B}\bullet \nabla )\vec{A}-\vec{B}(\nabla \bullet \vec{A})+\vec{A}(\nabla \bullet \vec{B})-(\vec{A}\bullet \nabla )\vec{B}\)
\(\left( \vec{A}\bullet \nabla \right)\vec{A}=\nabla \left( \frac{{{A}^{2}}}{2} \right)-\vec{A}\times \left( \nabla \times \vec{A} \right)\)
\(\nabla \bullet \left( \nabla \times \vec{A} \right)=div\bullet curl\vec{A}=0\)
\(\nabla \times \left( \nabla \varphi \right)=curl\times grad\varphi \)\(grad\phi =0\)
\(\nabla \times \left( \nabla \times \vec{A} \right)=\nabla \left( \nabla \bullet \vec{A} \right)-{{\nabla }^{2}}\vec{A}\)
\(\frac{D\left( {} \right)}{Dt}=\frac{\partial \left( {} \right)}{\partial t}+\left( \nabla \bullet \nabla \right)\left( {} \right)\)
矢量计算法:
Stokes定理:\(\oint_{c}{\vec{B}\bullet d\vec{l}=\int_{A}{\left( \nabla \times \vec{B} \right)}}\bullet d\vec{A}\)
散度定理:\(\int_{A}{\vec{B}\bullet d\vec{A}}=\int_{{{V}_{c}}}{\left( \nabla \bullet \vec{B} \right)d{{v}_{c}}}\).
2.2 引言
在流体力学中,用来描述流体物理状况的基本方程称为控制方程。其建立的基础是下列物理定律:
1)质量守恒定律(建立连续方程)
2)牛顿运动第二定律(建立动量方程)
3)热力学第一定律(建立能量方程)
4)热力学第二定律(建立导热方程)
5)流体的热力参数,可从流体的参数表,经验方程或理想化的模型得到。例如:对于完全气体这样的理想模型,理想气体状态方程可以说明热力参数间的关系:\(pv=nRT\)。
对于流体,应用上述定律推导可得多个不同控制方程(数学表达式),将这些控制方程有机得组合起来,就可得到关于指定流体变量之间的关系。需要说明的是,对于一些情况,不必要用到上述所有的控制方程。
本章主要应用前四条定律推导流体流动控制方程的普遍形式,以掌握描述流体流动的普遍方程。必须说明,我们的推导针对的是刚性的、非加速的(即惯性的)控制体,而且假设所研究的流体满足连续介质的要求(除非明确说明相反的情况)。推导控制方程时,首先推导积分形式,这种形式具有普遍性,可应用于任何形式的流动中;然后推导相应的微分形式,其可应用于无粘可压缩流体的绝热流动情况。
本章推导的控制方程是本书其余各章推演和分析方法的基础。
2.3 连续介质的数学描述
在推导流体流动控制方程之前,必须明确诸如连续性,系统,控制体,控制面,外延和内涵参数,参数场,拉格朗日和欧拉流动描述以及实质导数等概念。
2.3.1 连续性假设概念
流体定义为在剪应力作用下能够产生连续形变的物质。需要指出的是,这个定义的前提是流体处于静止状态时不存在剪应力。按照传统的物质形态划分,气体和液体均为流体。
实际上,流体是由大量微小的分子或原子组成的,而且每个分子都在不断地作无规则热运动。对于流体运动来说,用微观的研究方法太繁琐。气体动力学研究的是流体宏观运动,一般把流体看作连续的介质。连续性假设的内容是:流体充满一个容积时,不留任何自由的空隙,既没有真空的地方也不考虑分子的微观运动。
绝大多数工程研究仅关注流体的宏观或总体特性,而过多关心其流体微观或分子特性,流体微观特性对宏观的影响通过简单模型实现。当分子的平均自由程 和所要研究的物体的特征尺寸\(L\)相比非常小时,把流体看作是连续介质是合理的。通常认为,当\(l/L\ge 0.01\)时,连续介质模型不再适用。需要说明的是本书内容基于连续性假设的前提。
引入连续性假设的好处在于不必过分关心流体的微观运动,而把重点置于流体的宏观运动,这样使得问题的处理得到简化。
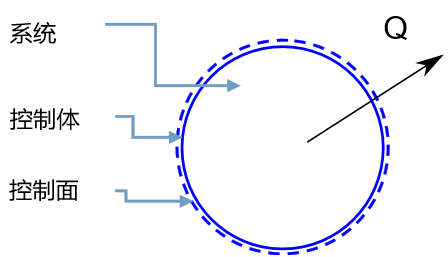
2.3.2 系统,控制体和控制面
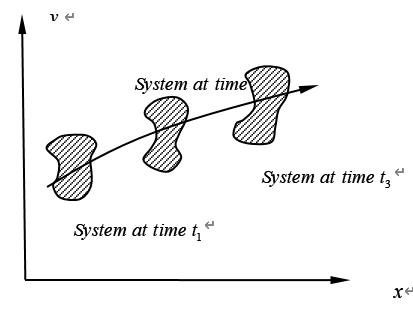
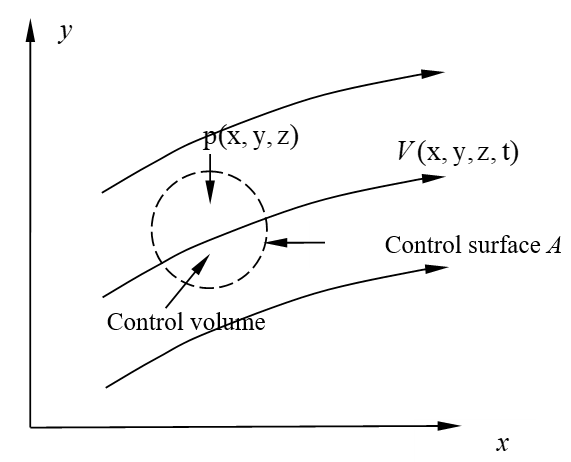
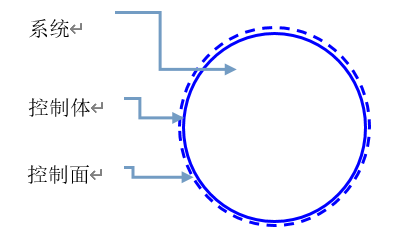
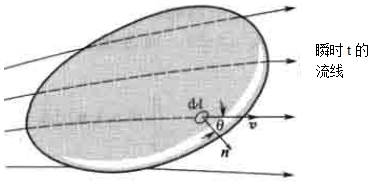
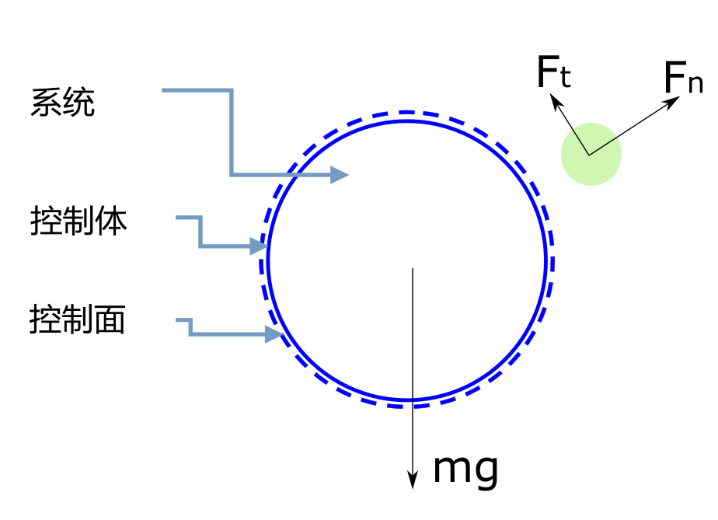
所谓系统(又称体系),是指一个指定的均匀物质集合,即指定的流体微团。质量既可以进入系统,也可以离开系统。系统以外的物质称为环境。控制流动过程的基本定律是对系统而言的。图2-1表示在空间中运动的系统。
图2-1 通过空间运动的系统
控制体是指流场中某一确定的空间区域,即流体可以通过控制体进行流动。通常,控制体可以改变形状和空间位置。然而,本书仅研究刚性控制体,如果控制体是运动的,则假设它仅作匀速运动,也就是研究无加速度或无惯性力的控制体。
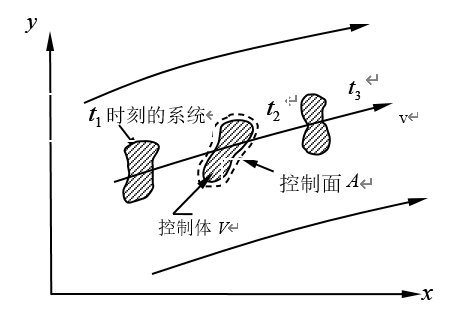
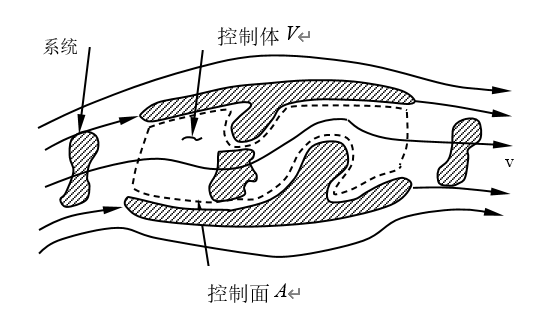
控制面是指完全包围控制体的假想可渗透表面。图2-2(a)说明在流动的流体中隔离出控制体时,系统、控制体和控制面的概念。图2-2(b)说明控制面与一个或多个流体不能穿过的固体边界面接触的情况。当然,对于既不与固体边界接触,又不平行于流体速度矢量\(\vec{V}\)的部分控制表面A,流体是可以流过的。
注意:惯性坐标系包括原始惯性坐标系和导出惯性坐标系。原始惯性坐标系由相对于指定的某些位置固定的刚性轴系组成,导出惯性坐标系是由相对于原始惯性坐标系以等速和无旋转运动的轴系组成。当选用参考惯性坐标系时,牛顿运动三大定律将有最简单的表达形式。
(a)在流动的流体中,无固体边界时的系统、控制面和控制体
(b)出现固体边界时的系统、控制面和控制体
图2-2 系统、控制面和控制体之间的关系
2.3.3 外延和内涵参数
外延参数是在所研究的体系下,其数值与质量有关(或取决于质量值)的参数。例如系统的容积、系统的质量以及系统的动量等。在本书中,外延参数尽可能用大写字母表示,例如:\(U\)表示内能,\(S\)表示熵等。质量是例外,考虑表达的习惯,虽然它是外延参数,但依然用小写字母\(m\)表示。通用的外延参数用符号\(N\)表示。
内涵参数是在所研究的体系下,其数值与质量无关的参数。内涵参数有两类,第一类是像压力、温度这样的内涵参数,它们明显与所包含的质量无关,仅与整个系统的状态有关,是表征系统状态的数值。第二类内涵参数是外延参数与质量的比值(即单位质量的值),例如:比内能\(u\)(单位质量的内能),比熵\(s\)(单位质量的熵),以及比焓\(h\)(单位质量的焓)等,第二类内涵参数通常用小写字母表示。通用内涵参数用符号\(n\)表示。对于满足连续介质要求的物质,通用内涵参数\(n\)定义为
\(n=\underset{\Delta m\to 0}{\mathop{\lim }}\,\frac{\Delta N}{\Delta m}=\frac{dN}{dm}\)
其中:\(\Delta N\)为微元系统的外延参数,\(\Delta m\)为微元系统的质量。
因此,对于系统,通用外延参数\(N\)的值可表达为
![]()
因为,密度定义为\(\rho ={dm}/{d{{V}_{c}}}\;\),即\(dm=\rho d{{V}_{c}}\),则方程(2.3.2)变为
\(N=\int_{{{\text{V}}_{c}}}{n\rho d{{V}_{c}}}\)
式中积分是在系统所占的容积\({{V}_{c}}\)上进行的。
对于与流动着的流体相联系的参数,如质量,动量,储能以及熵等,其相应的\(N\)和\(n\)的值为
以上关系式在下文推导流体通过控制体流动时的控制方程中需要用到。
2.3.4 参数场
在刚体动力学中,对质点或刚体而言,其参数(例如位置、速度、加速度等)均用时间的函数来描述。
在流体动力学中,由于流体与刚体存在差异,流体是可变形的,而且流动的流体中包含数目极大且具有相对运动特征的微团,因此,采用刚体动力学中所用的描述刚体参数的方法来描述流体参数在流体动力学中是不实际的。
在流体动力学中,为了表示不同流体微团,引入空间参数来表示出发于不同位置的流体微团;为了表示流体微团具有的物理量随时间的变化,引入时间参数。
对流动的流体所具有的参数(以后简称流体参数),需要用空间位置和时间位置共同来描述。由于流动参数是指定空间的时间参数,该参数本质为参数场的概念,这样通过参数场的引入就可以简化并准确地描述流体运动。
所谓参数场就是给定空间中参数的分布,其描述了参数在给定空间中随时间变化的规律。例如速度场就是速度矢量\(\vec{V}\)在空间x,y,z中t时刻的分布,其描述了速度矢量\(\vec{V}\)在空间x,y,z中随时间t的变化规律,可表示为\(\vec{V}(x,y,z,t)\)。人为确立参数场的概念有助于推演描述流体运动的数学公式。
有了参数场的概念,就不需要对每一个流体微团使用形如\({{\vec{V}}_{i}}={{V}_{i}}\left( t \right)\)的参数来描述,而是对流场中每一个空间位置给予 (x,y,z,t)的值,这样,就可以通过研究参数场\(\vec{V}\)来研究流体运动,而不是对每一个流体微团进行研究。
2.3.5 系统法或拉格朗日法
系统法或拉格朗日法是研究流体运动的方法之一。拉格朗日法的出发点是将流体看成无限多个流体微团组成的质点系,着手研究单个流体微团,并跟踪单个流体微团的运动历程,即它们位置随时间的变化规律,进一步得到该单个流体微团的速度、加速度等参数随时间的变化情况,然后再把所有流体微团的运动情况综合起来,得到整个流体的运动情况。该方法的实质是质点动力学研究方法的延续。系统法可用一个简单例子说明,每个流体质点好比一架飞机,通过在每架飞机安排一个观察员跟踪每架飞机的航线,再对所有观察员观察的每架飞机数据进行统计分析,就明晰了整个机群的动向。
如图2-3所示,跟踪单个流体微团路径的研究方法称为系统法或拉格朗日法。
采用系统法研究流体流动时遇到的第一个问题是如何在数学上区分大量流体微团。通常的做法是用流体微团在起始瞬间(或其它给定瞬间)时的位置坐标a、b、c来区分不同流体微团。这样不同的一组(a、b、c)就代表不同的流体质点。
采用系统法研究流体流动的第二个问题是用什么方程来描述流体的运动。通常的做法是用流体微团在空间中的位置坐标随时间的变化来描述流体质点的运动。
当时间改变时,微团在空间中的位置坐标(x,y,z)是参数a、b、c和时间的函数,即\[\left\{ \begin{align}
& x=x(a,b,c,t) \\
& x=x(a,b,c,t) \\
& x=x(a,b,c,t) \\
\end{align} \right.\](2.3.1)
式(2.3.1)就描述了流体运动规律,其称为流体质点的运动方程。在式(2.3.1)中,a、b、c称为拉格朗日法变数。对同一流体微团而言,a、b、c为常数,不随时间变化。
在式(2.3.1)中,如果固定a、b、c而令t改变,则得到某一流体质点的运动规律;如果固定t,而令a、b、c改变,则得到同一时刻不同流体质点的运动规律。
流体微团运动的速度 在直角坐标系中的三个分量为:\[\left\{ \begin{align}
& {{V}_{x}}=\frac{\partial x\left( a,b,c,t \right)}{\partial t} \\
& {{V}_{y}}=\frac{\partial y\left( a,b,c,t \right)}{\partial t} \\
& {{V}_{z}}=\frac{\partial z\left( a,b,c,t \right)}{\partial t} \\
\end{align} \right.\]
流体微团运动的速度 在直角坐标系中的三个分量为:\[\left\{ \begin{align}
& {{a}_{x}}=\frac{\partial V\left( a,b,c,t \right)}{\partial t} \\
& {{a}_{y}}=\frac{\partial V\left( a,b,c,t \right)}{\partial t} \\
& {{a}_{z}}=\frac{\partial V\left( a,b,c,t \right)}{\partial t} \\
\end{align} \right.\]
在大多数情况下,系统法或拉格朗日法不是十分有用,因为要跟踪数目巨大的流体微团非常困难,因此,需要探求新的研究流体流动的方法。
控制流体流动的基本定律总与有一定质量的系统相联系。因此,对系统必须用系统法或拉格朗日法才能写出基本定律,获得控制方程。
图2-3 研究流体运动的系统或拉格朗日法
2.3.6 控制体法或欧拉法
上一小节我们已经指出了采用拉格朗日法研究流体运动时的缺陷。本小节将介绍一种较为便捷的方法,即控制体法或欧拉法。
欧拉法的着眼点不是流体质点,而是空间。即将注意力集中在空间指定的容积上,即控制体上,研究并确定流经或占据容积的流体参数,进一步确定整个流体的参数,获得流体流动的规律。如图2-4所示,欧拉法着眼于控制体,故又称控制体法。欧拉法摆脱了跟踪研究流体微团的需要,利用场的描述就能完全确定流体参数。
例如:速度场 (x,y,z,t),从场的观点出发,其表示了给定空间、给定时刻速度参数分布;从欧拉观点出发,就表示了流体微团流动过程中,流经P(x,y,z)点处在时间t时的流体微团的速度。这样,当速度场 (x,y,z,t)已知,单个微团的轨迹就可通过速度场探究,从而使单个微团的参数得以确定。
在欧拉观点中,描述流体质点运动规律的方程就是流体的速度方程,在直角坐标系表达式为\[\left\{ \begin{align}
& {{V}_{x}}={{V}_{x}}\left( x,y,z,t \right) \\
& {{V}_{y}}={{V}_{y}}\left( x,y,z,t \right) \\
& {{V}_{z}}={{V}_{z}}\left( x,y,z,t \right) \\
\end{align} \right.\] (2.3.2)
要完全描述运动流体的状态还需要给出下列表示状态的方程\[\left\{ \begin{align}
& p=p\left( x,y,z,t \right) \\
& \rho =\rho \left( x,y,z,t \right) \\
& T=T\left( x,y,z,t \right) \\
\end{align} \right.\]
其中:变数\(x,y,z,t\)称为欧拉变数。
当速度已知后,出发于不同点(出发点用坐标\({{x}_{0}},{{y}_{0}},{{z}_{0}}\)表示)的单个微团的轨迹按照如下公式计算。
图2-4 研究流体运动的控制体或欧拉法
对于式(2.3.2),如果固定,x、y、z而令t改变,则式(2.3.2)中的函数代表了空间中某固定点上速度随时间的变化规律;如果固定t,,而令x、y、z改变,则带便了速度在空间中的分布。
需要指出,对于(2.3.2)的速度函数是定义在空间中的,它是空间坐标(x,y,z)的函数,其在数学上表示了一个场,因此,对流体速度研究归结于对场的研究。
在大多数流动情况下,并不需要关心单个微团的详细信息,因此,欧拉法是完全适合工程运用的方法。
总之,要讨论有关流动流体的质量,力,热,功,焓,熵等概念,要导出控制方程,必须针对一定的系统采用拉格朗日法进行研究。但拉格朗日法的使用存在一定困难。而控制体又不能用作导出控制方程的直接对象,因此,需要把二者结合起来,找出欧拉法和拉格朗日法之间的关系,使基本定律能用控制体的变量来表达。
2.3.7 实质导数
由于流体运动的控制方程针对系统才可用,因此,首先需要解决利用流动参数的场(即参数场)来表达流体微团参数对时间的导数,然后,找出拉格朗日法与欧拉法之间的联系。
在参数场中,流动参数对时间的导数称为流动参数的实质导数,也称为物质导数或微团导数,并以\({D\left( {} \right)}/{Dt}\;\)表示。
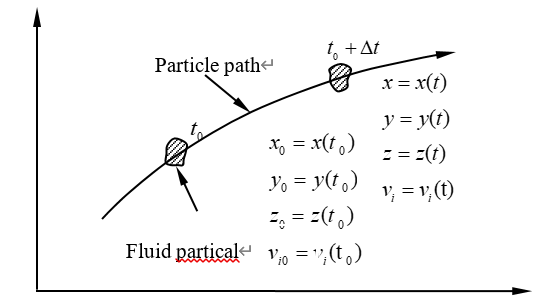
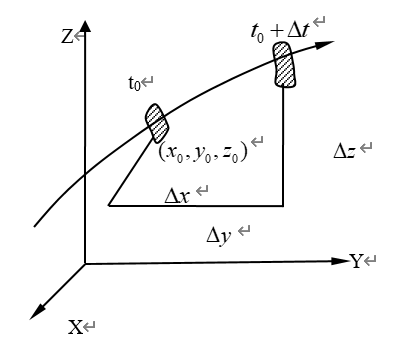
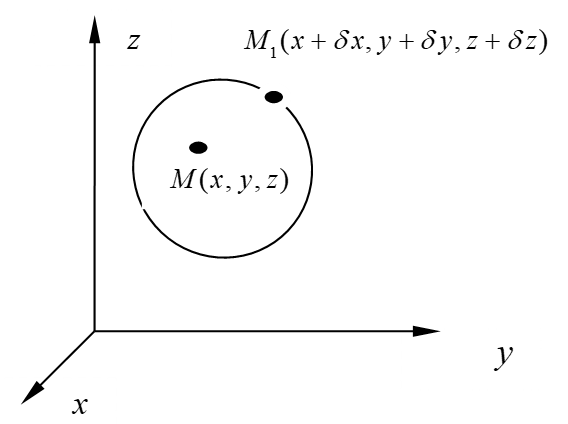
图2-5是在笛卡尔坐标系下拉格朗日空间中单个流体微团运动过程说明。
图2-5 拉格朗日空间
假设t0时刻,流体微团位于\(({{x}_{0}}{{\text{,}}_{{}}}{{y}_{0}}{{\text{,}}_{{}}}{{z}_{0}})\)处,此时,流体具有物理量为N;经\(\Delta t\)时间,流体微团运动到\(({{x}_{0}}+\Delta \text{x}{{\text{,}}_{{}}}{{y}_{0}}+\Delta \text{y}{{\text{,}}_{{}}}{{z}_{0}}+\Delta \text{z}{{\text{,}}_{{}}})\),流体具有物理量为\((N+\Delta \text{N})\)。
用N表示任意的系统外延参数;
在参数场中,N用N(x,y,z,t)说明。然而,在拉格朗日空间中,流体微团的坐标(x,y,z)也是时间的函数,即
\(x=x\left( t \right)\)\(y=y\left( t \right)\)\(z=z\left( t \right)\)
因此,对用拉格朗日空间表示的系统任意外延参数的表示法,与在参数场中的表示方式一样,也就是N(x,y,z,t)。
经过时间增量 ,外延参数N的变化可用泰勒级数的一次项来近似。这样
![]()
以\(\Delta t\)除式(2.3.3),并取当\(\Delta t\)趋近于零的极限。可取得系统在时间\({{t}_{0}}\)时任意外延参数N的时间变化率,即

在拉格朗日空间中,对系统,因为x=x(t)
![]()
式中: 是在时间 ,沿x方向的微团速度。
对方程(2.3.3)中的第二和第三项,采用类似的办法,可以得到\({{v}_{\left( {{t}_{0}} \right)}}\)和\({{w}_{\left( {{t}_{0}} \right)}}\),它们分别表示沿y方向和沿z方向的速度分量,这样,方程(2.3.4)转变为
![]()
用方程(2.3.6)表示的导数就是任意外延参数N的实质导数。如用专门符号D()/Dt表示,则任意外延参数N的实质导数为
\(\frac{DN}{Dt}\equiv \left[ \left( \frac{\partial N}{\partial t} \right)+u\left( \frac{\partial N}{\partial x} \right)+v\left( \frac{\partial N}{\partial y} \right)+w\left( \frac{\partial N}{\partial z} \right) \right]\)(2.3.7)
方程(2.3.7)右侧的第一项由可能出现的非定常流动产生,称为当地变化率;后三项中的每一项,由流场中微团位置的变化产生,称为迁移变化。
从实质导数的推演得知,流动参数的实质导数说明了在笛卡尔坐标系下,拉格朗日空间中,参数场中每一个流动参数的瞬时变化率,其说明了系统和参数场之间存在的某种联系。
因为参数场可直接用于流动的欧拉描述,因此,实质导数说明了流体流动中拉格朗日法与欧拉法之间存在的某种联系。
实质导数可以抽象出下列形式的算符
\(\frac{D\left( {} \right)}{Dt}=\frac{\partial \left( {} \right)}{\partial t}+u\frac{\partial \left( {} \right)}{\partial x}+v\frac{\partial \left( {} \right)}{\partial y}+w\frac{\partial \left( {} \right)}{\partial z}\)
应用矢量符号,实质导数可表示为
\(\frac{D\left( {} \right)}{Dt}\equiv \frac{\partial \left( {} \right)}{\partial t}+\left( \vec{V}\bullet \nabla \right)\left( {} \right)\)
上述表达式中,\({B}’\left( t \right)=A\left( t \right)\)和\(B\left( t \right)\)间的点表示标量积符号,必须保留。符号\(A\left( t \right)\)称为倒三角符号,在笛卡尔坐标系中定义为
\(\nabla =\frac{\partial }{\partial x}\vec{i}+\frac{\partial }{\partial y}\vec{j}+\frac{\partial }{\partial z}\vec{k}\)
2.4 加速度表达式
加速度\(A\left( t \right)\)是流体微团运动速度\(A\left( t \right)\)随流体流动时的时间变化率,故\(I\)是\(\int{A\left( t \right)dt}\)的实质导数。
\(\vec{a}=\frac{D\vec{V}}{Dt}=\frac{\partial \vec{V}}{\partial t}+\left( \vec{V}\bullet \nabla \right)\vec{V}\) (2.4.1)
这是一个加速度的矢量表达式,具有普遍的适应性,适用于任何坐标系。\(\frac{\partial \vec{V}}{\partial t}\)称为当地加速度,\(\left( \vec{V}\bullet \nabla \right)\vec{V}\)称为迁移加速度。
2.4.1 加速度在直角坐标系中的表达式
在直角坐标系中,通过(2.4.1)式来推导加速度的表达式。
在直角坐标系中:
\(\vec{V}=u\vec{i}+v\vec{j}+w\vec{k}\)
\(\frac{\partial \vec{V}}{\partial t}=\left( \frac{\partial u}{\partial t}\vec{i}+\frac{\partial v}{\partial t}\vec{j}+\frac{\partial w}{\partial t}\vec{k} \right)\)
\(\vec{V}\bullet \nabla =\left( u\vec{i}+v\vec{j}+w\vec{k} \right)\bullet \left( \frac{\partial }{\partial x}\vec{i}+\frac{\partial }{\partial y}\vec{j}+\frac{\partial }{\partial z}\vec{k} \right)=u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}+w\frac{\partial }{\partial z}\) (2.4.2)
将(2.4.2)代人(2.4.1)中,的加速度表达式为:
\(\begin{align}
& \vec{a}=\frac{\partial \vec{V}}{\partial t}+(u\frac{\partial }{\partial x}+v\frac{\partial }{\partial y}+w\frac{\partial }{\partial z})\vec{V}=\frac{\partial \vec{V}}{\partial t}+u\frac{\partial \vec{V}}{\partial x}+v\frac{\partial \vec{V}}{\partial y}+w\frac{\partial \vec{V}}{\partial z} \\
& =\left( \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z} \right)\vec{i}+\left( \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z} \right)\vec{j}+\left( \frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z} \right)\vec{k} \\
\end{align}\) (2.4.3)
也可将(2.4.3)式写成沿X、Y、Z方向的分量形式,为:\[\left\{ \begin{align}
& {{a}_{x}}=\frac{Du}{Dt}=\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z} \\
& {{a}_{y}}=\frac{Dv}{Dt}=\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z} \\
& {{a}_{y}}=\frac{Dw}{Dt}=\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z} \\
\end{align} \right.\](2.4.4)
例1 设速度场的欧拉描述为:
\(\vec{V}\left( x,y,t \right)={{e}^{xt}}\vec{i}+{{e}^{yt}}\vec{j}\)
试求在时间t=2时,位置(1,2)处微团的加速度。
解:由速度表达式可知:流动为直角坐标系中的二维流动。
由速度表达式亦可知,速度分量为
\(u={{e}^{xt}}\),\(v={{e}^{yt}}\),\(w=0\)
把速度分量代入加速度公式(2.4.3)中,得:
\(\vec{a}=\left( x{{e}^{xt}}+{{e}^{xt}}\bullet t{{e}^{xt}} \right)\vec{i}+\left( y{{e}^{yt}}+{{e}^{yt}}\bullet t{{e}^{yt}} \right)\vec{j}={{e}^{xt}}\left( x+t{{e}^{xt}} \right)\vec{i}+{{e}^{yt}}\left( y+t{{e}^{yt}} \right)\vec{j}\)
将\(t=2,x=1,y=2\)代入,得题目给定时刻和给定位置处流体微团的加速度。
\(\vec{a}={{e}^{2}}\left( 1+2{{e}^{2}} \right)\vec{i}+2{{e}^{4}}\left( 1+{{e}^{4}} \right)\vec{j}\)
例2 设流体运动以欧拉观点给出,流体运动的速度为 ,试将其转换到拉格朗日观点中去,即求出微团的运动方程。然后用两种观点分别求加速度
设\(\left( t=0x={{x}_{0}},y={{y}_{0}} \right)\)。
解:(1)从拉格朗日观点出发,求流体微团的运动方程
欧拉观点中的速度场与拉格朗日观点中的矢径相联系,为
\(\vec{V}=\frac{d\vec{r}}{dt}=\frac{dx}{dt}\vec{i}+\frac{dy}{dt}\vec{j}\)
因此有:\(\frac{dx}{dt}=u=ax+{{t}^{2}}\);\(\frac{dy}{dt}=v=by-{{t}^{2}}\)
或\(\frac{dx}{dt}-ax={{t}^{2}}\);\(\frac{dy}{dt}-by=-{{t}^{2}}\)
注意x,y是t的函数。以上两式是常微分方程。常微分方程解的公式为:
\(\frac{dx}{dt}+{{\text{P}}_{\left( t \right)}}x={{Q}_{\left( t \right)}}\),\(x{{e}^{\int{Pdt}}}=\int{Q{{e}^{\int{Pdt}}}dt}+C\)
并利用积分公式:
\(\int{{{u}^{n}}{{e}^{au}}du}=\frac{{{u}^{n}}{{e}^{au}}}{a}-\frac{n}{a}\int{{{u}^{n-1}}{{e}^{au}}du}\)
\(\int{u{{e}^{au}}du}=\frac{{{e}^{au}}}{{{a}^{2}}}\left( au-1 \right)\)
可求得:\(x=-\frac{{{t}^{2}}}{a}-\frac{2}{{{a}^{2}}}t-\frac{2}{{{a}^{2}}}+{{c}_{1}}{{e}^{at}}\)
\(y=\frac{{{t}^{2}}}{b}+\frac{2}{{{b}^{2}}}t+\frac{2}{{{b}^{2}}}+{{c}_{2}}{{e}^{bt}}\)
代入\(t=0x={{x}_{0}},y={{y}_{0}}\),求得常数
\({{c}_{1}}={{x}_{0}}+\frac{2}{{{a}^{2}}}\),\({{c}_{2}}={{y}_{0}}-\frac{2}{{{b}^{2}}}\)
这样,流体微团运动方程为:
\(\vec{r}=x\vec{i}+y\vec{j}\),
其中: \(x=-\frac{{{t}^{2}}}{a}-\frac{2t}{{{a}^{2}}}-\frac{2}{{{a}^{2}}}+{{x}_{0}}{{e}^{at}}+\frac{2}{{{a}^{2}}}{{e}^{at}}\)
\(y=\frac{{{t}^{2}}}{b}+\frac{2t}{{{b}^{2}}}+\frac{2}{{{b}^{2}}}+{{y}_{0}}{{e}^{bt}}-\frac{2}{{{b}^{2}}}{{e}^{bt}}\)
(2)从拉格朗日观点出发,求流体微团的加速度
加速度为:
\(\vec{a}=\frac{d{}^{2}\vec{r}}{d{{t}^{2}}}=\frac{d}{dt}\left( \frac{d\vec{r}}{dt} \right)=\frac{d}{dt}\left( \frac{dx}{dt}\vec{i}+\frac{dy}{dt}\vec{j} \right)\)
这时仍要注意,x,y是t的函数,求导得
\(\frac{dx}{dt}=-\frac{2t}{a}-\frac{2}{{{a}^{2}}}+a{{x}_{0}}{{e}^{at}}+\frac{2}{{{a}^{2}}}{{e}^{at}}-{{t}^{2}}+{{t}^{2}}\)
\(=a\left( -\frac{{{t}^{2}}}{a}-\frac{2t}{{{a}^{2}}}-\frac{2}{{{a}^{2}}}+{{x}_{0}}{{e}^{at}}+\frac{2}{{{a}^{2}}}{{e}^{at}} \right)+{{t}^{2}}\)
\(=ax-{{t}^{2}}=u\)
\(\frac{dy}{dt}=\frac{2t}{b}+\frac{2}{{{b}^{2}}}+b{{y}_{0}}{{e}^{bt}}-\frac{2}{{{b}^{2}}}{{e}^{at}}+{{t}^{2}}-{{t}^{2}}\)
\(=b\left( \frac{{{t}^{2}}}{b}+\frac{2t}{{{b}^{2}}}+\frac{2}{{{b}^{2}}}+{{y}_{0}}{{e}^{bt}}-\frac{2}{{{b}^{2}}}{{e}^{bt}} \right)-{{t}^{2}}\)
\(=by-{{t}^{2}}=v\)
代入加速度式,得
\(\vec{a}=\frac{d}{dt}\left( \left( ax+{{t}^{2}} \right)\vec{i}+\left( by-{{t}^{2}} \right)\vec{j} \right)\)
注意,跟踪微团运动,要求对时间和空间的导数,因此
\(\vec{a}=\left( \frac{\partial }{\partial t}\left( ax+{{t}^{2}} \right)+\frac{\partial }{\partial x}\left( ax+{{t}^{2}} \right)\frac{\partial x}{\partial t} \right)\vec{i}+\left( \frac{\partial }{\partial t}\left( by-{{t}^{2}} \right)+\frac{\partial }{\partial y}\left( by-{{t}^{2}} \right)\frac{\partial y}{\partial t} \right)\vec{j}\)
\(=\left( {{a}^{2}}x+\left( 2+at \right)t \right)\vec{i}+\left( {{b}^{2}}y-\left( 2+bt \right)t \right)\vec{j}\)
(3)从欧拉观点出发,求流体微团的加速度
从欧拉观点求加速度可直接利用公式(2.4.3),得
\(\vec{a}=\frac{D\vec{V}}{Dt}=\left( \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y} \right)\vec{i}+\left( \frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y} \right)\vec{j}\)
\(=\left( {{a}^{2}}x+\left( 2+at \right)t \right)\vec{i}+\left( {{b}^{2}}y-\left( 2+bt \right)t \right)\vec{j}\)
结论:两种观点求出的加速度相同。
2.4.2 流体加速度在圆柱坐标系中的表达式
我们已得到流体加速度的矢量通式(2.4.1)为:
\(\vec{a}=\frac{D\vec{V}}{Dt}=\frac{\partial \vec{V}}{\partial t}+\left( \vec{V}\bullet \nabla \right)\vec{V}\) (2.4.5)
设在圆柱坐标系中,三个坐标\(r,\theta ,z\),速度\(\vec{V}\)沿三个坐标\(r,\theta ,z\)坐标方向的分量为\({{v}_{r}},{{v}_{\theta }},{{v}_{z}}\),三个坐标\(r,\theta ,z\)方向的单位切矢量为\({{\vec{i}}_{r}},{{\vec{i}}_{\theta }},{{\vec{i}}_{z}}\)。
速度表达式为:
\(\vec{V}={{v}_{r}}{{\vec{i}}_{r}}+{{v}_{\theta }}{{\vec{i}}_{\theta }}+{{v}_{z}}{{\vec{i}}_{z}}\) (2.4.6)
在圆柱坐标系中逐项展开(2.4.5)式。
(2.4.5)式等号右边第一项为:
\(\frac{\partial \vec{V}}{\partial t}=\frac{\partial {{v}_{r}}}{\partial t}{{\vec{i}}_{r}}+\frac{\partial {{v}_{\theta }}}{\partial t}{{\vec{i}}_{\theta }}+\frac{\partial {{v}_{z}}}{\partial t}{{\vec{i}}_{z}}\) (2.4.7)
第二项中的
\(\left( \vec{V}\bullet \nabla \right)=\left( {{v}_{r}}{{{\vec{i}}}_{r}}+{{v}_{\theta }}{{{\vec{i}}}_{\theta }}+{{v}_{z}}{{{\vec{i}}}_{z}} \right)\bullet \left( \frac{\partial }{\partial r}{{{\vec{i}}}_{r}}+\frac{1}{r}\frac{\partial }{\partial \theta }{{{\vec{i}}}_{\theta }}+\frac{\partial }{\partial z}{{{\vec{i}}}_{z}} \right)={{v}_{r}}\frac{\partial }{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial }{\partial \theta }+{{v}_{z}}\frac{\partial }{\partial z}\) (2.4.8)
则(2.4.5)式等号右边第二项为
\(\begin{align}
& \left( \vec{V}\bullet \nabla \right)\vec{V}=\left( {{v}_{r}}\frac{\partial }{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial }{\partial \theta }+{{v}_{z}}\frac{\partial }{\partial z} \right)\left( {{v}_{r}}{{{\vec{i}}}_{r}}+{{v}_{\theta }}{{{\vec{i}}}_{\theta }}+{{v}_{z}}{{{\vec{i}}}_{z}} \right) \\
& =\left( {{v}_{r}}\frac{\partial {{v}_{r}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{\theta }}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{z}}}{\partial z} \right){{{\vec{i}}}_{r}}+{{v}_{r}}\left( {{v}_{r}}\frac{\partial {{{\vec{i}}}_{r}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{{\vec{i}}}_{r}}}{\partial \theta }+{{v}_{z}}\frac{\partial {{{\vec{i}}}_{r}}}{\partial z} \right) \\
& +\left( {{v}_{r}}\frac{\partial {{v}_{\theta }}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{\theta }}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{\theta }}}{\partial z} \right){{{\vec{i}}}_{\theta }}+{{v}_{\theta }}\left( {{v}_{r}}\frac{\partial {{{\vec{i}}}_{\theta }}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{{\vec{i}}}_{\theta }}}{\partial \theta }+{{v}_{z}}\frac{\partial {{{\vec{i}}}_{\theta }}}{\partial z} \right) \\
& +\left( {{v}_{r}}\frac{\partial {{v}_{z}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{z}}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{z}}}{\partial z} \right){{{\vec{i}}}_{z}}+{{v}_{z}}\left( {{v}_{r}}\frac{\partial {{{\vec{i}}}_{z}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{{\vec{i}}}_{z}}}{\partial \theta }+{{v}_{z}}\frac{\partial {{{\vec{i}}}_{z}}}{\partial z} \right) \\
\end{align}\) (2.4.9)
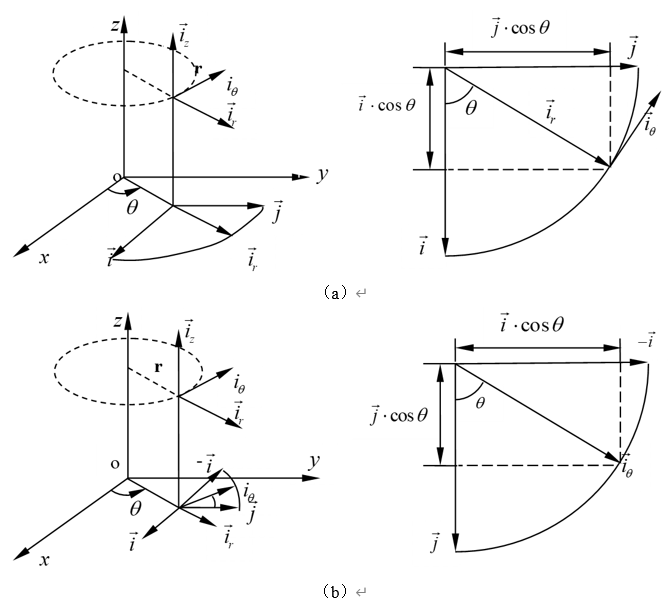
在(2.4.9)式中,需求出单位矢量\({{\vec{i}}_{r}},{{\vec{i}}_{\theta }},{{\vec{i}}_{z}}\)分别对r ,\(\theta \),z的偏导数。上述偏导数求解可通过\({{\vec{i}}_{r}},{{\vec{i}}_{\theta }},{{\vec{i}}_{z}}\)与\({{i}_{{}}},{{j}_{{}}},k\)之间的关系来实现。
\({{\vec{i}}_{r}},{{\vec{i}}_{\theta }},{{\vec{i}}_{z}}\)与\({{i}_{{}}},{{j}_{{}}},k\)之间的关系如图2-6所示。
图2-6 圆柱坐标在直角坐标系中表达式示意图
由图2-6(a)可得:
\({{\vec{i}}_{r}}=\cos \theta \vec{i}+\sin \theta \vec{j}\)
由图2-6(b)可得:
\({{\vec{i}}_{\theta }}=-\sin \theta \vec{i}+\cos \theta \vec{j}\)
另外 \({{\vec{i}}_{r}}=\vec{k}\)
分别将\({{\vec{i}}_{r}},{{\vec{i}}_{\theta }},{{\vec{i}}_{z}}\)对r,\(\theta \),z求导数,得
\(\frac{\partial {{{\vec{i}}}_{r}}}{{{\partial }_{r}}}=0\),\(\frac{\partial {{{\vec{i}}}_{r}}}{{{\partial }_{\theta }}}=-\sin \theta \vec{i}+\cos \theta \vec{j}={{\vec{i}}_{\theta }}\),\(\frac{\partial {{{\vec{i}}}_{r}}}{{{\partial }_{z}}}=0\)
\(\frac{\partial {{{\vec{i}}}_{\theta }}}{{{\partial }_{r}}}=0\),\(\frac{\partial {{{\vec{i}}}_{\theta }}}{{{\partial }_{\theta }}}=-\cos \theta \vec{i}-\sin \theta \vec{j}={{\vec{i}}_{r}}\),\(\frac{\partial {{{\vec{i}}}_{\theta }}}{{{\partial }_{z}}}=0\)
\(\frac{\partial {{{\vec{i}}}_{z}}}{{{\partial }_{r}}}=0\),\(\frac{\partial {{{\vec{i}}}_{z}}}{{{\partial }_{\theta }}}=0\),\(\frac{\partial {{{\vec{i}}}_{z}}}{{{\partial }_{z}}}=0\)
代入(2.4.9)式,并把相同单位矢量的项归类,得
\(\begin{align}
& \left( \vec{V}\bullet \nabla \right)\vec{V}=\left( {{v}_{r}}\frac{\partial {{v}_{r}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{r}}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{r}}}{\partial z}-\frac{v_{\theta }^{2}}{r} \right){{{\vec{i}}}_{r}} \\
& \text{ }+\left( {{v}_{r}}\frac{\partial {{v}_{\theta }}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{\theta }}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{\theta }}}{\partial z}+\frac{{{v}_{r}}{{v}_{\theta }}}{r} \right){{{\vec{i}}}_{\theta }} \\
& \text{ }+\left( {{v}_{r}}\frac{\partial {{v}_{z}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{z}}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{z}}}{\partial z} \right){{{\vec{i}}}_{z}} \\
\end{align}\) (2.4.10)
将(2.4.7)与(2.4.10)合并,得流体加速度在圆柱坐标系中的表达式为
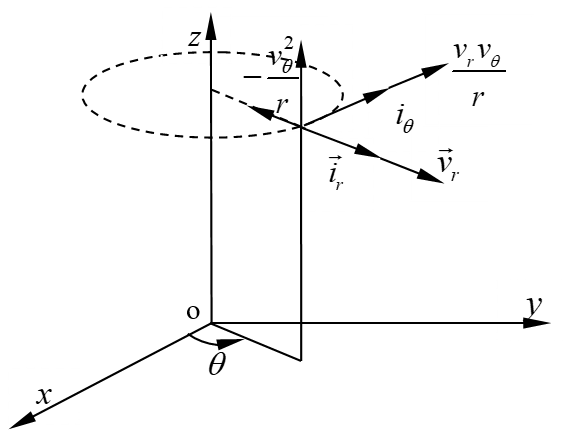
\(\vec{a}=\frac{D\vec{V}}{Dt}=\left( \frac{\partial {{v}_{r}}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{r}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{r}}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{r}}}{\partial z}-\frac{v_{\theta }^{2}}{r} \right){{\vec{i}}_{r}}+\left( \frac{\partial {{v}_{\theta }}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{\theta }}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{\theta }}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{\theta }}}{\partial z}+\frac{{{v}_{r}}{{v}_{\theta }}}{r} \right){{\vec{i}}_{\theta }}+\left( \frac{\partial {{v}_{z}}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{z}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{z}}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{z}}}{\partial z} \right){{\vec{i}}_{z}}\) (2.4.11)
式中对时间的偏导数表示速度分量的当地变化率,对坐标的偏导数表示速度分量的迁移变化率,而\(-\frac{v_{\theta }^{2}}{r}\)项表示微团做圆周运动时产生的向心加速度,\(\frac{{{v}_{r}}{{v}_{\theta }}}{r}\)项表示 方向改变时产生的切向附加加速度,如图2-7所示。
图2-7 加速度在圆柱坐标系中的附加项
经过类似的推导,可得流体加速度在球坐标系中的表达式,为:
\(\frac{D\vec{V}}{Dt}=\left( \frac{\partial {{v}_{r}}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{r}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{r}}}{\partial \theta }+\frac{{{v}_{\varphi }}}{r\sin \theta }\frac{\partial {{v}_{r}}}{\partial \varphi }-\frac{v_{\theta }^{2}}{r}-\frac{v_{\varphi }^{2}}{r} \right){{\vec{i}}_{r}}+\left( \frac{\partial {{v}_{\theta }}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{\theta }}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{\theta }}}{\partial \theta }+\frac{{{v}_{\varphi }}}{r\sin \theta }\frac{\partial {{v}_{\varphi }}}{\partial \varphi }+\frac{{{v}_{r}}{{v}_{\theta }}}{r}-\frac{{{v}_{\varphi }}^{2}\cot \theta }{r} \right){{\vec{i}}_{\theta }}+\left( \frac{\partial {{v}_{\varphi }}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{\varphi }}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{\varphi }}}{\partial \theta }+{{v}_{\varphi }}\frac{\partial {{v}_{\varphi }}}{\partial \varphi }+\frac{{{v}_{r}}{{v}_{\varphi }}}{r}-\frac{{{v}_{\theta }}{{v}_{\varphi }}\cot \theta }{r} \right){{\vec{i}}_{\varphi }}\)(2.4.12)
式中:\({{\vec{i}}_{r}},{{\vec{i}}_{\theta }},{{\vec{i}}_{\varphi }}\)分别为球坐标系中坐标r,\(\theta \),\(\varphi \)坐标轴上的单位切矢量,\({{v}_{r}},{{v}_{\theta }},{{v}_{\varphi }}\)分别为\(\vec{V}\)在坐标r,\(\theta \),\(\varphi \)上的分量。可以看出,(2.4.12)式中存在比圆柱坐标系中更加复杂的附加加速度。
2.5 流体微团运动的分解定理
2.5.1 直角坐标系中的流体微团运动的分解定理
一般情况下,刚体运动可分解为移动和绕某一瞬时轴的转动。对流体而言,除了移动和转动外,还有变形运动。研究流体微团的运动对理解流体流动的物理本质非常有帮助。
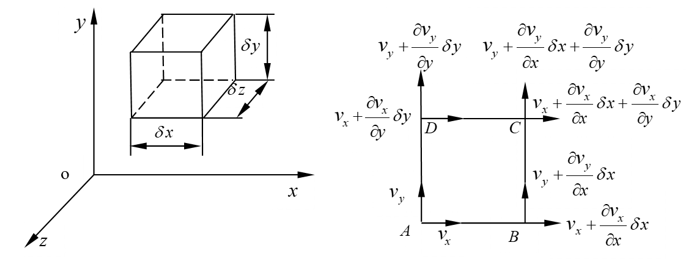
取一流体微团,如图2-8所示。
图2-8 流体微团示意图
设微团中心的速度为
\(\vec{V}={{v}_{x}}\vec{i}+{{v}_{y}}\vec{j}+{{v}_{z}}\vec{k}\) (2.5.1)
\({{M}_{1}}\)的速度为
\({{\vec{V}}_{1}}={{v}_{x1}}\vec{i}+{{v}_{y1}}\vec{j}+{{v}_{z1}}\vec{k}\) (2.5.2)
以M点的速度来表示\({{M}_{1}}\(点的速度,用泰勒级数略去二次以上的微量,有:\[\left. \begin{align}
& {{v}_{{{x}_{1}}}}={{v}_{x}}+\frac{\partial {{v}_{x}}}{\partial x}\delta x+\frac{\partial {{v}_{x}}}{\partial y}\delta y+\frac{\partial {{v}_{x}}}{\partial z}\delta z \\
& {{v}_{{{y}_{1}}}}={{v}_{y}}+\frac{\partial {{v}_{y}}}{\partial x}\delta x+\frac{\partial {{v}_{y}}}{\partial y}\delta y+\frac{\partial {{v}_{z}}}{\partial z}\delta z \\
& {{v}_{{{z}_{1}}}}={{v}_{z}}+\frac{\partial {{v}_{z}}}{\partial x}\delta x+\frac{\partial {{v}_{z}}}{\partial y}\delta y+\frac{\partial {{v}_{z}}}{\partial z}\delta z \\
\end{align} \right\}\](2.5.3)
上式也可写成矢量形式,为
\({{\vec{V}}_{1}}=\vec{V}+\left( \delta \vec{r}\centerdot \nabla \right)\vec{V)(2.5.4)
式中
\(\delta \vec{r}=\delta x\vec{i}+\delta y\vec{j}+\delta z\vec{k}\) (2.5.5)
式(2.5.3)说明,在某一点邻域上(即M1对M点)速度的改变量\(\left( {{{\vec{V}}}_{1}}-\vec{V} \right)\),决定于M点速度分量对坐标轴的九个偏导数,其中三个是同名偏导数,为:
\(\frac{\partial {{v}_{x}}}{\partial x},\frac{\partial {{v}_{y}}}{\partial y},\frac{\partial {{v}_{z}}}{\partial z}\)
六个是异名偏导数,分别为:
\(\frac{\partial {{v}_{x}}}{\partial y},\frac{\partial {{v}_{x}}}{\partial z},\frac{\partial {{v}_{y}}}{\partial x},\frac{\partial {{v}_{y}}}{\partial z},\frac{\partial {{v}_{z}}}{\partial x},\frac{\partial {{v}_{z}}}{\partial y}\)
下面分析这些流导数的物理意义。
为简便起见,取某瞬时t时一个无限小的矩形六面体微团,它在xoy平面上的投影为矩形ABCD,设A点的速度为\({{v}_{x}},{{v}_{y}}\),则其余各角点的速度如图2-9所示。
图2-9 流体微团速度示意图
如图2-9所示,在ABCD各角点的的速度中,出现了四个偏导数,两个同名偏导数\(\frac{\partial {{v}_{x}}}{\partial x},\frac{\partial {{v}_{y}}}{\partial y}\),两个异名偏导数\(\frac{\partial {{v}_{x}}}{\partial y},\frac{\partial {{v}_{y}}}{\partial x}\)。为了研究它们单独的影响,分别假设它们中的一种为零。
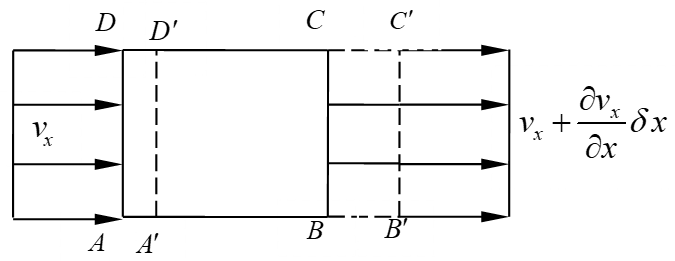
如设异名偏导数都等于零,而同名偏导数不等于零。则流体微团的ABCD将产生单纯的膨胀或压缩变形。如图2-10,仅看 方向,其伸长或压缩变形的速度(单位时间的变形)为\(\frac{\partial {{v}_{x}}}{\partial x}\delta x\),而相对的变形速度(单位时间和变形单位长度)称之为线变形率或线应变速度,为
\({{\varepsilon }_{xx}}={\frac{\partial {{v}_{x}}}{\partial x}\delta x}/{\delta x}\;=\frac{\partial {{v}_{x}}}{\partial x}\)
图2-10 线变形率示意图
同理,也可得其它两个同名偏导数为矩形微团分别沿 和 方向产生的线变形率。这样,便有
\({{\varepsilon }_{xx}}=\frac{\partial {{v}_{x}}}{\partial x},{{\varepsilon }_{yy}}=\frac{\partial {{v}_{y}}}{\partial y},{{\varepsilon }_{zz}}=\frac{\partial {{v}_{z}}}{\partial z}\) (2.5.6)
这三个方向的线变形率的代数和,就是流体微团在单位时间内体积的相对变化率,其值正好是散度,为
\(\frac{d\left( \delta {{V}_{c}} \right)}{d{{V}_{c}}dt}=\frac{\partial {{v}_{x}}}{\partial x}+\frac{\partial {{v}_{y}}}{\partial y}+\frac{\partial v{}_{z}}{\partial z}=div\vec{V}\) (2.5.7)
由此可得出结论:速度分量的同名偏导数分别表示微团在各方向的线变形率。它们的和,即散度,表示微团单位时间的相对体积变化率,也就是体积流率,源的强度。
如假设同名偏导数都等于零,而异名偏导数不等于零,则流体微团在xoy平面中图形ABCD的边线AB和AD将产生转动,如图2-11所示。
由图2-11可见,在单位时间内,B点相对于A点的转动量为\(\frac{\partial {{v}_{y}}}{\partial x}\delta x\),D点相对于A点的转动量为\(\frac{\partial {{v}_{x}}}{\partial y}\delta y\)。在一般情况下,边线AB和AD的转动速度不相等,结果使微团同时产生剪切变形和转动。
图2-11 剪切变形与转动示意图
经过dt时间后,AB边转过的角度为
\(d{{\alpha }_{1}}=\frac{\frac{\partial {{v}_{y}}}{\partial x}\delta x}{\delta x}dt=\frac{\partial {{v}_{y}}}{\partial x}dt\)
AD边转过的角度为
\(d{{\alpha }_{2}}=\frac{\partial {{v}_{x}}}{\partial y}dt\)
在dt时间内顶角A的变化量 表征流体微团在该时间内的剪切变形量,即
\(d\alpha =\left( \frac{\partial {{v}_{y}}}{\partial x}+\frac{\partial {{v}_{x}}}{\partial y} \right)dt\)
定义\(\frac{1}{2}\frac{d\alpha }{dt}\)为剪切角变形率(与材料力学中角应变相当),并用\({{\varepsilon }_{xy}}\)表示,则有
\({{\varepsilon }_{xy}}=\frac{1}{2}\frac{d\alpha }{dt}=\frac{1}{2}\left( \frac{\partial {{v}_{y}}}{\partial x}+\frac{\partial {{v}_{x}}}{\partial y} \right)\)
同理,也可得其它两个坐标轴上的剪切角变形率,这样便有\[\left. \begin{align}
& {{\varepsilon }_{xy}}=\frac{1}{2}\left( \frac{\partial {{v}_{y}}}{\partial x}+\frac{\partial {{v}_{x}}}{\partial y} \right) \\
& {{\varepsilon }_{yz}}=\frac{1}{2}\left( \frac{\partial {{v}_{z}}}{\partial y}+\frac{\partial {{v}_{y}}}{\partial z} \right) \\
& {{\varepsilon }_{zx}}=\frac{1}{2}\left( \frac{\partial {{v}_{x}}}{\partial z}+\frac{\partial {{v}_{z}}}{\partial x} \right) \\
\end{align} \right\}\](2.5.8)
由此可以得出结论:微团速度分量的两个异名偏导数平均值表示微团在对应坐标面中的剪切角变形率。
通常,我们以顶角A的平分线的旋转角速度表征微团的转动。由图2-11可见, 表征了流体微团的转动角度,规定以逆时针方向为正,则有
\(d\beta =\frac{1}{2}\left( d{{\alpha }_{1}}-d{{\alpha }_{2}} \right)\)
流体微团的转动角速度为
\({{\omega }_{z}}=\frac{1}{2}\left( \frac{d{{\alpha }_{1}}}{dt}-\frac{d{{\alpha }_{2}}}{dt} \right)=\frac{1}{2}\left( \frac{\partial {{v}_{y}}}{\partial x}-\frac{\partial {{v}_{x}}}{\partial y} \right)\)
同理可得流体微团绕x和y轴的转动角速度分量。这样便有\[\left. \begin{align}
& {{\omega }_{x}}=\frac{1}{2}\left( \frac{\partial {{v}_{z}}}{\partial y}-\frac{\partial {{v}_{y}}}{\partial z} \right) \\
& {{\omega }_{y}}=\frac{1}{2}\left( \frac{\partial {{v}_{x}}}{\partial z}-\frac{\partial {{v}_{z}}}{\partial x} \right) \\
& {{\omega }_{z}}=\frac{1}{2}\left( \frac{\partial {{v}_{y}}}{\partial x}-\frac{\partial {{v}_{x}}}{\partial y} \right) \\
\end{align} \right\}\](2.5.9)
将转动角速度进行矢量求和,得
\(\omega ={{\omega }_{x}}\vec{i}+{{\omega }_{y}}\vec{j}+{{\omega }_{z}}\vec{k}\)
\(=\frac{1}{2}\left| \begin{matrix}
{\vec{i}} & {\vec{j}} & {\vec{k}} \\
\frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\
{{v}_{x}} & {{v}_{y}} & {{v}_{z}} \\
\end{matrix} \right|=\frac{1}{2}rot\vec{V}\) (2.5.10)
由此可以得出结论:微团两个不同速度分量的异名偏导数相减的一半表示微团在对应坐标面中的旋转角速度;流体微团的旋转角速度等于速度矢量旋度的一半。
现在回到(2.5.3)式,研究流体微团的分解定理。为此,将(2.5.3)式的第一分式等号右边加减\(\frac{1}{2}\left( \frac{\partial {{v}_{y}}}{\partial x} \right)\delta y\),加减\(\frac{1}{2}\left( \frac{\partial {{v}_{z}}}{\partial x} \right)\delta z\),经整理得
\({{v}_{{{x}_{1}}}}={{v}_{x}}+\left( \frac{\partial {{v}_{x}}}{\partial x} \right)\delta x+\frac{1}{2}\left( \frac{\partial {{v}_{x}}}{\partial y}+\frac{\partial {{v}_{y}}}{\partial x} \right)\delta y+\frac{1}{2}\left( \frac{\partial {{v}_{z}}}{\partial x}+\frac{\partial {{v}_{x}}}{\partial z} \right)\delta z+\frac{1}{2}\left( \frac{\partial {{v}_{x}}}{\partial z}-\frac{\partial {{v}_{z}}}{\partial x} \right)\delta z-\frac{1}{2}\left( \frac{\partial {{v}_{y}}}{\partial x}-\frac{\partial {{v}_{x}}}{\partial y} \right)\delta y\)
同理得
\({{v}_{{{y}_{1}}}}={{v}_{y}}+\left( \frac{\partial {{v}_{y}}}{\partial y} \right)\delta y+\frac{1}{2}\left( \frac{\partial {{v}_{y}}}{\partial x}+\frac{\partial {{v}_{x}}}{\partial y} \right)\delta x+\frac{1}{2}\left( \frac{\partial {{v}_{z}}}{\partial y}+\frac{\partial {{v}_{y}}}{\partial z} \right)\delta z+\frac{1}{2}\left( \frac{\partial {{v}_{y}}}{\partial x}-\frac{\partial {{v}_{x}}}{\partial y} \right)\delta x-\frac{1}{2}\left( \frac{\partial {{v}_{z}}}{\partial y}-\frac{\partial {{v}_{y}}}{\partial z} \right)\delta z\)\({{v}_{{{z}_{1}}}}={{v}_{z}}+\left( \frac{\partial {{v}_{z}}}{\partial z} \right)\delta z+\frac{1}{2}\left( \frac{\partial {{v}_{z}}}{\partial y}+\frac{\partial {{v}_{y}}}{\partial z} \right)\delta y+\frac{1}{2}\left( \frac{\partial {{v}_{x}}}{\partial z}+\frac{\partial {{v}_{z}}}{\partial x} \right)\delta x+\frac{1}{2}\left( \frac{\partial {{v}_{z}}}{\partial y}-\frac{\partial {{v}_{y}}}{\partial z} \right)\delta y-\frac{1}{2}\left( \frac{\partial {{v}_{x}}}{\partial z}-\frac{\partial {{v}_{z}}}{\partial x} \right)\delta x\)
将线变形率(2.5.6),剪切角变形率(2.5.8)和转动角速度(2.5.9)的符号引入后,得到\[\left. \begin{align}
& {{v}_{{{x}_{1}}}}={{v}_{x}}+\left( {{\varepsilon }_{xx}}\delta x+{{\varepsilon }_{xy}}\delta y+{{\varepsilon }_{zx}}\delta z \right)+\left( {{\omega }_{y}}\delta z-{{\omega }_{z}}\delta y \right) \\
& {{v}_{{{y}_{1}}}}={{v}_{y}}+\left( {{\varepsilon }_{yy}}\delta y+{{\varepsilon }_{yz}}\delta z+{{\varepsilon }_{xy}}\delta x \right)+\left( {{\omega }_{z}}\delta x-{{\omega }_{x}}\delta z \right) \\
& {{v}_{{{z}_{1}}}}={{v}_{z}}+\left( {{\varepsilon }_{zz}}\delta z+{{\varepsilon }_{zx}}\delta x+{{\varepsilon }_{yz}}\delta y \right)+\left( {{\omega }_{x}}\delta y-{{\omega }_{y}}\delta x \right) \\
\end{align} \right\}\](2.5.11)
式(2.5.11)等号右边的第一列代表微团中心的平移运动;第二至四列表示微团的变形运动,其中第二列是只改变体积的线变形运动,而第三、四列表示只改变形状的剪切变形运动;第五、六列表示微团的转动运动。因此,得到微团运动的分解定理(或称柯西—海姆霍茨定理)。微团运动的分解定理说明流体微团的运动可以分解为三个组成部分:
1.随流体微团中心一起前进的平移运动;
2.变形运动,包括只改变体积的线变形运动和只改变形状的剪切变形运动;
3.绕流体微团瞬心的旋转运动。
与刚体运动相比,流体微团不同之处在于:(1)流体微团存在变形;(2)一般说来,流场中所包含不同流体微团运动参数是各不相同的。
以上是在直角坐标系中讨论了流体微团运动的分解。在圆柱坐标和球坐标系中,可通过类似的分析,得出类似的公式和相同的结论。不过,也可以不通过以上繁复的讨论和推导,而采用散度、旋度公式便可得到相应的变形和旋转公式。
2.5.2 圆柱坐标系中的流体微团运动的分解定理
在圆柱坐标系中,散度,即源的强度,体积变形率为
\(\nabla centerdot \vec{V}=div\vec{V}=\frac{1}{r}\frac{\partial \left( r{{v}_{r}} \right)}{\partial r}+\frac{1}{r}\frac{\partial {{v}_{\theta }}}{\partial \theta }+\frac{\partial {{v}_{z}}}{\partial z}\) (2.5.12)
因此,线变形率为
\({{\varepsilon }_{rr}}=\frac{1}{r}\frac{\partial \left( r{{v}_{r}} \right)}{\partial r},{{\varepsilon }_{\theta \theta }}=\frac{1}{r}\frac{\partial {{v}_{\theta }}}{\partial \theta },{{\varepsilon }_{zz}}=\frac{\partial {{v}_{z}}}{\partial z}\) (2.5.13)
\(\nabla \times \vec{V}=curl\vec{V}=\left| \begin{matrix}
\frac{{{{\vec{i}}}_{r}}}{r} & {{{\vec{i}}}_{\theta }} & \frac{{{{\vec{i}}}_{z}}}{r} \\
\frac{\partial }{\partial r} & \frac{\partial }{\partial \theta } & \frac{\partial }{\partial z} \\
{{v}_{r}} & r{{v}_{\theta }} & {{v}_{z}} \\
\end{matrix} \right|=\left( \frac{1}{r}\frac{\partial {{v}_{z}}}{\partial \theta }-\frac{\partial {{v}_{\theta }}}{\partial z} \right){{\vec{i}}_{r}}+\left( \frac{\partial {{v}_{r}}}{\partial z}-\frac{\partial {{v}_{z}}}{\partial r} \right){{\vec{i}}_{\theta }}+\left( \frac{\partial {{v}_{\theta }}}{\partial r}-\frac{1}{r}\frac{\partial {{v}_{r}}}{\partial \theta }+\frac{{{\text{v}}_{\theta }}}{r} \right){{\vec{i}}_{z}}\) (2.5.14)
因此,转动角速度为
\(\left\{ \begin{align}
& {{\omega }_{r}}=\frac{1}{2}\left( \frac{1}{r}\frac{\partial {{v}_{z}}}{\partial \theta }-\frac{\partial {{v}_{\theta }}}{\partial z} \right) \\
& {{\omega }_{\theta }}=\frac{1}{2}\left( \frac{\partial {{v}_{r}}}{\partial z}-\frac{\partial {{v}_{z}}}{\partial r} \right) \\
& {{\omega }_{z}}=\frac{1}{2}\left( \frac{\partial {{v}_{\theta }}}{\partial r}-\frac{1}{r}\frac{\partial {{v}_{r}}}{\partial \theta }+\frac{{{\text{v}}_{\theta }}}{r} \right) \\
\end{align} \right.\) (2.5.15)
只改变形状的剪切角变形率,是六个异名偏导数相加的平均值,只要将(2.5.15)适当改变就可得出\[\left\{ \begin{align}
& {{\varepsilon }_{r\theta }}=\frac{1}{2}\left( \frac{\partial {{v}_{\theta }}}{\partial r}+\frac{1}{r}\frac{\partial {{v}_{r}}}{\partial \theta }-\frac{{{\text{v}}_{\theta }}}{r} \right) \\
& {{\varepsilon }_{\theta z}}=\frac{1}{2}\left( \frac{1}{r}\frac{\partial {{v}_{z}}}{\partial \theta }+\frac{\partial {{v}_{\theta }}}{\partial z} \right) \\
& {{\varepsilon }_{zr}}=\frac{1}{2}\left( \frac{\partial {{v}_{r}}}{\partial z}+\frac{\partial {{v}_{z}}}{\partial r} \right) \\
\end{align} \right.\](2.5.16)
2.5.3 球坐标系中的流体微团运动的分解定理
在球坐标系中,散度,即源的强度,体积变形率为
\(div\vec{V}=\frac{1}{{{r}^{2}}}\frac{\partial \left( {{r}^{2}}{{v}_{r}} \right)}{\partial r}+\frac{1}{r\sin \vartheta }\frac{\partial \left( \sin \vartheta {{v}_{\theta }} \right)}{\partial \theta }+\frac{1}{r\sin \vartheta }\frac{\partial {{v}_{\varphi }}}{\partial \varphi }\)
因此,线变形率为
\({{\varepsilon }_{rr}}=\frac{1}{{{r}^{2}}}\frac{\partial \left( {{r}^{2}}{{v}_{r}} \right)}{\partial r};{{\varepsilon }_{\theta \theta }}=\frac{1}{r\sin \vartheta }\frac{\partial \left( \sin \vartheta {{v}_{\theta }} \right)}{\partial \theta };{{\varepsilon }_{\varphi \varphi }}=\frac{1}{r\sin \vartheta }\frac{\partial {{v}_{\varphi }}}{\partial \varphi }\)
因此,转动角速度为
\(\begin{align}
& curl\vec{V}=\left| \begin{matrix}
\frac{{{{\vec{i}}}_{r}}}{{{r}^{2}}\sin \varphi } & \frac{{{{\vec{i}}}_{\theta }}}{r\sin \varphi } & \frac{{{{\vec{i}}}_{\varphi }}}{r} \\
\frac{\partial }{\partial r} & \frac{\partial }{\partial \theta } & \frac{\partial }{\partial \varphi } \\
{{v}_{r}} & r\cdot {{v}_{\theta }} & r\sin \varphi \cdot {{v}_{\varphi }} \\
\end{matrix} \right| \\
& \\
\end{align}\)
2.6 系统和控制体之间的关系
自然界质量守恒,动量定律,能量守恒和热力学第二定律均对确定的流体微团,即“系统”,而言,和拉格朗日观点相对应;而流体流动通常通过场来描述,而场和欧拉观点相对应。为了通过场概念来描述流体流动,需要建立系统和控制体之间的关系。后面内容可以看出,流体流动几大方程的建立均应用了系统和控制体之间的关系。
在这一节讨论中,我们将解决如何将系统任意外延参数N随时间的变化率(即N的实质导数)表达为对控制体的表达式。
图2-12 系统和控制体之间的关系
图2-12表示直角坐标系\(x,y,z\)中的任意速度场\(V(x,y,z,t)\)。\({{V}_{c}}\)表示控制体,A表示包围控制体的表面积,即控制面。图中给出有限系统在t和\(\left( t+\Delta t \right)\)时刻的位置。
假设,控制体在\(x,y,z\)空间中固定。系统在时刻t占据与控制体相同的空间,用Ⅰ和Ⅱ两个区间表示;在时刻\(\left( t+\Delta t \right)\),系统占据Ⅱ和Ⅲ区间。
对系统,外延参数N对时间的变化率可以用下面的极限确定。
![]() (2.6.1)
(2.6.1)
其表示系统在时刻t所具有的外延参数N对时间的变化率。
方程(2.6.1)表示的导数是流动中流体微团的总导数,即流体微团具有的外延参数N的实质导数,引入实质导数的算符\(\frac{\text{D}\left( {} \right)}{Dt}\),得:
对图2-12所示的流体微团,方程(2.6.2)为
![]()
因为 \(N=\int_{{{V}_{c}}}{n\rho d{{V}_{c}}}\)
所以
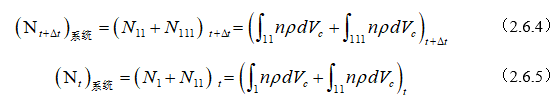
将(2.6.4)及(2.6.5)代入(2.6.3),并注意和的极限等于极限的和。得表达式
\(\frac{DN}{Dt}=\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{\left( {{\left( \int_{11}{n\rho d{{V}_{c}}} \right)}_{t+\Delta t}}-{{\left( \int_{11}{n\rho d{{V}_{c}}} \right)}_{t}} \right)}{\Delta t}+\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\left( \int_{111}{n\rho d{{V}_{c}}} \right)}_{t+\Delta t}}}{\Delta t}-\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\left( \int_{1}{n\rho d{{V}_{c}}} \right)}_{t}}}{\Delta t}\) (2.6.6)
对于方程(2.6.6)右边的第一项,当取\(\Delta t\)趋近于零的极限时,Ⅱ区与控制体\({{V}_{c}}\)相同,其变为
\(\frac{\partial }{\partial t}\int_{{{V}_{c}}}{n\rho d{{V}_{c}}}\) (2.6.7)
对于方程(2.6.6)右边的第二项,其中被积函数\(\left( n\rho d{{V}_{c111}} \right)\)是外延参数N经过时间 离开控制体进入Ⅲ区的数值,即
\({{\left( n\rho d{{V}_{c111}} \right)}_{t+\Delta t}}={{\left( \Delta {{N}_{111}} \right)}_{t+\Delta t}}\) (2.6.8)
以\(\Delta t\)相除,并取极限,当\(\Delta t\)趋近于零时,得控制体N的瞬时变化率
\(\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\left( \Delta {{N}_{111}} \right)}_{t+\Delta t}}}{\Delta t}={{\left( \frac{dN}{dt} \right)}_{out}}\)=N的流出率(2.6.9)
因为\(dN=ndm\), 的流出率可表示为
\(d\overset{\bullet }{\mathop{m}}\,=\rho \vec{V}\cdot d\vec{A}\) (2.6.10)
其表示流出控制体的质量流率\(d{{\overset{\bullet }{\mathop{m}}\,}_{out}}\)和通用外延参数\(N\)的单位值\(n\)的乘积。
对控制体\({{V}_{c}}\)而言,流体的质量流出率,可用\(\rho \),\(\vec{V}\)和微元面积\(dA\)表示。对如图2-13表示的微元控制面积\(dA\),通过\(dA\)的质量流率为
\(d\overset{\bullet }{\mathop{m}}\,=\rho V\cos \alpha dA\) (2.6.11)
用\(d\overset{\scriptscriptstyle\rightharpoonup}{A}\)表示面积矢量,大小为面积,方向沿微元面外法向,利用数量积的概念,得
\(d\overset{\bullet }{\mathop{m}}\,=\rho \vec{V}\cdot d\vec{A}\)
代入(2.6.10),得
\({{\left( \frac{dN}{dt} \right)}_{out}}=n\rho \vec{V}\cdot d{{\vec{A}}_{out}}\) (2.6.12)
因为任意外延参数 离开控制体进入Ⅲ区的N出量是通过控制面\({{A}_{out}}\)进行的,因此,将(2.6.12)对\({{A}_{out}}\)积分,其与(2.6.6)式的第二项相等,得
\(\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\left( \int_{111}{n\rho d{{V}_{c}}} \right)}_{t+\Delta t}}}{\Delta t}={{\int_{{{A}_{out}}}{\left( \frac{dN}{dt} \right)}}_{out}}=n\rho \vec{V}\cdot d{{\vec{A}}_{out}}\) (2.6.13)
方程(2.6.13)把原来流体在区间Ⅲ上的体积分转换成该流体流出控制体的那一部分控制面上的面积分。
方程(2.6.6)右边第三项可由计算第二项所用的方法类推,其中,被积函数是经过时间\(\Delta t\)进入控制体的N值。
图2-14表示流入控制体的流体质量流出律,和流入控制体时的微元控制面。注意,对于进入控制体的流体,角度\(\alpha \)总是大于90度而小于270度,因此,\(\cos \alpha \)总是负的(当然,质量流率总是正值)。于是,穿过微元面积\(dA\)的质量流率为
\(d\overset{\bullet }{\mathop{m}}\,=-\rho V\cos \alpha dA=-\rho \vec{V}\cdot d\vec{A}\)(2.6.14)
图2-13 控制体的质量流出率 图2-14 进入控制体的质量流入率
这样,方程(2.6.6)的第三项变为
\(-\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\left( \int_{1}{n\rho d{{V}_{c}}} \right)}_{t}}}{\Delta t}=-\underset{\Delta t\to 0}{\mathop{\lim }}\,\frac{{{\left( \int_{1}{nd\overset{\bullet }{\mathop{{{m}_{in}}}}\,} \right)}_{t}}}{\Delta t}=-{{\int_{{{A}_{in}}}{\left( \frac{dN}{dt} \right)}}_{in}}=\int_{{{A}_{in}}}{n\rho \vec{V}\cdot d{{{\vec{A}}}_{in}}}\) (2.6.15)
注意,上式已考虑了方程(2.6.6)第三项前的负号以及方程(2.6.14)的负号。这样,把原来在区间Ⅰ上的体积分可转换为流体流入控制体的那一部分控制面上的积分。
在整个控制面 上,将方程(2.6.13)与(2.6.15)相加得出
\({{\int_{{{A}_{out}}}{\left( \frac{dN}{dt} \right)}}_{out}}-{{\int_{{{A}_{in}}}{\left( \frac{dN}{dt} \right)}}_{in}}=\int_{A}{n\rho \vec{V}\cdot d\vec{A}}\) (2.6.16)
在方程(2.6.16)中,对于质量流出率,标量积\(\vec{V}\cdot d\vec{A}\)对\(DN/Dt\)产生正作用;对于质量流入率,标量积\(\vec{V}\cdot d\vec{A}\)对\(DN/Dt\)产生负作用。这与方程(2.6.6)中第二项和第三项的符号是一致的。
将方程(2.6.7)及方程(2.6.16)所取极限的结果代入方程(2.6.6),得
\(\frac{DN}{Dt}=\frac{\partial }{\partial t}\int_{{{V}_{c}}}{n\rho d{{V}_{c}}}+\int_{A}{n\rho \vec{V}\cdot d\vec{A}}\) (2.6.17)
这样,对一个系统而言,其在时刻 ,所具有的任何外延参数 的瞬时变化率,可用两项来表达:一项是相对于控制体的,另一项是相当于控制面的。前一项表示由于非稳态流动引起的控制体内N的变化率,而后一项表示相同时刻由于流动引起的通过控制面 的N的纯变化率。
方程(2.6.17)就是关于流动问题,系统和控制体法(拉格朗日和欧拉法)之间的关系。
对于固定形状的惯性控制体,对时间的导数能取入积分号,得到
\(\frac{DN}{Dt}=\int_{{{V}_{c}}}{\frac{\partial \left( n\rho \right)}{\partial t}}d{{V}_{c}}+\int_{A}{n\rho \vec{V}\cdot d\vec{A}}\) (2.6.18)
通过矢量关系,可将方程(2.6.17)变换成其它有用形式。采用散度定理,对任何矢量\(\vec{B}\),有
\(\int_{A}{\vec{B}\cdot d\vec{A}=\int_{{{V}_{c}}}{\nabla \cdot }}\vec{B}d{{V}_{c}}\) (2.6.19)
假如,\(\vec{B}\)取为\(n\rho \vec{V}\),则
\(\int_{A}{\left( n\rho \vec{V} \right)\cdot d\vec{A}=\int_{{{V}_{c}}}{\nabla \cdot }}\left( n\rho \vec{V} \right)d{{V}_{c}}\) (2.6.20)
将方程(2.6.20)代入(2.6.18),就可将流体所具有的外延参数N的实质导数表示为控制体的体积分
\(\frac{DN}{Dt}=\int_{{{V}_{c}}}{\left( \frac{\partial \left( n\rho \right)}{\partial t}+\nabla \cdot \left( n\rho \vec{V} \right) \right)}d{{V}_{c}}\) (2.6.21)
当外延参数N确定(即是质量,动量,能量或熵),则内涵参数n就已确定。
方程(2.6.21)中第二项的被积函数,通过下列矢量等式还可以进一步展开。设\(\Phi \)是任意标量,\(\vec{A}\)为任意矢量,则有
\(\nabla \cdot \left( \Phi \vec{A} \right)=\Phi \left( \nabla \cdot \vec{A} \right)+\vec{A}\left( \nabla \Phi \right)\) (2.6.22)
另外,外延参数N对微元系统的瞬时变化率也是一个有用的概念。假如,控制容积\({{V}_{c}}\)收缩到微元尺寸\(d{{V}_{c}}\),则方程(2.6.21)中积分的极限值是被积函数本身。再除以\(d{{V}_{c}}\),得到对于单位容积N变化率的表达式
\(\frac{DN/Dt}{d{{V}_{c}}}=\frac{\partial \left( n\rho \right)}{\partial t}+\nabla \cdot \left( n\rho \vec{V} \right)=\left( n\rho \right)_{t}^{{}}+\nabla \cdot \left( n\rho \vec{V} \right)\) (2.6.23)
式中,\(\left( n\rho \right)_{t}^{{}}=\frac{\partial {{\left( n\rho \right)}^{*}}}{\partial t}\)。
应用方程(2.6.23),可以将从积分方程(如方程(2.6.21))中获得相应的微分方程。
总之,方程(2.6.18)利用控制体参数来表达了系统的任意外延参数N的时间变化率。
2.7 连续方程
自然界无数事实证明,质量是不灭的。无论经过什么形式的运动,物质质量将保持不变,这一普遍规律被称为“质量守恒定律”。
下面我们将从“质量守恒定律”出发推导连续方程。
连续方程建立思想是将质量守恒定律应用于占据控制体的流体(系统)而得到连续方程。
有许多种建立连续方程的方法,这些方法和研究流体流动的两种方法(系统法和控制体法)相对应,下面我们将用不同的方法建立连续方程,目的是一方面理解研究流体流动的两种方法的区别,另一方面理解连续方程的物理本质。需要说明的是,这些方法最后结果都是相同的,各种方法起到相互印证作用。
(流体微团的)拉格朗日法
拉格朗日法研究对象为流体微团,该流体微团我们称为系统,在此我们采用的方法称为针对流体微团的拉格朗日法。
对系统,在不考虑核子和相对论影响时,质量守恒定律可理解为系统质量为常数。
图2-15 系统、控制体与控制面概念
如图2-15所示,在空间取一微元体,体积为\({{V}_{c}}\),该体积外表面为A,某时刻占据该体积\({{V}_{c}}\)的流体微团质量为m。
在拉格朗日观点中,质量为m流体微团即为“系统”。在欧拉观点中,体积\({{V}_{c}}\)即为“控制体”,外表面 为控制面。
用外延参数N表示系统的质量,即N=质量 ,因此方程(2.7.1)为
![]() (2.7.2)
(2.7.2)
控制体 内气体质量为 ,相应的内涵参数为\(n=1\)。由方程(2.6.18)得
\(\frac{DN}{Dt}=\int_{Vc}{\frac{\partial \left( n\rho \right)}{\partial t}}d{{V}_{c}}+\int_{A}{n\rho \vec{V}\bullet d\vec{A}}\)
当\(\frac{DN}{Dt}=0\),\(n=1\)时
\(\int_{Vc}{\frac{\partial \rho }{\partial t}}d{{V}_{c}}+\int_{A}{\rho \vec{V}\cdot d\vec{A}}=0\) (2.7.3)
方程(2.7.3)是质量守恒定律的积分形式。它对控制体可用,并称为积分形式连续方程。该方程要求满足流体连续介质假设,以及没有核子和相对论影响。对于定常流动,方程(2.7.3)第一项为零。
方程(2.7.3)表述的基本原理是在固定尺寸的惯性控制体 内单位时间积累的(流体)质量,等于单位时间穿过包围 的控制面A进入和离开 质量之差。
多维流动中,经常用到连续方程的微分形式,下面我们推导连续方程的微分形式。
采用散度定理(见方程(2.6.19)),方程(2.7.3)第二项为
\(\int_{A}{\rho \vec{V}\cdot d\vec{A}}\text{=}\int_{{{\text{V}}_{c}}}{\nabla \bullet \rho \vec{V}}d{{V}_{c}}\)
将上式代入(2.7.3),然后,当\(d\vec{S}={{n}^{0}}dS=dS\cos (n,x)\vec{i}+dS\cos (n,y)\vec{j}+dS\cos (n,z)\vec{k}=dydz\vec{i}+dxdz\vec{j}+dxdy\vec{k}\)趋近于零时,就可得到体积分的极限值。这种方法在推导方程(2.6.24)时曾用过。
对于N=质量,\(n=\text{1}\),则\(DN/Dt=0\)。方程(2.6.23)变成
\({{\rho }_{t}}+\nabla \cdot \left( \rho \vec{V} \right)=0\) (2.7.4)
其中:\({{\rho }_{t}}\equiv \frac{\partial \rho }{\partial t}\)
方程(2.7.4)就是流体流动连续方程的微分形式。应用某坐标系的 算符,就可获得该坐标系下的方程。对于常流,\({{\rho }_{t}}=0\)。
(针对有限体积的)控制体法
所谓(有限体积)控制体法包含两个方面(1)控制体为研究问题时在空间中所取有限体积,(2)研究方法为控制体法。
下面将从欧拉观点出发来推导连续方程,在空间中取一以面 为界的有限体积 为控制体,该有限体积由空间点组成,其固定于空间不随时间改变。
对占据控制体的流体应用质量守恒定律,即
(流出控制体的质量速率)-(流入控制体的质量速率)+(控制体内质量的积聚率)=0
如图2-16所示为流场内一个有限控制体。从控制体表面的面积微元\(d\vec{A}\)上流出的质量速率为\(\left( \rho v \right)\left( dA\cos \theta \right)\)。其中\(\left( dA\cos \theta \right)\)是面积\(d\vec{A}\)在以速度矢量\(\vec{v}\)为法线平面上的投影。\(\theta \)是速度矢量\(\vec{v}\)和\(d\vec{A}\)之间的夹角。
通过面积微元\(dA\)的质量速率为
\(dm=\rho \vec{v}\bullet d\vec{A}=\rho vdA\cos \theta \)
图2-16 通过控制体的流动
对整个控制表面进行积分,得到整个外表面质量流率
\(\int\limits_{A}{\rho \vec{v}\cdot d\vec{A}}\)
它是从控制体流出的净质量率。
如果质量是流入控制体,那么乘积\(\vec{v}\bullet d\vec{A}\)是负的。因此,如果积分值是正的就表示质量净流出,如果是负的就表示质量净流入,如果为0就表示控制体内的质量为常数。
控制体内的质量积聚率,可表示为
\(\int\limits_{Vc}{\frac{\partial \rho }{\partial t}d{{V}_{c}}}\)
因为整个控制体内质量是平衡的,所以积分表达式为
\(\int\limits_{Vc}{\frac{\partial \rho }{\partial t}d{{V}_{c}}+}\int\limits_{A}{\rho \vec{V}\cdot d\vec{A}}=0\)
将上面方程中的面积分通过散度定律变为体积分,并取\({{\text{V}}_{c}}\to 0\),可得
\({{\rho }_{t}}+\nabla \cdot \left( \rho \vec{V} \right)=0\)
(微元)控制体法
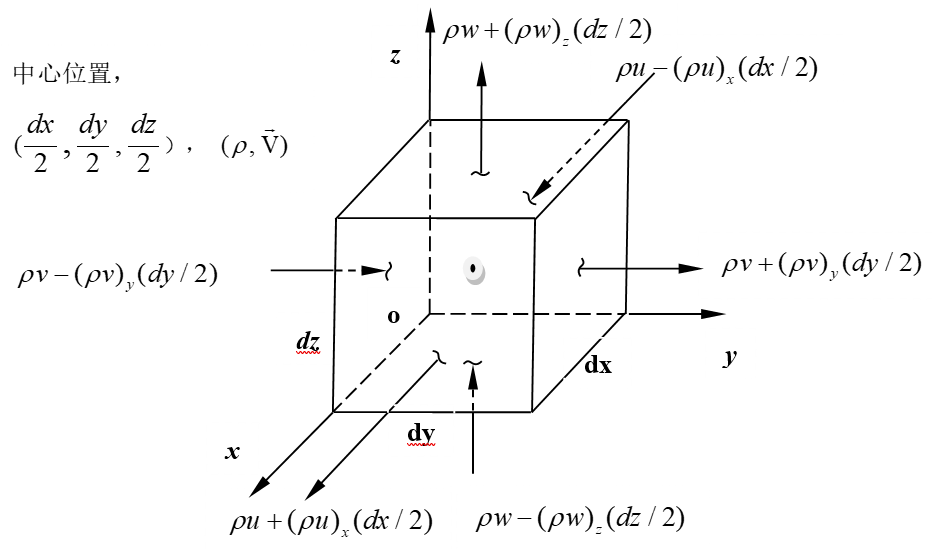
所谓(微元)控制体法包含两个方面(1)控制体为空间中微元体积,(2)研究方法为控制体法。
微元控制体法的基础是对微元控制体应用积分方程。应用欧拉观点,在笛卡尔坐标系中,对微元控制体应用质量守恒定律来建立连续方程。
图2-17 微元控制体
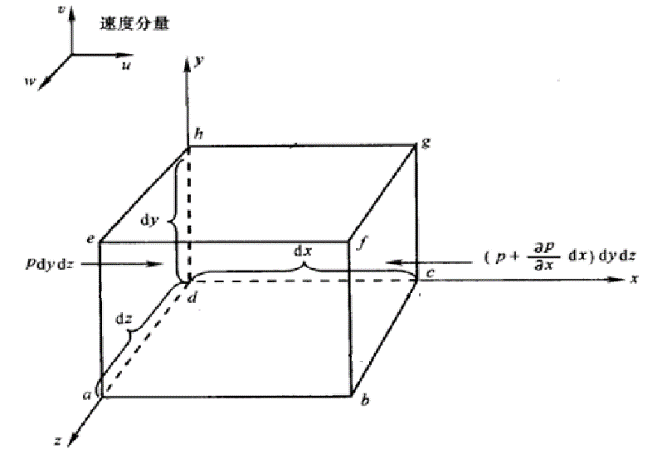
图2-17表示在笛卡尔坐标系中的微元控制体。设\(\rho \)和\(\vec{V}\)表示坐标为\(\left( \frac{dx}{2},\frac{dy}{2},\frac{dz}{2} \right)\)的微元控制体中心的参数。
对微元控制体可以假设,在其六个面的每一个面上流体参数是常数(一阶近似)。在微元控制体的背面,即面向 负方向的面,密度为\(\rho -{{\rho }_{x}}\left( \frac{dx}{2} \right)\),而在正面上,为\(\rho +{{\rho }_{x}}\left( \frac{dx}{2} \right)\)。对乘积\(\left( \rho u \right)\),\(\left( \rho v \right)\)和\(\left( \rho w \right)\)可写出类似的表达式,这里u,v和w是速度\(\vec{V}\)的笛卡尔分量。因此,在背面\(\left( \rho u \right)\)值为\(\left( \rho u \right)-{{\left( \rho u \right)}_{x}}\left( \frac{dx}{2} \right)\),而在正面,它为\(\left( \rho u \right)+{{\left( \rho u \right)}_{x}}\left( \frac{dx}{2} \right)\)。对其余四个面,可写出相似的表达式。流入背面的质量为
\(\left( \left( \rho u \right)-{{\left( \rho u \right)}_{x}}\left( \frac{dx}{2} \right) \right)dydz\) (2.7.5)
流出正面的质量为
\(\left( \left( \rho u \right)+{{\left( \rho u \right)}_{x}}\left( \frac{dx}{2} \right) \right)dydz\)
在微元控制体中沿x方向积累的质量为
\(\left( \left( \rho u \right)+{{\left( \rho u \right)}_{x}}\left( \frac{dx}{2} \right) \right)dydz-\left( \left( \rho u \right)-{{\left( \rho u \right)}_{x}}\left( \frac{dx}{2} \right) \right)dydz={{\left( \rho u \right)}_{x}}dxdydz\)
同理,沿 及沿 方向积累的质量分别为\({{\left( \rho v \right)}_{y}}dxdydz\)及\({{\left( \rho w \right)}_{z}}dxdydz\)。因此方程(2.7.3)中第二项
\(\int_{A}{\rho \vec{V}\cdot d\vec{A}}={{\left( \rho u \right)}_{x}}dxdydz+{{\left( \rho v \right)}_{y}}dxdydz+{{\left( \rho w \right)}_{z}}dxdydz\)
方程(2.7.3)中的非定常项是简单的
\(\int_{{{V}_{c}}}{\frac{\partial \rho }{\partial t}}d{{V}_{c}}={{\rho }_{t}}dxdydz\)
对于控制体来讲,其包含质量是守恒的,则
\(\int_{A}{\rho \vec{V}\cdot d\vec{A}}=\int_{{{V}_{c}}}{\frac{\partial \rho }{\partial t}}d{{V}_{c}}\)
\({{\rho }_{t}}dxdydz{{\left( \rho u \right)}_{x}}dxdydz+{{\left( \rho v \right)}_{y}}dxdydz+{{\left( \rho w \right)}_{z}}dxdydz\text{=}{{\rho }_{t}}dxdydz\)
两边除\(dxdydz\),可得
\({{\rho }_{t}}+{{\left( \rho u \right)}_{x}}+{{\left( \rho v \right)}_{y}}+{{\left( \rho w \right)}_{z}}=0\) (2.7.6)
方程(2.7.6)就是对笛卡尔坐标系中连续方程的微分形式。
将方程(2.7.6)表示为矢量形式,得
\({{\rho }_{t}}+\nabla \cdot \left( \rho \vec{V} \right)=0\) (2.7.7)
方程(2.7.7)与方程(2.7.4)是一致的。虽然应用了不同的方法,但结果与用拉格朗日法所获得结果相同。因为微元控制体法比较复杂,所以在今后将不采用。然而,应当指出,在研究传输现象(例如粘性、传导以及扩散等)时,微元控制体法显得更加直接。
各坐标系中连续方程的表达形式
上面在笛卡尔坐标系推导了连续方程的微分形式,对于其他坐标系的结果可用类似的方法导得。下面,将总结连续方程在不同坐标系表达式,以方便应用。需要指出的是,只要掌握散度在不同坐标系表达式,利用散度在不同坐标系表达式很容易写出连续方程在各种坐标系表达式。
1) 矢量形式连续方程
\(\frac{\partial \rho }{\partial t}+\nabla \bullet (\rho \vec{V})=0\).
2) 散度在正交曲线坐标系中表达式
散度为标量,表示单位体积通量的极限,表征源或汇的强度,计算公式为
\(div\overset{\to }{\mathop{a}}\,=\nabla \bullet \overset{\to }{\mathop{a}}\,=\frac{1}{H1\times H2\times H3}\left( \frac{\partial ({{a}_{1}}H2H3)}{\partial q1}+\frac{\partial ({{a}_{2}}H1H3)}{\partial q2}+\frac{\partial ({{a}_{3}}H1H2)}{\partial q3} \right)\)
3) 各坐标系连续方程表达式
正交曲线坐标系:\(\frac{\partial \rho }{\partial t}+\frac{1}{H1\times H2\times H3}\left( \frac{\partial (\rho {{v}_{1}}H2H3)}{\partial q1}+\frac{\partial (\rho {{v}_{2}}H1H3)}{\partial q2}+\frac{\partial (\rho {{v}_{3}}H1H2)}{\partial q3} \right)\text{=}0\)
直角坐标系:\(\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u)}{\partial x}+\frac{\partial (\rho v)}{\partial y}+\frac{\partial (\rho \omega )}{\partial z}=0\)
圆柱坐标系:\(\frac{\partial \rho }{\partial \tau }+\frac{1}{r}\frac{\partial (r\rho {{v}_{r}})}{\partial x}+\frac{1}{r}\frac{\partial (\rho {{v}_{\theta }})}{\partial \theta }+\frac{\partial (\rho {{v}_{z}})}{\partial z}=0\)
球坐标系:\(\frac{\partial \rho }{\partial \tau }+\frac{1}{r}\frac{\partial (\rho u)}{\cos \phi \partial \lambda }+\frac{1}{r}\frac{\partial (\rho v\cos \phi )}{\cos \phi \partial \phi }+\frac{1}{{{r}^{2}}}\frac{\partial (\rho w{{r}^{2}})}{\partial r}=0\)
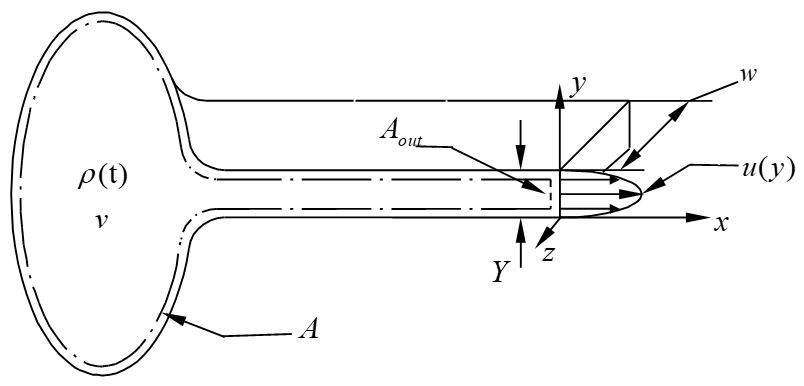
例3 空气通过矩形出口管流出贮箱。如图2-18所示。贮箱和出口的总容积以\({{V}_{c}}\)表示。如果出口管的高度\(Y\)比宽度\(W\)小,则在出口截面处速度分布为
\(u\left( y \right)=\left( \frac{4U}{{{Y}^{2}}} \right)\left( yY-{{y}^{2}} \right)\)
式中: 是最大速度。假设流动率足够小,以致整个贮箱和出口管的空气密度可以认为是均匀的(即\(\rho \ne \rho \left( x,y,z \right)\))。
(a)试推导出口处瞬时质量流率,以及在贮箱和出口管中空气密度时间变化率的表达式。
(b)某一具体的贮箱和出口管有总容积0.283\(\mathbf{a}(M)\),出口管高度Y=0.00254m,以及出口管宽度\(W=0.3048m\)。试计算在压力\(p=1.379\cdot {{10}^{5}}N/{{m}^{2}}\),温度\(T=277.8K\),以及最大出口速度 的瞬间,\({{\overset{\bullet }{\mathop{m}}\,}_{out}}\)和\(\frac{\partial \rho }{\partial t}\)之值。空气的气体常数为\(287.04J/kg\cdot K\)。
解:(a)定义贮箱和出口管的内壁,以及出口面积本身为控制面A。控制容积\(\mathbf{a}(M)\)由贮箱容积家出口管容积组成。对这样的控制体,连续方程为方程(2.7.3)。这样
\(\int_{{{V}_{c}}}{\frac{\partial \rho }{\partial t}}d{{V}_{c}}+\int_{{{A}_{out}}}{\rho \vec{V}\cdot d\vec{A}=0}\) (a)
式中:\({{\text{A}}_{out}}\)表示有质量流动的那部分控制面的总面积。
图2-18 例3示意图
控制体\({{V}_{c}}\)的瞬时质量流出率,由方程(a)的第二项得到
\({{\overset{\bullet }{\mathop{m}}\,}_{out}}=\int_{{{A}_{out}}}{\rho \vec{V}\bullet d\vec{A}}=\int_{{{A}_{out}}}{d{{\overset{\bullet }{\mathop{m}}\,}_{out}}}\) (b)
在贮箱中空气密度的时间变化率由方程(a)的第一项得到。如果密度在控制体上均匀,则\({\partial \rho }/{\partial }\;t\)不是\(x,y,z\)的函数。方程(a)的第一项变成
\(\int_{{{V}_{c}}}{\frac{\partial \rho }{\partial t}}d{{V}_{c}}=\frac{\partial \rho }{\partial t}{{V}_{c}}\) (c)
将(b),(c)代入(a)给出
\(\frac{\partial \rho }{\partial t}{{V}_{c}}+{{\overset{\bullet }{\mathop{m}}\,}_{out}}=0\) (d)
为了确定\({{\overset{\bullet }{\mathop{m}}\,}_{out}}\),注意
\(\vec{V}=\vec{i}\left( \frac{4U}{{{Y}^{2}}} \right)\left( yY-{{y}^{2}} \right)\) (e)
\(d\vec{A}=\vec{i}\left( dzdy \right)\) (f)
结果方程(b)变成
\({{\overset{\bullet }{\mathop{m}}\,}_{out}}=\rho \int_{0}^{Y}{\int_{0}^{\text{W}}{\left( \frac{4U}{{{Y}^{2}}} \right)\left( yY-{{y}^{2}} \right)dzdy}}\) (g)
\({{\overset{\bullet }{\mathop{m}}\,}_{out}}=\rho W\left( \frac{4U}{{{Y}^{2}}} \right)\left( \frac{Y{{y}^{2}}}{2}-\frac{{{y}^{3}}}{3} \right)\left| \begin{align}
& Y \\
& 0 \\
\end{align} \right.\) (h)
将方程(h)代入方程(d)给出
\(\frac{\partial \rho }{\partial t}=-\frac{2\rho UWTY}{3{{V}_{c}}}\) (i)
(b)在控制体内空气的瞬时密度通过应用对完全气体的热力学状态方程算得
\(\rho =\frac{p}{RT}=\frac{1.379\bullet {{10}^{5}}}{287.04\left( 277.8 \right)}=1.729kg/{{m}^{3}}\)
由方程(h)
\({{\overset{\bullet }{\mathop{m}}\,}_{out}}=\frac{2\rho UWY}{3}=\frac{2\left( 1.729 \right)\left( 30.48 \right)\left( 0.00254 \right)}{3}=0.0272kg/s\)
由方程(d)
\(\frac{\partial \rho }{\partial t}=-\frac{{{\overset{\bullet }{\mathop{m}}\,}_{out}}}{V{}_{c}}=-\frac{0.0272}{0.283}=-0.0961kg/{{m}^{3}}\cdot s\)
2.8 动量方程
动量方程建立基础是动量定律,即牛顿第二定律,动量方程建立思路是将动量定律应用于通过控制体流体的流动。
下面我们将从“动量定律”出发推导动量方程。
与连续方程类似,有多种方法来建立动量方程,下面我们将用不同的方法建立动量方程,不同方法所得的结果均相同,可以起到相互印证作用。
图2-19 系统、控制体与控制面
(流体微团的)拉格朗日法
把牛顿运动第二定律用到通过控制体流体流动所得的方程称为动量方程。
与推导连续方程类似,如图2-15所示,在空间取一微元体,体积为\({{V}_{c}}\),该体积外表面为 ,某时刻占据该体积\({{V}_{c}}\)的流体微团质量为m。
以流体微团为研究对象,牛顿运动第二定律为
![]() (2.8.1)
(2.8.1)
方程(2.8.1)表示:流动中,流体微元所受到的力等于流体微团所具有的动量随时间的变化率。
方程(2.8.1)中的导数是跟踪流体微团的导数,因此是实质导数,于是方程(2.8.1)可写成
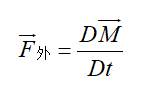 (2.8.2)
(2.8.2)
利用 和 的一般性质,对动量而言,\(N=\overrightarrow{M}=\int_{{{V}_{C}}}{\overrightarrow{V}\text{d}{{V}_{\text{c}}}}\),以及\(n=\overrightarrow{V}\)(见方程(2.3.5))。将这些结果代入方程(2.6.18),得
\({{\overrightarrow{F}}_{}}=\int_{{{V}_{_{C}}}}{{{(\rho \overrightarrow{V})}_{t}}\text{d}{{V}_{\text{c}}}}+\int_{A}{\overrightarrow{V}(\rho \overrightarrow{V}\cdot \text{d}\overrightarrow{A})}\) (2.8.3)
式中:下标t表示对时间t的偏微分。为了完成从系统法到控制体法的转变,必须把作用于系统上的外力表达为作用于控制体上的力。
(1)作用于流体上的纯外力
作用于流体上的外力可分为体积力\({{\overrightarrow{F}}_{B}}\)和表面力\({{\overrightarrow{F}}_{S}}\)
\({{\overrightarrow{F}}_{}}={{\overrightarrow{F}}_{B}}+{{\overrightarrow{F}}_{S}}\) (2.8.4)
体积力是作用在整个流体质量上的力。最普通的体积力是万有引力,其它重要的例子是带电流体上的电磁力。通常\({{\overrightarrow{F}}_{B}}\)可写为
\({{\overrightarrow{F}}_{B}}=\int_{{{V}_{C}}}{{{\overrightarrow{B}}_{\rho }}\text{d}{{V}_{\text{c}}}}\) (2.8.5)
式中:\(\overrightarrow{B}\)表示单位质量的体积力。
表面力是作用在与环境接触的系统表面上的力,以\({{\overrightarrow{F}}_{S}}\)表示。表面力又可分为法向力\({{\overrightarrow{F}}_{\text{n}}}\)和切向力\({{\overrightarrow{F}}_{t}}\)。表面力是法向力和切向力的矢量和,即
\({{\overrightarrow{F}}_{S}}={{\overrightarrow{F}}_{n}}+{{\overrightarrow{F}}_{t}}\)
在无粘性流体流动的情况下,法向力由压力引起,即
\({{\overrightarrow{F}}_{\text{n}}}=-\int_{A}{p\text{d}\overrightarrow{A}}\) (2.8.6)
在方程(2.8.6)中出现负号,是因为压力作用与在外表面上,方向指向外表面的内侧,而微元面积\(\text{d}\overrightarrow{A}\)的正法向是向外方向。对于无粘性流动,因为没有剪切力,\({{\overrightarrow{F}}_{t}}=0\)。对于粘性流动,表面力中有粘性剪应力。关于作用在粘性流体上法向和切向力的详细表达式,有兴趣的读者可以参考处理粘性流体流动的许多优秀著作。为了表示切向力的来源,将用\(\overrightarrow{F}\)剪表示\({{\overrightarrow{F}}_{t}}\),如同在分析一维流动时保持的那样的一般形式一样。
(2)对于控制体的动量方程
综合以上讨论的所有力,作用在系统上的纯外力\(\overrightarrow{F}\)外可表达为:
![]() (2.8.7)
(2.8.7)
将方程(2.8.7)代入方程(2.8.3)得动量方程。
\(\int_{{{V}_{C}}}{\overrightarrow{B}\rho \text{d}{{V}_{\text{c}}}}-\int_{A}{p\text{d}\overrightarrow{A}}+{{\overrightarrow{F}}_{}}=\int_{{{V}_{C}}}{{{(\rho \overrightarrow{V})}_{\text{t}}}\text{d}{{V}_{\text{c}}}}+\int_{A}{\overrightarrow{V}(\rho \overrightarrow{V}\cdot \text{d}\overrightarrow{A})}\) (2.8.8)
方程(2.8.8)即为动量方程的积分表达式,它是一矢量方程,其在每一个座标方向上的分量都保持独立的关系。
为了获得动量方程各分量方程的普遍形式,用单位矢量 表示 方向(例如,在笛卡尔座标系中,\({{x}_{i}}=x,yz\),而\({{\vec{n}}_{i}}=\vec{i}\),\(\vec{j}\)或\(\vec{k}\)),用\({{u}_{i}}\)表示对应坐标方向的速度分量。用\({{\vec{n}}_{i}}\)和方程(2.8.8)进行数量积,便获得方程(2.8.8)在\({{x}_{i}}\)方向的分量方程。
\(\int_{{{V}_{C}}}{{{B}_{i}}\rho \text{d}{{V}_{\text{c}}}}-\int_{A}{\text{p}{{\overrightarrow{n}}_{\text{i}}}\cdot \text{d}\overrightarrow{A}}{{\overrightarrow{n}}_{i}}+{{\overrightarrow{F}}_{}}=\int_{{{V}_{C}}}{{{(\rho {{u}_{i}})}_{t}}\text{d}{{V}_{\text{c}}}}+\int_{A}{{{u}_{i}}(\rho \overrightarrow{V}\cdot \text{d}\overrightarrow{A})}\) (2.8.9)
对定常流动,方程(2.8.9)右边第一项为0。
在许多应用中,不必要也不可能详细确定由于压力和剪切力产生的表面外力,感兴趣的仅是表面力的合力。例如喷气推进发动机(火箭、涡轮喷气或者冲压发动机)产生的合力,作用在没入流动流体物体上的总力,以及为了保持有流体流过的管道固定在应有位置上所需要的外力等。在这样的情况下,保持表面力为一般形式\(\overrightarrow{F}\)表更为方便,\(\overrightarrow{F}\)表是作用在控制体表面上所有外力的总和。这时,便得到动量方程的表达式为:
![]()
假设,在控制体内的动量变化和通过控制面的动量流通量可以求得,通过方程(2.8.10)便可用来计算作用在控制体表面上纯表面力的合力,而不需要详细知道压力或剪应力的分布。
(3)动量方程的微分形式
在推导动量方程的微分形式之前,必须确定剪切应力。如果保留剪应力,则它们与流场参数之间的关系是重要的。这样产生的微分方程称为Navier-Stokes方程。对于无粘性流体,![]()
通过应用散度定理(见方程(2.6.19)\(\int_{A}{\overrightarrow{B}\cdot \text{d}\overrightarrow{A}}=\int_{{{V}_{\text{c}}}}{\nabla \cdot \overrightarrow{B}\text{d}{{V}_{\text{c}}}}\)),方程(2.8.9)中的面积分可能转换为体积分。压力项变成
\(-\int_{A}{p\overrightarrow{{{u}_{i}}}\cdot \text{d}\overrightarrow{A}}=-\int_{{{V}_{\text{c}}}}{\frac{\partial p}{\partial {{x}_{i}}}}\text{d}{{V}_{c}}\) (2.8.11)
动量通量项变成
\(\int_{A}{{{u}_{i}}\rho \overrightarrow{V}\cdot \text{d}\overrightarrow{A}}=\int_{{{V}_{\text{c}}}}{\nabla \cdot \rho {{u}_{i}}\overrightarrow{V}}\text{d}{{V}_{\text{c}}}\) (2.8.12)
设 ,并将以上结果代入(2.8.9)得
\(\int_{{{V}_{\text{c}}}}{{{B}_{i}}\rho \text{d}}{{V}_{\text{c}}}-\int_{{{V}_{\text{c}}}}{\frac{\partial p}{\partial {{x}_{i}}}\text{d}}{{V}_{\text{c}}}={{\int_{{{V}_{\text{c}}}}{\rho {{u}_{i}}}}_{t}}\text{d}{{V}_{\text{c}}}+\int_{{{V}_{\text{c}}}}{\nabla \cdot \rho {{u}_{i}}\overrightarrow{V}}\text{d}{{V}_{\text{c}}}\)
当控制体\({{V}_{\text{c}}}\)缩小到微元容积\(\text{d}{{V}_{\text{c}}}\)时,积分值的极限就是被积函数本身,因此得
\(\rho {{B}_{i}}-\frac{\partial p}{\partial {{x}_{i}}}=\rho {{u}_{i}}{{}_{t}}+\nabla \cdot (\rho {{u}_{i}}\overrightarrow{V})\) (2.8.13)
展开方程(2.8.13)的右边(RHS),得。
\((RHS)=\rho {{({{u}_{i}})}_{t}}+{{u}_{i}}\left( {{\rho }_{t}}+\nabla \cdot (\rho \vec{V}) \right)+\rho (\vec{V}\cdot \nabla ){{u}_{i}}\) (2.8.14)
方括号中的表达式为质量守恒定律的表达式,方程(2.7.7),它恒等于0。因此,方程(2.8.14)简化为:
\(\left( RHS \right)=\rho \left( {{({{u}_{i}})}_{t}}+(\vec{V}\cdot \nabla ){{u}_{i}} \right)=\rho \frac{D{{u}_{i}}}{Dt}\) (2.8.15)
将方程(2.8.15)代入(2.8.13),得
\(\rho \frac{D{{u}_{i}}}{Dt}+\frac{\partial p}{\partial {{x}_{i}}}-\rho {{B}_{i}}=0\) (2.8.16)
方程(2.8.16)为微分形式动量方程的分量形式。
通过求分量方程的矢量和,可得动量微分方程的矢量形式。
\(\rho \frac{D\overrightarrow{V}}{D\text{t}}+\nabla \text{p}-\rho \overrightarrow{B}=0\) (2.8.17)
方程(2.8.17)即为著名的欧拉运动方程。其用于无粘流动。对于定常流,方程(2.8.15)中\({{u}_{i}}{{}_{t}}=0\),则方程(2.8.17)的第一项变成
\(\rho \frac{D\overrightarrow{V}}{D\text{t}}=\rho \overrightarrow{V}\cdot \nabla \overrightarrow{V}\)
因此,对于定常流,欧拉运动方程为
\(\rho \overrightarrow{V}\cdot \nabla \overrightarrow{V}+\nabla p-\rho \overrightarrow{B}=0\) (2.8.18)
(有限体积)控制体法
动量方程使用欧拉法进行推导的本质上是牛顿关于作用在一个质量上的一切力的总和等于其质量和其加速度的乘积这条定律的推广。对于变质量的情况,这条定律可改述为:一切力的总和必须等于单位时间内所涉及的流体质量的动量变化。
选取一个边长为\(dx\),\(dy\),\(dz\)的控制体,并把这控制体固定于坐标系上。将动量守恒定律应用于控制体,即可建立动量方程。
控制体形式的动量方程是最常用的基本方程之一。优点在于,只要知道了控制体进、出口的流动情况,就可以得出作用在控制体上的力,而无需知道控制体内部的流动细节。
对于质点系,牛顿运动第二定律为 。利用N和n的一般性质,\(N=\vec{M}=\int_{{{V}_{c}}}{\vec{V}d{{V}_{c}}}\),以及\(n=\vec{V}\),可得到x ,其中下标t表示对时间t的偏微分。
动量方程中的作用力为质量力和表面力,质量力的合力可表示为\({{\vec{F}}_{B}}=\int_{{{V}_{c}}}{\vec{R}\rho d{{V}_{c}}}\),其中\(\vec{R}\)表示单位质量流体的质量力。
一般情况下,控制体受到的表面力包括压力和黏性力,即法向力和切向力。对于理想流体,切向力为0,所以表面力仅为法向压力。作用在流体表面的压力和表面垂直并指向内部,即表面单位矢量向外为正,所以压力可以表示为\({{\vec{F}}_{p}}=\int_{A}{-p\cdot d\vec{A}}\),对于封闭表面,压力的合力为0。
于是控制体的动量方程为:
\({{\int_{{{V}_{c}}}{\left( \rho \vec{V} \right)}}_{t}}d{{V}_{c}}+\int_{A}{\vec{V}\left( \rho \vec{V}\cdot d\vec{A} \right)}=\int_{{{V}_{c}}}{\vec{R}\rho d{{V}_{c}}-\int_{A}{p\cdot d\vec{A}}}\) (2.8.19)
由\({{x}_{i}}\)方向的单位矢量和动量方程积分形式进行数量积,得\({{x}_{i}}\)方向的动量方程为:
\(\int_{vc}{{{R}_{i}}}\rho d{{v}_{c}}-\int_{A}{P{{{\vec{n}}}_{i}}}\cdot d\vec{A}=\int_{vc}{{{\left( \rho {{u}_{i}} \right)}_{t}}d{{v}_{c}}}+\int_{A}{{{u}_{i}}}\left( \rho \vec{V}\cdot d\vec{A} \right)\) (2.8.20)
其中,\(\int_{A}{P{{{\vec{n}}}_{i}}}\cdot d\vec{A}=\int_{{{V}_{c}}}{\nabla }\cdot \left( P{{{\vec{n}}}_{i}} \right)d{{V}_{c}}\),\(\int_{A}{{{u}_{i}}}\left( \rho \vec{V}\cdot d\vec{A} \right)=\int_{{{V}_{c}}}{\nabla }\cdot \left( {{u}_{i}}\rho \vec{V} \right)d{{V}_{c}}\)
于是动量方程可表示为:
\(\int_{{{V}_{c}}}{{{R}_{i}}}\rho d{{V}_{c}}-\int_{{{V}_{c}}}{\nabla \cdot \left( P{{{\vec{n}}}_{i}} \right)}d{{V}_{c}}=\int_{{{V}_{c}}}{{{\left( \rho {{u}_{i}} \right)}_{t}}d{{V}_{c}}}+\int_{{{V}_{c}}}{\nabla \cdot \left( {{u}_{i}}\rho \vec{V} \right)}d{{V}_{c}}\) (2.8.21)
当\({{V}_{c}}\to d{{V}_{c}}\)时,有
\({{R}_{i}}\rho -\nabla \cdot \left( P{{{\vec{n}}}_{i}} \right)=\left( \rho {{u}_{i}} \right)+\nabla \cdot \left( {{u}_{i}}\rho \vec{V} \right)\) (2.8.22)
展开并应用连续方程可得:
\({{R}_{i}}\rho -\nabla \cdot \left( P{{{\vec{n}}}_{i}} \right)=\rho \frac{D{{u}_{i}}}{Dt}\) (2.8.23)
求矢量和,得
\(\rho \vec{R}-\nabla P=\rho \frac{D\vec{V}}{Dt}\) (2.8.24)
当\(\vec{R}=0\) 时,方程变为:
\(\frac{D\vec{V}}{Dt}+\frac{1}{\rho }\nabla p=0\) (2.8.25)
便可以得到动量方程的微分形式。
(微元)控制体法
将牛顿第二定律应用在图2-19所示占据(微元)控制体的运动流体微团,就是:作用于微团上力的总和等于微团的质量与微团运动时加速度的乘积。这是一个矢量关系式,可以沿x,y,z轴分解成三个标量的关系式。下面分别建立x,y,z轴的动量方程。
x方向动量方程的建立
图2-20 运动的无穷小微团模型
(图中只画出了x方向的力,用于推导x方向动量方程)
微团运动纵观分析
先仅考虑x方向的动量分量,牛顿第二定律具有如下形式:
\({{F}_{x}}=m{{a}_{x}}\) (2.8.26)
其中:\({{F}_{x}}\) 和\({{a}_{x}}\) 分别是微团所受力(分力)和加速度在x方向的分量。
由于是无粘流动,微团受力包括直接作用于流体微团整个体积上的体积力和作用于微团表面的压力。
体积力表达式:
将作用在单位质量流体微团上的体积力记做\(f\),其x方向分量记做\({{f}_{x}}\)。流体微团的体积为\(dxdydz\),因此
作用在流体微团上的体积力的x方向分量=\(\rho {{f}_{x}}(dxdydz)\) (2.8.27)
表面力表达式:
仅考虑表现为表面压力的正应力,不考虑表现为由粘性引起的粘性力。
面\(adhe\)上的力:
存在沿x轴正向的压力\(pdydz\),同时存在沿x轴负向的应力\({{\tau }_{xx}}dydz\)。
面\(bcgf\)上的力:
存在压力 ,方向沿x轴负方向。。
合力:
综上所述,对运动的流体微团,x方向总的表面力为
\(\left( p-\left( p+\frac{\partial p}{\partial x} \right) \right)dxdydz\) (2.8.28)
x方向总的力\({{F}_{x}}\)为
\({{F}_{x}}=\text{-}\frac{\partial p}{\partial x}\text{d}x\text{d}y\text{d}z+\rho {{f}_{x}}\text{d}x\text{d}y\text{d}z\) (2.8.29)
式(2.8.29)给出了式(2.8.26)的左边。
下面考虑式(2.8.26)的右边。运动的流体微团,其质量是固定不变的,即
\(m=\rho dxdydz\) (2.8.30)
另外,我们知道流体微团的加速度就是速度变化的时间变化率。所以,加速度的x方向分量,记做\(n=e\),直接就等于u.的时间变化率。但由于我们考虑运动的流体微团,因此这个时间变化率是由物质导数给出的,即
\(e={{e}_{i}}+{{e}_{k}}+{{e}_{p}}+{{e}_{o}}\) (2.8.31)
将式(2.8.26)与式(2.8.29)到式(2.8.31)综合起来,我们得到:
\(\rho \frac{Du}{Dt}=-\frac{\partial p}{\partial x}+\rho {{f}_{x}}\) (2.8.32a)
这就是无粘流动x方向的动量方程。
用同样的办法,可得到y方向和z方向的动量方程
\(\rho \frac{Dv}{Dt}=-\frac{\partial p}{\partial y}+\rho {{f}_{y}}\) (2.8.32b)
\(\rho \frac{Dw}{Dt}=-\frac{\partial p}{\partial z}+\rho {{f}_{z}}\) (2.8.32c)
方程(2.8.32a、b、c)分别是x、y、z方向的动量方程。注意到,它们都是偏微分方程,是通过将基本的物理学原理应用于无穷小流体微团直接得到的。同时,由于流体微团是运动的,所以方程(2.8.32a、b、c)是非守恒形式的。它们都是标量方程,统称为纳维—斯托克斯方程。
按照下面的方法,可以得到纳维—斯托克斯方程的守恒形式。
根据物质导数的定义,可将方程(2.8.32a)的左边写成:
\(\rho \frac{Du}{Dt}=\rho \frac{\partial u}{\partial t}+\rho \vec{V}\bullet \nabla u\) (2.8.33)
另外,展开下面的导数
\(\frac{\partial (\rho u)}{\partial t}=\rho \frac{\partial u}{\partial t}+u\frac{\partial \rho }{\partial t}\)
整理,得
\(\rho \frac{\partial u}{\partial t}=\frac{\partial (\rho u)}{\partial t}\text{-}u\frac{\partial \rho }{\partial t}\) (2.8.34)
利用标量与向量乘积的散度的向量恒等式,有
\(\nabla \bullet (\rho u\vec{V})=u\nabla \bullet (\rho \vec{V})+(\rho \vec{V})\bullet \nabla u\)
改写为:
\((\rho \vec{V})\bullet \nabla u=\nabla \bullet (\rho u\vec{V})\text{-}u\nabla \bullet (\rho \vec{V})\) (2.8.35)
将式(2.8.34)和式(2.8.35)代人式(2.8.33),得
\(\rho \frac{Du}{Dt}=\frac{\partial (\rho u)}{\partial t}\text{-}u\frac{\partial \rho }{\partial t}\text{+}\nabla \bullet (\rho u\vec{V})\text{-}u\nabla \bullet (\rho \vec{V})\text{=}\frac{\partial (\rho u)}{\partial t}\text{-}u\left( \frac{\partial \rho }{\partial t}+\nabla \bullet (\rho \vec{V}) \right)\text{+}\nabla \bullet (\rho u\vec{V})\) (2.8.36)
此式右边方括号里的表达式就是连续性方程的左边,所以方括号中的项等于零,于是(2.8.36)可以简化为:
\(\rho \frac{Du}{Dt}=\frac{\partial (\rho u)}{\partial t}\text{+}\nabla \bullet (\rho u\vec{V})\) (2.8.37)
再将式(2.8.37)代人式(2.8.32a),得
\(\frac{\partial (\rho u)}{\partial t}+\nabla \bullet (\rho u\vec{V})=-\frac{\partial p}{\partial x}+\rho {{f}_{x}}\) (2.8.38a)
同样,方程(2.8.32b、c)可以写成:
\(\frac{\partial (\rho v)}{\partial t}+\nabla \bullet (\rho v\vec{V})=-\frac{\partial p}{\partial y}+\rho {{f}_{y}}\) (2.8.38b)
\(\frac{\partial (\rho w)}{\partial t}+\nabla \bullet (\rho w\vec{V})=-\frac{\partial p}{\partial z}+\rho {{f}_{z}}\) (2.8.38c)
方程(2.8.38a)到方程(2.8.38c)就是纳维—斯托克斯方程的守恒形式。
不同坐标系中动量方程的表达式
上面在笛卡尔坐标系推导了动量方程,接下来将总结动量方程在不同坐标系下的表达式,以方便应用。对于无粘流体,不考虑体积力的情况下,动量方程
\(\rho \frac{D\overrightarrow{V}}{D\text{t}}+\nabla \text{p}-\rho \overrightarrow{B}=0\)
由于\(\overrightarrow{B}\text{=}0\),则上式可以简化为
\(\frac{D\overrightarrow{V}}{Dt}+\frac{\nabla p}{\rho }=0\)
不同坐标系下的动量方程表达方式如下:
直角坐标系
x方向:\(\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}+\frac{1}{\rho }\frac{\partial p}{\partial x}=0\)
y方向:\(\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}+\frac{1}{\rho }\frac{\partial p}{\partial y}=0\)
z方向:\(\frac{\partial w}{\partial t}+u\frac{\partial w}{\partial x}+v\frac{\partial w}{\partial y}+w\frac{\partial w}{\partial z}+\frac{1}{\rho }\frac{\partial p}{\partial z}=0\)
圆柱坐标系
r方向:\(\frac{\partial {{v}_{r}}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{r}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{r}}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{r}}}{\partial z}+\frac{1}{\rho }\frac{\partial p}{\partial r}-\frac{{{v}_{\theta }}^{2}}{r}=0\)
方向:\(\frac{\partial {{v}_{\theta }}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{\theta }}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{\theta }}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{\theta }}}{\partial z}+\frac{1}{\rho }\frac{\partial p}{r\partial \theta }+\frac{{{v}_{r}}{{v}_{\theta }}}{r}=0\)
z方向:\(\frac{\partial {{v}_{z}}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{z}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{z}}}{\partial \theta }+{{v}_{z}}\frac{\partial {{v}_{z}}}{\partial z}+\frac{1}{\rho }\frac{\partial p}{\partial z}=0\)
球坐标系
r方向:\(\frac{\partial {{v}_{r}}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{r}}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{r}}}{\partial \theta }+\frac{{{v}_{\varphi }}}{r\sin \theta }\frac{\partial {{v}_{r}}}{\partial \varphi }+\frac{1}{\rho }\frac{\partial p}{\partial r}-\frac{{{v}_{\theta }}^{2}\text{+}{{v}_{\varphi }}^{2}}{r}=0\)
方向:\(\frac{\partial {{v}_{\theta }}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{\theta }}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{\theta }}}{\partial \theta }+\frac{{{v}_{\varphi }}}{r\sin \theta }\frac{\partial {{v}_{\theta }}}{\partial \varphi }+\frac{1}{\rho r}\frac{\partial p}{\partial \theta }-\frac{{{v}_{r}}{{v}_{\theta }}\text{+}{{v}_{\varphi }}^{2}\cot \theta }{r}=0\)
方向:\(\frac{\partial {{v}_{\varphi }}}{\partial t}+{{v}_{r}}\frac{\partial {{v}_{\varphi }}}{\partial r}+\frac{{{v}_{\theta }}}{r}\frac{\partial {{v}_{\varphi }}}{\partial \theta }+\frac{{{v}_{\varphi }}}{r\sin \theta }\frac{\partial {{v}_{\varphi }}}{\partial \varphi }+\frac{1}{\rho r\sin \theta }\frac{\partial p}{\partial \varphi }\text{+}\frac{{{v}_{r}}{{v}_{\varphi }}\text{+}{{v}_{\theta }}{{v}_{\varphi }}\cot \theta }{r}=0\)
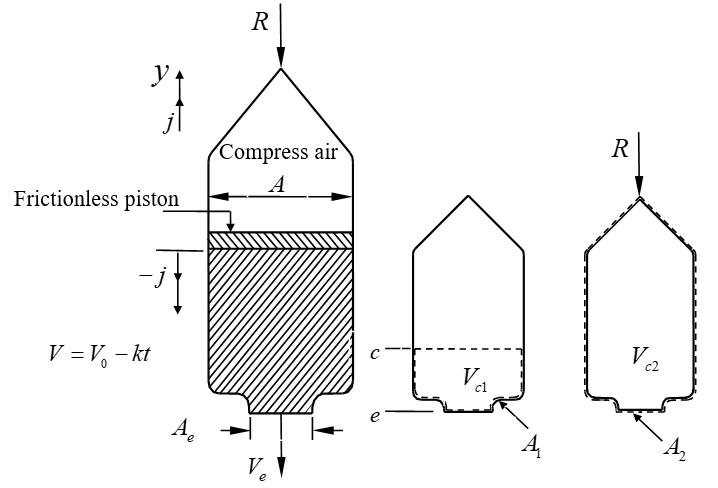
例4 图2-21表示一个模型火箭。该火箭通过火箭内压缩空气膨胀,推动活塞运动,进而使得水从尾部喷射推进。火箭内水面移动速度为\(V={{V}_{0}}-kt\)。水室内横截面积为A,而收缩喷管的出口面积为\({{A}_{e}}=A/2\)。火箭的初始质量为\(M\)。而水的密度\(\rho \)是常数。试求为了固定火箭所需要的约束力\(R\)。注意,火箭推力在数值上等于\(R\),而作用方向相反。
解:
图2-21 例4示意图
在解题前必须做某些简化假设。假设忽略压缩空气和无摩擦活塞的质量,速度\(V\)和\({{V}_{\text{e}}}\)在它们各自的截面上均匀,以及在喷管出口截面上喷射压力\({{P}_{\text{e}}}\)均匀并且等于大气压力。
(a)首先必须求\({{V}_{\text{e}}}\text{t}\)。因此,定义控制容积\({{V}_{\text{c1}}}\),如图2-21所示。对于\({{V}_{\text{c1}}}\)应用连续方程,方程(2.7.3),产生
\(\int_{{{V}_{c1}}}{(\frac{\partial \rho }{\partial t})}d{{V}_{c1}}+\int_{{{A}_{1}}}{\rho \overrightarrow{V}\cdot d\overrightarrow{A}}=0\) (a)
因为密度是常数,故(a)式为
\(\int_{{{A}_{1}}}{\overrightarrow{V}\cdot d\overrightarrow{A}}=0\) (a)
公式(a)在所有表面展开 \(\int_{{{A}_{c}}}{\overrightarrow{V}\cdot d\overrightarrow{A}}+\int_{{{A}_{e}}}{\overrightarrow{V}\cdot d\overrightarrow{A}}+\int_{{{A}_{}}}{\overrightarrow{V}\cdot d\overrightarrow{A}}=0\)
下表面
上表面 \({{\overrightarrow{V}}_{e}}=-\overrightarrow{j}{{V}_{e}}\) \(d{{\overrightarrow{A}}_{e}}=-\overrightarrow{j}d{{A}_{e}}\) (b)
\(\overrightarrow{V_{c}^{{}}}=-\overrightarrow{j}V\) \(d\overrightarrow{A}=\overrightarrow{j}dA\) (c)
其余表面,速度矢量和面积矢量垂直,无质量流出。
将(b)、(c)代入方程(a),并简化产生
\({{A}_{e}}{{V}_{e}}-AV=0\) (d)
\({{V}_{e}}=\frac{AV}{{{A}_{e}}}=2({{V}_{0}}-kt)\) (e)
(b)其次,从控制容积\({{V}_{c2}}\),如图2.8.1所示,求火箭瞬时质量。
对这种情况,连续方程(2.7.3)变成
\(\int_{{{V}_{c2}}}{\frac{\partial \rho }{\partial t}}d{{V}_{c}}+\int_{{{A}_{2}}}{\rho \overrightarrow{V}\cdot d\overrightarrow{A}}=0\) (f)
方程(f)中的第一项可写成
\(\int_{{{V}_{c2}}}{\frac{\partial \rho }{\partial t}}d{{V}_{c}}=\frac{\partial {{M}_{(t)}}}{\partial t}\) (g)
式中:\({{M}_{(t)}}\)是控制体\({{V}_{c2}}\)内水,空气和火箭元件的总质量。
方程(f)中第二项是简单的,
\(\int_{{{A}_{2}}}{\rho \overrightarrow{V}\cdot d\overrightarrow{A}}=\int_{{{A}_{e}}}{\rho (-\overrightarrow{j}{{V}_{e}})}\cdot (-\overrightarrow{j}d{{A}_{e}})=\rho {{V}_{e}}{{A}_{e}}=2\rho {{A}_{e}}({{V}_{0}}-kt)\) (h)
将方程(g)和(h)代入(f)产生
\(\frac{\partial M}{\partial t}+2\rho {{A}_{e}}({{V}_{0}}-kt)=0\) (i)
对方程(i)积分产生
\(\int_{{{M}_{0}}}^{M}{dM}=-\int_{0}^{t}{2\rho {{A}_{e}}({{V}_{0}}-kt)dt}\) (j)
\({{M}_{(t)}}={{M}_{0}}-2\rho {{A}_{e}}({{V}_{0}}t-\frac{1}{2}k{{t}^{2}})\) (k)
(c)现在对控制体 应用动量方程,求在火箭上的反作用力。
\({{V}_{c2}}\),动量方程(2.8.10)为:
\({{\overrightarrow{F}}_{}}+\int_{{{V}_{\text{c}2}}}{\overrightarrow{B}\rho \text{d}{{V}_{\text{c}}}}={{\int_{{{V}_{c2}}}{\rho \overrightarrow{V}}}_{\text{t}}}d{{V}_{c}}+\int_{{{A}_{2}}}{\overrightarrow{V}\rho \overrightarrow{V}\cdot d\overrightarrow{A}}=0\) (l)
接下来将逐项研究方程(l)中的各项。
事实上,对方程(l)只要在\(\overrightarrow{j}\)方向上的应用。\(\overrightarrow{F}\)表为作用在控制面A2上的表面力。因此作用在A2上的所有的压力都等于外界大气压力Pe(包括火箭喷管出口截面上的水压力Pe),所以表面力中没有压力项。作用在A2上的唯一的表面力是使火箭保持固定所需要的约束力(\(\text{-}\overrightarrow{\text{j}}R\)。
\(\int_{{{V}_{c}}}{\overrightarrow{B}\rho d{{V}_{c}}}\)为体积力,由重力引起的体积力为(\(\text{-}\overrightarrow{\text{j}}{{M}_{g}}\))。
\(\int_{{{V}_{c2}}}{{{(\rho \overrightarrow{V})}_{t}}dV}\)为控制体\({{V}_{c2}}\) 内的惯性力变化。因为在控制体内水的速度为\(\text{-}\overrightarrow{\text{j}}V\),因此
\(\int_{{{A}_{2}}}{\overrightarrow{V}(\rho\overrightarrow{V}\cdot\overrightarrow{A})}\)为控制面上的动量流通量,
代入方程(l),并消去\(\overrightarrow{j}\)得
(m)
\(-R-{{M}_{\text{g}}}=\frac{\partial }{\partial t}(-VM)-\rho {{A}_{e}}{{V}_{e}}^{2}\)
方程(m)中的右边第一项可写成
\(\frac{\partial }{\partial t}(-VM)=-M\frac{\partial V}{\partial t}-V\frac{\partial M}{\partial t}\) (n)
将方程(l)及\(V={{V}_{0}}-kt\) 代入方程(n)右边产生
\(\frac{\partial }{\partial t}(-VM)=-kM\text{+2}\rho {{A}_{e}}{{({{V}_{0}}-kt)}^{2}}\) (o)
将方程(o)代入方程(m)并解出R产生
\(R=-(g+k)-\text{2}\rho {{A}_{e}}{{({{V}_{0}}-kt)}^{2}}\text{+}\rho {{A}_{e}}{{V}_{e}}^{2}\)
将方程(k)及(e)代入上式,最后得
\(R=-(g+k)[{{M}_{0}}-\text{2}\rho {{A}_{e}}({{V}_{0}}t-\frac{k{{t}^{2}}}{2})]\text{+}\rho {{A}_{e}}{{V}_{e}}^{2}{{({{V}_{0}}-kt)}^{2}}\) (p)
上面的例子是应用动量方程求解非定常流动问题很好的说明。它生动地表明,为了获得问题的解,需要对所研究的进行必要假设和近似。
2.9 能量方程
在推导能量方程之前,有必要明晰能量、功和热力学第一定律等概念。
1)能量概念
系统能量是系统在某一状态下所具有的全部能量。本课程仅考虑系统涉及物理变化和化学变化时各种能量,而不考虑电能和原子能。至于化学能,在有化学反应的气体流动中予以考虑,现在只是仅研究没有化学反应的有关物理过程的各种能量。
无化学反应的物理过程包括的能量
对于没有化学反应的物理过程,能量包括三种:一是系统作整体宏观运动时所具有的宏观动能EK;二是在重力场中,系统位于某一高度Z所具有的势能EP;三是与系统整体运动和重力场无关,系统内部气体分子作无规则运动所具有的内部能量U(简称内能),因此,系统的总能量为
\(E={{E}_{K}}+{{E}_{P}}+U\)
若系统只有一公斤工质,则总能量为
\(\text{e}={{e}_{K}}+{{e}_{P}}+u\)
式中: \({{e}_{K}}=\frac{{{V}^{2}}}{2}\) \(J/kg\);
\({{e}_{p}}=gz\) \(J/kg\);
u——-内能 \(J/kg\);
V——-系统作整体运动的速度 \(m/s\);
z——-焓系统距海平面的高度\(m\);
气体分子作无规则运动所具有的内部能量由四部分组成:(1)气体分子作无规则的平移运动所具有的平移动能;(2)多原子组成的分子作旋转运动所具有的旋转动能;(3)分子内部的原子作振动所具有的振动动能;这三种能量均为温度的函数。此外,还有由于分子间作用力所形成的势能,这种能量随分子间距离变化而变化,亦即决定于比容。综上所述,可得气体的内能决定于气体的温度和比容,将它们写成数学关系,即
\(U=f(T,\text{v})\)
由于温度和比容是状态参数,所以内能也是一个状态参数,其具有全微分性质,将它们写成数学关系,即
\(\int_{1}^{2}{dU={{U}_{2}}-{{U}_{1}}=\Delta U}\)
对完全气体,分子之间无作用力,所以内能中无势能,而仅有三种动能,因此,完全气体的内能仅是温度的函数,即\(U=f(T)\)
可见,只要起始和终了温度相同,不论变化过程的途径如何,完全气体的内能变化也都相等。
具有化学反应的过程包括的能量
对具有化学反应的过程,物质内能包括两大部分内容。一部分是物理内能,用符号\({{U}_{ph}}\) 表示,它是前面介绍的“物质内部的热量”,本质是分子热运动的动能和分子之间相互作用力所形成的势能;对完全气体来说,它仅决定于气体温度。另一部分是化学(内)能,用符号\({{U}_{ch}}\)表示,它决定于物质内部结构,而与物质所处的物理状态无关。一般是对1摩尔(mol)或对1千摩尔(kmol)物质而言。设1千摩尔(kmol)物质的内能用符号(\(\mu u\)表示,单位为kJ/kmol,则\((\mu u)={{(\mu u)}_{ph}}+{{(\mu u)}_{ch}}\)
或 \(U={{(U)}_{ph}}+{{(U)}_{ch}}\)
显然,对具有化学反应的过程来讲,物质内能的概念比无化学反应的过程有所扩大,它包括了物理内能和化学内能。对只是讨论工质成分不改变的物理过程,过程前后的化学成分不变,所有化学能也不改变,所有化学能可以不予考虑。
在燃烧反应中,系统向外界放出能量,系统内能下降。系统和外界交换的热量叫做反应热。反应热可以为正,也可以为负。在热化学中,规定系统向外界放热为正,外界向系统加热为负。反应热用\(\overline{Q}\)表示,以与前面所用相区别。
2)容积功概念
如下图所示,
图2-22 容积功示意图
当气缸内的气体处于与外界压力相等的条件下,活塞静止不动。假设由于某种原因,气缸内的气体进行可逆的膨胀过程。假设此时气缸内气体压为p,活塞面积为A,则气体作用在活塞上的总作用力为pA,当活塞向右移动一微小距离dx,气体对活塞所做的功为
\(\text{d}W=pAdx=pdV\)
上式称为容积功。当dV>0,即气体膨胀,容积功为正,又称为膨胀功;反之,dv<0,气体被压缩,容积功为负,又称为压缩功。由于功和容积为广延量,所以\(\text{d}W=mdw\),\(\text{dV}=mdv\),所以1公斤气体所做的容积功为
\(\text{dw}=pdv\)
活塞从位置1移动到位置2,气体所做的容积功为\({{w}_{12}}=\int_{1}^{2}{pdv}\)。
式中:v ——-比体积。
注意:
(1)容积功是过程量,而不是状态量,\(\int_{1}^{2}{pdv}\) 不能写成\({{w}_{2}}-{{w}_{1}}\) ,而只能写成w12。
(2)只有可逆过程才能用上述各式来计算气体对外做的容积功。
3)焓的概念
在一些热力学方程式中,u和pv同时出现,因此用状态参数焓来代替u和pv两项,不仅可以简化方程,而且有助于热力计算。
定义: \(H=U+pV\)
式中:H——-焓,J;U——-内能,J;V——-体积,m3。
对于1公斤工质,则比焓
\(h=u+pv\)
式中:h——-焓,J/kg;u——-内能,J/kg;v——-比容,\(\frac{{{m}^{3}}}{kg}\) 。
由于内能u,压力p和比容v都是状态参数,所以h也是一个状态参数。因此,两状态之间焓的变化为
\(\Delta h={{h}_{2}}-{{h}_{1}}=\int_{1}^{2}{dh}\)
无化学反应的热力学第一定律
热力学第一定律表达为,外界对体系的加热量等于热力学能的增加与对外做功之和,表达式为:\(Q=\Delta U+W\)
对于微元过程,上式可写成\(\delta Q=\text{d}U+\delta W\)
式中,Q——-过程中体系与外界之间交换的热量,对体系加热取正,反之,体系向外散热,取负;
W—–过程中体系与外界之间交换的功,体系对外界做功,取正,反之,外界对体系做功,取负;
——体系热力学能的增加。
不论对于完全气体或真实气体,过程可逆或者不可逆,流动气体或静止气体,热力学第二定律都是适用的。对于1公斤工质,热力学第一定律解析式为
\(q=\Delta u+w\)
\(\delta q=du+\delta w\)
4)能量方程的建立
能量方程建立的基础是能量守恒,与连续和动量方程的建立思路类似,能量方程建立思路是将能量方程应用于占据控制体的流体。
建立能量方程的微元控制体如图2-18所示,Q为系统和外界的换热,W为系统对外界做功,我们以占据控制体的流体(系统)为研究对象。
对于单位质量的连续介质系统,热力学第一定律可以写成
\(\delta Q=de+\delta W\)
或
\(de=\delta Q-\delta W\) (2.9.1)
式中de由与流体相联系的各种形式的贮能组成。对流动的流体,单位质量所具有的贮能假设仅限于热能,动能和位能。因此,单位质量流体的贮能为
\(e=u+\frac{{{V}^{2}}}{2}+gz\) (2.9.2)
对于质量为m的流体,总能量是E=me,方程(2.9.1)变成
\(dE=\delta Q-\delta W\) (2.9.3)
式中:\(\delta Q\)和\(\delta W\)应用于整个系统。
在这里,Q和W没有遵循外延参数大写,内涵参数小写的规定,而遵循了能量方程中所采用术语的习惯,即大写字母Q和W表示热和功。我们规定,当采用 时,Q和W是以单位质量为基础,当采用E时,Q和W应用于整个系统的质量;当采用\(\frac{de}{dt}\) 时,\(\overset{\cdot }{\mathop{Q}}\) 和\(\overset{\cdot }{\mathop{W}}\)表示对每单位质量;而当采用\(\frac{dE}{dt}\)时,\(\overset{\cdot }{\mathop{Q}}\) 和\(\overset{\cdot }{\mathop{W}}\)表示对整个系统的质量。
图2-23 控制体示意图
为了推导关于控制体的热力学第一定律表达式,采用如图2-23所表示的控制体物理模型。图中示意地指出轴功,剪切功,热交换以及穿过控制体边界的质量流量。
方程(2.9.3)是对于流体微团的,但通过以相除,它可转化为系统总能量对时间的变化,于是
\(\frac{dE}{dt}=\delta \overset{\cdot }{\mathop{Q}}\,+\delta \overset{\cdot }{\mathop{W}}\) (2.9.4)
方程(2.9.4)表示系统具有的总能量E对时间的变化率,即跟踪流体质点的系统总能量时间变化率,是实质导数。因此 \(\frac{DE}{Dt}=\delta \overset{\cdot }{\mathop{Q}}\,+\delta \overset{\cdot }{\mathop{W}}\,\) (2.9.5)
在这种情况下,\(N=E=\int_{V}{(u+\frac{{{V}^{2}}}{2}}+gz)\rho d{{V}_{c}}\),以及\(n=e=u+\frac{{{V}^{2}}}{2}+gz\)。将 和 代入方程(2.6.18)产生
\(\frac{DE}{Dt}=\int_{V}{\frac{\partial }{\partial t}\left[ \rho (u+\frac{{{V}^{2}}}{2}+gz) \right]d{{V}_{c}}+\int_{A}{(u+\frac{{{V}^{2}}}{2}+gz)(\rho \overrightarrow{V}\cdot d\overrightarrow{A})}}\) (2.9.6)
为了把对系统的热力学第一定律转换成对控制体的,热和功必须用关于控制体的流动参数表示。
(1)对控制体的热交换
外界对控制体的热交换总数(以Q表示)是外界对瞬时占据控制体的流体质量的热交换总数。外界传向系统的热交换为正,反之系统传向外界的热交换为负。通常热交换可由传导,对流以及辐射引起。因此
Q=传导+对流+辐射 (2.9.7)
为了用控制体的流动参数明确表示\(\delta Q\),必须确定不同的热交换过程(传导、对流及辐射)和流动参数之间相互的关系。在本书,热交换过程的细节是不研究的,这样热交换的作用将保留其普遍形式\(\delta Q\)。这样做,在控制方程中就包含了热交换的一般影响项,并且可以研究一维问题。
(2)控制体所做的功
控制体对环境所做功定义为正功,这种功具有两种主要类型。第一种为轴功,W轴表示,指流体通过穿过系统边界的旋转轴对外界所做的功。例如运行压气机,起重机以及别的机械所做的都是轴功。第二种是表面力所做的功,这种功通过流体穿过控制体边界,或者通过控制体边界的运动产生。前一种表面力所做的功叫做流动功。
如早先所指出的那样,表面力分为由压应力产生的法向力和由剪应力产生的切向力。由于,剪应力所做功的表达式在此不进行推演。剪切力所做的功以W剪表示,并在方程中保留其一般形式。
压应力所做的功是将质量推出控制体所做的功(正功),或者是环境把质量推入控制体时所接受的功(负功)。
图2-24 法向力所作的流动功示意图
图2-24用于确定由法向力所做的流动功。作用在无限小矢量面积\(d\overrightarrow{A}\) 上的法向力为
\(d\overrightarrow{{{F}_{n}}}=pd\overrightarrow{A}\) (2.9.8)
由方程(2.9.8)给出的微元力\(d\overrightarrow{{{F}_{n}}}\)是控制体内的流体作用在环境上的力,因此是正值。通过以\(\overrightarrow{V}\)的数值乘在\(\overrightarrow{V}\)方向的\(d\overrightarrow{{{F}_{n}}}\)分量,得到所做功的变化率,这样
\(d\overset{\cdot }{\mathop{{{W}_{n}}}}\,=d{{F}_{n}}\cdot V\cdot \cos \alpha =d\overrightarrow{{{F}_{n}}}\cdot \overrightarrow{V}\) (2.9.9)
\(d\overset{\cdot }{\mathop{{{W}_{n}}}}\,=p\overrightarrow{V}\cdot d\overrightarrow{A}=pv(p\overrightarrow{V}\cdot d\overrightarrow{A})\) (2.9.10)
我们规定,当系统把质量推出控制体时,系统做正功,反之亦然。
由法向力做的总功,通过\(\delta \overset{\cdot }{\mathop{W}}\,\) 在整个控制面上积分得到,为
\(\overset{\cdot }{\mathop{{{W}_{n}}}}\,=\int_{A}{\delta }\overset{\cdot }{\mathop{{{W}_{n}}}}\,=\int_{A}{pv(}p\overrightarrow{V}\cdot d\overrightarrow{A})\) (2.9.11)
方程(2.9.11)既包括正功,又包括负功,功的符号由标量积\(\overrightarrow{V}\cdot d\overrightarrow{A}\) 的符号确定。
这样,瞬时占据控制体的流体对外界所做总功变化率为
![]()
(3)对控制体的能量方程
当把方程(2.9.5)、(2.9.6)、(2.9.7)和(2.9.12)联立起来可得到由控制体参数表示的热力学第一定律方程,它称为能量方程,为
合并面积分项,得
注意,由压应力引起的流动功\(\int_{A}{pv(\rho \overrightarrow{V}\cdot d\overrightarrow{A})}\)已并入方程(2.9.6)贮能项的比内能。产生表达式\((u+pv)\)。根据定义,\(u+pv\text{=h}\),h为比焓。由于,内能u和流动功pv总是在表面积分中一起发生,可以采用流体比焓,正如在方程(2.9.13)中表示的那样,采用比焓是方便的。然而,应当记住,第一个积分表示了非定常贮能,因为它不包含流动功,在这个积分中显示为内能u。
(4)能量方程的微分形式
根据散度定理,把积分形式的能量方程(2.9.13)中的面积分项转换为体积分,方程(2.9.13)中的
\(\int_{A}{\left( h+\frac{{{V}^{2}}}{2}+gz \right)}(\rho \overrightarrow{V}\cdot d\overrightarrow{A})=\int_{V}{\nabla \cdot [\left( h+\frac{{{V}^{2}}}{2}+gz \right)\rho \overrightarrow{V}]d{{V}_{c}}}\)
这样,方程(2.9.13)变为
令控制体缩小到微元控制体 ,这时积分值就是被积函数本身,上式变成 ![]()
通过对方程(2.9.14)中的非定常流动项加减,\({{[\rho (pv)]}_{t}}\),非定常流动项变成
\(\frac{\delta }{\delta t}\left[ \rho \left( h+\frac{{{V}^{2}}}{2}+gz \right) \right]-{{P}_{t}}\) (2.9.15)
式中:\({{p}_{t}}=\frac{\partial p}{\partial t}\)。
展开方程(2.9.14)中的非定常流动项和能量流通项,像推导微分形式的动量方程中一样[见方程(2.8.14)],并使用连续方程,能量方程(方程(2.9.14))的最后形式为

对于定常流动,\(\frac{D}{Dt}=(\overrightarrow{V}\cdot \nabla )\)且,Pt=0。
方程(2.9.16)中的轴功,剪切功和热交换项仅表示这些过程会出现。对于它们的具体计算,需要推导出与其相适应的利用流动参数和梯度表示的功和与热交换方程。
不同坐标系中能量方程的表达式
上面在笛卡尔坐标系推导了能量方程,接下来将总结能量方程在不同坐标系下的表达式,以方便应用。对于无粘流体,绝热流动,且无轴功的情况下,能量方程
可简化为
\(\rho \frac{D}{Dt}\left( h+\frac{{{V}^{2}}}{2}+gz \right)-\frac{\partial p}{\partial t}=0\)
不同坐标系下的能量表达方式如下:
例5 考察2.7中的第一个例子描述的贮箱和出口管。假设空气质量流出率足够的小,以至于贮箱和出口管内的一切参数都可以认为是均匀的(即不是x,y,z的函数),并假设空气对贮箱的热交换率为1055J/s。对于该例中给定的条件,试确定贮箱中空气内能的瞬时变化率(即 )。
解:取贮箱和出口管共同作为控制体Vc 。假设没有轴功和剪切功,忽略体积力的影响。对于所包含的低速度,动能也可忽略。这样,方程(2.9.13)变成
方程(a)中的非定常项可写成
式中,\(\frac{\partial \rho }{\partial t}=-{{\dot{m}}_{out}}/{{V}_{c}}\) [见前例的方程(d)]。因此
方程(a)中能量流通量项可写成
将(d),(e)代入(a),得
对完全气体,\(u={{C}_{v}}T\) 以及\(h={{C}_{p}}T\) 。从方程(f)解出 得
这里,对完全气体,\({{C}_{p}}-{{C}_{v}}=R\) 。
方程(h)即是所要求的 \(\partial u/\partial t\)与其它流动参数间的关系。
从该例,\(V=0.283{{m}^{3}},{{\dot{m}}_{out}}=0.272kg/s,\rho =1.729kg/{{m}^{3}},T=277.8K\) ,将这些数值代入(h),可以得到
2.10 熵方程
通过工程热力学知识可知,热力过程可以通过压容图表示,但压容图不能表示系统温度变化,也不能表示系统与外界换热,这样就需要引入熵的概念,以表述系统温度和系统与外界的换热。
熵是状态参数,无法测量,仅可通过使用其它状态参数来进行计算。
对可逆过程,熵定义为系统与外界交换的热量除以当时气体热力学温度,用公式表示为
\(ds=\frac{dQ}{T}\)
对于不可能热力过程
\(ds>\frac{dQ}{T}\)
这就是热力学第二定律。
流体力学中,熵方程建立基础是热力学第二定律,与前面几大方程建立思路类似,熵方程建立思路是将热力学第二定律应用于占据控制体的流体,如图2-25所示。
图2-25 系统、控制体与控制面
对系统而言,热力学第二定律(即熵方程)为\(ds\ge \frac{\delta Q}{T}\)
式中等号用于可逆过程,不等号用于不可逆过程。
像推导能量方程一样,符号Q表达具有普遍意义的热交换,而不考虑热交换的机理。对于质量为m的系统,系统的总熵S=ms ,上面的方程变成
\(dS\ge \frac{\delta Q}{T}\)(2.10.1)
因为,(2.10.1)对于流体微团有效,系统熵S的时间变化率就是S的实质导数。因此
\(\frac{DS}{DT}\ge \frac{\delta \dot{Q}}{T}\)(2.10.2)
利用参数N和n ,\(N=S=\int_{{{V}_{\text{c}}}}{s\rho d{{V}_{c}}}\) ,以及n=s 。将 n=s代入方程(2.6.18)得
方程(2.10.3)称为为积分形式的熵方程。
熵方程的微分形式建立,可通过使用散度定理[方程(2.6.19)],将面积分转换为体积分,并将控制体收缩到微元控制体,积分值等于被积函数本身,方程(2.10.3)为
展开方程(2.10.4),并舍弃包含连续方程的项,得
对定常流动,方程(2.10.5)为
正如在推导能量方程中所指出的那样,方程(2.10.5)中的热交换Q 必须用流动参数表达。方程(2.10.5)适应于一切有热交换作用的流体流动。
不同坐标系中熵方程的表达式
上面在笛卡尔坐标系推导了熵方程,接下来将总结熵方程在不同坐标系下的表达式,以方便应用。
2.11 小结
本章中,我们已经把表示控制流体流动定律的方程推导为对控制体的积分和微分形式。为参考方便,将这些方程分别总结于表2.1和表2.2。
控制方程的积分形式在研究一维流动时采用,见表2.1。
表2.1 控制方程的积分形式
控制方程的微分形式以保留为函数形式的 , , 进行推导。因此,这些过程的影响仅作定性的考虑,其在解微分方程前或者省略,或者用流动参数及其梯度表示。控制方程的微分形式在研究多维流动中采用,见表2.2。
表2.2 对流体流动控制方程的微分形式
习题
1.有一不可压缩流体的流动,x方向的速度分量为\(u=a{{x}^{2}}+by\) ,z方向的速度分量为零,求y方向的速度分量v,其中a和b为常数。已知y=0时,v=0。
2.设某一流体流动为u=2y+3z 、v=3z+x 、w=2x+4y ,该流体的粘性系数\(\mu =0.008N\cdot s/{{m}^{2}}\),求其切应力。
3.已知流体质点在坐标系原点上的速度为0,且速度分量为u=5x 、v=-3y ,请问:可以构成不可压缩流体运动的第三个分量w应该是什么?
4.在二维流动中,速度分量\(u={{y}^{2}}-{{x}^{2}}\) 、v=2xy 。试计算在点(2,2)处,
(a)速度\(\overrightarrow{V}\) 的大小;(b)\(\overrightarrow{V}\) 与x 轴的夹角;(c)当流体微团通过该点时的加速度。
5.试证明下述不可压缩流体的运动不可能存在。
u=x,v=y ,w=z
6.已知\(\overrightarrow{V}=\left\{ a{{x}^{2}},a{{y}^{2}},-a{{z}^{2}} \right\}\),式中a为常数,试求(1,1,1)处,
(a)相对线变形率;(b)单位时间的相对体积变化率;(c)剪切角变化率;(d)转动角速度,并对整个流场和该点的流动做简要分析。
7.设有二维、定常、不可压流动,其x方向的速度分量为 ,试求x方向的速度分量\(u={{e}^{-x}}\cosh y+1\) 。(当y=0时,v=0 )
8.试证明,在封闭容器中不可压缩流体的能量耗损率为
式中 \(\Phi \)为耗损函数。
9.假定流管形状不随时间变化,设A为流管的横断面积,且在A断面上的流动物理量是均匀的,试证明连续方程具有下述形式。