三维装药一维内弹道计算
1 背景及意义
随着大装填和大长径比发动机需求增强,往往需要减小发动机装药通道的面积,这将增大发动机工作过程中通道内的燃气速度,当通道内燃气速度增大到一定程度时,会导致侵蚀燃烧的出现。侵蚀燃烧一般会使推进剂燃速增大(偶见减小,本文不作考虑),对发动机的内弹道造成明显影响,此外,在侵蚀燃烧的影响下,位于下游的装药提前烧尽,将使对应部位的绝热层或壳体更早地暴露于燃气中,给发动机的安全带来挑战。因此,对于工作过程中存在侵蚀燃烧现象的发动机,研究其侵蚀燃烧特性,对内弹道揭示和提升发动机安全性是非常有意义的。
侵蚀燃烧是由平行于燃面以较高速度流动的燃气向推进剂表面传递的更高的热流率引起的。在发动机中,喉部面积与装药末端通道面积之比(喉通比),是决定通道末端速度的关键,当喉通比增大到一定程度时,装药通道中下游会达到较高的速度,从而出现侵蚀燃烧。在发动机工作前期,由于装药通道面积最小,喉通比最大,因此侵蚀燃烧最为明显,并且侵蚀燃烧可能与点火燃气共同作用,使得发动机内出现更高的压强峰,在影响内弹道性能的同时,给壳体结构带来很大的考验。不同位置处的装药将依次烧尽,拖尾段开始的时刻提前、持续时间变长,发动机的推力曲线偏离预定方案,并且使得发动机重心变化更难预测,这些因素都可能给整个飞行任务带来不利影响。而拖尾阶段开始时发动机内余药更多,这些推进剂在拖尾段不能被很好地利用,相当于进一步增加了发动机的消极质量。图 5-1给出了受侵蚀影响的大长径比发动机的内弹道曲线示意图,其中可以清晰地看出侵蚀燃烧对发动机内弹道的影响主要集中在发动机工作初期并影响拖尾段。

图 1 侵蚀燃烧现象对发动机内弹道的影响
降低开发成本和提高可靠性是固体火箭发动机 (SRM) 领域的两个重要研究课题。两者都需要对 SRM 的工作过程进行更好地模拟(例如,推力或压力与时间的关系)。准确的性能预测将减少对昂贵测试的需求,从而降低每个 SRM 的开发成本。即使是标称性能,在许多情况下就算是使用当前最先进的软件仍然无法准确模拟(预测)。几个关键的物理现象仍然没有得到很好的理解,其中最重要的就是临界固体推进剂的燃速。除了标称性能之外,还有非设计性能,特别是由于内部声学和压力相关燃速之间的耦合而导致发动机的不稳定性。相比于正常、稳定的行为,不稳定的行为更加难以预测。在这两个领域中,发动机性能的关键未知因素是推进剂燃速,这可能是影响发动机性能的唯一最重要的因素,但人们对此还认识不足。已知影响燃速但仍知之甚少的因素包括内部发动机横流(侵蚀燃烧)、与加压速率相关的非稳态燃烧(动态燃烧)和辐射传热。
目前的研究表明,随着 L* 值的降低,燃烧的动态过程和侵蚀燃烧变得越来越重要。一个简单的零维发动机质量平衡的例子表明,L* 是表明动态燃烧重要性的主要参数。侵蚀燃烧对横流质量通量敏感,它受两个与 L* 相关但不完全由 L* 决定的装药几何特征的影响。第一个特征是通气面积;靠近后端的限制性通气面积(即小水力直径)会增加侵蚀燃烧。第二个特征是 L/D 比值,该值越大,则流经给定通气面积的质量越大,从而增强侵蚀燃烧。轴向压力分布也与内部流动条件有关。对于小到中等 L/D 比值,燃烧表面上的压力相当均匀,用零维模型来描述其内部的流动(控制体积质量平衡)就足够了(侵蚀燃烧可以忽略不计)。然而,随着 L* 的减小和 L/D 的增加,轴向压降、轴向加速流动和侵蚀燃烧效应变得更加重要;对于侵蚀燃烧预测,内流模型必须至少为一维(轴向解析)。对于潜入喷管和通气面积和/或轴向燃烧表面积的突然变化,一维流动模拟可能不够,必须实施 二维或三维流动模型。
这项工作的目标是发展一种分析/模拟能力,可用于1) 进一步研究侵蚀燃烧和动态燃烧的影响,2)使用简化的物理模型在较长的时间尺度上进行仿真,以减少计算需求。因此,需要一套适合于分离和理解侵蚀燃烧、增压速率依赖的动态燃烧效应及其耦合效应内弹道分析模型。推进剂的燃烧表面积是决定进入内通道的质量流量的关键。一般来说, 零维、一维和二维的燃面退移模型在用作内弹道仿真时误差过大,不能接受。为了准确地模拟SRM的性能,需要在整个燃烧期间对固体推进剂装药的瞬时几何形状进行建模[1,2]。对固体推进剂装药几何形状在燃烧过程的演变进行建模。同时也允许商用CAD程序的初始装药设计和整个火箭燃烧的持续时间内的三维燃面退移计算。将装药几何模型与流场求解器相结合,模拟了全燃烧过程,并研究了侵蚀燃烧对SRM内弹道的影响。
在装药设计一章中,介绍了基于ACIS、GPU和LevelSet方法的三维装药设计和计算软件。能够比较准确地模拟三维装药在肉厚方向上的演化,并提供零维和一维内弹道计算所需要的装药参数,为内弹道仿真提供初始数据。
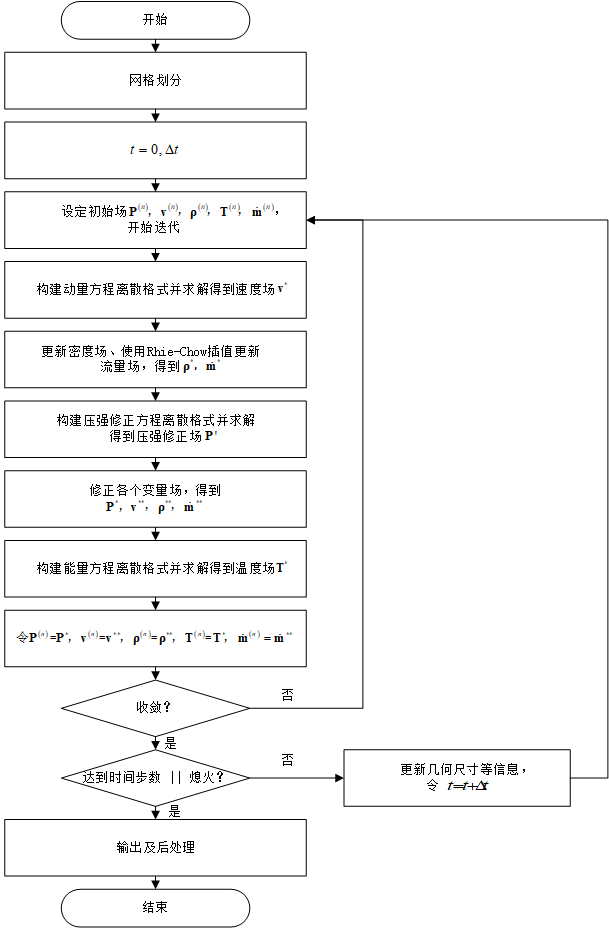
内弹道仿真模型利用燃面退移模拟与零维或一维的SRM 内弹道模拟燃速和内流场模型相结合。由于各种物理现象(例如冲击波、传热等)具有固有的传播速度,流体动力学和固体推进剂燃烧对数值格式的稳定性有不同的时间步长要求[3]。为了减少计算时间,当这些现象结束或收敛到准稳态时,便应用替代模型进行计算。此外,由于显著的装药几何演化(即发动机燃尽)的时间尺度远大于流体动力学和固体推进剂燃烧的时间尺度,在整个发动机完全燃烧过程的模拟中,有必要将装药几何结构与流场和燃速模型耦合。使用计算机辅助设计 (CAD) 工具进行复杂的装药设计、用户友好的界面、快速的表面演化和可变的时间步长,在相对较短的时间内为复杂的发动机获得了合理的固体推进剂装药几何演化结果,可用的 PC 处理速度。通过将装药设计所获得的描述的推进剂表面演化与流场求解器和燃烧模型相结合,可以模拟 SRM 的全燃烧内弹道,并且可以研究动态和侵蚀燃烧对发动机性能的影响。针对三维数值模拟所带来的资源消耗和过长的计算时间,采用一维准定常和非定常模型,预估三维装药的一维内弹道。
2 药柱几何和燃面退移模型
复杂的三维固体火箭推进剂装药的初始装药设计和燃烧表面演化是SrmStudio装药设计的重要组成部分,它包含三种方法:基于ACIS几何造型方法、GPU并行计算方法和LevelSet方法。这三种方法已经经过大量的工程应用,所得结果稳定可靠,燃面计算精度误差在0.1%以下。ACIS几何造型方法,利用图形交并差运算,认为装药是由外轮廓线形成的回转体,减去内腔形体所形成的。GPU并行计算则是将装药离散化,并计算距离场,通过差值运算获得燃面肉厚的对应关系。该软件可以将商业CAD绘制的任何装药图形直接导入,进行快速装药计算。这种方法不再受药型的影响,只要指定燃面,即可进行计算。LevelSet方法使用带符号的最小距离函数 (MDF) 进行建模,如相关论文 [4] 中所述。 初始推进剂装药几何形状由商业 CAD 软件建模,推进剂段的 MDF 由本程序自动生成。 在建立推进剂几何形状的初始 MDF 后,通过操纵初始 MDF 模拟后续的推进剂表面退移和燃尽。 计算沿轴线方向的燃烧周长、湿周长和通气面积,用于一维流场模拟,并且可以在数值上集成用于零维模拟。必要时还会计算端部燃烧表面积、燃烧室和喷管体积。
在装药计算时,需要指定一维内弹道计算所需数据。程序将自动将轴线方向分割成nx等分,计算时分别给出各个截面燃烧周长和通气面积,输出二维表格,供一维内弹道计算调用。

图2 装药计算与内弹道计算网格划分示意图。
3 一维内弹道仿真模型
流场模型通过假设燃烧推进剂的质量加入和通过喷管的质量排出相等,来求解零维或一维内部流动(如压力、速度等)。在零维模型中,诸如压力、温度、质量流率、燃速、总表面积和燃烧室容积等参数都是标量。零维流模型对发动机的性能给出了一个初步的近似值,但由于偶尔需要模拟一维非稳态事件,如侵蚀燃烧和声学不稳定性,也采用了一维流场求解器。流场参数的径向和方位角变化,包括燃速,被认为是可以忽略的。
Aslam–Xu–Stewart (AXS)[5]模型用于求解固体火箭发动机的一维流场。AXS 是一个不稳定的反应流偏微分方程解算器。由于对不含铝推进剂进行仿真是这项工作的主要目的,推进剂燃烧假定在进入燃烧室之前完成,并假定燃烧产物处于化学平衡。因此,禁用了AXS模型的轴向反应功能。原来的AXS模型已经修改,以体现推进剂燃烧所带来的质量流入,如图方程(1).采用三阶 Runge-Kutta 时间和三阶通量分裂空间方法求解此控制方程,
\({\begin{array}{*{20}{c}}{\frac{{\partial \rho A}}{{\partial t}} + \frac{{\partial \rho VA}}{{\partial x}} = {\rho _p}{r_b}S}\\{\frac{{\partial \rho VA}}{{\partial t}} + \frac{{\partial \left( {\rho {V^2} + p} \right)A}}{{\partial x}} = p\frac{{\partial A}}{{\partial x}}}\\{\frac{{\partial \rho {e_T}A}}{{\partial t}} + \frac{{\partial \left( {\rho {e_T} + p} \right)A}}{{\partial x}} = {\rho _p}{r_b}S\left( {{h_f} + \frac{1}{2}V_f^2} \right)}\end{array}}\) (1)
其中
\({{e}_{T}}=\frac{p}{\left( k-1 \right)\rho }+\frac{{{\text{V}}^{2}}}{2}\) (2)
并且
\({{V}_{f}}=\frac{{{\rho }_{p}}{{r}_{b}}}{\rho }=\frac{{{\rho }_{p}}{{r}_{b}}R{{T}_{f}}}{p}=\frac{{{\rho }_{p}}{{r}_{b}}{{C}_{pf}}\left( k-1 \right){{T}_{f}}}{kp}\) (3)
也可以用一维准定常模型来进行计算:
\(\left. {\begin{array}{*{20}{l}}{\frac{{dP}}{{dx}} = \frac{{\rho {V^2}}}{{{A_p}}}\frac{{{a^2}}}{{{a^2} – {V^2}}}\frac{{d{A_p}}}{{dx}} – \frac{{{\rho _p}rV\Pi }}{{{A_p}}}\left[ {\frac{{2{a^2} + \left( {k – 1} \right){V^2}}}{{{a^2} – {V^2}}}} \right]}\\{\frac{{dV}}{{dx}} = \frac{{{\rho _p}r\Pi }}{{\rho {A_p}}}\frac{{{a^2} + k{V^2}}}{{{a^2} – {V^2}}} – \frac{{{a^2}V}}{{{A_p}\left( {{a^2} – {V^2}} \right)}}\frac{{d{A_P}}}{{dx}}}\\{{C_p}T + \frac{{{V^2}}}{2} = {C_p}{T_0}}\\{P = \rho RT}\end{array}} \right\}\) (4)
零维内弹道模型在短时间内冻结燃烧室总体积和燃烧表面积,同时迭代时间并进行几次燃烧室压力迭代。通过在整个燃烧表面上施加均匀的燃速,表面周期性地演化。重复以上步骤,计算新的几何模型,直到燃尽。
对于一维模拟,使用准定常和非定常模型计算轴向压力、速度、温度和其他内部流动参数(方程1-3)。燃气质量生成率由燃速(燃速模型)、燃烧周长(推进剂几何演化模型)、网格间距和固体推进剂密度的乘积计算(方程5)。前端和后端设置为反射型壁面和出口边界条件。
\({{\dot{m}}_{i}}={{r}_{b}}*\prod{_{b}{{\rho }_{p}}\Delta x}\) (5)
出于数值稳定性的考虑,时间步长是有规律的,依据CFL条件,限制时间步长为最大波速在火箭中传播一个网格的时间,
\(\Delta t=CFL*\left[ \frac{\Delta x}{\max \left| u+a \right|} \right]\) (6)
为了确定耦合系统的时间步长,CFL数由用户控制,但必须小于1。如果一个不同的模块(例如,燃速)需要的时间步长小于气体动力学规定的 CFL 条件,系统时间步长将相应减少。
一维弹道模块具有捕捉轴向压力变化的能力,这对于研究侵蚀燃烧和模拟点火瞬态是有用的,在后续的工作中可以用于模拟轴向激波的传播和非线性声不稳定性 。由于采用了空间均匀网格,流场求解器计算时要特别注意端面燃烧部位的移动所带来的问题。在几何条件突然变化的位置,AXS 模型会有比较大的误差。.
4 侵蚀燃速模型
固体推进剂的燃烧机理相当复杂,燃烧过程受局部的流动、化学和热现象的影响。由于计算能力的限制以及对燃烧过程的理解有限,许多固体推进剂燃速模型都经过了一系列的简化。由于其更复杂的理论公式,非准稳态(即动态)燃烧模型比准稳态燃烧模型需要更多的计算时间。本文使用的燃速模型,考虑了如下的发动机工况,包括准稳态、非线性非稳态(取决于增压率)和侵蚀性(取决于横流速度)燃烧。随着初始瞬态的减小,非准稳态(动态)燃烧收敛到准稳态燃烧。在点火和初始增压后的适当点,将模型切换到准稳态燃烧模型,可以消除了时间步长限制稳定性要求,并减少了计算需求。因此,动态燃烧模型仅适用于非稳态事件非常重要的持续时间(例如,点火后不久),一旦这些瞬态事件消失,则可以使用准稳态燃速模型。当动态燃速与准稳态燃速之差小于准稳态燃速的1% 时,采用准稳态燃速模型。
在固体火箭发动机领域,学者们发展出了多种推进剂燃烧理论及燃速模型。在不考虑侵蚀燃烧的情况下,使用最多的燃速模型是圣罗伯定律(Saint Rober’s law)
\(r=a{{P}^{n}}\) (7)
公式中a为燃速系数,n为压强指数,对于特定的推进剂,这两个参数在一定范围内可以认为是常数。
上式将燃速表示成了压强的公式,表示了压强对燃速的重要作用。除了压强之外,其他一些因素也会对燃速产生影响,比如推进剂初温、压强变化率、推进剂附近气流的速度等。众多研究表明,推进剂的燃速会受到其表面附近与平行流动的气流的影响。在过去的一个多世纪,为了对侵蚀燃烧进行解释和预测,研究人员们进行了大量的理论和实验研究,也为其产生的原因提出了多种理论模型,一些综述文献包括[6-8]。一般认为,侵蚀燃烧引起的燃速增加是由流动带来的燃气向推进剂的传热量增加而引起的。由于侵蚀燃烧涉及到多个物理化学过程,这些过程既难以测量,又难以建模,因此侵蚀燃烧的真正机理至今尚未被完全揭示,不过,在长期的研究过程中,学者们已经对侵蚀燃速规律有了不少的认识,并提出了多种侵蚀燃速模型。
最简单的侵蚀燃速模型要属线性模型。Crawford和Kenshner[9]对一维稳态绝热流动进行了数值仿真,结果表明,侵蚀比与气流速度成正比。Green[10]在对不同的复合推进剂进行实验研究后认为,在压强一定的情况下侵蚀比与通道的质量流率成正比,且与喉通比成正比。Vandenkerckhove[11]在对双基推进剂进行研究后认为,随着通道流速的提高,湍流会逐步侵入嘶嘶区,从而增加对推进剂表面的传热,从而引起侵蚀燃烧现象,这一理论解释了临界速度的存在。他还提出了侵蚀比与气流速度之间的线性关系,这一关系后续又被Rout[12]和Razdan[13]等人使用和修正。Blatz[14]指出沿着发动机通道,气流压强降低、速度增加,因此推进剂的基础燃速略有降低,而侵蚀燃速会上升,在此基础上进行了一维稳态分析并提出了侵蚀比与密流之间的线性关系。
以上的各种线性模型把侵蚀比(推进剂在侵蚀燃烧条件下的总燃速与无侵蚀燃烧时的基础燃速之比)当作是某一变量的线性函数,这类模型一般可以写为形式[8]
\(\varepsilon \left( z \right) = \left\{ \begin{array}{l}1,{\rm{ }}z < {z^*}\\1 + {k_z}\left( {z – {z^*}} \right),{\rm{ }}z \ge {z^*}\end{array} \right.\) (8)
式中:
ε —— 侵蚀比;
z —— 影响侵蚀比的变量,如气流速度、通道密流等;
z* —— 开始发生侵蚀燃烧时变量z的临界值;
kz —— 比例系数。
线性模型具有非常简单的形式,却可以在一定程度上反映出主要因素对侵蚀燃速的影响。在通过与实验对比,选取适当的临界变量z*及比例系数\({{k}_{z}}\)后,使用该类模型可以得到较为准确的内弹道计算结果。不过,由于其形式较为简单,这个系列的模型一般只能揭示一到两个因素对侵蚀燃速的影响。
侵蚀燃烧在具有高气体横流速度的固体火箭发动机中变得非常重要,因为增加了固体推进剂的传热,从而提高了局部燃速。这通常发生在具有大纵横比(L/D)或收缩流设计(如星形尾部装药)的发动机中。这项工作采用了LR模型的几种变体,该模型将火焰区向固体推进剂的传热分为两种独立的机制[15]。第一,主要燃烧区的传热仅取决于压力(如本文前面讨论的)。第二,由于燃烧气体流过表面,取决于横流速度。L-R模型是另一种著名的侵蚀燃速模型。勒努尔(Lenoir)和罗比拉德(Robillard)[15]将推进剂在侵蚀条件下的总燃速视为基础燃速与侵蚀燃速之和
\(r={{r}_{0}}+{{r}_{be}}\) (9)
式中:
r —— 总燃速;
r0 —— 基础燃速(无侵蚀燃烧时的推进剂燃速);
\({{r}_{be}}\) —— 侵蚀燃速(由侵蚀燃烧引起的燃速增量)。
他们假定侵蚀燃速与推进剂表面的对流换热系数成正比,利用了考虑加质流情况下的平板对流换热模型,得到了如下半经验公式
\(r=a{{P}^{n}}+\frac{\alpha {{G}^{0.8}}}{{{L}^{0.2}}{{e}^{\frac{\beta r{{\rho }_{p}}}{G}}}}\) (10)
式中:
P —— 压强;
G —— 通道密流;
L —— 从发动机头部到所考虑位置的轴向距离;
α —— 待定参数,一般通过实验与试算结合得到,;
\(\alpha=\left[0.0288{C}_{pg}{\mu}_{g}^{0.2}{Pr}^{-2/3}\right]\frac{1}{{\rho}_{c}{C}_{pc}}\left(\frac{{T}_{f}-{T}_{s}}{{T}_{s}-{T}_{0}}\right)\)
β —— 待定参数,通过实验与试算结合得到。
在L-R模型提出之后,其他一些学者对其进行了不同程度的发展。King[16]在考虑了侵蚀燃速的存在对推进剂表面热反馈的影响后,得到了与L-R模型精度接近的模型。劳伦斯(Lawrence)[17]对L-R模型进行了一定的修正,他使用装药通道直径作为特征长度,并且把原L-R公式右边项中的总燃速r用基础燃速r0来代替,从而使燃速公式变为显式,减小了计算总燃速所需的计算量。通过实验对不同种类的复合推进剂在不同流动条件下的燃速进行测试,并与初始L-R模型进行了对比后,劳伦斯认为采用修正模型可以得到更加准确的侵蚀燃速结果。劳伦斯的改进模型可能是L-R系列模型中使用最为广泛的一种,在侵蚀燃烧、内弹道计算、以及发动机点火过程模拟等方面被多次引用[18-21]。
Lawrence的模型使用了通道水力直径Dh作为特征长度,但是仍然以平板对流公式来计算换热系数,这可能会带来一定的误差。西北工业大学马艳杰[22]使用了适于圆形通道的对流换热系数公式(Dittus-Boelter公式),结合通道的水力直径作为特征长度,对自由装填药柱发动机进行了模拟,起到了良好的效果。
Nickerson[23]在著名的发动机计算软件SPP中,对L-R公式中的特征长度进行了另一种修正,使用以下表达式来代替式(10)中L的值
\(f\left( {{D}_{h}} \right)=0.90+0.189{{D}_{h}}\left[ 1+0.043{{D}_{h}}\left( 1+0.023{{D}_{h}} \right) \right]\) (11)
使得L-R公式对大型发动机的计算更加准确。
这些改进保留了原始LR模型的传热理论,但也提高了模型预测大型发动机侵蚀燃烧贡献的能力。方程式(12)是SPP作者推荐的侵蚀燃烧模型,因为它提供了最多的通用性[19]。
\({{r}_{be}}=\alpha \frac{{{G}^{0.8}}}{{{\left[ f\left( {{D}_{h}} \right) \right]}^{0.2}}}{{e}^{-\frac{\beta {{r}_{b}}{{\rho }_{p}}}{G}}}\) (12)
Yamada[22]使用侧面带有小孔的通道来模拟推进剂表面的燃气流入,在此基础上进行了模拟实验。通过模拟实验,他认为推进剂表面的热流与通道内气流的湍流强度成正比,进而与侵蚀燃速成正比。据此,他对L-R公式进行了一定的修正。对于侵蚀燃烧开始发生的临界速度,他提出了与Vandenkerckhove[11]类似的解释:沿着气流通道向下游方向,气流速度逐渐增大,湍流强度逐渐增加,层流边界层厚度逐渐减小,当层流层厚度减小到与火焰前沿相同后,湍流便开始对推进剂表面传热产生影响,从而引发了侵蚀燃烧现象。根据这一解释,对于基础燃速较高的推进剂,由于其火焰前沿与推进剂表面较近,更难被湍流所影响,因此出现的侵蚀现象更弱,这一结论与大量实验相吻合。Yamada还指出,负侵蚀现象有可能是由较弱的湍流引起的,而较强的湍流则会引起正侵蚀。
尽管L-R系列模型可以得到与实验吻合度相当高的内弹道计算结果,但是其准确度非常依赖于模型中的两个待定参数α和β。通常情况下,这两个参数需要通过计算与实验相互对比来获得。由于这两个常数既与推进剂有关,又与具体的发动机参数有关,这使得模型对实验有较强的依赖。只要相关参数有所变动,就需要进行大量的试算才能得到与实验相符的结果,这使得L-R模型难以在实验前预测发动机的侵蚀特性。
1997年,Mukunda和Paul[25]从L-R模型出发,进行了数学物理简化以及无量纲处理等步骤,提出了一种新的模型。与L-R模型类似,Mukunda模型中同样存在着两个待定参数,不过他们通过将模型与实验进行对比,得到了与大量推进剂试样实验及发动机实验吻合得较好的两个常数的值,这使得他们的模型成为了适用于不同推进剂、不同发动机的普适模型。之后,他们又对模型进行了改进[26],使其适合于具有复杂三维构型的发动机。除了普适性外,Mukunda模型中的侵蚀比使用显式表达式,与L-R模型相比,计算量更小。目前Mukunda模型也被一些研究所证实和采用[22,27]。
除了以上介绍的三类侵蚀燃速模型外,还有一些其他的侵蚀燃速模型。如Dickinson模型[28]及Hasegawa[29]对其所作的修正模型。Ishihara[30]在他的模型中引入一个“嘶嘶区变量Φ”的概念,指出Φ是影响推进剂表面热传导的主要因素,并得到了推进剂燃速与Φ之间的关系式。在国内,张宜[31]等人通过实验总结出使用通道内的湍流参数(湍动能k和粘性耗散率ε)来表示侵蚀比的经验公式。
此外,也有一些学者从机理方面对侵蚀燃烧进行解释和预测,提出了一些侵蚀模型。King的综述文献[7]对多种复合推进剂的侵蚀效应进行了实验及讨论,结果表明,粘合剂种类、催化剂、氧燃比、铝的含量等因素,对侵蚀效应的影响都是通过影响推进剂初始燃速来发挥作用的。也就是说,在压强、温度等外界一致的情况下,如果两种推进剂的初始压强相同,那么在相同的流速下,侵蚀效应是非常接近的。这与Vandenkerckhove[11]和Yamada[24]的观点接近。King还提出了两个不同的复合推进剂侵蚀模型[32,33],以及双基推进剂侵蚀模型[34]。Razdan[35]对复合推进剂表面及附近的流场进行了二维稳态模拟,计算过程中考虑了推进剂表面的化学反应和湍流边界层,分析了湍流对侵蚀燃烧的影响。Cai[36]对复合推进剂及其附近的燃气进行了考虑化学反应的二维轴对称耦合计算,得到了包含侵蚀燃烧影响在内的推进剂燃速数值的计算模型。上述各种燃速模型有利于揭示侵蚀燃烧的作用机制,让人们了解侵蚀燃烧的本质。不过目前来说,由于这些模型涉及到的计算量一般较大,有的还需要考虑推进剂内部的微观结构,因此不适合用于发动机内弹道计算及由此进行的侵蚀特性预估。
可以看到,现有的用于计算侵蚀燃速的模型中,普遍含有待定参数。这些待定参数同时受推进剂及发动机的影响,因此一般需要通过试算与实验来共同确定,这使得这些模型只能在实验后通过调整相关参数来复现实验结果,而无法在实验前对发动机进行较为准确的内弹道计算,以做出侵蚀特性预估。Mukunda等人虽然称他们的模型是普适的,但实际上也只是通过与大量实验对比,获得了一对应用范围较广的参数值,这期间有对某些实验结果的妥协,因此对于某些发动机,模型所建议的参数并不完全适用[22]。为了对发动机进行侵蚀特性预估,在发动机设计阶段就发现发动机中的侵蚀规律,从而减少实验次数,并提前发现可能的改进方向,需要一种对实验依赖较少的模型来计算侵蚀燃速模型。
5 算例
将研究结果按照图2所示,编制成计算机程序,并对一三段装药发动机进行内弹道计算,结果与试验吻合较好。
图3内弹道计算框图
使用基于水平集方法的燃面退移模型,实现了对任意三维装药发动机的燃面捕捉,从而可以获取计算N-S方程源项的燃烧周长及通道面积数据。这扩展了本文的内弹道计算模型,使其能够对任意三维装药发动机进行一维瞬态内弹道。为了验证此方法,对某一使用三维药柱较大长径比发动机进行了内流场计算,并对侵蚀特性进行了分析。
为了满足任务要求,本文考虑的发动机有着较为复杂的装药结构,其示意图见图 3。
图3 装药示意图
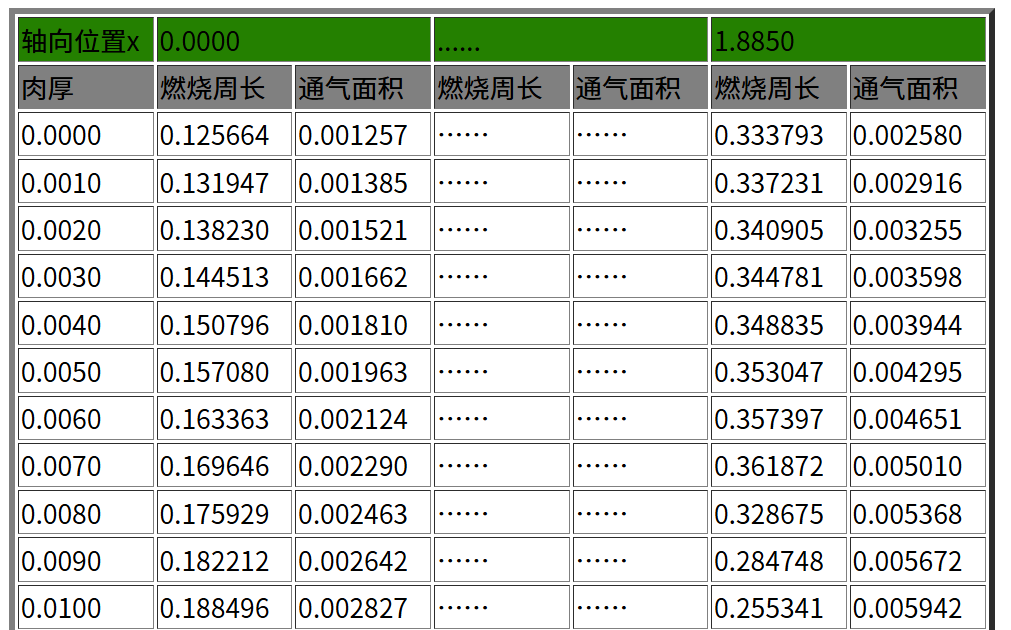
对侵蚀燃烧的研究表明,由于侵蚀燃烧的存在,发动机末端装药将先被烧尽,末端的绝热层暴露于燃气的时间更长,因此,在三段装药中,使用了不同的绝热层厚度。在装药的起终点,如前、后封头,以及各段药的连接位置处,出于热防护及结构限制等因素,有较厚的绝热层,这使得这些部位的装药外表面并非规则的圆柱面,当燃面退移到这些位置时,截面的燃烧周长及通气面积等参数显然不能简单地表示为肉厚的解析式。此外,在后段装药的两个尺寸截面的过渡位置,其几何参数的计算也较为复杂。
总之,该发动机的药型较为复杂,在多个位置处,燃烧周长及通道面积的计算并不容易。对此类发动机,使用前述提到的水平集方法燃面退移模型,是非常适用且必要的。本文采用SrmStudio软件计算装药在不同截面处燃烧周长及肉厚数据,可以被内弹道计算程序调用。
图 4 不同位置燃面肉厚数据表
对发动机进行了一维瞬态内弹道计算,得到了压强-时间曲线,以及发动机工作过程中的流动及侵蚀燃烧结果。计算时,先使用了基于水平集方法的燃面退移模型来计算燃烧周长及通道面积,得到几何信息数据库,再使用上一章的内弹道计算模型进行内弹道计算,计算过程中截面上的几何参数由截面的轴向位置及肉厚作为检索依据,从几何信息数据库插值而来。
表1 发动机热力学参数表
| 参数名 | 参数值 |
| a (50°C) | 6.5e-5 |
| n | 0.3 |
| 推进剂初温/K | 323 |
| 点火温度/K | 700 |
| 燃气燃温/K | 3162 |
| 燃气定压比热比/ | 1866 |
| 燃气分子量 | 26.9 |
| 燃气动力粘度/Pa·s | 9e-5 |
| 燃气导热率/ | 0.26 |
在得到几何信息数据库后,将之保存在文件中,供内弹道计算函数使用。
压强曲线结果及分析
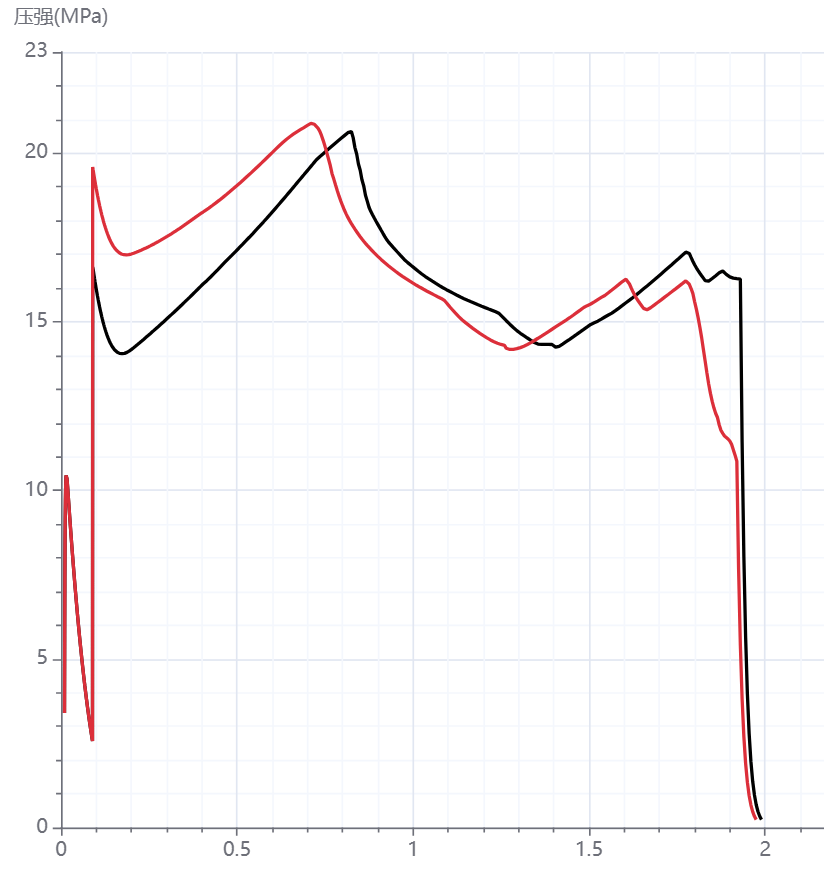
图5显示了实验与计算所得的发动机头部压强曲线,其中计算曲线分为了考虑侵蚀燃烧与不考虑侵蚀燃烧两种情况。图中,根据曲线的变化趋势,将整个发动机工作过程粗略地分为了三个阶段。
图5 内弹道计算结果,黑色是不考虑侵蚀,红色是考虑侵蚀
第一个阶段表示后段装药燃尽之前的阶段。由曲线可以看到,在发动机点火后,燃烧室内压强迅速上升,在点火燃气与侵蚀燃烧的作用下,产生一个较大的初始压力峰,并伴有尾部压强降低。回顾整个压强曲线,可以发现,对于本发动机,由于药型较为复杂,各个截面上的燃烧周长及通气面积不易表示成肉厚的解析式,因此需要使用基于水平集方法的燃面退移模型,进行相关参数的数值计算。经过计算,得到的压强曲线与实验吻合得很好,说明燃面退移模型与一维瞬态内流场计算模型之间得到了正确的耦合。根据分析,可以发现发动机中三段装药从后至前,分别在不同的时刻烧尽,使得后段的绝热层暴露的时间更长,这表明了在中下游使用更厚绝热层的必要性和合理性。
使用扩展模型对某型复杂三维装药发动机进行了计算,得到了发动机几何信息数据库,以及与实验吻合得很好的压强曲线,验证了扩展的内弹道模型的正确性。
零维流场模型适用于一维现象(如侵蚀燃烧或显著轴向压降)不显著的发动机。零维分析可提供发动机内部压力的合理估计,并可预测重要现象,如动态燃烧产生的初始压力峰值。
一维模拟的结果表明,这种水平的流场模拟能够为小型和大型固体火箭发动机产生合理的结果,前提是包含了精确的三维装药几何信息。
通过将新的三维装药几何模拟与零维和一维流场计算相耦合,对SRM非定常内部流动和燃烧进行了模拟。由于三维流场分析在计算上非常大,因此在必要时保留三维性(固体推进剂装药演变),同时进行合理的降维(流场和燃速)以减少计算时间是这项工作的一个重要结果。仍然能够捕捉重要的发动机现象,如轴向压降、侵蚀燃烧效应。
- Gossant, B., “Solid Propellant Combustion and Internal Ballistics,” Solid Rocket Propulsion Technology, 1st English ed., edited by A. Davenas, Pergamon Press, New York, 1993, pp. 111–
- Yildirim, C., and Aksel, M. H., “Numerical Simulation of the Grain Burnback in Solid Propellant Rocket Motor,” AIAA Paper 2005-4160, July 2005.
- Stewart, D. S., Tang, K. C., Brewster, M. Q., Yoo, S. H., and Kuznetsov, I. R., “Multi-Scale Modeling of Solid Rocket Motors: Time Integration Methods from Computational Aerodynamics Applied to Stable Quasi-Steady Motor Burning,” AIAA Paper 2005-0357, Jan. 2005.
- Willcox,M.A.,Brewster,M.Q.,Tang,K.C.,andStewart,D.S.,“Solid Propellant Grain Design and Burnback Simulation Using a Minimum Distance Function,” Journal of Propulsion and Power, Vol. 23, No. 2, March–April 2007, pp. 465–
- Xu, S., Aslam, T., and Stewart, D. S., “High Resolution Numerical Simulation of Ideal and Non-Ideal Compressible Reacting Flows with Embedded Internal Boundaries,” Combustion Theory and Modeling, Vol. 1, No. 1, 1997, pp. 113–
- Landsbaum EM. Erosive Burning of Solid Rocket Propellants-A Revisit. Journal of Propulsion and Power, 2005, 21(3): 470–477.
- King MK. Erosive burning of solid propellants. Journal of Propulsion and Power, 1993, 9(6): 785–805.
- Arkhipov VA, Zarko VE, Zharova IK, et al. Solid propellant combustion in a high-velocity cross-flow of gases (review). Combustion, Explosion, and Shock Waves, 2016, 52(5): 497–513.
- Crawford B, Kershner R. Rocket fundamentals. NDRC Division, 1944, 3.
- Green L. Erosive Burning of Some Composite Solid Propellants. Journal of Jet Propulsion, 1954, 24(1): 9–15.
- Vandenkerckhove JA. Erosive Burning of a Colloidal Solid Propellant. Journal of Jet Propulsion, 1958, 28(9): 599–603.
- Rout R, Mukunda H, Jain V. Erosive burning characteristics of solid propellant rocket motor. 14th Joint Propulsion Conference. Las Vegas,NV,U.S.A.: American Institute of Aeronautics and Astronautics, 1978.
- Razdan MK, Kuo KK. Measurements and Model Validation for Composite Propellants Burning under Cross Flow of Gases. AIAA Journal, 1980, 18(6): 669–677.
- Blatz PJ. A simplified approach to erosive burning. Symposium (International) on Combustion, 1961, 8(1): 745–753.
- Lenoir JM, Robillard G. A mathematical method to predict the effects of erosive burning in solid-propellant rockets. Symposium (International) on Combustion, 1957, 6(1): 663–667.
- King MK. A Modification of the Composite Propellant Erosive Burning Model of Lenoir and Robillard. Combustion and Flame, 1975(24): 365–368.
- Deverall L. The experimental and theoretical comparison of the erosive burning characteristics of composite propellants. 3rd Solid Propulsion Conference. Atlantic City, NJ, U.S.A.: American Institute of Aeronautics and Astronautics, 1968.
- Peretz A, Kuo KK, Caveny LH, et al. Starting Transient of Solid-Propellant Rocket Motors with High Internal Gas Velocities. AIAA Journal, 1973, 11(12): 1719–1727.
- Nagaoka T, Shirota K, Koreki T, et al. An experimental study on erosive burning in solid propellant motors. Tokyo, Japan: 1973: 83–90.
- Willcox MA, Brewster MQ, Tang KC, et al. Solid Rocket Motor Internal Ballistics Simulation Using Three-Dimensional Grain Burnback. Journal of Propulsion and Power, 2007, 23(3): 575–584.
- Rettenmaier AK, Heister SD. Experimental Study of Erosive and Dynamic Burning in Polybutadiene-Based Composite Propellants. Journal of Propulsion and Power, 2013, 29(1): 87–94.
- Ma Y, Bao F, Hui W, et al. An Approach to Analysing Erosive Characteristics of Two-Channel Combustion Chambers. International Journal of Aerospace Engineering, 2019, 2019: 1–9.
- Nickerson G, Coats D, Dang A, 等. The Solid Propellant Rocket Motor Performance Prediction Computer Program (SPP), Version 6.0. Air Force Astronautics Laboratory, Volumes I-VI, 1987.
- Yamada K, Goto M, Ishikawa N. Simulative Study on the Erosive Burning of Solid Rocket Motors. AIAA Journal, 1976, 14(9): 1170–1176.
- Mukunda HS, Paul PJ. Universal behaviour in erosive burning of solid propellants. Combustion and Flame, 1997, 109(1–2): 224–236.
- Mukunda HS, Paul PJ, Javed A, et al. Extension of the universal erosive burning law to partly symmetric propellant grain geometries. Acta Astronautica, 2014, 93: 176–181.
- Javed A, Chakraborty D. Universal erosive burning model performance for solid rocket motor internal ballistics. Aerospace Science and Technology, 2015, 45: 150–153.
- Dickinson LA, Jackson F, Odgers AL. Erosive Burning of Polyurethane Propellants in Rocket Engines. Williams and Wilkins, Baltimore, MD,: Elsevier, 1960: 754–759.
- Hasegawa H, Hanzawa M, Tokudome S-I, et al. Erosive Burning of Aluminized Composite Propellants: X-Ray Absorption Measurement, Correlation, and Application. Journal of Propulsion and Power, 2006, 22(5): 975–983.
- Ishihara A, Kubota N. Erosive burning mechanism of double-base propellants. Symposium (International) on Combustion, 1988, 21(1): 1975–1981.
- 张宜, 夏祥兴, 李宜敏. 复合推进剂侵蚀燃烧特性的k-ε参数表征. 推进技术, 1988(5): 47–51.
- King MK. A Model of Erosive Burning of Composite Propellants. Journal of Spacecraft and Rockets, 1978, 15(3): 139–146.
- King M. A model of the effects of pressure and crossflow velocity on composite propellant burning rate. 15th Joint Propulsion Conference. Las Vegas,NV,U.S.A.: American Institute of Aeronautics and Astronautics, 1979.
- King MK. Model for Prediction of Double-Base Propellant Burn Rate, Including Cross-Flow Effects. AIAA Journal, 1982, 20(10): 1432–1439.
- Razdan MK, Kuo KK. Erosive Burning Study of Composite Solid Propellants by Turbulent Boundary-Layer Approach. AIAA Journal, 1979, 17(11): 1225–1233.
- Cai W, Thakre P, Yang V. A Model of AP/HTPB Composite Propellant Combustion in Rocket-Motor Environments. Combustion Science and Technology, 2008, 180(12): 2143–2169..