金属壳体安全系数与可靠性
金属壳体安全系数与可靠性
计算参数
壳体直径D(mm):
D的偏差±(mm):
壳体壁厚δ(mm):
δ的偏差±(mm):
壳体材料的强度极限σb(MPa):
σb的偏差±:(MPa)
燃烧室最大工作压力Pmax(MPa):
Pmax的偏差±:(MPa)
安全系数n:
可靠性R:
燃烧室壳体的安全系数与可靠性
在燃烧室壳体设计时,要保证它有足够大的安全系数,例如安全系数nb>1和np>1。然而,这并不意味着壳体就能绝对可靠地工作。有时尽管安全系数远远大于1,但仍可能是不安全的。因此,就有必要了解壳体工作的可靠性与哪些因素有关以及安全系数与可靠性之间的关系如何,并根据规定的可靠性要求来确定壳体应具有的安全系数。
一、壳体的可靠性概率
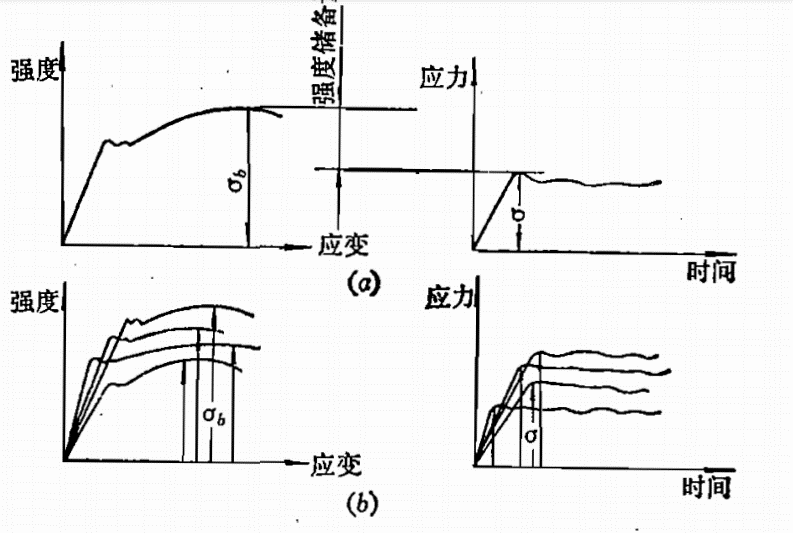
把材料的力学特性和壳体的应力都看作是一些确定的量,如图1(a)所示。但实际上它们都是一些随机变量,如图1(b)所示。通常,安全系数定义为
\(n=\frac{{{{\bar{x}}}_{2}}}{{{{\bar{x}}}_{1}}}\) (1)
式中 \({{\bar{x}}_{1}}\) —代表壳体内的最大广义应力的平均值,或代表燃烧室最大压力的平均值;\({{\bar{x}}_{2}}\)——代表材料强度极限的平均值,或代表壳体爆破压力的平均值。
图1材料的力学特性和壳体的应力
亦即,\({{n}_{b}}={{\bar{\sigma }}_{b}}/{{\bar{\sigma }}_{b\max }}\) ;\({{n}_{p}}={{\bar{\sigma }}_{p}}/{{\bar{\sigma }}_{p\max }}\)
实际上,σb和σmax以及pb和Pmax,都是具有某种分布特性的随机变量。通常假设它们都是按正态曲线(高斯曲线)分布的,其标准偏差各为σ1和σ2。
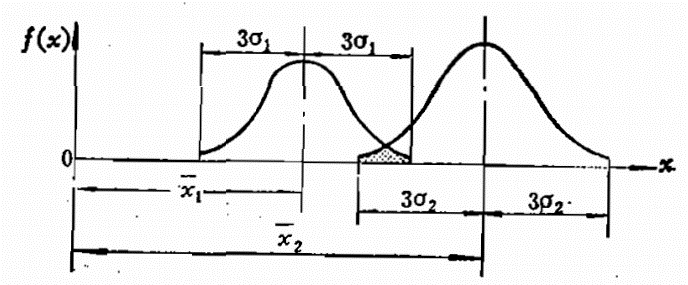
图2壳体应力\({{\bar{x}}_{1}}\)和材料强度\({{\bar{x}}_{2}}\) 的分布曲线
因此,
\(\left\{ {\begin{array}{*{20}{c}}{{x_1} = {{\bar x}_1} \pm 3{\sigma _1}}\\{{x_2} = {{\bar x}_2} \pm 3{\sigma _2}}\end{array}} \right.\) (2)
\({{\bar{x}}_{1}}\)和\({{\bar{x}}_{2}}\)的概率分布曲线如图2所示。由图可见,尽管\({{\bar{x}}_{2}}>{{\bar{x}}_{1}}\) ,但在该两条曲线的重叠部分,仍存在\({{\bar{x}}_{1}}>{{\bar{x}}_{2}}\)的可能性,也就是说,仍存在着壳体发生破坏的可能性。由概率理论得知,若有k个独立的随机变量\({{\bar{x}}_{1}}\),各变量的标准偏差为σi,则由k个随机变量组成的系统z的标准偏差为
\(\sigma =\sqrt{{{\sum\limits_{i=1}^{k}{\left( \frac{\partial z}{\partial {{x}_{i}}} \right)}}^{2}}\sigma _{i}^{2}}\) (3)
表1列出了由两个以下的独立变量所组成的简单系统z的平均值\(\bar z\)及其标准偏差σ。
表1简单系统z的平均值和标准偏差
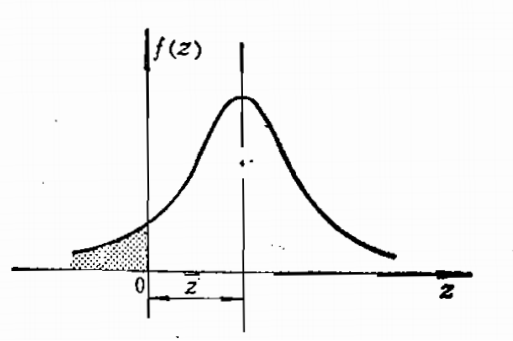
设x₁和x₂均按正态曲线分布,且其标准偏差各为σ₁和σ₂。若令z=x₂-x1,则z也按正态曲线分布,如图3所示。由表2可知,其标准偏差为
图3 z的正态分布曲线
\(\sigma=\sqrt{{\sigma}_{1}^{2}+{\sigma}_{2}^{2}}\) (4)
z的平均值为
\(\bar z={\bar x}_{2}-{\bar x}_{1}\)(5)
z的分布密度函数为
\(f\left( z \right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left[ -\frac{{{\left( z-\bar{z} \right)}^{2}}}{2{{\sigma }^{2}}} \right]\) (6)
令\[y=\left( z-\bar{z} \right)/\sigma \] ,则
\(f\left( y \right)=\frac{1}{\sigma \sqrt{2\pi }}\exp \left[ -\frac{{{y}^{2}}}{2} \right]\) (6’)
由图3可见,z=x₂-x₁>0的概率(可靠性概率)为正态曲线的大部分;而z=x₂—x₁<0的概率(破坏概率)为正态曲线的阴影部分。因此,壳体可靠性概率为
\(R\left( z>0 \right)=\frac{1}{\sqrt{2\pi }}\int\limits_{-\frac{{\bar{z}}}{\sigma }}^{\infty }{\exp }\left[ -\frac{{{y}^{2}}}{2} \right]dy\) (7)
可靠性概率R与\({\bar z}/{\sigma}\)的函数关系可以做成表格查询,也可编程计算。壳体的破坏概率为
Pf=1-R (8)
若已知材料强度极限(或壳体爆破压力)的平均值\({\bar x}_{2}\)及其标准偏差σ₂,同时也知道壳体最大广义应力(或燃烧室最大工作压力)的平均值\({\bar x}_{1}\)及其标准偏差σ₁,则可以由式(5)、(4)算出\(\bar z\)和σ。然后,根据算出的\(\bar z/{\sigma}\)值查表4-4,得出可靠性概率R。
二、安全系数与可靠性概率的关系
由式(7)或表得知,可靠性概率R是\(\bar z/{\sigma}\)的函数,且\(\bar z/{\sigma}\)愈大,R也愈大。因此,欲求安全系数n与可靠性概率R之间的关系,必须首先求出安全系数n与\(\bar z/{\sigma}\)之间的关系。
由式(4)、(5)和(1)得
\(\bar{z}/\sigma =\frac{x2-x1}{\sqrt{{{\sigma }_{1}}^{2}+{{\sigma }_{2}}^{2}}}=\frac{\frac{{{{\bar{x}}}_{2}}}{{{{\bar{x}}}_{1}}}-1}{\sqrt{{{\left( \frac{{{\sigma }_{1}}}{{{{\bar{x}}}_{1}}} \right)}^{2}}+{{\left( \frac{{{x}_{2}}}{{{{\bar{x}}}_{1}}} \right)}^{2}}{{\left( \frac{{{\sigma }_{2}}}{{{{\bar{x}}}_{2}}} \right)}^{2}}}}=\frac{n-1}{\sqrt{{{\left( \frac{{{\sigma }_{1}}}{{{{\bar{x}}}_{1}}} \right)}^{2}}+{{\left( n \right)}^{2}}{{\left( \frac{{{\sigma }_{2}}}{{{{\bar{x}}}_{2}}} \right)}^{2}}}}\) (9)
若已知材料强度极限(或壳体爆破压力)的相对偏差% \({\left( {\frac{{{\sigma _2}}}{{{{\bar x}_2}}}} \right)}\)和壳体最大广义应力(或燃烧室最大压力)的相对偏差\({\left( {\frac{{{\sigma _1}}}{{{{\bar x}_1}}}} \right)}\),根据规定的可靠性概率要求,由式(9)即可求出壳体应具有的安全系数。
由式(9)可知,n增大、\({\left( {\frac{{{\sigma _2}}}{{{{\bar x}_2}}}} \right)}\),和\({\left( {\frac{{{\sigma _1}}}{{{{\bar x}_1}}}} \right)}\)减小均可使R提高。若相对偏差不变,增大安全系数固然能提高可靠性概率,但壳体壁厚会增大,使结构重量增大,可见这并不是一种恰当的办法。采用减小相对偏差的办法,例如提高材料的机械强度、减小机械强度的偏差(严格控制原材料的质量和热处理规范)以减小相对偏差\({\left( {\frac{{{\sigma _2}}}{{{{\bar x}_2}}}} \right)}\),降低推进剂燃速、药柱尺寸和喷管喉部面积的偏差以减小相对偏差\({\left( {\frac{{{\sigma _1}}}{{{{\bar x}_1}}}} \right)}\),皆能有效地提高可靠性概率。
举例,已知某燃烧室壳体的筒体两端分别与室盖和喷管采用卡环连接。壳体直径D=127±0.26mm,壁厚δ=2.5±0.12mm。壳体材料的强度极限σb=380±42MPa,燃烧室最大工作压力Pmax=12±1.2兆帕。试计算该壳体的安全系数n6和可靠性概率R。
根据给定的参数,3σp=1.2(MPa),σp=0.4(MPa);3σb=42(MPa), σb =14(MPa);3σR=0.13×10-⁸(米),σR=0.043×10-⁸(米);3σδ=0.12×10⁻³(米); σδ=0.04×10-³(米)。
将壳体视为受内压力载荷作用的长圆筒来处理。σθ=pmax R/δ;σx=pmax R/2δ;σr≈0。
最大广义应力为
\[\sigma =\sqrt{{{\left( {{\sigma }_{x}}-{{\sigma }_{\theta }} \right)}^{2}}+{{\left( {{\sigma }_{\theta }}-{{\sigma }_{r}} \right)}^{2}}+{{\left( {{\sigma }_{x}}-{{\sigma }_{r}} \right)}^{2}}}=\frac{\sqrt{3}}{2}{{\sigma }_{\theta }}\]
安全系数为
\(n=\frac{{{\sigma }_{b}}}{{{\sigma }_{\max }}}\)
已知\(\sigma =\frac{\sqrt{3}}{2}\frac{{{P}_{\max }}R}{\delta }\),令W=pmaxR,则由表1可知:
\[\bar{W}={{\bar{P}}_{max}}\bar{R}\] (MPa/米),W的标准偏差为
\({{\sigma }_{w}}=\sqrt{{{{\bar{p}}}^{2}}_{\max }\sigma _{R}^{2}+{{R}^{2}}\sigma _{p}^{2}}\) (MPa/m)
已知\({{\sigma }_{\max }}=\frac{\sqrt{3}}{2}\frac{{\bar{W}}}{\delta }\) ,由表1可知,σmax的标准偏差为
\({{\sigma }_{\sigma }}=\sqrt{\frac{{{{\bar{W}}}^{2}}\sigma _{\delta }^{2}+\sigma _{w}^{2}\bar{\delta }_{{}}^{2}}{{{{\bar{\delta }}}^{4}}}}\)
求:
\[\frac{{{\sigma }_{1}}}{{{{\bar{x}}}_{1}}}=\frac{{{\sigma }_{\sigma }}}{{{\sigma }_{\max }}}\]
\[\frac{{{\sigma }_{2}}}{{{{\bar{x}}}_{2}}}=\frac{{{\sigma }_{\sigma b}}}{{{\sigma }_{b}}}\]
由式(9)得\[{{\bar{z}}}/{\sigma }\;\] ,查表或计算,可得系统可靠性R概率,进而求得失效概率Pf=1-R。