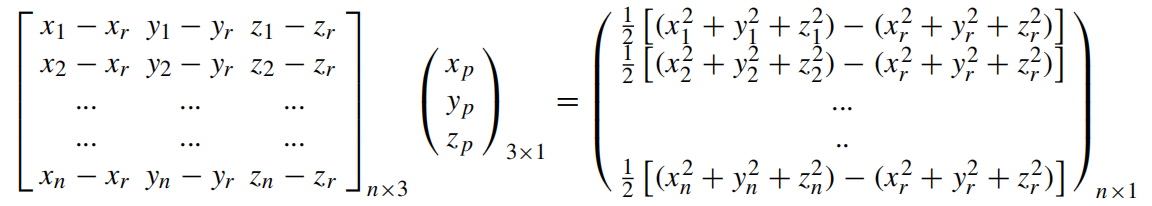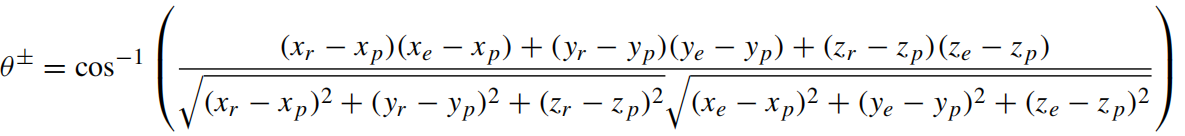使用3-D DIC对大型固体火箭助推器的柔性喷喷管系统（FNS）进行性能表征

本文介绍了用于大型固体火箭助推器喷管的柔性喷管系统（FNS）的各种性能参数的测量方法，如枢轴点偏移、摆动角度和喷管运动的对称性。本文尝试使用枢轴点坐标作为主数据来估计上述参数。为此，利用矢量化试验中基于立体的三维数字图像相关（3-D DIC）系统在喷管模拟器上方获得的参考点轨迹。提出并验证了一种线性最小二乘法（LLS）方法，用于从三维DIC轨迹定位枢轴点。进一步分析枢轴点位置和实测DIC位移，以评估目标参数。结果表明，使用3-D DIC系统通过简化的测量方案为执行器的性能提供了保障。此外，它还生成了有用的附加数据，作为衍生产品，与传统测量相当。因此，预计FNS表征所需的数据减少、测试时间和资源将大大减少。

引言

固体火箭发动机（SRM）具有高推重比、高可靠性和高推进剂密度特点。大型固体助推器常使用二次喷射推力矢量控制（SITVC）或柔性喷管控制（FNC）系统。在当前情况下，大多数新型固体火箭都配置了FNC系统，因为它的设计简单可靠。典型的FNC系统利用带有柔性密封件的柔性接头配置和一对称为柔性喷管系统（FNS）的执行器以及相关的控制电子设备，以满足飞行过程中的矢量控制需求。

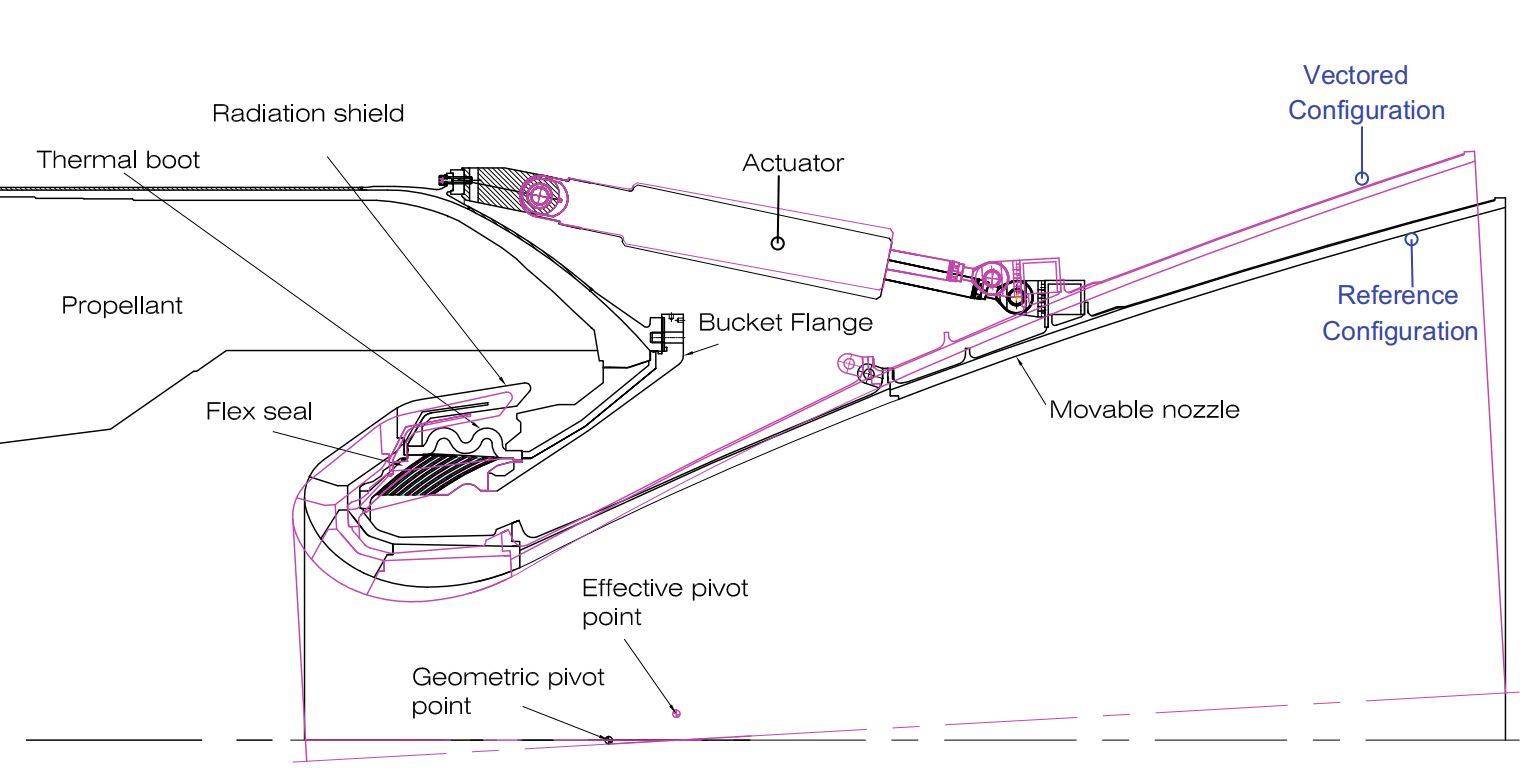
FNS属于一类柔性机构，采用一种称为柔性密封的柔性接头，该接头通常是一个圆柱体，带有具有交替层的球形金属体和弹性体（橡胶）（如图1 ）。喷管的运动是通过弹性材料的变形实现的， 根据设计，所有刚性体都具有共同的几何中心。柔性密封件预计在这个几何中心有一个枢轴点，称为几何枢轴点（GPP），现实情况，由于 （i） 柔性密封件在腔室压力下的变形，（ii） 弹性体的粘弹性行为，以及 （iii） 由于作动器运动引起的不对称，实际或有效枢轴点与 GPP 存在偏移。有效枢轴点如图1所示，与喷管的初始位置和摆动位置不同。柔性接头枢轴点偏移的量化，对于摆动喷管的动态包络至关重要。此外，由于驱动系统是位置或行程控制的，因此柔性接头枢轴点动力学对喷管的摆动角度有重要影响。

图1 使用柔性喷管系统（FNS）的喷管的横截面线图，其中显示了喷管从参考状态到摆动状态的驱动过程中的几何和有效枢轴点

在S200中，FNS在驱动平面上配置了±5.5°的摆角能力，在合成平面上配置了±7.8°的摆角能力。两个相距 90° 的电动液压作动器有助于实现喷管的全轴矢量控制能力。需要确定该FNS有效枢轴点的偏移，以获得对设计和配置的保障。此外，也有报道称，当燃烧室压力发生变化时，枢轴点位置会发生变化。除枢轴点偏移外，基于FNS的推力矢量控制（TVC）系统的性能还对喷管摆动角度、作动器行程对称性、推力矢量轴（推力线对准）等参数敏感。上面强调的所有参数对于FNS系统的正常运行都起着至关重要的作用。

在本文中，仅使用一个基于立体相机的3-D DIC设备报道了测量枢轴点坐标、其偏移、摆动角度和喷管运动对称性的简易方法。此时，DIC已成为一种用于全场位移和应变测量的先进且成熟的非接触式光学技术[7,8]。这种技术的二维版本最初是由Peters等人提出的，它可以仅使用单个相机（单目视觉）测量平面物体上的平面内位移和应变。

由于真实物体不是平面的，二维DIC随后通过结合立体摄影测量（双目视觉）的原理而成熟为三维DIC，其中采用了一对相机[11-14].3-D DIC可以测量任何感兴趣的实际物体的三维位移和表面应变[7,8,15,16]。近年来，研究工作更多地集中在仅使用单个相机来获得三维位移和应变[17-22]。这些努力将彻底改变DIC领域，并有望显着降低高速和动态应用的系统成本。

本文使用立体相机单独使用3-D DIC进行实验，因此讨论将仅限于此类布局。此外，由于3-D DIC可以捕获物体在微米到数百毫米范围内的三维运动，而不会影响任何精度；它有助于仅使用一个 3-D DIC 系统精确测量柔性喷管的多个性能参数。在此，简要总结了用于测量灵敏喷管性能参数的现有技术[23]，参考文献[23]中使用了许多位移传感器来确定枢轴点的偏移，但枢轴点的坐标和其他参数尚未确定。参考文献[24]，位移传感器和倾角仪仅用于估计喷管旋转角度。参考文献[25]报道了使用红外光电法确定喷管轴线和矢量角。激光跟踪仪已被用于测量喷管矢量角[26]和推力线测量[27]。Guo等[28]的工作结合了四个光标测量相机来测量喷管的角度和运动，其中提出了所涉及的算法。文献[29]提出了一种很有前途的方法，利用单相机测量喷管在较高速度下的摆动角度，其中再次使用了复杂的算法。参考文献[31]中采用了一种类似但稍微简单的方法来测量喷管的摆动中心，该喷管仅限于进行平面运动的喷管。在单台仪器设置中，只有可数数量的论文确定了多个喷管性能参数。然而，参考文献[30]中进行了一个值得注意的尝试，用于估计相对较小的喷管的喷管运动参数，例如旋转中心和摆动角度。此外，参考文献[30]中使用的算法复杂，方法与本文提出的方法不同。值得注意的是，到目前为止，还没有尝试使用3-D DIC的惊人能力来测量大型喷管的性能参数。

文献综述表明，矢量喷管的摆动角度（驱动角度/喷管旋转）和推力线对准（喷管轴/推力矢量轴）进行了多次尝试。其中许多论文利用非接触式和/或光学技术来测量喷管的性能参数。然而，到目前为止，除了参考文献之外，还没有确定枢轴点坐标[30,31]。

本文提出的目标参数估计的基本要求之一是枢轴点坐标的确定。如本文所述，将 3-D DIC 与线性最小二乘法 （LLS） 算法结合使用将有助于确定备受关注的枢轴点坐标。LLS算法利用从3-D DIC获得的喷管模拟器上参考点的轨迹来预测枢轴点坐标。轨迹基本上是图像每一帧中参考点的动态位移。利用合成数据验证了该算法，并估计了不同振幅的随机噪声的实验不确定度。随着置信度的提高，在喷管矢量循环中测量了实际枢轴点坐标。因此，找到枢轴点偏移变得直截了当，而其他参数则使用实体几何形状的已知公式和“测量程序”中描述的三维DIC生成的数据进行估计。将3-D DIC位移得出的数据与试验台中可用的测量仪器进行比较，以进行验证并找到进一步的改进范围。实验、测量程序和结果的细节将在后面的章节中介绍，并附有简要结论。

实验细节

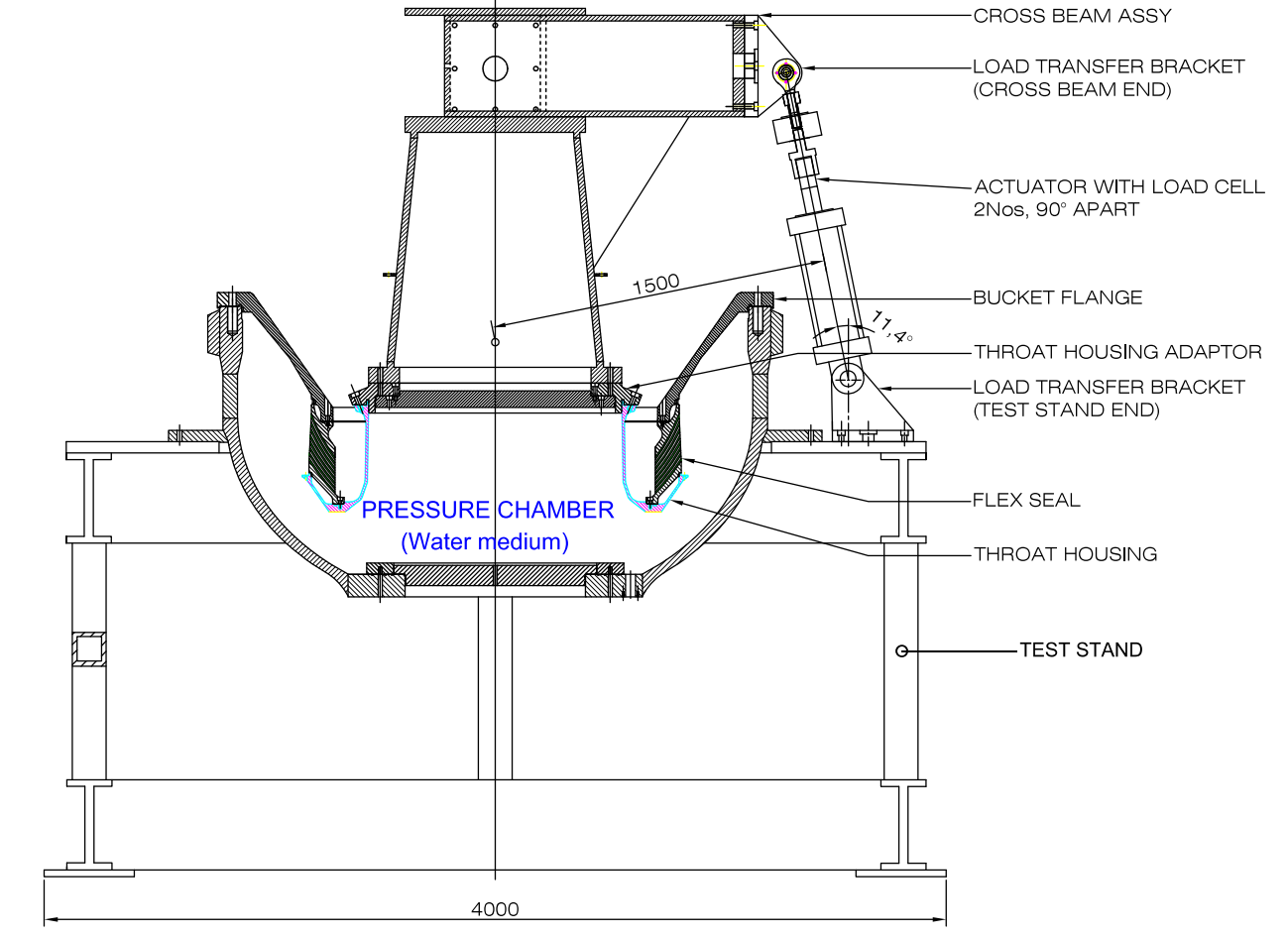
柔性密封件（见图1和图2）是FNS中最重要的元素，通过耐压试验（PPT）、零定位试验（NPT）和矢量试验（VT）等一系列地面试验证明了每种柔性密封的功能和结构。NPT和VT在PPT之后进行。PPT完成后无需组装喷管。PPT设置通过组装两个作动器和一个称为横梁组件¹的喷管模拟器进行修改，如图2所示，用于NPT和VT。两个作动器连接到横梁的臂上（图2）。图 2 中的线图仅显示一个作动器，而另一个作动器将沿着纸平面的法线图 3a 中以摄影方式显示了横梁组件的等距视图，两个作动器 A1 和 A2 连接到虚拟喷管的臂。

图2喷管矢量试验装置示意图。试验台的各种元件都有标记。在这里，柔性密封是在各种燃烧室压力下进行评估的部件。

在矢量测试中，FNS分别在5 bar、23 bar、35 bar和38.5bar等四个压力水平下进行测试，分别模拟发动机退位、平衡、最大期望和验证压强下喷管施加的载荷。在每个燃烧室压力下，作动器的归零，然后执行A1作动器、A2作动器和A1-A2组合作动器的进行。增压顺序为5 bar、23 bar、38.5 bar和35 bar。因此，文中出现各种数据，都会遵循上述压力顺序。对于38.5bar室压力测试，没有进行组合A1-A2驱动，因为这将使FNS超出设计限制。此外，据估计，在35 bar下，A1-A2组合驱动期间，弯曲密封中产生的应变大于38.5 bar时的单个作动器测试。因此，在35 bar测试之前进行了38.5 bar测试。

图3 数字照片a横梁组件(喷管模拟器)显示A1和A2作动器和轴向LVDT, b在矢量测试期间用于表征摆动喷管系统的三维DIC配置，显示参考点或跟踪点。

如图3（b）所示，在横梁组件顶部的3-D DIC设置用于获取所有目标参数。在此设置中，使用两台500万像素的单色CCD相机（Point Grey，德国制造）和8毫米固定焦距镜头（德国施耐德制造）布置在目标表面上方约500毫米处进行立体成像。随机斑点图案（图4（a）和（b））是在A4尺寸上生成的’喷管模拟器是一种称为横梁组件的虚拟喷管。此后，喷管模拟器、横梁组件和虚拟喷管的名称将在正文中互换使用。

图4从假喷管顶部看到的随机图案立体视图;a左相机图像，b右相机图像。同样，c和d分别从左、右相机视图显示用于立体校准的圆形网格模式

白纸用黑色喷漆，并用胶水牢固地贴在成像表面。需要注意的是，上述粘接后的随机模式足以较好地跟踪刚体位移，建立三维DIC的全局坐标系，采用标准圆网格模式(图4(c)和(d))按照[32]中的步骤进行立体标定。各种立体参数被存储并输入到DIC分析程序VIC3D中。在驱动过程中，使用VICSNAP以0.5 Hz的频率远程自动抓取图像[32]，满足所有安全协议。成像区域是这样选择的，在随机模式之外有足够的空间可用来捕获驱动器的向前和向后的冲程。立体摄像机所覆盖的区域在500mm×500mm附近，测量了大约2000像素的图像帧。DIC分析使用91个pixel×91像素子集，其中15个像素作为网格步长。选择大的子集是因为用于测量的稀疏随机模式(黑点密度较小)。这种子集大小的选择提供了图像相关所需的独特指纹，从而导致更好的测量精度和更平滑的位移场。在当前的测试设置中，面内和面外位移精度分别优于0.025 mm(考虑0.1像素精度)和0.05 mm(考虑0.2像素精度)。这里需要强调的是，[32]中的程序声称比报道的程序具有更好的亚像素精度。

在图3(b)的设置中，成像平面为x-y平面，其中DIC坐标系的x轴和y轴分别与A1作动器和A2作动器的运动几乎对齐。因此，在a1驱动期间，参考点的轨迹将在x-z平面(x>z)内，在A2驱动期间，轨迹将在y-z平面(y>z)内。z坐标是在DIC中获得的面外轨迹数据。三维DIC设置，轴向在横梁上方(图3(b))，将有助于定位支点w.r.t，一个参考点几乎穿过喷管轴，位于横梁的顶部平面。横梁顶面的位置是已知的，因此它被用作几何参考来测量和解释感兴趣的参数。

矢量测试只会产生横梁组件的刚体运动。在理想条件下，跟踪横梁顶部的单个参考点(图3(b))就足以估计目标参数。因此，从DIC测量到参考点的位移可以解释为记录时间运动时的轨迹。从在图4(a)和(b)中，在随机图案上绘制两条垂直的铅笔线，几乎对齐致动器的运动，以粗略地了解致动器的物理参考轴。选择这些线(图4(a)和(b)在喷管轴的交点作为跟踪其时间运动(轨迹)的参考点/区域。然而，既然目的也是为了从横梁组件的倾斜角度测量驱动角，进行全场测量。使用VIC3D[32]分析了两条线交叉处70mm×70mm的区域，并绘制了位移图。随后，提取了以上述参考点为中心的2mm×2mm较小面积（但由于驱动过程中横梁倾斜而无法选择较大的区域进行平均）的数据，得到了x、y和z平面上的时间刚体运动。平均值旨在提高测量的保真度。因此，轨迹实际上是在代表参考点的矢量化周期中提取平均数据的较小区域的动态位移。
值得注意的是，3-D DIC是作为表征FNS的新测量方案引入的。因此，除了DIC测量外，测试台还像往常一样配备了位移传感器（线性可变位移传感器（LVDT）和倾角仪。此外，柔性密封件还配备了应变片。四个轴向LVDT用于测量喷管模拟器的轴向运动，两个LVDT用于直接测量执行器的行程。LVDT 的冲程为 300 mm，精度为全范围的 0.1%。矢量测试在角度控制模式下进行。因此，放置了两个倾角计对准执行器，并将角度数据用于反馈控制回路。通过DIC估计的参数将与“结果和讨论”中的LVDT测量值进行比较。因此，它将验证DIC的测量结果，并可能有助于确定需要改进的领域

测量程序

在本节中，我们介绍了使用3-DIC数据测量枢轴点坐标、其偏移、驱动角度和喷管运动的对称性所遵循的程序。为了估计所有这些参数，虚拟喷管（横梁组件）上参考点的轨迹似乎就足够了。然而，全场数据将用于寻找驱动角度的替代方法。

线性最小二乘法（LLS）求枢轴点坐标算法

本文提出了一种线性最小二乘法（LLS），用于从横梁（假喷管）上参考点的轨迹求枢轴点的位置。借助3-D DIC，在矢量序列中跟踪参考点的运动。应该注意的是，参考点是空间中的任意点，仅在坐标为 （x=0，y=0，z=0） 的 3-D DIC 轴中定义。在执行器的单个驱动测试中，参考点将在空间中进行二维运动，描述执行器平面上的圆弧，而与枢轴点的位置无关。如果幸运的是，DIC中所选的参考点仍保留在包含枢轴点的平面上，则可以将圆的中心视为枢轴点。然而，在现实中，由于包含枢轴点的平面是未知的;DIC中选择的参考点将任意但略微偏离包含枢轴点的平面，图5所示为图5所示，该参考点以夸张的方式从包含枢轴点的平面偏移，以便视觉欣赏。在图5中，假设参考点在驱动过程中在y-z平面内运动。在这种情况下，需要 x、y 和 z 偏移来获取枢轴点的坐标并测量枢轴半径。当执行器的组合运动时，也会出现类似的情况，即参考点将遵循合成平面中的圆弧。如果考虑所有三个驱动测试（A1，A2和组合A1-A2）在单次测试压力下的轨迹数据，则在空间中将有三个弧具有三个曲率。其中两个是相互垂直的，具有几乎相似的曲率，而另一个

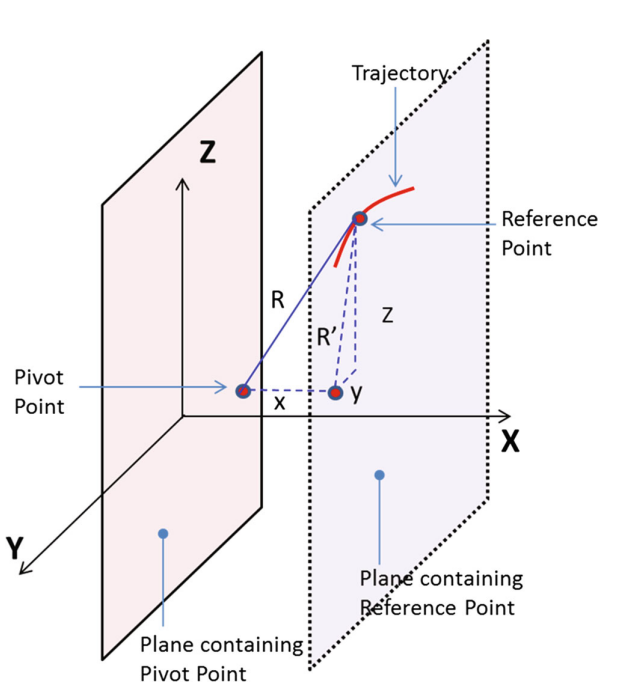
图5 图中显示了不落在包含枢轴点的平面上的参考点所追踪的轨迹。参考点在 y-z 平面上移动，偏移量为与包含枢轴点的平面的 x 距离。此处的轴以粗体大写字母 X、Y 和 Z 显示，其中坐标表示为小写字母（x、y 和 z）

一个将是它们在一个结果平面中的结果。由于作动器的运动在所有轴上几乎是对称的，因此预计所有三个轨迹都将是一个球体的一部分，这里称为枢轴球体。同样，如果考虑单个作动行程（A1或A2或A1-A2组合）的轨迹数据，则将导致具有单一曲率的圆弧。因此，可以使用经典的立体几何方法找到枢轴点坐标。考虑所有作动周期的查找枢轴点坐标的方法如下所述。

考虑到上述讨论，中心与原点偏移 （x_o，y_o，z_o） 的球体方程由下式
给出：（x-x_o）²+（y-y_o）²+（z-z_o）²=r²， （1）

其中，x，y，z 是球体上任何一点的坐标，r 是球体的半径。

现在，将方程（1）中球体中心的坐标替换为枢轴点坐标（x_p，y_p，z_p），并将参考点（x_r，y_r，z_r）作为球体上的坐标之一，球体方程的形式为
（x_r-x_p）²+（y_r-y_p）²+（z_r-z_p）²=r²。       (2)

这里需要注意的是，参考点的位置是从DIC中知道的，需要确定的未知数是枢轴点坐标（x_p，y_p，z_p）和半径r，从DIC得到的轨迹包含许多点，这些点都假定位于球体上。考虑到轨迹中的第i个点与坐标为（x_i，y_i，z_i），球体方程可以表示为
（x_i-x_p）²+（y_i-y_p）²+（z_i-z_p）²=r²。      (3)

式（2）和（3）可以用来消解r.因此，可以将轨迹、参考点和枢轴点上的广义坐标表达式得到为
（x_i-x_r）x_p+（y_i-y_r）y_p+（z_i-z_r）z_p=（1/2）[(x_i²+y_i²+z_i²)-( x_r²+y_r²+z_r²)]。     (4)

上述等式（4）包含了LHS上的未知数（x_p，y_p，z_p），RHS具有来自DIC的所有测量数据。

（5）

等式（5）可以用简化的方式表示为 AX = B。我们至少需要三个方程（轨迹上的三个点，距参考点的一部分）来获得 （x_p，y_p，z_p） 的唯一解。然而，由于从DIC得到的轨迹包含三个以上的数据点，因此线性方程组的方程多于未知方程。因此，采用线性最小二乘求解法得到未知数。

X=(A^TA)^-1A^TB     (6)

一旦使用公式（6）确定枢轴点坐标，则可以使用公式（2）估计枢轴半径。上述过程适用于任意参考点。但是，在作动测试的第一个周期中，参考点的坐标值将为（0,0,0）。因此，将上述线性方程（5）
的集合进一步简化，将（x_r，y_r，z_r）代为（0,0,0）。在这种情况下，数据分析变得更加简单。

通过考虑执行器单独驱动和组合驱动过程中的整个轨迹，可以得到在单一压力下的一个枢轴中心和一个枢轴半径。因此，如果考虑不同压力下的轨迹，可以得出随压力变化的偏移。为了找到各个驱动周期中的偏移，可以考虑来自单个执行器和组合执行器运动的数据。在这些情况下，由于轨迹是圆的一部分，因此只能使用上述类似的最小二乘法解确定枢轴点的两个坐标。从每个执行器运动获得的数据将提供各个执行器平面中的坐标。可以将圆拟合的LLS的这些平面偏移量（2-D LLS）与球拟合的LLS偏移量（3-D LLS）进行比较，以找出所有压力循环中的极端偏移。然而，在单个驱动测试（平面圆LLS）中，

由于无法从弧的平面或二维性质中获得第三个坐标，因此无法找出枢轴半径。

测量驱动角度的程序

测量枢轴点坐标的过程考虑了单个点的轨迹。因此，仅通过跟踪参考点，可以通过矢量构造获得驱动角，下面将其做为方法-1进行详细说明。此外，由于3-D DIC能够在喷管模拟器顶部的平面上提供全场位移，因此可以通过测量假喷管的倾斜度直接获得驱动角度。倾斜测量的驱动角度在下面的方法 2 中进行了描述。考虑两种测量驱动角度的方法的主要目的是通过DIC找出最佳的测量方法。此外，还可以将DIC测量的角度与倾角仪测量值进行比较以进行验证。

方法-1

从3-D DIC获得的轨迹数据包含了在过程中向前和向后运动的极值点

矢量周期。由于枢轴点坐标已经可用，因此可以通过考虑参考点的坐标和矢量循环中喷管位移的极值点的简单矢量构造来找出驱动角度。

现在，将行程的极值点坐标视为 （x_e,y_e,z_e），即先前定义的参考点和枢轴点的坐标，两个向量可以构造为

${{M}_{pr}}=\left( {{x}_{r}}-{{x}_{p}} \right)\hat{i}+\left( {{y}_{r}}-{{y}_{p}} \right)\hat{j}+\left( {{z}_{r}}-{{z}_{p}} \right)\hat{k}$

和

${{M}_{pe}}=\left( {{x}_{e}}-{{x}_{p}} \right)\hat{i}+\left( {{y}_{e}}-{{y}_{p}} \right)\hat{j}+\left( {{z}_{e}}-{{z}_{p}} \right)\hat{k}$

(7)

其中 M_pr 和 M_pe 分别是将枢轴点连接到参考点和枢轴点连接到行程的极值点的向量。其中，i、j 和 k 是沿 DIC 坐标系的 x、y 和 z 轴的单位法向量。

现在，驱动角度 θ^± 可以从矢量的点积估计为

θ^±=cos^-1（Mpr·Mpe）    (8)

其中，θ⁺ 和 θ^– 分别为前向和后向行程定义，‘·’表示点积。公式 8 使用坐标信息后可以扩展为

(9)

方法-2

通过考虑假喷管上与执行器平面对齐的两个点的轴向偏转，可以直接测量驱动角度。由于VIC3D将度量坐标以及轴向偏转数据作为一个整体场提供，因此测量非常简单 在这里，虚拟喷管上的两个空间点由距离“△l_i”隔开，该距离与A_i对齐;执行器用于查找相应执行器的致动角度。由于从DIC可以求出这两点的相对轴向偏转“△w_i”，因此可以得到驱动角为：

$\theta _{i}^{\pm }={{\tan }^{-1}}\left( \frac{\Delta {{w}_{i}}}{\Delta {{l}_{i}}} \right)$   (10)

其中i是 1 或 2，具体取决于所考虑的执行器。

测量喷管运动对称性的程序

从目前的实验安排来看，3-D DIC数据无法提供驱动行程的直接测量。但是，由于跟踪了喷管上的物理点，因此可以推断出喷管运动的对称性：该参数将间接指示行程对称性。尽管如此，由于可以解释喷管的直接运动，因此它将为FNS的性能提供很大的信心。

为了测量喷管运动的对称性，需要测量跟踪点（参考点）从轨迹的平均位置（参考位置）到轨迹的极端矢量位置（终点）的行程，用d^±表示。现在，喷管的运动或实际位移可以表示为

${{d}^{\pm }}=\sqrt{{{\left( {{x}_{r}}-{{x}_{e}} \right)}^{2}}+{{\left( {{y}_{r}}-{{y}_{e}} \right)}^{2}}+{{\left( {{z}_{r}}-{{z}_{e}} \right)}^{2}}}$

其中 d+ 和 d- 分别是矢量周期内向前和向后行程中的运动（位移）。其他符号有其通常的含义。

前行程和后行程位移之差称为喷管运动’△d’的不对称性，表示为

△d=|d⁺|-|d^–|，(12)

其中 ||是绝对值。如果两个运动都被认为是正数，则△d=|d⁺-d^–|。在“结果与讨论”中，将比较 LVDT 的实际行程和 3-D DIC 喷管运动，以了解 FNS 的物理行为。

LLS算法定位枢轴点的验证

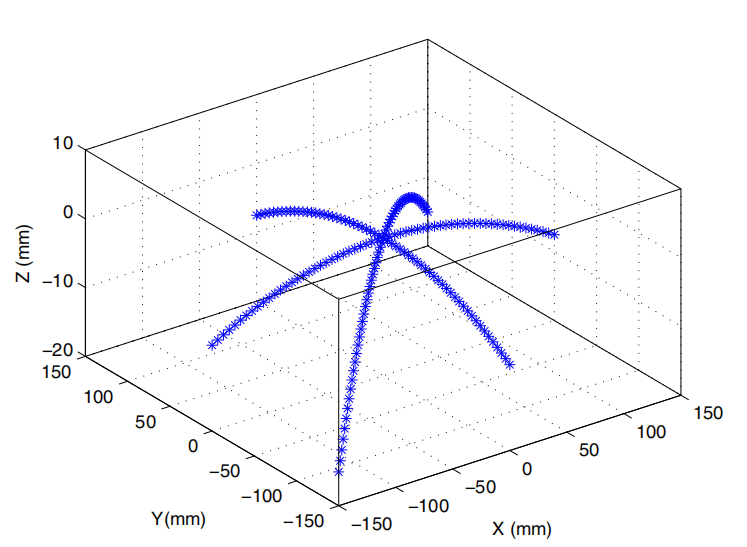
上述过程是在MATLAB平台中实现的。为了验证代码，在MATLAB中生成了合成轨迹，如图6所示。最初，考虑到球体的中心位于 （0,0,0） 和半径为 1500 mm，构建了三个弧。其中两条圆弧分别对准 x 轴和 y 轴。第三条弧线是根据前两条弧线的结果生成的。现在，为了模拟 DIC 数据，球体中心偏移 （0,0，-1500 mm），以获得参考点为(0,0,0).考虑这种坐标变换后，合成轨迹中的x和y坐标在-150 mm至150 mm之间变化，而z在7.5 mm至15 mm之间变化，见图6。

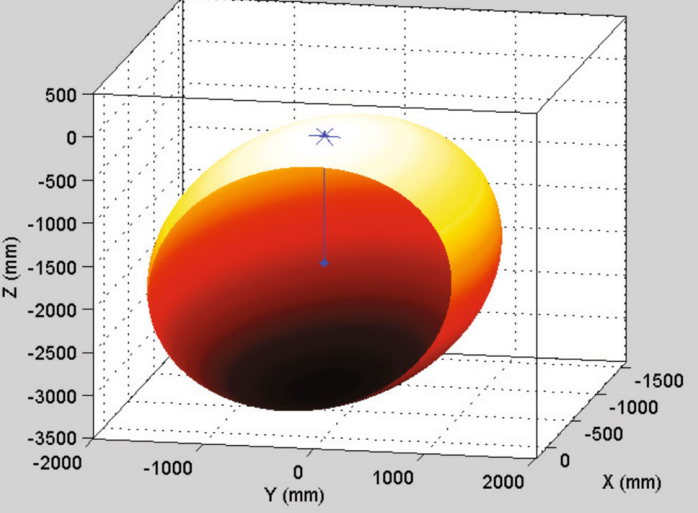
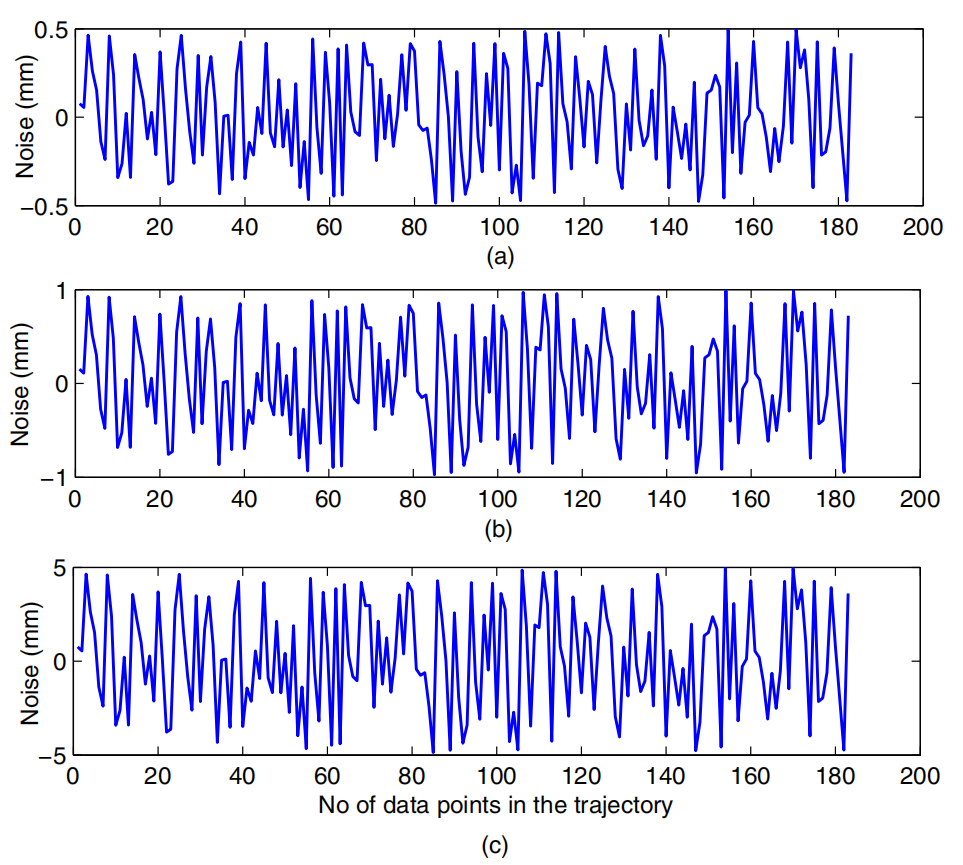
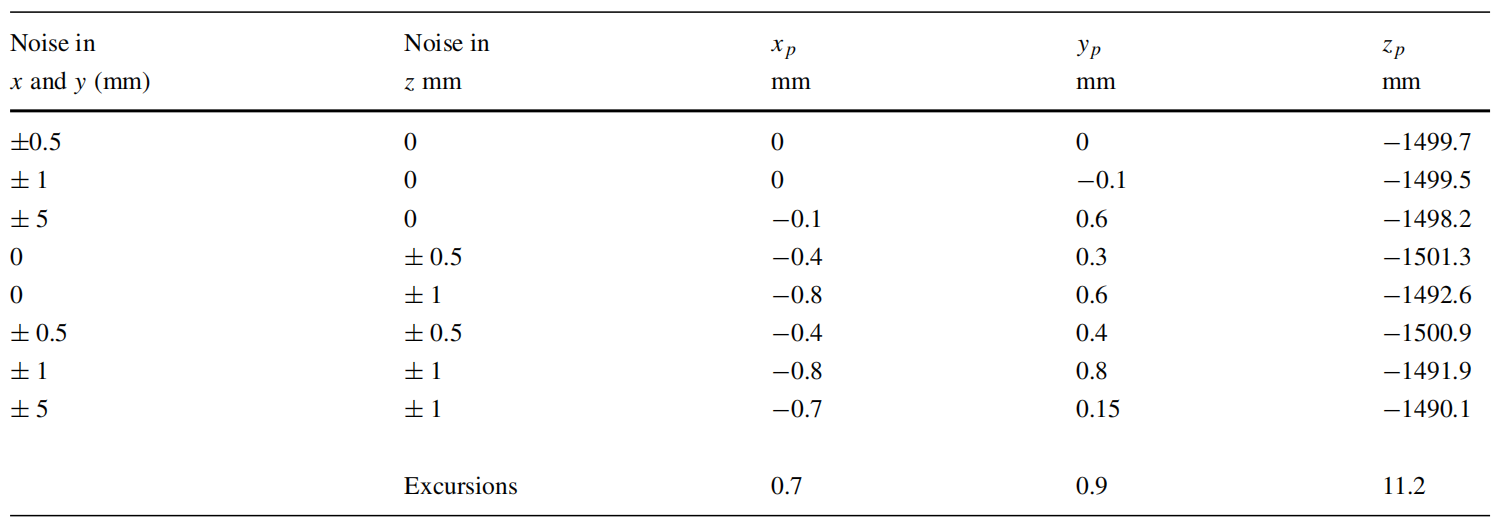
首先，在算法中利用图6所示的合成数据，得到枢轴点的坐标，得到的坐标与（0,0，-1500mm）与模拟的枢轴点坐标完全匹配。使用合成数据和LLS算法获得的枢轴球体的剖面图如图7所示，其中可以看到轨迹数据和枢轴半径。因此，上一节中概述的过程运行良好。现在，为了理解估计枢轴点的不确定性，将图8所示的各种大小的实验随机噪声添加到合成轨迹中。除此之外，还可能增加由于试验台的微小振动而产生的噪声。因此，为不确定性分析提供了实验噪声的额外余量。表 1. 报告了用各种噪声组合确定的枢轴点，可以看出面内噪声对枢轴点坐标的影响可以忽略不计。然而，z位移噪声对枢轴点坐标的干扰最大。x、y 和 z 位移噪声的组合具有与单独的 z 噪声几乎相似的效果。值得注意的是，由于驱动角度较小，与 x 和 y 位移相比，参考点的 z 位移较小（7.5 至 15 mm）。因此，z运动中的小噪声会在枢轴点z坐标中产生明显的效果。本文认为，z位移中最大为1 mm的实验噪声被认为是一种夸大其词，以理解噪声的极端影响。同样，在不确定性分析中考虑了 x 和 y 的 5 mm 噪声。在此重申，使用3-DDIC时的面内位移测量精度为0.025 mm（考虑0.1像素精度），在面外位移测量精度为0.05 mm（考虑0.2像素精度）。因此，不确定性分析中假设的噪声可以作为保守估计。表 1 显示，在干扰的极端情况下，x 和 y 坐标的最大不确定性为 1 mm，而 z 坐标的最大不确定性为 10 mm。这些噪声导致的不确定性较小在确定实际枢轴半径时大于 1%，并且在

图6 表示参考点在三维空间中轨迹的合成数据

图7 使用LLS方法拟合后的合成数据与球体的拟合 球体顶部的三个弧线表示在不同平面上的驱动。球体从一侧切开，以可视化枢轴中心的位置和枢轴半径

图8 在合成数据中加入a±0.5 mm、b±1 mm和c±5 mm的随机噪声，了解它们对枢轴点偏移的影响

枢轴点 Z 坐标。正在进行的部分中模拟的不确定性为使用所提出的程序以足够的精度确定枢轴点偏移提供了进一步的信心。

结果与讨论

在本节中，将介绍通过DIC分析测量的FNS的性能参数。使用DIC轨迹数据和全场位移测量了枢轴点的坐标和其他与性能相关的量。DIC测量值将与测试装置中可用的其他常规测量值进行比较。

枢轴点和枢轴半径偏移

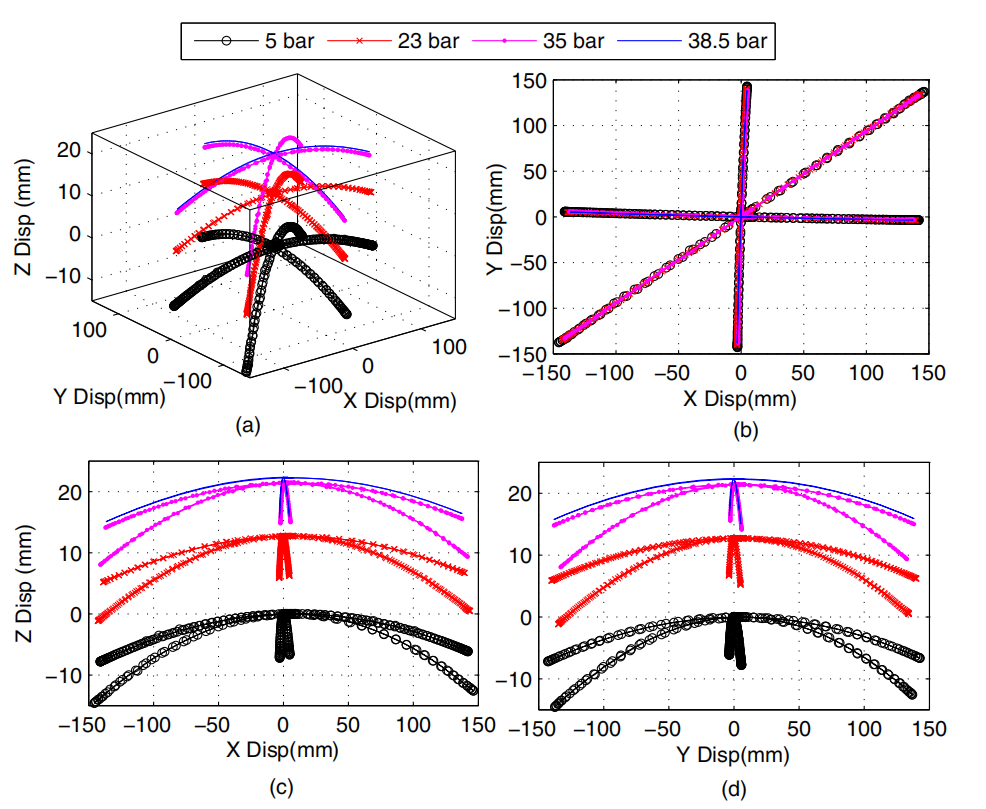
从3-D DIC获得的轨迹在不同腔室压力下如图9（a）所示。x-y、x-z 和 y-z 平面上的相同数据分别显示在图 9（b）、（c） 和 （d） 中。这里需要注意的是，与合成轨迹不同，致动器的运动平面会略微偏离 DIC 坐标轴。

表1 随机噪声对枢轴点坐标确定和偏移的影响

图9 在不同压力下，驱动试验中横梁顶部的参考点轨迹分别显示在xyz空间、b xy平面、cxz平面和dyz平面上。在这些轨迹中，Al 和 A2 驱动几乎与 x 和 yaxes 对齐。

实际上，将 DIC 的一个轴与执行器运动对齐是很困难的，因为测试是远程进行的，并且 DIC 设置已经安装好。因此，预计 DIC 轴会从执行器轴略有移动 [图 9（b）、（c） 和 （d））。然而，通过考虑来自DIC的合适合成位移，总是可以找到点在驱动平面中的轨迹。

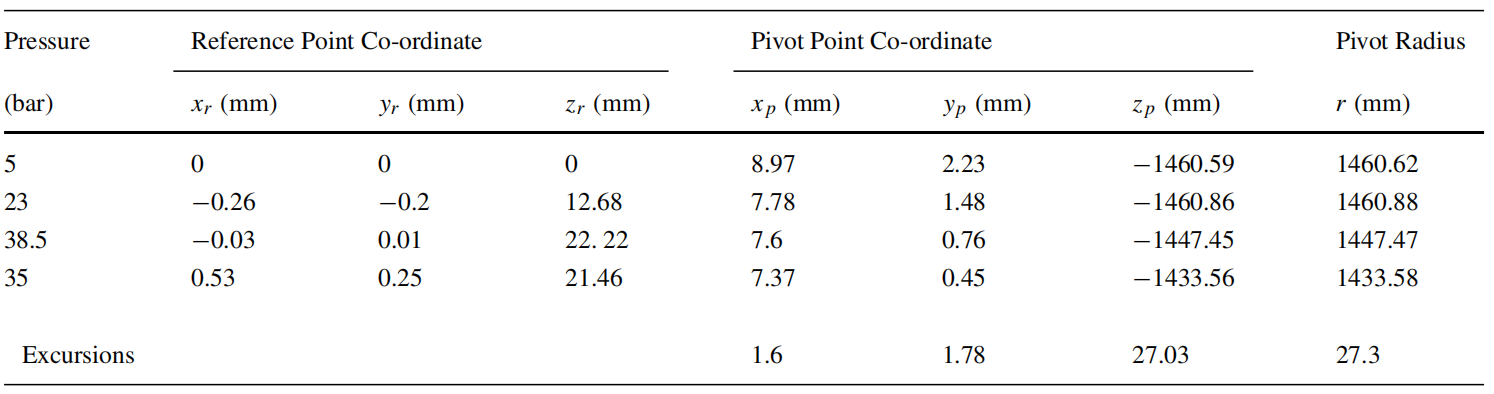
表2报告了在三维LLS算法中，考虑到A1、A2和A1-A2组合驱动的整个轨迹，在不同压力下得到的参考点和枢轴点的坐标。在表 2 中，x、y 和 z 坐标表示枢轴点相对于跟踪点（参考点）的位置。通过考虑整个数据集，如果假设x轴和y轴与A1和A2执行器平面匹配，z轴与喷管轴匹配，则坐标可以直接解释。例如，x>0 表示枢轴点位于参考点的右侧，从虚拟喷管顶部的摄像头观察到，同样，y>0 表示枢轴点垂直于参考点上方，z<0 表示枢轴点轴向低于参考点，反之亦然。

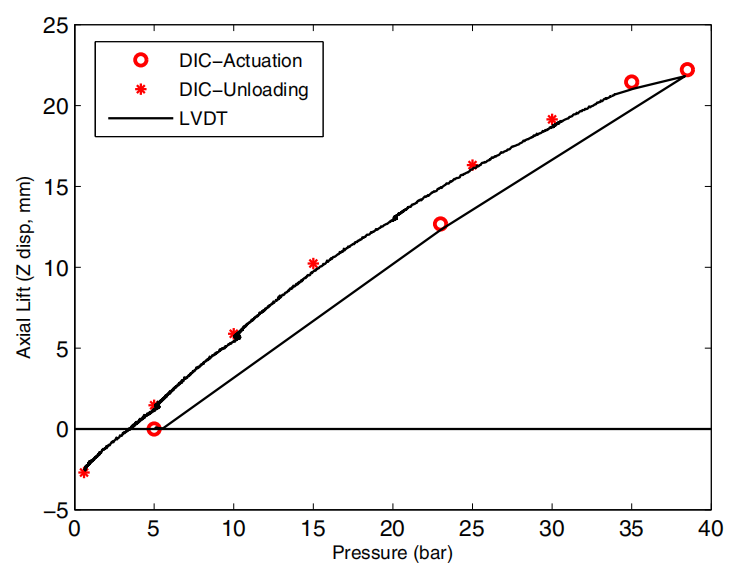
本文略有离题，比较了DIC的轴向位移和4个轴向LVDT的平均位移（图10）。从图 9 和表 2 可以明显看出，当腔室中的压力增加时，参考点会向上升高。实际上，当腔室压力增加时，挠性密封会受到压缩，从而引起虚拟喷管的轴向向上刚体运动。图10显示了DIC与LVDT测量结果的良好一致性。在该图中，在两次测量中都可以看到轴向位移的滞后行为。由于柔性密封是一种压力密封的柔性接头，由钢垫片和橡胶的交替层组成，因此预计橡胶将表现出粘弹性。

表2 不同压力下得到的参考点（跟踪点）和枢轴点的坐标

图10 与LVDT测量值相比，喷管模拟器在加压和减压过程中在不同压力下的升程测量值

在这种材料行为下，观察到的滞后行为是合理的。这种行为在参考文献[23]中也有报道。在这里，必须注意的是，由于DIC参考图像是在5 bar下拍摄的，并且LVDT数据也进行了相应调整，因此在0.6 bar压力下的位移为负。从上述推论可以看出，DIC能够提供与LVDTs相当的轴向位移，此外，在目前的实验中，DIC测量的精度将优于300 mm行程的LVDT。因此，这些LVDT可以用3-D DIC代替。测试台仪器的这种简化可以节省时间和资源。

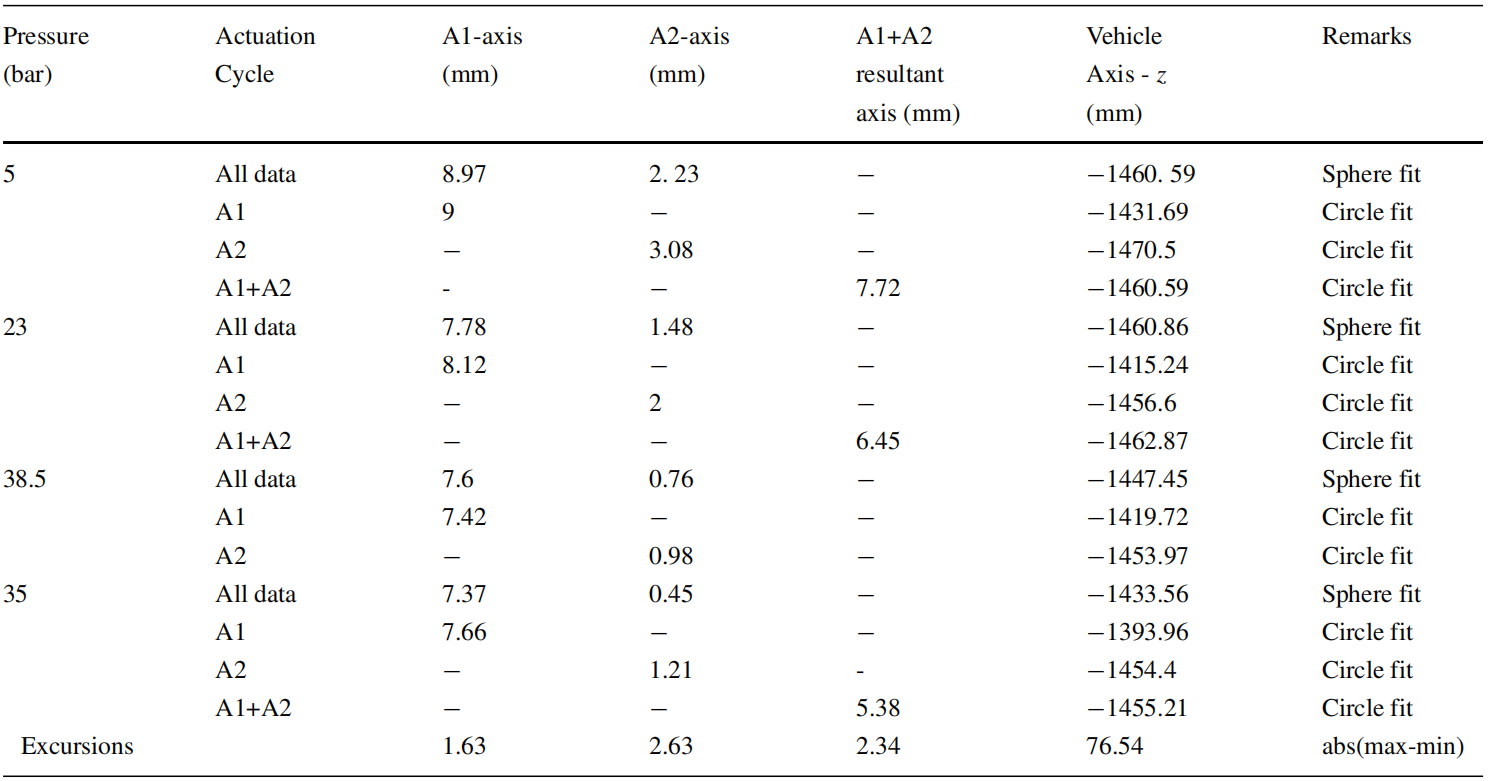
现在，表2中的偏移数据显示，x_p和y_p坐标的偏移小于2 mm，而z_p和r的偏移小于30 mm。枢轴半径 ‘r’（ 将枢轴点连接到参考点的线是枢轴半径;从切割侧见图 7。）测量值在设计范围内，看到的偏移比预期的要小得多。为了估计极端偏移，轨迹数据在A1、A2和A1-A2中，使用LLS算法分别考虑圆拟合的驱动周期，并按表 3.报告的单个驱动数据估计偏移，为了补偿A1和A2平面的偏移，表3考虑了平面内x和y数据的结果，以使其与执行器平面对齐。可以看出，平面内偏移对偏移的影响可以忽略不计。A1、A2 和 A1-A2 组合平面的偏移小于 3 毫米，而轴向偏移增加到近 77 毫米。然而，通过这些对枢轴点偏移的严格估计，其幅度小于80 mm，与[23]中报告的值相当。轴坐标的偏移约为枢轴半径的 5% 由于柔性密封的结构限制，这种偏移对于基于 FNS 的喷管是可以接受的 此外，在设计过程中，这种小的偏移已经在喷管的动态包络中得到解决。

驱动角度的估计

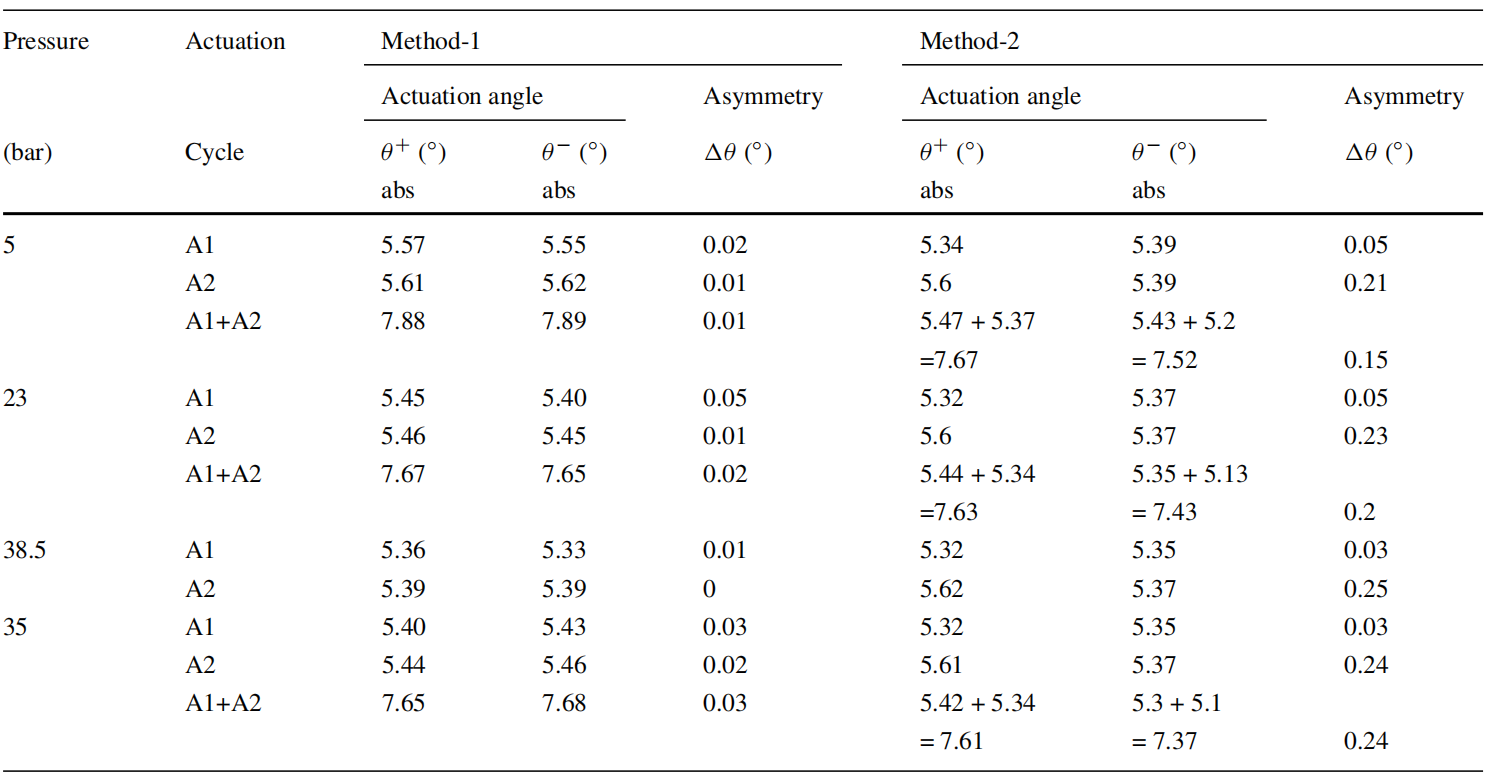
现在，由于已经掌握了枢轴点、假喷管位移的极值和参考点等信息，因此可以使用公式（9）给出的方法-1来估计驱动角度。同样，如公式（10）给出的方法-2中所述的假喷管倾斜的直接测量可以从全场数据中估计出来。表4报告了两种方法测量的驱动角度。在此表中，显示了每个执行器在不同压力下的向前和向后行程的数据。从方法记录的最大角度不对称-1 为 0.05°，小于单侧行程的 1% 然而，方法 2 的不对称性在一定程度上较大（0.25 度），相当于单侧行程的 4.4%。此外，表 4 显示，随着腔室压力的增加，驱动角度呈减小趋势，根据方法 1（35 bar 时除外）。从方法 2 中看不到这种趋势，并且在所有腔室压力下，该方法的驱动角度几乎是可重复的。由于测试是在角度控制模式下进行的，因此预计驱动角度不会有任何变化。使用方法 1 看到的趋势是用于计算角度的公式 （9） 所固有的。此公式使用枢轴点和其中的参考点坐标。这些坐标在所有压力下都不会保持不变。此外，枢轴点作为浮点显示较大的偏移。因此，方法2为直接方法，在估计驱动角度时更为可取。

使用表 4 中的方法 2 获得的执行器角度小于预期的 5.5° 执行器角度。必须注意的是，对于闭环反馈控制，使用了两个相距 90° 对准执行器的倾角仪的数据。这些倾角仪从假喷管的轴线偏移，并放置在 3-D DIC 测量值下方 1 米处的平台上。由于倾角仪是控制执行器的唯一选项，因此从该测量中获取的反馈实际上可能无法反映实际的矢量角度。这种反馈控制也会影响执行器的行程，如下一节所述（表5）。DIC 测得的驱动角度几乎与喷管的轴线重合，在 A1 和 A2 轴的角度中显示出一些缺陷和不对称性。因此，在未来的测试中，可以使用DIC数据来解决这一缺陷。

表3 不同腔室压力下的枢轴点坐标以及每个坐标的偏移（显示在最底部行）

估计喷管运动的对称性

由于测试是在角度控制模式下使用倾角仪反馈进行的，因此预计这将对FNS的行程对称性产生影响，如上一节所述。需要注意的是，与用于此目的的 LVDT 不同，DIC 数据无法直接测量执行器行程。但是，由于 DIC 正在跟踪虚拟喷管的实际运动，因此可以从该运动中解释行程对称性。为了理解这种行为，比较了 DIC 参考点的实际位移 （d±） 和放置在执行器上的 LVDT 的直接行程 （s±），用于向前和后向行程。

表4 在执行器向前和向后行程期间，使用方法-1和方法-2在不同压力下获得的驱动角度

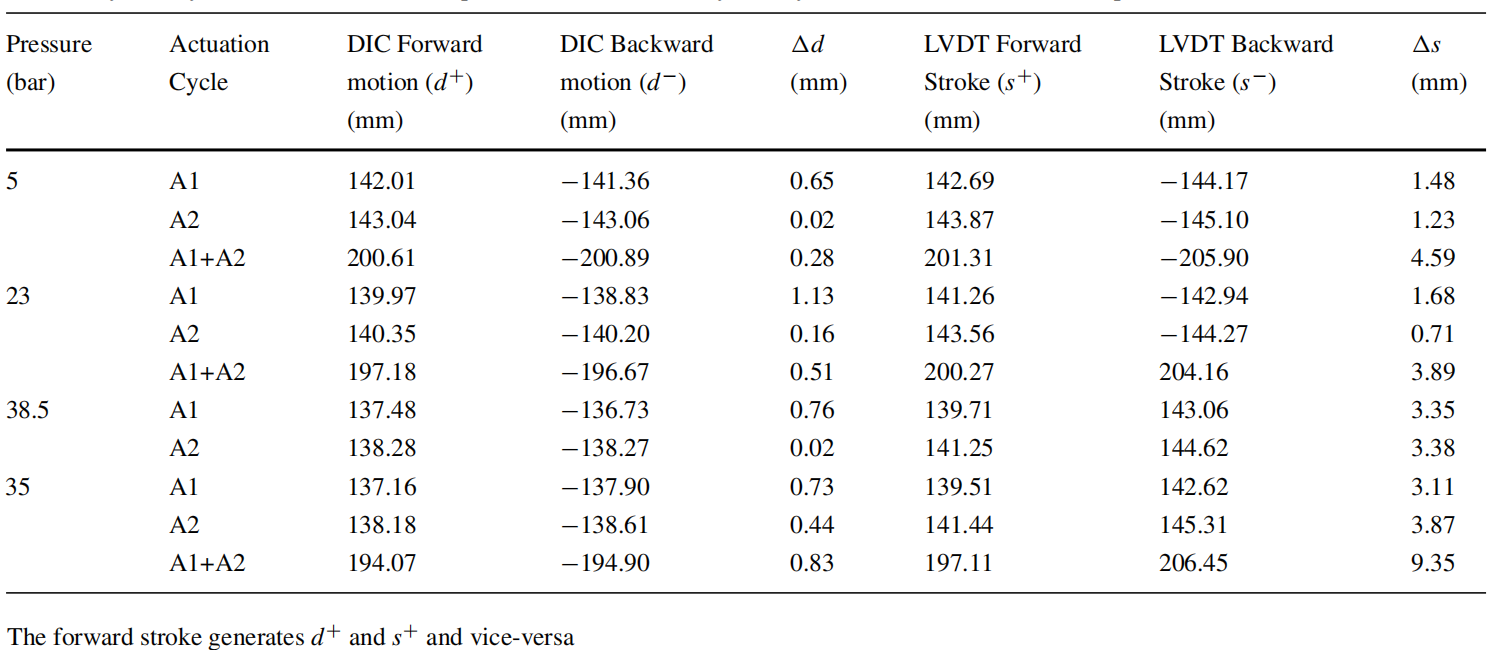
表5 不同压力下测得的喷管运动对称性（d±，公式（12））和冲程对称性（LVDT）

使用公式（12）对不同压力下的每个执行器测量的DIC测量运动进行估计。DIC数据和LVDT数据如表5所示。

1.13 mm（单侧运动的不到 1%），而从 LVDT 测量的直接行程显示出更大的不对称性。冲程中的这种行为可能是由于角度控制驱动、执行器安装不对称以及 LVDT 与执行器轴线的轻微错位造成的。尽管如此，DIC测量的喷管运动显示出更好的对称性，并为FNS的设计和功能提供了更多的信心。上一节中报告的驱动角度数据也很好地证实了喷管运动的对称性

从表5可以推断出，喷管位移（d=）比从 LVDTs.It 测量的执行器行程（s±）小2 mm至3 mm，必须注意的是，使用DIC测量的枢轴半径略小于1500 mm，而执行器轴距枢轴点的距离为1500 mm（图2）。假喷管上的参考点本身就会在径向位置产生这样的缺陷，这导致了上述观察结果。除了这个推论之外，DIC位移类似于执行器的行程。

结束语

成功地利用立体三维DIC系统估计了FNS系统的性能参数，即

（i）枢轴点偏移，

（ii）驱动角度；

（ii）单一设置中喷管运动的对称性。

估计上述参数所需的主要数据之一是枢轴点的坐标。为此，本文开发了一种涉及线性最小二乘法（LLS）的程序。利用仿真轨迹数据验证了开发的程序，并量化了实验不确定性。此过程用于在喷管模拟器上查找枢轴点和枢轴半径从参考点轨迹的偏移。枢轴半径和枢轴点轴坐标的偏移分别小于30 mm（<2%）和80 mm（<6%）。同样，驱动角度和喷管运动的不对称性小于1%。本文估计的枢轴点偏移与[23]一致，但所提出的程序比参考文献[23]简单得多。此外，在文献[23]中，只报告了枢轴点偏移，而没有确定枢轴点的实际坐标或枢轴半径。仅从一个 3-D DIC 设置中获取许多性能参数的工作简化了仪器方案。

此处报告的性能参数为FNS的设计和配置提供了信心。使用立体 3-D DIC 系统和简单的算法使测量更简单、更快速 此外，3-D DIC 设置可以提供虚拟喷管的轴向升程作为附加数据。因此，它提供了一个范围，可以通过用 DIC 替换轴向 LVDT 来简化现有测试协议。此外，将来将尝试提供来自 DIC 的实时驱动角度作为控制喷管驱动装置的输入。因此，所提方法有望克服现有方法中仪器的复杂性、数据减少的困难和工时要求。计划遵循拟议的程序来表征未来的 FNS，以减少测试期间的仪器要求。

参考文献

1.Woodberry RFH(1975)Fexible joints for thrust vector controls, AIAA and SAE 11th Propulsion Conference,Anaheim,California AIAA-75-1221

2.KobalterGFFexible nozzle fora thrust vector control system,US Patent No-US3860134 A

3.Nagappa R,Kurup MR,Muthunayagam AE(1989)ISRO’S solid rocket motors.ActaAstronaut 19(8):681-697

4.Report NASA(1974)Solid rocket thrust vector control NASA- SP-8114

5.Donat JR(1993)Solid rocket motor nozzle flexseal design sen- sitivity,AIAA,AHS,and ASEE,Aerospace Design Conference Irvine,California AIAA-93-1122

6.YongbinZ(2007)Discussion on control precision of single swing nozzle.Mod Def Technol 35(3):54-57

7.Sutton MA,Orteu JJ,Schrier HW (2009)Image correlation for shape,motion and deformation measurement.Springer,USA

8.Bomert M,Hild F,Orteu JJ,Roux S (2012)Digital Image Correlation.In:Grediac M,Hild F,Pineau A (Eds)Full-Field Measurements and Identification in Solid Mechanics.Wiley- ISTE,chapter 6,pp 157-190

9.Peters WH,Ranson WF(1982)Digital image techniques in experimental stress analysis.Opt Eng 21(3):427-431

10.Peters WH,Ranson WF,Sutton MA,Chu TC,Anderson J

(1983)Application Of DigitalCorrelationMethods To RigidBody Mechanics.OptEng 22(6):226738

11.Kahn-Jetter ZL,Chu TC(1990)Three-dimensional displacement measurements using digital image correlation and photogrammet- ric analysis.Exp Mech 30(1):10-16

12.Luo PF,Chao YJ,Sutton MA,Peters WH(1993)Accurate measurement of three-dimensional deformations in deformable and rigid bodies using computer vision.Exp Mech 33(2):123- 132

13.Cardenas-Garcia JF,Yao HG,Zheng S(1995)3D Reconstruction of objects using stereo imaging.Opt Lasers Eng 22(3):193-213

14.Helm JD,McNeill SR,Sutton MA(1996)Improved three- dimensional image correlation for surface displacement measure- ment.Opt Eng 35(7):1911-1920

15.Sutton MA,McNeill SR,Helm JD,Chao YJ(2000)Advances in two-dimensional and three-dimensional computervision.In: Rastogi PK(ed)Photomechanics.Springer,Berlin Heidelberg, pp 323-372

16.OrteuJJ (2009)3-D Computervision in experimental mechanics Opt Lasers Eng 47(34):282-291

17.Quan C,Tay C,Sun W,He X(2008)Determination of three- dimensional displacement using two-dimensional digital image corelation.Appl Opt47(4):583-593

18.Xia S,Gdoutou A,Ravichandran G (2013)Diffraction assisted image correlation:a novel method for measuring three- dimensional deformation using two-dimensional digital image correlation.Exp Mech53(5):755-765

19.PanB,Yu LP,Zhang QB(2018)Review of single-camera stereo- digital image correlation techniques for full-field 3D shape and deformation measurement.Sci China Tech Sci61(1):2-20

20.Li J,Dan X,Xu W,Wang Y,Yang G,Yang L (2017)3D Digital image correlation using singlecolor camera pseudo-stereosystem Opt Laser Technol 95:1-7

21.Li J,Zhang B,Kang X,Xu W,Yang G,Yang L(2018)Single camera 3D digital image correlation using a polarized system Instrum Exp Tech61(1):99-105

22.Zhong FQ,Shao XX,QuanC(2018)3D digital image corelation using a single 3-CCD colour camera and dichroic filter.Measur Sci Technol29(4):045401

23.Gaffin RD(1977)Space shuttle solid rocket booster nozzle flexible seal pivot point dynamics,AIAA/SAE 13th Propulsion Conference,Forida,AIAA-P-77-986

24.Yoo JS(2010)First Korea space launch vehicle kick motor movable nozzle motion.J Space Craft Rocket 47(1):153-168

25.Zhang LF,Guo YB,Chen G,Ye D,Chen RS(2010)Estimation of nozzle axis and vector angle by infrared photoelectric measurement technology.J Harbin Inst Technol 42(1):24-28

26.Seely J,TorickR,Mascio W(1990)Nozzlevector angledetermina- tion using a laser measurement system,AIAA/SAE/ASME/ASEE 26th Joint Propulsion Conference,Orlando,Forida,AIM-90-2082

27.ZhangCF,TangWY,LiHP,Wang J,Chen JC(2007)Application of lasertracker to thrust line measurement of solid rocket motor.J Solid Rocket Technol 30(6):548-551

28.Guo Y,Chen G,Ye D,Yu X,Yuan F(2013)2-DOF angle measurement of rocket nozzle with multivision,Advanced Mechanical Engineering,ArticleID942580.Hindwai Publication Cairo.https:/doi.org/10.1155/2013/942580J

29.Qu Y,Yang H(2015)High-speed measurement of nozzle swing angle of rocket engine based on monocular vision,Ninth International Symposium on Precision Engineering Measurement and Instrumentation.Proc SPIE9446(1-9):944647

30.Guo Y,Ye D,Chen G,Yuan F(2012)Binocular vision-vased measurement for motion parameters of rocket nozzle.Appl Mech Mater 220-223:1056-1061

31.Wang X,Tan J,Zhao Q,Ling Q(2015)Computer vision-based swing center testing method for flexible joint,Seventh Interna- tional Symposium on Precision Mechanical Measurements.Proc SPIE 9903(1-7):990320

32.VIC3D and VICSNAP The 3-D DIC commerical code and the image cpaturing software,Supplied byM/s Correlated Solutions, USA

译自：

Experimental Techniques (2019) 43:429–443，https://doi.org/10.1007/s40799-018-0282-x