固体发动机喷管扩散段内部型面一维优化设计探讨

本文在一维两相平衡流动理论基础上，对于一组给定设计参数，根据提高质量比、减少扩散损失的最佳化工程准则，分析确定使喷管扩散段长度最短的内部优化型面为一特定系数的三次多项式。同现有儿种典型的喷管相比，若推力和扩散损失相同，其扩散段长度要短11.9～17.3%,扩散段拐点至出口重量约轻14.2～21.1%。本文提出的优化型面在大的和高膨胀比特别是长度受到限制的喷管上使用，更具有其实用价值。

符 号

v₀ ——燃气出口速度

g ——重力加速度

ξ ——膨胀比

\(\dot m\) ——秒流量

F ——推力

C_F ——推力系数.

I_sp——比 冲

μ ——质量比

R_eq——两相平衡流气体常数

K _eq——两相平衡流气体比热比

T ——温度

P ——压力

ε ——扩散损失

W ——喷管扩散段部分重量

L ——喷管扩散段沿轴向长度

γ ——材料比重

δ ——材料厚度

y ——喷管扩散段内部型面表达式，径向坐标

x ——轴向坐标

A ——面 积

r——半径

r_td——喉部下游壁面曲率半径

η₁，η₂，…，η_i——长度系数

α_M——特型喷管初始膨胀半角

α_co——锥形喷管初始多胀半角

d₁,…;d_4——待定系数

b₁,…,b₄——待定系数

C₁,…,C₄——待定系数

d₄₁,…,d_4i——待定系数

上 标

— 相对值

‘ 一阶导数

下 标

c——燃烧室

e、e₂——出口或端部

a—— 环境

t—— 喉部

co——锥形

d ——双圆弧

P ——抛物线

tw ——二次多项式

th ——三次多项式

i——扩散段拐点

opt ——优 化

em——等效平均

1 ——绝热层

2——外 壳

/ 表示之比

—表示从某处到某处

一、引言

在固体发动机中，喷管和燃烷室一样，是组成发动机最主要的部件之一。高温燃气在喷管内膨胀流动，把燃气的热能转变成动能，高速喷出而产生推力。因此，喷管设计的好坏对燃气流动影响很大，直接关系到喷管效率和推力大小。所以，喷管扩散段内部型面的没计在整个喷管设计中占有极为重要的地位。

在含铝固体推进剂中，金属粉末经燃烧后形成金属氧化物，由于它的气化温度很高，所以在燃烧室的温度、压力条件下，它以凝聚相形态存在。因此，燃烧产物实际上是含有气体和凝相这两种物质的两相流动。两相流动是一个很复杂的过程。鉴于目前二维两相流动计算尚不能用于喷管设计，因而现有喷管设计仍以一维流动理论为基础，由此可得出发动机性能及推进剂特性与发动机设计之间的关系，并为计算及比较所有类型的火箭发动机性能提供了基础[1]。为了近似地考虑非一维流动及其它多种因素的影响，可通过引入修正因子的方法来改善一维流动理论所得到的结果。比如，计及非一维流动的扩散损失、化学不平衡损失、两相流滞后损失、喷管潜入损失及与边界层有关的传热和摩擦损失[2],就能在一维两相平衡流动理论基础上较准确地予示喷管的推力和比冲等各种性能参数。

二、喷管流动及性能参数

假定燃气为一维两相平衡等熵定常流动，则根据热力学和流体力学不难推得有关喷管流动及性能参数的下列公式[1]:

燃气出口速度

\( {v}_{e}=\sqrt{2g \frac{{K}_{eq}}{{K}_{eq}-1} {R}_{eq} {T}_{c} \left[ 1-{\left( \frac{{P}_{e}}{{P}_{c}}\right)}^{\frac{{K}_{eq}-1}{{K}_{eq}}} \right]}\)

膨胀比

\(\xi = \frac{{A}_{e}}{{A}_{t}}=\frac{\sqrt{\frac{{K}_{eq}-1}{{K}_{eq}+1}}{\left( \frac{2}{{K}_{eq}+1}\right) }^{\frac{1}{{K}_{eq}-1}}}{\sqrt{\left[ {\left( \frac{ {P}_{e}}{{P}_{c}} \right)}^{\frac{2}{{K}_{eq}}}-{\left(\frac{ {P}_{e}}{{P}_{c}} \right) }^{\frac{{K}_{eq}+1}{{K}_{eq}}}\right]}} \)

秒流量

\( {\dot m}=\sqrt{{K}_{eq}}{\frac {2}{{K}_{eq}+1}}^{\frac{{K}_{eq}+1}{2{K}_{eq}-1}} \sqrt{g} \frac{{P}_{c}{A}_{t}}{sqrt{{R}_{eq}{T}_{c}}}\)

推力

\( F=\frac{{\dot m}{V}_{e}}{g}+{A}_{e}{{P}_{e}-{P}_{a}} \)            (4)

推力系数

\({C}_{F}={\frac{2}{{K}_{eq}+1}}^{\frac{1}{{K}_{eq}-1}}\sqrt{\frac{{K}_{eq}-1}{{K}_{eq}+1}} \left\{ \frac{2{K}_{eq}}{{K}_{eq}-1} \sqrt{1-{\left( \frac{{P}_{e}}{{P}_{c}} \right)}^{\frac{{K}_{eq}-1}{{K}_{eq}}}}+\frac{{\left( \frac{{P}_{c}}{{P}_{e}}\right)}^{\frac{1}{{K}_{eq}}}}{\sqrt{1-{\left( \frac{{P}_{c}}{{P}_{e}} \right)}^{\frac{{K}_{eq}-1}{{K}_{eq}}}}}\left( \frac{{P}_{e}-{P}_{a}}{{P}_{c}} \right) \right\}\)             (5)

比冲

\({I}_{sp}=\frac{{V}_{e}}{g}+\frac{{A}_{e}}{\dot m} \left( {P}_{e}-{P}_{a}\right)\)        (6)

扩散攒失[2]

\(\varepsilon=\frac{1-\cos \frac{(\alpha+{\theta}_{e})}{2}}{1}\)           (7)

三、现行设计常用的扩散段内部型面

按照总体要求，依据一维两相平衡流理论可确定膨胀比及喷管喉部几何尺寸，进行喷管设计。喷管入口型面通常选用椭圆和锥形，喉部多用圆弧加圆柱段，其下游壁面曲率半径的选取往往受喷管摆动角度、具体结构的限制，根据经验，一般取喉部半径的一至二倍左右，视具体情况而定。至于初始膨胀半角，锥形喷管一般取15°～30°,特型喷管大约是20°～24°[3]。在上述诸参数选定之后，关键就是如何合理地选择并确定喷管扩散段的内表面的形状。

从喷管扩散段的内部型面来看，基本上可以分为两种：一种是锥形的，另一种是特型的，也称特性喷管，其扩散段的母线是曲线型的。曲面形状设计方法较多，其实质都是依据燃气流经扩散段形成超音速气流的流线外边界来确定。这种形状象钟的喷管，其扩散半角从喉部处的大约35°连续地变到出口处的10°左右。气流通过喉部后，急速膨胀，而后又使气流转向轴向流动，以减小径向分速损失，所以特型喷管具有效率高和重量轻等优点。

锥形喷管构造简单，容易制造，但扩散损失较大，所以通常用在小型发动机上；对于大的和高膨胀比的发动机，则要采用特性喷管。目前，由于二维两相流计算方法尚未用于喷管设计，故现行喷管扩散段设计多采用双圆弧或近似作图法求得的抛物线内部型面，可以缩短喷管长度，减轻结构重量。

四、扩散段内部型面的优化设计

众所周知，只有当任务规定之后，发动机的最佳化才能以一种合理的方式实现。在某一给定任务范围内，可以考虑多种不同的最佳化准则，如象质量载荷对起飞总质量之比\(u={m}_{u}/{m}_{D}\)(工程准则),或质量载荷对工作全部耗资的最大比\(u={m}_{u}/c\)(经济准则)。按照所用准则之不同，最佳化系统便不同[1]。

通常在衡量发动机的性能时，有一个重要的综合指标，就是发动机单位重量所获得的冲量，即所谓冲量重量比

\(\frac{I}{{W}_{m}}=\frac{{I}_{sp}{W}_{p}}{{W}_{m}}={I}_{sp}\mu\)

显而易见，要设计高质量高水平的发动机，必须努力减少结构重量，提高质量比；减少扩散等损头，增大比冲，这是本文述及的喷管扩散段内部型面优化设计所依据的工程准则。前面亦已提过，在大的和高膨胀比的发动机上采用双圆弧或近似作图法求得的抛物线型喷管，可以缩短长度，减轻结构重量。现在的问题是，在喷管的膨胀比、喉部半径、喉部壁面曲率半径、初始膨胀半角、出口半角等一组参数皆确定的情况下，是否可以用其它型面的扩散段代替双固弧或抛物线型扩散段，进一步缩短喷管长度、减轻结构重量?这就是本文所要探讨的问题。

在最佳性能问题上，热交换、化学不平衡和喷管的烧蚀是可以忽略的，扩散和两相流的共同作用明显地影响喷管的效率和设计[3]。本文已假定为一维两相平衡流动，故对欲比较的诸喷管来说，在推力和扩散损失相同条件下求得最短长度的喷管作为优化喷管则是本文的目的。为此，将下面五种可供选择的扩散段型面的喷管长度进行比较，就能分析求得优化的喷管扩散段内部型面。

可供选择的喷管扩散段型面有：

锥形喷管

\({y}_{co}={a}_{1}+{b}_{1}x\)                     (8)

抛物线喷管

\({y}_{p}={a}_{2}+\sqrt{{b}_{2}(x-{c}_{2})}+{y}_{0}\)            (9)

双圆弧喷管

\({}_{}=\sqrt{{r}^{2}-{(x-{x}_{0})}^{2}}\)            (10)

二次多项式喷管

\({y}_{tw}={a}_{3}+{b}_{3}x+{c}_{3}{x}^{2}\)                 (11)

三次多项式喷管

\({y}_{th}={a}_{4}+{b}_{4}x+{c}_{4}{x}^{2}+{c}_{5}{x}^{3}\)                 (12)

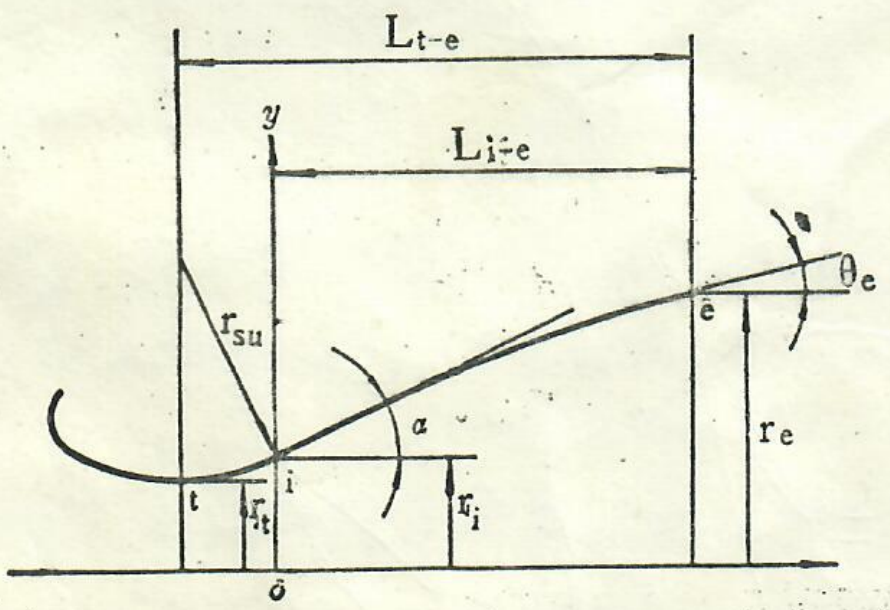
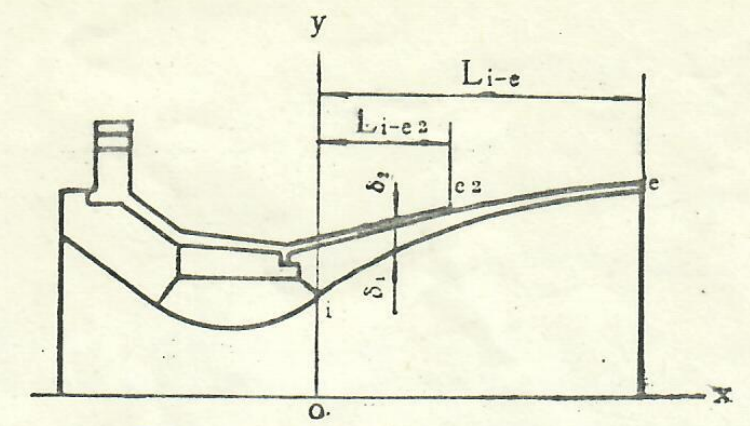
式中诸待定系数由给定的边界条件来确定，参数定义如图1所示。

图1特型喷管扩散段内部型面示意图

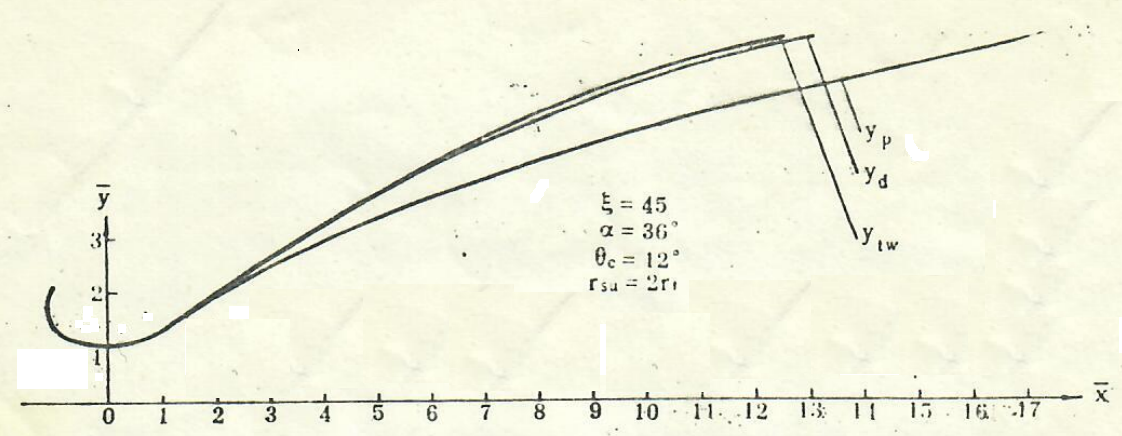
图2为喷管喉部半径、喉部下游壁面曲率半径、初始膨胀半角、出口半角皆相同情况下地物线、二次多项式、双圆弧喷管内部型面示意图。当α=36°及θe=12°时，若采用二次多项式扩散段型面，可较双圆弧缩短5.18%。

图2抛物线，二次多项式与双四弧扩散段内部型面的比较

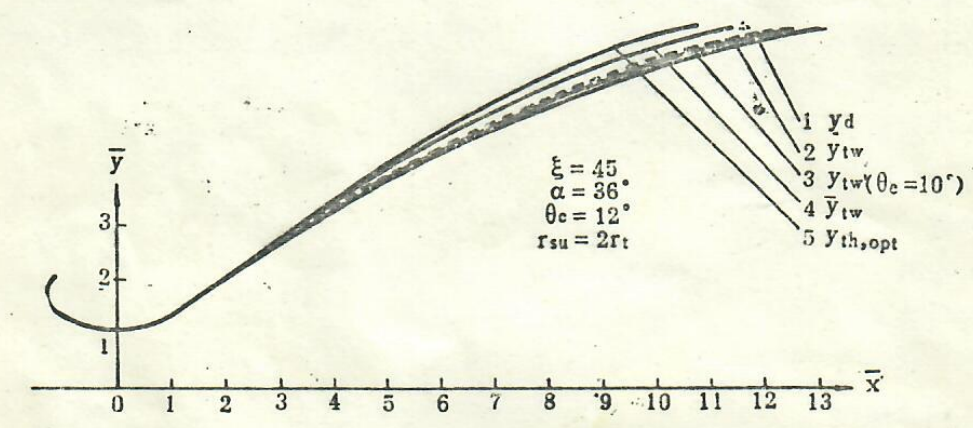
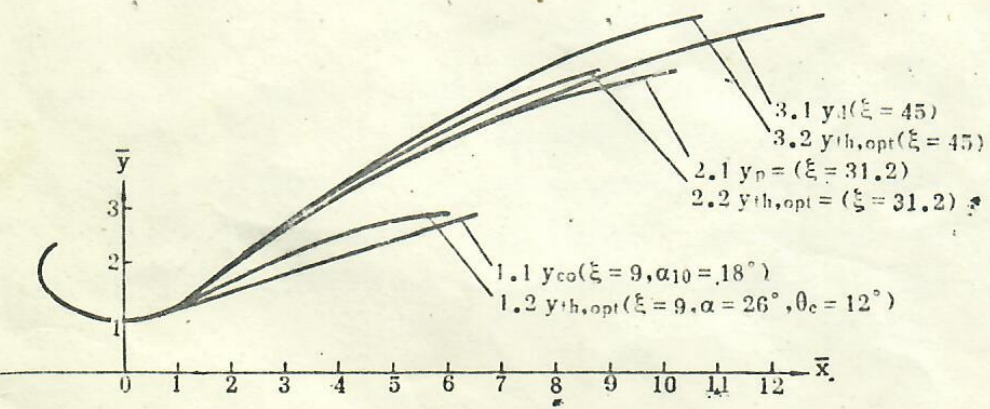
图3为喷管喉部半径、喉部下游壁面曲率半径、初始膨胀半角、出口半角皆相同情况下三次多项式、二次多项式、双圆弧扩散段内部型面示意图。若扩散段长度相同，三次多项式扩散段的出口半角可选取的比二次多项式扩散段的出口半角小一些，于是扩散损失也就小一些。图3中的虚线即为0e=10°的三次多项式扩散段内部型面。

图3二，三次多项式，双圆弧与优化扩散段内部型面的比较

在出口半角相同情况下，为了缩短喷管长度，三次多项式扩散段的长度应尽可能地选取较二次多项式的短一些，但又不能太短，避免使型面过度弯曲而增大扩散损失。据此可推导求得三次多项式扩散段型面拐点至出口的最短长度为3(r_e-r_i)/(2tgα+tgθ_e),此长度对应的型面即为所求的优化型面(见附录):

\({\bar {y}}_{th,opt}=1+{\bar r}_{su}(1-\cos \alpha)+\text{tg} \alpha {\bar x}-\frac{(\text{tg} \alpha -\text{tg} {\theta}_{e}){(2\text{tg} \alpha +\text{tg} {\theta}_{e})}^{2}}{27{\left[ \sqrt{\xi}-1-{\bar r}_{su}(1-\cos \alpha) \right]}^{2}}{({\bar x})}^{3}\)                (13)

图3中的曲线5就是给定条件下的优化型面。为了便于比较，在图中还同时给出η=0.9的三次多项式型面和二次多项式及双圆弧型面。

五、优化型面与几种常用扩散段型面的比较

1.喷管扩散段拐点至出口长度的比较

根据诸扩散段型面表达式和优化型面喷管的长度，易推得下列诸表达式：优化三次多项式型面与锥形长度之比为

\({L}_{th,opt/co}=\frac{{L}_{th,opt}}{{L}_{co}}=\frac{3 \text{tg} {\alpha}_{co} [\sqrt{\xi}-1+{\bar r}_{su}(\cos \alpha -1)]}{(2 \text{tg} \alpha +\text{tg} {{\theta}_{e}} )[\sqrt{\xi}-1+{\bar r}_{su}(\cos {\alpha}_{co} -1)]}\)     (14)

优化三次多项式型面与抛物线型面长度之比为

\({L}_{th,opt/p}=\frac{{L}_{th,opt}}{{L}_{p}}=\frac{6 \text{tg} \alpha+\text{tg}{\theta}_{e}}{(2 \text{tg} \alpha+\text{tg}{\theta}_{e})( \text{tg} \alpha+\text{tg}{\theta}_{e})}\)   (15)

优化三次多项式型面与双圆弧型面长度之比为

\({L}_{th,opt/d}=\frac{{L}_{th,opt}}{{L}_{d}}=\frac{3(\cos {\theta}_{e}-\cos \alpha)}{(2 \text{tg} \alpha+\text{tg}{\theta}_{e})( \sin \alpha+\sin {\theta}_{e})}\)   (16)

优化型面与二次多项式型面长度之比为

\({L}_{th,opt/tw}=\frac{{L}_{th,opt}}{{L}_{tw}}=\frac{3(\text{tg} \alpha+\text{tg}{\theta}_{e})}{2(2 \text{tg} \alpha+\text{tg}{\theta}_{e})}\)   (17)

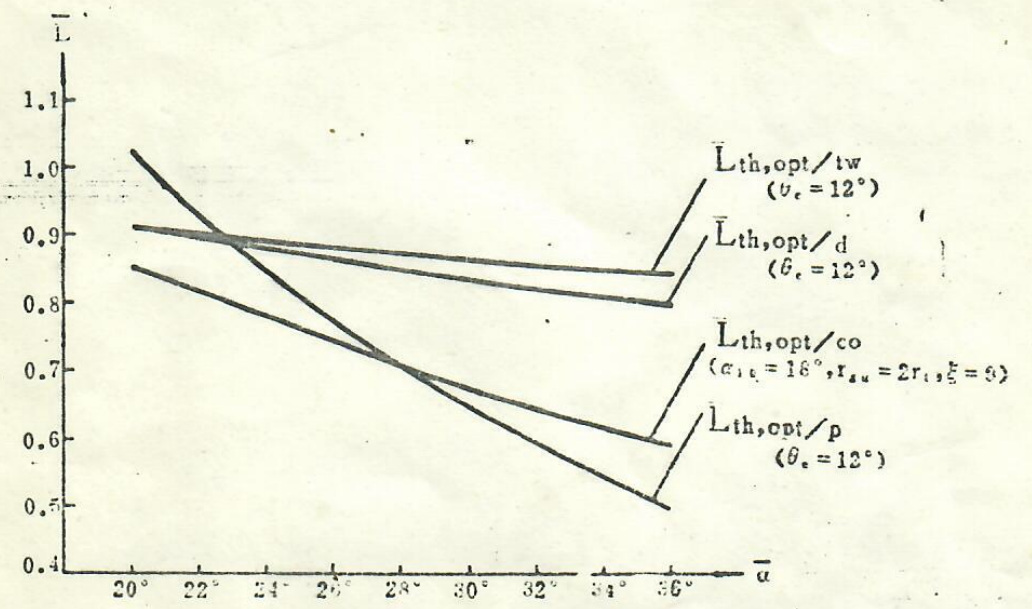
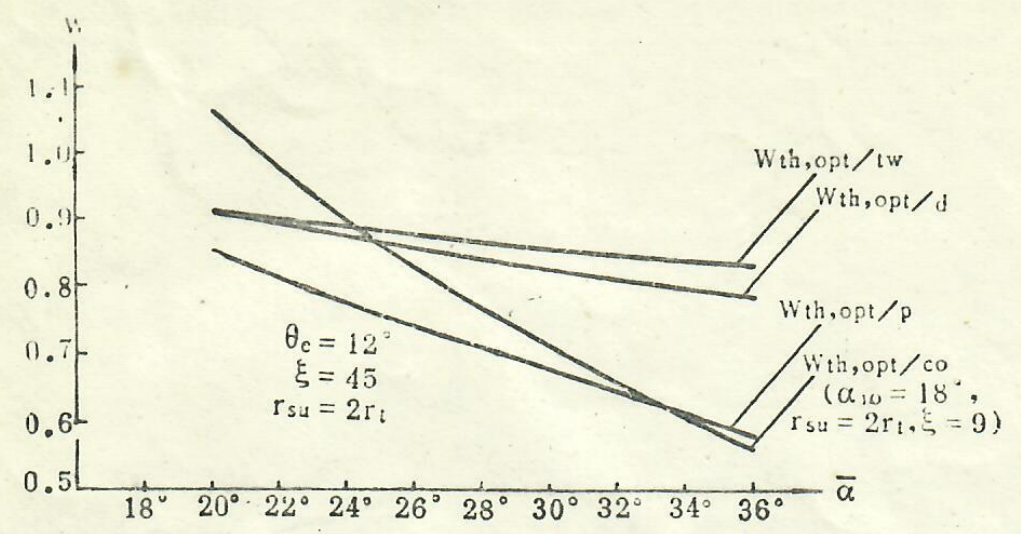
图4表明\({L}_{th,opt/co},{L}_{th,opt/p},{L}_{th,opt/d},{L}_{th,opt/tw}\) 随初始膨胀半角α的变化情况，皆随α增加而减少，在任何情况下其值都小于1(对于锥形喷管，α应大于20.5°),进而说明优化三次多项式型面喷管扩散段长度是最短的。

图4优化型面与儿种常用型面扩散段拐点至出口长度的比较

2.喷管扩散段拐点至出口重量的比较

欲精确地比较喷管的重量，须待具体方案确定之后才好进行。现在，为了便于说明问题，我们采用下面近似方法进行比较。

如图5所示，喷管扩散段拐点至出口重量为：

图5计算扩散段重量用的喷管结构示意图

\(W={\rho}_{1}\pi \int\limits_{0}^{{L}_{i-e}}{\left[ {(y+{\delta}_{1})}^{2}-{y}^{2}\right] dx}+{\rho}_{2}\pi \int\limits_{0}^{{L}_{i-e2}}{\left[ {(y+{\delta}_{1}+{\delta}_{2})}^{2}-{(y+{\delta}_{1})}^{2}\right] dx}\)

\(={{\rho }_{1}}\pi \int\limits_{0}^{{{L}_{i-e}}}{\left[ (2y{{\delta }_{1}}+\delta _{1}^{2}) \right]dx}+{{\rho }_{2}}\pi \int\limits_{0}^{{{L}_{i-e2}}}{\left[ 2\left( y+{{\delta }_{1}} \right){{\delta }_{2}}+\delta _{2}^{2} \right]dx}\)

\(={{\rho }_{1}}\pi \int\limits_{0}^{{{L}_{i-e}}}{\left[ (2y{{\delta }_{1}}+\delta _{1}^{2}) \right]dx}+{{\rho }_{2}}\pi \int\limits_{0}^{{{L}_{i-e2}}}{\left[ 2y{{\delta }_{1}}+2{{\delta }_{1}}{{\delta }_{2}}+\delta _{2}^{2} \right]dx}\)                  (18)

令：\({{\delta }_{1m}}=\frac{\int\limits_{0}^{{{L}_{i-e}}}{\left[ (2y{{\delta }_{1}}+\delta _{1}^{2}) \right]dx}}{\int\limits_{0}^{{{L}_{i-e}}}{2ydx}}\)

\({{\delta }_{2m}}=\frac{\int\limits_{0}^{{{L}_{i-e2}}}{\left[ 2y{{\delta }_{1}}+2{{\delta }_{1}}{{\delta }_{2}}+\delta _{2}^{2} \right]dx}}{\int\limits_{0}^{{{L}_{i-e}}}{2ydx}}\)

则：\(W=2\pi \left({\rho}_{1}{\delta}_{1m}+{\rho}_{2}{\delta}_{2m}\right) \int\limits_{0}^{{L}_{i-e}}{2ydx}\)

假定诸喷管扩散段等效平均的绝热层厚度\({\delta}_{1m}\)和等效平均外壳厚度\({\delta}_{2m}\)皆分别相等，所用材料相同，则优化型面喷管与诸喷管扩散段拐点至出口重量之比可用简化形式来表达。

与锥形、抛物型、双圆弧重量之比略。

图6表明优化型面与上述各种型面扩散段相对重量随初始膨胀半角的变化情况，可以看出，除锥形喷管外，对于任何α值都小于1;对于锥形喷管，当α大于22°时，\(\bar W\) 之值也小于1,表明优化型面扩散段较常用型面扩散段拐点至出口的重量都轻。

3.优化型面与现有三种典型喷管扩散段型面的比较

图6优化型面与几种常用型面扩散段拐点至出口重量的比较

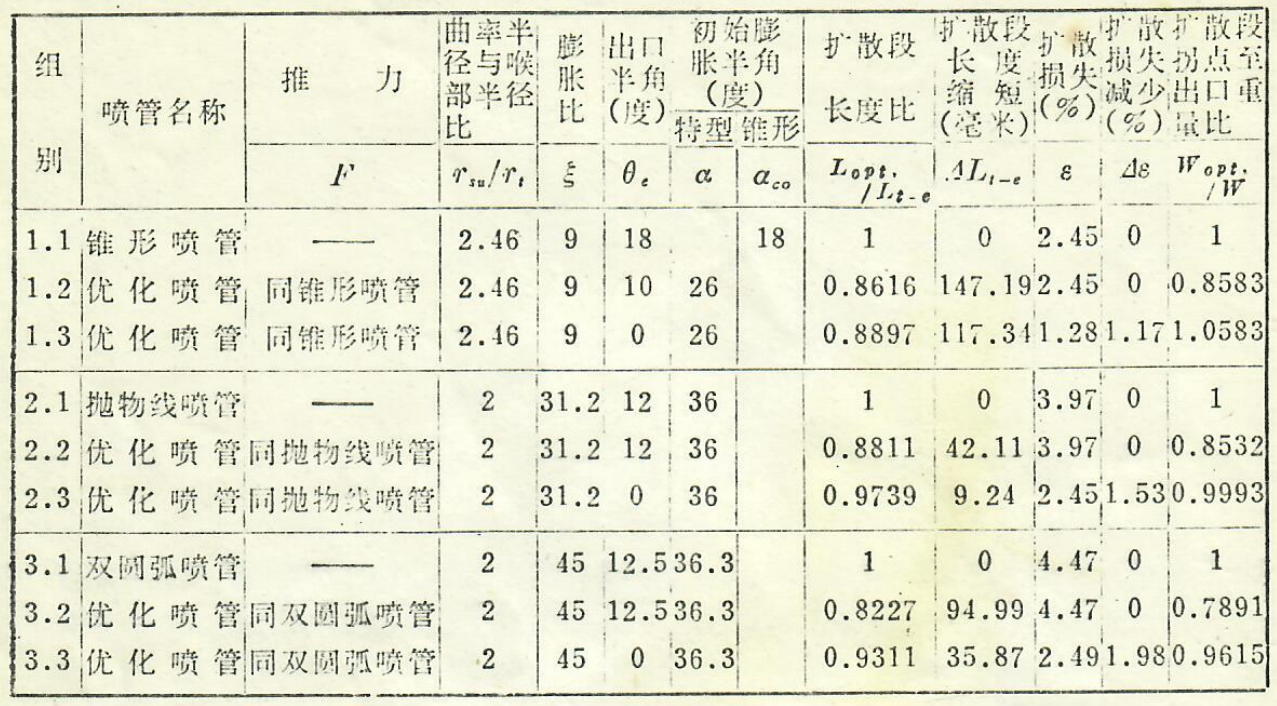
图7分别表明锥形、抛物线(近似作图法求得)、双圆弧等现有三种典型喷管与相应的优化喷管内部型面的比较情况。从图上不难看出，优化型面扩散段的长度较相应的三种典型喷管长度都要短一些。表1列出比较结果。从表中可以发现，若推力和扩散损失皆相同，对于锥形、抛物线、双圆弧喷管来说，其相应的优化型面喷管扩散段长度分别要短147,19、42.11、94.99毫米，扩散段拐点至出口的重量分别约减轻14.2%、14.7%、21.1%;若推力相同、扩散损失有所减少，则对于锥形、抛物线、双圆弧喷管来说，其相应的优化喷管扩散段的长度分别要短117.34、9.24、35.87毫米，扩散损失分别减少1.17%、1.53%、1.98%;若保持推力和扩散段长度相同，则可分别求得一组α和θe,使扩散损失最小，此型面即为优化型面，这里不一一赘述于上述喷管的优化喷管。

图7优化型面与三种典型扩散段型面的比较

表1三欠多项式优化型面喷管与三种典型喷管几何及性能参数的比较

五、结 论

1.在推力和扩散损失相同条件下，选择合适的初始膨胀半角，采用本文给出的优化型面代替锥形喷管，可获得长度最短的喷管；还可获得推力相同，而喷管长度和扩散损失皆小于锥形喷管的优化喷管。

2. 在推力和扩散损失相同条件下，采用本文给出的优化型面代替抛物线、双圆弧和二次多项式型面喷管，可获得长度最短的喷管；还可获得推力相同，然而长度和扩散损失皆小。

3.本文给出的优化型面在大的和高膨胀比喷管特别是长度受到限制的喷管上使用，更具有其实用价值。

参 考 文 献

[1] F.A.Williams x.C.Huang M. Barrere, cFuidmenta! Aspecis of SolidPrapellant Rockeisy AGAR Dograph. 116.1969.

[2] D.E.Coats,et al’cA Computer Program for the Prediction of SolidPropellant Rosket Motor Performancey VolumeⅡAD-A015141 July.1975.

[3] L.J.Jacques cGeneral Principles For the Aerodynamic Design of. SolidRocket Nozzles》AIAA Paper No. 75-1338.

论文作者：王成轩

附录: 优化三次多项式型面的确定

根据型面表达式和给定边界条件易求得:

\({L}_{i-e,tw}=\frac{2}{\text{tg}\alpha+\text{tg}{\theta}_{e}} \left({r}_{e}-{r}_{i} \right)\)

\({c}_{4}=\frac{3({r}_{e}-{r}_{i})}{{L}_{i-e,th}^{2}}-\frac{2 \text{tg} \alpha +\text{tg}{\theta}_{e}}{{L}_{i-e,th}}\)

\(d=\frac{ \text{tg} \alpha +\text{tg}{\theta}_{e}}{{L}_{i-e,th}^{2}}-\frac{2({r}_{e}-{r}_{i})}{{L}_{i-e,th}^{3}}\)

令:\(\eta=\frac{{L}_{i-e,th}}{{L}_{i-e,tw}}\)

将\({{L}_{i-e,th}}=\eta{{L}_{i-e,tw}}\)代入上式,则有:

\(d=\left(1+\frac{1}{\eta}\right)\frac{{ \text{tg} \alpha +\text{tg}{\theta}_{e}}^{3}}{4{\eta}^{2}{({r}_{e}-{r}_{i})}^{2}}\)                (1)

显然，欲缩短三次多项式扩散段的长度应取:

η_opt<…<η_i<…<η₂<η₁<1            (2)

y_th,1<y_th,2<…<y_th,i<…<y_th,opt   (x>0)     (3)

因为

\({d}_{2}-{d}_{1}=\frac{({\eta}_{2}-{\eta}_{1})[(1-{\eta}_{1}){\eta}_{2}^{2}+(1-{\eta}_{2}){\eta}_{1}^{2}+{\eta}_{1}{\eta}_{2}]{( \text{tg} \alpha +\text{tg}{\theta}_{e})}^{3}}{4{\eta}_{1}^{3}{\eta}_{2}^{3}{({r}_{e}-{r}_{i})}^{2}}<0\)

所以

\({d}_{2}<{d}_{1}\)

同样有

d_opt<…<d_i<…<d₂<d₁

可因为由(3)得

\({y}_{th,2}-{y}_{th,1}=({c}_{4,2}-{c}_{4,1})x+({d}_{2}-{d}_{1}){x}^{3}>0\)

但

\({d}_{2}-{d}_{1}<0\)

所以

\({c}_{4,2}-{c}_{4,1}>0\)

同样有:

_C4,1<c_4,2<…<c_4,i<…<c_4,opt            (5)

然而,优化三次多项式型面扩散段的长度又不能取得太短,以避免型面过度弯曲而增大扩散损失。根据这一要求,应使曲线斜率

\({y}_{th}{‘} \le \text{tg} \alpha ,   (x \ge 0)\)

这就保证型面上任一点的扩散损失皆不大于初始路胀处的扩散损失,α根据目前设计惯例选取。据此即有：

\(\text{tg}\alpha+2{c}_{4,opt}x+3{d}_{opt}{x}^{2} \le \text{tg} \alpha\)

即

\(2{c}_{4,opt}+3{d}_{opt}{x} \le 0\)

但由式(2)、(1)得

\({d}_{opt}<0\)

所以

\({c}_{opt} \le 0\)

又据式(5),应取:

\({c}_{4,opt}=0\)

则

\({L}_{i-e,th,opt}=\frac{3}{2\text{tg}\alpha-\text{tg}{\theta}_{e}}{({r}_{e}-{r}_{i})}\)

由此可得到优化三次多项式型面的表达式为:

\({\bar {y}}_{th,opt}=1+{\bar r}_{su}(1-\cos \alpha)+\text{tg} \alpha {\bar x}-\frac{(\text{tg} \alpha -\text{tg} {\theta}_{e}){(2\text{tg} \alpha +\text{tg} {\theta}_{e})}^{2}}{27{\left[ \sqrt{\xi}-1-{\bar r}_{su}(1-\cos \alpha) \right]}^{2}}{({\bar x})}^{3}\)

\({\bar {y}}_{th,opt}=\frac{{y}_{th,opt}}{{r}_{t}}=1+{\bar r}_{su}(1-\cos \alpha)+\text{tg} \alpha {\bar x}-\frac{(\text{tg}\alpha-\text{tg}{\theta}_{e}){(2\text{tg}\alpha+\text{tg}{\theta}_{e})}^{2}}{27{\left[ \sqrt{\xi}-1-{{\bar r}_{su}}(1- \cos \alpha) \right] }^{2}}{(\bar {x})}^{3}\)

式中：\({\bar r}_{su}=\frac{{r}_{su}}{{r}_{t}}, {\bar x}=\frac{x}{{r}_{t}}\)