固体火箭发动机燃烧不稳定研究进展与展望
围绕固体火箭发动机燃烧不稳定的研究现状及未来发展趋势进行了探讨 。为了深入认识固体火箭发动机中的燃烧不稳定现象 ,并形成对其进行准确预示和有效抑制的方法 , 需要解决理论 、计算及实验多方面的基础问题 :燃烧不稳定的物理机制 ,不稳定的预示方法 ,发动机中各种增益和阻尼因素的特征 ,振荡增长过程中触发和极限环形成的机理 ,不稳定抑制技术及地面实验的等效分析方法 。最后给出了总结与建议 , 明确了固体火箭发动机燃烧不稳定研究的目标和方向。
1 引 言
尽管固体火箭发动机作为航天发射助推器或各类武器主动力的成功应用已经超过 50 年 ,但大型分段发动机 、各种尺度的战术导弹发动机都曾被燃烧不稳定困扰[1-5],燃烧不稳定问题始终是工业界和学术界面临的严峻挑战 。 固体推进剂组元众多 ,反应复杂 ;燃烧在高温 、高压下进行 ,气相燃烧在近表面1mm 内 的 薄 层 中 完 成 ,实 验 研 究 的 难 度 大 。建 立 准确的燃烧模型 ,尤其是动态燃烧模型当前仍是一个难点 。推进剂的燃烧耦合响应是发动机燃烧不稳定最主要的增益因素 ,燃烧增益难以准确建模导致燃烧不稳定难以准确预示 ,金属的分布式燃烧使燃烧响应的预测更加复杂 。尽管在理论上难以准确预示燃烧不稳定 ,但是由于影响燃烧不稳定的主要增益和阻尼因素大致清楚[6-7],采用综合治理的手段可以抑制大多数发动机中出现的燃烧不稳定问题[8]。 由于对燃烧不稳定的产生没有准确的预测方法 ,在实际工作中该问题至今仍表现出多发性和顽固性 ,加上有些时候导弹总体对发动机技术指标的限制 ,使得一些发动机的燃烧不稳定问题非常棘手 。 因而 ,在固体火箭发动机燃烧流动领域 ,不稳定燃烧存在诸多需要解决的重要问题[9]。
本文将对固体火箭发动机燃烧不稳定的产生机理 、理论分析方法 、主要增益与阻尼 、预示方法和地面实验验证方法做较为详细的综述 ,并对未来的发展提出研究建议 。
2 典型的固体发动机燃烧不稳定
目前固体发动机主要出现两类典型的燃烧不稳定问题 :涡脱落主导的燃烧不稳定和燃烧响应主导的燃烧不稳定 。
2.1 涡脱落主导的燃烧不稳定
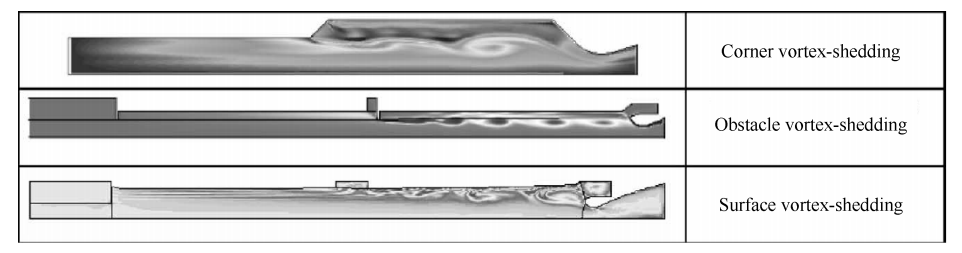
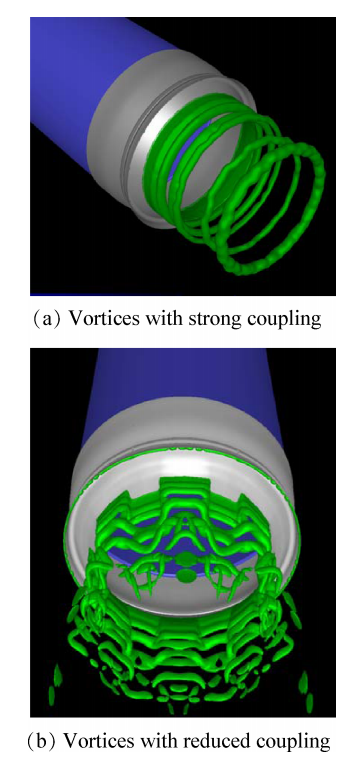
固体火箭发动机中有三种形式的涡脱落(图 1):转 角 涡 脱 落(Corner vortex shedding)、障 碍 涡 脱 落(Obstacle vortex shedding)和表面涡脱落( Surface vor⁃ tex shedding)。 转角涡脱落容易出现在中小尺度的固体 火 箭 发 动 机 中(如 战 术 导 弹 发 动 机),后 两 种 主 要发 生 在 分 段 固 体 发 动 机 中(如 大 型 固 体 运 载 火 箭 和助推器)。
图1 SRM中的涡脱图
对于航天发射用大型分段式固体发动机的燃烧不稳定问题 ,早在 20 世纪 90 年代欧洲研究者就开展了深入研究[10-11]。法国的 ASSM(Aerodynamics of seg⁃ mented solid motors)和 POP(Pressure oscillations program)研发计划发现了表面涡脱落和铝燃烧对燃烧不稳 定 的 增 益 作 用[5],同 时 也 发 现 P230 缩 比 发 动 机 内由燃烧形成的头部空腔和嵌入喷管带来的尾部空腔对 压 强 振 荡 都 有 明 显 的 增 益 作 用[12-13],如 图 2 所 示 。与 欧 洲 在 AIAA 会 议 上 大 量 报 道 研 究 进 展 不 同 ,在1995 年 Flandro[14]提出涡对火箭发动机稳定性影响之后,美国在发动机内涡脱落方面的研究报道较少 。
图2 SRM中的声涡耦合
总之 ,对涡脱落主导的燃烧不稳定问题的相关研究较多 ,能够较好地解决工程上所遇到的此类燃烧不稳定问题 。但是 ,目前关于声涡耦合规律的研究 ,更多的是通过实验和数值模拟来分析声涡耦合现象的发生条件及其抑制方法 。从学术角度来看 ,仍不清楚声涡耦合过程中声对涡调制作用的详细机制 。 大量的研究均表明 ,导致声涡耦合的频率不是一 个 固 定 的 点 ,而 是 一 定 的 频 率 范 围 。 文 献[15]和
[16]研 究 了 声 对 涡 的 调 制 作 用 ,在 保 持 流 动 参 数 不变的条件下 ,通过外加激励或改变结构长度改变声场的频率 ,都可以观察到涡卷起与合并以适应声频率的现象 。在固体火箭发动机燃烧室内 ,何种结构和流动条件下产生的涡能够被调制 ,目前还缺乏深入的研究 。
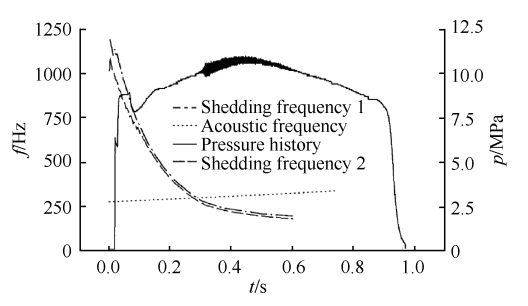
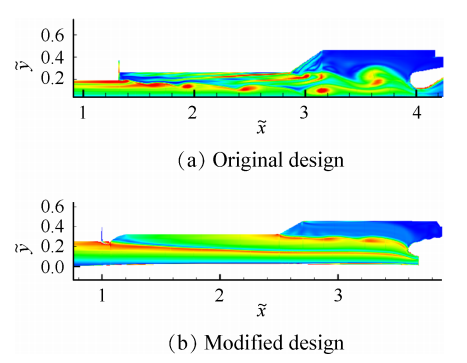
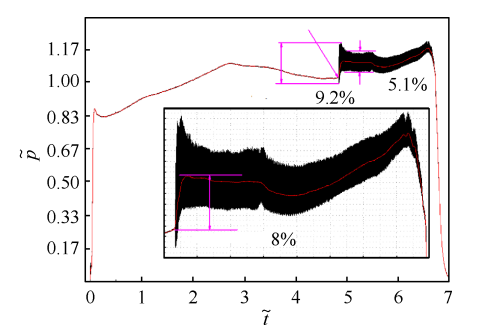
涡脱落导致的压强振荡一般振幅较小 ,但在燃烧响应的共同作用下 ,压强振荡可以达到很高的水平(图3)。 这种压强振荡在工程上相对容易抑制 ,当前的大涡模拟技术能够很好地模拟 ,并通过结构改进抑制 ,图 4 展示的是某发动机出现的涡脱落以及通过改进结构后涡脱落的抑制情况 。文献[17]采用 一种新的分段发动机前端绝热结构 ,通过三维构型设计使得障碍涡脱落的相干性降低(如图 5),减小涡脱落撞击喷管后产生的声激励 ,相对于对称结构设计 ,这种三维结构可以明显降低分段发动机中的压强振荡 。
图3 SRM中的不稳定燃烧,图中压力和时间作无因次化处理
图4 修改后装药抑制涡脱落,x,y作无因次化处理
图5 三维和轴对称构型下不同相干涡脱落
2.2 燃烧响应主导的燃烧不稳定
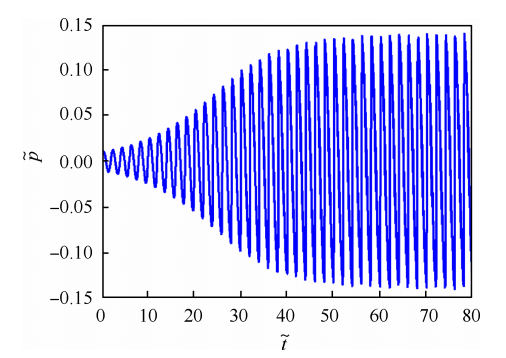
战术导弹用固体火箭发动机的燃烧不稳定通常出现在发动机工作的末期 ,此时发动机燃烧室中没有明显的转角 ,内部结构和流动条件也不大可能产生表面涡 ,针对某发动机的数值模拟工作验证这一点 。这种燃烧不稳定具有典型的非线性燃烧不稳定的特征 ,即触发 、平均压强上升和极限环振荡 ,如图 6所示 。 发动机在某种扰动的激励下触发燃烧不稳定 ,并迅速达到极限环状态 。改变推进剂配方 、降低压强耦合响应对此类燃烧不稳定有一定的抑制效果 ,但并不完全奏效 。 当前 ,此类燃烧不稳定无论在理论上和工程上都非常棘手 ,目前尚无可靠的方法预示此类燃烧不稳定 。
2.3 线性和非线性燃烧不稳定
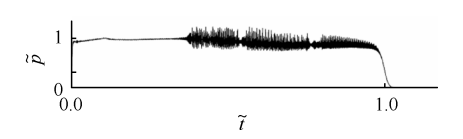
在描述不稳定燃烧行为时 ,会用到线性不稳定与非线性不稳定的概念 。笼统地讲 ,线性不稳定意味着压强振荡的振幅是指数形式增长 ,而非线性燃烧不稳定则表现为典型的非线性特性:触发 、平均压强上升和极限环振荡 。两种不稳定行为之间并非是绝对孤立的 ,通常情况下 ,线性不稳定在经过初始增长之后 ,由于增益和阻尼的动态变化 ,非线性占据主导作用 ,最终会发展为极限环振荡(见图 7)。 如果发动机工作时总是会出现燃烧不稳定,则认为发动机是线性不稳定的;如果同样的发动机在某些状态下是稳定的,而在另外一些特定工作或激励状态下表现出燃烧不稳定,则认为该发动机是非线性不稳定的 。
图 6 非线性燃烧不稳定
图 7 线性和非线性燃烧不稳定
在进行燃烧稳定性理论分析时 ,同样会出现线性与非线性的概念 ,此处是指所用的分析方法是线性模型或非线性模型 。线性模型是基于线性化分析方法建立的模型 ,只能预示燃烧不稳定的发生趋势 ;非线性模型则是基于非线性分析方法建立的模型,可以预测稳定性区间、触发条件和最终的极限环振幅 。
3 燃烧不稳定预示方法
基于固体火箭发动机的设计参数和固体推进剂性能参数进行燃烧稳定性的预示对工程研制非常重要 ,但由于燃烧不稳定现象的复杂性 ,目前仍无令人满意的通用方法 。 当前对固体火箭发动机燃烧不稳定的研究大体可以分为三类:理论分析方法 、实验方法和数值模拟方法 。一个有效的不稳定预示方法 ,需要以适当的理论分析为基础 ,结合相应的实验验证 ,补充一定的数值模拟 ,建立起燃烧稳定性边界与发动机参数间可靠的关联规律 。 因此 ,理论分析研究在燃烧不稳定预示中扮演着至关重要的角色 。
从数学上讲 ,燃烧稳定性的传统理论分析方法可分为线性方法和非线性方法 。线性分析方法将发动机简化为一个线性系统 ,其稳定性由总增益系数的正负来判断 ,正的增益系数意味着发动机内部的小扰动将被逐渐放大 ,即有不稳定的产生 。发动机在产生线性不稳定之后 ,振幅经过短暂的指数增长之后 ,大多数发动机会由于非线性的作用而产生极限环振荡 ,即压强振荡幅值会维持一定的水平 ,此时已发展为非线性不稳定 。有些发动机会表现出双稳定性 ,即发动机是线性稳定的(总增益系数为负),但是当扰动幅值较大时则会激发出非线性不稳定行为 。此时线性简化模型显然不再适用 ,需要在线性分析的基础上考虑非线性效应 :一方面可以预测发动机在大扰动下激发非线性不稳定的临界幅值 ,另一方面也可以刻画平均压强上升和极限环振荡等远离线性区的动力学行为 ,从而描述发动机非线性燃烧不稳定的剧烈程度 。
3.1 线性分析方法
对于燃烧响应主导的燃烧不稳定分析 ,Culick 做出了诸多开创性工作 :包括推进剂燃烧响应及燃烧室动力学分析两方面 。在推进剂燃烧响应方面 ,Culick[18]对 1950~ 1960 年间提出的诸多燃烧响应模型进行了系统性研究 ,揭示了这些模型间的联系 ,并将其归 为 一 类 模 型 ,被 统 称 为 准 稳 态 均 质 一 维(Quasi- steady homogeneous one-dimensional,QSHOD)模 型 。在燃烧室动力学方面 ,建立了燃烧室内流动的完整的控制方程 ,并提出基于 Galerkin 法的系统性分析方法,成为后来理论分析的基础[19]。
美 国 于 1976 年 开 发 出 标 准 的 稳 定 性 预 测 程 序( SSP),综 合 发 动 机 内 各 物 理 过 程 的 线 性 行 为 特 征 ,对 发 动 机 是 否 具 有 产 生 声 不 稳 定 的 趋 势 进 行 预 测 。该程序包含的激励和阻尼机制全面 ,拓展性强 ,因此得到了广泛的应用 。 国内当前对固体发动机的燃烧稳定性分析也大多采用线性分析方法 。
另一方面 ,涡脱落主导的燃烧不稳定问题的核心不稳定机理为流动不稳定 ,因此相关研究主要集中在侧向加质管流的稳定性方面 。 由于侧向加质管流在实际研究中多使用多孔介质作壁面 ,因此该流动又称为多孔介质管流 ,最早由 Berman 提出并求出其稳态解[20]。 Culick[21]和 Flandro[22]基于稳态解发展了侧向加质流场对各种小扰动的稳定性分析方法 ,因此该问题也称为 Taylor-Culick(TC)流 。TC 流的流动稳定性分析可以揭示发动机中仅侧向加质影响时 ,涡在扰动作用下的动力学特性及流动不稳定产生的机理 。
TC 流的流动不稳定分析属于流动稳定性的线性分析范畴:首先对 TC 流的 Navier-Stokes 方程在稳态解附近进行线性化处理 ,得到线性扰动方程 ;然后研究线性扰动方程在各种形式的扰动波作用下的时空发展特性 ,从而预测不稳定的产生 。 由于扰动方程的复杂性 ,声涡耦合产生的不稳定很难像燃烧响应主导的不稳定那样使用解析的方法进行分析 ,而是需 要 采 用 半 解 析 或 数 值 的 方 法 ,例 如 Majdalani等[23-25]的多尺度渐进匹配展开分析 、Boyer 等[26]的谱方法分析等 。 国内结合分段发动机的流动稳定性也开展了类似的研究工作 ,谱方法中存在的网格依赖性或区域依赖性问题基本得到解决[27-28]。这些不稳定分析方法的本质是求解扰动方程的特征值问题 ,计算结果对于一定参数范围内的不同形式扰动都适用,具有一定普适性 。
3.2 非线性分析方法
发动机燃烧不稳定的一个显著特征就是周期性大幅度的压强振荡 ,但因为数学分析的复杂性 ,非线性 分 析 方 法 的 进 展 一 直 比 较 缓 慢 。例 如 ,早 在 1964年 ,Brownlee[29]就发现了不稳定燃烧时燃烧室内声波会 发 生 非 线 性 畸 变 ,直 到 Flandro[30]引 入 能 量 平 衡 法对积分系统进行分析才能较准确地将这一因素纳入考虑 。
Flandro 等[31]将固体火箭发动机燃烧不稳定的非线性特性总结为:压强极限环境振荡 、平均压强上升以及触发现象 。从实际应用的角度 ,燃烧稳定性的
线性分析方法有两个主要缺陷:其一 ,只能预示发动机在某状态下是否会因小扰动作用而出现燃烧不稳定 ,并不能得出不稳定的严重程度 ,即无法得出压强振荡的振幅 、无法计算出平均压强上升的情况 ;其二 ,无法预示线性稳定的发动机在大扰动下是否会被触发燃烧不稳定 ,这种燃烧不稳定似乎表现出的某种随机性——地面试验和部分飞行试验中发动机都能正常工作 ,但在特殊飞行条件下可能出现不稳定 。从数学上讲 ,这两个缺陷都是由于线性分析方法中忽略非线性项 ,从而无法准确描述大幅度扰动的动力学特性所导致的 。 这种不准确分为两个层
次 :第一 ,分析结果定性准确而定量不准确 ,这种不准确对应于第一个问题 ,即线性分析方法可以预测不稳定的发生 ,但无法给出具体振荡幅值 、压强上升等定量信息 ;第二 ,分析结果定性也不准确 ,非线性系统在参数变化时可能会出现解的性质和数目的变化 ,大振幅扰动通常会将系统带到另一个状态 ,这种不准确对应于触发现象,线性分析方法完全失效 。
对于线性分析方法定性准确而定量不准确的情形 ,可以引入适当的修正 。 法国的“ 软件和工程组织”(SEA)将两种非线性模型(气体动力学方法和能量平衡法)应用到 SSP 中以预测振幅 。对于简单的圆柱形通道 ,两种方法的结果相近 ;针对星孔装药 ,前者得出的结果较为合适 。 由此可见 ,国外对复杂装药构型固体发动机的燃烧不稳定问题还没有一个非常准确的预测方法 ,同时由简单圆柱形通道得出的结论不能直接应用到复杂装药构型的固体发动机中 。 1995 年 Flandro[14]引入了新的旋流修正来保证无滑移边界条件 ,此外还删除了速度耦合项 ,因为通过实 验 测 得 速 度 耦 合 响 应 存 在 很 大 的 困 难 ,2003 年 又引入涡量和粘性修正[32];同时 ,Flandro 等[31]对发动机中出现的极限振幅 、触发振幅和燃烧室平衡压强变化的真正原因给出了解释 ;此外 ,Flandro 等[33]还研究了平行波入射对燃烧不稳定触发机理的影响 。尽管Flandro 等[34-35]在 2004 年的研究成果能够很好地解释某一发地面实验的典型非线性不稳定特征 ,但是在更多的实际发动机分析中还是存在很大的问题 。 Flandro 等 从 能 量 守 恒 的 角 度 出 发 ,以 Culick 的 气 体
动力学方法为基础 ,提出了预测非线性燃烧不稳定的 能 量 平 衡 方 法[30-31]。该 方 法 根 据 Brownlee 的 实 验观察 ,假设压强振荡达到极限振幅状态后 ,振荡波是一种前沿陡峭的行激波 ,激波带来的熵增导致系统能量的耗散 ,从而使振幅稳定在极限状态 。 能量平衡法的计算中所需要的数据有工作压强 、燃烧室结构参数 、推进剂燃速和导纳函数等 。其中 ,推进剂和发动机结构参数均是已知的或经过计算可以得到的 ,只有推进剂的声导纳需要通过实验得到 。该方法是基于积分形式的流体力学方程组进行分析 ,因此计算中不会出现大型偏微分方程组求解 ,可以通过简单的数值计算对极限振幅与平均压强变化进行耦合求解 ,可以对发动机平均压强上升 、压强振荡及触发等非线性行为进行预测 ,计算效率高于理论模型预示方法和 CFD 方法 。
对于另一种情况 ,即线性分析结果定性上也不正确的情形 ,则必须依赖于非线性动力学分析 。 Baum 等[36],Culick 等[37]及 Wicker 等[38]等指出,触发现象在数学上是由亚临界分岔导致的双稳态区导致的 ,其必要条件是非线性的燃烧响应 。其中 ,Baum, Levine 引入了压强线性 、速度非线性的燃速模型 ,Cu ⁃ lick 引入了基于 Galerkin 模态系数的一般非线性燃速模 型 ,而 Wicker 则 引 入 了 包 含 压 强 和 速 度 二 阶 非 线性项的燃速模型 。基于这些不同的燃速模型的非线性分析都可以获得类似的亚临界分岔特性 。 印度理工 学 院 Madras 分 校 的 Mariappan 等[39]则 引 入 了 准 稳态一维均质燃速模型作为燃速控制方程与燃烧室非线性声学方程耦合进行研究 ,并提出了一种新的燃烧不稳定机制 。
Sujith 团 队 将 流 体 动 力 学 不 稳 定 领 域 的 非 正 交(或 非 模 态)不 稳 定 机 制 引 入 到 热 声 耦 合 系 统 中 ,具体 到 固 体 火 箭 发 动 机 ,燃 烧 室 声 学 系 统 和 推 进 剂 燃烧响应这两个系统都存在非正交效应[40]。这一不稳定 机 制 出 现 在 模 态 不 正 交 的 系 统 中 :扰 动 引 入 系 统后 ,即使该系统线性稳定 ,在各个模态上的扰动分量都 衰 减 ,但 由 于 模 态 间 投 影 不 为 0,总 的 扰 动 仍 可 能在 一 定 时 间 内 增 长 ;虽 然 这 一 暂 态 增 长 在 线 性 系 统中最终还是会衰减 ,但对于非线性系统 ,若暂态增长的 幅 值 比 较 高 ,则 相 当 于 向 系 统 中 引 入 了 一 个 大 扰动 ,可能导致触发不稳定 。Mariappan 等[39]证实了固体火箭发动机非线性声学方程与准稳态一维均质燃速 方 程 的 耦 合 系 统中 确 实 存 在 这 种 机 制 :在 某 线 性稳 定 工 况 下 ,引 入 1% 的 小 扰 动 ,系 统 最 终 进 入 了 不稳定状态 。
上述研究都是围绕燃烧响应主导的燃烧不稳定展开的 。对于涡主导的燃烧不稳定 ,非线性分析困难得多 。这是由于涡的产生和发展过程是一个复杂的大尺度多维流体动力学过程 ,很难像燃烧响应那样简化为简单微分方程或代数方程 。 因此 ,对于涡主导的燃烧不稳定现象 ,虽然涡本身是对流控制下典型的非线性过程 ,目前成熟的理论分析仍止步于上节所述的线性分析方法 。鉴于此 ,对该现象的研究通常采用理论与数值模拟及实验相结合的形式 : Apte 等[41-43]对自由发展及外加激励情况下的侧向加质流动开展数值研究 ,总结了不稳定现象的规律 ,并通过大涡模拟研究了燃烧室中不同位置处涡的特征及转捩特征,总结了侧向加质导致的流场新特性;La⁃ boureur 等[44]设 计 了 多 孔 介 质 腔 实 验 ,对 数 值 方 法 进行了校核 ,研究了流道高度与流动不稳定的关系 。欧 洲 学 者 开 展 的 POP 研 究 项 目 中 ,燃 烧 不 稳 定 是 围绕实际发动机/模型实验结果开展的 ,通过对涡量项合理的建模和校正 ,可以构造出比较准确的发动机一 维 非 定 常 流 动 模 型 ,例 如 Laureti 等[45]的 模 型 可 以复现实验中的不稳定曲线 。此外,法国 Vuillot[11]使用两种理论模型(含 Flandro 脱落涡项修正的线性声平衡法和基于不稳定可压 N-S 方程的完全数值模拟)对Ariane-5 的 MPS P230 助 推 器 1/15 缩 比 模 型(LP3)进行 了 模 拟 ,结 果 表 明 :前 者 虽 然 预 测 成 功 ,但 Flandro方法对很多参数相当敏感 ;与此相比后者的使用相对简单 ,但其网格数量是一个棘手的问题 ,使用该模型进行全尺寸发动机稳定性预测是一个相当大的挑战 ,但可行性已经得到验证 。对于采用复杂装药的发动机 、分段发动机等 ,燃烧不稳定性预示更为复杂 ,由于发动机尺度过大 ,全尺寸大涡模拟等数值方法在工程研制上难以接受 。
综上所述 ,无论是燃烧响应主导的燃烧不稳定还是涡主导的燃烧不稳定 ,在实验室研究和实际工程 应 用 中 都 表 现 出 典 型 的 非 线 性 特 征 ,但 目 前 仍 没有完全令人满意的理论对其进行描述 ,现有理论远远无法满足对发动机不稳定进行预示的需求 ,亟需寻求突破 。
4 主要增益与阻尼
增益与阻尼的准确数值或经验表达式是各类燃烧不稳定预示方法都必需的数据或模型 ,对于非线性预示方法来说 ,还需要增益与阻尼的高阶表达式 。压强耦合响应 、速度耦合响应 、分布式燃烧 、粒子阻尼和喷管阻尼是当前燃烧不稳定分析中最重要的增益和阻尼项 。
4.1 压强耦合响应
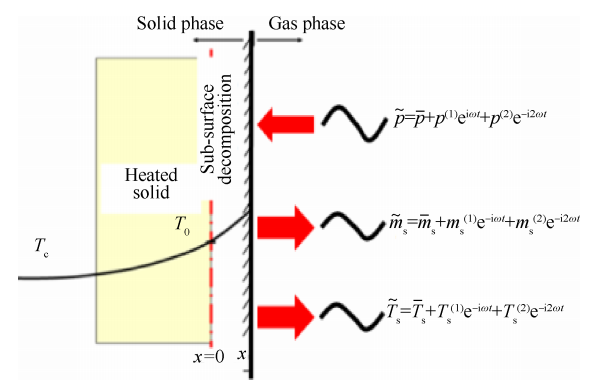
在理论方面 ,主要采用 QSHOD,Z-N 和 BDP 模型描述压强耦合响应 。在实验方面 ,固体推进剂燃烧的压强耦合响应数据主要通过 T 型燃烧器实验获得 ,通过增大外加脉冲激励 ,可以获得推进剂的高阶压强耦合响应函数 。
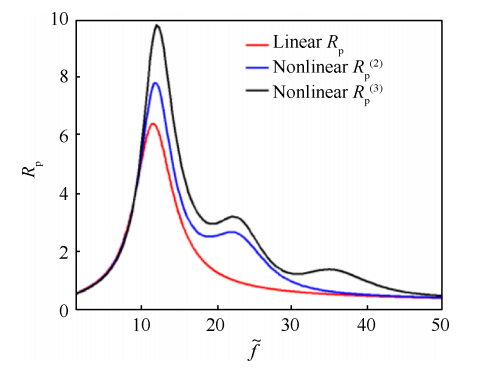
QSHOD 模型是假设固相转化气相过程发生在一个薄层界面内 ,通过求解固相温度场 、气相温度场以及在界面上二者能量平衡 ,经过线性化处理后 ,获得响 应 函 数 的 统 一 表 达 式 ,即“ 两 参 数 ”表 达 式 。 QSHOD 方法在一定程度上提供了一种解释 ,能够加深人们对线性燃烧响应机理的了解 。但是 ,其不能考虑燃烧响应与压强振荡幅值之间的关系 ,而在压强振荡的增长过程中 ,随着压强振荡幅值的变化必然会导致近表面燃烧的变化 ,从而导致燃烧响应程度的变化 。非线性燃烧不稳定的典型特征是压强振荡频谱分布中包含了多个不同频率的波 ,且较大的振幅发生在几个低频处 。对于这种多阶模态共存的情况 ,固体推进剂的燃烧响应过程不再是单一频率作用 ,而是多阶模态共同作用 ,燃烧响应表现出非线性特性 ,需要用非线性压强耦合响应函数来表征 。金秉宁等[46-47]以线性 QSHOD 模型为基础 ,考虑非线性压强振荡中的前三阶振荡幅值 ,在模型气固交界面的边界条件进行非线性非稳态处理 ,获得了非线性压强耦合响应模型 ,并获得了各阶模态振荡幅值对非线性燃烧响应函数的影响规律 ,如图 8 和图9 所示 。 可以看出 ,压强耦合响应函数的线性和非线性结果存在明显的差别 。从最终的表达形式来看 ,扩展至三阶的压强耦合响应表达式已经非常复杂 ,进一步向五阶扩展难度较大 。
图8 影响燃面的压强震荡
图9 刺激作用下压强耦合响应函数
压 强 耦 合 响 应 的 另 一 个 理 论 计 算 模 型 是 Z-N (Zel ’dovitch-Novozhilov)模 型 。Z-N 认 为 气 相 流 动 、化学反应过程及推进剂的固相分解过程特征时间远小 于 固 相 导 热 过 程 ,因 此 整 个 系 统 中 起 主 导 作 用 的是 最 慢 的 固 相 导 热 过 程 。基 于 这 一 认 识 ,可 以 假 设在 非 定 常 情 形 下 燃 速 、燃 温 及 表 面 热 流 间 仍 满 足 定常 情 形 下 的 函 数 关 系 ,由 此 得 到 的 推 进 剂 非 定 常 响应 模 型 即 为 Z-N 模 型 。 目 前 对 QSHOD 模 型 及 Z-N模型的分析在本质上是小扰动假设下原控制方程的一 阶 或 二 阶 近 似 ,无 法 满 足 发 动 机 燃 烧 不 稳 定 研 究对更高阶表达式(一般需要五阶)的需求 。目 前 在 模 型 扩 展 至 高 阶 方 面 的 研 究 表 明 , QSHOD 模型与 Z-N 模型具有定量的线性等价性 ,在绝大多数参数范围内的非线性响应也定性地等价 :两种模型燃速响应的变化趋势一致 ,但 QSHOD 模型的 燃 速 振 幅 和 分 岔 点 都 比 Z-N 模 型 高 很 多 ;当 推 进剂能量较高时 ,两者的响应有较大的差异 ,Z-N 模型基本保持原有性态而 QSHOD 模型迅速失稳 。
实验方面 ,根据测量方式的不同可以分为直接测量法和间接测量法 。直接测量方法可以同时获得响应函数 Rp(或者导纳函数 Ab)的实部和虚部,但装置较为复杂 ,并且需要具备微波和磁场技术 ,较难广泛开展应用 。 间接测量法是通过分析燃烧过程中的非稳态动力学过程 ,将压强耦合响应与压强振荡联系起 来 ,从 而 获 得 响 应 函 数 Rp 实 部 或 者 导 纳 函 数 的 实部 ,主要方法有 T 型燃烧器法 、旋转阀法和阻抗管法 。其中 ,T型燃烧器以其成熟的技术被研究者广泛采用 ,通过不断改进 ,在不同实验室对不同成分配方的推进剂进行了测量 ,可获得一些较为满意的数据 。现阶段 ,双脉冲激励 T 型燃烧器方法是适合科学研究和工程研制需求的可靠方法 。
双脉冲激励 T 型燃烧器方法可以开展线性和非线性测量[47]。线性响应函数测量方法是基于小扰动理论 ,利用外部脉冲激励装置 ,在 T 型燃烧器内产生小幅振荡 ,通过改变 T 型燃烧器的长度 ,获得不同压强振荡基频下的压强耦合响应 ;分别测量不同振荡基频条件下的压强耦合响应函数值 ,最终获得不同振荡频率条件下的压强耦合响应函数 。
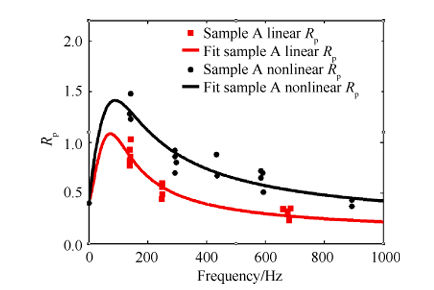
考虑振幅对压强耦合响应影响的非线性响应函数是预示触发和压强振荡非线性增长的关键 。不同的触发强度意味着推进剂燃烧区域存在不同的压强扰动 ,导致不同的压强耦合响应 。非线性响应函数测量方法的核心是如何给 T 型燃烧器施加大振幅的压强激励 ,在不改变 T 型燃烧器长度前提下 ,获得可分辨的高阶燃烧响应以及不同振荡幅值条件下的燃烧响应 。北京理工大学的苏万兴等[48]尝试在推进剂试件中间加一层黑火药 ,来增强 T 型燃烧器内部的压强激励 ,但是由于端面燃烧试件易产生边缘效应 ,导致推进剂并不是按照理想的端面退移 ,这样会给实验结果带来较大的不确定性 。作者所在的课题组通过改进脉冲激励装置的压强和位置 ,从而产生与实际发动机非线性振荡特性相类似的多阶模态共存的压强振荡 ,通过对各阶模态振荡特性分析 ,从而同时获得各阶模态的推进剂非线性压强耦合响应函数特性[49],图 10 为同一种推进剂配方的线性和非线性法测量结果对比 。
图10 试验中线性和非线性压力耦合响应函数比较
含铝复合推进剂压强耦合响应函数会受发动机工作参数和推进剂配方参数的影响 。通常情况下 ,随着工作压强的增高 ,推进剂压强耦合响应会在整个振荡频域范围内均呈整体型增大 ,并且响应函数的峰值频率会向高频移动 。在设计发动机时 ,发动机声腔频率尽量要避开固体推进剂燃烧响应函数峰值频率 ,或者推进剂响应函数峰值频率要尽量避开发动机声腔频率 。发动机试车数据表明 ,飞行过载和自 旋 均 会 对 压 强 耦 合 响 应 函 数 产 生 影 响 ,但 该 方面的研究在国内外相关文献中均未见报道 。 因而 ,飞行状态对压强耦合响应的影响将是今后研究的重点之一 。
推进剂配方参数对压强耦合响应函数有较大的影响 。对于同一发动机而言 ,不同配方推进剂在发动机中表现出的稳定性明显不同 。推进剂配方参数中氧化剂 AP 粒度级配 ,RDX 或 HMX 粒度与含量 ,金属铝粉的粒度 、级配与含量等均对压强耦合响应函数有较大的影响 。 目前 ,针对 AP 和 RDX 的配比以及金属 Al 粉的粒度与级配等变化开展了大量的试验研究,获得了相关的影响规律[47]。
4.2 速度耦合响应
除了压强耦合响应的影响 ,速度耦合响应同样是导致发动机非线性燃烧不稳定的主要增益因素 。目前对于速度耦合响应的产生机理有了一些认识 ,但仍缺乏可靠的实验数据支撑 ,使得对速度耦合响应如何导致非线性燃烧不稳定的产生仍没有明确的认识 。
Baum 等[36]的早期研究认为 ,非线性速度耦合响应是导致触发的主要诱因 。实际发动机的燃烧不稳定抑制研究表明 ,仅依靠压强耦合响应函数测量难以完全解决实际发动机中出现的非线性燃烧不稳定问题 。对于侧向加质的固体火箭发动机 ,当推进剂主要燃面与声振速度平行时 ,需要考虑速度耦合的增益作用 。从热声耦合的角度来看 ,速度耦合与压强耦合有明显的不同 ,压强耦合在整个振荡区域内均表现出增益作用 ,而速度耦合在不同振荡区域内可表现出增益作用,也可以表现出抑制作用 。
McClure[50]从理论上证明了速度耦合响应与压强耦 合 响 应 对 于 燃 烧 不 稳 定 的 增 益 同 等 重 要 。 Yang等[51]研究认为 ,不同于压强耦合响应特性 ,速度耦合响应还依赖于燃烧室内的流场环境,在较大的速度耦合响应作用下,线性稳定的发动机可以被触发产生非线性不稳定 。Cai 等[52]对固体火箭发动机中 AP/HTPB复合推进剂瞬态燃烧过程进行数值模拟 ,研究认为速度振荡可引起推进剂燃烧表面的火焰波动 ,使得对固相的热反馈过程表现出非线性特性 。
在 实 验 研 究 方 面 ,Stepp[53]通 过 T 型 燃 烧 器 实 验获得了双基推进剂在声腔二阶频率下的速度耦合响
应值 ,但实验结果难以分离驱动药和待测药的响应特性 ,且测量流程复杂 、实验工作量大 、声腔二阶频率触发控制要求较高 ,使得该方法较难有效地获得速 度 耦 合 响 应 特 性 。 Brown 等[54]采 用 旋 转 阀 技 术 产生可控频率和幅值的速度振荡 ,从而通过实验获得两种低燃速无铝固体推进剂的速度耦合响应函数 ,但该方法对相角精确化的控制和高压动密封的要求较高,实验测量较难开展 。
速度耦合响应同样受到振荡幅值的强烈影响 ,推进剂表面不同程度的速度振荡导致火焰脉动的程度不同 ,影响到推进剂表面的扩散燃烧过程 ,获得速度耦合响应的非线性表达式在非线性不稳定的预示中同样重要 。
作者所在的课题组采用 T 型燃烧器技术 ,建立了一种含铝固体推进剂速度耦合响应函数的实验测量方 法[55],初 步 的 实 验 研 究 结 果 表 明 速 度 耦 合 响 应 函数值比压强耦合响应函数值高一个数量级 ,表明速度耦合响应确实是不可忽略的重要影响因素 。获得准确的速度耦合响应模型还需要开展大量深入细致的实验研究与理论分析工作 。
4.3 粒子阻尼
固体推进剂燃烧产物中的凝相粒子可以对声场产生阻尼作用 ,造成声能损失 ,明显改善发动机的燃烧稳定性 。粒子阻尼主要是凝相粒子的动力松弛和热松弛造成的 ,即凝相粒子的速度和温度滞后于气相声振 ,由于粘性损失和导热而产生声能损失 。粒子阻尼对声不稳定燃烧有很强的阻尼作用 ,在发动机燃烧室内带来的声能损失常常占到总声能损失的三分之一以上,远远大于气相阻尼和结构阻尼等 。
几十年来国内外学者从理论分析 、试验测试以及数值模拟三个方面对粒子阻尼做了大量的研究工作 ,对粒子阻尼特性有了定量的认识 。研究惰性粒子对固体火箭发动机不稳定燃烧影响的理论中 ,应用较广的是粒子松弛理论 ,当惰性粒子的动力驰豫时间与声振荡的特征时间相等时 ,惰性粒子的阻尼效应最大 。 目前 ,已经有比较成熟的方法计算粒子阻尼特性 ,可以考虑频率和粒子多重尺寸分布对阻尼特性的影响 ,为发动机稳定性预估提供可靠的
数据[3,56]。
近年来 ,随着对非线性燃烧不稳定研究的深入 ,对发动机中粒子阻尼特性有了更为深入的认识 ,可以从发动机飞行状态变化和压强振荡增长等动态的角度理解粒子阻尼 。在固体火箭发动机做机动飞行时 ,横向过载会引起燃烧室内部凝相粒子的定向运动 ,这种定向运动会改变凝相粒子在燃烧室中的空间分布 ,从而影响粒子的阻尼特性 ,甚至会诱发燃烧不稳定 。在极限环振荡的发展过程中 ,由于声对粒子的操纵作用 ,也可能导致粒子尺寸沿发动机纵向方向重新分布 ,引起粒子阻尼特性的改变 ,并参与压强振荡非线性增长过程中的增益与阻尼博弈 。获得粒子阻尼的动态变化对预示非线性不稳定的产生和发展非常重要,也是目前正在研究的问题 。
4.4 喷管阻尼
喷管阻尼是发动机中最重要的阻尼机制 ,粗略估计可达系统总阻尼的 50% 左右 。非线性燃烧不稳定的准确预示也需要获得在各阶声学模态下的喷管阻尼 。 喷管阻尼是指声波和平均气流通过喷管时以透射和对流的方式对声能造成的散失 。它是一种边界阻尼 ,由声场与平均流之间的相互作用造成的损失 。 由于固体发动机不稳定燃烧以轴向振型为主 ,喷 管 进 口 截 面 恰 好 处 于 燃 烧 室 声 压 波 腹 位 置 ,而 此处的平均气流速度又恰好比较高 ,这导致声能透射和对流损失都比较大 。 喷管的收敛半角 、型面结构 、是否潜入 、潜入空腔的体积大小等因素将对喷管阻尼会有较大的影响 。对于不稳定燃烧研究而言 ,最大限度地增大喷管阻尼将提高发动机的工作稳定性 。
喷管阻尼理论最初是在液体火箭发动机的研制中发展起来的 。Crocco 等[57]发展了喷管声导纳线性理论 ,为喷管声导纳的研究奠定了基础 。在其研究中 ,假设平均流是一维无旋流 ,而声波是三维有旋运动 ,并且在理论分析中考虑了熵波 。Zinn 等[58-59]基于短喷管理论对喷管阻尼特性进行了理论预估 ,并对小尺寸喷管导纳特性进行了冷气试验 ,其试验结果与理论预估结果非常一致 ,提出了喷管阻尼的工程预 估 公 式 。Janardan 等[60]与 其 合 作 者 开 展 了 喷 管 阻尼试验研究 ,结果表明 ,锥型收敛段喷管阻尼要优于等曲率型收敛段喷管阻尼 ,但其实验只能在冷流条件下进行 ,且测量结果不能直接应用于实际发动机 ,还需要进行一定的转换 。
喷管阻尼系数的常用计算方法包括传统方法 、特征值法和衰减法 。其中 ,传统计算方法简单快速 ,仍广泛应用 。 由于传统方法采用了短喷管理论计算喷管导纳 ,并忽略了燃烧室平均流场的影响 ,因此喷管阻尼系数准确性降低 ,且计算结果与喷管收敛段几何构型和声学模态的阶数无关 ,已不满足现阶段燃烧不稳定预估模型的要求 。French[61]利用 CFD 技术求得燃烧室-喷管的稳态平均流场 ,然后代入到声
波速度势方程求解燃烧室-喷管整体的声学模态 ,进而求得喷管阻尼系数 。该方法考虑了燃烧室流场对喷管阻尼系数的影响 ,结果比较准确 ,但是用 CFD 计算燃烧室流场的计算量大 ,尤其是当发动机结构尺寸较大时计算量问题格外突出 。北京理工大学的孙兵兵等[62]采用脉冲衰减法对喷管阻尼特性进行了深入全面的数值计算 ,探索了燃烧室长度 、喷喉半径 、喷管收敛半角 、潜入式喷管空腔体积 、喷管收敛段型面 、平均压强等因素对喷管阻尼特性的影响规律 。
作者所在的课题组在传统方法的基础上 ,提出一种喷管阻尼系数的改进算法[63]。此算法未采用短喷管理论并考虑了燃烧室平均流场的影响 ,利用线性化欧拉方程分别计算喷管导纳和燃烧室声学模态 ,进而得到喷管阻尼系数 ,计算量大大减少 ,可以很方便地嵌套进燃烧不稳定分析程序中 。在此基础上 ,对喷管阻尼的影响因素展开研究 ,总结了模态阶数 、喷管收敛段几何构型 、发动机长径比 、喉通比和特征时间等喷管阻尼影响因素对喷管阻尼系数的影响规律 。
4.5 分布式燃烧
对固体发动机中铝的分布式燃烧的重视起始于欧 洲 的 分 段 发 动 机 压 强 振 荡 研 究 ,Dupays[64]在 2002年详细论述了发动机中两相非稳态流动和分布式燃烧对压强振荡的作用 。分布式燃烧的研究涉及两个层次的内容 :第一是固体推进剂中铝在发动机条件下燃烧过程和模型的研究 ,这是分布式燃烧研究的基础 。第二是从热声耦合的角度 ,分析发动机燃烧流动状态下分布式燃烧对压强振荡的贡献 。
美国 、俄罗斯 、法国和意大利对固体推进剂中铝的燃烧开展了较为深入的研究 ,对铝的表面团聚 、燃烧产物的最终物理和化学状态有了比较深入的认识 。Beckstead 对推进剂中铝的燃烧过程进行了全面的 描 述[65],Sundaram 等[66]对 纳 米 和 微 米 铝 的 燃 烧 理论做了系统的综述 。作者所在的课题组通过粒子收集[67]、物 理 与 化 学 特 性 分 析[68]和 数 字 全 息[69]等 手 段对固体推进剂中铝的表面团聚和燃烧产物特性开展了全面的研究 ,积累了大量的实验经验和数据 ,为建立最终的发动机条件下铝的分布式燃烧模型奠定了基础 。
在 分 布 式 燃 烧 对 燃 烧 不 稳 定 的 作 用 方 面 ,Du ⁃ pays[64]的 研 究 表 明 ,燃 烧 室 中 小 粒 度 的 燃 烧 铝 液 滴(初始粒径 30μm,燃烧残余物 3μm)对压强振荡有放大 作 用 ,而 大 液 滴(初 始 粒 径 125μm,燃 烧 残 余 物60μm)对 其 有 衰 减 作 用 。 Gallier 等[70]通 过 数 值 模 拟发现 ,纯气相燃烧流动稳定的简单药型发动机 ,在考虑铝燃烧后会出现燃烧不稳定 ,分析认为 ,该不稳定是由燃烧室声学和铝的非稳态燃烧释热耦合而导致的热声不稳定 ;通过变参数分析发现 ,铝燃烧区域的尺寸是最重要的作用因素 。最近 ,Genot 等[71]通过数值模拟对发动机中铝的分布式燃烧开展了更为深入的研究 ,发现压强振荡导致铝粒子燃烧时间的振荡 ,从而导致燃烧室燃烧释热区间的剧烈变化 ,这种释热区间的变化是热声不稳定的源头 。
上述数值模拟工作表明 ,发动机内特定尺寸铝粒子的分布式燃烧会诱发燃烧不稳定 ,但是这些工作都是基于单一粒径假设 。真实发动机中铝粒子从推进剂表面逃逸时的粒径分布非常复杂 ,而且粒径分布与推进剂配方和发动机的工作压强有关 。 另外 ,实验研究表明 ,同一推进剂在同样的工作压强下燃烧时 ,表面团聚物的尺寸存在一定程度的散布 ,这种散布会影响最终的释热几何区间 ,使得发动机的燃烧不稳定诱发和演化机理更为复杂 。 因此 ,建立一种与推进剂配方关联 、考虑不确定性分布 、考虑不同振荡环境的分布式燃烧模型 ,对非线性燃烧不稳定的准确预示非常关键 。
5 触发与极限环的形成过程
非线性燃烧不稳定的触发现象表现为不稳定只在特定扰动下才会产生 ,其数学本质是发动机系统在该工况下存在双稳态(双稳定解)。 这一现象给实际发动机带来的挑战有两方面 ,一是在现有线性理论下被判定稳定的发动机仍可能出现燃烧不稳定[6-7]。二是即使通过试验验证的发动机在实际使用中仍可能在飞行过载等外界因素影响下出现燃烧不稳 定[72]。尽 管 该 现 象 的 重 要 性 很 早 就 被 指 出 了[30],但由于固体发动机系统的复杂性 ,理论建模和分析难度大 ,目前对触发现象的机理和影响因素研究都不能满足工程需要 。
目前对非线性不稳定的触发机制 ,普遍认为主要由推进剂非定常燃烧响应的非线性特征决定 。 Baum 等[36]在线性压强耦合响应函数的基础上引入压强线性 、速度非线性的非线性燃速响应函数用于触发现象研究 。 Culick 等[37]提出将燃速响应函数表示为各声模态的压强 、速度扰动系数的多项式函数 ,并将其与燃烧室非线性声学模型耦合组成发动机系统模型 ,从数值分岔分析和两模态截断理论分析两个角度证实了触发不稳定的双稳态机理 。Wicker 等[38]则进一步从两模态截断模型出发对触发现象的影响
因素进行了研究 。但是 ,这些模型中所考虑的增益 、阻尼因素较少 ,建立的模型也比较简单 ,其理论分析却已经非常困难 。 因此,如何处理模型复杂化的需求与理论分析手段有限的矛盾是一个亟待解决的问题。
非线性燃烧不稳定被某种激励触发后 ,压强振荡的振幅通常首先服从线性规律按指数增长 。 随着振幅的增大 ,非线性效应逐渐增强 ,增益和阻尼会随着振幅的增大而改变 ,从而使系统的净增益发生变化 。 当发动机系统内各因素的增益和阻尼作用达到动态平衡时 ,压强振荡进入极限环状态 。显然 ,这 一过程的分析需要将包括推进剂燃烧响应及燃烧室声学振荡在内的各种物理 、化学过程的非线性特征都考虑在内 。
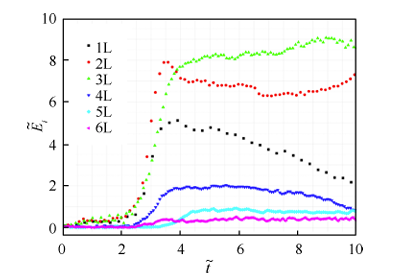
按 照 Flandro 的 理 论[30-31],在 压 强 振 荡 的 增 长 过程中 ,由于低阶能量的饱和 ,能量逐渐由低阶向高阶传递 ,引起高阶振荡并导致波形畸变 ,从而产生激波 。 由激波产生的能量损失带来新的阻尼效应 ,与其它增益 、阻尼因素共同决定了极限环状态的产生 。实际情况却远比这更复杂 ,图 11 是某发动机压强振荡增长过程中能量在不同振动模态之间的分布 ,可以发现 ,前三阶几乎同时增长 ,在快速增长的后期第二阶增长最快 。Flandro 理论中所引入的假设与图 11所示的实验现象并不一致 。而且 ,Flandro 对各增益 、阻尼的建模也没有深入 ,它们在振幅增大的情况下的变化规律也将影响各阶能量的传递规律 。 应当说 ,目前对不稳定发展过程中极限环的形成过程的了解非常有限 ,进一步深入研究振荡演化过程及其能量传递规律 ,对于选择合适的不稳定抑制方法来说非常有帮助 。
图11 压强振荡过程中1阶到6阶饱和能量
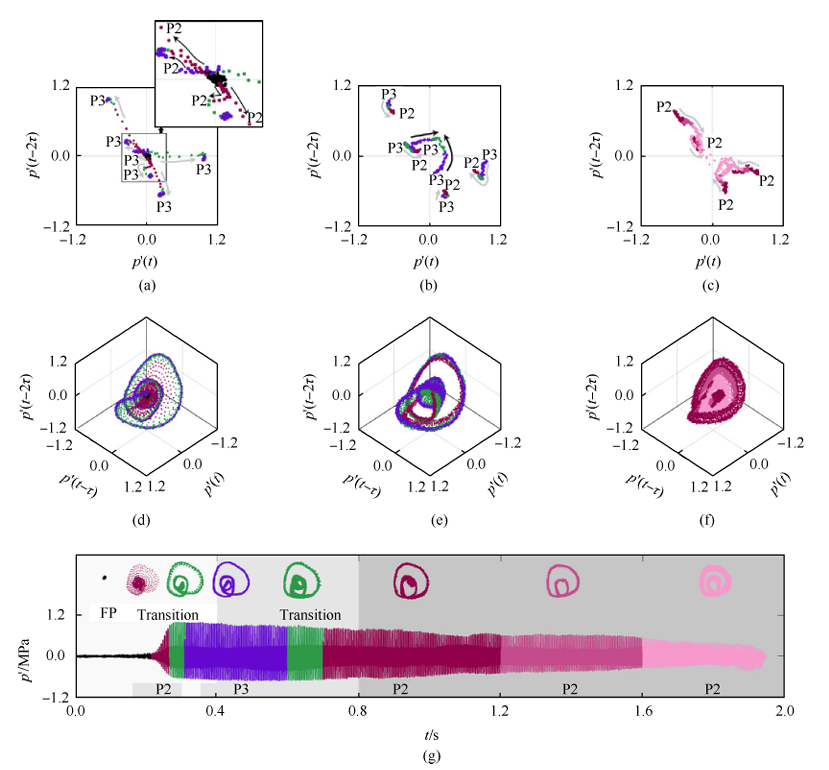
在关于燃烧不稳定的传统认识中 ,压强振荡频率应当是燃烧室声模态基频的整数倍 。但是 ,通过对实际发动机的燃烧不稳定压强信号 分 析 却 发 现[73]:在 极 限 环 振 荡 中 可 能 出 现 倍 周 期信号 ,即压强振荡的周期是燃烧室声模态周期的整数 倍(如 图 12)。 即 ,振 荡 信 号 的 频 率 不 再 是 传 统 认识中必为基频的 n 倍,而是伴随出现了基频的 1/m,这一发现可能蕴含着新的现象和规律 。
图12 燃烧不稳定性中 SRM 的庞加莱映射和相图通过相空间重构[73]:
(a)~(c)庞加莱映射,(d)~(f)重构相图,(g)时间序列(τ – 相重构的时间延迟,’ – 扰动值)
应用非线性时间序列分析方法中的相空间重构法 ,可以得到各个时间区间内极限环的几何特征 ,极限环的“ 圈数 ”即对应了周期的倍数 。 由于不同周期的极限环反映了发动机系统不同的状态 ,因此该方法的应用有助于对燃烧不稳定全过程中发动机的变化进行深入研究 。 同时 ,这种振荡模式的识别也是对发动机燃烧不稳定状态进行辨识和控制的基础 。
6 燃烧不稳定的抑制和地面实验验证
文 献[3]介 绍 了 美 国 在 固 体 火 箭 发 动 机 燃 烧 不稳 定 方 面 的 教 训 ,文 献[6]和[7]详 细 介 绍 了 美 国 在战术导弹用固体发动机燃烧不稳定方面的实验工作 ,国内近年来也探索出了一些燃烧不稳定的抑制方法 。尽管当前还不能定量描述燃烧不稳定的生成和发展 ,工程中还是可以采取一些措施抑制燃烧不稳定:
(1)控 制 铝 粉 的 表 面 质 量 和 粒 度 。 铝 的 表 面 氧化膜晶体结构对推进剂的燃烧响应存在较大的影响 ,在铝粉生产过程中 ,控制生产工艺以避免表面产生 α -Al2 O3 对 于 抑 制 燃 烧 不 稳 定 非 常 关 键 。 实 验 表明 ,铝粉的粒度对燃烧响应也有较大的影响 ,铝粉的粒度增大导致响应函数峰值增大 ,且峰值频率向低频移动 ,在实际发动机中 ,需要根据推进剂的综合性能要求合理选择铝粉的级配 。
(2)增加惰性粒子 。在推进剂中加入 ZrC 来抑制燃烧不稳定已经被实验证实 。惰性粒子添加有两种方式 :一种是加入到推进剂配方中 。 由于燃烧不稳定通常发生在发动机工作的末期 ,这种方法会带来
较大的不必要的比冲损失 ;另一种方法是将惰性粒子加入到后段绝热层中 ,当发动机后段推进剂耗尽 ,绝热层中的惰性粒子释放,增加阻尼 。
(3)控制推进剂的 AP 级配 。细粒度 AP 超过 10%的推进剂会使一些发动机出现明显的燃烧不稳定 ,非常粗(>200μm)的 AP 含量太多,也会使压强耦合响应增强 ,引起发动机不稳定 。 因此 ,推进剂配方应根据综合性能的要求合理选择 AP 的级配 。
(4)改 变 发 动 机 的 装 药 结 构 形 式 。 理 论 分 析 和实验研究都证实了在发动机后段有推进剂燃烧的情况下较少产生燃烧不稳定 ,尽管采用这种装药结构形式比较困难 ,但是还是提供了一种抑制不稳定的思路 。
除了上述措施之外 ,尽可能从结构上增加声阻尼 ,例如改善头部几何结构 ,改变喷管结构 ,也是燃烧不稳定抑制的常用方法 。 目前工程上主要采用试错法来解决燃烧不稳定问题 ,考虑尽可能多的因素 ,然后通过点火实验验证 。
由于飞行实验的代价太大 ,地面实验验证对于抑制燃烧不稳定至关重要 。如果发动机是线性不稳定的 ,发动机地面点火试车就可以再现压强振荡 ,不稳定抑制措施的地面实验验证难度相对较小 。如果发动机处于双稳定性状态 ,地面实验的难度就要大很多 。
当前 ,发动机非线性燃烧不稳定的地面实验方法主要有两种 :一是在地面静止台架上开展全尺寸点火实验 ,在某一时刻用脉冲器向发动机燃烧室施加激励 ,触发燃烧不稳定 ;二是采用将被测试的发动机放置在火箭橇上 ,利用火箭橇模拟飞行过程中发动机所承受的过载[72]。这两种方法都可以再现燃烧不稳定 ,但是问题是:地面实验状态与飞行状态有何关联? 脉冲器施加的外部激励强度和飞行状态下发动机受到的扰动是同一类的激励吗? 如果是同一类的激励,激励的强度如何等效?
火箭橇实验能够在一定程度上模拟飞行过载 ,但发动机受到的约束状态与飞行状态差别较大 ,实验成本和花费的时间要远高于静止实验台实验 。对于固体火箭发动机燃烧不稳定抑制技术验证来说 ,其关键技术在于 :在建立准确的增益和阻尼动态变化模型的基础上 ,开展发动机燃烧稳定性非线性分析 ,获得外部激励和飞行状态的等效方法 ;在此基础上 ,发展一种飞行状态下所产生激励的等效地面模拟方法 。
7 总 结
(1)固 体 火 箭 发 动 机 的 非 线 性 燃 烧 不 稳 定 目 前仍然是学术界和工业界面临的严峻挑战 ,想要抑制燃烧不稳定 ,需要从燃烧室系统非线性动力学的角度理解燃烧不稳定 ,获得主要增益和阻尼因素的高阶非线性模型或数值计算方法 。
(2)由 于 推 进 剂 非 稳 态 燃 烧 和 系 统 增 益 与 阻 尼机理的复杂性 ,短期内建立完整 、准确的非线性不稳定分析方法存在很大的难度 ,解决工程问题需要理论分析与实验研究相结合 。
(3)从工程研制需求来看 ,近期目标是建立考虑因素比较完善的非线性不稳定预示方法 ,为飞行状态和地面静止实验时发动机受到的激励建立等效分析方法是最为紧要的 。
(4)从长远来看 ,固体推进剂燃烧和铝分布式燃烧的精细化模型是燃烧不稳定准确预示的关键 ,这需要集中优势力量 、学术界和工程界联合攻关 ,搞清不同配方条件下推进剂的细观燃烧机理 、铝的表面团聚和分布式燃烧机理 ,建立起可靠的燃烧描述模型,为不稳定分析提供准确的增益数据 。
(5)工 程 实 践 中 传 统 的 燃 烧 不 稳 定 抑 制 方 法 通常是修改几何构型以增加阻尼 、调节推进剂配方以降低增益 ,这种方法通常需要多次试错 、代价不菲 。最近在铝基复合燃料压强指数控制方面的进展可能是燃烧不稳定抑制的新方向,值得进一步深入研究 。致 谢:感谢国家自然科学基金的资助 。
参考文献
[ 1 ] 刘佩进 ,金秉宁 ,李 强 . 战术导弹固体发动机燃烧不 稳 定 研 究 概 述[J]. 固 体 火 箭 技 术 ,2012,35(4): 446-449.
[ 2 ] 王 宁 飞 ,张 峤 ,李 军 伟 ,等 . 固 体 火 箭 发 动 机 不 稳定 燃 烧 研 究 进 展[J]. 航 空 动 力 学 报 ,2011,26(6): 1405-1414.
[ 3 ] Blomshield F S. Lessons Learned in Solid Rocket Com ⁃ bustion Instability[ R]. AIAA 2007-5803.
[ 4 ] Casalis G,Boyer G,Radenac E. Some Recent Advances in the Instabilities Occurring in Long Solid Rocket Motors [ R]. AIAA 2011-5642.
[ 5 ] Fabignon Y ,Dupays J ,Avalon G ,et al. Instabilities and Pressure Oscillations in Solid Rocket Motors[J]. Aerospace Science and Technology,2003(7): 191-200.
[ 6 ] Blomshield F S,Crump J E,Mathes H B,et al. Stability Testing of Full-Scale Tactical Motors[J]. Journal of Pro– pulsion and Power,1997,13(3):349-355.
[ 7 ] Blomshield F S,Mathes H B,Crump J E,et al. Nonlin ⁃ ear Stability Testing of Full-Scale Tactical Motors[J]. Journal of Propulsion and Power ,1997 ,13(3): 356- 366.
[ 8 ] 胡 大 宁 ,何 国 强 ,刘 佩 进 ,等 . 翼 柱 型 药 柱 固 体 火 箭发动机不稳定燃烧研究[J]. 固体火箭技术 ,2010,33 (5):502-506.
[ 9 ] 吕 翔 ,何 国 强 ,刘 佩 进 ,等 . 固 体 发 动 机 燃 烧 流 动基 础 问 题 与 研 究 建 议[J]. 宇 航 学 报 ,2019,40(10): 1157-1166.
[10] Culick F E C. Unsteady Motions in Combustion Cham ⁃ bers for Propulsion Systems[ R]. RTO–AG–AVT–039, 2006.
[ 11 ] Vuillot F. Vortex Shedding Phenomena in Solid Rocket Motors[J]. Journal of Propulsion and Power ,1995 ,11 (4):626-639.
[12] Prévost M ,Godon J C ,Innegraeve O. Thrust Oscilla ⁃ tions in Reduced Scale Solid Rocket Motors,Part I:Ex ⁃ perimental Investigations[ R]. AIAA 2005-4003.
[ 13 ] Prévost M ,Le Quellec A ,Godon J C. Thrust Oscilla ⁃ tions in Reduced Scale Solid Rocket Motors,a New Con ⁃ figuration for the MPS of Ariane 5[ R]. AIAA 2006- 4418.
[14] Flandro G A. Effects of Vorticity on Rocket Combustion Stability[J]. Journal of Propulsion and Power,1995,11 (4):607-625.
[15] Kailasanath K,Gardner J H,Boris J P,et al. Numerical Simulations of Acoustic-Vortex Interactions in a Central- Dump Ramjet Combustor[J]. Journal of Propulsion and Power,1987,3(6):525-533.
[16] Kailasanath K,Gardner J H,Boris J P,et al. Acoustic- Vortex Interactions and Low-Frequency Oscillations in Axisymmetric Combustors[J]. Journal of Propulsion and Power,1989,5(2): 165-171.
[17] Telara M ,Paglia F ,Stella F ,et al. ARIANE 5 P230 SRM Frontal Thermal Protection Evolution: Numerical Simulation[ R]. AIAA 2006-5242.
[18] Culick F E C. A Review of Calculations for Unsteady Burning of a Solid Propellant[J]. AIAA Journal,1968,6 (12):2241-2255.
[19] Culick F E C. Nonlinear Behavior of Acoustic Waves in Combustion Chambers—II[J]. Acta Astronautica,1976, 3(9/10):735-757.
[20] Berman A S. Laminar Flow in Channels with Porous Walls[J]. Journal of Applied Physics ,1953,24:1232- 1235.
[ 21 ] Culick F E C. Rotational Axisymmetric Mean Flow and Damping of Acoustic Waves in a Solid Propellant Rocket [J]. AIAA Journal,1966,4(8): 1462-1464.
[22] Flandro G A. Solid Propellant Acoustic Admittance Cor⁃ rections[J]. Journal of Sound and Vibration,1974,36, 297-312.
[ 23 ] Majdalani J ,Flandro G A. The Oscillatory Pipe Flow with Arbitrary Wall Injection[J]. Proceedings of the Roy- al Society of London ,Series A:Mathematical,Physical and Engineering Sciences,2002,458:1621-1651.
[24] Majdalani J,Saad T. The Taylor-Culick Profile with Ar⁃ bitrary Headwall Injection[J]. Physics of Fluids,2007, 19(9).
[25] Majdalani J. Multiple Asymptotic Solutions for Axially Travelling Waves in Porous Channels[J]. Journal of Flu– id Mechanics,2009,636:59-89.
[26] Boyer G,Casalis G,Estivalèzes J-L. Stability Analysis and Numerical Simulation of Simplified Solid Rocket Mo ⁃ tors[J]. Physics of Fluids,2013,25(8).
[27] 杨尚荣 . 固体火箭发动机侧向加质流稳定性分析[ D].西安:西北工业大学,2014.
[28] 李 阳,刘佩进,金秉宁 . 基于 Collocation 方法的 Tay⁃ lor-Culick 模型流动稳定性的特征向量分析[J]. 固体火箭技术,2018,41(6):684-687.
[29] Brownlee W G. Nonlinear Axial Combustion Instability in Solid Propellant Motors[J]. AIAA Journal ,1964 ,2 (2):275-284.
[30] Flandro G A. Energy Balance Analysis of Nonlinear Com ⁃ bustion Instability[J]. Journal of Propulsion and Power, 1985,1(3):210-221.
[ 31 ] Flandro G A ,Fischbach S R ,Majdalani J. Nonlinear Rocket Motor Stability Prediction: Limit Amplitude, Triggering,and Mean Pressure Shift[J]. Physics of Flu – ids,2007,19(9).
[32] Flandro G A ,Majdalani J. Aeroacoustic Instability in Rockets[J]. AIAA Journal,2003,41(3):485-497.
[ 33 ] Flandro G A,Fischbach S. Effect of Parallel Wave Inci⁃ dence on Combustion Instability Driving Mechanisms [ R]. AIAA 2007-5807.
[34] French J C,Flandro G A,Majdalani J. Improvements to the Linear Standard Stability Prediction Program( SSP) [ R]. AIAA 2004-4181.
[35] Flandro G A,Majdalani J,French J C. Incorporation of Nonlinear Capabilities in the Standard Stability Predic ⁃ tion Program[ R]. AIAA 2004-4182.
[36] Baum J D,Levine J N,Lovine R L. Pulsed Instability in Rocket Motors :A Comparison Between Predictions and Experiments[J]. Journal of Propulsion and Power, 1988,4(4):308-316.
[37] Culick F E C,Burnley V,Swenson G. Pulsed Instabili⁃ ties in Solid-Propellant Rockets[J]. Journal of Propul– sion and Power,1995,11(4):657-665.
[38] Wicker J M,Greene W D,Kim S-I,et al. Triggering ofLongitudinal Combustion Instabilities in Rocket Motors – Nonlinear Combustion Response[J]. Journal of Propul– sion and Power,1996,12(6): 1148-1158.
[39] Mariappan S,Sujith R I. Thermoacoustic Instability in a Solid Rocket Motor:Non-Normality and Nonlinear Insta ⁃ bilities[J]. AIAA 2010-1517.
[40] Balasubramaniank K , Sujith R I. Non-Normality and Nonlinearity in Combustion-Acoustic Interaction in Diffu ⁃ sion Flames[J]. Journal of Fluid Mechanics , 2008, (594):29-57.
[41 ] Apte S , Yang V. Unsteady Flow Evolution in Porous Chamber with Surface Mass Injection,Part 1:Free Oscil⁃ lation[J]. AIAA Journal,2001,39(8): 1577-1586.
[42] Apte S , Yang V. Unsteady Flow Evolution in Porous Chamber with Surface Mass Injection ,Part 2:Acoustic Excitation[J]. AIAA Journal,2002,40(2):244-253.
[43 ] Apte S V ,Yang V. A Large-Eddy Simulation Study of Transition and Flow Instability in a Porous-Walled Cham ⁃ ber with Mass Injection[J]. Journal of Fluid Mechanics, 2003,477:215-225.
[44] Laboureur D ,Tóth B ,Anthoine J. Investigation of the Taylor-Culick Flow Through Particle Image Velocimetry and Numerical Simulation[J]. AIAA Journal,2010,48 (6): 1077-1084.
[45] Laureti M,Rossi G,Favini B,et al. P80 SRM Pressure Oscillations Reconstruction[ C]. Cincinnati :2018 Joint Propulsion Conference,2018.
[46] 刘 佩 进 ,金 秉 宁 ,魏 祥 庚 ,等 . 固 体 推 进 剂 非 线 性 压强 耦 合 响 应 特 性 分 析[J]. 推 进 技 术 ,2016,37(9): 1601-1608.( LIU Pei-jin,JIN Bing-ning,WEI Xiang- geng,et al. Analysis of Nonlinear Pressure Coupled Re ⁃ sponse[J]. Journal of Propulsion Technology,2016,37 (9): 1601-1608.)
[47] 金 秉 宁 . 固 体 推 进 剂 非 线 性 压 强 耦 合 响 应 特 性 研 究[ D]. 西安:西北工业大学,2016.
[48] Su Wanxing,Wang Ningfei,Li Junwei,et al. Improved Method of Measuring Pressure Coupled Response for Composite Solid Propellants[J]. Journal of Sound and Vi- bration,2014,333:2226-2240.
[49] 金秉宁 ,刘佩进 ,魏少娟 . 固体推进剂非线性压强耦合 响 应 特 性 实 验 研 究[J]. 含 能 材 料 ,2019,27(4): 290-296.
[50] McClure F T. Erosion Mechanism for Nonlinear Instabili⁃ ty in the Axial Modes of Solid Propellant Rocket Motors [J]. ARS Journal,1962,32(3):374-378.
[ 51 ] Yang V,Hsieh K C. Velocity-Coupled Flow Oscillations in a Simulated Solid-Propellant Rocket Environment[ R]. AIAA 88-0543.
[52] Cai W,Thakre P,Yang V. A Model of AP/HTPB Com ⁃
posite Propellant Combustion in Rocket-Motor Environ ⁃ ments[J]. Combustion Science and Technology ,2008, 180(12):2143-2169.
[ 53 ] Stepp E E. Effect of Pressure and Velocity Coupling on Low-Frequency Instability[J]. AIAA Journal ,1967 ,5 (5):945-948.
[54] Brown R S ,Erickson T E ,Babcock W R. Combustion Responses Function Measurements by the Rotating Valve Method[J]. AIAA Journal,1974,12(11): 1502-1510.
[55] 金 秉 宁 ,刘 佩 进 ,Hichem Rezaiguia,等 . 固 体 推 进 剂速度耦合响应函数测量实验方法研究[J]. 推进技术 , 2019,40(1): 192-198.(JIN Bing-ning,LIU Pei-jin, Hichem Rezaiguia , et al. Research on Experimental Method for Measuring Velocity-Coupled Response Func ⁃ tion of Solid Propellant[J]. Journal of Propulsion Tech – nology,2019,40(1): 192-198.)
[56] 金 秉 宁 ,刘 佩 进 ,杜 小 坤 ,等 . 复 合 推 进 剂 中 铝 粉 粒度 对 分 布 燃 烧 响 应 和 粒 子 阻 尼 特 性 影 响[J]. 推 进 技术 ,2014,35(12): 1701-1706. (JIN Bing-ning,LIU Pei-jin,DU Xiao-kun,et al. Effects of Different Alumi⁃ num Particle Sizes in Composite Propellant on Distribut⁃ ed Combustion Response and Particle Damping[J]. Jour– nal of Propulsion Technology ,2014 ,35(12): 1701- 1706.)
[57] Crocco L,Sirignano W A. Behavior of Supercritical Noz ⁃ zles under Three Dimensional Oscillatory Conditions[ R]. AGARD–OGRAPH-117,1967.
[58] Zinn B T. Nozzle Damping in Solid Rocket Instabilities [J]. AIAA Journal,1973,11(11): 1492-1497.
[59] Bell W A,Daniel B R,Zinn B T. Experimental and The ⁃ oretical Determination of the Admittances of a Family of Nozzles Subjected to Axial Instabilities[J]. Journal of Sound and Vibration,1973,30(2): 179-190.
[60] Janardan B A,Zinn B T. Rocket Nozzle Damping Char⁃ acteristics Measured Using Different Experimental Tech ⁃ niques[J]. AIAA Journal,1977,15(3):442-444.
[ 61 ] French J C. Nozzle Acoustic Dynamics and Stability Mod ⁃ eling[J]. Journal of Propulsion and Power ,2011 ,27 (6): 1266-1275.
[62] 孙 兵 兵 ,李 军 伟 ,苏 万 兴 ,等 . 固 体 火 箭 发 动 机 喷 管阻 尼 特 性 的 数 值 仿 真[J]. 航 空 动 力 学 报 ,2016,31 (9):2290-2297.
[ 63 ] Liu Peijin,Wang Muxin,Yang Wenjing,et al. Modified Computation of the Nozzle Damping Coefficient in Solid Rocket Motors[J]. Acta Astronautica,2018 ,143:391- 397.
[64] Dupays J. Two-Phase Unsteady Flow in Solid Rocket Mo ⁃ tors[J]. Aerospace Science and Technology ,2002 ,6: 413-422.
[65] Beckstead M W . A Summary of Aluminum Combustion[ R]. RTO–EN-023,2004.
[66] Sundaram D S,Puri P,Yang V. A General Theory of Ig ⁃ nition and Combustion of Nano- and Micron-Sized Alu ⁃ minum Particles[J]. Combustion and Flame , 2016, 169:94-109.
[67] 敖 文 ,刘 佩 进 ,吕 翔 ,等 . 固 体 推 进 剂 燃 烧 过 程铝 团 聚 研 究 进 展[J]. 宇 航 学 报 ,2016,37(7): 371- 380.
[68] 刘 欢 ,刘 佩 进 ,胡 松 启 ,等 . 收 集 处 理 方 法 对 含 铝固 体 推 进 剂 凝 相 燃 烧 产 物 特 性 影 响[J]. 推 进 技 术 , 2019,40(1): 206-214.( LIU Huan,LIU Pei-jin,HU Song-qi,et al. Effects of Collection and Treatment Meth ⁃ ods on Characteristics of Condensed Combustion Prod ⁃ ucts of Aluminized Solid Propellant[J]. Journal of Pro– pulsion Technology,2019,40(1):206-214.)
[69] 金秉宁 ,刘佩进 ,王志新 . 数字全息在固体推进剂铝燃烧三维测量中的应用研究[J]. 推进技术 ,2018,39 (9): 2102-2109.(JIN Bing-ning,LIU Pei-jin,WANG
Zhi-xin. Application of Digital Holography in 3D Mea⁃ surement of Aluminum Combustion in Solid Propellant [J]. Journal of Propulsion Technology ,2018 ,39(9): 2102-2109.)
[70] Gallier S,Godfroy F. Aluminum Combustion Driven In ⁃ stabilities in Solid Rocket Motors[J]. Journal of Propul– sion and Power,2009,25(2):509-521.
[ 71 ] Genot A,Gallier S,Schuller T. Thermo-Acoustic Insta ⁃ bilities Driven by Fuel Droplet Lifetime Oscillations[ C]. Dublin: 37 th International Symposium on Combustion, 2018.
[72] 张 翔 宇 ,甘 晓 松 ,高 波 ,等 . 固 体 火 箭 发 动 机 火 箭橇 过 载 模 拟 试 验 方 法[J]. 固 体 火 箭 技 术 ,2016,39 (6):751-754.
[73 ] Guan Yu , Liu Peijin ,Jin Bingning , et al. Nonlinear Time-Series Analysis of Thermoacoustic Oscillations in a Solid Rocket Motor[J]. Experimental Thermal and Fluid Science,2018,98:217-226